Abstract
Persistent homology is a relatively new tool often used for qualitative analysis of intrinsic topological features in images and data originated from scientific and engineering applications. In this paper, we report novel quantitative predictions of the energy and stability of fullerene molecules, the very first attempt in employing persistent homology in this context. The ground-state structures of a series of small fullerene molecules are first investigated with the standard Vietoris-Rips complex. We decipher all the barcodes, including both short-lived local bars and long-lived global bars arising from topological invariants, and associate them with fullerene structural details. By using accumulated bar lengths, we build quantitative models to correlate local and global Betti-2 bars respectively with the heat of formation and total curvature energies of fullerenes. It is found that the heat of formation energy is related to the local hexagonal cavities of small fullerenes, while the total curvature energies of fullerene isomers are associated with their sphericities, which are measured by the lengths of their long-lived Betti-2 bars. Excellent correlation coefficients (> 0.94) between persistent homology predictions and those of quantum or curvature analysis have been observed. A correlation matrix based filtration is introduced to further verify our findings.
Keywords: persistent homology, filtration, fullerene, isomer, nanotube, stability, curvature
1 Introduction
Persistent homology, a method for studying topological features over changing scales, has received tremendous attention in the past decade.14, 59 The basic idea is to measure the life cycle of topological features within a filtration, i.e., a nested family of abstract simplicial complexes, such as Vietoris-Rips complexes, Čech complexes, or alpha complexes.15 Thus, long-lived topological characteristics, which are often the intrinsic invariants of the underlying system, can be extracted; while short-lived features are filtered out. The essential topological characteristics of three-dimensional (3D) objects typically include connected components, tunnels or rings, and cavities or voids, which are invariant under the non-degenerate deformation of the structure. Homology characterizes such structures as groups, whose generators can be considered independent components, tunnels, cavities, etc. Their times of “birth” and “death” can be measured by a function associated with the filtration, calculated with ever more efficient computational procedures,11–13, 37 and further visualized through barcodes,23 a series of horizontal line segments with the x-axis representing the changing scale and the y-axis representing the index of the homology generators. Numerous software packages, such as Perseus, Dionysus, and Javaplex,47 based on various algorithms have been developed and made available in the public domain. As an efficient tool to unveil topological invariants, persistent homology has been applied to various fields, such as image analysis,5, 40, 45 chaotic dynamics verification,30, 36 sensor network,44 complex network,29, 34 data analysis,4 geometric processing,16 and computational biology.10, 22, 31, 55 Based on persistent homology analysis, we have proposed molecular topological fingerprints and utilized them to reveal the topology-function relationship of biomolecules.54 In general, persistent homology is devised as a robust but qualitative topological tool and has been hardly employed as a precise quantitative predictive tool.1, 3
To the best of our knowledge, persistent homology has not been applied to the study of fullerenes, special molecules comprised of only carbon atoms. The fullerene family shares the same closed carbon-cage structure, which contains only pentagonal and hexagonal rings. In 1985, Kroto et al.33 proposed the first structure of C60, which was then confirmed in 1990 by Krätschmer et al.32 in synthesizing macroscopic quantities of C60. Enormous interest has been aroused by these interesting discoveries. However, there are many challenges. Among them, finding the ground-state structure has been a primary target.
In general, two types of approaches are commonly used.2, 7, 18, 20, 35, 56 The first method is based on the geometric and topological symmetries of fullerene.18, 20, 35 In this approach, one first constructs all possible isomers, and then chooses the best possible candidate based on the analysis of the highest-occupied molecular orbital (HOMO) energy and the lowest-unoccupied molecular orbital (LUMO) energy.35 In real applications, to generate all possible isomers for a fullerene with a given atom count is nontrivial until the introduction of Coxeter’s construction method9, 18 and the ring spiral method.35 In Coxeter’s method, the icosahedral triangulations of the sphere are analyzed to evaluate the possible isomer structures. This method is mathematically rigorous. However, practical applications run into issues with low-symmetry structures. On the other hand, based on the spiral conjecture20, the ring spiral method simply lists all possible spiral sequences of pentagons and hexagons, and then winds them up into fullerenes. When a consistent structure is found, an isomer is generated; otherwise, the sequence is skipped. Although the conjecture breaks down for fullerenes with 380 or more atoms, the spiral method proves to be quite efficient.20
For each isomer, its electronic structure can be modeled simply by the Hückel molecular orbital theory,46 which is known to work well for planar aromatic hydrocarbons using standard C-C and C-H σ bond energies. Similarly, the bonding connectivities in fullerene structures are used to evaluate orbital energies. The stability of the isomers, according to Manolopoulus,35 can then be directly related to the calculated HOMO-LUMO energy gap. However, this model falls short for large fullerene molecules. Even for small structures, its prediction tends to be inaccurate. One possible reason is fullerene’s special cage structures. Instead of a planar shape, the structure usually has local curvatures, which jeopardizes the σ-π orbital separation.17, 20 To account for curvature contributions, a strain energy is considered. It is found that the stain energy reaches its minimum when pentagonal faces are as far away as possible from each other. This is highly consistent with the isolated pentagon rule (IPR) — the most stable fullerenes are those in which all the pentagons are isolated.20
Another approach to obtain ground-state structures for fullerene molecules is through simulated annealing.2, 7, 56 This global optimization method works well for some structures. However, if large energy barriers exist in the potential, the whole system is prone to be trapped into metastable high-energy state. This happens as breaking the carbon bonds and rearranging the structure need a huge amount of energy. A revised method is to start the system from a special face-dual network and then employ the tight-binding potential model.56, 57 This modified algorithm manages to generate the C60 structure of Ih symmetry that has the HOMO-LUMO energy gap of 1.61 eV, in contrast to 1.71 eV obtained by using the ab initio local-density approximation.
In this paper, persistent homology is, for the first time, employed to quantitatively predict the stability of the fullerene molecules. The ground-state structures of a few small fullerene molecules are first studied using a distance based filtration process. Essentially, we associate each carbon atom of a fullerene with an ever-increasing radius and thus define a Vietoris-Rips complex. The calculated Betti numbers (i.e., ranks of homology groups), including β0, β1 and β2, are provided in the barcode representation. To further exploit the persistent homology, we carefully discriminate between the local short-lived and global long-lived bars in the barcodes. We define an average accumulated bar length as the negative arithmetic mean of β2 bars. As the local β2 bars represent the number of cavities of the structure, when β2 becomes larger, interconnectedness (and thus stability) tends to increase, and relative energy tends to drop. Therefore, the average accumulated bar length indicates the level of a relative energy. We validate this hypothesis with a series of ground-state structures of small fullerenes. It is found that our average accumulated bar length can capture the energy behavior remarkably well, including an anomaly in fullerene C60 energy. Additionally, we explore the relative stability of fullerene isomers. The persistence of the Betti numbers is calculated and analyzed. Our results are validated with the total curvature energies of two fullerene families. It is observed that the total curvature energies of fullerene isomers can be well represented with their lengths of the long-lived Betti-2 bars, which indicates the sphericity of fullerene isomers. For fullerenes C40 and C44, correlation coefficients up to 0.956 and 0.948 are attained in the distance based filtration. Based on the flexibility-rigidity index (FRI),51–53 a correlation matrix based filtration process is proposed to validate our findings.
The rest of this paper is organized as follows. In Section 2, we discuss the basic persistent homology concepts, including Simplices and simplicial complexes, chains, homology, and filtration. Section 3 is devoted to the description of algorithms. The alpha complex and Vietoris-Rips complex are discussed in some detail, including filtration construction, metric space design, and persistence evaluation. In Section 4, persistent homology is employed in the analysis of fullerene structure and stability. After a brief discussion of fullerene structural properties, we elaborate on their barcode representation. The average accumulated bar length is introduced and applied to the energy estimate of the small fullerene series. By validating with total curvature energies, our persistent homology based quantitative predictions are shown to be accurate. Fullerene isomer stability is also analyzed by using the new correlation matrix based filtration. This paper ends with a conclusion.
2 Rudiments of Persistent Homology
As representations of topological features, the homology groups are abstract abelian groups, which may not be robust or able to provide continuous measurements. Thus, practical treatments of noisy data require the theory of persistent homology, which provides continuous measurements for the persistence of topological structures, allowing both quantitative comparison and noise removal in topological analyses. The concept was introduced by Frosini and Landi21 and Robins,42 and in the general form by Zomorodian and Carlsson.59 Computationally, the first efficient algorithm for Z/2 coefficient situation was proposed by Edelsbrunner et al.14 in 2002.
2.1 Simplex and Simplicial Complex
For discrete surfaces, i.e., meshes, the commonly used homology is called simplicial homology. To describe this notion, we first present a formal description of the meshes, the common discrete representation of surfaces and volumes. Essentially, meshing is a process in which a geometric shape is decomposed into elementary pieces called cells, the simplest of which are called Simplices.
Simplex
Simplices are the simplest polytopes in a given dimension, as described below. Let v0, v1, ..vp be p+1 affinely independent points in a linear space. A p-simplex σp is the convex hull of those p+1 vertices, denoted as σp = convex < v0, v1, …, vp > or shorten as σp =< v0, v1, …, vp >. A formal definition can be given as,
| (1) |
The most commonly used simplices in R3 are 0-simplex (vertex), 1-simplex (edge), 2-simplex (triangle) and 3-simplex (tetrahedron) as illustrated in Fig. 1.
Figure 1.
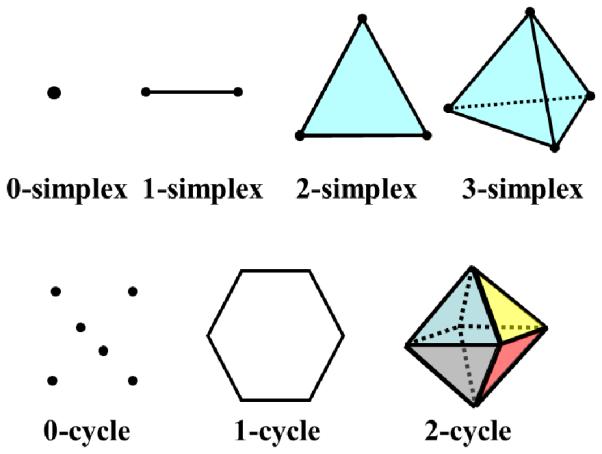
Illustration of 0-simplex, 1-simplex, and 2-simplex in the first row. The second row is simple 0-cycle, 1-cycle and 2-cycle.
An m-face of σp is them-dimensional subset of m+1 vertices, where 0 ≤ m ≤ p. For example, an edge has two vertices as its 0-faces and one edge as its 1-face. Since the number of subsets of a set with p+ 1 vertices is 2p+1, there are a total of 2p+1 - 1 faces in σp. All the faces are proper except for σp itself. Note that polytope shapes can be decomposed into cells other than simplices, such as hexahedron and pyramid. However, as non-simplicial cells can be further decomposed, we can, without loss of generality, restrict our discussion to shapes decomposed to simplices as we describe next.
Simplicial Complex
With simplices as the basic building blocks, we define a simplicial complex K as a finite collection of simplices that meet the following two requirements,
Containment: Any face of a simplex from K also belongs to K.
Proper intersection: The intersection of any two simplices σi and σj from K is either empty or a face of both σi and σj.
Two p-simplices σi and σj are adjacent to each other if they share a common face. The boundary of σp, denoted as ∂σp, is the union (which can be written as a formal sum) of its (p-1)-faces. Its interior is defined as the set containing all non-boundary points, denoted as σ - ∂σp. We define a boundary operator for each p-simplex spanned by vertices v0 through vP as
| (2) |
where indicates that vi is omitted and Z/2 coefficient set is employed. It is the boundary operator that creates the nested topological structures and the homomorphism among them as described in the next section.
If the vertex positions in the ambient linear space can be ignored or do not exist, the containment relation among the simplices (as finite point sets) defines an abstract simplicial complex.
2.2 Homology
A powerful tool in topological analysis is homology, which represents certain structures in the meshes by algebraic groups to describe their topology. For regular objects in 3D space, essential topological features are connected components, tunnels and handles, and cavities, which are exactly described by the 0th, 1st, and 2nd homology groups, respectively.
Chains
The shapes to be mapped to homology groups are constructed from chains defined below. Given a simplicial complex (e.g., a tetrahedral mesh) K, which, roughly speaking, is a concatenation of p-Simplices, we define a p-chain as a formal linear combination of all p-Simplices in K, where ai ∈ Z/2 is 0 or 1 and σi is a p-simplex. Under such a definition, a 0-chain is a set of vertices, a 1-chain is a set of line segments which link vertices, a 2-chain is a set of triangles which are enclosed by line segments, and a 2-chain is a set of tetrahedrons which are enclosed by triangle surfaces.
We extend the boundary operator ∂p for each p-simplex to a linear operator applied to chains, i.e., the extended operator meet following two conditions for linearity,
| (3) |
where ci and cj are both chains and λ is a constant, and all arithmetic is for modulo-2 integers, in which 1 + 1 = 0.
An important property of the boundary operator is that the following composite operation is the zero map,
| (4) |
which immediately follows from the definition. Take the 2-chain c = f1 + f2 as an example, which represents a membrane formed by two triangles, f1 =< v1, v2, v3 > and f2 =< v3, v2, v4 >. The boundary of c is a 1-chain, which turns out to be a loop,
| (5) |
The boundary of this loop is thus
| (6) |
Simplicial homology
Simplicial homology is built on the chain complex associated to the simplicial complex. A chain complex is a sequence of abelian groups (C1, C2, … , Cn) connected by the homomorphism (linear operators) ∂p, such that ∂p ⚬ ∂p+1 = 0 as in Eq.(4).
| (7) |
The chain complex in the definition of simplicial homology is formed by Cp, the space of all p-chains, and ∂p, the boundary operator on p-chains. Since ∂p ⚬ ∂p+1 = 0, the kernel of the boundary operator p-chains is a subset of the image of the boundary operator of p + 1-chains. The p-chains in the kernel of the boundary homomorphisms ∂p are called p-cycles (p-chains without boundary) and the p-chains in the image of the boundary homomorphisms ∂p+1 are called p-boundaries. The p-cycles form an abelian group (with group operation being the addition of chains) called cycle group, denoted as Zp = Ker ∂p. The p-boundaries form another abelian group called boundary group, denoted as Bp = Im ∂p+1.
Thus, p-boundaries are also p-cycles as shown in Fig. 2. As p-boundaries form a subgroup of the cycles group, the quotient group can be constructed through cosets of p-cycles, i.e., by equivalence classes of cycles. The p-th homology, denoted as Hp, is defined as a quotient group,
Figure 2.
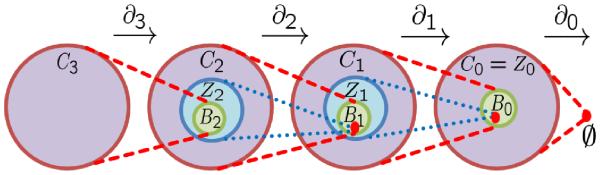
Illustration of boundary operators, and chain, cycle and boundary groups in R3 • Red dots stand for empty sets.
| (8) |
where Ker ∂p is the collection of p-chains with empty boundary and Im ∂p+1 is the collection of p-chains that are boundaries of p + 1-chains.
Noticing that all groups with p > 3 cannot be generated from meshes in R3, we only need chains, cycles and boundaries of dimension p with 0 ≤ p ≤ 3. See Fig. 2 for an illustration.
We illustrate simplexes and cycles including 0-cycle, 1-cycle, and 2-cycle in Fig. 1. Basically, an element in the p-th homology group is an equivalence class of p-cycles. One of these cycles c can represent any other p-cycle that can be "deformed" through the mesh to c, because any other p-cycle in the same equivalence class differ with c by a p-boundary b = ∂(∂1+∂2 + …),where each ∂i is a p+l-simplex. Adding the boundary of ∂i has the effect of deforming c to c + ∂σi by sweeping through ∂i. For instance, a 0-cycle vi is equivalent to vj if there is a path < vi,vk1 > + < vk1,vk2 > + · · · + < vkn,vj >. Thus each generator of 0th-homology, (like a basis vector in a basis of the linear space of 0th-homology) represents one connected component. Similarly, 1-cycles are loops, and 1st-homology generators represent independent nontrivial loops, i.e., separate tunnels; 2-homology generators are independent membranes, each enclosing one cavity of the 3D object.
Define βp = rank(Hp) to be the p-th Betti number. For a simplicial complex in 3D, β0 is the number of connected components; β1 is the number of tunnels; and β2 is the number of cavities. As Hp is the quotient group between Zp and Bp, we can also compute Betti numbers through,
| (9) |
Note, however, Hp is usually of much lower rank than either Zp or Bp.
2.3 Persistent Homology
Homology generators identify the tunnels, cavities, etc., in the shape, but as topological invariants, they omit the metric measurements by definition. However, in practice, one often needs to compare the sizes of tunnels, for instance, to find the narrowest tunnel, or to remove tiny tunnels as topological noises. Persistent homology is a method of reintroducing metric measurements to the topological structures.14, 59
The measurement is introduced as an index ito a sequence of nested topological spaces {Xi}. Such a sequence is called a filtration,
| (10) |
Since each inclusion induces a mapping of chains, it induces a linear map for homology,
| (11) |
The above sequence describes the evolution of the homology generators. We follow the exposition in Ref.38 and define by a composition mapping from . . A new homology class c is created (born) in if it is not in the image of . It dies in Xj if it becomes trivial or is merged to an “older” (born before i) homology class, i.e., its image in is in the image of , unlike its image under .
As shown in Fig. 3, if we associate with each space a value hi denoting “time” or “length”, we can define the duration, or the persistence length of the each homology generator c as
Figure 3.
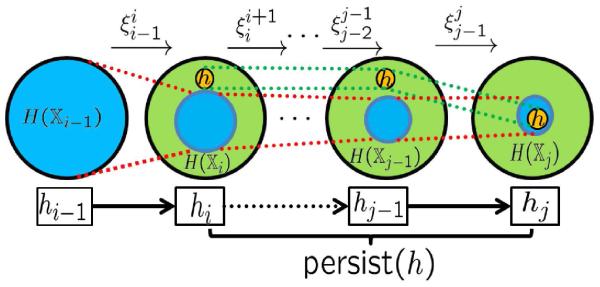
Illustration of the birth and death of a homology generator c
| (12) |
This measurement hi is usually readily available when analyzing the topological feature changes. For instance, when the filtration arises from the level sets of a height function.
3 Algorithms for persistent homology
In computational topology, intrinsic features of point cloud data, i.e., a point set S ⊂ Rn without additional structure, are common subjects of investigation. For such data, a standard way to construct the filtration is to grow a solid ball centered at each point with an ever-increasing radius. If the differences between points can generally be ignored, as is the case for fullerenes, a common radius r can be used for all points. In this setting, the radius r is used as the parameter for the family of spaces in the filtration. As the value of r increases, the solid balls will grow and Simplices can be defined through the overlaps among the set of balls. In Figure 4, fullerene C60 is used to demonstrate this process. There are various ways of constructing abstract simplicial complexes from the intersection patterns of the set of expanding balls, such as Čech complex, Vietoris-Rips complex and alpha complex. The corresponding topological invariants, e.g., the Betti numbers, are in general different due to different definitions of simplicial complexes. In this section, we discuss computational algorithms for the design of filtrations, the construction of abstract simplicial complexes, and the calculation of Betti numbers.
Figure 4.
Illustration of filtrations built on fullerene C60. Each point or atom in the point cloud data (i.e., coordinates) of the C50 is associated with a common radius r which increases gradually. As the value of r increases, the solid balls centered at given coordinates grow. These balls eventually overlap with their neighbors at certain r values. Simplices indicating such neighborhood information can be defined through abstract r-dependent simplicial complexes, e.g., alpha complexes and Rips complexes. Note that in the last chart, we have removed some atoms to reveal the central void.
Alpha complex
One possible filtration that can be derived from the unions of the balls with a given radius around the data points (as shown in Figure 4) is the family of d-dependent Čech complexes, each of them is defined to be a simplicial complex, whose k-Simplices are determined by (k + 1)-tuples of points, such that the corresponding d/2-balls have a non-empty intersection. However, it may contain many Simplices for a large d. A variant called the alpha complex can be defined by replacing the d/2-ball in the above definition by the intersection of the d/2-ball with the Voronoi cells for these data points. In both cases, they are homotopic to the simple unions of balls, and thus produce the same persistent homology. Interested readers are referred to the nerve theorem for details.58
Vietoris-Rips complex
The Vietoris-Rips complex, which is also known as Vietoris complex or Rips complex, is another type of abstract simplicial complex derived from the union of balls. In this case, for a k-simplex to be included, instead of requiring that the (k + 1) d/2-balls to have a common intersection, one only needs them to intersect pairwise. The Čech complex is a subcomplex of the Rips complex for any given d, however, the latter is much easier to compute and is also a subcomplex of the former at the filtration parameter of .
Euclidean-distance based filtration
It is straightforward to use the metric defined by the Euclidean space in which the data points are embedded. The pairwise distance can be stored in a symmetric distance matrix (dij), with each entry dij denoting the distance between point i and point j. Each diagonal term of the matrix is the distance from a certain point to itself, and thus is always 0. The family of Rips complexes is parameterized by d, a threshold on the distance. For a certain value of d, the Vietoris-Rips complex can be calculated. In 3D, more specifically, for a pair of points whose distance is below the threshold d, they form a 1-simplex in the Rips complex; for a triplet of points, if the distance between every pair is smaller than d, the 2-simplex formed by the triplet is in the Rips complex; whether a 3-simplex is in the Rips complex can be similarly determined. The Euclidean-distance based Vietoris-Rips complexes are widely used in persistent homology due to their simplicity and efficiency.
Correlation matrix based filtration
Another way to construct the metric space is through a certain correlation matrix, which can be built, e.g., from theoretical predictions and experimental observations. From a previous study on protein stability, flexibility-rigidity index (FRI) theory has been proven accurate and efficient.51 The reason for its success is that the geometric information is harnessed properly through the special transformation to a correlation matrix. The key to this transformation is the geometric to topological mapping. Instead of direct geometric information of the embedding in the Euclidean space, a mapping through certain kernel functions is able to interpret spatial locations of atoms in a particular way that reveals the atom stability quantitatively. We believe that this functional characterization is of importance to the study of not only proteins, but also other molecules.
Here, we present a special correlation matrix based Vietoris complex on the FRI method. In order to define the metric used, we briefly review the concepts of the FRI theory. First, we introduce the geometry to topology mapping.51–53 We denote the coordinates of atoms in the molecule we study as r1, r2, · · · , rj , · · · , rN, where rj ∈ R3 is the position vector of the jth atom. The Euclidean distance between ith and jth atoms rij can then be calculated. Based on these distances, topological connectivity matrix can be constructed with monotonically decreasing radial basis functions. A general form for a connectivity matrix is,
| (13) |
where wj is associated with atomic types, parameter ηj > 0 is the atom-type related characteristic distance, and Φ(rij; ηj) is a radial basis correlation kernel.
The choice of kernel is of significance to the FRI model. It has been shown that highly predictive results can be obtained by the exponential type and Lorentz type of kernels.51–53 Exponential type of kernels is
| (14) |
and the Lorentz type of kernels is
| (15) |
The parameters κ and υ are adjustable.
We define the atomic rigidity index µi for ith atom as
| (16) |
A related atomic flexibility index can be defined as the inverse of the atomic rigidity index.
| (17) |
The FRI theory has been intensively validated by comparing with the experimental data, especially the Debye-Waller factor (commonly known as the B-factor).51 While simple to evaluate, their applications in B-factor prediction yield decent results. The predicted results are proved to be highly accurate while the procedure remains efficient. FRI is also used to analyze the protein folding behavior.53
To construct an FRI-based metric space, we need to design a special distance matrix, in which the functional correlation is measured. If we directly employ the correlation matrix in Eq. (13) for the filtration, atoms with less functional relation form more Simplices, resulting in a counter-intuitive persistent homology. However, this problem can be easily remedied by defining a new correlation matrix as Mij = 1 − Cij, i.e.,
| (18) |
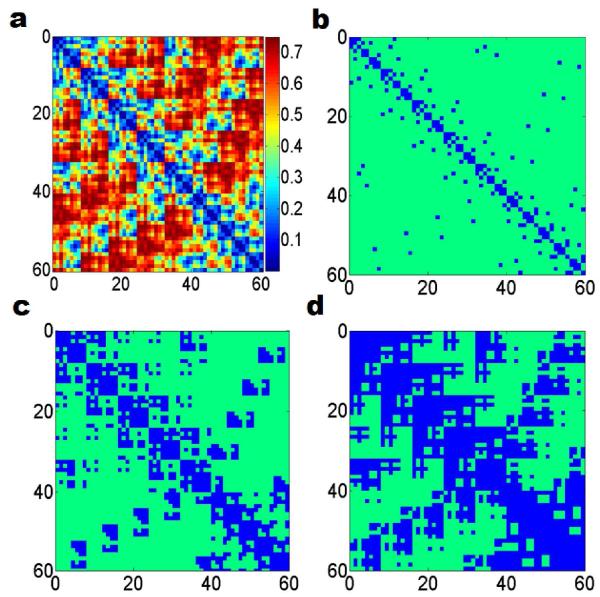
Thus a kernel function induces a metric space under this definition. Figure 5(a) demonstrates such a metric space based filtration of fullerene C60, in which we assume wj = 1 since only one type of atom exists in this system. The generalized exponential kernel in Eq. (14) is used with parameters κ = 2.0 and η = 6.0ÅA.
Figure 5.
Correlation matrix based filtration of fullerene C60 (labels on both axes are atomic numbers). A correlation matrix is constructed from the FRI theory. As the filtration parameter increases, the Rips complex based on this matrix expands accordingly. (a) The correlation based matrix for fullerene C60; (b), (c) and (d) demonstrate the connectivity between atoms at the filtration threshold d = 0.lA, 0.3A, and 0.5A, respectively. The blue color entries represent the pairs already forming simplices.
With the correlation matrix based filtration, the corresponding Vietoris-Rips complexes can be straight-forwardly constructed. Specifically, given a certain filtration parameter h0, if the matrix entry Mij ≤ h0, an edge formed between ith and jth atoms, and a simplex is formed if all of its edges are present. The complexes are built incrementally as the filtration parameter grows. Figures 5(b), (c) and (d) illustrate this process with three filtration threshold values h = 0.1Å, 0.3Å and 0.5Å, respectively. We use the blue color to indicate formed edges. It can be seen that simplicial complexes keep growing with the increase of filtration parameter h. The diagonal terms are always equal to zero, which means that N atom centers (0-Simplices) form the first complex in the filtration.
4 Application to fullerene structure analysis and stability prediction
In this section, the theory and algorithms of persistent homology are employed to study the structure and stability of fullerene molecules. The ground-state structural data of fullerene molecules used in our tests are downloaded from the CCL webpage and fullerene isomer data and corresponding total curvature energies24 are adopted from David Tomanek’s carbon fullerene webpage. In these structural data, coordinates of fullerene carbon atoms are given. The collection of atom center locations of each molecule forms a point cloud in R3. With only one type of atom, the minor heterogeneity of atoms due to their chemical environments in these point clouds can be ignored in general. We examined both distance based and correlation matrix based metric spaces in our study. The filtration based on the FRI theory is shown to predict the stability very well.
Before we discuss the more informative persistent homology of fullerenes, we discuss the basic structural properties simply based on their Euler characteristics (vertex number minus edge number plus polygon number). The Euler characteristic, as a topological property, is invariant under non-degenerate shape deformation. For a fullerene cage composed of only pentagons and hexagons, the exact numbers of these two types of polygons can be derived from the Euler characteristic. For instance, if we have np pentagon and nh hexagons in a CN fullerene cage, the corresponding numbers of vertices, edges and faces are (5np + 6nh)/3, (5np + 6nh)/2 and np + nh, respectively, since each vertex is shared by three faces, and each edge is shared by two faces. As the fullerene cage is treated as a two dimensional surface, we have the Euler characteristic (5np + 6nh)/3 − (5np + 6nh)/2 + (np + nh) = 2, according to Euler’s polyhedron formula, since it is a topological sphere. Thus, we have np = 12, which means a fullerene cage structure must have 12 pentagons and correspondingly N/2 − 10 hexagons. Therefore, for a CN fullerene cage, we have N vertices, 3N/2 edges and N/2 + 2 faces.
4.1 Barcode representation of fullerene structures and nanotube
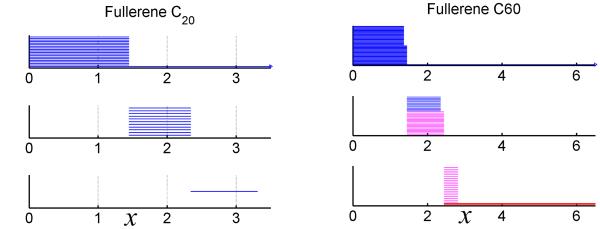
Barcodes for fullerene molecule
In Fig. 6, we demonstrate the persistent homology analysis of fullerene C20 and C60 using the barcode representation generated by Javaplex.47 The x-axis represents the filtration parameter h. If the distance between two vertices is below or equal to certain h0, they will form an edge (1-simplex) at h0. Stated differently, the simplical complex generated is equivalent to the raidus filtration with radius parameter h/2. In the barcode, the persistence of a certain Betti number is represented by an interval (also known as bar), denoted as . Here j ∈ {0, 1, 2} as we only consider the first three Betti numbers in this work. From top to bottom, the behaviors of β0, β1, and β2 are depicted in three individual panels. It is seen that as h grows, isolated atoms initialized as points will gradually grow into solid spheres with an ever-increasing radius. This phenomenon is represented by the bars in the β0 panel. Once two spheres overlap with each other, one β0 bar is terminated. Therefore, the bar length for the independent 0-th homology generator (connected component) , denoted as , indicates the bond length information of the molecule. As can be seen from Fig. 6, for fullerene C20, all β0 bar lengths are around 1.45Å and the total number of components equals exactly to 20. On the other hand, fullerene C60 has two different kinds of bars with lengths around 1.37Å and 1.45Å, respectively, indicating its two types of bond lengths.
Figure 6.
Illustration of the barcodes for fullerene C20(left chart) and C60 (right chart) filtration on associated Rips complexes. Each chart contains three panels corresponding to the Betti number sequences β0, β1 and β2, from top to bottom.
More structure information is revealed as β1 bars, which represent independent noncontractible 1-cycles (loops), emerge. It is seen in the fullerene C20 figure, that there are 11 equal-length β1 bars persisting from l.45Å to 2.34Å. As fullerene C20 has 12 pentagonal rings, the Euler characteristics for a 1D simplicial subcomplex (1-skeleton) can be evaluated from the Betti numbers,
| (19) |
Here β0, nvertice, and nedge are 1, 20, and 30, respectively. Therefore, it is easy to obtain that β1 = 11 for fullerene C20, as demonstrated in Fig. 6. It should be noticed that all β1 bars end at filtration value h = 2.34Å, when five balls in each pentagon with their ever-increasing radii begin to overlap to form a pentagon surface.
Even more structur al information can be derived from fullerene C60’s β1 barcodes. First, there are 31 bars for β1. This is consistent with the Euler characteristics in Eq. (19), as we have 12 pentagons and 20 hexagons. Secondly, two kinds of bars correspond to the coexistence of pentagonal rings and hexagonal rings. They persist from 1.45Å to 2.35Å and from 1.45Å to 2.44Å , respectively.
As the filtration progresses, β2 bars (membranes enclosing cavities) tend to appear. In fullerene C20, there is only one β2 bar, which corresponds to the void structure in the center of the cage. For fullerene C60, we have 20 β2 bars persisting from 2.44Å to 2.82Å, which corresponds to hexagonal cavities as indicated in the last chart of Fig .1. Basically, as the filtration goes, each node in the hexagon ring joins its four nearest neighbors, and fills in the relevant 2-simplices, yielding a simplical complex whose geometric realization is exactly the octahedron. There is another β2 bar due to the center void as indicated in the last chart of Fig.6, which persists until the complex forms a solid block. Note that two kinds of β2 bars represent entirely different physical properties. The short-lived bars are related to local behaviors and fine structure details, while the long-lived bar is associated with the global feature, namely, the large cavity.
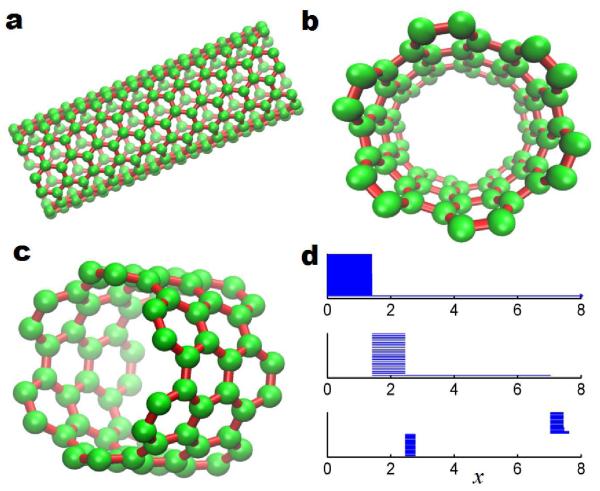
Barcodes for nanotube
Another example of nanotube is demonstrated in Fig. 7. The nanotube structure is const ructed using the software TubeApplet webpage . We set tube indices to (6,6), the number of unit cell to 10, tube radius to 4.05888, and lattice constant to 2.454Å. We extract a segment of 3 unit cells from the nanotube and employ the persistent homology analysis to generate it barcodes. Our results are demonstrated in Fig. 7. Different from fullerene molecules, the nanotube has a long β1 bar representing the tube circle. It should also be noticed that β2 barcodes are concentrated in two different regions. The first region is when x is around 2.5 to 2.7. The β2 barcodes in this domain are generated by hexagonal rings on the nanotube. The other region appears when x is slightly larger than 7.0. The corresponding β2 barcodes are representation of the void formed between different layer of carbons.
Figure 7.
Illustr ation of persistent homology analysis for a nanotube. (a) The generated nanotube structure with 10 unit layers. (b) and (c) A 3 unit layer segment extracted from the nanotube molecule in a. (d) Barcodes representation of the topology of the nanotub e segment.
Unlike commonly used topological methods20, persistent homology is able to provide a multiscale representation of the topological features. Usually, global behavior is of major concern. Therefore, the importance of the topological features is typically measured by their persistence length. In our analysis, we have observed that except for discretization errors, topological invariants of all scales can be equally important in revealing various structural features of the system of interest. In this work, we demonstrate that both local and global topological invariants play important roles in quantitative physical modeling.
4.2 Stability analysis of small fullerene molecules
From the above analysis, it can be seen that detailed structural information has been incorporated into the corresponding barcodes. On the other hand, molecular structures determine molecular functions.51–53 Therefore, persistent homology can be used to predict molecular functions of fullerenes. To this end, we analyze the barcode information. For each Betti number βj, we define an accumulated bar length Aj as the summation of barcode lengths,
| (20) |
where is the length of the ith bar in the j-th-homology barcode. Sometimes, we may only sum over certain types of barcodes. We define an average accumulated bar length as , where N is the total number of atoms in the molecule.
Zhang et al.56, 57 found that for small fullerene molecule series C20 to C70, their ground-state heat of formation energies gradually decrease with the increase of the number of atoms, except for C60 and C70. The decreasing rate, however, slows down with the increase of the number of atoms. With data adopted from Ref.,56 Fig. 8 demonstrates this phenomenon. This type of behavior is also found in the total energy (STO-3G/SCF at MM3) per atom,39 and in average binding energy of fullerene C2n which can be broken down to n dimmers (C2).6
Figure 8.
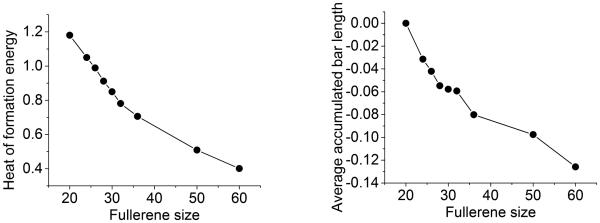
Comparison between the heat of formation energies computed using a quantum theory56 (left chart) and average accumulated bar length (right chart) for fullerenes. The units for the heat of formation energy and average accumulated bar length are eV/atom and Å/atom, respectively Although the profile of average accumulated bar length of fullerenes does not perfectly match the fullerene energy profile, they bear a close resemblance in their basic characteristics.
To understand this behavior, many theories have been proposed. Zhang et al.57 postulate that the fullerene stability is related to the ratio between the number of pentagons and the number of atoms for a fullerene molecule. Higher percentage of pentagon structures results in relatively higher levels of the heat of formation. On the other hand, a rather straightforward isolated pentagon rule (IPR) states that the most stable fullerenes are those in which all the pentagons are isolated. The IPR explains why C60 and C70 are relatively stable as both have only isolated pentagons. Raghavachari’s neighbour index41 provides another approach to quantitatively characterize the relative stability. For example, in C60 of In symmetry, all 12 pentagons have neighbour index 0, thus the In C60 structure is very stable.
In this work, we hypothesize that fullerene stability depends on the average number of hexagons per atom. The larger number of hexagons is in a given fullerene structure, the more stable it is. We utilize persistent homology to verify our hypothesis. As stated in Section 4.1, there are two types of β2 bars, namely, the one due to hexagon-structure-related holes and that due to the central void. Their contributions to the heat of formation energy are dramatically different. Based on our hypothesis, we only need to include those β2 bars that are due to hexagon-structure-related holes in our calculation of the average accumulated bar length B2. As depicted in the right chart of Fig. 8, the profile of the average accumulated bar length closely resembles that of the heat of formation energy. Instead of a linear decrease, both profiles exhibit a quick drop at first, then the decreasing rate slows down gradually. Although our predictions for C30 and C32 fullerenes do not match the corresponding energy profile precisely, which may be due to the fact that the data used in our calculation may not be exactly the same ground-state data as those in the literature,57 the basic characteristics and the relative relations in the energy profile are still well preserved. In fact, the jump at the C60 fullerene is captured and stands out more obviously than the energy profile. This may be due to the fact that our method distinguishes not only pentagon and hexagon structures, but also the size differences within each of them. We are not able to present the full set of energy data in Ref.56 because we are limited by the availability of the ground-state structure data.
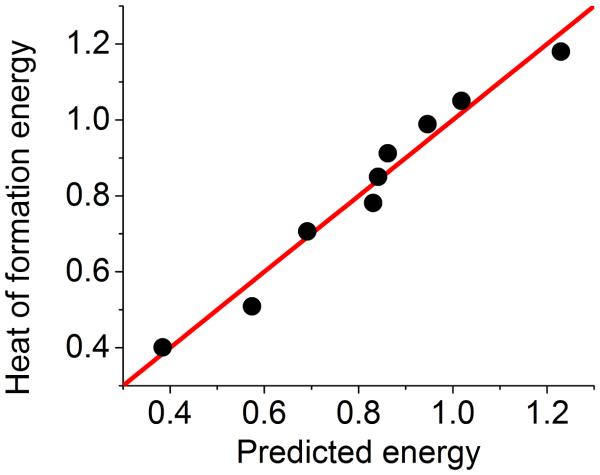
To quantitatively validate our prediction, the least squares method is employed to fit our prediction with the heat of formation energy, and a correlation coefficient is defined,51
| (21) |
where represents the heat of formation energy of the ith fullerene molecule, and is our theoretical prediction. The parameter and are the corresponding mean values. The fitting result is demonstrated in Fig. 9. The correlation coefficient is close to unity (0.985), which indicates the soundness of our model and the power of persistent homology for quantitative predictions.
Figure 9.
The comparison between quantum mechanical simulation results56 and persistent homology prediction of the heat of formation energy (eV/atom). Only local β2 bars that are due to hexagon structures are included in our average accumulated bar length B2. The correlation coefficient from the least-squares fitting is near perfect (Cc = 0.985).
4.3 Total curvature energy analysis of fullerene isomers
Having demonstrated the ability of persistent homology for the prediction of the relative stability of fullerene molecules, we further illustrate the effectiveness of persistent homology for analyzing the total curvature energies of fullerene isomers. Fullerene molecules CN are well-known to admit various isomers,19 especially when the number (N) of atoms is large. In order to identify all of the possible isomers for a given N, many elegant mathematical algorithms have been proposed. Coxeter’s construction method9, 18 and the ring spiral method35 are two popular choices. Before discussing the details of these two methods, we need to introduce the concept of fullerene dual. Mathematically, a dual means dimension-reversing dual. From Euler’s polyhedron theorem, if a spherical polyhedron is composed of nvertice vertices , nedge edges and nface faces, we have the relation nvertice − nedges + nface = 2. Keeping the nedge unchanged while swapping the other two counts, we have its dual, which has nvertice faces and nface vertices. For example, the cube and the octahedron form a dual pair, the dodecahedron and the icosahedron form another dual pair, and the tetrahedron is its self-dual. This duality is akin to the duality between the Delaunay triangulation and the corresponding Voronoi diagram in computational geometry.
In fullerenes, each vertex is shared by three faces (each of them is either a pentagon or a hexagon). Therefore, fullerene dual can be represented as a triangulation of the topological sphere. Based on this fact, Coxeter is able to analyze the icosahedral triangulations of the sphere and predict the associated isomers. This method, although mathematically rigorous, is difficult to implement for structures with low symmetry, thus is inefficient in practical applications.20 On the other hand, in the Schlegel diagram,43 each fullerene structure can be projected into a planar graph made of pentagons and hexagons. The ring spiral method is developed based on the spiral conjecture,20 which states “The surface of a fullerene polyhedron may be unwound in a continuous spiral strip of edge-sharing pentagons and hexagons such that each new face in the spiral after the second shares an edge with both (a) its immediate predecessor in the spiral and (b) the first face in the preceding spiral that still has an open edge.” Basically, for fullerenes of N atoms, one can list all possible spiral sequences of pentagons and hexagons, and then wind them up into fullerenes. If no conflict happens during the process, an isomer is generated. Otherwise, we neglect the spiral sequence. Table 1 lists the numbers of isomers for different fullerenes,20 when enantiomers are regarded as equivalent 1. It is seen that the number of isomers increases dramatically as N increases. Total curvature energies of many fullerene isomers are available at the carbon fullerene webpage.
Table 1.
Numbers of isomers for small fullerenes.
| Natom | 20 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 50 | 60 |
| Nisomer | 1 | 1 | 1 | 2 | 3 | 6 | 6 | 15 | 17 | 40 | 271 | 1812 |
In 1935, Hakon defined sphericity as a measure of how spherical (round) an object is.26 By assuming particles having the same volume but differing in surface areas, Hakon came up with a sphericity function,26
| (22) |
where Vp and Ap are the volume and the surface area of the particle. Obviously, a sphere has sphericity 1, while the sphericity of non-spherical particles is less than 1. Let us assume that fullerene isomers have the same surface area as the perfect sphere Ap = 4πR2, we define a sphericity measure as
| (23) |
where Vs is the volume of a sphere with radius R. By the isoperimetric inequality, among all simple closed surfaces with given surface area Ap, the sphere encloses a region of maximal volume. Thus, the sphericity of non-spherical fullerene isomers is less than 1. Consequently, in a distance based filtration process, the smaller sphericity a fullerene isomer is, the shorter its global β2 bar will be.
On fullerene surface, the local curvature characterizes the bond bending away from the plane structure required by the sp2 hybrid orbitals.28 Therefore, the relation between fullerene curvature and stability can be established and confirmed by using ab initio density functional calculations.24 However, such an analysis favors fullerenes with infinitely many atoms. Let us keep the assumption that for a given fullerene CN, all its isomers have the same surface area. We also assume that the most stable fullerene isomer CN is the one that has a near perfect spherical shape. Therefore, each fullerene isomer is subject to a (relative) total curvature energy Ec per unit area due to its accumulated deviations from a perfect sphere,
| (24) |
| (25) |
where Γ is the surface, µ is bending rigidity, κ1 and κ2 are the two principal curvatures, and κ0 = 1/R is the constant curvature of the sphere with radius R. Here, H and K are the mean and Gaussian curvature of the fullerene surface, respectively. Therefore, a fullerene isomer with a smaller sphericity will have a higher total curvature energy. Based on the above discussions, we establish the inverse correlation between fullerene isomer global β2 bar lengths and fullerene isomer total curvature energies.
Obviously, the present fullerene curvature energy (24) is a special case of the Helfrich energy functional for elasticity of cell membranes27
| (26) |
where, C0 is the spontaneous curvature, and KC and KG are the bending modulus and Gaussian saddle-splay modulus, respectively. The Gauss - Bonnet theorem states that for a compact two-dimensional Riemannian manifold without boundary, the surface integral of the Gaussian curvature is 2πχ, where χ is the Euler characteristic. Therefore, the curvature energy admits a jump whenever there is a change in topology which leads to a change in the Euler characteristic. A problem with this discontinuity in the curvature energy is that the topological change may be induced by an infinitesimal change in the geometry associated with just an infinitesimal physical energy, which implies that the Gaussian curvature energy functional is unphysical. Similarly, Hadwiger type of energy functionals, which make use of a linear combination of the surface area, surfaced enclosed volume, and surface integral of mean curvature and surface integral of Gaussian curvature,25 may be unphysical as well for systems involving topological changes. However, this is not a problem for differential geometry based multiscale models which utilize only surface area and surface enclosed volume terms,8, 48–50 as we employ the Eulerian representation and the proposed generalized mean curvature terms but not Gaussian curvature terms. Moreover, in the present model for fullerene isomers, there is no topological change.
To verify our assumptions, we consider a family of isomers for fullerene C40. It has a total of 40 isomers. We compute the global β2 bar lengths of all isomers by Euclidean distance filtration and fit their values with their total curvature energies with a negative sign. Figure 10 (right chart) shows an excellent correlation between the fullerene total curvature energies and our persistent homology based predictions. The correlation coefficient is 0.956, which indicates that the proposed persistent homology analysis of non-sphericity and our assumption of a constant surface area for all fullerene isomers are sound. In reality, fullerene isomers may not have an exactly constant surface area because some distorted bonds may have a longer bond length. However, the high correlation coefficient found in our persistent homology analysis implies that either the average bond lengths for all isomers are similar or the error due to non-constant surface area is offset by other errors.
Figure 10.
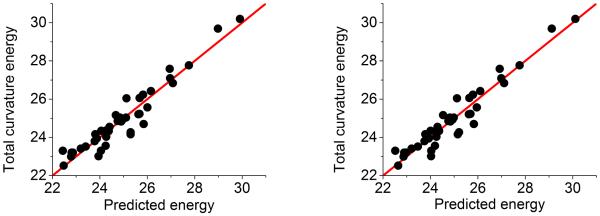
Comparison between the distance filtration (left chart) and the correlation matrix filtration (right chart) in fullerene C40 stability analysis. Fullerene C40 has 40 isomers. Each of them has an associated total curvature energy (eV). We calculate our average accumulated bar lengths from both distance filtration and the correlation matrix based filtration, and further fit them with total curvature energies. The correlation coefficients for our fitting are 0.956 and 0.959, respectively. It should be noticed that only the central void related β2 bars (i.e., the long-lived bars) are considered. The exponential kernel is used in matrix filtration with parameter η = 4 and κ = 2.
To further validate our persistent homology based method for the prediction of fullerene total curvature energies, we consider a case with significantly more isomers, namely, fullerene C44, which has 89 isomers. In this study, we have again found an excellent correlation between the fullerene total curvature energies and our persistent homology based predictions as depicted in the right chart of Fig. 11. The correlation coefficient for this case is 0.948. In fact, we have checked more fullerene isomer systems and obtained similar predictions.
Figure 11.
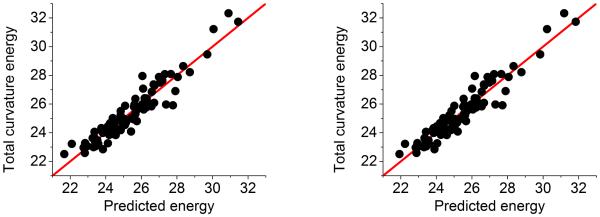
Further validation of our method with 89 isomers for fullerene C44. The correlation coefficients for distance filtration (left chart) and correlation matrix based filtration (right chart) are 0.948 and 0.952, respectively. In the latter method, the exponential kernel is used with parameter η = 4 and κ = 2.
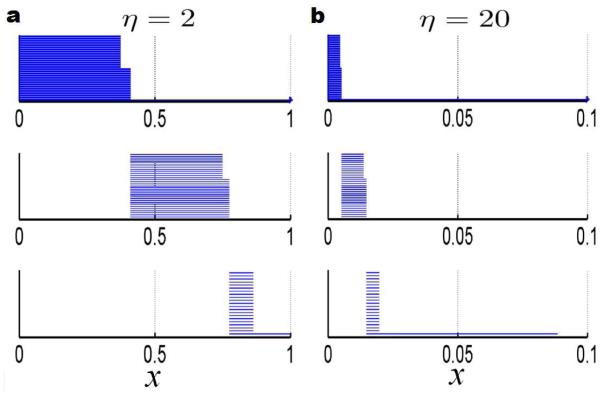
Finally, we explore the utility of our correlation matrix based filtration process for analysis of fullerene total curvature energies. In place of Euclidean distance based filtration, the correlation matrix based filtration is employed. To demonstrate the basic principle, Eq. (18) with the generalized exponential kernel in Eq. (14) is used in the filtration. We assume wij = 1 as fullerene molecules have only carbon atoms. To understand the correlation matrix based filtration method, the fullerene C60 is employed again. We fixed the power κ = 2, and adjust the value of characteristic distance η. Figure 12 gives the calculated barcodes with η = 2 and η = 20. It can be seen that these barcodes share a great similarity with the Euclidean distance based filtration results depicted in the right chart of Figure 6. All of topological features, namely, two kinds of bonds in β0, the pentagonal rings and the hexagonal rings in β1, and also the hexagonal cavities and the central void in β2 are clearly demonstrated. However, it should be noticed that, unlike the distance based filtration, the matrix filtration does not generate linear Euclidean distance relations. However, relative correspondences within the structure are kept. For instances, in β2 bars, the bar length ratio between the central void part and the hexagonal hole part in Fig. 12 is drastically different from its counterpart in Fig. 6. From our previous experience in flexibility and rigidity analysis,51–53 these rescaled distance relations have a great potential in capturing the essential physical properties, such as, flexibility, rigidity, stability, and compressibility of the underlying system.
Figure 12.
Illustration of the persistent barcodes generated by using correlation matrix based filtrations with different characteristic distances. The exponential kernel model with power κ = 2 is used. The characteristic distances in the left and right charts are respectively η = 2 and η = 20.
Similarly, the global β2 bar lengths obtained from the correlation matrix based filtration are utilized to fit with the total curvature energies of fullerene isomers. The correlation coefficients for the correlation distance matrix filtration are 0.959 and 0.952, respectively for C40 and C44 fullerene isomers. The corresponding results are demonstrated in the right charts of Figs. 10 and 11, respectively. It can be seen that the correlation matrix filtration is able to capture the essential stability behavior of fullerene isomers. In fact, results from correlation matrix based filtrations are slightly better than those of Euclidean distance based filtrations. In correlation matrix based filtrations, the generalized exponential kernel is used with parameter η = 4 and κ = 2. These parameters are chosen based on our previous flexibility and rigidity analysis of protein molecules. Overall, best prediction is obtained when the characteristic distance is about 2 to 3 times of the bond length and power index κ is around 2 to 3. Fine tuning of the parameters for each single case may yield even better result. However, this aspect is beyond the scope of the present work.
5 Conclusion
Persistent homology is an efficient tool for the qualitative analysis of topological features that last over scales. In the present work, for the first time, persistent homology is introduced for the quantitative prediction of fullerene energy and stability. We briefly review the principal concepts and algorithms in persistent homology, including simplex, simplicial complex, chain, filtration, persistence, and paring algorithms. Euler characteristics analysis is employed to decipher the barcode representation of fullerene C20 and C60. A thorough understanding of fullerene barcode origins enables us to construct physical models based on local and/or global topological invariants and their accumulated persistent lengths. By means of an average accumulated bar length of the second Betti number that corresponds to fullerene hexagons, we are able to accurately predict the relative energies of a series of small fullerenes. To analyze the total curvature energies of fullerene isomers, we propose to use sphericity to quantify the non-spherical fullerene isomers and correlate the sphericity with fullerene isomer total curvature energies, which are defined as a special case of the Helfrich energy functional for elasticity. Topologically, the sphericity of a fullerene isomer is measured by its global 2nd homology bar length in the barcode, which in turn gives rise to the prediction of fullerene isomer total curvature energies. We demonstrate an excellent agreement between total curvature energies and our persistent homology predictions for the isomers of fullerene C4 and C44. Finally, a new filtration based on the correlation matrix of the flexibility and rigidity index is proposed and found to provide even more accurate predictions of fullerene isomer total curvature energies.
Acknowledgments
This work was supported in part by NSF grants IIS-0953096, IIS-1302285 and DMS-1160352, NIH grant R01GM-090208 and MSU Center for Mathematical Molecular Biosciences initiative. GWW acknowledges the Mathematical Biosciences Institute for hosting valuable workshops. KLX thanks Bao Wang for useful discussions.
References
- [1].Adcock A, Carlsson E, Carlsson G. The ring of algebraic functions on persistence bar codes. arXiv:1304.0530. 2013 [Google Scholar]
- [2].Ballone P, Milani P. Simulated annealing of carbon clusters. Physical Review B. 1990;42(3201-3204) doi: 10.1103/physrevb.42.3201. [DOI] [PubMed] [Google Scholar]
- [3].Bendich P, Chin S, Clarke J, deSena J, Harer J, Munch E, Newman A, Porter D, Rouse D, Strawn N, Watkins A. Topological and statistical behavior classifiers for tracking applications. arXiv:1406.0214. 2014 [Google Scholar]
- [4].Carlsson G. Topology and data. Am. Math. Soc. 2009;46(2):255–308. [Google Scholar]
- [5].Carlsson G, Ishkhanov T, Silva V, Zomorodian A. On the local behavior of spaces of natural images. International Journal of Computer Vision. 2008;76(1):1–12. [Google Scholar]
- [6].Chang YF, Zhang JP, Sun H, Hong B, An Z, Wang RS. Geometry and stability of fullerene cages: C24 to C70. International Journal of Quantum Chemistry. 2005;105(2):142–147. [Google Scholar]
- [7].Chelikowsky JR. Nucleation of C60 clusters. Phys. Rev. Lett. 1991 Nov;67:2970–2973. doi: 10.1103/PhysRevLett.67.2970. [DOI] [PubMed] [Google Scholar]
- [8].Chen Z, Baker NA, Wei GW. Differential geometry based solvation models I: Eulerian formulation. J. Comput. Phys. 2010;229:8231–8258. doi: 10.1016/j.jcp.2010.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Coxeter HS. A spectrum of mathematics. Auckland University Press; Auckland: 1971. Virus macromolecules and geodesic domes; pp. 98–107. [Google Scholar]
- [10].Dabaghian Y, Memoli F, Frank L, Carlsson G. A topological paradigm for hippocampal spatial map formation using persistent homology. PLoS Comput Biol. 2012;8(8):e1002581. doi: 10.1371/journal.pcbi.1002581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dey TK, Li KY, Sun J, David CS. Computing geometry aware handle and tunnel loops in 3d models. ACM Trans. Graph. 2008;27 [Google Scholar]
- [12].Dey TK, Wang YS. Reeb graphs: Approximation and persistence. Discrete and Computational Geometry. 2013;49(1):46–73. [Google Scholar]
- [13].Edelsbrunner H, Harer J. Computational topology: an introduction. American Mathematical Soc.; 2010. [Google Scholar]
- [14].Edelsbrunner H, Letscher D, Zomorodian A. Topological persistence and simplification. Discrete Comput. Geom. 2002;28:511–533. [Google Scholar]
- [15].Edelsbrunner H, Mucke EP. Three-dimensional alpha shapes. Physical Review Letters. 1994;13:43–72. [Google Scholar]
- [16].Feng X, Tong Y. Choking loops on surfaces. IEEE Transactions on Visualization and Computer Graphics. 2013;19(8):1298–1306. doi: 10.1109/TVCG.2013.9. [DOI] [PubMed] [Google Scholar]
- [17].Fowler PW, Austin SJ, Manolopoulos DE. Competing factors in fullerene stability. Physics and Chemistry of the Fullerenes. 1994;443(41-62) [Google Scholar]
- [18].Fowler PW, Cremona JE, Steer JI. Systematics of bonding in non-icosahedral carbon clusters. Theor. Chim. Acta. 1988;73(1-26) [Google Scholar]
- [19].Fowler PW, Heine T, Mitchell D, Orlandi G, Schmidt R, Seifert G, Zerbetto F. Energetics of fullerenes with heptagonal rings. J. Chem. Soc. Faraday Trans. 1996;92(12) [Google Scholar]
- [20].Fowler PW, Manolopoulos DE. An atlas of fullerenes. Clarendon press; Oxford: 1995. [Google Scholar]
- [21].Frosini P, Landi C. Size theory as a topological tool for computer vision. Pattern Recognition and Image Analysis. 1999;9(4):596–603. [Google Scholar]
- [22].Gameiro M, Hiraoka Y, Izumi S, Kramar M, Mischaikow K, Nanda V. Topological measurement of protein compressibility via persistence diagrams. preprint. 2013 [Google Scholar]
- [23].Ghrist R. Barcodes: The persistent topology of data. Bull. Amer. Math. Soc. 2008;45:61–75. [Google Scholar]
- [24].Guan J, Jin ZQ, Zhu Z, Tománek D. Local curvature and stability of two-dimensional systems. preprint. 2014 [Google Scholar]
- [25].Hadwiger H. Vorlesungen Über Inhalt, Oberfläche und Isoperimetrie. Springer; 1975. [Google Scholar]
- [26].Hakon W. Volume, shape and roundness of quartz particles. Journal of Geology. 1935;43:250–280. [Google Scholar]
- [27].Helfrich W. Elastic properties of lipid bilayers: Theory and possible experiments. Zeitschrift für Naturforschung Teil C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- [28].Holec D, Hartmann MA, Fischer FD, Rammerstorfer FG, Mayrhofer PH, Paris O. Curvature-induced excess surface energy of fullerenes: Density functional theory and monte carlo simulations. Phys. Rev. B. 2010;81:235403. [Google Scholar]
- [29].Horak D, Maletic S, Rajkovic M. Persistent homology of complex networks. Journal of Statistical Mechanics: Theory and Experiment. 2009;2009(03):P03034. [Google Scholar]
- [30].Kaczynski T, Mischaikow K, Mrozek M. Computational homology. Springer-Verlag; 2004. [Google Scholar]
- [31].Kasson PM, Zomorodian A, Park S, Singhal N, Guibas LJ, Pande VS. Persistent voids a new structural metric for membrane fusion. Bioinformatics. 2007;23:1753–1759. doi: 10.1093/bioinformatics/btm250. [DOI] [PubMed] [Google Scholar]
- [32].Kratschmer W, Lamb LD, Fostiropoulos K, Huffman D. Solid C60: a new form of carbon. Nature. 1990;347(354-358) [Google Scholar]
- [33].Kroto HW, Heath JR, Obrien SC, Curl RF, Smalley RE. C60:buckminster fullerene. Nature. 1985;318(162-163) [Google Scholar]
- [34].Lee H, Kang H, Chung MK, Kim B, Lee DS. Persistent brain network homology from the perspective of dendrogram. Medical Imaging, IEEE Transactions on. 2012 Dec;31(12):2267–2277. doi: 10.1109/TMI.2012.2219590. [DOI] [PubMed] [Google Scholar]
- [35].Manolopoulos DE, May JC, Down SE. Theoretical studies of the fullerenes: C34 to C70. Chemical Physics Letters. 1991;181(105-111) [Google Scholar]
- [36].Mischaikow K, Mrozek M, Reiss J, Szymczak A. Construction of symbolic dynamics from experimental time series. Physical Review Letters. 1999;82:1144–1147. [Google Scholar]
- [37].Mischaikow K, Nanda V. Morse theory for filtrations and efficient computation of persistent homology. Discrete and Computational Geometry. 2013;50(2):330–353. [Google Scholar]
- [38].Munch E. Applications of persistent homology to time varying systems. Dissertation of Duke University. 2013 [Google Scholar]
- [39].Murry RL, Strout DL, Scuseria GE. Theoretical studies of fullerene annealing and fragmentation. International Journal of Mass Spectrometry and Ion Processes. 1994;138(113-131) [Google Scholar]
- [40].Pachauri D, Hinrichs C, Chung M, Johnson S, Singh V. Topology-based kernels with application to inference problems in alzheimer’s disease. Medical Imaging, IEEE Transactions on. 2011 Oct;30(10):1760–1770. doi: 10.1109/TMI.2011.2147327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Raghavachari K. Ground state of C84: two almost isoenergetic isomers. Chemical Physics Letters. 1992:397–400. [Google Scholar]
- [42].Robins V. Towards computing homology from finite approximations. Topology Proceedings. 1999;24:503–532. [Google Scholar]
- [43].Schlegel V. Theorie der Homogen Zusammengesetzten Raumgebilde. Dresden, Druck von E. Blochmann und Sohn; 1883. [Google Scholar]
- [44].Silva VD, Ghrist R. Blind swarms for coverage in 2-d. In Proceedings of Robotics: Science and Systems. 2005:01. [Google Scholar]
- [45].Singh G, Memoli F, Ishkhanov T, Sapiro G, Carlsson G, Ringach DL. Topological analysis of population activity in visual cortex. Journal of Vision. 2008;8(8) doi: 10.1167/8.8.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Streitwieser A. Molecular orbital theory for organic chemists. Wiley; New York: 1961. [Google Scholar]
- [47].Tausz A, Vejdemo-Johansson M, Adams H. Javaplex: A research software package for persistent (co)homology. 2011 Software available at http://code.google.com/p/javaplex. [Google Scholar]
- [48].Wei GW. Differential geometry based multiscale models. Bulletin of Mathematical Biology. 2010;72:1562–1622. doi: 10.1007/s11538-010-9511-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Wei G-W. Multiscale, multiphysics and multidomain models I: Basic theory. Journal of Theoretical and Computational Chemistry. 2013;12(8):1341006. doi: 10.1142/S021963361341006X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Wei G-W, Zheng Q, Chen Z, Xia K. Variational multiscale models for charge transport. SIAM Review. 2012;54(4):699–754. doi: 10.1137/110845690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Xia KL, Opron K, Wei GW. Multiscale multiphysics and multidomain models — Flexibility and rigidity. Journal of Chemical Physics. 2013;139:194109. doi: 10.1063/1.4830404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Xia KL, Wei GW. A stochastic model for protein flexibility analysis. Physical Review E. 2013;88:062709. doi: 10.1103/PhysRevE.88.062709. [DOI] [PubMed] [Google Scholar]
- [53].Xia KL, Wei GW. Molecular nonlinear dynamics and protein thermal uncertainty quantification. Chaos. 242014:013103. doi: 10.1063/1.4861202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Xia KL, Wei GW. Persistent homology analysis of protein structure, flexibility and folding. International Journal for Numerical Methods in Biomedical Engineerings. 2014;30:814–844. doi: 10.1002/cnm.2655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Yao Y, Sun J, Huang XH, Bowman GR, Singh G, Lesnick M, Guibas LJ, Pande VS, Carlsson G. Topological methods for exploring low-density states in biomolecular folding pathways. The Journal of Chemical Physics. 2009;130:144115. doi: 10.1063/1.3103496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Zhang BL, Wang CZ, Ho KM, Xu CH, Chan CT. The geometry of small fullerene cages: C20 to C70. The Journal of Chemical Physics. 1992;97(5007) [Google Scholar]
- [57].Zhang BL, Xu CH, Wang CZ, Chan CT, Ho KM. Systematic study of structures and stabilities of fullerens. Physical Review B. 1992;46(11) doi: 10.1103/physrevb.46.7333. [DOI] [PubMed] [Google Scholar]
- [58].Zomorodian A. Topology for Computing. Cambridge Monographs on Applied and Computational Mathematics; 2009. [Google Scholar]
- [59].Zomorodian A, Carlsson G. Computing persistent homology. Discrete Comput. Geom. 2005;33:249–274. [Google Scholar]