Operating characteristics of statistical methods for detecting gene-by- measured environment interaction in the presence of gene-environment correlation under violations of distributional assumptions

Abstract

Accurately identifying interactions between genetic vulnerabilities and environmental factors is of critical importance for genetic research on health and behavior. In previous work (Van Hulle et al. 2013) we explored the operating characteristics for a set of biometric (e.g., twin) models (Rathouz et al. 2008) for testing gene-by-measured environment interaction (G×M) in the presence of gene-by-measured environment correlation (r_GM) where data followed the assumed distributional structure. Here we explore the effects that violating distributional assumptions have on the operating characteristics of these same models even when structural model assumptions are correct. We simulated N=2000 replicates of n=1000 twin pairs under a number of conditions. Non-normality was imposed on either the putative moderator or on the ultimate outcome by ordinalizing or censoring the data. We examined the empirical type I error rates and compared BIC values. In general, non-normality in the putative moderator had little impact on the type I error rates or BIC comparisons. In contrast, non-normality in the outcome was often mistaken for or masked G×M, especially when the outcome data were censored.

In the past few decades it has become increasingly clear that any inquiry into the roots of psychopathology such as anxiety or depression, as well as other complex behaviors, requires accounting for possible interactions and correlations between genetic vulnerabilities and environmental factors. Historically, genetically informative models assumed that genetic and environmental influences on a particular trait were static across the population. But growing evidence points both to differential effects of the same environmental exposure across genotypes (gene-by-environment interaction) and to differential environmental exposures across genotypes (gene-by-environment correlation). Several methods have been proposed to model these more complex relationships, particularly within the context of twin and family studies (Eaves & Erkanli, 2003; Price & Jaffee, 2008; Purcell, 2002; Rathouz, Van Hulle, Rodgers, Waldman, & Lahey, 2008).

An important methodological consideration with the models proposed by ourselves and others in this recent literature is that these are full probability, non-linear structural equations models (SEM). As such, they are based on distributional assumptions, such as multivariate normality of latent genetic and latent environmental factors. In practice, many phenotypes of interest are not normally distributed. Data may be ordinal (e.g. behavior ratings of impulsivity), skewed (e.g. symptom counts of depression) or censored (e.g. age-of-onset). In contrast to recent work, classical twin and adoption study data analysis methods—which do not posit any interaction effects—rely on linear SEMs. Whereas normality may be a useful working assumption in these models, valid inferences are often based only on assumptions about the first two moments (mean, variance and covariance) of the data. Violations of normality have a negligible effect on parameter estimates in such models, and methods are available to adjust standard errors for bias due to non-normality. In the presence of gene-by-environment interactions, however, because they involve the product or square of latent normal quantities, the manifest variables will be non-normal by construction. Alternatively, when the latent factors are normal and do not interact, but the latent errors or measurement errors are non-normal, the manifest variables will also be non-normal. Therefore, when the scale of measurement of the variable(s) of interest is inherently non-normal, it is questionable as to whether the data can distinguish between these two fundamentally different scenarios. The issue of robustness of current G×M analysis methods to violation of distributional assumptions is therefore critical to behavior genetic designs being used in investigations of psychopathology, in particular where many phenotypes are measured with highly skewed distributions (e.g. symptom counts), and requires thorough exploration before any of these methods can be reliably used in such studies.

The goal of the current paper is to explore the existence and severity of consequences of such violations of distributional assumptions on statistical tests and estimators. We consider bivariate behavior genetic designs involving a measured environment M and its potential moderating effects (G×M) on variance components impacting on a phenotype of interest P. The models allow for correlation between M and variance components of P (rGM). The specific question is whether, in the context of the set of models laid out in Purcell (2002) and in Rathouz et al. (2008), the data are able to distinguish between non-normality in manifest variables due to G×M versus that due to measurement properties of the phenotype.

In our previous work (Van Hulle, Lahey, & Rathouz, 2013), we evaluated the Type I error rates, power, and performance of the Bayesian Information Criterion (BIC) for testing and comparing a subset of the models proposed in Rathouz et al. (2008), equations for which are shown in Table 1. In that paper, data were simulated under a variety of conditions both with and without G×M interactions. To briefly summarize, we found that: (i) when comparing the Cholesky with G×M model with the various submodels, the false positive rates consistently fell short of the nominal Type I error rates (α =.10, .05, .01); (ii) with larger sample sizes (N=2000),in nearly all cases the correct model had the lowest BIC value across all possible models; (iii) with lower sample sizes (N=500), models specifying non-linear main effects were more difficult to distinguish from models containing interaction effects. In that paper, all simulated latent quantities and error variables were normally distributed, thus matching the distributional assumptions of the models. For the current study, we examined Type I error rates and performance of the Bayesian Information Criterion (BIC) for nested and non-nested models under similar data generating mechanisms as in Van Hulle et al. (2013), but where violations of normality in the measurement process were imposed on either the moderator (M) or the phenotype (P).

Table 1.

Bivariate variance components models for latent component-by-measured environment (G×M) interaction.

Model	Equation
Classical ACE modela	$$M={\mu }_M+a_M{A}_M+c_M{C}_M+e_M{E}_M$$ (1)
Bivariate cholesky	$$P={\mu }_P+a_C{A}_M+c_C{C}_M+e_C{E}_M+a_U{A}_U+c_U{C}_U+e_U{E}_U$$ (2)
Bivariate cholesky with G×M	$$P={\mu }_P+(a_C+{\alpha }_{C}M)A_M+(c_C+{\kappa }_{C}M)C_M+(e_C+{\varepsilon }_{C}M)E_M+(a_U+{\alpha }_{U}M)A_U+(c_U+{\kappa }_{U}M)C_U+(e_U+{\varepsilon }_{U}M)E_U.$$ (3)
Nonlinear main effects model with G×M	$$P={\mu }_P+{\beta }_{1}M+{\beta }_2{M}^2+(a_U+{\alpha }_{U}M)A_U+(c_U+{\kappa }_{U}M)C_U+(e_U+{\varepsilon }_{U}M)E_U.$$ (4)
Nonlinear main effects	$$P={\mu }_P+{\beta }_{1}M+{\beta }_2{M}^2+a_U{A}_U+c_U{C}_U+e_U{E}_U.$$ (4*)
Linear main effects only	$$P={\mu }_P+{\beta }_{1}M+a_U{A}_U+c_U{C}_U+e_U{E}_U.$$ (4†)

^ashown here for the putative moderator.

Note: P refers to a phenotype of interest, M refers to a putative moderator, a, c, and e refer to additive genetic, shared environment, and non-shared environment influences respectively, and μ is the mean. A, C, and E are standard normal latent variables. The subscript “C” refers to factors that affect both M and P, and the subscript “U” refers to factors that are unique to P.

Methods

Model specification and data generation

For the purposes of the current study M refers to a putative moderator and P to an outcome of interest. We chose M rather than E to highlight that the moderator may not be strictly environmental in nature. G×M refers to generic interaction effects that encompass interactions between the moderator and latent additive genetic (A) or latent shared (C) or non-shared (E) environmental influences. We refer in the same generic sense to correlations between A, C, or E, and the moderator as r_GM. Further details on notation and interpretation are given in Van Hulle et al. (2013).

Jointly, the classical twin model and the bivariate Cholesky model, (1) and (2) in Table 1, allow for r_GM in the form of genetic (a_C), shared (c_C), and non-shared (e_C) environmental influences common to M and P (denoted here by the subscript “C”). Corresponding influences unique to P (denoted by the subscript “U”) are given by a_U, c_U, and e_U in (2). The remaining models are variations on (2) that together with (1) allow for both r_GM and G×M. Model (3) is the “Cholesky G×M” model proposed by Purcell (2002), and model (4) is a special case of (3) proposed by Rathouz et al. (2008) that replaces the common effects on P with direct (or “main”) effects of M on P. The remaining two are: a non-linear main effects model that drops G×M in the unique influences on P (4*), and a model that further drops the non-linear effect of M on P (4†).

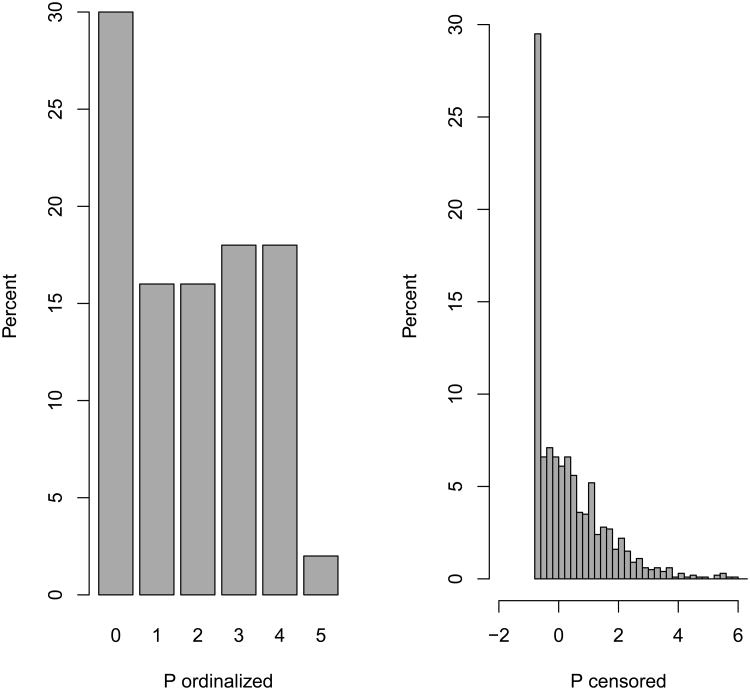
To address the aims of this study, data were simulated for M under the classical twin model (1) and for P under models (2), (3), (4), (4*), and (4†). We simulated data using code written in Stata 12.1 (StataCorp, 2011) under the multiple specifications for each model shown in Table 2. To introduce violations of distributional assumptions, we either censored or ordinalized the manifest measures M or P. For censoring, scores in the bottom 30% of the distribution were given the value of the 30^th percentile (e.g. -0.6 in Figure 1) to simulate a floor effect. For ordinalizing, the data were assigned a score from 0 to 5, with the bottom 30% assigned a score of 0, the top 2% assigned a score of 5, and the remaining data evenly distributed between scores of 2, 3, and 4 (see Figure 1). For each DGM in Table 2, non-normality was imposed on either M or P (but not both simultaneously) resulting in a total of 44 distinct data generating mechanisms (DGMs). Note that for DGMs where P contained interaction effects and non-normality was imposed on M, P was generated after M was censored or ordinalized. We wanted to approximate a situation where the underlying mechanisms giving rise to the phenotype of interest were truly non-normal in nature.

Table 2.

Models and data generation mechanism (DGM) parameter values used in data simulation.

Model DGM		Simulation Condition		Simulation Parameter Values	Nested in
		Correlation or Non-Linear Main Effect	Interaction
Cholesky (2)	A.	High rAM & Low rEM	---	aC= .5; $a_U=\sqrt{.9-a_C^2}$; eC=.1; $e_U=\sqrt{.9-e_C^2}$	(3), (5)
	B.	Low rAM & High rEM	---	aC= .1; $a_U=\sqrt{.9-a_C^2}$ eC=.5; $e_U=\sqrt{.9-e_C^2}$	(3), (5)
Cholesky with G×M (3)	A.	High rAM & Low rEM	High A×M, Low E×M	aC=.5; αC=.5*aC; $a_U=\sqrt{.9-a_C^2}$; αU=.5*aU; eC=.1; εC=.25*eC; $e_U=\sqrt{.9-e_C^2}$; εU=.25*eU
	B.	High rAM & Low rEM	Low A×M, High E×M	aC=.5; αC=.25*aC; $a_U=\sqrt{.9-a_C^2}$; αU=.25*aU; eC=.1; εC=.5*eC; $e_U=\sqrt{.9-e_C^2}$; εU=.5*eU
	C.	Low rAM & High rEM	High A×M, Low E×M	aC=.1; αC=.5*aC; $a_U=\sqrt{.9-a_C^2}$; αU=.5*aU; eC=.5; εC=.25*eC; $e_U=\sqrt{.9-e_C^2}$; αU=.25*eU
	D.	Low rAM & High rEM	Low A×M, High E×M	aC=.1; αC=.5*aC; $a_U=\sqrt{.9-a_C^2}$; αU=.25*aU; eC=.5; εC=.5*eC; $e_U=\sqrt{.9-e_C^2}$; εU=.5*eU
Nonlinear Main Effects With G×M (4)	A.	Large	Low A×M, Low E×M	${\beta }_1=\sqrt{{.5}^2+{.1}^2}$; β2=.25*β1; $a_U=\sqrt{.9-{.5}^2}$; αU=.25*aU; $e_U=\sqrt{.9-{.1}^2}$; εU=.25*eU	(3)
	B.	Small	Low A×M, Low E×M	${\beta }_1=\sqrt{{.5}^2+{.1}^2}$; β2=.125*β1; $a_U=\sqrt{.9-{.5}^2}$; αU=.25*aU; $e_U=\sqrt{.9-{.1}^2}$; εU=.25*eU	(3)
Nonlinear Main Effectsonly (4*)	A.	Large	---	${\beta }_1=\sqrt{{.5}^2+{.1}^2}$; β2=.25*β1 $a_U=\sqrt{.9-{.5}^2}$; $e_U=\sqrt{.9-{.1}^2}$	(3), (4)
	B.	Small	---	${\beta }_1=\sqrt{{.5}^2+{.1}^2}$; β2=.125*β1 $a_U=\sqrt{.9-{.5}^2}$; $e_U=\sqrt{.9-{.1}^2}$	(3), (4)
Linear Main Effects only (4†)		---	---	${\beta }_1=\sqrt{{.5}^2+{.1}^2}$ $a_U=\sqrt{.9-{.5}^2}$; $e_U=\sqrt{.9-{.1}^2}$	(2), (4*)

Note: DGM = data generating mechanism. DGM numbers correspond to model numbers in Table 1, with A-D enumerating specific simulation conditions. For all simulation conditions, a_M = e_M = √.9, c_M = √.1 and c_U = √.2; for DGM's 3A-D, interaction between shared environment and the moderator κ_C = κ_U = .01 and main effect of shared environment common to M and P, c_C =.01; for DGM's 4A-B interaction between the shared environment and the moderator, κ_U = .01.

Figure 1.

Example of distribution of simulated data after ordinalizing (left panel) or censoring (right panel). Data were ordinalized by grouping the top 2%, the bottom 30%, and evenly dividing the remaining scores. Data were censored by replacing scores in the bottom 30% with the value of the 30^th percentile.

Note: For left panel Mean = 1.8, SD = 1.6, Skew = 0.2, Kurtosis = -1.3; for right panel Mean = 0.4, SD = 1.2, Skew = 1.6, Kurtosis = 3.2.

Data were simulated such that a high gene-moderator correlation (r_AM) was paired with low environment moderator correlation (r_EM) and vice versa, and a high gene-by-moderator interaction (A×M) was paired with low environment-by-moderator interaction (E×M) and vice versa, with the exception of DGM (4). For DGM's that included r_AM, high correlations were set at 0.5 and low correlations were set at 0.1, with the same values assigned to high and low r_EM. For DGM (3), high A×M was defined as interactions with the common (α_C) and unique (α_U) influences on P set to one half of the main effect of common (a_C) and unique (a_U) genetic influences on P. Low A×M was defined as one quarter of the main effect of common or unique genetic influences. Doing so ensured that the effect of A_M or A_U on P would be either absent (high A×M) or reduced by half (low A×M) when M is two standard deviations below its mean. An analogous definition was used to specify high and low E×M (ε_C, ε_U). Similarly, for DGMs (4) and (4*), the quadratic main effect of M on P (β₂), was set such that the effect of M on P was absent (large) or reduced by half (small) when M was two standard deviations below its mean. Note that for simplification, shared environment correlations and interactions with M, c_C, κ_C, and κ_U, were set to .01 where applicable and were not considered further. All values are collected and presented in Table 2.

For each of the 44 scenarios, we simulated sample sizes of n=1000 pairs (500 each of MZ and DZ pairs). All simulations were performed with 2000 replicates.

Data analysis

We used the structural equation modeling software Mplus 6.1 (Muthén & Muthén, 2011) to fit the models (2), (3), (4), (4*), and (4†) to each set of replicates. In our analysis, we treated ordinal and censored data as continuous because the integration algorithm needed to calculate the log-likelihood is not available for categorical or censored data in Mplus and because treating the data as continuous reflects the lack of concordance between the data generation and the modeling assumptions. We calculated the empirical Type 1 error rates for nominal rates of 0.1, 0.05, and 0.01 for nested models. These analyses evaluate the ability of the maximum likelihood statistical procedure to detect when non-linear (latent or manifest) model terms are needed. G×M interactions were tested by comparing the Cholesky with G×M model (3) to the non-linear main effects with G×M model (4), and to the non-linear main effects only model (4*) and the classical bivariate Cholesky (2). The non-linear main effects with G×M model (4) was compared to the non-linear main effects only model (4*). Finally, the non-linear main effects model (4*) and the Cholesky (2) were compared to a linear effects only model (i.e. β₂ = 0). We also empirically assessed the degree to which BIC could differentiate nested or non-nested models when neither model reflected the true DGM. A BIC difference of 10 corresponds to a Bayesian odds of 150:1 that the model with the more negative value is the better fitting model (Raftery, 1995). Thus, a difference of 10 should be considered “very strong” evidence in favor of the model with the more negative value. We computed the difference in BIC for each pair of models and indicate how often one model was chosen over the other. We interpreted BIC differences between -10 and 10 as indicating that the models were equivocal (i.e. described the data equally well). For each DGM, we determined the best model among all the alternatives according to lowest BIC, allowing us to see how often the correct model was chosen and, when it was not, which other models were chosen.

Results

Type I error rate for comparing nested models

For each hypothesis test, when data were generated under the null model, we present the empirical (i.e., simulated) Type I error rates for nominal rates of 0.1, 0.05, and 0.01 in Tables 3 (ordinalized) and 4 (censored). The first column lists the alternative model, H_A, and the second column lists the null model used to generate the data, H₀. For example, the first row in Table 3 indicates that when data are generated under the Non-linear main effects model (4) with large β₂ and M is ordinalized, the number of false positives (4.9%) is about half the expected rate for alpha=.10 when comparing the Cholesky with G×M model (3) to Non-linear main effects with G×M model (4). In general, when M is ordinalized the Type I error rates, though not perfect, are close to or lower than the nominal values and in line with the results reported in Van Hulle et al. (2013). Tests of the common G×M influences (model (4) vs model (3), for example, were underpowered. Tests of the unique G×M influences (e.g. model (4*) vs model (4) or the non-linear main effect (model (4*) vs model (4†)) were well calibrated. When P is ordinalized, the error rates tend to be lower than expected (in keeping with our earlier findings) when comparing two models with interaction effects (e.g. (3) vs (4)), However, empirical Type I error rates are higher than expected when the true model does not contain G×M (or G×M was weak) but the alternative model does. That is, when G×M is present, the LRT is underpowered. However, in the absence of true G×M, non-normality in the phenotype P is mistaken for interaction effects. We found similar results when M or P are censored (Table 5). The empirical Type I error rates are lower than expected when M is censored but generally in keeping with our earlier findings with normally distributed data. A notable exception occurred when comparing the Cholesky G×M model (3) with the Cholesky model (2) when M is censored. In this case, Type I error rates were much higher than expected. We cannot at this time fully explain this discrepancy. When P is censored, the true model is overwhelmingly rejected in favor of a model containing G×M in cases where DGM's had weak or no G×M effects. When β₂ in model (4) was large, the magnitude of the non-linear main effect overwhelmed the violation of assumptions and led to good performance in the Type I error rates.

Table 3.

Ordinalized data simulation: Percent of simulated LRT statistics under the null hypothesis exceeding critical value for pairs of nested models based on 2000 replicates of N=1000.

			% Type I error rates
	DGM		LRT df	Ordinalized on M			Ordinalized on P
Model for HA	Model for H0	Condition of H0		10	5	1	10	5	1
Cholesky with G×M (3)	NL main effects with G×M (4)	Large β2	4	4.9	2.4	0.3	3.0	1.0	0.2
		Small β2	4	4.4	1.8	0.1	1.9	0.7	0.2
	NL main effects (4*)	Large β2	7	5.9	2.6	0.6	4.4	2.2	.25
		Small β2	7	5.7	2.5	0.5	15.4	8.8	2.1
	Choleskya (2)	high rAM	6	7.2	3.4	0.7	22.9	13.4	3.2
		low rAM	6	8.2	3.9	0.7	35.3	21.4	6.6
NL main effects with G×M (4)	NL main effects (4*)	Large β2	3	9.3	4.8	0.8	8.8	3.6	0.9
		Small β2	3	8.0	4.1	1.0	31.9	20.5	6.9
NL main effects (4*)	Lin main effectsa (4†)		1	10.8	4.6	1.4	17.6	10.3	2.3
Cholesky (2)	Lin Main effects (4†)		2	8.3	4.4	0.7	9.4	4.8	0.7

Note: P refers to a phenotype of interest, M refers to a putative moderator. LRT refers to the likelihood ratio test.

^aDGM does not contain G×M effects.

Table 4.

Censored data simulation: Percent of LRT statistics under the null hypothesis exceeding critical value for pairs of nested models based on 2000 replicates of N=1000.

			% Type I error rates
	DGM		LRT df	Censored on M			Censored on P
Model for HA	Model for H0	Condition of H0		10	5	1	10	5	1
Cholesky with G×M (3)	NL main effects with G×M (4)	large β2	4	4.9	2.2	0.3	9.3	4.8	0.9
		small β2	4	4.9	1.6	0.3	5.4	2.2	0.5
	NL main effects (4*)	large β2	7	5.7	2.8	0.5	82.5	82.4	81.7
		small β2	7	5.5	2.5	0.5	100	100	100
	Cholesky (2)	high rAM	6	23.0	15.1	4.2	100	100	100
		low rAM	6	50.2	37.5	16.2	100	100	100
NL main effects with G×M (4)	NL main effects (4*)	large β2	3	8.7	4.5	0.9	83.7	83.1	81.7
		small β2	3	8.8	4.2	0.7	100	100	100
NL main effects (4*)	Lin main effectsa (4†)		1	10.4	5.3	1.1	67.3	54.0	30.8
Cholesky (2)	Lin Main effects (4†)		2	8.0	4.3	0.7	8.8	4.5	0.5

Note: P refers to a phenotype of interest, M refers to a putative moderator. LRT refers to the likelihood ratio test.

^aDGM does not contain G×M effects.

Table 5.

Ordinalized data simulation: Percent each model is favored via comparison of BIC values^a for all pairwise comparisons, and percent each model has lowest BIC: n=1000.

	DGM												DGM
	CHOL				CHOLG×M								NLMainG×M				NLMain
	2A		2B		3A		3B		3C		3D		4A		4B		4*A		4*B
	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P
CholG×M					100.0	98.3	100.0	100.0	100.0	75.3	100.0	100.0	100.0	96.9	100.0	98.1	96.7	11.0	1.0
Equivocal						0.5				5.6				3.1		1.9	3.3	59.0	21.7	2.3
Chol	100.0	100.0	100.0	100.0		1.2				19.1								30.0	77.3	97.7
CholG×M	5.2	1.0	7.7	30.5	27.5	0.4	0.6	2.8	2.0	39.7	24.6	19.7
Equivocal	58.7	37.5	66.1	63.4	65.0	33.6	30.7	47.4	48.3	32.3	65.8	66.3
NLMainG×M	36.1	61.5	26.2	6.1	7.5	66.0	98.7	49.8	49.7	28.0	9.6	14.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0
CholG×M	0.2		0.2	6.2	100.0	97.8	100.0	100.0	100.0	83.9	100.0	100.0	99.0	65.9	99.0	93.0
Equivocal	9.2	5.0	13.0	47.7		2.2				3.6			1.0	33.1	1.0	7.0
NLMain	90.6	95.0	86.8	46.1						12.5				2.0			100.0	100.0	100.0	100.0
NLMainG×M					100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0
Equivocal	2.7	12.3	1.8	20.8													1.0	1.2	1.3	8.5
NLMain	97.3	87.7	98.2	79.2													99.0	98.8	98.7	91.5
NLMainG×M					100.0	98.6	100.0	100.0	100.0	74.7	100.0	100.0	100.0	100.0	100.0	100.0	100.0	85.1	38.0	7.8
Equivocal	1.0	5.7				0.2				5.3								14.9	60.9	90.1
Chol	99.0	94.3	100.0	100.0		1.2				20.0									1.1	2.1
NLMain					23.2	86.9	31.2	15.9	8.8	30.1	14.5	83.2	100.0	85.8	75.6	4.9	100.0	100.0	97.6	86.0
Equivocal	40.4	65.9	32.2	8.1	50.7	11.1	64.8	71.0	51.4	55.2	39.3	15.6		14.2	24.4	95.1			2.4	14.0
Chol	59.6	31.4	67.8	91.9	23.1	2.0	4.0	13.1	39.8	14.7	46.2	1.2
Lowest Overall BICb
CholG×M					62.5	6.3	5.0	14.4	14.0	49.2	59.3	50.6
NLMainG×M					37.5	92.5	95.0	85.6	86.0	36.8	40.7	49.4	100.0	100.0	100.0	100.0
NLMain	5.6	14.7	2.4														100.0	100.0	100.0	100.0
Chol	94.4	85.3	97.6	100.0		1.2				13.9

^aabsolute BIC difference >10

^bPercentage of replicates for which indicated model has minimum BIC across models (2), (3), (4), and (4*).

Note: P refers to a phenotype of interest, M refers to a putative moderator. Bold indicates the correct model.

As shown in Figure 1, we imposed rather severe deviations from normality on the data. To see if LRT improved with less severe deviations from normality we simulated data (2000 replicates) under models (2) and (4†) without G×M. We again imposed two types of non-normality on P: censored (bottom 10% and top 5%) and ordinalized, such that distribution of P was roughly bell-shaped with scores divided into groups of size 12%, 20%, 30%, 20%, 10%, and 8% and assigned a value from 0 to 5 (See Supplemenatary Figure 1). Type I error rates were reduced modestly (by 2-4%) when P was ordinalized, but the empirical error rates were still higher than expected. When we imposed a less severe censoring scheme on P, the empirical error rates were reduced dramatically (see Supplementary Table 1) and were generally in line with the empirical error rates reported in our paper on normally distributed data (Van Hulle et al., 2013).

BIC for general model comparison

The Bayesian Information Criterion (BIC) is often used to choose one best-fitting among two or more nested or non-nested models. It imposes a greater penalty on complexity than the likelihood ratio test. We generated data under a variety of models (2), (3), (4) and (4*), and calculated the BIC difference for every pairwise model comparison, nested and non-nested. For each pair of model comparisons, the percentage of replicates for which BIC differences indicated that one model is favored over the other is given in Table 5 (ordinal data) and Table 6 (censored data). The results largely mirror the LRT's. That is, when the data are ordinalized the correct model (or the model that most closely approximates the correct model) is favored over the incorrect model the majority of the time and the correct model nearly always has the lowest BIC among the 5 alternatives, with one notable exception. When data are generated under the Cholesky with G×M model (3), the non-linear main effects with G×M (4) is equivocal to or preferred over the true model (3) in the majority of cases, regardless of whether M or P was ordinalized. In many cases (38 to 95%), model (4) has the lowest BIC among the five alternatives. When P is censored (Table 6), models that include G×M are preferred to models that do not even when the DGM does not include G×M, such as models (2) and (4*). For instance, when P is censored and the DGM is the non-linear main effects model (4*), a model with G×M effects is preferred over the true model in a majority of replicates. In fact, model (4) had the lowest BIC in 80%-100% of replicates when the DGM was model (4*). As with ordinalized data, non-linear main effects with G×M model (4) is consistently preferred over or equivocal to the Cholesky G×M model (3) when data were generated under the latter. In our previous work we showed that with smaller samples sizes, it is difficult to detect significant differences among α_C, κ_C, and ε_C and we replicated that finding here with data distributions that deviate from normality.

Table 6.

Censored data simulation: Percent each model is favored via comparison of BIC values^a for all pairwise comparisons, and percent each model has lowest BIC: n=1000.

	DGM												DGM
	CHOL				CHOLG×M								NLMainG×M				NLMain
	2A		2B		3A		3B		3C		3D		4A		4B		4*A		4*B
	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P	M	P
CholG×M		51.0		77.7	100.0	100.0	100.0	100.0	100.0	100.0	84.8	100.0	100.0	100.0	100.0	100.0		100.0		100.0
Equivocal		41.6		1.5							3.1						1.1
Chol	100.0	7.4	100.0	20.8							12.1						98.9		100.0
CholG×M	3.6	1.3	15.2	33.6	4.4	1.3	3.3	2.2	13.3	32.0	19.0	64.2		0.2
Equivocal	55.7	40.4	67.5	59.8	58.3	39.6	52.1	49.1	66.1	61.2	68.6	27.4		0.4
NLMainG×M	40.7	58.3	17.3	6.6	37.4	59.1	44.6	48.7	20.6	6.8	12.4	8.4	100.0	99.4	100.0	100.0	100.0	100.0	100.0	100.0
CholG×M		66.0	1.0	97.5	99.0	100.0	99.0	100.0	100.0	100.0	85.7	100.0	98.7	100.0	99.0	100.0		63.1		83.6
Equivocal	6.8	29.0	22.4	2.5	1.0		1.0				2.9		1.3		1.0			14.8		15.3
NLMain	93.2	5.0	76.6								11.5						100.0	22.1	100.0	1.1
NLMainG×M		89.8		96.9	100.0	100.0	100.0	100.0	100.0	100.0	86.0	100.0	100.0	100.0	100.0	100.0		79.3		99.5
Equivocal	2.6	10.2	3.6	3.1							2.6						1.2	3.1	1.0	0.5
NLMain	97.4		96.4								11.4						98.8	17.6	99.0
NLMainG×M		76.1		64.5	100.0	100.0	100.0	100.0	100.0	100.0	84.6	100.0	100.0	100.0	100.0	100.0	5.0	100.0		100.0
Equivocal	2.2	2.1	3.3	24.8							2.9						83.1		49.0
Chol	97.8	21.8	96.7	10.7							12.5						11.8		51.0
NLMain	0.8	0.4	1.2		10.0	100.0	4.6	86.8	1.4	70.3	45.0	100.0	68.8	100.0	28.0	89.6	78.9	83.4	99.0	99.2
Equivocal	54.7	68.2	40.7	16.3	55.3		64.6	12.5	30.8	23.1	37.8		31.2		72.0	10.4	21.1	2.7	1.0	0.8
Chol	44.5	31.4	58.1	83.7	34.6		30.8	0.7	67.8	6.6	17.2							13.9
Lowest Overall BICb
CholG×M		7.8		60.2	20.8	9.7	16.3	13.6	40.0	67.7	44.0	62.5
NLMainG×M		85.2		33.1	79.2	90.3	83.7	86.4	60.0	32.3	42.6	37.5	100.0	100.0	100.0	100.0		80.7		100.0
NLMain	14.3	0.4	11.0								3.4						100.0	19.3	99.0
Chol	85.7	6.5	89.0	6.7							9.5								1.0

^aabsolute BIC difference >10.

^bPercentage of replicates for which indicated model has minimum BIC across models (2), (3), (4), and (4*).

Note: P refers to a phenotype of interest, M refers to a putative moderator.Bold indicates the correct model; italics indicates A×M or E×M detected when it does not hold (i.e.DGM is Chol or NLMain)

Discussion

Our goal was to follow-up our earlier work describing the operating characteristics of alternative models testing for G×M by extending that work to some commonly occurring deviations from normality. In our previous work, we showed that deviations from expected Type I error rates were mild to moderate. In this study, we show that when data fail to meet distributional assumptions, deviations from expected Type I error rates are unpredictable and in some cases quite extreme.

In general, violations of normality in the moderator M have little impact on the operating characteristics of the models. Tests of non-linear main effects vs common G×M are somewhat underpowered, whereas tests of unique G×M or non-linear main effects are calibrated as expected, in keeping with our earlier work. In contrast, when the ultimate phenotype P violates assumptions of normality, G×M may be detected when it does not exist. In addition, it is difficult to distinguish among G×M interactions that involve latent factors that are common to the putative moderator M and outcome variable P when the data are non-normally distributed. In cases where P was ordinalized, tests of G×M were underpowered when the data generating model and alternative models both contained unique G×M and/or strong non-linear main effects. The true model was rejected in favor of a model with G×M effects more often than expected when the data generating model lacked G×M effects or such effects were small. These issues were exacerbated when P was censored. Under the censoring scheme imposed here, the null model was rejected in favor of a model containing G×M effects or non-linear main effects the vast majority of the time when the data generating model lacked or had only weak G×M effects or non-linear main effects.

These results were generally supported by BIC comparisons. BIC differences were largely in the expected direction when P was ordinalized. However, when P was censored, BIC tests led to favoring models with G×M or non-linear effects over those that do not even when the true model does not include any G×M or non-linear effects. For instance, when the data were generated under the Cholesky with high r_GM, and P was censored, the non-linear main effects with G×M model had the lowest BIC value in 85% of replicates. Perhaps more troubling is the failure to detect G×M when it does exist. In particular, it was difficult to distinguish between moderation of the genetic and environmental influences common to M and P and non-linear main effects. This was true whether M or P were ordinalized or censored. However, when data were censored, common G×M effects were mistaken for non-linear main effects in the majority of replicates under most conditions. Unfortunately, these problems cannot be solved with transformation “to normality” before analysis because such transformation may then serve to eliminate G×M should it actually exist.

This study shows that violations of normality, particularly in the phenotype of interest, result in problems in both distinguishing non-linearity from G×M and in detecting moderation of the common factors influencing both the moderator and the phenotype. Underlying G×M effects themselves may lead to mild deviations from normality in the phenotype. Therefore, researchers should interpret model fitting results with caution when the phenotypic data may deviate from distributional assumptions.