Model-based estimation of loop gain using spontaneous breathing: A validation study

Abstract

Non-invasive assessment of ventilatory control stability or loop gain (which is a key contributor in a number of sleep-related breathing disorders) has proven to be cumbersome. We present a novel multivariate autoregressive model that we hypothesize will enable us to make time-varying measurements of loop gain using nothing more than spontaneous fluctuations in ventilation and CO₂. The model is adaptive to changes in the feedback control loop and therefore can account for system non-stationarities (e.g. changes in sleep state) and it is resistant to artifacts by using a signal quality measure. We tested this method by assessing its ability to detect a known increase in loop gain induced by proportional assist ventilation (PAV). Subjects were studied during sleep while breathing on continuous positive airway pressure (CPAP) alone (to stabilize the airway) or on CPAP + PAV. We show that the method tracked the PAV-induced increase in loop gain, demonstrating its time-varying capabilities, and it remained accurate in the face of measurement related artifacts. The model was able to detect a statistically significant increase in loop gain from 0.14 ± 10 on CPAP alone to 0.21 ± 0.13 on CPAP + PAV (p < 0.05). Furthermore, our method correctly detected that the PAV-induced increase in loop gain was predominantly driven by an increase in controller gain. Taken together, these data provide compelling evidence for the validity of this technique.

1. Introduction

Ventilatory control instability or high loop gain (LG) is a key factor in the pathogenesis of a variety of sleep-related breathing disorders, including Cheyne–Stokes respiration (Bradley and Floras, 2003; Javaheri, 1999; Xie et al., 2002), sleep at altitude in adults (Berssenbrugge et al., 1983; Burgess et al., 2004, 2008; Salvaggio et al., 1998), periodic breathing in neonates (Rigatto and Brady, 1972a,b; von Czettritz et al., 1996; Wilkinson et al., 2007), and obstructive sleep apnea (OSA) (Wellman et al., 2004; Younes et al., 2001). In general, LG is a measure of the stability of a system (e.g. an electrical or a physiological system) controlled by negativefeedback loops. In the case of respiration, LG represents the sensitivity of the negative feedback loop that controls ventilation. LG is defined as the ratio of a corrective response (e.g., hyperpnea) to a disturbance (e.g., apnea). A high LG (large ventilatory response to a disturbance) may develop into self-sustaining oscillations i.e. instability. On the other hand, a low LG (small ventilatory response to a disturbance) is more likely to exhibit stable breathing. The two key components of LG are controller gain and plant gain (see Fig. 1). Controller gain reflects chemoresponsiveness, or the hypoxic and hypercapnic ventilatory responses. Plant gain reflects the effectiveness of ventilation at eliminating CO₂. LG is a frequency dependent variable and therefore increases as a function of the circulatory delay and other time dependent variables. A non-invasive method for measuring LG could allow diagnose the contribution of LG to disordered breathing and then potentially treat the condition by using for example, oxygen or acetazolamide (Edwards et al., 2012; Wellman et al., 2008) to lower LG. However, such clinical utility of LG has been limited thus far by the fact that measurements from spontaneous breathing have proven inaccurate, and invasive measurements are impractical clinically (Francis et al., 2000).

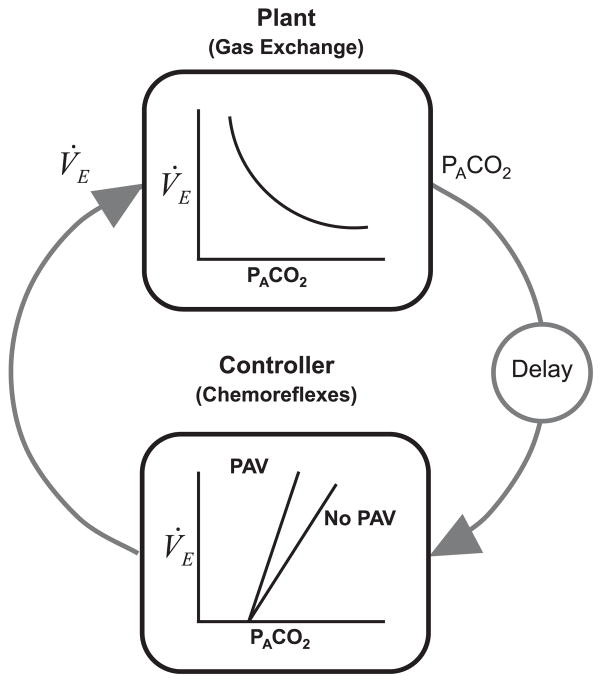
Fig. 1.

Schematic diagram of the respiratory control system. The plant represents the gas-exchange system. The input to the plant is ventilation (V˙_E), and the output is the alveolar gas tension (P_ACO₂). The delay term represents the time it takes for the pulmonary capillary blood to reach the chemoreceptors. During sleep, the controller primarily represents the ventilatory response to CO₂, i.e. chemorelfexes. PAV works by generating pressure at the airway in proportion to a person’s inspiratory effort, thereby resulting in an increase in controller gain. The product of the plant and controller gains equals the loop gain.

Existing invasive measures for LG include proportional assist ventilation (PAV) (Meza and Younes, 1996), pressure support ventilation (for controller gain) (Dempsey et al., 2004), and pseudo-random binary CO₂ stimulation (Ghazanshahi and Khoo, 1997). All of these techniques are labor intensive and could only be performed by an experienced investigator in a research laboratory. In contrast, the technique proposed in this paper could be used by anyone with access to ventilation and CO₂ time series collected during spontaneous breathing, albeit with continuous positive airway pressure (CPAP) to stabilize the upper airway.

Previous autoregressive models for estimating LG have been proposed (Asyali et al., 2002; Ghazanshahi and Khoo, 1997; Khoo et al., 1995; Modarreszadeh et al., 1995; Nemati et al., 2011). However, they are confounded by artifacts in the signal and only provide a single value of LG for the entire block of data analyzed. Therefore, the presence of changing physiological states that occur naturally during sleep (e.g. sleep-wake transitions, arousals from sleep, changes in controller sensitivities with changes in sleep-state) cannot be evaluated. The first iteration of the multivariate autoregressive model proposed in this paper was validated in an anesthetized, upper-airway bypassed animal preparation (Nemati et al., 2011). The primary goal of this study was to expand on our previous model to provide a continuous method for the measurement of LG and its components (controller and plant gain) during sleep in humans as well as to make the method more resistant to artifact noise. In the current study, we aimed to validate this technique in human subjects by testing its ability to detect a directional change in LG produced by PAV.

2. Methods

2.1. Subjects

Thirteen CPAP treated OSA subjects (age: 45 ± 10 yrs) were recruited from the sleep laboratory at Brigham and Women’s Hospital. All OSA subjects had an apnea/hypopnea index >10 events/h during supine non-rapid eye movement (NREM) sleep and a documented CPAP use of >5 h per night for at least two months prior to the study. Eight healthy controls (age: 35 ± 10 yrs) were also recruited from the community. Subjects were excluded if they were taking any medication known to influence breathing, sleep/arousal or muscle physiology. Additionally, subjects were excluded if they had a history of renal failure, neuromuscular disease or other major neurological disorders, uncontrolled diabetes, heart failure, central sleep apnea/Cheyne–Stokes respiration, uncontrolled hypertension, thyroid disease, or any other unstable medical condition. Female subjects were screened to ensure that they were not pregnant. All subjects gave written, informed consent before participation in this study, which was approved by the Partners Healthcare Human Research Committee.

2.2. Experimental setup and protocol

Subjects underwent a clinical polysomnogram (PSG) to confirm the presence or absence of OSA and a research PSG to validate the proposed LG estimation algorithm.

2.2.1. Clinical PSG

Subjects were asked to sleep supine for the majority of the night with the standard clinical montage of electroencephalography (EEG; C3/A2, O2/A1), electrooculography, and submental and anterior tibialis electromyography. Oxygen saturation was monitored by using a pulse oximeter attached to the index finger. Airflow was measured using nasal pressure and a thermistor. Piezo-electric bands around chest and abdomen monitored respiratory movements. Data were collected and stored using the Alice digital PSG system (Philips Respironics, Murrysville, PA). Sleep state, arousals, and respiratory events were scored according to standard AASM Criteria (Iber, 2007).

2.2.2. Research PSG

Sleep electrodes were attached similar to the clinical PSG. In addition, subjects were also fitted with a nasal mask (Gel Mask; Respironics, Murrysville, PA) attached to a pneumotachometer (model 3700A; Hans-Rudolph, Kansas City, MO) and pressure transducer for measuring airflow (Validyne, Northridge, CA). CO₂ was continuously recorded from a catheter placed inside the nostril with (Vacumed capnograph, Ventura, CA). The mask was connected to a BiPAP Vision mechanical ventilator (Philips Respironics) which is capable of delivering CPAP alone or in combination with PAV. After the monitoring equipment was placed on the subjects, they lay down in the supine position and breathed on their prescribed level of CPAP (for OSA subjects) or 4 cmH₂O for controls. Once asleep, PAV was slowly increased as high as possible until the patient awoke. Several PAV increases were performed during the night. We estimated LG from 5 to 10 min segments of spontaneous breathing during NREM sleep while subjects breathed on CPAP alone or on CPAP + PAV. A paired t-test was used to compare the LG on CPAP alone to the LG on CPAP + PAV. LG is known to be elevated on PAV (Meza and Younes, 1996) and thus if our algorithm detected a significantly higher LG on PAV, this would be interpreted as confirmation that our technique is capable of detecting a directional change in LG, thereby lending validity to the technique.

2.3. Preprocessing and signal quality index

Working with physiological measurements usually involves dealing with common problems such as movement artifact or measurement error. For example, PET_CO2 can sometimes be inaccurate due to low expiratory volume or mask leak, which would confound the estimation of LG. We proposed a framework for including measures of the quality of the experimentally recorded signals, thus mitigating the influence of such artifacts on the estimation of LG. Signals for flow and PCO₂ were processed according to the steps described previously (Nemati et al., 2011) to extract the breath-by-breath time series data for minute ventilation (V˙_E) and end-tidal PCO₂ (PET_CO2). Briefly, V˙_E was calculated for each breath as V_T/T_tot, where V_T is the tidal volume and T_tot is the duration of the breath (see Fig. 2). A breath-by-breath signal quality index for PET_CO2 (SQI_CO2) was created by fitting a line to the expiratory (end-tidal) portion of the PCO₂ waveform, as shown in Fig. 3 (also see Fig. 2 panel E). A flat line (i.e., slope = 0) indicates that the measured end-tidal CO₂ is of high quality, while non-zero slopes correspond to end-tidal CO₂ estimates with low signal quality. Moreover, since it is physiologically unlikely to see more than 5 mmHg change in end-tidal CO₂ in consecutive breaths, such observations with greater than 5 mmHg change were assigned a lower signal quality (see Appendix B for details). The resulting breath-to-breath V˙_E and PET_CO2time-series, representing deviations from a steady-state baseline during spontaneous breathing, and the corresponding SQI_CO2, were used for estimating LG as described below.

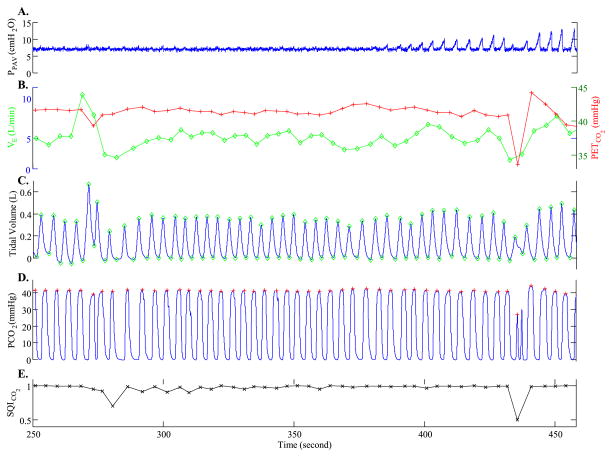
Fig. 2.

Example of recorded waveforms and derived time series. (A) Pressure setting of PAV. This subject was breathing on 7 cmH₂O CPAP until PAV was initiated (time = 380 s) and slowly ramped up, as evident by the increasingly larger inspiratory pressures delivered. (B) Derived minute ventilation (V˙_E ; open circles) and end-tidal PCO₂ (PET_CO2 ; + symbols) time-series. (C) Tidal volume waveform with marked peaks and troughs. (D) PCO₂ waveform with marked PET_CO2 values. (E) A derived breath-by-breath index of PET_CO2 signal quality (SQI_CO2). Note that, due to a shallow breath at ~430 s, PET_CO2 drops suddenly to below 35 mmHg. However, since the end-expiratory portion of the waveform is not flat, the corresponding PET_CO2 is a poor estimate of the alveolar PCO₂ level. The associated SQI_CO2 for this breath is 0.5, indicating that this breath should be trusted less when fitting the data to estimate LG.

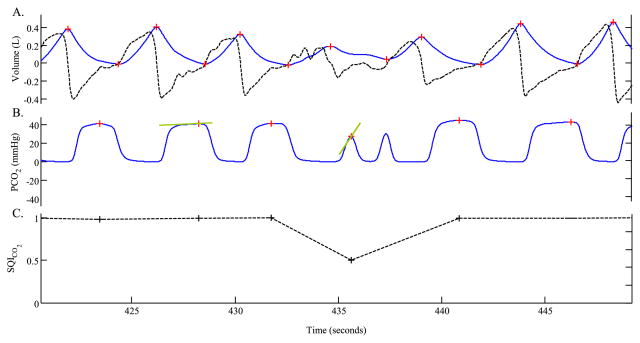
Fig. 3.

Signal quality index for CO₂. Panel A shows a flow signal (dark, dotted line) and the corresponding tidal-volume signal (blue, solid line). Note that, the PET_CO2 corresponding to breath #4 is about 28 mmHg. Such a sudden drop in PaCO₂ is unlikely to be physiological. Breath #4, therefore, is assigned a low signal quality index, as shown in panel C.

2.4. Calculations of controller, plant, and loop gain

Along with signal quality index, we also developed an adaptive LG estimation technique that accounts for nonstationarity in chemoreflex system characteristics (e.g., as a result of changes in sleep stages, body position, etc.). A non-stationary time series is one in which the statistics of the underlying random process (e.g., mean, variance) change over time. This notion is relevant to the current study in which PAV, and therefore LG, was slowly increased over time, which induced non-stationarity into the ventilatory control system. These PAV data therefore, represent an ideal dataset in which to test the ability of our algirithm to deal with non-stationarities.

Our autoregressive model includes two main variables, V˙_E and PET_CO2, as a linear function of their previous values and random fluctuations. The model with maximal memory (lag) of p breaths that reflects the interaction between V˙_E and PET_CO2 can be represented as follows

$$y(n)=\sum _{k=1}^p{a}_n(k)y(n-k)+w(n)$$ (1)

where

$$y(n)=\left(\begin{array}{c}{\stackrel{.}{V}}_E(n)\\ P_{{\text{CO}}_2}(n)\end{array}\right),a_n(k)=\left(\begin{array}{cc}{a}_{n_{{\stackrel{.}{V}}_E{\stackrel{.}{V}}_E}}(k)& a_{n_{{\stackrel{.}{V}}_E,{\mathit{PCO}}_2}}(k)\\ a_{n_{P{\text{CO}}_2,{\stackrel{.}{V}}_E}}(k)& a_{n_{PC{O}_2,PC{O}_2}}(k)\end{array}\right),w(n)=\left(\begin{array}{c}{w}_{{\stackrel{.}{V}}_E}(n)\\ w_{PC{O}_2}(n)\end{array}\right)$$

The vector y(n) includes V˙_E and PET_CO2 at breath n; y(n − k) lists the values of these two variables at the kth previous breath; w(n) represents the variations in V˙_E and PET_CO2 that are not explained by the chemical control system properties, and are therefore considered to be the result of external noise; and the matrices a_n(k) for k = 1, …, p represent the model coefficients that can vary over time and relate y(n − k) to y(n); As an example, when p = 1, Eq. (1) reduces to the following system of equations:

$$\begin{array}{l}{\stackrel{.}{V}}_E(n+1)=a_{n_{{\stackrel{.}{V}}_E,{\stackrel{.}{V}}_E}}(1){\stackrel{.}{V}}_E(n)+a_{n_{{\stackrel{.}{V}}_E,{\text{PCO}}_2}}(1)P_{{\text{CO}}_2}(n)+w_{{\stackrel{.}{V}}_E}(n+1)\\ P_{{\text{CO}}_2}(n+1)=a_{n_{{\text{PCO}}_2,{\stackrel{.}{V}}_E}}(1){\stackrel{.}{V}}_E(n)+a_{n_{{\text{PCO}}_2,{\text{PCO}}_2}}(1)P_{{\text{CO}}_2}(n)+w_{{\text{PCO}}_2}(n+1).\end{array}$$ (2)

It was shown in our previous work (Nemati et al., 2011) that the parameters characterizing the autoregressive model of breathing (the autoregressive coefficients) can be used to derive controller gain, plant gain, and loop gain at different frequencies (or cycle-durations) of interest. For example, identification of the controller gain was accomplished by considering the effects of PCO₂ fluctuations on ventilation over time and adjusting the relevant coefficients to achieve the most accurate prediction of ventilation. Here, similar to the model order in our previous work, V˙_E depends on the past four values of V˙_E and PET_CO2, and PET_CO2 depends only on the previous value of PET_CO2 and V˙_E. The details of our autoregressive model are given in Appendix A. When dealing with frequency-dependent quantities (controller, plant, and loop gains) we considered the average value of these quantities in the medium frequency range of 5–15 breaths/cycle. Since the medium frequency band spans the range of cycle-durations of periodic breathing commonly observed experimentally in human subjects (Ghazanshahi and Khoo, 1997; Nemati et al., 2011), we focused on the controller, plant, and loop gain values measured in this band.

A Kalman smoother algorithm was used for the estimation of LG. The Kalman smoother algorithm (Tarvainen et al., 2006) consists of a Kalman filter and a fixed-interval smoother that uses both the preceding and succeeding recorded values in the time series to obtain a more accurate and refined parameter estimation (see Appendix A). The model fitting procedure involved tweaking the model parameters to achieve the lowest discrepancy between the model prediction and the actual observed values of ventilation and blood gasses (i.e., a penalty term was imposed proportional to the magnitude of the discrepancy, and the parameter fitting objective was to minimize the penalty term). In order to minimize the deleterious effects of artifacts, we used our breath-by-breath indices of signal quality for PCO₂ to lower the contribution of poor signal quality breaths to the penalty function (Nemati et al., 2010). Fig. 4 shows an example PAV trial (panel A), breath-by-breath signal CO₂ signal quality time series (panel B), and the corresponding adaptive estimates of controller, plant and loop gain, before (panel C) and after (panel D) including signal quality indices.

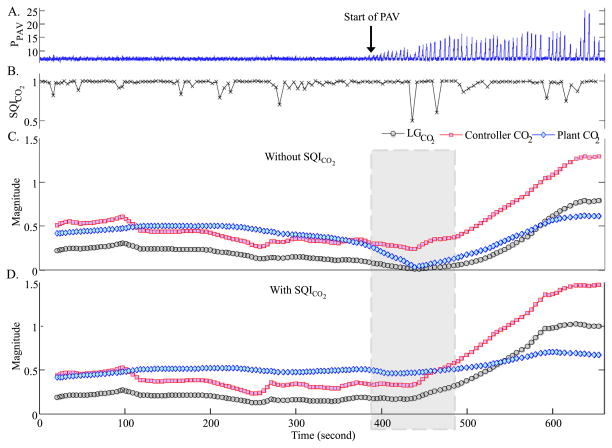
Fig. 4.

Adaptive estimation of controller, plant, and loop gain with and without the SQI_CO2. Starting around 400 s, PAV was progressively increased (panel A). Our derived breath-by-breath index of PET_CO2 quality (SQI_CO2) is shown in panel B. Adaptive estimation of the controller, plant, and loop gain of the system before and after including the SQI_CO2 are presented in panels C and D, respectively (the confidence bounds associated with individual estimates are omitted for clarity). Inclusion of the SQI_CO2 in panel D resulted in a better estimate of the plant gain and the loop gain around the 430 s mark (note that the controller gain drops to zero in panel C due to artifactual measurements of end-tidal CO₂ around the 430 s time mark). Note how the adaptive algorithm detected a progressively larger value of the controller gain, which resulted in progressive increase in system loop gain. This example lends strong credibility to the value of incorporating a signal quality index into the parameter estimation algorithm.

2.5. Statistical analysis

Paired t-tests were used to compare the LG on and off PAV. As a secondary analysis, unpaired t-tests were used to compare LG between healthy controls and OSA subjects, as previous studies have shown that OSA patients tend to have a higher LG. A p value of less than 0.05 was considered significant. Values are presented as means ± standard deviation.

3. Results

3.1. Respiratory variables and experimentally derived system properties

The average respiratory variables for the baseline (CPAP only) and the PAV (CPAP + PAV) conditions are shown in Table 1. As expected, PAV induced a small increase in V_T and T_TOT, with the net effect of a slight increase in V˙_E and decrease in PET_CO2. Table 1 shows a breakdown of the respiratory variables according to the patient population (control versus OSA). OSA subjects exhibited a small but significantly higher V˙_E both during baseline and on PAV.

Table 1.

Break-down of respiratory variables to control and OSA subgroups.

Subject	Baseline			PAV
	Control (N = 8)	OSA (N = 13)	Overall (N = 21)	Control (N = 8)	OSA (N = 13)	Overall (N = 21)
VT (L)	0.39 ± 0.07	0.43 ± 0.09	0.42 ± 0.08	0.42 ± 0.08	0.47 ± 0.09	0.45 ± 0.09†
TI (s)	1.77 ± 0.20	1.77 ± 0.31	1.77 ± 0.27	1.82 ± 0.28	1.73 ± 0.31	1.76 ± 0.29
TTOT (s)	4.30 ± 0.53	4.20 ± 0.72	4.24 ± 0.64	4.37 ± 0.65	4.30 ± 0.71	4.33 ± 0.67†
V˙E (L min−1)	5.43 ± 0.59	6.27 ± 1.03*	5.96 ± 0.96	5.77 ± 0.74	6.71 ± 1.22*	6.35 ± 1.14†
PETCO2 (mmHg)	40 ± 4	41 ± 3	40 ± 3	39 ± 4	39 ± 3	39 ± 3†

^*p < 0.05 between OSA and controls.

^†p < 0.05 between baseline and PAV.

3.2. Effect of PAV on controller, plant, and loop gain

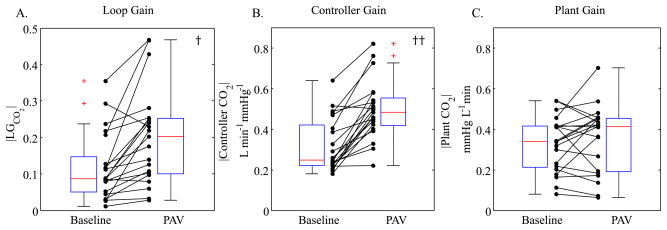
Fig. 5 provides a comparison of LG (panel A), controller gain (panel B) and plant gain (panel C), for the individual subjects between baseline and PAV. The autoregressive technique was able to detect the PAV-induced increase in LG (p < 0.05). Moreover, it detected that the increase was predominantly driven by an increase in controller gain (p < 0.005) which is what one would expect when breathing on PAV.

Fig. 5.

Group comparison of Baseline (CPAP only) and PAV (CPAP + PAV) loop gains (panel A), controller gains (panel B), and plant gains (panel C). LG increased from 0.14 ± 0.10 to 0.21 ± 0.13, predominantly due to a significant increase in controller gain from 0.36 ± 0.14 to 0.54 ± 0.14 L min⁻¹ mmHg⁻¹. Plant gain did not change significantly (from 0.35 ± 0.13 to 0.33 ± 0.14 mmHg L⁻¹ min). The † and †† indicate a statistically significant difference (p < 0.05 and p < 0.005, respectively).

3.3. Baseline controller, plant, and loop gain in OSA versus controls

Compared to controls, OSA subjects had an elevated controller gain (control 0.24 ± 0.04 versus OSA 0.36 ± 0.15; p < 0.05) and a higher LG (control 0.07 ± 0.04 versus OSA 0.14 ± 0.10; p < 0.05). No significant differences between plant gains were observed (control 0.28 ± 0.12 versus OSA 0.35 ± 0.13) (Fig. 6).

Fig. 6.

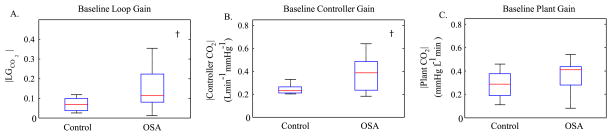
Comparison of baseline loop gain, controller gain and plant gain between healthy controls and OSA subjects. (A) OSA subjects had higher loop gain (control 0.07 ± 0.04 versus OSA 0.14 ± 0.10). (B) OSA subjects had an elevated controller gain (control 0.24 ± 0.04 versus OSA 0.36 ± 0.15). (C) No significant differences between plant gains were observed (control 0.28 ± 0.12 versus OSA 0.35 ± 0.13). † indicates a statistically significant difference (p < 0.05).

4. Discussion

The major contribution of the current study is the introduction of a parameter estimation technique capable of adapting to the changes in LG. The estimation technique successfully tracked changes in LG induced by PAV which is an established technique for raising LG. Furthermore, the proposed framework is also non-invasive (i.e., based on spontaneous breathing) and, through the use of signal quality indices, mitigates the deleterious effects of recording artifacts on the parameter estimation procedure. This is the first time that a technique has been shown to successfully estimate LG from spontaneous, unobstructed breathing in humans.

There have been several previous attempts to estimate LG from spontaneous breathing. For example, breath-to-breath variability in ventilation has been studied extensively (Bruce, 1996; Khoo, 2000), with the periodic component of variability generally attributed to the chemoreflex feedback mechanism, and the non-periodic component ascribed to neural, vagal, behavioral, and other factors external to the chemoreflex feedback loop. Furthermore, several authors have employed system identification techniques based on autoregressive models that make use of the breath-to-breath dependence of ventilation on arterial blood gas tensions (via chemoreceptors) as well as dependence of O₂/CO₂ on ventilation (due to gas exchange) (Khoo and Marmarelis, 1989; Mitsis et al., 2009; Nemati et al., 2011). Lastly, many researchers have used autoregressive modeling in the presence of exogenous stimulations (e.g., pseudorandom binary sequences of inhaled CO₂) in an attempt to estimate LG during sleep (Ghazanshahi and Khoo, 1997; Modarreszadeh and Bruce, 1994; Modarreszadeh et al., 1995). However, none of these techniques has emerged as a useful and reliable tool for noninvasively estimating LG, possibly because recordings of respiratory variables are noisy and non-stationary. Therefore, estimation algorithms must be appropriately tailored to deal with these issues. The proposed technique overcomes these obstacles and makes it possible to track LG over time and in the presence of state changes or measurement artifacts.

4.1. OSA and ventilatory stability

Further validation of our LG estimation algorithm comes from the fact that our findings agree with previous LG studies in OSA patients. Our technique determined that OSA subjects have elevated controller gain compared to healthy controls with no difference in plant gain and overall, the LG was found to be higher in OSA subjects. These findings are consistent with studies by Younes et al. (2001) and Wellman et al. (2004) which underscores the potential value of this technique in managing OSA patients with drugs to lower LG.

In a study previously published by our group (Jordan et al., 2005), the LG values for OSA subjects were found to be slightly higher than the LG values estimated from our autoregressive method. The difference may in part be the result of slightly different LG definitions used in the two studies; the LG determined with PAV is the LG at the 180° phase angle, whereas with the current technique it is the average LG within a frequency band. While the 180° phase angle likely lies somewhere within this frequency band, it could nevertheless produce a slightly different LG value than the autoregressive technique presented here. Furthermore, in the paper by Jordan et al. (2005), PAV failed to produce periodic breathing in several individuals and LG had to be quantified as a “less than” value, which generally tends to be higher than the “equal to” values. Therefore, the LG values presented in their work are slightly higher than the ones presented here.

4.2. Methodological considerations

The credibility of LG measurement on the basis of PAV, and the effects of CPAP/PAV on the ventilatory control variables have been reviewed extensively before (Younes et al., 2001). This makes the PAV data used in this study ideal for validating our proposed method, both because there is no other gold standard with which to validate our method and because PAV produces a time-varying increase in LG, allowing the adaptiveness of our algorithm to be tested.

Although we selected periods of stable NREM sleep without evidence of clinical arousals, we cannot discount the influence of more subtle EEG changes. Future works should either model the influence of arousals on ventilation or include signal quality indices that minimize the contribution of large arousal-related ventilation on the estimation procedure.

Our technique would need to be modified if there were frequent large breaths or long pauses. Our patients did not have these variations in their breathing pattern. The technique could be modified to deal with pauses (e.g. central apneas) by inserting breaths with zero tidal volume. We believe that variations in the breathing rate (e.g. small fluctuations in expiratory time) will not affect our method and in fact is one way that the ventilation could physiologically decrease/increase (by varying respiratory rate). Therefore, if the inspiratory volume is scaled up or down when it is divided by the breath duration, this is the true ventilation that we want the model to capture.

5. Conclusions

Our results demonstrate that the proposed autoregressive model is able to track small changes in LG during sleep without using invasive methods. It could therefore be used clinically for the identification of patients with ventilatory control abnormalities. In particular, selection of patients for interventions that lower LG (e.g., supplemental oxygen or acetazolamide) may provide patients with attractive treatment alternatives.

Appendix A

A.1. System non-stationarity and adaptive estimation

To accommodate non-stationarity, we allow the autoregressive coefficients to vary gradually over time, yielding estimates of controller, plant, and loop gain that change smoothly over time. The adaptive analog of our autoregressive model is given by the following matrix equation:

$$y(n)=\sum _{k=1}^p{a}_n(k)y(n-k)+w(n),$$ (A1)

where the subscript n in term a_n(k) signifies that the model coefficients can vary over time. One may cast the problem of estimating the set of parameters ${\{a_n(k),k=1,\cdots ,p\}}_{n=1}^N$, where N is the length of time series (or the total number of available breaths), into a general Kalman filter state-space framework by defining the following system of equations:

$$A_{n+1}=A_n+d_n$$ (A2)

$$y_n=H_n{A}_n+w_n,$$ (A3)

where A_n is a vector of autoregressive coefficients (of dimension m × m × p) at the n-th breath, y_n is a vector of respiratory variables as defined in Eq. (A1), H_n is a matrix of previous values of y (y_n−1, …, y_n−p) structured such that the multiplication of H_n by A_n is equivalent to the summation term in Eq. (A1), and the noise terms d_n and w_n are zero-mean, uncorrelated random variables with covariance matrices Q_n and R_n. Eq. (A1) imposes a smoothness constraint on the A_n coefficients, where the degree of deviation depends directly on the size of Q_n. The solution to the problem of finding the sequence of (latent state) variables A₁, ···, A_n given all the observations up to and including time n is given by the Kalman filter (Arnold et al., 1998). In this work, we use the Kalman Smoother algorithm as described in reference (Tarvainen et al., 2006). The Kalman Smoother provides a solution to the problem of inferring the entire sequence of state variables A₁, ···, A_N given all the N observations y₁, …, y_N. This is achieved by performing a forward Kalman filter, followed by a backward smoothing step based on the RTS algorithm (Rauch et al., 1965).

A.2. Calculation of loop, controller, and plant gains from transfer path functions

Eq. (A1) is a discrete convolution and it becomes multiplicative in the frequency domain. Define the Fourier transform of a signal in the time domain by $Q(f)={\sum }_{k}q(k)exp(-2\pi \sqrt{-1}fk)$ where k indexes the time domain and f indexes the frequency domain. The Fourier transform of Eq. (A1) is therefore

$$Y(f)=A(f)Y(f)+W(f)$$ (A4)

Here we present the time domain variables in lower case and frequency domain variables in upper case and the dependence on frequency f will be omitted for notational simplicity. Note that the summation over time defining $A(f)={\sum }_{p=1}^{p}a(k)exp(-2\pi \sqrt{-1}fp)$ only includes the previous P points where P is the maximal lag in the model of Eq. (A1). Eq. (A4) for each individual component of Y can be written as

$$Y_i[\sum _{j\ne i}{T}_{j\to i}{Y}_j]+T_{i\to i}{W}_i$$ (A5)

where T_j→i are the transfer path functions (TPF) from the jth signal to the ith signal and are defined as

$$T_{j\to i}=\{\begin{array}{cc}\frac{A_{ij}}{1-A_{ii}},& i\ne j\\ \frac{1}{1-A_{ii}},& i=j\end{array}$$ (A6)

TPFs represent the effect of one variable on another in the control system and therefore correspond to the controller and plant gains.

A.3. Measurement noise and signal quality index

The Kalman estimator for the model coefficients is given by the following equation:

$${\stackrel{⌢}{A}}_n={\stackrel{⌢}{A}}_{n-1}+K_n{r}_n$$ (A7)

where Ȃ_n is a vector of all estimated model coefficients at the n-th breath, r_n = y_n − H_nȂ_n−1 is an error term capturing the discrepancy between our model prediction for the ventilatory variables and the actual observed values, and K_n is a weighting factor, also known as the Kalman gain. Intuitively, Eq. (A7) states that our best estimate of A_n is a weighted combination of our previous estimate Ȃ_n−1 (the first term of the sum) and a second term related to the discrepancy between our model prediction and our actual measurements (that is, the model residual, r_n).

In this work, we made the weighting factor K_n to be directly (although nonlinearly) proportional to the signal quality associated with the n-th measurement. This form of penalty creates a nonlinear function for the noise covariance to ensure that noisy signals are not trusted and has been previously shown to work well in practice (Nemati et al., 2010; Li et al., 2008). Algorithmically, this is achieved by defining a modified covariance matrix, denoted by $R_n^{\prime }$, which is a monotonically decreasing function of the signal quality (the higher the signal quality, the smaller $R_n^{\prime }$):

$$R_n^{\prime }\leftarrow R_{n}exp(1/{\text{SQI}}_n^2-1),$$ (A8)

where SQI_n is the signal quality of the ventilatory variables at the n-th breath, and may be replaced by various measures of the underlying signal quality, such as the SQI_CO2 described in Section B1. This nonlinear weighting function therefore tends to one as the value of SQI_n tends to one, at which point the modified covariance matrix $R_n^{\prime }$ will be equal to R_n. Note that, if separate signal quality measures are available for each measurement then the diagonal elements of the R_n are individually modified.

To illustrate the benefits of this weighting scheme, consider the two cases presented in Fig. A1. Fig. A1A shows a time series that for the first three samples stays at its baseline value, where our “static” (non-adaptive) model prediction yields residuals of zeros. Substituting zeros for r₁, …, r₃ in Eq. (A7) yields the previous model parameters. However, starting at the fourth sample the time series changes its baseline and therefore the model prediction no longer corresponds to the actual values of the time series, resulting in a non-zero residual. Substituting a non-zero value for r₄ in Eq. (A7) results in a new estimate of model parameters, in a manner that depends on the value of the weighting factor K₄. Now, consider the case presented in Fig. A1B, where the variations in the values of the time series are due to measurement errors, as reflected by a reduced signal quality (0.5 versus 1). In this case, although a nonzero residual (say at the second sample) favors a change in model parameters, the reduction in the weighting factor K₂ (due to a reduced signal quality) pushes the balance of Eq. (A7) towards accepting the previous estimates of the model parameters. In particular, the weighting scheme allows us to minimize the influence of artifacts, related to possible mismatch between PET_CO2 and alveolar PCO₂, on parameter estimation through assignment of an appropriate SQI_CO2 as discussed in Section B.

Fig. A1.

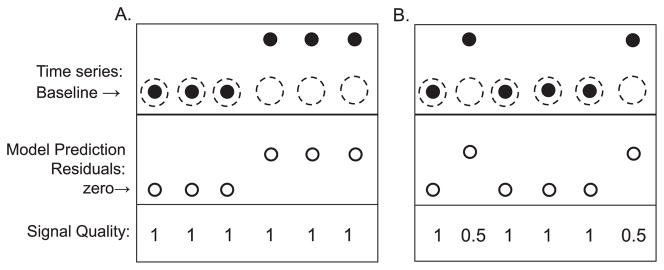
Schematic illustration of the effects of non-stationarity vs. measurement noise. The closed circles are the actual data, and the open circles are the model-predicted data. In panel A, during the first few samples, the system is in a steady state. However, on the fourth sample, the steady state suddenly increases. The sudden change in baseline results in a prediction error, i.e. the model incorrectly predicts the steady state on the last three breaths shown by dashed circles (ordinarily, with a time-invariant model, this would lead to parameter estimates that are halfway between the two steady states). With a time-varying model, the parameter estimates can change as the baseline changes. In order to determine if deviations from the baseline represent noise or a true change in steady state, a signal quality index is used. Panel B shows a stationary time series that is corrupted by random measurement noise (second and sixth samples). In this case, the time varying model does not change its parameters because of the poor quality index associated with samples 2 and 6. In general, it is difficult to distinguish between the two cases A and B. However, inclusion of a signal quality index can mitigate this ambiguity.

For the sake of completeness, the modified Kalman smoother algorithm which additionally incorporates the proposed signal quality indices is summarized in Table A1. We initialized the state vector Ȃ₀, the a priori covariance matrix ${\widehat{P}}_1^{-}$, and the autoregressive noise covariance matrix R₀ by fitting (static) autoregressive models to the first 50 breaths from all the subjects and the resulting parameters were averaged (the same initial values were used for all the subjects). The forgetting factor λ was set equal to 4/60~0.0667, which roughly corresponds to a 60 s time constant (assuming a breath-to-breath interval of 4 s). Note that, our implementation of the adaptive autoregressive algorithm accommodates “structured” autoregressive modeling (i.e., when different orders are used for different variables). The above two-pass algorithm has been coded in MATLAB^™ and is available online at the Physionet website.

Given the smoothed state estimates ( ${A^{\prime }}_n^s$) at each data sample n, we derived estimates of controller, plant, and loop gain using the method we described in our previous work (Nemati et al., 2011). Furthermore, we took the associated uncertainty to be equal to the summation of the diagonal elements of the smoothed state covariance estimate ( ${\widehat{P}}_n^s$).

Table A1.

Summary of the adaptive estimation algorithm.

Initialization

Initialize Ȃ0 and ${\widehat{P}}_1^{-}$, λ, R0

Forward pass

1. For n from 1 to N

2. Construct the data history matrix Hn

3. Compute: one step prediction of observation: ${\stackrel{⌢}{x}}_n=H_n{\stackrel{⌢}{A}}_n^{-}$

4. Compute residuals: rn = xn − x̑n

5. Update the covariance matrix: $R_n=(1-\lambda )R_{n-1}+\lambda r_n{r}_n^T$, and compute $R_n^{\prime }$ according to Eq. (A8)

6. Compute Kalman Gain: $K_n={\stackrel{⌢}{P}}_n^{-}{H}_n^T/\left(H_n{\stackrel{⌢}{P}}_n^{-}{H}_n^T+R_n^{\prime }\right)$

7. Compute state estimate: Ȃn = Ȃn−1 + Knen

8. Compute estimated state covariance: ${\stackrel{⌢}{P}}_n={\stackrel{⌢}{P}}_n^{-}-K_n{H}_n{\stackrel{⌢}{P}}_n^{-}$

9. Update state noise covariance: Wn = λPn

10. Calculate a priori estimated state covariance: ${\stackrel{⌢}{P}}_{n+1}^{-}={\stackrel{⌢}{P}}_n+W_n$

END

Backward pass

For n from N − 1 to 1

Let $S_n=\widehat{P}n/{\stackrel{⌢}{P}}_{n+1}^{-}$

1. Compute smoothed estimated state covariance: $${\widehat{P}}_n^s={\stackrel{⌢}{P}}_n+S_n\left({\widehat{P}}_{n+1}^s-{\widehat{P}}_{n+1}^{-}\right)S_n^T$$

2. Compute smoothed state estimate: ${\stackrel{⌢}{A}}_n^s={\stackrel{⌢}{A}}_{n-}{S}_n\left({\stackrel{⌢}{A}}_{n+1}^s-{\stackrel{⌢}{A}}_n\right)$

END

Note, the initial smoothed estimate at step N for the backward pass is the final state estimate for the forward pass: ${\stackrel{⌢}{A}}_N^s={\stackrel{⌢}{A}}_N$

Similarly, ${\widehat{P}}_{n+1}^s={\stackrel{⌢}{P}}_N$

Appendix B

B.1. Signal quality for CO₂

Because PCO₂ can sometimes be inaccurate due to low expiratory volume and mask leak, a breath-by-breath signal quality index (SQI_CO2) was defined as follows (see Fig. 3). First, we fit a line through the end-tidal portion of the PCO₂ waveform for each breath, and the slope of the line was recorded (S). A flat line (i.e., S = 0) indicates that the measured end-tidal CO₂ is of high quality, while non-zero slopes correspond to end-tidal CO₂ estimates with low signal quality. Next, since it is physiologically not possible to see more than 5 mmHg change in PCO₂ from one breath to the next, if the corresponding PCO₂ was different by more than 5 mmHg from the preceding PCO₂, a penalty of 0.2 points was imposed. Similarly, if the corresponding PCO₂ was different by more than 10 mmHg from the preceding PCO₂, a larger penalty of 0.4 points was imposed. The final value of the SQI_CO2 was set equal to max (0.5, 1-S-penalty). For example, a slope of S = 0.15, and a 6 mmHg change in PCO₂ (penalty = 0.2), results in an SQI_CO2 of 1–0.15–0.2 = 0.65.