Causal diagrams for empirical legal research: a methodology for identifying causation, avoiding bias and interpreting results

Abstract

In this paper we introduce methodology—causal directed acyclic graphs—that empirical researchers can use to identify causation, avoid bias, and interpret empirical results. This methodology has become popular in a number of disciplines, including statistics, biostatistics, epidemiology and computer science, but has yet to appear in the empirical legal literature. Accordingly we outline the rules and principles underlying this new methodology and then show how it can assist empirical researchers through both hypothetical and real-world examples found in the extant literature. While causal directed acyclic graphs are certainly not a panacea for all empirical problems, we show they have potential to make the most basic and fundamental tasks, such as selecting covariate controls, relatively easy and straightforward.

1. Introduction

Scholars spend significant time and energy seeking to identify cause and effect relationships that exist in their data. Even a brief review of the extant legal literature suggests that state-of-the-art statistical analysis is now routine; every stage of empirical research— from data collection to model choice to presentation of findings—is more advanced and sophisticated than was typical in the empirical literature just a decade ago.

Surprisingly, one aspect of causality that researchers have spent very little time exploring is the precise nature of the underlying relationships between and among the variables of interest. Understanding this basic structural framework is essential for a number of empirical tasks, such as specifying sound statistical models, avoiding bias and confounding, and accurately interpreting results. In fact, pursuing an empirical project without a map of the cause and effect relations is a bit like undertaking a construction project without a detailed blueprint: success is possible, but the likelihood of confusion and error increases quite a bit absent a good plan.

In this paper we describe the use of causal directed acyclic graphs as a formal methodology for reasoning about cause and effect relationships and about qualitative assumptions in empirical research. Pearl (1995) introduced these diagrams into the causal inference literature and showed how they could be useful in reasoning about causal structures and in determining what variables an investigator needs to control for in answering specific causal queries. These diagrams are similar to (and sometimes even used synonymously with (Edwards 1991)) Bayes' nets or influence diagrams, but causal directed acyclic graphs specifically allow for causal or counterfactual interpretation, as we clarify below. We will demonstrate how the use of such graphs can assist researchers in interpreting their empirical analyses. As we discuss, this causal directed acyclic graph methodology generalizes and formalizes, within a causal context, ideas from the structural equation modeling and path analysis literature that have been popular in the legal and social sciences.¹ The causal directed acyclic graph methodology, while building on existing ideas also offer innovations and advantages for empirical scholars seeking to make causal claims and for this reason has become popular in statistics, biostatistics, epidemiology and computer science—we argue here that it could be of use in empirical legal research as well.²

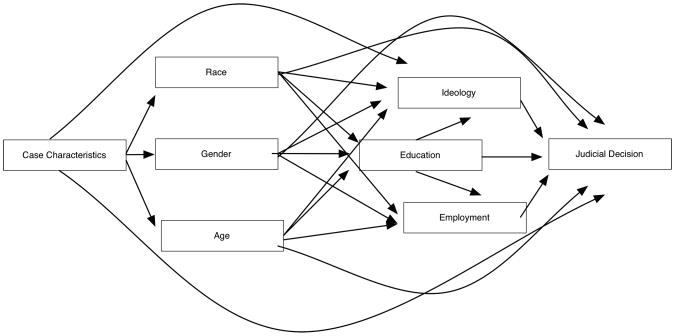
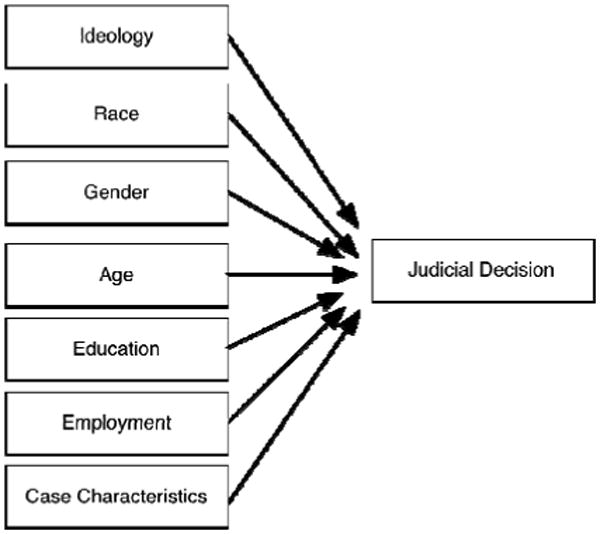
To give just one example of how causal diagrams can aid empirical researchers, consider a study of judicial behavior by Adam Cox and Thomas Miles (2008) investigating the effects of individual judges' characteristics on federal judicial decision making in the voting rights context. For their project, the authors collected data on these background characteristics (ideology, gender, race, age, education, employment experience prior to the bench), along with case characteristics, and the final judicial decision in the legal controversy. They were particularly interested in the effects of ideology and race³ on judicial decisions but they also comment on the effects of various other demographic characteristics of the judges. The causal relationships of these variables might be as depicted in figure 1 below, suggesting that each of the variables has a direct and unmediated effect on the unit of analysis, the judicial decision, but are not related to each other except as “parents” of the decisions themselves. As will be seen below, this structure would warrant the analytic approach taken by Cox and Miles in the presentation and interpretation of their findings.

Figure 1. A Simple Underlying Causal Structure.

Alternatively, the variables in Cox and Miles' study could be related as depicted in figure 2, implying a far more complex (and perhaps more realistic) set of relationships. The unit of analysis is the case and the case characteristics now affect both judicial decisions and the likelihood that litigation will take place in courts with judges of a particular race, gender, age or ideology—plaintiffs are likely to file claims with judges deemed friendly to their legal claims. The various variables are essentially viewed as characteristics of the case itself. However, because of the cause relationships between the judge's race, gender, and ideology and education and employment these variables will have causal relationships amongst one another as indicated in the diagram. Gender, race and age have direct effects on the variables education, ideology, employment, and judicial decisions, as well as indirect effects on ideology, employment, and judicial decision as mediated through education. Education has a direct effect on ideology, employment, and judicial decisions and an indirect effect on judicial decisions as mediated through ideology and employment. Indeed, only ideology and employment have a direct unmediated effect on judicial decisions in both figures 1 and 2.).

Figure 2. A More Complex Set of Structural Relationships.

In sum, we suggest that both case and individual judge characteristics directly affect the outcome unit of analysis, i.e. the judicial decision. Further, case characteristics directly affect only litigation-relevant judge characteristics along with the final judicial decision. Several of the background judge characteristics do not affect each other because they are temporally unchanging, such as race and gender.

Deciding which diagram better describes the structural relationships between these variables requires that investigators rely on theory and qualitative assumptions, and the distinction is key for purposes of making good modeling decisions and interpreting empirical results correctly. If, on the one hand, figure 1 reflects the true structure of the data, then, as will be made clear below, the total and direct effects on judicial decisions are equal for each of the seven variables, and the choice of statistical controls for assessing these effects is relevant only for purposes of precision (that is to say, the controls are useful for decreasing the standard error of the estimate). If figure 2 is the true model, on the other hand, then the estimates of the total and direct effects of race, gender or age will in general diverge; indeed they could have different signs—the direct effect could be negative while the overall total effect could be positive. Parsing total effects and direct effects of, say race, in the context of figure 2 would require the authors to adjust for education, employment, ideology, gender, age and case characteristics for the direct effect, but only case characteristics for the total effect. Moreover, and perhaps more importantly, the estimated total effect of ideology, education, and employment are likely to be biased if figure 2 is correct and the authors fail to control for gender, race and age. After our exposition of the theory of causal directed acyclic graphs we will return to these and other issues and show how the assumptions made by empirical scholars could have notable affects on results.⁴

We would like to point out an important fact that is often overlooked by researchers before continuing: interpreting coefficients from a regression is never free of assumptions vis-à-vis the structural relationships between and among variables. Whenever a regression coefficient is interpreted causally, assumptions are necessarily being made about how the variables in the regression are related; causal diagrams, as we will show below, are useful because they make explicit what scholars often assume implicitly and sometimes inadvertently. Our goal in this article is to demonstrate how causal diagrams can aid empirical scholars in clarifying their theory about the data and in the subsequent task associated with interpreting empirical results. This will increase the likelihood that investigators will make sound qualitative assumptions, pursue the best modeling strategy for identifying causal effects, and interpret results in a useful and precise manner.⁵

Before outlining the ways in which causal diagrams can advance the goals and aims of empirical legal research, we first describe the formal rules and principles for constructing and reasoning about these diagrams. Section 2 describes the mechanics of constructing causal graphs and shows why the graphs are useful for clarifying qualitative modeling assumptions, a necessary step for addressing problems of confounding and selection bias. Section 3 explains how and why the graphs enable researchers to determine what independence and conditional independence relations hold amongst variables. Section 4 turns directly to the issues of confounding and selection and illustrates how investigators can use causal graphs to examine problems of confounding and selection bias and to estimate the causal effects of an intervention, treatment, or policy change from non-experimental data. Section 5 discusses the way in which directed acyclic graphs can address the issues associated with controlled directed effects. In section 6.1, we demonstrate how to apply the causal directed acyclic graph framework to questions that emerge in the context of legal research with the help of a case study that focuses on the Cox and Miles' (2008) investigation outlined above. In Section 6.2, thanks to Cox and Miles' generous decision to share their dataset, we re-fit the data to new statistical models that account for the bias and confounding that we believe exists in their study. Through this re-estimation process, we demonstrate the ways in which causal diagrams could have improved and made more precise the empirical results reported by Cox and Miles; specifically, we note that the authors systematically report both inflated and deflated coefficients. The authors' claim with respect to ideology is perhaps overstated, but their causal claims with respect to race, age, and employment are quite a bit stronger than they may realize. Section 7 offers concluding remarks and notes the variety of empirical legal studies that could benefit from the methodology that we present here.

Finally, we would like to note that our presentation here is intended to be an introduction to the theory and uses of causal diagrams. We seek to demonstrate how legal scholars are able to use the graphs for the most basic questions that emerge in all empirical studies. There are many other empirical issues that can be addressed through the use of causal graphs that we do not discuss here, such as issues involving mutual causation, interaction, and qualitative information about signs. We encourage scholars to consult the broad, emerging literature in statistics, biostatistics, epidemiology and computer science for more-in-depth discussion of these and other issues.

2. Causal theory and Directed Acyclic Graphs

The first step in creating a causal directed acyclic graph requires the construction of a network or diagram representing the investigator's understanding of the relationships and dependencies between and among variables. The graph consists of a set of nodes (the variables) and a set of directed edges (arrows) that link the nodes. A path is an unbroken, nonintersecting sequence of edges that may go along with or against the arrows. A directed path is a path that follows the edges in the direction of the arrows. Relationships such as A ← B → C and A→ B→ C are both paths but only the latter is directed path as it follows the edges in the direction indicated by the graph's arrow. A node X_i that has a directed edge into node X_j indicates the former is the “parent” (or “direct cause”) of the latter; in this case X_j is said to be a “child” of X_i. A node X_i is an “ancestor” (or “indirect cause”) of X_j if there is a directed path from X_i to X_j; in this case X_j is said to be a “descendent” of X_i. If there is no node on the graph which has a directed path back to itself, then the graph is said to be acyclic. In this essay we consider graphs that are both directed and acyclic and for this reason are called directed acyclic graphs (DAGs) (Pearl 2009; Greenland, Pearl, & Robins 1999).

The directed graphs that are acyclic preserve the notion that causes must precede their effects. Systems exhibiting mutual causation can be handled on a causal directed acyclic graph by representing the same variable at different times by different nodes. Representing systems in which causation amongst variable is mutual and simultaneous is more difficult but some progress can be made even in these settings (White & Chalak, 2009).

A directed acyclic graph is said to be a causal directed acyclic graph if two conditions are met. First, the arrows on the graph must have a causal interpretation in the sense that interventions on a parent node should affect the values of the child node. Second, for a graph to be a causal directed acyclic graph it is necessary that any common cause of two variables on the graph is also on the graph. If there is a variable that is only a cause of one other variable on the graph, it may be included or omitted from the graph; however, if the variable is a cause of two or more other variables on the graph then it must be included. As will be seen below this requirement that any common cause of two variables on the graph must also be on the graph is important for reasoning about confounding and causal relationships.

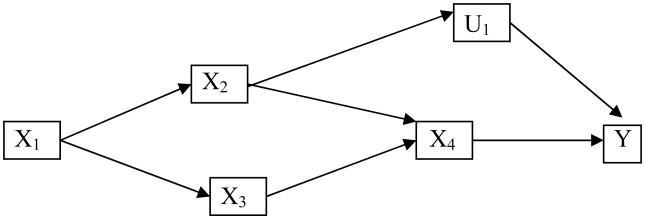
Figure 3 presents a modified example of a causal graph from Judea Pearl's 2009 book, Causality: Models, Reasoning, and Inference (Pearl 2009, 15). The graph indicates the relationship among and between five separate variables. Assume, for purposes of discussion, that it represents the relations among the seasons of the year (X₁), sprinkler systems (X₂), rainfall (X₃), wet pavement (X₄) and accidents (Y). The DAG shows that X₁ is a parent of both X₂ and X₃; that X₂ and X₃ are parents of X₄; and that X₄ is a parent of Y. In the terminology given above, we could also describe X₁, X₂, X₃ and X₄ as ancestors of Y; we could describe X₂, X₃, X₄ and Y as descendents of X₁. All of these concepts will become useful in our discussion below. Moreover, it is easy to see that X₂ ← X₁ → X₃ and X₁→ X₂→ X₄ → Y are both paths but only the latter is a directed path.

Figure 3. A Directed Acyclic Graph with Five Variables (Pearl 2009, 15).

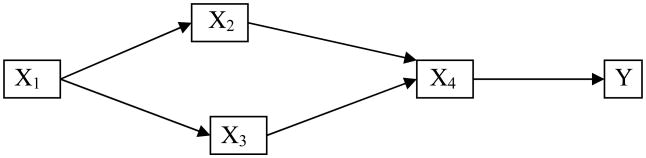
The graph reflects our intuitions, understanding, and beliefs about the world and it is meant to convey underlying assumptions of analysis. The absence of a direct link between X₁ and Y, for example, captures our understanding that the influences of seasonal variation on sidewalk accidents is mediated through various other conditions and are not direct causes of accidents. Springtime, for example, does not directly cause one to slip on the sidewalk; rather springtime leads to more rain and higher levels of sprinkler use, which in turn, leads to wet pavement, which is the direct and proximate cause of observed accidents in this model. The intuitions represented in the graph also coincide with independence conditions. As will be seen below, the graph implies that knowing X₄ renders Y independent of the set {X₁, X₂, X₃}. If further thought and consideration lead us to believe that the variables are related in a different manner, then the graph must be updated to reflect this new understanding. We show how slight modifications in the graph reflect different assumptions in our discussion below.

More extended discussion of causal directed acyclic graphs can be found in the work of Pearl (1995 Pearl (2009) and Greenland, Pearl and Robins (1999). In the appendix we discuss some more technical material on how causal directed acyclic graph are related to structural equation modeling. Importantly, these causal directed acyclic graph generalize structural equation modeling ideas in the legal and social sciences by not imposing assumptions about linearity or normality; causal directed acyclic graphs in fact do not impose any assumptions concerning functional form or distributions (see the online appendix for further details). This considerable increased generality, however, comes at a price. Unlike traditional structural equation modeling techniques, the use of causal directed acyclic graphs generally does not entail estimating path coefficient; because causal DAGs do not make assumptions about functional form it will often not be possible to characterize the relationships between variables as a single path coefficient. Causal DAGs rather are conceptual tools, which allow the researcher to draw conclusions about confounding and to clarify structural assumptions. The conclusions drawn will apply irrespective of the functional form relating the variables. However, to conduct empirical analyses, the use of causal DAGs will be supplemented by regression analyses and thus also with additional assumptions about function form.

3. Causal Diagrams and Independence Relations

It is easy to see that causal DAGs provide an intuitive and straightforward means for expressing qualitative assumptions about the relationships of the variables of interest. The graphs, however, can also highlight hidden complexities about these relationships that researchers ignore in the absence of the DAG. Consider the variable X₄ in figure 3 and note that X₂ and X₃ both have directed edges into X₄. Because X₄ is the effect of two separate causes, we will say that X₄ is a “collider variable” on the path X₂ → X₄ ←X₃. Colliders take on special importance because they reflect the fact that two parents can be marginally independent but can become dependent if we condition on their common effect.

It may seem surprising and perhaps counter-intuitive that conditioning on a node could actually create dependence, rather than block it. Observations on common consequences of two independent variables tend to render those causes dependent, because information about one of the causes tends to make the other more or less likely given the consequences that have occurred (Pearl 2009; Morgan & Winship 2007). Stephen Morgan and Christopher Winship provide a useful example to illustrate the point. Consider a team of researchers who plan to study the applicant pool of a particular university. The admission criteria at the university calls for either a high SAT score or a high level of extra-curricular activities. These two factors are likely to be negatively correlated in the admitted student population, but uncorrelated in the applicant pool, the population of interest. Thus if the researchers decide to adjust for the admission decision in their study, they would uncover a strong correlation between SAT scores and extra-curricular activities when in fact no such correlation exists in the applicant pool generally (Morgan and Winship 2007, 66-67). This pattern is sometimes referred to as selection bias in the legal and social science literature and can be induced by adjustment for collider variables in some contexts—a problem we discuss further below.

Formally, a collider is defined as a node on a particular path such that both the preceding and subsequent nodes on the path have directed edges going into that node. Note that a collider is specific to a path. Thus X₄ is a collider on the path X₂ → X₄ ←X₃ but X₄ is not a collider on the path X₂ → X₄ →Y. A path between two nodes, A and B, is said to be blocked conditional on some set of variables Z if either there is a variable in Z on the path that is not a collider or if there is a collider on the path such that neither the collider itself nor any of its descendants are in Z. If all paths between A and B are blocked given Z then it can be shown that A and B are independent conditional on Z. Thus in figure 3, X₂ and X₃ will be conditionally independent given X₁ since the path X₂ ← X₁ →X₃ is blocked by X₁ which is in the conditioning set and the path X₂ → X₄ ←X₃ is blocked by X₄ which is a collider on the path. Thus all paths between X₂ and X₃ are blocked conditional on X₁ and so X₂ and X₃ are conditionally independent given X₁. However, using these rules of conditional independence we can see that X₂ and X₃ will not be conditionally independent given X₁ and X₄. When we condition on X₄ the path X₂ → X₄ ←X₃ is no longer blocked conditional on X₁ and X₄ because we are now conditioning on the collider X₄. These rules concerning blocked paths allow us to assess any independence relation on the graph. Essentially, statistical association between two variables A and B can arise in one of three ways. First, A might be a cause of B (or B a cause of A) and this creates association between the two variables. Second, A and B might be statistically associated because of some common cause C of both A and B, even if neither A nor B is a cause of the other. Third, A and B might be associated if we condition on a common effect of A and B (or, more generally, if we condition on a common effect of two variables one of which is associated with A and one of which is associated with B).

The next section describes the relationship between causal DAGs and the estimation of causal effects, shows how it is possible to use the graph to identify causal effects, and relates this discussion to methods and criteria for addressing problems of confounding and selection biases.

4. Using DAGs for the Identification of Causal Effects

Suppose we have observational data and that we have constructed a causal diagram representing the relationships and dependencies of the variables of interest as discussed above. We want to estimate the causal effect of a specific intervention, policy program, or medical procedure (set X= x) on an outcome of interest (Y). The question arises as to what adjustments must be made to avoid confounding. Adjustments are essentially equivalent to dividing the population into groups that are homogenous relative to some factor, say Z, and assessing the effect of the intervention on the outcome in each homogenous group and then averaging the results (Pearl 2009, 78). Such a procedure is often carried out in conjunction with modeling by means of regression techniques.

Confounding occurs when an unblocked “back-door” path exists from the treatment or intervention to the outcome, thereby allowing additional factors, other than treatment, to affect the dependent variable of interest. A back-door path from X to Y is a path that begins with an edge going into X. The effect of X on Y is unconfounded when all back-door paths between the treatment and the outcome are blocked by the set of pretreatment variables for which adjustment is made. More formally, let Y_x denote the value of Y which would be obtained, if possibly contrary to fact, there were an intervention to set X to the value x. Variables of the form Y_x are sometimes referred to as counterfactual variables or potential outcomes (Rubin, 1974). We cannot in general draw inferences about counterfactual variables for a particular individual but under certain assumptions we can draw inferences about the probability distributions or expectations over a population of counterfactual variables. We say that the effect of X on Y is unconfounded given Z if P(Y_x | Z = z) = P(Y | Z = z, X =x). The quantity P(Y_x | Z = z) is not in general empirically observable from observational data since we do not in general know what would happen under interventions to set X to x. In contrast the quantity P(Y | Z = z, X =x) is empirically observable. When the effect of X on Y is unconfounded given Z we can estimate counterfactual probabilities P(Y_x | Z = z) using observed probabilities P(Y | Z = z, X =x). The condition referred to as unconfoundedness is sometimes also referred to as “the conditionally ignorable treatment assignment” in the literature on causation (Rubin 1990; Greenland, Pearl and Robins 1999).

These concepts become transparent and easy to understand with the help of a causal DAG and Judea Pearl's back-door criterion, a simple graphical test that researchers can use to determine whether the effect of X on Y is confounded. We first set out a general version of the result and then provide some specific examples of its application. A set of variables, Z, satisfies the back-door criterion relative to the ordered pair X and Y in a DAG if

1. no node in Z is a descendant of X; and

2. Z blocks every path between X and Y that begins with an arrow into X (i.e. all backdoor paths from X to Y).

If the set of variables Z satisfies this criterion, then the causal effect of X on Y is identified and given by the formula

$$P({\mathrm{y}}_{\mathrm{x}}={\sum }_{\mathrm{z}}P(\mathrm{y}|)\mathrm{x},\mathrm{z})P(\mathrm{z})$$

To understand how the back-door criterion operates, reconsider figure 3 and assume we seek to identify the effects of wet pavement (X₄) on the likelihood of accidents (Y). Because all paths to Y must enter through X₄ we easily can see there is no back-door path from X₄ to Y and thus it is possible to identify the causal effects of the treatment without controlling for any variables whatsoever. Thus, we do not need to make any adjustments to the model, and the expected value of the causal effect of the treatment on the outcome of interest is equal to E(Y_x4) = E(Y| X₄ = x₄). The total effect of the wet pavement on accidents, comparing wet pavement to dry pavement, would then be given by E(Y_x4=1) - E(Y_x4=0) = E(Y| X₄ = 1) - E(Y| X₄ = 0).

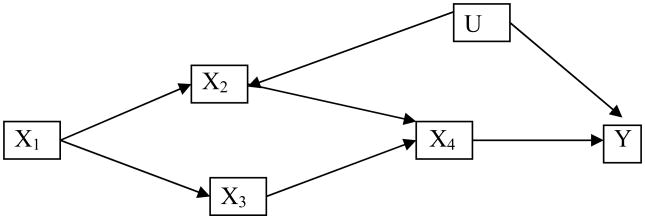
Now assume that the DAG we have constructed for identifying the effects of wet pavement on accidents is presented in figure 4.

Figure 4. Causal Directed Acyclic Graph with Unobserved Variable, U₁.

Note: Controlling for X₂ satisfies the back-door criterion for the effect of X₂ on Y.

Suppose that sprinkler systems often jut out of the ground in a manner that makes accidents happen irrespective of whether the pavement is wet and that U₁ indicates whether the sprinkler system is jutting out of the ground. Suppose we only have data on X₁, X₂, X₃, X₄ and Y but not U₁. Note that if figure 4 is in fact a correct representation of the causal relationships then figure 3 is not a causal DAG because not all of the effect of X₂ on Y is mediated by X₄. In this case, figure 3 could be made into a causal DAG by adding an arrow from X₂ directly to Y; then both figures 3 and 4 would be causal DAGs but figure 4 would simply be a more elaborate causal DAG. In any case, if figure 4 indicates a correct depiction of the causal relationships we have possible confounding bias because we have two back-door paths from X₄ to Y. Namely, we have X₄ ←X₂ → U₁ → Y and X₄ →X₃ → X₁ → X₂ → U₁ → Y. The back-door criterion, however, indicates that it is nonetheless possible to identify the causal effects of X₄ on Y if we adjust for X₂. Using the criteria set out above, X₂ is not a descendant of X₄ and it blocks all back-door paths from X₄ to Y. Thus adjusting for X₂ in our model means that the expected value of the effect of wet pavement on accidents is E(Y_x4) = Σ_x2 E[Y| X₄ = x₄, X₂ = x₂]P(X₂ = x₂) —an equation that is similar to the generalized version presented above. The total effect of the wet pavement on accidents, comparing wet pavement to dry pavement, would then be given by

$$\mathrm{E}({\mathrm{Y}}_{\mathrm{x}4=1})-\mathrm{E}({\mathrm{Y}}_{\mathrm{x}4=0})={\sum }_{\mathrm{x}2}\mathrm{E}[\mathrm{Y}|{\mathrm{X}}_4=1,{\mathrm{X}}_2={\mathrm{x}}_2]P({\mathrm{X}}_2={\mathrm{x}}_2)-{\sum }_{\mathrm{x}2}\mathrm{E}[\mathrm{Y}|{\mathrm{X}}_4=0,{\mathrm{X}}_2={\mathrm{x}}_2]P({\mathrm{X}}_2={\mathrm{x}}_2).$$

What if X₂ it self was unobserved—would the analysis change? If X₂ were unobserved we could not satisfy the back-door criterion using the variables for which we had data and thus the causal effects of wet pavement on the likelihood of accidents would be confounded. This is because we would not be able to find a set of Z variables that included nondescendants of X₄ and that would block all back-door paths from X₄ to Y. Even if we adjusted for X₁ and X₃ we would still have the unblocked path X₄ ←X₂ → U₁ → Y and thus our estimate of the effect of X₄ on Y would be confounded by the uncontrolled for effects of X₂ and U₁.

One of the important and interesting features of the back-door criterion is that it may lead to different modeling approaches than are commonly adopted by empiricists. One familiar approach for addressing possible confounding, for example, is to control for any and all pre-treatment variables. This approach has the perceived advantage of assuring that the investigator will adjust for all possible confounders and in the worse case scenario will not affect the results if no confounding in fact exists. But there are also disadvantages to this approach. Adjusting for numerous and possible unnecessary variables requires far more information and thus may be costly; it may pose problems if the sample size is limited; and if the controls are correlated only with treatment (and not the outcome) the estimates will be less efficient and thus statistical significance could be lost. Moreover, as we will see below, it can sometime even introduce bias! For all these reasons, parsimony should be preferred in modeling—and the back-door criterion facilitates this goal.

To see how the common approach of adjusting for all pre-treatment covariates differs from the approach that relies on the back-door criterion, reconsider figures 3 and 4. Using the former strategy, a researcher would control for X₁, X₂, and X₃ in order to identify the effects of X₄ on Y; the back-door criterion, however, calls for no adjustments in figure 3 and for adjusting only for X₂ in figure 4. This difference is important because more complex DAGs would lead to far more adjustments under the common approach but not necessarily under the back-door criterion.

Not only will the back-door criterion often lead to fewer adjustments, the method enables researchers to avoid confounding when it would be induced by the rule of thumb that calls for controlling for all pre-treatment variables. Consider figure 5, where the variables U₁ and U₂ indicate unobservable and unmeasurable variables. If the researcher controls for X₃, a pretreatment variable, she will unwittingly open a back-door path from X₄ to Y (namely, X₄ ← U₂ → X₃ ← U₁ → Y) that cannot be blocked due to the existence of unobservable variables. This problem emerges because X₃ is a collider variable on this path (i.e. an effect of two different causes). As noted above, when we adjust for a collider variable, we create an association with two otherwise independent variables, which in this context creates confounding. Thus if the researcher constructed a DAG similar in substance to figure 5 with a collider variable present and adopted the common approach of controlling for all pretreatment variables—she would create confounding when it could be avoided if she relied on the backdoor criterion.

Figure 5.

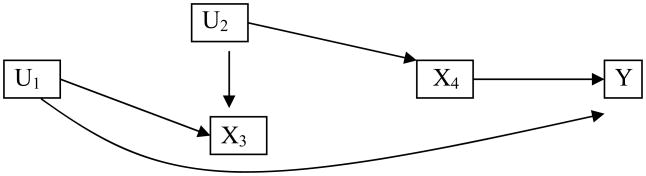
Directed Acyclic Graph with Two Unobserved Covariates.

Note: Adjusting for X₃, a “collider” variable induces correlation between U₁ and U₂ and confounds the results of X₄ on Y.

We are now in a position to set out a more conceptually detailed description of the back-door criterion that will assist researchers in the decision of when to control and when not to control for pretreatment variables. For purposes of this discussion, we label a directed path such as A→B→C as a chain, a non-directed path such as A ←B→ C as a fork, and a collider variable as one that is the effect of two separate causes, such as B in the path A→B←C. Recall we seek a set of variables, Z, that satisfies the back-door criterion relative to the ordered pair X and Y in a DAG. According to Pearl's test, we can say that the back-door criterion is satisfied if Z contains non-descendents of X and if every backdoor path from X to Y contains

1. a chain, A →B → C, where the middle node B is in Z, or

2. a fork, A ←B → C, where the middle node B is in Z, or

3. a collider variable B, A →B ←C, such that the middle node B is not in Z and such that no descendant of the collider is in Z.

With these criteria, investigators are able to conceptualize the problem of confounding in a clear and unambiguous manner. Moreover, as we show in our discussion below, the criterion allows for a systematic procedure that is applicable to diagrams of any shape, size, or complexity. Finally, the back-door criterion enables the analyst to search for the optimal and minimal set of covariates (see Pearl 2009, 80 for further discussion).

5. Controlled directed effects

One further issue concerning the identification of causal effects may be of interest. Consider again the causal DAG in figure 4. Suppose we are interested in the effect of sprinkler systems (X₂) on accidents (Y). Part of this effect may be mediated because the sprinkler systems make the pavement wet; this part of the effect is said to be mediated through X₄. Part of the effect of the sprinkler system on accidents may occur directly because the systems jut out of the ground in a manner that make accidents more likely. We may be interested principally in the direct effect of the sprinkler system on accidents controlling for wet pavement.

More generally, if some variable X is a cause of some outcome Y and if M is a variable on a directed path from X to Y, we may be interested in the direct effect of X on Y controlling for M. We let Y_xm denote the value of Y which would be obtained, if possibly contrary to fact, there were interventions to set X to the value x and M to the value m. The controlled direct effect is then defined as Y_x=1,m - Y_x=0,m. Note that this controlled effect may be different for different values of m. Thus in the context of the sprinkler example we might be interested in the direct effect of the sprinkler systems on accidents intervening to make the pavement wet; this would be denoted by Y_x2=1,x4=1 - Y_x2=0,x4=1 and this quantity captures the “jutting out” effects of sprinkler systems being on when the pavement is wet. Note that here the mediator M that we are controlling for is the variable X₄ indicating whether the pavement is wet. Alternatively, we might be interested in the direct effect of the sprinkler systems on accidents intervening to make the pavement dry; this would be denoted by Y_x2=1,x4=0 - Y_x2=0,x4=0 and would capture the “jutting out” effects of sprinkler systems being on when the pavement is dry.

In general controlling for a post-treatment variable can introduce bias (Rosenbaum, 1984; Pearl, 2001) in the analysis of total effects. However, under certain circumstances the results of such analyses can be interpreted as direct effects (Pearl, 2001). Causal diagrams clarify the assumptions required for such a causal interpretation. We can draw conclusions about the identification of controlled direct effects using a generalization of the backdoor path criterion. Specifically, if there is some set of variables Z which are not descendents of either X or M and if (i) all backdoor paths from X to Y that do not pass through M are blocked by Z and (ii) all backdoor paths from M to Y are blocked by Z and X then inferences can be drawn about the probability distribution of counterfactuals of the form Y_xm. Basically these conditions amount to Z sufficing to block all the backdoor paths from (X,M) jointly to Y. Specifically if the conditions above hold then

$$P({\mathrm{y}}_{\mathrm{x}\mathrm{m}})={\sum }_{\mathrm{z}}P(\mathrm{y}|\mathrm{x},\mathrm{m},\mathrm{z})P(\mathrm{z})$$

More general conditions for identification are also available (Pearl 2001) but the conditions given above will suffice for the purposes of our discussion. In the context of the sprinkler example, we see that if we want the direct effect of sprinkler systems (X₂) on accidents (Y) controlling for wet pavement (X₄) we do not need to adjust for anything. There are no backdoor paths from X₂ to Y that do not pass through M (=X₄) and thus the first condition above is satisfied. Furthermore, X₂ blocks all backdoor paths from X₄ to Y. We could then simply regress Y on X₂ and X₄ and the coefficient for X₂ would represent the direct effect. Estimating the total effects of the sprinker system on accidents would, in contrast, require the investigator to control only for X₁ or X₃ to avoid confounding.

It is important to note that to identify controlled direct effects there are two backdoor path conditions given above that must be satisfied, not just one. In addition to the condition that the backdoor paths from X to Y must be blocked by Z, the backdoor paths from M to Y must be blocked by (X, Z). Both conditions are needed if we want to estimate controlled direct effects. That is to say, we must not just adjust for variables that confound the relationship between intervention X and outcome Y but also for those variables that confound the relationship between the mediator M and the outcome Y. If we do not control for variables that confound the relationship between the mediator M and the outcome Y (i.e. if the second condition is not satisfied) then our estimate of controlled direct effects will be biased (Judd & Kenny 1981; Robins & Greenland 1992; Cole & Hernán 2002). Other more subtle definitions of direct and indirect effects, which allow for the partitioning of a total effect into a direct and indirect effect are also available (Pearl 2001).

6. Improving Empirical Research with DAG Methodology

We now turn from abstract rules and hypothetical examples to Cox and Miles' study, Judging the Voting Rights Act, with which we began our discussion. We use the causal DAG methodology to illustrate the assumptions that authors often unknowingly make in their empirical work and, at the same time, demonstrate just how causal DAGs can aid researchers in basic empirical tasks. In Section 6.1, we note that Cox and Mile's regression analyses depend on the accuracy of figure 1 (presented the introduction); the authors' estimates, however, are confounded if figure 2 is a better depiction of the data. In Section 6.2, we refit the data to the models assuming the accuracy of figure 2 and highlight the qualitative and quantitative changes that emerge between our findings and those presented by Cox and Miles in their study.

6.1 Cox and Miles' Causal Assumptions and the Potential for Confounding

In the introduction, we presented, in figures 1 and 2, DAGs depicting possible cause and effect relationships between and among the variables of interest. If figure 1 is accurate, the authors need not worry about possible confounding. Nor is there any distinction to be made between total and direct effects because these two effects are identical in figure 1 for all variables. One could regress judicial decisions on each of the variables one by one to obtain total effects. Alternatively, if figure 1 is correct then one could also regress judicial decisions on all seven variables simultaneously and use this regression to also obtain the causal effects. The difference between the two is that the latter approach will produce more precise estimates.

If figure 2 is accurate, confounding is a potential problem for purposes of estimating the effects of ideology, education, and employment. This is because open back-door paths exist from these variables to the outcome of interest. For ideology, there are back-door paths to judicial decisions including “ideology←gender→judicial decisions” and “ideology←race→judicial decisions” and “ideology←age→judicial decisions”; similar backdoor paths exist for employment and education. In figure 2 gender, race and age are confounded only by case characteristics. Thus if control is made only for the characteristics of the case, the total effect of gender, race or age could be estimated. Moreover, in figure 2, ideology and employment, are the only variables with causal effects that are not mediated by intervening variables and thus the total and direct effects are identical for these nodes, but not for any other node in the figure.

Cox and Miles present their multivariate regression analysis for the effect of ideology on individual judicial decisions and we reproduce these regression estimates in table 1 below. In each of the regression models reported in this table, Cox and Miles regress judicial decisions on ideology and a number of variables recording characteristics of the case including—in different variations as depicted in columns 1, 2, and 3 of the table. They do not, however, control for race, gender, age or education and yet as noted above, if the structural relationships given in figure 2 are correct this would indicate that all of the estimates of the effect of ideology are confounded. To obtain unconfounded estimates of the effect of ideology under figure 2, one would have to control for race, gender, age and education, as well as the characteristics of the case.

Table 1.

Cox and Miles (2008), Table 5, Columns 1-3 Reporting Probit Findings on the Likelihood of Voting for Section 2 Liability.

Variable	(1) Cox & Miles Table 5, col. 1	(2) Cox & Miles Table 5, col. 2	(3) Cox & Miles Table 5,col. 3
Judge was Democratic Appointee	.145** (.035)	.151** (.039)	.158** (.044)
Judge was Democratic Appointee * Year After 1994	-	-	.004 (.06)
Year Was After 1994	-.123** (.035)	-	-
Case Occurred in South	.016 (.043)	-	-
Appellate Case	-.084 (.038)	-.102* (.042)	-.101** (-.053)
Challenge to At-large Election	.104 (.049)	.078 (.054)	.077 (.055)
Challenge to Reapportionment Plan	.054 (.049)	.034 (.055)	.034 (.055)
Challenge to Local Election Practice	.005 (.043)	-.018 (.05)	-.018 (.05)
Plaintiffs Were African-American	.027 (.046)	.114* (.049)	.114** (.049)
Case Occurred in Jurisdiction Covered by §5	.046 (.044)	.045 (.05)	.044 (.055)

Note:

^*indicates significant P<.10 and

^**indicates significant at P<.05. With the exception of Model (1), all regression include fixed-effects controls for judicial circuits and years.

Cox and Miles do not completely ignore the effects of race, gender, age, education and employment on judicial decisions. Table 2 reproduces the authors' regression estimates in models that account for these characteristics. Consider first the regression model presented in column 1 with ideology, race, gender and the characteristics of the case as covariates. If our figure 2 is a correct representation of the causal relationships amongst the variables, then the estimate for race reported by Cox and Miles cannot be interpreted as the direct effect of race, controlling for ideology, because ideology is confounded by education and age, which are not controlled for, and thus the set of controls does not satisfy the second backdoor path criterion for direct effects as presented in the previous section. Furthermore, the estimate for race cannot be interpreted as the total effect of race because the analysis controls for judge's ideology, which is a descendent of race in figure 2. Similarly, the estimate for gender cannot be interpreted as the direct effect of gender on judicial decisions controlling for ideology because ideology is confounded by education and age, which are not in the model; nor can their estimate for gender be interpreted as a total effect because control is being made for ideology, which is a descendent of gender.

Table 2. Cox and Miles (2008), Table 6, Columns 1-3 Reporting Probit Findings on the Likelihood of Voting for Section 2 Liability.

Variable	(1) Cox & Miles Table 6, col. 1	(2) Cox & Miles Table 6, col. 4	(3) Cox & Miles Table 6, col. 5	(4) Cox & Miles Table 6, col. 6
Judge was Democratic Appointee	.125** (.04)	.140** (.037)	.166** (.039)	.155** (.038)
Judge was African-American	.300** (.09)	-	-	-
Judge was Female	-.020 (.056)	-	-	-
Age	-	.003 (.002)	-	-
Judge Attended Ivy League College	-	-	.018 (.051)	-
Judge Attended Elite Law School	-	-	-.078* (.041)	-
Judge Previously Served as Law Clerk	-	-	.016 (.044)	-
Judge Previously Served in State Leg or Exec Branch	-	-	-	.021 (.039)
Judge Previously Served on State Court	-	-	-	-.056 (.040)
Judge Previously Served in Federal Leg. or Exec. Branch	-	-	-	.002 (.04)

Note:

^*means significant P<.10 and

^**indicates significant at P<.05. The regressions include the same controls as in Model (2) of Table 5: controls for whether the case occurred in a jurisdiction covered by section 5, whether the case was an appeal, whether the plaintiffs were African-American, whether the challenge was to an at-large lection scheme or a reapportionment plan, whether the governing body challenged was local, and fixed-effect controls for judicial circuits and years.

If our figure 2 is correct then to obtain the direct effect of race, controlling for ideology and education, one could regress judicial decisions on race, gender, age, education, ideology and case characteristics; similarly to obtain the direct effect of gender, controlling for ideology and education, one could again simply regress judicial decisions on race, gender, age, education, ideology and case characteristics. Note, however, that these direct effects controlling for ideology and education, would include the effects of race (or gender) mediated by employment. One could alternatively obtain estimates of the direct effects of race (or gender), controlling for ideology, education, and employment, on judicial decisions by regressing judicial decisions on race, gender, age, ideology, education, employment and case characteristics.⁶ These direct effect estimates would then not include effects of race on judicial decisions mediated through prior employment but it would include the effects mediated through other “life experiences” due to race, a possible mechanism suggested by Cox and Miles. To obtain the total effect of race one could regress judicial decisions on race and characteristics of the case; to obtain the total effect of gender one could regress judicial decisions on gender and characteristics of the case. However, if figure 2 is correct, the regression analysis of Cox and Miles reported in Column 1 (in which judicial decision is regressed on race, gender, ideology and the characteristics of the case) cannot be interpreted as any of the aforementioned effects because ideology is confounded by education and age and no control is made for education and age in this model.

We now turn to Cox and Miles' discussion of the effects of age, education and employment. Again assuming that our figure 2 is correct, the age coefficient reported in table 2 column 2 (in which judicial decision is regressed on ideology, age and the characteristics of the case) cannot be interpreted as a direct effect of age on judicial decisions controlling for ideology because ideology is confounded by education, race and gender which are not in the model; nor can their estimate for age be interpreted as a total effect of age because control is being made for ideology which is a descendent of age. To obtain the direct effect of age on judicial decisions controlling for ideology and education one could regress judicial decisions on race, gender, age, education, ideology and case characteristics. To obtain the total effect of age on judicial decisions one could regress judicial decisions on simply age and the characteristics of the case.

Cox and Miles report the results of a regression of judicial decisions on ideology, education and the characteristics of the case (table 2, column 3), and results of a regression of judicial decisions on ideology, employment and the characteristics of the case (table 2, column 4). However, if figure 2 is correct, the estimates from these regressions cannot be interpreted as the total effects—nor as the direct effects—of education and employment on judicial decisions. This is because the effects of education and employment on judicial decisions are confounded by race, gender, and age; there are unblocked backdoor paths from education and employment to judicial decision through race, gender and age. To obtain the total effect of education on judicial decisions, one could regress judicial decisions on education, race, gender, age and the characteristics of the case. Note that race, gender, age and the characteristics of the case block all backdoor paths from education to judicial decisions in figure 2. To obtain the direct effect of education, controlling for ideology and employment, on judicial decisions, one could regress judicial decisions on education, ideology, employment, race, gender, age and the characteristics of the case. In figure 2, the total and direct effects of employment on judicial decisions coincide. To obtain the effect (total or direct) of employment on judicial decisions, one could regress judicial decisions on education, race, gender, age and the characteristics of the case.

In summary, if the regression analyses in tables 1 and 2 are to be interpreted as Cox and Miles suggest, the causal diagram depicted in our figure 1 must be correct, but we believe that figure 2 is a more realistic description of the data. Cox and Miles would have more closely approximated the effects of interest, therefore, had they carried out their regression analyses that we suggested above. In the next section, we explore whether and how Cox and Miles' empirical results would change if they relied upon the directed acyclic graphing methodology.

6.2 Re-analysis of the Cox and Miles Data

While many of the estimates in the Cox and Miles' study are confounded, it is nonetheless possible that these effects remain statistically and substantively significant even when the proper controls are included in the model. Indeed, we find that many (but by no means all) of Cox and Miles' qualitative conclusions survive our re-analysis—but their quantitative conclusions tend to be consistently over- and understated given the problems of bias and confounding in their choice of variables to include in their statistical models.

To enable our re-analysis of the data, Cox and Miles generously agreed to share their data and for this reason we are able to compare precisely how the differing estimation strategies can and will affect the parameters of interest. To begin our investigation, we first fit the data to Cox and Miles' statistical model, assuming with the authors that figure 1 above accurately reflects the underlying relationships between and among the variables. As expected, we were able to replicate their findings with only minor differences;⁷ the results of this replication process are presented in table 3, columns 1, 2, and 3. We then re-fit the data, assuming the variables as depicted in figure 2. Our results are juxtaposed to those found by Cox and Miles' in table 3, columns 1(a), 2(a), and 3(a).

Table 3. Replication of Cox and Miles' Table 5, columns (1)-(3) and Re-Estimation of Results to Account for Bias and Confounding (standard errors in parentheses).

Variable	(1) Replication of Cox & Miles Table 5, col. 1	(1a) VanderWeele & Staudt Model	(2) Replication of Cox & Miles Table 5, col. 2	(2a) VanderWeele & Staudt Model	(3) Replication of Cox & Miles Table 5,col. 3	(3a) VanderWeele & Staudt Model
Judge was Democratic Appointee	.145* (.03)	.121** (.03)	.151** (.039)	.104** (.04)	.149** (.04)	.099* (.05)
Judge was Democratic Appointee * Year After 1994	-	-	-	-	.004 (.08)	.01 (.08)
Year Was After 1994	-.12** (.03)	-.14** (.03)	-	-	-	-
Case Occurred in South	.01 (.04)	.01 (.04)	-	-	-	-
Appellate Case	-.08** (.03)	-.09** (.04)	-.102** (.042)	-.11** (.04)	-.101** (.04)	-.11** (.04)
Challenge to At-large Election	.10** (.05)	.08* (.04)	.078 (.051)	.06 (.05)	.077 (.05)	.06 (.05)
Challenge to Reapportionment Plan	.05 (.05)	.03 (.05)	.034 (.053)	.008 (.05)	.034 (.05)	.008 (.05)
Challenge to Local Election Practice	.004 (.04)	.005 (.04)	-.018 (.05)	-.02 (.04)	-.018 (.04)	-.02 (.04)
Plaintiffs Were African-American	.02 (.04)	.01 (.04)	.114** (.04)	.11** (.04)	.113** (.04)	.11** (.04)
Case Occurred in Jurisdiction Covered by §5	.04 (.04)	.05 (.04)	.045 (.05)	.03 (.05)	.044 (.055)	.03 (.05)
Judge's Age	-	.003** (.001)	-	.005** (.002)	-	.005** (.002)
Judges' Race	-	.27** (.08)	-	.36** (.09)	-	.36** (.09)
Judge's Gender	-	.003 (.05)	-	.02 (06)	-	.02 (.06)
Judge Attended Ivy League College	-	-.003 (.05)	-	.02 (.05)	-	-.02 (.05)
Judge Attended Elite Law School	-	-.07* (.04)	-	-.07* (.04)	-	∼7 ∼4
Judge Previously Served as Law Clerk	-	.09* (.05)	-	∼8 ∼5	-	.08 (.05)
Circuit Fixed Effects	No	No	Yes	Yes	Yes	Yes
Year Fixed Effects	No	No	Yes	Yes	Yes	Yes
N	679	677	652	650	652	650

Notes: The dependent variable is a pro-plaintiff outcome code =1 and 0, otherwise. All models are probit models but are directly interpretable: the coefficients report the change in probability that the judge will vote for the plaintiff at the mean value of all the other variables in the model.

^*indicates significant at P<.10 and

^**indicates significant at P<.05.

The first thing to note about table 3 is that, at least in the voting rights context, the qualitative effects of ideology are robust to various sets of controls. Specifically, the role of ideology is both positive and is statistically significant (with p-values of approximately 0.05 or less). This finding confirms Cox and Miles' claim that ideology is causally related to pro-plaintiff outcomes and Section 2 liability in particular. The authors' modeling strategy, however, has inflated the size of this effect in every context. After including the proper controls, we obtained estimates that were 2.4 - 5 percentage points lower than those obtained by Cox and Miles; given the relatively small size of the coefficients in all the models, this means that due to confounding Cox and Miles have overestimated the effects of ideology by 19%, 45%, and 50% in column 1, 2, and 3, respectively.⁸ Although accounting for this inadvertent exaggeration does not change the authors' underlying claim with respect to the positive effects of ideology in this particular, in other situations such changes can have a substantive effect even on qualitative conclusions given the possibility of a change in the sign of the coefficient—a problem that we show in fact emerges in the context of gender.

After identifying the effects of ideology, Cox and Miles turn to the judges' other personal characteristics: race, gender, education, and past employment. With minor exceptions, we were again able to replicate the authors' findings and we present these results in columns 1, 2, and 3 of table 4 below.⁹ We then adopted the modeling strategy that we believe better accounts for the true underlying causal relationships and present our findings in columns 1(a), 2(a), and 3(a) below.

Table 4. Replication of Cox and Miles' Table 6, columns (1), (5) and (6) and Re-Estimation of Results to Account for Bias and Confounding (standard errors in parentheses).

Variable	(1) Replication of Cox & Miles Table 6, col. 1	(1a) VanderWeele & Staudt Model	(2) Replication of Cox & Miles Table 6, col. 5	(2a) VanderWeele & Staudt Model	(3) Replication of Cox & Miles Table 6, col. 6	(3a) VanderWeele & Staudt Model
Judge was Democratic Appointee	.124** (.04)	.104** (.04)	.166** (.04)	.104** (.04)	.154** (.03)	.113* (.04)
Judge was African-American	.300** (.09)	.36** (.09)	-	.362** (.09)	-	.377** (.09)
Judge was Female	-.020 (.05)	.02 (.06)	-	.02 (.06)	-	.02 (.06)
Age	-	.005** (.002)	-	.005** (.002)	-	.006** (.002)
Judge Attended Ivy League College	-	.02 (.05)	.018 (.05)	.02 (.05)	-	.01 (.05)
Judge Attended Elite Law School	-	-.11* (.04)	-.078* (.04)	-.07* (.05)	-	-.08 (.04)
Judge Previously Served as Law Clerk	-	.08 (.05)	.016 (.05)	.08 (.06)	-	.09* (.05)
Judge Previously Served in State Leg or Exec Branch	-	-	-	-	.021 (.04)	.01 (.04)
Judge Previously Served on State Court	-	-	-	-	-.056 (.04)	-.08* (.04)
Judge Previously Served in Federal Leg. or Exec. Branch	-	-	-	-	.002 (.04)	-.05 (.04)
N	652	650	652	650	652	650

Notes: The dependent variable is a pro-plaintiff outcome code =1 and 0, otherwise. All models are probit models but are directly interpretable: the coefficients report the change in probability that the judge will vote for the plaintiff at the mean value of all the other variables in the model.

^*indicates significant at P<.10 and

^**indicates significant at P<.05. The regressions include controls for whether the case occurred in a jurisdiction covered by section 5, whether the case was an appeal, whether the plaintiffs were African-American, whether the challenge was to an at-large lection scheme or a reapportionment plan, whether the governing body challenged was local, circuit fixed effects, and year fixed effects.

Beginning first with the effects of race. We again find support for Cox and Miles' claim that a judge's race affects the likelihood of voting in favor of Section 2 liability, but in this context we believe the authors reported deflated coefficients. They find that controlling for ideology African-American judges are 30% more likely to vote in favor of liability than white judges,¹⁰ but we find the actual direct effect is 6-8 percentage points higher.¹¹ This means that the authors underestimated causal effects of race by 17-20%.¹² These findings, along with those discussed immediately above with respect to ideology suggest that race has quite a bit stronger effect on outcomes than the authors believe, while ideology has less of an effect than estimated. We deem these twin findings of our modeling process to be important for at least two reasons. First, identifying unbiased effects of the variables allows researchers to have better confidence in their empirical claims and in inferences about causation. Without addressing the problem of confounding, causal claims are completely unwarranted. Second, our findings make Cox and Miles' study all the more important to the literature. As they note, quite a few scholars have investigated the effects of ideology on judicial decision-making but few have explored the effects of race and those that have done so have produced null findings. Cox and Miles' data—after attempting to address the problems of bias and confounding by appropriate covariate control—not only suggests that race is an important factor to consider but that the direct effect of race is roughly 250% greater than that of ideology in the decision-making context when it comes to voting rights claims.¹³ This is a finding that is important for understanding and predicting judicial outcomes and also for the judicial appointment process.

With respect to the direct effects of gender, our models produce contrasting qualitative results: Cox and Miles suggest that gender has a negative effect on the likelihood of voting for Section 2 liability while our revised model suggests the effects are positive. By underestimating the effects of gender on judicial outcomes, in short, the authors misidentified the sign of the coefficient. In neither approach, however, do the results achieve statistical significance as shown in columns 1 and 1(a) of table 4.¹⁴

With respect to the direct effects of education, presented in columns 2 and 2(a) of table 4, our qualitative results are very similar: we, like Cox and Models, find positive but statistically insignificant effects associated with college and clerking, and negative, slightly significant effects caused by a judge's decision to attend an elite law school.¹⁵ A comparison of the two sets of findings however, suggests that of Cox and Miles' education coefficients are slightly overstated.

Columns 3 and 3(a) depict the effects of past employment experience: our models again produce similar qualitative results except with respect to a judge's past experience on a state court. We estimated the total and directs effects (they coincide as note above) of a judge's state court experience and identified a 8% decrease in the likelihood of a judge voting for the plaintiff and this finding is statistically significant at the p ≤ .10 level. Cox and Miles also estimated the effects of state court experience to be negative but not at a statistically significant level—an imprecise estimate most likely due to the decision to exclude the confounding variables, race, gender, age, and education.

Finally, Cox and Miles' findings suggest that age plays no direct role in a judge's propensity to vote for or against the plaintiff (see table 2, column 2 above), but we consistently find a positive and statistically significant effect for age in every model we estimate. For every year a judge grows older, our models suggest that the likelihood of voting for Section 2 liability increases by .3% - .6%.¹⁶ This means that the oldest judge in the database (90 years of age) is 18% - 34% more likely to render a pro-plaintiff vote that the youngest judge (31 years of age). Without the proper controls for race, gender, and education in the estimation of this direct effect, this finding was not observed.

We summarize the differences between our findings and Cox and Miles' findings in table 5 below. As the table indicates, our methodology slightly weakens the authors' conclusions with respect to ideology, but strengthens the conclusions with respect to race. Moreover, we identify a statistically significant role for both age and past service on a state court—findings left hidden in Cox and Miles' study due to bias and confounding. In short, while we admire Cox and the Miles' work, we believe the comparisons presented below confirm our claim that empirical researchers should spend more time and energy considering the underlying causal relationships of the variables of interest prior to specifying and fitting statistical models. This will help assure scholars' claims about causality are justifiable, will avoid problems of under- and overestimation of target parameters, and will potentially enable more precise estimates.

Table 5. Summary of Conclusions with Respect to Cox and Miles' Study on the Voting Rights Act.

Variable	Cox & Miles' Coefficients	Change in Statistical Significance
Judge was Democratic Appointee	Overestimated by 19-50%	Yes; while still statistically significant not always at p≤ .05 as authors suggest
Judge was African-American	Underestimated by 17-20%	No
Judge was Female	Sign change: estimated negative when in fact positive	No
Age	Underestimated by 0-50%%	Yes; finding is statistically significant but authors argued it was not
Judge Attended Ivy League College	Underestimated by 9%	No
Judge Attended Elite Law School	Overestimated by 11%	No
Judge Previously Served as Law Clerk	Underestimated by 80%	No
Judge Previously Served in State Leg or Exec Branch	Overestimated by 210%	No
Judge Previously Served on State Court	Underestimated by 30%	Yes; finding is statistically significant but authors argued it was not
Judge Previously Served in Federal Leg. or Exec. Branch	Sign Change: estimated positive when in fact negative	No

7. Conclusion

Recent methodological advances associated with graphical modeling of causal relationships have made it possible to address the barriers to causal inference in a remarkably simple and straightforward, yet rigorous, manner. Specifically, directed acyclic graph methods or causal DAGs, developed primarily in statistics, epidemiology and computer science, enable empirical researchers to construct diagrams that not only make modeling assumptions explicit, but also to determine when these assumptions are sufficient for obtaining consistent estimates, and how to specify a closed-form model for determining the quantity of interest when identification is possible (Pearl 2009; Greenland, Pearl, and Robins 1999). We discussed these methods in the context of empirical legal research and show how investigators can use DAGs to address the most basic and fundamental tasks of empirical research.

We have described the formal rules governing inferences about confounding that can be drawn from the causal directed acyclic graph. The graphs themselves encode structural assumptions. Legal researchers will use substantive knowledge and potentially prior studies to draw these graphs. In cases in which the causal structure of the graph is not clear, it is possible to draw several graphs and consider how conclusions about confounding varies with each graph and how the results of empirical analyses vary when control is made for different variables based on conclusions drawn from each graph.

Several broad intuitive conclusions emerge from the use of these causal directed acyclic graphs in reasoning about confounding. First, if the total effect of a particular variable is of interest, then control should generally not be made for intermediates on the pathway from the variable of interest to the outcome but for total effects control should be made for variables that affect both the exposure variable of interest and the outcome. If controlled direct effects are of interest, and control for one or more intermediates along the pathway is made then it is also necessary to make control for variables that confound the relationship between the intermediates and the outcome. An important implication of these guidelines is that separate regressions will often be required for different effects of interest. Variables that confound one effect of interest may not confound another; variables that are on the pathway for a certain effect of interest may not be on the pathway for some other effect. For each effect of interest, a researcher should use the guidelines given above to determine for what variables control should be made. If the effect of interest changes the variables for which control is to be made will often change as well.

It should be noted that to obtain valid estimates of causal effects, control needs to be made for a set of variables that suffice to control for confounding; if there are important unmeasured variables on a causal direct acyclic graph for which control cannot be made then it may not be possible to identify the causal effect of interest. In such cases sensitivity analysis techniques (Rosenbaum and Rubin, 1983; Imbens, 2003; VanderWeele and Arah, 2011) can be useful in assessing the extent to which an unmeasured confounding variable would have to be related to both the treatment or exposure of interest and the outcome in order to invalidate the qualitative conclusions drawn from the analysis.

These intuitive rules described above can help legal researchers in their decisions about which variables to include in a model when seeking to identify the particular effect is of interest. In cases in which it is not clear whether control should be made for a variable the precise rules described in section 4 concerning blocked paths can be used to guide the researcher's decision-making. We demonstrated how these rules could be applied to an empirical study of judicial decision-making in the voting rights context. Specifically, with the help of the DAG framework, we demonstrated how even widely admired studies can be plagued with problems of over- and underestimation of coefficients and imprecise results when the underlying causal structure of the variables is not rigorously investigated. Importantly, the methodology can be applied to a wide range of empirical legal studies, not only to those investigating judicial decision making: indeed, virtually every legal empirical researcher who estimates a statistical model would benefit by making qualitative assumptions about their data explicit with the help of a DAG.

This paper is merely an introduction to the topic; many other extensions to the causal DAG framework are possible (Pearl 2009; Hernán et al. 2004; VanderWeele & Robins,2007; VanderWeele et al. 2008; White & Chalak, 2009; Shpitser et al., 2010) and we encourage empirical legal researchers to consult the literature further.

Online Appendix

A causal DAG, such as that in figure 3, can be viewed as a set of non-parametric structural equations (Pearl, 2009) such that each variable X_i is given by the equation

$${\mathrm{X}}_{\mathrm{i}}=f_{\mathrm{i}}(p{a}_i,{\mathrm{\epsilon }}_i),i=1,\dots ,n$$ (1)

where pa_i are the parents of X_i on the graph and the ε_i are mutually independent random variables that the researcher chooses not to include in the graph. Put differently, equation (1) indicates that the variable X_i is a function of its direct causes (its parents) as well as a disturbance term. This equation is completely nonparametric in the sense that it does not assume anything about the functional form of the relationships among and between the variables. Moreover, it can be interpreted as a generalization of the linear structural equation model that has become popular in the legal and social science, namely

$${\mathrm{X}}_{\mathrm{i}}=\sum {\beta }_{ik}{\mathrm{x}}_k+{\mathrm{\epsilon }}_i,i=1,\dots ,n$$ (2)

As Pearl notes, a set of equations (in either form (1) or (2) above) is a structural model if each equation represents an autonomous process or mechanism (Pearl 2009, 27). If each process determines the value of exactly one variable (the dependent variable) then the model is a structural causal model. Figure 3 represents a causal model with each node representing an autonomous process and thus can be represented by the following equations

$$\begin{array}{c}{\mathrm{x}}_1={\mathrm{\epsilon }}_1\\ {\mathrm{x}}_2=f_2({\mathrm{x}}_1,{\mathrm{\epsilon }}_2)\\ {\mathrm{x}}_3=f_3({\mathrm{x}}_1,{\mathrm{\epsilon }}_3)\\ {\mathrm{x}}_4=f_4({\mathrm{x}}_3,{\mathrm{x}}_2,{\mathrm{\epsilon }}_4)\\ \mathrm{y}=f_5({\mathrm{x}}_4,{\mathrm{\epsilon }}_5)\end{array}$$

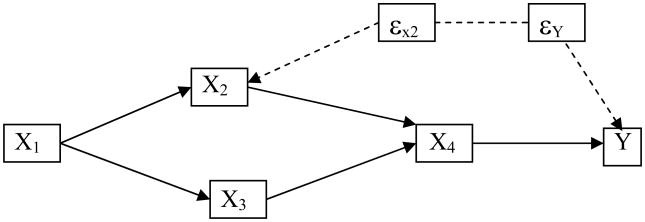
For purposes of constructing a causal graph it is important to recall that the error terms in the model are assumed to be mutually independent. The requirement that the error terms are mutually independent is essentially equivalent to the requirement that any common cause of two or more variables on the graph must also be on the graph (Pearl 2009). If any factors are believed to influence two or more variables (thus violating the independence assumption) then they must enter the analysis as an unmeasured variable and must be depicted on the graph. Figure A.1 uses dotted lines to indicate that the error terms, ε₂ and ε_Y, are not mutually independent (perhaps we believe that people who use sprinkler systems are particularly prone to sidewalk accidents).

Figure A.1. Directed Acyclic Graph with Mutually Independent Errors but with an Unobserved Variable, U.

Correlated errors could substantially change the conclusions drawn from a diagram. With respect to figure 3, for example, we claimed that knowing X₄ renders Y independent of the set {X₁, X₂, X₃} but this no longer holds true if we thought there were correlated errors as in figure A.1. Typically instead of using correlated errors as in figure A.1 we would represent these relations by adding an unmeasured common cause U of X₂ and Y as in figure A.2

Figure A.2. Directed Acyclic Graph with Unobservable Errors that Violate the Mutual Independence Assumption; Errors, ε₂ and ε_Y, are Correlated.

Recall that X_i is a node in a causal diagram and pa_i are the parents or direct causes of that node. The joint probability function for a causal DAG can be given by

$$\mathrm{P}(\mathrm{X})=\mathrm{\Pi }p({\mathrm{X}}_{\mathrm{i}}|p{a}_{Xi},)i=1,\dots ,n$$ (3)

Specifically, with respect to figure 3 above, we can calculate the joint probability function as follows

$$\mathrm{P}({\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,{\mathrm{x}}_4,\mathrm{y})=P({\mathrm{x}}_1)P({\mathrm{x}}_2|{\mathrm{x}}_1)P({\mathrm{x}}_3|{\mathrm{x}}_1)P({\mathrm{x}}_4|{\mathrm{x}}_2,{\mathrm{x}}_3)P(\mathrm{y}|{\mathrm{x}}_4)$$ (4)

The joint probability function, along with the functional relationships depicted in the DAG (such as those in equation (1) above), enable a researcher to identify exactly how an intervention, policy change, or new medical procedure will change the distribution of interest. Consider a simple intervention in which a variable, say X_i, is forced to take on a fixed value, x_i. Formally, when we fix the value of X_i or intervene we effectively remove the equation x_i = f_i(pa_i, ε_i) from the model and substitute X_i = x_i in all the remaining equations, which in turn allows for a prediction of the effects of the intervention on the new probability function. In effect, (3) above would be transformed as follows

$$\mathrm{P}({\mathrm{x}}_1,\dots {\mathrm{x}}_{\mathrm{n}};\text{after setting}{\mathrm{X}}_{\mathrm{i}}\text{to}{\mathrm{x}}_{\mathrm{i}})=\{\begin{array}{cc}{\mathrm{\Pi }}_{\mathrm{j}\ne \mathrm{i}}P(x_j|p{a}_j)& \text{if}{\mathrm{X}}_{\mathrm{i}}={\mathrm{x}}_{\mathrm{i}}\\ 0& \text{if}{\mathrm{X}}_{\mathrm{i}}\ne {\mathrm{x}}_{\mathrm{i}}\end{array}$$ (5)

With respect to figure 3, if we fix the variable X₂ = 1 (i.e. we fix the sprinkler system to be “on”) the resulting joint distribution for the remaining variables is

$$\mathrm{P}({\mathrm{x}}_{1\mathrm{x}2=1},{\mathrm{x}}_{3\mathrm{x}2=1},{\mathrm{x}}_{4\mathrm{x}2=1},{\mathrm{y}}_{\mathrm{x}2=1})=P({\mathrm{x}}_1)P({\mathrm{x}}_3|{\mathrm{x}}_1)P({\mathrm{x}}_4|{\mathrm{x}}_3,{\mathrm{x}}_2=1)P(\mathrm{y}|{\mathrm{x}}_4)$$ (6)

Examining the joint distribution after intervening on some variable is valuable because it highlights the fact that only descendants of the variable intervened upon, here X₂, are affected by this action and thus the marginal probabilities are unaltered for the ancestors of the intervention variable. An examination of the difference between equations (4) and (6) clearly shows this. Moreover, these properties lead directly to a formula that allows researchers to identify the casual effects on a specific variable. For example, the distribution and expected value of the variable Y in figure 3, intervening to set X₂ =1, is

$$\mathrm{P}({\mathrm{y}}_{\mathrm{x}2=1})={\sum }_{\mathrm{i}\ne 2}P(\mathrm{y}|p{a}_Y){\mathrm{\Pi }}_{\mathrm{i}\ne 2}P({\mathrm{x}}_{\mathrm{i}}|p{a}_i\text{and})$$ (7)

$$\mathrm{E}({\mathrm{y}}_{\mathrm{x}2=1})={\sum }_{\mathrm{i}\ne 2}\mathrm{E}[\mathrm{y}|p{a}_Y]{\mathrm{\Pi }}_{\mathrm{i}\ne 2}P({\mathrm{x}}_{\mathrm{i}}|pa)$$ (8)

The implication of the analyses above is significant. The above results show that if all the direct causes of the treatment variable are observable, then it is possible to infer post-intervention distributions from pre-intervention distributions. In short, causal DAGs allow us to estimate the causal effects of an intervention from non-experimental or observational data—the very point of many empirical legal studies. The backdoor path criterion stated in section IV above allows for the derivation of simpler expression for causal effects and allows one to potentially identify the causal effects of an intervention in which some members of pa_i might be unobserved.