Using Solutes and Kinetics to Probe Large Conformational Changes in the Steps of Transcription Initiation

Summary

Small solutes are useful probes of large conformational changes in RNA polymerase (RNAP)-promoter interactions and other biopolymer processes. In general, a large effect of a solute on an equilibrium constant (or rate constant) indicates a large change in water-accessible biopolymer surface area in the corresponding step (or transition state), resulting from conformational changes, interface formation, or both. Here, we describe nitrocellulose filter binding assays from series used to determine the urea dependence of open complex formation and dissociation with Escherichia coli RNAP and λP_R promoter DNA. Then, we describe the subsequent data analysis and interpretation of these solute effects.

1. Introduction

1.1 Solute Interactions and Solute Effects

Small solutes are emerging as useful probes and perturbants of intermediates and transition states and of overall changes in surface area in transcription initiation and other protein and nucleic acid processes. In general, large amounts of protein and nucleic acid surface are buried or exposed when interfaces are made or disrupted or in coupled conformational changes. The effect of a solute on an equilibrium constant (or rate constant) is determined by its favorable or unfavorable interactions with the functional groups on the surface buried or exposed in the corresponding step (or transition state).

These solute effects vary widely for different solutes and different surfaces. For example, urea interacts favorably with most protein and nucleic acid functional groups. High concentrations (typically more than 4 M) of urea denature proteins and nucleic acids at 25 °C because urea interacts favorably with the amide and hydrocarbon groups exposed in unfolding proteins and with the nucleobase groups exposed in melting nucleic acid helices (1). At lower concentrations, these same interactions cause urea to disfavor steps in transcription initiation that bury RNA polymerase (RNAP) or promoter DNA surface, and to favor the reverse direction of these steps (described below). Glycine betaine (GB) and proline, on the other hand, interact unfavorably with many protein functional groups and with nucleic acid phosphates and therefore stabilize proteins (though not nucleic acids) against denaturation (1, 2) and favor the early and late steps in transcription initiation that bury RNAP and promoter DNA surface ((3) and unpublished data for proline). Replacement of KCl by potassium glutamate (KGlu) has a qualitatively similar effect to replacing urea by GB in that this replacement favors protein folding and assembly (but not DNA helix formation), and therefore favors the early and late steps in transcription initiation (4).

Solute effects are analyzed and interpreted using the slope of a plot of the logarithm of the observed equilibrium constant (lnK_obs) or rate constant (lnk_obs) versus solute concentration ([solute]). These plots are typically linear up to at least 1 M [solute]. Their slopes, closely related to what are called solute m-values, can be analyzed at several levels, starting with the qualitative level discussed above, where the sign of the effect reports on whether surface is buried or exposed in the step (when lnK_obs is analyzed) or the formation of the transition state (when lnk_obs is analyzed) and the magnitude of the effect reports on how much surface is involved. As examples of this technique, details of the use of urea and GB to probe conformational changes and interface formation in the steps of forming and stabilizing the open promoter complex by E. coli RNAP are provided in this article (3–6).

1.2 Mechanism of Formation and Stabilization of the Open Promoter Complex in Transcription Initiation

The mechanism of transcription initiation by E. coli and T7 phage RNAP have been extensively investigated and are model systems for transcription initiation. Both polymerases form the open complex by a “bind-bend-melt” mechanism (7, 8). Kinetic studies using E. coli RNAP (R) and the P_R promoter (P) of phage λ show that a minimum of four steps and three kinetically-significant intermediates (designated I₁, I₂, I₃) are involved in formation of the transcriptionally-competent open complex (RP_o) by the bacterial polymerase: [Mechanism 1 goes here] Immediately after mixing RNAP and λP_R promoter DNA under conditions typically used to study transcription initiation, relatively unstable closed complexes designated I₁ are formed (9). For λP_R, I₁ does not appear to be a single species but rather an ensemble (i.e a mixed population) of relatively unstable closed complexes which dissociate rapidly to free RNAP and promoter DNA and therefore equilibrate with each other and with free promoter on the time scale required to convert to I₂. Likewise in a λP_R dissociation kinetics experiment, the relatively unstable open intermediates I₃ and I₂ convert rapidly back to the stable open complex (RP_o) on the time scale required for I₂ to convert to I₁. The interconversion I₁ ⇄ I₂, opening and closing the 13 base pair transcription bubble (9), is the rate-determining step in both directions for λP_R, with the highest free energy transition state (TS) in Mechanism 1. While RP_o is relatively well-characterized, much less is known about these intermediates and TS (8). This information is needed to determine the mechanism of operation of RNAP as a molecular DNA-opening machine. The use of solutes as probes of large conformational changes and interface formation in these intermediates and transition state, as illustrated in this chapter, provides information that is not readily obtained by other methods.

1.3 Examples of Solute Effects on Steps of Transcription Initiation and their Interpretation

Solutes can be used as probes for the change in surface area in a step or the formation of a transition state. As an example from transcription initiation, the equilibrium constant and both rate constants for the interconversion of I₁ and I₂, the step which includes opening/closing the 13 base pair initiation bubble, are independent of urea and of the choice of anion (Cl⁻ versus Glu⁻) and only weakly dependent on salt concentration (3–5). This contrasts greatly with the situation for DNA melting in solution, where the equilibrium constant for opening DNA oligomers of this length is a strong function of urea and salt concentration, and provides one of several lines of evidence that DNA opening occurs in the active site cleft of RNA polymerase in an environment very different from that of the solution.

As a second example of the use of solutes as probes, the dissociation rate constant k_d is a strong function of urea, GB, and salt concentration, and is profoundly affected by replacing Cl⁻ by Glu⁻ (3–5). Effects of urea and KCl are entirely in the equilibrium constant K₃ for the conversion of the initial open complex I₂ to the stable open complex RP_o and provide strong evidence for folding and assembly of approximately120 residues of downstream mobile elements (DME) (6) of WT RNAP on duplex DNA as part of stabilizing the λP_R open complex by a factor of about 10⁵ (4, 5)

In addition to their use as probes, solutes can also be used as selective perturbants. As one example, because urea and KCl are found to destabilize RP_o greatly with respect to I₂, but do not affect the rate of conversion of I₂ to I₁, rapid increases in concentration of these solutes create a transient, majority population (called a burst) of the otherwise-undetectable intermediate I₂ for characterization by DNA footprinting (9). In another study, GB was used to increase the I₁ binding constant and hence increase the size of the burst population of I₁, and to reduce the rate of its conversion to open complexes, to footprint I₁ in manual mixing experiments (10). The original papers should be consulted for details of these experiments.

In what follows, we describe the methods used to perform nitrocellulose filter binding assays to study the urea dependence of the kinetics of RP_o formation and of RP_o dissociation into free RNAP and promoter DNA. We then explain the data analysis required to determine the solute concentration dependences of the individual steps of Mechanism I, and describe the conclusions we have reached using such analyses in our studies of the mechanism with λP_R.

2. Materials

2.1. Reagents

1. RNAP: Prepare using standard protocols, such as described in (reference chapter in this volume describing this prep). Dialyze into RNAP Storage Buffer (see below), divide into 100 µL aliquots, and store at −80°C. Store a 100 µL aliquot at −20°C while in use.

2. Radiolabeled DNA: Use T4 Polynucleotide Kinase (New England Biolabs) and γ ³²P-labeled ATP (Perkin Elmer) to ³²P-label one primer, then use this primer to amplify the fragment containing the promoter via PCR. Purify PCR fragment from an agarose gel. Store at 4°C (see Note 1).

3. 8× Transcription Buffer Salts: 320 mM Tris (pH 8.5 at room temperature), 960 mM KCl, 80 mM MgCl₂. Dissolve 3.876 g Tris HCl, 7.157 g KCl, and 1.626 g MgCl₂ into about 90 mL deionized H₂O. Adjust pH to 8.5 using HCl. Bring to 100 mL with deionized H₂O in a volumetric flask. Store at 4°C.

4. 4× Transcription Buffer Salts: 160 mM Tris (pH 8 at assay temperature), 480 mM KCl, 40 mM MgCl₂. Combine 25 mL 8× Transcription Buffer Salts with about 20 mL deionized H₂O. Equilibrate at intended assay temperature and adjust the pH to 8.0 using HCl. Bring to 50 mL in a volumetric flask using deionized H₂O. Store at 4°C.

5. 1 M dithiothreitol (DTT). Mix 0.154 g DTT with 1 mL deionized H₂O. Vortex to dissolve. Filter using a 0.45 µm syringe filter. Store at −20°C in 50 µL aliquots.

6. 50 mg/mL bovine serum albumin (BSA). Mix 100 mg with 2 mL deionized H₂O. Filter using a 0.45 µm syringe filter. Store at −20°C in 50 µL aliquots.

7. 50 mg/mL heparin. Mix 100 mg with 2 mL deionized H₂O. Filter using a 0.45 µm syringe filter. Store at −20°C in 50 µL aliquots. (See Note 2).

8. RNAP Storage Buffer: 50% v/v glycerol, 10 mM Tris (pH 7.5 at 4°C), 100 mM NaCl, 0.1 mM DTT, 0.1 mM Na₂EDTA. Dissolve 0.061 g Tris HCl and 0.292 g NaCl in about 20 mL deionized H₂O. Add 10 µL 0.5 M Na₂EDTA (pH 8.0 at room temperature) and 5 µL 1 M DTT. Equilibrate at 4°C in a water bath and adjust pH to 7.5 using HCl. Bring to 25 mL with deionized H₂O in a volumetric flask. Bring to 50 mL with glycerol in a volumetric flask. Store at −20 °C.

9. 6 M Urea in 1× Transcription Buffer Salts (see Note 3): 43 mm (millimolal) Tris (pH 8 at assay temperature), 129 mm KCl, 10.7 mm MgCl₂, 6 M urea. Combine 12.5 mL 4× Transcription Buffer Salts and 6.25 mL RNAP Storage Buffer. Bring to 50 mL with deionized H₂O in a volumetric flask. Dissolve 18.018 g dry urea into a small amount of this solution of 1× Transcription Buffer Salts. Transfer this solution into a 50 mL volumetric flask and add additional 1× Transcription Buffer Salts to bring the final volume to 50 mL (see Note 4 and Section 3.1). Store at 4 °C.

10. Filter Binding Wash Buffer: 10 mM Tris (pH 8.0 at room temperature), 100 mM NaCl, 0.1 mM Na₂EDTA. Dissolve 5.844 g NaCl and 1.211 g Tris in about 950 mL deionized H₂O. Add 200 µL 0.5 M Na₂EDTA stock (pH 8.0 at room temperature). Adjust pH using HCl. Bring to 1 L with deionized H₂O. Store at 4°C.

2.2 Supplies and equipment

1. 0.45 µm nitrocellulose filters (Schleich and Schuell). Soak in deionized H₂O at least 30 minutes prior to assay. Store at 4°C in deionized H₂O.

2. 10-place filter-holding vacuum manifold capable of achieving pressures of 15–30 inches of Hg (Hoefer Scientific, San Francisco, CA).

3. Three-syringe Rapid Quench-Flow Fast Mixer (Model RQF-3; KinTek Co. Austin, TX) with temperature-regulated water bath for rapid-mix, rapid-quench experiments.

4. Approximately 20 1.5 mL microcentrifuge tubes with holes made in the top. (see Note 5).

5. Scintillation counter (Hewlett-Packard Tri-Carb 2100 TR).

6. Laboratory timer for manual mixing experiments.

3. Methods

This section provides details of nitrocellulose filter binding kinetics experiments that detect long-lived competitor-resistant (CR) open complexes and serve to determine the dependences of equilibrium and rate constants of individual steps in Mechanism I on solute concentration. For λP_R under the wide range of solution conditions investigated, the kinetics of open-complex dissociation are single exponential, as are the kinetics of association when one reactant (typically RNAP) is in excess. Under such conditions, overall rate constants for dissociation (k_d) and association (β_CR or α_CR; see Equations 2–4 below) are directly determined from filter binding experiments. From the dependence of α_CR on RNAP concentration, the equilibrium constant K₁ and rate constant k₂ in Mechanism 1 are determined. A different assay, capable of detecting I₁ directly, is necessary to obtain individual rate constants k₁ and k₋₁ in addition to K₁. Rapid destabilization of RP_o using high concentrations of salt or urea yields a burst of I₂, allowing one to determine k₋₂ directly and therefore dissect k_d to obtain K₃ (and in favorable cases k₃ and k₋₃ (5)).

Filter binding studies of the effects of different solutes and solute concentration on the observable rate constants k_d and β_CR or α_CR are analyzed similarly to determine which individual rate or equilibrium constants are affected by that solute, and by how much. Methods described below are for the destabilizing solute urea, which favors the exposure of RNAP and DNA surface and hence destabilizes both binding and folding steps. In most cases these methods are easily adapted to study protein-stabilizing solutes like GB and proline, effects of which on protein folding are comparable in magnitude but opposite in direction to urea. (See Note 6.)

It is important to note that solute-as-probe experiments typically are performed in the solute concentration range 0 – 1 M. Higher concentrations of protein-stabilizing solutes can be used if needed to detect small effects, but higher concentrations of urea and other destabilizing solutes should generally be avoided. In experiments using urea as a perturbant to rapidly destabilize RP_o (5), concentrations of urea in the molar range can be used because RNAP in promoter complexes is stabilized against subunit dissociation and unfolding by binding free energy.

Below, we describe assays utilizing both manual mixing and rapid quench-flow fast mixing with a three syringe mixer. For best results, fast mixing should be used for reactions with half-lives shorter than about 100 seconds. For λP_R these include studies of the kinetics of RP_o formation at temperatures above 20 °C and of RP_o dissociation at high urea or salt concentrations. However, slower reactions can be easily (and more efficiently) assayed using manual mixing (see (3–6, 11)). In fast mixing experiments, each time point is an individual reaction that proceeds for a defined amount of time and then is stopped with a quench solution. In manual mixing experiments, individual aliquots are taken from the same large continuous reaction at different times and quenched.

In general, for fast mixer reactions, approximately 19 µL of each reactant in sample ports A and B are combined at time t = 0 in the instrument’s reaction loop. At a later time t, approximately 150 µL (consisting of the combined reaction mixtures and the buffers from push syringes A and B used to drive the reaction mixtures together) are combined with half this volume of the quenching reagent loaded into push syringe C and immediately expelled through the exit line (total volume: approximately 220 µL). Only minimal instructions are given here for use of the RQF-3 Rapid Quench-Flow Fast Mixer. For more comprehensive instructions, the instrument manual should be consulted.

3.1 Preparation of Reaction Mixtures

Filter binding assays are performed in 1× Transcription Buffer, which consists of the following concentrations in the absence of urea: 120 mM KCl (129 mm (millimolal)), 10 mM (10.7 mm) MgCl₂, 40 mM (43mm) Tris pH 8.0 at assay temperature, 1 mM DTT, 100 µg/mL bovine serum albumin (BSA), and (from storage buffer) 12.5 mM (13.3 mm) NaCl and 6.25% v/v (855 mM, 913 mm) glycerol. This solution can be prepared by mixing one-fourth the final volume 4× Transcription Buffer Salts, one eighth the final volume RNAP Storage Buffer, 1/1000^th the volume 1M DTT stock, and 1/500^th the volume 50 mg/mL BSA stock with deionized H₂O.

As described in Section 2.1, we add dry urea to 1× Transcription Buffer to make our urea stock solutions. This procedure maintains the molal concentrations of the other components constant, and does not significantly change the molar concentrations of other species at final urea concentrations less than 1 M, though the favorable interaction of urea with KCl reduces the effective salt concentration (i.e., the salt activity (1)).

In general, reaction volumes should be large enough to allow for the production of 12–18 time points, which should be sufficient to determine a time course of competitor-resistant open complex formation or dissociation (see Note 7). All volumes described below have been chosen to achieve this number of data points.

All solutions used should be equilibrated at the assay temperature 5–15 minutes prior to initiation of an experiment.

3.2 Nitrocellulose Filter Binding (see Note 8)

1. Use a pair of tweezers to place a nitrocellulose filter over a manifold port under vacuum. Place one of the provided stainless steel chimney weights over the filter (leaving the center of the filter accessible via the hole in the weight). Open the port to remove water from the filter, close the port, and cover filter with 200–500 µL Filter Binding Wash Buffer.

2. To bind an experimental sample, open the port to pull through the Wash Buffer. Apply the sample to the center of the filter. Wash with 200–500 µL Wash Buffer. Close the port, and remove the filter from the manifold.

3. Dry the filter completely. Insert the filter into a scintillation vial and determine its radioactive counts per minute (cpm) using a scintillation counter (see Note 9).

3.3 Examples of Assays to Determine Solute Effects on Kinetics of Open Complex Formation

3.3.1 Manual Mixing Association Experiment at 0.5 M urea

1. Prepare Solutions:

   1. DNA Mix (800µL total): Combine 66.7 µL 6 M Urea in 1× Transcription Buffer Salts, 183 µL 4× Transcription Buffer Salts, 0.80 µL 1 M DTT, 1.60 µL 50 mg/mL BSA, 91.6 µL RNAP Storage Buffer, X µL of radiolabeled DNA (final concentration 50–500 nM; see Note 10), and (456 – X) µL of deionized H₂O.
   2. RNAP Mix (750 µL total): Combine 62.5 µL 6 M Urea in 1× Transcription Buffer Salts, 172 µL 4× Transcription Buffer Salts, 0.75 µL 1 M DTT, 1.50 µL 50 mg/mL BSA, Y µL RNAP in Storage Buffer (to obtain a final concentration twice as large as that desired in the association reaction), (85.9 – Y) µL Storage Buffer, and 427 µL deionized H₂O (see Note 11).
   3. Competitor Mix (500 µL, for 50 µg/mL heparin in assay): Combine 41.7 µL 6 M Urea in 1× Transcription Buffer Salts, 115 µL 4× Transcription Buffer Salts, 0.5 µL 1 M DTT, 1.0 µL 50 mg/mL BSA, 57.3 µL RNAP Storage Buffer, 3 µL 50 mg/mL heparin, and 285 µL dH₂O. Aliquot 20 µL of this mix into one tube per filter for the experiment.

2. Before initiating the reaction, remove 50 µL of DNA Mix and combine it with 50 µL of 1× Transcription Buffer and 20 µL Competitor Mix. Filter 100 µL of this to determine the background filter retention of DNA (cpm_bkgd; see section 4.1).

3. At time 0, combine 750 µL DNA Mix and 750 µL RNAP Mix. Vortex gently or pipet to mix.

4. At various time points, remove a 100 µL aliquot of the DNA-RNAP reaction mixture, quench by combining it with 20 µL of Competitor Mix in a separate tube for 10 s, and filter 100 µL of the quenched solution. Take enough long time points to accurately define the plateau cpm value (see Note 7).

5. At the end of the assay, remove two separate aliquots of 100 µL, and combine each with 20 µL Competitor Mix. Filter 100 µL of one of the 120 µL samples 10 seconds after mixing to determine the cpm value for this population of 100% CR complexes (cpm_{100% CR}, used in determining filter efficiency; see section 4.1). Remove 100 µL from the other 120 µL sample and divide it into 20 µL aliquots. Spot these aliquots onto previously dried filters to determine the total cpm in each filtered aliquot (cpm_TOT, used in determining the fraction of competitor-resistant filter retainable complexes, θ; see section 4.1).

3.3.2 Rapid-Mix Rapid-Quench Association Experiment at 0.5 M Urea

1. Prepare solutions:

   1. DNA Mix (500µL total) and RNAP Mix (500 µL): Same proportions of reagents as in the corresponding mixes detailed in Section 3.3.1.1.
   2. Push Buffer for DNA and RNAP Mixes (10 mL total): Combine 833 µL 6 M Urea in 1× Transcription Buffer, 2290 µL 4× Transcription Buffer Salts, 10 µL 1 M DTT, 20 µL 50 mg/mL BSA, 1150 µL RNAP Storage Buffer, and 5700 µL deionized H₂O. Remove 100 µL for determination of cpm_bkgd and cpm_TOT.
   3. Competitor Mix (5 mL total, for 50 µg/mL heparin in assay): Combine 417 µL 6 M Urea in 1× Transcription Buffer Salts, 1.15 mL 4× Transcription Buffer Salts, 5 µL 1 M DTT, 10µL 50 mg/mL BSA, 573 µL RNAP Storage Buffer, 15 µL 50 mg/mL heparin, and 2.83 mL deionized H₂O.

2. Load Push Buffer into the left (A) and right (B) vertical drive syringes of a KinTek RQF-3 Rapid Quench-Flow Fast Mixer. Load Competitor Mix into the center (C) drive syringe.

3. Load the DNA Mix into the instrument’s left (A) sample port. Load Push Buffer (set aside in step 1c) into the right (B) sample port. Perform two reactions, mixing DNA Mix with Push Buffer in the reaction loop for 1 second. Filter one of the expelled samples to determine cpm_bkgd. Apply the other expelled sample onto a set of dry filters to determine cpm_TOT. Clean sample port B and load RNAP Mix.

4. Generate time points for the association of RNAP and DNA by allowing individual reactions to proceed for defined times prior to being quenched and expelled. Take enough long time points to accurately define the plateau cpm value (see Note 7). Collect the expelled volumes by inserting the exit line on the fast mixer into a 1.5 mL microcentrifuge tube into which a hole has been made in the top (see Note 5). Filter the entire expelled sample as described in Section 3.2.

3.4 Examples of Assays to Determine Solute Effects on Kinetics of Open Complex Dissociation

3.4.1 Manual Mixing Dissociation Experiment at 2 M urea

1. Prepare solutions:

   1. RP_o Mix (810 µL total): Combine 233 µL 4× Transcription Buffer Salts, 0.93 µL 1 M DTT, 1.9 µL 50 mg/mL BSA, X µL of radiolabeled DNA solution (final concentration 50–500 nM (see Note 8)), and (578 – X) µL deionized H₂O (resulting in a volume of 814 µL). Remove 105 µL of this mix and combine with 15 µL Storage Buffer (resulting in 120 µL). To the remaining 709 µL, add 101 µL RNAP in Storage Buffer. Incubate at 37°C for 30–60 minutes to form open complexes.
   2. Urea/Competitor Mix (750 µL total, for 50 µg/mL heparin in assay): Combine 500 µL 6 M Urea in 1× Transcription Buffer Salts, 62.5 µL 4× Transcription Buffer Salts, 0.75 µL 1 M DTT, 1.5 µL 50 mg/mL BSA, 31.3 µL RNAP Storage Buffer, 1.5 µL 50 mg/mL heparin, and 153 µL deionized H₂O.

2. Before initiation of dissociation reaction, remove 60 µL from RP_o Mix and incubate at 37 °C to ensure the association reaction proceeds to completion (an additional 5–10 half-lives). Combine with 60 µL of 1× Transcription Buffer containing 100 µg/mL heparin, incubate for 10 seconds, and filter 100 µL to determine cpm_100%CR. To the 120 µL sample from Section 1.a. above, add 120 µL Urea/Competitor Mix. Filter 100 µL of this to determine cpm_bkgd. Remove 100 µL and spot onto a set of dry filters to determine cpm_TOT.

3. To the remaining 750 µL of RP_o Mix, add 750 µL of Urea/Competitor Mix at time 0. At various time points, remove 100 µL of the dissociation reaction and filter as described in Section 3.2.

3.4.2 Rapid-Mix Rapid-Quench Dissociation Experiment at 2 M urea

1. Prepare solutions:

   1. RP_o Mix (500 µL total): Combine 155 µL 4× Transcription Buffer Salts, 0.61 µL 1 M DTT, 1.24 µL 50 mg/mL BSA, X µL of radiolabeled DNA solution (final concentration 50–500 nM (see Note 10)), and (386 – X) µL deionized H₂O (resulting in a volume of 543 µL). Remove 105 µL of this mix and combine with 15 µL Storage Buffer (resulting in 120 µL). To the remaining 438 µL, add 62.5 µL RNAP in Storage Buffer. Incubate at 37°C for 30–60 minutes to form open complexes.
   2. Urea/Competitor Mix (5 mL total): Same proportions of reagents as in the corresponding mixes detailed in Section 3.4.1.1.
   3. Push Buffer for RP_o Mix (10 mL total): Combine 2.50 mL 4× Transcription Buffer Salts, 10 µL 1 M DTT, 20 µL 50 mg/mL BSA, 1.25 mL RNAP Storage Buffer, and 6.22 µL deionized H₂O.
   4. Quench Buffer (10 mL total): Combine 2.5 mL 4× Transcription Buffer Salts, 10 µL 1 M DTT, 20 µL 50 mg/mL BSA, 1.25 mL RNAP Storage Buffer, 10 µL 50 mg/mL heparin, and 6.21 mL dH₂O.

2. Load 5 mL Push Buffer for RP_o Mix into the left (A) vertical drive syringe of a KinTek RQF-3 Rapid Quench-Flow Fast Mixer. (Set aside 5 mL Push Buffer for RP_o Mix for later determination of cpm_100%CR.) Load Urea/Competitor Mix into the right (B) drive syringe. Load Quench Buffer into the center (C) drive syringe.

3. Load mixture containing DNA in 1× Transcription Buffer (removed before addition of RNAP in production of RP_o Mix) into the instrument’s left (A) sample port. Load Urea/Competitor Mix into the right (B) sample port. Perform two reactions, mixing DNA with Urea/Competitor Mix for 1 second. Filter one of the expelled samples to determine cpm_bkgd. Apply the other expelled sample onto a set of dry filters to determine cpm_TOT. Clean sample port A and load RP_o Mix.

4. Generate time points for the dissociation of RP_o by allowing individual reactions to proceed for defined times prior to being quenched and expelled (see Note 12). Collect and filter the expelled volumes as described in Section 3.3.2.

5. After all experimental time points are collected at the desired temperature, bring the temperature of the water bath connected to the fast mixer to 37 °C. Replace the urea solutions with Push Buffer for RP_o. Mix and filter several samples with very short incubation times to determine cpm_100%CR.

4. Data analysis

4.1 Determination of θ_t

The first step in the analysis of filter binding kinetic data is to calculate θ_t, the fraction of promoter DNA in competitor-resistant (CR) complexes at time t. CR complexes are operationally defined as those which survive a 10 s challenge with an inert (non-displacing) competitor like heparin (for λP_R; see Note 2) or unlabeled promoter DNA. For λP_R, because RP_o is generally much more stable than I₃ and I₂, it is usually the dominant competitor-resistant open complex, though I₃ may also be significant at lower temperatures. Values of θ_t are calculated by dividing the background-corrected counts per minute (cpm) for a time point filter by the total cpm per sample bound and correcting for filter efficiency (E), defined as the fraction of labeled promoter DNA retained on the filter under conditions where 100% of promoter DNA is bound in a CR complex in solution (E = cpm_100%CR/cpm_TOT; see Notes 13 and 14).

$${\mathrm{\theta }}_{\mathrm{t}}=(1/\mathrm{E})({\text{cpm}}_{\mathrm{t}}-{\text{cpm}}_{\text{bkgd}})/{\text{cpm}}_{\text{TOT}}$$ (1)

In RP_o formation kinetics experiments, if the long-time plateau value of θ_t (called θ_t=∞) is significantly less than 1, then RP_o formation is reversible and the kinetics are for the approach to an equilibrium distribution of RP_o, intermediate complexes and free promoter DNA. If θ_t=∞ = 1, then RP_o formation is irreversible.

4.2 Determination of the Observed Rate Constant for RP_o Formation

In excess RNAP, single-exponential kinetics of formation of CR complexes at λP_R (primarily RP_o) are observed under all conditions investigated. In these experiments, the observed rate constant for formation of these CR (open) complexes is called β_CR, and is determined by fitting θ_t versus time to the first order rate equation

$${\mathrm{\theta }}_{\mathrm{t}}={\mathrm{\theta }}_0+({\mathrm{\theta }}_{\mathrm{t}=\infty }-{\mathrm{\theta }}_{\mathrm{o}})(1-e^{-{\beta }_{CR}t})$$ (2)

where θ_o is the fitted value of θ_t at t = 0 (typically θ_o less than 0.1) and θ_t=∞ is the long-time (plateau, equilibrium) value of θ_t (11, 12). Equivalently, β_CR can be fit using the decay to equilibrium equation

$$\mathrm{\Delta }{\mathrm{\theta }}_{\mathrm{t}}=\mathrm{\Delta }{\mathrm{\theta }}_{\mathrm{o}}{e}^{-{\beta }_{CR}t}$$ (3)

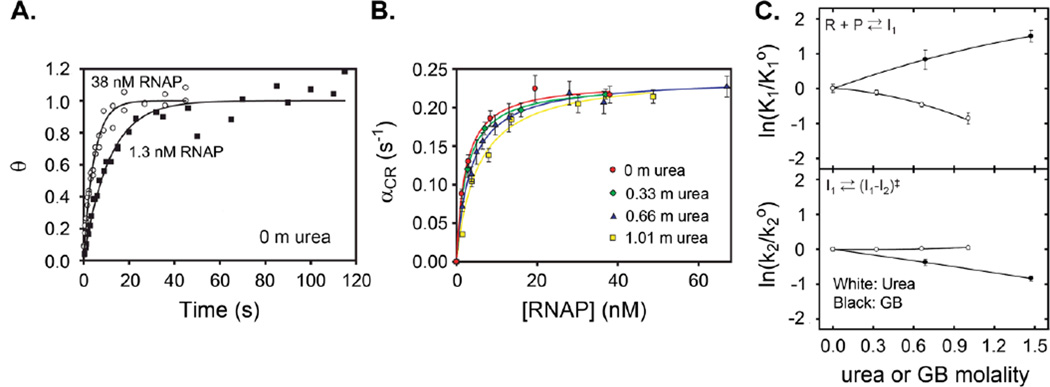
where Δθ_t = θ_t=∞ - θ_t and Δθ_o = θ_t=∞ - θ_o. Representative kinetic data for the formation of RP_o using wild-type RNAP and λP_R DNA are shown in Fig. 1.A., plotted as θ_t versus t.

Figure 1.

Data showing the determination of the urea dependences of K₁ and k₂. A. Rate constants of formation of filter-retainable open complexes (β_CR) are determined at 25°C in BB^assoc_urea at 0 m urea at 38 and 1.3 nM active RNAP using Equation 2. B. Data obtained for α_CR are fit to Equation 5 as a function of active [RNAP] to obtain fits for K₁ and k₂ at varying concentrations of urea. C. Values of K₁ and k₂ are plotted as functions of urea and GB to determine solute concentration dependences, or “m-values”. Figure reproduced from (3) with permission (ACS Publications).

Where association is reversible (i.e., where θ_t=∞ is less than 1), then β_CR is interpreted as the decay-to-equilibrium rate constant, while if association is irreversible (θ_t=∞ = 1), β_CR is interpreted as the rate constant α_CR for formation of competitor-resistant complexes. In general, β_CR is related to α_CR by

$${\mathrm{\alpha }}_{\mathrm{C}\mathrm{R}}={\mathrm{\beta }}_{\mathrm{C}\mathrm{R}}-{\mathrm{k}}_{\mathrm{d}}={\mathrm{\beta }}_{\mathrm{C}\mathrm{R}}{\mathrm{\theta }}_{\mathrm{t}=\infty }$$ (4)

where k_d is the dissociation rate constant. Where possible, α_CR should be determined under conditions where RP_o formation is irreversible (β_CR >> k_d, so that α_CR = β_CR). Where decay-to-equilibrium studies are necessary, the best way to determine α_CR from β_CR is to obtain an independent determination of k_d. (see Note 15).

4.3 Determination of K₁ and k₂

The quantities K₁ and k₂ in Mechanism 1 are determined from analysis of the dependence of α_CR on RNAP concentration in excess RNAP and at sufficiently high concentrations of DNA and RNAP that the kinetics of the initial diffusion-limited promoter binding step are not rate-determining. Single-exponential kinetics of CR complex formation indicates that all intermediates (I₁ in Mechanism 1) formed before the rate-determining step (I₁ → I₂ in Mechanism 1) are in rapid equilibrium with each other and with free promoter DNA under the conditions investigated to date. For this situation, the rate constant α_CR for RP_o formation is a hyperbolic function of RNAP concentration (11–13):

$${\mathrm{\alpha }}_{\mathrm{C}\mathrm{R}}={\frac{K_1{k}_2{[RNAP]}_{\mathit{\text{tot}}}}{1+K_1[RNAP]}}_{\mathit{\text{tot}}}$$ (5)

where K₁ is the equilibrium constant for I₁ formation, k₂ is the rate constant for the DNA opening step that converts I₁ to I₂, and [RNAP]_tot is the total concentration of active RNAP (see Note 16). Nonlinear fitting of α_CR versus [RNAP]_tot is used to determine K₁ and k₂ (as in Fig. 1.B).

4.4 Determination of Observed Dissociation Rate Constant k_d

The first order kinetics of dissociation of open complexes, made irreversible by the presence of an inert (non-displacing) competitor (see Note 2), are analyzed by the rate equation

$${\mathrm{\theta }}_{\mathrm{t}}={\mathrm{\theta }}_{\mathrm{t}=\infty }+({\mathrm{\theta }}_0-{\theta }_{\mathrm{t}=\infty })(e^{-k_{d}t})$$ (6)

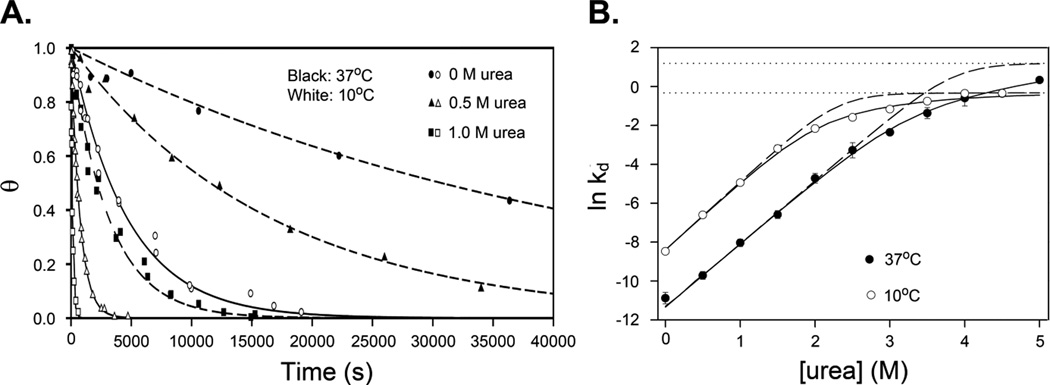
to obtain the dissociation rate constant k_d (see Fig. 2.A.): In Equation 6, θ_t=∞ is the fitted value of θ_t at completion of dissociation (typically θ_t=∞ less than 0.15), and θ₀ is the fitted initial value of θ (typically θ₀ ≈ 1).

Figure 2.

Data showing the determination of the urea dependences of k₋₂ and K₃. A. Rates of dissociation of filter-retainable open complexes are determined at 10 and 37°C in DB at 0, 0.5, and 1 M urea using Equation 6. B. Data obtained for ln(k_d) are fit as a function of urea concentration. Nonlinear fits are shown with (solid lines) and without (dashed lines, using Equation 7) consideration of the urea dependence of the term k₋₂/k₋₃. (For detailed analysis, see (5).) Horizontal dotted lines represent values of k₋₂, while the initial slopes of the fits determine the m-value -dlnK₃/d[urea]. Figure reproduced from (5) with permission (Elsevier).

Single exponential kinetics of dissociation of RP_o are observed after addition of an inert competitor because intermediates in dissociation formed before the rate-determining step (i.e. I₃ and I₂ in Mechanism 1) are unstable relative to RP_o and rapidly equilibrate with one another and with RP_o before the rate-determining conversion of I₂ to I₁. For this situation, k_d is interpreted (12) as

$${\mathrm{k}}_{\mathrm{d}}\approx {\mathrm{k}}_{-2}/(1+{\mathrm{K}}_3)$$ (7)

where K₃ is the overall equilibrium constant for the conversion of I₂ to RP_o. For most conditions investigated, K₃ is much greater than 1 for competitor-initiated dissociation experiments for λP_R and therefore k_d ≈ k₋₂/K₃. For dissociation initiated by a rapid shift to 1.1 M KCl (or 4 M urea), making K₃ much less than 1, the observed dissociation rate constant k_d ≈ k₋₂. Dissociation kinetics experiments initiated by upshifts to less extreme concentrations of urea have been used to determine rate constants k₃ and k₋₃ and establish the existence of the intermediate I₃ (5).

4.5 Interpreting Effects of Solutes

Effects of solutes on biopolymer processes arise from interactions of the solute with the biopolymer surface that is buried or exposed in the process (14). If the interaction of the solute with the biopolymer surface is favorable, relative to interactions with water, then addition of the solute will favor the direction of the process that exposes the biopolymer surface to water. Urea and Hofmeister salt ions like GuH⁺, I⁻ and SCN⁻ are protein denaturants because they interact favorably (or at least not unfavorably) with the amide and hydrocarbon surface of the protein that is exposed when the protein unfolds. On the other hand, osmolytes like GB and proline and Hofmeister salt ions like Glu⁻, F⁻ and SO₄²⁻ are protein stabilizers because their interactions with amide and aliphatic hydrocarbon surface of proteins are unfavorable relative to interactions with water. Effects of a solute on the rate constant for a step of a process are interpreted analogously in terms of interactions of the solute with the biopolymer surface that is buried or exposed in forming the high-free-energy transition state in that step (see (15)).

4.5.1 Interpreting Solute Effects on Equilibrium Constants

The effect of a solute on the equilibrium constant for a step is interpreted in terms of interactions of the solute with the biopolymer surface that is buried or exposed. For the conversion of reactant X to product Y, where the observed equilibrium constant K_obs = ([Y]/[X])_eq at solute concentration [solute] and K_obs,o is the corresponding equilibrium constant in the absence of that solute,

$$\text{ln}{\mathrm{K}}_{\text{obs}}=\text{ln}{\mathrm{K}}_{\text{obs},\mathrm{o}}+{\mathrm{\alpha }}_{\mathrm{X}\to \mathrm{Y}}\mathrm{\Delta }\mathrm{A}\mathrm{S}{\mathrm{A}}^{\mathrm{X}\to \mathrm{Y}}[\text{solute}]$$ (8)

where ΔASA^X→Y is the change in water-accessible surface area in the conversion of X to Y and the proportionality constant α_X→Y is the “interaction potential” quantifying the interaction of the solute with a unit area (i.e. 1 Ų) of a surface with the composition specified by ΔASA^X→Y. Predicted values of α_X→Y for interactions of urea with the predominantly hydrocarbon surfaces involved in various protein processes are generally in the range - (2.5 ± 0.5) × 10⁻⁴ M⁻¹ (1). Therefore, as proposed originally by Myers et al. (16), urea can be used semiquantitatively as a probe of ΔASA in protein processes irrespective of the composition of the ΔASA. In particular, urea is an unambiguous probe for distinguishing steps with large changes in ASA (e.g. I₂ → RP_o, which has very large urea dependence of K_obs, indicating a very large reduction in ASA (see Fig. 1.C.)) from those with small or compensating changes in ASA (e.g., I₁ → I₂, which has no urea dependence of K_obs, indicating small or compensating changes in ASA (see Fig. 2.B.)).

Values of α_X→Y for interactions of GB or proline with different surfaces can differ by as much as an order of magnitude, making them less easily interpretable and less useful as general probes of ΔASA in structurally uncharacterized processes (2). However, these solutes should prove very useful in conjunction with urea for beginning to characterize the composition of the ΔASA, in addition to the amount. For the surface exposed in local or global protein unfolding (approximately 70% hydrocarbon, 20% amide, 10% other polar or charged), effects of GB and proline are opposite in sign and slightly larger in magnitude than those of urea (2).

4.5.2 Interpreting Solute Effects on Rate Constants

For the interconversion of reactant X and product Y via high free energy transition state TS, with single exponential kinetics and observed forward and back rate constants k_f and k_b:

$$\text{ln}{\mathrm{k}}_{\mathrm{f}}=\text{ln}{\mathrm{k}}_{\mathrm{f},\mathrm{o}}+{\mathrm{\alpha }}_{\mathbf{X}\to \mathrm{T}\mathrm{S}}\mathrm{\Delta }\mathrm{A}\mathrm{S}{\mathrm{A}}^{\mathrm{X}\to \mathrm{T}\mathrm{S}}[\text{solute}],\text{and ln}{\mathrm{k}}_{\mathrm{b}}=\text{ln}{\mathrm{k}}_{\mathrm{b},\mathrm{o}}+{\mathrm{\alpha }}_{\mathrm{Y}\to \mathrm{T}\mathrm{S}}\mathrm{\Delta }\mathrm{A}\mathrm{S}{\mathrm{A}}^{\mathrm{Y}\to \mathrm{T}\mathrm{S}}[\text{solute}]$$ (9)

Protein folding transition states (TS) have recently been characterized using effects of denaturants (urea or guanadinium chloride) on folding and unfolding rate constants (15). The slopes of linear plots of ln(k) versus [denaturant] (closely related to kinetic m-values) for folding and unfolding of thirteen globular proteins were analyzed together with data on the temperature dependences of these rate constants (activation heat capacities) to quantify the amounts of amide and hydrocarbon ASA buried in folding to and from TS. From these data, we conclude that folding to TS preferentially buries amide surface and that the amount of amide and hydrocarbon surface buried in folding to TS in most cases exceeds that buried in forming all the native secondary structure of the protein.

For RNAP, the only rate constants that have been characterized in this way are k₂ and k₋₂ for the step that includes DNA opening (see Fig. 1.C. and Fig. 2.B.). For this step, neither k₂ nor k₋₂ depends on urea concentration. Additionally, k₂ is found to be independent of salt concentration and is unchanged when Cl⁻ is replaced by Glu⁻, variables which greatly affect other steps in the mechanism of transcription initiation. We conclude that DNA opening occurs in the active site cleft, greatly reducing effects of solutes and salts from what would be observed for DNA melting in solution. Also, or alternatively, burial of RNAP surface in this step may compensate for the exposure of DNA surface upon melting. Investigation of effects of other solute probes on this step will help distinguish between these two scenarios.

4.5.3 Example Application of Solute Dependence: DME Assembly in Late Steps of RP_o Formation

Recent work has shown the useful application of solute concentration dependence to the study of large conformational changes in the late steps of RP_o formation. The slope of the initial linear region of a plot of ln(k_d) versus urea for RP_o complexes at λP_R is approximately 3.0 M⁻¹ (see Fig. 2 B); an increase in urea concentration from 0 to 1 M therefore increases k_d by a factor of e³, about 20-fold. In this urea concentration range, k_d ≈ k₋₂/K₃ (Equation 7). Dissociation experiments after an upshift to high concentrations of urea in Fig. 2B reveal that k₋₂ is independent of urea concentration, so the entire effect of urea on α_X→YΔASA^X→Y is on the equilibrium constant K₃ for the conversion I₂ → RP_o. Therefore, lnK₃ decreases with increasing [urea] with a slope α_I2→RPoΔASA^I2→RPo = −3.0 M⁻¹. Interpreted as a protein folding or a subunit assembly process involving the DME of RNAP, using α_{I2→ RPo} = (2.5 ± 1) × 10⁻⁴ M⁻¹ (see above) indicates that ΔASA^{I2 → RPo} is about 1.2 × 10⁴ A². Folding buries 80–100 A² per amino acid residue buried (ref?), so this ΔASA^I2→RPo corresponds to 120–150 buried residues. The effect of GB on dissociation is similar in magnitude and opposite in sign to that of urea, consistent with this interpretation.

Many important questions remain about this folding transition in the late steps of the mechanism, including which regions of RNAP and promoter DNA are responsible for it, and its role in transcription initiation. Analysis of amino acid sequences of the beta and beta prime subunits with the program PONDR (Predictions of Natural Disordered Regions; (17, 18)) predicted regions of RNAP that are disordered in holoenzyme and that might fold in RP_o formation, contributing to the massive urea dependence of the step I₂→RP_o (3). Several such unfolded regions, located at the downstream end of the cleft, are now designated downstream mobile elements (DME) (6). Variants of RNAP with deletions in these regions are being investigated to determine their effect on K₃ and its urea dependence. For example, deletion of residues 1149–1190 of the β’ subunit of RNAP removes most of a DME called the β’ jaw (19, 20). This deletion (termed “ΔJAW RNAP”) reduces the urea dependence of K₃ from −3.0 M⁻¹ to −2.0 M⁻¹, reducing the predicted number of residues folded in this step from 120–150 for WT RNAP to 80–100 for ΔJAW RNAP and suggesting that these 42 residues of the jaw are unstructured in the unbound WT RNAP holoenzyme and fold as part of the conformational changes that stabilize the initial open complex I₂ (6). We find that the urea dependence of k_d for RP_o formed at the T7A1 promoter is similar to that seen for λP_R (ER, unpublished data), indicating that a similar folding transition occurs to stabilize the initial open complex at this promoter. Solute studies performed at other promoters, as well as determinations of clamp width by FRET (21), RNAP-DNA crosslinking, or other methods will help to answer questions about the generality and physiological role of this massive conformational change late in the mechanism of transcription initiation.