A Generative Model for Probabilistic Label Fusion of Multimodal Data

Abstract

The maturity of registration methods, in combination with the increasing processing power of computers, has made multi-atlas segmentation methods practical. The problem of merging the deformed label maps from the atlases is known as label fusion. Even though label fusion has been well studied for intramodality scenarios, it remains relatively unexplored when the nature of the target data is multimodal or when its modality is different from that of the atlases. In this paper, we review the literature on label fusion methods and also present an extension of our previously published algorithm to the general case in which the target data are multimodal. The method is based on a generative model that exploits the consistency of voxel intensities within the target scan based on the current estimate of the segmentation. Using brain MRI scans acquired with a multiecho FLASH sequence, we compare the method with majority voting, statistical-atlas-based segmentation, the popular package FreeSurfer and an adaptive local multi-atlas segmentation method. The results show that our approach produces highly accurate segmentations (Dice 86.3% across 22 brain structures of interest), outperforming the competing methods.

1 Introduction

Registration-based segmentation [1] is popular in brain image analysis because the relatively low variability of this organ (compared to the mediastinal or abdominal regions) allows for accurate registrations and therefore good segmentation results. The principle of registration-based segmentation is straightforward: assuming that an image with manually labeled structures (henceforth an “atlas”) is available, this image can be spatially mapped or deformed (i.e., “registered”) to a different target image. The registration outputs a deformation field that can be used to warp (“propagate”) the atlas labels in order to obtain an estimate of the labeling (“segmentation”) of the target image.

Registering and propagating the labels from a single atlas achieves limited accuracy because a single example cannot sufficiently represent the whole population of potential test data. This is a particularly limiting factor when pathology might be present in the images. A possible way of overcoming this limitation is using a statistical atlas, which models the intensity and/or label distribution in a population from a collection of atlases. For example, instead of a discrete label at each voxel, a statistical atlas has a vector of label probabilities representing the prior probability of observing a segmentation label at that location. Statistical atlases have two major advantages over using a single template: 1. the image is a summary of the population that was used to build the atlas and therefore it is more likely that a given target image can be successfully registered to it; and 2. the fact that the labels are probabilistic rather than deterministic can overcome, to some extent, inaccuracies in the registration.

Building a statistical atlas from a set of labeled images is computationally expensive: it is typically an iterative process which requires registering the images to the current estimate of the atlas, updating this estimate by averaging the warped images, registering the images again, and so on [2]. However, once the statistical atlas has been built, only one registration is required to propagate the label probabilities from the atlas to a target image. These propagated probabilities are usually interpreted as a Bayesian prior that, combined with a likelihood term (computed from the image intensities), provides posterior probabilities for the possible labels at each voxel location [3,4,5].

Even though probabilistic atlases have been successfully applied in brain MRI segmentation, they still have difficulties representing larger anatomical variations. A computationally taxing, though effective way of handling such cases is registering each available atlas to the target image independently. Even though this multiplies the registration time by the number of atlases N, one would hope that, if enough training data is available, at least one or two atlases will be registered successfully to the test image. The question is then how to automatically decide from which atlases the labels should be picked to render the final segmentation. We call this problem label fusion.

1.1 Label Fusion

The popularity of label fusion algorithms is rising mainly for two reasons. First, the maturity of registration algorithms allows them to produce excellent results. The second reason is that the increasing processing power of computers alleviates the high computational demand associated with this technique. Label fusion techniques are based on weighting the contributions of the atlases depending on their similarity to the target image after registration. There are two major families of label fusion techniques: those that allow the weights to change across spatial locations and whose that do not.

In global weighting methods, the weight of the contribution of each atlas to the segmentation is the same for every voxel of the target image. In “majority voting” [6], all atlas are weighted equally, independently of their similarity to the target image after registration. Therefore, the most frequent propagated label is selected at each voxel. The main limitation of this method is that, since atlases are equally weighted, underrepresented features in the training data are often outweighted by the more frequent variations. In “best atlas selection” [7], the labels are propagated only from the atlas which is most similar to the test image after warping. This represents a considerable waste of CPU time dedicated to registering atlases, whose labels are never used. SIMPLE (Langerak et al. [8]) computes a joint segmentation using majority voting, estimates the performance of the individual atlases given the current segmentation, defines weights based on the performances and finally uses these weights to update the estimated segmentation. The performances of the atlases and the fused segmentation are iteratively updated until convergence. In [9], global weights are defined based on the normalized mutual information (MI) of each atlas and the target image after registration.

Locally-weighted label fusion techniques achieve higher segmentation accuracy [10] by exploiting the fact that different atlases might have been correctly registered in different parts of the target image. Therefore, it makes sense to borrow labels from different atlases at different locations. STAPLE [11] weights the propagated labels according to an estimated accuracy level, while incorporating consistency constraints. However, it is limited by the fact that it does not consider the intensities of the target image in the segmentation. An ad-hoc fusion method is proposed by Isgum et al. in [12]. They compute the local weight of each atlas at each voxel as the inverse of the absolute intensity difference of the target and registered images. The weighting maps are convolved with a Gaussian kernel to ensure the smoothness of the output. A more principled version of this method is proposed by Sabuncu et al. in [13]. They define a generative model in which a discrete membership field specifies the index of the atlas from which the intensity and label where borrowed at each voxel. Variational expectation maximization is used to infer the most likely labels in this framework. The fusion weights are given by the posterior distribution of the membership field in light of the observed data.

Furthermore, local label fusion has been extended to a nonlocal framework by Coupé et al. in [14]. They compare the local appearance of the target volume with patches of the atlases centered not only at the voxel at hand but also at shifted locations, and use the resulting similarity metrics to weight the label corresponding to each patch. Because they explore the neighborhood of each voxel, they do not need the registration to be precise, hence a linear transform (which can be quickly optimized) rather than a deformable registration method can be used. Other recent works on label fusion have explored ways of improving the segmentation based on exploiting the correlations of the errors from the different atlases to enhance the fusion [15], using advanced similarity metrics derived from manifold learning for the weighting [16] and developing hierarchical schemes for the fusion depending on the local label confidence [17].

1.2 Label Fusion in Intermodal and in Multimodal Setups

There are certain scenarios, where we cannot assume consistency between the intensity values of the atlases and the target image. This is particularly a problem in MRI, in which the intensities depend heavily on the selected pulse sequence, imaging hardware and acquisition parameters. Even though histogram matching and intensity standardization techniques (such as [18]) can alleviate this problem, they are only applicable if the type of MRI contrast of the input images is the same (e.g., T1-weighted).

The intermodality¹ registration literature has coped with the issue of intensity variation mainly through metrics based on global MI. We will assume here that the registration of the atlases to the target image has already been solved. In case of multimodal target data, the registration can either use heuristics (e.g., using the average MI between the target and all the atlases) or estimate the true multichannel MI via high-dimensional histograms [19] or entropic spanning graphs [20].

Global label fusion approaches can be easily generalized to the inter / multimodal case using MI to compute global “distances” between images. This is the case for best template selection [7] and Cao et al.’s manifold learning approach [16]. For majority voting, SIMPLE and STAPLE, generalization is not even needed because they do not rely on the intensities of the images, and they are thus independent of the modalities or number of image channels of the data.

Local fusion approaches, which are the most appealing ones due to their excellent performance, are however harder to extend to inter- and multimodal scenarios: techniques that rely on computing local similarities by directly comparing image intensities (e.g., Isgum et al. [12]) cannot be used. In the multimodal case, if one of the channels matches the modality of the atlas, it would be possible to discard the rest of the channels and use a intramodal algorithm. However, this strategy is suboptimal in the sense that it does not consider data that might convey important information.

Another option would be to use MI or normalized cross correlation (NCC) to define local weights. However, both MI and NCC require a number of image samples for estimation, which represents a compromise between localization and metric reliability if it is to be computed at a certain voxel using the local neighborhood. Moreover, neither MI nor NCC decay very fast with poorly aligned images. Therefore, one typically needs to define a function that maps them to weights, enhancing the differences in metric values (e.g. w = [NCC]^α, with α > 1). Despite these disadvantages, this type of heuristics could be used to generalize the methods by Isgum et al., Coupé et al. [14] and Wang et al. [15] to intermodal and multimodal settings. Sabuncu et al.’s method [13], which produces excellent results in an intramodality brain MRI segmentation problem, relies on a principled generative model in which the intensity of the target image at a voxel location is assumed to be equal to the intensity of one of the deformed atlases at the same location plus Gaussian noise. This generative model was modified to accommodate the intermodality case in [21].

1.3 Contribution of This Paper

To the best of our knowledge, no prior work has been carried out that deals with how to carry out label fusion on multimodal data. In a previous conference paper [21], we presented a generative model for multi-atlas image segmentation across modalities. Rather than directly comparing the intensities of the registered atlases and the target image, we proposed exploiting the consistency of voxel intensities within the segmentation regions, as well as their relation with the propagated labels. Here we extend this framework to the multimodal case as well as present some improvements in the inference algorithm that yield improved segmentation results. In particular, we use expectation maximization (EM) rather than k-means to compute the estimates of the image intensity parameters.

The rest of the paper is organized as follows. Section 2.1 describes the generalization of the framework to multimodal data, as well as the improved inference algorithm based on EM. Section 3 presents the experimental setup, in which we use the proposed method and a number of competing algorithms (majority voting, FreeSurfer [22], statistical-atlas-based segmentation and a NCC-adaption of Isgum et al.’s algorithm) to segment brain MRI data from a multiecho FLASH sequence. Finally, Section 4 discusses the results and future directions of work and concludes the paper.

2 Methods

The proposed method relies on a generative model of image data. We first describe the model and then propose a method to carry out inference in order to obtain the segmentation corresponding to a target image.

2.1 Generative Model

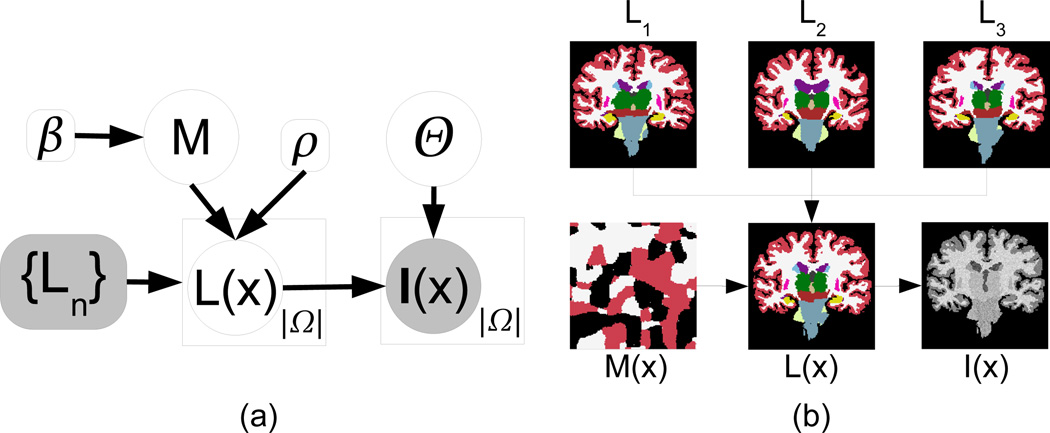
The generative model displayed in Figure 1 (see corresponding equations in Table 1) was used in this study:

1. We assume that a set of N atlases (each with ℒ different labels) has been registered to a common space (which is the space of the target scan). We name the propagated label maps {L_n} = L₁, …, L_N. Rather than using the discrete propagated labels directly in the fusion, we assume that each voxel in the (deformed) atlases has an associated vector of label probabilities which is built through a logOdds model [23] with slope ρ. This model is described by Equation 1 in Table 1, where $D_n^l$ is the signed distance transform corresponding to label l in atlas n; it is greater than zero inside the object, zero on the boundary, and less than zero outside. The logOdds model essentially replaces the discrete labels by smoother probability maps which can, to some extent, compensate for inaccuracies in the registration (in a similar way as statistical atlases).

2. A discrete field of memberships M such that M(x) ∈ {1, …, N} is sampled from a Markov random field (MRF) parametrized by the smoothness constant β (Equation 2 in the table, where 𝒩(x) represents the 6-neighborhood of x). Higher values of β encourage larger clusters of voxels with the same label. The field M(x) indicates from which atlas the generated image borrows the information at each voxel location x in the image domain Ω.

3. From {L_n} and M, the “real”, underlying segmentation of the data L(x) is generated by sampling at each voxel location x from the probability vector specified by atlas L_M(x) at x (Equation 3 in the table).

4. Given the label of a voxel L(x), the “real”, underlying image intensity I^*(x) is sampled from a multivariate Gaussian distribution associated with that label (Equation 4 in Table 1). Each of the ℒ Gaussians is described by a C × 1 mean vector μ_l and a C × C covariance matrix Σ_l (where C is the number of image channels). We assume a flat prior for the Gaussian parameters i.e., p(μ_l) ∝ 1, p(Σ_l) ∝ 1.

5. I^*(x) is corrupted by a multiplicative bias field B(x), which is modeled through a set of low-spatial-frequency basis functions {ψ_k(x)} to yield the final observed intensities I(x) (Equation 5 in the table, where the exponential ensures that the field is non-negative). The bias field is described by the vectors of coefficients {b_k}, where b_k = [b_{k, 1}, …, b_k,C]^T groups the C coefficients (one per channel) for basis function ψ_k. Note that we allow a different set of coefficients per image channel, i.e. we assume that the bias fields for the different channels are independent. As for the parameters of the Gaussian distributions, we also assume a flat prior for the bias field coefficients: p({b_k}) ∝ 1. Henceforth, we use the variable Θ to refer to the whole set of intensity parameters i.e., Θ = {{b_k}, {μ_l }, {Σ_l}} and p(Θ) ∝ 1.

Fig. 1.

a) Graphical model of the image generation process. Random variables are in circles and constants are in boxes. Observed variables are shaded. Plates indicate replication. b) Illustration of the generative process: three deformed atlases are combined through the membership field M(x) to yield the labels L(x). The image intensities I(x) are obtained by sampling a Gaussian distribution for each label. We purposely chose the Gaussian parameters to make I(x) resemble a T1-weighted MRI scan.

Table 1.

Equations corresponding to the graphical model in Figure 1(a)

$p(L(\mathbf{x})=l|L_n)=\text{exp}[\rho D_n^l(\mathbf{x})]/{\sum }_{l\prime =1}^{ℒ}\text{exp}[\rho D_n^{l\prime }(\mathbf{x})]$ $M~\frac{1}{Z_{\beta }}{\prod }_{x\in \Omega }\text{exp}(\beta {\sum }_{\mathbf{y}\in 𝒩(\mathbf{x})}\delta (M(\mathbf{x})=M(\mathbf{y})))$ L(x) ~ p(L(x) = l|LM(x)) ${\mathbf{I}}^{*}(\mathbf{x})~{(2\pi )}^{-\frac{C}{2}}{\left|{\Sigma }_{L(\mathbf{x})}\right|}^{-\frac{1}{2}}\text{exp}[-\frac{1}{2}{({\mathbf{I}}^{*}(\mathbf{x})-{\mathit{\mu }}_{L(\mathbf{x})})}^T{\Sigma }_{L(\mathbf{x})}^{-1}({\mathbf{I}}^{*}(\mathbf{x})-{\mathit{\mu }}_{L(\mathbf{x})})]$ I(x) = B(x)I* (x), with B(x) =diag(exp [−∑k bk ψk(x)])

It is worth to note that some segmentation methods are particular cases of this generative model. For example, by setting β = 0, ρ → ∞, Σ_l = lim_α→∞ αId (where Id is the identity matrix) we obtain majority voting. Setting β → ∞ and ρ → ∞ amounts to best atlas selection. Finally, making β = 0 gives a model which is very similar to statistical-atlas-based segmentation [3]. The main difference is that, instead of registering a pre-built statistical atlas (a parametric model), we have a nonparametric approach in which an atlas is constructed directly in target image space by registering all the atlases to the dataset to segment.

2.2 Segmentation Using Bayesian Inference

We can use Bayesian inference to compute the most likely segmentation by maximizing the posterior probability of the labels L(x) given the available information, i.e., the image intensities I(x) and the deformed atlases {L_n}:

$$\mathrm{L̂}=\underset{L}{\text{argmax}}p(L|I,\{L_n\})=\underset{L}{\text{argmax}}{\int }_{\Theta }p(L,\Theta |I,\{L_n\})d\Theta =\underset{L}{\text{argmax}}{\int }_{\Theta }p(L|\Theta ,I,\{L_n\})p(\Theta |I,\{L_n\})d\Theta$$ (1)

In our previous conference paper, we attempted to maximize p(L, Θ|I, {L_n}) with respect to {L, Θ}, which was achieved with a coordinate ascent algorithm, i.e., alternatively optimizing for L and Θ. This is a k-means style algorithm. However, when we compute the most likely Θ, we are not interested in the labels L, hence a better strategy would be to integrate out L. This leads to the EM algorithm proposed in this paper, in which soft label assignments (rather than hard, like in k-means) are used to update Θ.

Looking at Equation 1, we see that it involves a high-dimensional integral over the parameters in Θ. However, we can make the assumption that the statistical distribution of these parameters given the observed data I and {L_n} is sharp, i.e., p(Θ|I, {L_n}) ≈ δ(Θ − Θ̂), where δ(·) is Kronecker’s delta and Θ̂ = argmax_Θ p(Θ|I, {L_n)}. This assumption can be quite realistic, since we do not expect the values of Θ to deviate much from Θ̂ without considerably decreasing the likelihood of the model. Then, the integral disappears and the most likely labels are (approximately) given by:

$$\mathrm{L̂}\approx \underset{L}{\text{argmax}}p(L|\mathrm{\Theta ̂},I,\{L_n\})$$ (2)

We will first discuss how to obtain the optimal estimate of Θ̂. Then, we will describe a method to compute the most likely segmentation with Equation 2.

Computing the Most Likely Image Intensity Parameters

The optimal point estimate of the image intensity parameters Θ is given by:

$$\mathrm{\Theta ̂}=\underset{\Theta }{\text{argmin}}(-\text{log}p(I|\Theta ,\{L_n\}))$$ (3)

$$=\underset{\Theta }{\text{argmin}}(-\text{log}[\sum _L\sum _{M}p(I,L,M|\Theta ,\{L_n\})])$$ (4)

where we have used p(Θ) ∝ 1. Equation 4 is computationally intractable due to the sum over all possible membership fields ∑_M, which does not factorize over voxels. Instead, we use variational EM (VEM) to minimize an upper bound. We define the free energy J as:

$$J=-\text{log}p(I|\Theta ,\{L_n\})+KL[q(M)\Vert p(M|I,\Theta ,\{L_n\})]$$ (5)

$$=-H(q)-\sum _{M}q(M)\text{log}p(I,M|\Theta ,\{L_n\})$$ (6)

where H(·) is Shannon’s entropy, KL(·‖·) is the Kullback-Leibler divergence and q(M) is a statistical distribution over M, which approximates the posterior probability p(M|I, Θ, {L_n}). The free energy J is a bound of the target function to minimize (Equation 3) because the KL divergence is nonnegative. The standard computational trick in VEM is to assume that q(M) factorizes:

$$q(M)=\prod _{\mathbf{x}\in \Omega }{q}_x(M(\mathbf{x})),$$

which eventually makes the intractable sum tractable. The idea is to minimize J by iteratively optimizing for q(M) (expectation or E step) and Θ (maximization or M step):

• –
  E step: to optimize J for q(M), it is easier to work with Equation 5, since the only term depending on q(M) is the KL divergence. We have

  $$\mathrm{q̂}=\underset{q}{\text{argmin}}\sum _{M}q(M)\text{log}\frac{q(M)}{p(M|I,\Theta ,\{L_n\})}=\underset{q}{\text{argmin}}\sum _{M}q(M)\text{log}\frac{q(M)}{p(M){\sum }_{L}p(I|L,\Theta )p(L|M,\{L_n\})}=\underset{q}{\text{argmin}}(\sum _{\mathbf{x}\in \Omega }\sum _{n=1}^N{q}_x(n)\text{log}{q}_x(n)-\beta \sum _{\mathbf{x}\in \Omega }{E}_{q_x}[\sum _{\mathbf{y}\in 𝒩(\mathbf{x})}{q}_y(M(\mathbf{x}))]-\dots \dots -\sum _{\mathbf{x}\in \Omega }\sum _{n=1}^N{q}_x(n)\text{log}[\sum _{l=1}^{ℒ}p(I(\mathbf{x})|{\Theta }_l)p(L_{M(\mathbf{x})}=l)])$$
  Building the Lagrangian with a multiplier for the constraint ∑_n q_x(n) = 1 and taking derivatives with respect to q_x, we obtain:

  $$q_x(M(\mathbf{x}))=\frac{\text{exp}[\beta {\sum }_{\mathbf{y}\in 𝒩(\mathbf{x})}{q}_{\mathbf{y}}(M(\mathbf{x}))]{\sum }_{l=1}^{ℒ}p(I(\mathbf{x})|{\Theta }_l)p(L_{M(\mathbf{x})}(\mathbf{x})=l)}{{\sum }_{n=1}^N\left(\text{exp}\right[\beta {\sum }_{\mathbf{y}\in 𝒩(\mathbf{x})}{q}_{\mathbf{y}}(n)]{\sum }_{l\prime =1}^{ℒ}p(I(\mathbf{x})|{\Theta }_{l\prime })p(L_n(\mathbf{x})=l\prime ))},$$ (7)

  which can be solved with fixed point iterations. Note that the constraint q_x ≥ 0 is implicitly enforced due to the nonnegative nature of probabilities and of the exponential function.
• –
  M step: to optimize J with respect to Θ, we focus on Equation 6 instead (since the entropy does not depend on Θ):

  $$\mathrm{\Theta ̂}=\underset{\Theta }{\text{argmax}}f(\Theta )=\underset{\Theta }{\text{argmax}}\sum _{\mathbf{x}\in \Omega }\sum _{n=1}^N{q}_x(n)\text{log}(\sum _{l=1}^{ℒ}[p(I(\mathbf{x})|{\Theta }_l)p(L_n(\mathbf{x})=l)]).$$ (8)
  Here, one must be careful with the scaling of the Gaussian probability density function:

  $$p(\mathbf{I}(\mathbf{x})|{\Theta }_l)=\text{exp}[\sum _{c=1}^C\sum _k{b}_{k,c}{\psi }_k(\mathbf{x})]𝒢({\mathbf{I}}^{*}(\mathbf{x});{\mathit{\mu }}_l,{\mathbf{\Sigma }}_l)$$

  where 𝒢 is the probability density function of the multivariate Gaussian distribution. Taking matrix derivatives of Equation 8 with respect to μ_l and Σ_l (see [24]), we obtain the following update equations:

  $${\mathit{\mu }}_l\leftarrow \frac{{\sum }_{\mathbf{x}\in \Omega }{w}_l(\mathbf{x}){\mathbf{I}}^{*}(\mathbf{x})}{{\sum }_{\mathbf{x}\in \Omega }{w}_l(\mathbf{x})},{\mathbf{\Sigma }}_l\leftarrow \frac{{\sum }_{\mathbf{x}\in \Omega }{w}_l(\mathbf{x})({\mathbf{I}}^{*}(\mathbf{x})-{\mathit{\mu }}_l){({\mathbf{I}}^{*}(\mathbf{x})-{\mathit{\mu }}_l)}^{\mathrm{T}}}{{\sum }_{\mathbf{x}\in \Omega }{w}_l(\mathbf{x})}$$ (9)

  where

  $$w_l(\mathbf{x})=\sum _{n=1}^N{q}_x(n)\frac{p(\mathbf{I}(\mathbf{x})|{\Theta }_l)p(L_n(\mathbf{x})=l)}{{\sum }_{l\prime =1}^{ℒ}p(\mathbf{I}(\mathbf{x})|{\Theta }_{l\prime })p(L_n(\mathbf{x})=l\prime )}$$

For the bias field parameters {b_k}, the derivatives of the target function in Equation 8 are:

$$\frac{\partial f}{\partial {\mathbf{b}}_k}\sum _{\mathbf{x}\in \Omega }{\psi }_k(\mathbf{x})\sum _{n=1}^N\frac{{\sum }_{l=1}^{ℒ}p(\mathbf{I}(\mathbf{x})|{\Theta }_l)p(L_m(\mathbf{x})=l)[\mathbf{I}\mathbf{d}-{\mathbf{\Sigma }}_l^{-1}({\mathbf{I}}^{*}(\mathbf{x})-{\mathit{\mu }}_l){\mathbf{I}}^{*\mathrm{T}}(\mathbf{x})]}{{\sum }_{l\prime =1}^{ℒ}p(\mathbf{I}(\mathbf{x})|{\Theta }_{l\prime })p(L_m(\mathbf{x})=l\prime )}$$ (10)

and we use a quasi-Newton algorithm with line search (BFGS [25]) to numerically find the optimum. Because the bias field has a low number of degrees of freedom, the first iteration of the VEM algorithm already produces a relatively good estimate of the coefficients. Therefore, the BFGS algorithm converges very quickly (one or two steps) in successive iterations.

Computing the Final Segmentation

Once we have the estimate Θ̂, computing the most likely segmentation in Equation 2 is straightforward. Replacing the posterior probability of M by its approximation q(M) in Equation 2, we have:

$$\mathrm{L̂}\approx \underset{L}{\text{argmax}}p(L|I,\mathrm{\Theta ̂},\{L_n\})\approx \sum _{M}p(L|M,I,\mathrm{\Theta ̂},\{L_n\})q(M)=\prod _{\mathbf{x}\in \Omega }\sum _{n=1}^N{q}_x(n)\frac{p(I(\mathbf{x})|{\mathrm{\Theta ̂}}_{L(\mathbf{x})})p(L_n(\mathbf{x})=L(\mathbf{x}))}{{\sum }_{l\prime =1}^{ℒ}p(I(\mathbf{x})|{\mathrm{\Theta ̂}}_{l\prime })p(L_n(\mathbf{x})=l\prime )}$$

Since this expression factorizes over voxels, the most likely label at location x is just:

$$\mathrm{L̂}(\mathbf{x})=\underset{l}{\text{argmax}}\sum _{n=1}^N{q}_x(n)\frac{p(I(\mathbf{x})|\mathrm{\Theta ̂})p(L_n(\mathbf{x})=l)}{{\sum }_{l\prime =1}^{ℒ}p(I(\mathbf{x})|{\mathrm{\Theta ̂}}_{l\prime })p(L_n(\mathbf{x})=l\prime )}$$ (11)

The complete segmentation algorithm is summarized in Table 2.

Table 2.

Summary of the proposed multimodal label fusion framework

Compute the most likely image intensity parameters: 0. Initialize qx(n) = 1/N, Σl = limα →∞ αId (equivalent to majority voting). 1. Update q with Equation 7 until convergence. 2. Update means and variances with Equation 9. 3. Update the bias field using the derivatives in Equation 10. 4. Go to 1 until convergence. Compute the most likely segmentation for each voxel using Equation 11 and the latest estimate of q from step I.1.

3 Experiments and Results

3.1 Datasets

We used two different datasets in this study, one for training and one for testing. The training dataset (i.e., the atlases) consists of 39 T1-weighted scans acquired with a MP-RAGE sequence in a 1.5T scanner with the following parameters: TR=9.7ms, TE=4.ms, TI=20ms, flip angle = 10°, 1 mm. isotropic resolution. Thirty-six brain structures were manually delineated by expert human raters using the protocol described in [26]. We note that these are the same subjects that were used to construct the probabilistic atlas in FreeSurfer [22]. As in [21,13], rather than using all 36 structures in the evaluation, we consider a representative subset here: left and right white matter (WM), cerebral cortex (CT), lateral ventricle (VE), cerebellum white matter (CWM), cerebellum cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HP) and amygdala (AM).

The test dataset [27] consists of eight multimodal brain MRI scans acquired with a multiecho FLASH sequence in a 1.5T scanner with the following parameters: TR=20ms, TE = minimum, flip angle = {3°, 5°, 20°, 30°}, 1 mm. isotropic resolution. There are therefore C = 4 channels available, one per value of flip angle. The lowest flip angles produce PD-weighted images, whereas the higher angles yield T1-weighted data. The same set of 36 structures was labeled using the same protocol. These manual annotations were drawn on the images corresponding to the largest flip angles, i.e., T1-weighted scans.

3.2 Preprocessing

All the scans from both datasets were first skull-stripped using ROBEX [28]. For the test dataset, we only used the T1-weighted volume as input to the skull stripping module. The training images were then deformed to the test images using a nonlinear, symmetric, diffeomorphic registration method (ANTS [29], version 1.9). For the registration metric, we used the mean mutual information (computed with 32 bins) between the four fixed images (i.e., the four flip angles) and the moving image. The executed command was:

ANTS 3 −m MI[fix1,mov1,0.25,32] … −m MI[fix4,mov4,0.25,32]
       −r Gauss[3,0] −t SyN[0.25] −i 11×51×51×15 −o output

The resulting warps were used to deform the distance transforms of the different labels and atlases $D_n^l$, which are in turn used to compute label probabilities for each voxel of the target image to segment with Equation 1 in Table 1.

In addition to registering the atlases to the target images (used in label fusion), we built a single probabilistic atlas via an iterative, unbiased approach [2] as described as follows. First, we used the FreeSurfer pipeline to obtain intensity-standardized images. The atlases were then spatially normalized by registering with a population template image (which was the average intensity image computed based on the latest registrations). Since the images were intensity normalized, we used cross correlation as the registration similarity metric. Hence, this time the command was:

ANTS 3 −m CC[fix,mov,1,5] −r Gauss[3,0] −t SyN[0.25]
       −i 11×51×51×15 −o output

After a round of registration (where all atlases were registered with the current template), the template was updated as the average intensity image. Then, the atlases were re-registered to the template and this whole cycle was iterated until the intensity template converged. The final warps were then used to deform the corresponding manual annotations and compute label probabilities for each voxel in the statistical atlas as:

$$p(L(\mathbf{x})=l)=(1/N)\sum _{n=1}^N\delta (L_n(\mathbf{x})=l).$$ (12)

The obtained template was registered to the test images using the mean mutual information metric, as described above. The resulting deformations were used to propagate the label probabilities of Equation 12 to the target image space.

3.3 Experimental Setup

We used the N = 39 atlases to segment the eight multimodal volumes using a number of competing approaches:

• –Majority voting. Rather than using discrete labels (i.e., ρ = ∞ in the logOdds model), we use ρ = 1, which is shown in [13] to constitute a better prior by introducing some “fuzziness”, which can partially compensate for inaccurate registration. The performance of majority voting marks the accuracy that can be reached with registration only.
• –The statistical atlas, which was constructed by co-registering the atlases as described in Section 3.2. The algorithm to obtain the segmentation given the (registered) statistical atlas is very similar to our method in Section 2.2. We actually used the same implementation assuming a single atlas for which the label probabilities are not given by the logOdds model, but by Equation 12 instead. The basis for the bias field model {ψ_l(x)} was set to a third-degree polynomial, which, in 3D, yields 20 coefficients per image channel. Rather than iterating through all voxels in the estimation of the bias field (Equations 8 and 10), we only used a randomly selected subset (10% of the total number of voxels |Ω|) to speed up the algorithm. The estimate will still be reliable thanks to the low number of degrees of freedom of the field.
• –An ad-hoc locally-weighted label fusion method. To estimate the local similarity, we computed the 10^th power of the NCC of the two images in a 7 × 7 × 7 voxel window around the location of interest. We also considered using MI instead of NCC, but NCC performed better in pilot experiments and also has the advantage that it can efficiently be computed using integral images [30]. Since four channels are available for the target image to analyze, we simply took the average NCC of the four. The coefficient of the exponential (10) was coarsely tuned based on visual inspection of the results on a T1-weighted MRI scan of the first author’s brain, preprocessed in the same way as the test data.
• –The proposed framework. We used ρ = 1.0, β = 0.75, which we borrowed from [13]. A third-order polynomial was again used for the bias field modeling, using 10% of the available image data for the estimation. The iterative EM algorithm was stopped when no parameter in Θ changed more than 0.1% or when the maximal number of iterations (set to 25) was reached.
• –Finally, it is also interesting to segment the data using only one of the channels in order to estimate the benefit of using all four channels. As a representative, state-of-the-art method, we used FreeSurfer to segment the T1-weighted channel (i.e., flip angle = 30°). Using FreeSurfer also has the advantage that it was trained on the same training data used in this study, enabling a fair comparison. Moreover, the fact that it uses the same set of labels facilitates the comparison with the other methods.

In order to evaluate the accuracy of the aforementioned approaches, we used the popular Dice coefficient (Dice = 2|A ∩ M|/[|A| + |M|]), where A and M denote the automatic and manual segmentations, respectively; and |·| denotes the volume.

3.4 Results

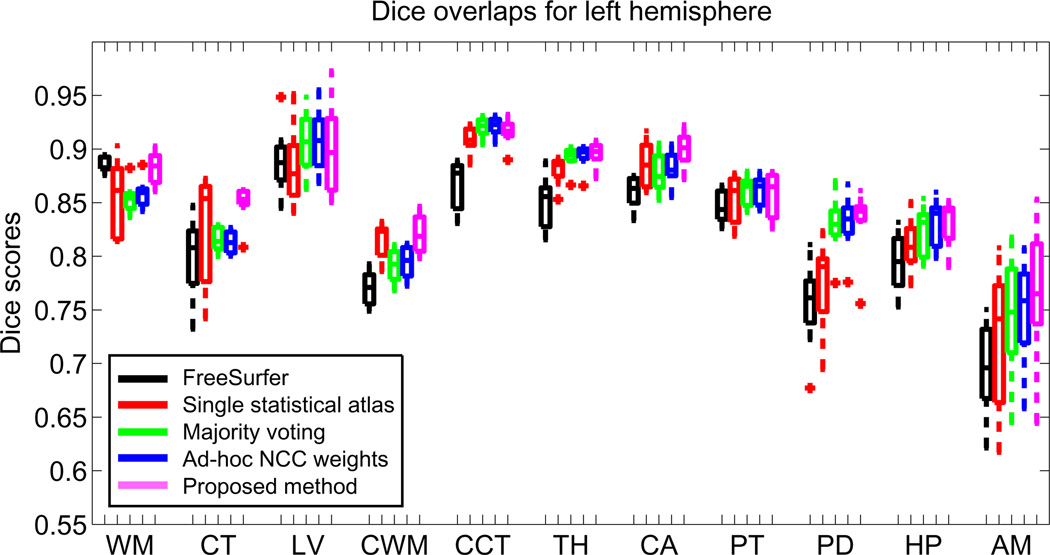
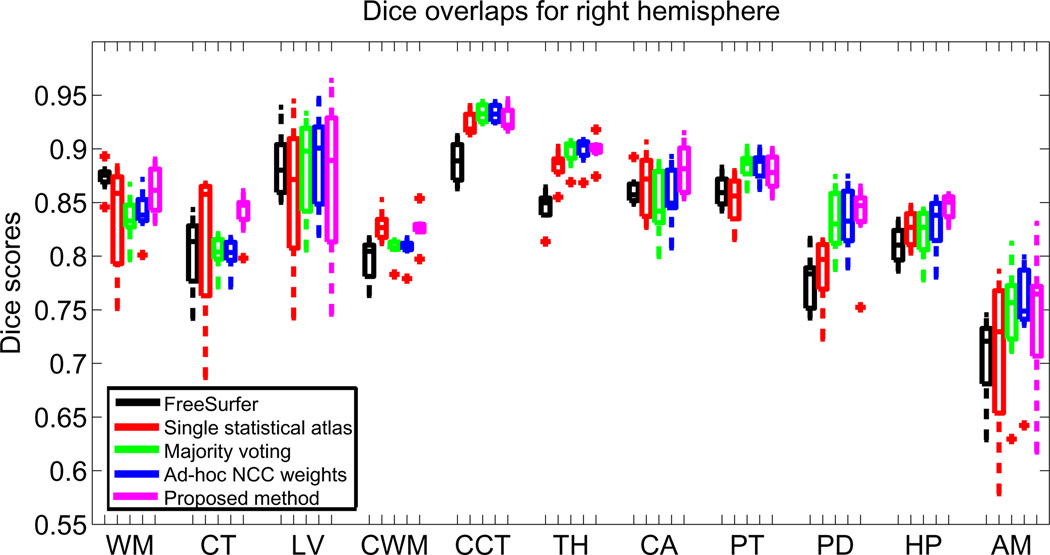
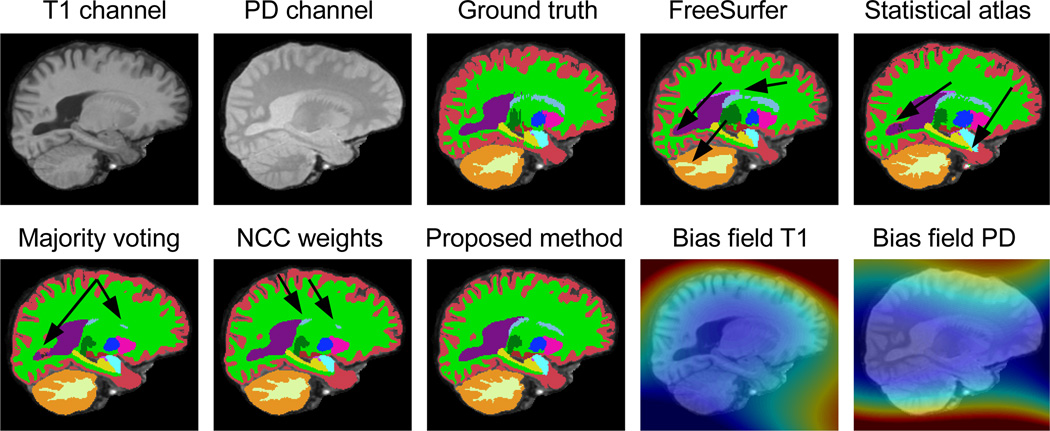
Figures 2 and 3 display, for each hemisphere, the boxplots for the Dice overlaps corresponding to the structures of interest listed in Section 3.1. The mean Dice scores for each hemisphere are listed in Table 3. Table 4 displays p-values corresponding to paired t-tests comparing the different competing methods with the proposed algorithm. Finally, Figures 4 and 5 show sample segmentations from the different methods.

Fig. 2.

Boxplot of Dice overlap scores corresponding to the 11 structures of interest for the left hemisphere; see Section 3.1 for the abbreviations. Horizontal box lines indicate the three quartile values. Whiskers extend to the most extreme values within 1.5 times the interquartile range from the ends of the box. Samples beyond those points (outliers) are marked with crosses.

Fig. 3.

Boxplot of Dice overlap scores corresponding to the 11 structures of interest for the right hemisphere; see caption of Figure 2

Table 3.

Mean Dice scores (in %) across the 11 structures of interest for each method: left hemisphere (top row), right hemisphere (middle), and both combined (bottom)

Method	FreeSurfer	Stat.atlas	Maj.Vot.	Ad-hoc NCC	This study
Left hemisphere	82.4	84.4	85.4	85.6	86.4
Right hemisphere	83.2	84.1	85.1	85.4	86.1
Both	82.8	84.3	85.2	85.5	86.3

Table 4.

p values corresponding to paired t-tests comparing the Dices scores from the different methods with those from the proposed approach

Method	FreeSurfer	Stat.atlas	Maj.Vot.	Ad-hoc NCC
Left hemisphere	4.1 · 10−19	2.3 · 10−11	2.3 · 10−6	1.6 · 10−4
Right hemisphere	9.4 · 10−12	5.0 · 10−11	1.4 · 10−4	9.6 · 10−3
Both	7.9 · 10−29	5.0 · 10−21	1.9 · 10−9	8.9 · 10−6

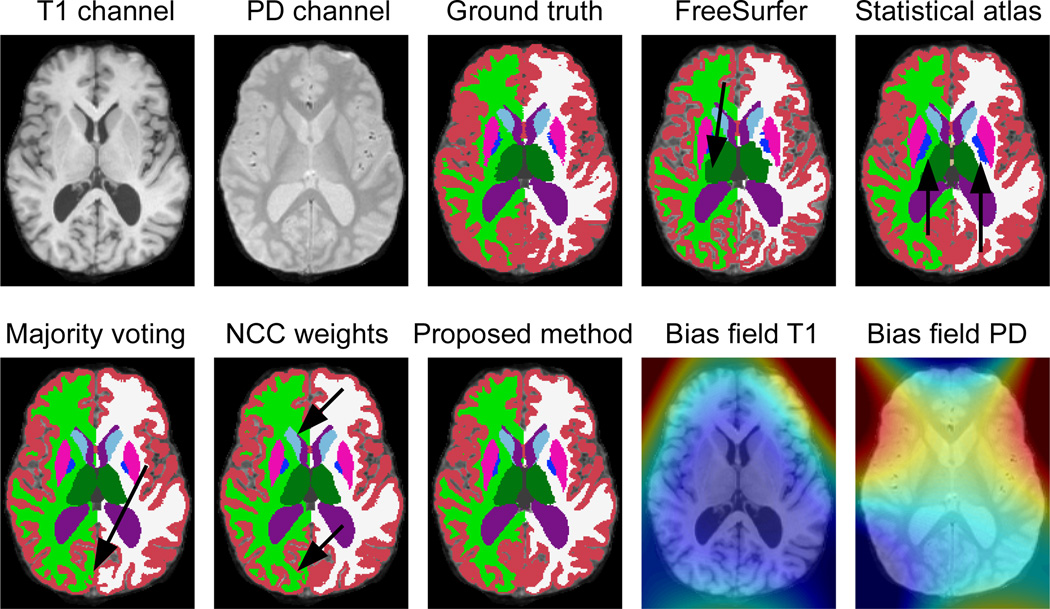
Fig. 4.

Sagittal slice of a sample scan: input data (two of the four channels), ground truth, outputs from the different algorithms, and bias fields estimated by our method (blue=0.85, red=1.15). The arrows point to mistakes made by the different algorithms.

Fig. 5.

Axial slice of a sample scan and its automated segmentations (see caption of Figure 4)

FreeSurfer is the one of the best performers only in the cortex. For the other structures, it is consistently inferior to the other methods, which take advantage of the multimodal nature of the target images. It is important to mention that the T1-weighted volume, which is the one we feed to the FreeSurfer pipeline, has relatively poor white matter / gray matter contrast (see for instance Figure 4), which explains the low Dice overlaps produced by this method compared with previously reported results (e.g. [13]).

Majority voting, thanks to the good performance of the registration method and the large number of atlases, outperforms FreeSurfer and also the method based on a single statistical atlas. Even though the statistical atlas produces better results for the cortices of the cerebrum and the cerebellum, which are very difficult to register, it performs considerably worse in the subcortical structures. In this case, the flexibility of having the 39 atlases registered independently represents an advantage over the single registration of the statistical atlas.

When the locally-computed NCCs are used to assign different weights to the atlases at each voxel, a small (Dice increment 0.3%) but significant (p < 10⁻⁵) improvement is achieved. When we use the generative model proposed here, we obtain as good results as the statistical atlas on the cortices, significantly outperforming the other multi-atlas methods (majority voting and NCC-based). Furthermore, the proposed method also provides slightly better results majority voting and the NCC-based algorithm for the subcortical structures.

Sample segmentations are displayed in Figures 4 and 5. The segmentations are in general poor in the cortex (red label), but quite accurate for the subcortical structures. The arrows pinpoint the typical mistakes made by the other methods as explained above. In Figure 4, FreeSurfer makes quite a few mistakes around the lateral ventricle (in purple) and in the cerebellum. The statistical atlas, next to mistakes in the ventricle, also displays a leak in the hippocampal label (yellow). Majority voting cannot capture the large ventricle, which is anatomically infrequent. The ad-hoc locally-weighted model produces a poor segmentation for the caudate nucleus (light blue). The proposed algorithm, on the other hand, provides a robust segmentation across all structures.

In figure 5, FreeSurfer (next to oversegmenting the cortex) severely undersegments the thalamus. The statistical atlas undersegments the left and right pallidum (dark blue), whereas majority voting shows some problems with the cortex. So does the ad-hoc NCC method, which also undersegments the right caudate nucleus (oversegmenting the right lateral ventricle). Again, the proposed algorithm produces the most accurate segmentation across the different structures.

4 Discussion

In this paper we have presented a multimodal label fusion scheme that does not make any assumptions about the relation between the intensities of the deformed atlases and the target images. Instead, the framework uses a principled generative model to take advantage of the consistency of intensities within image regions. This is done by assuming that the intensities corresponding to each label follow a multivariate Gaussian distribution. The results show that the presented approach outperforms: 1. majority voting, which does not consider the intensities of the target images; 2. FreeSurfer, a state-of-the-art segmentation tool that only takes advantage of one of the channels of the target data; 3. using a single statistical atlas (which takes advantage of all the channels); and 4. a heuristic rule for locally weighted label fusion.

The proposed method has the disadvantage that the Gaussian intensity distribution assumption might break down because of the nature of the data or if two structures with different intensity profiles share the same label. For example one might only be interested in one structure such as the hippocampus, in which case a single Gaussian might not be an appropriate model for the background intensities. One possible solution would be to use a mixture of Gaussians. In this case, one must be careful because excessive flexibility in the intensity model might lead to leaks in the segmentation.

Another disadvantage of the presented framework is that the parameters β and ρ are fixed by the user. It would be desirable to allow the inference method to handle them automatically, either by computing point estimates (as we did with Θ here) or integrating them out. Exploring this direction, as well as incorporating the registration into the framework (rather than considering it a preprocessing step) remains as future work.