Practical estimate of gradient nonlinearity for implementation of ADC bias correction

Abstract

Purpose

This work describes an efficient procedure to empirically characterize gradient nonlinearity and correct for the corresponding ADC bias on a clinical MRI scanner.

Methods

Spatial nonlinearity scalars for individual gradient coils along superior and right directions were estimated via diffusion measurements of an isotropic ice-water phantom. Digital nonlinearity model from an independent scanner, described in literature, was rescaled by system-specific scalars to approximate three-dimensional bias correction maps. Correction efficacy was assessed by comparison to unbiased ADC values measured at isocenter.

Results

Empirically estimated nonlinearity scalars were confirmed by geometric distortion measurements of a regular grid phantom. The applied nonlinearity correction for arbitrarily oriented diffusion gradients reduced ADC bias from ~20% down to ~2% at clinically-relevant offsets both for isotropic and anisotropic media. Identical performance was achieved using either corrected DWI intensities or corrected b-values for each direction in brain and ice-water. Direction-average trace image correction was adequate only for isotropic medium.

Conclusion

Empiric scalar adjustment of an independent gradient nonlinearity model adequately described DWI bias for a clinical scanner. Observed efficiency of implemented ADC bias correction quantitatively agreed with previous theoretical predictions and numerical simulations. The described procedure provides an independent benchmark for nonlinearity bias correction of clinical MRI scanners.

INTRODUCTION

Absolute apparent diffusion coefficient (ADC) has been suggested as a potential biomarker for cancer diagnosis and treatment monitoring (1-4). There is interest in minimizing scanning time to obtain quantitative ADC in as few measurements as possible for clinical research applications (3-5), particularly when multiple b-values are needed to distinguish individual components of diffusion weighted signal (3,6,7). At isocenter, any three orthogonal diffusion weighted imaging (DWI) measurements are sufficient to characterize a diffusion tensor trace, ADC, for tissue of arbitrary anisotropy (8-10). Better than 3% reproducibility of ADC measurements at isocenter was demonstrated for multi-center, multi-platform studies using an ice-water phantom (11). For DWI measurements away from the isocenter, gradient nonlinearity bias was detected as a primary source of ADC errors (> 10%) on clinical scanners (11,12). This systematic bias is specific to gradient design, which differs among clinical vendors and even with the same vendor (12-15). The systematic deviations from gradient linearity are currently not routinely corrected for diffusion measurements on commercial MRI systems. The resulting ADC errors confound multi-institutional efforts to standardize and validate ADC biomarkers in clinical trials (4,11,16). Removal of the detected instrumental bias is desired to establish confidence levels for ADC measurements in clinical body oncology applications (3-7).

Unlike the rotation-invariant unbiased ADC, systematic nonlinearity bias possesses tensor properties due to spurious gradients generated both along and orthogonal to the primary gradient directions (13-15). Theoretical description for medium of arbitrary anisotropy predicts that this bias is dependent on the mutual orientation of tissue diffusion tensor and applied diffusion gradient direction (17,18). Thus, comprehensive correction of nonlinearity bias (17) necessitates full diffusion tensor imaging (DTI) experiment (more than six DW directions) followed by eigenvalue calculation to obtain unbiased ADC, which limits its practical value for clinical applications (3-5). Recent research (18), based on numerical simulation for medium of arbitrary anisotropy and gradient system described in (13), has shown that adequate approximation of the ADC nonlinearity bias can be achieved by squaring projection of nonlinearity tensor onto the corresponding diffusion gradient direction.

Similar to routine geometric distortion correction (13,14), nonlinearity bias correction in diffusion measurements requires information on spatial dependence of gradient fields (15). For commercial scanners, this proprietary information is usually known to system engineers (12), but is not provided to the general MRI user (14). Alternatively, system nonlinearity can be characterized by empirical mapping of gradient fields using a distortion phantom, e.g. (13), however this is tedious and difficult to automate in the clinical setting. The availability of a minimal effort procedure, to quickly and independently characterize system nonlinearity, would be desirable both to enable correction of ADC bias for the clinical scanners that do not provide built-in correction tools (11), as well as benchmark alternative bias correction algorithms as they become available from vendors (12).

This work outlines and implements an independent procedure to empirically describe gradient nonlinearity and correct for the corresponding bias in clinical ADC measurements. A system-specific nonlinearity tensor approximation is proposed by three-dimensional rescaling of digital gradient field maps for a similar (horizontal-bore) geometry, described in literature (13). The rescaling is performed numerically using three characteristic nonlinearity scalars obtained empirically for each of the three gradient coils. An efficient method is introduced to estimate these nonlinearity scalars from the minimum number of experiments. Finally, practical implementation of the theoretical framework for ADC bias correction, introduced in (18), is illustrated for arbitrary orthogonal DWI gradients both in an isotropic ice-water phantom and in anisotropic brain tissue on a representative clinical scanner. The correction efficiency is evaluated by comparison to known values or unbiased (isocenter) measurements for individual diffusion directions as well as trace DWI.

METHODS

The implemented empiric workflow included steps to characterize and correct for gradient nonlinearity of an arbitrary horizontal-bore MRI scanner. The characteristic nonlinearity scalars for the given gradient coil system were obtained by measuring ADC bias in an isotropic (ice-water) phantom as a function of right and superior offset for diffusion gradients applied along the primary coil axes. An independent model of gradient nonlinearity for a representative horizontal-bore system was derived numerically based on literature (13) and digitized on a discrete Cartesian 3D-grid. To approximate 3D nonlinearity maps for gradient coils of the actual scanner, the independent model nonlinearity grid was rescaled according to measured characteristic nonlinearity scalars. The digital 3D corrector maps were generated for the set of orthogonal diffusion gradient orientations. The above steps were performed once for the gradient system. Further steps included a procedure to correct acquired DWI for an object of arbitrary geometry to produce an unbiased ADC estimate and compare the measurements with those that are free of bias (e.g., isocenter) to evaluate performance.

(1) Diffusion Phantoms

The isotropic phantom was constructed from a single 172-mL (29mm diameter) tube filled with distilled water and surrounded by ice-water envelope for temperature control to 0°C (18,19). This phantom provided the universal ADC standard with known diffusion coefficient of 1.1×10⁻³ mm²/s (20) and measurement accuracy within 2% at isocenter (11,19). Compliant with local Institutional Review Board policies, DWI scans of the human brain for a consented volunteer provided an anisotropic phantom.

(2) DWI acquisition and ADC measurements

The DWI measurements were performed on a 3T Ingenia MRI scanner (Philips Medical Systems, Best, The Netherlands). The following diffusion-weighted single-shot echo-planar acquisition parameters were used for the ice-water phantom: repetition time TR = 8000ms, echo time TE = 98ms, acquisition matrix = 128×128, FOV = 240 × 240mm, 25 slices, 6mm thick, 4mm gap, bandwidth = 2.65kHz/pixel, single average, no parallel imaging, b-values = 0 and 1000s/mm²; and for brain: TR = 8434ms, TE = 72ms, FOV = 224 × 224mm; 60 slices, 2mm thick, 1mm gap, bandwidth = 1.89kHz/pixel, two averages, b-values = 0 and 800s/mm². Two sets of DWI waveforms were used with diffusion gradients applied on three orthogonal axes (U ≡ (u₁, u₂, u₃); ${\mathit{u}}_i^T{\mathit{u}}_j\equiv {\delta }_{ij}$): “LAB” directions, U = I = [(1,0,0)^T, (0,1,0)^T, (0,0,1)^T], and “non-LAB directions, $\mathit{U}=[{(\frac{1}{2},\frac{1}{2},\frac{1}{\sqrt{2}})}^T,{(\frac{1}{2},\frac{1}{2},\frac{1}{\sqrt{2}})}^T,{(\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}},0)}^T]$. Sixteen-direction DTI, including non-LAB, was also acquired for the brain tissue to provide an ADC benchmark as an average of diffusion tensor eigenvalues. Second order volume-shim encompassing the object was used for all measurements.

For both U-gradient waveforms, the ADC was measured for the three separate DWI directions and the trace DWI, defined as the signal geometric mean of individual diffusion directions. Off-center measurements for the ice-water phantom were performed using torso coil and repositioning the ice-water phantom with 80mm offset in superior/inferior (SI) and 45mm offset in right/left (RL) directions. Axial and sagittal slices were acquired for SI and RL offset directions, respectively. The axis of the phantom tube was oriented perpendicular to the DWI slices. The stack of slices from both offsets provided a spatial extent of approximately +/−140 mm with approximately 40 individual offset measurements in the SI and RL directions. Axial ADC measurements for brain were performed using head coil near the isocenter, as well as a table offset superiorly by 120mm to move both coil and anatomy away from isocenter.

ADC was measured from a 10mm circular ROIs placed in the middle of the ice-water tube and from irregular (FA-specific) ROIs for the brain tissue. The AP location for the ROIs varied between −20 and 15mm. Typically, 12-15 offsets (ROIs) were used for right and superior ADC bias measurements with the ice-water phantom. Measurement uncertainty was defined as two standard deviations of the ADC pixel noise within an ROI (~90 pixels). The gradient nonlinearity bias was estimated as a deviation from the true (known) ADC value of 1.1×10⁻³ mm²/s (20) for the isotropic ice-water and as a deviation from the unbiased values at the isocenter for the brain tissue.

(3) Characterization of system nonlinearity

A characteristic nonlinearity scalar for an individual gradient coil along one of the LAB axes was determined as an offset value along this axis where the observed ADC bias for this gradient coil exceeded the measurement uncertainty within an ROI. System nonlinearity scalars were estimated from the ADC bias measurements for individual diffusion directions using LAB-DWI (U = I) on the ice-water phantom as a function of right (R) and superior (S) offsets and normalizing to the true ADC value 1.1×10⁻³ mm²/s (20). The measured bias dependencies were fit to a quadratic function of offset, and an offset value corresponding to above 5% bias was used as a bulk nonlinearity scalar along the offset direction. As predicted by (18), the two (R and S) offset experiments with LAB diffusion gradients directly provided squared RL- and SI-scalars for the three diagonal elements of the nonlinearity tensor ($l_{xx}^2$, $l_{yy}^2$ and $l_{zz}^2$). The anterior/posterior (AP)-scalar was inferred from presumed cylindrical symmetry of the gradient coil geometry (13,15,18): l_ii (r_AP)=l_jj (r_RL).

An alternative (standard) estimate of the nonlinearity scalars was performed from a 3D T1 weighted scan of a regular grid phantom by manual measurements of the geometric distortion ratio, $l_{ii}\left(\mathit{r}\right)=\frac{\Delta r_i^d\left(\mathit{r}\right)}{\Delta r_i^{true}\left(\mathit{r}\right)}$, of the distorted inter-grid spacing, $\Delta r_i^d\left(\mathit{r}\right)$, without vendor's geometric correction, to the true spacing, $\Delta r_i^{true}\left(\mathit{r}\right)=15mm$, along RL and SI directions, i = x, z. The absolute error of the manual distance measurements for inter-grid spacing was about 2-3mm. The empiric estimates of the bulk nonlinearity scalars for the gradient coils thus obtained were further validated by system application scientists using information of their gradient design.

Using spherical harmonic coefficients provided in (13) for an independent system, digital 3D-maps for individual gradient coil fields, $B_z^{G_i}\left(\mathit{r}\right)$, i = X, Y, Z, were generated on a discrete spatial 3D-grid, r = r_xyz, sampled every 5mm within FOV = 500mm (21). These field maps were then numerically differentiated along Cartesian grid and normalized by the effective gradient strength at the isocenter to produce baseline model maps (i.e. 3D look-up tables) for the diagonal components of gradient nonlinearity tensor (17, 21): $l_{ii}\left({\mathit{r}}_{xyz}\right)=\frac{1}{\Vert {\mathit{G}}_{io}\Vert }\frac{\partial {\mathit{B}}_z^{{\mathit{G}}_i}}{\partial {\mathit{r}}_i}$. The baseline nonlinearity scalars of the independent model system (13) were obtained for each gradient coil by examining $l_{ii}^2\left({\mathit{r}}_{R∕S}\right)$ offset dependence for the bias values corresponding to those measured for the actual scanner.

The ratio of the baseline model scalar to the nonlinearity scalar measured for the actual scanner (at the same bias level) along a particular Cartesian direction was used to rescale the grid spacing of the independent model. This rescaling procedure was equivalent to spatial reshaping of the digital 3D objects by either compression or expansion. The resulting rescaled maps provided a digital 3D approximation for gradient coil nonlinearity of the actual scanner. The reshaped discrete $l_{ii}\left({\mathit{r}}_{xyz}\right)=l_{ii}^{xyz}$ 3D-maps were then interpolated with cubic splines on a uniform Cartesian grid sampled every 3.2mm within FOV = 320mm. In all further calculations, the derived (i.e. scaled) nonlinearity maps were used unaltered for all experimental data generated using the given gradient system.

(4) Nonlinearity bias correction

In contrast to the theoretical formalism of (18), digital 3D corrector maps, C^k, for k^th DWI direction were generated in discrete form using diagonal nonlinearity elements, $l_{ii}^{xyz}$, that were empirically derived by above-described rescaling of independent model (13), and ignoring all off-diagonal cross-terms, l_i≠j~0,

$$C_{xyz}^k={\left[{\Sigma }_i^{X,Y,Z}{l}_{ii}^{xyz}{u}_{ik}^2\right]}^2.$$

These “master” correctors were obtained once for a specific U and used for subsequent correction of arbitrary objects, scan geometries, and nominal b-values. Consistent with the experimental measurements (see section-2), the master correctors were constructed for two U-scenarios of the three orthogonal diffusion gradients.

For experimental data, each master corrector map, $C_{xyz}^k$, was resampled on a uniform spatial grid by cubic-spline interpolation to produce C^k_fps according to DICOM header information for the specific imaged volume (namely, FOV, pixel and slice spacing, slice location and orientation, as well as table offset). Here (f, p, s) denote voxel indices in frequency, phase and slice dimensions respectively. This custom-geometry corrector was then applied voxel-by-voxel to yield corrected DWI intensities (18), ${\left(S_{b^k}^c\right)}_{fps}=S_0^{\frac{{C^k}_{fp{s}^{-1}}}{{C^k}_{fps}}}{S}_{b^{\prime }}^{\frac{1}{{C^k}_{fps}}}$, and produce a corrected ADC by $AD{C}_c=\frac{1}{3b_0}{\sum }_k^3(ln{S}_0-ln{S}_{b^k}^c)$. Alternatively, corrected b-maps, ${\left(b_c^k\right)}_{fps}=b_0{C^k}_{fps}$, were used with uncorrected DWI intensities, $S_{b^{\prime }}^k$, to produce a corrected ADC by $AD{C}_c=\frac{1}{3b_o}{\sum }_k^3\frac{ln{S}_o-ln{S}_{b^{\prime }}^k}{C^k}$. Consistent with the acquisition conditions, the nominal b-values of b₀ = 800 and 1000 were included in the ADC analysis. All calculations were automated using Matlab 7 (Mathworks, Natick MA).

RESULTS

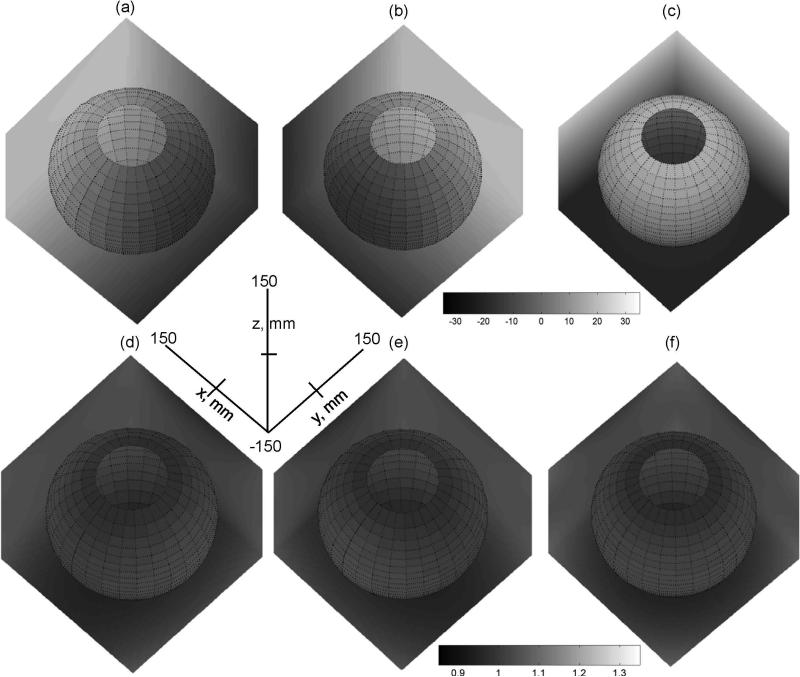
Figure 1 illustrates digital three-dimensional gradient filed maps, $B_z^{G_i}\left({\mathit{r}}_{xyz}\right)$ (a-c), and primary nonlinearity maps, l_ii (r_xyz) (d-f), for the independent model of (13) within the FOV = 300mm. (The full gray-scale range of the plots corresponds to FOV = 500mm, as described in Methods (21).) The direction of growing intensity for the field maps (a-c) points along the primary axis of the gradient coil, while deviation from unity for the nonlinearity maps (d-f) reflects spatial non-uniformity of the corresponding gradients. The most uniform gradients are achieved at isocenter, while nonlinearity is growing moderately toward the FOV edges, as is evident from the gray-scale variation across the boundary planes. Furthermore, both gradient fields and nonlinearity for Y-coil (b,e) are rotated by 90-degrees around z-axis in respect to X-coil maps (a,d), while Z-coil field (c) and nonlinearity (f) are symmetric in xy-plane. Three unidirectional cross-sections through the isocenter would provide the characteristic x,y,z-spatial scalars for each individual (model) gradient nonlinearity map, l_ii. However, above noticed symmetries suggest that six of nine scalars would be sufficient.

Figure 1.

3D digital gray-scale maps within FOV = 300mm for gradient fields and their first derivatives along primary directions for X,Y, and Z-gradients described by independent model (13, 21): (a) $B_z^X$, (b) $B_z^Y$, (c) $B_z^Z$, (d) l_xx, (e) l_yy, (f) l_zz. The x,y,z-axes provide common spatial coordinates directions for all 3D maps. Gray-scale bars provide the range for depicted field maps (a-c) and gradient nonlinearity (d-f). The same gray-scale range is used for the 3D maps in a row. Spatial dependence is represented by gray-scale changes at boundary planes (X=150mm, Y=150mm, Z=−150mm) and spherical slice through the FOV. The unbiased (uniform) MR gradients in (d-f) correspond to value of one (at isocenter). The deviation from uniformity (bias) is visually estimated by the gray-scale variation away from isocenter.

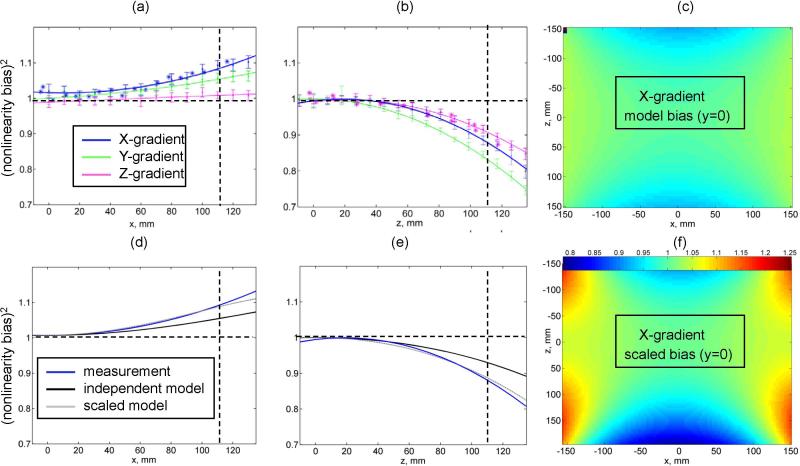
For the actual clinical scanner, the unidirectional nonlinearity bias is efficiently measured for all coils simultaneously in a single LAB-DWI experiment for the isotropic (ice-water) phantom as a function of the right (Figure 2a) and superior (Figure 2b) offsets from the magnet isocenter. The solid colored lines in Figures 2a and 2b correspond to unidirectional quadratic fits for the nonlinearity bias of the three individual gradient coils. The equivalence of gradient nonlinearity characteristics obtained through the ADC bias measurements (Fig.2a,b data with error bars) to conventional measurement of geometric distortion on a regular grid phantom, (Fig.2a,b asterisks) is evident from good agreement between the results both for the right offset for the X-gradient coil (Fig.2a, blue line) and for the superior offset for the Z-coil (Fig.2b, magenta line). Deviation of 2-4% from unity observed for geometric distortion data near zero-offset reflect the error for manual measurement of distorted inter-grid spacing. The ADC error-bars of 2-3% are determined primarily by signal-to-noise within ROI and nominally independent of the offset. Small (< 2%) deviations of the ADC bias from unity near the magnet isocenter observed for some coils suggest negligible effect of the cross-terms between diffusion and imaging gradients, as predicted in (18). Observed effect of shim imperfections, pronounced at larger offsets, also stays within the measurement uncertainty. Overall, absolute nonlinearity bias for all coils is higher for the superior compared to the right offset (Fig.2b versus Fig.2a). The highest absolute system nonlinearity is observed for the Y-coil along SI direction (Fig.2b, green line).

Figure 2.

Measured ADC nonlinearity bias (ADC_measured/ADC_known) for ice-water phantom is plotted for X (blue), Y(green) and Z(magenta) gradient coil as a function of right offset (a) and superior offset (b). Error bars correspond to a standard deviation over 10 mm diameter circular ROI (approx. 90 pixels). Solid lines correspond to quadratic fit for the measured bias. Asterisks mark results for geometric distortion measurements performed on a regular grid phantom along x (blue) and z (magenta) directions. Vertical scatter of asterisks near zero offset reflects the distortion measurement error (2-4%). Horizontal dashed lines mark expected value for linear gradients. Vertical lines at ~110mm offset mark the characteristic scalar measurement for gradient nonlinearity. (d) and (e) panes illustrate linear rescaling (dotted gray) of the independent model (black line) to the characteristic system scale (blue line) for X gradient coil. (f) shows results of 2D rescaling for independent model map in (c) at y=0 by characteristic z and x scalars measured from (d) and (e). Common nonlinearity range used for (f) and (c) maps is indicated by a color-bar.

Figures 2d and 2e illustrate the qualitative agreement between nonlinearity trends measured for the X-coil of the actual scanner (blue lines) with the unidirectional cross-sections (black lines) through the digital 3D nonlinearity maps (Fig.1d) generated for an independent horizontal-bore scanner (13). However, as is evident from the intersection with the vertical dashed guide line at 110mm offset (Fig.2d,e), the measured nonlinearity bias of the actual scanner is steeper than that of the literature model (13). For the X-gradient coil, the same ~5% right-nonlinearity bias is measured for the actual scanner at 110mm as for the model system (13) at 150mm, indicating that the 3D model nonlinearity of the X-coil along RL-direction, l_xx, requires ~30% compression (Fig.2d, gray line). Similarly, z-scalar for the needs ~20% compression (Fig.2e, gray line); and y-scalar of l_xx (given by x-scalar of l_yy due to RL-AP symmetry) requires ~25% compression as well. Figure 2f illustrates the results of the non-uniform compression of the Cartesian grid for the 2D cross-section (y = 0 plane) of the digital X-coil nonlinearity map, $l_{xx}^{xyz}$ (Fig.2c), for the independent model system (13). The desired compression of the 2D map for the independent model (Fig.2c) to the actual scanner scale (Fig.2f) is evident from the changes in the heat-map color, especially near the edges. A similar process was followed for the reshaping of the Y-coil nonlinearity map (Fig.1e), l_yy. In contrast, the characteristic z-scalar for the Z-coil needed 10% expansion, while x- and y-scalars did not change appreciably. Hence, 3D-map of the baseline model (13) for the Z-coil nonlinearity (Fig.1f), l_zz, had to be stretched along SI. Slight deviations of the rescaled model from actual measured bias both before and after point of “matched” nonlinearity scale (in Fig.2d,e: gray versus blue line) are within the measurement uncertainty (<2%, Fig.2a,b error bars) over the full 300mm FOV.

The resulting rescaled nonlinearity maps that provide 3D approximation for the system-specific nonlinearity of individual coils are shown in Figures 3a-c. Relative nonlinearity scale of Fig.3a-c (gray-scale bar) is kept the same as in Fig.1d-f to illustrate changes in the extent of nonlinearity between obtained (rescaled) system approximation and original independent model of (13). Higher nonlinearity is evident for rescaled X- and Y-gradient maps in Fig.3a,b versus original model in Fig.1d,e, while Z-gradient is virtually unchanged (Fig.3c versus Fig.1f). The resulting pixel-wise RMS deviation from linearity (l_ii – 1) for all three gradients in Fig.3a-c within FOV = 300mm was 4.5% (RMS bias). The retrospective comparison of the rescaled nonlinearity maps to system design maps produced an RMS of 1.1% and less than 3% absolute deviation for more than 90% of pixels within 300mm FOV, confirming adequate approximation of system nonlinearity.

Figure 3.

Gray-scale plots of primary rescaled nonlinearity maps, $l_{ii}^{xyz}$, for FOV = 300mm: (a) X-gradient, (b) Y-gradient, (c) Z-gradient, and corrector maps, $C_{xyz}^k$, for non-LAB DWI: (d) C¹, (e) C², (f) C³. The x,y,z-axes provide common spatial coordinates and directions for all 3D maps. Gray-scale bars provide the range for depicted gradient nonlinearity (a-c) and DWI bias (d-f). A single gray-scale range is used for the 3D maps in a row. The same nonlinearity scale is used for (a-c) as in Fig.1(d-f). The unbiased (uniform) gradients correspond to value of one (at isocenter). The deviation from uniformity (bias) is visually estimated by the gray-scale changes away from isocenter. Spatial dependence is represented by gray-scale variation at boundary planes (X=150mm, Y=150mm, Z=−150mm) and spherical slice through the FOV.

Figures 3d-f show corrector maps obtained as linear combinations of the squared nonlinearity maps for individual coils (Fig.3a-c) weighted by non-LAB diffusion gradient direction in coil coordinates, as described in Methods. Since both X- and Y-gradients are active for all no-LAB DWI directions, similar spatial symmetries are observed for the corresponding corrector maps (Fig.3d-f). In case of LAB gradients, when single gradient is active per DWI direction, the individual correctors (not shown) would simply represent the squares of the corresponding nonlinearity maps (Fig.3a-c). The 3D corrector maps also provided a description of the spatial distribution for the expected diffusion weighting bias along individual DWI directions (18). Thus, different absolute bias is expected at the same spatial location depending on DWI direction (Fig.3). The direction-average (isotropic trace) corrector map, constructed within FOV of nearly quadratic gradient nonlinearity, would exhibit negligible dependence on DWI direction: pixel-wise difference below 2% for LAB versus non-LAB scenario.

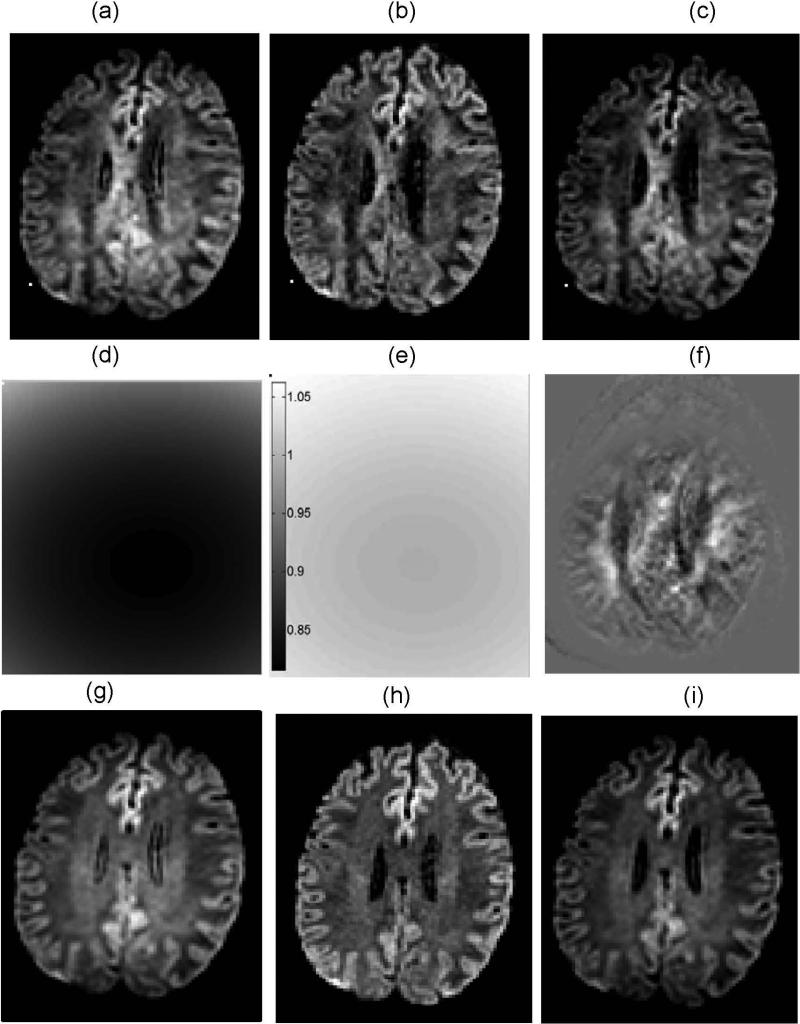
Figure 4 illustrates performance of the correctors based on the above described approximate gradient coil nonlinearity maps (Fig.3) when applied to data generated independently from brain tissue using non-LAB gradients. The observed diffusion weighting at the superior offset (z ~ 130mm, Fig.4a,g) and close to the isocenter (z ~ 10mm, Fig.4b,h) agree with the predicted bias (Fig.4d,e). Up to 20% percent b-value “under-weighting” is predicted for the superior offset (Fig.4d), while negligible bias (<3%, Fig.4e) is expected for the bulk of the image slice acquired close to the isocenter (Fig.4b,h). Corrected DWI intensities shown in (Fig.4c,i) are close to the unbiased measurement (Fig.4b,h) both for a single diffusion direction (Fig.4b,c) and the trace (geometric average) image (Fig.4h,i). Direction-average correction applied directly to the biased trace image (Fig.4g) is not equivalent to the geometric average of individually corrected images (Fig.4i) and results in the anatomy-specific deviations (Fig.4f). These deviations are clearly pronounced for highly anisotropic corpus callosum (CC), while less significant for isotropic cerebrospinal fluid (CSF).

Figure 4.

DWI bias correction illustrated for a single slice through the brain anatomy for the first non-LAB DWI direction (a-c) and the trace image (g-i): (a,g) biased by underweighting at superior offset of z~130mm; (b,h) negligible bias for z~10mm; (c,i) corrected diffusion weighting for z~130mm; (d) 2D corrector (bias) map corresponding to (a); (e) 2D corrector (bias) map for (b); (f) difference between trace DWI corrected for individual directions (i) and single “average corrector” trace image (not shown). Positive difference in (f) is illustrated by pixels brighter than (zero) background outside of the brain. Magnitude images are plotted for all panes but (f), with black color corresponding to zero-magnitude. Same window leveling is used for DWI (a-c) and (g-i). (d) and (e) share the same gray-scale bar.

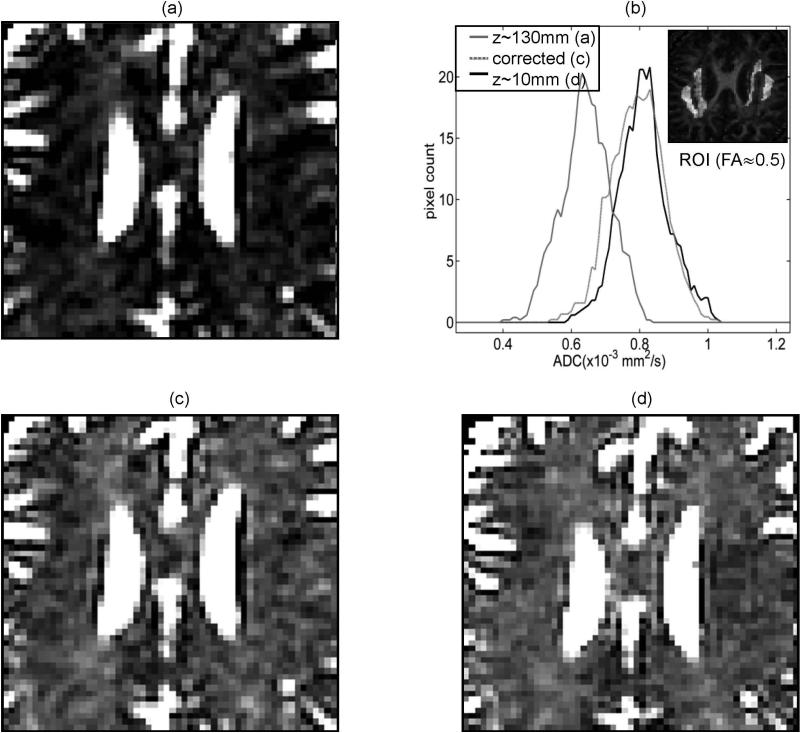
Figure 5 illustrates the efficiency of the nonlinearity bias correction for ADC as a result of the individual DWI corrections. Both for the anisotropic and the isotropic brain tissue (Fig.5b insert), the original ADC bias of −15 to −20% at the offset z~130 mm (e.g., 0.65±0.07 × 10⁻³mm²/s for FA(ROI)~0.5, Fig.5a,b, and 2.5±0.2 × 10⁻³mm²/s for CSF (histograms not shown)) is effectively reduced down to −1.5 to −2.5% (ADC_c (FA~0.5) = 0.81±0.08 × 10⁻³mm²/s and ADC_c (FA~0.0) = 2.9±0.2 × 10⁻³mm²/s). Similar correction efficiency was observed for the direction specific DWI-ADC bias (reduced from original ~14% down to ~2%) in an isotropic ice-water phantom with the LAB gradients (data not shown). The width of the ADC distribution is not significantly altered by the bias correction (Fig.5b). Different original bias is observed for the isotropic CSF versus the anisotropic brain tissue (~15% versus ~20%) at close spatial locations. The original ADC bias measured by 16-direction DTI (0.66±0.05 × 10⁻³mm²/s at z~130mm versus 0.82±0.05 × 10⁻³mm²/s at z~10mm) is nominally the same as that of 3-direction DWI (0.65±0.07 × 10⁻³mm²/s versus 0.81±0.07 × 10⁻³mm²/s). ADC calculation either from the corrected DWI intensities or from the corrected b-values produced identical results (zero difference) independent of the anisotropy and the applied diffusion gradient direction. Trace image correction using direction-average corrector map was effective only for the ADC of the isotropic CSF, and less efficient (4-6% residual ADC bias) for the anisotropic corpus callosum brain tissue.

Figure 5.

ADC bias correction illustrated for pixels of arbitrary anisotropy in the same slice as in Figure 4, zoomed on corpus callosum region: (a) biased ADC for superior offset z~130mm; (c) corrected ADC bias for z~130mm; (d) negligible ADC bias for z~10mm. (b) shows ADC histograms (smoothed by 3-point moving-average), corresponding to (a) – solid gray, (c) – dotted gray and (d) – solid black ADC maps, for ROI with FA~0.5. ROI selection is illustrated by bright pixels in the insert of the FA map in (b). Same window leveling is used for ADC maps in (a), (c) and (d).

DISCUSSION

The described results provide experimental evidence that empiric approximation of three primary gradient nonlinearity maps enables reasonably efficient correction of ADC bias for medium of arbitrary anisotropy. An adequate approximation for nonlinearity of a given scanner is obtained by spatial rescaling of independent model for gradient system of similar geometry (13). Consistent with prediction from numerical simulations (18), the experimentally observed ADC bias is effectively reduced by 85-90% both for anisotropic and isotropic brain tissue independent of applied DWI directions. ADC correction implemented using b-value maps is shown to be fully equivalent to using corrected DWI intensities. The implemented correction procedure has negligible effect on the measurement noise. For isotropic medium, a single direction-average corrector map could be constructed to apply directly to the trace image, nominally independent of chosen DWI direction. However for anisotropic media, DWI correction using an average corrector map for a biased trace image is less efficient than correction of individual DWI directions.

In general, an empirical spatial mapping of the gradient fields is a daunting task requiring multi-plane measurements and recursive data fitting (13). Since the bulk of the ADC nonlinearity error is described by the three diagonal elements of the nonlinearity tensor (18), for the majority of clinical ADC applications (3-5) it is sufficient to characterize the 3D bias using gradient nonlinearity, l_ii(r), along the primary (i^th) direction and ignoring spurious gradients (off-diagonal i ≠ j nonlinearity components). In principle, 3D maps for diagonal elements of the nonlinearity tensor can be measured at finite grid locations directly from spatially dependent geometric distortions on a regular grid phantom (13,17). However, finite grid dimension of the phantom would require resampling and interpolations of the maps for the actual DWI experiments, while measurement uncertainties could make this interpolation unstable and limit reproducibility.

Therefore, a low-effort practical alternative, as proposed in this work, is to use an analytical (i.e. noiseless) model (13) and measure only the bulk (six) primary nonlinearity scalars. The independent baseline nonlinearity model can be adopted from a gradient system of similar (horizontal-bore) geometry (13). This procedure allows for stable and straightforward interpolation for any experimental FOV and arbitrary scan geometry. Since this procedure is based on linear rescaling, it does not preserve higher spatial derivatives of the spherical harmonics model. Thus, slight deviations of the scaled maps from the actual system nonlinearity are expected both before and after the offset point where the scalars are exactly “matched”. As is evident from this work, these deviations are tolerable and fall within ADC uncertainty for an experimental measurement.

Compared to standard geometric distortion measurements, the proposed method is more sensitive to the shim quality, since higher experimental uncertainties may confound the measurements of nonlinearity scalars at large offsets. Careful adjustment of phantom elevation and scan geometry, as well as averaging of measurements from symmetric offsets may be needed to achieve consistent scalar measurements (within ±10mm). An additional, major, limitation is in the choice of independent baseline model. The maximum nonlinearity ranges are fixed by the design coefficients of that model, and cannot be exceeded by proposed simple spatial reshaping of the nonlinearity maps. Furthermore, the relative weight of higher order harmonics (3^rd, 5^th, and 7^th) included in the independent model (13) cannot be changed, preventing extrapolation of the rescaled nonlinearity maps to large FOV (more than ¾ of bore diameter). To alleviate these limitations, different baseline model could be chosen, or existing model rescaled in intensity of nonlinearity in addition to spatial grid rescaling. Even though proposed approximation enables independent ADC bias correction on a clinical system, the superior performance is expected for correction using full system design information.

In conclusion, this work described a viable procedure to independently characterize gradient nonlinearity on a clinical scanner and correct for the observed spatial non-uniformity bias in ADC in a few measurements. Application of the proposed corrections effectively removed ADC bias for off-center measurements both in isotropic (ice-water, CSF) and highly anisotropic medium (e.g. corpus callosum).