Using Markov Chains to predict the natural progression of diabetic retinopathy

Abstract

AIM

To study the natural progression of diabetic retinopathy in patients with type 2 diabetes.

METHODS

This was an observational study of 153 cases with type 2 diabetes from 2010 to 2013. The state of patient was noted at end of each year and transition matrices were developed to model movement between years. Patients who progressed to severe non-proliferative diabetic retinopathy (NPDR) were treated. Markov Chains and Chi-square test were used for statistical analysis.

RESULTS

We modelled the transition of 153 patients from NPDR to blindness on an annual basis. At the end of year 3, we compared results from the Markov model versus actual data. The results from Chi-square test confirmed that there was statistically no significant difference (P=0.70) which provided assurance that the model was robust to estimate mean sojourn times. The key finding was that a patient entering the system in mild NPDR state is expected to stay in that state for 5y followed by 1.07y in moderate NPDR, be in the severe NPDR state for 1.33y before moving into PDR for roughly 8y. It is therefore expected that such a patient entering the model in a state of mild NPDR will enter blindness after 15.29y.

CONCLUSION

Patients stay for long time periods in mild NPDR before transitioning into moderate NPDR. However, they move rapidly from moderate NPDR to proliferative diabetic retinopathy (PDR) and stay in that state for long periods before transitioning into blindness.

INTRODUCTION

Diabetic retinopathy (DR) is a common complication of diabetes and despite the availability of effective treatment it remains one of the leading causes of visual loss. The vision 2020 protocol projects DR and glaucoma as “emerging” causes of blindness in developing countries^[1]. It was noted from previous research that there is a direct relationship between the duration of diabetes mellitus (DM) and the frequency and severity of DR^[2]. Of concern, it was reported that by 2030, 85% of the world's diabetic population will be in developing countries and the prevalence of diabetes in India is set to more than double from 31 million in 2000 to 79 million in 2030^[3]. The report acknowledges that these projections could be gross underestimations as they are based on levels of obesity, which is rising at an alarming rate. The estimated number of people with DM by country is shown in the Figure 1^[4].

Figure 1. Top 10 countries with highest number of people with diabetes for 2000 and 2030 (projected).

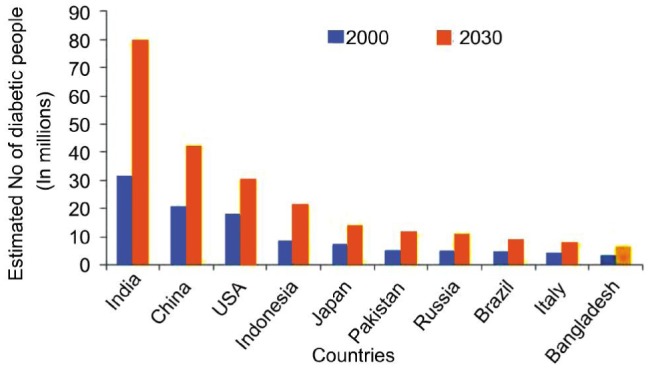
Reducing the impact of DR is highly desirable from both a social and economic perspective. In the US, the estimated economic burden from four major adult vision problems (including DR), refractive errors, visual impairment and blindness was $35.4 billion^[5]. In the UK, the economic cost of partial sight and blindness was estimated at £21 billion^[6]. On the other hand, conservative estimates show that the economic burden of diabetes alone in India is to the tune of $2.2 billion^[7]. A theme emerging from the literature on DM and DR is the significance of early detection and prevention, thereby improving patient quality of life. Often, the initial diagnosis of DR tends to be in the mature stages of the condition, so the focus is on slowing the process of progression to more advanced stages and ideally encourage healthy lifestyle which can slow the progression of DR^[7]. The main purpose of this study is to use Markov Chains to model the progression of DR based on data from observational study of 153 patients^[8].

SUBJECTS AND METHODS

In this observational study of 153 eyes (worst eye considered) who visited the Eye Camp in the calendar year of 2010 and were followed up each year till 2013. We identify DR stages based on Early Treatment Diabetic Retinopathy Study (ETDRS) classification. We exclude patients who underwent recent eye surgery; cases with macular ischemia or other eye diseases that can interfere with the examination of fundus and angiography. We ignored patients with macular edema which can occur in the presence of proliferative and non-proliferative stages of the disease prior to pan retinal photocoagulation consideration and can also lead to severe vision loss. Lastly, patient records with ambiguity or missing information due to non-attendance at the end of follow-up period were excluded from this study. All patients were assigned a reference number and we tracked the progression of DR using this reference number only.

As this study is an observational study, treatment intervention is most likely to occur for patients who reach stage 3 [severe non proliferative DR (NPDR)]. This means that the data does not strictly represent the natural progression of the condition. Rather than excluding these patients from the analysis we adjust the outcome as in previous studies^[9]. Although the Wisconsin Epidemiologic Study of DR (WESDR) studies include treatment as a stage, they acknowledged few practical limitations which places caution over interpretation of results. The key ones being the interval censored nature of the data which means there is limited certainty about the year of intervention and the severity of patient within a specified stage that underwent treatment.

The natural progression of DR is shown in the Figure 2.

Figure 2. Stages of the natural progression of diabetic retinopathy.

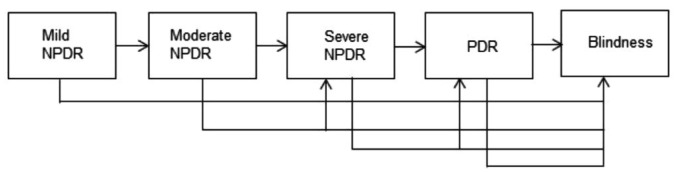
NPDR: Non-proliferative diabetic retinopathy; PDR: Proliferative diabetic retinopathy.

For the purpose of this study the model assumes a unidirectional flow of progression from mild NPDR to Blindness. However, it is worth mentioning that patients may skip one or more stages to move to an advanced stage. Also, in this study we did not observe patients regressing (i.e. moving to previous stages) and no patient observed in this study progressed to death. This unidirectional approach to modelling DR contrasts to research carried out by where patients who developed DR regressed^[10],^[11]. In this study, it was reported that among 26 patients who developed DR, the HbA1c level at one year of discharge of one in five patients whose retinopathy regressed was lower than the remaining patients whose retinopathy did not regress^[10].

As with many chronic diseases, a patient's history of DR can be visualised as a progression through several distinct states of severity. The Markov process has been a convenient method to describe random processes that evolve over time. In case of modelling DR, Markov Chains has been successfully used in previous studies^[12]–^[14]. In a homogenous discrete-time Markov Chain model was used to describe the natural progression from year to year^[11]. While in the WESDR included three observations per patient with inter-observation periods of four and six years^[13]. However, the WESDR study is limited to young-onset insulin dependent patients and only considered the right eye. Also, being an observational study, WESDR modelled two additional states namely treatment intervention and death. However, they explicitly mentioned the absence of information on severity of DR at the time of treatment and year of the treatment intervention.

Typically, Markov Chain is a process that consists of a finite number of states and some known probabilities. Initially, patients are placed in one of the states and the probabilities of transition to other states are defined within a specified time period, known as a Markov cycle. The key to the Markov model is the Markov Property which states that given the entire past history of the subject, the present state depends only on the most recent past state. This memory-less property allows the model to be described in terms of a single-cycle transition matrix ^[14]. In this study, we are modelling a progressive DR with five states ordered from least (mild NPDR) to most severe (blindness). A progressive DR in this context means the state of the patient can never improve and is represented by the matrix M. This matrix is often called a transition matrix because it expresses the probability of movement from one state to another state (Table 1).

Table 1. A transition matrix which shows the probability of movement from one state to another state in the cycle of diabetic retinopathy.

DR stages	Mild (S1)	Moderate (S2)	Severe (S3)	PDR (S4)	Blindness (S5)
Mild (S1)	θ11	θ12	θ13	θ14	θ15
Moderate (S2)	θ21	θ22	θ23	θ24	θ25
Severe (S3)	θ31	θ32	θ33	θ34	θ35
PDR (S4)	θ41	θ42	θ43	θ44	θ45
Blindness (S5)	θ51	θ52	θ53	θ54	θ55

In the matrix M (Table 1), θ_ij represents the probability of moving from state i to state j during one year. In other words, i represent the starting location and j represents the ending location. For example, θ₁₂ represents the probability of patient moving from state 1 (mild NPDR) to state 2 (moderate NPDR) and state 5 in the above matrix represents an absorbing state (i.e. a patient entering this state cannot leave).

One of the early studies in this subject was WESDR, which investigated the prevalence, incidence and progression of DR. In this study, treatment interventions and death was included and the study was conducted for a period of two years ^[14]. However, in this study they seldom used an entire suite of covariates to understand transition rates. In the study carried out in the United Kingdom, it incorporated a hidden Markov Model for simultaneously estimating transition rates and misclassification probabilities. In the study of abdominal aortic aneurysms by ultrasonography, the disease is staged by severity according to successive ranges of aortic diameter ^[15]. In Taiwan, the natural progression of DR was observed over a three year period from 1999 to 2002 in 971 patients diagnosed with type 2 diabetes. The multi-state Markov Model used showed that on average, the mean duration of disease transition from mild NPDR to proliferative DR (PDR) was 14.97y. In addition, the study concluded the average duration of DR from non-existence to blindness was approximately 26.5y^[16]. Another study carried out in Taiwan, modelled the natural progression of DR after treatment (including metabolic control and laser photocoagulation) from no DR to blindness. They concluded that, on average, the average time spent from no DR to blindness is 23.02y ^[17]. However, due to the variation of patients observed in this study, we could not generalise the treatment. In Singapore, using 124 retinal photographs were analyzed to understand the transition of patients from normal retinal to PDR. Using a three-layered feed forward neural network, classification of the four eyes resulted in a sensitivity of more than 90% for the classifier with the specificity of 100% was achieved ^[18].

RESULTS

Of the 153 eyes observed and treated, we present descriptive statistics of the patients in Table 2 (continuous) and Table 3 (categorical attributes). We observed patients in the age range of 40 to 78; clearly skewed to the older population, with a wider spread in duration of diabetes. The wide spread in attribute values is explained by the groups that present the various stages of the progression (mild NPDR to blindness). Also, we observed a fairly even split in male (53%) and female patients (47%) who participated in this study.

Table 2. The descriptive statistics of key attributes recorded in this study.

Attributes	Minimum	Maximum	Mean	SD
Age	40	78	57.07	9.20
Age at onset of diabetes	21	67	45.19	8.74
Duration of diabetes	1	38	11.88	7.71
Central foveal thickness	130	670	292.27	117.57
Fasting blood sugar	70	314	146.74	52.21
Post prandial blood sugar	90	590	205.88	88.49
Hb1AC	4	11.70	7.49	2.10
Low density lipoprotein	50	209	120.47	39.99
High density lipoprotein	29	89	49.31	12.57
Triglycerides	55	367	179.79	65.28

SD: Standard deviation.

Table 3. The descriptive statistics of key categorical attributes recorded in this study.

Attributes	Y (%)	N (%)
Insulin use	52	48
Hypertension	54	46
Nephropathy	18	82
Smoking	29	71
Alcohol	27	73
Surgery in eye	17	83
Family history	58	42
Anemia	44	56

In Table 3, we observe a vast majority of patients examined in this study had no previous surgery in eye, no history of nephropathy, do not smoke or consume alcohol. However, due to the self reported nature of the question, the responses to smoking and alcohol need to be treated with caution. We observed a slight majority in patients who are insulin dependent, report hypertension and present with a family history of diabetes. The relationship between key attributes recorded in this study is shown in Table 4.

Table 4. The correlation matrix of the key attributes recorded in this study.

Key variables	Age	Duration	FBS	PPBS	Hb1AC	LDL	HDL	TG
Age	1
Duration	0.469b	1
FBS	-0.007	0.274b	1
PPBS	0.091	0.238b	0.613b	1
Hb1AC	0.157a	0.477b	0.545b	0.436b	1
LDL	0.057	0.263b	0.205b	0.335b	0.493b	1
HDL	-0.111	-0.120	-0.157	-0.333b	-0.305b	-0.291b	1
TG	0.177a	0.220b	0.060	0.363b	0.226b	0.385b	-0.359b	1

^aCorrelation is significant at the 0.01 level (2-tailed); ^bCorrelation is significant at the 0.05 level (2-tailed). FBS: fasting blood sugar; PPBS: Post parandial blood sugar; LDL: Low density lipoprotein; HDL: High density lipoprotein; TG: Triglycerides.

The matrix (Table 4) shows the linear relationship summarized by the Pearson correlation co-efficient (r) between attributes measured in this study. It does not explain anything about causation or the direction of relationship. We observed a strong positive relationship (r=0.477, P<0.001) between Hb1AC and duration of diabetes. This suggests that as duration of diabetes increases, Hb1AC increases. On the other hand, a negative relationship (r=-0.359, P<0.001) between Triglycerides and High Density Lipoprotein. In both cases, given that P<0.001 means that there is less than 0.001 probability that a correlation co-efficient this big would have occurred by chance in a sample of 153 patients (as indicated by the two asterisks after the co-efficient). Hence, this gives us confidence around our interpretations of coefficients as genuine.

The matrix (Table 5) gives the transition probabilities between time of first visit and the status at the follow up of one year. Of the 153 eyes observed and treated, we represent the transition matrix (M1) in a tabulated form as Table 5.

Table 5. The transition of 153 eyes observed in study from mild NPDR to blindness from the time of first visit to end of year 1.

DR stages	Mild (S1)	Moderate (S2)	Severe (S3)	PDR (S4)	Blindness (S5)
Mild (S1)	0.80	0.12	0.08	0	0
Moderate (S2)	0	0.44	0.30	0.26	0
Severe (S3)	0	0	0.46	0.50	0.04
PDR (S4)	0	0	0	0.88	0.12
Blindness (S5)	0	0	0	0	1

The matrix (M1) shows that 80% of patients who were classified as mild NPDR (state 1) at the time of first visit were in that state at the end of year 1. Although we did not observe any case progress from state 1 to state 5 at the end of year 1, we observed just over one in ten cases progress from PDR (state 4) to blindness (state 5).

To verify the adequacy of the model, we compared observed (O) and expected (E) values at year 3, as shown in matrix (M2) which is tabulated as Table 6. To obtain the expected values in the M2, we multiply each successive power of the initial transition matrix by the initial state vector.

Table 6. Compares the observed (O) and expected (E) proabilities of patients moving from mild NPDR to blindness from year 1 to end of year 3.

DR stages	Mild (S1)	Moderate (S2)	Severe (S3)	PDR (S4)	Blindness (S5)
Mild (S1)	0.52 (E)	0.14 (E)	0.15 (E)	0.17 (E)	0.01 (E)
	0.50 (O)	0.12 (O)	0.18 (O)	0.20 (O)	0.00 (O)
Moderate (S2)		0.08 (E)	0.18 (E)	0.62 (E)	0.11 (E)
		0.12 (O)	0.22 (O)	0.60 (O)	0.06 (O)
Severe (S3)			0.09 (E)	0.69 (E)	0.20 (E)
			0.14 (O)	0.66 (O)	0.21 (O)
PDR (S4)				0.68 (E)	0.32 (E)
				0.75 (O)	0.25 (O)
Blindness (S5)					1

Thus, P(n)=P(n-1)×P. So to compute P3 (i.e. the state at year 3 since first visit) as P(0)×P2

The fitted values are close to observed values and the goodness of fit² (5, N=153)=2.14, P=0.70 which suggests that a five-state Markov model is adequate. Also, it is worth stating that rows in the M2 are rounded to two decimal places and may not sum to one.

Now, for a stationary Markov Chain with m transient states and m–s recurrent states, the one step ahead transition probability matrix (Matrix P) can be written as follows.

In the above matrix, Q refers to the m×m transition probability matrix (shown as matrix M1 above). R refers to the m×(m–s) transition probability matrix for movement from the transition states to the recurrent states, the matrix 0 is a (m-s)×m matrix with all elements equal to zero and represent the zero probabilities to move from recurrent to transient states. P1 represents the (m-s)×(m-s) transition probability matrix for movements between the recurrent states. The following property of Q is useful in modelling progression in DR.

Now, the expected number of visits from transient state i to transient state j before moving to a recurrent state is equal to the (i, j)^th element of (I–Q)⁻¹. This expected number of visits to a state can also be interpreted as the amount of time spent in that state. The expected number of time units that the process will be in a state in a single visit is called the mean sojourn time of state i.

The sum of the i^th row of the (I–Q)⁻¹ is the expected amount of time for which the process remains in transient states before moving to a recurrent state if the system starts in the i^th transient state.

The sum of the rows of the matrix is given by the expression below.

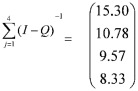In this study, each time unit is defined as one year. So if a patient enters the model in a mild NPDR state, he/she is expected to stay in the mild NPDR state for 5 time units (or years), be in the moderate NPDR state for 1.07 time units, be in the severe NPDR state for 1.33 time units and be in the PDR state for 7.88 time units. After all these visits to the transient states, the patient is expected to move to blindness state.

It is widely accepted that early detection of retinal abnormalities is essential in preventing DR and loss of vision. Treatments such as photocoagulation can decrease vision loss. However, it is usually not possible to restore visual acuity once it has deteriorated. Thus the optimal time for treatment using this approach is before visual acuity is impaired^[19]. Fundus photography can be used to track the progression of the disease or efficacy of the treatments. However, the utility of using fundus photography is limited because of its costs, specialist equipment and expertise in using equipment. In most severe cases of DR, vitrectomy is clearly beneficial. However, this intervention is indicated only when DR has progressed to a measurably advanced stage in which some visual acuity has already been lost^[20]. In cases where macular edema is present, the use of intravitreal triamcinolone acetonide may be done in the office setting using sterile techniques. Although this is recognised as another mode of therapy for refractory diabetic macular edema, there is limited literature published in the known risks of intravitreal delivery including endophthalmitis, glaucoma, cataract and retinal detatchment. Also, as is widely accepted, vascular endothelial growth factors have been implicated as an important factor in increasing vascular permeability in patients with DR. There are several anti-vascular endothelial growth factor (VEGF) drugs that are used in management of diabetic macular edema, including pegaptanib, bevacizumab and ranibizumab. Pegaptanib is an aptamer which binds to and thus neutralises VEGF-165, whereas ranibizumab, an antibody fragment and bevacizumab, a whole antibody binds to all isoforms of VEGF. However, apart from its pro-angiogenic role in pleiotropic functions range from inducing survival of endothelial cells to potent vasodilation. Consequently, although VEGF blockage may be useful in arresting DR, the unwanted side effects such as hypertension and poterinuria (due to glomerular dysfunction) are most frequent^[21].

DISCUSSION

As the global prevalence of diabetes increases, the number of people with DR will increase too. This was reported to increase more significantly in developing countries^[22]. To add to this, there is no nationwide study published on prevalence of DR in India and the current level of awareness among general population of DR is low^[19],^[23]. This research work is one of the very few studies that analyze the progression of DR among DM patients using Markov chains in the sub-continent. In this study, 153 eyes were observed at the end of year one and tracked at the end of year three. All cases observed in this study showed unidirectional flow from NPDR to blindness unlike previous research where patients regressed. In order to model the natural progression of DR in these patients, an absorbing Markov chain model is proposed. Although termed as “natural progression”, this is strictly not true as treatment intervention commences for patients who reach stage 3 (severe NPDR). The absorbing model proposed for this study is a five state model (i.e. stages namely mild NPDR, moderate NPDR, severe NPDR, PDR and blindness). The final state blindness is an absorbing state (i.e. a patient entering this state cannot leave).

The first year transition matrix of initial state of patients at the end of year one was constructed and we obtained the year 3 matrix. We validated the year 3 results from the transition matrix by comparing it with actual data. The results from Chi-square test confirmed that there was statistically no significant difference which provided assurance the model was robust and could be used for estimating the mean sojourn times (i.e. the amount of time units the process will be in a state in one visit). On estimating the mean times, we concluded that patients tend to stay longer in mild NPDR state (5y) before moving swiftly through moderate (1.07y) and severe NPDR (1.33y) to stay for the longest period in the PDR state (nearly 8y) before transitioning into blindness. This study offers insight for ophthalmic practitioners into periods of stay at each state thereby providing opportunity for targeted interventions at stages prior to stage 3 (severe NPDR). Overall, it is therefore expected that such a patient entering the model in a state of mild NPDR will enter blindness after 15.29y. This compares to 14.97y recorded in Taiwan from moving from NPDR to PDR and this study did not include an absorbing state such as blindness, also it was not clear which phase of NPDR was recorded as the starting point. Another study in Taiwan reported it takes, on average, 23.02y to transition from no DR to blindness. However, in this particular study, the group included a treatment intervention of metabolic control and laser photocoagulation.

Despite improvements in methodology and data quality over previous studies, we acknowledge the limitations as we feel the model maybe simplified. An inherent limitation of Markov models is the memory less property wherein the transition probabilities is only dependent on the most recent past and not any stage prior to that. This may contrast reality where patients who have been compliant with blood glucose management over a number of years are more likely to remain compliant compared to patients who has been erratic is less likely to comply with the new cycle. This behaviour clearly has an impact on the rate of DR progression to subsequent stages. One suggestion is to introduce additional stages in the model and record transition probabilities. However, it was subsequently acknowledged that this would complicate the model and is not a practically viable solution^[24]. By acknowledging these practical challenges, this study recommends three areas that future research could focus. Firstly, developing hidden Markov models for detecting micro aneurysms as they are the first visible clinical signs of DR, comparing results with survival data mining techniques such as Cox regression models and lastly, segmentation of foveal avascular zone in digital angiograms using Markov random fields^[25]–^[27].