Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Feb 12;5:8407. doi: 10.1038/srep08407

Pangea breakup and northward drift of the Indian subcontinent reproduced by a numerical model of mantle convection

Masaki Yoshida 1,a, Yozo Hamano 1
PMCID: PMC4325333  PMID: 25673102

Abstract

Since around 200 Ma, the most notable event in the process of the breakup of Pangea has been the high speed (up to 20 cm yr−1) of the northward drift of the Indian subcontinent. Our numerical simulations of 3-D spherical mantle convection approximately reproduced the process of continental drift from the breakup of Pangea at 200 Ma to the present-day continental distribution. These simulations revealed that a major factor in the northward drift of the Indian subcontinent was the large-scale cold mantle downwelling that developed spontaneously in the North Tethys Ocean, attributed to the overall shape of Pangea. The strong lateral mantle flow caused by the high-temperature anomaly beneath Pangea, due to the thermal insulation effect, enhanced the acceleration of the Indian subcontinent during the early stage of the Pangea breakup. The large-scale hot upwelling plumes from the lower mantle, initially located under Africa, might have contributed to the formation of the large-scale cold mantle downwelling in the North Tethys Ocean.

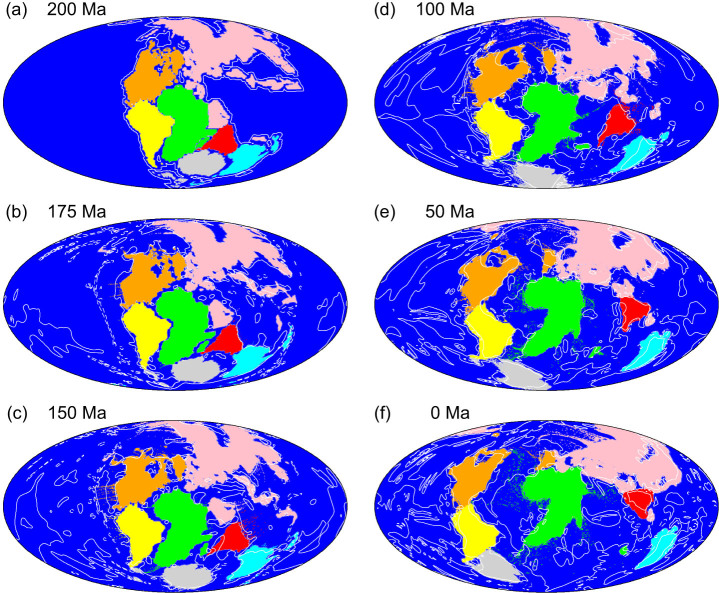
Recent plate reconstruction models, based on detailed geological and geomagnetic datasets, have illustrated the specific processes of both the breakup of the supercontinent Pangea and the subsequent continental drift1. During the breakup of Pangea, the Indian subcontinent became isolated from the southern part of Pangea, called Gondwanaland, at around 130 Ma, moved northwards, and eventually collided with Eurasia to form the Himalayas at around 40–50 Ma2,3,4,5 (Fig. 1). The reason why the Indian subcontinent moved at such a high speed of up to c. 20 cm yr−1 6,7 remains a controversial issue in geodynamics. Numerical simulation of mantle convection under Earth-like conditions provides a unique approach for clarifying this issue by investigating time-dependent mantle convection. Here, numerical simulation of 3-D mantle convection is reported, considering the supercontinent Pangea, to determine the geodynamic mechanisms of the Pangea breakup, the subsequent continental drift, and the high-speed northward drift of the Indian subcontinent.

Figure 1. Time sequence of drifting continental blocks at each age from 200 Ma to the present1.

Figure 1

Open in a new tab

The Indian subcontinent that moved towards the north and collided with Eurasia is highlighted by thick contour lines. This map was produced using the Generic Mapping Tools56.

The mantle was modelled as a Boussinesq fluid with an infinite Prandtl number and realistic Rayleigh number confined in 3-D spherical shell geometry. Conservation equations for mass, momentum, and energy, which govern mantle convection, and the advection equation for those materials compositionally different from the mantle material, were solved using finite-volume-based mantle convection code8,9 (see Methods for details). Impermeable, shear-stress-free conditions were imposed on both the top and bottom surface boundaries of the spherical shell. The temperature was fixed at the top surface boundary, whereas adiabatic conditions were imposed on the bottom surface boundary.

The simulations in the present study were performed for a period of 200 Myr (i.e., from 200 Ma to the present) to study the behaviour of continental drift and the pattern of mantle convection when the supercontinent Pangea, modelled as a collection of chemically buoyant, highly viscous continental blocks, was imposed a priori at the beginning of the simulation.

The lowermost part of Earth's present-day mantle is characterized by the two seismically slow domains beneath Africa and the South Pacific10,11. While we do not know the thermal heterogeneity in the mantle hundreds of millions of years ago, it is reasonable to suppose that it would have differed from that inferred for the present-day mantle. However, in the present study, based on the assumption that the two large-scale upwelling plumes (i.e., thermo-chemical piles) under Africa and the South Pacific12,13,14,15,16,17, the planetary-scale subduction zone2,3,18 and the resulting degree-two thermal structure of the Earth's mantle interior have persisted throughout the last several hundred million years, the initial state of the lateral temperature anomaly in the mantle at 200 Ma was derived from the S-wave global seismic tomography model, S40RTS19.

The seismic velocity anomaly from the S40RTS model was converted to a temperature anomaly using results from mineral physics20 (Supplementary Fig. 1). The temperature anomaly from the S40RTS model was imposed within the mantle for depths greater than 660 km, and the temperature anomaly in the upper mantle was uniformly set at zero (Supplementary Fig. 2b–f). This is because the thermal heterogeneity in the upper mantle derived from the original seismic tomography model represents the present-day tectonic characteristics, i.e., the configuration of subducting plates as high velocity anomalies, the distribution of plate divergence as low velocity anomalies, and the distribution of neutrally buoyant continental roots (i.e., tectosphere) as high velocity anomalies above c. 300 km21.

Following the previous work9, the geometry of the modelled Pangea was taken from the digital data of the coastline of Pangea at 200 Ma1. Pangea was initially broken up into seven major continental blocks (i.e., Eurasia, Africa, North America, South America, Antarctica, Australia, and the Indian subcontinent; Supplementary Fig. 2a), and the continental boundaries were treated as a narrow oceanic mantle. The thickness of Pangea was initially set to 202 km. The density difference between the chemically buoyant Pangea and the ambient mantle was taken to be −100 kg m−322,23. The viscosity ratio between the highly viscous Pangea and the ambient mantle (ΔηC) was taken as a free parameter, and it was varied from 102 to 104 in the present study. Considering the thermal insulation effect of the supercontinent, as suggested by several numerical models24,25,26,27,28,29,30,31, the temperature of the subcontinental mantle beneath Pangea, from depths of 202–660 km, was assumed to be ΔTe higher than that of the mantle beneath oceanic regions at the same depths (see the Discussion section for further details on the thermal insulation effect). In the present study, ΔTe was taken to be +200 K (or lower for some models).

To study the mantle dynamics associated with the breakup of Pangea, previous work has imposed rigid continental blocks in 3-D spherical models of mantle convection and has solved continental drift using a kinematic approach32. In contrast, our numerical model allows the highly viscous continental material to deform and drift independently under the convective force of the ambient mantle8,9.

Results

The models performed in the present study are listed in Table 1. The main free parameter was the viscosity ratio between the highly viscous lithosphere of Pangea and the ambient mantle, ΔηC; other free parameters were the viscosity contrast between the top surface and the underlying mantle due to the temperature-dependent viscosity, ΔηT (see Methods), and the excess temperature anomaly of the subcontinental mantle beneath Pangea, ΔTe.

Table 1. Models examined in the present study.

Model name ΔηC ΔηT ΔTe [K] λa Figure(s)
C30 103 0 +200 1 2, 3, 4, 5, 6
C20 102 0 +200 1 5, S3
C25 102.5 0 +200 1 5, S4
C35 103.5 0 +200 1 5, S5
C40 104 0 +200 1 5, S6
C30NL 103 0 +200 0 S8
C20NL 102 0 +200 0  
C30T10 103 101 +200 1 5
C30T20 103 102 +200 1 5
C30T30 103 103 +200 1 5
C30H000 103 0 0 1 5, 6, S7
C30H050 103 0 +50 1 5
C30H100 103 0 +100 1 5
Open in a new tab

aSee Eq. (11); when λ = 0, there is no lateral temperature anomaly in the lower mantle for the initial field.

Figure 2 shows the time sequence of the position of drifting continents for Model C30 with ΔηC = 103, which ensures dynamic stability of the drifting continents33,34,35,36. Figure 3 shows the time sequence for 3-D views of mantle convection and drifting continents for Model C30. The modelled Pangea broke up and each continental block moved with time following the initiation of the simulation. The “present-day” continental distribution at 0 Ma obtained in this simulation roughly resembles the present-day continental distribution of the real Earth, although certain blocks (i.e., Antarctica) are not located in their true present-day locations (Fig. 2f).

Figure 2. Time sequence of the positions of drifting continents for Model C30 with a viscosity ratio between Pangea and the ambient mantle (ΔηC) of 103.

Figure 2

Open in a new tab

The Indian subcontinent is indicated in red. White contour lines show the temperature anomaly (i.e., the deviation from the horizontally averaged temperature) of the upper mantle at a depth of 358 km. Contour intervals are 250 K. Solid and dashed lines represent positive and negative temperature anomalies, respectively. This map was produced using the Generic Mapping Tools56.

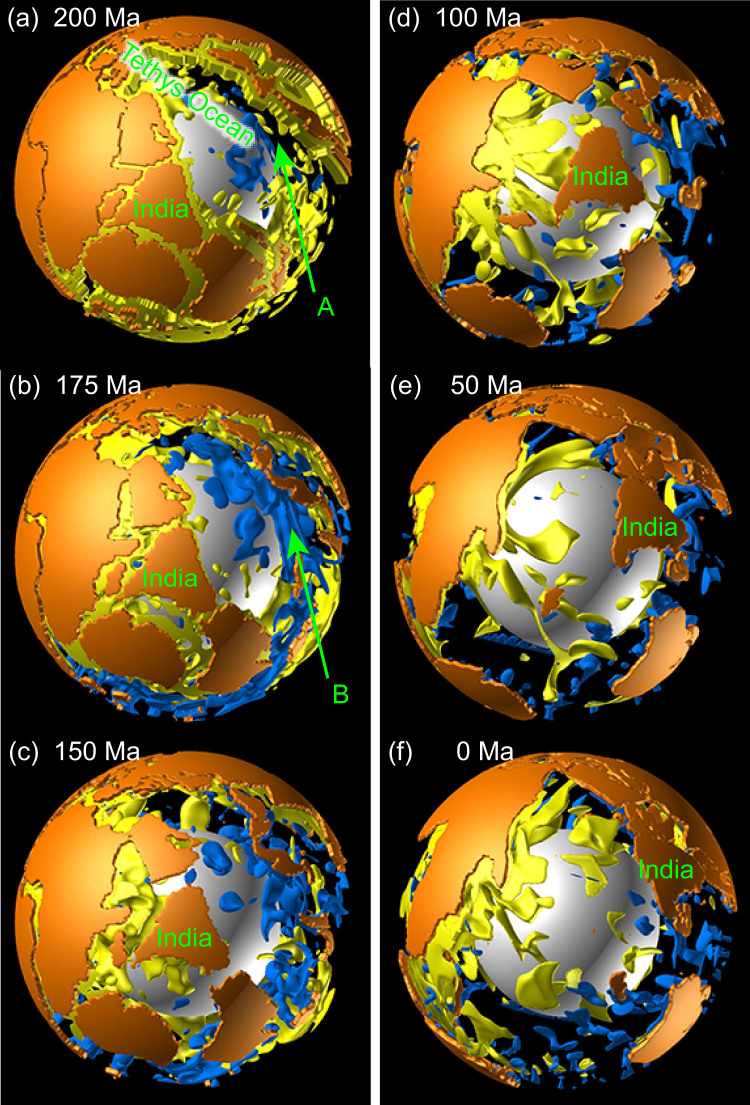
Figure 3. Time sequence of 3-D views of mantle convection and drifting continents for Model C30 with ΔηC = 103.

Figure 3

Open in a new tab

The cyan and yellow isosurfaces of the temperature anomaly (i.e., the deviation from the laterally averaged temperature at each depth) indicate −250 K and +100 K, respectively. The isosurfaces of the temperature anomaly at depths of less than 202 km are omitted for clarity. Positions of the continents are represented by orange regions. White sphere indicates the bottom of the mantle. This figure was produced using the commercial visualization software AVS/Express.

The most notable feature of this result is that the Indian subcontinent moved towards the north at high speed following its separation from Gondwanaland, before it eventually collided with Eurasia (Fig. 2f). Our numerical simulation revealed that a major factor in the high-speed northward drift of the Indian subcontinent was the large-scale cold mantle downwelling that developed spontaneously in the North Tethys Ocean (B in Fig. 3b), attributed to the overall shape of the supercontinent Pangea. This mantle downwelling flow was minor in the initial state of the temperature anomaly in the mantle (A in Fig. 3a). These cold downwellings originated from the subduction of surface oceanic mantles, which eventually joined with the cold suboceanic mantle initially present in this region (Supplementary Fig. 2c–f). This numerically-obtained large-scale downwelling in the North Tethys Ocean region is consistent with the subduction history of the Indian region compiled by both seismic tomography and plate reconstruction37. In addition, a global plate reconstruction model demonstrated that the age of oceanic lithosphere in the North Tethys Ocean was c. 180 Ma, the oldest ocean floor in the world of the day1, which means that mantle downwellings developed preferentially from this region. The large-scale hot upwelling plumes from the lower mantle, initially located under Africa (A in Fig. 4), might have contributed to the formation of the large-scale cold mantle downwelling in the North Tethys Ocean.

Figure 4. This figure shows Figure 3b from a different viewpoint.

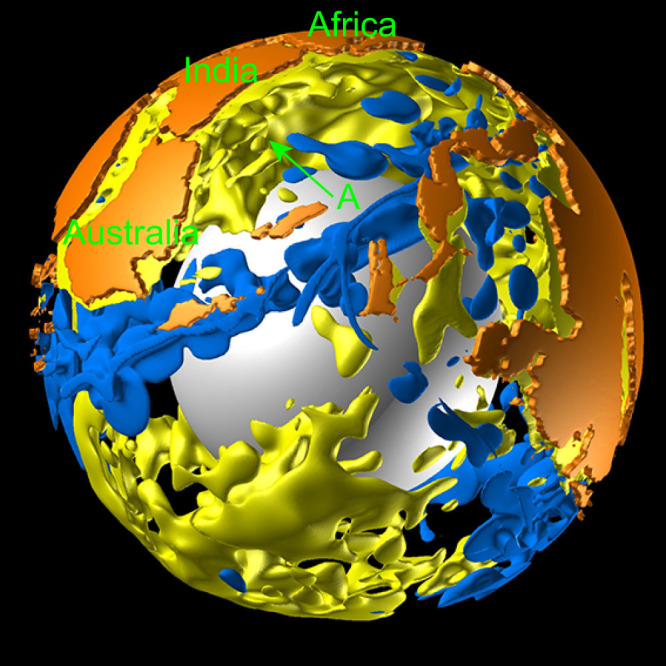
Figure 4

Open in a new tab

This figure was produced using the commercial visualization software AVS/Express.

The northward drift of the Indian subcontinent observed in Fig. 2 is a robust feature observed in all of the models of the present study. When ΔηC = 102 (i.e., one order of magnitude smaller than for the model shown in Fig. 2) and 102.5 (Models C20 and C25, respectively), the Indian subcontinent still moved northwards and collided with Eurasia, although all the continental blocks were considerably deformed over time because of their dynamical weakness (Supplementary Figs. 3 and 4). On the other hand, when ΔηC = 104 (i.e., one order of magnitude larger than for the model shown in Fig. 2) and 103.5 (Models C40 and C35, respectively), continental blocks were less deformed by mantle convection because the advection of the continental material was decoupled from the ambient mantle convection. Therefore, the time required to move the Indian subcontinent and to reproduce the present-day continental distribution was much longer. Thus, continental drift is not realized within the time scale of the real Earth when ΔηC is larger than 103 (Supplementary Figs. 5 and 6).

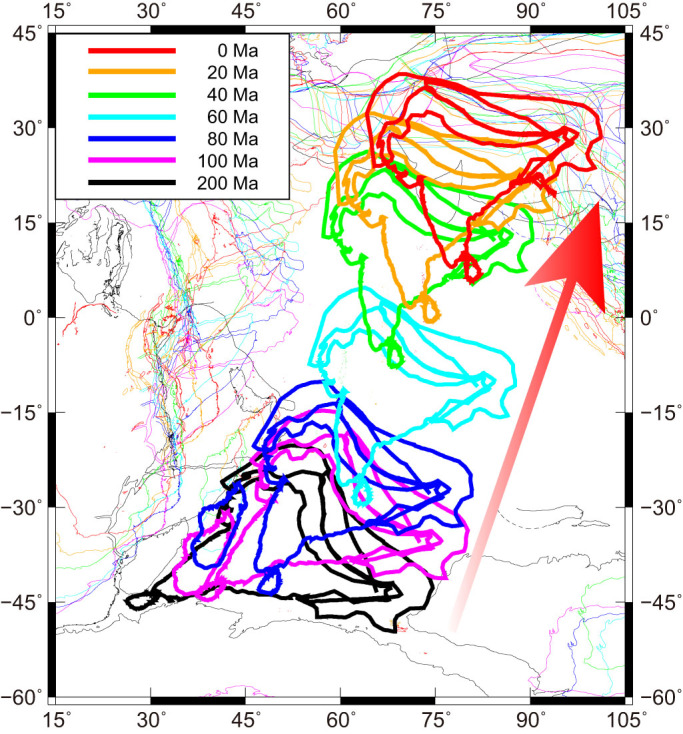
Figure 5 shows the time tracking of the “centre” of the Indian subcontinent for 250 Myr from 200 Ma along latitudinal and longitudinal directions for the models examined in the present study. This result quantitatively revealed that the trace of the Indian subcontinent was sensitive to the choice of ΔηC, and, when ΔηC = 103, the Indian subcontinent gradually accelerated before it collided with Eurasia, and then slowed down after the collision event.

Figure 5.

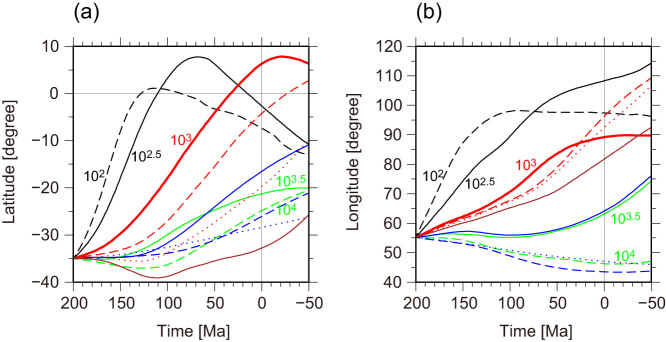
Figure 5

Open in a new tab

Time tracking of the “centre” of the Indian subcontinent for 250 Myr from 200 Ma along (a) latitudinal and (b) longitudinal directions for the no-temperature-dependent-viscosity models with ΔηC = 102 (black dashed lines; Model C20), 102.5 (black solid lines; Model C25), 103 (red solid lines; Model C30), 103.5 (green solid lines; Model C35), and 104 (green dashed lines; Model C40); for the temperature-dependent models with ΔηC = 103 and ΔηT = 101 (blue solid lines Model C30T10), ΔηC = 103 and ΔηT = 102 (blue dashed lines; Model C30T20), and ΔηC = 103 and ΔηT = 103 (blue dotted lines; Model C30T30); and for the models with ΔηC = 103 and an excess temperature anomaly beneath Pangea of ΔTe = +100 K (red dashed lines; Model C30H100), +50 K (red dotted lines; Model C30H050), and 0 K (i.e., no excess temperature anomaly; brown solid lines; Model C30H000).The “centre” is defined at the location of −35°N and 50°E at 200 Ma.

Here, we demonstrate the results of additional simulations using a numerical model of mantle convection with temperature-dependent viscosity to show the dynamic effects of a laterally viscosity heterogeneity on the Pangea breakup and subsequent continental drift. The activation parameter, E ≡ ln(ΔηT), that controls the viscosity contrast between the top surface and the underlying mantle (see Eq. (7) in Methods), was set to 2.30 (i.e., ΔηT = 101; Model C30T10), 4.61 (ΔηT = 102; Model C30T20), and 6.91 (ΔηT = 103; Model C30T30) in the present study.

Figure 5 shows that the Indian subcontinent slowed down with increasing ΔηT (see the three blue lines in Fig. 5) because the high viscosity of the top surface thermal boundary layer blocked the acceleration of the continental drift on the modelled Earth. This result implies that a yielding rheology (i.e., pseudo visco-plastic rheology) was required to reproduce plate-like behaviour in the highly viscous thermal boundary layer38,39,40, which reproduces the variety of “plate boundary forces” acting on the continental margins41.

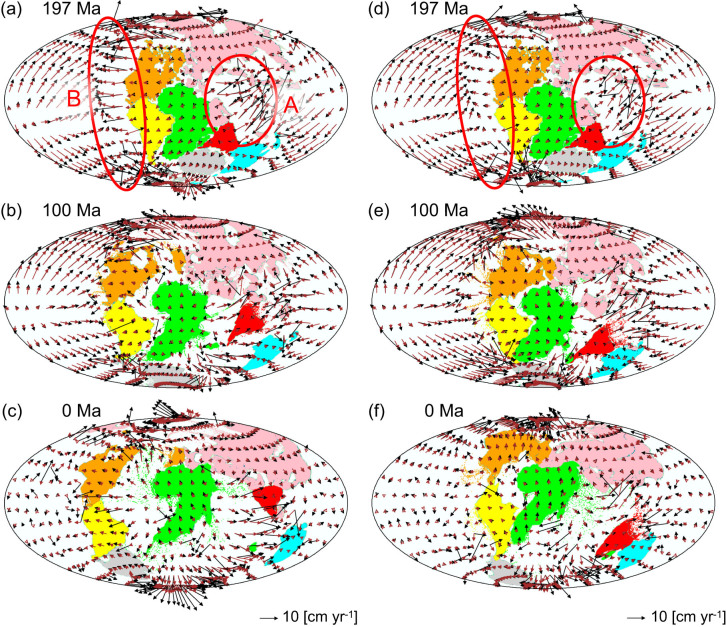
Figure 6 illustrates the effects of the high-temperature anomaly (HTA) region due to the thermal insulation effect beneath Pangea, by showing the time sequence of the drifting continents and velocity fields at the top surface boundary and at a depth of 302 km for the model with ΔηC = 103, both with (Fig. 6a–c; Model C30) and without (Fig. 6d–f; Model C30H000) the HTA region. When the HTA region beneath Pangea is considered, the speed of the lateral flow of mantle around Pangea is fast during the early stage of the Pangea breakup (i.e., 197 Ma), compared with the model that does not include the HTA region (cf. red circles in Fig. 6a and d). In the absence of the HTA region, the Indian subcontinent eventually moved towards the north, but it did not reach Eurasia in the Northern Hemisphere (Fig. 6e and f). As a result, the “present-day” continental distribution at 0 Ma exhibits less similarity to that of the present-day continental distribution of the real Earth, compared with the model that included the HTA region (Fig. 6f, see also Supplementary Fig. 7). This result demonstrates that the strong lateral mantle flow caused by the HTA region beneath Pangea (A in Fig. 6a) enhanced the acceleration of the Indian subcontinent during the early stage of the Pangea breakup. In addition, the strong lateral mantle flow caused by the HTA region (B in Fig. 6a) served as the driving force behind the westward drift of North and South America, which led to the formation of the Atlantic Ocean, elongated from north to south.

Figure 6. Time sequence of the positions of drifting continents and the velocity fields at the top surface (black arrows) and at a depth of 302 km (brown arrows) for the model with ΔηC = 103, and with (a to c; Model C30) and without (d to f; Model C30H000) the high temperature anomaly beneath Pangea.

Figure 6

Open in a new tab

This map was produced using the Generic Mapping Tools56.

When the temperature anomaly of the subcontinental mantle beneath Pangea, ΔTe, decreased below +200 K, the time required to move the Indian subcontinent and to reproduce the present-day continental distribution increased significantly (Model C30H100 with ΔTe = +100 K, Model C30H050 with ΔTe = +50 K, and Model C30H000 with ΔTe = 0 K, shown as dashed and dotted red lines and solid brown lines in Fig. 5, respectively). On the other hand, when ΔTe was +200 K and the lateral temperature anomaly in the lower mantle, which was derived from the S40RTS tomography model, was not considered (i.e., λ = 0 in Eq. (11), see Methods), the Pangea breakup and subsequent continental drift appears to be realized within the time scale of the real Earth. However, the Indian subcontinent and Africa stuck together over time and the “present-day” continental distribution at 0 Ma obtained in this simulation did not resemble the actual present-day continental distribution (Supplementary Fig. 8). These results suggest that the existence of both the HTA region in the upper mantle and the lateral temperature anomaly in the lower mantle are required for the formation of the present-day continental distribution.

Discussion

One of the major findings of the present study is that the degree of deformation of continents depends largely on the value of ΔηC and that the stable continental drift observed in the real Earth is realized under severely limited ΔηC. This implies that the drag force due to the non-uniform lateral mantle flow acting on the base of the continents increases the local deformation of the continental material, which makes it difficult to move the continents rigidly. In fact, when ΔηC is small (e.g., ΔηC ≤ 102.5), the greater the continent's size, the larger the degree of continental deformation is (Supplementary Figs. 3 and 4). When the value of ΔηC is a moderate value for realizing realistic continental drift with minimal deformation (ΔηC = 103 in the present model; Fig. 2), the speed of flow in the subcontinental mantle is close to the speed of continental drift (Fig. 6a–c). In this case, when the size of the continent is small, the drag force acting on the base of the continent is relatively uniform such that the continental block moves with only small deformation. This is an important reason why the small Indian subcontinent moved at high speed without considerable deformation.

A previous numerical study of mantle convection models with temperature-, phase-, and composition-dependent viscosity and yield stress (i.e., pseudo visco-plastic rheology) revealed that the behaviour of continental drift following the breakup of Pangea is very sensitive to the magnitude of yield stress, and suggested that the actual continental drift of the Earth is accomplished by mantle convection within limited geophysical conditions9. However, for the simulation approach used in this study, the subsequent pattern of drifting continents depends on the initial mantle convection pattern. The dynamic role of lateral viscosity heterogeneity in the Pangea breakup and the subsequent continental drift remains to be explained in future studies. In particular, an understanding of the effects of plume heat flux on the acceleration and deceleration of the Indian plate before its collision with Eurasia is required, using future 3-D numerical models with temperature-dependent rheology of mantle materials, as suggested by a previous numerical model5.

Our systematic case study suggested that the existence of the widespread HTA region beneath Pangea, due to the thermal insulation effect, enhanced the acceleration of the Indian subcontinent during the early stage of the Pangea breakup. Indeed, whether such a HTA region was widespread beneath Pangea is a controversial issue in geoscience27 ever since the hypothesis by Don L. Anderson who proposed that the breakup of Pangea would be caused by a temperature increase beneath Pangea due to the thermal insulation effect29. This was supported by several numerical studies of mantle convection24,25,26,27,28,29,30,31, whereas other numerical studies insisted that there was no significant temperature increase caused by the continental assembly42,43. This latter conflicting result was due to the relative dominance of cold downwelling in mantle convection, which causes a shorter convection wavelength and a lower mantle temperature associated with a decrease in heat transport efficiency44. Our model simply assumed that the widespread temperature increase beneath Pangea existed which in our modelling (Supplementary Fig. 2b) caused the continental breakup and may underlie intermittent eruption of continental flood basalts4,27,45. However, there is a possibility that the temperature anomaly beneath Pangea may be spatially non-uniform due to the active subduction of oceanic plates along the margins of Pangea. The effect of the spatially non-uniform HTA region on the breakup of Pangea and the subsequent continental drift should be investigated carefully in future.

To summarize the results of the present study, it was determined that the high-speed northward drift of the Indian subcontinent was likely caused by large-scale mantle downwelling that developed spontaneously in the North Tethys Ocean, attributed to the overall shape of the supercontinent Pangea. This result implies that the high-speed northward drift of the Indian subcontinent and the resulting Indo-Asian convergence at around 40–50 Ma was destined when the supercontinent Pangea was formed at around 300 Ma.

It is about one hundred years since the publication of the first edition of “Die Entstehung der Kontinente and Ozeane (The Origin of Continents and Oceans)”46 by Alfred Wegener, who first proposed the theory of continental drift in 1912. Now, we can approximately reproduce the process of continental drift, from the breakup of Pangea at about 200 Ma to the present-day continental distribution, using a numerical simulation model of 3-D spherical mantle convection with an infinite Prandtl number and an Earth-like Rayleigh number. Arthur Holmes, a British geologist, first proposed that the cause of continental drift was subcrustal convection currents within the Earth47. Our numerical simulations demonstrated that toroidal flow of the surface boundary layer, generated by the lateral viscosity heterogeneity between the highly viscous continents and the oceanic mantle, played a significant role in the modelled Pangea breakup and implied that the primary driving force of continental dispersal was both mantle convection (i.e., large-scale mantle upwelling/downwelling flows) and plate tectonics (i.e., plate boundary forces).

Methods

The mantle was modelled as a Boussinesq fluid with an infinite Prandtl number and realistic Rayleigh number confined in 3-D spherical shell geometry (r, θ, ϕ) with a thickness of 2867 km. Mantle convection was numerically solved using the finite-volume-based mantle convection code, ConvGS8,9. The number of computational grids was taken to be 128 (r) × 128 (θ) × 384 (ϕ) × 2 (for Yin and Yang grids48). Impermeable, shear-stress-free conditions were imposed on both the top and bottom surface boundaries of the spherical shell. The temperature was fixed at the top surface boundary, whereas adiabatic conditions were imposed on the bottom surface boundary.

The dimensionless conservation equations for mass, momentum, and energy, which govern mantle convection under the Boussinesq approximation, and the advection equation for those materials compositionally different from mantle material, were expressed, respectively, as:

graphic file with name srep08407-m1.jpg
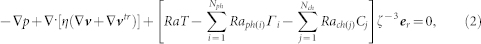graphic file with name srep08407-m2.jpg
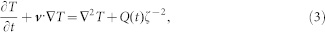graphic file with name srep08407-m3.jpg
graphic file with name srep08407-m4.jpg

where v represents the velocity, p the dynamic pressure, η the viscosity, t the time, T the temperature, Q the time-dependent radioactive heat production rate per unit mass, Γi the phase function (0 ≤ Γi ≤ 1)49, Cj the composition (0 ≤ Cj ≤ 1), i the index of each phase in the mantle, j the index of each material compositionally different from mantle material, and er the unit vector in the upward radial direction.

The dimensionless parameters were the thermal Rayleigh number Ra, the phase Rayleigh number Raph(i), the compositional Rayleigh number Rach(j), the internal heating number Q, and the mantle/shell radius ratio ζ:

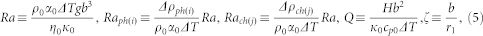graphic file with name srep08407-m5.jpg

where the definitions and values of the symbols are as listed in Supplementary Table 1.

The thermal Rayleigh number Ra was fixed at 5.72 × 107 (corresponding to a reference viscosity of 1021 Pa s and a temperature difference across the mantle of 2500 K). The internal heat production depends on time, considering the decay of radioactive elements in the chondritic mantle9,50. The olivine to wadsleyite phase transition at a reference depth of 410 km, the wadsleyite to ringwoodite phase transition at a depth of 520 km, and the ringwoodite to perovskite + magnesiowüstite phase decomposition at a depth of 660 km were imposed in the model (see Supplementary Table 1).

The viscosity of the mantle in the present model depends on the phase and composition according to a dimensionless formulation:

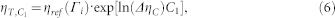graphic file with name srep08407-m6.jpg

where C1 is the composition that represents continental (C1 = 1) and mantle (C1 = 0) materials, and ΔηC is the viscosity ratio between the continental and mantle materials, which is taken as a free parameter. The reference viscosity at each phase ηref(Γi = 1,2) is set to 1 in the olivine, wadsleyite, and ringwoodite phases, and ηref(Γi = 3) is set to 30 in the perovskite + magnesiowüstite phase51,52,53.

Note that the temperature-dependence of viscosity was not considered in the present model because activation parameters of rocks in the deep mantle have not yet been determined, even in recent mineral physics experiments20. Notwithstanding, in the present study, we also obtained results from additional simulations with a numerical model of mantle convection using a temperature-dependent viscosity, to show the dynamic effect of laterally variable rheology on the Pangea breakup and the subsequent continental drift.

For the temperature-dependent viscosity model, Eq. (6) was replaced by

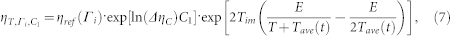graphic file with name srep08407-m7.jpg

where Tave(t) is the dimensionless average temperature of the entire mantle at each time step, and E ≡ ln(ΔηT) is the activation parameter that controls the viscosity contrast between the top surface and the underlying mantle.

Based on the half-space cooling model54, the initial condition for the depth profile of dimensionless temperature is given by

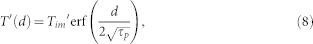graphic file with name srep08407-m8.jpg

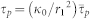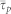where the prime indicates a dimensionless value, Tim' is the dimensionless initial mantle temperature of 0.52 (corresponding to 1573 K), d is the depth (i.e., d = 0 and 1 at the top and bottom boundaries, respectively), Inline graphic, and Inline graphic is set at the typical age of the lithosphere (100 Myr).

In the present model, we assumed that the seismic velocity perturbation depends on the temperature perturbation alone. The initial state of the lateral temperature anomaly in the mantle at 200 Ma was derived from the S-wave global seismic tomography model, S40RTS19. The seismic velocity anomaly δVs from the S40RTS model was converted to the temperature anomaly δT:

graphic file with name srep08407-m9.jpg

where δVs is the deviation from the PREM55, and the temperature derivative of the seismic velocity anomaly as a function of depth obtained by mineral physics experiment20 (Supplementary Fig. 1):

graphic file with name srep08407-m10.jpg

In addition, considering the thermal insulation effect of the supercontinent24,25,26,27,28,29,30, the temperature of the subcontinental mantle beneath Pangea from depths of 202 to 660 km is assumed to be ΔTe higher than that of the mantle beneath the oceanic regions at the same depths.

Finally, the dimensionless initial temperature field in the mantle at the beginning of the simulation was

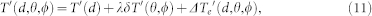graphic file with name srep08407-m11.jpg

where λ is 0 or 1, and ΔTe' is the dimensionless excess temperature anomaly of the subcontinental mantle beneath Pangea. When λ is 0, there is no lateral temperature anomaly for the initial temperature field.

The obtained temperature anomaly in the mantle is shown in Supplementary Fig. 2b–f.

Author Contributions

M.Y. designed the project and carried out the numerical simulations and data analyses. M.Y. and Y.H. discussed the results and prepared the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep08407-s1.pdf (1.3MB, pdf)

Acknowledgments

Digital data for the coastline of Pangea are taken from GPlates 1.4 software (http://www.gplates.org/). Some figures were produced using the Generic Mapping Tools. The calculations presented herein were performed using the supercomputer facilities (SGI ICE X) at JAMSTEC. This work was supported by a Grant-in-Aid for Scientific Research (B) from Japan Society for the Promotion of Science (JSPS KAKENHI Grant Number 23340132).

References

  1. Seton M. et al. Global continental and ocean basin reconstructions since 200 Ma. Earth-Science Rev. 113, 212–270 (2012). [Google Scholar]
  2. Scotese C. R. in PALEOMAP Progress Rep. 90-0497 (Department of Geology, University of Texas, 2001). [Google Scholar]
  3. Collins W. J. Slab pull, mantle convection, and Pangaean assembly and dispersal. Earth Planet. Sci. Lett. 205, 225–237 (2003). [Google Scholar]
  4. Storey B. C. The role of mantle plumes in continental breakup: case histories from Gondwanaland. Nature 377, 301–308 (1995). [Google Scholar]
  5. van Hinsbergen D. J. J., Steinberger B., Doubrovine P. V. & Gassmöller R. Acceleration and deceleration of India-Asia convergence since the Cretaceous: Roles of mantle plumes and continental collision. J. Geophys. Res. 116, B06101 (2011). [Google Scholar]
  6. Kumar P. et al. The rapid drift of the Indian tectonic plate. Nature 449, 894–897 (2007). [DOI] [PubMed] [Google Scholar]
  7. Aitchison J. C., Ali J. R. & Davis A. M. When and where did India and Asia collide? J. Geophys. Res. 112, B05423 (2007). [Google Scholar]
  8. Yoshida M. Mantle temperature under drifting continents during the supercontinent cycle. Geophys. Res. Lett. 40, 681–686 (2013). [Google Scholar]
  9. Yoshida M. Effects of various lithospheric yield stresses and different mantle-heating modes on the breakup of the Pangea supercontinent. Geophys. Res. Lett. 41, 3060–3067 (2014). [Google Scholar]
  10. Dziewonski A. M., Foret A. M., Su W.-J. & Woodward R. L. in Relating Geophysical Structures and Processes: The Jeffreys Volume, AGU Geophys. Monog., 76 (eds Aki, K. & Dmowska, R.) 67–105 (Am. Geophys. Un., 1993). [Google Scholar]
  11. Garnero E. J., Thorne M. S., McNamara A. K. & Rost S. in Superplumes: Beyond Plate Tectonics (eds Yuen, D. A., Maruyama, S., Karato, S. & Windley, B. F.) 139–158 (Springer, 2007). [Google Scholar]
  12. Torsvik T. H., Smethurst M. A., Burke K. & Steinberger B. Large igneous provinces generated from the margins of the large low-velocity provinces in the deep mantle. Geophys. J. Int. 167, 1447–1460 (2006). [Google Scholar]
  13. Torsvik T. H., Steinberger B., Cocks L. R. M. & Burke K. Longitude: Linking Earth's ancient surface to its deep interior. Earth Planet. Sci. Lett. 276, 273–282 (2008). [Google Scholar]
  14. Burke K., Steinberger B., Torsvik T. H. & Smethurst M. A. Plume Generation Zones at the margins of Large Low Shear Velocity Provinces on the core-mantle boundary. Earth. Planet. Sci. Lett. 265, 49–60 (2008). [Google Scholar]
  15. Torsvik T. H., Burke K., Steinberger B., Webb S. J. & Ashwal L. D. Diamonds sampled by plumes from the core-mantle boundary. Nature 466, 352–355 (2010). [DOI] [PubMed] [Google Scholar]
  16. Bower D. J., Gurnis M. & Seton M. Lower mantle structure from paleogeographically constrained dynamic Earth models. Geochem. Geophys. Geosyst. 14, 44–63 (2013). [Google Scholar]
  17. Bull A. L., Domeier M. & Torsvik T. H. The effect of plate motion history on the longevity of deep mantle heterogeneities. Earth. Planet. Sci. Lett. 401, 172–182 (2014). [Google Scholar]
  18. Richards M. A., Jones D. L., Duncan R. A. & De Paolo D. J. Flood basalts and hotspot tracks: plume heads and tails. Science 254, 263–267 (1991).17787974 [Google Scholar]
  19. Ritsema J., Deuss A., van Heijst H. J. & Woodhouse J. H. S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 184, 1223–1236 (2011). [Google Scholar]
  20. Karato S. Deformation of Earth materials: Introduction to the rheology of the solid Earth. 463 (Cambridge Univ. Press, 2008). [Google Scholar]
  21. Conrad C. P., Behn M. D. & Silver P. G. Global mantle flow and the development of seismic anisotropy: Differences between the oceanic and continental upper mantle. J. Geophys. Res. 112, B07317 (2007). [Google Scholar]
  22. Rolf T. & Tackley P. J. Focussing of stress by continents in 3D spherical mantle convection with self-consistent plate tectonics. Geophys. Res. Lett. 38, L18301 (2011). [Google Scholar]
  23. Poudjom Djomani Y. H., O'Reilly S. Y., Griffin W. L. & Morgan P. The density structure of subcontinental lithosphere through time. Earth Planet Sci. Lett. 184, 605–621 (2001). [Google Scholar]
  24. Yoshida M., Iwase Y. & Honda S. Generation of plumes under a localized high viscosity lid on 3-D spherical shell convection. Geophys. Res. Lett. 26, 947–950 (1999). [Google Scholar]
  25. Phillips B. R. & Bunge H.-P. Heterogeneity and time dependence in 3D spherical mantle convection models with continental drift. Earth Planet. Sci. Lett. 233, 121–135 (2005). [Google Scholar]
  26. Phillips B. R. & Bunge H.-P. Supercontinent cycles disrupted by strong mantle plumes. Geology 35, 847–850 (2007). [Google Scholar]
  27. Coltice N., Phillips B. R., Bertrand H., Ricard Y. & Rey P. Global warming of the mantle at the origin of flood basalts over supercontinents. Geology 35, 391–394 (2007). [Google Scholar]
  28. Heron P. J. & Lowman J. P. The effects of supercontinent size and thermal insulation on the formation of mantle plumes. Tectonophys. 510, 28–38 (2011). [Google Scholar]
  29. Anderson D. L. Hotspots, polar wander, Mesozoic convection and the geoid. Nature 297, 391–393 (1982). [Google Scholar]
  30. Gurnis M. Large-scale mantle convection and the aggregation and dispersal of supercontinents. Nature 332, 695–699 (1988). [Google Scholar]
  31. Heron P. J. & Lowman J. P. The impact of Rayleigh number on assessing the signicance of supercontinent insulation. J. Geophys. Res. 119, 711–733 (2014). [Google Scholar]
  32. Baumgardner J. R. in Flow and Creep in the Solar System: Observations, Modeling, and Theory (NATO Science Series C) (eds Stone, D. B. & Runcorn, S. K.) 207–224 (Kluwer Academic Publishers, 1993). [Google Scholar]
  33. Lenardic A. & Moresi L.-N. Some thoughts on the stability of cratonic lithosphere: effects of buoyancy and viscosity. J. Geophys. Res. 104, 12747–12758 (1999). [Google Scholar]
  34. Doin M.-P., Fleitout L. & Christensen U. Mantle convection and stability of depleted and undepleted continental lithosphere. J. Geophys. Res. 102, 2771–2787 (1997). [Google Scholar]
  35. Shapiro S. S., Hager B. H. & Jordan T. H. Stability and dynamics of the continental tectosphere. Lithos 48, 115–133 (1999). [Google Scholar]
  36. Yoshida M. Dynamic role of the rheological contrast between cratonic and oceanic lithospheres in the longevity of cratonic lithosphere: A three-dimensional numerical study. Tectonophys. 532–535, 156–166 (2012). [Google Scholar]
  37. Hafkenscheid E., Wortel M. J. R. & Spakman W. Subduction history of the Tethyan region derived from seismic tomography and tectonic reconstructions. J. Geophys. Res. 111, B08401 (2006). [Google Scholar]
  38. Yoshida M. Mantle convection with longest-wavelength thermal heterogeneity in a 3-D spherical model: Degree one or two? Geophys. Res. Lett. 35, L23302 (2008). [Google Scholar]
  39. Foley B. J. & Becker T. W. Generation of plate-like behavior and mantle heterogeneity from a spherical, viscoplastic convection model. Geochem. Geophys. Geosyst. 10, Q08001 (2009). [Google Scholar]
  40. van Heck H. J. & Tackley P. J. Planforms of self-consistently generated plates in 3D spherical geometry. Geophys. Res. Lett. 35, L19312 (2008). [Google Scholar]
  41. Forsyth D. & Uyeda S. On the relative importance of the driving forces of plate tectonics. Geophys. J. R. Astron. Soc. 43, 163–200 (1975). [Google Scholar]
  42. O'Neill C., Lenardic A., Jellinek A. M. & Moresi L. Influence of supercontinents on deep mantle flow. Gondwana Res. 15, 276–287 (2009). [Google Scholar]
  43. Lenardic A. et al. Continents, supercontinents, mantle thermal mixing, and mantle thermal isolation: Theory, numerical simulations, and laboratory experiments. Geochem. Geophys. Geosyst. 12, Q10016 (2011). [Google Scholar]
  44. Grigné C., Labrosse S. & Tackley P. J. Convective heat transfer as a function of wavelength: Implications for the cooling of the Earth. J. Geophys. Res. 110, B03409 (2005). [Google Scholar]
  45. Courtillot V., Jaupart C., Manighetti I., Tapponnier P. & Besse J. On causal links between flood basalts and continental breakup. Earth. Planet. Sci. Lett. 166, 177–195 (1999). [Google Scholar]
  46. Wegener A. Die Entstehung der Kontinente and Ozeane. 1st edn, (Friedrich Vieweg & Sohn, 1915). [Google Scholar]
  47. Holmes A. Radioactivity and earth movements. Geol. Soc. Glasgow Trans. 18, 559–606 (1931). [Google Scholar]
  48. Yoshida M. & Kageyama A. Application of the Yin-Yang grid to a thermal convection of a Boussinesq fluid with infinite Prandtl number in a three-dimensional spherical shell. Geophys. Res. Lett. 31 L12609 (2004). [Google Scholar]
  49. Christensen U. R. & Yuen D. A. Layered convection induced by phase transitions. J. Geophys. Res. 90, 10291–10300 (1985). [Google Scholar]
  50. Schubert G., Turcotte D. L. & Olson P. Mantle Convection in the Earth and Planets. (Cambridge Univ. Press, 2001). [Google Scholar]
  51. Hager B. H. in Glacial Isostasy, Sea-Level and Mantle Rheology (eds Sabatini, R., Lambeck, K. & Boschi, E.) 493–513 (Kluwer Academic Publishers, Dordrecht, The Netherlands, 1991). [Google Scholar]
  52. Bunge H.-P., Richards M. A. & Baumgardner J. R. The effect of depth dependent viscosity on the planform of mantle convection. Nature 379, 436–438 (1996). [Google Scholar]
  53. Ricard Y., Richards M., Lithgow-Bertelloni C. & Stunff Y. L. A geodynamic model of mantle density heterogeneity. J. Geophys. Res. 98, 21895–21909 (1993). [Google Scholar]
  54. Turcotte D. L. & Schubert G. Geodynamics. 3rd edn, (Cambridge Univ. Press, 2014). [Google Scholar]
  55. Dziewonski A. M. & Anderson D. L. Preliminary reference earth model. Phys. Earth Planet. Int. 25, 297–356 (1981). [Google Scholar]
  56. Wessel P., Smith W. H. F., Scharroo R., Luis J. F. & Wobbe F. Generic Mapping Tools: Improved version released. EOS Trans. AGU 94, 409–410 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep08407-s1.pdf (1.3MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES