LIGSIFT: an open-source tool for ligand structural alignment and virtual screening

Abstract

Motivation: Shape-based alignment of small molecules is a widely used approach in computer-aided drug discovery. Most shape-based ligand structure alignment applications, both commercial and freely available ones, use the Tanimoto coefficient or similar functions for evaluating molecular similarity. Major drawbacks of using such functions are the size dependence of the score and the fact that the statistical significance of the molecular match using such metrics is not reported.

Results: We describe a new open-source ligand structure alignment and virtual screening (VS) algorithm, LIGSIFT, that uses Gaussian molecular shape overlay for fast small molecule alignment and a size-independent scoring function for efficient VS based on the statistical significance of the score. LIGSIFT was tested against the compounds for 40 protein targets available in the Directory of Useful Decoys and the performance was evaluated using the area under the ROC curve (AUC), the Enrichment Factor (EF) and Hit Rate (HR). LIGSIFT-based VS shows an average AUC of 0.79, average EF values of 20.8 and a HR of 59% in the top 1% of the screened library.

Availability and implementation: LIGSIFT software, including the source code, is freely available to academic users at http://cssb.biology.gatech.edu/LIGSIFT.

Supplementary information: Supplementary data are available at Bioinformatics online.

Contact: skolnick@gatech.edu

1 INTRODUCTION

Identification of new lead molecules is a major challenge in the drug discovery process, as the experimental screening of large chemical databases is very expensive and depends on how representative the library is. Virtual screening (VS) approaches are frequently used for lead identification, which can be then verified under laboratory settings. VS approaches can be broadly classified into protein-centric approaches (e.g. docking) and ligand centric approaches. Protein-centric approaches do not depend on known ligand information and are generally expected to perform better, as they enable one to explicitly evaluate protein–ligand interactions. However, these approaches rely heavily on the quality of the receptor structure and suffer from inherent limitations of the applied protocol. Ligand centric VS methods, on the contrary, do not need receptor information and often use known ligands as a seed to identify potential binders based on their 2D or 3D similarity to the known active molecule (Eckert and Bajorath, 2007). 2D VS methods generally represent a molecule as a vector with entries indicating the presence or absence of molecular features. These methods are popular, as they provide a fast and easy way of fishing out similar active molecules. However, the scaffold hopping potential of such methods is controversial (Renner and Schneider, 2006), and both molecular size and complexity negatively affect the search performance of such methods (Holliday et al., 2003).

In contrast, 3D VS methods are computationally taxing due to complexities associated with ligand flexibility and determination of the optimal 3D alignment. Nevertheless, with improvement in computational power, 3D VS methods have become popular, as they capture the physical and functional features required for the biological interaction and are generally capable of scaffold hopping (Quintus et al., 2009; Rush et al., 2005). The scaffold hopping potential of 3D methods not only help to reduce false negatives during VS experiments, but also provide important insights for bioisostere replacement (Jennings and Tennant, 2007), potential off-target interactions and cross-reactivity of existing drugs.

Three-dimensional methods for aligning small molecules consist of three basic components: (a) a descriptor to represent the molecule, (b) a scoring function to assess the alignment quality and (c) an optimization procedure to find the best possible alignment with respect to the chosen scoring function. Common choices of descriptors include molecular interaction field-based (Cheeseright et al., 2008), pharmacophore-based (Sperandio et al., 2007) and shape-based representations of small molecules. A number of algorithms for shape-based VS have emerged in the last few years; each seeks to maximize the shape overlap between the pair of molecules under consideration. Most use atom centered, smooth Gaussian functions to model molecular volume, as it helps to achieve rapid overlay and can also be performed relatively easily using simple mathematical operations. For example, Rapid Overlay of Chemical Structures (ROCS), a highly popular closed-source algorithm, uses a Gaussian description of the molecular shape and chemical nature of the ligand (Grant et al., 1996; Grant and Pickup, 1995) for ligand screening. Similarly, Align-it^TM, an open-source tool uses a Gaussian description of molecular pharmacophores, but follows a different optimization approach to find the best overlay (Taminau et al., 2008). These and other similar tools use the Tanimoto Coefficient (TC) or similar size-dependent functions for measuring molecular similarity (Hamza et al., 2012; Holliday et al., 2003). Moreover, these scoring functions lack a statistical model that can indicate the significance of structural/chemical match between molecules (Baldi and Nasr, 2010).

In this study, we present a new open-source, ligand-based VS algorithm that provides a size-independent scoring function to measure shape and chemical similarity and also reports the P-value to assess the statistical significance of the match between a pair of molecules. Performance evaluation of LIGSIFT on the 40 targets in the Directory of Useful Decoys (DUD) set shows overall improved performance compared with other well-established shape-based VS methods such as ROCS and Align-it^TM.

2 METHODS

2.1 Molecular representation and alignment

The 3D structure of a small molecule is represented using atom-based descriptors in LIGSIFT (supplementary Table S1). The molecular shape-density of every heavy atom i is described using a spherical Gaussian function:

$${\rho }_i\left(\mathit{r}\right)={\phi }_i\exp \left\{-{\alpha }_i{\left(r-R_i\right)}^2\right\},\text{\hspace{1em}where}{\alpha }_i=\pi {\left(\raisebox{1ex}{$3{\phi }_i$}\!\left/ \!\raisebox{-1ex}{$4\pi {\sigma }_i{}^3$}\right.\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$$ (1)

is the decay factor, φ_i = 2√2 is the amplitude, R_i is the atomic coordinate for the ith atom and σ_i is its van der Waals radius. The chemical nature of pharmacophore heavy atoms (supplementary Table S1) is identified using SMARTS expressions in OpenBabel (O'Boyle et al., 2008), and is modeled using the same Gaussian description as the atomic shape. Additionally, the spatial orientation of some atom-types (H-bond donor and acceptor) is calculated based on the position of neighboring atoms (supplementary Table S1).

Using this model, the shape/chemical density of any molecule can be calculated as the sum of atomic densities, defined as:

$$\text{V}={\displaystyle \sum _{i=1}^n{\displaystyle \int d\mathit{r}{\rho }_i}}(r)$$ (2)

and the overlap between two molecules A and B is calculated as the sum of the overlaps of individual atoms’ Gaussian functions:

$$\begin{array}{l}{V}_{\text{AB}}={\displaystyle \sum _{i\in A}{\displaystyle \sum _{j\in B}{\displaystyle \int dr{\rho }_i\left(r\right)}}}{\rho }_j\left(r\right)\\ ={\displaystyle \sum _{i\in A}{\displaystyle \sum _{j\in B}{\rho }_i{\rho }_j\exp \left(-\frac{{\alpha }_i{\alpha }_j{d}_{ij}^2}{{\alpha }_i+{\alpha }_j}\right)}}{\left(\frac{\pi }{{\alpha }_i+{\alpha }_j}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\end{array}$$ (3)

where i and j are the heavy atom indices of molecules A and B, ρ_i and ρ_j are the atomic Gaussian distributions of each atom and d_ij is the distance between atom i and j.

To identify the correct shape and chemical similarity between molecules A and B, we need to first identify the relative poses of A and B that maximizes V_AB. To achieve this, two types of quickly identifiable initial alignments are used. The first type of initial alignment is generated by aligning the principal axes of the moment of inertia tensors of molecules A and B. This procedure helps to quickly scan the complete 3D space with minimum iterations, but is more suitable for aligning molecules of similar size. The second type of initial alignment is based on a three-atom superposition of an atomic triad selected from A and B. Although a systematic search would involve all combinations of atom pairs from both the molecules and would provide a very close to optimal alignment, this is not a practical solution for fast VS applications. Therefore, only pairs of atoms having similar chemical nature are used as triad pairs to generate sub-optimal initial alignments.

Starting from each sub-optimal initial alignment, the optimal non-sequential alignment is identified using the Jonker–Volegenant shortest augmenting path algorithm (Jonker and Volgenant, 1987), which aims to minimize the total cost of misaligning heavy atom pairs. A cost matrix is calculated for every heavy atom pair ($i\in \text{A},j\in \text{B}$), where the cost (C_ij) for aligning atom i and j is defined as:

$$C_{ij}=k-V_{ij}\text{,}$$ (4)

where V_ij is the overlap of the atomic Gaussian distribution between atom i and j, and k = 100 is an arbitrary constant larger than V_ij. When evaluating chemical similarity, V_ij is evaluated as zero for atom pairs with dissimilar chemical types, in order to encourage matches between atom pairs with same or similar chemical type.

Finally, a short Metropolis Monte-Carlo simulation with rigid body rotation and translation of coordinates is performed to refine and maximize the overlap (V_AB) between molecules A and B.

2.2 Molecular similarity of overlapped structures

Once the relative pose of molecules A and B that results in maximum overlap (V_AB) is identified, the scaled TC (sTC) score is calculated as:

$$\text{sTC}=\frac{\text{TC}+s_0}{1+s_0}\text{,}\text{where TC}=\frac{V_{\text{AB}}}{V_{\text{A}}+V_{\text{B}}-V_{\text{AB}}}$$ (5)

Here, TC is the Tanimoto coefficient of the shape/chemical similarity, V_A and V_B are the shape/chemical densities of molecules A and B calculated using the Gaussian model (Equation 2). s₀ in Equation(5) is the scaling factor that ensures that the mean molecular similarity scores are size-independent and is calculated as:

$$s_0=\frac{\left(a+b\ln \left(V_{\text{A}}\right)+c\ln \left(V_{\text{B}}\right)+d\ln \left(V_{\text{A}}+V_{\text{B}}\right)\right)-e}{e-1}$$ (6)

To estimate s₀, we need a random background distribution of molecular similarity (MS) scores consistent with the conformational variability of small molecules. Therefore, a conformational pool of 737 PubChem molecules of various sizes was generated using RDKit’s distance-geometry conformer generator. For each molecule, a maximum of 50 low-energy conformers were generated, and each conformer was structurally aligned with 11 604 representative PDB ligands. In addition, all PDB ligands were also aligned to each other. Pairwise TC values for shape similarity and chemical similarity obtained after aligning molecule pairs of various sizes were used for calculating s₀ (using Equation 6). This scaling of TC values ensures that the molecular similarity scores are size-independent for random match between ligands. The parameters for a, b, c, d and e in Equation 6 for different optimization schemes (shape similarity, chemical similarity and combination of shape and chemical similarity) are listed in supplementary Table S2.

Figure 1 shows the distribution of scaled TC mean and unscaled TC mean obtained for random structural alignments. Both scaled shape and chemical similarity scores have a narrow distribution with a maximum density near 0.49 and 0.42, respectively, reflecting that the mean scores for alignment between random pair of molecules are size independent. Meanwhile, molecular similarities measured using unscaled TC have a large spread, which reflects their size dependence.

Fig. 1.

Distribution of mean shape and chemical similarity scores for random pairs of molecules of various sizes

2.3 Statistical significance of molecular similarity

The statistical significance of the sTC between any two molecules is estimated by comparing the similarity score with values obtained for the alignment between random molecule pairs. The structure similarity of random pairs of various sizes was calculated using the same procedure as described above for calculating s₀ and modeled by Gumbel distribution fitting in the R evir package. A statistical model of fitted distributions was obtained through linear regression fits

$$\begin{array}{l}\mu =a+b{V}_{\text{A}}+c{V}_{\text{B}}+d\ln (V_{\text{A}}+V_{\text{B}})\text{+}e\left|V_{\text{A}}-V_{\text{B}}\right|\\ \sigma =a+b\ln (V_{\text{A}})+c\ln (V_{\text{B}})+d\ln (V_{\text{A}}+V_{\text{B}})\text{,}\end{array}$$ (7)

where μ is the location parameter and σ is the scale parameter of the fitted Gumbel distributions. Parameters a to e in Equation (7) for estimating P-values are listed in supplementary Table S3. The P-values of sTC scores can be then calculated by:

$$P\text{value}=1-\exp \left\{-\exp \left(-z\right)\right\}\text{,where}z=\frac{\text{MS}-\text{score}-\mu }{\sigma }$$ (8)

is the z-score of sTC, μ and σ are parameters computed based on the fitted statistical model (Equation 7). Observed and modeled distributions for molecules of various sizes are shown in supplementary Figures S1 and S2.

2.4 Validation dataset

For the validation, we have used a standard database of active and decoy molecules for 40 pharmaceutically relevant protein targets, listed in the DUD (Huang et al., 2006). For each active molecule, there are approximately 36 physically similar but topologically dissimilar decoys, selected based on matching molecular weight, number of hydrogen-bond donor and acceptors, number of rotatable bonds and log P. Duplicate entries were removed; thus only a single entry for each molecule in the database is retained. The list of all the 40 targets along with the number of actives and decoys is found in supplementary Table S4.

To evaluate the effect of conformational flexibility on VS, conformational models of the ligand derived from the 40 DUD protein–ligand complexes and database molecules were generated using OMEGA (Hawkins et al., 2010) with default settings.

2.5 Evaluation of VS

To evaluate the performance of different screening approaches, we used the standard evaluation metrics: (a) the receiver operating characteristic (ROC) curve and (b) the enrichment factor (EF) of screened compound library and (c) the hit rate (HR). The ROC curve plots the true positive rate as a function of false positive rate. The area under the curve (AUC) is frequently used to quantify the shape of the ROC curve, with values in the range [0–1], with 0.5 indicating random performance.

For evaluating the performance in the top x% of the screened library, a common metric EF has been applied, which is defined as:

$${\text{EF}}^{x\text{\%}}=\frac{{\text{True Positives}}^{x\text{\%}}/N_{\text{selected}}^{x\text{\%}}}{N_{\text{actives}}/N_{\text{total}}}$$ (9)

We have used EF^1%_, EF^5% and EF^10% to analyze the performance.

A known problem of EF is its dependency on the ratio of active and decoy molecules in the database. Therefore, we have used an additional metric HR, defined as:

$${\text{HR}}^{x\text{\%}}=\frac{{\text{EF}}_{\text{actual}}^{x\%}}{{\text{EF}}_{\text{ideal}}^{x\%}}\times 100$$ (10)

where ${\text{EF}}_{\text{ideal}}^{x\%}$ is the ideal EF that would be obtained in x^% of the database.

3 RESULTS

VS was performed for all the 40 DUD targets using bioactive and both single and multiple database conformers and database molecules were ranked using various shape and chemical similarity metrics. Multi-conformer models of database molecules were generated using OMEGA (OpenEye Inc.).

3.1 Effect of size-independent scoring function on VS

A common problem in VS is the large number of false negative predictions. One possible cause is the size dependence of the scoring functions that are used in scoring and ranking. We sought to address this problem by scaling a widely used metric TC, so that it becomes size independent (scaled TC). To examine the effect of scaling, independent of the contribution from different conformers of the database molecules, we used a single conformer per database molecule, as provided in the downloaded DUD structure file, which was generated using CORINA (Huang et al., 2006). Table 1 shows the average AUC and EF values obtained for the 40 DUD targets, using the bioactive query conformer and a single conformer of the database molecules (see Section 2.4). The same molecular overlay was used for both TC and sTC.

Table 1.

VS performance on 40 DUD targets using scaled and unscaled TC scoring functions

Ranking score	AUC av|sd	EF1% av|sd	EF5% av|sd	EF10% av|sd
TCshape+chem	0.73 ± 0.20	17.0 ± 10.9	7.3 ± 4.8	4.4 ± 2.5
TCshape	0.68 ± 0.21	13.6 ± 11.2	5.7 ± 4.4	3.7 ± 2.4
TCchem	0.77 ± 0.20	17.6 ± 10.8	8.0 ± 5.3	4.8 ± 2.6
sTCshape+chem	0.75 ± 0.20	17.1 ± 11.1	7.4 ± 4.9	4.4 ± 2.5
sTCshape	0.70 ± 0.21	13.5 ± 11.3	5.8 ± 4.4	3.7 ± 2.5
sTCchem	0.78 ± 0.19	17.9 ± 10.8	8.1 ± 5.3	4.9 ± 2.7

av: average; sd: standard deviation; TC: Tanimoto coefficient; sTC: scaled TC

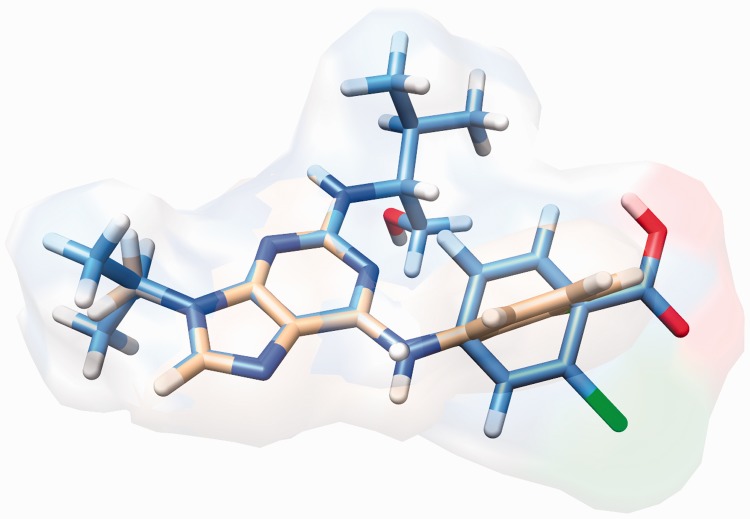
Overall, sTC shows a small improvement in both average AUC and EFs on the DUD set. In most cases, AUC and EF values either remain unchanged or the improvement was marginal, because the size of seed ligand and database molecules are mostly similar in the DUD set (supplementary Table S5). Only for the targets where database molecules were of much different size than the seed ligand does the advantage of scaling TC become apparent on average (supplementary Table S5). To examine this, we increased the size and heterogeneity of database molecules by including active and decoy molecules from other 39 proteins in the DUD set. We observe (supplementary Table S6) that as the size of database molecules diverge from the seed ligand, the difference between AUC and EF1% of sTC and unscaled TC becomes larger. This suggests that sTC helped to rank active molecules, which had statistically more significant matches but lower TC scores higher than those that had statistically less significant but higher TC scores. For example, Figure 2 shows structural superposition of a cdk2 active molecule ZINC03814437, on the seed ligand taken from cdk2 receptor structure (PDB: 1ckp). As the size of the active database molecule (in tan) is smaller than the seed ligand (in cyan), the large volume of the seed ligand overwhelms the unscaled chemical TC score of TC = 0.415. Based on TC, ZINC03814437 is ranked at position 123 (6.7% of database). For sTC, the chemical similarity is scaled, so the same overlap has a sTC = 0.54, which ranks the active molecule at position 62 (3.3% of database); highlighting the advantage of a size-independent scoring function.

Fig. 2.

Structural superposition of the active molecule ZINC03814437 (tan) on seed cdk2 ligand (cyan), using LIGSIFT

3.2 VS performance of LIGSIFT

The performance of LIGSIFT is next benchmarked using the bioactive conformation of the seed ligand and modeled multiple conformations of database molecules. Table 2 shows the AUC values of the ROC curves (supplementary Fig. S3) for each of the 40 DUD targets.

Table 2.

Area under the ROC curves for all 40 DUD targets using X-ray conformation of seed ligand and modeled conformers of database molecules

DUD target	LIGSIFT (sTC)	LIGSIFT (TC)	Align-It	ROCS#
ACE	0.79	0.78	0.86	0.70
ACHE	0.80	0.80	0.82	0.77
ADA	0.73	0.74	0.88	0.86
ALR2	0.69	0.66	0.71	0.57
AMPC	0.93	0.94	0.89	0.82
AR	0.83	0.83	0.79	0.79
CDK2	0.71	0.69	0.45	0.68
COMT	0.90	0.81	0.79	0.32
COX1	0.62	0.62	0.68	0.53
COX2	0.95	0.95	0.95	0.93
DHFR	0.97	0.97	0.97	0.92
EGFR	0.93	0.93	0.94	0.95
ER agonist	0.92	0.92	0.87	0.94
ER antagonist	0.90	0.90	0.94	0.98
FGFR1	0.62	0.60	0.59	0.49
FXA	0.77	0.76	0.62	0.39
GART	0.86	0.87	0.92	0.93
GPB	0.94	0.94	0.94	0.92
GR	0.87	0.84	0.56	0.79
HIVPR	0.79	0.77	0.78	0.56
HIVRT	0.78	0.76	0.63	0.66
HMGA	0.96	0.95	0.92	0.92
HSP90	0.87	0.87	0.65	0.66
INHA	0.72	0.73	0.77	0.72
MR	0.89	0.87	0.72	0.87
NA	0.96	0.97	0.88	0.97
P38	0.51	0.50	0.45	0.52
PARP	0.68	0.69	0.94	0.58
PDE5	0.57	0.56	0.64	0.53
PDGFRB	0.46	0.44	0.23	0.34
PNP	0.98	0.98	0.95	0.91
PPAR γ	0.85	0.84	0.91	0.92
PR	0.79	0.78	0.66	0.67
RXR α	0.98	0.98	0.98	0.96
SAHH	0.97	0.97	0.96	0.97
SRC	0.38	0.37	0.38	0.38
THROMBIN	0.59	0.56	0.69	0.66
TK	0.92	0.92	0.78	0.86
TRYPSIN	0.64	0.55	0.75	0.78
VEGFR2	0.67	0.64	0.29	0.43
Average AUC	0.79±0.20	0.78±0.20	0.75±0.23	0.73±0.2

#AUC values are taken from Kirchmair et al. (2009).

TC: Tanimoto Coefficient; sTC: scaled TC

Overall, LISIFT shows very good VS performance. The average AUC for the 40 targets is 0.79 ± 0.20, which is better than the well-established shape-based VS tools like ROCS (AUC = 0.73 ± 0.2), that uses a similar combo scoring function, and is much better than available open source tools like Align-It^TM (AUC = 0.75 ± 0.23). For 38 targets, LIGSIFT VS rankings were better than random (AUC > 0.5), while it failed for two targets: PDGFRB and SRC. The control methods, Align-It and ROCS, also failed on these two target proteins (AUC < 0.5), in addition to another three and four other proteins (Table 2), respectively. A detailed analysis of these two failed target proteins suggests that the seed ligand may not be a good representative for fishing out other active molecules for this receptor. For instance, when we used other active molecules in the database as our seed molecule, AUC values as well as EF and HR generally improved for both the proteins (supplementary Table S7). As expected, the performance using these database seed molecules depends on how well they represent other actives molecules in the database. These cases highlight the applicability and advantage of using multiple seed ligands to identify similar active molecules from the database.

Nevertheless, as observed in case of single conformers, even when we use multiple database conformations, the size-independent scaled TC (sTC) scoring performs slightly better than simply using the unscaled TC as the metric. A closer examination of the results highlights that AUC of the ROC curves improved for 20 of the 40 proteins (underlined values in Table 2), suggesting that the scaling of the similarity scores was helpful in alleviating false negatives for 50% of the test proteins.

The VS results are further analyzed using the EF (Equation 9), with the results summarized in Table 3. Using chemical similarity, LIGSIFT achieved an average EF of 20.8 ± 12.6, highlighting the ability of the method to recognize active molecules at the beginning of ranked database. High enrichment rates (EF1% >30) were observed for 15 proteins: ACHE, ADA, AMPC, AR, COMT, COX2, DHFR, GPB, HMGA, HSP90, INHA, MR, NA, PNP and RXR; while no enrichment (EF1% = 0) was observed for SRC (supplementary Table S8).

Table 4.

HR of various shape-based VS methods on DUD targets

Method	HR1% av | sd	HR5% av | sd	HR10% av | sd
Align-It	48.0 ± 35.5	40.6 ± 29.6	49.4 ± 31.8
ROCS#	54.6 ± 36.3	38.3 ± 30.0	46.0 ± 30.4
LIGSIFT(comb TC)	56.3 ± 36.1	44.5 ± 30.2	52.3 ± 29.7
LIGSIFT(shape TC)	47.9 ± 35.9	37.2 ± 27.6	45.3 ± 28.5
LIGSIFT(chem TC)	58.9 ± 35.7	46.4 ± 30.2	53.8 ± 29.8
LIGSIFT(comb sTC)	56.4 ± 36.2	45.1 ± 30.3	53.4 ± 30.1
LIGSIFT(shape sTC)	48.3 ± 36.1	37.7 ± 27.5	45.9 ± 29.0
LIGSIFT(chem sTC)	59.0 ± 35.6	46.6 ± 30.2	54.5 ± 29.9

#HR values calculated using EF data reported in (Kirchmair et al., 2009).

av: average; sd: standard deviation; comb: combined shape and chemical similarity scores (1:1)

Table 3.

EF comparisons of shape-based VS methods

Method	EF1% av | sd	EF5% av | sd	EF10% av | sd
Align-It	16.9 ± 12.5	8.1 ± 5.9	4.9 ± 3.2
ROCS#	19.4 ± 12.9	8.4 ± 6.0	5.2 ± 3.0
LIGSIFT(comb TC)	19.8 ± 12.7	8.9 ± 5.5	5.2 ± 3.0
LIGSIFT(shape TC)	16.9 ± 12.6	7.4 ± 5.5	4.5 ± 2.9
LIGSIFT(comb TC)	20.7 ± 12.6	9.3 ± 6.0	5.4 ± 3.0
LIGSIFT(comb sTC)	19.8 ± 12.7	9.0 ± 6.1	5.3 ± 3.0
LIGSIFT(shape sTC)	17.0 ± 12.6	7.5 ± 5.5	4.6 ± 2.9
LIGSIFT(chem sTC)	20.8 ± 12.6	9.3 ± 6.0	5.4 ± 3.0

#EF values are taken from ref (Kirchmair et al., 2009).

TC: Tanimoto Coefficient; sTC: scaled TC; av: average; sd: standard deviation; comb: combined shape and chemical similarity scores (1:1)

These values are comparable to those reported for ROCS (EF1% = 19.4 ± 12.9) (Kirchmair et al., 2009), and much better than what is obtained using Align-It (EF1% = 16.9 ± 12.5). However, the enrichment of active molecules using ROCS VS is null (EF1% = 0) for four proteins (FGFR1, GART, TRYPSIN and VEGFR2), while Align-It failed on three proteins (COMT, PR and VEGFR2).

Although the AUC of ROC curves along with EF1% are commonly used for evaluating VS performance, a known disadvantage of EF is its dependence on the ratio of actives and decoys in the database, which makes comparison of various methods on different datasets ambiguous. Therefore, we additionally used the Hit Rate (Equation 10) for evaluating VS performance. The average hit rate of LIGSIFT in the top 1% of the screened library was 59%, better than the ROCS hit rate of 54.6 and the Align-It hit rate of 48.0%. These results clearly show that on average LIGSIFT ranks a large number of active molecules as best among the screened molecules in the database. For example, 22 of the 40 DUD proteins achieved a hit rate >50%, while only two proteins had a hit rate of <10% (supplementary Table S9).

It is interesting to note that even though multiple ligand conformations should result in better molecular overlap and is expected to have better VS performance, the observed improvement in average AUC was marginal (increasing from 0.78 to 0.79). The average EF1% showed the largest improvement, increased from 17.9 to 20.8. To examine the effect of molecular flexibility on VS performance, we further analyzed EF1% for molecules with different molecular flexibility (supplementary Table S10), measured by their number of rotatable bonds, but found no correlation between molecular flexibility and VS performance.

4 DISCUSSION AND CONCLUSION

Shape-based ligand structural alignment has multiple applications, the most practical being drug discovery. Even though there is a rapid increase in the number of tools developed for this purpose, the metrics used for evaluating molecular similarity in these applications are size dependent and lack statistical significance quantification.

Here, we have developed a new algorithm (LIGSIFT) for the structural overlay of small molecules and quantification of molecular similarity (both shape and chemical) using a size-independent scoring function (sTC). This score is essentially a scaled TC based on a random background distribution of shape and chemical TC calculated for millions of overlays of molecules of various sizes. A rigorous benchmark and evaluation done using three standard metrics, namely AUC of ROC curve, EF and Hit Rate (HR), highlight the improvements in VS using scaled TC (sTC) over commonly used size-dependent ranking functions like TC, especially for database molecules that have different size than seed ligand.

In a commonly used DUD benchmark dataset, LIGSIFT performs better (AUC = 0.79 ± 0.2) than other well-established shape-based VS methods like ROCS (reported AUC = 0.73 ± 0.2) (Kirchmair et al., 2009), ShaEP (reported AUC = 0.64 ± 0.17) (Vainio et al., 2009), MolShaCS (reported AUC = 0.63 ± 0.08) and Align-It (0.75 ± 0.2). Overall, for 95% of the test proteins, the VS performance of LIGSIFT was non-random and the hit rate of active molecules was >10% in the top 1% of screened library.

While these results are encouraging, we noticed that using a given seed ligand, LIGSIFT was able to retrieve only half of the active molecules in nearly 55% of the tested proteins. This phenomenon is not restricted to only LIGSIFT, but was also observed for other shape-based VS tools, suggesting that a single-seed ligand contains a limited imprint of the physicochemical information of the ligand-binding site and may not be sufficient for identifying all active molecules present in the ligand database. In addition, it is also possible that these missed active molecules bind at a different location on the protein. For these cases, it might be useful to use a diverse set of known active ligands as seeds. If other active molecules are unknown, ligands from homologous proteins can be useful as seeds in VS experiments. In future work, we will explore this option in further detail.