Abstract
The multilevel summation method (MSM) offers an efficient algorithm utilizing convolution for evaluating long-range forces arising in molecular dynamics simulations. Shifting the balance of computation and communication, MSM provides key advantages over the ubiquitous particle–mesh Ewald (PME) method, offering better scaling on parallel computers and permitting more modeling flexibility, with support for periodic systems as does PME but also for semiperiodic and nonperiodic systems. The version of MSM available in the simulation program NAMD is described, and its performance and accuracy are compared with the PME method. The accuracy feasible for MSM in practical applications reproduces PME results for water property calculations of density, diffusion constant, dielectric constant, surface tension, radial distribution function, and distance-dependent Kirkwood factor, even though the numerical accuracy of PME is higher than that of MSM. Excellent agreement between MSM and PME is found also for interface potentials of air–water and membrane–water interfaces, where long-range Coulombic interactions are crucial. Applications demonstrate also the suitability of MSM for systems with semiperiodic and nonperiodic boundaries. For this purpose, simulations have been performed with periodic boundaries along directions parallel to a membrane surface but not along the surface normal, yielding membrane pore formation induced by an imbalance of charge across the membrane. Using a similar semiperiodic boundary condition, ion conduction through a graphene nanopore driven by an ion gradient has been simulated. Furthermore, proteins have been simulated inside a single spherical water droplet. Finally, parallel scalability results show the ability of MSM to outperform PME when scaling a system of modest size (less than 100 K atoms) to over a thousand processors, demonstrating the suitability of MSM for large-scale parallel simulation.
1. Introduction
Significant long-range electrostatic interactions arise in many biomolecular systems, such as negatively charged DNA and RNA, polar or charged membranes, ion channels, and electrostatic steering of protein–protein and enzyme–substrate association. Accordingly, electrostatic interactions need to be accurately represented in molecular modeling calculations. The computational cost increases in principle as N2, where N is the number of charged particles in the system.
The evaluation of electrostatic interactions can, through the use of the fast Fourier transform (FFT), be approximated with controlled accuracy by two finite range calculations, one in real space and one in reciprocal space. However, these FFT-based approximation methods, including particle–mesh Ewald (PME)1,2 and particle–particle particle–mesh (PPPM),3 generally require simulations to describe infinite three-dimensional lattices where each lattice cell is filled with a copy of the simulated system. As a result, the simulations include unwanted interactions with the copies. To prevent artifacts due to copy–copy interactions, the biologically relevant components of each copy must be surrounded by ample solvent to guarantee enough spacing between copies, unfortunately increasing system size and, thereby, computational cost. Moreover, the communication cost of calculating in parallel the two 3-D FFTs required by PME and PPPM outpaces the computational cost as the number of atoms and number of processors increase, due to the necessity of exchanging data between all of the processors involved in the FFT calculation. On massively parallel computers routinely employed today for large system molecular dynamics (MD) simulations, the FFT communication becomes the main performance bottleneck, and efforts to maintain scalability for PME have inspired various strategies, such as reserving a subset of processors for the FFT calculation.4 Alternative methods for calculating electrostatics, including the real-space convolution method implemented in the special-purpose Anton 2 supercomputer,5 have been developed to avoid the FFT communication bottleneck. In particular, the multilevel summation method (MSM) effectively replaces the nonscalable FFT communication by more densely localized convolution calculations that permit better parallel scaling and utilization of modern vector computational hardware units.
An example where MSM is methodologically more suitable than PME arises in studies of the asymmetric environment across a membrane bilayer, where one might want to employ periodic boundaries along the surface but not along the membrane normal. If PME is employed and fully periodic boundary conditions are required, one needs to use a dual-membrane–dual-volume strategy, where two spatially separated membranes are included6 and the computational cost is doubled.
Interest in supporting systems having planar geometry has led to the development of a 2-D Ewald summation method,7 although this method has not yet been implemented in any mainstream MD software. Efforts have also been made to circumvent the enforced periodicity from PME by creating a nonperiodic “energy step” at the edge of a periodic simulation cell to maintain asymmetric ion concentrations across a membrane,8 but this approach cannot maintain a charge gradient across a membrane. Non-Ewald methods,9 such as the Wolf method10 and the isotropic periodic sum method with discrete fast Fourier transform (3D-IPS/DFFT)11 (the latter available in the Amber MD package12) can also be applied to nonfully periodic systems, but good accuracy for heterogeneous systems requires a large long-range cutoff value.13 MSM has the advantage of providing a unified methodology that can treat periodic, semiperiodic, and nonperiodic boundary conditions with a single algorithm that, furthermore, offers good parallel scalability.
MSM, employing so-called nested interpolation of softened pair potentials in real space, follows a strategy for long-range force calculation that differs from the one employed by PME. MSM was initially introduced for solving integral equations14 and later applied to long-range electrostatic interactions in 2-D.15 The method was then extended to calculate continuous forces in 3-D suitable for MD simulation in case of nonperiodic boundary conditions,16 intended originally to replace the functionality of the fast multipole method (FMM).17,18 MSM was further generalized to handle periodic boundary conditions.19 The use of multiple spatial scales in MSM makes it better suited than PME to multiple time stepping20 that is employed in the time integration of MD simulations.
The difficulties with the parallel scaling of PME and other FFT-based methods for ever greater numbers of processors have generated renewed interest in FMM for improving the scalability of MD,21,22 despite known stability problems caused by FMM producing discontinuous potentials and forces that require the use of computationally costly high order approximations.23 The calculation of highly accurate electrostatic forces provides no discernible benefit to MD, which instead requires continuous forces for the energy conserving integration methods used for simulating long time scales. There is also no added benefit from using adaptive solvers, such as FMM or other related oct-tree methods, due to the general uniformity of the particle density arising in applications of MD simulation to biomolecular systems. MSM has a hierarchical structure similar to that of FMM, allowing good parallel scalability while also producing continuous forces that provide stable dynamics without the high computational cost.16 A GPU-accelerated implementation of MSM has been developed already to calculate maps of the Coulombic potential.24−26 The methodology of MSM can also be applied to other pairwise potentials without truncation,27 most significantly to dispersion forces28 (the long-range part of van der Waals forces), which have critical effects on membrane properties.29,30
In the present study, we compare MSM with PME, both as implemented in version 2.10 of the MD program NAMD,31,32 for accuracy and efficiency. The parallelization of MSM in NAMD is distinguished from other recent parallelization efforts33 by making use of a combined domain decomposition and force decomposition approach to provide scaling to large numbers of processors, together with fine-grained SIMD (single instruction, multiple data) parallelism employed to greatly enhance the performance of the local grid calculations. The practical accuracy produced by MSM, although shown to be less than that typical for PME, is sufficient to reproduce the PME calculations of various structural, dynamic, dielectric, and mechanical properties of water. In particular, excellent agreement between MSM and PME is found for interface potentials at air–water and membrane–water interfaces, for both periodic and semiperiodic simulations, indicating that long-range Coulomb interactions are well represented with MSM regardless of boundary condition. Applications demonstrate also the suitability of MSM for systems with semiperiodic and nonperiodic boundaries. Semiperiodic simulations have been performed for membrane electroporation induced by an imbalance of charge across a membrane and also for ion conduction through a graphene nanopore with an ion gradient. Standard use of PME for either system would require the aforementioned dual-membrane–dual-volume strategy, doubling the system size. Nonperiodic simulations have also been performed for two well-studied proteins, each inside a spherical water droplet, to further validate the use of MSM. Generally speaking, the additional modeling options offered by MSM to representative systems makes MSM more efficient than PME by reducing the number of atoms needed for simulation. Parallel scalability results are also presented that show the ability of MSM to outperform PME when scaling a system of modest size (less than 100 K atoms) to over a thousand processors, demonstrating the suitability of MSM for large-scale parallel simulation. We conclude that the improved modeling offered by MSM, in combination with sufficient accuracy, better parallel scaling than PME, and availability in a mainstream MD program, makes MSM a compelling alternative to PME.
2. Multilevel Summation Method
For the convenience of the reader, we provide below a brief overview of the multilevel summation method (MSM) algorithm. Detailed discussions including the error analysis employed are available elsewhere.16,19 Readers interested only in the use of MSM, not in its algorithmic underpinnings, may proceed to Section 3.
2.1. Algorithm
MSM approximates the Coulombic potential energy for a system of N particles, having position ri and charge qi,
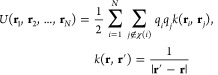 |
1 |
where χ(i) denotes for each i the set of atom indices to be excluded from the summation, which includes j = i and, typically for the simulation of biomolecules, also those atoms j that are either covalently bonded to i or to another atom that is covalently bonded to i. The interaction kernel k is split into the sum of a short-range part k0 smoothly truncated at cutoff distance a and slowly varying parts k1,k2,...,kL–1,kL smoothly truncated at cutoff distances 2a, 4a,...,2L–1a, ∞, respectively,
The splitting can be defined systematically in terms of a single unparameterized softening function γ(R) that softens 1/R for R ≤ 1,
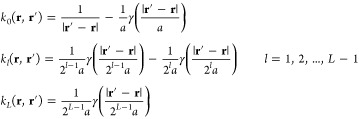 |
2 |
The slowly varying parts are interpolated from grids of spacing h, 2h,...,2L–2h, 2L–1h, respectively, for which interpolation operators 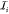 are defined in terms of interactions between
grid point positions rml = (xm, yml, zm)T and their
corresponding nodal basis functions ϕml,
are defined in terms of interactions between
grid point positions rml = (xm, yml, zm)T and their
corresponding nodal basis functions ϕml,
| 3 |
where m and n index the grid points. The nodal basis functions can be defined in terms of a single dimensionless basis function Φ,
Interpolation by piecewise polynomials of degree p provides local support for Φ with stencil size p + 1. Continuous forces, deemed important for energy conservation when simulating over long time scales,34,35 are produced from a continuously differentiable Φ and sufficient continuity from γ. Details regarding the softening and interpolation basis functions are provided in Section 2.2. The approximation is made efficient by nesting the interpolation between levels,
| 4 |
The CHARMM force field prescribes a cutoff distance of a = 12 Å for calculating van der Waals forces,36 which we adopt, for the sake of efficiency, in calculating all short-range nonbonded interactions. The choice of grid spacing h = 2.5 Å, which is slightly larger than the interatomic spacing, works effectively in practice. The computational work per grid point is bounded by a constant, and the number of grid points is reduced by about a factor of 1/8 at each successive level. The computational cost of MSM is O((p3 + (a/h)3)N), and analysis of the error19 shows an asymptotic bound of the form
Experiments in the present study test C1 cubic interpolation (p = 3) with C2 splitting,16 for which the functional forms of Φ and γ, given in Section 2.2, are among the lowest order choices that produce continuous forces.
The Coulombic potential energy is approximated by substituting eqs 4 and 2 into eq 1,
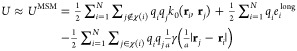 |
5 |
where the first summation is the exact short-range part, the second summation is the approximate long-range part, and the final summation removes the excluded interactions from the long-range part. The eilong long-range electrostatic potential is
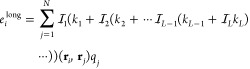 |
6 |
The short-range part of eq 5 simply evaluates all particle pair interactions within the cutoff distance a. The algorithm for eilong in eq 6 is made efficient by factoring the interpolation operator in eq 3, calculating at each grid point intermediate charge qm and potential eml. The order of the calculation is the following:
| 7 |
| 8 |
| 9 |
| 10 |
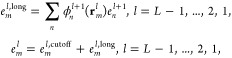 |
11 |
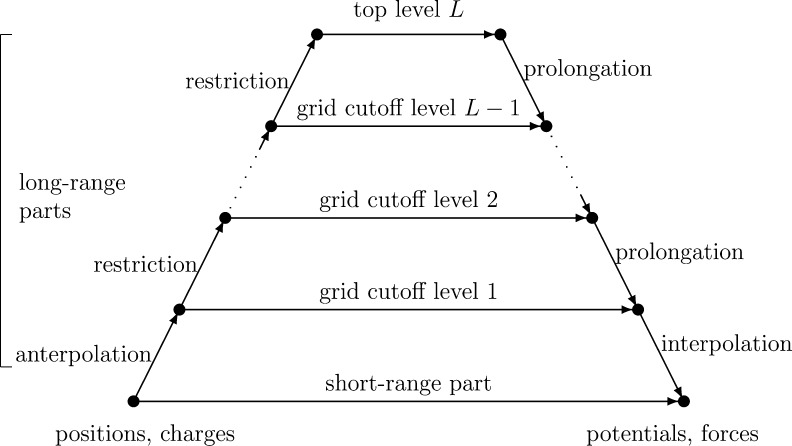
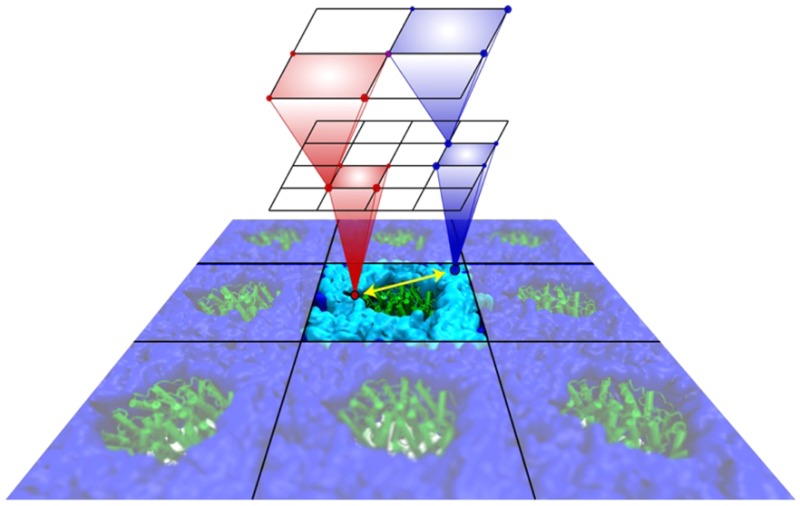
| 12 |
Figure 1 shows a diagram depicting the computational steps and their dependencies. The bottom–left shows the particle positions and charges, and the calculated potentials and forces are on the bottom–right. The gridded charges are calculated for each level moving up the left side, and the gridded potentials are calculated moving down the right side. The horizontal arrows represent the calculation of the short-range part along the bottom and the grid cutoff calculations for each grid level, all of which collectively require the majority of the computational effort. Forces are obtained analytically by taking the negative gradient of eq 5,
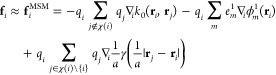 |
13 |
Figure 1.
Algorithmic steps for MSM.
The interpolation of atomic potentials from the finest grid in eq 12 evaluates for each atom position the nearby nodal basis functions requiring O(p3) operations per atom. The anterpolation (the adjoint of interpolation)14 in eq 7 performs similar work to spread atomic charges to the grid. All of the other functions ϕml and kl are evaluated at grid points, so can be calculated a priori. The restrictions in eq 8 and prolongations in eq 11 are gridded versions of anterpolation and interpolation, each requiring just O(p) operations per grid point when exploiting the regularity of the nodal basis function stencil by factoring the sums along each dimension. After a sufficient number of restrictions, the top level grid calculation in eq 10 is performed between all pairs of a bounded number of grid points. Most of the computational work for the long-range part is due to the grid cutoff calculation in eq 9, which evaluates pairs within a cutoff distance of 2a/h grid points, requiring O((a/h)3) operations per grid point. The partial potential em is the convolution of grid charges qnl with the stencil kl (rm, rnl) = kl(0,rm–n) for |m – n| < 2a/h as the convolution kernel.
An alternative approximation scheme is available through Hermite interpolation, an approach that exactly reproduces function values and derivatives at grid points, discussed in more detail in Section 2.2. When one extends Hermite interpolation to three dimensions, there arise 23 = 8 values per grid point that can account for all selections of zero or one derivatives independently in each dimension. The calculation of the grid point interactions is then expressed as 8 × 8 matrix–vector products, which have a straightforward mapping to CPU vector instructions, as discussed in Section 2.5. The increase in density of the grids is offset by doubling the finest level grid spacing, so that roughly the same amount of arithmetic operations are required for Hermite as for cubic interpolation. The accuracy of Hermite interpolation with doubled grid spacing is shown to be between that of cubic and quintic interpolation.19
Periodicity along a dimension is accomplished by including the periodic images of atoms contained within the cutoff distance into the short-range part of eq 5 and wrapping around the respective edges of the grid when calculating the long-range part. The top level is reduced, in this case, to a single grid point, for which the charge will be zero, if the system of atoms is neutrally charged, or will be set to zero, which effectively acts as a neutralizing background potential.19 The use of periodic boundary conditions imposes additional constraints on the grid spacing and the number of grid points along each periodic dimension. The grid spacing must exactly divide the periodic cell length, with the number of grid points chosen to be a power of 2 to maintain the doubling of the cutoff distance and grid spacing at each successive level. By permitting the number of grid points to also have up to one factor of 3, the grid spacings Δx, Δy, Δz can always be chosen so that 2 Å ≤ Δx, Δy, Δz < 3 Å. This strategy also benefits SIMD implementation discussed in Section 2.5, where an odd number of grid points along a dimension will need to be processed only once, namely on the top level.
2.2. Softening and Interpolation Functions
The function γ(R) that softens 1/R for R ≤ 1 is defined in terms of a truncated Taylor series expansion of s–1/2 about s = 1 and substituting R2 = s. For example, the softening used in this study with cubic interpolation is
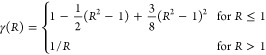 |
giving C2 continuity at the unit sphere and C∞ continuity everywhere else. Additional advantages of an even-powered softening are that γ((1/a)(x2 + y2 + z2)1/2) has bounded derivatives and can be calculated without square roots.
A piecewise interpolating polynomial of odd degree p having C1 continuity, as needed for producing continuous forces, can be constructed as a linear blending of the two degree p – 1 interpolating polynomials centered on consecutive nodes. The dimensionless basis function Φ(ξ) for cubic interpolation used in this study is
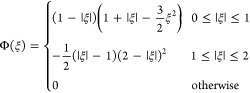 |
Higher order interpolation with quintic (p = 5), septic (p = 7), and nonic (p = 9) polynomials provides improved accuracy, but at greater computational cost. Empirical results show for degree p interpolation the optimality of using C(p+1)/2 softening.19
An alternative approach for interpolating with C1 continuity is to construct the Hermite interpolant that reproduces the function values and first derivatives at nodes. Hermite interpolation along one dimension requires two basis functions, Φ[0](ξ) for the function values and Φ[1](ξ) for the first derivatives:
Performing Hermite interpolation in 3-D requires storing 23 = 8 values per grid point, to account for 0 or 1 partial derivatives independently along the coordinate dimensions. The 8-element vector of nodal basis functions is similarly constructed by all products of Φ[0] and Φ[1] independently for each of the three coordinates. The algorithmic calculations in eqs 7–12 are modified accordingly. The anterpolation in eq 7 becomes multiplication of an 8-vector by a scalar, and the interpolation in eq 12 becomes the inner product of two 8-vectors. The restriction in eq 8 and prolongation in eq 11 become 8 × 8 matrix–vector products, where the restriction matrices are transposes of the prolongation matrices. The grid cutoff calculations in eq 9 and eq 10 are also 8 × 8 matrix–vector products. The grid spacing for Hermite interpolation is doubled from that of cubic interpolation to compensate for the “density” of each grid point increasing by a factor of 8. A more detailed mathematical description is available elsewhere.19
2.3. Comparison with PME Algorithm
Both MSM and PME perform a splitting of the interaction potential, PME into two parts and MSM into L + 1 parts. Both methods perform a charge-spreading (anterpolation) step to a grid of charges and an interpolation step from a grid of potentials. The major difference between the two methods is that PME transforms the grid of charges using a discrete 3-D fast Fourier transform (FFT), followed by a simple scaling of the transformed charges in Fourier space and a second FFT to transform back to the grid potentials, while MSM performs nested interpolation entirely in real space. The use of the FFT for PME is predicated on the assumption that the molecular system is periodic in all three dimensions, whereas MSM can be used flexibly with or without periodic boundary conditions.
Although the asymptotic complexity of PME is O(N log N) due to the use of the FFT, the overall operation count of PME is relatively small for moderate system sizes, as the FFT by itself is economical in the number of arithmetic operations required. However, computing the FFT requires large strided memory accesses that are inefficient for modern computer architectures. Moreover, the FFT does not provide good parallel scaling, as the communication pattern for implementing a 3-D FFT is many-to-many, essentially the same as a matrix transpose. MSM uses a hierarchical algorithm with close neighbor communication and arithmetically dense localized 3-D convolutions that map well to multicore processors with vectorized instructions. In spite of having a higher operation count for moderate system sizes, the use in MSM of a more efficient communication pattern combined with more effective use of computer processing resources offers better parallel scaling and performance compared to PME.
The numerical accuracy of MSM compared to PME is addressed in Figures 2 and 3 for simulations of an equilibrated 50 Å cube of 4142 water molecules. The figure compares NAMD’s MSM using cubic, Hermite, and quintic interpolation, discussed above, to NAMD’s smooth PME method using quartic and sexic interpolation of the structure factors.2 The employed PME grid spacings of 1.2 and 1.5 Å are representative of the method’s use in practice; for instance, GROMACS4 uses 1.2 Å as its default spacing and NAMD uses 1.5 Å as its default maximum spacing to provide a safety check to the user. The relative error in average mass-weighted force plotted in Figure 2 is calculated as
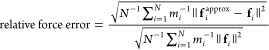 |
14 |
with mass mi for each atom. The exact forces fi have been calculated from a highly accurate PME force calculation using octic (eighth order) interpolation with the cutoff between short- and long-range parts set to 40 Å and the grid spacing set to 0.1 Å, making use of the fact that PME converges to the Ewald summation in the limit as the cutoff goes to infinity and the grid spacing goes to zero. The error in potential energy presented in Figure 3 has been averaged over ν = 1000 frames of a 2 ns trajectory,
measured relative to a highly accurate PME calculation of the potential Un. MSM provides lower numerical accuracy than PME, but force errors within 1% are deemed sufficient for MD applications, so that the force error is not greater than the error incurred from time stepping employed in the integration of the Newtonian equations of motion. Energy conservation for cubic MSM with the 12 Å cutoff between short- and long-range parts adopted here has been verified by simulating the cube of water for 1 ns in the NVE ensemble with 1 fs time stepping and observing that the standard deviation of total energy σE is 0.3% of either the standard deviation of the kinetic energy or the standard deviation of the potential energy, which is within the 20% criterion considered for energy conservation in an MD simulation.37−39
Figure 2.
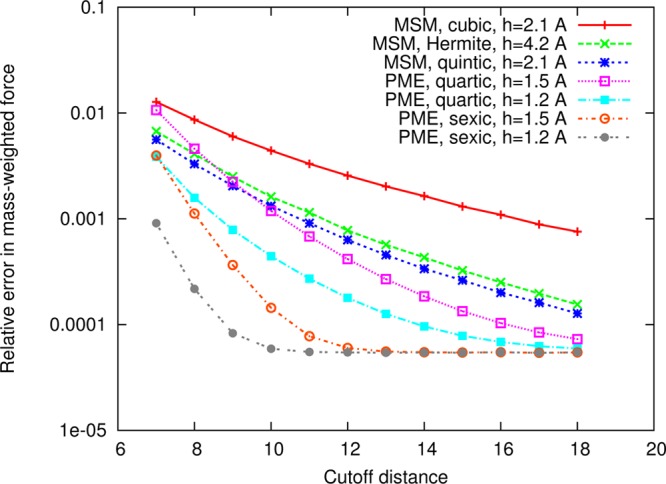
Comparison of the force accuracy of MSM and PME in NAMD. Shown is the relative error in mass-weighted force versus cutoff distance for simulations of a 50 Å cube of 4142 water molecules. For MSM, the cutoff distance is used to control accuracy for a given interpolation and splitting. Although MSM provides lower numerical accuracy than PME (specifically, there is about one digit of precision difference at the 12 Å cutoff distance between cubic MSM and quartic PME with 1.2 Å grid spacing), force errors within 1% (i.e., less than 0.01) are deemed sufficient for application of MD to biomolecular systems.
Figure 3.
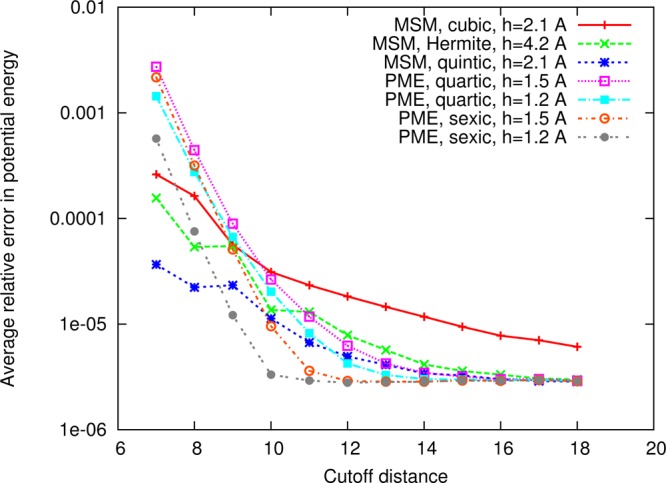
Comparison of the potential energy accuracy of MSM and PME in NAMD. Shown for the 50 Å cube of 4124 water molecules is the relative error in potential energy, averaged over 1000 frames of a 2 ns simulation trajectory, plotted versus cutoff distance.
2.4. Distributed Memory Parallelization
The parallelization of MSM is implemented using Charm++, the parallel language extension of C++ used by NAMD that provides a message-driven programming paradigm expressed as asynchronously executable objects.40,41 NAMD employs a hybrid data and force decomposition for scalable parallelism, decomposing the atoms spatially into uniform patches and also decomposing into objects the work of calculating the short-range nonbonded forces between nearest neighbors.31,32 MSM and PME both make use of the existing infrastructure in NAMD for calculating their short-range parts, modifying the functional form of the interaction to fit each respective method. For the long-range part of MSM, the grids are decomposed into blocks of grid points, analogous to the NAMD patches. As with the short-range force calculation, sufficient work for scalable parallelization is available by carrying out the grid cutoff calculations involving interactions between neighboring MSM grid blocks through separately schedulable work objects. The restriction and prolongation calculations introduced above require a much smaller amount of work, so they are best kept on the same processor as their corresponding grid blocks, as the overhead of communicating data to a remote processor exceeds the runtime of the actual calculation step. Similarly, the anterpolation and interpolation calculations involving atom coordinates are kept processor-wise with the patches.
Each MSM grid block receives charges from below, either from anterpolation at the patch level or from restriction of a lower grid level. After all expected sub-blocks of charge are received and summed, the grid block, assuming that it is not the top-level block, performs a restriction to a local buffer and sends sub-blocks of the restricted charge up to the upper level grid blocks. After sending the restricted charges, the grid block sends its charges to all of the block interaction work objects to which it contributes. A block interaction work object receives a block of charges and performs its part of the grid cutoff calculation to a block of potentials, then sends that block of potentials to its designated grid block. After all expected contributions to its block of potentials are received and summed by the grid block, including contributions from block interaction work objects and from prolongation of a higher grid level, the grid block will either send the potentials back to the patch level for interpolation, if it is a first level grid block, or it will perform a prolongation to a local buffer and send sub-blocks of the prolongated potential down to the lower level grid blocks.
Performance is improved through static (i.e., not measurement-based) load balancing of the work objects and through Charm++ message-driven task prioritization. The MSM grid blocks are assigned to the multiprocessor nodes in a round-robin manner; for large processor counts, the processors will outnumber the grid blocks. The MSM block interaction work objects are similarly assigned so as to achieve an even node-level load distribution, with preference given to nodes that hold either the source charge block or the target potential block for a given block interaction, in order to reduce the amount of internode communication required. Once the node assignments have been made, the grid blocks and block interaction work objects for each node are equitably divided among its processors. Message priorities are assigned to give highest priority first to sending restricted charges from the lowest grid levels up to the highest, followed by the block interactions and prolongated potentials from the highest grid levels down to the lowest. The idea is to prioritize the critical path of communication that goes through the top grid level and back, in an effort to reduce the latencies involved with receiving all contributions to a grid block of potentials from prolongation and grid cutoff calculation before further prolongation or interpolation can occur. MSM makes use of the existing NAMD reduction infrastructure for summing the long-range potential energy.
2.5. SIMD and Vector Parallelization
Nearly all contemporary microprocessors offer some degree of support for fine-grained parallel computing using so-called single-instruction multiple-data (SIMD) processing units that execute, in lock-step, the same arithmetic operation in parallel on several independent data values. CPU and GPU SIMD hardware is programmed using single-program multiple-data (SPMD) programming languages such as CUDA,24,25 OpenCL,42 ISPC, and OpenMP (with SIMD directives), or at the machine instruction level through the use of vendor-specific assembly language or so-called compiler intrinsic functions. The MSM algorithm is well suited to fine-grained parallel execution on such CPU and GPU architectures, due to its predictably and uniformly strided memory access patterns, and because its innermost loops over grids can be decomposed into operations on vectors that match the size and stride of the SIMD processing units provided by the underlying computing hardware.
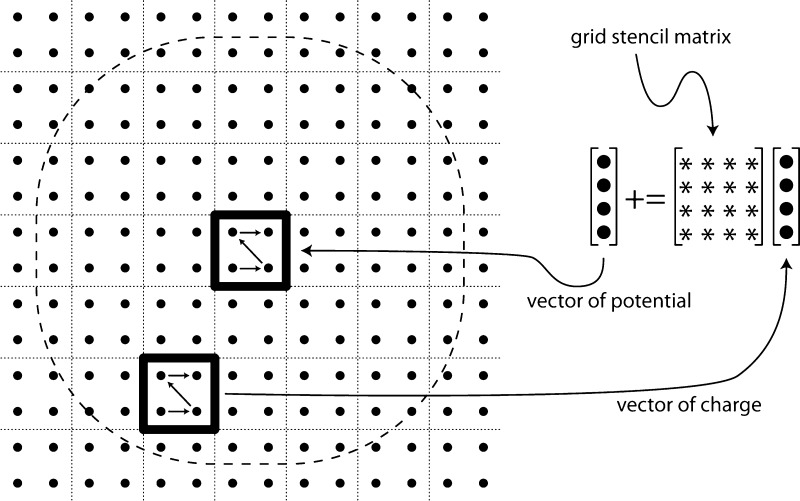
MSM with Hermite interpolation is capable of most naturally utilizing the SIMD processing units of CPUs, available through the Intel x86 compiler intrinsics for SSE2 (up to 4-element vector instructions) or AVX (up to 8-element vector instructions). Hermite interpolation directly computes 8-element grid points, with grid point interactions expressed as 8 × 8 matrix–vector products. A single precision implementation of Hermite interpolation can map each grid point directly to two SSE2 registers or to a single AVX register. With the matrices stored in row–major order, the matrix–vector multiplication can be implemented in AVX using 8 multiply–add instructions or twice as many for SSE. A similar optimization is available to the other interpolation schemes that employ single-element grid points. The optimization involves clustering the grid points into 23-point cubes. With this data reorganization, the clustered grid point interactions can be expressed as 8 × 8 matrix–vector products using the same vector instructions as used for Hermite interpolation. The grid point clustering might require up to one extra layer of grid point padding in each of the x-, y-, and z-directions. Figure 4 illustrates the grid cutoff calculation from eq 9 modified to operate on a sequence of vectors, where a vector of potentials for a clustered grid point is calculated by summing over the “sphere” of clustered grid points comprising vectors of charge.
Figure 4.
Grid point clustering algorithm for calculating eq 9. The algorithm is illustrated in 2-D. For each cluster of grid point potentials, the algorithm loops over the sphere of charge clusters and sums their contributions, calculating the sum of matrix–vector products. The clustered charges and potentials are stored contiguously as vectors that match the processor’s SIMD vector length. The grid stencil matrix elements are the precomputed kl(rml, rn) values corresponding to the positions of the individual grid points.
Many-core processors such as GPUs and the Intel Xeon Phi natively operate on larger vector lengths. Xeon Phi processors support vector lengths of up to 16 single precision floating point values, and contemporary GPUs natively operate on even larger vectors or arrays containing 64 to more than 512 elements at a time. In the case of Xeon Phi, it should be possible to organize the MSM data structures and use vector mask operations to process two pairs of 8-element vectors per instruction. A GPU implementation of MSM can be constructed by clustering grid points into much larger tiles, and using a 3-D work decomposition, with each GPU thread block or workgroup assigned to different tiles. The most critical issue for GPU performance is the use of memory layouts for the clustered grid point tiles that enable so-called coalesced memory access patterns that minimize the number of hardware memory cycles. The best parallel work decomposition strategy for GPUs hinges upon the amount of parallelism available in the work assigned to one GPU. For MSM workloads that result in a sufficiently large number of grid points, a spatially oriented decomposition of grid point tiles and their associated interactions allows the use of so-called gather style algorithms that perform potential accumulation in on-chip registers. For MSM workloads that present the GPU with insufficient work for the spatial approach to be profitable, a parallel decomposition over interactions between MSM grid blocks will provide increased parallelism using a scatter type algorithm, at the cost of an extra parallel reduction step required for summing the partial potentials for each MSM grid block prior to transferring results back to the host CPU.
3. Simulation Protocols
All simulations were carried out with a developmental version of NAMD32 implementing the parallelized MSM algorithm that has been subsequently released in NAMD version 2.10. A modified TIP3P water model in the CHARMM force field was used.36 The r-RESPA multiple time-step integrator43 was applied with time steps of 2 and 4 fs for short-range nonbonded and long-range electrostatic interactions, respectively. The SETTLE algorithm44 maintained rigid geometry for water molecules while RATTLE45 constrained the length of covalent hydrogen bonds. The calculation of nonbonded interactions excluded pairs of atoms covalently bonded to each other or to a common atom. Temperature was set to 300 K for all systems by a Langevin thermostat. All semiperiodic systems were initially equilibrated for 500 ps with full periodic boundary conditions in the NPT ensemble, where pressure was kept constant at 1 atm by the Langevin piston method,46 before running production simulations in the NVT ensemble using semiperiodic boundary conditions.
Electrostatic interactions are treated either using MSM or PME.2 The NAMD cutoff distance, set to 12 Å, defines both the van der Waals truncation distance and the splitting between short- and long-range parts of the electrostatic interactions for both methods. The MSM simulations use the default cubic interpolation with C2 splitting and the default grid spacing of 2.5 Å, except for the performance comparison, which uses Hermite interpolation with C3 splitting and a grid spacing of 5 Å. The PME simulations use the default quartic interpolation with a grid spacing of 1.2 Å.
Below we explain how semiperiodic and completely nonperiodic systems are simulated in the case of MSM electrostatic force evaluation. In the case of fully periodic systems, PME and MSM simulations are specified identically in NAMD, except for the choice of electrostatic algorithm.
Semiperiodic System
For semiperiodic systems, the periodicities are established by defining just one or two of the three cell basis vectors. MSM does not require any special conditions for the cell basis vectors, except for linear independence. However, any constraints for containing atoms within the boundaries along nonperiodic dimensions are best described by establishing orthogonal periodic basis vectors aligned to the axes of the x,y,z-coordinate system chosen accordingly. To demonstrate the use of MSM, we consider a membrane bilayer with asymmetric content across the membrane in the form of a difference in ion concentration above and below the membrane. For this purpose, we utilize a simulation cell that is periodic in the x,y-plane only. Along the z-axis, we keep the simulated system constrained by a harmonic restoring potential to a finite interval with a lower and upper boundary at z = ± a. The boundary is realized through a containing force along the z-direction of −k (z – a), for z > a and +k (z + a), for z < −a, where k = 3 kcal/(mol·Å2); the condition is implemented using the TclBC scriptable boundary condition feature of NAMD.
Nonperiodic System
To demonstrate a simulation of a completely nonperiodic system, we consider a protein solvated together with ions in a spherical water droplet. The components of the system, in particular the water molecules, have a strong tendency to remain together at room temperature when placed in vacuum, though once in a while a water molecule or even more rarely an ion or the whole protein will evaporate. To prevent such evaporation from happening, we surround a water droplet by a repulsive boundary surface of a radius a chosen 5 Å larger than the radius of the droplet. For this purpose we introduce a repulsive radial force directed toward the center with magnitude k (r – a), for r > a; here, r is the radial position of any atom in the system and the force constant is k = 10 kcal/(mol·Å2), implemented using the spherical boundary condition feature of NAMD. The center of mass of the protein is constrained to the center of mass of the droplet in order to keep the protein near the droplet center and well solvated.
4. Results and Discussion
In the following, we illustrate the capabilities of molecular dynamics simulations with NAMD stemming from the MSM algorithm. We first demonstrate the accuracy of the MSM algorithm and of its implementation in NAMD through comparison with NAMD simulations based on the well-tested PME algorithm. We then present results of simulations for semiperiodic and nonperiodic systems, until now unfeasible in NAMD having relied on the PME algorithm. We finally compare the scaling of NAMD on multiprocessor machines running PME- and MSM-based simulations side-by-side.
4.1. Water Properties
Water is fundamental to molecular processes in living cells, often due to the electrostatic interactions among water molecules themselves and among water molecules and proteins or ions that give rise to strong dielectric screening. Accordingly, water is an excellent test bed for the computational treatment of electrostatic forces. Indeed numerous structural, dynamic, dielectric, and mechanical properties of water can serve to illustrate the accuracy of electrostatic force descriptions by means of MSM and PME, for example, density, radial distribution function, diffusion constant, dielectric constant, distance-dependent Kirkwood factor or surface tension. To compare simulation results obtained with MSM and PME electrostatic descriptions, a box of water was simulated for 6 ns in an NPT ensemble with a modified TIP3P water model in the CHARMM force field.36 The resulting water properties are compared in Table 1 and Figure 5. For all water properties calculated, agreement is found between MSM and PME, indicating that MSM furnishes the same accuracy as PME in electrostatic descriptions.
Table 1. Comparison of Water Properties Determined from Simulations Based on PME or MSM Electrostatic Force Evaluation.
| water property | PME | MSM |
|---|---|---|
| density (kg/m3) | 1006 ± 3 | 1008 ± 2 |
| diffusion constant (×10–5 cm2/s) | 5.2 ± 0.2 | 5.2 ± 0.1 |
| dielectric constant | 104 ± 2 | 102 ± 2 |
| surface tension (dyn/cm2) | 53 ± 3 | 52 ± 3 |
Figure 5.
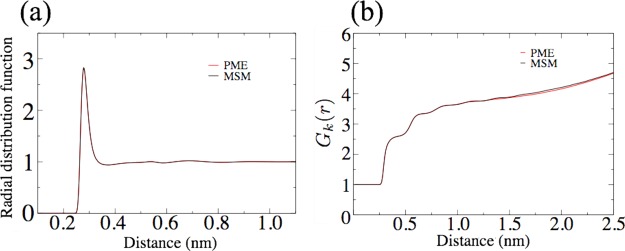
Comparison of PME and MSM algorithms via simulation of a water box. Properties compared are the water oxygen–oxygen radial distribution function (a), a structural property, and the Kirkwood G-factor (b), a dielectric property.
The water self-diffusion constant was obtained from the mean-square displacement using the Einstein relation. The surface tension was calculated by Lz(−(Pxx + Pyy)/2 + Pzz)/2, where Pij is the ij component of the pressure tensor, and Lz is the length of the simulation cell in the direction normal to the surface. The distance-dependent Kirkwood G-Factor was resolved as contributions from spherical shells of radius R by employing
where μj is the dipole moment of water and μ is the dipole magnitude. The dielectric constant ε was calculated using
where the collective rotational dipole moment is MD = ∑j = 1Nμj.
4.2. Interface Potentials at Air–Water and Membrane–Water Interfaces
A key electrostatic property of water arises at the water-membrane interface in living cells and at the air–water interface47,48 in the form of the so-called interface potential. This potential results from an alignment of water dipole and quadrupole moments. Long-range electrostatic interaction is essential for the magnitude of the potential. Only reliable electrostatic treatments can predict the correct interface potential.47,48 As shown in Figure 6, MSM gives the same interface potential as PME, at both air–water and membrane–water interfaces, in case of either a fully periodic boundary or a semiperiodic boundary. The results show that MSM provides a reliable description of the long-range electrostatic interaction. If truncated electrostatic interactions are applied with a cutoff of 1.2 nm, an interface potential that is too large is found, as seen in Figure 6. Only by elongating the electrostatic interactions, for example, by elongating the cutoff to 1.6 nm, is the calculated interface potential close to the value determined by means of simulations employing MSM or PME that account for the full long-range interaction.
Figure 6.
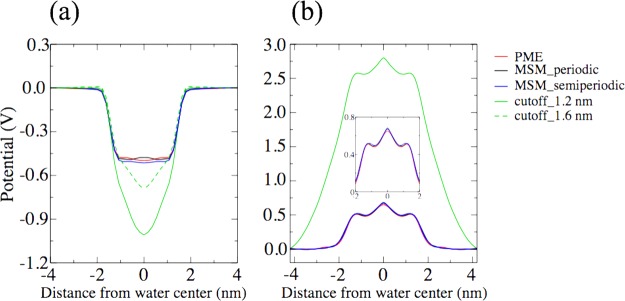
Comparison of PME and MSM algorithms in simulations determining interface potentials. Compared are resulting electrostatic potentials at an air–water interface (a) and at a membrane (POPC)–water interface (b). The distances from water layer center and membrane center are measured along the interface normal.
All interface potentials Ψ(z) were calculated via
where ρ(z) is the charge density as a function of z.
4.3. Membrane Electroporation in a Semiperiodic Simulation
Cellular membranes surrounding living cells commonly maintain a voltage gradient for battery-like energy storage and for fueling many types of membrane processes such as ATP synthesis or ion vectorial transport. The potential is due to a difference in charge distribution across the membrane. In the case that the charge distribution difference and, along with it, the electrical field become too large, a pore is formed in the membrane in a process termed electroporation.49−52 For example, by having more cations on one side of the membrane and more anions on the other, a strong electric field can be generated across the membrane, thereby inducing electroporation.53,54
In simulations employing PME, an electric field across a membrane, created by having different numbers of cations and anions on each side of the membrane, requires actually two different water compartments containing positive and negative ions separated by two membranes in order to permit a periodic boundary condition along the membrane normal. In case of simulations employing MSM without periodicity in the z-direction, only a single membrane is required to separate positive and negative ions, roughly halving the computational effort while describing a situation that is more realistic than arising in the case of PME-based simulations.
MD simulations with MSM were performed for a membrane bilayer made of POPC lipids and employing semiperiodic boundary conditions. With an average NaCl concentration of 0.15 M, but more Na+ ions on one side of the membrane and more Cl– on the other, an electric field of 0.7 V/nm was created across the membrane. The numbers of cations and anions were equal and the system charge was neutral. Within 1 ns, a water pore developed in the membrane. As illustrated through a simulation snapshot in Figure 7, ions diffused through the pore from one side of the membrane to the other. Lipid head groups kept interacting with the ions within the pore and created a toroidal pore structure. Exactly the same behavior resulted in simulations with PME, but requiring two membranes.53
Figure 7.

Formation of a pore in a membrane induced by an ion concentration difference. A majority of cations were placed on one side of the membrane and a majority of anions on the other side, creating an electric field across the membrane. The electric field causes membrane pore formation. For lipids and water molecules, the following coloring has been chosen: carbon (green); oxygen (red); nitrogen (blue); phosphorus (tan); hydrogen (white). Ions are shown in yellow. For the sake of clarity, lipid tail hydrogen atoms are not shown.
4.4. Ion Conduction through a Graphene Nanopore in a Semiperiodic Simulation
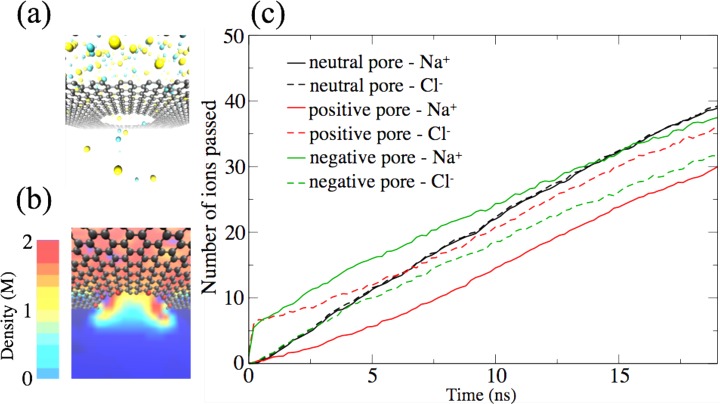
Bioengineering is today developing nanoscale sensors for medical diagnostics, for example, for cost-effective DNA sequencing. One type of sensor involves nanopores situated in graphene sheets, the sheets acting much like a cellular membrane. MD simulations offer guidance to nanosensor development by offering engineers microscopic views of the measuring processes involving nanosensors. The ability of MSM to simulate single membranes, illustrated above, can be put to good use in the case of graphene nanopores. We illustrate this capability of MSM by describing ion conduction through a nanopore embedded into a single graphene sheet. The sheet separates, just as the membrane in the previous example, ions initially at different concentrations above and below the graphene sheet.
In the simulations, we chose the edge of the graphene nanopore to contain either electrically neutral or positively or negatively charged atoms. After carrying out MSM-based simulations on the respective semiperiodic systems, we compared the ion conductance through neutral, positive, and negative graphene nanopores, where 2 M NaCl, described by CHARMM force parameters,55 was placed on one side of the graphene and none on the other side. The nanopore measured 6 nm in diameter, with 30 carbon atoms forming the pore edge. To charge the nanopore, 12 carbon atoms distributed evenly along the pore edge were selected, and unit positive or negative charges were placed on them. In comparison to employing charged chemicals to decorate the pore,56 nanopores with these charged carbon atoms have the same physical pore size as the neutral pore. To neutralize the overall system charge, 12 additional Na+ or Cl– were added to the 2M-concentration side when the nanopore edge was negative or positive, respectively.
Right after the simulation started, ions diffused through the nanopore regardless of the pore charges, as shown in Figure 8a. In the cases of charged nanopore edges, counterions translocated faster than the co-ions, until the charges on the two sides of graphene became equal. The simulations revealed that both positive and negative ions diffuse through the nanopore at the same rate, regardless of pore edge charge, as shown by the slope of ion passage in Figure 8c. For the charged nanopore edges, however, the ion translocation rates are smaller than in the case of the neutral nanopore. The ion translocation rate through a neutral pore is 2.1 ns–1, while it is 1.7 ns–1 for the positively charged pore edge and 1.6 ns–1 for the negatively charged pore edge. For charged nanopore edges, counterions tend to localize around the pore region. As shown in Figure 8b, ion density is high around the charged pore region. Therefore, the effective nanopore size is reduced for charged nanopores, and thus, ion translocation rates are smaller.
Figure 8.
Semiperiodic simulation based on the MSM algorithm describing ion conduction through graphene nanopores. (a) Simulation setup for a neutral nanopore. Sodium ions are colored yellow and chloride ions green. Graphene carbon atoms are colored gray. For the sake of clarity, water molecules are not shown. (b) Ion density profile around a nanopore with a charged edge. Charged edge carbon atoms are shown in red. (c) Number of ions passed through the pore at time t. The slope of the curves shown is the translocation rate, which is affected by the nanopore edge charge.
All simulations were terminated at 18 ns, at which point the ion concentration difference between the two sides of the graphene sheet had decreased to ∼70% of its original value.
4.5. Water Droplet in Nonperiodic Simulation
MSM can be applied not only to semiperiodic systems but also to systems without any periodic boundary. For example, proteins can be simulated in a large water droplet with MSM. The total number of water molecules in a droplet is smaller than the number of water molecules in a periodic rectangular or dodecahedral box of the same maximum dimension. Moreover, simulations with nonzero net charge can be performed with MSM on a nonperiodic droplet, while the net charge must be chosen to vanish for PME-based simulations.
One needs to be aware that biomolecules in single droplets are subject to water surface tension created naturally by the water–air boundary. Such tension arises for droplets suspended in air and can be significant for droplets of small size. In the case of bulk water surface tension does not arise, neither in a real system nor in a system simulated with periodic boundary conditions and completely filled elementary cells. Such avoidance of surface tension may be an advantage of fully periodic MSM and PME calculations; future calculations will test if this advantage is really significant.
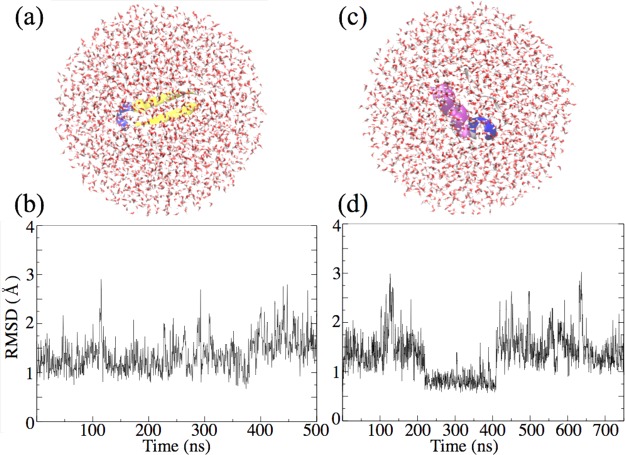
To illustrate the possibility of simulations of a single water droplet, small proteins, β-hairpin57 and tryptophan cage (PDB: 1L2Y), were each simulated in a small spherical water droplet. Each protein was placed at the center of the droplet, which was 20 Å larger than the radius of gyration of the proteins, as shown in Figure 9. The β-hairpin is composed mostly of β-sheet structure, whereas the tryptophan cage is composed mostly of α-helical structure. The protein structures were monitored by means of the root-mean-square displacement (RMSD) as shown in Figure 9; both proteins maintain their structures over 1 μs of simulation, as indicated by RMSD values of less than 2 Å for most of the simulation time.
Figure 9.
Nonperiodic simulations based on the MSM algorithm describing a β-hairpin protein motif (a) and the protein Trp-cage (c) inside a water droplet. Protein structures are characterized color-wise as follows: β-sheet (yellow); α-helix (purple); ordered turn (blue); disordered coil (white). The RMSD values for β-hairpin and Trp-cage, defined here with reference to initial structure, are shown in parts b and d, respectively.
Comparing the nonperiodic MSM approximation to an exact electrostatics calculation over all pairs of interacting atoms, the droplet containing the β-hairpin showed a difference of 0.5 kcal/mol from a total energy of −2.3 × 104 kcal/mol, with a relative error in average mass-weighted force of 8.5 × 10–3, as measured by eq 14.
4.6. Performance Comparison
Performance and scaling of MSM and PME are comparable, despite the fact that the NAMD implementation of PME has had many more years of development effort than MSM. MSM is shown to perform best with Hermite interpolation, an approach that, as mentioned previously, exactly reproduces function values and derivatives at grid points. The 8 × 8 matrix–vector products resulting from Hermite interpolation in three dimensions are calculated very efficiently using CPU vector instructions.
A comparison of the NAMD implementations of MSM and PME was performed on the β-hairpin protein solvated in a cubic box of 3757 water molecules for a total of 11.5 K atoms and simulated with multiple time step integration, in which long-range electrostatic forces were evaluated every 4 fs using 16 processors (1 node) in a Dell PowerEdge compute node of the TACC Stampede system. The comparison shows that PME achieves a simulation rate of 18 ns per day, whereas MSM using Hermite interpolation with C3 splitting achieves 15 ns per day and using cubic interpolation with C2 splitting only 11 ns per day.
However, a comparison for the case of a larger simulation using more processor cores demonstrates the scaling benefits of MSM. The NAMD benchmark system ApoA1 (92 K atoms)58 simulated with 1 fs single time stepping using varying numbers of Cray XE6 nodes (32 cores per node) of the Blue Waters JYC test computer system shows that, while PME achieves faster simulation rates for smaller core counts, MSM achieves comparable scaling results with slightly faster simulation rates for larger core counts. Figure 10 plots the results showing nanoseconds per day versus number of cores. Table 2 lists the performance measured in milliseconds per time step. The performance crossover point occurs between 256 and 512 cores; the MSM performance continues to scale up to 1536 cores, whereas the PME performance reaches a plateau at 1024 cores.
Figure 10.
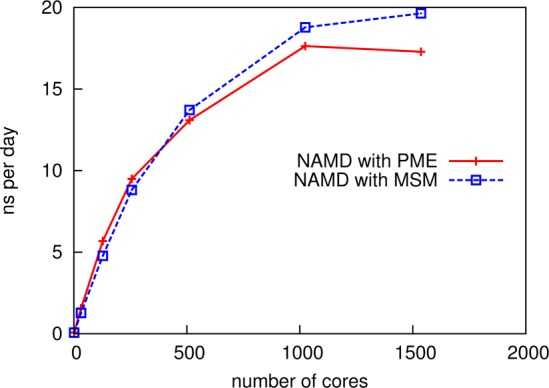
Performance of MSM and PME on ApoA1 (92 K atoms) with 1 fs time stepping, on a Cray XE6 (32 cores per node). MSM using Hermite interpolation with C3 splitting, a 5 Å grid spacing, and 12 Å splitting distance achieves 19.6 ns/day with 1536 cores, whereas PME using quartic interpolation with 1.2 Å grid spacing, and 12 Å splitting distance tops out at 17.6 ns/day with 1024 cores. Performance of MSM here exceeds PME at 512 cores and higher.
Table 2. NAMD Performance Data, Measured in Milliseconds per Integration Time Step, for Parallel Scaling of a Simulation of ApoA158 on a Cray XE6 (32 Cores per Node).
| no. of cores | with PME, ms/step | with MSM, ms/step |
|---|---|---|
| 1 | 1139 | 1381 |
| 32 | 55.5 | 68.1 |
| 128 | 15.2 | 18.1 |
| 256 | 9.1 | 9.8 |
| 512 | 6.6 | 6.3 |
| 1024 | 4.9 | 4.6 |
| 1536 | 5.0 | 4.4 |
5. Conclusion
The multilevel summation method (MSM) has recently been implemented in the molecular dynamics program NAMD31,32 and provides now a successful alternative in computing electrostatic forces arising in molecular dynamics (MD) simulations of biomolecular systems. The practical accuracy produced by MSM, although less than the numerical accuracy available in typical use of particle–mesh Ewald (PME),1,2 is sufficient for MD, as shown by a comparison of calculated water properties such as density, diffusion constant, dielectric constant, surface tension, radial distribution function, and distance-dependent Kirkwood G-Factor. Agreement is also found between MSM and PME in calculations of the interface electrostatic potential at air–water and membrane–water interfaces.
MSM has key advantages over PME. With nested interpolation of softened pair potentials in real space, MSM permits simulations without periodic boundary conditions in some or all of the simulated dimensions. Instead, PME in its common implementations can only be applied with fully periodic boundary conditions. For example, simulations with MSM can be performed with periodic boundary conditions along the x,y-directions but not along the z-direction. Such simulations allow different ion concentrations to be placed on either side of a membrane bilayer, producing membrane pore formation in MSM-based simulations. A related example for now feasible simulations with NAMD is ion conduction through neutral and charged graphene nanopores in the presence of a large ion gradient. MSM can be further applied to spherical systems without any periodicity. To illustrate this, two proteins, a β-hairpin motif and the protein tryptophan cage, have been simulated in spherical water droplets. In this case, the simulation with MSM not only may be more realistic but also requires a smaller atom count, roughly described by the ratio (4πr3/3)/8r3 ≈ 0.5; now with MSM available, the argument that periodic systems, even though larger per elementary cell, avoid surface effects such as surface tension, can actually be tested. In any case, the simulation examples described in the present study demonstrate that MSM offers flexibility in regard to boundary conditions and provides more alternatives in simulation design than does PME.
Moreover, MSM offers improved parallel scalability over PME. Unlike the PME algorithm that is based on the Fourier transform, requiring communication that poses a limit to scalability, MSM instead has a hierarchical structure with highly localized arithmetic operations that permit effective utilization of modern vector computational hardware units. According to our performance benchmarks, the superior scalability of MSM makes it competitive with PME and actually faster than PME in case of simulations of large systems.
Ongoing is the development of improved interpolation for MSM to provide higher accuracy for a given polynomial degree p without increasing the computational cost. Future work includes also the calculation of dispersion forces without truncation with MSM-based NAMD; these forces, in particular, their long-range contribution, are considered to be important for membrane properties.29,30 With support in NAMD also for long-range dispersion forces, the present CHARMM-prescribed 12 Å cutoff/splitting distance can be used as a true control for MSM accuracy. High performance simulations will then be able to achieve practical accuracy with a reduced splitting distance, where a splitting distance of between 8 and 9 Å is expected to double the overall simulation performance. Other future work includes extending our earlier development efforts on GPU-accelerated MSM for calculating electrostatic potential maps25 to support MSM-based NAMD on large-scale GPU-accelerated parallel computers.
Acknowledgments
The authors are grateful to Eric Bohm and Yanhua Sun for discussions regarding MSM parallelization and implementation. The research has been supported through grants by the National Institutes of Health (5 R01 GM098243-02, R01-GM067887, 9P41GM104601, U54 GM087519) and by the National Science Foundation (CHE0957273, PHY1430124). The authors also acknowledge supercomputer time on Stampede at the Texas Advanced Computing Center (TACC), provided by grant MCA93S028 from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (OCI-1053575), and the Blue Waters sustained-petascale computing project supported by NSF awards OCI-0725070 and ACI-1238993, the state of Illinois, and “The Computational Microscope” NSF PRAC awards OCI-0832673 and ACI-1440026.
Author Contributions
⊥ D.J.H. and Z.W. contributed equally to this study.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
References
- Darden T.; York D.; Pedersen L. G. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar]
- Hockney R. W.; Eastwood J. W.. Computer Simulation Using Particles; McGraw-Hill: New York, 1981. [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
- Shaw D. E.; Grossman J. P.; Bank J. A.; Batson B.; Butts J. A.; Chao J. C.; Deneroff M. M.; Dror R. O.; Even A.; Fenton C. H.; Forte A.; Gagliardo J.; Gill G.; Greskamp B.; Ho C. R.; Ierardi D. J.; Iserovich L.; Kuskin J. S.; Larson R. H.; Layman T.; Lee L.-S.; Lerer A. K.; Li C.; Killebrew D.; Mackenzie K. M.; Mok S. Y.-H.; Moraes M. A.; Mueller R.; Nociolo L. J.; Peticolas J. L.; Quan T.; Ramot D.; Salmon J. K.; Scarpazza D. P.; Schafer U. B.; Siddique N.; Snyder C. W.; Spengler J.; Tang P. T. P.; Theobald M.; Toma H.; Towles B.; Vitale B.; Wang S. C.; Young C.. Anton 2: Raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer. Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, 2014; pp 41–53.
- Sachs J. N.; Crozier P. S.; Woolf T. B. Atomistic simulations of biologically realistic transmembrane potential gradients. J. Chem. Phys. 2004, 121, 10847–10851. [DOI] [PubMed] [Google Scholar]
- Lindbo D.; Tornberg A.-K. Fast and spectrally accurate Ewald summation for 2-periodic electrostatic systems. J. Chem. Phys. 2012, 136, 164111. [DOI] [PubMed] [Google Scholar]
- Khalili-Araghi F.; Ziervogel B.; Gumbart J. C.; Roux B. Molecular dynamics simulations of membrane proteins under asymmetric ionic concentrations. J. Gen. Physiol. 2013, 142, 465–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda I.; Nakamura H. Non-Ewald methods: Theory and applications to molecular systems. Biophys. Rev. 2012, 4, 161–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf D.; Keblinski P.; Phillpot S.; Eggebrecht J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r–1 summation. J. Chem. Phys. 1999, 110, 8254–8282. [Google Scholar]
- Wu X.; Brooks B. R. Using the isotropic periodic sum method to calculate long-range interactions of heterogeneous systems. J. Chem. Phys. 2008, 129, 154115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salomon-Ferrer R.; Case D. A.; Walker R. C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar]
- Takahashi K. Z.; Narumi T.; Yasuoka K. Cutoff radius effect of the isotropic periodic sum and Wolf method in liquid–vapor interfaces of water. J. Chem. Phys. 2011, 134, 174112. [DOI] [PubMed] [Google Scholar]
- Brandt A.; Lubrecht A. A. Multilevel matrix multiplication and fast solution of integral equations. J. Comput. Phys. 1990, 90, 348–370. [Google Scholar]
- Sandak B. Multiscale fast summation of long range charge and dipolar interactions. J. Comput. Chem. 2001, 22, 717–731. [Google Scholar]
- Skeel R. D.; Tezcan I.; Hardy D. J. Multiple grid methods for classical molecular dynamics. J. Comput. Chem. 2002, 23, 673–684. [DOI] [PubMed] [Google Scholar]
- Greengard L.; Rokhlin V. A fast algorithm for particle simulation. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar]
- Greengard L.; Rokhlin V. A new version of the fast multipole method for the Laplace equation in three dimensions. Acta Numerica 1997, 6, 229–269. [Google Scholar]
- Hardy D. J.Multilevel summation for the fast evaluation of forces for the simulation of biomolecules. Ph.D. thesis, University of Illinois at Urbana–Champaign, Champaign, IL, 2006; Also Department of Computer Science Report No. UIUCDCS-R-2006-2546, May 2006. [Google Scholar]
- Barash D.; Yang L.; Qian X.; Schlick T. Inherent speedup limitations in multiple time step/particle mesh Ewald algorithms. J. Comput. Chem. 2003, 24, 77–88. [DOI] [PubMed] [Google Scholar]
- Andoh Y.; Yoshii N.; Fujimoto K.; Mizutani K.; Kojima H.; Yamada A.; Okazaki S.; Kawaguchi K.; Nagao H.; Iwahashi K.; Mizutani F.; Minami K.; Ichikawa S.-i.; Komatsu H.; Ishizuki S.; Takeda Y.; Fukushima M. MODYLAS: A highly parallelized general-purpose molecular dynamics simulation program for large-scale systems with long-range forces calculated by fast multipole method (FMM) and highly scalable fine-grained new parallel processing algorithms. J. Chem. Theory Comput. 2013, 9, 3201–3209. [DOI] [PubMed] [Google Scholar]
- Ohno Y.; Yokota R.; Koyama H.; Morimoto G.; Hasegawa A.; Masumoto G.; Okimoto N.; Hirano Y.; Ibeid H.; Narumi T.; Taiji M. Petascale molecular dynamics simulation using the fast multipole method on K computer. Comput. Phys. Commun. 2014, 185, 2575–2585. [Google Scholar]
- Bishop T. C.; Skeel R. D.; Schulten K. Difficulties with multiple time stepping and the fast multipole algorithm in molecular dynamics. J. Comput. Chem. 1997, 18, 1785–1791. [Google Scholar]
- Stone J. E.; Phillips J. C.; Freddolino P. L.; Hardy D. J.; Trabuco L. G.; Schulten K. Accelerating molecular modeling applications with graphics processors. J. Comput. Chem. 2007, 28, 2618–2640. [DOI] [PubMed] [Google Scholar]
- Hardy D. J.; Stone J. E.; Schulten K. Multilevel summation of electrostatic potentials using graphics processing units. J. Paral. Comput. 2009, 35, 164–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le L.; Lee E. H.; Hardy D. J.; Truong T. N.; Schulten K. Molecular dynamics simulations suggest that electrostatic funnel directs binding of Tamiflu to influenza N1 neuraminidases. PLoS Comput. Biol. 2010, 6, e1000939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. S.; Salsbury F. R. Jr.; Olson M. A. An efficient hybrid explicit/implicit solvent method for biomolecular simulations. J. Comput. Chem. 2004, 25, 2038–2048. [DOI] [PubMed] [Google Scholar]
- Tameling D.; Springer P.; Bientinesi P.; Ismail A. E. Multilevel summation for dispersion: A linear-time algorithm for r–6 potentials. J. Chem. Phys. 2014, 140, 024105. [DOI] [PubMed] [Google Scholar]
- Wennberg C. L.; Murtola T.; Hess B.; Lindahl E. Lennard-Jones lattice summation in bilayer simulations has critical effects on surface tension and lipid properties. J. Chem. Theory Comput. 2013, 9, 3527–3537. [DOI] [PubMed] [Google Scholar]
- Huang K.; García A. E. Effects of truncating van der Waals interactions in lipid bilayer simulations. J. Chem. Phys. 2014, 141, 105101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalé L.; Skeel R.; Bhandarkar M.; Brunner R.; Gursoy A.; Krawetz N.; Phillips J.; Shinozaki A.; Varadarajan K.; Schulten K. NAMD2: Greater scalability for parallel molecular dynamics. J. Comput. Phys. 1999, 151, 283–312. [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore S. G.; Crozier P. S. Extension and evaluation of the multilevel summation method for fast long-range electrostatics calculations. J. Chem. Phys. 2014, 140, 234112. [DOI] [PubMed] [Google Scholar]
- Skeel R. D.; Hardy D. J. Practical construction of modified Hamiltonians. SIAM J. Sci. Comput. 2001, 23, 1172–1188. [Google Scholar]
- Engle R. D.; Skeel R. D.; Drees M. Monitoring energy drift with shadow Hamiltonians. J. Comput. Phys. 2005, 206, 432–452. [Google Scholar]
- MacKerell A. D. Jr.; Bashford D.; Bellott M.; Dunbrack R. L. Jr.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher I. W. E.; Roux B.; Schlenkrich M.; Smith J.; Stote R.; Straub J.; Watanabe M.; Wiorkiewicz-Kuczera J.; Yin D.; Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- van Gunsteren W. F.; Berendsen H. J. C. Algorithms for macromolecular dynamics and constraint dynamics. Mol. Phys. 1977, 34, 1311–1327. [Google Scholar]
- Berendsen H. J. C.; van Gunsteren W. F.. Practical algorithms for dynamic simulations. Proceedings of the International School of Physics; “Enrico Fermi”: Amsterdam, 1986; pp 43–65. [Google Scholar]
- Berendsen H. J. C.; van Gunsteren W. F.. Molecular Liquids; Springer: New York, 1984; pp 475–500. [Google Scholar]
- Kalé L. V.; Krishnan S. In Parallel Programming Using C++; Wilson G. V., Lu P., Eds.; MIT Press: Cambridge, MA, 1996; pp 175–213. [Google Scholar]
- Kalé L. V.; Bohm E.; Mendes C. L.; Wilmarth T.; Zheng G. In Petascale Computing: Algorithms and Applications; Bader D., Ed.; Chapman & Hall/CRC Press: Boca Raton, FL, 2008; pp 421–441. [Google Scholar]
- Stone J. E.; Gohara D.; Shi G. OpenCL: A parallel programming standard for heterogeneous computing systems. Comput. in Sci. and Eng. 2010, 12, 66–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuckerman M.; Berne B. J.; Martyna G. J. Reversible multiple time scale molecular dynamics. J. Chem. Phys. 1992, 97, 1990–2001. [Google Scholar]
- Miyamoto S.; Kollman P. A. SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water molecules. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
- Andersen H. C. Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. J. Chem. Phys. 1983, 52, 24–34. [Google Scholar]
- Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar]
- Feller S. E.; Pastor R. W.; Rojnuckarin A.; Bogusz S.; Brooks B. R. Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem. 1996, 100, 17011–17020. [Google Scholar]
- Lin J.-H.; Baker N. A.; MacCammon J. A. Bridging implicit and explicit solvent approaches for membrane electrostatics. Biophys. J. 2002, 83, 1374–1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prausnitz M. R.; Bose V. G.; Langer R.; Weaver J. C. Electroporation of mammalian skin: A mechanism to enhance transdermal drug delivery. Proc. Natl. Acad. Sci. U.S.A. 1993, 90, 10504–10508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver J. C.; Chizmadzhev Y. A. Theory of electroporation: A review. Bioelectrochem. Bioenerg. 1996, 41, 135–160. [Google Scholar]
- Tieleman D. P.; Leontiadou H.; Mark A. E.; Marrink S. J. Simulation of pore formation in lipid bilayers by mechanical stress and electric fields. J. Am. Chem. Soc. 2003, 125, 6382–6383. [DOI] [PubMed] [Google Scholar]
- Tieleman D. P. The molecular basis of electroporation. BMC Biochem. 2004, 5, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurtovenko A. A.; Vattulainen I. Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: Atomistic molecular dynamics study. J. Am. Chem. Soc. 2005, 127, 17570–17571. [DOI] [PubMed] [Google Scholar]
- Gurtovenko A. A.; Vattulainen I. Ion leakage through transient water pores in protein-free lipid membranes driven by transmembrane ionic charge imbalance. Biophys. J. 2007, 92, 1878–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venable R. M.; Luo Y.; Gawrisch K.; Roux B.; Pastor R. W. Simulations of anionic lipid membranes: Development of interaction-specific ion parameters and validation using NMR data. J. Phys. Chem. B 2013, 117, 10183–10192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sint K.; Wang B.; Král P. Selective ion passage through functionalized graphene nanopores. J. Am. Chem. Soc. 2008, 130, 16448–16449. [DOI] [PubMed] [Google Scholar]
- Munoz V.; Thompson P.; Hofrichter J.; Eaton W. Folding dynamics and mechanism of β-hairpin formation. Nature 1997, 390, 196–199. [DOI] [PubMed] [Google Scholar]
- Phillips J. C.; Wriggers W.; Li Z.; Jonas A.; Schulten K. Predicting the structure of apolipoprotein A-I in reconstituted high density lipoprotein disks. Biophys. J. 1997, 73, 2337–2346. [DOI] [PMC free article] [PubMed] [Google Scholar]