Hopping Diffusion of Nanoparticles in Polymer Matrices

Abstract

We propose a hopping mechanism for diffusion of large nonsticky nanoparticles subjected to topological constraints in both unentangled and entangled polymer solids (networks and gels) and entangled polymer liquids (melts and solutions). Probe particles with size larger than the mesh size a_x of unentangled polymer networks or tube diameter a_e of entangled polymer liquids are trapped by the network or entanglement cells. At long time scales, however, these particles can diffuse by overcoming free energy barrier between neighboring confinement cells. The terminal particle diffusion coefficient dominated by this hopping diffusion is appreciable for particles with size moderately larger than the network mesh size a_x or tube diameter a_e. Much larger particles in polymer solids will be permanently trapped by local network cells, whereas they can still move in polymer liquids by waiting for entanglement cells to rearrange on the relaxation time scales of these liquids. Hopping diffusion in entangled polymer liquids and networks has a weaker dependence on particle size than that in unentangled networks as entanglements can slide along chains under polymer deformation. The proposed novel hopping model enables understanding the motion of large nanoparticles in polymeric nanocomposites and the transport of nano drug carriers in complex biological gels such as mucus.

1. Introduction

Mobility of nonsticky nanoparticles in complex fluids,^1,2 including polymer solutions and melts,³⁻¹⁰ biomacromolecular solutions,¹¹⁻²¹ cells,²²⁻²⁷ extracellular environments,^28,29 and colloidal suspensions,³⁰ reflects local structure and dynamics of these complex matrices. In previous work,^31,32 we showed that the motion of particles in polymer liquids (solutions and melts) is different on short and long time scales because it is determined by the dynamics of surrounding polymers. At relatively short time scales the motion of particles is subdiffusive as it is coupled to the segmental dynamics of polymers, whereas at relatively long times the particle motion is diffusive. The terminal diffusion coefficient of particles does not depend on the polymer molecular weight if the particle size is smaller than the entanglement length of the polymer liquids. The diffusion coefficient of particles larger than the entanglement length decreases with 3.4 power of the molecular weight of linear polymers, because particles probe the terminal dynamics of entangled polymers. These predictions have been verified by a recent systematic experimental study.³³ The diffusion coefficient of these large particles decreases with increasing matrix viscosity; however, the large particles can still move as the polymer liquids relax, no matter how slow the relaxation is. The question then is as follows: What is the particle mobility in polymers that cannot relax, for example, in permanently cross-linked networks? Can particles move through permanently cross-linked networks if their size is larger than the network mesh size? A prior work⁴³ addressed this question via a mode-coupling approach and obtained the fact that the hopping distance of large particles in polymer melts increases with particle size, while the hopping energy barrier asymptotically varies proportionally to the particle volume, which is qualitatively different from the results of our paper. On the basis of our prior work,^31,32 we present a systematic scaling description for diffusion of such large particles in both unentangled and entangled polymer solids (networks and gels) and entangled liquids (melts and solutions).

We argue that in permanently cross-linked networks the only way for a particle with size exceeding the network mesh size to leave a confinement cage is by hopping—waiting for the fluctuation of a gate (loop) between two neighboring confinement cages to become large enough to slip around the particle. To describe the particle hopping diffusion, we introduce two important parameters, hopping free energy barrier and hopping step size. The free energy barrier is determined by the deformation of a loop (gate) as it slips around the particle. To describe particle confinement in unentangled networks with strongly overlapping chains and to estimate the hopping step size, we introduce a model of “overlapping elementary networks”.

The idea of hopping diffusion of particles in unentangled permanent networks is extended to describe diffusion of particles in entangled polymer networks, which contain both permanent cross-links and topologically trapped entanglements. Unlike the fixed permanent cross-links, entanglements can slide along polymer chains. Therefore, the confinement cages due to entanglements are “softer” in comparison to the network cages formed by permanent cross-links. Consequently, there is a range of particle sizes for which the particle diffusion is dominated by hopping of particles between entanglement cages.

Unlike entangled polymer networks, there are no permanent cross-links in entangled polymer liquids; polymers in entangled liquids can relax on long time scales. We show that there is a certain (polymer molecular weight dependent) particle size above which the hopping diffusion of particles between entanglement cages becomes very difficult; it is relatively easier for the very large particle to diffuse at long time scales by “waiting” for the entangled polymer liquid to relax and flow around the particle.

The paper is structured as follows. In section 2, we discuss hopping diffusion of large particles in unentangled polymer solids (networks and gels). To estimate the step size and entropic free energy barrier for hopping, we model the “real” unentangled network by many overlapping “elementary” networks. Hopping diffusion of particles in entangled polymer solids is discussed in section 3. Section 4 presents the diffusion of probe particles in entangled polymer liquids. Specifically, we compare the particle motion due to the relaxation of polymer chains and that due to hopping and calculate the range of parameters for which each of two diffusion modes dominates. Concluding remarks are presented in section 5.

2. Unentangled Polymer Solids (N_x < N_e)

A typical polymer network has both chemical cross-links and topological entanglements. The properties of the polymer network are dominated by the type of constraints that has higher density. Therefore, we distinguish two types of networks: unentangled and entangled polymer networks, depending on the relative values of network mesh size and entanglement length scale. The network mesh size is defined as the average distance between two neighboring permanent cross-links along the chain and can be measured by the value of unentangled network elastic modulus. The entanglement length is measured by the magnitude of entanglement plateau modulus.³⁴⁻³⁶ The case of high density of permanent cross-links, with the network mesh size smaller than the entanglement length, is classified as unentangled polymer network. In the opposite case of entangled polymer network the network mesh size is larger than the entanglement length and the network properties are dominated by the topological entanglements between network strands.

Consider the motion of a probe particle of size d in a dry, monodisperse unentangled permanently cross-linked network above its glass transition temperature T_g and crystallization transition temperature T_c. Let us denote the number of Kuhn monomers between two neighboring cross-links by N_x and the size of a network strand by a_x ≃ bN_x^1/2, where b is Kuhn length. In a typical network there are many network strands overlapping within the volume pervaded by a network strand (see Figure 1). The overlap parameter P ≃ N_x^1/2 is defined as the number of network strands within the volume a_x³ ≃ (bN_x^1/2)³ pervaded by one network strand.

Figure 1.

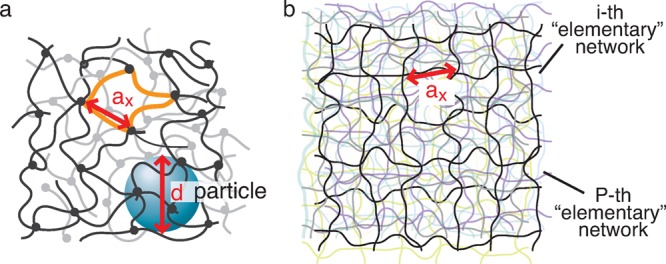
Unentangled polymer network modeled by overlapping “elementary” networks. (a) Schematic visualization of a particle of size d in an unentangled polymer network with strands of average size a_x. The solid circles represent permanent cross-links. There are P ≃ N_x^1/2 network strands within the pervaded volume a_x³ of a network strand. (b) The unentangled polymer network is modeled by P overlapping yet independent “elementary” polymer networks, with details discussed in Appendix A. One of these “elementary” networks is shown by bright black lines while the remaining P – 1 “elementary” networks are shown by dimmed color lines.

2.1. Hopping Diffusion

A large probe particle of size d (d > a_x) is confined inside the unentangled network, as shown in Figure 1a. However, it is still possible for this particle to escape from the cage formed by network strands confining the particle. This escape–a hopping step–occurs by a large fluctuation of the one of these strands. To understand this process, we model the monodisperse unentangled network by P overlapping yet independent “elementary” networks, as shown in Figure 1b. The details of this representation are discussed in Appendix A. There is on the order of one network strand per volume a_x³ in each of these “elementary” networks.

The “elementary” networks are not static; instead, they are fluctuating all the time. The fluctuation of an “elementary” network cage can be large enough to allow one of the network strands to slip around the particle. In this case a hopping event occurs and the particle enters a neighboring cage of the network. We use the model of “elementary” networks to elucidate the hopping diffusion of large particles.

2.1.1. Hopping Step Size

Each of P “elementary” networks constrains the particle independently and tends to localize the particle at the “center” of its own cage. We model the constraint from an “elementary” network by a virtual chain with one of its two ends attached to the particle center and the other anchored at the center of the “elementary” network cage, as illustrated by the dashed lines and black dots in Figure 2a. The number of monomers, n_cage, per virtual chain is determined by equating its elastic energy and the elastic deformation energy of an “elementary” network when the particle is shifted from its equilibrium position by a distance δr (see Appendix C):

1

which gives

2

Figure 2.

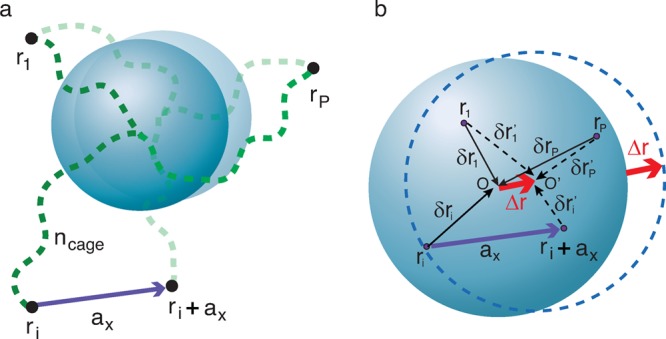
Step size of a large probe particle hopping between two neighboring cages in a monodisperse unentangled polymer network. (a) The unentangled polymer network is modeled by P overlapping “elementary” networks with their network cage centers r₁, ..., r_i, ..., r_P (dots) randomly distributed around the fluctuation center of the particle (its equilibrium position). The constraint applied to a large particle of size d > a_x from an “elementary” network is modeled by a virtual chain with n_cage monomers. The virtual chain has one of its two ends attached to the particle center, and the other anchored to the center of a cage of ith “elementary” network, as shown by the black dots. (b) During a single hopping event the particle leaves its initial equilibrium position O and arrives at a neighboring equilibrium position O′ with a step size Δr. This hop is achieved by the particle leaving the confinement cage of the “elementary” network i with the center r_i that is most likely to be the furthest from the initial equilibrium position O of the particle and entering the neighboring cage of the same “elementary” network with the center at r_i + a_x, while staying in the same cages of all the rest “elementary” networks.

Instead of fluctuating around the cage “center” in a particular “elementary” network, the particle finds an “optimal” position at which the restoring forces from all the “elementary” networks are balanced. The centers of cages in P “elementary” networks are randomly distributed within the volume on the order of a_x³ around the equilibrium position of the probe particle, as illustrated in Figure 2b. At this equilibrium position the net force exerted by these P “elementary” networks on the particle is zero. The restoring force f_j applied to the particle from the jth “elementary” network is linearly proportional to the deviation δr_j of the particle from the “center” of the “elementary” network cage, f_j = [k_BT/(b²n_cage)] δr_j, as the confinement potential is parabolic (see eq 1 and Appendix C). Assuming that all virtual chains have the same number of monomers n_cage, we have

3

The hopping step size for a large probe particle (d > a_x) moving through the unentangled network is much smaller than that for an “elementary” network because the particle is constrained by many surrounding overlapping “elementary” networks. During a single hopping step the particle moves by a displacement Δr and arrives at a new equilibrium position. The particle most likely escapes from the cage of an “elementary” network i, whose center is at the maximum distance from the equilibrium position of the particle, as the corresponding free energy barrier is the lowest compared with that of other “elementary” networks.³⁸ Consequently, after leaving the cage center r_i of the “elementary” network i, the particle enters the neighboring cage, whose center r_i + a_x is separated by a vector a_x from the old cage, and deviates by a vector δr_i^′ = δr_i + Δr – a_x from the new equilibrium position. Note that deviations from the cage centers of all other P – 1 “elementary” networks to the new equilibrium position of the particle are changed by a vector Δr (see Figure 2). Since at this new equilibrium position the net force exerted on the particle by P “elementary” networks is still zero, one obtains the equation for the step size Δr of particle hop

4

Equation 4 can be rewritten using eq 3 as PΔr – a_x = 0, which gives the magnitude of the step size of particle hop in a dry network

5

It is important to emphasize that this displacement Δr is P ≃ N_x^1/2 times smaller than the hopping step size a_x ≃ bN_x^1/2 in a single “elementary” network.

2.1.2. Hopping Entropic Free Energy Barrier

To hop from one cage to a neighboring one, the large probe particle has to overcome a free energy barrier, which is defined as the difference between the maximum and the initial elastic deformation energy of the network strands during the hopping event. To estimate the energy barrier, one might think that it is necessary to consider the deformation energy of all P (d³/a_x³) network strands affected by the large probe particle,⁴³ which is the number of network strands d³/(b³N_x) within its pervaded volume d³. However, not all of the affected network strands are deformed in the same way during a single hopping event. Indeed, it is enough for one network loop to slip around the particle for this particle to hop between neighboring cages. Stretching the slipping loop also results in further deformation of loops connected to it. However, deformation of all other affected loops can be taken into account using the concept of “virtual chains”, which, effectively, only renormalizes the length of the slipping loop. The size of a loop in “elementary” networks is about a_x (see Appendix A).

The energy barrier due to the slipping loop corresponds to the “transition” state in which the large particle is leaving the initial cage and is at the onset of entering the neighboring cage (see “transition” state in Figure 3). In this state the network loop is stretched from length a_x to the order of particle size d (in fact, the peripheral length πd of the particle). Therefore, the entropic free energy barrier contributed from the deformation of the loop slipping around the particle (barrier loop) during a single hopping event is

6

Figure 3.

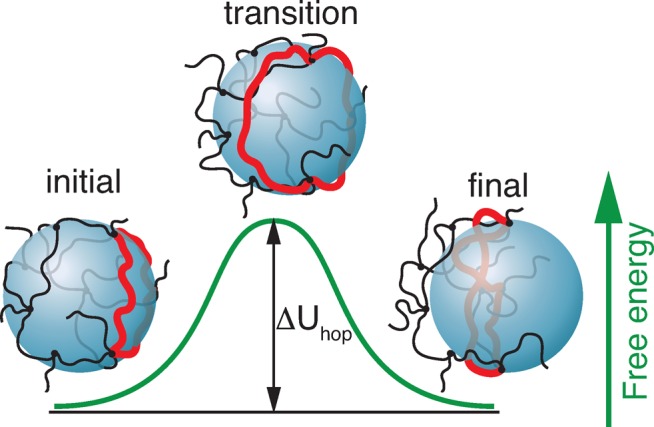
Illustration of a large probe particle hop from one network cage to a neighboring cage with only one network loop (highlighted by red) slipping around the particle.

2.2. Dry Unentangled Polymer Networks

A loop of size larger than d can slip around the particle, resulting in a hopping step. The hopping free energy barrier (eq 6) determines the probability of a loop fluctuating to a size larger than the particle size d. This probability is proportional to ∫_d^∞ dx exp (−x²/a_x²)/a_x. The waiting time for this hopping step in a dry unentangled polymer network is

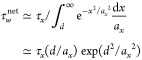7

where

8

is the Rouse relaxation time of a network strand, at which a loop attempts to slip around the particle but is unlikely to succeed utill τ_w^net. The monomer relaxation time τ₀ in eq 8 is

9

with ζ corresponding to the monomeric friction coefficient.

The mean-square displacement for a large particle hopping in a dry unentangled polymer network is proportional to the number of steps t/τ_w^net that the particle makes during a certain period of time

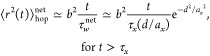10

The hopping process occurs on time scales longer than the relaxation time of a network strand τ_x, but with a very small probability to succeed during this relatively short time interval. The probability of a hop increases with time interval and becomes significant enough for a successful hopping to occur at the waiting time scale τ_w^net (eq 7). In addition to hopping the particle is fluctuating within the network cells without leaving them at times longer than relaxation time of a network strand τ_x. We model the total restoring force on the particle due to P “elementary” networks by elastic force from a composite virtual chain, which consists of P virtual chains with n_cage monomers connected in parallel, as shown in Figure 2. The number of monomers n_cage/P of such a composite virtual chain determines the mean-square fluctuations of the particle on time scales longer than network strand relaxation time:

11

One can use microrheological approach to estimate the network modulus from the amplitude of these thermal fluctuations of the particle: G_x ≃ k_BT/(d⟨r²⟩_fluct^net) ≃ k_BTP/a_x³ (see eq C.3).

We would like to stress that the particle motion at times t > τ_x is due to the superposition of the two processes: fluctuations around the center of a network cage but without leaving it (eq 11) and hopping between neighboring network cages (eq 10). The contribution to the particle mean-square displacement from hopping ⟨r² (t)⟩_hop^net becomes important at certain time scale τ_hop, at which ⟨r²(t)⟩_hop^net is comparable to the mean-square displacement ⟨r²⟩_fluct due to particle fluctuations within the confinement cage. This gives the crossover time at which hopping diffusion becomes observable

12

The mean-square displacement of the particle does not significantly increase until time scale τ_hop^net, as shown in Figure 4. At time scales longer than τ_hop the mean-square displacement of large particles is dominated by the hopping diffusion (see eq 10):

13

The particle diffusion coefficient due to hopping in a dry unentangled network (see eq 10) is

14

For a relatively large particle, the hopping diffusion is extremely slow as the mean-square displacement of particles decreases exponentially with the square of particle size.

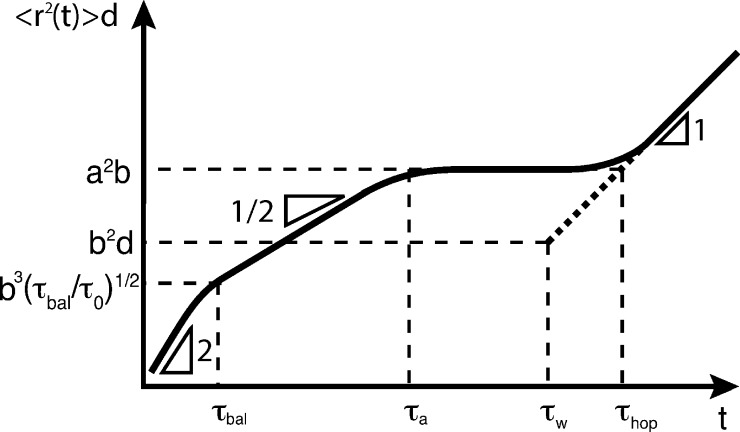
Figure 4.

Time dependence of the product of mean-square displacement ⟨Δr²(t)⟩ and the particle size d for large particles subjected to the confinement from cages of size a. The motion of large particles (d > a) is not affected by confinement cells at time scales shorter than the relaxation time τ_a (see eq 23) of a strand. The particle motion is ballistic at very short time scales (t < τ_bal; eq 18) and crosses over into subdiffusive at longer time scales (τ_bal < t < τ_a). At time scales longer than τ_a the particles are trapped by confinement cells; they cannot move until time scale τ_w, at which the particles start to hop between neighboring confinement cells. The hopping diffusion becomes experimentally observable on time scale τ_hop, at which mean-square displacement of the particle due to hopping becomes comparable to that due to fluctuations of the particle within a confinement cell, a²b/d (eq 11). For dry unentangled polymer networks a ≡ a_x, τ_a ≡ τ_x (eq 8), τ_w ≡ τ_w^net (eq 7), and τ_hop ≡ τ_hop (eq 12); for entangled polymer networks and melts, a ≡ a_e, τ_a ≡ τ_e (eq 23), τ_w ≡ τ_w^ent (eq 22), and τ_hop ≡ τ_hop (eq 26). Logarithmic scales.

At times shorter than the relaxation time τ_x (eq 8), the motion of a large probe particle (d > a_x) is unaffected by network cages and is similar to particle movement in polymer melts. The particle motion on times t < τ_x is subdiffusive with the mean-square displacement proportional to the square root of time, since particle motion is coupled to the segmental dynamics of network strands, as shown by the solid line with the slope 1/2 in Figure 4.³¹

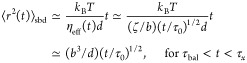15

The effective viscosity η_eff(t) “felt” by the particle during time interval t corresponds to a melt with chains containing (t/τ₀)^1/2 monomers coherently moving at this time.³¹

At times shorter than the crossover time τ_bal, the particle moves along ballistic trajectories. The mean-square velocity of the particle v is determined by the equipartition theorem

16

Substituting r = υt in eq 16 we find the particle mean-square displacement for ballistic motion (see Figure 4):

17

Matching eqs 15 and 17 at t = τ_bal gives the crossover time between the ballistic and subdiffusive regimes:

18

The width of the ballistic regime is determined by the time scale τ_bal. For large particles with higher density ρ_b in liquids of low viscosity, it is possible that τ_bal > τ₀, or mb/(ζτ₀d) > 1. This dimensionless ratio can be written as mb/(ζτ₀d) ≃ (d/b)² (η_ref/η_s)², where the reference viscosity η_ref = (ρ_bk_BT/b)^1/2 is determined by the particle density ρ_b and Kuhn length b with a typical value η_ref ∼ 10^–4 Pa·s. Thus, for the ratio of the particle to Kuhn monomer size larger than the ratio of viscosities d/b > η_s/η_ref the ballistic regime ends at time scales longer than τ₀ and “eats” part of the subidiffusion regime. Indeed, the ballistic regime is experimentally observable by using particle tracking of ultrahigh temporal-spatial resolutions.⁴⁴ The ballistic regime puts the short-time cutoff at τ_bal to the application of microrheology, since the particle motion at time scales t < τ_bal is not coupled to the modes of the probed matrix. The long-time cutoff to the application of microrheology is determined by the hopping process, as the finite zero-shear-rate viscosity predicted by the generalized Stokes–Einstein approach from particle diffusion at time scales t > τ_hop^net does not correspond to the infinite zero-shear-rate viscosity of a permanent network.

2.3. Unentangled Polymer Gels

An unentangled polymer gel can be treated as an “effective” unentangled dry polymer network in which the “effective” monomers are correlation blobs. Therefore, the results of particle hopping in dry polymer networks can be directly applied to polymer gels with hopping step size b replaced by the correlation length ξ (see eq D.2) and other parameters replaced by concentration dependent ones (see eqs D.3 and D.4 in Appendix D). The key elements for hopping diffusion of large particles in unentangled polymer gels are summarized in Table 1 and their detailed discussion is presented in Appendix D.

Table 1. Parameters for Hopping Diffusion of Particles in Unentangled Polymer Solids and Entangled Solids and Liquids^a.

	unentangled solids		entangled solids and liquids
	dry networks	gels	dry networks and melts	gels and solutions
Δr	b	ξ	b	ξ
ΔU/kBT	d2/ax2	d2/ax2	d/ae	d/ae
Dhop	(b2/(τxd/ax)) exp(−d2/ax2)	(ξ2/(τxd/ax)) exp(−d2/ax2)	(b2/τe) exp(−d/ae)	(ξ2/τe) exp(−d/ae)

^aΔr is the hopping step size, ΔU is the entropic free energy barrier, and D_hop is the hopping diffusion coefficient. Length scales: b is the size of a Kuhn monomer, ξ is correlation length, a_x is the network strand size, and d is the particle size. Time scales: τ₀ is the monomeric relaxation time, τ_ξ is relaxation time of correlation volume, τ_x and τ_e correspond to the relaxation time of a network and entanglement strand respectively.

Note that we consider above only monodisperse polymer networks. However, real polymer networks are polydisperse as they are typically made of strands of different molecular weight. The motion of a large particle in real polymer networks could be affected by the polydispersity. Interestingly, we find that there is still a window in which the particle motion is not affected by the network polydispersity even for particles larger than the average network loop size (see Appendix B). Within this window, the variation of energy barriers due to polydispersity is smaller than the thermal energy k_BT. As a result, polydispersity of the network becomes important only for very large particles with size larger than average loop size d > a_xl̅^1/2, in which l̅ ≃ ln P is the average number of network strands in a loop (see Appendix A). These particles diffuse extremely slow with exponentially small diffusion coefficient. This interesting behavior will be the subject of future explorations.

3. Entangled Polymer Solids: Entanglement Cages Are “Softer”

Fluctuations of chains in polymer solids (networks and gels) are suppressed by both permanent cross-links and entanglements. In entangled polymer solids the density of permanent cross-links is lower than the density of entanglements so that the tube diameter a_e is smaller than the network mesh size a_x. The hopping diffusion of large particles with size a_e < d < a_x²/a_e in entangled polymer solids can be readily obtained by extending the results of hopping diffusion of large particles in unentangled polymer solids with a_x < a_e (see section 2). However, unlike the loop formed in permanently cross-linked networks, the loop formed by entanglements does not have fixed number of monomers. Indeed, the number of monomers contained in a particular loop increases when the loop slides over the particle because some chain segments far from the particle are pulled in as the particle slips through the loop. The number of monomers n in the loop is determined by the condition that the tension in the loop is balanced by the tube tension kT/a_e:

19

in which the term k_BTd/(nb²) corresponds to the tension in the loop of n monomers, and the tube diameter (entanglement length) a_e ≃ bN_e^1/2 with N_e being the number of monomers per entanglement strand. Therefore, the number of monomers in the loop that slides over the particle is

20

and the free energy barrier for particle hopping between entanglement cages is

21

This free energy barrier for the probe particle to hop between entanglement cages (eq 21) has a weaker (linear) dependence on particle size d/a_e in comparison to the quadratic dependence for cross-linked networks (see eq 6). This linear free energy barrier (eq 21) represents the softening of the confining potential due to the increase in the distance between entanglements under network stretching.³⁷ Notice that the polydispersity of chain lengths does not affect the barrier energy (eq 21) in the case of lightly cross-linked networks (N_x > N_e). Our prediction for the particle size dependence of free energy barrier in entangled polymer melts (eq 21) is different from prediction of ref (43).

The waiting time for the particle to hop between two neighboring entanglement cages is (see eq 7)

22

in which the relaxation time of an entanglement strand is

23

This waiting time (eq 22) increases exponentially with the relative size of the particle d with respect to the size of an entanglement strand a_e, but with a relatively weaker dependence on particle size d than that for unentangled polymer solids (see eq 7). This weaker dependence is due to the lower energy of nonaffine deformation of entanglement strands (see eq 21) in comparison with stronger affine deformation of unentangled polymer networks and gels (see eq 6). For instance, for particles with size d twice larger than the entanglement mesh a_e or network mesh size a_x (d/a_e = d/a_x = 2) the ratio of two waiting times is τ_w^ent/τ_w ≃ exp ((d/a_e) – (d/a_x)²) ≃ exp (2–2²) ≃ 10^–1.

Since the particle “feels” network modulus G_e ≃ k_BT/(a_e²b), the mean-square fluctuations of the particle trapped by the entanglement net is:

24

The ballistic and subdiffusive motion at shorter time scales are similar to the case of unentangled networks (eqs 15 and 17) with the crossover time at the upper boundary of subdiffusive regime equal to the relaxation time of entanglement strand τ_e, see Figure 4.

Mean-square displacement of a large probe particle (d > a_e) due to hopping is proportional to the number of hops that the particle makes during a certain time period t with the same step size b as in the case of unentangled dry network (eq 5)

25

which is determined by the relative size of the particles with respect to the entanglement mesh size a_e. The crossover time at which the mean-square particle displacement due to hopping diffusion ⟨r²⟩_hop^ent (eq 25) becomes comparable to the mean square particle fluctuation in an entanglement cage ⟨r²⟩_fluct (eq 24) is

26

Diffusion coefficient of large probe particles in entangled polymer solids is exponentially small

27

Mobility of relatively large particles (a_e < a_x < d < d_e ≃ a_x²/a_e) is affected by both entanglements and permanent cross-links, but dominated by the entanglements. This is because the entropic free energy barrier due to permanent cross-links, k_BT(d/a_x)², is smaller than that from entanglements, k_BT(d/a_e), for a_e < a_x < d < d_e. The two barriers are on the same order at d ≃ d_e ≃ a_x²/a_e. The motion of a very large particle (d > d_e > a_x) is dominated by permanent cross-links and essentially not affected by entanglements, because the entanglements are under large deformation due to the presence of the very large particle, leading to the slippage of them toward the permanent cross-links, as discussed in detail in Appendix E. Therefore, the particle diffuses as if it is in unentangled polymer networks (see Section 2). The crossover at d ≃ d_e ≃ a_x²/a_e between entanglement and cross-link dominated regimes can be approximately described by the sum of the two free energy barriers

28

The terminal diffusion coefficient of particles of different sizes in an entangled polymer network is presented by the solid line in Figure 5. Hopping diffusion of a particle in entangled polymer gels is similar to that in entangled polymer networks, with the hopping step size b replaced by correlation length ξ (eq D.2) and corresponding parameters replaced by concentration dependent ones (see Appendices D and F). The key elements for hopping diffusion of large particles in entangled polymer gels are summarized in Table 1.

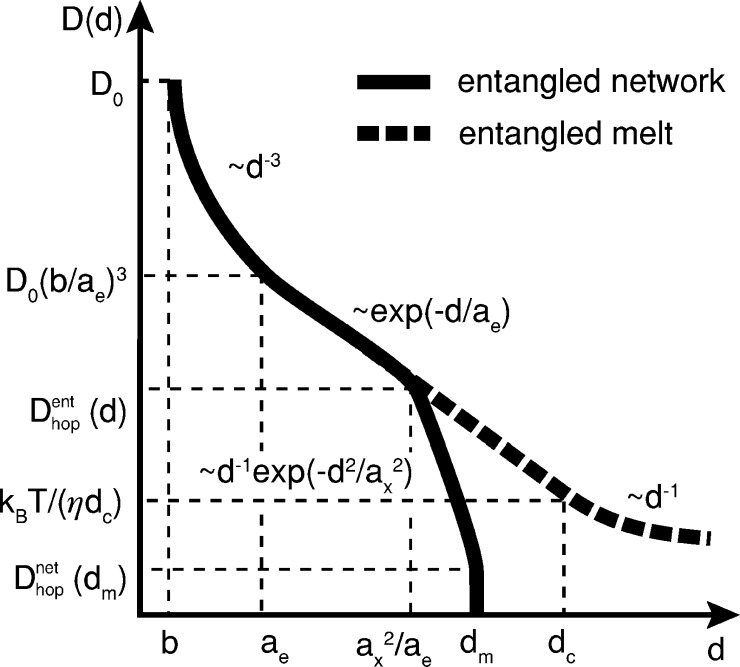
Figure 5.

Particle diffusion coefficient. Dependence of particle diffusion coefficient D(d) on particle size d in entangled polymer networks (solid line) and entangled polymer melts (dashed line). In an entangled polymer networks, for small particles with size d < a_e, the particle diffusion coefficient is inversely proportional to the minus third power of particle size: D ∼ d^–3.³¹ Particles of intermediate sizes (a_e < d < a_x²/a_e) experience hopping diffusion between entanglement cages: D ∼ exp(−d/a_e) (see eq 27). Large particles in permanent networks (a_x²/a_e < d < d_m (eq B.19)) experience hopping diffusion between network cages: D ∼ exp(−d²/a_x²)/d (see eq 14). Extremely large particles d > d_m are permanently trapped in the network. In an entangled polymer melt, the particle motion is dominated by hopping diffusion for particles with size a_e < d < d_c: D ∼ exp(−d/a_e) (see eqs 27 and 34). Particles larger than d_c have to wait for the polymer melt relax to diffuse and they “feel” the bulk viscosity: D ∼ 1/d. D₀ ≃ k_BT/(η_sb) corresponds to the diffusion coefficient of a monomer. Y-axis is logarithmic; X-axis is linear.

4. Entangled Polymer Liquids: Competition between Hopping Diffusion and Chain Reptation

In our previous work,³¹ we discussed the motion of particles in entangled polymer liquids. Here we revisit this problem taking into account the contribution of hopping to particle mobility. The motion of large particles (d > a) in entangled polymer liquids is due to both hopping mechanism and chain relaxation by reptation. In order to diffuse, the particles either have to hop between confinement cages or wait for polymer liquids to flow around these particles. The particle motion is not affected by the entanglements at time scales shorter than the relaxation time τ_e of an entanglement strand (see Figure 6 and ref (31)). At time scales longer than τ_e, the large particles are trapped by entanglement cages and cannot move further until a certain time scale τ_liq. The physical meaning of the onset time scale τ_liq of particle diffusion is determined by the fastest of the two processes that dominates the particle motion at long time scales. The motion of large particles in entangled polymer liquids due to chain reptation process has been discussed in ref (31). In section 3, we have discussed the mechanism of hopping diffusion of large particles in entangled polymer solids. These results can be directly applied to describe the hopping diffusion in entangled polymer liquids (melts and solutions) for large particles with size d larger than the entanglement strand size a_e ≃ bN_e^1/2. In the following, we compare the mean-square displacement of large particles in entangled polymer melts due to hopping mechanism and the mean-square displacement due to the chain relaxation (reptation) process.

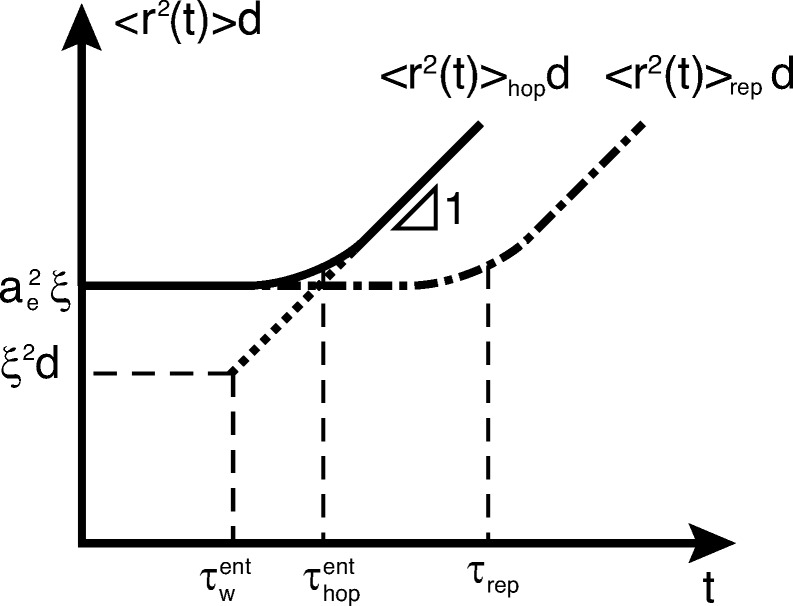
Figure 6.

Time dependence of mean-square displacement of large particles (d > a_e) in entangled polymer liquids. Illustration of the case at which τ_liq is determined by hopping process with τ_liq ≃ τ_hop^ent if d < d_c or N > N_c (eqs 33 and 34) with mean-square displacement described by eq 26, as shown by the solid curve. The motion of large probe particles at time scales shorter than τ_e is not affected by entanglement.³¹ At time scales longer than τ_e large probe particles are trapped by entanglement mesh, but they do not have to wait for the polymer liquids to relax to move further (dash-dotted line); instead, they can diffuse by hopping between neighboring entanglement cages (solid line with unit slope for t > τ_hop). Logarithmic scales.

The motion of large particles (d > a_e) in entangled polymer liquids due to hopping is the same as that presented in section 3; the mean-square displacement on time scale t > τ_e is described by eq 26. Another process contributing to the particle motion at time scales longer than τ_e is chain reptation.³¹ Large probe particles can also diffuse by waiting for polymer chains to relax at reptation time scale τ_rep

29

which increases as cube of degree of polymerization N and τ_e is the relaxation time of entanglement strand (eq 23) containing N_e Kuhn segments.

Mean-square displacement of large particles due to chain reptation process is

30

in which η ≃ [k_BT/(ba_e²)]τ_e(N/N_e)³ is bulk viscosity of entangled polymer melts. Assuming no coupling between the two processes (chain reptation and hopping diffusion) the net mean-square displacement of the large probe particle in entangled polymer melts can be written as the sum of contributions from both processes

31

in which τ_hop^ent is the crossover time between fluctuation plateau and hopping diffusion (eq 26).

The corresponding terminal particle diffusion coefficient is

32

The polymer relaxation (reptation) time increases as power law of the degree of polymerization (eq 29), and at the crossover value of the degree of polymerization N_c the reptation time τ_rep becomes comparable to τ_hop^ent.

33

The description of particle mobility in entangled polymer melts can be extended to polymer solutions by substituting Kuhn monomer size b by the correlation length ξ (eq D.2) and including concentration dependence of all other quantities, N_e (eq F.3) and a_e (eq F.1) as shown in Appendix F.

The mean-square displacement of the large probe particle in polymer liquids with degree of polymerization larger than N_c is dominated by the hopping diffusion (see solid line in Figure 6). The mobility of probe particles in liquids with shorter polymers (N < N_c) is dominated by chain relaxation process. Note that the reptation time τ_rep is independent of the particle size, whereas the time scale τ_hop^ent increases exponentially with particle size d (see eq 26). Therefore, for a polymer solution with fixed polymer length N and concentration above the entanglement onset we can introduce the crossover particle size d_c

34

at which the hopping time scale τ_hop^ent is comparable to the reptation time τ_rep. Note that in the second line of eq 34, we are assuming d_c ∼ a_e, as the numerical solution of eq 34 gives d_c on the order of a_e.

Thus, there is an interval of particle sizes (a_e < d < d_c) for which the terminal particle diffusion coefficient is dominated by the contribution from hopping diffusion, whereas for particles with size d larger than d_c (see eq 34) it is dominated by the contribution from chain reptation process.

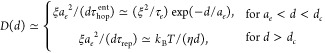35

The interval of particle sizes (a_e < d < d_c) within which the particle motion is dominated by the hopping process is of significant width to be tested by experiments or computer simulations. For instance, the crossover particle size could be of one order of magnitude larger than the tube diameter (d_c ≃ 10a_e) in a highly entangled polymer liquid with N/N_e ≃ 50 entanglements per chain and typical ratio of tube diameter a_e and correlation length ξ of a_e/ξ ≃ 5. The motion of very large particles with size larger than d_c (eq 34) is diffusive with their terminal diffusion coefficient inversely proportional to the bulk viscosity and the particle size. Note that above we describe the dependence of terminal particle diffusion coefficient D(d) on particle size d. By including the concentration and molecular weight dependencies of corresponding parameters, ξ, a_e, τ_e, and η, one can obtain the dependence of particle diffusion coefficient D on solution concentration ϕ, and degree of polymerization N (polymer molecular weight M), as discussed in Appendix F.

To summarize: (1) There is a range of particle sizes (a_e < d < d_c (eq 34)) in which the particle motion is mainly determined by hopping diffusion; (2) the hopping diffusion coefficient of large particles decreases exponentially with increasing particle size d (eq 27 and Table 1); (3) very large particles with size greater than d_c have to wait for polymer liquids to relax and flow around them in order to diffuse.³¹ The dependence of terminal diffusion coefficient of particles on their sizes in an entangled polymer melt is presented by the dashed line in Figure 5. Note that microrheological approach works only for these very large particles with d > d_c, while for smaller particles it leads to the underestimation of polymer viscosity due to faster particle diffusion by hopping process.

5. Conclusion

In this work, we have discussed the mobility of large particles subjected to topological constraints. The topological constraints could be network cages in unentangled polymer solids (networks and gels), entanglement nets in polymer liquids (melts and solutions), or both entanglements and network cages in entangled polymer solids. We introduce a novel hopping mechanism to describe the diffusion of large particles with size d larger than the network mesh size a_x and/or the entanglement mesh size a_e. We argue that although the large particles experience the topological constraints from the network (entanglement) cages, they can still diffuse by waiting for the fluctuations of the surrounding confinement cages, which could be large enough to slip around the particle.

In unentangled polymer solids (a_x < a_e) the large particles are trapped by network cages at long time scales (t > τ_x). To move (hop) between cages, these particles have to wait for time τ_w, at which the fluctuations of network strands become large enough to allow the particles to hop between cages. The hopping step occurs by just one network loop out of many overlapping ones that slips over the particle. The resulting hopping step size Δr of a particle is on the order of a monomer size in dry polymer networks or melts and on the order of correlation length in gels and entangled polymer solutions. Note that this hoping step size is much smaller than the network mesh size and is independent of particle size d, which is qualitatively different from prediction in ref (43). Hopping diffusion coefficient of large particles in unentangled networks exhibits exponential dependence on the square of the ratio between the particle size and the network strand size: D_hop^net ∼ (a_x/d) exp (−d²/a_x²).

In addition to permanent cross-links, polymer solids can also contain entanglements. Particles diffusing in weakly cross-linked polymer solids are primarily constrained by entanglements. Unlike the chemical cross-links, the constraining effect due to entanglements softens upon chain elongation and thus the corresponding free energy barrier for hopping diffusion between neighboring entanglement cages is weaker. The corresponding diffusion coefficient of large particles (a_e < d < d_e ≃ a_x²/a_e) in entangled networks has relatively weaker dependence on particle size, D_hop^ent ∼ exp (−d/a_e), in comparison to unentangled networks. We would like to stress that our model predicts linear dependence of the hopping energy barrier on particle size d, which is qualitatively different from that in ref (43), in which the hopping barrier is expected to be asymptotically proportional to the particle volume d³. It is worthwhile to note that the barrier height predicted in ref (43) is similar to our estimate for the energy of embedding a particle into the polymer network (Appendix C).

In contrast to particle motion in entangled permanently cross-linked networks, for which hopping is the only mechanism allowing long-time diffusion, large particles in entangled polymer liquids can also diffuse by allowing these liquids to flow around them at time scales longer than the relaxation time. We show that particles with intermediate size a_e < d < d_c (see eq 34) diffuse primarily by hopping between neighboring entanglement cages, while extra large particles (d > d_c > a_e) have to wait for the polymer liquids to relax as the entropic energy barrier for hopping between neighboring entanglement cages becomes extremely high.

The hopping process provides the mechanism for diffusion of particles with size several times larger than the mesh size of unentangled polymer networks and tube diameter of entangled polymer solids and liquids. For instance, recent experiments studying the diffusion of gold nanoparticles with size slightly larger than the entanglement length in polystyrene solutions show that the particles experience viscosity smaller than the macroscopic value.⁴¹ It is possible that the diffusion coefficient of these particles with size d > a_e is due to hopping. We are looking forward to more systematic experimental and computer simulation tests that will provide more information about diffusion of particles with size larger than the network (entanglement) mesh size. Furthermore, a natural extension of the results presented in this paper could be the mobility of particles in reversible polymer liquids⁴² and solids,⁴⁵ which will be presented in a future publication.

Appendix

A. Concept of “Elementary” Networks

Consider the motion of a probe particle of size d in a dry, monodisperse unentangled permanently cross-linked network. Let us denote the number of Kuhn monomers between two neighboring cross-links by N_x and the size of a network strand by a_x ≃ bN_x^1/2, where b is Kuhn length. In a typical network there are many network strands overlapping within the volume pervaded by a network strand. The overlap parameter P ≃ N_x^1/2 is defined as the number of network strands within the volume a_x³ ≃ (bN_x^1/2)³ pervaded by one network strand.

To understand how this strong overlap of network strands affects the topological structure of the network, we consider an ideal, unentangled polymer network, formed by end-linking monodisperse precursor linear polymers. Each cross-link joins f ends of such polymers. The topology of the network is fixed once the network is formed. The network has a topological Cayley tree-like structure, as illustrated in Figure 7a for example of f = 4. The number of network strands at the lth generation is (f – 1)^l−1, which grows exponentially with the generation number of the tree. These network strands heavily overlap with each other, resulting in many network strands within the pervaded volume of a particular strand. As a result, network strands form loops that contain many generations of the tree per loop, as shown by the colored, thick lines in Figure 7a. In contrast, there are not many small loops, as network strands on these topological scales are connected into a treelike structure.

Figure 7.

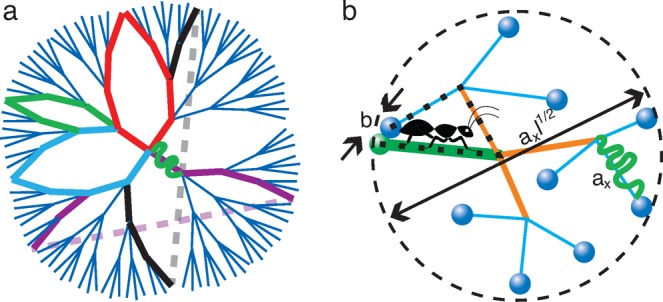
Illustration of loops in a network formed by end-linking a melt of unentangled linear chains by cross-links with functionality f = 4. Network strands, consisting of Kuhn segments with size b, have random conformation, as shown by the curved lines, and represented by straight lines of size a_x. (a) Topological illustration of treelike structure of the network (Flory model). In reality, the network stands strongly overlap with each other; the network strands belonging to higher generations of the tree meet and form loops, as shown by the colored, thick (both solid and dashed) lines. Dashed lines denote bonds between pairs of strands that are close in space, but remote on topological tree. b) An ant walking along the network strands arrives at its starting monomer (green circle) after l steps of size a_x. Line thickness corresponds to the generation of steps on the tree. The path of the ant forms a loop (dotted lines) with the size about a_xl^1/2. There are (f – 1)^l−1 chain ends (blue circles) randomly distributed in the volume (a_xl^1/2)³.

To estimate the loop size, we imagine that an ant starts from one end of a network strand, walks along network strands with step size of the network strand size a_x, passing the cross-links, and reaches the starting monomer of the strand after l steps along the loop, as illustrated in Figure 7b for l = 3. The number of possible ways to form a loop of l network strands by end-linking the first network strand and one of the network strands at the lth generation of the Cayley tree is (f – 1)^l−1. The probability that two ends of such tree are inside the contact volume b³ is

A.1

where (a_xl^1/2)³ is the volume pervaded by linear chain of l network strands and P ≃ a_x/b = N_x^1/2 is the overlap parameter of network strands. An average number, l̅, of network strands in a loop is determined by the condition φ(l̅) ≃ 1, which gives

A.2

The size of such a loop is a_l ≃ a_xl̅^1/2, logarithmically larger than the network strand size, a_x. Below we use this ideal network model, with cross-link functionality of f = 4 as an example, to discuss the diffusion of a large particle in the network.

Diffusion of a large particle in the unentangled network involves stretching of the loop due to its slipping around the particle. To understand how the large embedded particle deforms the minimal loops of real networks (Figure 8a), we first consider a simplified picture by modeling the unentangled polymer network as P* independent, overlapping de Gennes c* networks of minimal loops,³⁴ as illustrated in Figure 8b. Each c* network has overlap parameter on the order of unity. Similar to the “real” network, a loop in a c* network has l̅ ≃ ln P network strands connected by cross-links most of which are bifunctional, as shown in Figure 8b.

Figure 8.

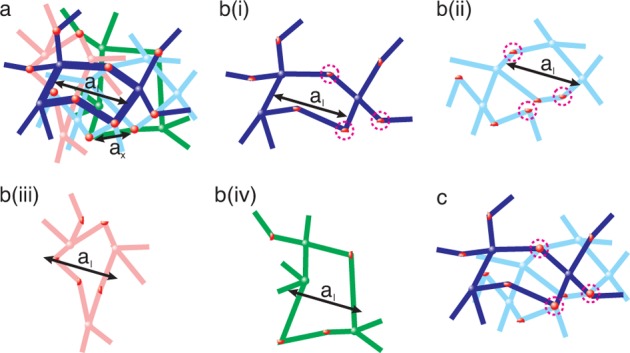
Unentangled network formed in a melt of precursor linear polymers by end-linking them using cross-links with functionality f = 4. (a) A loop of an unentangled polymer network consists on average of l̅ ≃ ln P network strands, as shown by the thick lines. The overlap parameter of network strands P ≫ 1, and typical loop size, a_l ≃ a_xl̅^1/2, is larger than network strand size, a_x. (b) The unentangled network can be constructed using P* de Gennes c* networks as building blocks. Each c* network has the overlap parameter of network strands on the order of unity. Each color represents one c* network. A minimal loop in a c* network has l̅ network strands connected to each other mostly by bifunctional units, as illustrated by red half-circles. (c) By random cross-linking bifunctional units of P* overlapping c* networks, one can construct a “real” unentangled polymer network, shown in part (a). Taking two c* networks, parts b(i) and b(ii), for example, the cross-linking process is represented by unifying two half circles to form a full circle, labeled by dashed circles.

Unlike the overlap parameter P of strands of a real network, P* denotes the overlap parameter of all linear strands of overlapping c* networks. Therefore, the value of P* ≃ (N_xl̅)^1/2 ≃ N_x^1/2(ln N_x)^1/2, as a mesh loop in such networks consists on average of N_xl̅ monomers.

At equilibrium, the particle is located in entropic cages in each of c* networks. Each c* network pulls the particle towards the center of its network cage. At the center of the cage, c_i, the elastic force applied to the particle is zero in the absence of other c* networks. However, the particle is confined by all c* networks. Therefore, the average position of the geometric center of the particle, r, is not at the equilibrium position c_i of any particular c* network and is determined from the minimum of free energy. The total deformation energy is the sum of the contributions from P* unconnected c* networks:

A.3

The elastic constant, k⁰, of an unconnected c* network is (see Appendix B.2)

A.4

where a_l is root mean square fluctuation of a strand size in an unconnected c* network. The size of these fluctuations is on the order of the average loop size a_l ≃ a_xl̅^1/2, and does not depend on network deformation.

While the above results are for P* unconnected c* networks, in reality c* networks are strongly connected; each loop in a “real” network is connected to neighboring loops, as illustrated in Figure 9a. Therefore, the deformation of one loop affects other connected loops. To describe correlated deformation of these loops, we allow bifunctional connections along strands of c* networks to randomly pairwise cross-link to form tetrafunctional cross-links, connecting different c* networks, as illustrated by the transition from half to full circles in Figure 8c. Such random cross-linking of on average l̅ ≃ ln P bifunctional units per loop results in formation of a “real” polymer network from P* initially unconnected overlapping c* networks.

Figure 9.

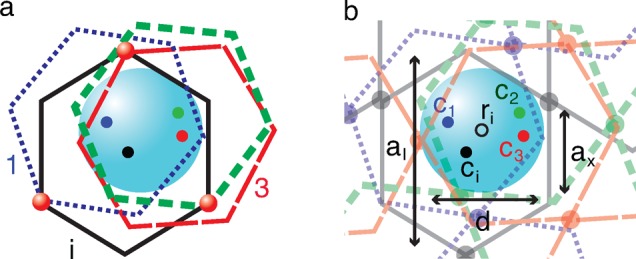
Connection between different loops. (a) A network loop i (solid line) deformed by the particle is directly connected through tetrafunctional cross-links (circles) to different loops (1, 2, and 3, different styles and colors). We also show positions of the centers of corresponding confinement cages. The conformations of strands in a “real” network are not straight and cages consist of several loops. (b) The loops are parts of different c* networks, shown by dimmed lines. The cage is composed of loops of c* network i and l̅ directly connected loops of different c* networks (j = 1, 2, 3). The coordinate r_i of the cage center in a real network is the average of the corresponding center coordinates c₁, c₂, c₃ and c_i; see eq A.8

The deformation of a single c* network after such cross-linking is affected by the c* networks connected to it. Below we show that elastic properties of real networks do not depend on the number l̅ of strands in a loop. Therefore, the total deformation energy of the real network due to the inserted large particle can be expressed as a sum over P ≃ N_x^1/2 inter-connected c* networks and contains two parts:

A.5

The “diagonal” elastic constants, k_ii, account for the deformation of network strands within c* network i. The “off-diagonal” constants, k_ij,i≠j, account for correlations in deformation of network strands in c* networks i and j due to their connectivity. Since we take the number P of c* networks in eq A.5, which is slightly less than the number P* ≃ Pl̅^1/2 in eq A.3, elastic constant k_ii and center of cage coordinates c_i are renormalized. Equating the corresponding quadratic terms in eqs A.3 and A.5, (1/2)P*k⁰r² = (1/2)Pk_iir², we find k_ii = k⁰l̅^1/2. The distance between neighboring cages |Δc_i| ≃ a_l is weakly affected by this renormalization.

Since two bifunctional units of the loop after cross-linking form one tetrafunctional cross-link, there are about l̅ tetrafunctional cross-links per loop. These tetrafunctional cross-links connect the loop to l̅ neighboring loops from different c* networks, as illustrated by the dashed circles in Figure 8. We call such loops with shared tetrafunctional cross-links “directly connected”. Therefore, about l̅ loops from other c* networks are directly connected to a particular loop in given c* network. These loops “directly connected” to loop i are deformed by the large particle in parallel with the loop i.

“Off-diagonal” elastic constant k_ij depends on connectivity of deformed loops in c* networks i and j. If a loop of c* network j is directly connected to a loop of network i (see Figure 9a), deformations of both loops are strongly correlated and off-diagonal elastic constant is on the same order of magnitude as the diagonal one, k_ij ≃ k_ij ≃ l̅^1/2k⁰. If these loops are only indirectly connected, correlations in their displacements are relatively weak. The connectivity can be characterized by the minimal chemical path connecting loops i and j through network strands (see Figure 7). Note that there is only one path connecting any two cross-links separated by number of strands l < l̅, suggesting that the real network has a treelike structure on scales shorter than loop size a_l ≃ a_xl̅^1/2.

Consider a loop in c* network i which is indirectly connected to a loop in network j by a path containing l > 0 minimal N_x-strands. Correlations between deformations of the two loops quickly decay with the number of network strands l along the shortest chemical path connecting the loops, since the elastic stress applied to a deformed strand is divided between all (exponentially large number of) strands at distance l. Therefore, the elastic constant, k_ij, corresponding to such “indirect” connection of loops is relatively weak compared to “diagonal” and “direct” constants.

Equation A.5 can be rewritten as the sum of P independent quadratic potentials

A.6

where the elastic constant k is obtained using eq A.4 with a_l ≃ a_xl̅^1/2

A.7

by neglecting the contribution of weak “indirect” elastic constants k_ij and using k_ij ≃ k_ii ≃ l̅^1/2k⁰ for l̅ pairs of directly connected c* network loops. Equation A.7 is in agreement with independent calculation of the elastic constant of elementary network in Appendix B.2. The eqs A.6 and A.7 allow us to interpret P inter-connected c* networks as P independent elementary networks. Comparing to eqs A.5 and A.6 we find that the coordinate of the center of the ith elementary network cage is related to corresponding P coordinates of c* networks as

A.8

The ratio k_ij/k is about 1/l̅ for c* networks i and j with directly connected loops, as for a particular c* network i there are about l̅ directly connected c* networks j. This ratio k_ij/k is relatively small for c* networks i and j with indirectly connected loops. Therefore, r_i in eq A.8 can be interpreted as the average of positions of centers c_j for l̅ directly connected cages, as illustrated in Figure 9b.

We would like to emphasize the importance of eq A.6. It suggests that the deformation of a real unentangled network can be interpreted as the deformation of P unconnected networks. We call them “elementary” networks; the elastic modulus k of an “elementary” network is represented by eq A.7, and the center of the cage of i-th “elementary” network r_i is described by eq A.8. Notice that eq A.7 indicates that the amplitude of fluctuations of a cross-link in elementary networks is a_x, which is smaller than the loop size a_l.

Elementary networks represent elastic and fluctuation properties of a “real” network. Fluctuations of a strand of “real” network can be described by the composite chain model³⁵ that includes one “real” network strand and two virtual chains, as shown in Figure 10. A virtual chain has size about a_x, although it represents the tree of much larger size on the order of a_l. Therefore, the fluctuation of ends of real chains is also about a_x and is smaller than the loop size, a_x < a_l.

Figure 10.

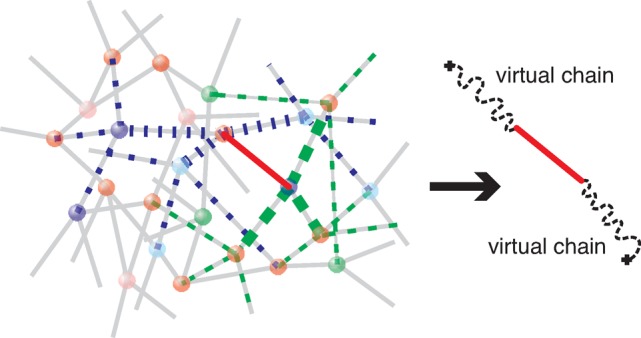
A composite chain³⁵ of a “real” network in Figure 8a consisting of a real chain (solid red) connected by its ends to two virtual chains, as shown in the right figure. Virtual chains represent treelike series of strands, as shown by dotted and dashed lines of different colors respectively (left figure); lines of different thickness corresponds to generations along the tree.

The size of a cage that confines the particle in “elementary” network can be interpreted as the step size, Δr_i, of the particle hopping between neighboring “cages”. This step size can be estimated using the connection between elementary and c* networks (see eq A.8). During a single hop, not only one loop of a c* network is strongly deformed, but l̅ loops directly connected to this particular loop are deformed by the particle. Therefore, although the distance between two neighboring cage centers in an inter-connected c* network is |Δc_j| ≃ a_l, the hopping step size

A.9

in an “elementary” network is relatively smaller, due to simultaneous deformation of l̅ directly connected network strands. The mean square of the step size is

A.10

suggesting that the cage size of an “elementary” network is also a_x.

Since all l̅ directly connected loops of real network deform in parallel, when the particle hops between elementary network cages, in fact they deform simultaneously with l̅ cages of different c* networks. Deformation energy of an unconnected c* network cage is

A.11

The energy barrier for hopping diffusion between “elementary” network cages is l̅ times higher than ΔU*:

A.12

The “elementary” network model is used to calculate the key parameters, step size and energy barrier, for hopping diffusion of a large particle in an unentangled network.

B. Polydispersity of Polymer Networks

There are two major sources of variation in loop size. The first is related to variations in the number of network strands per loop, and the second is related to variations in the number of monomers per strand. Below we consider both of them in more details.

B.1. Statistics of the Number l of Network Strands per Loop

We approximate the probability distribution of the number l of network strands in a loop by eq A.1 with cutoff at l = l_max:

B.1

Near the cutoff we can expand (l_max/l)^3/2 in this expression in powers of l_max – l:

B.2

The cutoff l_max can be found from normalization condition

B.3

Substituting expansion B.2 we obtain

B.4

Two constants in this equation can be simplified after changing the summation index k = l_max–l:

B.5

Expanding the upper limit in these sums to infinity we find

B.6

At large l_max ≫ 1, we can neglect correction term 1/l_max in eq B.4 and obtain

B.7

Similar calculation of the average number of strands in a loop gives

B.8

where

B.9

and we substituted expansion B.2 and neglected the correction term ∼1/l_max similarly to eq B.4. Therefore, the average l̅ almost coincides with the cutoff l̅ ≃ l_max.

Mean square variation of the strand number in a loop is calculated similarly to eq B.9:

B.10

At P ≫ 1 we get ≪l̅². Therefore, we can neglect fluctuations of the number of strands in a loop.

B.2. Statistics of Energy Barriers

The variation of the number of monomers N in a strand can be described by Poisson distribution

B.11

where N̅ is average number of strand monomers. The dispersion of this distribution is

B.12

Below, we discuss how such strong polydispersity in strand length affects energy barriers.

For a polydisperse network eqs A.11 and A.12 for the energy barrier take the form:

B.13

where the number of Kuhn segments in a loop of i-th c* network is

B.14

This free energy barrier varies between different locations within the polymer network due to the polydispersity of loop sizes. It could therefore be possible that a large particle is localized within a particular region of the network surrounded by small loops (large free energy barrier for the particle to escape). In this case the particle motion is affected by the polydispersity of the network loops. If the particle size is not very large, however, it is possible that the particle diffusion is not affected by network polydispersity, because the variation of the free energy barrier caused by the difference in loop length is less than thermal energy k_BT.

To explore this variation, we expand eq B.13 in the variation of the number of monomers per strand δN_ij = N_ij – N̅

B.15

Assuming that δN_ij is uncorrelated for different strands, the variation of the sum is

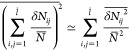B.16

In the case of Poisson distribution, eq B.12, this equation becomes Σ_i,j2 = 2l̅². Typical value of the sum in eq B.15 is

B.17

Therefore, the variation of the barrier energy δ(ΔU):

B.18

The crossover particle size d_m is given by the condition |δ(ΔU)|_d=dm ≃ k_BT, which gives

B.19

For particles with size smaller than this crossover value the fluctuation of the free energy barrier is less than k_BT. Therefore, the particles diffuse as if they are in a monodisperse network and the polydispersity of network loops is not essential. Note that the particles in this regime are still subjected to the confinement of the network cages, as their size d is larger than the size a_x of the network cage, but they do not “feel” the polydispersity of the network. At the crossover particle size d_m, the particle diffusion coefficient drops by the factor of e^–l ≃ 1/P ≪ 1. The current paper focuses on this very interesting regime (a_x < d < d_m) in which large particles feel the confinement from the network cages, but not the polydispersity of the network loops.

C. Linear Restoring Force Confining a Particle in a Network Cage

If a large particle (d > a_x) deviates from the center of the network cage by a small distance, the “elementary” network tends to drag the particle towards the center of the cage with a restoring force. To estimate this restoring force, we need to calculate the change in the deformation free energy of the network due to a small displacement of the particle while it stays in the same cage.

C.1. Embedding Energy

At equilibrium position the particle “sits” in the network, expelling about (d/a_x)³ “elementary” network strands to space just outside the particle. These chains are stretched very inhomogeneously, with the strongest stretching of chains displaced from the center of the particle. Stretching factor λ(r) of chains that were at distance r from the particle center decays as λ²(r) = d²/r², which can be understood as the ratio of surfaces d² after displacement to particle boundary and r² before such deformation. Therefore, the elastic energy of all such chains is

C.1

in which dn(r) ≃ r²dr/a_x³ corresponds to the number of such chains in an elementary network displaced from distances (r, r + dr) from the center of the particle. Thus, the energy of embedding the particle into the elementary network is on average on the order of k_BT per “elementary”network chain extruded from the particle volume.

The large particle also deforms the network strands that were outside of volume occupied by the particle, r > d. The strain at distance r from the center of the probe particle in the “elementary” network induced by the embedded particle is ϵ(r) ≃ d³/r³, in which d³ stands for the volume of the particle. Therefore, the elastic deformation energy U_out for network strands that were outside the particle is

C.2

which is on the same order as the energy of elastic deformation of all chains that were within the pervaded volume of the particle. The total embedding energy U_elem ≡ U_in+U_out presents the energy required to embed the particle into the elementary network: U_elem ≃ G_elemd³, where G_elem ≃ k_BT/a_x³ is the modulus of the elementary network. This result for embedding energy U_emb ≃ G_xd³ is also valid for a real unentangled network consisting of P elementary networks with elastic modulus

C.3

C.2. Deformation Energy

Consider the deformation of chains that were located inside the angular sector dΩ_e with center at r_i and direction of unit vector e due to particle displacement by a vector δr from its equilibrium position r_i in the center of a cage in the ith “elementary” network. Since the surface of the displaced particle is shifted from (d/2)e to (d/2)e – δr, its radius in the direction e becomes |(d/2)e – δr|≃ d/2 – (δre) for small displacement δr ≪ d. The corresponding change of deformation energy of an elementary network is obtained by summing the changes of chain deformation energies (see eqs C.1 and C.2) in all angular sectors dΩ_e:

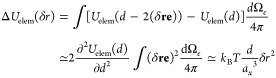C.4

Since this deformation energy is parabolic function of δr, the restoring force is linearly proportional to the distance δr from the current location of the particle to its equilibrium position r_i:

C.5

For an unentangled polymer network that is modeled by P overlapping but noninteracting elementary networks, the total change in the deformation energy becomes k_BTP(d/a_x³)δr² for the particle with displacement δr from its free energy minimum O, see Figure 2. Recall that the hopping step size for a particle in an unentangled dry polymer network is about b (eq 5) and the network strand size a_x ≃ bN_x^1/2 ≃ bP. Therefore, the change in the deformation free energy is about k_BTd/(a_xP), which is much smaller than the deformation energy k_BT(d/a_x)² of a single slipping loop as P ≫ 1. Therefore, for both “elementary”and unentangled polymer networks the entropic energy barrier for hopping diffusion can be approximated as the deformation free energy of the slipping loop (eq 6).

D. Diffusion of Particles in Unentangled Polymer Gels

Consider a gel prepared by cross-linking polymer chains in a solution. The properties of a gel depend on the preparation conditions (see Chapter 7 in ref (35)). To keep our calculations simple we limit our consideration to particle diffusion in gels at preparation conditions.

An unentangled polymer gel can be treated as an “effective” unentangled dry polymer network in which the “effective” monomers are correlation blobs. Therefore, the results obtained for particle hopping in dry polymer networks can be readily applied to polymer gels with hopping step size b replaced by the correlation length ξ and other parameters replaced by the concentration dependent ones:

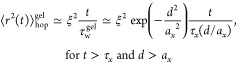D.1

However, this is not observable for time window τ_x < t < τ_hop^gel, in which the particle displacement due to hopping is smaller than that arising from fluctuations. In eq D.1, the concentration dependent correlation length ξ is³⁶

D.2

where v is the scaling exponent that depends on the solvent quality (v = 1/2 in a Θ solvent and v = 3/5 in an athermal or good solvent). In eq D1, τ_w^gel is the waiting time for particle hopping in an unentangled polymer gel which has the same expression as τ_w in eq 7 but with network strand size a_x and relaxation time τ_x replaced by the concentration-dependent ones (Chapter 9 in ref (35)):

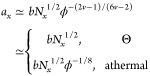D.3

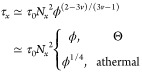D.4

The contribution to the mean-square displacement of a large particle due to hopping ⟨r²⟩_hop^gel is comparable to the mean-square fluctuations of the trapped particle ξa_x/d at time scale τ_hop^gel (see eq 12).

D.5

The mean-square displacement of the particle at time scales longer than τ_x can be approximated as the sum of mean-square displacement due to fluctuation ξa_x²/(dP) and mean-square displacement due to hopping (eq D.1)

D.6

and the corresponding terminal particle diffusion coefficient is

D.7

The terminal diffusion coefficient of a large probe particle (d > a_x) in unentangled polymer gels exhibits exponential dependence on the square of ratio of the particle size d to network strand size a_x (see eq D.7). One can rewrite eq D.7 as a function of polymer concentration in the gel using eqs D.2 and D.4:

D.8

The terminal particle diffusion coefficient is reciprocally proportional to the fourth power of concentration in Θ solvents, D ∼ ϕ^–4, while in athermal and good solvent concentrations, the dependence enters not only in the coefficient (as −15/8 power) but also in the exponential through the concentration dependence of the barrier height.

E. Entanglement Effects Disappear for Very Large Particles in Entangled Networks with a_e < a_x²/a_e < d

Consider the motion of large particles in entangled polymer solids with low density of cross-links (d > a_x²/a_e > a_e). Intuitively the motion of particles with size d > a_e is expected to be affected by the entanglements. However, for particles larger than the crossover size d_e defined in eq E.1 below (a_e < d_e < d) the confinement from entanglements is not important. Indeed, the local entanglements that surround these very large particles do not “exist” anymore, because they are under large deformation, leading to the slippage of entanglements towards to the permanent cross-links,³⁷ as shown in Figure 11. Therefore, the hopping diffusion of very large particles d > d_e in entangled polymer solids with low density of cross-links (a_x > a_e) is controlled by the permanent networks and is similar to the diffusion of large particles in unentangled polymer solids (see section 2). At the crossover particle size d_e the tube diameter a_e^′ of stretched network becomes comparable to the network strand: a_e ≃ a_x. Taking into account the fact that the tube diameter increases from a_e to a_e^′ ≃ a_e(d_e/a_e)^1/2 due to non-affine deformation of entanglements,³⁷ the crossover particle size is

E.1

which is about a_x/a_e times of the network strand size a_x. Mobility of relatively large particles (a_x < d < d_e ≃ a_x²/a_e) is affected by both entanglements and permanent cross-links, but dominated by the entanglements. This is because the entropic free energy barrier due to permanent cross-links, k_BT(d/a_x)², is smaller than that from entanglements, k_BT(d/a_e), for a_x < d < d_e. Therefore, the particle motion is similar to that discussed in section 3.

Figure 11.

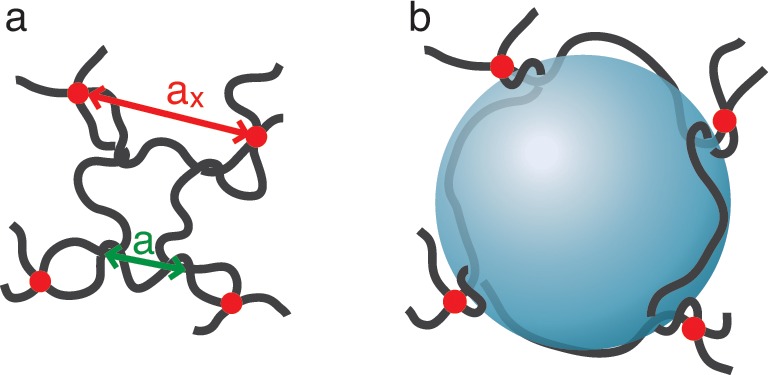
Very large particles do not “feel” confinement from entanglements in networks with low density of cross-links (a_e < a_x). (a) A polymer network with low density of cross-links, at which the entanglement length a_e is smaller than the network mesh size a_x. (b) Very large particles (d > d_e ≃ a_x²/a_e, eq E.1) result in large deformation of local entanglements, pushing them toward the permanent cross-links, and therefore do not “feel” the existence of entanglements.

F. Particle Diffusion Coefficient in Entangled Polymer Liquids

F.1. Dependence of Particle Diffusion on Solution Concentration

The contribution from hopping diffusion to the concentration-dependent terminal diffusion coefficient can also be applied to describe diffusion of particles with size d larger than the tube diameter a_e(1) of entangled polymer melts without solvent. In addition to the two regimes expected for particles smaller than the tube diameter a_e(ϕ), there is an additional regime in which the terminal particle diffusion coefficient is affected by entanglements. This regime begins at the solution concentration ϕ_ae=d, at which the tube diameter a_e (see eq F.1) is on the order of the particle size d: a_e(ϕ_ae=d) ≃ d. Concentration dependence of the tube diameter is

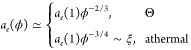F.1

where ϕ is volume fraction of polymer solutions.⁴⁰ Therefore, the corresponding crossover concentration is

F.2

In this regime (ϕ > ϕ_ae=d), the terminal particle diffusion coefficient is determined either by hopping diffusion or chain reptation process (see eq 32). Recalling the relations τ_e ≃ τ₀(ξ/b)³(a_e/ξ)⁴ (see eq 23) and τ_rep ≃ τ_e(N/N_e(ϕ))³ (see eq 29) and using eqs 9, D.2, 26, F.1 and the concentration dependence of the degree of polymerization between entanglements

F.3

one can simplify eq 32 to obtain the concentration dependence of terminal particle diffusion coefficient by summing the two contributions:

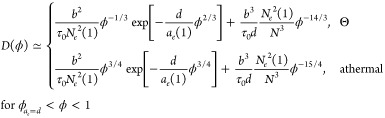F.4

In entangled polymer liquids of relatively short polymers (N_e < N < N_c) the terminal diffusion coefficient is mainly controlled by chain reptation process (see the second term in eq F.4). The crossover degree of polymerization N_c increases exponentially with relative particle size d/a_e (see eq 33). For example, for a_e/ξ ≃ 5 and d/a_e ≃ 4 we have N_c ≃ 4N_e; if a_e/ξ ≃ 5 and d/a_e ≃ 10 we have N_c ≃ 22N_e.

In solutions of long polymers (N > N_c) there are two cases for the terminal particle diffusion coefficient depending on particle size. If the size of particles is not too large: a_e(1) < d < d_c(1), where d_c(1) represents the value of crossover particle size d_c (see eq 34) in polymer melt (ϕ = 1)

F.5

the terminal particle diffusion coefficient is dominated by the contribution from hopping.

For particles with size larger than d_c(1), the hopping diffusion still dominates as long as the solution concentration is below ϕ_dc, at which the particle size d is comparable to crossover size d_c(ϕ_dc) (see eq 34). Using eqs D.2, 23, F.1 and F.3, one can transform eq 34 into logarithmic concentration dependence of the crossover particle size d_c(ϕ) below which the particle motion is dominated by hopping diffusion.

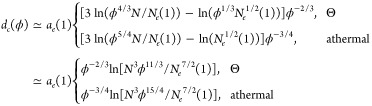F.6

Note that in this calculation the solution volume fraction ϕ is above the entanglement volume fraction ϕ_e, suggesting that the variation of the solution concentration is limited. Typically for polymer solutions with long polymers N > N_c(ϕ), the crossover particle size d_c(ϕ) decreases slowly by less than 10% as solution concentration increases by 20%. It suggests that changing the solution concentration will not significantly enlarge the window within which the particles experience hopping-dominated diffusion.

Particles with size d larger than d_c(1) are expected to experience full solution viscosity above the crossover concentration ϕ_dc and the terminal particle diffusion coefficient is dominated by the contribution from chain reptation process (see eq 30).

F.2. Dependence of Particle Diffusion Coefficient on Polymer Length

Consider the motion of large probe particles (d > a_e) of fixed size in entangled polymer liquids with different degrees of polymerization N but with the same concentration ϕ. The contribution of hopping diffusion to the particle terminal diffusion coefficient is not important if the degree of polymerization N is smaller than the crossover value N_c (see eq 33). Within the window N_e < N < N_c the terminal particle diffusion coefficient is dominated by the contribution from chain reptation process and the large particles “feel” bulk solution viscosity at times longer than solution relaxation time τ_rep. The terminal particle diffusion coefficient is reciprocally proportional to the solution viscosity η and decreases with increasing degree of polymerization N as

F.7

The terminal particle diffusion coefficient will be mainly controlled by the hopping diffusion for polymer liquids with very high degree of polymerization (N > N_c). For instance, using eq 35, one can estimate the ratio of particle diffusion mechanism due to hopping diffusion to that due to chain reptation:

F.8

This is about 7 for a_e/ξ ≃ 5, d/a_e ≃ 5, and N/N_e ≃ 10. For polymers with very high degree of polymerization (N > N_c) the diffusion coefficient is independent of polymer molecular weight (see eq 27).

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States