Abstract
The Ewald, Particle Mesh Ewald (PME), and Fast Fourier–Poisson (FFP) methods are developed for systems composed of spherical multipole moment expansions. A unified set of equations is derived that takes advantage of a spherical tensor gradient operator formalism in both real space and reciprocal space to allow extension to arbitrary multipole order. The implementation of these methods into a novel linear-scaling modified “divide-and-conquer” (mDC) quantum mechanical force field is discussed. The evaluation times and relative force errors are compared between the three methods, as a function of multipole expansion order. Timings and errors are also compared within the context of the quantum mechanical force field, which encounters primary errors related to the quality of reproducing electrostatic forces for a given density matrix and secondary errors resulting from the propagation of the approximate electrostatics into the self-consistent field procedure, which yields a converged, variational, but nonetheless approximate density matrix. Condensed-phase simulations of an mDC water model are performed with the multipolar PME method and compared to an electrostatic cutoff method, which is shown to artificially increase the density of water and heat of vaporization relative to full electrostatic treatment.
1. Introduction
It is well-known that the molecular modeling of many biological processes requires a rigorous treatment of the long-ranged electrostatic interactions.1−5 Furthermore, recent years have seen the development of many promising next-generation force fields and fast ab initio methods that endeavor to generalize the electrostatic interactions to higher-order atomic multipoles.6 Specific examples include the following: polarizable force fields, such as AMOEBA;7−12 density-based force fields, such as GEM13−16 and S/G-1;17 force fields that model the perturbative or many-body expansion of the energy;18−21 hybrid quantum mechanical/molecular mechanical (QM/MM) methods;22 and molecular orbital-based quantum mechanical force fields (QMFFs), such as the embedded fragment model,23 X-Pol,24−29 and the closely related modified “divide-and-conquer” (mDC) methods.30−32 The use of higher-order atomic multipoles in these examples, and many other models, offer the promise of improved accuracy, but at a larger computational cost.33−35 In order to elucidate the strengths and weaknesses of proposed models, it is necessary to make comparison to experiment, which often requires their application within molecular simulations under periodic boundary conditions. At the same time, these applications provide empirical measures of the preliminary model’s true computational cost. Therefore, fast electrostatic algorithms must be developed that are equipped to handle generalized charge densities, so that new models can be applied and tested.
The Ewald,36 Particle Mesh Ewald37−40 (PME), and Fast Fourier–Poisson41 (FFP) methods are three algorithms used to evaluate the long-ranged electrostatic interactions of periodic systems. These methods were originally designed to accommodate systems consisting of point charges; therefore, modifications to their original formulations are required to apply them to models employing multipolar charge densities. In the present work, we derive a unified set of equations for the Ewald, PME, and FFP methods using a spherical tensor gradient operator formalism that extend these methods to arbitrary multipole order. Expressions for the energies, forces, and the generalized multipolar potentials required to incorporate the electrostatics into the QMFF self-consistent field (SCF) procedure are provided. Previous works have extended these methods within the framework of Cartesian point multipoles and Cartesian Gaussians,42−47 as opposed to the solid harmonic multipoles considered here. Other related works were not formulated to arbitrary multipole order48,49 or led to a formulism that did not prove to be computationally efficient.50 The efficiency of our formulation is demonstrated through QMFF molecular dynamics applications described below and extended in Part 2 of this series.51 During preparation of this manuscript, Simmonett52 has independently reported an extension of PME for use with solid harmonic multipoles that shares many characteristics with the PME method presented here; however, our analysis extends significantly beyond ref (52) by comparing the accuracy and performance of Ewald, PME, and FFP methods as stand-alone electrostatic methods and upon implementation within a linear-scaling QMFF.
The paper is organized as follows. Section 2 describes the generalized charge density; derives equations for the generalized Ewald, PME, and FFP methods; and discusses net charge corrections, error analysis, and the integration of the methods into the mDC QMFF. Section 3 compares the accuracy and computational cost of the methods, as a function of multipolar order and within the context of condensed-phase molecular simulations of water.
2. Methods
2.1. The Charge Density
Our goal is to compute the electrostatic interaction of a neutral charge density ρ(r) with itself and its periodic images:53
| 1 |
where the unit cell defining the periodicity is described by the lattice vectors a1, a2, a3 and reciprocal-space vectors a1*, a2, a3*; and the periodic images are replicated by integer lattice translations n = n1a1 + n2a2 + n3a3. The energy (given by eq 1) is finite only when the charge density is neutral; however, a widely used approximation for the treatment of charged systems will be discussed in Section 2.6. Furthermore, we adopt the standard convention of removing the infinite self-energy of point charges (and point multipoles) whenever those energies may appear. Upon replicating all integer translations of the aperiodic density, ρ(r), the edges of a lattice with the same shape, orientation, and dimensions can be redrawn about any origin; and the periodic density filling each cell will contain exactly one instance of ρ(r) that appears to have been “wrapped” into the cell’s interior. The apparent wrapping of ρ(r) to the cell boundary is an illusion formed by the effluence of density emanating from the other translations, upon making ρ(r) periodic. The aperiodic density is not required to be confined within a primary unit cell to achieve this effect. Nor is it a requirement for the evaluation of eq 1, because the electrostatic potential of ∑nρ(r + n) is periodic.
The methods presented in this work are solutions to eq 1 for a density composed of atom-centered point multipole expansions. There are various ways of defining what is meant by a multipole expansion. The two most common ways being Cartesian multipoles44 or those based on spherical harmonics.52,54,55 Our definition of a multipole moment is the inner product of a density with a real-valued regular solid harmonic:56
| 2 |
An auxiliary basis of charge density χlμ(r), satisfying
| 3 |
is thus well-suited to describe an atomic multipole expansion. The definition of Clμ(r) is closely related to the scaled regular solid harmonics frequently encountered in fast multipole methods.54,57−59 In brief, the real-valued scaled regular solid harmonics Rlmc/s(r) are the real Rlm(r) = ReRlm(r) and imaginary Rlms(r) = ImRlm(r) components of the complex-valued scaled regular solid harmonics:58
| 4 |
where
| 5 |
is an associated Legendre polynomial. Because the complex-valued harmonics are symmetry related Rlm*(r) = (−1)mRl,–m(r), the real-valued harmonics are fully described by the set of non-negative m values. The notation is simplified, when appropriate, through the introduction of a Greek subscript whose sign merely acts to symbolize the cosine/sine designation57
| 6 |
The real-valued regular solid harmonics
| 7 |
differ only by factors
| 8 |
that are chosen to reproduce Racah’s normalization
| 9 |
In the interest of writing the expression for a point multipole, we begin by deducing the form of a Gaussian multipole function from eqs 3 and 9:
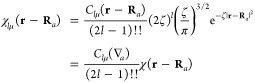 |
10 |
where
| 11 |
is a Gaussian monopole, ∇a = {d/dXa,d/dYa,d/dZa} are gradients with respect to the Gaussian center, and Clμ(∇) is a spherical tensor gradient operator60 (STGO). A STGO is constructed by replacing the Cartesian coordinate arguments of the solid harmonic with their corresponding Cartesian derivative operators. The STGO obeys several mathematical properties.61,62 The present work specifically makes use of the STGO chain-rule identity,
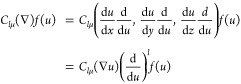 |
12 |
which follows from the homogeneity of solid harmonics Clμ(ar) = alClμ(r). The application of eq 12 to the last line of eq 10 establishes the relationship between χlμ(r – Ra) and a Gaussian monopole. A Dirac delta function is a Gaussian monopole in the limit of infinite exponent:
| 13 |
and a point multipole is this limit applied to eq 10:
| 14 |
Thus, a sum of atom-centered point multipole expansions is
| 15 |
2.2. Plane Waves
Methods for solving eq 1 avoid the infinite sum of explicit lattice translations by approximating a periodic density with a finite number of plane wave basis functions ⟨r|k⟩ ≡ eikT·r. The description of these methods is greatly simplified using Dirac notation, which we briefly summarize here. In this notation, the spatial representation of a function is equivalently written ⟨r|f⟩ = f(r); a complex conjugate is ⟨f|r⟩ = f*(r); the inner product of two functions ⟨f|g⟩ = ∫f*(r)g(r) d3r integrates all space or, if both functions are periodic, the volume of the unit cell; and we reserve |k⟩ to index the plane wave basis functions. This index is meant to be the function’s “angular wave number”, which is defined as k = 2π(k1a1* + k2a2 + k3a3*). From these definitions, one can show that the basis is orthogonal ⟨k|k′⟩ = δk,k′V, where V = a1 · a2 × a3 is the unit-cell volume; they obey a trivial addition theorem ⟨r + r′|k⟩ = ⟨r|k⟩⟨r′|k⟩; they are eigenfunctions of the gradient operator ∇⟨r|k⟩ = ik⟨r|k⟩; and the electrostatic potential of a plane wave basis function
| 16 |
becomes particularly amenable to computation. Finally, it is easy to show that the plane waves are eigenfunctions of the STGO,
| 17 |
via direct application of eq 12 with u = ikT·r.
Plane waves can be used as a basis to represent real, periodic functions:
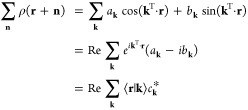 |
18 |
where ck = ak + ibk. Complex numbers have been introduced to compactly express two independent linear least-square fit problems: the representation of the even (cosine) and odd (sine) character of the density. One can show that the two least-square fit solutions for ak and bk are equivalent to having chosen
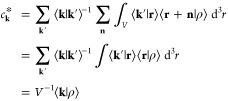 |
19 |
to minimize the sum of squared errors ⟨Δ|Δ⟩, defined by
| 20 |
In other words, eq 19 is identical to having determined ak and bk by solving the two (uncoupled) equations
and
respectively. By integrating over the volume of a unit cell, the first line of eq 19 effectively integrates one instance of ρ(r) that has been wrapped into the cell’s interior. The second line of eq 19 exploits the periodicity of the plane waves by “unwrapping” the density and modifying the integration limits accordingly.
One can deduce that cos(−x) = cos(x) and sin(−x) = −sin(x) imply the symmetries a–k = ak, b–k = −bk, and c–k = ck*. As a consequence of these symmetries,
and, therefore, the sum over allk in eq 18 naturally acts to cancel the imaginary components from each term. That is, although each term is complex, the other half of the sum adds its conjugate. The appearance of “Re” in our description of Ewald, PME, and FFP is to remind the reader that the imaginary numbers vanish and only the real component of each term thus needs to be computed. Equation 18 is often referred to as a “complex-to-real” reverse (or inverse) Fourier transform and is typically implemented within computer software to utilize only a subset of symmetry-unique ck* values that are provided as input.
Weighted least-squares fits can be performed to generalize the plane wave expansion described above. These fits produce coefficients
| 21 |
that minimize the sum of squared errors ⟨Δ|Ô|Δ⟩ weighted by a linear Hermitian operator Ô. In the general case, the components of ck store the result of a fit that may have required a coupled (as opposed to independent) solution to ak and bk. For the specific case ⟨r|Ô|r′⟩ = |r – r′|–1, eq 21 is called an “electrostatic fit”. The coefficients of an electrostatic fit reduce to eq 19, because the plane waves are eigenfunctions of the Coulomb operator (eq 16). In other words, eq 19 are the plane wave expansion coefficients that best reproduce the electrostatic potential of the periodic density.
2.3. Multipolar Ewald
One could, in principle, directly project ρ(r) into the periodic basis and compute the interaction from the plane wave representation; in practice, however, this is intractable because an infinite number of plane waves would be required to model δ(r). Therefore, the Ewald method abandons the direct solution of eq 1, preferring instead to decompose the periodic density into smooth and discontinuous components:
| 22 |
whereby the smooth model density composed of Gaussians
| 23 |
is well-approximated from a linear least-squares fit to reasonably few plane waves:
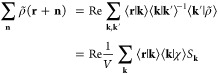 |
24 |
Furthermore, the model density was chosen to reproduce the long-range electrostatic potential of the point multipoles to ensure that only short-ranged corrections are required. In our notation, ⟨k|ρ̃⟩ and ⟨k|χ⟩ = e–(k2/4ζ) are Fourier coefficients of the Gaussian density and Gaussian monopole, respectively. The summation over k in eq 24 is a reverse Fourier transform, and Sk is a “structure factor”.
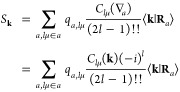 |
25 |
The Ewald energy is the interaction of ρ(r) with the electrostatic potential of the plane wave projected periodic Gaussian density ϕ̃(r) (see eq 32) upon correcting the short-ranged differences between the point and Gaussian potentials Δϕ(r) (see eq 27):
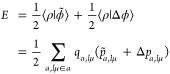 |
26 |
where p̃a,lμ = ∂⟨ρ|ϕ̃⟩/∂qa,lμ and Δpa,lμ = ∂⟨ρ|Δϕ⟩/∂qa,lμ are the corresponding “multipolar potentials”. The real-space corrections to the potential, energy, and multipolar potential are given as follows:
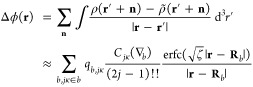 |
27 |
| 28 |
| 29 |
where
| 30 |
These corrections are assumed to be sufficiently short-ranged, such that only nearby minimum image separations Rab and |r – Rb| need to be considered. An efficient algorithm for computing eq 30 and its gradients, particularly for low-order harmonics, is described in ref (56). The application of that algorithm requires the following definition of the “auxiliary vector”:
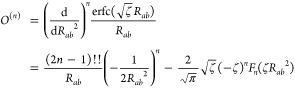 |
31 |
where Fn(x) is the Boys function.63
The reciprocal-space Ewald potential, energy, multipolar potential, and contribution to the gradient are readily obtained upon noting ⟨δ|k⟩ = 1.
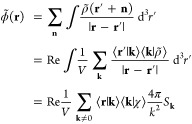 |
32 |
| 33 |
| 34 |
| 35 |
The extension of Ewald to atom-centered point multipole expansions presented here differs from the standard point-charge Ewald method only by the inclusion of STGOs in the structure factor and real-space correction.
2.4. Multipolar Particle Mesh Ewald
A linear-scaling implementation of the real-space Ewald corrections requires only short-range cutoffs and a sufficiently large Gaussian exponent; however, by fixing the cutoff—and, hence, the exponent—the computational complexity of the reciprocal-space Ewald potential then scales with O(N2), because
-
(1)
the number of plane waves must increase with the size of the system, to maintain consistent resolution of the periodic density, and
-
(2)
the calculation of each Sk requires a summation over the number of particles.
In the unlikely event that the particles happened to be positioned such that they formed a uniformly spaced grid, however, then the expression for Sk would become a sum over grid points (see eq 48) and the contribution of all grid points to all Sk could be computed O(N log N) using a Fast Fourier Transform (FFT). The novelty of PME is its coercion of the particle positions to exploit this otherwise unlikely scenario to speed the calculation of the reciprocal-space potential and energy.
PME approximates the particle positions with a linear combination of predefined uniformly spaced FFT grid points Rt,
| 36 |
that can be used to compute Fourier coefficients from numerical quadrature. The Gaussian quadrature of plane waves is equivalent to Simpson’s integration rule performed on a regular grid:
| 37 |
where fk is a discrete Fourier transform (DFT):
| 38 |
t is the index of the grid (t = (t1, t2, t3)) and Rt is the location of a FFT grid point:
N1, N2, and N3 are the number of FFT grid points in each lattice direction; N = N1N2N3.
θ is a Cardinal B-spline weight evaluated about a particle position:
| 39 |
In our notation, the argument of Mn(u) is meant to be periodically wrapped into the range (−Nd/2,Nd/2].
Mn is a Cardinal B-spline function that holds recursion properties for efficient evaluation of their values and gradients.38
| 40 |
The B-spline weights are real ⟨r|θ⟩ = ⟨θ|r⟩, have even symmetry ⟨−r|θ⟩ = ⟨r|θ⟩, sum to one (∑t⟨Rt – r|θ⟩ = 1 ∀r), and are nonzero only for those grid points near the particle. The number of grid points contributing to the approximate position of a particle is determined from the chosen B-spline order without regard to the FFT grid spacing.
Following the work of Schoenberg,64−66 previous descriptions38 of PME have used Cardinal B-splines as a linear basis to construct “exponential Euler splines.” In that point of view, the structure factors are computed from approximate plane waves that are spline-evaluated at the actual particle positions. We below choose an alternate perspective by applying eq 36 to obtain the same outcome, which we then relate to ref (38).
The charge density is composed of atom-centered functions; therefore, it is convenient to re-express eq 36 as
| 41 |
which is deduced from the invariance of the relative particle and grid positions upon their simultaneous reflection about the origin and subsequent translation by +r; that is, Ra → r – Ra and Rt → r – Rt. An atom-centered Gaussian is thus approximated by a linear combination of Gaussians centered about the FFT grid points:
| 42 |
However, this has the unintended consequence of making the approximate Gaussian appear artificially diffuse as the B-spline order is increased. Fortunately, if the B-spline is of sufficient order to be accurately integrated by the discrete Fourier transform, then the Fourier coefficients of the approximate Gaussian
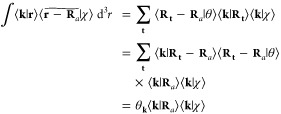 |
43 |
are those of the true Gaussian,
| 44 |
scaled
by the B-spline DFT
coefficients θk. Note that θk = θk*, because the B-splines are even
functions. Repeating this procedure for  , or any function |f⟩,
yields analogous results. In other words, the Fourier coefficients
of an approximately positioned function should be scaled by θk–1.
, or any function |f⟩,
yields analogous results. In other words, the Fourier coefficients
of an approximately positioned function should be scaled by θk–1.
Let us continue on a brief aside that relates eq 36 to the exponential Euler splines used in ref (38) by considering its application to ⟨k|k′⟩ = δk,k′V in the manner above using either of the relations
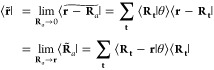 |
45 |
The result ∫V⟨k|r⟩⟨r̃|k′⟩ d3r = θk⟨k|k′⟩ implies the need to effectively renormalize an “approximate plane wave” upon grid interpolation; that is, ⟨r|k⟩ ≈ ⟨r̃|k⟩θk–1, which are the exponential splines. The relationship between eq 36 and the exponential Euler splines is the interpretation of whether it is the approximate plane wave or the Fourier coefficient of the approximately positioned function that is renormalized:
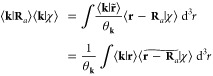 |
46 |
The subtle distinction between these interpretations has no practical consequence on the PME method other than, perhaps, how the mathematical terms are grouped together; eq 47 scales the structure factor by θk–1, whereas ref (38) absorbs it into the definition of Sk.
The periodic representation of the model Gaussian density (eq 23) composed of the approximate Gaussians (eq 42) is, upon scaling the Fourier coefficients,
| 47 |
where the PME structure factor,
| 48 |
is the forward DFT of
| 49 |
whose evaluation avoids O(N2) operations by the locality of θ(r).
The PME reciprocal-space potential is the electrostatic potential of eq 47,
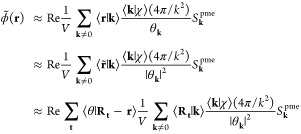 |
50 |
and yields the following PME reciprocal-space energy, multipolar potential, and contribution to the gradient:
| 51 |
| 52 |
| 53 |
The extension of PME to atom-centered point multipole expansions presented here differs from the standard point charge PME method only by the inclusion of STGOs acting upon the B-spline in eqs 49–51 and, like Ewald, the real-space correction (eqs 27 and 28).
Although the STGO has many remarkable properties61 when acting upon a spherical function, a regular or irregular solid harmonic, or a product of the these functions, the B-spline weights cannot take advantage of these properties. Instead, one must treat the STGO as a linear combination of gradient operators,
| 54 |
whose coefficients are exactly those that relate Clmc/s(r) to Cartesian monomials:67
| 55 |
where
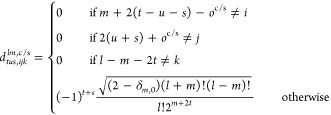 |
56 |
and oc = 0 and os = 1. In the above notation, m = |μ|, Clμ≥0(∇) = Clmc(∇), and Clμ<0(∇) = Clm(∇).
2.5. Multipolar Fast Fourier–Poisson Method
Fast Fourier–Poisson (FFP), like Ewald, abandons the direct solution to eq 1 by introducing a Gaussian density whose potential can be determined from a plane wave expansion.41 Unlike the Ewald method, FFP evaluates the plane wave expansion coefficients from numerical quadrature to take advantage of FFTs. The electrostatic potential of the plane-wave-resolved Gaussian density is computed in Fourier space, evaluated on a regular grid by means of a reverse FFT, and then used to numerically integrate the Coulomb self-energy of the Gaussian density. Therefore, the FFP real-space corrections account for the short-ranged differences between the Gaussian and point interaction energies:
| 57 |
The plane wave representation of the periodic model density composed of the Gaussian multipoles is
| 58 |
where
| 59 |
The evaluation of ⟨Rt|ρ̃⟩ avoids O(N2) operations by evaluating χlμ(Rt – Ra) only for minimum image distances within a suitable cutoff. The real-space energy corrections, ΔTlμ,jκ, vanish when the Gaussians do not overlap
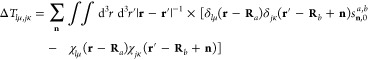 |
60 |
where sn,0a,b = 1 − δn10δn20δn30δab). Therefore, eq 60 is well-approximated by computing the integrals for the short-ranged, minimum-image Rab separations only. Explicit expressions for the real-space energy correction, multipolar potentials, and gradient contribution are analogous to those shown in eqs 28–31 upon substituting ζ with ζ/2, which arises from the Gaussian product theorem.
The FFP reciprocal-space energy, multipolar potential, and contribution to the gradient are as follows:
| 61 |
| 62 |
| 63 |
The gradient of the Gaussian basis,
| 64 |
is efficiently computed using the following derivative properties:58
| 65 |
| 66 |
| 67 |
When negative m values are encountered, the reader is implicitly instructed to apply the symmetry property Rl,–mc/s(r) = ±(−1)mRlm(r), which follows directly from Rlm*(r) = (−1)mRl,–m(r), where the plus/minus sign (±) corresponds to the cosine/sine designation.
2.6. Correction for Charged Systems
Let ⟨r|ĵ|r′⟩ = ∑n|r – r′ + n|–1; then, we can rewrite eq 1.
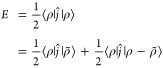 |
68 |
If the net charge is nonzero (∫ρ(r) d3r = Q), then the system is nonphysical and this definition of the energy is infinite. Although it is possible to neutralize the density in arbitrarily different ways to produce different energies, a particularly convenient choice is made by introducing a uniform background density,68
| 69 |
and ∑nρ̅(r + n) = Q/V, everywhere. With this choice of neutralization, the energy is
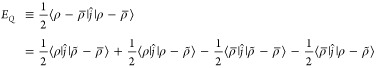 |
70 |
However, 1/2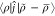 = 1/2⟨ρ|ϕ̃⟩,
as written in the previous sections, by virtue of excluding the k = 0 term in the Ewald summation, because it is charge-neutral.
Similarly, 1/2
= 1/2⟨ρ|ϕ̃⟩,
as written in the previous sections, by virtue of excluding the k = 0 term in the Ewald summation, because it is charge-neutral.
Similarly, 1/2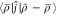 vanishes, because the exclusion of the k = 0 term produces
a potential composed of functions that
are each orthogonal to a constant over the range of the unit cell.
The last term in eq 70 vanishes, by symmetry,
for all nonzero multipoles and is well-approximated by an integral
over all space if ζ is sufficiently large to extinguish the
correction potential within the bounds of the unit cell (in a minimum
image context). As a result of these properties, the energy of a charged
system is
vanishes, because the exclusion of the k = 0 term produces
a potential composed of functions that
are each orthogonal to a constant over the range of the unit cell.
The last term in eq 70 vanishes, by symmetry,
for all nonzero multipoles and is well-approximated by an integral
over all space if ζ is sufficiently large to extinguish the
correction potential within the bounds of the unit cell (in a minimum
image context). As a result of these properties, the energy of a charged
system is
| 71 |
An analogous result is written for FFP by replacing ζ with ζ/2.
For completeness, we note that it has been pointed out69,70 that eq 1 is absolutely convergent only if the total dipole moment of the system μ is zero; however, it is otherwise only conditionally convergent. In other words, the asymptotic value of eq 1 is dependent on the shape of the supercells used to replicate the system. A “dipole surface” term 2π|μ|2/[(2εS + 1)V] can be applied to mimic an infinite spherical sample of a cubic cell; however, this energy is usually ignored in Ewald implementations,38 because its application to charged systems has a dependence on an arbitrary origin and it produces discontinuous energy changes when charged residues are wrapped into the primary unit cell.71 By ignoring this term, we are said to employ “tinfoil boundary conditions”, because it is equivalent to embedding the crystal inside a perfect conductor (εS → ∞).
2.7. Error Analysis
Figure 1 compares the Ewald energy (eq 26) to a brute force evaluation of eq 1, as a function of replicated unit cell length. The fundamental unit cell is a 10 Å cube containing three-point multipoles:
| 72 |
where R = (1 Å)ẑ. The unit cell is replicated by extending the sides of the cell to form increasingly larger cubes. The various lines in Figure 1 indicate the nonzero angular moment in eq 72. The “relative energy error” is defined as
where E is the Ewald energy evaluated with |kmax| = 256 and En is eq 1 after replication to the specified size. The relative error is bounded by ≥10–15, because of our use of double-precision arithmetic. The loss of one or two additional digits of precision should be expected, because of the accumulation of round-off errors.
Figure 1.
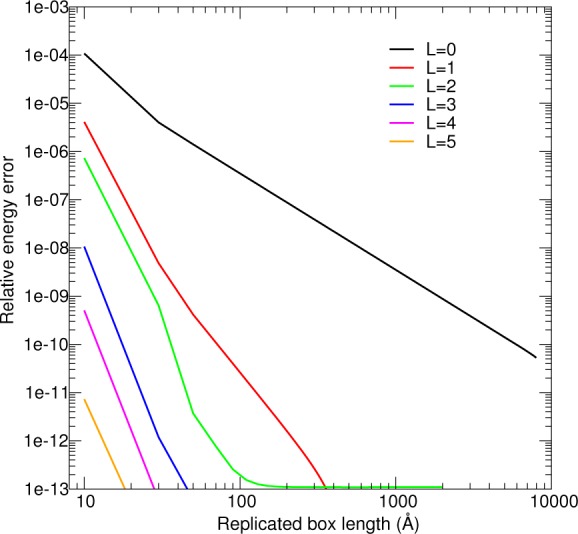
Comparison between the Ewald energy to the energy computed from explicit replication of a unit cell, as a function of replicated cell length for systems composed of the indicated multipole orders.
Figure 2–4 make use of an ad hoc three-site water model to analyze the relative force errors and the real-space and reciprocal-space timings of Ewald, PME, and FFP, as a function of atomic multipole order. These three figures are the analysis of a box of 1024 waters whose bulk density has been equilibrated with TIP4P-Ew at 298 K. The 3-site multipolar water models used to perform the analysis are systematically constructed from a 5-site charge-only water model. The 3- and 5-site water models use the DFTB372 gas-phase structure of water (these coordinates are superimposed onto the TIP4P-Ew waters): ROH = 0.957143 Å, RHH = 1.572691 Å, ∠HOH = 110.4812° (the 5-site model includes two additional charges located at the O–H bond midpoints). The atom charges (a.u.) (qO5-site = −0.12404869708, qH = 0.66106645662) and the bond charges (qB5-site = −0.59904210808) were computed from the isolated water DFTB3 density matrix; that is, qO is the one-center atomic orbital (AO) product contribution to the Mulliken charge of O, and qB5-site is the Mulliken bond charge between O and H. The multipole moments of the 3-site model are constructed from a Mulliken-like partitioning and subsequent solid harmonic translation of the 5-site model bond charges:
| 73 |
| 74 |
The intrawater interactions are excluded when analyzing the relative force errors with these models.
Figure 2.
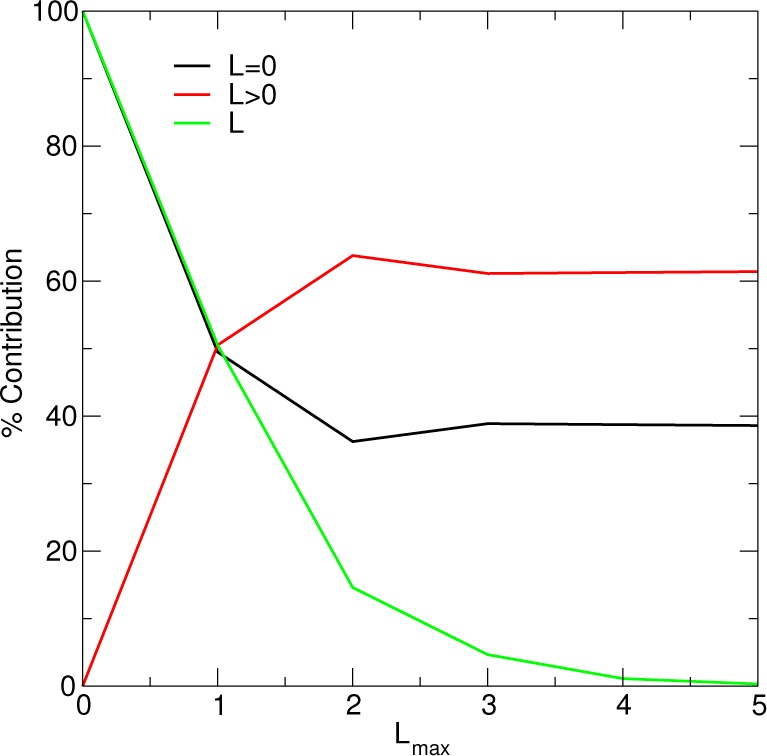
Decomposition of the intermolecular electrostatic forces using a box of 1024 waters. Lmax indexes the ad hoc 3-site water model being considered, as distinguished by the multipole expansion order on the oxygen.
Figure 4.
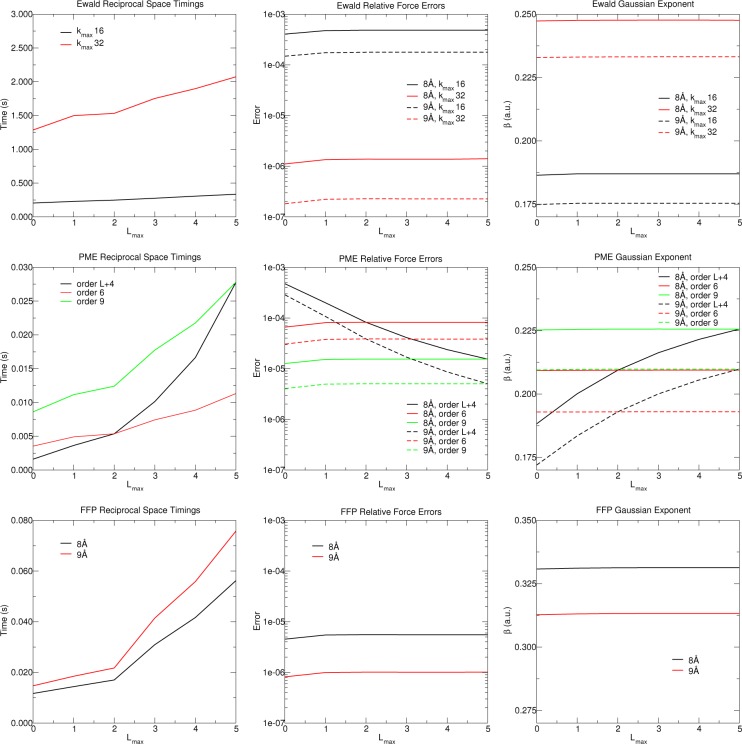
Reciprocal-space evaluation timings (left column), relative force errors (RFEs) (middle column), and the Gaussian exponents (right column) chosen to minimize the RFEs of Ewald (top row), PME (middle row), and FFP (bottom row), using the box of 1024 waters. Lmax indexes the ad hoc 3-site water model being used.
In order to interpret the results in Figure 4, it is useful to understand how the multipole order influences the magnitude of the forces. For this purpose, Figure 2 decomposes the intermolecular electrostatic forces within the 1024 water box by the percent contributed from the charge–charge interactions, the non-“charge−charge” interactions, and those interactions that involve a particular angular momentum L. Let FL be the 3 N vector of atomic forces for a system of waters composed of the ad hoc 3-site water model using an order L multipole expansion. The “percent contribution” of the charges, the multipoles, and a particular multipole L to the forces are respectively chosen to be
| 75 |
| 76 |
| 77 |
The relative force errors (RFEs) in Figure 4 are calculated using the expression
| 78 |
where Fref,L is the vector of Ewald forces evaluated with |kmax| = 128 and whose real-space corrections include all N2 minimum image interactions. The Gaussian exponent has been nonlinearly optimized to minimize each RFE, and their values are shown in Figure 4 using the convention β = ζ1/2.
The timings reported in Figures 3, 4, and 6 were performed on an Intel Xeon E5520 2.27 GHz workstation consisting of a total of 8 cores, and the software was rudimentarily parallelized with OpenMP to make use of all cores.
Figure 3.
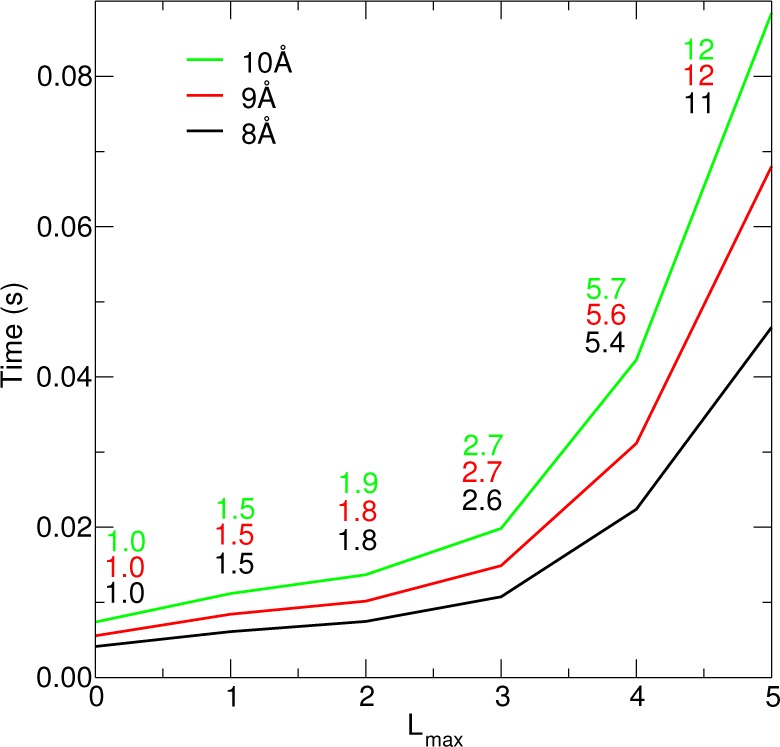
Wall clock time required to evaluate the real-space corrections (eq 29) for a box of 1024 waters using different real-space cutoffs. Lmax indexes the ad hoc 3-site water model being used. The inset values are timing ratios T(Lmax)/T(0), that is, the slow-down relative to the charge-only model.
Figure 6.
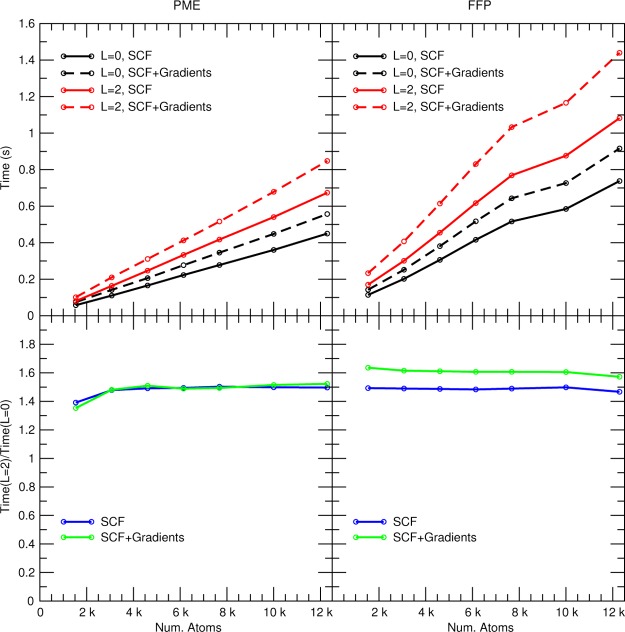
SCF and SCF + gradient timings using the mDC quantum force field for a series of water boxes. “L = 0” indicates that only atomic charges were used to compute electrostatics, whereas “L = 2” indicates that up to quadrupoles were used on the heavy atoms.
2.8. Implementation within the mDC Quantum Force Field
The analyses in Figures 5, 6, and 7, and the data shown in Table 1, were produced from condensed-phase calculations using the mDC linear scaling quantum force field.31 In brief, the quantum mechanical treatment of the entire system is replaced by a series of quantum calculations for each molecule. Although the molecular orbitals of each fragment are not directly coupled, the subsystems remain coupled through the interactions of their electron densities and empirical potentials. Specifically, the mDC method performs DFTB3/3OB semiempirical calculations72 of each molecule while subjecting them to an effective chemical potential arising from the intermolecular interactions. This idea is conceptually similar to “density functional embedding theory”;73 however, mDC replaces the rigorous evaluation of the embedding potential with computational tractable empirical approximations that are tuned for high accuracy. The standard DFTB3 semiempirical model evaluates the electrostatic interactions from Mulliken charges that are updated until self-consistency is reached. In the mDC formalism described below, the standard DFTB3 treatment continues to be used for those atoms within a common fragment; however, we concoct an auxiliary set of atomic multipoles from the density matrix to improve the intermolecular interactions. The multipolar potentials arising from those interactions enter the fragment Fock matrices as an effective external chemical potential, and the multipoles are updated at each step of the SCF procedure. Let EA be the DFTB3 energy for molecule A consisting of atoms located at RA; then, the mDC energy is
| 79 |
where NA is the number of electrons in fragment A, qa,lμ is an atomic multipole moment determined from the DFTB3 density matrix, and pa,lμ = ∂Einter/∂qa,lμ is the multipolar potential describing the effective external potential experienced by atom a. With this convention, the σ-spin Fock matrix used to construct the orbitals of molecule A is given as
| 80 |
As explained in ref (31), the atomic charges are computed from a biased Mulliken partition of the density matrix, and the higher-order multipole moments (up to quadrupoles for heavy elements) are computed from the single-center AO–product components of the density matrix. The intermolecular interaction energy Einter consists of Lennard-Jones potentials and the electrostatic interaction of the atomic multipoles. The electrostatic energy and multipolar potentials are evaluated using either the Ewald, PME, or FFP methods described in the previous sections. Because the multipole moments are dependent on the density matrix and the Fock matrix is dependent on the interactions with the other molecules, the mDC energy must be optimized until a mutual convergence is met for all molecules.
Figure 5.
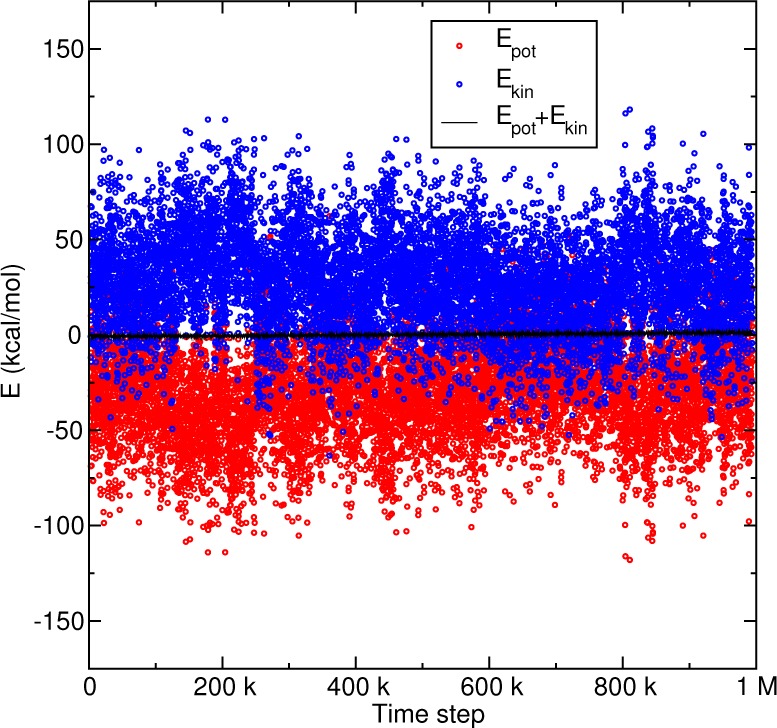
Conservation of the mDC total energy for 1 million steps in a NVE simulation of N,N-dimethylglycine, using the multipolar PME method with 6th order B-splines.
Figure 7.
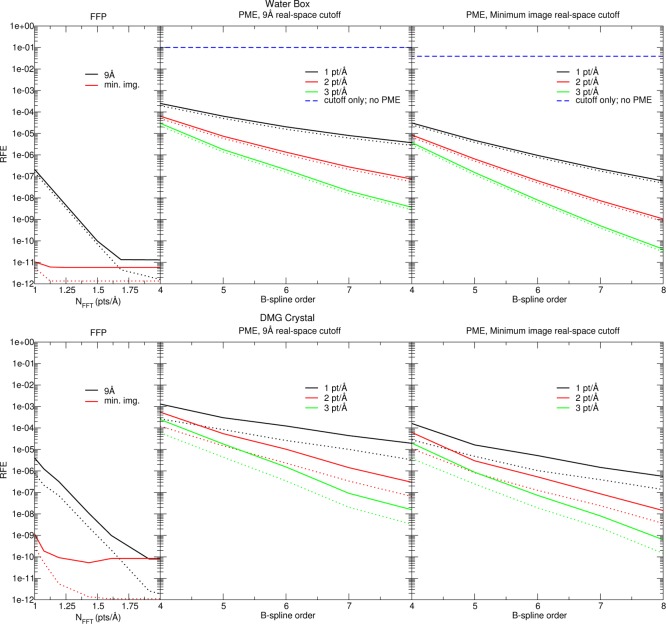
RFEs observed with the mDC linear-scaling quantum force field using various methods of computing the electrostatic interactions. The top portion of the figure shows a box of 1024 waters, whereas the bottom of the figure shows a supercell of N,N-dimethylglycine containing 4608 atoms. Errors are reported relative to FFP evaluated with 3 points/Å and a minimum image (“min img.”) short-range correction. The label “9 Å” indicates the range used for the short-range real-space corrections and, for FFP, the evaluation of the model Gaussian density at the FFT grid points. Dotted lines indicate the ability of the electrostatics protocol to reproduce the electrostatic component of the force, using the atomic multipoles obtained from the reference FFP calculation. The dashed lines are mDC RFEs, using cutoff-based electrostatics without any Ewald treatment.
Table 1. Effect of Electrostatic Cutoff on the Condensed-Phase Properties of Water at 298 K.
Figure 5 illustrates the quality of the mDC forces by demonstrating conservation of the total energy in a NVE simulation of an N,N-dimethylglycine (DMG) crystal at 225 K. The crystal consists of 288 DMG residues (4608 atoms) constructed from supercell replication of the experimentally determined X-ray structure74 and was simulated at the experimental density with a locally modified development version of PMEMD75 that incorporates the mDC method. The simulation was performed using a 0.5 fs time step for 1 million steps, and the electrostatics were computed with sixth-order B-spline PME, a 9 Å real-space cutoff, and a 1 pt/Å FFT grid density.
Figure 6 demonstrates linear scaling of the mDC method for a series of water boxes. In addition, timings were recorded for an ad hoc mDC model that limits the intermolecular interactions to monopoles for the sole purpose of determining the relative cost of incorporating atomic quadrupoles. The PME calculations were performed with sixth-order B-splines, a real-space cutoff of 9 Å, and an FFT grid density of 1 point/Å. The FFP calculations were performed with an FFT grid density of 1 point/Å and a cutoff of 9 Å in both the real- and reciprocal-space calculations, that is, the evaluation of the model Gaussian density at the FFT grid points.
Unlike the ad hoc water models used in Figure 4, mDC self-consistently models each molecule’s polarization in response to its environment (the other molecules). Because the polarization is induced from the environment’s electrostatic potential, the electrostatic protocol indirectly introduces atomic force errors by altering the electronic polarization. Within the mDC method, the change in polarization is produced from the difference in the multipolar potential contributions to the Fock matrix. Figure 7 decomposes the mDC force errors to quantify the extent to which the protocols indirectly effect the forces through their difference in polarizations. First, a mDC calculation is performed using a reference electrostatic protocol to produce a SCF converged energy (EmDC,ref) and charge density (qref). The dotted lines in Figure 7 are the RFEs computed from the vectors of intermolecular electrostatic forces evaluated with qref
| 81 |
| 82 |
where Eelec,model and Eelec,ref are the model and reference intermolecular electrostatic energies, respectively. A second mDC calculation is then performed using a model electrostatic protocol throughout the SCF procedure to produce a converged energy EmDC,model and charge density qmodel. The solid lines in Figure 7 are the RFEs computed from
| 83 |
| 84 |
which are evaluated with different electrostatic protocols and charge densities. The dashed lines in Figure 7 are computed from eqs 83 and 84, where EmDC,model is evaluated using a molecule-based cutoff electrostatic protocol; that is, no treatment for periodicity was applied beyond employing the minimum image convention within the cutoff radius. The electrostatic interactions between the waters were smoothly switched off from 8 Å to 9 Å, based on the O–O separation. All reference calculations were performed with FFP using a 3 point/Å grid density and a full minimum image treatment of the short-range corrections and reciprocal-space evaluation.
The PME and electrostatic cutoff methods are compared in Table 1, which examines how these methods effect the density and heat of vaporization of liquid water at 298 K. These properties were computed from 8-ns simulations of 512 waters in the NPT ensemble using the Monte Carlo barostat,75 and the Andersen thermostat,76 as implemented in PMEMD. A time step of 1 fs was used in conjunction with SHAKE77,78 to constrain the internal structure of the waters to the isolated DFTB3 geometry. The parameters of the mDC water model used to generate these properties are described in Part 2 of this series.51
3. Results and Discussion
3.1. Comparison to Brute Force Replication
Figure 1 establishes the correctness of the Ewald formulas for various multipole orders by comparing its energy to brute force evaluation of eq 1. Analogous plots for FFP and PME with suitably dense FFT grids and B-spline order are indistinguishable from the Ewald results shown in Figure 1. The errors in the energy flatten to a constant in the range of 10–13–10–14, because the large number of calculations involved in the brute force evaluation suffer from a loss of numerical precision. As the multipole order is increased, the energy converges more quickly, because the Coulomb interactions decay by r–la–lb–1. When L ≥ 4, the range of the interactions become so small that the energy is well-approximated by the minimum-image interactions.
3.2. Errors and Timings as a Function of Multipole Order
Before comparing the Ewald, PME, and FFP RFEs, it is useful to briefly discuss the relative magnitude of the forces associated with increasing the multipole order. As shown in Figure 2, the charge–charge interactions represent 40%–50% of the force when higher-order multipoles are used in the ad hoc water model. Furthermore, higher-order multipoles progressively contribute less to the force, since their interactions become shorter-ranged. All interactions involving the octupoles within the Lmax = 3 water model, for example, contribute <5% to the force, whereas all interactions involving L = 5 contribute <0.5%.
The wall-clock time required to evaluate the real- and reciprocal-space contributions to the multipolar potentials, as a function of multipole expansion order, are displayed in Figures 3 and 4, respectively. The real-space corrections evaluated from eqs 29 and 30 and the algorithm in ref (56) are particularly efficient for Lmax ≤ 3. For higher-order expansions, techniques based on rotations into an internal-coordinate system can be used to further improve performance;52,79 however, considering the short-range and relative insignificance of these interactions, it can be verily questioned if practical models for condensed-phase simulations will consider their additional cost worthwhile. Including quadrupoles on the oxygen causes the real-space evaluation timings to slow down by a factor of 1.8, relative to a charge-only model. Comparison of the reciprocal-space timings in Figure 4 suggests that, for this system of 1024 waters, FFP and Ewald are ∼2 and ∼100 times slower than PME, respectively, for comparable error levels. Furthermore, the evaluation of the real-space corrections at Lmax = 2 with a cutoff of 9 Å are approximately twice as slow as the sixth-order B-spline PME reciprocal-space evaluation times.
The optimized Gaussian exponents shown in Figure 4 are far more sensitive to the choice of real-space cutoff than they are to multipole order. As the real-space cutoff is increased, the Gaussian exponent decreases to become better resolved in the plane wave basis, and this consequently decreases the errors of the reciprocal-space forces. Similarly, increasing the PME B-spline order affords the opportunity to increase the Gaussian exponent to reduce the errors in the real-space correction without sacrificing accuracy in the reciprocal-space potential.
3.3. Comparisons within a Linear-Scaling Quantum Force Field Framework
Much of this manuscript uses the word “error” to describe a difference between an accurate electrostatics protocol and a more approximate treatment. However, this phrasing should not be misconstrued to incorrectly suggest that the PME gradients are inconsistent with the PME energy, for example. To emphasize this, Figure 5 demonstrates conservation of total energy in a NVE simulation of DMG for 1 million time steps evaluated with the mDC quantum force field, whose electrostatics are computed with PME. If there were an inconsistency between the energy and forces, then we would observe a significant drift in the energy as time is propagated; however, we do not observe a drift.
The mDC method is linear scaling when using either PME or FFP, as illustrated in Figure 6. When evaluated with PME, a box of 4096 waters can be SCF converged within <0.7 s. Furthermore, our timings indicate that the use of quadrupoles slows the mDC calculation by a factor of 1.5, relative to a charge-only model. This is slightly less than the ratio observed in Figure 3, because the mDC and charge-only mDC evaluations share common operations that are independent of the multipole order used in their intermolecular electrostatics (for example, their Fock matrix diagonalizations). The number of SCF cycles required to reach convergence is not particularly sensitive to the size of the system, which can be inferred from the linear-scaling shown in Figure 6. The SCF convergence rate is largely determined by the quality of the initial guess orbitals. In practice, the difference between MD steps is so small that convergence can typically be reached within 4–6 cycles.
Ewald, PME, and FFP are approximate, but their accuracy can be systematically improved by adjusting the number of plane waves, the Gaussian exponent, and the real-space correction cutoff. In the analysis of Figure 4, we examine how these parameters alter the electrostatic energy protocol by quantifying their effect on atomic forces (for a fixed charge density), −∂E/∂R|q, while ignoring their effect on electrostatic potentials ∂E/∂q|R. However, the parameters do effect the electrostatic potentials. Furthermore, the electrostatic potentials enter the Fock matrix via eq 80. Therefore, the parameters indirectly effect the charge density through the propagation of electrostatic potential “errors” within the SCF, which cause its convergence to a different density matrix. In other words, not only will ab initio methods (or any polarizable model) suffer from the “primary error” associated with the partial derivative −∂E/∂R|q, they also incur a “secondary error” when the model and reference forces are evaluated about different charge densities. The dotted lines in Figure 7 are the primary electrostatic errors; that is, they are the RFEs associated with the electrostatic forces evaluated from the atomic multipoles generated from the reference calculation. The solid lines in Figure 7 contain both the primary and secondary errors produced when the reference and approximate electrostatic protocols are used throughout the SCF procedures to yield two slightly different densities.
The reader may first notice that the primary FFP errors decrease and converge, with respect to FFT grid density quickly; however, the secondary errors trail off at 10–11 to 10–10. This limit is ultimately caused by our SCF numerical convergence criteria. The errors in Figure 7 were generated with a 10–12 tolerance on the maximum value appearing in the “error matrix”, that is, the commutator between the Fock matrix and the density matrix.
As expected, one observes a decrease in error as the PME B-spline order is increased, the FFT grid density is increased, and as the real-space cutoff is increased. The mDC RFEs observed in water and DMG parallel the primary errors; however, the DMG secondary errors are significantly larger than those observed in water. The reason for this is because a DMG molecule contains 16 atoms, whereas water contains 3. By having more AOs, the DMG molecules are more likely to converge to a slightly different density matrix.
Before PME was popularized in MD simulations,37,38 electrostatic cutoffs were often used, and many of the original water models were thus parametrized using a cutoff protocol. It was later found that application of those water models with PME caused significant changes in the thermodynamic properties of liquid water,80−82 and it has been suggested that new water models not be parametrized using cutoffs,81 because their application within simulations of biomolecules often necessitates the use of an Ewald treatment.83,84 Nonetheless, some recently developed water models have continued to be parametrized using cutoffs.85 Therefore, we are obliged to investigate by how much this may effect condensed-phase properties. First, in Figure 7, we note that a cutoff of 9 Å produces an RFE value of 0.1, in comparison to the RFE value observed with a sixth-order B-spline PME with a grid spacing of 1 point/Å FFT (2 × 10–5). Furthermore, even if all N2 minimum image interactions were computed without PME, the RFE is still 0.04. Finally, we performed MD simulations using a parametrized mDC water model to obtain an equilibrated density and heat of vaporization, as shown in Table 1, and we reperformed the simulations using switched-cutoff electrostatics to make comparison. In agreement with previous works,80,81 we observe that cut-off electrostatics cause the density of water to increase, and because the interactions in this range are attractive overall, this also causes the heat of vaporization to increase.
4. Conclusion
This work presented extensions of the Ewald, Particle Mesh Ewald (PME), and Fast Fourier–Poisson (FFP) methodologies to systems composed of point multipole expansions to arbitrary order by making use of the spherical tensor gradient operator. The timings and errors inherent to these methods were compared using ad hoc water models and with a parametrized water based on the modified divide-and-conquer (mDC) linear-scaling quantum force field. These comparisons lead us to conclude that (i) the FFP method is approximately twice as slow as the PME method at comparable error levels; (ii) the inclusion of quadrupoles in the linear-scaling force field slow the calculations by 1.5, relative to a charge-only model; and (iii) with the exception of the Ewald method, the real-space corrections are more expensive than the reciprocal-space calculations for typical cutoff values. Furthermore, our results suggest that the evaluation of multipolar electrostatics involving orders greater than 3 could likely be computed to an acceptable error using an electrostatic cutoff, because of their overall short-range and relative insignificance, in comparison to lower-order interactions.
The relative force errors exhibited within mDC were decomposed into primary and secondary errors, where the primary errors directly result from the approximations within the PME or FFP algorithms for a given density, and the secondary errors are the propagation of the model’s electrostatic potential within the self-consistent field (SCF) procedure, resulting in a different converged density matrix. It is found that the force errors closely follow the primary errors, and the magnitude of the secondary errors is related to the number of atomic orbitals (AOs). Nevertheless, the presence of these “errors” does not imply that the mDC forces are inconsistent with its energy, which was demonstrated with an NVE simulation that was devoid of an energy drift. Instead, these differences merely reflect how similar an electrostatic protocol is to another reference protocol.
Finally, the importance of using an Ewald treatment in simulations, as opposed to using electrostatic cutoffs, was emphasized by comparing the density and heat of vaporization of water. The electrostatic cut-off method was found to artificially increase the density and heat of vaporization of water.
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM62248). Computational resources from the Minnesota Supercomputing Institute for Advanced Computational Research (MSI) were utilized in this work. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (Grant No. OCI-1053575).
The authors declare no competing financial interest.
This article was published ASAP on January 14, 2015. A sentence in section 2.2 has been modified. The correct version was published on January 15, 2015.
Funding Statement
National Institutes of Health, United States
References
- York D. M.; Darden T.; Pedersen L. G. J. Chem. Phys. 1993, 99, 8345–8348. [Google Scholar]
- York D. M.; Yang W.; Lee H.; Darden T.; Pedersen L. G. J. Am. Chem. Soc. 1995, 117, 5001–5002. [Google Scholar]
- Cheatham T. E. III; Young M. A. Biopolymers 2000, 56, 232–256. [DOI] [PubMed] [Google Scholar]
- Cisneros G. A.; Karttunen M.; Ren P.; Sagui C. Chem. Rev. 2014, 114, 779–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisneros G. A.; Babin V.; Sagui C. In Biomolecular Simulations: Methods and Protocols; Monticelli L., Salonen E., Eds.; Methods in Molecular Biology, Vol. 924; Springer Science + Business Media: New York, 2013; pp 243–270. [DOI] [PubMed] [Google Scholar]
- Cardamone S.; Hughes T. J.; Popelier P. L. A. Phys. Chem. Chem. Phys. 2014, 16, 10367–10387. [DOI] [PubMed] [Google Scholar]
- Ponder J. W.; Wu C.; Ren P.; Pande V. S.; Chodera J. D.; Schnieders M. J.; Haque I.; Mobley D. L.; Lambrecht D. S.; DiStasio R. A. Jr.; Head–Gordon M.; Clark G. N. I.; Johnson M. E.; Head-Gordon T. J. Phys. Chem. B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y.; Wu C.; Ponder J. W.; Ren P. J. Comput. Chem. 2011, 32, 967–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren P.; Ponder J. W. J. Phys. Chem. B 2004, 108, 13427–13437. [Google Scholar]
- Grossfield A.; Ren P.; Ponder J. W. J. Am. Chem. Soc. 2003, 125, 15671–15682. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. J. Chem. Theory Comput. 2013, 9, 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semrouni D.; Cramer C. J.; Gagliardi L. Theor. Chem. Acc. 2014, 134, 1590. [Google Scholar]
- Chaudret R.; Gresh N.; Narth C.; Lagardere L.; Darden T.; Cisneros G. A.; Piquemal J.-P. J. Phys. Chem. A 2014, 118, 7598–7612. [DOI] [PubMed] [Google Scholar]
- Duke R. E.; Starovoytov O. N.; Piquemal J.-P.; Cisneros G. A. J. Chem. Theory Comput. 2014, 10, 1361–1365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisneros G. A. J. Chem. Theory Comput. 2012, 8, 5072–5080. [DOI] [PubMed] [Google Scholar]
- Elking D. M.; Cisneros G. A.; Piquemal J.-P.; Darden T. A.; Pedersen L. G. J. Chem. Theory Comput. 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudret R.; Gresh N.; Narth C.; Lagardère L.; Darden T. A.; Cisneros G. A.; Piquemal J.-P. J. Phys. Chem. A 2014, 118, 7598–7612. [DOI] [PubMed] [Google Scholar]
- Mas E. M.; Bukowski R.; Szalewicz K.; Groenenboom G. C.; Wormer P. E. S.; van der Avoird A. J. Chem. Phys. 2000, 113, 6687–6701. [DOI] [PubMed] [Google Scholar]
- Medders G. R.; Babin V.; Paesani F. J. Chem. Theory Comput. 2014, 10, 2906–2910. [DOI] [PubMed] [Google Scholar]
- Piquemal J.; Chevreau H.; Gresh N. J. Chem. Theory Comput. 2007, 3, 824–837. [DOI] [PubMed] [Google Scholar]
- Gresh N.; Cisneros G. A.; Darden T. A.; Piquemal J.-P. J. Chem. Theory Comput. 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nam K.; Gao J.; York D. M. J. Chem. Theory Comput. 2005, 1, 2–13. [DOI] [PubMed] [Google Scholar]
- Gordon M. S.; Freitag M. A.; Bandyopadhyay P.; Jensen J. H.; Kairys V.; Stevens W. J. J. Phys. Chem. A 2001, 105, 293–307. [Google Scholar]
- Gao J.; Truhlar D. G.; Wang Y.; Mazack M. J. M.; Löffler P.; Provorse M. R.; Rehak P. Acc. Chem. Res. 2014, 47, 2837–2845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Sosa C. P.; Cembran A.; Truhlar D. G.; Gao J. J. Phys. Chem. B 2012, 116, 6781–6788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song L.; Han J.; lin Lin Y.; Xie W.; Gao J. J. Phys. Chem. A 2009, 113, 11656–11664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie W.; Orozco M.; Truhlar D. G.; Gao J. J. Chem. Theory Comput. 2009, 5, 459–467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie W.; Gao J. J. Chem. Theory. Comput. 2007, 3, 1890–1900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P.; Truhlar D. G.; Gao J. Phys. Chem. Chem. Phys. 2012, 14, 7821–7829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giese T. J.; Chen H.; Dissanayake T.; Giambaşsu G. M.; Heldenbrand H.; Huang M.; Kuechler E. R.; Lee T.-S.; Panteva M. T.; Radak B. K.; York D. M. J. Chem. Theory Comput. 2013, 9, 1417–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giese T. J.; Chen H.; Huang M.; York D. M. J. Chem. Theory Comput. 2014, 10, 1086–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giese T. J.; Huang M.; Chen H.; York D. M. Acc. Chem. Res. 2014, 47, 2812–2820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handley C. M.; Hawe G. I.; Kell D. B.; Popelier P. L. A. Phys. Chem. Chem. Phys. 2009, 11, 6365–6376. [DOI] [PubMed] [Google Scholar]
- Kramer C.; Gedeck P.; Meuwly M. J. Chem. Theory Comput. 2013, 9, 1499–1511. [DOI] [PubMed] [Google Scholar]
- Devereux M.; Raghunathan S.; Fedorov D. G.; Meuwly M. J. Chem. Theory Comput. 2014, 10, 4229–4241. [DOI] [PubMed] [Google Scholar]
- Ewald P. P. Ann. Phys. 1921, 64, 253–268. [Google Scholar]
- Darden T.; York D.; Pedersen L. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Hsing L.; Pedersen L. G. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar]
- Cerutti D. S.; Duke R. E.; Darden T. A.; Lybrand T. P. J. Chem. Theory Comput. 2009, 5, 2322–2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerutti D. S.; Case D. A. J. Chem. Theory Comput. 2010, 6, 443–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- York D. M.; Yang W. J. Chem. Phys. 1994, 101, 3298–3300. [Google Scholar]
- Toukmaji A.; Sagui C.; Board J.; Darden T. J. Chem. Phys. 2000, 113, 10913–10927. [Google Scholar]
- Nymand T. M.; Linse P. J. Chem. Phys. 2000, 112, 6152–6160. [Google Scholar]
- Sagui C.; Pedersen L. G.; Darden T. A. J. Chem. Phys. 2004, 120, 73–87. [DOI] [PubMed] [Google Scholar]
- Schnieders M. J.; Fenn T. D.; Pande V. S.; Brunger A. T. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2009, D65, 952–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisneros G. A.; Piquemal J.; Darden T. A. J. Chem. Phys. 2006, 125, 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darden T. A.Extensions of the Ewald method for Coulomb Interactions in crystals. In International Tables for Crystallography, Reciprocal Space, 3rd Edition; Springer: Dordrecht, The Netherlands, 2008; Vol. B, pp 458–483. [Google Scholar]
- Aguado A.; Madden P. A. J. Chem. Phys. 2003, 119, 7471–7483. [Google Scholar]
- Laino T.; Hutter J. J. Chem. Phys. 2008, 129, 074102. [DOI] [PubMed] [Google Scholar]
- Zielinski F.; Popelier P. L. A. J. Mol. Model. 2014, 20, 2256. [DOI] [PubMed] [Google Scholar]
- Giese T. J.; Panteva M. T.; Chen H.; York D. M.. J. Chem. Theory Comput. DOI: 10.1021/ct500799g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmonett A. C.; Pickard F. C. IV; Schaefer H. F. III; Brooks B. R. J. Chem. Phys. 2014, 140, 184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Equation 1 can be equivalently expressed with n appearing in the denominator instead of the numerator by transforming the integration variable with the substitution u = r′ + n, so that r′ = u – n.
- Giese T. J.; York D. M. J. Comput. Chem. 2008, 29, 1895–1904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giese T. J.; York D. M. J. Chem. Phys. 2011, 134, 194103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giese T. J.; York D. M. J. Chem. Phys. 2008, 128, 064104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson M. A.; Sałek P.; Macak P.; Helgaker T. J. Chem. Phys. 2004, 121, 2915–2931. [DOI] [PubMed] [Google Scholar]
- Pérez–Jordá J. M.; Yang W. J. Chem. Phys. 1996, 104, 8003–8006. [Google Scholar]
- Pérez-Jordá J. M.; Yang W. J. Chem. Phys. 1997, 107, 1218–1226. [Google Scholar]
- Hobson E. W. Proc. London Math. Soc. 1892, 24, 55–67. [Google Scholar]
- Giese T. J.; York D. M. In Many-Body Effects and Electrostatics in Biomolecules; Cui Q., Meuwly M., Ren P., Eds.; Pan Stanford Publishing: Singapore, in press. [Google Scholar]
- Weniger E. J. Collect. Czech. Chem. Commun. 2005, 70, 1225–1271. [Google Scholar]
- Helgaker T.; Jørgensen P.; Olsen J.. Molecular Electronic-Structure Theory; John Wiley & Sons: Hoboken, NJ, 2000. [Google Scholar]
- Schoenberg I. J. J. Approx. Theory 1983, 39, 324–337. [Google Scholar]
- Schoenberg I. J.Euler’s contribution to cardinal spline interpolation: The exponential Euler splines. In Leonhard Euler 1707–1783; Birkhäuser Verlag: Basel/Boston/Stuttgart, 1983; pp 199–214. [Google Scholar]
- Schoenberg I. J.Cardinal interpolation and spline functions IV. The exponential Euler splines. In Linear Operators and Approximation; Birkhäuser Verlag: Basel, Switzerland, Boston, MA, Stuttgart, Germany, 1972; pp 382–404. [Google Scholar]
- Ishida K. J. Chem. Phys. 1998, 109, 881–890. [Google Scholar]
- Bogusz S.; Cheatham T. E. III; Brooks B. R. J. Chem. Phys. 1998, 108, 7070–7084. [Google Scholar]
- Smith E. R. Proc. R. Soc. London, Ser. A 1981, 375, 475–505. [Google Scholar]
- De Leeuw S. W.; Perram J. W.; Smith E. R. Proc. R. Soc. London, Ser. A 1983, 388, 177–193. [Google Scholar]
- Brooks B. R.; Brooks C. L. III; MacKerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaus M.; Goez A.; Elstner M. J. Chem. Theory Comput. 2013, 9, 338–354. [DOI] [PubMed] [Google Scholar]
- Libisch F.; Huang C.; Carter E. A. Acc. Chem. Res. 2014, 47, 2768–2775. [DOI] [PubMed] [Google Scholar]
- Kapustin E. A.; Minkov V. S.; Stare J.; Boldyreva E. V. Cryst. Growth Des. 2014, 14, 1851–1864. [Google Scholar]
- Case D. A.; Babin V.; Berryman J. T.; Betz R. M.; Cai Q.; Cerutti D. S.; Cheatham T. E. III; Darden T. A.; Duke R. E.; Gohlke H.; Goetz A. W.; Gusarov S.; Homeyer N.; Janowski P.; Kaus J.; Kolossváry I.; Kovalenko A.; Lee T. S.; LeGrand S.; Luchko T.; Luo R.; Madej B.; Merz K. M.; Paesani F.; Roe D. R.; Roitberg A.; Sagui C.; Salomon-Ferrer R.; Seabra G.; Simmerling C. L.; Smith W.; Swails J.; Walker R. C.; Wang J.; Wolf R. M.; Wu X.; Kollman P. A.. AMBER 14; University of California: San Francisco, CA, 2014. [Google Scholar]
- Andersen H. C. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar]
- Miyamoto S.; Kollman P. A. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
- Ryckaert J. P.; Ciccotti G.; Berendsen H. J. C. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
- Hättig C. Chem. Phys. Lett. 1997, 268, 521–530. [Google Scholar]
- Horn H. W.; Swope W. C.; Pitera J. W.; Madura J. D.; Dick T. J.; Hura G. L.; Head-Gordon T. J. Chem. Phys. 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- Rick S. W. J. Chem. Phys. 2004, 120, 6085–6093. [DOI] [PubMed] [Google Scholar]
- van der Spoel D.; van Maaren P. J. J. Chem. Theory Comput. 2006, 2, 1–11. [DOI] [PubMed] [Google Scholar]
- York D. M.; Wlodawer A.; Pedersen L. G.; Darden T. Proc. Natl. Acad. Sci. U.S.A. 1994, 91, 8715–8718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheatham T. E. III; Miller J. L.; Fox T.; Darden T. A.; Kollman P. A. J. Am. Chem. Soc. 1995, 117, 4193–4194. [Google Scholar]
- Han J.; Mazack M. J. M.; Zhang P.; Truhlar D. G.; Gao J. J. Chem. Phys. 2013, 139, 054503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kell G. S. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar]
- Wagner W.; Pruß A. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar]