Estimation of the Standardized Risk Difference and Ratio in a Competing Risks Framework: Application to Injection Drug Use and Progression to AIDS After Initiation of Antiretroviral Therapy

Abstract

There are few published examples of absolute risk estimated from epidemiologic data subject to censoring and competing risks with adjustment for multiple confounders. We present an example estimating the effect of injection drug use on 6-year risk of acquired immunodeficiency syndrome (AIDS) after initiation of combination antiretroviral therapy between 1998 and 2012 in an 8-site US cohort study with death before AIDS as a competing risk. We estimate the risk standardized to the total study sample by combining inverse probability weights with the cumulative incidence function; estimates of precision are obtained by bootstrap. In 7,182 patients (83% male, 33% African American, median age of 38 years), we observed 6-year standardized AIDS risks of 16.75% among 1,143 injection drug users and 12.08% among 6,039 nonusers, yielding a standardized risk difference of 4.68 (95% confidence interval: 1.27, 8.08) and a standardized risk ratio of 1.39 (95% confidence interval: 1.12, 1.72). Results may be sensitive to the assumptions of exposure-version irrelevance, no measurement bias, and no unmeasured confounding. These limitations suggest that results be replicated with refined measurements of injection drug use. Nevertheless, estimating the standardized risk difference and ratio is straightforward, and injection drug use appears to increase the risk of AIDS.

There have been repeated calls for epidemiologists to present estimates of risk based directly on the survival function (1–5). Risk differences and ratios based on the survival function are superior to contrasts based on the rate, hazard, or odds because the risk is a collapsible parameter (5, 6). For a collapsible parameter, in the absence of confounding, the crude and covariate-adjusted population values are the same; this is not the case for noncollapsible parameters. In addition, risk differences and ratios are more easily communicated to scientists and the lay community.

Epidemiologists are increasingly using regression models that properly account for competing risks (7). However, to date, there are relatively few published examples of “risk” estimated from epidemiologic data using the survival function with adjustment for multiple measured confounders (3). One obstacle to the presentation of such estimates is the lack of examples to familiarize epidemiologists with the methods needed to produce estimates that account for confounding by measured factors. Moreover, these methods are complicated when there are competing risks that preclude participants from incurring the event of interest (7, 8), and in this setting, even fewer examples are found (9). Here, among human immunodeficiency virus (HIV)–infected therapy initiators, we estimate the effect of injection drug use on the risk of acquired immunodeficiency syndrome (AIDS) with death before AIDS as a competing risk. Our goal is to illustrate the estimation of risk in the presence of multiple confounders and competing risks.

METHODS

Study sample

The National Institutes of Health–funded Centers for AIDS Research Network of Integrated Clinical Systems (CNICS) was initiated in September 2006 to develop a comprehensive and standardized clinical data repository from point-of-care electronic medical record systems to support population-based HIV research (10). The CNICS includes data on more than 25,000 HIV-positive adults engaged in clinical care from January 1, 1995, to the present at 8 centers for AIDS research (University of Alabama at Birmingham (Birmingham, Alabama); Case Western Reserve University (Cleveland, Ohio); Fenway Community Health Center of Harvard University (Boston, Massachusetts); Johns Hopkins University (Baltimore, Maryland); University of California, San Francisco (San Francisco, California); University of California, San Diego (San Diego, California); University of North Carolina (Chapel Hill, North Carolina); and University of Washington (Seattle, Washington)). The frequency of follow-up averages every 3 months; however, patients can be seen more or less often depending on provider scheduling recommendations. The CNICS is a dynamic cohort with approximately 1,400 new patients enrolling and 10% of existing patients leaving care each year (10). Institutional review boards at each site approved study procedures. Participants provided written informed consent or contributed administrative and clinical data with a waiver of written informed consent where approved by the local institutional review board.

We included the 7,936 CNICS participants who initiated therapy without an AIDS diagnosis between January 1, 1998, and December 31, 2012. Therapy initiation was defined as the date of initiation of a regimen consisting of 3 or more antiviral agents. We included participants with documented prior mono/dual antiretroviral therapy exposure. We excluded the 188 (2%) patients who were missing injection drug use classification, and the 566 (7%) patients who did not have a measured CD4 cell count (in cells/mm³) and viral load (in log₁₀ copies/mL) within 180 days before to 14 days after therapy initiation. Sex and race (Caucasian vs. other) were recorded for each participant at cohort entry. Age and calendar year were recorded at therapy initiation.

The exposure of interest was injection drug use. Reported history of injection drug use was elicited at cohort entry as a possible transmission factor. Such a reported history is an imperfect proxy for current injection drug use, to the extent that behaviors go unreported or change over time. Moreover, in this example, the confounding variables were determined at therapy initiation, which was a median of 92 days after injection drug use was assessed. We defer these points until the discussion.

The outcome of interest was first incident AIDS diagnosis after therapy initiation. Time at risk was measured in days from therapy initiation to the first date of AIDS diagnosis, death, dropout (>12 months without contact), 6 years, or December 31, 2012 (December 31, 2011, for the Johns Hopkins University site because of a lag in death updates).

Statistical methods

In the absence of the competing risk of death, the cumulative incidence of AIDS at time t is simply the complement of the survivor function of time until AIDS diagnosis, R(t) = 1 – S(t) = P(T_i ≤ t), where T_i is a continuous random variable denoting time from therapy initiation to AIDS for i = 1 to 7,182 patients, R(0) = 0, and R(∞) = 1 (11).

In the presence of the single competing risk of all-cause mortality before AIDS, the cumulative incidence of AIDS at time t is the joint probability of incurring either event by time t and that the event is AIDS, R_j(t) = P(T_i ≤ t, J_i = j), where J_i is a discrete random variable denoting AIDS (j = 1) or all-cause mortality before AIDS (j = 2). Here, again R₁(0) = 0, but now R₁(∞) = P(J_i = 1) ≤ 1, which is the eventual risk of AIDS (7).

Let A_i be a discrete random variable denoting exposure to injection drugs (a = 1) or not (a = 0) for patient i. Let $T_i^a$ be the potential (i.e., factual or counterfactual) time from therapy initiation to AIDS or death before AIDS for patient i, and $J_i^a$ be the analogous potential event-type indicator, under (possibly counterfactual) exposure A = a, where $J_i^a=1$ denotes AIDS, and $J_i^a=2$ denotes deaths before AIDS. Then the potential cumulative incidence of AIDS at time t is $R_1^a(t)=P(T_i^a\le t,J_i^a=1)$ (12). Although we are interested in the entire function over time t, we concentrate inference on AIDS incidence at times t = 2 years and 6 years from therapy initiation. Our estimands are then the AIDS risk difference $\text{RD}(t)=R_1^1(t)-R_1^0(t)$ and AIDS risk ratio $\text{RR}(t)=R_1^1(t)/R_1^0(t)$ at t = 2 and 6.

To accommodate censoring, let $T_i^{\ast }=min(T_i,C_i)$, where C_i is a continuous random variable denoting right censoring because of dropout or administrative end of follow-up, and let j = 0 when $T_i^{\ast }=C_i$. Below, we assume that administrative censoring is noninformative, and censoring because of dropout is noninformative given measured covariates.

We estimate $R_1^a(t)$ as follows:

$${\hat{R}}_1^a(t)=\sum _{t_k\le t}\{{\hat{S}}^{\hat{W}(t)}(t_{k-1})\}\left\{\frac{d_1^{\hat{W}(t)}(t_k)}{n_1^{\hat{W}(t)}(t_k)}\right\},$$

where t_k are the ordered event times, ${\hat{S}}^{\hat{W}(t)}(t)$ is the Nelson-Aalen estimator of the overall inverse probability (IP)–weighted survival function (i.e., ${\hat{S}}^{\hat{W}(t)}(t)=\exp \{-{\hat{H}}^{\hat{W}(t)}(t)\}$, where ${\hat{H}}^{\hat{W}(t)}(t)=\sum _{t_k\le t}{d}^{\hat{W}(t)}(t_k)/n^{\hat{W}(t)}(t_k)$), $d^{\hat{W}(t)}(t_k)$ is the IP-weighted number of events at ordered event time t_k (i.e., AIDS cases and deaths), and $n^{\hat{W}(t)}(t_k)$ is the IP-weighted number at risk at time t_k. One could alternatively use the Kaplan-Meier estimator of the survival function, which is asymptotically equivalent to the Nelson-Aalen estimator; however, the Nelson-Aalen estimator is reported to have better finite-sample properties (13, p. 94). Using the Kaplan-Meier estimator, ${\hat{R}}_1^a(t)+{\hat{R}}_2^a(t)+{\hat{S}}^{\hat{W}(t)}(t)=1$. This formula for $R_1^a(t)$ cumulatively sums the probability of surviving all events multiplied by the instantaneous cause-specific hazard of having the event of interest in the IP-weighted data. Thus, the cumulative incidence function, $R_1^a(t)$, is a partition of the cumulative incidence function for the composite outcome (e.g., R₁(t) + R₂(t) = 1 – S(t)). Next, we describe its calculation with additional detail.

First, we estimate the IP of exposure weights. Specifically, we fit a linear-logistic model P(A_i = 1|L_i) = expit(α₀ + α₁L_i), where expit = exp(·)/{1 + exp(·)}, and L is a vector of measured confounders. Specifically, L consisted of age (spline), CD4 cell count (spline), viral load (spline), indicators for male sex, black race, Hispanic ethnicity, prior mono/dual antiretroviral therapy, calendar year of therapy initiation, and study site. Splines were restricted quadratic with 4 knots placed at the 5th, 35th, 65th, and 95th percentiles of the confounder's distribution in the study sample (14). IP exposure weights were then constructed as ${\hat{W}}_i^1=\hat{P}(A_i=a)/\hat{P}(A_i=a|L_i)$, where the stabilizing factor $\hat{P}(A_i=a)$ is given by the marginal proportion at exposure level a in the study sample.

Second, we estimate the IP of dropout weights. Specifically, we partition the 6-year follow-up period into quintiles defined by the distribution of dropouts (i.e., 1.42, 1.92, 2.56, and 3.47 years from therapy initiation). Then we fit a pooled linear-logistic model P{D_i(q) = 0|L_i} = expit(β_0,q + β₁L_i), where D_i(q) is an indicator of dropout during interval q, and L is the same vector of measured covariates as defined above for confounding. IP dropout weights were then constructed as

$${\hat{W}}_i^2(t)=\prod _{q\le t}\hat{P}\{D_i(q)=0\}/\hat{P}\{D_i(q)=0|L_i\},$$

where the stabilizing factor $\hat{P}\{D_i(q)=0\}$ is given by the marginal proportion who had not dropped out by time q. Although we used the same vector of covariates for dropout as used for confounding, it is not necessary that the same vector be used for both.

The final IP of exposure and dropout weight was defined as ${\hat{W}}_i(t)={\hat{W}}_i^1{\hat{W}}_i^2(t)$. The mean overall IP weight was 1.00 (range, 0.27–13.09). The mean exposure IP weight was 1.00 (dropout IP weight, 1.00), (range, 0.29–13.09; dropout range, 0.73–1.83). Results were not meaningfully altered when overall IP weights were censored (sometimes referred to as truncated) to the interval 1/10, 10 (15).

Third, we estimate the overall Nelson-Aalen IP-weighted survival function, as well as the IP-weighted hazard for AIDS, and combine information as shown in ${\hat{R}}_1^a(t)$ above. Our estimator requires no tied event times within or between the AIDS events and the competing risk of death to allow a simple partition of event types, so we randomly jitter the observed times up to 1 day. When applied to unweighted data, this approach yields an estimate of the cumulative incidence function (16), which equals the function obtained from the SAS macro CUMINCID (17) or the R package CMPRSK (R Foundation for Statistical Computing, Vienna, Austria).

We obtain 95% confidence intervals as a measure of uncertainty due to sampling error using a nonparametric bootstrap. Specifically, we resampled 7,182 patients at random with replacement with equal probability 200 times and conducted the above procedure (including estimation of the IP weights). The standard deviation of the 200 bootstrap resamples is used as an estimate of the standard error. In the Appendix, we present a limited simulation, which provides experimental evidence in support of this approach under the null hypothesis.

For our estimator to consistently estimate RD(t) and RR(t), we make several assumptions; namely, we assume treatment-version irrelevance (18), no interference, positivity (19), conditional exchangeability (20), no measurement bias (21), and correct specification of the exposure and dropout models. We address each of these assumptions in detail in the discussion. SAS, version 9.3, software (SAS Institute, Inc., Cary, North Carolina) was used for all analyses.

RESULTS

Eighty-three percent of the 7,182 patients were male, 33% were African American, 14% were Hispanic, and 11% reported prior mono/dual antiretroviral therapy. At therapy initiation (i.e., study entry), patients were a median of 38 years of age with a median CD4 count of 287 cells/mm³ and a median viral load of 4.49 log₁₀ copies/mL (Table 1). The 1,143 of 7,182 patients who reported injection drug use were 3 years older when they initiated therapy 1 calendar year earlier than non–injection drug users, with a lower CD4 cell count and higher viral load (Table 1).

Table 1.

Characteristics of 7,182 HIV-Positive Adults Who Initiated Antiretroviral Therapy Between 1998 and 2012, CNICS

Characteristic	Injection Drug Use						Overall (n = 7,182)
	Yes (n = 1,143)			No (n = 6,039)
	Median (IQR)	No.	%	Median (IQR)	No.	%	Median (IQR)	No.	%
Age, years	40 (34–46)			37 (30–44)			38 (31–45)
Year of ART initiation	2006 (2002–2009)			2007 (2003–2009)			2006 (2003–2009)
CD4 count, cells/mm3	260 (153–396)			292 (170–434)			287 (168–428)
Viral load, log10 copies/mL	4.51 (3.75–5.06)			4.48 (3.49–5.04)			4.49 (3.53–5.04)
Prior mono/dual ART		138	12		671	11		809	11
Male		925	81		5,035	83		5,969	83
African American		378	33		2,000	33		2,378	33
Hispanic		111	10		864	14		975	14

Abbreviations: ART, antiretroviral therapy; CNICS, Centers for AIDS Research Network of Integrated Clinical Systems; HIV, human immunodeficiency virus; IQR, interquartile range.

During the 6-year study follow-up, 22,927 person-years accrued, during which 660 incident AIDS cases were observed, yielding a rate of 2.88 AIDS cases per 100 person-years (Table 2). These rates were 4.39 AIDS cases per 100 person-years among the 1,143 who reported injection drug use and 2.60 AIDS cases per 100 person-years among the 6,039 who did not report injection drug use. The rate of death before AIDS was 0.99 deaths per 100 person-years. This rate was 1.94 deaths per 100 person-years among the 1,143 patients who reported injection drug use and 0.82 deaths per 100 person-years among the 6,039 patients who did not report injection drug use. Thirty-six percent of the 7,182 patients were censored alive and AIDS free before 6 years of follow-up, or on December 31, 2012 (December 31, 2011, for the Johns Hopkins University site).

Table 2.

Disposition of 7,182 HIV-Positive Adults Who Initiated Antiretroviral Therapy Between 1998 and 2012, Followed for Up to 6 Years, CNICS

Characteristic	Injection Drug Use				Overall(n = 7,182)
	Yes (n = 1,143)		No (n = 6,039)
	No.	%	No.	%	No.	%
Person-years at risk	3,556		19,371		22,927
Incident AIDS	156	14	504	8	660	9
Death (from all causes)	69	6	158	3	227	3
Dropout	416	36	2,202	36	2,618	36

Abbreviations: AIDS, acquired immunodeficiency syndrome; CNICS, Centers for AIDS Research Network of Integrated Clinical Systems; HIV, human immunodeficiency virus.

The 6-year crude AIDS risks were 19.47% among those who reported injection drug use and 11.60% among those who did not, yielding a risk difference of 7.87 (95% confidence interval (CI): 4.73, 11.0) and a risk ratio of 1.68 (95% CI: 1.41, 2.00; Table 3). Figure 1 provides a visual display of both the crude risk of AIDS and death by time from therapy initiation.

Table 3.

Crude and Standardized 2-Year and 6-Year Risks of AIDS by Injection Drug Use in 7,182 HIV-Positive Adults Who Initiated Antiretroviral Therapy Between 1998 and 2012, CNICS

Risk Type	AIDS Incidence, %		Risk Difference	95% CIa	Risk Ratio	95% CIa
	Injection Drug Use	No Injection Drug Use
Crude
2-Year	10.22	6.61	3.61	1.75, 5.47	1.55	1.27, 1.89
6-Year	19.47	11.60	7.87	4.73, 11.0	1.68	1.41, 2.00
Standardizedb
2-Year	8.13	6.82	1.31	−0.46, 3.08	1.19	0.95, 1.50
6-Year	16.75	12.08	4.68	1.27, 8.08	1.39	1.12, 1.72

Abbreviations: AIDS, acquired immunodeficiency syndrome; CI, confidence interval; CNICS, Centers for AIDS Research Network of Integrated Clinical Systems; HIV, human immunodeficiency virus.

^a Standard error based on standard deviation of 200 nonparametric bootstrap resamples.

^b Standardized for age (spline), CD4 cell count (spline), indicators for male sex, black race, Hispanic ethnicity, prior mono/dual antiretroviral therapy, calendar year of antiretroviral therapy initiation, and study site.

Figure 1.

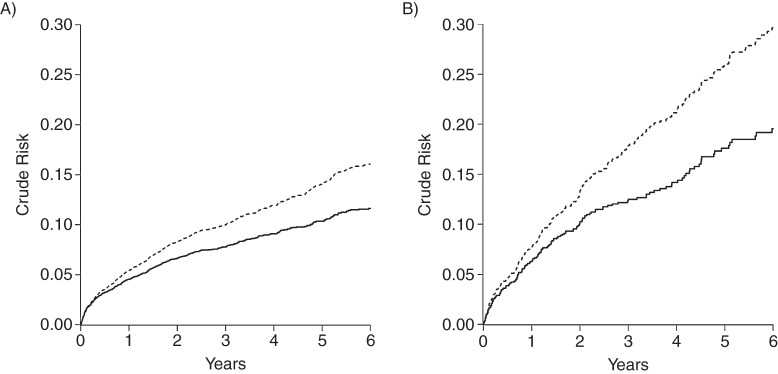
Crude risk of acquired immune deficiency syndrome (AIDS) (solid line) and death (dashed line, stacked) among 7,182 human immunodeficiency virus–positive adults from the Centers for AIDS Research Network of Integrated Clinical Systems who initiated antiretroviral therapy between 1998 and 2012. A) For non–injection drug users, B) for injection drug users.

After accounting for confounding and dropout by characteristics measured at therapy initiation and the competing risk of death, we found that the 6-year standardized AIDS risks were 16.75% for injection drug users and 12.08% for nonusers, yielding a 6-year standardized risk difference of 4.68 (95% CI: 1.27, 8.08) and a 6-year standardized risk ratio of 1.39 (95% CI: 1.12, 1.72). The standardized risk ratio was 17% (i.e., 1–1.39 / 1.68) smaller than the crude risk ratio. As expected, the 6-year standardized risk ratio was less precise (ratio of upper to lower CI = 1.54) compared with the 6-year crude risk ratio (ratio of upper to lower CI = 1.42) because of the accounting for possible confounding and selection bias. Figure 2 provides a visual display of both the standardized risk of AIDS and death by time from therapy initiation. Figure 3 provides a nuanced view of the standardized risk difference and risk ratio as they evolve over time from therapy initiation.

Figure 2.

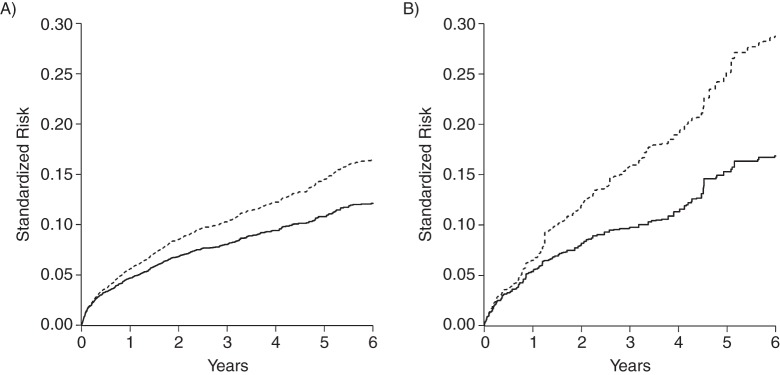
Standardized risk of acquired immune deficiency syndrome (AIDS) (solid line) and death (dashed line, stacked) among 7,182 human immunodeficiency virus–positive adults from the Centers for AIDS Research Network of Integrated Clinical Systems who initiated antiretroviral therapy between 1998 and 2012. A) For non–injection drug users, B) for injection drug user.

Figure 3.

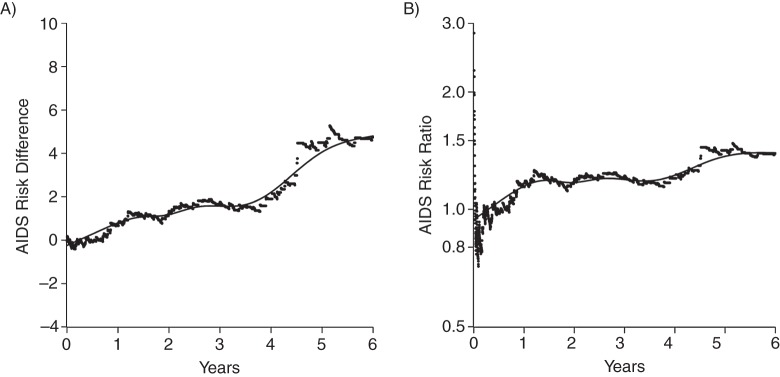
Standardized acquired immune deficiency syndrome (AIDS) A) risk difference and B) risk ratio for injection drug use among 7,182 human immunodeficiency virus–positive adults from the Centers for AIDS Research Network of Integrated Clinical Systems who initiated antiretroviral therapy between 1998 and 2012. Dots placed at times of incident AIDS cases with overlaid smoothing spline.

DISCUSSION

After accounting for measured covariates and the competing risk of death, we observed a 6-year risk of AIDS among injection drug users that was 39% larger than that of nonusers; the 6-year risk for nonusers was 12.08%. This modestly higher risk is consistent with those reported in existing literature. For instance, using a subset of the data used here, Moore et al. (22) reported on 2,141 patients followed from starting therapy between 1995 and 2002, of whom, 827 had a history of injection drug use. Summarizing their results over calendar years, they observed a rate ratio for AIDS-defining illness of 1.26 (95% CI: 1.11, 1.43) compared to those without a history of injection drug use and adjusted for age, sex, race, prior AIDS-defining illness, and baseline CD4 count and viral load. More recently, Qian et al. (23) reported on 1,712 patients followed for up to 7 years from starting therapy, of whom, 262 had a history of injection drug use. They reported a hazard ratio for AIDS or death of 1.83 (95% CI: 1.09, 3.06) compared to those without a history of injection drug use and adjusted for age, sex, race, prior antiretroviral therapy, and baseline CD4 count and viral load. However, prior work did not report absolute risks and accounted for the competing risk of death by censoring (22) or using a composite endpoint (23).

Our findings are subject to several limitations. First, to obtain results, we assume our exposures map to well-defined interventions. This assumption is implied by the simplified consistency statement, $T_i=T_i^a$ for A_i = a. A general consistency statement is $T_i=T_i^{a,k(a)}$ for A_i = a, K_i(a) = k(a), where K(a) are the possibly a-dependent K versions of exposure. In our setting, no exposure to injection drugs (a = 0) is well defined because there is arguably only 1 version. However, exposure to injection drugs (a = 1) has many possible versions and is therefore not very well defined. For example, those exposed could be infrequently injecting cocaine or frequently injecting heroine. With multiple versions of exposure, to apply inferences directly to other populations (where the mixture of exposure versions may differ), we must assume exposure/treatment-version irrelevance, $T_i^{a,k(a)}=T_i^{a,k^{\mathrm{\prime }}(a)}$ for all i, a, and k(a) ≠ k′(a). Informally, we must assume that the potential outcomes do not depend on the version of the exposure. For additional details on treatment-version irrelevance, please see the article by Vanderweele (24). We do not believe exposure-version irrelevance holds in the present illustrative setting. As is commonly the case, we are limited by the coarseness of the information collected (e.g., we do not have information on injection frequency or type). Therefore, because there may be a modest effect of injection drug use on AIDS incidence, future work is needed to explore the exposure response with more refined measurements of injection drug use. A related point regarding exposure measurement error is discussed below.

Second, we assumed positivity. In our setting, this assumption states that we must have both exposed and unexposed, P(A = a|L = l) > 0, as well as nondropouts, P{D(q) = 0|L = l} > 0, at every level of the confounders, P(L = l) ≠ 0. These assumptions were relaxed somewhat by smoothing over the data through the use of a linear-logistic model for P(A = a|L = l) and a linear-pooled logistic model for P{D(q) = 0|L = l}, with continuous components of L specified using splines (rather than an indicator for each level), as well as by omission of several terms for the products between confounders. It did not appear that relaxing of the positivity assumption in this way reintroduced confounding or selection bias, and positivity appeared to hold based on exploration of the data including additional product terms and using finer control for continuous covariates and time, as previously illustrated (15).

Third, we assumed conditional exchangeability. Conditional exchangeability is equivalent to the assumption of no unmeasured confounders and no unmeasured selection bias. An Achilles heel of observational science is the ever-present threat of unmeasured confounding. It remains possible that further adjustment for unmeasured factors would further reduce (or enhance) the effect reported. Although dropout was common at 36%, concern over selection bias due to this dropout rate is limited by the fact that we observed the same proportion of dropout among injection drug users and nonusers. We coarsened the time scale to improve estimation of the dropout weights. In principle, such coarsening may reintroduce some selection bias. In practice, our results were insensitive to inclusion of the dropout weights.

Fourth, we assume that injection drug use, AIDS incidence, death, and confounders are measured with negligible error. This assumption likely holds for all-cause mortality, AIDS incidence, and several demographic confounders (e.g., age, sex). Although AIDS incidence is likely well measured, in the current era of effective therapies, AIDS incidence may become less common and therefore less germane than total mortality. Here, we focus on AIDS incidence, which was more common than death during the study period. Injection drug use is likely measured with nonnegligible error. However, Qian et al. (23) demonstrated in a single-site clinical HIV cohort with similar demographic distributions that a reported history of injection drug use had 91% sensitivity and 88% specificity for current injection drug use. Such strong measurement properties limit the extent of measurement bias. Given the prospective nature of our study, we expect exposure misclassification to be nondifferential with respect to AIDS and death. With our binary classification of injection drug use, we therefore expect that the limited measurement bias is toward the null (21). Methods to account for exposure measurement exist (25, 26), but they must be adapted to the current setting and are beyond the scope of this paper. On a related note, epidemiologists demand temporal order between exposure and disease but often neglect the temporality between confounders and exposure (27). Here, we knowingly account for covariates that are assessed after exposure; we do so under the assumption that injection drug use is fixed over this relatively short time period.

It is not uncommon for epidemiologists to report rates (e.g., 4.39 AIDS cases per 100 person-years among those who reported injection drug use). One might apply a competing risks extension (28) of the so-called exponential formula (29) to these crude rates found in Table 2 and obtain a 6-year crude risk in the injection drug users of 23.14%, rather than the 19.47% shown in Table 3. This difference between estimates may be due to the fact that the cause-specific hazards of AIDS and/or death are not constant over the 6 years after therapy initiation, which is a restrictive assumption of this rate-based approach (30), although a piecewise approach could be used to relax this assumption.

One might have censored the competing deaths and used an IP-weighted Cox proportional hazards model (where deaths are combined with dropouts). The resulting standardized cause-specific hazard ratio of 1.31 (95% CI: 1.06, 1.62) is roughly similar to the 6-year risk ratio shown in Table 3, yet the absolute risk estimates themselves are numerically larger and would diverge more so had we observed a greater proportion of competing deaths. This is because, when using standard survival analysis techniques, a portion of the censored deaths are implicitly “redistributed” to become AIDS cases after death. This is due to the fact that the risk defined as the cumulative incidence, $R_1^a(t)$, is a function of the composite survival curve (i.e., a function of both cause-specific hazard functions). Therefore, when risk is based upon a single cause-specific hazard, it will increasingly overestimate $R_1^a(t)$ as the frequency of competing events increases. Therefore, one should not interpret the cause-specific hazard ratio as a risk ratio. Rather, the cause-specific hazards for each event are to be interpreted as “momentary event forces” acting together to determine event times (31). In addition, one might adjust for measured confounders using proportional hazards regression rather than standardize using IP weights. Such an approach results in a covariate-conditional effect estimate rather than a covariate-marginal estimate and is therefore often subject to issues of interpretability regarding the noncollapsibility of the hazard ratio (5, 32). Specifically, for noncollapsible parameters like the hazard, rate, and odds ratios, the population value of the covariate-conditional parameter may depend on which covariates are included in the linear predictor of the regression model even in the absence of confounding. For example, expected estimates of the hazard ratio from 2 large, well-conducted randomized trials may not be comparable when different covariates are included in the 2 models, even when it may be assumed that confounding is not present because of randomization.

We define our parameter of interest using potential outcomes, such that we are estimating a so-called causal effect. Indeed, what we have proposed is a marginal structural competing-risks model for a time-fixed exposure. However, we purposefully avoided the use of the term “causal” because the assessment of causality often requires more than a single consistently estimated parameter based on potential outcomes. The methods presented here to estimate the standardized risk difference and standardized risk ratio are straightforward to implement using standard software. These methods can be extended easily to handle multiple exposure groups or categorized continuous exposures. In principle, and under additional assumptions, these methods can be extended to handle left-truncated data that arise when one uses an alternate timescale, such as age. Finally, these methods can be extended to handle time-varying exposures (3, 33).

In summary, we present results that suggest a modestly higher 6-year risk of AIDS among injection drug users compared with nonusers. Strengths of this study include the large, representative cohort of HIV-infected patients, high-quality study measurements, and quantitative methods tailored to the question at hand.

APPENDIX

Here, we present results of an experiment to assess whether the proposed approach provides a valid estimate of the risk difference and risk ratio under the null hypothesis. We permuted injection drug use exposure in 500 copies of our data while maintaining the observed proportion exposed. Whatever the true effect of injection drug use on acquired immune deficiency syndrome (AIDS) risk, the expected association in such permuted data should be null.

In each of the 500 permutations of the data, we conducted the analyses described in the main text for the 6-year AIDS risk. The average 6-year risks were 12.94 in the “exposed” group and 12.93 in the “unexposed” group, yielding a 6-year AIDS risk difference of 0.01 and a risk ratio of 1.00. The average standard errors for the risk difference and risk ratio were 1.42 (empirical standard error, 1.48) and 0.11 (empirical standard error, 0.11), respectively. The 95% confidence interval coverage for the risk difference and risk ratio were 93.8% and 94.2%, respectively. These experimental results suggest that the proposed approach is approximately unbiased for the risk difference and ratio with approximately correct estimates of precision and appropriate confidence interval coverage, at least at the null. Limitations notwithstanding, this simulation provides experimental support for the proposed method.