Pharmacokinetic-Pharmacodynamic Model To Evaluate Intramuscular Tetracycline Treatment Protocols To Prevent Antimicrobial Resistance in Pigs

Abstract

High instances of antimicrobial resistance are linked to both routine and excessive antimicrobial use, but excessive or inappropriate use represents an unnecessary risk. The competitive growth advantages of resistant bacteria may be amplified by the strain dynamics; in particular, the extent to which resistant strains outcompete susceptible strains under antimicrobial pressure may depend not only on the antimicrobial treatment strategies but also on the epidemiological parameters, such as the composition of the bacterial strains in a pig. This study evaluated how variation in the dosing protocol for intramuscular administration of tetracycline and the composition of bacterial strains in a pig affect the level of resistance in the intestine of a pig. Predictions were generated by a mathematical model of competitive growth of Escherichia coli strains in pigs under specified plasma concentration profiles of tetracycline. All dosing regimens result in a clear growth advantage for resistant strains. Short treatment duration was found to be preferable, since it allowed less time for resistant strains to outcompete the susceptible ones. Dosing frequency appeared to be ineffective at reducing the resistance levels. The number of competing strains had no apparent effect on the resistance level during treatment, but possession of fewer strains reduced the time to reach equilibrium after the end of treatment. To sum up, epidemiological parameters may have more profound influence on growth dynamics than dosing regimens and should be considered when designing improved treatment protocols.

INTRODUCTION

Although the phenomenon of antimicrobial resistance is well established, its persistent increase and alarming proportions continue to threaten the ability of antimicrobials to treat infections. Antimicrobial exposure is an important driver of high resistance levels. Decline in the development of new antibiotics calls for optimal use of the available drugs. Antimicrobial usage in food production animals contributes significantly to increased antimicrobial resistance in these animals (1). The reduced use of antimicrobials can reduce the resistance load; however, treatment of infection is necessary to ensure a sufficient level of animal welfare and health. Antimicrobials are mainly used treat infections caused by pathogenic bacteria, but knowledge of the mobile genetics of antimicrobial resistance has resulted in an expanding focus on bacterial ecology. For pathogens, the normal commensal bacterial flora within the animal is of interest as a potential genetic partner in the transmission of antibiotic resistance genes (2). Several classes of antimicrobials, such as β-lactams, aminoglycosides, tetracyclines, and sulfonamides, are used in both human and veterinary medicine (3). Therefore, the development of antimicrobial resistance in livestock is of public health concern due to the risk of transmission of resistant zoonotic, as well as commensal, bacteria to humans through the food chain.

It is unrealistic and unethical to stop antimicrobial use in intensive pig production, where the pig sector accounted for ca. 80% of the veterinary use of antibiotics in Denmark in 2012, with tetracycline being the most frequently used drug (3–5). Tetracycline is commonly used against intestinal diseases in weaning pigs, both metaphylactically and therapeutically in Denmark (5). Metaphylactic use of antimicrobial agents is defined as the pen treatment of both clinically ill and healthy animals, whereas therapeutic use is defined as the prescription of antibiotics to a diagnosed clinically ill animal. Therapeutic treatments with tetracycline are often via intramuscular (i.m.) injection, whereas metaphylactic delivery is commonly via food or water medication of the pen. Farmer and veterinarians decide the treatment method after consultation depending on the different factors, where metaphylactic treatment is possible and legal only if 25% of the total pigs in a section of a herd are sick (6). In this regard, therapeutic treatment has the advantage over metaphylactic treatment of treating sick animals only. Tetracyclines have been known for decades to lead to widespread antimicrobial resistance among bacteria in the intestines of pigs (7). Tetracyclines are also used in humans, accounting for 11% of the total consumption of antimicrobials in the primary health care industry in Denmark in 2012 (5). Therefore, there is a need to improve tetracycline dosing strategies to minimize resistance without compromising treatment efficacy.

Escherichia coli is one of the commensal bacteria used as an indicator of antimicrobial resistance in animals, humans, and food products, and it shows high potential transmission via the food chain. For example, an antimicrobial-resistant strain of E. coli has survived processing and chilling better than the parental antimicrobial-sensitive strain (8–10). On average, 36% of detected E. coli were tetracycline resistant in the Danish surveillance on pigs in 2012 (5). This surveillance has shown consistently high levels of tetracycline resistant E. coli in the past 5 years, indicating that tetracycline-resistant E. coli are endemic in the pig production.

In the last decade, pharmacokinetic (PK) and pharmacodynamic (PD) models have been used to assess the development of antimicrobial resistance. Mathematical modeling techniques are frequently used to estimate resistance and assess drug efficacy (11). Such models, based on in vitro and in vivo studies, allow rapid analysis of dosing strategies to help overcome the problem of the development and emergence of antimicrobial resistance (12). Traditional methods for optimizing treatment strategies are generally based on point estimates (e.g., the MIC, maximum drug concentration [C_max], and the area under the concentration time curve [AUC]) (13–15). In contrast, recent models include the dynamics of both PK and PD processes over time, providing deeper insight and a more accurate description of the impact of antimicrobial dosing strategies (16–21). However, these studies were based on the in vitro growth of bacterial populations and were limited to a few (sometimes only one) clinical bacterial strains across the susceptible and resistant subpopulations, providing a poor reflection of the within host bacterial dynamics.

Recently, mathematical models have been used to simulate in vivo scenarios that either are not possible, too expensive, or too time-consuming in practice to assess the impact of dosing factors (e.g., duration, frequency, dose, etc.) on the growth of antimicrobial-resistant bacteria (22–24). These studies focused on the impact of dosing factors on the total resistance level but did not account for differences in the numbers of competing strains or the composition of strains with different susceptibilities on the effect of a given treatment strategy. Therefore, high and persistent levels of tetracycline-resistant E. coli need to be addressed via the modeling approaches that consider the multiple strain composition. In the present study, we investigated not only the effect of dosing factors but also the effect of strain composition and the number of competing strains on the formulation of treatment strategies for minimum growth of E. coli-resistant bacteria.

We attempted to optimize i.m. tetracycline treatment in order to minimize the level of antimicrobial resistance to tetracycline in a treated pig. Our primary objectives were to use a mathematical model to (i) predict competitive growth of randomly selected E. coli strains in a pig under drug exposure based on in vivo PK data from tetracycline i.m. treatment, (ii) assess the optimum dosing frequency and treatment duration to suppress or delay the growth of resistant strains, and (iii) analyze the effect of both the composition and the number of competing strains on resistance levels.

MATERIALS AND METHODS

The model includes the growth of multiple strains under dynamic equilibrium in a pig after i.m. treatment. The dynamic equilibrium of growing strains was established by introducing a constant “outflow rate” into the model. The growth of the strains in the model was affected by antimicrobial concentration and by the total bacterial count, whereas the antimicrobial concentration was dependent on a combination of dosing factors (frequency, duration, etc.). The composition of multiple strains was made by random selection of strains with growth characteristics determined in vitro.

In vivo pharmacokinetics.

The plasma concentrations of tetracycline in pigs after i.m. treatment were modeled using data from the literature on the plasma concentrations of oxytetracycline in pigs after administration of the drug i.m. (25), where the plasma concentrations of oxytetracycline were determined at different time points over 48 h after drug administration in 12 healthy pigs. A two-compartment PK model was fitted to the mean values of the plasma concentration and time profile to estimate the transfer rate parameters, as shown in Fig. 1 and equations 1, 2, and 3.

$$\frac{d{C}_g}{dt}=-k_a{C}_g$$ (1)

$$\frac{d{C}_c}{dt}=k_a{C}_g+k_{21}{C}_p-(k_{12}+k_{el})C_c$$ (2)

$$\frac{d{C}_p}{dt}=k_{12}{C}_c-k_{21}\hspace{0.17em}{C}_p$$ (3)

FIG 1.

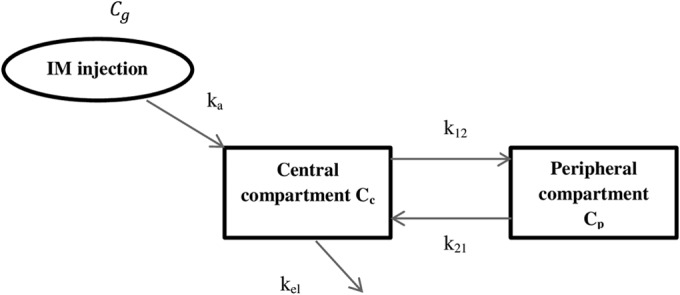
Two-compartmental PK-model with central compartment being the plasma compartment and peripheral compartment being tissue compartment. k_a is the first-order absorption rate as drug is being absorbed from intramuscular injection site C_g.

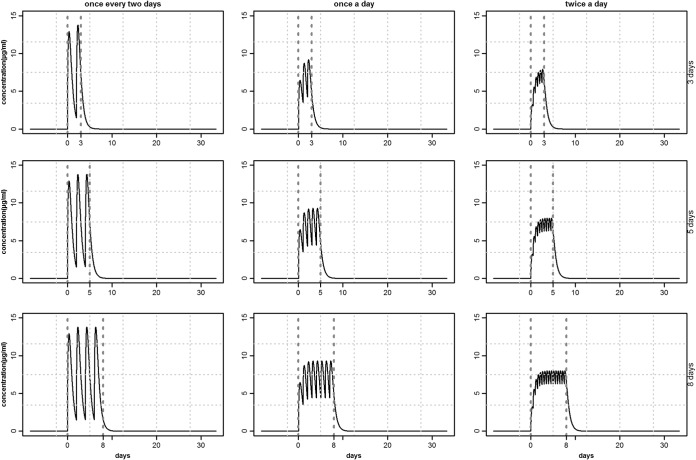
These equations represent changes in drug concentrations, C_c and C_p, over time in the central (plasma) and peripheral (tissue) compartments, respectively, where k_a is the drug absorption rate from diffusion compartment C_g, k₁₂ and k₂₁ are the transfer rates between the two compartments, and k_el is the elimination rate from the central compartment (Fig. 1). The estimated rates (k_a, k₁₂, k₂₁, and k_el) were used to produce different concentration-time profiles for different combinations of treatment durations and dosing frequencies that deliver the same daily dose of 20 mg/kg. Three treatment durations (3, 5, and 8 days) and three dosing frequencies (once every 2 days, once per day, and twice per day) were selected, giving a total of nine combinations of concentration profiles.

Growth parameters.

The in vitro growth of 50 E. coli strains in the presence of tetracycline were previously assessed using a PD E_max model (A. Ahmad, C. Zachariasen, L. E. Christiansen, K. Græsbøll, N. Toft, L. Matthews, P. Damborg, J. E. Olsen, Y. Agersø, and S. S. Nielsen, submitted for publication). The relationship between the tetracycline concentration (c) and the estimated net bacterial growth rates α was analyzed using the model:

$$\alpha \left(c\right)={\alpha }_{\text{max}}-\frac{{\alpha }_{\text{max}}{\left(\frac{c}{{\text{EC}}_{50}}\right)}^{\gamma }}{1+{\left(\frac{c}{{\text{EC}}_{50}}\right)}^{\gamma }}$$ (4)

where α_max is the bacterial growth rate in the absence of the drug (maximum effect), EC₅₀ is the drug concentration at which the drug effect is reduced to 50%, and γ denotes the Hill coefficient, which is a measure of the steepness of the sigmoid relationship between the concentration (c) and the net growth rate at around EC₅₀ (27). The estimated model parameters (α_max, EC₅₀, and γ; see the supplemental material), which described the growth response to the antimicrobial, were used to construct the PK-PD model. These 50 E. coli strains were randomly selected from among 160 porcine indicator E. coli isolates from the Danish Integrated Antimicrobial Resistance Monitoring and Research Program (DANMAP) in 2010 (28). A cutoff value of 8 μg/ml between susceptible and resistant E. coli strains was also adopted from DANMAP 2010.

Mathematical model for competitive growth.

We modeled the changes in bacterial counts of individual bacterial strains in a pig using growth parameters from the PD model combined with the in vivo drug profile using an ordinary differential equation given by the following equation:

$$\frac{d{N}_i}{dt}=({\alpha }_{\max \hspace{0.17em}}-\frac{{\alpha }_{\max \hspace{0.17em}}{c}^{\gamma }}{\mathrm{E}{{\mathrm{C}}_{50}}^{\gamma }+c^{\gamma }})\left(\frac{N_{\max \hspace{0.17em}}-N_i}{N_{\max \hspace{0.17em}}}\right)\left(\frac{N_{\max \hspace{0.17em}}-\Sigma N_i}{N_{\max \hspace{0.17em}}}\right)N_i-\phi N_i$$ (5)

The left side of the equation shows the change in bacterial counts for strain i (N_i). The first term in parentheses on the right side of the equation gives the drug efficacy as a function of the three PD model parameters (α_max, EC₅₀, and γ) and the in vivo drug concentration-time profile c. The remaining parenthetic terms are density-dependent limitations to growth, which depend on the carrying capacity, the N_max, and the total bacterial counts summed over all competing strains in the pig (ΣN_i). The final term is the excretion of strains from a pig with an outflow rate (ϕ) (29).

Both the composition and the diversity of E. coli vary considerably between pigs; up to 10 different E. coli strains were found in the intestinal flora of healthy domestic pigs (30). To capture the effect of number of competing strains on resistance levels, simulations were run with 12, 6, and 3 strains. A plasma concentration profile was used for bacterium-drug interaction after i.m. injection because the plasma concentration is often used as a surrogate for the concentration at the actual interaction site, in this case the intestine (31).

The carrying capacity N_max was set to 10¹⁰ bacteria (23, 29, 32). An outflow rate, ϕ, of 0.01 of strains was taken from a published experimental study that estimated this rate as the hourly fractional inflow and outflow of E. coli “free-living” in the large intestine from an in vivo study in postweaned dairy calves (22, 33). The model was initiated by selecting 12 strains with one-third resistant and assigning growth parameters to these strains as described above. The model was initially run without drugs to attain the dynamic equilibrium in the absence of selection pressures. Initial values of individual strains were randomly selected between 10⁶ and 10⁹, with the sum not exceeding the carrying capacity of 10¹⁰.

Treatment was introduced once the equilibrium with 12 E. coli competing in the intestinal flora of a pig was attained, and the first treatment day was denoted day 0. The 12 E. coli strains were randomly selected from among the 50 E. coli strains representing the pig population of Denmark. We considered the treatment of weaning pigs, since the proportion of antimicrobial use is much higher in weaning pigs compared to finishers and sows (5). Therefore, the model was allowed to run for a period of 35 days after treatment (a period during which the pig will leave the weaner section) to assess the effect of dosing factors on growth dynamics and resistance levels when pigs leaves the weaning section. To capture the variation in growth characteristics and susceptibility levels in the mix of strains, simulations were repeated 100 times, with the strains sampled randomly each time from the collection of 50 E. coli strains with known growth characteristics. We report the mean with a simulation envelope of the sum of susceptible and resistant strains for these 100 repetitions.

The procedure was repeated with treatment protocols based on different combinations of dosing factors, as indicated in Fig. 2. To compare across treatment protocols, the same strains and initial values were used. Different numbers of competing strains (6 and 3) in a pig were also considered. Since ca. 30% of detected E. coli were tetracycline resistant in the Danish surveillance of pigs in 2011, competing strains were selected with one-third (33.3%) of them being resistant (5). Thus, in the competition between 12, 6, and 3 strains, 4, 2, and 1 strains were found to be resistant, respectively. The model was written in R version 3.0.1 for Windows (“Frisbee Sailing”) (34); all data were also analyzed and plotted using R.

FIG 2.

Tetracycline plasma concentration profiles for different combinations of dosing frequency (from left to right) and treatment duration (from top to bottom), with the same per day dose (20 mg/kg) of i.m. injection treatment. The vertical dotted lines demarcate the treatment interval.

RESULTS

Concentration-time profiles.

The plasma concentration profiles C_c in a pig following an i.m. tetracycline treatment of 20 mg/kg/day for different dosing combinations are shown in Fig. 2. An increase in dosing frequency (Fig. 2, left to right) maintained the concentration above a certain level, but also reduced the peak concentration. Increasing the duration (Fig. 2, top to bottom) did not increase the peak value, but extended the time above a threshold concentration level. These concentration-time profiles (Fig. 2) were fed into the model (equation 5) and thus shape the treatment strategy results. The maximum peak concentration attained in these protocols was ∼10 μg/ml, which was far below the susceptibility levels of resistant strains. As a result, all of the resistant strains had a competitive advantage, irrespective of the treatment protocols and their susceptibility levels.

Model outputs.

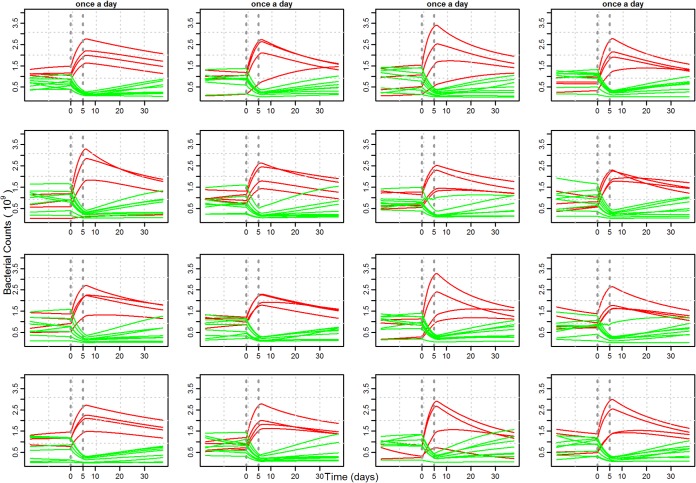
A sample of 16 repetitions out of 100 performed on 12 competing strains under the same treatment protocol (once a day for 5 days) is given in Fig. 3. The period prior to day 0 (when treatment started) was to allow a dynamic equilibrium to be established in the absence of treatment. Dynamic equilibrium in the present study refers to the coexistence of multiple strains in a pig, where only small changes happen over long periods of time, unless the system is disturbed by, e.g., an antimicrobial treatment. After a disturbance, the system will again return to a state of equilibrium, which may or may not differ from the original one. In our case, a dynamic equilibrium was only possible when ϕ < α_max for all competing strains. If ϕ was larger than the growth rates, then the strains would all vanish with time. The dynamic equilibrium was disrupted by the treatment, and it took various lengths of time posttreatment to return to equilibrium (Fig. 3). All resistant strains (red lines) among a total of 12 competing strains showed clear growth advantages during the treatment period. This led to a high resistant proportion at the end of treatment and time to regain the dynamic equilibrium posttreatment (Fig. 3).

FIG 3.

Example of competitive growth of 12 strains (lines) with 16 repeats (one per plot). In each repeat, 12 strains were drawn randomly from 50 strains, with one-third of the total pool being resistant (red lines). Both the treatment duration (5 days) and the dosing frequency (once a day) are the same in all 16 plots. The treatment window is demarcated with vertical lines.

Repetitions performed for 12 competing strains under the same treatment protocol showed a large variation in the growth of individual strains, with each repeat corresponding to a different sample of 12 strains with various susceptibility levels and growth parameters (Fig. 3). Growth dynamics, both during and after treatment, and the time taken by these individual strains to regain the equilibrium were quite different in repetitions (Fig. 3).

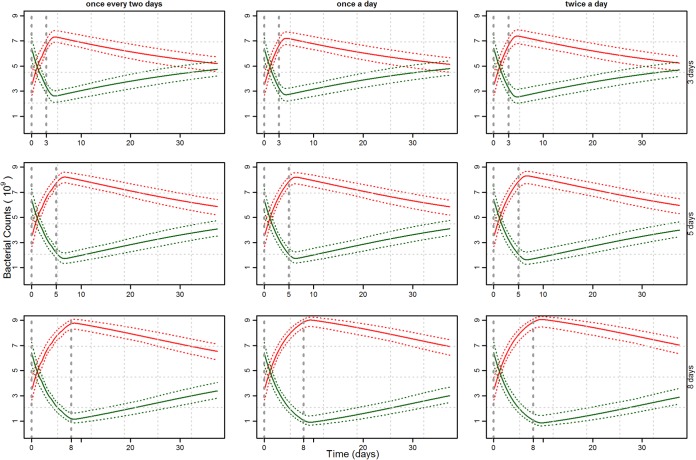
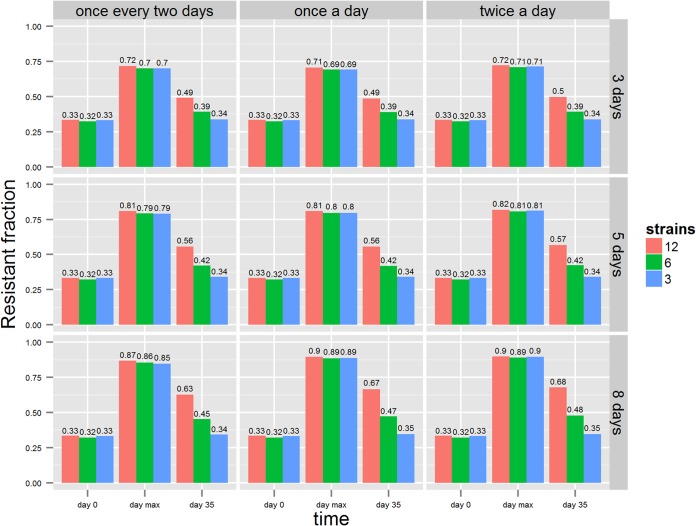
The overall variation across the sum of all susceptible and all resistant strains was much less, as shown by the simulation envelope (Fig. 4). All combinations of dosing factors resulted in a very high resistant proportion at the end of treatment, irrespective of the susceptibility levels of the strains (Fig. 4). Longer durations of treatment clearly increase resistance levels, whereas changing dosing frequencies appeared to result in almost no difference in resistance. The difference in dosing duration resulted in various lengths of time posttreatment to return to equilibrium (Fig. 4). The resistance fractions were quantified at three time points (day 0, day maximum [max], and day 35) to expose the difference between dosing protocols (Fig. 5).

FIG 4.

Mean and simulation envelope of the total pool of susceptible (green) and total pool of resistant (red) bacterial counts from 100 repeats of a composition with 12 strains at all nine combinations of treatments' duration and dosing frequency, as given in Fig. 2.

FIG 5.

Fraction of resistant counts at day 0 (before treatment), at “max” (i.e., the maximum fraction after treatment), and at day 35. Different dosing frequencies—low (once every 2 days), normal (once a day), and high (twice a day)—are shown as subplots. Each color bar represents treatment duration.

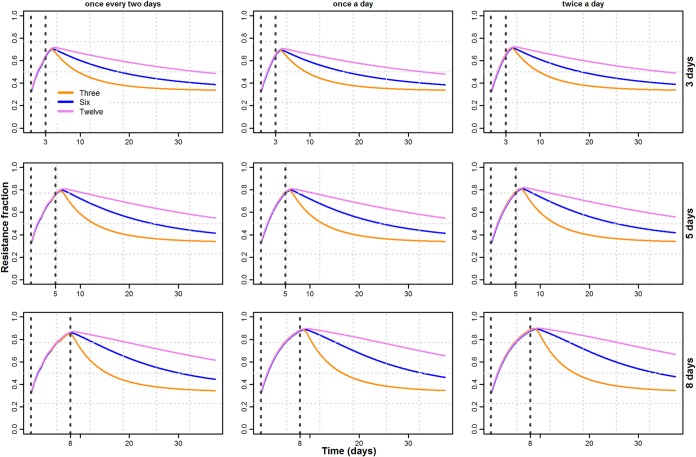
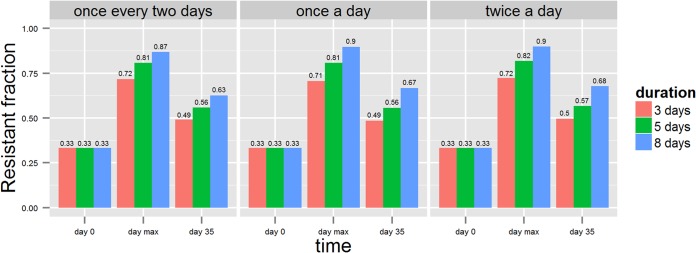
The proportion of resistant counts was sensitive to the number of competing strains (Fig. 6). A decrease in the number of competing strains also decreased the time to reach equilibrium. The difference in times was longer for longer treatment durations, whereas the dosing frequency seemed to have no effect on the differences in time (Fig. 7).

FIG 6.

Fraction of total resistant counts at nine combinations of treatment factors where different colors represent the number of competing strains (i.e., 3, 6, and 12).

FIG 7.

Resistance levels at three time points with day 0 (when treatment started), day “max” (the maximum resistance level), and day 35 (weaning end) for all nine combination of dosing factors, with each color bar representing the number of competing strains.

DISCUSSION

We developed a model that simulates how multiple bacterial strains in a pig under different treatment protocols may compete. The total population of strains was affected by different antimicrobial treatment protocols. We have demonstrated that the less time the strains are under antimicrobial pressure, the less time it takes for susceptible strains to overcome competition from the resistant ones. In other words, given a constant daily dose, it is better to treat for short periods with any dosing frequency. However, short treatment durations may not adequately treat the infection, a factor to be considered in the treatment evaluations (35). Variation in the total resistance level under the same treatment is insensitive to the composition of the strains but sensitive to the number of strains, with fewer strains resulting in a more rapid return to equilibrium.

The effect of treating infections caused by bacterial pathogens on the development and growth of antimicrobial resistance in commensal bacteria is of considerable concern (35–38). High levels of resistance are generally considered to be strongly correlated with selection pressures from antimicrobial use. Since treatment is necessary on animal welfare grounds, careful investigation of dosing factors (dosing frequency, treatment duration, dose level, etc.) could provide alternate treatment protocols to help reduce the development of resistance. Here, we used a mathematical model to investigate the relationship between dosing factors and resistance levels in the presence of multiple competing strains. Limiting growth factors were used in the model to reflect the in vivo situation for dynamic equilibrium of multiple strains (30).

In contrast to most previous simulation studies, antimicrobial pressure was not assumed to be constant during the treatment but varied according to simulated plasma concentration-time profiles based on a two-compartment PK model (22–24). Key parameters were estimated by fitting this model to the in vivo profile of tetracycline plasma concentration in a pig following i.m. treatment, derived from a previously published study (25). This approach allows a subsequent PD model to reproduce realistic changes in antimicrobial pressure in the pig. Treatment protocols that have been investigated previously considered the effect of treatment on a single or few clinical strains only, whereas we have shown here that both the number of competing strains and the strain composition also have an impact on the evaluation of treatment protocols. We considered the growth of multiple strains in our model growing under dynamic equilibrium. This was achieved by introducing a double term including carrying capacity N_max in equation 5, a form which differs from the very simple rate models. This term is necessary, since the strain with the highest growth rate will otherwise outgrow all of the other strains and equilibrium cannot be established. A biological interpretation of the terms may be that the total population, ΣN_i, cannot exceed N_max because the total nutrition present is limited, and it is assumed that a single strain cannot utilize all types of nutrients and therefore cannot outgrow all other strains. Furthermore, the growth parameters of competing strains were estimated previously from in vitro growth, making our study, to our knowledge, the first to include population representative strains.

Our previous analysis of the growth of E. coli strains indicated that there was no fitness cost to resistance (29). Thus, using these population representative strains sets our model apart from previous models, which have assumed a fitness cost for resistant strains. Mutation and conjugation mechanisms were not considered in the model, as they would be expected to have insignificant effects compared to the already established resistance prior to treatment. The plasma concentration of tetracycline was used instead of the drug concentration at the interaction site since plasma concentrations are considered an appropriate surrogate marker in most PK studies (39). A single pig treatment regardless of diseased status of the pig was considered; thus, no transmission factors were included in the model, and the model is consequently limited to a single pig in isolation. The outflow rate was kept constant throughout the investigated period, but in principle it could be varying with the varying disease status of a pig.

We examined the competitive growth of E. coli strains, characterized by their in vitro drug response, in a pig using in vivo drug concentration profiles in plasma. The goal was to evaluate the extent to which different dosing factors suppress the growth of resistant strains when growing under dynamic equilibrium conditions. Due to the competitive advantage of resistant strains, all treatments showed an increase in resistance level, as shown in previous studies (5, 11). Consequently, it would be preferable to have less time under treatment to reduce the competitive growth of these resistant strains. High peak concentrations may also lead to high resistance levels at the end of treatment. All dosing protocols showed rapid dominance of resistant strains during the treatment, in agreement with results from other studies (11, 40). There was a very small apparent effect of dosing frequency, whereas previous studies showed that an increased dosing frequency could reduce resistance (15, 16, 36). This could have arisen because of the large difference in MIC values of susceptible and resistant strains (see the supplemental material). Increased dosing frequencies could not produce sufficiently high drug concentrations to affect the resistant strains. Thus, adjusting the dosing frequency does not seem to be an appropriate approach. A more prolonged treatment resulted in a greater resistance and consequently took longer to return to equilibrium. This is undesirable because the longer the period before return to equilibrium, the greater the risk of transmission of resistant strains to other pigs and humans, although this has not been explicitly modeled in the present study. In reality, treatment durations depend on the efficacy of the treatment, but it may also be possible to reduce the duration with a higher daily dose level to achieve the desired efficacy and lower resistance levels (24). The effect of the number of strains on resistance levels has not been investigated previously. Our results indicate that the total resistant level is largely insensitive to strain composition (Fig. 4) but that the number of competing strains is an important determinant of the return time to equilibrium (Fig. 7).

To conclude, the simulation model used in the present study was used to investigate resistance dynamics under in vivo antimicrobial exposures. Short treatment duration resulted in the shortest time for strains to return to equilibrium, while higher numbers of competing strains substantially increased this time. Our predictions have provided new insights into the relationship between drug dosing factors and drug resistance. Specifically, we have shown that both the dosing factors and the strain composition have an impact on the resistance development, and taking these into account could be helpful in the design of new treatment protocols.

The distribution of different strains may depend not only on the pig but also on the herd or a section of a herd. When designing the treatments, predictions from the present study could be used to redesign the dosing regimens for i.m. injection treatments using tetracycline in pigs. Moreover, accounting for the number of strains and their composition would help to improve the design of treatment protocols.