Comparison of the Accuracy and Precision of Pharmacokinetic Equations To Predict Free Meropenem Concentrations in Critically Ill Patients

Abstract

Population pharmacokinetic analyses can be applied to predict optimized dosages for individual patients. The aim of this study was to compare the prediction performance of the published population pharmacokinetic models for meropenem in critically ill patients. We coded the published population pharmacokinetic models with covariate relationships into dosing software to predict unbound meropenem concentrations measured in a separate cohort of critically ill patients. The agreements between the observed and predicted concentrations were evaluated with Bland-Altman plots. The absolute and relative bias and precision of the models were determined. The clinical implications of the results were evaluated according to whether dose adjustments were required from the predictions to achieve a meropenem concentration of >2 mg/liter throughout the dosing interval. A total of 157 free meropenem concentrations from 56 patients were analyzed. Eight published population pharmacokinetic models were compared. The models showed an absolute bias in predicting the unbound meropenem concentrations from a mean percent difference (95% confidence interval [CI]) of −108.5% (−119.9% to −97.3%) to 19.9% (7.3% to 32.7%), while absolute precision ranged from −249.1% (−263.4% to −234.8%) to 31.9% (17.6% to 46.2%) and −178.9% (−196.9% to −160.9%) to 175.0% (157.0% to 193.0%). A dose change was required in 44% to 64% of the concentration results. Seven of the eight equations evaluated underpredicted free meropenem concentrations. In conclusion, the overall accuracy of these models supports their inclusion in dosing software and application for individualizing meropenem doses in critically ill patients to increase the likelihood of achievement of optimal antibiotic exposures.

INTRODUCTION

Meropenem, a carbapenem antibiotic with broad-spectrum activities against both Gram-positive and Gram-negative bacteria, is commonly used in critically ill patients with life-threatening infections. Vital to the success of this treatment is early and appropriate antibiotic therapy. Selecting the correct dose is as important, but this process is highly challenging in critically ill patients because of the variable and difficult-to-predict pharmacokinetics in these patients (1, 2). Dose optimization of meropenem should be considered imperative because suboptimal antibiotic exposures might jeopardize the clinical outcomes and potentially increase the emergence of antibiotic resistance (3).

Meropenem is a time-dependent antibiotic: its clinical and microbiological efficacy is related to the percentage of the dosing interval in which the free drug concentration remains above the MIC of the pathogenic organism (fT_>MIC) (4, 5). The in vitro bactericidal activity of carbapenems is optimal at an fT_>MIC of ≥40%; however, a target fT_>MIC of 100% has been suggested in critically ill patients (6). Population pharmacokinetic models that quantify the effect of demographic, pathophysiological, and other drug-related factors on drug disposition should be considered valuable in the critical care setting for accurately predicting individualized and optimized antibiotic doses for patients who exhibit profoundly altered and rapidly changing pharmacokinetics. The models can be applied to predict appropriate empirical doses or be used to guide dose adaptation as part of a therapeutic drug monitoring (TDM) intervention.

Several pharmacokinetic models have been developed for meropenem from different subpopulations of patients (7–14). In order to establish a TDM program for meropenem to optimize meropenem dosing, the question arises as to which pharmacokinetic model best predicts the meropenem concentrations in a heterogeneous cohort of critically ill patients.

The aim of this study was to measure the agreement between observed free meropenem concentrations from a mixed cohort of critically ill patients and the free concentrations predicted by the population pharmacokinetic models. We then sought to rank the predictive performance of the identified models and compared them according to the frequency of dose adjustments prompted by the results based on the model predictions versus the observed concentrations.

MATERIALS AND METHODS

Patient selection and data collection.

The TDM data collection and observational study was approved by the local hospital and university ethics committees (Royal Brisbane and Women's Hospital and The University of Queensland) with a waiver for informed consent granted because of the retrospective nature of the study. Data were available for critically ill patients aged 18 years and older who had received meropenem and had at least one set of two serum samples available from routine clinical TDM (samples were taken at the middle of the dosing interval and as a trough sample). Patients receiving renal replacement therapy were excluded from the study. Data were collected between 2011 and 2014.

Demographic and laboratory data collected included sex, age, height, total body weight, and serum creatinine concentrations. The creatinine clearance was calculated using the Cockcroft and Gault equation (15). A corresponding daily measured serum creatinine concentration was used for each pair of data. Subjects with a serum creatinine concentration of <0.4 mg/dl had their creatinine concentration set to 0.4 mg/dl (7). Subjects aged 65 years or older with a serum creatinine concentration of <0.9 mg/dl had their creatinine values set to 0.9 mg/dl to estimate their creatinine clearance for predictions using the Crandon et al. method (9). Dosage and blood sampling histories, including the date, time, dosage, and duration of infusion were also collected.

Determination of meropenem concentrations.

Plasma unbound concentrations of meropenem were determined by using published validated high-performance liquid chromatography (HPLC) assays (16, 17). Briefly, to measure the unbound drug concentrations, plasma samples were filtered using an Amicon Ultra 0.5-ml 30,000-molecular-weight-cutoff centrifugal filter device. The ultrafiltrates were mixed with morpholineethanesulfonic acid (MES) buffer (pH 6.6) and analyzed by using HPLC. The concentration ranges of the standard curves were 0.1 to 50 mg/liter. The coefficients of variation (CV) for interassay and intra-assay precision were 2.6% and 2.6 to 4.2%, respectively, and the accuracy was 7.2%.

Requirement for dose adjustment.

The clinical implications of the results were evaluated by comparing the need for dose adjustment of the observed and the predicted concentrations. The chosen trough concentration target was 100% ƒT_>MIC where the chosen MIC was the meropenem breakpoint for Pseudomonas aeruginosa of 2 mg/liter available from the European Committee of Antimicrobial Susceptibility Testing (http://www.eucast.org/). For interpreting the need for dose adaptation, if the trough concentration was <2 mg/liter, the dose was increased, and if the trough concentration exceeded 15 mg/liter, the dose was decreased. The dose adjustments were not required when the predicted or observed trough concentration was between 2 mg/liter and 15 mg/liter.

Evaluation of population pharmacokinetic models.

The dosing application used to predict serum meropenem concentrations, taking into account the patient demographic and laboratory information for these analyses, was ID-DOS (individually designed optimum dosing strategies) (http://www.optimum-dosing-strategies.org/). ID-ODS is a simulation tool powered by R software (version 2.15.3; Institute for Statistics and Mathematics [http://www.r-project.org/]) with an extensive model library built from population pharmacokinetic models published in the peer-reviewed literature. Based on the patient demographic information readily available at the bedside, ID-ODS incorporates Monte Carlo simulation and Bayesian feedback into the design of personalized dosing regimens via a graphical user interface. The meropenem concentration-time profiles were computed based on first-order 1- and 2-compartment intravenous (i.v.) infusion models written in the R language using the published mean population pharmacokinetic parameter values for drug clearance, volume of distribution (V), and transfer rate constants. A change in the calculated pharmacokinetic parameters was allowed to ensure that changing physiological variables were incorporated during the time course of the therapy. Protein binding of 2% was assumed to calculate the free meropenem concentrations as all models included only described total meropenem concentrations (18). Prediction errors were evaluated based on the absolute and relative bias and precision. The absolute bias and precision were established with the Bland-Altman method using the calculated mean percent difference and 95% limits of agreement, respectively (19). The relative bias and precision were established by calculating the delta mean prediction errors (ΔME) and the delta mean squared prediction errors (ΔMSE) and their 95% confidence intervals (CI), respectively (20). Categorical and continuous variables were evaluated by the Mann-Whitney U test and the Student t test, respectively, as appropriate, using R software.

RESULTS

Patient characteristics and dosing data.

The TDM data from 56 adult patients with a total of 157 collected samples were included in this analysis. The mean number of concentrations per subject was 2.8. The patients' demographic and clinical characteristics are shown in Table 1. Renal function varied among patients as characterized by the serum creatinine concentrations. The majority of patients received conventional doses of meropenem (1 g every 8 h as a 0.5-h infusion), with 12% of the patients receiving higher doses up to 2 g as a 3-h extended infusion regimen.

TABLE 1.

Demographics and clinical characteristics of the patients studied^a

Characteristicb	Value
Age (yr)	55 (36−63)
BMI (kg/m2)	24.2 (21.5−27.6)
Weight (kg)	75 (60−95)
Serum creatinine concn (μmol/liter)	72 (46.2−108.7)
Creatinine clearance (ml/min)c	99.9 (73−128.76)
Infection type (%)
Abdominal	17
Respiratory	44
CNS	15
Other	24

^aData are presented as median (interquartile range [IQR]) except where otherwise indicated. The plasma creatinine concentrations were measured on the day of sampling; other parameters were measured upon admission.

^bBMI, body mass index; CNS, central nervous system.

^cCreatinine clearance was estimated by the Cockcroft-Gault formula.

Comparative accuracy of observed concentrations with model-based predictions.

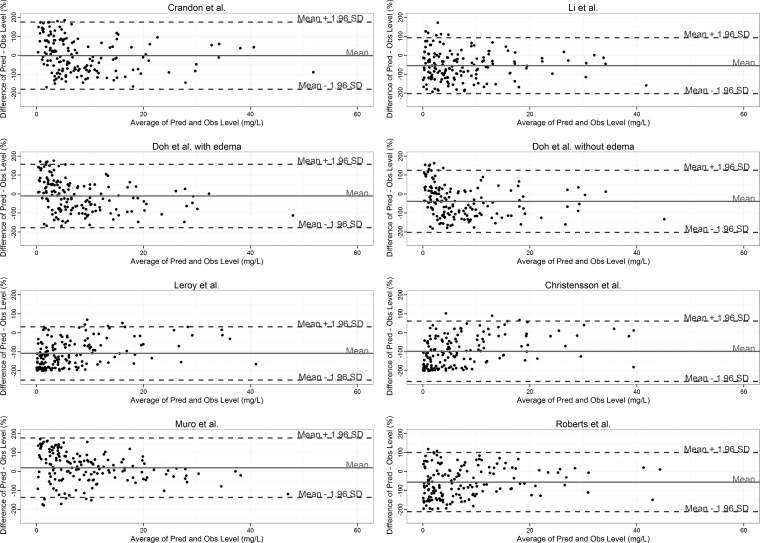
Eight population pharmacokinetic models were used to predict the meropenem concentrations for the individual patients (Table 2). The absolute bias ranged from a mean percent difference (95% CI) of −108.5% (−119.9% to −97.3%) for the Leroy et al. equation (11, 13) to 19.9% (7.3% to 32.7%) for the Muro et al. model (14). The biases of two equations were not different from zero with means (95% CI): Crandon et al. (9), −1.9% (−16.2% to 12.3%); and Doh et al. with edema (8), −10.29% (−23.7% to 3.1%). The Leroy model was found to be the most precise with the narrowest range of the 95% limits of agreement (95% CI) of −249.1% (−263.4% to −234.8%) to 31.9% (17.6% to 46.21%) for predicting the observed concentrations. The relative percent plots for all models are shown in Fig. 1.

TABLE 2.

Equations of the evaluated methods for the prediction of meropenem pharmacokinetic parameters in adult patients

Study (reference), no. of patients in the study	Equationa
Noncompartmental analysis models
Leroy et al. (11,13), n = 32	CL (ml/min) = 1.85 · CLCR + 24.9; Vss (liters) = 0.264 · TBW if CLCR = >80 ml/min; Vss (liters) = 0.212 · TBW if CLCR is 30−80 ml/min; Vss (liters) = 0.342 · TBW if CLCR = <30 ml/min
Christensson et al. (12), n = 23	CL (ml/min/1.73 m2) = 1.71 · CLCR + 14; Vss (liters) = 0.21 · TBW if CLCR = >80 ml/min/1.73 m2; Vss (liters) = 0.2 · TBW if CLCR = 30−80 ml/min/1.73 m2; Vss (liters) = 0.23 · TBW if CLCR = <30 ml/min/1.73 m2
One-compartment population pharmacokinetic model
Muro et al. (14), n = 68	CL (liters/h) = 11.1 · (mSCR/0.7)−1; V (liters) = 33.6
Two-compartment population pharmacokinetic models
Crandon et al. (9), n = 21	K (h−1) = 0.392 + 0.003 · CLCR; V1 (liters) = AdjBW · 0.239
Li et al. (7), n = 79	CL (liters/h) = 14.6 · (CLCR/83)0.62 · (AGE/35)−0.38; V1 (liters) = 10.8 · (TBW/70)0.99; V2 (liters) = 12.6
Doh et al. (8), n = 59	CL (liters/h) = 4.45 + 10.5 · (CLCR/138); V1 (liters) = 17 + 11.1 · EDEMA; V2 (liters) = 10.1
Roberts et al. (10), n = 10	CL (liters/h) = 13.6 · (6/CLCR); V1 = 7.9; V2 = 14.8

^aCL, meropenem plasma clearance; CL_CR, creatinine clearance; V_ss, steady-state volume of distribution; TBW, total body weight, mSCR, modified serum creatinine; V, volume of distribution for one-compartment model; K, elimination rate constant from the central compartment; V₁, volume of distribution of the central compartment; V₂, volume of distribution of the peripheral compartment; AdjBW, adjusted body weight; EDEMA, indicator for the presence (1) or absence (0) of edema.

FIG 1.

Bland-Altman plots of relative differences between predicted (Pred) and observed (Obs) unbound meropenem concentrations against the means of predicted and measured unbound concentrations for the models tested. The Li et al. data are from reference 7, and the Roberts et al. data are from reference 10. SD, standard deviation. The biases and 95% limits of agreement are shown as solid and broken horizontal lines, respectively.

The relative predictive performances of these eight predictors were also compared. Table 3 presents the relative performances of the 8 equations ranked in terms of ΔME and ΔMSE against the constant prediction value (mean of the observed concentrations). Compared to this naive predictor, the one-compartment model by Muro et al. (14) developed in Japanese patients was found to be the least biased with a ΔME (95% CI) of 0.02% (−1.19% to 1.24%) and the most precise as established by the ΔMSE (95% CI) of −55.04% (−82.82% to −27.26%). To further evaluate whether the Muro model is statistically superior to the other methods, we compared the predictions of the other 7 methods against those generated by the Muro model as shown in Table 4. Predictions by the Muro model compared to those of the others were more precise, represented by the consistently negative ΔMSE values. The positive ΔME values suggest that all models tend to underpredict concentrations compared to the Muro model. The results of this analysis confirm the suitability of the Muro method for accurately and precisely predicting free meropenem concentrations in a heterogeneous cohort of critically ill patients.

TABLE 3.

Evaluation of the predictive performance of the studied models

Model	Bias and precision relative to naive predictora
	ΔME (mg/liter)			ΔMSE (mg/liter)
	Mean	95% CI	Rank	Mean	95% CI	Rank
Crandon et al. (9)	−1.82	−3.28 to −0.36	2	−26.27	−58.5 to 5.95	5
Li et al. (7)	−4.25	−5.55 to −2.95	5	−29.02	−49.95 to −8.01	4
Doh et al. with edema (8)	−2.96	−4.29 to −1.63	3	−35	−58.4 to −11.58	3
Doh et al. without edema (8)	−4.31	−5.69 to −2.93	6	−19.8	−39.02 to −0.57	6
Leroy et al. (11, 13)	−5.34	−6.69 to −4	8	−13.13	−35.39 to 9.12	8
Christensson et al. (12)	−4.45	−5.85 to −3.05	7	−16.02	−40.13 to 8.09	7
Muro et al. (14)	0.02	−1.19 to 1.24	1	−55.04	−82.82 to −27.26	1
Roberts et al. (10)	−3.37	−4.66 to −2.08	4	−36.54	−57.37 to −15.7	2

^aThe bias and precision of the models were ranked according to the delta mean prediction error (ΔME) and delta mean square prediction error (ΔMSE) in relation to a naive predictor (mean of all observed concentrations), respectively.

TABLE 4.

Evaluation of the predictive performance of the studied models relative to the Muro et al. (14) model

Model	Bias and precision relative to Muro model
	ΔMPE		ΔMSPE
	Mean	95% CI	Mean	95% CI
Crandon et al. (9)	1.84	0.77 to 2.92	−28.76	−53.9 to −3.58
Li et al. (7)	4.27	3.57 to 4.98	−26.01	−50.36 to −1.67
Doh et al. with edema (8)	2.98	2.25 to 3.71	−20.03	−39.37 to −0.69
Doh et al. without edema (8)	4.33	3.57 to 5.09	−35.24	−58.05 to −12.42
Leroy et al. (11, 13)	5.37	4.72 to 6.02	−41.91	−69.79 to −14.03
Christensson et al. (12)	4.47	3.85 to 5.09	−39.02	−68.3 to −9.73
Roberts et al. (10)	3.39	1.45 to 5.33	−149.75	−206.44 to −93.06

Requirement for dose adjustment.

Figure 2 summarizes the differences in the predictions from the models studied in terms of whether a dose adjustment (or not) is indicated for the 81 opportunities for dose modification evaluated. In this figure, the decision to decrease, increase, or maintain the total daily dose requirement to achieve the prespecified 100% ƒT_>MIC target is color coded with white, black, and gray colors, respectively. In the ideal situation and when the decision to adjust (or not) for all models is in agreement with the conclusion made based on the observed concentration, for the given ith opportunity, the colors moving across the mosaic plot horizontally will be the same as the color in the observed column. An example of this type of agreement is represented by the 70th dose adjustment decision coded black to increase the daily dose administered, which was based on the observed concentrations and predictions by all models. Dose adjustment decisions predicted by the Muro model agreed with those determined by the observed concentrations 64% of the time (P = 0.22). The methods of Crandon et al. (9), Li et al. (7), and Doh et al. (with or without edema) (8) would have led to similar dose adjustment changes of 62% (P = 0.51), 62% (P < 0.05), 60% (P = 0.69), and 59% (P < 0.05) of the time as determined by observed concentrations, respectively. The other three methods agreed with the decisions based on the observed concentrations <55% (P < 0.05 for all three) of the time.

FIG 2.

Dose adjustment decisions based on meropenem concentrations predicted by the models studied using 100% fT_>MIC (MIC = 2 mg/liter) as the pharmacokinetic/pharmacodynamic target for dose adjustment. w.ed., with edema; w.o.ed., without edema.

DISCUSSION

The population pharmacokinetics of meropenem has been studied extensively in critically ill patients (7–14). To the best of our knowledge, no report has compared the predictive performance of the existing pharmacokinetic models when applied to a heterogeneous cohort of critically ill patients. Our results demonstrate considerable differences in both accuracy and precision among the published models. These disagreements are likely due to a number of factors, including the patient population that the models were derived from and the methods applied in the pharmacokinetic modeling procedure. The model of Crandon et al. (9) and that of Doh et al. in burned patients (8), which incorporates the presence of edema in estimating the volume of distribution (V) of the central compartment, showed no significant bias in the prediction of observed concentrations. The similarity of the predictions by these two methods is not unexpected, as the method by Doh et al. was developed in burn patients in the hypermetabolic phase, a physiologic state that is known to alter the pharmacokinetics (8, 10). When the Doh et al. model was evaluated without edema, where the volume of distribution is nearly 30% lower than with edema, an increase in the magnitude of bias was observed.

While showing the absence of significant bias, the Crandon et al. model (9) was the least precise of all as evidenced by the widest 95% limits of agreement. Indeed, the importance of the accuracy of the estimated model parameters has little value if they are not precise. The covariate relationship between creatinine clearance and the elimination rate constant included in the Crandon et al. model resulted in a slope parameter mean of 0.007 h⁻¹ and a corresponding CV of 157.1%. This large CV is a likely contributing factor to the observed widest range of the 95% limits of agreement (21). The magnitude of variation is also larger than that observed for any other parameters of the competing models. The models with and without edema by Doh et al. were both moderately precise (8).

Two other methods by Li et al. (9) and Roberts et al. (10) exhibited very similar degrees of bias and precision. Both models were found to consistently underpredict concentrations to a greater degree than the three above-mentioned models. The Li model accounted for the effects of creatinine clearance, age, body weight, and gender in a mixed population of patients with mainly intra-abdominal infections and community-acquired pneumonia (7). The high bias with the mean percent difference of −54.8% and low precision with a CV of nearly 300% may be a result of the heterogeneous cohort of the population studied by Li et al., which did not solely include critically ill patients. The study by Roberts et al. exclusively evaluated patients with critical illnesses, but excluded those with renal dysfunction, making it difficult to accurately characterize the relationship between renal function and meropenem clearance for a wide range of patients at all levels of renal dysfunction, similar to the group studied here (10).

The Leroy et al. (11, 13) and Christensson et al. (12) methods showed the highest degrees of bias based on our evaluation. Leroy et al. developed the model for meropenem in both healthy subjects and patients with renal impairment, while Christensson et al. evaluated the pharmacokinetics of meropenem in patients with various degrees of renal impairment (12). The use of noncompartmental methods in both analyses, in addition to the population studied, is likely to account for the inferior results displayed by these two studies. Given that these studies were performed under controlled conditions that are not fully representative of the diverse patient populations in which meropenem was used in the critically ill patients studied here, a lack of accuracy and precision for these models is expected.

The model of Muro et al., which was developed in Japanese hospitalized patients and included a covariate relationship for modified serum creatinine concentration and for meropenem clearance was the only model that slightly overestimated concentrations (14). Meropenem is predominantly excreted via the kidneys and, consequently, clearance of the drug is significantly affected by renal impairment (22). In this study, to avoid a discrepancy between the renal function and the measured serum creatinine concentration, a value less than the lower limit of normal (established at 0.4 mg/dl) was rounded up to 0.4 mg/dl and was defined as a modified serum creatinine concentration. Then, the serum creatinine concentration was normalized in the study to the population median value of 0.7 mg/dl during the covariate analysis, which appears to have led to more meaningful estimations of model parameters that are useful in a wider critically ill patient group.

When we analyzed the ΔME against a naive predictor (average of the observed concentrations), it was evident that, in general, most of the models underpredicted the meropenem free concentrations. Based on this analysis, the model of Muro et al. (14) was also found to be the least biased and most precise compared to the absolute standard versus all of the other methods when applied to predict meropenem concentrations in this critically ill patient cohort. The superiority of the Muro model for predicting free meropenem concentrations in this group of critically ill patients was further confirmed by comparing the predictive errors among the models using the Muro model as the standard.

The utility of the TDM and subsequent dose adjustment based on measured concentrations to achieve optimal beta-lactam exposure was confirmed by Roberts et al. in a study of critically ill patients (23). To enhance the accuracy of predictions in support of optimal dose adjustments of these agents, TDM practices should be supplemented with optimal sampling strategies and adaptive feedback control. Once the observed serum meropenem concentrations become available, preferably collected at the optimal sampling times to ensure the most precise estimation of patient-specific pharmacokinetic parameters, computerized decision support equipped with Bayesian adaptive feedback control can be used to establish meropenem dosing regimens designed to achieve the desired therapeutic targets as precisely as possible for individual patients (24). The clinical implications of the information provided by our work is clearly demonstrated in the predicted levels from the Muro model, leading to similar choices for dose adjustment the great majority of the time, compared to the results based on the observed concentrations, which in turn supports the incorporation of this best performing model into a TDM program focusing on the dose individualization of meropenem in critically ill patients.

Limitations of the study.

First, the small cohort of patients available for analysis might be considered a limitation of the study. However, this is the largest unbound meropenem concentration data set used for comparing the models studied and so furthers our understanding of the field. Second, the heterogeneous nature of this patient cohort may not match the characteristics of the patients that were included in the different meropenem population models. Therefore, these models may be more accurate in critically ill patient populations more closely matching those from their studies. Third, our predictions have used the population mean estimates from the contributing models and have not simulated incorporating measures of between-subject variability. While our approach is pragmatic and suitable for describing model accuracy in empirical dosing, it would not describe the true pharmacokinetic variability present. Fourth, we assigned a fixed 2% protein binding of meropenem to the simulations from the models which had used total concentrations. This approach may have led to some inaccuracies, given that some authors have described both higher and lower protein binding in critically ill patients (25).

In conclusion, to the best of our knowledge, this is the first paper comparing the predictive performance of published meropenem pharmacokinetic models applied to data obtained from a heterogeneous cohort of critically ill patients. While accuracy of the models might generally be considered sufficient, we found that the majority of the models tended to underestimate meropenem concentrations, which in some circumstances could potentially jeopardize the likelihood of achieving an optimal pharmacokinetic/pharmacodynamic target when they are applied in clinical practice. The pharmacokinetic model developed by Muro et al. (14) demonstrated the best predictive performance in this context. However, given the vast heterogeneity among critically ill patients' clinical presentations and their pharmacokinetics, the characteristics of pharmacokinetic models and the targeted populations should be fully considered when population models are used to predict the optimal dose of meropenem in critically ill patients.