Cytoskeletal forces during signaling activation in Jurkat T-cells

Cytoskeletal forces are implicated in T-cell–receptor activation, but their determinants are not known. Traction force microscopy was used to measure forces generated during T-cell activation. Whereas actin dynamics were essential for force generation, myosin contractility played a limited role. T-cells were also found to be mechanosensitive.

Abstract

T-cells are critical for the adaptive immune response in the body. The binding of the T-cell receptor (TCR) with antigen on the surface of antigen-presenting cells leads to cell spreading and signaling activation. The underlying mechanism of signaling activation is not completely understood. Although cytoskeletal forces have been implicated in this process, the contribution of different cytoskeletal components and their spatial organization are unknown. Here we use traction force microscopy to measure the forces exerted by Jurkat T-cells during TCR activation. Perturbation experiments reveal that these forces are largely due to actin assembly and dynamics, with myosin contractility contributing to the development of force but not its maintenance. We find that Jurkat T-cells are mechanosensitive, with cytoskeletal forces and signaling dynamics both sensitive to the stiffness of the substrate. Our results delineate the cytoskeletal contributions to interfacial forces exerted by T-cells during activation.

INTRODUCTION

T-lymphocytes are central effectors of the adaptive immune response, circulating through the body and scanning antigen-presenting cells (APCs) for their cognate antigens (Monks et al., 1998; Wulfing and Davis, 1998). Contact and adhesion between the T-cell and the APC results in T-cell spreading on the APC, ensuring close proximity between the cells. Receptors on the T-cell surface (TCRs) recognize peptide–major histocompatibility complex (MHC) complexes on the APC surface. This results in the activation of TCRs and the formation of signaling microclusters that consist of activated TCR and various downstream signaling molecules (Bunnell et al., 2002; Campi et al., 2005; Douglass and Vale, 2005; Yokosuka et al., 2005; Varma et al., 2006). Despite extensive study of the biochemical signaling pathways involved, much further work is required to elucidate the precise mechanism of T-cell activation (Choudhuri and van der Merwe, 2007).

Signaling activation of T-cells critically depends upon T-cell adhesion to the APC (Kandula and Abraham, 2004) and extensive rearrangements of the actin cytoskeleton and cell deformation (Yu et al., 2013). These observations suggest that physical forces exerted on the TCR may contribute to activation by facilitating conformational changes in the TCR/CD3 complex, resulting in signaling activation, TCR clustering, and the assembly of signaling microclusters (Ma et al., 2008; Ma and Finkel, 2010). Alternatively, the applied forces may act directly on signaling molecules, resulting in conformational changes that activate additional signaling cascades (Babich et al., 2012; Yu et al., 2012). In support of these views, direct application of external forces to stimulatory beads or antigen-coated AFM tips can lead to activation of the TCR (Kim et al., 2009; Li et al., 2010; Husson et al., 2011). A recent study using primary human CD4⁺ cells on elastomer pillar arrays coated with anti-CD3 or MHC peptides showed that T-cells exert traction forces in response to CD3 or CD28 stimulation (Bashour et al., 2014), suggesting that cellular forces may be directly involved in T-cell activation.

In most adherent cells, stresses are generated by the coordinated action of actin polymerization and myosin contraction, which drive actin flows. Although several studies suggest that cytoskeletal dynamics plays a crucial role in TCR signaling (Wulfing and Davis, 1998; Jacobelli et al., 2004; Kumari et al., 2012; Yi et al., 2012; Hammer and Burkhardt, 2013; Yu et al., 2013), the delineation of contributions of different cytoskeletal components to force generation is unclear. Regardless of the origin of the force, the overall magnitude of generated forces will depend on the elastic properties of the cellular actin network and the dynamics of actin assembly and disassembly. The effective internal stress generated in the viscoelastic actin network can be estimated from the material parameters of the cell (Betz et al., 2011). Independent measures of Jurkat cell stiffness suggest that these are soft (Young's modulus, ∼50–100 Pa [pN/μm²]; Rosenbluth et al., 2006), which likely limits the peak internal stresses to 100 Pa at best. Whether these forces are sufficient for activation is unknown, although force probe experiments suggest that primary T-cells pull and engulf anti-CD3–coated beads with small loading rates (Husson et al., 2011). However, the small size of the beads precludes any analysis of the forces exerted across the entire cell–substrate contact, which can be significantly larger.

Here we use traction force microscopy to measure the forces exerted by T-cells during activation. We find that Jurkat T-cells are weak force generators on anti-CD3–coated elastic substrates, exerting peak stresses reaching 20–30 Pa and total forces of a few nanonewtons, which is consistent with the amount of externally applied force required for T-cell activation (Kim et al., 2009). We find that these forces are largely driven by actin polymerization dynamics. Myosin contractility contributes to the generation of forces during the early phase of stimulation but is not required for the maintenance of force at later times. We find that T-cell signaling activation is sensitive to the stiffness of the activating substrates, as previously observed (Judokusumo et al., 2012), and this mechanosensitivity is correlated with increased cytoskeletal forces. Our results suggest that forces generated by the actomyosin cytoskeleton are sufficient for receptor activation in T-cells and modulate the efficacy of signal transduction.

RESULTS

Traction forces generated by Jurkat T-cells

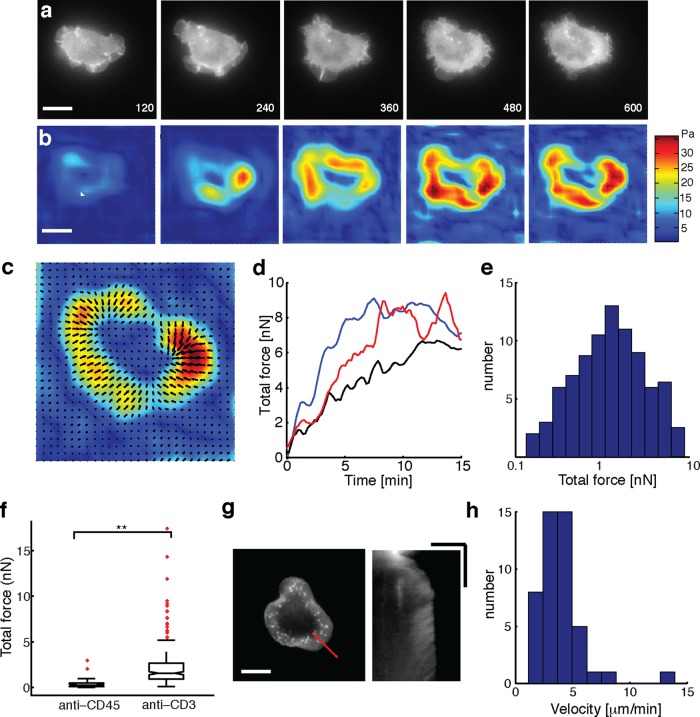
To measure the forces exerted by T-cells, we performed traction force microscopy, which allows the measurement of spatially resolved traction stresses (Dembo and Wang, 1999). Jurkat T-cells expressing enhanced green fluorescent protein (EGFP)–actin were allowed to spread on polyacrylamide gels coated with anti-CD3 antibody and embedded with fluorescent beads on the top surface as fiduciary markers. We imaged the spreading dynamics of cells starting from the earliest time points before the cell established contact with the substrate and continued imaging for at least 15 min. Typically, cells were completely spread before 15 min, as shown in the EGFP-actin images (Figure 1a) of a typical cell spreading on a gel of stiffness 1.7 kPa (which approximates the stiffness of APCs; Rosenbluth et al., 2006). To measure the traction stresses exerted by cells, we tracked the fluorescent beads using particle image velocimetry (PIV). The first frame of the live-cell image sequence, before the cell exerted traction on the surface, was used as the “zero displacement” or reference image. Unconstrained Fourier transform traction cytometry (FTTC; Butler et al., 2002) was used to calculate the traction stress map from the measured bead displacements at different times (Figure 1b). The average traction stresses exerted by cells were in the range of 5–10 Pa, whereas the peak traction stresses exerted were in the range of 10–30 Pa, in the same range as stresses exerted by neuronal growth cones (Betz et al., 2011; Koch et al., 2012). By contrast, rapidly migrating keratocytes and strongly adherent fibroblasts are known to exert traction stresses in the range of 100 Pa to several kilopascals (Lee et al., 1994; Dembo and Wang, 1999).

FIGURE 1:

Jurkat T-cells are weak generators of traction force. (a) Time-lapse fluorescence images of EGFP-actin expressing Jurkat T-cells spreading on an anti-CD3–coated elastic substrate (of stiffness 1.2 kPa). Scale bar, 10 μm. (b) Time-lapse images of traction stress color maps for the same cell as in a. The colors correspond to magnitudes of stresses as indicated in the color bar. (c) Vector map of traction force vectors showing the direction of exerted traction stresses. Scale bar, 10 μm. (d) Development of total force as a function of time for three example cells. Black trace corresponds to the cell in a. (e) Histogram of total traction force exerted by Jurkat T-cells (N = 95). (f) Comparison of traction stresses generated by cells on substrates coated with stimulatory antibody anti-CD3 and nonstimulatory antibody anti-CD45. (g) Snapshot of an EGFP-actin cell on an elastic substrate (left; scale bar, 10 μm), and a kymograph (right) drawn along the dashed line. The linear streaks illustrate actin retrograde flow in the cell periphery. Scale bar, 5 μm (horizontal), 5 min (vertical). (h) Histogram of retrograde flow speeds of cells spreading on gels in the stiffness range 1–2 kPa (N = 46).

We found that the traction stress was concentrated at the periphery of the spread area coincident with lamellipodia. The stresses exerted were higher a few micrometers internal to the periphery of the cell, which corresponded to actin-dense regions. Stresses were exerted centripetally and directed toward the cell center, as seen in the spatial map of vectors corresponding to the exerted stresses (Figure 1c). We used EGFP-actin images to track cell edges (as shown by the black line in Figure 1c) and obtain the contact area of the spreading cell at each time point. The total force exerted by the cell was calculated using F = ∫∫|T (x,y)|dxdy, where T(x, y) is the traction stress at the location (x, y). The force exerted by the cell rapidly increased over the first 5 min after initiation of spreading, until it reached a maximum and subsequently either saturated over the rest of the observation period or showed a slight decrease (Figure 1d). The total force exerted by cells (average force between 14 and 15 min of spreading initiation on gels of stiffness 1–2 kPa) showed considerable variation, with a median value of 2 nN (Figure 1e). Based on the observed stiffness of Jurkat cells (Young's modulus E ≈ 50–100 Pa; Rosenbluth et al., 2006), the expected value of maximum force is F ≈ E × area ≈ 2–5 nN.

We further verified that the observed forces were specific to TCR-ligand–mediated activation and spreading. Cells barely spread or established attachments on elastic substrates coated with poly-l-lysine alone, indicating that anti-CD3 coating was essential for spreading and force exertion. On substrates coated with the nonstimulatory antibody anti-CD45, cells established contact and spread but to a smaller extent than on stimulating surfaces. The total forces exerted by cells on a nonstimulating surface were significantly lower than the forces exerted on stimulating surfaces (anti-CD3 coated; Figure 1f). This indicates that the observed forces are largely a direct consequence of TCR–ligand binding leading to T-cell activation.

A previous study on neurons established a connection between traction forces exerted by cells, cell stiffness, and internal cellular forces with the rate of actin retrograde flows in the cell lamellipodia (Betz et al., 2011). We examined whether the actin flows in Jurkat T-cells were consistent with these observations. We quantified the rate of actin flow using kymography of actin structures in the lamellipodia of spread cells (Figure 1g). The distribution of actin flow speeds for cells spreading on gels of stiffness 1–2 kPa is shown in Figure 1h. The median value of retrograde flow of actin was measured to be 3 μm/min, which was consistent with other soft cells such as hippocampal neurons (Koch et al., 2012).

Role of the actin cytoskeleton in force generation

We next sought to examine the molecular basis of force generation and maintenance in Jurkat T-cells. The actomyosin cytoskeleton is likely the most important component responsible for force generation in these cells, similar to other cell types (Mossman et al., 2005; Babich et al., 2012). We perturbed the activity of the actomyosin cytoskeleton using small-molecule inhibitors, which are powerful agents for rapid and reversible inhibition of target molecules. Because preincubation of cells with inhibitors can affect cell spreading, we added inhibitors to cells after they had spread and measured the changes in cellular traction stress after inhibitor application. Unless specified, we added inhibitors to cells after 15 min of stimulation on anti-CD3–coated gels of stiffness in the range of 1–2 kPa and continued to image the bead movements and EGFP-actin dynamics simultaneously for an additional 15 min in order to measure the effect of the drug on forces. This method allows us to examine the effects of inhibitors on a single-cell basis and additionally avoid the problems of population averaging on cells that exhibit some heterogeneity in their exerted forces.

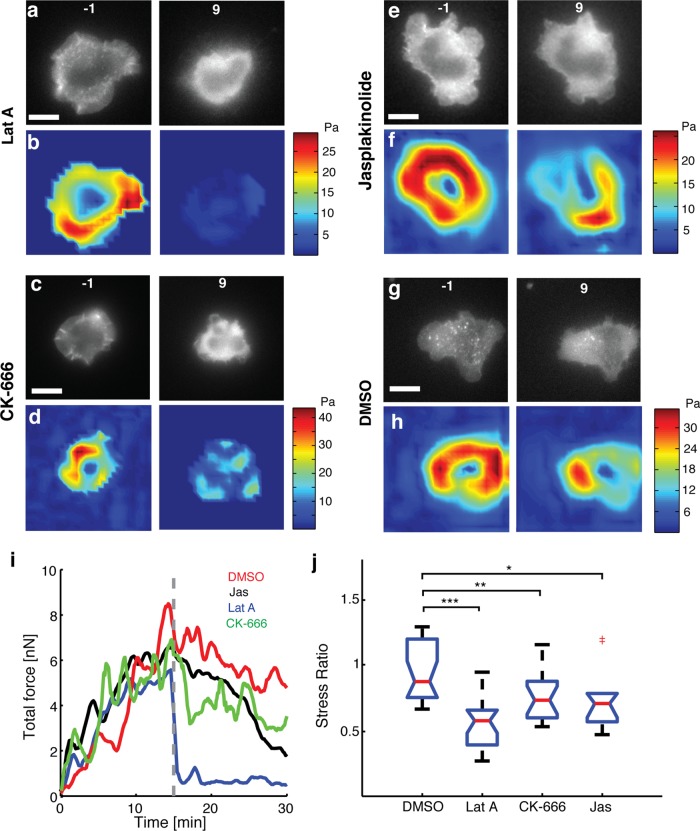
We first focused on the role of actin polymerization and depolymerization dynamics on cellular traction forces with latrunculin-A (Lat-A) to inhibit polymerization of actin, jasplakinolide (Jasp) to stabilize preexisting actin filaments, and CK-666 to inhibit the activity of Arp2/3, an actin-nucleating protein. Inhibition of actin polymerization by Lat-A resulted in the disruption of preexisting lamellipodia and actin-rich structures visible in the cell surface contact zone (Figure 2a), with a reduction in traction (Figure 2b). Application of Lat-A 5 min after initiation of spreading resulted in similar disruption of actin and loss of traction (unpublished data). Initial TCR signaling upon stimulation has been shown to result in immediate recruitment of signaling proteins that subsequently lead to Arp2/3 activation (Billadeau et al., 2007; Burkhardt et al., 2008; Beemiller and Krummel, 2010; Dustin and Groves, 2012). Hence the Arp2/3 complex might also be important in mechanically linking TCR to the F-actin cytoskeleton and therefore involved in the force generation process. Inhibition of Arp2/3 activation by addition of CK-666, an inhibitor that locks the Arp2/3 complex in an inactive conformation (Nolen et al., 2009), led to the retraction of lamellipodia and termination of edge dynamics (Figure 2c). This is in accordance with several previous observations that the Arp2/3 complex is essential for maintaining lamellipodial structure (Gomez et al., 2007). Consistent with our expectations, addition of CK-666 led to a reduction in the traction forces, as seen from the before-and-after traction maps (Figure 2d). CK-666 application also led to a reduction in F-actin intensity and retrograde flow but not a complete inhibition of actin flow (Supplemental Figure S1). Stabilization of F-actin upon addition of Jasp reduces the retrograde flow of actin in cells (Babich et al., 2012). Addition of 1 μM Jasp resulted in the reduction of traction forces in most cells, as shown in the traction maps before and after inhibitor addition (Figure 2, e and f). However, the effect of Jasp was somewhat variable, with some cells showing little effect of Jasp on actin flow and edge dynamics. These cells typically did not show a decrease in traction. As a control, addition of dimethyl sulfoxide (DMSO) carrier alone did not significantly affect the actin structures in the cell or the traction forces generated (Figure 2, g and h, and Supplemental Figure S1).

FIGURE 2:

Loss of F-actin dynamics reduces cellular force generation. Fluorescence images of EGFP-actin expressing Jurkat T-cells on an elastic substrate 1 min before (left) and 9 min after (right) application of (a) 1 μM latrunculin-A, (c) 100 μM CK666, (e) 1 μM jasplakinolide, and (g) 0.1% DMSO. Color maps of traction stresses of the same cells before (left) and after (right) addition of (b) 1 μM latrunculin-A, (d) 100 μM CK666, (f) 1 μM jasplakinolide, and (h) 0.1% DMSO. (i) Total traction force as a function of time for a representative cell in each of the conditions described. The dashed line represents the time point at which the drug was added. (j) Comparison of the after-to-before ratios of traction stresses for application of Lat-A (N = 20 cells), CK666 (N = 17 cells), and Jasp (N = 10 cells) with control (DMSO carrier, N = 20 cells). The average stresses in a 3-min time interval just before addition of drug and in the time interval 9–12 min after addition of drugs were used to compute the ratios. *p < 0.05, **p < 0.01, ***p < 0.001.

Representative curves of the time evolution of total traction force upon addition of inhibitors or control (DMSO carrier alone) are shown in Figure 2i. The force dropped significantly and rapidly after the addition of Lat-A, whereas addition of CK-666 and Jasp led to a decrease in force with a more gradual decline compared with Lat-A. To characterize the change in stress upon inhibitor application for a population of cells, we quantified the ratio of mean stress after (between 9 and 12 min) and before (−3 to 0 min) application of drug for each cell. Lat-A treatment decreased the traction stresses by almost 50% (ratio, 0.55), whereas CK-666 resulted in a stress ratio of 0.75, and the stress ratio for Jasp addition was 0.85 (Figure 2j). All of these were significantly different from the control (stress ratio, 0.95). Comparisons made at different time points after drug application showed similar reductions in traction stress (Supplemental Figure S2). Our results indicate that actin polymerization and depolymerization dynamics, as well as retrograde flows of actin, are important for the generation of forces in Jurkat T-cells. We also found that inhibitors targeting the microtubule cytoskeleton and dynein motors did not have any significant effect on the traction forces (Supplemental Figure S3).

Role of myosin activity in force generation

To examine the effect of myosin IIA activity on traction stress generation in Jurkat T-cells, we used blebbistatin, a specific inhibitor of the ATPase activity of myosin IIA (Cheung et al., 2002); ML-7, a myosin light chain kinase inhibitor (Saitoh et al., 1987); and Y-27632, a specific Rho-kinase (ROCK) inhibitor (Uehata et al., 1997). The inhibitors were added in the same manner as the actin inhibitors (15 min after spreading initiation), and the stress ratios after and before drug application were compared with the corresponding control conditions.

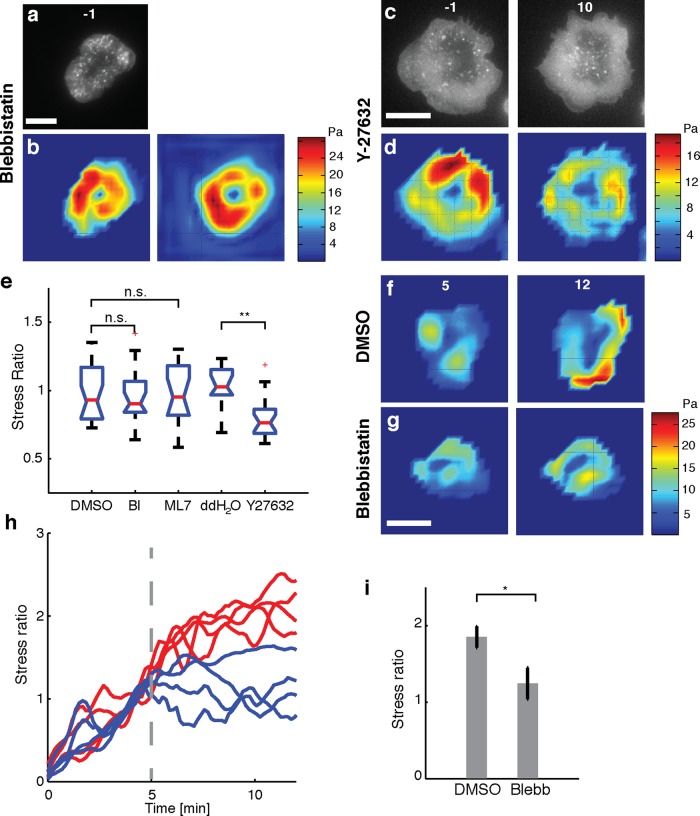
We first examined the effect of blebbistatin on traction force generation. Because blue light inhibits blebbistatin, we turned off the 491-nm illumination just before adding 50 μM blebbistatin to spreading Jurkat cells and compared the traction stress, as shown in the “before” and “after” stress maps (Figure 3, a and b) for a representative cell. Qualitatively, we found that the cell edge continued to behave in a dynamic manner upon blebbistatin addition. We measured actin retrograde flow in the presence of blebbistatin using TagRFP-T–actin–labeled cells and found that the flow was largely intact, indicating that myosin IIA does not play a significant role in maintaining actin flow in these cells (Supplemental Figure S2). We also found that myosin activity contributed to the formation of the actin ring (Supplemental Figure S4). We noted that the average stress ratio (0.96) was not significantly different from the control (stress ratio, 0.95; Figure 3e). We further found that 10 μM ML-7 had no effect on the traction stresses (stress ratio, 0.97; Figure 3e). On the other hand, treatment with 100 μM Y-27632 decreased the stresses exerted, as shown in the stress maps (Figure 3, c and d). The cell contact area did not decrease upon drug application, and actin lamellipodial structures were maintained even after the addition of Y-27632 (Figure 3, c and d). However, there was a slight decrease in the dynamics of the cell edge upon Y-27632 addition. The summary data show a modest decrease in stresses (stress ratio, 0.8) as compared with the double-distilled H₂O control (Figure 3e).

FIGURE 3:

Effect of myosin II activity on cellular force generation. (a) Fluorescence image of an EGFP-actin Jurkat T-cell on an elastic substrate 1 min before addition of 50 μM blebbistatin. (b) Traction stress color map of the same cell 1 min before (left) and 9 min after (right) addition of blebbistatin. (c) Fluorescence images of an EGFP-actin Jurkat T-cell on an elastic substrate 1 min before (left) and 9 min after (right) application of 100 μM Y-27632. (d) Traction stress color maps of the same cell before and after addition of Y-27632. (e) Comparison of the after-to-before ratios of traction stresses upon addition of blebbistatin (N = 20 cells) and ML7 (N = 17 cells) with control (DMSO carrier) and comparison of traction stress ratios upon addition of Y-27632 (N = 20 cells) with double-distilled H₂O control (N = 11 cells). The average stresses in a 3- min time interval just before addition of drug and in the time interval 9–12 min after addition of drug were used to compute the ratios. **p < 0.01. (f, g) Traction stress color maps for example cells (at the indicated time points after stimulation). Drug or vehicle was added at 5 min after stimulation (f, DMSO; g, blebbistatin). (h) Traces of the total force exerted by four example cells with drug addition 5 min after stimulation (vertical dashed line). The total force is normalized to the value exerted at 5 min after stimulation. Red lines indicate vehicle, and blue lines indicate the time of blebbistatin addition. (i) Summary statistics of the stress ratio after drug addition for cells averaged between 9 and 12 min after stimulation. N = 13 for blebbistatin and N = 12 for DMSO (p < 0.05, Wilcoxon's rank sum test). Scale bars, 10 μm.

Because myosin II contraction affects conjugate formation (Ilani et al., 2009) and T-cell activation in the early stages (Yu et al., 2012), it is possible that myosin II is required for the initial generation of forces but not at later stages. To test this, we applied blebbistatin 5 min after the initiation of spreading and examined the effect on the exerted forces. We found that whereas the total force exerted by the cell continued to increase until saturation upon vehicle (DMSO) application (Figure 3f), the total force exerted by the cell plateaued near the value at 5 min or decreased slightly upon blebbistatin application. However, blebbistatin did not abolish the forces (Figure 3, g and h), and a few cells continued to show increase in traction. Summary data of the stress ratios after and before treatment show that blebbistatin-treated cells have a significantly lower stress ratio than DMSO (carrier)-treated cells. This confirms that myosin II is required for the initial phase of force generation but is not involved at later time points (Figure 3i).

Effect of substrate stiffness on cellular forces, morphology, and signaling

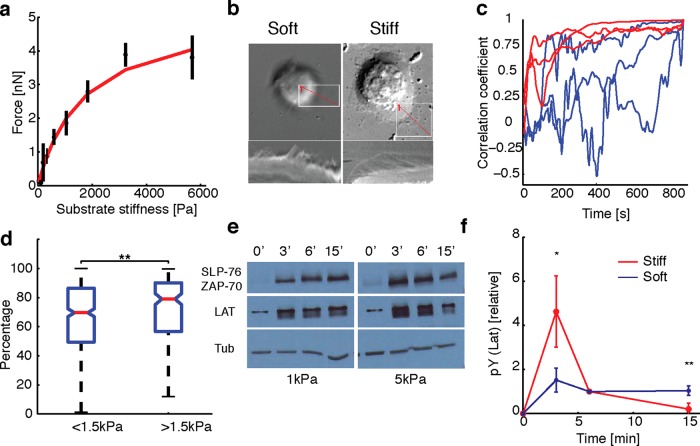
Many types of cells that interact with soft materials have the ability to sense the stiffness of their mechanical environment and respond to it by exerting larger forces on stiffer substrates (Janmey and McCulloch, 2007). Whether Jurkat cells respond similarly to substrate stiffness is not known. Recent experiments suggest that physical forces, such as those generated by the actin cytoskeleton, may be important for T-cell signaling. To examine whether Jurkat cells are sensitive to substrate stiffness, we fabricated polyacrylamide gels with varying concentrations of cross-linker to change the elastic modulus of the gels. We used gels that ranged in stiffness from 200 Pa to ∼6 kPa embedded with beads and imaged for traction force measurements as before. For comparison of forces between gels of different stiffness, we calculated the average traction stress exerted by stably spread cells between minutes 14 and 15 after spreading initiation. We found that the total force exerted by cells increased for soft substrates and rapidly saturated for stiffer substrates, as shown in Figure 4a. Similar results were obtained for earlier time points (unpublished data). Our observations suggest that Jurkat T-cells have the ability to sense the substrate stiffness and modulate the internally generated cytoskeletal forces as a function of substrate stiffness.

FIGURE 4:

Substrate stiffness affects traction forces and signaling. (a) Average total force exerted by cells (between 14 and 15 min of spreading initiation) as a function of gel stiffness (N = 500). The data are fit to 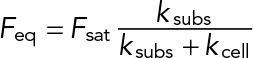(red curve) with F_sat = 5 nN, and k_cell = 1 nN/μm (corresponding to 1.5 kPa). (b) Top, DIC images of two representative cells spreading on soft (200 Pa) and stiff (10 kPa) gels. Kymographs of edge dynamics for the two cells along the locations indicated by the red lines. (c) Example time traces of Pearson coefficient between cell edge's radial position profile at 15 min and at earlier time points for cells spreading on soft (blue) and stiff (red) gels. (d) Comparison of the percentage of time for which the cell edge profile had correlation coefficient >0.5 compared with the profile at 15 min for softer (<1.5 kPa stiffness) and stiffer (>1.5 kPa stiffness) gels. The difference between the two conditions is significant (t test, p < 0.001) and indicates that cell edges are more dynamic on softer gels. (e) Western blot analysis of tyrosine phosphorylation (pY) levels (of LAT and ZAP70/SLAP76 substrates) at the indicated times on two different gel stiffnesses (∼1 and ∼5 kPa). (f) Densitometry analysis of relative pY levels (for LAT substrate) as a function of time for cells on soft gels (blue curve, ∼1 kPa) and stiff gels (red curve, ∼ 5 kPa). Analysis represents average of five different experiments.

The sigmoid fit to the traction–stiffness relationship (Figure 4a) suggested an operational definition in which gels with stiffness <1.5 kPa could be denoted as soft and gels of higher stiffness as stiff. We then examined whether cell morphology and edge dynamics showed distinct behaviors depending on gel stiffness. We found that cells were more dynamic, with cell edges displaying extensive protrusions and retractions and cell shape remodeling on soft gels. On stiff gels, cells typically spread out smoothly, with the cell edge advancing in a more isotropic manner. Furthermore, cell edge dynamics continued for a much longer period of time on softer gels, whereas on stiffer gels, cell edges either remained stably spread with minimal edge dynamics or retracted. This is illustrated in Figure 4b with kymographs drawn radially across the cell for representative cells on soft (left) and stiff (right) gels. We quantified the dynamics of cell morphology by comparing the radial distance profile (from the cell center around the cell edge as tracked from EGFP-actin images) at 15 min with that at each earlier time point. We calculated the Pearson correlation coefficient of these two profiles as the cell edge evolved in time. Representative time courses of the correlation coefficient for cells spreading on soft (<1.5 kPa, blue) and stiff (>1.5 kPa, red) gels are shown in Figure 4c. On stiff gels, the correlation coefficient was small initially, indicating considerable edge dynamics, but approached 1 as the cell periphery remained stable and persistent. However, on softer gels, the correlation coefficient remained low throughout, indicating ongoing edge dynamics through the duration of the movie. To quantify the population response to substrate stiffness, we calculated the percentage of time, P(t), that the correlation coefficient was >0.5, that is, with a shape similar to that at 15 min (Figure 4d). We found that cells on soft gels were significantly more dynamic, with low P(t) (t test, p < 0.001) compared with those on stiffer gels. These observations demonstrate that cell morphologies are more dynamic on soft substrates.

Recent work has shown that primary T-cells show enhanced signaling on stiff elastic substrates compared with softer ones (Judokusumo et al., 2012). However, the softest substrates used in that study were much stiffer than the stiffest ones used in our study. We confirmed that Jurkat T-cells showed phosphotyrosine (pY) signaling on the anti-CD3–coated gels of different stiffnesses used in our study and not on poly-l-lysine–coated gels (Supplemental Figure S5). We next examined whether the differences in observed forces and morphology at varying gel stiffness were associated with differences in signaling activation. Because it is difficult to sample signaling on a continuous range of substrate stiffnesses, we chose two specific stiffness values (∼1 and ∼5 kPa) as representative soft and stiff substrates, respectively. We allowed the cells to spread on gels for specific times (3, 6, and 15 min) before lysing them in situ and used the cell lysates for SDS–PAGE analysis. Western blotting for pY residues was used to analyze the relative pY levels at various time points on gels of different stiffness. Figure 4e shows the results of a representative SDS–PAGE analysis for soft (1 kPa) and stiff (∼5 kPa) gels. As seen from the bands of pY labeling, signaling is activated in cells spreading on both types of gels and appears to peak within 3 min of contact formation. However, for stiff gels, pY levels decrease after 6 min, whereas for soft gels, the pY levels appear to persist for a longer time (as the band appears more intense even at later time points). To quantify the development of signaling, we calculated the relative pY levels for the 35- to 40-kDa band, likely corresponding to phosphorylated LAT, for soft and stiff gels. We found that pY levels peaked at ∼3 min on stiff gels and rapidly declined, whereas on softer gels, the levels were lower but sustained even at 15 min after stimulation (Figure 4f). We observed the same trend for bands corresponding to ZAP70/SLP76. Our results suggest that the temporal evolution of early signaling in Jurkat T-cells is sensitive to substrate stiffness.

DISCUSSION

Mechanical forces have been implicated to play a role in TCR signaling and activation. Here we measured the traction stresses generated by Jurkat T-cells and transmitted through TCRs to the contacting surface. We find that T-cells are soft and weak force generators exerting average stresses on the order of 10–20 Pa during activation by anti-CD3–coated substrates. The stresses are distributed peripherally around the contact zone. The forces peak rapidly upon stimulation and are maintained for several minutes after initiation of spreading during signaling activation. Moreover, these forces are specifically generated in response to CD3 stimulation, as shown for human primary CD4⁺ cells (Bashour et al., 2014). Overall, the forces are of lower magnitude than those associated with integrin receptors in adherent cells.

In many adherent cells, integrins serve as the primary mediators of adhesion, and integrin-mediated adhesion plays an important role in T-cell activation (Grakoui et al., 1999; Alon and Dustin, 2007; Scholer et al., 2008). It is likely that Jurkat cells may exert lower stresses on substrates coated with integrin ligands—for example, VCAM in addition to anti-CD3—due to the reduction of retrograde flow (Nguyen et al., 2008). However, experiments measuring forces applied on beads covered with anti-CD3 plus anti–lymphocyte function-associated antigen-1 (LFA-1) displayed only subtle differences and similar loading rates compared with beads coated with anti-CD3 alone (Husson et al., 2011).

Previous studies established that actin cytoskeletal dynamics is essential for TCR signaling and activation (Babich et al., 2012). We found that an intact and dynamic F-actin cytoskeleton was essential for the exertion of traction stresses by Jurkat T-cells. As expected, inhibition of actin polymerization with Lat-A significantly decreased the forces generated. We also found that the Arp2/3 complex was required for force production, suggesting that the biochemical pathway that leads to Arp2/3 activation and actin polymerization (Goley and Welch, 2006) might also link activated TCR to the actin cytoskeleton physically (Billadeau et al., 2007). The decrease in forces upon Arp2/3 inhibition was not as severe as that due to Lat-A, suggesting that other pathways, such as formin-dependent ones leading to actin polymerization, may also contribute to force production. We further found that actin flow speeds were reduced by the inhibition of CK666. This reduction of flow speeds is consistent with observations in neuronal growth cones (Yang et al., 2012). Because it is known that formin-mediated actin polymerization plays a significant role in T-cell activation (Gomez et al., 2007), it is possible that formin-mediated actin polymerization is able to maintain actin structures and support traction forces in the absence of Arp2/3-mediated actin assembly. Stabilization of F-actin by Jasp consistently led to a reduction in forces in cells in which actin flows and edge dynamics were inhibited upon Jasp treatment. In some cells, however, in which Jasp treatment did not affect the actin dynamics or flow, the stresses remained unaffected. These results point to a relationship between actin flows and stress generation. We have not been able to relate actin flows to local forces due to the limitations of wide-field imaging, but this will be a subject of future study.

Myosin IIA-driven contraction of actomyosin networks is the major contributor to actin retrograde flow in neuronal growth cones and filopodia (Van Goor et al., 2012) and contributes 90% of the traction stress exerted by mouse embryonic fibroblasts (Cai et al., 2006). The role of myosin II in TCR signaling has not been unequivocally established. The primary form of myosin II present in T-cells is myosin IIA, with a very small fraction of myosin IIB (Jacobelli et al., 2004; Ilani et al., 2009). Although some studies showed that myosin II inhibition has no effect on actin retrograde flow or microcluster transport (Jacobelli et al., 2004; Babich et al., 2012; Beemiller et al., 2012; Yu et al., 2012), others showed that myosin IIA inhibition results in fewer and more unstable conjugates between T-cells and stimulatory cells, as well as reduction in microcluster formation and transport in primary and Jurkat T-cells stimulated by antigens presented on bilayer substrates (Ilani et al., 2009; Yi et al., 2012). We find that suppression of myosin IIA activity by blebbistatin and ML7 application did not affect the maintenance of traction forces in cells that were already spread. On the other hand, application of blebbistatin during the early phase of spreading retarded further development of tractions, which is consistent with the observation that myosin inhibition reduces the stability of T-cell-APC conjugates.

In contrast, inhibition of Rho-kinase by Y-27632 modestly decreased the forces. It is possible that inhibition of Rho-kinase has additional effects on the actin cytoskeleton, which may result in decreased traction. Alternatively, Y-27632 may slow down the movement of actomyosin structures such as actin arcs, which may exert a contractile force and contribute to the forces (Yi et al., 2012). Overall, our results suggest that myosin plays a limited role in the maintenance of force but is required for the proper development of force during early spreading. This is consistent with the transient effect of myosin on microcluster movement in primary T-cells spreading on patterned bilayers (Yu et al., 2012). A better understanding of the relationship between gradients of actin retrograde flow and traction stress requires a more careful characterization of actin dynamics using fluorescence speckle microscopy. Although in general, myosin IIA contractility is essential for the transmission of tractions to integrin-dependent adhesions (Cai et al., 2006; Fournier et al., 2010; Aratyn-Schaus et al., 2011; Koch et al., 2012), the extent of stress reduction upon myosin IIA inhibition is variable (Cai et al., 2006; Meili et al., 2010). Dictyostelium cells lacking an analogous myosin show only modest (50%) inhibition (Del Alamo et al., 2007), suggesting that additional mechanisms, possibly due to actin retrograde flow, can maintain and transmit sufficiently high tractions.

We found that Jurkat T-cells exert larger forces on substrates of increased stiffness (in the stiffness range of 200 Pa to 6 kPa), indicating that they are able to sense the substrate rigidity over this large range and modulate their force generation accordingly. Many cell types, including fibroblasts, neutrophils, and neurons, have been shown to be mechanosensitive, being able to exert increasing force on substrates of greater stiffnesses (Lo et al., 2000; Chan and Odde, 2008; Oakes et al., 2009). This appears to be in contrast to a recent study on human primary CD4⁺ cells spreading on anti-CD3–coated micropillar arrays (Bashour et al., 2014), which did not show any change in traction force per pillar as a function of pillar stiffness. However, our results are consistent with a previous study using red blood cells as a force probe, which showed that T-cells engage anti-CD3–coated beads and pull with loading rates that increased with probe stiffness (Husson et al., 2011). Mouse primary T-cells have been found to respond to the mechanical stiffness of substrates, with increased interleukin-2 production and enhanced tyrosine phosphorylation on stiffer polyacrylamide gels (Judokusumo et al., 2012). However, the stiffness range explored in those studies was considerably higher (10–200 kPa), and traction forces were not measured. In vivo, T-cells spread on APCs that are soft (in the stiffness range of a few hundred pascals to 1 kPa; Rosenbluth et al., 2006), suggesting that our observations of enhanced dynamics of the cell edge on soft gels may be physiologically relevant to T-cell function.

We also found altered cell morphology on gels of different rigidities. On soft substrates, the cell edge was observed to be highly dynamic, undergoing repeated rounds of protrusion and retraction. The repeated edge dynamics may result from repeated bursts of actin polymerization leading to multiple leading edges and formation of fresh signaling clusters at the nascent cell periphery. In contrast, on stiff substrates, the cell-edge expansion is smoother, without repeated protrusions. Previous studies have shown that the continuous recycling of signaling intermediates (tyrosine kinases and substrates) is essential for maintaining levels of pY after cell spreading (Bunnell et al., 2002; Lee et al., 2002; Campi et al., 2005; Varma et al., 2006). Thus it is likely that the continued cell-edge dynamics of cells on softer substrates may mediate the sustained signaling observed on these substrates.

The response of Jurkat cells to substrate stiffness can be explained using a model derived from active matter theory (Marcq et al., 2011). In a simple one-dimensional version of this model, the extracellular environment can be represented by a linear spring of length l_subs(t) at time t, rest length l_0,subs(t), and spring constant k_subs. The cell exerts an active stress (σ_a) resulting from actin polymerization and myosin contractility, which consumes energy by ATP hydrolysis. Force balance leads to a simple expression for the force, 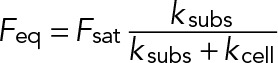, where F_eq is the steady-state force; 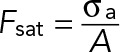, where A is the cell area; k_subs is the effective spring constant for the substrate (0.1–10 nN/μm for the gel stiffnesses considered here); and k_cell is the stiffness of the cell (∼1 nN/μm). Thus, on soft substrates, the steady-state force exerted by the cell linearly increases with stiffness and saturates when K_ext ≫ K_cell. Given our measured saturating force of 5 nN and the typical cell area A ≈ 100 μm², we can estimate the peak active stress, 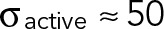Pa, which is in agreement with the measured Young's moduli of Jurkat cells (Rosenbluth et al., 2006). The same model can also be used to estimate the maximal strain rate that can be exerted by these cells, which will pull on TCR–ligand bonds. Assuming a linear force–velocity relationship (appropriate for overdamped systems), the loading rate can be estimated as 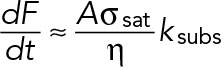, where 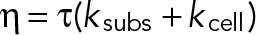is the viscous dissipation in the actin gel and A is the area over which the stress is exerted. Again, using our estimated values for these parameters 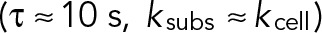, a typical bead (area, ∼1 μm²) would experience a loading rate of ∼2–3 pN/s, which is well in agreement with observed rates experienced by anti-CD3–coated beads in a force sensor apparatus (Husson et al., 2011).

The molecular mechanisms that underlie mechanosensing remain a topic of intense study (Moore et al., 2010). A number of studies suggest that integrins may serve as putative mechanosensors (Alon and Dustin, 2007). We find that Jurkat cells exhibit mechanosensitivity even without integrin engagement, suggesting that these mechanisms may be quite general. Jurkat cells also lack CasL (a p130Cas homologue), a protein implicated in mechanosensitivity (Sawada et al., 2006; Yu et al., 2012), but other possible candidates include PLC-γ (Babich et al., 2012). In conclusion, our studies show that mechanosensitivity may be a general feature of T-cells. Our results place constraints on the forces that these cells are able to generate and thereby apply on TCR–ligand linkages to potentially initiate signaling.

MATERIALS AND METHODS

Cells and reagents

Jurkat E6-1 cells transfected with EGFP-actin were cultured in RPMI 1640 supplemented with 10% fetal bovine serum and 1% penicillin-streptomycin. TagRFP-T sequence was cloned from pcass TagRFP-T (a gift from Morgan Huse, Rockefeller University, New York, NY) into pEGFP-actin (Clontech, Mountain View CA) to create pTagRFP-T–actin and then further cloned into Z4-MSCV-TagRFP-T (a gift from Morgan Huse) to create Z4-MSCV-TagRFP-T–actin, allowing retroviral bicistronic expression of TagRFP-T–actin and a Zeocin-resistant gene. Retroviruses were generated according to standard protocol with Phoenix Amphotropic cells and transduced into Jurkat E6-1 cells by spin infection. The cells were then selected in 200 μg/ml Zeocin for 2 wk and sorted with fluorescence-activated cell sorting to obtain TagRFP-T–actin cells.

Anti-CD3 was purchased from eBioscience (San Diego, CA). Y27632 was purchased from SelleckChem (Houston, TX). (–)-Blebbistatin and jasplakinolide were purchased from Calbiochem (Billerica, MA). Forty percent acrylamide, 2% Bis-acrylamide, ammonium persulfate, and tetramethylethylenediamine were purchased from Bio-Rad (Hercules, CA). FluoSphereRed microspheres, 0.2 μm, were purchased from Molecular Probes (Eugene, OR). Poly-l-lysine, ML-7, latrunculin-A, and nocodazole were purchased from Sigma-Aldrich (St. Louis, MO). Sylgard 164 elastomers were purchased from Ellsworth Adhesives (Germantown, WI). Stainless steel microspheres were purchased from Salem Balls (Canton, CT). Polystyrene microspheres were purchased from Polysciences (Warrington, PA). Hydrazine hydrate was purchased from Acros (Pittsburgh, PA).

Fabrication and calibration of polyacrylamide gels

Traction force microscopy procedures were followed as described in Sabass et al. (2008), with a slight modification to form a thin and dense layer of fluorescent beads trapped on top of the polyacrylamide gel. Before coating of proteins, the top of the gel was observed under an epifluorescence microscope (TE2000; Nikon, Tokyo, Japan) at 10× magnification in rhodamine channel to ensure that a monolayer of densely spaced beads was present. Suitable gels were then attached to the bottom of a MatTek 35-mm dish (MatTek, Ashland, MA) with Sylgard 164 silicone elastomer (Dow Corning, Midland, MI). Poly-l-lysine, 0.01%, was coated on polyacrylamide with the hydrazine hydrate method. After coating with poly-l-lysine, the gel was washed three times with phosphate-buffered saline, and 10 μg/ml anti-human CD3 (Hit3a) was added to the gel and incubated either at 37°C for 2 h or 4°C overnight. Fluorescently labeled Hit3a was used to verify that antibody coating did not depend on substrate stiffness (unpublished data). After each image acquisition, gel height was determined by microscope's focusing mechanism and corrected for axial scaling. Stainless steel balls (1/64-, 1/32-, and 3/64-in. diameter) or polystyrene balls (for gels with Young modulus <300 Pa) were then added to where the time series was taken. Steel balls were removed by a magnetic stir bar, and polystyrene balls were removed by bulb aspiration for a few times. The indentation caused by the ball and the gel height at that spot were recorded. The acrylamide concentration was changed from 2 to 8% with the cross-linker (Bis) concentration kept fixed at 0.1% in order to change the gel stiffness. The Young's modulus of each individual gel used for the experiments was calculated using a Hertz model for an elastic substrate with finite thickness (Pelham and Wang, 1997) rather than using an average relation between gel stiffness and Bis concentration. Typically, gels with acrylamide/Bis ratios of 2:0.1, 3:0.1, 4:0.1, and 5:0.1 were measured to have an average stiffness of 0.8, 1, 3, and 5 kPa, respectively.

Microscopy

Live-cell movies of cell spreading were taken over 15 min at a frame rate of 5 s per frame in bright-field differential interference contrast (DIC), FluoSphereRed, and GFP channels. Images were collected using an inverted microscope (TE2000 PFS; Nikon, Melville, NY) with a cooled charge-coupled device camera (CoolSNAP HQ2; Photometrics, Tucson, AZ). EGFP-actin and fluorescent receptors were imaged with total internal reflection fluorescence using a 60×/1.49 numerical aperture objective lens, a 491-nm laser (100 mW; Andor, South Windsor, CT) for EGFP excitation, and a 561-nm laser (75 mW; Andor) for FluoSphereRed excitation. The imaging medium used was L-15, and the dish was kept at 37°C throughout data acquisition by means of an airstream incubator (Nevtek, Williamsville, VA). Illumination wavelength and exposure times were controlled using a multibandpass dichromatic mirror (Chroma, Rockingham, VT) and bandpass excitation and emission filters (Chroma) in electronic filterwheel/shutter devices (Sutter Instruments, Novato, CA). In inhibitor addition experiments, data acquisition was paused at 15 min. Inhibitors were added at an equal volume as the imaging medium and double in target final concentration were added, and data acquisition was resumed for 5–15 min. For blebbistatin experiments, we inserted a filter in the light path to block blue-green illumination.

Data analysis

The image sequences in FluoSphereRed channel were denoised and input into the freely available MATLAB package MatPIV for particle image velocimetry analysis. The first image in the sequence before the cells contacted the substrate was taken as the zero-displacement image, and sample drift was corrected for by tracking the displacements of fiduciary beads far away from any cells, using particle-tracking algorithms. Displacement vector maps generated were then input into an unconstrained FTTC algorithm implemented in MATLAB (Butler et al., 2002) and extended to include finite-thickness correction (Del Alamo et al., 2007). The analysis was carried out for every frame in the image sequence, and the analyzed traction stress data were presented as traction stress magnitude and vector maps image sequences, respectively. Cells showing significant above-background displacements and traction were chosen by observation for cell edge tracking and further analysis. The method was sufficiently sensitive to detect bead displacements in gels up to 6 kPa, as verified by single-particle tracking (Supplemental Figure S6). Cell edge tracking was implemented as described in Lam Hui et al. (2012). The centroid of the tracked cell area in the first frame was treated as the cell's center. At each frame, the radial distance and angle of each piece of the cell edge from the centroid was recorded and grouped into bins of 6°. The radial edge profile of the cell at each time point was represented by the average radial distance in each bin. Pearson's correlation coefficient of the radial edge profile was calculated in MATLAB. Stress vectors calculated at each grid point from FTTC were assigned to neighboring pixels, and average traction stress magnitude was obtained by integrating the magnitudes of stress vectors at every pixel inside the cell boundary, irrespective of the stress direction (presented in Figures 1–3). We noted that on gels of high stiffness, the bead displacements caused by the cell were small, whereas the background noise in PIV tracking remained the same, resulting in higher background traction compared with data from cells spreading on a soft substrate, owing to the fact that the calculated traction stress is proportional to the substrate Young's modulus. To eliminate the bias, we used the traction stress measured at the first frame as the background and subtracted this from the stresses at later times to obtain the effective traction stress exerted by the cell. Typically, we found that the stress measured in the first frame was comparable to the traction field outside the cell boundary and was ∼1 Pa.

Densitometry analysis

We first normalized the intensity within the 35- to 40-kDa band by tubulin intensity at every time point. Then we calculated the normalized difference as (ratio − ratio_{0 min})/(ratio_{6 min} − ratio_{0 min}).

Abbreviations used:

AFM

atomic force microscope

APC

antigen-presenting cell

ATP

adenosine triphosphate

CD

cluster of differentiation

DMSO

dimethyl sulfoxide

EGFP

enhanced green fluorescent protein

FTTC

Fourier transform traction cytometry

LAT

linker for activation of T-cells

LFA-1

lymphocyte function–associated antigen 1

MHC

major histocompatibility complex

PIV

particle image velocimetry

pY

phosphotyrosine

ROCK

Rho-associated protein kinase

SLP76

SH2-domain containing leukocyte protein of 76 kDa

TCR

T-cell receptor

VCAM

vascular cell adhesion molecule

ZAP70

zeta-chain association protein kinase 70.