Theoretical Analysis of Dynamic Processes for Interacting Molecular Motors

Abstract

Biological transport is supported by collective dynamics of enzymatic molecules that are called motor proteins or molecular motors. Experiments suggest that motor proteins interact locally via short-range potentials. We investigate the fundamental role of these interactions by analyzing a new class of totally asymmetric exclusion processes where interactions are accounted for in a thermodynamically consistent fashion. It allows us to connect explicitly microscopic features of motor proteins with their collective dynamic properties. Theoretical analysis that combines various mean-field calculations and computer simulations suggests that dynamic properties of molecular motors strongly depend on interactions, and correlations are stronger for interacting motor proteins. Surprisingly, it is found that there is an optimal strength of interactions (weak repulsion) that leads to a maximal particle flux. It is also argued that molecular motors transport is more sensitive to attractive interactions. Applications of these results for kinesin motor proteins are discussed.

1. Introduction

A central role in supporting many cellular processes is played by several classes of enzymatic molecules that are known as motor proteins or molecular motors [1–5]. They use the chemical energy released from hydrolysis of adenosine triphosphate (ATP) to drive cellular transport along cytoskeleton filaments. Single-molecule properties of various molecular motors are now well investigated both experimentally and theoretically [4–6]. However, cellular cargoes are often moved by groups of motor proteins, and microscopic mechanisms of collective motor behaviors remain not well understood [5,7,8]. Recent experiments on kinesin motor proteins indicate that motors bound to the microtubule filament interact with each other [9–11]. The evidences for this behavior are found from observations that kinesins on microtubules phase segregate into more dense and less dense patches, and from measurements of different times to be bound to the filament depending on the presence of neighbors [9–11]. It was estimated that these interactions are weakly attractive (1.6 ± 0.5k_BT) [9]. It raises a question on a fundamental role of this phenomenon in collective motion of motor proteins. Various chemical transitions such as bindings, unbindings, hydrolysis and steppings should be affected by this potentials, influencing the overall dynamics of motor proteins. However, the impact of such interactions on transport of molecular motors is not fully explored [7]. There are several investigations addressing collective dynamics of interacting motor proteins [12–14, 24]. But the main limitation of these studies is a phenomenological description of interactions that does not provide a quantitative description for chemical transitions in motor proteins.

One of the most powerful tools in investigating multi-particle non-equilibrium systems is a class of models called totally asymmetric simple exclusion processes (TASEP) [15–17]. It is known that these models successfully capture essential properties of a large number of physical, chemical and biological systems [16–22]. Different versions of TASEP have been extensively employed in studies of various aspects of biological molecular motors [8, 13, 16, 19, 23, 24], providing an important microscopic insights on these complex processes. TASEP with interactions have been studied before, but only for the particles on the ring [13], or with phenomenologically defined interactions [24–26].

In this paper, we investigate the effect of inter-molecular interactions on collective dynamics of motor proteins by introducing a new TASEP model with interactions. The most important advance of our method is that interactions are taken into account using a fundamental thermodynamic procedure. It provides a direct way of coupling microscopic properties of motor proteins with their collective dynamic features. To make the model more realistic we use open boundary conditions since the cytoskeleton filaments have finite length. Using various mean-field analytical methods and extensive Monte Carlo simulations we compute particle currents and density profiles for molecular motors. It provides us with a direct method to address the fundamental role of interactions. Our analysis suggests that there is an optimal interaction strength, corresponding to weak repulsions, that leads to the maximal particle flux. It is also found that interactions introduce significant correlations in the system and modify phase diagrams. In addition, dynamic properties of molecular motors are influenced stronger by attractive interactions.

2. Theoretical Description

2.1. Model

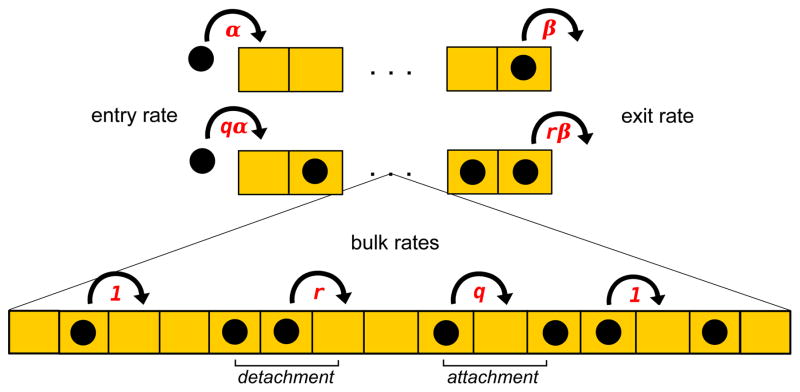
We consider a transport of molecular motors on the cytoskeleton filaments as a multi-particle motion along a lattice segment with L sites as illustrated in Fig. 1. The model assumes very long filaments, L ≫ 1. For each lattice site i (1 ≤ i ≤ L) we assign an occupation number τ_i, which is zero if the site is empty or τ_i = 1 if the site is occupied. Each site cannot be occupied by more than one particle. It is assumed that each two particles sitting on neighboring sites interact with each other with an energy E (E > 0 correspond to attractions and E < 0 describe repulsions). A single motor that is not a part of the particles cluster can move forward with the rate 1 if it moves to the site without neighbors (Fig. 1). There is no energy change in this case. However, if the particle hops into another cluster it moves with rate q ≠ 1 because the energy of the system changed by creating a new pair of neighbors (see Fig. 1). Similarly, for the particle breaking from the cluster its forward rate is equal to r ≠ 1 when the particle does not have neighbors in the new position. But for the case when one pair is broken and another one is created the stepping rate is equal to 1 since there is no overall energy change (Fig. 1). Creating and breaking the pair of particles can be viewed as opposite chemical transitions, so the detailed balance arguments can be applied,

Figure 1.

Schematic picture of TASEP model with interacting particles

$$\frac{q}{r}=exp(\frac{E}{k_{B}T}).$$ (1)

It is important to note that the motor protein stepping along the cytoskeleton filaments is a complex process that combines chemical transformations and mechanical motion. However, it can be viewed as a set of reversible chemical transitions between spatially separated biochemical states [3, 5]. For this reason, the stepping can be well approximated as a single reversible chemical reaction, justifying the application of the detailed balance arguments.

To simplify analysis, we assume that the energy E is equally split between creation and breaking processes, providing explicit expressions for the stepping rates q and r,

$$q=exp(\frac{E}{2k_{B}T}),r=\frac{1}{q}=exp(\frac{-E}{2k_{B}T}).$$ (2)

The splitting of the interaction potential between the rates q and r is not unique, but other possibilities can be easily explored in our method. In addition, it can be shown that particle dynamics is similar for all cases. Furthermore, our computer simulations (not shown here) indicate that qualitative behavior of the system is independent of the energy splittings.

Eqs. (2) have a clear physical meaning. For attractive interactions (E > 0) the particle moves faster (q > 1) to create a new pair since the energy of the system decreases by E. Breaking out of the cluster increases the energy by E and the transition rate is slower (r < 1). Similar arguments can be given for repulsive interactions (E < 0). When there is no interactions (E = 0) we have q = r = 1 and the original TASEP with only hard-core exclusions is recovered.

This model is related to a class of lattice-gas models studied by Katz, Lebowitz and Spohn, which are known as KLS models [26,27]. This approach has been employed for understanding non-equilibrium properties of multi-particle systems. However, our method is not the same as the KLS model. The main difference is that our transition rates are determined from fundamental thermodynamic arguments, while the KLS models are generally inconsistent with thermodynamics. It is important to emphasize that generally stochastic models are not derived from the first principles. So their applications for real systems in Chemistry, Physics and Biology must be accompanied by fundamental constraints. The requirement of thermodynamic consistency is such constraint. This is the main reason why the KLS models cannot be used for analyzing interactions in motor proteins, although they are still important for clarifying general principles of non-equilibrium systems. Furthermore, the importance of thermodynamic constraints can be seen from the fact that the number of possible stationary phases decreases in comparison with the KLS models predictions, as we show below. At the same time, for weak interactions both approaches converge, as expected. We also note here that, in contrast to some previous studies, our thermodynamically consistent method accounts for interactions in all chemical transitions in the system. In addition, it differs from other TASEPs with interactions [13, 24, 25, 29, 30] because in our model the stepping rates depend on the state of four consecutive lattice sites.

Interactions also modify the boundary transitions as shown in Fig. 1. The entrance rate is equal to α if no particle pair created, while the rate is equal to qα when the pair creation is involved. Similarly, the exit rate of the single particle is given by the rate β, while exiting with breaking from the cluster changes the rate to rβ.

2.2. Simple Mean-Field Theory

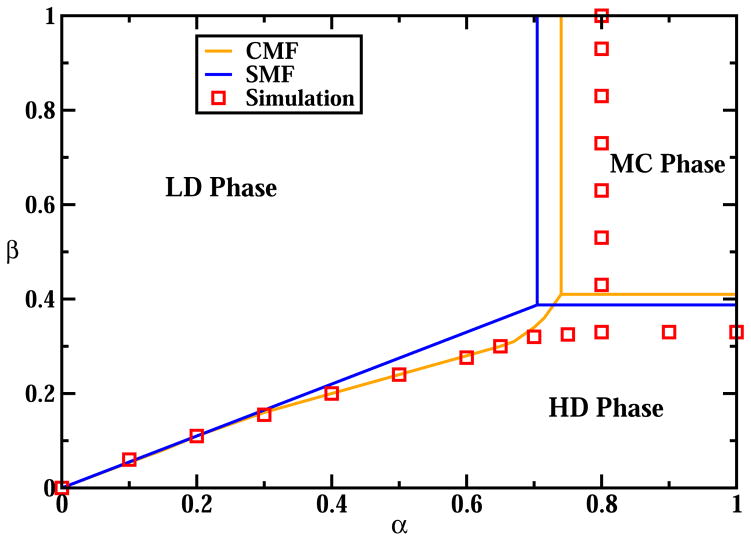
To analyze the system we start with the simplest mean-field (SMF) approach that neglects all correlations in the system. It assumes that for any two sites on the lattice their occupancies are independent of each other, i.e., Prob(τ_i, τ_j) ≈ Prob(τ_i) * Prob(τ_j) for 1 ≤ i, j ≤ L. The particle density at every site is associated with an average occupancy, ρ =< τ >, and it reaches a constant value in the bulk of the system. It can be shown that, similarly to the classical TASEP without interactions, there are three stationary phases, low density (LD), high density (HD) and maximal current (MC), as illustrated in Fig. 2.

Figure 2.

Stationary phase diagram for TASEP with inter-molecular interactions. The case of weakly repulsive interactions, E = −1.2 K_BT, is shown.

When dynamics at the entrance is rate-limiting we have a low-density (LD phase). In this case the temporal evolution of the particle density ρ at every lattice site can be described by

$$\frac{d\rho }{dt}=\alpha {(1-\rho )}^2+q\alpha \rho (1-\rho )-\rho {(1-\rho )}^3-r{\rho }^2{(1-\rho )}^2-{\rho }^3(1-\rho )-q{\rho }^2{(1-\rho )}^2$$ (3)

This equation suggests that the change in the particle density is determined by the difference in the particle fluxes. The first two terms on the right side correspond to the entrance current, while the last four terms are for the bulk current that leaves the giving lattice site. At the stationary state, we have $\frac{d\rho }{dt}=0$, and this equation can be solved exactly, producing following expression

$${\rho }_{LD}=\frac{q-\sqrt{q^2-4\alpha q(q-1)}}{2(q-1)}.$$ (4)

For q = 1 it reduces to ρ_LD = α, as expected for the standard TASEP without interactions. From this equation and using Eq. (3) the expression for the current can be also derived,

$$J_{LD}=\alpha \frac{\alpha q(q-1)-1+\sqrt{q^2-4\alpha q(q-1)}}{q-1},$$ (5)

which in the limit q → 1 produces J_LD = α (1 − α).

For the case when the exiting becomes the rate-limiting step the system is in a high-density (HD) phase. In this case, the time evolution of the particle density is given by

$$\frac{d\rho }{dt}=\rho {(1-\rho )}^3+r{\rho }^2{(1-\rho )}^2+{\rho }^3(1-\rho )+q{\rho }^2{(1-\rho )}^2-\beta \rho (1-\rho )-r\beta {\rho }^2.$$ (6)

In the steady-state limit we obtain,

$${\rho }_{HD}=\frac{q-2+\sqrt{q^2-4\beta (q-1)}}{2(q-1)},$$ (7)

while for the current we have

$$J_{HD}=\beta \frac{\beta (q-1)-1+\sqrt{q^2-4\beta (q-1)}}{q(q-1)}.$$ (8)

When there are no interactions in the system (q = 1) the particle density and the current reduce to the values for the standard TASEP, ρ_HD = 1 − β and J_HD = β(1 − β).

In the bulk of the system the steady-state particle current is independent of entry and exit rates. It can be expressed in terms of an average density ρ in the following form,

$$J=\rho {(1-\rho )}^3+r{\rho }^2{(1-\rho )}^2+{\rho }^3(1-\rho )+q{\rho }^2{(1-\rho )}^2,$$ (9)

where $q=\frac{1}{r}=exp(\frac{E}{2k_{b}T})$. In this situation, the current can reach its highest value and this phase is known as a maximal current (MC) phase. In the case of no interactions (E = 0 and q = r = 1) we obtain the parabolic expression J = ρ(1 − ρ) for the current as expected for the standard TASEP model without interactions. The MC phase is specified by a condition that $\frac{\partial J}{\partial \rho }=0$, which leads to the following expression,

$$(2\rho -1)[-1+\rho (4-2q-2r)+{\rho }^2(2r+2q-4)]=0.$$ (10)

This equation has only one real root, $\rho =\frac{1}{2}$. Substituting $\rho =\frac{1}{2}$ into Eq. (9), we obtain the following expression for the maximal current as a function of interaction energy,

$$J_{MC}=\frac{1}{8}+\frac{r+q}{16}=\frac{1}{8}+\frac{exp(\frac{E}{2k_{b}T})+exp(\frac{-E}{2k_{b}T})}{16}.$$ (11)

For E = 0 (q = r = 1) it yields $J_{MC}=\frac{1}{4}$, as expected for the standard TASEP model without interactions. In the MC phase the bulk density reaches the maximal value of ρ_MC = 1/2.

Our computer simulations indicate that LD-MC and HD-MC transitions are continuous. We use then the continuity of the stationary current at transition to determine the boundary lines separating LD and MC and HD and MC phases. The equality of the stationary current at the boundary J_MC = J_LD yields the following expression,

$$\alpha {(1-\rho )}^2+q\alpha \rho (1-\rho )=\rho {(1-\rho )}^3+r{\rho }^2{(1-\rho )}^2+{\rho }^3(1-\rho )+q{\rho }^2{(1-\rho )}^2.$$ (12)

Since in the MC phase the density is equal to ρ = 1/2 the boundary in terms of the entrance rate is given by

$${\alpha }_b=\frac{1+q}{4q}.$$ (13)

Similarly, we can determine the boundary between the HD and MC phases,

$${\beta }_b=\frac{1+q}{4}.$$ (14)

However, the transition between LD and HD phases is discontinuous and it involves a density jump. Then from the condition of equal current at the phase line, J_HD = J_LD, we derive

$$\beta {\rho }_{HD}(1-{\rho }_{HD})+r\beta {\rho }_{HD}^2=\alpha {(1-{\rho }_{LD})}^2+q\alpha {\rho }_{LD}(1-{\rho }_{LD}),$$ (15)

Using Eqs. (4) and (7) it can be shown that it leads to a simple relation for this phase boundary,

$$\beta =q\alpha .$$ (16)

2.3. Cluster Mean-Field Theory

The fact that the SMF method neglects correlations is the main reason for not satisfactory description of TASEP with stronger inter-molecular interactions. To develop a more reasonable analysis we propose to use a mean-field approach that takes into account some correlations. Our idea is to fully describe particle dynamics inside of a cluster of several lattice sites, but correlations between states of different clusters will be neglected. In our calculations clusters with 2 lattice sites are utilized. In this approach, the occupation of four consecutive sites is written as Prob(τ_i−1, τ_i, τ_i+1, τ_i+2) ≈ Prob(τ_i−1, τ_i)*Prob(τ_i+1, τ_i+2). The method is called a cluster mean-field (CMF). There are four possible states for each two-site cluster depending on the occupancy of sites that can be labeled as (1,1), (1,0), (0,1) and (0,0). We define P₁₁, P₁₀, P₀₁ and P₀₀ as probabilities to be found in one of these configurations, respectively. The normalization requires that P₁₁ + P₁₀ + P₀₁ + P₀₀ = 1. The average bulk density and the current can be expressed in terms of these functions,

$$\begin{array}{l}{\rho }_{\mathit{bulk}}=\frac{1}{2}\sum _{{\tau }_1}\sum _{{\tau }_2}{\tau }_{1}P({\tau }_1,{\tau }_2)+\frac{1}{2}\sum _{{\tau }_1}\sum _{{\tau }_2}{\tau }_{2}P({\tau }_1,{\tau }_2)\\ =\frac{1}{2}\sum _{{\tau }_1}\sum _{{\tau }_2}[{\tau }_{1}P({\tau }_1,{\tau }_2)+{\tau }_{2}P({\tau }_1,{\tau }_2)]\\ =P_{11}+\frac{P_{01}+P_{10}}{2}.\end{array}$$ (17)

In CMF all dynamic properties for TASEP with interactions can be obtained by analyzing changes of cluster probabilities with time. The temporal evolution of two-site probabilities in the bulk is governed by a set of Master equations:

$$\frac{d{P}_{11}}{dt}=q{P}_{01}{P}_{01}+P_{11}{P}_{01}-r{P}_{11}{P}_{00}-P_{11}{P}_{01};$$ (18)

$$\frac{d{P}_{00}}{dt}=q{P}_{01}{P}_{01}+P_{11}{P}_{01}-r{P}_{11}{P}_{00}-P_{11}{P}_{01};$$ (19)

$$\begin{array}{l}\frac{d{P}_{01}}{dt}=P_{10}[P_{10}{P}_{01}+P_{00}^2+P_{00}{P}_{01}+P_{00}{P}_{10}]+r{P}_{10}[P_{11}{P}_{00}+P_{01}^2+P_{00}{P}_{01}+P_{01}{P}_{11}]\\ +P_{10}[P_{10}{P}_{11}+P_{11}^2+P_{11}{P}_{01}+P_{01}{P}_{10}]+q{P}_{10}[P_{00}{P}_{10}+P_{10}^2+P_{11}{P}_{10}+P_{00}{P}_{11}]\\ -P_{01}[q{P}_{00}{P}_{01}+P_{00}^2+P_{00}{P}_{10}+q{P}_{10}{P}_{01}+P_{00}{P}_{01}+q{P}_{01}^2+P_{00}{P}_{11}+q{P}_{11}{P}_{01}]\\ -P_{01}[q{P}_{11}{P}_{01}+P_{11}^2+P_{11}{P}_{10}+q{P}_{10}{P}_{01}+q{P}_{01}^2+P_{00}{P}_{11}+P_{11}{P}_{01}+q{P}_{00}{P}_{01}];\end{array}$$ (20)

$$\begin{array}{l}\frac{d{P}_{10}}{dt}=2r{P}_{11}{P}_{00}+P_{01}{P}_{00}+P_{01}{P}_{11}-P_{10}[P_{10}{P}_{01}+P_{00}^2+P_{00}{P}_{01}+P_{00}{P}_{10}]\\ -r{P}_{10}[P_{11}{P}_{00}+P_{01}^2+P_{00}{P}_{01}+P_{01}{P}_{11}]-P_{10}[P_{10}{P}_{11}+P_{11}^2+P_{11}{P}_{01}+P_{01}{P}_{10}]\\ -q{P}_{10}[P_{00}{P}_{10}+P_{10}^2+P_{11}{P}_{10}+P_{00}{P}_{11}].\end{array}$$ (21)

From Eqn. (18) at the stationary state we obtain,

$$q{P}_{01}^2=r{P}_{11}{P}_{00},$$ (22)

while equations Eqs. (20) and (21) yield,

$$\begin{array}{l}{P}_{10}^2[P_{01}(2-r-q)+q]+P_{10}[P_{00}+P_{11}+r{P}_{01}+P_{00}{P}_{11}(q+r-2)]\\ -2q{P}_{01}^2-P_{00}{P}_{01}-P_{11}{P}_{01}=0.\end{array}$$ (23)

So far, we have three equations with four unknown two-site cluster probabilities probabilities and we need one more. The last equation can be derived from the expression for the current.

$$J=q{P}_{01}^2+r{P}_{11}{P}_{00}+P_{11}{P}_{01}+P_{00}{P}_{01}=2r{P}_{11}{P}_{00}+\sqrt{P_{11}{P}_{00}}(P_{00}+P_{11}),$$ (24)

where Eq(22) was used to eliminate P₀₁. Using the normalization condition, the average density from Eq.(17) can be written as,

$$\rho =\frac{1}{2}(1+P_{11}-P_{00}).$$ (25)

Now we can define a new variable η such that

$$\eta =P_{11}+P_{00}.$$ (26)

Then the particle current can be expressed as a function of ρ and η. Then applying the condition of maximal current, ∇J(ρ, η) = 0, it can be shown that $\rho =\frac{1}{2}$. It suggests that P₁₁ = P₀₀ = qP₀₁. Utilizing this condition together with the normalization, we obtain the following cubic equation for P₀₁,

$$P_{01}^3[-1-2q+2q^2+4q^3-q^4-2q^5]+P_{01}^2[1-2q-10q^2+2q^3+5q^4]+P_{01}[2q-q^2-4q^3]+q^2=0.$$ (27)

The physically reasonable root (0 < P₀₁ < 1) of this equation can be found, and it is used then to calculate the current via the relation $J=4q{P}_{01}^2$. Various cluster probabilities can be interpreted as a measure of clustering in the lattice. For very strong repulsion, P₁₁ → 0 and no clusters form. As the interaction energy becomes more attractive P₁₁ increases and the particles have larger tendency to form clusters.

At the entrance, cluster probabilities satisfy the following master equations,

$$\frac{d{P}_{11}}{dt}=q\alpha P_{01}-r{P}_{11}{P}_{00}-P_{11}{P}_{01};$$ (28)

$$\frac{d{P}_{00}}{dt}=P_{00}{P}_{01}+q{P}_{01}{P}_{01}-\alpha P_{00};$$ (29)

$$\frac{d{P}_{10}}{dt}=\alpha P_{00}+r{P}_{11}{P}_{00}+P_{11}{P}_{01}-P_{10}[P_{00}+P_{01}+q{P}_{11}+q{P}_{10}];$$ (30)

$$\frac{d{P}_{01}}{dt}=P_{10}[P_{00}+P_{01}+q{P}_{11}+q{P}_{10}]-q\alpha P_{01}-P_{00}{P}_{01}-q{P}_{01}{P}_{01}.$$ (31)

At the stationary state it can be shown that

$$P_{00}=\frac{q{P}_{01}^2}{\alpha -P_{01}};$$ (32)

$$P_{11}=q(\alpha -P_{01});$$ (33)

$$q{P}_{10}^2+P_{10}(P_{00}+P_{01}+q{P}_{11})-q\alpha P_{01}-\alpha P_{00}=0.$$ (34)

Using the normalization condition, P₁₀ = 1 − P₀₀ − P₁₁ − P₀₁, we obtain,

$$\begin{array}{l}{P}_{01}^2(q-1)+P_{00}^2(q-1)-q{P}_{11}+P_{00}(1-2q)+P_{01}(1-2q)+P_{11}{P}_{00}(q-1)\\ +P_{11}{P}_{01}(q-1)+2P_{00}{P}_{01}(q-1)+q-q\alpha P_{01}-\alpha P_{00}=0.\end{array}$$ (35)

Then from Eqs. (32) and (33) we derive the final expression for P₀₁.

$$\begin{array}{l}{P}_{01}^4(2q^3-5q^2+4q-1)\\ +P_{01}^3(-2\alpha q^3+7\alpha q^2+3q^2-7q\alpha -3q+2\alpha +1)\\ +P_{01}^2({\alpha }^2{q}^3-4{\alpha }^2{q}^2-5\alpha q^2+5{\alpha }^{2}q+5q\alpha +q-{\alpha }^2-2\alpha )\\ +P_{01}({\alpha }^3{q}^2+3\alpha q^2-2q{\alpha }^3-2q{\alpha }^2-2q\alpha +{\alpha }^2)\\ +q{\alpha }^2-q^2{\alpha }^3=0.\end{array}$$ (36)

It can be solved numerically, which leads to calculating all other properties in the LD phase.

In the HD phase the exit is controlling the dynamics, and cluster probabilities evolve as given by

$$\frac{d{P}_{11}}{dt}=q{P}_{01}{P}_{01}+P_{11}{P}_{01}-r\beta P_{11};$$ (37)

$$\frac{d{P}_{00}}{dt}=\beta P_{01}-r{P}_{11}{P}_{00}-P_{00}{P}_{01};$$ (38)

$$\frac{d{P}_{01}}{dt}=P_{10}[P_{00}+P_{10}+r{P}_{11}+r{P}_{01}]-P_{11}{P}_{01}-q{P}_{01}{P}_{01}-\beta P_{01};$$ (39)

$$\frac{d{P}_{10}}{dt}=P_{01}{P}_{00}+r{P}_{11}{P}_{00}+r\beta P_{11}-P_{10}[P_{00}+P_{10}+r{P}_{11}+r{P}_{01}].$$ (40)

At the steady state we obtain:

$$P_{11}=\frac{q{P}_{01}^2}{r\beta -P_{01}};$$ (41)

$$P_{00}=\beta -q{P}_{01};$$ (42)

$$P_{10}^2+P_{10}[P_{00}+r{P}_{11}+r{P}_{01}]-\beta r{P}_{11}-\beta P_{01}=0.$$ (43)

Again using the normalization condition one can calculate,

$$\begin{array}{l}{P}_{01}^2(1-r)+P_{00}^2(1-r)+P_{11}(r-2)-P_{00}+P_{01}(r-2)+P_{11}{P}_{00}(1-r)\\ +P_{00}{P}_{01}(1-r)+2P_{11}{P}_{01}(1-r)+1-\beta P_{01}-r\beta P_{11}=0.\end{array}$$ (44)

Eliminating P₀₀ and P₁₁ from this expression yields

$$\begin{array}{l}{P}_{01}^4(2q^5-5q^4+4q^3-q^2)\\ +P_{01}^3(3q^4-3q^3+q^2+2q\beta -7q^2\beta +7\beta q^3-2\beta q^4)\\ +P_{01}^2(q^3-{\beta }^2+q^3{\beta }^2-5\beta q^3-3q^2{\beta }^2+5\beta q^2+4q{\beta }^2-2q\beta )\\ +P_{01}({\beta }^2-{\beta }^3-2q{\beta }^2-2\beta q^2+3{\beta }^2{q}^2)\\ +q{\beta }^2-q{\beta }^3=0.\end{array}$$ (45)

This equation can be solved numerically exactly for P₀₁, and all other properties can be obtained as explained above.

Phase diagram for the CMF method can be obtained using the same approach as was explained for SMF. We apply the condition J_LD = J_MC to determine the boundary between LD and MC phases

$$\alpha P_{00}+q\alpha P_{01}=q{P}_{01}{P}_{01}+r{P}_{11}{P}_{00}+P_{11}{P}_{01}+P_{00}{P}_{01}.$$ (46)

In the MC phase we have ρ_bulk = 0.5, and it leads to P₁₁ = P₀₀. Combining this equality with Eqs. (32) and (33) the following quadratic equation is derived,

$${\alpha }^2-4\alpha P_{01}+4P_{01}^2=0.$$ (47)

It has only one solution at α_b = 2P₀₁ where P₀₁ is solution of the Eq. (27). Similarly, for the boundary between HD and MC phases we obtain β_b = 2qP₀₁. To determine the phase boundary between LD and HD phases we must solve the equation J_LD = J_HD, producing

$$\alpha P_{00}+q\alpha P_{01}=\beta P_{01}+r\beta P_{11}.$$ (48)

It can be further simplified into

$${\beta }^2(P_{01}-\alpha )+q{\alpha }^2\beta -q^2{\alpha }^2{P}_{01}=0.$$ (49)

Solving this equation for β leads us to

$$\beta =\frac{q\alpha P_{01}}{\alpha -P_{01}}.$$ (50)

From Eq. (50) it can be shown that $P_{01}=\frac{\alpha \beta }{q\alpha +\beta }$. After substituting it into Eq. (36) we obtain the following relation for the boundary between LD and HD phases,

$$\begin{array}{c}{\beta }^4(1-q)+{\beta }^3(-1+3\alpha +2q-2q\alpha )+{\beta }^2(-\alpha +{\alpha }^2-q+q\alpha +q{\alpha }^2+2q^2\alpha +q^2{\alpha }^2-q^3{\alpha }^2)\\ +\beta (-q{\alpha }^2-2q^2\alpha +2q^2{\alpha }^2+2q^2{\alpha }^3+q^3{\alpha }^2-q^3{\alpha }^3)-q^3{\alpha }^2+q^4{\alpha }^3=0.\end{array}$$ (51)

3. Monte Carlo Simulations and Discussions

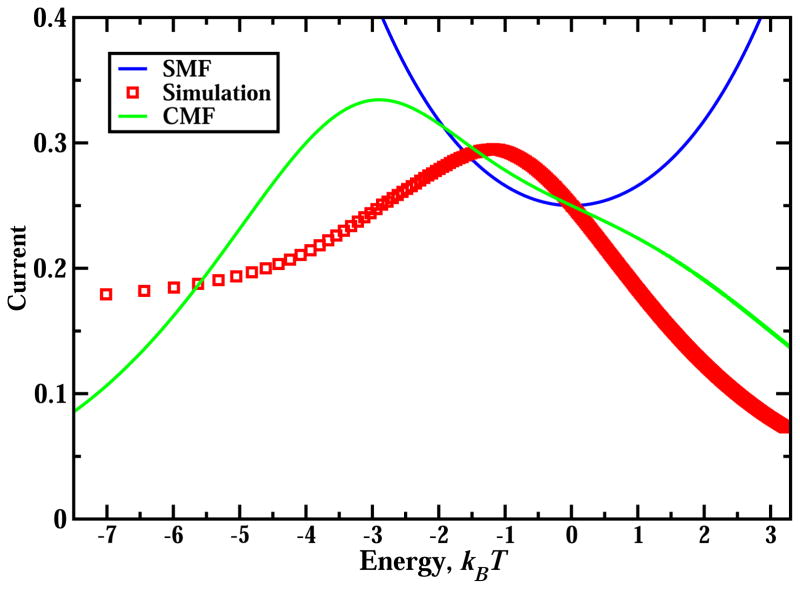
We performed extensive Monte Carlo simulations to test our theoretical predictions. Our chosen lattice size, L = 1000, is large enough to avoid finite size and boundary effects. A random sequential update was utilized for all simulations. The particle current and density profiles were averaged over 10⁸ Monte Carlo steps and the first 20% were discarded to ensure the system had reached the steady state. Comparing theoretical predictions of SMF approach with Monte Carlo computer simulations (Figs. 2 and 3) we can see that it is a reasonable approximation for very weak interactions (E ≈ 0), while for stronger attractions or repulsions the simple mean-field method does not work well. The calculated density profiles in SMF deviate from computer simulations results (see Fig. 3). But the strongest argument against using SMF for TASEP with interactions comes from the analysis of Eq. (11) for the current in the MC phase. It predicts that for |E| ≫ 1 the current is increasing without a bound, which is clearly an unphysical result. In the case of strong attractions particles will tend to stay in one big cluster that cannot move because particle breaking from the cluster is not possible. In this case the current is expected to go to zero. For strong repulsions the situation is different. In this case any particle cannot have neighbors so that the system behaves like TASEP with particles that cover 2 sites, for which precise estimates for the current are known, $J=1/{(\sqrt{2}+1)}^2\approx 0.17$ [28]. Our computer simulations agree with these predictions (see Fig. 4).

Figure 3.

Density profiles TASEP with inter-molecular interactions for E = −1.2 K_BT. (a) LD phase with α = 0.4 and β = 0.8; (b) HD phase with α = 0.8 and β = 0.2

Figure 4.

Maximal current as a function of the interaction strength. Lines are predictions from mean-field calculations. Symbols are from Monte Carlo computer simulations.

It is interesting to discuss why SMF provides a qualitatively reasonable picture of the phase diagram, while for particle currents it fails completely. The phase diagram is quantified by different particle densities, and for densities correlations are less important than for currents that are determined by the simultaneous occupancies of several neighboring lattice sites.

Theoretical framework of the CMF method along with computer simulations allows us to investigate the fundamental effect of interactions on multi-particle dynamics in the TASEP model. It has been argued above that particle currents should diminish for strong attractions and repulsions. It suggests that there is an intermediate strength of interactions where the maximal flux might be achieved. Our calculations support these arguments as illustrated in Fig. 4. We found that this optimal strength corresponds to weak repulsions with E^* ≈ −3k_BT in CMF, while the simulations indicate E^* ≈ −1.2k_BT. The surprising observation is that optimal conditions do not correspond to the case of no interactions, as one would expected from naive symmetry arguments. These arguments are that for attractive interactions the flux should be smaller because of particles clustering, while repulsions decrease the current by slowing the particles that are close to each other. In addition, the optimal particle flux can be larger than the current for the system with only hard-core exclusions. The computer simulations predict J_max ≈ 0.29, which is 16% more than the maximal current for TASEP without interactions J_max = 0.25. Thus, inter-molecular interactions might significantly modify particle fluxes.

It could be also observed that the effect of interactions on particle dynamics in TASEP is not symmetric with respect to E = 0. The results of the CMF calculations and Monte Carlo computer simulations suggest that there is more sensitivity for attractive interactions. The phase diagram also depends on the sign and strength of interactions. Fig. 5 shows the position of the triple point (that connects LD, HD and MC phases) at different values of E. One can see that increasing repulsions shrinks the MC and HD phases, and the LD phase occupies the largest fraction of the parameters space. For strong attractions the result is opposite. The HD phase dominates, while the LD and MC phase significantly diminish. These observations can be easily explained. Repulsions decrease the effective entrance rate into the system, making it a rate-limiting step for a larger range of parameters. This corresponds to expanding the LD phase. For attractions the exit rate slows down significantly because particles leaving the system sometimes should break from the clusters. This is not favorable from the energetic point of view. In this case, the HD phase dominates the system.

Figure 5.

Coordinates of the triple points on phase diagrams as a function of the interaction strength. Lines correspond to predictions from two types of mean-field calculations. Symbols are results from computer simulations.

It is interesting to apply our theoretical analysis for real motor proteins. Experimental studies show that kinesins molecular motors bound to cytoskeleton filaments experience a short-range attractive interactions of order E = 1.6 ± 0.5k_BT [9]. Comparing this with plots in Fig. 4 we conclude that kinesins probably do not function at the most optimal regime with the maximal particle current. However, they operate at conditions where small changes in interactions might lead to large modifications in dynamic properties. It suggests that kinesins might be optimized not for the maximal flux but for supporting robust cellular transport via tuning its intermolecular interactions. It allows molecular motors to compensate for fluctuations due to collisions with other molecules and from external loads. We hypothesize that this collective dynamic behavior of kinesins might be the most efficient from energetic point of view. This picture agrees with current views on mechanisms of cooperativity in multiple kinesins [5, 7]. However, we should notice that our model of motor protein dynamics is oversimplified. It ignores many important processes such as back steppings, bindings to the filaments and unbindings from them, and hydrolysis. It is not clear what effect the inter-molecular interactions will have if all relevant chemical transitions are included.

4. Summary and Conclusions

In conclusion, we developed a new theoretical approach to investigate the effect of inter-molecular interactions on dynamics of cellular molecular motors that move along cytoskeleton filaments. Our method is based on employing totally asymmetric simple exclusion processes that are known to be successful for analysis of non-equilibrium multi-particle phenomena. The important part of the method is a thermodynamically consistent procedure that allowed us to quantitatively describe the effect of inter-molecular interactions. Theoretical calculations indicate that interactions bring significant spatial correlations in the system that could be partially captured by considering dynamics of clusters. It is found that there is an optimal strength of interactions at which the particle current reaches the maximum, while for large attractions or repulsions the fluxes disappear. For TASEP these optimal conditions correspond to weak repulsions. This observation is unexpected since from naive symmetry arguments the case of no interactions seems to be optimal. Interactions also modify stationary phase diagrams. For repulsions the LD phase becomes the most important, while for attractions the HD phase dominates. Our analysis also show that dynamic properties are more sensitive to attractive interactions. The implications of these observations for kinesins motor proteins are discussed. It is argued that kinesins might be functioning under conditions to support the robustness of the cellular transport instead of the maximal fluxes. At the same time, it was noticed that our theoretical analysis does not account for several important transitions in motor proteins that might limit its applicability in the current form. It will be important to extend our method to include these features and to test our theoretical predictions for other classes of motor proteins.