BIOPHYSICAL CHARACTERISATION OF THE UNDER-APPRECIATED AND IMPORTANT RELATIONSHIP BETWEEN HEART RATE VARIABILITY AND HEART RATE

Abstract

Heart rate variability (beat-to-beat changes in the RR interval) has attracted considerable attention over the last 30+ years (PubMed currently lists >17,000 publications). Clinically, a decrease in heart rate variability is correlated to higher morbidity and mortality in diverse conditions, from heart disease to foetal distress. It is usually attributed to fluctuation in cardiac autonomic nerve activity. We calculated heart rate variability parameters from a variety of cardiac preparations (including humans, living animals, Langendorff-perfused heart and single sinoatrial nodal cell) in diverse species, combining this with data from previously published papers. We show that regardless of conditions, there is a universal exponential decay-like relationship between heart rate variability and heart rate. Using two biophysical models, we develop a theory for this, and confirm that heart rate variability is primarily dependent on heart rate and cannot be used in any simple way to assess autonomic nerve activity to the heart. We suggest that the correlation between a change in heart rate variability and altered morbidity and mortality is substantially attributable to the concurrent change in heart rate. This calls for re-evaluation of the findings from many papers that have not adjusted properly or at all for heart rate differences when comparing heart rate variability in multiple circumstances.

Introduction

Early scientists believed that the heart beat was metronomic until, in 1733, Reverend Stephen Hales made the observation that the pulse rate varied with respiration.¹ In the 1960's, advances in electrocardiogram (ECG) recording allowed quantification of beat-to-beat variation in R-wave to R-wave interval (RR interval) dubbed ‘heart rate variability’ (HRV).² Thereafter, an explosion of investigation into HRV occurred - PubMed currently lists >17,000 HRV-related articles. Diverse parameters describing different characteristics of HRV have been proposed.³ In the general population, having a low HRV is associated with increased morbidity and mortality from various causes, not all cardiac.⁴ For example, Dekker et al. demonstrated that decreased HRV was a predictor of death from all causes, including cancer.⁵ There is ample evidence too of changes in HRV that occur in response to disease, both cardiac and non-cardiac. For example, decreased HRV is correlated to higher morbidity and mortality in patients following myocardial infarction.⁶ In addition to ischaemic heart disease, significant changes in HRV are also documented in many other common conditions, including heart failure, hypertension, prior to arrhythmia onset, left ventricular hypertrophy, hypertrophic cardiomyopathy, and in non-cardiac conditions including sepsis, foetal distress, diabetes, stroke, depression and obstructive airways disease (for review, see²). HRV was heralded as a useful non-invasive method for predicting clinical risk in these diverse disease states.

Underlying HRV is believed to be fluctuating behaviour in the limbs of the cardiac autonomic nervous system. Prior to the advent of HRV, the ability of scientists and physicians to non-invasively estimate cardiac autonomic innervation was limited. A significant literature concerning HRV from bench to bedside continues to be produced today.

In this study, we have investigated HRV in a variety of species and cardiac preparations. Our results argue that, rather than being a pure marker of cardiac autonomic nervous system activity, HRV is primarily dependent on heart rate, with HRV increasing when the RR interval increases (i.e. when heart rate slows), and decreasing when the RR interval decreases (i.e. when heart rate quickens). This lends weight to the theory that the correlation between a decrease in heart rate variability and higher morbidity and mortality is the consequence of the concurrent increase in heart rate. It follows that observed differences in HRV between two or more scenarios should, therefore, always take into account the heart rate present when HRV was measured, otherwise conclusions drawn may be flawed.

Methods

Experiments performed for this study focussed upon three different cardiac preparations: the conscious in vivo human and rat, isolated denervated Langendorff-perfused heart (rabbit, rat) and isolated sinoatrial node cell (‘SANC’, rabbit). The species employed in each of these situations varied, as did the experimental conditions used, and these are described in the Online Data Supplement (ODS). Human studies were approved by the local ethics committee at the Manchester Royal Infirmary, and subjects gave their informed consent. Studies on the rat in vivo were approved by the Norwegian Council for Animal Research; the protocol used had the ID number 1980 and was carried out in accordance with the Guide for the Care and Use of Laboatory Animals by the European Commission Directive 86/609/ECC. Studies on the Langendorff-perfused rabbit and rat heart were performed in accordance with the Animals (Scientific Procedures) Act 1986 from the UK Home Office, with animals being sacrificed using approved Schedule 1 procedures. Studies on the isolated SANC from the rabbit were conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals

HRV analysis

Continuous recordings of single channel ECG data from the conscious human or rat and the isolated rabbit and rat Langendorff-perfused heart, and spontaneous action potentials recorded from the isolated rabbit SANC were subjected to HRV analysis in multiple domains along identical lines, as detailed in the ODS. Stationary time epochs of 2·5 min (150 s) were used. Because of the varying heart rates in different species the number of data points differed among species. We repeated the data analysis with a fixed number of data points (500 heart beats) and did not observe significant differences in the results compared to the analysis using fixed time epochs of 2.5 min (data not shown). For simplicity, only the standard deviation of normal beat to normal beat intervals (SDNN) and RMSSD are presented as parameters reflecting HRV herein.

Computer modelling

The Zhang et al.⁷ deterministic ordinary differential equation (ODE) model for the electrophysiology of a rabbit central SANC was implemented in this study for the advanced computer modelling study. Further details of the model are given in the ODS.

Results

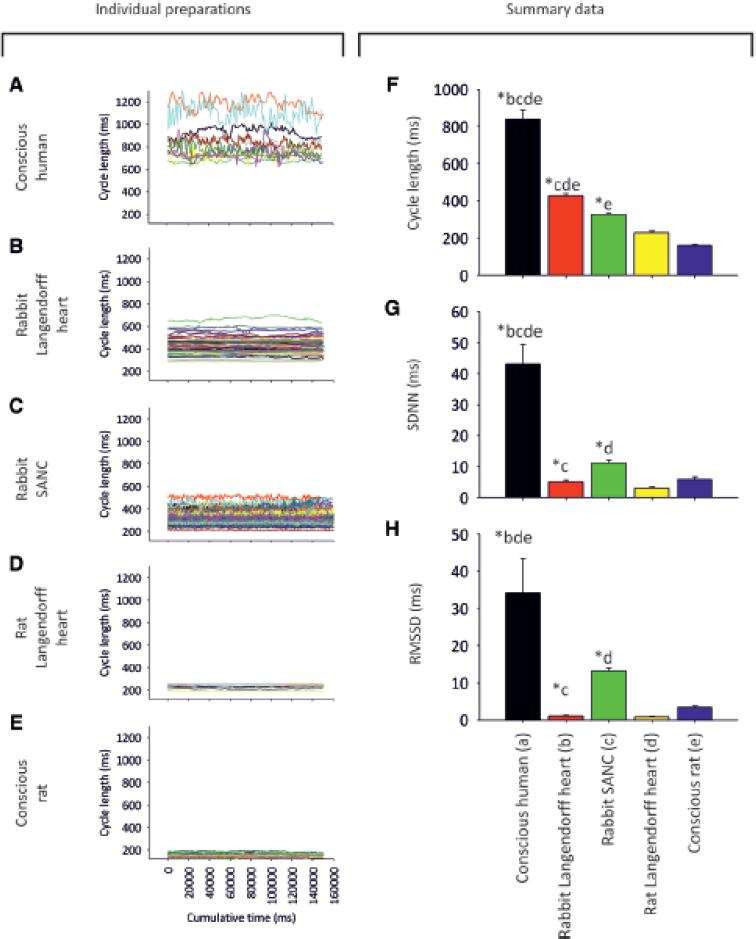
We measured baseline HRV in the conscious human (n=11) and rat (n=11), isolated denervated Langendorff-perfused heart from the rabbit (n=58) and rat (n=8), and isolated denervated rabbit SANC (n=67). Fig. 1A-E shows tachograms for the different preparations, demonstrating marked differences in HRV under baseline conditions; the data are summarised in Fig. 1F-H. Corresponding power spectra and total power summary data are shown in the ODS (Fig. S1). HRV as a result of fluctuation in autonomic nerve activity is expected to be present in the conscious animal, but absent in the isolated denervated preparations; however, the pattern of HRV did not conform to this assumption. As expected, HRV in terms of SDNN, RMSSD and total power was high in the conscious human (Fig. 1A, G, H and Fig. S1) and low in the isolated denervated preparations (Fig. 1B-D, G, H and Fig. S1). However, in the conscious rat with an intact autonomic nervous system, HRV was also low (Fig. 1E, G, H and Fig. S1). The baseline cycle length (CL; same as RR or NN interval) also varied widely between preparations (Fig. 1F). The preparation with the longest CL was the conscious human (mean±SEM, 839±50 ms). The Langendorff-perfused rabbit heart (428±10 ms) and rabbit SANC (327±7 ms) had the next-longest CLs, followed by the Langendorff-perfused rat heart (229±8 ms). The preparation with the shortest CL was the conscious rat (161±4 ms). Below we argue that HRV is strongly dependent on CL: the shorter the CL, the less the HRV. This explains the low HRV in the conscious rat, which had the shortest CL (Fig. 1E, F). However, there is not a perfect correspondence between HRV and CL – the HRV in the two Langendorff heart preparations is lower than expected on the basis of CL alone. We re-examine the differences in baseline HRV in the five preparations in Fig. 5A.

Fig. 1. Differences in HRV among different cardiac preparations (baseline conditions).

A-E, tachograms (150 s stationary epochs) from: A, conscious human (n = 11); B, Langendorffperfused rabbit heart (n = 58); C, rabbit SANC (n = 67); D, Langendorff-perfused rat heart (n = 8); E, conscious rat (n = 11). Individual experiments are plotted in unique colours. F-H, summary of baseline differences in CL and HRV among cardiac preparations. Mean (+SEM) CL (F), SDNN (G) and RMSSD (H) for different preparations. Asterisk and letters atop bars demonstrate statistically significant differences from other lettered bars (P<0·05; 1-way ANOVA).

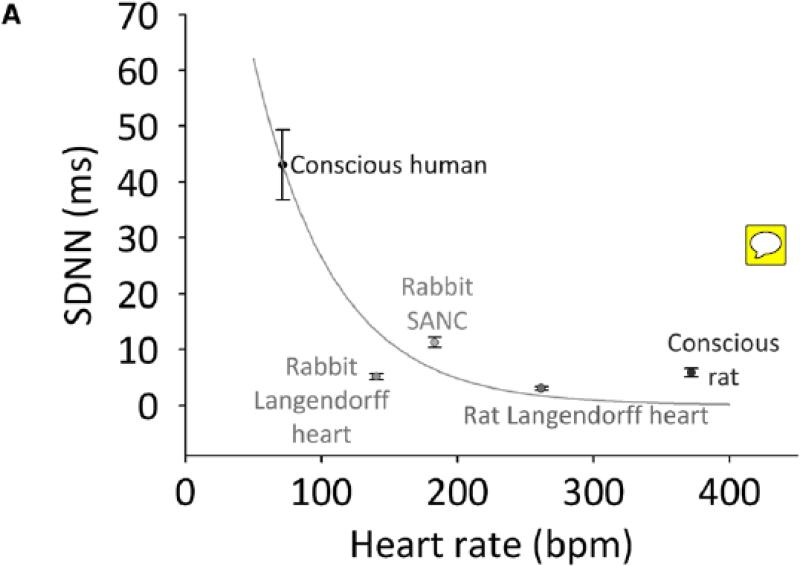
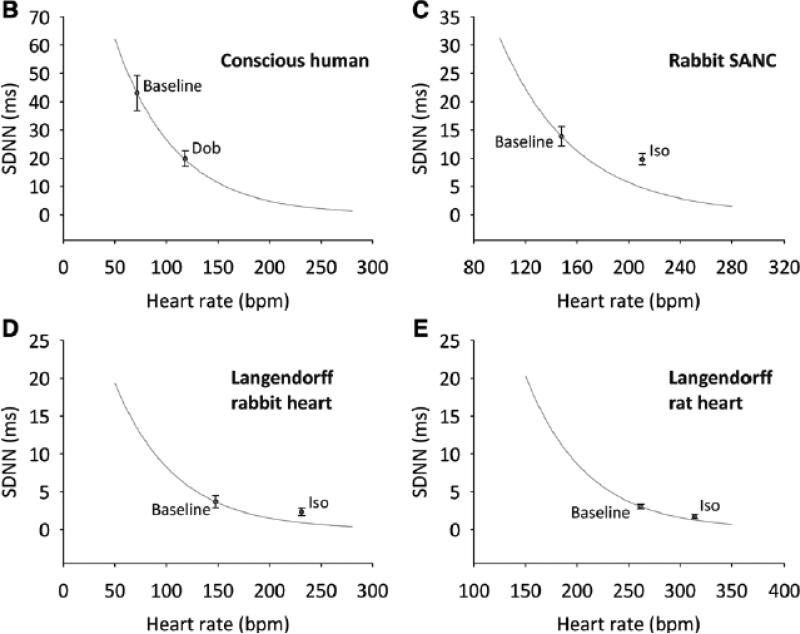
Fig. 5. Application of a correcting factor facilitates clarification of whether changes in HRV are attributable to heart rate differences alone.

Analysis of baseline differences in HRV among different preparations (A); analysis of changes in HRV following administration of β-agonists to different preparations (B-E). SDNN is plotted against heart rate. Predicted effect of heart rate on SDNN is plotted (green lines) using calculated correcting factor from Fig. 3C. Conscious human data (A) or baseline data (B-E) are arbitrarily used as starting point from which to calculate the effect of heart rate on SDNN.

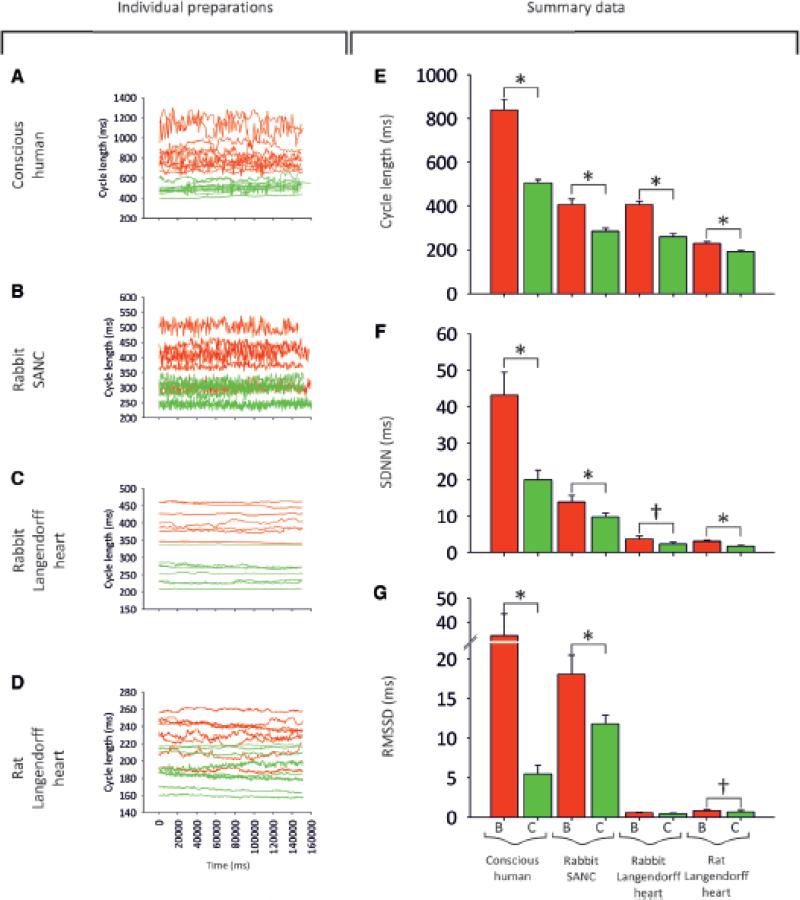
Despite clear inter-preparation differences in HRV, β-adrenergic stimulation has the same effect on HRV in the conscious animal, isolated denervated heart and isolated denervated SANC - Fig. 2A shows the effect of the β-adrenergic agonist, dobutamine, on the CL and HRV in the conscious human (n = 11). As expected, dobutamine caused a dramatic decrease in the CL (Fig. 2A, E), and along with it a decrease in measured parameters of HRV (Fig. 2F, G). The effect of β-adrenergic stimulation (using isoprenaline as the agonist) was also investigated in the rabbit SANC (Fig. 2B) and in the Langendorff-perfused rabbit (Fig. 2C) and rat (Fig. 2D) heart. β-adrenergic stimulation had a similar effect on CL, causing it to significantly shorten in all preparations studied (Fig. 2E). It also had a similar effect on HRV, causing it to decrease in all preparations studied (Fig. 2F, G). Could the decrease in HRV in all preparations simply be accounted for by the decrease in CL?

Fig. 2. Effect of β-agonists on HRV in different cardiac preparations.

A-D, tachograms demonstrating the effect of β-agonists on HRV. A, before and after dobutamine in conscious humans. B, data before and after 100 nM isoprenaline in rabbit SANC. C, data before and after 100 nM isoprenaline in Langendorff-perfused rabbit hearts. D, data before and after 100 nM isoprenaline in Langendorff-perfused rat hearts. Baseline data = red, data in presence of β-adrenergic agonist = green. E-G, summary of the effect of β-adrenergic agonists on HRV. Mean (+SEM) CL (E), SDNN (F), and RMSSD (G) under baseline conditions (= ‘B’; red bars) and with β-adrenergic agonist (= ‘C’; green bars) for the different preparations. Asterisk and bar = statistically different (P<0·05; 1-way ANOVA). Sword and bar = P=0·1>P>0·05.

Relationship between HRV and heart rate

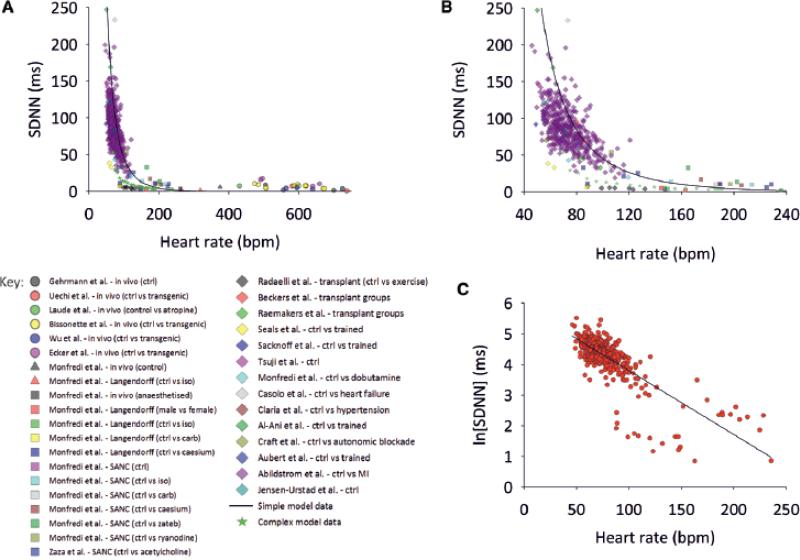
Fig. 3A summarises all data obtained from the conscious human and rat, the Langendorffperfused rabbit and rat heart, and the rabbit SANC – SDNN is used as the parameter of HRV and is plotted against heart rate. Fig. 3B shows the same data, but only up to heart rates of 240 beats/min. Fig. 3A, B also shows data from many other studies, including data from the healthy conscious human, athletically-trained conscious human, conscious human exposed to autonomic blockade, conscious human with heart failure, conscious human with hypertrophic cardiomyopathy, conscious human with myocardial infarction, conscious human heart transplant recipient, conscious mouse (wild type and transgenic) and rabbit SANC (control and exposed to acetylcholine, ACh) (see ODS for details of studies included). Despite the fact that the SDNN (along with other HRV parameters) will have been measured in different ways (over different sampling time periods, for example), and that the data are from different species, different preparations, different disease states, different conditions and different laboratories, all the data are clustered and approximately fall along a common exponential decay-like curve: there is an exponential decay-like decrease in SDNN when heart rate increases (Fig. 3A, B). Fig. S2 in the ODS shows that sub groups of the data in Fig. 3A, B show the same relationship between HRV and heart rate as the whole data (Fig. 3A, B). Fig. 3C shows a semi-logarithmic plot of the same data: the natural logarithm of the SDNN is plotted against the heart rate and there is a linear relationship, as is expected for an exponential decay-like process; it can be calculated from this linear relationship that for every 10 beats/min increase in heart rate, log_n(SDNN) decreases by 0·169 ms (standard error of estimate = 0.41, R² = 0.68). It follows that the SDNN at a given heart rate (HR) is given by the following:

$$SDNN=SDN{N}_{reference}{e}^{-\frac{(HR-H{R}_{reference})}{58.8}}$$ [1]

where SDNN_reference is the SDNN at a reference heart rate, HR_reference

Fig. 3. Relationship between HRV (SDNN) and heart rate – comparison of theory and experiment.

A, relationship between SDNN and heart rate. Data from experiments undertaken in this paper and elsewhere, and our mathematical models are plotted. Basic key under panel A; for detailed key see ODS. B, relationship between SDNN and heart rate (heart rate range 40-240 beats/min only). C, relationship between log_n(SDNN) and heart rate (same data as A). Black line shows that for every 10 beats/min increase in heart rate, log_n(SDNN) decreases by 0·17 ms.

A simple mathematical model of the relationship between HRV and heart rate

In the sinoatrial node, the membrane depolarizes throughout diastole (the pacemaker potential). If the pacemaker potential is monophasic, the rate of change of membrane potential, $\frac{d{V}_m}{dt}$, is roughly constant. This is driven by a roughly constant inward ionic current, I_tot, the total of the various ionic currents flowing during diastole, including rapid and slow delayed rectifier K⁺ currents (I_K,r and I_K,s), funny current (I_f) , background Na⁺ current (I_b,Na), T-type Ca²⁺ current (I_Ca,T) and Na⁺-Ca²⁺ exchange current (‘Ca²⁺ clock current’, I_NaCa) etc. $\frac{d{V}_m}{dt}$ is related to I_tot in the following way:

$$\frac{d{V}_m}{dt}=-\frac{I_{tot}}{C_m}$$ [2]

where C_m is cell capacitance. If ΔV_m is the difference between the maximum diastolic potential (peak negative potential after the action potential; ~-60 mV) and the threshold potential (~-40 mV), then the diastolic interval (DI; time between spontaneous action potentials) is given by:

$$DI=\frac{\Delta V_m}{\left(\frac{d{V}_m}{dt}\right)}orDI=-\frac{\Delta V_m{C}_m}{I_{tot}}$$ [3]

Consider a fluctuating perturbing force that results in HRV (perhaps a change in autonomic nerve activity in the conscious animal, some unknown process in the isolated heart, or a fluctuation in the Ca²⁺ clock in the isolated SANC). This results in a fluctuating ionic current, I_per (perhaps ACh-activated K⁺ current, I_K,ACh, or I_NaCa; the nature of I_per is speculated upon further in the ODS), across the SANC membrane. During diastole (i.e. the pacemaker potential) this will change $\frac{d{V}_m}{dt}$. The change in $\frac{d{V}_m}{dt}$, i.e. $\Delta \frac{d{V}_m}{dt}$, is given by:

$$\Delta \frac{d{V}_m}{dt}=-\frac{I_{per}}{C_m}$$ [4]

If one assumes that I_tot and I_per are constant throughout the pacemaker potential, the rate of change of membrane potential during the pacemaker potential will now be $\frac{d{V}_m}{dt}+\Delta \frac{d{V}_m}{dt}$, in other words $-\frac{I_{tot}}{C_m}-\frac{I_{per}}{C_m}$, or $-\left(\frac{I_{tot}+I_{per}}{C_m}\right)$. This will result in a change in DI (ΔDI):

$$\Delta DI=\frac{\Delta V_m{C}_m}{I_{tot}}-\frac{\Delta V_m{C}_m}{I_{tot}+I_{per}}or\Delta DI=\Delta V_m{C}_m\left(\frac{1}{I_{tot}+\frac{1}{I_{tot}+I_{per}}}\right)$$ [5]

Because

$$CL=DI+APD,$$ [6]

where APD is action potential duration, there will be a change in CL (ΔCL) which will be the same as the change in DI, i.e. ΔCL = ΔDI (assuming APD is constant). I_per fluctuates from beat to beat (thus explaining HRV). If it is assumed that during one diastolic interval the amplitude of I_per is sufficient to change the CL by one standard deviation, then (from equations [5] and [6]):

$$SDNN=-\Delta V_m{C}_m\left(\frac{1}{I_{tot}}-\frac{1}{I_{tot}+I_{per}}\right).$$ [7]

An increase in heart rate (decrease in CL) is achieved by an increase in I_tot (from 30 to 100 beats/min, calculation using equations [3] and [6] shows that I_tot will increase ~4·2×, from -0·22 to -0·91 pA). Equation [6] shows that as the heart rate increases (i.e. as I_tot increases), the SDNN decreases, because $(\frac{1}{I_{tot}}-\frac{1}{I_{tot}+I_{per}})$ will tend to zero. Equation [7] was solved numerically assuming that ΔV_m = 20 mV, C_m = 20 pF and I_per = 0 · 085 pA. Heart rate was calculated from the CL given by equations [3], [5] and [6] (APD assumed to be 160ms). The solid line in Fig. 3A, B shows the calculated relationship between the SDNN and heart rate based on this model. It is a steep exponential decay-like relationship and the line goes through the majority of the experimentally measured points. This suggests that heart rate is a major determinant of the changes in HRV in the clinical and experimental studies.

The model highlights two reasons for the decrease in SDNN at high heart rates. These reasons are robust and model independent. Firstly, a perturbing influence will produce a change in dV_m/dt that is likely to be roughly constant at all rates, and a change in slope of the pacemaker potential will obviously have a greater effect on the DI at longer baseline DIs. Secondly, the relationship between DI (SDNN is a DI) and heart rate is nonlinear and hyperbolic, because the two are inversely related. This acts to steepen the relationship between SDNN and heart rate.

Fig. S3 in the ODS shows the effect of I_per on the calculated relationship between HRV in terms of SDNN and heart rate – an increase in I_per effectively shifts the curve to higher heart rates.

The relationship between HRV and heart rate as determined by a biophysically-detailed model

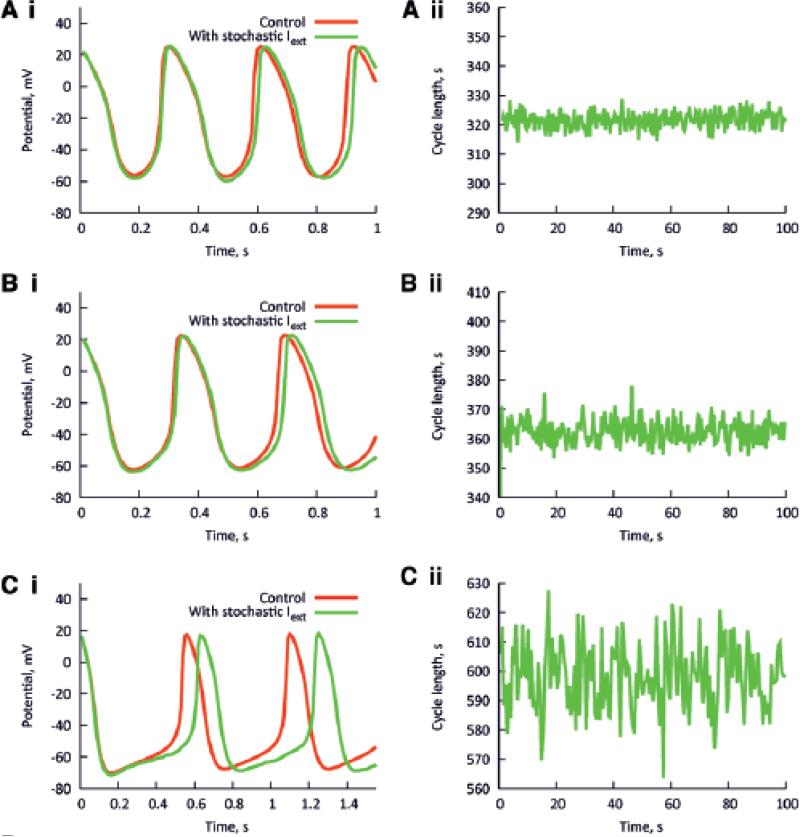
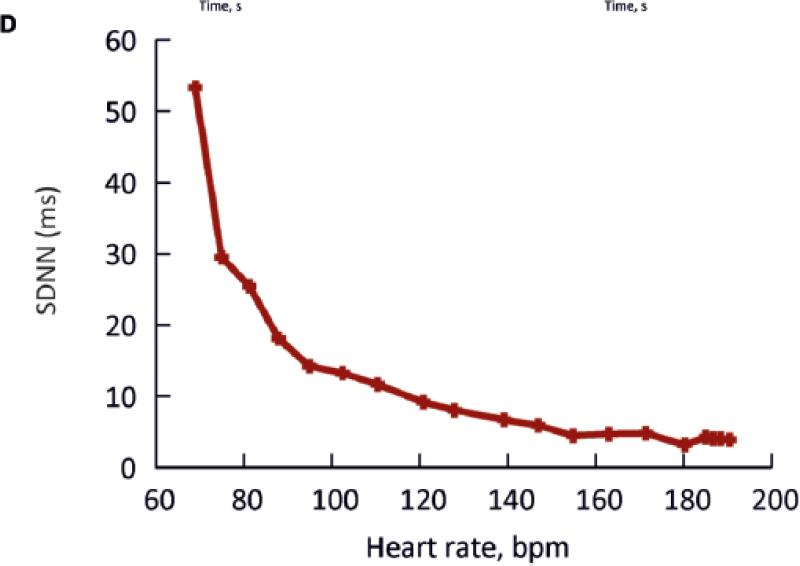
To confirm the dependence of HRV on heart rate, simulations were carried out using a biophysically-detailed model of the sinoatrial node action potential. The model of a rabbit central SANC (with C_m = 20 pF) from Zhang et al.⁷ was employed. Fig. 4Ai shows simulated pacemaker action potentials with no perturbing current (red traces), and with a perturbing current (green traces). The maximum I_per was 20 pA, but the average value of I_per was 0·132 pA, similar to the value of I_per used in the simple model. Fig. 4Aii shows the corresponding tachogram. The pacemaker rate of the model was modulated by changing the modelled ACh concentration (0-0·04 μM). The maximum amplitude of I_per (20 pA) was kept constant. The pacemaker rate was fastest in Fig. 4A (ACh concentration, 0 μM) and slowest in Fig. 4C (ACh concentration, 0·04 μM). In the absence of ACh, when the pacemaker rate was high, the perturbing current produced a small beat-to-beat change in the CL (Fig. 4Ai). When the pacemaker rate was slowed by ACh, the identical perturbing current produced a greater beat-to-beat change in CL (Fig. 4Ci). The tachograms from the simulations confirm that the HRV was greater at the slower heart rates (Fig. 4A-Cii). The calculated SDNN from the model is plotted against the heart rate in Fig. 4D. The data from Fig. 4 are shown in Fig. 3A as grey squares. It is clear that they fall comfortably within the scatter of clinical and experimental data points.

Fig. 4. Relationship between HRV and heart rate predicted by a biophysically detailed model.

Computed action potentials from a SANC model with (green) and without (red) a maximum 20 pA perturbing current (I_per) at fast (top, e.g. Ai) to slow (bottom, e.g. Ci) rates, and corresponding tachograms (Aii – Cii). Rate was varied by altering I_K,ACh. D, relationship between SDNN and heart rate in this model.

A detailed analysis of changes in HRV in different preparations at baseline and with β-adrenergic stimulation

With the above considerations in mind, we were able to produce curves of expected change in SDNN with heart rate (shown as the green lines in Fig. 5) and compare these to experimentally observed changes in HRV, in order to determine whether an experimentally observed difference in HRV (in terms of SDNN) between two experimental conditions can be explained simply by the difference in heart rate. Fig. 5A shows the relationship between SDNN and heart rate in several different experimental preparations: the conscious human and rat, Langendorff-perfused rabbit and rat heart, and rabbit SANC (same data as shown in Fig. 1). The green line demonstrates the expected change in SDNN with heart rate (based on a decrease in log_n(SDNN) of 0·169 ms for every 10 beats/min increase in heart rate – as calculated from Fig. 3C), arbitrarily using data for the conscious human as the starting point (thus explaining why the line passes exactly through the conscious human data point; the choice of starting point makes no difference to the analysis). It is apparent that the decrease in HRV in the rabbit SANC, Langendorff-perfused rat heart, and conscious rat can be largely accounted for by the higher heart rate in these preparations (the data points lie above the green line). However, the decrease in HRV in the Langendorff-perfused rabbit heart may not be completely accounted for by the higher heart rate in this preparation (the point lies below the green line).

Fig. 5B-E shows a similar analysis of the effect of β-stimulation on HRV in the conscious human (Fig. 5B), rabbit SANC (Fig. 5C), and Langendorff-perfused rabbit (Fig. 5D) and rat (Fig. 5E) heart. In each case, the decrease in HRV seen following exposure to catecholamine can be completely explained by the increase in heart rate (the dobutamine/isoprenaline points lie on or above the green lines). Such an understanding of the expected change in HRV where heart rate is different between experimental preparations or conditions is essential when trying to determine whether there is a heart rate-independent difference in HRV between two or more situations.

Fig. 5 is a graphical method of correcting for changes in heart rate. It is also possible to correct for heart rate numerically:

$$cSDNN=\frac{SDNN}{e^{-\frac{HR}{58.8}}}$$ [8]

where cSDNN is the corrected SDNN (at a heart rate of 0 beats/min) and HR is the heart rate. Fig. S4 in the ODS shows that it is possible to eliminate the heart rate dependence of the HRV data in Fig. 3 using this correction factor. Equation 8 can be rewritten to give corrected SDNN_ref at any reference heart rate (HR_ref):

$$SDN{N}_{ref}=\frac{SDNN}{e^{\left(\frac{H{R}_{ref}-HR}{58.8}\right)}}$$ [9]

Discussion

We have demonstrated in detail that substantial HRV exists in isolated cardiac preparations without autonomic connections. This HRV exists under baseline conditions and is modified by drugs that modify beating rate, including exposure to a β-adrenergic agonist. We have shown that regardless of species, preparation, conditions, method of determination and laboratory, there is a unique exponential decay-like relationship between HRV (as measured by the SDNN) and heart rate (Fig. 3). This is true both in the healthy and diseased heart. Using mathematical modelling, we propose a biophysical explanation for the relationship between HRV and heart rate: at high heart rates, the ratio of the perturbing current, I_per (regardless of its nature), to the intrinsic ionic current, I_tot, driving the pacemaker potential becomes vanishingly small and the effect of I_per becomes negligible. This can be stated in another way: I_per will change the slope of the pacemaker potential by roughly the same amount regardless of rate; the effect of this change will be smaller the higher the heart rate. As such, HRV is primarily dependent on heart rate and cannot be used in any simple way to assess autonomic nerve activity to the heart. Although our analysis has focussed on SDNN, our arguments are germane to many commonly used methods to measure HRV.

Earlier indications of a relationship between HRV and heart rate

It has long been suspected that heart rate has a significant effect on HRV. Mangin et al.⁸ studied this relationship in conscious rats, showing that SDNN, RMSSD and the sum of low- and high-frequency power are all significantly correlated with CL. Coumel et al.⁹ also demonstrated a significant relationship between SDNN and heart rate (correlation coefficient, 0·79). Neither of these studies quantitatively established the impact of heart rate on HRV. Zaza et al., however, did.¹⁰ Using isolated rabbit SANCs and modifying heart rate using ACh, they were able to demonstrate that the relationship between concentration of ACh and CL was not linear, nor was the relationship between CL and diastolic depolarization rate.¹⁰ This hinted at a strong rate-dependency of several commonly used indices of HRV, including SDNN. Despite this paper being published >10 years ago, there continues to be a marked under-appreciation of this relationship. Our work aims to further clarify the importance of this, and the need to make allowances for it.

Zaza et al.¹⁰ used model data to calculate that log_n(SDNN) decreases by 0·17 ms for every 10 beats/min increase in heart rate. Similarly, Tsuji et al.^{11, 12} used two hour snapshots of ambulatory cardiac monitoring to define that log_n(SDNN) decreased by 0·16 ms for every 10 beats/min increase in heart rate. In our study, log_n(SDNN) decreased by 0·169 ms for every 10 beats/min increase in heart rate (Fig. 3B). The similarity of these numbers demonstrates the highly conserved relationship between HRV and heart rate. Simillarly, our simple model predicts that log_n(SDNN) decreases by 0·24 ms per 10 beat/min increase in heart rate (Fig. 3A, B, solid line).

Sacha et al.¹³ have pointed out that the variation in CL (RR interval) for a given variation in heart rate is greater at slower heart rates, because of the inverse relationship between heart rate and CL, and suggested a “correction procedure”, which could “eliminate” this effect. We agree that this is one reason why SDNN varies with heart rate - as stated above it acts to steepen the relationship between SDNN and heart rate. However, the primary reason why SDNN varies with heart rate is the non-linear relationship between the change in CL (ΔCL) and CL (for a given I_per) - the correction procedure from Sacha et al.¹³ does not take this into account.

Multiple ‘non-linear’ methods for the interpretation of HRV have been developed over the last several years (for example, approximate entropy¹⁴), yet their take-up has been limited. It remains unclear whether these do indeed give a true heart rate-independent means with which to assess HRV.

Can HRV be corrected for the effect of heart rate?

Previously, several authors have attempted to correct for the effect of heart rate on HRV by normalising HRV parameters by simply dividing them by the heart rate at that point in time (e.g. ¹⁵). Such linear corrections are inadequate to correct the non-linear relationship between HRV and heart rate. This is demonstrated by Fig. S5 in the ODS. In the power spectrum of HRV, the high frequency band is said to represent parasympathetic activity, the low frequency (at least in part) sympathetic activity.³ Via the mechanisms proposed in the present study, heart rate is expected to affect both frequency components equally. Some investigators argue that the ratio of the high frequency to low frequency components is the best measure of autonomic nerve activity to the heart¹⁰ and undoubtedly the mechanisms proposed in the present study are not expected to affect this ratio. However, for independent reasons the validity of this ratio has been challenged.¹⁶

Tsuji et al.^{11, 12} used a good method. They studied HRV (SDNN) in 736 human subjects enrolled in the Framingham study, finding that HRV was correlated with the heart rate (in the manner that can be explained by the present study). However, they¹² showed that age was an independent factor determining HRV, with HRV being lower in older subjects for a given heart rate. They were able to separate age from heart rate, because of the large number of subjects investigated. If it is assumed that HRV is primarily the result of fluctuations in autonomic nerve activity in the conscious human (see above), the study of Tsuji et al.¹² suggests a decrease in autonomic nerve activity with age.

Fig. 5 shows a graphical method of separating an independent factor from the effect of heart rate. For example, Fig. 5A suggests that HRV in Langendorff-perfused rabbit hearts (compared to the conscious human) is lower than can be accounted for by the higher heart rate, suggesting that I_per in the Langendorff-perfused rabbit heart is lower than in the conscious human. This is not unexpected - there is no fluctuating autonomic nerve activity in Langendorff-perfused rabbit hearts.

Finally, the easiest method to correct for heart rate is to use equation 8 as shown by Fig. S4 in the ODS.

Relationship between HRV and morbidity and mortality

The higher morbidity and mortality associated with decreased HRV has been presumed to be the consequence of autonomic imbalance (sympathetic excess, parasympathetic withdrawal, even bilateral autonomic withdrawal).^{2, 3} This must now be reinterpreted. We argue that HRV is a non-linear measure of heart rate and, therefore, the higher morbidity and mortality associated with a decrease in HRV is likely to be the result of the concurrent increase in heart rate. Of course, the autonomic nervous system has a role to play in heart rate control, although it is not the sole factor. That heart rate itself is an important mediator of risk is established, and has been borne out by the fact that a high heart rate is correlated with adverse outcomes.¹⁷ Indeed, heart rate lowering drugs (β-blockers¹⁸ and ivabradine¹⁹) are known to ameliorate morbidity and mortality in diverse cardiovascular diseases. Although it is possible that β-blockers have some effect on the autonomic nervous system in addition to their bradycardic action, the same could not be said for the ‘pure heart rate lowerer’ ivabradine.

Perspectives

HRV is widely used as a measure of autonomic tone to the heart as well as patient morbidity and mortality, and there are more than 17,000 papers on the topic. We have demonstrated that regardless of the cardiac preparation (from human to rabbit isolated sinus node myocyte) and presence or absence of disease or physiological modification, HRV is inextricably linked to heart rate in an exponential manner – the lower the heart rate, the greater the heart rate variability. We have illustrated and explained this relationship with two independent biophysical models. Our findings have significant implications for the many studies that have been and continue to be produced in which either no account is taken of the heart rate at which HRV is calculated, or in which the effect of heart rate has been improperly corrected for. Future studies concerning HRV should rigorously and openly correct for differences in heart rate before drawing conclusions.

Novelty and Significance.

What is new? A unique relationship exists between HRV and heart rate across diverse cardiac preparations, both innervated and denervated, from the living animal all the way down to the fundamental building block of automaticity, the sinoatrial node cell. This relationship is independent of the conditions or duration over which HRV is recorded, and persists even when drugs or gene modification are used to affect cellular processes. We have modelled this relationship using diverse biophysical models of differing complexity. We have suggested how to adequately correct for the phenomenon. What is relevant? Our findings are significant because many papers have previously been published using HRV data that are not corrected for heart rate. Papers continue to be published apace with this fundamental flaw, and yet with simple correction, the effect of heart rate could be removed and true differences in HRV revealed. This has ramifications for the handling of blood pressure variability data. Summary. HRV data should always adequately take into the account the heart rate at which they were measured.

Glossary

APD

Action potential duration

bpm

Beats/min

CL

Cycle length

C_m

Cell capacitance

DI

Diastolic interval

Δ

Change of

ECG

Electrocardiogram

HRV

Heart rate variability

I_b,Na

Background inward Na⁺ current

I_ca,T

T-type Ca²⁺ current

I_f

Funny current

I_NaCa

Na⁺-Ca²⁺ exchange current

I_K,ACh

ACh-activated K⁺ current

I_K,r

Rapid delayed rectifier K⁺ current

I_K,s

Slow delayed rectifier K⁺ current

I_per

Perturbing current underlying HRV

Itot

Total ionic current during the pacemaker potential

RR

R wave to R wave interval

SANC

Sinoatrial node cell

SDNN

Standard deviation of normal beat to normal beat intervals

t

Time

V_m

Membrane potential