Finding Genetic Overlaps Among Diseases Based on Ranked Gene Lists

Abstract

To understand disease relationships in terms of their genetic mechanisms, it is important to study the common genetic basis among different diseases. Although discoveries on pleiotropic genes related to multiple diseases abound, methods flexibly applicable to various types of datasets generated from different studies or experiments are needed to gain big pictures on the genetic relationships among a large number of diseases. We develop a set of genetic similarity measures to gauge the genetic overlap between diseases, as well as several estimators of the number of overlapping disease genes between diseases. These methods are based on ranked gene lists so that they could be flexibly applied to different types of data. We first investigate the performance of the genetic similarity measure for evaluating the similarity between human diseases in simulation studies. Then we apply the method to diseases in the OMIM database. We show that our proposed genetic measure achieves superior performance in explaining phenotype similarities between diseases compared to simpler methods. Furthermore, we identified common genes underlying the genetic overlap between disease pairs. With an example of five vision-related diseases, we demonstrate how our methods can provide insights into the relationships among diseases based on their shared genetic mechanisms.

1. Introduction

Exploring the genetic basis of complex human diseases has long been an important aspect in understanding disease etiology. Genome-wide association studies (GWAS) have succeeded in identifying an immense amount of variants associated with various traits. Gene expression studies have identified many genes and pathways whose expression profiles change with different phenotypes. These findings have provided major insights into the biological mechanisms of common genetic variants underlying complex traits, especially human diseases. Susceptibility genes common to different related diseases are found in numerous studies (Hindorff et al., 2009; Jawaheer et al., 2001; Danoy et al., 2010; Smyth et al., 2008; Scherrer et al., 2003; Blonigen et al., 2005; Toulopoulou et al., 2007; Kalaria and Ballard, 1999; Eyre et al., 2010), providing evidence in neurology, psychiatry, and some other autoimmune diseases that several different diseases may share a certain extent of genetic overlap. These studies suggest that exploring the common genetic risk factors for related diseases or phenotypes can help advance our understanding of disease etiologies (Blonigen et al., 2005). The genetic overlap can also help identify new disease genes and suggest important common biological pathways that could be informative in identifying therapeutic targets for multiple diseases (Eyre et al., 2010).

On the other hand, the rising interest in identifying pleiotropic genes from the genetic findings of related diseases (Sivakumaran et al., 2011) calls for efficient methods to identify disease-associated variants common to multiple diseases. To study the genetic overlap among different phenotypes, Rzhetsky et al. (2007) proposed a probabilistic model to describe the linkage of an individual's genetic variation to multiple disease status at different stages of one's life, and built a phenotypic disease network consisting of 657 diseases. This analysis indicated that genetic overlap among different disease phenotypes is so prevalent that most disorders studied are rooted in these shared genetic variations one way or another. Cotsapas et al. (2011) developed a method called cross phenotype meta-analysis (CPMA), which detects the association of an SNP to multiple phenotypes, and clustered SNPs potentially associated with multiple immune diseases. Suthram et al. (2010) used gene expression data of several diseases and a protein interaction network to study the common “functional modules” for diseases. Linghu et al. (2009) studied the association between diseases by their mutual predictability, a quantitative measure of how genes related to one disease can predict the genes related to the other disease. Another study in genetic overlap is between Crohn's disease (CD) and psoriasis (PS) (Ellinghaus et al., 2012). Indications of overlapping genetic or environmental factors between these two diseases include the observation that the two diseases occur together more frequently than expected, and that individual GWAS studies for each of them find common SNPs that are associated with both diseases.

Moreover, when there are multiple studies for each disease, the study of genetic overlap among diseases may involve ranking genes for each study first then using data integration methods to integrate multiple ranked lists (Adler et al., 2009; Boulesteix and Slawski, 2009; Deng et al., 2008; Jurman et al., 2012; Lin and Ding, 2009; Lin, 2010; Pihur et al., 2009). Therefore, it is necessary to consider the problem of finding genetic overlap among diseases under a more general setting, based on ranked lists of genes that could be obtained from any heterogeneous types of studies, rather than from a specific type of data or a homogeneous study. A closely related article (Natarajan et al., 2012) studied the problem of list-intersection test for gene lists, including its control of Type I error, within set FDR and sensitivity. Several other studies (Jurman et al., 2012; Subramanian et al., 2005; Fury et al., 2006; Yang et al., 2006; Roider et al., 2009; Plaisier et al., 2010; Ni and Vingron, 2012; Antosh et al., 2013) also addressed related topics of detecting overlap between ranked gene lists. However, most methods either use a fixed cutoff position and only consider intersection between lists on top of it, or use a weighting parameter to impose a higher weight on the top part of lists; or by using varying cutoffs to select the one that produces the most significant result, then evaluate the significance of that result, which induces heavier computation burden.

In this article we develop novel methods to study disease relationships based on their genetic similarity. We find in simulation studies a parameter-free statistic and an estimator of the genetic overlap size that show relatively good performance, indicating strong medical significance in application. Then we apply our proposed WeiSumE genetic similarity measure to detect genetic overlaps between diseases from the OMIM database. In addition, we include another application on diseases in the catalog of GWAS from National Human Genome Research Institute in the Supplementary Material (available online at www.liebertonline.com/cmb).

2. Methods

We propose two sets of statistics based on ranked lists to detect and measure the extent of genetic overlap between diseases given a list of genes ranked according to the importance of their contributions to each disease: scan statistics K_r and S_M, and weighted sum statistics WeiSumE and WeiSumV.

Figure 1 is a schematic outline of the workflow of our methods. Given two diseases A and B, we obtain for each disease a list of genes ranked by their strength of association to the disease, regardless of the types of experiments that produce these ranks. Then based on our proposed genetic similarity measures, we compute the value of dissimilarity between diseases A and B, and similarly for all other disease pairs, giving a dissimilarity matrix. Finally, we identify the common genes contributing to the genetic overlap between each disease pair and depict the pattern of the genetic overlap among the diseases of interest. In addition, we propose three estimators for the number of overlapping disease genes.

FIG. 1.

Outline of the methods. Given two diseases A and B, we obtain for each disease a list of genes ranked by their strength of association to the disease, regardless of the types of experiments that produce these ranks. Then based on our proposed genetic similarity measures, we can compute the value of dissimilarity between diseases A and B, and similarly for all other disease pairs, giving a dissimilarity matrix. The dissimilarity matrix provides a quantitative estimate of the genetic overlapping pattern among a set of diseases, which is readily applicable to further analysis. Furthermore, we can identify the genes underlying the genetic overlaps and provide an overlapping pattern for a set of diseases of interest.

2.1. Testing whether genetic overlap exits using scan statistics

2.1.1. A basic statistic and its extensions

Given n genes and the ranked list of these genes according to their relationship to each of two diseases, we first introduce a basic statistic that measures the extent of the genetic overlap between the two diseases, then propose some extensions on this statistic.

Suppose through some previous studies we are given two ranked lists, and in each list genes are ranked decreasingly based on their contributions to a disease. To address the question of whether the two diseases have a common genetic foundation in their respective etiologies, or in other words a significant “genetic overlap,” we develop a basic statistic to describe the extent of this “genetic overlap” as follows. Let G_d(k), d = 1, 2 denote the set of top k ranked genes in list d corresponding to the d-th disease. We propose the following statistic:

where Φ is the empty set. If two diseases have genetic overlaps, K is expected to be small. Under the null model that the two ranked lists are random shuffling of the genes, the p-value can be defined as

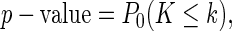where k is the observed value of K for the two diseases.

This formulation of the null is equivalent to fixing the order of the n genes for one disease, randomly order the genes for the other disease, and let

where O_i is the ranking order of the i-th gene for the second disease. Therefore, K follows the distribution of a shuffled order of one sequence under the null hypothesis, and the p-value is:

Derivation of Equation 1 is given in section S2.1 in the Supplementary Materials.

We can further extend the above studies to r ≥ 1 overlaps. Let K_r be the minimum number of top ranked genes needed to observe r overlapping genes. We use K_r as a statistic to test the hypothesis that the two gene lists have overlaps versus the null hypothesis that the two ranks are not related (randomly shuffled) (Chen and Karlin, 2007; Karlin and Chen, 2004). Similarly, the p-value is:

where c is the observed value of K_r. Derivation of Equation 2 is given in section S2.2 of the Supplementary Materials.

As in the use of r-scan statistics to locate genes or transcription factor–binding site clusters (Chen and Karlin, 2007; Karlin and Chen, 2004; Ewens et al., 2006; Karlin and Brendel, 1992; Smith et al., 2005), there is no gold standard for determining the optimal value of r for the K_r statistics, and actually, the optimal value of r may really depend on the diseases of interest.

We may fix a prespecified value of r and use the statistic K_r as a test statistic. For a fixed type I error α, we can find a threshold k_r(α) to be the maximum c such that the p-value defined in Equation 2 is less than or equal to α. We reject the null hypothesis that the two genetic diseases have no overlapping genes if the observed K_r is less than or equal to k_r(α). This test is valid in the sense that it has a controlled type I error rate, and it should have reasonable power under the alternative hypothesis, since K₁ should be small, and in turn, all K_r's should be smaller than expected under the null model.

In reality, we do not know the true number of overlapping disease genes, which makes it hard to fix r in advance. In order to estimate r from the data rather than prespecifying it, we propose an alternative test statistic as follows.

2.1.2. An alternative test statistic

Under the null hypothesis that the two diseases do not have overlapping genes, we expect that the p-value using K_r, p_r, will approximate a uniform distribution within the unit interval [0, 1], although they are not independent for given diseases. On the other hand, under the alternative hypothesis that the two diseases do have overlapping genes, the value of p_r is expected to decrease until r reaches the true number of overlaps. Thus, we can choose the smallest p-value among 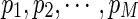, where M is the maximum number of genes we consider. Let

Note that R_M is a random variable. The alternative statistic we use to test the null hypothesis versus the alternative hypothesis is

where is the observed value of for the real data.

It is important to note that S_M cannot be regarded as a p-value of the test though, since we are taking the minimum of all p_r for 1 ≤ r ≤ M. Instead it should be regarded as a test statistic.

Since S_M follows the same distribution for a given total number of genes (n) and the maximum number of genes to consider (M) under the null model, we may obtain the distribution of S_M first using simulations as described in section S2.3 in the Supplementary Material.

2.2. Testing whether genetic overlap exits using weighted sums

Section 2.1 proposed two sets of test statistics based on the number of overlapping genes up to a certain position to gauge the overlap between two ranked lists. In this section, we will discuss a different set of test statistics that take the complete overlapping pattern across two ranked lists into account. Yang et al. (2006) proposed a similarity score (OrderedList), defined as the weighted sum of the number of overlapping genes X_i on top of the lists up to each position i, with an exponentially decreasing weight e^-βi, which we refer to later as WeiSumO:

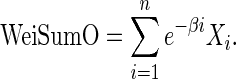However, it is not clear how to choose parameter β for real studies.

Based on this idea, we proposed two weighted sums that normalize the number of overlapping genes X_i by its expectation (WeiSumE) or by its standard deviation (WeiSumV):

where

since X_i follows a hypergeometric distribution Hyper(i; i, n).

Each of the three definitions of weighted sum statistics generates a weighted sum corresponding to a certain β value, therefore giving three sets of statistics with respect to a set of possible β values. Simulations can be used to obtain the null distributions and p-value p_β for each β. Note that when β = 0, WeiSumE simplifies to WeiSumE* as defined in Equation 11.

Similarly, as in section 2.1, for each of the three weighted sums we also propose one single statistic across a series of β's by choosing the minimum p-value:

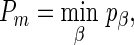where p_β is the p-value given by a weighted sum statistic with a specific β.

For the choice of β's we adopt the default series of β values in the R package OrderedList (Yang et al., 2006; Lottaz et al., 2006). There they set a minimum weight to 10⁻⁵, and the magnitude of β determines up to what position of the list the assigned weight e^−βi = 10⁻⁵. Then they set a series of positions i = 100, 150, 200, 300, 400, 500, 750, 1000, 1500, 2000, 2500, and take the corresponding β = − log(10⁻⁵)/i as the default β series. In addition, we also add β = 0, imposing no exponential decay.

To determine p_β's and the p-value of the single statistic p_m for each weighted sum (denoted as WeiSumX) out of WeiSumO, WeiSumE, and WeiSumV for a given list pair, we follow the procedure described in section S2.4 in the Supplementary Material.

2.3. Estimating the number of overlapping disease genes

To determine the number of overlapping associated genes, we may look at R_M as defined in Equation 3, which gives the minimum p-value, and take the number of overlaps on top of the lists up to as an estimator:

Note that ô₁ might not always equal R_M since the number of overlaps actually observed in the top 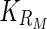genes may be larger than R_M. In addition, we propose a few alternative approaches to determine the number of overlapping genes.

For any gene g, define the Bernoulli trial B_g = 1 if the gene ranks among the top K_r genes for both diseases, and B_g = 0 otherwise:

where O is the number of overlapping genes in the top K_r of the ranked lists.

Let 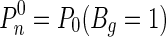, the probability of a gene ranked among top K_r among both lists of length n, under the null hypothesis H₀ that the two diseases do not overlap. Then:

Also, the expected position on the list where the first overlap occurs under the null model is:

Intuitively, a true overlapping gene associated with both diseases is more likely to occur as an overlap before a random overlap occurs, as we scroll down the lists. Therefore, we can estimate the maximum position on the list where there is expected to be less than one random overlap, and take the number of overlaps observed up to that position as an estimator of the number of overlapping genes:

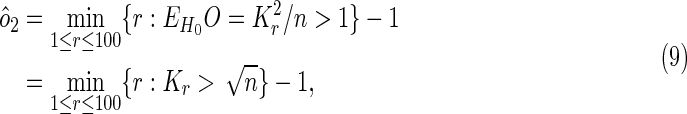or the number of overlaps observed earlier than the position in which a first random overlap is expected to occur under the null model:

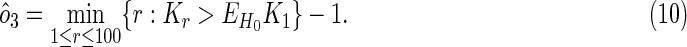3. Results

3.1. Simulation results summary

We conduct simulation studies to evaluate the performance of our methods under different conditions and compare the best performing statistic from each category with one another in Table 1. The simulation procedures and results are in Supplementary Material section S1.3. (Supplementary material is available online at www.liebertonline/cmb)

Table 1.

Comparison of Different Statistics in Simulation Studies

n	1000	6000	11000	25000
K1	32	56	63	63
S1	32	56	63	63
WeiSumE*	27	46	66	94
pm	32	53	64	73

For each length of gene list n, the number of parameter settings out of a total of 144 different settings of a method shows the highest power, including ties, taking p-value threshold of 0.05.

We find that one of our proposed statistics, WeiSumE*, excels in detecting genetic overlap between longer gene lists, especially for n = 25000, which is about the number of genes in the full human genome, therefore is most suitable for the study of human diseases:

where X_i is the number of overlapping genes between two ranked gene lists among the top i ranked genes, and n is the total number of genes in a list. This is a special case of the set of WeiSumE statistics as explained in the Methods section. However, we will refer to it as WeiSumE in the Results section for convenience.

Table 2 gives an example of the mean squared error of different estimators of the number of overlapping genes in one parameter setting. It shows that ô₃ gives the most reliable estimation of the number of disease genes, especially for human data (n ∼ 25, 000).

Table 2.

The Mean Squared Error of Different Estimators of the Number of Overlapping Genes When σ² = 0.1

σ2	0.1
n(×1000)	1	6	11	25
ô1 (M = 5)	7.92	9.76	10.61	11.78
ô1 (M = 10)	9.46	12.68	13.88	15.79
ô1 (M = 20)	26.62	30.39	33.17	36.65
ô2	2.52	3.47	4.09	5.03
ô3	2.67	3.44	3.74	4.35

The σ² is a parameter describing the accuracy of the ranking algorithm; the higher σ² is, the less accurate the ranking algorithm is. In addition, n × 1000 is the total number of genes in the genome, and M is the cutoff position for a ô₁, where only up to M overlapping genes are considered.

3.2. Genetic overlap of OMIM diseases

We apply our proposed genetic similarity measures to study diseases from the OMIM database online and use ENDEAVOUR (2.44) (Aerts et al., 2006; Tranchevent et al., 2008) to rank the human genes. ENDEAVOUR is a gene prioritization tool with various options of data sources. To ensure the reliability of ranking, we consider diseases with at least five associated genes recorded in the OMIM database, which gives a total of 89 diseases. Then for each disease, we take its corresponding OMIM genes as the training genes to input into ENDEAVOUR, including all data sources provided, and rank all the human genes.

3.2.1. Consistency among different phenotype similarities

Before we move on to studying the genetic relationships among the 89 OMIM diseases, it would be interesting to look at their phenotype similarity first. We investigate three phenotype similarity measures: HPO (Robinson et al., 2008), MimMiner (van Driel et al., 2006) and another similarity matrix provided in Lage et al. (2007). Supplementary Figure S1 shows the rank of one similarity measure score versus another. Note that for each pair of similarity measures, we only display disease pairs available in both phenotype similarity matrices. As is shown in the figure, the three phenotype similarity measures weakly correlate with each other, demonstrating the lack of consistency in such produced disease relationships.

3.2.2. Explaining phenotype similarity with genetic similarity

Seeing that consistency among different phenotype similarities is low, we proceed to ask how well the genetic similarity measure WeiSumE can explain the phenotype similarity, taking MimMiner as an example. For comparison, we also consider two other simpler measures of genetic similarity to see if the phenotype similarity can be explained with them as well. The first one (#OMIM) is simply the number of genes present in the OMIM database for both diseases. Another measure (HyperP) is the p-value of a hypergeometric test using a fixed cutoff, which is the probability of observing at least the number of overlapping genes between the two lists up to a fixed cutoff position under the null hypothesis that the two lists are random permutation of each other. We rank the WeiSumE genetic similarity, #OMIM similarity, HyperP similarity, and the MimMiner phenotype similarity of all disease pairs, and compare all three genetic overlap measures with MimMiner to obtain the average density fold change of each method, as shown in Figure 2. It shows that WeiSumE performs the best out of the three methods from a genetic point-of-view to explain the MimMiner phenotype similarity without having to set a cutoff threshold as in HyperP.

FIG. 2.

Performance of WeiSumE explaining the MimMiner phenotype similarity, compared with two other simpler methods, #OMIM and HyperP, with different cutoff positions. The average fold change is used as a measure for performance here; detailed definitions and explanations are in the Supplementary Material section S1.1.1. In particular, HyperP similarity performance is listed with varying cutoff positions 10, 20, 50, 100, 200, 500, 1000.

Next we look into the disease pairs, where the genetic similarity and phenotype similarity disagree. For example, the disease pair peeling skin syndrome and hypotrichosis 2 (HYPT2) displays very low MimMiner phenotype similarity but very high genetic similarity. According to OMIM description, both diseases are caused by mutations in the CDSN gene, where peeling skin syndrome is caused by a homozygous mutation and HYPT2 is caused by a heterozygous mutation. Therefore, despite the lack of phenotype similarity, this pair of diseases do share a common genetic basis. A contrary example is the pair of maturity-onset diabetes of the young (MODY) and noninsulin-dependent diabetes mellitus (NIDDM), which shows high MimMiner phenotype similarity but very low genetic similarity. MODY is an autosomal dominant form of diabetes caused by insulin secretion defects, while NIDDM is a polygenic disease characterized by insulin resistance. Therefore, these two subtypes of diabetes must be treated differently despite their resemblance in phenotypes. These examples of discrepancy between genetic and phenotype similarity demonstrate the importance of relating diseases based on their genetic mechanisms, since effective drug treatments and therapeutic interventions shall address the underlying mechanisms of diseases, rather than phenotypic symptoms.

3.2.3. Identifying common genes underlying the genetic overlap

Having studied the ability of our proposed genetic similarity measure to explain the phenotype similarity, we attempt to further identify the common genes underlying the respective genetic mechanisms of the two diseases. For this purpose we propose several estimators of the number of common disease genes based on ranked gene lists in the Methods section, and take the estimated number of overlapping genes from the top of the lists to be the common genes underlying the two disease mechanisms. From simulation study results shown in Table 2, we will use the ô₃ estimator.

In views of the genetic overlap sizes of disease pairs, as shown in Supplementary Figure S2, the majority of disease pairs share genetic overlap to some extent, mostly around 1 to 16 overlapping genes. The pleiotropy of genes, on the other hand, are moderate: Out of the full human genome that we ranked, 2920 genes are considered pleiotropic by our method. The distribution of pleiotropy extent of the genes is shown in Supplementary Figure S3. We find that the extent of pleiotropy varies significantly. Some genes are extremely pleiotropic and relate to a vastly diverse set of diseases, the most of which being the CREBBP (CREB binding protein) gene. This gene plays important roles in many biological activities. For instance, CREBBP may function as tumor suppressor gene or oncogene in prostate cancer, and may serve as potential therapeutic target (Shaikhibrahim et al., 2011). Mutations in CREBBP result in neural tube defects in mice (Bhattacherjee et al., 2009) and modest associations were also observed in humans (Lu et al., 2010). Both results were reconfirmed in our study.

Next we take five eye-related diseases—Leber optic atrophy, macular degeneration (age-related, 1; ARMD1), cataract (autosomal dominant), retinitis pigmentosa (RP), and colorblindness (partial, Deutan series; CBD)—as examples and demonstrate how our genetic overlap measures explain their common genetic basis. We plot in Figure 3 a heat map showing the dissimilarity quantile matrix of the five diseases measured by WeiSumE dissimilarity measure, where each value is the fraction of the WeiSumE distribution shown in Supplementary Figure S4 among all disease pairs that is less than the dissimilarity value of the given disease pair. This figure provides clear evidence that cataract (autosomal dominant), RP and CBD (partial, Deutan series) share a substantial common genetic basis, while Leber optic atrophy and ARMD1 appear to be genetically more distant to any other of the five diseases.

FIG. 3.

A heatmap of the WeiSumE dissimilarity quantile matrix among five eye-related diseases.

To further investigate the genes that contribute to their genetic overlap, Figure 4 shows a Venn diagram of the number of genes underlying the genetic overlap among the five diseases. There is no gene underlying all five eye-related diseases, conforming to the pattern shown in Figure 3 that Leber optic atrophy and ARMD1 are genetically distant to the other three diseases. However, it is interesting that two genes are identified to be underlying the genetic overlap among four diseases, each contributing to Leber optic atrophy or ARMD1 and the closely related three diseases, despite the low genetic overlap of Leber optic atrophy or ARMD1 and the three. Under close investigation, we find that these two genes are CDH23 (cadherin-related 23) and COL7A1 (collagen, type VII, alpha 1), both widely pleiotropic, residing within the very tail of the pleiotropy extent distribution in Supplementary Figure S3. CDH23, contributing to Leber optic atrophy and the three close diseases, is underlying the genetic overlap of 171 disease pairs; COL7A1, contributing to ARMD1 and the three close diseases, is underlying the genetic overlap of 1085 disease pairs. Mutations within both genes are shown in the literature (Schultz et al., 2011; Dighiero et al., 2004) to potentially cause vision loss. In contrast, the 32 genes underlying the genetic overlap of cataract, RP, and CBD include genes that are more specific to the three diseases, therefore contributing more significantly to their genetic overlap. One example is the gene PDE6A (phosphodiesterase 6A, cGMP-specific, rod, alpha), contributing to the genetic overlap among the three diseases exclusively. According to NCBI records, this gene encodes a subunit of a key phototransduction enzyme and participates in processes of transmission and amplification of the visual signal.

FIG. 4.

This Venn diagram shows the number of overlapping genes among any subset of diseases from the five eye-related diseases.

4. Discussion

The traditional disease classification system groups diseases with similar clinical symptoms and phenotypic traits. Thus, diseases with entirely different underlying pathologies could be grouped together, leading to similar treatment design. Such problems may be avoided if diseases can be classified based on their genetic mechanisms. In fact, recent research showed that multiple diseases could share the same set of malfunctional genes. Grouping diseases with similar pathogenesis mechanisms could inspire novel strategies for effective repositioning existing drugs and therapies. The key challenge is how to assess the genetic similarity between two diseases, and how to identify the contributing genes.

In this article, we aim to detect and identify genetic overlaps among different diseases. Two groups of statistics and three estimators of the number of overlapping genes are developed. The first group is based on scan statistics considering the number of overlapping top ranked genes between two lists. The second group is based on the weighted sum of the numbers of overlapping top ranked genes between two lists. We evaluate the effectiveness of these statistics by comparing their power in detecting genetic overlaps under a variety of scenarios. We also study the effects of various parameters such as the reliability of the ranking, the number of associated genes, the number of overlapping associated genes, and the total number of genes under study. As expected, the reliability of the ranking significantly affects the power of these statistics.

In addition, the two groups of statistics have different merits. The scan-based statistics can be applied to situations in which only a fraction of the top ranked genes are available for each disease, which is the case for the NIH catalog of GWAS, where only associations with p-value less than 10⁻⁵ are reported. Among this group, the statistic K₁ performs reasonably well in most situations. However, these statistics are generally less powerful than the weighted sum statistics that consider all the elements in the lists. Among the weighted sum statistics, WeiSumE performs very well in most scenarios we studied. Moreover, it overcomes the difficulty of choosing weights for different diseases.

For applications, we use WeiSumE to measure genetic overlap among diseases in the OMIM database based on ranked gene lists produced by ENDEAVOUR. We show that our method demonstrates superior performance relative to other simpler methods in explaining the phenotype similarity. Furthermore, we look into disease pairs displaying major discrepancy between their genetic and phenotypic similarity. For disease pairs high in genetic similarity but low in phenotypic similarity, the known common genetic variants responsible for these disease pairs support their common genetic basis. On the other hand, some disease pairs show high phenotype similarity but low genetic similarity since mutations responsible for these diseases may be involved in different pathways. In addition, we show the overall pattern of genetic overlap sizes between disease pairs that we study, and the pattern of pleiotropy extent of genes. Finally we demonstrate in a specific example of five vision-related diseases how our methods can provide important biological insights into their genetic mechanisms.

Despite these significant findings, this study has some limitations. First, the similarity measures depend purely on the ranked gene lists without explicitly considering their reliability. When experimental data from multiple studies for each disease are available, we may be able to associate with each gene a confidence score that describes quantitatively how the gene is related to the disease. Instead of transforming the confidence score to a rank, which may reduce the power of detecting the genetic overlaps, we can use the confidence score directly to study the disease relationships. Second, the statistics in this article depend on the number of overlapping genes among the top genes for both lists. They have the advantages of being simple and easy to compute. Nevertheless we may also consider statistics depending on the number of overlapping genes among different numbers of top genes in the first list and the second list. Finally, we use simulations to approximate the distributions of several statistics studied in this article. Theoretical results on their distributions will help to compute the statistical significance more accurately and efficiently. These are the topics for future studies.

Acknowledgments

We thank K.U. Leuven (Katholieke Universiteit Leuven) and VIB (Flanders Interuniversity Institute for Biotechnology) for providing the ENDEAVOUR software. This research was supported by National Institutes of Health (P50HG002790 and 1 U01 HL108634). Q.C. was partially supported by the Viterbi Fellowship.

Author Disclosure Statement

No competing financial interests exist.