Abstract
Immunoassays are one of the most versatile and widely performed biochemical assays and, given their selectivity and specificity, are used in both clinical and research settings. However, the high cost of reagents and relatively large sample volumes constrain the integration of immunoassays into many applications. Scaling the assay down within microfluidic devices can alleviate issues associated with reagent and sample consumption. However, in many cases a new device is designed and empirically optimized for each specific analyte, a costly and time consuming approach. In this paper, we report the development of a microfluidic bead-based immunoassay which, using antibody coated microbeads, can potentially detect any analyte or combination of analytes for which antibody coated microbeads can be generated. We also developed a computational reaction model and optimization algorithm that can be used to optimize the device for any analyte. We applied this technique to develop a low volume IL-6 immunoassay with high sensitivity (358 fM, 10 pg/mL) and a large dynamic range (4 orders of magnitude). This device design and optimization technique can be used to design assays for any protein with an available antibody and can be used with a large number of applications including biomarker discovery, temporal in vitro studies using a reduced number of cells and reagents, and analysis of scarce biological samples in animal studies and clinical research settings.
Keywords: Immunoassay, Microfluidic, Computational Fluid Dynamics, Multi-Objective Optimization
1 Introduction
The immunoassay is one of the most common biochemical tests performed in both clinical and research settings (Diercks et al. 2009). This technique takes advantage of highly selective antibody-antigen interactions to measure any biomolecular structure or particle for which antibodies are available. These include drugs, biomarkers, hormones, cytokines, antibodies, viruses, and bacteria (Henares et al. 2008). Immunoassays have found a broad range of applications in medical diagnostics (e.g., HIV, prostate specific antigen, pregnancy, sexually transmitted diseases, etc.), proteomics, and biological research in general (Wild 2005).
Despite their widespread use, the disadvantages include high cost due to expensive antibodies and reagents, the requirement for highly trained operators, the amount of labor associated with each assay, and long incubation times due to the large distances molecules must diffuse in order to react (Ng et al. 2010). Furthermore, the required sample volume is a limitation in certain applications (Phillips 2004). Microfluidic technology has the potential to mitigate these drawbacks that plague conventional immunoassays. First, miniaturization decreases both sample and reagent usage (Bange et al. 2005) directly resulting in a significant cost reduction and facilitating analysis of scarce samples that can not be analyzed using conventional techniques (Phillips 2004). The small scale also decreases diffusional distances and increases the binding surface area to sample volume ratio producing faster reactions (Derveaux et al. 2008). Furthermore, microfluidic devices are easily automated, allowing for high-throughput and highly reproducible assays (Bange et al. 2005; Derveaux et al. 2008).
Performing microimmunoassays using packed beds of microbeads as the antibody immobilization surface affords additional advantages. This provides rapid and efficient mixing across relatively large distances (Seong and Crooks 2002; Derveaux et al. 2008), alleviating a common problem in microfluidics due to the low Reynolds number flow regime resulting from the small dimensions of microfluidic channels (Beebe et al. 2002). These benefits were shown in a previous study, where a 90-fold reduction in assay time was observed compared to its bench-top counterpart performed in a 96-well plate (Sato et al. 2000). Moreover, altering the capture antibody on the microbead surface can easily change the analyte specificity of the assay utilizing the same device. Finally, millions of beads can be conjugated to antibodies in a single batch, allowing highly reproducible assays between devices (Wilson et al. 2006).
Previous reports have described immunoassay conditions for a specific analyte with a given number of antibodies and each application has required individual empirical optimization (Diercks et al. 2009; Sato et al. 2002; Sato et al. 2000; Shin et al. 2007; Kong et al. 2009; He et al. 2009). Unfortunately, empirical optimization is costly and time consuming as this approach requires many devices and experiments. An alternative strategy is to develop a predictive mathematical model using computational fluid dynamics (CFD) combined with antibody-antigen reaction modeling within microchannels. In addition to eliminating the need for large numbers of experiments, an improved understanding of the effects of various design and operating parameters can be used to predict immunoassay performance for a given application. Unfortunately, the limited models of antibody-antigen reactions in microfluidic systems have only studied surface based reactions and have lacked experimental validation (Lionello et al. 2005a, b; Winz et al. 2007). Nevertheless, the work of Zimmerman et al. demonstrated that a computational model enables the prediction of operating parameters best suited for a particular application, i.e. minimal assay time, high sensitivity, or large dynamic range (Zimmermann et al. 2005).
In this report, a microfluidic platform to perform sandwich immunoassays utilizing antibody-conjugated microbeads is designed and tested. In addition, a predictive CFD based model of antibody-antigen interactions in a packed bed format within a microchannel is developed and experimentally validated. The model is utilized in conjunction with mathematical optimization techniques in order to aid in the development of the device as well as to understand the key factors affecting assay performance. The optimal conditions determined from the mathematical optimization are then used to demonstrate a highly sensitive, low-volume microimmunoassay with large dynamic range and a greatly reduced reagent consumption and cost. The combination of the presented device and optimization methodology can be further extended to develop an assay for any analyte for which antibodies are available. Therefore, this technology may be translated to improve many research and clinical applications which rely on high-throughput studies and/or the analysis of scarce biological samples.
2 Microfluidic Device Design and Assay Operating Principle
The device is designed to perform parallel low volume sandwich immunoassays on a single chip using antibody-conjugated microbeads, allowing a single design to be used to measure any analyte with an available antibody pair. The operating principal of the microimmunoassay is shown in Fig. 1a. Antibody conjugated microbeads are first immobilized via a mechanical trap. The sample solution then flows over the beads allowing incubation of the sample with the antibodies. A wash is performed to remove any non-specifically bound proteins, followed by labeling with a biotinylated detection antibody. Following a wash step, streptavidin-phycoerythrin flows to bind a fluorescent tag to the antibody sandwich. Subsequent to an additional wash step, the beads can be analyzed on chip using fluorescence microscopy. Alternatively, the beads can be collected and analyzed via flow cytometry allowing for the potential for multiplexing with this device using Luminex optically encoded microbeads (Houser 2012).
Fig. 1.
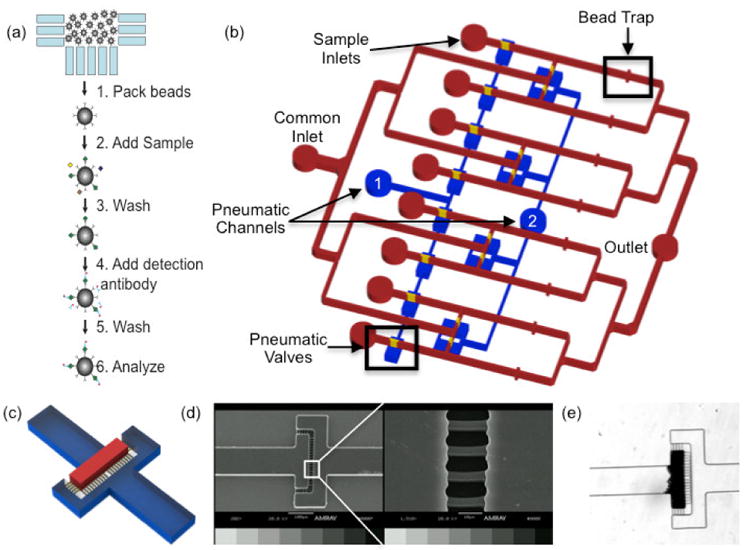
a) Microimmunoassay principle. Antibody conjugated microbeads are packed into the bead traps. Sample is then flowed over the bead beds followed by a wash step. Detection antibody is then added, the beads are washed, and the sample is ready for analysis b) Schematic representation of the microimmunoassay device. A common inlet is used for flowing all assay reagents including blocking buffer, wash buffer, antibody coated microbeads, detection antibodies, and fluorophores. Individual sample inlets allow for the simultaneous analysis of eight samples. Downstream of each sample inlet, an array of 3 μm channels acts as a bead trap to create a packed bed that functions as a reaction chamber. A common outlet discards waste from the assay and also is used as an inlet during collection of the microbeads at the completion of the assay. Pneumatic valves are used to direct fluid flow throughout the assay. Whenever the common inlet is in use, pneumatic channel 1 is pressurized so fluid flows from the common inlet through the bead traps. During sample incubation and bead collection, pneumatic channel 2 is pressurized to prevent mixing between adjacent channels. c) 3D schematic of the bead traps. The bead bed is immobilized in the area denoted in red and the bead trap is comprised of the array of yellow features d) SEM image of the bead trap e) Brightfield micrograph of a packed bed of microbeads upstream of the bead trap
A schematic of the device is shown in Fig. 1b. Pneumatic valves are incorporated into the design to divert fluid flow to desired regions of the device (Unger et al. 2000). With this design, only two pneumatic valves are needed to facilitate eight parallel reactions, which can be easily scaled-up to process additional samples on a single chip. A common inlet is used for the introduction of assay reagents (i.e., blocking buffer, wash buffer, microbeads, detection antibodies, and fluorophores). When flow is present through the common inlet, pneumatic valve 1 is closed to divert fluid flow through the reaction zones and away from sample inlets. Individual sample inlets facilitate flowing multiple samples simultaneously as well as the collection of each individual bead population at the completion of the assay. Pneumatic valve 2 is closed during the incubation and collection steps to prevent mixing of adjacent fluid streams and bead loss through the common inlet, respectively. Downstream of each sample inlet, a bead trap immobilizes the microbeads for the duration of the assay while permitting fluid to flow through the bead bed. The bead trap consists of an array of 3 μm wide channels, considerably narrower than the diameter of the beads in our experiments, shown in Fig. 1c. These features are 7 μm tall as we found that this is tallest we could reproducibly fabricate these features with good resolution, as shown in the scanning electron micrograph in Fig 1d. A picture of an immobilized packed bead bed is shown in Fig. 1e.
The bead trap is designed to minimize flow resistance as this is a major concern with packed beds (Derveaux et al. 2008). Therefore, the channel doubles in width from 100 to 200 μm at the bead trap. This halves the fluid velocity through the bed and allows the same number of beads to be packed in a bed half as long, decreasing the pressure drop resulting from the packed bed by a factor of 4 (Bird et al. 2006). In addition, channels are oriented both parallel and orthogonal to fluid flow which has been shown to greatly reduce clogging of microbeads in microfluidic channels (Andersson et al. 2001).
3 Mathematical Modeling and Optimization
3.1 Theoretical Background
Equations
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
| (Eq. 4) |
| (Eq. 5) |
| (Eq. 6) |
| (Eq. 7) |
| (Eq. 8) |
| (Eq. 9) |
The model is constructed in two parts, first, the fluid flow through the packed bed and second, the transport and surface binding of the analyte. The fluid flow is governed by the volume averaged Navier-Stokes equation (Eq. 1) and the continuity equation (Eq. 2), where ρ is the fluid density, v is the fluid velocity vector, P is pressure, μ is fluid dynamic viscosity, and f represents external forces. Within microfluidic systems, the Reynolds number is very low and flow is therefore laminar. It is assumed that the fluid is incompressible (i.e. of constant density) and fully developed at the inlet. Therefore, the left side of Eq. 1 can be assumed to be zero (Bird et al. 2006).
The presence of the packed bed is accounted for as a volume-averaged pressure drop term, Pbed, which reflects the average frictional loss as fluid moves through the bed. This pressure drop can be estimated using the Ergun equation for laminar flow (Eq. 3), where ε is the void fraction and Dp is the diameter of the particles that comprise the packed bed. This frictional loss term is set to zero outside the packed bed and Eq. 4 is solved in conjunction with the continuity equation for incompressible fluids (Eq. 2) to obtain the coarse grained velocity field throughout the packed bed (Wilkes 2006). This approach is meant to account for the overall effect of the packed bead bed on the fluid dynamics within our model. It is important to note that this volume-averaged method is not intended to represent microscopic flow profiles within the bed.
Analyte transport and binding are governed by the Convection-Diffusion equation with an added source term for the binding reaction derived from mass conservation of the analyte (Eq. 5), where V is total volume of the packed bed, C is the analyte concentration in the bulk fluid, D is the effective analyte diffusivity, Γs is the surface concentration of the bound analyte, and ABead and VBead are the surface area and volume per bead, respectively. The effective molecular diffusion coefficient was used in lieu of the effective dispersion coefficient as dispersion is negligible in all geometries considered in our simulations (Squires and Quake 2005). This equation considers the rate of change of the total number of molecules of the analyte, given by the volume of fluid εV and bulk concentration C, or the area of the bead surface (the bead phase volume (1-ε)V scaled by the bead surface area to volume ratio ABead /VBead) and surface concentration Γs. Applying mass conservation shows that rate of change of the number of analyte molecules in a fluid element in the packed bed is given by the diffusive and convective transport rate of molecules in and out of the element and the rate of loss due to binding to the surface. Second order binding kinetics determines the rate of surface binding with rate constants kon and koff and the total density of binding sites available Γs max − Γs, shown in Eq. 6. Summing the convective and diffusive transport terms with the binding term yields the full reaction diffusion equation (Eq 5). The surface reaction can then be converted to a volumetric reaction by rewriting the Γs in the last term in Eq. 5 as a ratio of the number of moles (N) to the area of bead and multiplied by ABead VBead-1, yielding Eq. 7. The ABead terms cancel, and the number of moles per bead volume can then be replaced with a volumetric concentration, ΓV, as shown in Eq. 8. This equation can then be inserted into Eq. 5 to produce Eq. 9. This derivation is consistent with validated chromatography models (Dimartino et al. 2011; Boi et al. 2007).
3.2 Computational Methods
The simulation is restricted to the packed bed within the device as we assume negligible analyte binding occurs on the channel walls upstream of the reaction chamber. All operations pertaining to the mathematical model (i.e., generating geometries, meshing, and solving) are performed within Ansys Workbench (Ansys, Inc, Canonsburg, PA) in different subprograms handling each individual unit operation. The first step is the construction of a simplified 3D model of the reaction chamber consisting of the bead bed and a 7 μm tall outlet region in Ansys DesignModeler. This geometry is then imported into Ansys Meshing, where it is discretized and a mesh is created. The mesh is then imported into Fluent, a computational fluid dynamics software package, where the fluid flow and transport-binding equations are solved simultaneously. The physical velocity porous formulation in Fluent is used to model the presence of random close packed beads and incorporate the pressure drop and velocity change due to the packed bed (Eq. 3) in order to solve the modified Navier-Stokes equation (Eq. 4). The transport-binding equation (Eq. 9) is solved using a user-defined function. The concentration of analyte, capture molecule, and captured analyte complex are each modeled as scalar fields defined across each cell in the mesh geometry using the user-defined scalar mode. The convection terms are provided by the fluid velocity field, and analyte diffusivity is estimated from molecular weight (He and Niemeyer 2003) with corrections for the tortuosity of the packed bed (Froment et al. 1990). The consumption and production of the reaction species (e.g. the last term on the right of Eq.9) are modeled as source terms. The solution methods in Fluent are as follows: SIMPLE scheme for pressure velocity coupling, Green-Gauss Node Based gradient calculation method, Standard pressure equation solver, Second Order Upwind discretization scheme for momentum and user defined scalars, first order implicit transient formulation, and the default adaptive time stepping method (ANSYS 2010). The output of the model is moles of analyte bound at each time step, calculated by a volume integral of the molar concentration of the antibody-analyte complex over the reaction volume. A text file is written containing the amount of protein bound at each time step. For the validation experiments, the constants used are for a model system of streptavidin coated beads and biocytin-Alexafluor 488 solutions. The Design of Experiments (DOE) and optimization were performed using parameters for IL-6 and typical binding constants for antibody-antigen interactions. Table 1 contains the values for the constants used in simulations.
Table 1.
Constants used in simulations.
| Constant | Biocytin-Alexafluor488 | IL-6 |
|---|---|---|
| ε | 0.36a | |
| ρ (kg m-3) | 998.2b | |
| μ (kg m-1 s-1) | 0.001003b | |
| Dp (μm) | 5.8c | 6.5c |
| Γmax (mol m-3) | 0.0889c | 0.013857c |
| kon (M-1 s-1) | 107 d | 106 e |
| koff (s-1) | 10-5 d | 10-3 e |
| D (m2 s-1) | 7.292 × 10-11 f | 2.206 × 10-11 f |
(Dullien 1991),
As per manufacturer specifications,
3.3 Optimization Platform
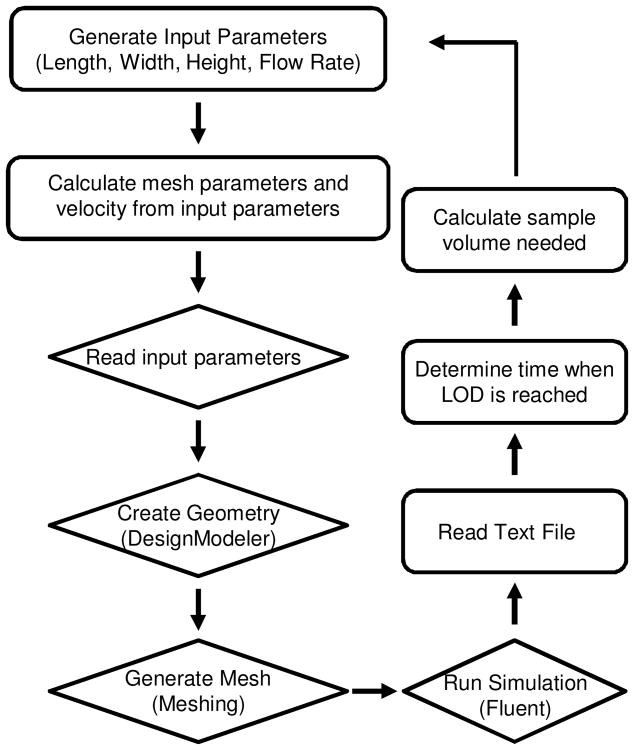
An optimization software package, modeFrontier (ESTECO, Trieste, Italy), is used to sequentially iterate the simulations during the DOE and optimization runs. The workflow for the DOE and optimization studies is shown in Fig. 2. Ranges for the length, width, and height of the reaction chamber and flow rate are defined by the user. For each simulation, the software calculates the flow velocity, minimum mesh element size, maximum mesh face size, and maximum mesh element size based on the input parameters. These calculated parameters are fed into Ansys Workbench which completes the simulation workflow described above. The output text file is read by modeFrontier at the completion of the simulation and used to calculate the amount of flow time needed to reach the limit of detection (LOD). We used the LOD of a typical flow cytometer of 750 fluorescein molecules per event as provided by the manufacturer (BD 2010). However, our goal is to optimize the device for Luminex bead based multiplex assays that utilize phycoerythrin. To estimate the LOD using this fluorophore, we assumed brightness at the same concentration using the same excitation source is proportional to the ratio of the product of the extinction coefficient and the quantum yield (Lichtman and Conchello 2005). Therefore, we estimated the LOD to be 42 phycoerythrin molecules per bead. The incubation time needed to reach this threshold is multiplied by the flow rate, yielding the sample volume required to reach the detection limit.
Fig. 2.
Schematic representation of the optimization workflow. Operations in rectangles and diamonds are performed in modeFrontier and Ansys Workbench, respectively. The velocity and meshing parameters are calculated from the input parameters and fed into Ansys Workbench. The geometry is created in Ansys DesignModeler and exported to Ansys Meshing to discretize the volume. Ansys Fluent solves the governing equation and outputs a text file containing the amount of protein bound in the bead bed at each time step calculated as a volume integral of antibody-antigen complex concentration across the reaction volume. The text file is read by modeFrontier and the data is used to determine the time at which the LOD has been reached. The sample volume is calculated from the product of incubation time required to reach the LOD and the flow rate. For DOE, the process is repeated for the next set of input parameters from the full factorial experimental design. For optimization studies, the algorithm adjusts the input parameters in an attempt to minimize the design objectives
3.4 Design of Experiments and Optimization
The goal of these studies is to determine the assay parameters that will minimize the required sample volume and incubation time. The design parameters of the proposed device are the length, width, and height of the bead bed. The height will be limited to between 25 and 41 microns, as shorter channels are highly susceptible to clogging of microbeads and fabricating taller channels becomes a more difficult and tedious fabrication process. The width (W) will be constrained between 25 and 300 μm, as our experience with this device has shown that wider channels results in uneven packing of bead beds. The length (L) of the bed will be constrained between 25 and 50 μm. Model convergence becomes an issue with a bed length of less than 25 μm, and the pressure drop across the bed becomes too large with a length over 50. Additionally, these parameters dictate the number of antibody-conjugated beads as determined by multiplying the volume of the reaction chamber by the solid volume fraction and dividing by the volume of a single bead. Furthermore, the operating parameter of interest is the flow rate of the sample solution. The flow rate was constrained to between 5 nL/min (the slowest flow able to be generated using our syringe pump) and 100 nL/min. With these constraints, the concentration of analyte at the inlet was set to 358 fM (10 pg/mL IL-6 (Toumpanakis and Theodoros 2007)) in an effort to optimize a highly sensitive assay.
Exploration of the effects of assay parameters within the design space was accomplished by utilizing DOE. Three levels were used for the length, width, and height, corresponding to the constraints specified above as well as a center point. For the flow rate, 15 levels were used in an effort to determine the reaction limited and transport limited operating states of the immunoassay. The experimental matrix was constructed utilizing a full factorial experimental matrix totaling 405 combinations. This relatively large number of simulations was utilized to capture any possible non-linear effects (Montgomery 2009). The calculation of incubation time and volume needed to reach the detection limit as well as the determination of main factor and interaction effects was performed in modeFrontier.
Multi-objective optimization was performed in modeFrontier using the Hybrid algorithm. In brief, an initial group of 10 design combinations was generated using a Uniform Latin Hypercube DOE. A child population was then created using a sequential quadratic programming (SQP) algorithm, a gradient based method using derivative approximations (ESTECO 2013). The combined population was then evaluated by a second generation non-dominated sorting genetic algorithm (NSGAII) (Deb et al. 2002) that identified the optimal designs. The best designs were chosen to become the new parent population and the process was repeated for a total of 1000 simulations. Minimization of the time to perform the assay and the necessary sample volume were set as design objectives. At the conclusion of the simulations, the software determined Pareto-optimal solutions. The data was exported to Excel (Microsoft, Redmond, WA) and Matlab (Mathworks, Natick, MA) for plotting.
4 Experimental Methods
4.1 Device Fabrication
The device consists of two layers to facilitate the incorporation of pneumatic valves. Therefore, molds are fabricated on two separate silicon wafers, one for the fluidic network and one for the control layer using standard photolithography techniques (Madou 2002). The fluidic layer requires three separate photolithography steps. First, the beads traps are patterned using SU-8 2007 (MicroChem Corp., Newton MA) at a height of 7 μm. These features are only 3 μm wide, so the temperature was ramped during all baking steps to reduce interfacial stress and prevent delamination. In addition, the exposure dose was reduced approximately 40% compared to manufacturer recommendations to improve resolution (Chan-Park et al. 2004). A flood exposure was performed after development followed by a hard bake to mitigate the effect of underexposure on the mechanical integrity of the features. The valve layer is then patterned in a 36 μm layer of AZ9260 (AZ Electronic Materials) deposited in 3 sequential 12 μm spin coating steps, each followed by a baking step. Following development, the wafer is baked above the glass transition temperature of the photoresist causing reflow, rounding the features and allowing complete closure of the channels at these locations (Fordyce et al. 2012; Unger et al. 2000). The final layer of the fluidic channel structure is fabricated using a 41 μm layer of SU-8 2025 according to manufacturer recommendations, as is the control layer on a separate wafer.
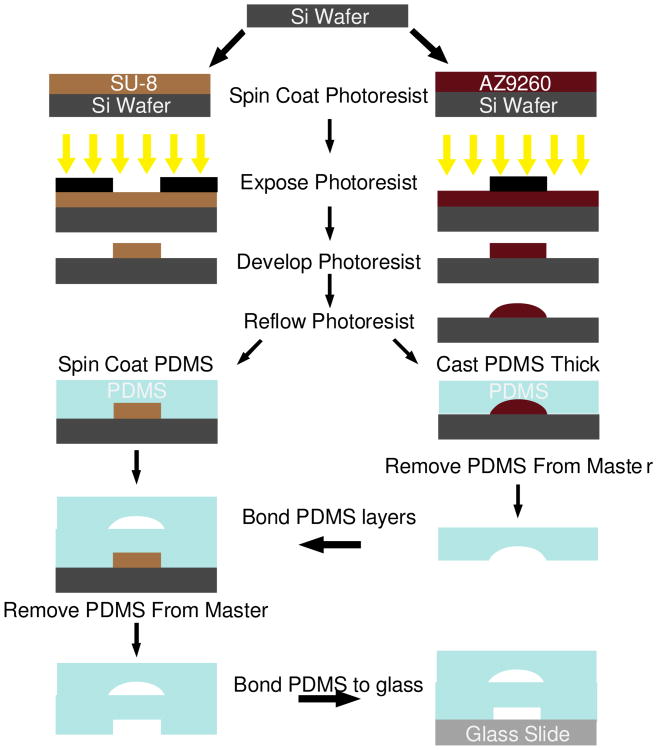
The fluidic mold is then cast in Smooth-Cast 325 Colormatch polyurethane (Smooth-On, Inc., Easton PA, 48841) as previously described (Desai et al. 2009) to prevent wearing of the silicon mold during repeated replica molding processing. The device is then fabricated using multilayer soft lithography techniques (Xia and Whitesides 1998; Unger et al. 2000). Briefly, the control wafer is spin coated with a 60 μm layer (Schneider et al. 2009) of (poly)dimethylsiloxane (PDMS) (Sylgard 184, Dow Corning, Midland, MI). The fluidic network is then cast with a thick layer of PDMS. The fluidic network is removed from the mold; the outlets are punched, and the devices are cleaned with scotch tape. The fluidic network is bonded to the thin layer utilizing oxygen plasma treatment followed by manual alignment using a stereomicroscope. After bonding is complete, the assembly is removed and bonded to a glass slide (Bhattacharya et al. 2005). A schematic of the fabrication process is shown in Fig. 3
Fig. 3.
Schematic of the device fabrication procedure, with each photolithography step represented by a single color in the device schematic in Fig. 1b. All layers are fabricated using SU-8 with the exception of the valve seats which are made using AZ9260. Photolithography is performed using standard techniques. The AZ9260 layer is reflowed after development to create rounded channel architecture necessary for complete pneumatic valve closure. The fluidic layer and control layers are fabricated on two separate wafers. The fluidic layer is created by casting a thick layer of PDMS, while the control layer is spin-coated with PDMS yielding a thin layer. The thick layer is bonded to the thin layer, and then both layers are bonded to a glass slide
4.2 Model Validation Experiments
Devices were primed by submerging them in deionized (DI) water under vacuum overnight. Once primed, the control lines were pumped with DI water to remove any remaining bubbles. The control channels were then connected to a compressed air tank equipped with a precision air regulator (McMaster Carr, Robbinsville, NJ, 6162K22). Prior to the assay, the channels are pressurized until closure and the pressure is not changed for the duration of the assay (typically around 40 psi). All reagents were loaded into 1 mL Luer-Lok syringes (BD Biosciences, San Jose CA, 309628) fitted with 30 gauge needles (BD Biosciences, San Jose CA, 305128) connected to Tygon microbore tubing (US Plastic Corporation, Lima OH, 56514) and infused using a syringe pump (Harvard Apparatus, Holliston, MA, 55-3333). First, the devices are flowed with 0.5% bovine serum albumin (BSA) in phosphate buffered saline (PBS) for 5 minutes at 10 μL/min to prevent analyte adsorption to the channel walls. Then, the device is flushed with PBS for 5 minutes at 10 μL/min to remove the unbound BSA.
The mathematical model was validated using a model antibody antigen binding system comprised of streptavidin coated beads (5.8 μm diameter, Bang's Laboratories, Inc., Fishers, IN, CM01N) and Alexa Fluor 488 biocytin (Molecular Probes, Eugene, OR, A12924). The microbeads were first washed in PBS by suspending 10 μl of beads in 990 μL of PBS and then resuspending in 1 mL Ficoll-Paque Plus (GE Healthcare). The bead solution was flowed into the channels at 10 μL/min until the beds were packed with the pneumatic valve 1 closed. The device was then flushed with PBS to fully pack the bead beds and remove the Ficoll-Paque from the device. Each sample inlet was then connected to a separate syringe loaded in a syringe pump with a multi syringe rack (Harvard Apparatus, Holliston, MA, 70-2020) and samples were flowed at 500 nL/min for 3 hours over the bead bed with pneumatic valve 2 closed to prevent mixing of sample streams. For the time-lapse validation experiments, a 10 ng/mL solution of biocytin-Alexafluor 488 was made in PBS and loaded into eight separate syringes and images were taken at 3 minute intervals. For the validation experiments performed using different concentrations, 10-fold dilutions were made (10 ng/mL, 1 ng/mL, 100 pg/mL, and 10 pg/mL biocytin-AlexaFluor 488) and each concentration was loaded into two syringes to perform duplicate measurements. In both experiments, PBS was flowed at 10 μL/min for 5 minutes with pneumatic valve 1 closed immediately following incubation as a wash step. Next, all valves were opened and the sample syringes were removed, leaving only the tubing connected to the sample inlets. Another wash was performed at 10 μL/min for an additional 5 minutes to remove any residual sample from the tubing. Finally, PBS was flowed by hand through the outlet to collect the beads. The samples were then analyzed via flow cytometry.
4.3 Fluorescence Microscopy and Time Lapse Model Comparison
Fluorescent images were taken using an Olympus IX81 inverted microscope (Center Valley, PA) equipped with a XM10 digital camera and an automated stage and an EXFO X-Cite 120 fluorescent light source. Image capture and processing was performed using Olympus cellSens Dimension software. Images were captured at 3 minute intervals and processed by manually creating masks of the bead bed and a background area within the microchannel upstream of the beads. The mean fluorescence intensity of the background was subtracted from the beads at each frame and the data was exported to Excel. The data was normalized by subtracting the minimum value of the time series and dividing by the range of fluorescence intensities. To validate the model's predictive capabilities, binding was modeled at the same flow rate and concentration and the data was normalized by dividing the amount bound at each time step by the amount bound at 3 hours.
4.4 Flow Cytometry
Beads were suspended in PBS, transferred to BD Falcon round bottom tubes (BD Biosciences, San Jose, CA, 352008), and vortexed prior to analysis. Samples were analyzed using a BD FACSCalibur and the mean fluorescence intensity of each bead population was extracted with BD CellQuest Software (BD Biosciences, San Jose, CA).
4.5 Flow Cytometry Data Analysis and Model Comparison
A standard curve using the same beads as the on-chip experiments was generated by incubating varying concentrations of biocytin-Alexafluor488 with a fixed number of microbeads in an Eppendorf tube and vortexing overnight. The beads were washed 3 times, resuspended in PBS, and analyzed via flow cytometry. Normalized fluorescence intensity was calculated by dividing the mean fluorescence of each data point by the measured fluorescence of the highest concentration. The saturation concentration was identified as the lowest concentration that resulted in the maximum measured fluorescence. Normalized concentration was then calculated by dividing each concentration by the saturation concentration, and a plot of normalized concentration vs. normalized fluorescence was created and fitted with a 5-parameter logistic fit using Matlab.
The data from the validation experiments was then analyzed by normalizing the results from each experiment by dividing each measurement by the average of the highest concentration. The normalized data was processed using the 5-parameter logistic fit to yield normalized binding. To test the model accuracy, binding was simulated under the same flow rate and concentrations used in experiments. The predicted binding from the simulation was normalized by dividing the amount bound at 3 hours for each concentration by the concentration of binding sites on the beads as per manufacturer specifications.
4.6 On-Chip Immunoassay Experiment
On-chip immunoassay was performed using the Bio-Plex Pro Human Cytokine IL-6 antibody set, Cytokine Reagent Kit, and cytokine standards (Bio-Rad Laboratories Inc, Hercules, CA, 171304070M, 171D50001, and 171B5006M, respectively). All reagents were prepared as per manufacturer recommendations, with the standards reconstituted and diluted in 0.5% BSA in PBS. The device was operated similarly to the validation experiments described previously with some minor changes. First, Bio-Plex Pro assay buffer was used in the channel blocking and bead collection steps. In addition, Bio-plex Pro wash buffer was used instead of PBS for all wash steps. Finally, the flow rate for the sample, biotinylated detection antibody, and streptavidin-phycoerythrin incubation steps were 5, 50, and 50 nL/min and performed for 4.5, 1.5, and 0.5 hours, respectively. At the completion of the assay, the beads were collected and transferred to a 96 well plate and analyzed using the Bio-Plex 200 system as per manufacturer recommendations. The raw event data for each bead was exported into Matlab for analysis.
4.7 Scanning Electron Microscopy
Silicon molds were cleaned using filtered compressed air and IPA, cut and taped to sample mounts. Samples were then coated using a SCD 004 Sputter Coater (Balzers Union Limited, Balzers Union Limited, Liechtenstein) loaded with a gold/palladium target and imaged using an Amray 1830I Scanning Electron Microscope (Amray, Inc., Bedford MA).
4.8 Statistical Analyses
Regression analysis was performed by plotting the normalized predicted binding versus the normalized experimental binding under the same conditions, fitting a linear regression, and calculating the R2 value in Excel. The experimental and simulated data were also compared by a lack of fit sum of squares test. This test is performed by calculating an F-statistic (F*) which takes into account the error between the model and experimental results (lack of fit) as well as the experimental variance (pure error). The null hypothesis is no lack of fit exists between the model and experimental data. If the test statistic is greater than a critical value (Fcritical) at a chosen significance level (α), the null hypothesis is rejected (Montgomery 2009). Since accepting the null hypothesis will allow us to conclude that the model accurately predicts our experimental system, a high significance level (α=0.25) was chosen to ensure model validity. One-way analysis of variance (ANOVA) with α=0.05 was performed using Kaleidagraph (Synergy Software, Reading, PA). This statistical test determines whether the differences between the mean of two or more groups are statistically significant or not significant (NS), with a null hypothesis that the means of the groups are equal. In both the lack of fit sum of squares test and ANOVA, the p-value represents the probability of obtaining a test statistic at least as extreme as was observed, given that the null hypothesis is true. Full factorial experimental matrix generation, DOE data analysis, and selection of optimal designs were performed in modeFrontier.
5 Results and Discussion
5.1 Model Validation
Prior to performing optimization the mathematical model was experimentally validated in order to ensure its accuracy. For the validation experiments, a model system for antibody antigen binding consisting of streptavidin coated microbeads and biocytin-AlexaFluor 488 was employed. This approach has been used in prior publications as a model system of antibody-antigen binding as it provides several advantages (Yoo et al. 2011; Sasso et al. 2010). These include increased reaction speed, lower cost compared to antibody conjugated beads, and a one step reaction allowing for direct interrogation in real time using fluorescent microscopy. This allows binding curves to be experimentally constructed in order to directly compare CFD simulations to experimental results.
The first validation experiment was performed by flowing 10 ng/mL biocytin-AlexaFluor488 over a packed bed of streptavidin coated microbeads at a flow rate of 500 nL/min through all eight sample inlets simultaneously. The fluorescence intensity in the bead bed was captured over time and compared to normalized predicted binding of the mathematical model using the same inlet concentration and flow rate. The comparison of the predicted and experimental results is shown in Fig. 4. Visual inspection of the results reveals a strong agreement between the predicted values of the mathematical model and the observed results in the device. The error, defined as the difference between the model prediction and experimental results, is largest initially while the rate of binding is highest and decreases as the binding curve plateaus. The accuracy of the simulations is further validated through statistical analysis. Regression analysis shows a very good correlation between the data as shown in Fig. 4a (R2=0.99063). In addition, a lack of fit sum of squares test was performed and revealed that no significant differences exist between the model predictions and experimental results (F*=0.47326<Fcritical at α=0.25). At the conclusion of these time-lapse experiments, the beads were collected and analyzed via flow cytometry with the results shown in Fig. 4b. The data shows that measurements in the device are reproducible and independent of position (NS, p=0.14 by one way ANOVA). This will ensure that measurements from different channels are comparable to facilitate the construction of standard curves and quantification of sample concentrations.
Fig. 4.
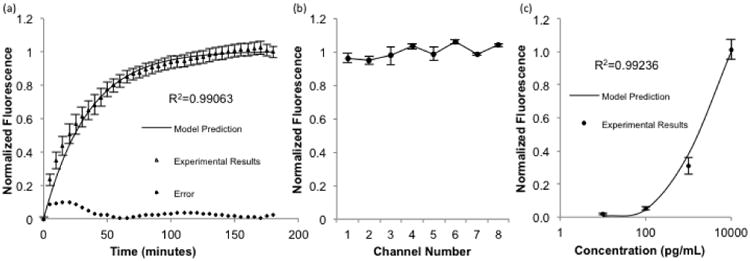
a) Comparison of model predictions with time lapse fluorescence data using 10 ng/mL concentrations of biocytin-Alexafluor 488 in all eight sample inlets. Error is defined as the difference between the model prediction and experimental results (n=24, R2=0.99063, p>0.25 by lack-of-fit sum of squares test) b) Beads from the time lapse experiment were collected and analyzed by flow cytometry, with no significant difference in the measured fluorescence between device channels (n=6, NS, p=0.14 by one way ANOVA) c) Different concentrations were each flowed through two sample inlets, collected, analyzed by flow cytometry, and compared with model predictions. (n=6, R2=0.99236, p>0.25 by lack-of-fit sum of squares test). Error bars represent standard error of the mean
For the second validation experiment, 4 different concentrations of biocytin-AlexaFluor488 were flowed simultaneously over the bead beds at 500 nL/min for 3 hours. The beads were then washed and collected for analysis using flow cytometry. Identical conditions were simulated, and a comparison of the results is shown in Fig. 4c. Once again, a good correlation was observed through regression analysis (R2=0.99236) and the lack of fit sum of squares test confirmed the model is accurate (F*=0.16<Fcritical at α=0.25). Together, the validation experiments provide statistical evidence that the mathematical model accurately predicts binding in our experimental system. Therefore, it can be appropriately utilized to aid in optimization of assay parameters to minimize the amount of required sample volume and incubation time.
5.2 Exploration of Design Parameters Using DOE
With a validated mathematical model, a full factorial DOE was used to explore the effect of the design parameters. The length, width, and height of the reaction zone were varied at three levels. These parameters also determine the number of antibody-coated microbeads that are modeled. The different combinations of geometric parameters resulted in 27 different possible numbers of beads. The flow rate was modeled at 15 levels to determine when the transition occurs from the reaction to transport limited regimes. Three levels were used for all other parameters to ensure the ability to investigate possible nonlinear effects.
The importance of each factor on the design objectives was determined by ranking the main factor and interaction effects. The effect sizes, which represent the strength of the relationship between the input parameter and a respective output parameter, were calculated in modeFrontier from the entire full factorial design dataset and the results are shown in Fig. 5. An interaction effect, denoted by an asterisk, signifies that the effect of an input variable is not constant as the range of another parameter is varied. For example, if varying one input parameter when a second input parameter is at its minimum value affects the output differently than if the second input is at its maximum value, an interaction effect exists. The results of the DOE clearly demonstrate that the flow rate is the most important input parameter in determining the amount of sample volume needed, as its effect is almost three times as large as any other parameter. The only other factors that substantially affect volume are the interaction of the flow rate with each of the geometric parameters, each contributing to approximately the same extent. This can be explained by the fact that in these simulations the reaction volume (i.e. the product of length, width, and height) determines the number of microbeads and therefore antibodies that are present. However, alone each factor has almost no effect. Since only the interaction between the flow rate and the geometric parameters affects volume, this suggests that these parameters do not have an effect over the entire range of flow rates that were studied.
Fig. 5. Results of DOE. Effect of input parameters on a) required sample volume and b) incubation time required to reach the LOD. An asterisk denotes an interaction between two factors. H=Height, L=Length, Q=Flow Rate, W=Width.
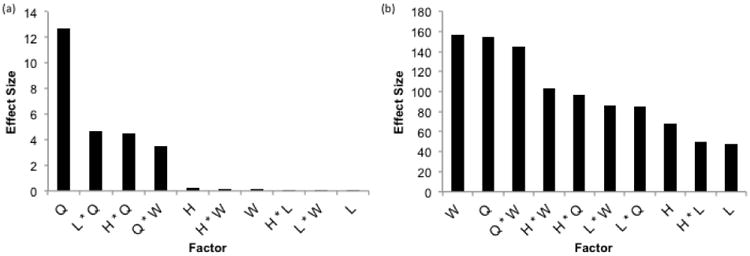
The most important factors in determining incubation time needed to reach the LOD are width and the flow rate. These factors alone had a very similar effect size, with the interaction between the two having a slightly smaller effect. This can be explained by the fact that the velocity is dependent on the flow rate and cross sectional area of the channel, i.e. the product of width and height. It is the velocity, not the flow rate, which determines the local concentrations of analyte and therefore the binding rate, as can be seen in Eq. 5. Consequently, the interaction between width and height is the next most significant factor, followed closely by the height and flow rate interaction. It is logical to hypothesize that the height should affect time at the same magnitude as the width since they equally determine the velocity. However, width was varied over the largest range of any geometric parameter, thus having the largest effect on velocity and as a result, the incubation time. The interactions of the length with the width and flow rate were the next two largest effects, with the remainder of the factors impacting incubation time to a lesser extent. With these results, it is seen that the incubation time is much more sensitive to the geometry than the required sample volume.
Due to the presence of interactions between design parameters revealed by the DOE, the results of the simulations were further analyzed. At higher flow rates, the amount of time required to perform the assay is relatively unchanged, regardless of the number of beads in the bed, shown in Fig. 6a&b. As the flow rate is decreased, the effect is greatly augmented. However, the sample volume remains essentially unaffected by the number of beads and is virtually solely dependent on the flow rate as shown in Fig. 6c. Since the required assay time is generally unaffected at higher flow rates, binding is not dependent on the amount of sample delivered to the reaction region. Furthermore, the efficiency of the reaction, defined as the fraction of protein flowed through the channel that binds, is very low at higher flow rates as shown in Fig. 6d. However, at lower flow rates the number of beads has a clear effect on incubation time. Together, these results suggest the existence of different operating regimes that occur within our design space as the balance between convection, diffusion, and reaction is altered.
Fig. 6.
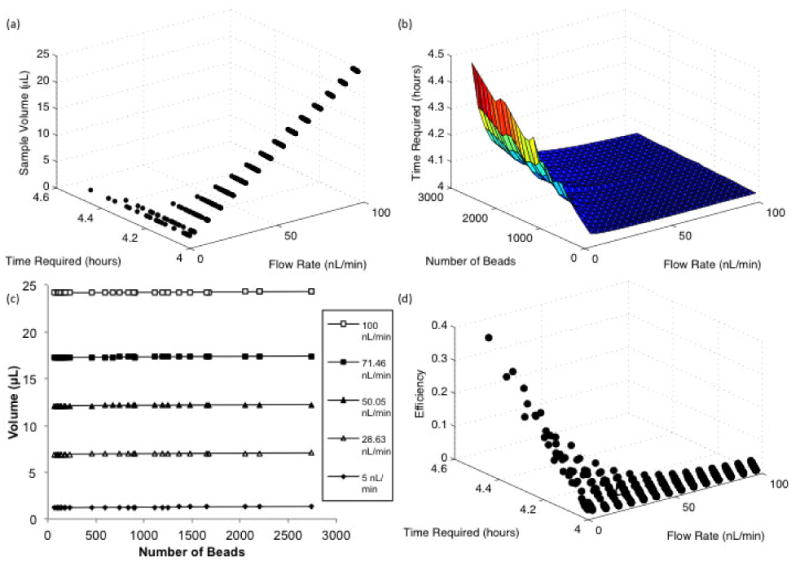
Full Factorial DOE results a) Effect of the flow rate on the time and volume required to reach the limit of detection b) Effect of the number of beads on the time to reach LOD at different flow rates c) Effect of number of beads on the sample volume at selected flow rates d) Relationship between the flow rate, time required to reach the LOD, and the binding efficiency defined as the fraction of protein flowed through the channel that is bound
In order to investigate the balance between these phenomena the Peclet and Damkohler numbers were studied since these dimensionless quantities relate convection with diffusion, and reaction and convection, respectively (Fogler 1999). The effect of these numbers on the product of time and volume was investigated and is shown in Fig. 7. It is obvious that it is most advantageous to minimize the Peclet number. At higher Peclet numbers, convection occurs faster than diffusion and the reaction zone is not well mixed. However, minimizing the Peclet number is not sufficient as a concomitant increase in the Damkohler number to approximately 40 is necessary in order to minimize time and volume required for the assay. This signifies an increase in the residence time of the sample within the bed accomplished by decreasing the fluid velocity resulting in more time for the protein to bind. However, a large bead bed and slowed convection causes the solution concentration to decrease along the length of the bed. This results in increased assay time, causing a plateauing of the effect of increasing the Damkohler number at a low Peclet number.
Fig. 7.
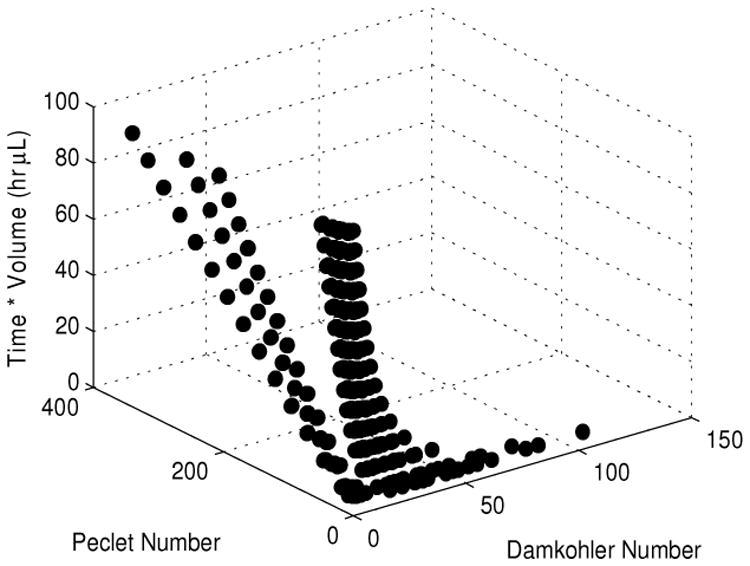
Effect of the Damkohler Number and the Peclet Number on the product of the incubation time required to reach the LOD and the necessary sample volume. Low Peclet numbers (<10) and Damkohler Numbers greater than 40 results in the minimization of the incubation time and sample volume needed to perform an assay.
These conclusions explain the results of the full factorial matrix (Fig. 6). The increased convection at higher flow rates does not allow enough time for the reaction to occur resulting in a reaction-limited regime where the rate of binding is only determined by the affinity of the antibody for the protein. As convection is slowed, the efficiency increases. However, a point is reached where the reaction is occurring faster than protein can be transported to the bead surface (i.e. higher Damkohler and low Peclet numbers) and the amount of time required to reach the limit of detection begins to increase. At the transition between these two regimes, the product of sample volume and reaction time are minimized. In the presented design space, this occurs when the Peclet number is less than 10 and the Damkohler number approaches 40, as shown in Fig. 7.
5.3 Model-driven Multi-Objective Optimization
Optimization was performed using the Hybrid Algorithm in modeFrontier with the same parameter constraints as the DOE. This technique is a combination of a NSGAII algorithm and an SQP optimizer and was chosen for its ability to handle multiple objectives with continuous variables. All the simulations included in the optimization and the optimal designs of the Pareto frontier as are shown in Fig. 8a and Fig. 8b, respectively. In result of the trade-off between time and volume, no design combination exists that minimizes both objectives. Therefore, a large number of designs are selected as optimum as shown in Fig. 8c. These designs encompass a large range of flow rates, but the number of beads converges to the lower range of the allowable number of beads, shown in Fig. 8d. This corroborates the fact that a high efficiency is not an important design consideration as efficiency increases with the number of beads in the reaction region. In addition, amongst the optimal parameter combinations very little incubation time must be sacrificed to greatly reduce sample volume. While this holds true when the number of beads is low, this trade off becomes more pronounced as the bead number is increased, as shown in Figs. 6a&b.
Fig. 8.
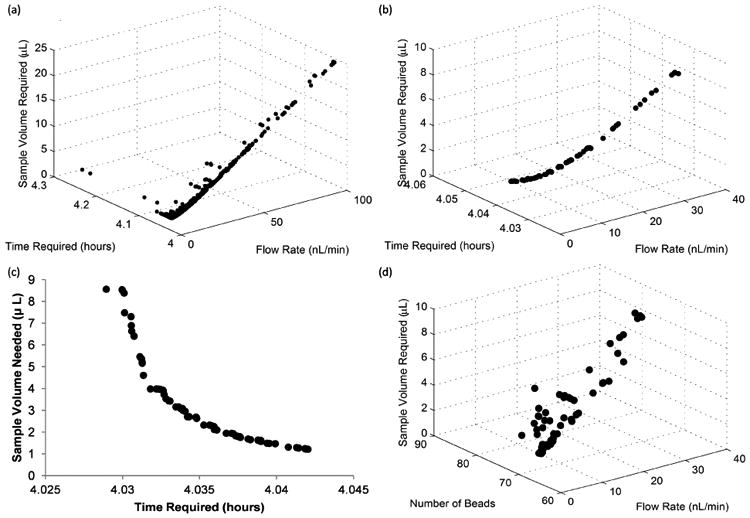
Optimization results a) All design points included in the optimization b) Designs selected as optimal designs. c) Trade off between design objectives of optimal designs d) Number of beads for optimal designs shown in b.
Although the optimization algorithm minimized the number of microbeads in the chosen Pareto designs (Fig 8d), the number of beads required for analysis is an important consideration that must be accounted for in our experimental system. The Bio-Plex 200 system used in our on-chip experiments requires a minimum of 50 beads to perform an assay. To ensure that sufficient beads are recovered from the device, it is necessary to incubate more than the minimum number of beads to account for bead loss during the collection step. From our DOE, we concluded that the number of beads did not affect the amount of volume needed (Fig 6c), and only affect the time required by about 30 minutes, across the entire design space (Fig 6b). From an experimental standpoint, a modest increase in incubation time is a necessary trade off required to ensure sufficient bead recovery. In addition, the relatively small increase in incubation time over the large range of bead numbers tested (70 to more than 2700) we can conclude that small variations will not significantly impact the results of the assay. This is advantageous in practice, as precise control of the number of beads in each channel is difficult to achieve. Small imperfections and inconsistencies between bead traps or debris trapped in the device during fabrication may cause changes in channel resistance and therefore alter the distribution of beads. These practical concerns led us to fill the reaction zone of our device approximately halfway with beads, yielding about 900 beads per channel. With this bed size, we incubated at a flow rate of 5 nL/min for 4.5 hours, slightly longer than our computational results suggest, to mitigate the effects of possible flow instabilities produced by the syringe pump at this very low flow rate. In our device, these parameters translate to a Peclet number of 1.29 and a Damkohler Number of 34.3, which provides a good balance between sample consumption and assay time (see Fig. 7).
5.4 Optimized Low Volume Immunoassay
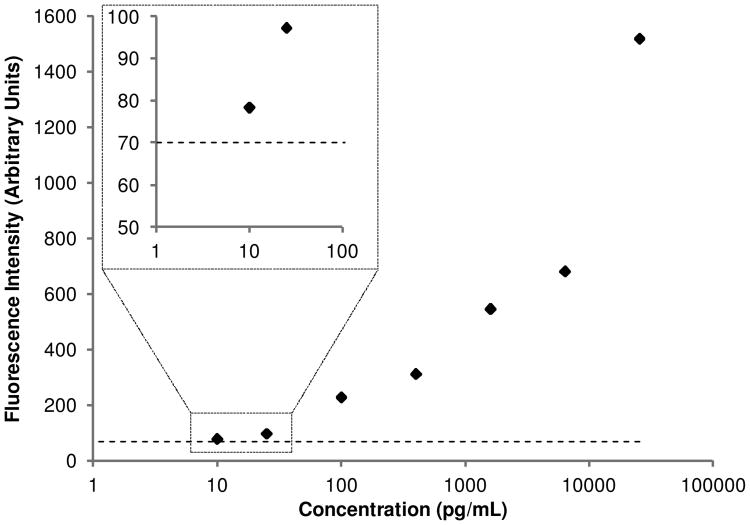
To demonstrate the utility of the mathematical model and optimization platform, a low volume on-chip immunoassay was performed using a commercially available IL-6 kit. A standard curve was constructed consisting of 7 samples. A blank condition of 0.5% BSA with no IL-6 was also run to quantify the noise floor attributed to background proteins. Sample was flowed at 5 nL/min for 4.5 hours, consuming only 1.35 μL of sample. In addition, only 4.5 μL of detection antibody was used, a greater than 10 fold reduction compared to bench-top assays, resulting in a significant decrease in cost per sample. The standard curve resembles that of a standard bench-top assay using this kit, and the fluorescence intensity of the 10 pg/mL condition was greater than the blank, shown in Fig. 9. The measurement of the noise floor in conjunction with the clear difference observed in the fluorescence between the 25 pg/mL and 10 pg/mL samples was used to determine that 10 pg/mL is above the detection limit of the assay. While it is ideal to calculate the LOD from the standard deviation of two independents measurements of a blank sample within a single device, this approach has been used previously to determine the LOD with only one sample (Sasso et al. 2012). This allowed maximization the number of samples processed in order to demonstrate the large dynamic range of the assay, ranging from 10 to 25,699 pg/mL. Therefore, the optimization studies were successful in designing a low volume immunoassay while maintaining high sensitivity and a large dynamic range.
Fig. 9. Results of low volume on chip IL6 immunoassay with optimal parameters. The dotted line represents the noise floor of the assay, determined by measuring the fluorescence of a sample containing no IL-6.
The computational platform presented mitigates the need for empirical assay optimization. Performing sufficient experiments to meticulously explore the design space would be completely unfeasible, even when employing a partial factorial design with only three levels. However, the complicated relationship between the design variables and objectives would most likely not be captured without an increased number of flow rates. In addition, experimental error resulting from expected variations in device fabrication, bead packing, and syringe pump flow rates would require replicate experiments. Together, the computational platform presented is a cheaper, less laborious, and more useful approach than empirical optimization. In addition, it can be used to optimize the device for different beads, proteins, and/or antibody affinities by simply altering constants. To the best of our knowledge, this is the first report of a model describing the reaction on the surface of microbeads in a packed bed configuration within a microfluidic device. Previous reports have modeled surface based reactions (Lionello et al. 2005a, b; Winz et al. 2007) and even attempted to optimize assays (Zimmermann et al. 2005). However, these studies were not experimentally validated and did not perform mathematical optimization.
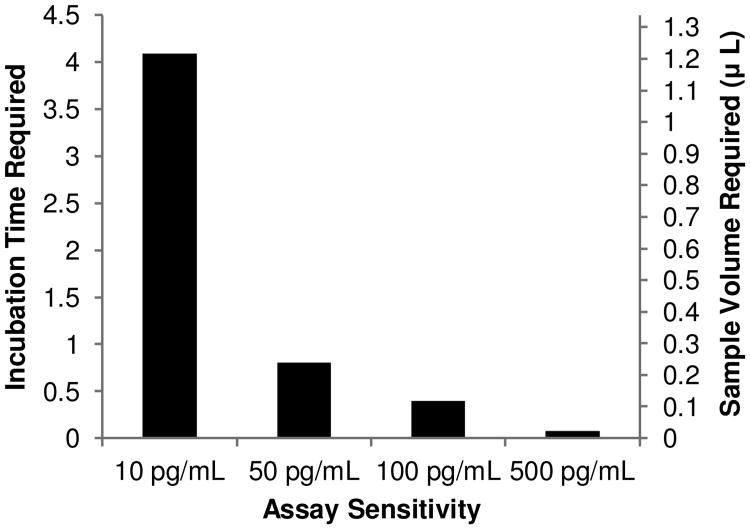
In conjunction with the optimization workflow, the device presented represents a platform technology with the ability to detect virtually any protein with an available antibody pair. In addition, it allows for the analysis of scarce samples while maintaining a high sensitivity and large dynamic range. However, the relatively long assay time (4.5 hours of sample incubation) may not be optimal for certain applications. This lengthy incubation is the result of reaction rate and cannot be increased, but a shorter incubation time is possible by sacrificing the high sensitivity of the assay. A previous report showed that a microfluidic immunoassay could be performed with an incubation time of only 20 minutes (Sato et al. 2000). However, this assay was performed with an analyte concentration approximately four orders of magnitude greater than what was used in this study. This holds true in our system, as the desired LOD of the assay affects the required incubation time to a much higher degree than any of the input parameters explored in the DOE. For example, decreasing the assay sensitivity from 10 pg/mL to 50 pg/mL of IL-6 (358 fM to 1.79 pM) reduces the incubation time to less than 1 hour, as shown in Fig. 10. In addition, the number of captured molecules needed to reach the limit of detection can be decreased by using quantum dots for fluorescence labeling (Medintz et al. 2005) or introducing a signal amplification technique such as rolling circle amplification (Konry et al. 2011) to further decrease assay time and improve the sensitivity of this device. Furthermore, by incorporating Luminex beads the device can be expanded for multiplexing in a miniscule sample volume. This also results in a significant cost savings by drastically reducing the amount of antibodies and reagents needed. Finally, although the current design possesses only 8 reaction zones, the design is scalable and can be easily expanded to facilitate many more samples.
Fig. 10. Effect of the desired assay sensitivity on the incubation time and sample volume required to perform the assay at a flow rate of 5 nL/min.
6 Conclusions
In this work, we present a bead based microimmunoassay platform and computational assay optimization methodology which allow for a single device to be tailored to many analytes with minimal experimentation. Together, the advantages of this approach make it amendable to a variety of applications. One example is the analysis of cellular secretion profiles through in vitro studies. Typically, each time point of interest is assigned to an individual well to acquire sufficient volume for protein analysis. With this device, small volumes could be extracted at each time point, creating temporal secretion profiles using a single well. This capability will greatly reduce the amount of cells and media needed to carry out these studies. In addition, in vivo applications exist, for example analyzing scarce samples such as cerebrospinal fluid (CSF) in rodent models (Shapiro et al. 2011; Stammers et al. 2012). Moreover, the high-throughput, low-cost, and multiplexing capabilities of this technology also make it suitable for biomarker discovery studies (Shoemaker et al. 2012). Finally, this could be used in a clinical setting for the analysis of scarce clinical samples from pediatric or neonate patients (Phillips 2004).
Acknowledgments
This work was partially funded by the National Institute of Health Grants P41EB002503 and UH2TR000503, the National Institute of Health Rutgers Biotechnology Training Program (T32GM008339), and the National Science Foundation Integrated Science and Engineering of Stem Cells Program (DGE0801620). The authors would like to thank Dr. Sara Salahi, Dr. Kellie Anderson, and Anwesha Chaudhury for productive conversations regarding computational and optimization issues, Dana Barrasso for guidance pertaining to statistical analysis, Dr. Bhaskar Mitra for support in developing the fabrication protocols, and modeFrontier customer support for extensive troubleshooting of the optimization platform.
References
- Andersson H, van der Wijngaart W, Stemme G. Micromachined filter-chamber array with passive valves for biochemical assays on beads. Electrophoresis. 2001;22(2):249–257. doi: 10.1002/1522-2683(200101)22:2<249::AID-ELPS249>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- ANSYS. Fluent 13.0-User Manual 2010 [Google Scholar]
- Bange A, Halsall H, Heineman W. Microfluidic immunosensor systems. Biosensors and Bioelectronics. 2005;20(12):2488–2503. doi: 10.1016/j.bios.2004.10.016. [DOI] [PubMed] [Google Scholar]
- BD. BD FACSCalibur Flow Cytometry System Technical Specifications. BD Biosciences. 2010 http://www.bdbiosciences.com/documents/FACSCalibur_FlowCytometry_TechSpec.pdf.
- Beebe DJ, Mensing GA, Walker GM. Physics and Applications of Microfluidics in Biology. Annual Review of Biomedical Engineering. 2002;4(1):261–286. doi: 10.1146/annurev.bioeng.4.112601.125916. [DOI] [PubMed] [Google Scholar]
- Bhattacharya S, Datta A, Berg JM, Gangopadhyay S. Studies on surface wettability of poly (dimethyl) siloxane (PDMS) and glass under oxygen-plasma treatment and correlation with bond strength. Microelectromechanical Systems, Journal of. 2005;14(3):590–597. [Google Scholar]
- Bird RB, Stewart WE, Lightfoot EN. Transport phenomena. Wiley; 2006. [Google Scholar]
- Boi C, Dimartino S, Sarti GC. Modelling and simulation of affinity membrane adsorption. Journal of Chromatography A. 2007;1162(1):24–33. doi: 10.1016/j.chroma.2007.02.008. [DOI] [PubMed] [Google Scholar]
- Chan-Park MB, Zhang J, Yan Y, Yue C. Fabrication of large SU-8 mold with high aspect ratio microchannels by UV exposure dose reduction. Sensors and Actuators B: Chemical. 2004;101(1):175–182. [Google Scholar]
- Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evolutionary Computation, IEEE Transactions on. 2002;6(2):182–197. [Google Scholar]
- Derveaux S, Stubbe BG, Braeckmans K, Roelant C, Sato K, Demeester J, Smedt SC. Synergism between particle-based multiplexing and microfluidics technologies may bring diagnostics closer to the patient. Anal Bioanal Chem. 2008;391(7):2453–2467. doi: 10.1007/s00216-008-2062-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai SP, Freeman DM, Voldman J. Plastic masters—rigid templates for soft lithography. Lab Chip. 2009;9(11):1631–1637. doi: 10.1039/b822081f. [DOI] [PubMed] [Google Scholar]
- Diercks A, Ozinsky A, Hansen C, Spotts J, Rodriguez D, Aderem A. A microfluidic device for multiplexed protein detection in nano-liter volumes. Analytical Biochemistry. 2009;386(1):30–35. doi: 10.1016/j.ab.2008.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimartino S, Boi C, Sarti GC. A validated model for the simulation of protein purification through affinity membrane chromatography. Journal of Chromatography A. 2011;1218(13):1677–1690. doi: 10.1016/j.chroma.2010.11.056. [DOI] [PubMed] [Google Scholar]
- Dullien FA. Porous media: fluid transport and pore structure. 1991. Access Online via Elsevier. [Google Scholar]
- ESTECO. modeFRONTIER 4 User Manual 2013 [Google Scholar]
- Fogler HS. Elements of chemical reaction engineering 1999 [Google Scholar]
- Fordyce PM, Diaz-Botia C, DeRisi JL, Gomez-Sjoberg R. Systematic characterization of feature dimensions and closing pressures for microfluidic valves produced via photoresist reflow. Lab Chip. 2012 doi: 10.1039/c2lc40414a. [DOI] [PubMed] [Google Scholar]
- Froment GF, Bischoff KB, De Wilde J. Chemical reactor analysis and design. Vol. 2. Wiley; New York: 1990. [Google Scholar]
- Haynes WM, Lide DR, Bruno TJ. CRC Handbook of Chemistry and Physics 2012-2013. CRC press; 2012. [Google Scholar]
- He H, Yuan Y, Wang W, Chiou NR, Epstein AJ, Lee LJ. Design and testing of a microfluidic biochip for cytokine enzyme-linked immunosorbent assay. Biomicrofluidics. 2009;3(2):022401. doi: 10.1063/1.3116665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He L, Niemeyer B. A novel correlation for protein diffusion coefficients based on molecular weight and radius of gyration. Biotechnology progress. 2003;19(2):544–548. doi: 10.1021/bp0256059. [DOI] [PubMed] [Google Scholar]
- Henares TG, Mizutani F, Hisamoto H. Current development in microfluidic immunosensing chip. Anal Chim Acta. 2008;611(1):17–30. doi: 10.1016/j.aca.2008.01.064. [DOI] [PubMed] [Google Scholar]
- Houser B. Bio-Rad's Bio-Plex(R) suspension array system, xMAP technology overview. Archives of physiology and biochemistry. 2012;118(4):192–196. doi: 10.3109/13813455.2012.705301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong J, Jiang L, Su X, Qin J, Du Y, Lin B. Integrated microfluidic immunoassay for the rapid determination of clenbuterol. Lab Chip. 2009;9(11):1541–1547. doi: 10.1039/b818430e. [DOI] [PubMed] [Google Scholar]
- Konry T, Smolina I, Yarmush JM, Irimia D, Yarmush ML. Ultrasensitive Detection of Low - Abundance Surface - Marker Protein Using Isothermal Rolling Circle Amplification in a Microfluidic Nanoliter Platform. Small. 2011;7(3):395–400. doi: 10.1002/smll.201001620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtman JW, Conchello JA. Fluorescence microscopy. Nature Methods. 2005;2(12):910–919. doi: 10.1038/nmeth817. [DOI] [PubMed] [Google Scholar]
- Lionello A, Josserand J, Jensen H, Girault HH. Dynamic protein adsorption in microchannels by “stop-flow” and continuous flow. Lab Chip. 2005a;5(10):1096–1103. doi: 10.1039/b506009e. [DOI] [PubMed] [Google Scholar]
- Lionello A, Josserand J, Jensen H, Girault HH. Protein adsorption in static microsystems: effect of the surface to volume ratio. Lab Chip. 2005b;5(3):254–260. doi: 10.1039/b411179f. [DOI] [PubMed] [Google Scholar]
- Madou MJ. Fundamentals of microfabrication: the science of miniaturization. CRC; 2002. [Google Scholar]
- Medintz IL, Uyeda HT, Goldman ER, Mattoussi H. Quantum dot bioconjugates for imaging, labelling and sensing. Nature materials. 2005;4(6):435–446. doi: 10.1038/nmat1390. [DOI] [PubMed] [Google Scholar]
- Montgomery D. Design and analysis of experiments. 7th. John Wiley & Sons; New York: 2009. Design and analysis of experiments. John Wiley & Sons, New York. [Google Scholar]
- Ng AHC, Uddayasankar U, Wheeler AR. Immunoassays in microfluidic systems. Anal Bioanal Chem. 2010;397(3):991–1007. doi: 10.1007/s00216-010-3678-8. [DOI] [PubMed] [Google Scholar]
- Phillips TM. Rapid analysis of inflammatory cytokines in cerebrospinal fluid using chip-based immunoaffinity electrophoresis. Electrophoresis. 2004;25(1011):1652–1659. doi: 10.1002/elps.200305873. [DOI] [PubMed] [Google Scholar]
- Piran U, Riordan WJ. Dissociation rate constant of the biotin-streptavidin complex. Journal of Immunological Methods. 1990;133(1):141–143. doi: 10.1016/0022-1759(90)90328-s. [DOI] [PubMed] [Google Scholar]
- Sasso LA, Johnston IH, Zheng M, Gupte RK, Ündar A, Zahn JD. Automated microfluidic processing platform for multiplexed magnetic bead immunoassays. Microfluid Nanofluid. 2012;13(4):603–612. doi: 10.1007/s10404-012-0980-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasso LA, Undar A, Zahn JD. Autonomous magnetically actuated continuous flow microimmunofluorocytometry assay. Microfluid Nanofluid. 2010;9(2-3):253–265. doi: 10.1007/s10404-009-0543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato K, Tokeshi M, Odake T, Kimura H, Ooi T, Nakao M, Kitamori T. Integration of an immunosorbent assay system: Analysis of secretory human immunoglobulin A on polystyrene beads in a microchip. Anal Chem. 2000;72(6):1144–1147. doi: 10.1021/ac991151r. [DOI] [PubMed] [Google Scholar]
- Sato K, Yamanaka M, Takahashi H, Tokeshi M, Kimura H, Kitamori T. Microchip - based immunoassay system with branching multichannels for simultaneous determination of interferon - γ. Electrophoresis. 2002;23(5):734–739. doi: 10.1002/1522-2683(200203)23:5<734::AID-ELPS734>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Schneider F, Draheim J, Kamberger R, Wallrabe U. Process and material properties of polydimethylsiloxane (PDMS) for Optical MEMS. Sensors and Actuators A: Physical. 2009;151(2):95–99. doi: 10.1016/j.sna.2009.01.026. [DOI] [Google Scholar]
- Seong GH, Crooks RM. Efficient mixing and reactions within microfluidic channels using microbead-supported catalysts. Journal of the American Chemical Society. 2002;124(45):13360–13361. doi: 10.1021/ja020932y. [DOI] [PubMed] [Google Scholar]
- Shapiro JS, Stiteler M, Wu G, Price EA, Simon AJ, Sankaranarayanan S. Cisterna magna cannulated repeated CSF sampling rat model-effects of a gamma-secretase inhibitor on Aβ levels. Journal of Neuroscience Methods. 2011 doi: 10.1016/j.jneumeth.2011.12.010. [DOI] [PubMed] [Google Scholar]
- Shin KS, Lee SW, Han KC, Kim SK, Yang EK, Park JH, Ju BK, Kang JY, Kim TS. Amplification of fluorescence with packed beads to enhance the sensitivity of miniaturized detection in microfluidic chip. Biosensors and Bioelectronics. 2007;22(9):2261–2267. doi: 10.1016/j.bios.2006.11.011. [DOI] [PubMed] [Google Scholar]
- Shoemaker LD, Achrol AS, Sethu P, Steinberg GK, Chang SD. Clinical Neuroproteomics and Biomarkers: From Basic Research to Clinical Decision Making. Neurosurgery. 2012;70(3):518. doi: 10.1227/NEU.0b013e3182333a26. [DOI] [PubMed] [Google Scholar]
- Squires TM, Quake SR. Microfluidics: Fluid physics at the nanoliter scale. Reviews of modern physics. 2005;77(3):977. [Google Scholar]
- Stammers AT, Liu J, Kwon BK. Expression of inflammatory cytokines following acute spinal cord injury in a rodent model. J Neurosci Res. 2012;90(4):782–790. doi: 10.1002/jnr.22820. [DOI] [PubMed] [Google Scholar]
- Toumpanakis D, Theodoros V. Molecular mechanisms of action of Interleukin-6 (IL-6) Pneumon. 2007;20:154–167. [Google Scholar]
- Unger MA, Chou HP, Thorsen T, Scherer A, Quake SR. Monolithic Microfabricated Valves and Pumps by Multilayer Soft Lithography. Science. 2000;288(5463):113–116. doi: 10.1126/science.288.5463.113. [DOI] [PubMed] [Google Scholar]
- Wild D. The immunoassay handbook. Gulf Professional Publishing; 2005. [Google Scholar]
- Wilkes JO. Fluid mechanics for chemical engineers. Prentice Hall PTR; 2006. [Google Scholar]
- Wilson R, Cossins AR, Spiller DG. Encoded microcarriers for high-throughput multiplexed detection. Angew Chem-Int Edit. 2006;45(37):6104–6117. doi: 10.1002/anie.200600288. [DOI] [PubMed] [Google Scholar]
- Winz R, de los Rıos Gonzalez A, von Lieres E, Schmittel M, Wiechert W. Simulation of a micro-analytical device for adsorbing substances from a fluid. Proceedings of the European Comsol Conference; Grenoble. 2007. pp. 736–741. [Google Scholar]
- Xia YN, Whitesides GM. Soft lithography. Annu Rev Mater Sci. 1998;28:153–184. [Google Scholar]
- Yoo SK, Kim YM, Yoon SY, Kwon HS, Lee JH, Yang S. Bead Packing and Release Using Flexible Polydimethylsiloxane Membrane for Semi-Continuous Biosensing. Artificial Organs. 2011:no–no. doi: 10.1111/j.1525-1594.2011.01240.x. [DOI] [PubMed] [Google Scholar]
- Zimmermann M, Delamarche E, Wolf M, Hunziker P. Modeling and optimization of high-sensitivity, low-volume microfluidic-based surface immunoassays. Biomedical microdevices. 2005;7(2):99–110. doi: 10.1007/s10544-005-1587-y. [DOI] [PubMed] [Google Scholar]