Objective function to obtain multiple representative waveforms for a novel helical CT scan protocol

Abstract

Purpose:

To develop objective functions for selecting multiple representative respiratory waveforms. A specific application considered is to reduce the number of swiping scans in a novel helical CT scan protocol to harvest efficiency and dose reduction benefit.

Methods:

The authors consider a general class of potential objective functions consisting of weighted norms on pointwise profile differentials. The authors utilize the Lagrangian approach and derive proper conditions on the formulation based on first and second order optimality conditions. The derived objective functions are applied to clinically acquired respiratory trajectories for swipe subset selection to verify the validity and generality of the proposed rationale. An end-to-end 4DCT reconstruction comparison is performed using a swipe subset of data corresponding to 3 out of the full 25 waveforms to assess the consequence in image quality and dose.

Results:

Their results show that maximizing the proposed objective function with the suggested parameters yields maximal spread of trajectories among the selected subset. 4DCT Reconstruction using the chosen subset of data indicates the potential for further dose reduction by about 5 to 10 folds without significant sacrifice in image quality. Experimental results also support further generalization to include slice prioritization.

Conclusions:

The authors have derived a formulation that is both simple and general as a metric to quantify the spread of a set of respiratory trajectories, which can be used for subset selection with potential computation and dose reduction benefit when applied to a newly developed helical 4DCT scan protocol.

1. INTRODUCTION AND PURPOSE

Despite the development of highly conformal delivery techniques utilizing various modulation and sophisticated treatment planning, the effective conformality of dose received by the patient is challenged by the presence of respiration-induced motion—such motion drives instantaneous anatomy to deviate from the one used for planning.¹ The use of 4DCT generates important knowledge about respiratory profiles and supports further 4D-based planning.² Current clinical 4DCT is subject to two major issues: (1) image artifacts that distort the structure of interest and provide misleading information about motion;^3,4 (2) concerns over imaging dose, since 4DCT would require “covering” each voxel for various motion states.

Recently, a new method for acquisition and analysis of 4DCT scans has been proposed.⁵ The scan protocol utilizes fast helical imaging, with multiple swipes acquired with alternating longitudinal scan directions. A breathing surrogate is simultaneously measured and used to assign breathing phases to voxels covered by the beam. Unlike conventional gating or sorting based approach that aims to scan the whole volume at a few fixed well-spaced breathing phases, this new method⁶ constructs voxel-specific motion and intensity models. A distinctive consequence of this “voxel” perspective is that the breathing phases observed are allowed to vary among different voxels. These special characteristics, however, are not fully exploited in the current low-dose helical scan protocol which acquires several swiping scans consecutively and only uses the synchronized breathing surrogate measurement retrospectively for voxelwise phase assignment. A sufficiently large number of helical swipes are acquired during scanning to ensure sufficient voxelwise phase coverage, and it is likely that many scans are acquired at similar breathing phases. (Breathing phase in this context refers to the amplitude and rate of breathing at the time each computed tomography (CT) slice is acquired.) It was speculated that a “gating” scheme may potentially reduce the number of scan acquisitions required to accurately model lung motion. In this work, we aim to harness the “relaxed” phase coverage requirement and explore the possibility of using a smaller number of helical swipes to obtain a close-to-uniform distribution of phase coverage for each voxel as a set. Furthermore, it is quite feasible to trigger the scanner in response to a continuously observed surrogate (e.g., RPM and bellows) signal. A smaller number of swipes in combination with such prospective control scheme would implicate lower imaging dose for 4DCT. We will present a solid optimization-based scan selection recipe to this end.

2. METHOD

The breathing surrogate (obtained in this case using an abdominal bellows) is synchronized with the CT acquisition so that the motion status is associated with each voxel (as a function of couch longitudinal position z). Therefore, if we have a limited “budget” to perform multiple low-dose helical scans, it is most ideal that each voxel is scanned at a set of motion status with the largest spread in breathing amplitude to best cover all possible scenarios. Without loss of generality, we use the lung volume calibrated to bellows reading as function of z in the current context.

To properly “spread” the observed motion states for each voxel, we first consider a simplified situation where the overall range of variation is fixed. Let the motion profile values at scan location z (indicated by longitudinal table location) be x = (x₁, …, x_N+1) corresponding to the (N + 1) motion status (indicated by lung volume in our context). Without loss of generality, we can sort the elements in x in ascending order $\tilde{\mathit{x}}$ and examine the non-negative interval values $\mathit{y}=\{y_i={\tilde{x}}_{i+1}-{\tilde{x}}_i\}$.

Intuitively, spreading the state x drives all y_i to be close to a single value. We seek a metric M(y) such that maximizing M(y) would yield unique y_i values. In other words,

$${\displaystyle argmaxM\left(\mathit{y}\right)=[c,\hspace{0.17em}c,\dots ,c],}$$ (1)

where c is some constant.

Such function M is not unique: if M is any such function, then composing it with a monotone increasing function g yields another function $\tilde{M}=g\circ M$ which has the same maximizer. We can further restrict this function M to be concave, smooth, and simple numerically.

Arguably, the simplest and most intuitive function could be of the following form:

$${\displaystyle M(\mathit{y};p)=\sum _i{y}_i^p.}$$ (2)

When p = 2, this corresponds to sum of square metric.

We proceed to examine the range of p values that satisfies Eq. (1). Write out the Lagrangian as

$${\displaystyle L(\mathit{y},\mathrm{\lambda };p)=\sum _i{y}_i^p+\mathrm{\lambda }(\sum _i{y}_i-c),}$$ (3)

where λ is the Lagrangian multiplier.

The first order stationarity condition for $\hat{\mathit{y}}$ is

$${\displaystyle \frac{d}{d{y}_i}L=p{y}_i^{p-1}+\mathrm{\lambda }=0,\forall i.}$$ (4)

The stationary solution is given by y_i = (−λ/p)^1−p for all i. Note that p = 0 corresponds to a degenerate scenario with M(y) = N in Eq. (2) which is of no interest.

We check the second order condition to ensure the proper type of stationarity

$${\displaystyle \frac{d^2}{d{y}_i^2}L=p(p-1)y_i^{p-2}.}$$ (5)

For y to be local maximum, we need d²/dy_i²L < 0. Since p and y_i are both non-negative, the appropriate condition is p ∈ (0, 1).

3. APPLICATION TO RESPIRATORY TRACE SELECTION

3.A. Qualitative assessment of trajectory selection property

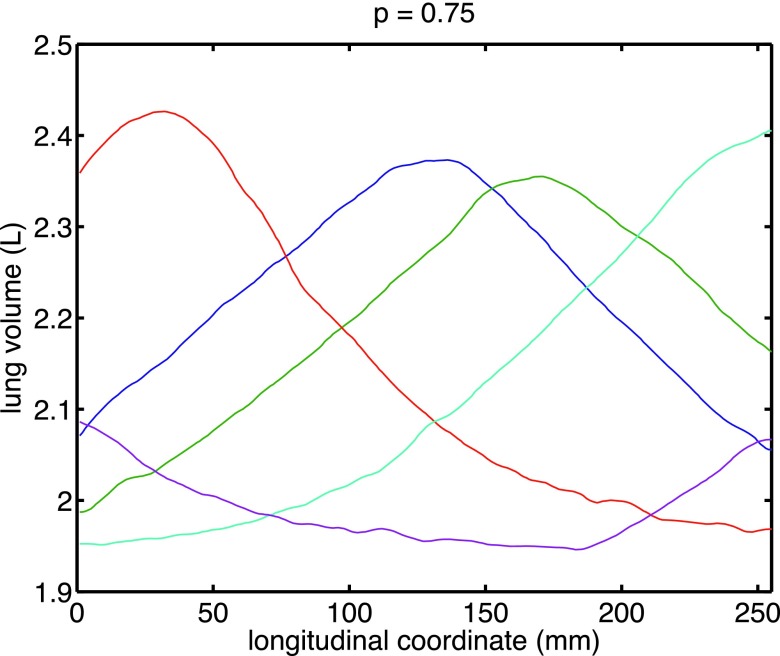
Aiming to select a subset with the maximal variation in motion profile, we select the subset of motion profiles that maximizes Eq. (2). Figures 1 and 2 reports the optimal five-subset corresponding to different choices of p.

FIG. 1.

Example of a desired subset of trajectories for scanning among a large set of 25 breathing trajectories measured with current nonselective helical protocol.

FIG. 2.

Comparison of “optimal” trajectory subset corresponding to different choices of power p.

Visual inspection of the optimal curve set corroborates with our theoretical derivation that maximizers for p < 1 provide the same desired spread in the selected subset. In addition, the choice for p = 1, though it does not satisfy our second order condition, seems to behave similarly.

We may further consider a scenario where the significance for “representativeness of motion” varies in a slicewise fashion. For example, respiration has a small impact, if any, on the motion, in the shoulder and hip area, so it is less important to capture their observations at all typical breathing phases; on the other hand, such representation is critical for high-quality 4D reconstruction for the lung region. To this end, Eq. (2) is extended to

$${\displaystyle M_{\mathrm{aggregate}}=\sum _z{\alpha }_{z}M\left({\mathit{y}}_z\right)=\sum _l{\alpha }_z\sum _i{y}_{i,z}^p,}$$ (6)

where M given in Eq. (2) with p < 1.

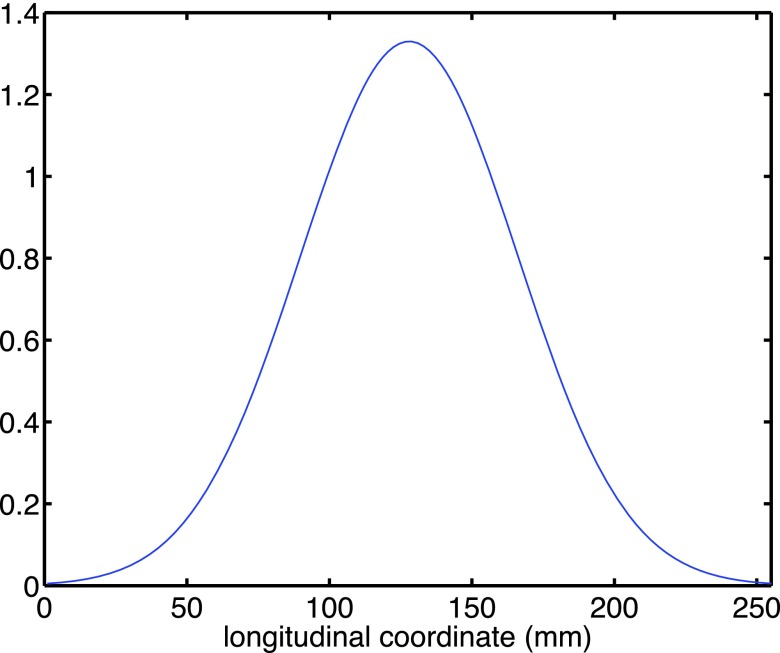
We illustrate the effect of this “slicewise modulation” with an example where the central region (e.g., lung) is emphasized and the peripheral region (the two ends of scanning range) is discounted with a bump-like function in Fig. 3.

FIG. 3.

An example bump function to emphasize motion spread for centrally located slices.

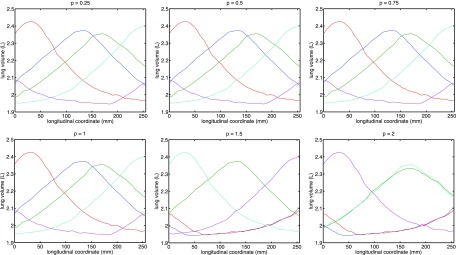
The selection results corresponding to various p’s are reported in Fig. 4. Inspection of these results gives rise to three observations:

• 1.Any p ∈ (0, 1) yields a subset of trajectories that provides the desired spread for centrally located slices, which corroborates our derivation.
• 2.The introduction of slicewise weighting has a smaller-than-expected impact on the general spread: the selected respiratory trajectories still have decent spread in the end-slices despite that the objective has relaxed the requirement for such. A probable reason is that the profiles roughly conformed to a phase-shifted wave pattern, and maximal spread in the central-slice induce reasonable spread everywhere.
• 3.Unlike the unweighted situation, the results for p = 1 are less desirable. This implies that it is preferable to set p to be properly within the open interval (0, 1) to ensure robust behavior.

FIG. 4.

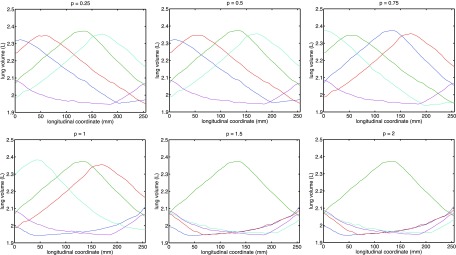
Comparison of optimal trajectory subset corresponding to different choices of power p with slicewise modulation.

3.B. End-to-end 4DCT verification

To examine the end-to-end impact of the proposed trajectory selection scheme on 4DCT reconstruction, we applied the same 4DCT reconstruction technique to the full 25 succes sive swipes⁵ versus a subset of only 3 swipe scans selected by the proposed method, which we refer to as “full” and “partial” hereafter.

Under Internal Review Board approval, patients were imaged under free-breathing conditions 25 successive times in alternating directions, using the low-dose fast helical protocol with a 64-slice CT scanner (Somatom Definition Flash, Siemens Healthcare, Forchhiem, Germany). Images were acquired with beam collimation of 64 * 0.6 mm, a pitch of 1.2, and scanner rotation period of 0.285 s, and a table velocity of 161.7 mm/s, requiring approximately 2.5 s to scan the entire lung volume. The scans used 120 kV and 40 effective mA s/slice. The total computed tomography dose index volume (CTDI_vol) for the whole 25 swiping scans was 4.22 cGy, about one third less compared to the 6.9 cGy CTDI_vol value from a current clinical slow-helical 4D-CT protocol (Siemens Sensation Open, 800 mA s, spiral pitch 0.1). A 4DCT reconstruction that allows for reconstruction of image at arbitrary user-selected phase has been developed, by combining nonrigid registration and fitting based on a 5D breathing motion model.⁷ By contrast to conventional 4DCT reconstruction approaches based on gating, the 5D perspective treats 4DCT as a continuum of intensity variations, governed by breathing dynamics.

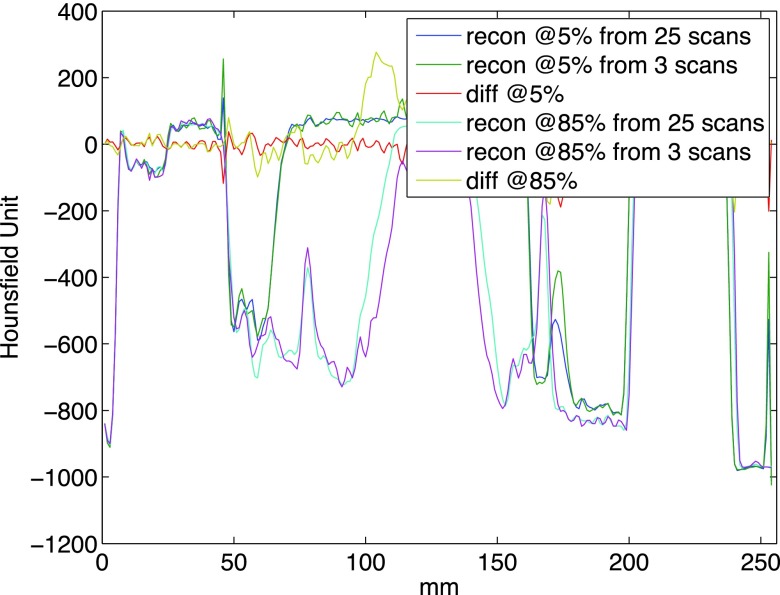
Utilizing a subset of the swipes is expected to have multiple impacts on the 4DCT reconstruction outcome, specifically (1) there is a higher possibility that a particular voxel has not received sufficient phase coverage; (2) the quality of image registration may degrade due to larger deformation to be addressed; (3) the average image is expected to have lower signal-to-noise ratio (SNR) given fewer realizations to be fused; (4) estimation of motion model could suffer from noisier registration. The nonlinear and cascaded nature of the reconstruction process makes it difficult to quantitatively predict the degradation. To reflect an extreme case, we picked the best three swiping scans with the proposed method and repeated the whole process. Figure 5 shows the CT volumes recovered at two arbitrarily picked phases of 5% and 85%. Little visual difference exists between the reconstructions based on the full and partial protocols. To assess the ability to capture proper physiological motion, a profile was generated at the same superior–inferior location from the four reconstructions: reconstruction based on 3 scans has demonstrated a similar ability to capture the range of motion as the 25 scan set. The profile views in Fig. 6 further verify this qualitative observation.

FIG. 5.

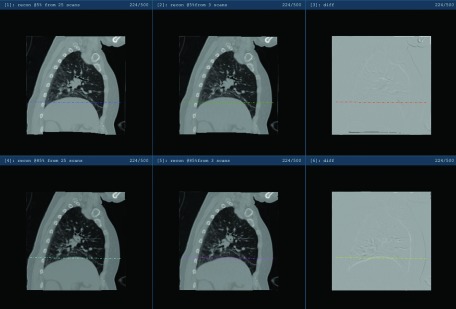
Illustration of the reconstructed 5% and 85% phases based on 25 and 3 scans, respectively. Upper row: reconstruction for 5% phase; bottom row: reconstruction for 85% phase. Left column: reconstruction based on 25 swipes; middle column: reconstruction based on 3 swipes; right column: intensity difference image between the full and partial protocols based reconstruction.

FIG. 6.

Profile illustration of the reconstructed 5% and 85% phases based on 25 and 3 scans, respectively, at the level indicated in Fig. 5, along the anterior–posterior direction.

To quantitative assessment, the impact on image quality, SNR, and contrast-to-noise (CNR) ratio were calculated from the full and partial experiments. The mean μ and standard deviation σ of the intensity value (in Hounsfield unit scale) in the central pulmonary artery and the paraspinal muscle were measured at the level of the pulmonary trunk bifurcation using a region of interest (ROI) within a homogeneous area. The SNR and CNR were calculated based on $\mathrm{SNR}\stackrel{△}{=}{\mu }_{\mathrm{vessel}}/{\sigma }_{\mathrm{vessel}}$ and $\mathrm{CNR}\stackrel{△}{=}{\mu }_{\mathrm{vessel}}\hspace{0.17em}-\hspace{0.17em}{\mu }_{\mathrm{muscle}}/{\sigma }_{\mathrm{vessel}}$, respectively and reported in Table I.

TABLE I.

Image quality comparison.

	25 scans					3 scans
	μvessel	μmuscle	σvessel	SNR	CNR	μvessel	μmuscle	σvessel	SNR	CNR
Reconstruction at 5% phase	78.96	−35.44	43.65	1.81	2.62	81.50	−38.25	54.96	1.48	2.18
Reconstruction at 85% phase	77.26	−31.55	47.22	1.64	2.30	79.8	−34.13	46.82	1.70	2.43

Overall, there is no significant difference in SNR and CNR between the reconstruction of the two protocols. The mean intensity values within the ROI are comparable for both the full and partial protocols. In the reconstruction for 5% exhale phase, the partial exhibits higher variation in the ROI located in pulmonary vessel, possibly explained by deformation vector field (DVF) of lower quality. The larger variation σ_vessel leads to lower SNR and CNR for the partial protocol. This degradation is not consistent and is absent from the reconstructions at the 85% inhale stage.

4. DISCUSSION AND CONCLUSIONS

We have presented a simple yet general objective formula tion whose maximization leads to a subset of respiratory trajectories, which provides (close-to) uniform coverage of the breathing states. A preliminary end-to-end test in the context of a helical low-dose 4DCT protocol shows that utilizing a small subset of 3 swiping scans as suggested provides comparable reconstruction quality compared to the normal full protocol of 25 swiping scans. Retrospectively, it allows one to perform 4DCT reconstruction on a subset of scans that are most complementary in information contents, thus reducing the computation burden. In the current 4D helical analysis step, each registration (including segmentation of lung and bronchi as preprocessing) takes about 20 min/registration, construction of the motion model takes approximately 60 min with most time spent on loading the DVFs into memory for a least-squared fit to the 5D model,⁷ and subsequent reconstruction at arbitrary phase is a forward propagation step that takes a few minutes. Therefore, the overall computation cost roughly scales linearly with the number of swiping scans. Compared to the full protocol that takes about a full day (20∗25 + 60 min), the partial protocol takes about an hour to complete, enabling a more efficient clinical turn-around.

The scan selection occurs within 25 swipes of fast helical scans of approximately 2.5 s each. Therefore, the overall data acquisition completes within 1 min in the worst-case scenario. Combined with the previously discussed registration + reconstruction, the overall clinical work flow takes about an hour. This may be slightly longer than the order of 15 to 30 min in some efficient clinics using commercial scanning and reconstruction protocols, but we feel the additional time is justified by the significant reduction in image artifacts, improved flexibility in reconstruction phase, and lower dose. Further numerical speedup is being investigated to enhance the computational efficiency of the proposed scheme.

More importantly, combined with motion profiling-based prediction⁸ and surrogate-based scanning trigger, this scheme would enable prospective near-optimal acquisition for a smaller number of helical swipes. Given the uncertainty in prospective predicting waveforms, it would be sensible to use a slightly larger number of swipes than the three we tested or develop a adaptive scheme. Even with the conservative estimate of using five to six swipes, it will effectively reduce the scanning by four to five folds, corresponding to a CTDI_vol in the range of 0.84–1.01 cGy, compared to the full protocol of 4.22 cGy and the clinical slow helical protocol of 6.9 cGy.

The proposed method provides a rationale to acquire decent phase coverage for all voxels with fast low-dose helical scanning protocols. This type of data is compatible with a large class of model-based 4DCT reconstruction algorithms,^9,10 beyond the 5D-model based approach used here.