Abstract
The capture and subsequent analysis of rare cells, such as circulating tumor cells from a peripheral blood sample, has the potential to advance our understanding and treatment of a wide range of diseases. There is a particular need for high purity (i.e., high specificity) techniques to isolate these cells, reducing the time and cost required for single-cell genetic analyses by decreasing the number of contaminating cells analyzed. Previous work has shown that antibody-based immunocapture can be combined with dielectrophoresis (DEP) to differentially isolate cancer cells from leukocytes in a characterization device. Here, we build on that work by developing numerical simulations that identify microfluidic obstacle array geometries where DEP–immunocapture can be used to maximize the capture of target rare cells, while minimizing the capture of contaminating cells. We consider geometries with electrodes offset from the array and parallel to the fluid flow, maximizing the magnitude of the resulting electric field at the obstacles' leading and trailing edges, and minimizing it at the obstacles' shoulders. This configuration attracts cells with a positive DEP (pDEP) response to the leading edge, where the shear stress is low and residence time is long, resulting in a high capture probability; although these cells are also repelled from the shoulder region, the high local fluid velocity at the shoulder minimizes the impact on the overall transport and capture. Likewise, cells undergoing negative DEP (nDEP) are repelled from regions of high capture probability and attracted to regions where capture is unlikely. These simulations predict that DEP can be used to reduce the probability of capturing contaminating peripheral blood mononuclear cells (using nDEP) from 0.16 to 0.01 while simultaneously increasing the capture of several pancreatic cancer cell lines from 0.03–0.10 to 0.14–0.55, laying the groundwork for the experimental study of hybrid DEP–immunocapture obstacle array microdevices.
I. INTRODUCTION
The capture of rare cells from a peripheral blood sample has the potential to advance our understanding and treatment of a wide range of diseases.1 Circulating tumor cells (CTCs) are one example of a rare cell; shed into the circulatory system from a primary tumor, they are theorized to contribute to cancer metastasis and the formation of secondary tumors away from the primary site.2 There is a need for devices that can capture CTCs and other rare cells at high purity (i.e., high specificity; capturing the target rare cells while minimizing the capture of contaminating cells) to facilitate subsequent downstream analyses. This is particularly true for single-cell genetic analyses, such as gene expression3–6 and copy number analysis studies;7–9 a higher sample purity reduces the time and cost required by reducing the number of single-cell analyses performed on contaminating cells.
Microfluidic devices have demonstrated impressive advances in the high efficiency isolation of CTCs and other rare cells using immunocapture (i.e., operating with high sensitivity; capturing most of the target rare cell population),6,10–13 but researchers often report low purity. We have previously shown that the immunocapture can be combined with dielectrophoresis (DEP) to achieve a synergistic effect in a Hele-Shaw characterization microdevice, increase the capture of pancreatic cancer cells while decreasing the capture of contaminating cells.14 This Hele-Shaw device was designed to quantify shear- and DEP-dependent capture on a flat, two-dimensional surface; it is not designed to differentially attract rare cells to the capture surface while reducing the capture of contaminating cells. Here, we aim to extend that work by developing numerical simulations that identify three-dimensional microfluidic device geometries optimized for the high efficiency, high purity isolation of rare cells using DEP–immunocapture.
DEP is an electrokinetic body force, which acts on polarizable particles in a non-uniform electric field, and has been used in a wide range of microfluidic devices to separate cell populations based on differences in their electrical properties due to differences in cell origin or disease state.1,15 The time-averaged DEP force, , on a spherical particle is given by
| (1) |
where εm is the permittivity of the medium, a is the particle radius, is the real part of the complex Clausius-Mossotti factor, and is the magnitude of an externally applied electric field of angular velocity ω, ; bolded variables denote vectors, and an undertilde denotes the complex representation of two real quantities. The complex Clausius-Mossotti factor is given by
| (2) |
where , , and σ is the conductivity; the subscripts p and m denote the particle and medium, respectively. As dielectrophoresis is governed only by the real part of the complex Clausius-Mossotti factor, we depict in the remainder of this work as fCM for convenience. When fCM > 0, a particle experiences positive DEP (pDEP) and is attracted to regions of high field magnitude and repelled from regions of low field magnitude; the reverse is true when fCM < 0 and a particle experiences negative DEP (nDEP). It is possible to select the frequency f so that target rare cells (e.g., CTCs) undergo pDEP while contaminating leukocytes (e.g., peripheral blood mononuclear cells, PBMCs) undergo nDEP.16–24
DEP has been used with microfluidic obstacle arrays to concentrate micro- and nanoscale beads,25,26 and to enrich cancer cell lines by DEP trapping.18 Separately, these obstacle arrays have been used to generate size-dependent collision dynamics, bringing target cells into contact with the antibodies on the obstacle surface, while displacing contaminating cells onto trajectories with infrequent cell–obstacle collisions; this technique has been termed geometrically enhanced differential immunocapture (GEDI).6,11,27 This work focuses on combining differential DEP response in obstacle arrays with immunocapture, so as to capture target cells on the obstacle surfaces using antibody-antigen binding. Although the ideal DEP–obstacle array system would generate a uniformly high electric field around the obstacles, attracting cells experiencing pDEP to the obstacle capture surface, such a device would require electrodes on the side of each obstacle and would be difficult to fabricate using conventional techniques. Here, we propose a practical alternative: a pair of electrodes, offset from an array of dielectric obstacles, that generate a spatially varying electric field around the obstacles themselves. This arrangement addresses the practical concerns of fabrication but results in regions of both high and low electric field magnitude around the obstacles (Fig. 1, right inset), requiring careful consideration of where to place the electrodes to achieve the desired effect.
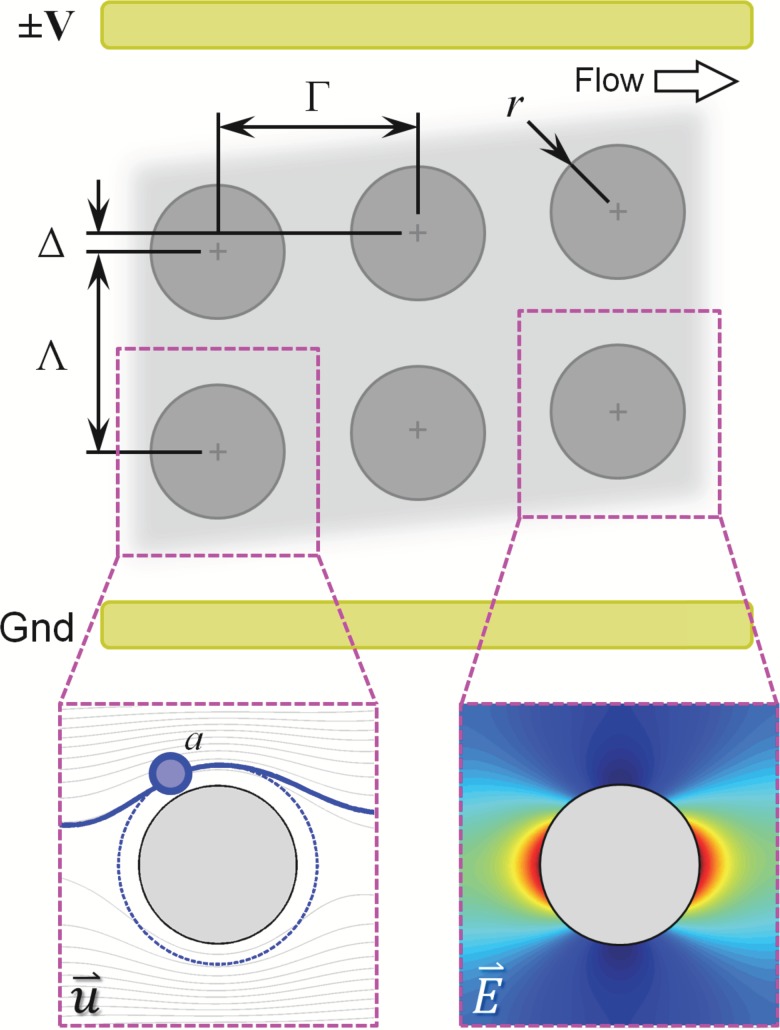
FIG. 1.
Antibody-functionalized obstacle arrays in a 2D microfluidic device can be used to engineer differential particle transport (left inset) and cell capture probabilities as a function of cell type, cell diameter (2a), array geometry (row spacing, Γ; column spacing, Λ; obstacle diameter, 2r; row offset, Δ), and flow rate. This paper studies the effect of DEP-assisted immunocapture, generated by applying an AC electric field to electrodes offset from the array and parallel to the direction of fluid flow. Target cells undergoing positive DEP (pDEP) are attracted to the high electric field magnitude regions at the obstacles leading and trailing edges (right inset), where the shear stress is low and the residence time is long (supporting the capture of the target cells); although they are also repelled from the low field magnitude regions at the obstacle shoulders, the locally high shear stress and short residence time minimizes the impact on overall capture. Likewise, contaminating cells undergoing negative DEP (nDEP) are repelled from regions where capture is likely (i.e., the obstacles' leading edge) and attracted to regions where capture is unlikely (i.e., the obstacles' shoulder).
Two geometric configurations are possible for the electrode pair: electrodes offset from and along the length of the array (i.e., parallel to the fluid flow, as in Fig. 1), or electrodes offset from and across the width of the array (i.e., parallel to the inlet and outlet ends of the array). In this work, we are interested in target cells that undergo pDEP and contaminating cells that undergo nDEP. As such, electrodes along the length of the array offer a synergistic benefit with immunocapture: the magnitude of the resulting electric field is maximized at the obstacles' leading and trailing edges (Fig. 1, right inset), attracting our target cells using pDEP to those regions, where shear stress is low and the residence time is long; we have previously shown that this is where capture is most likely to occur.28 The electric field magnitude is minimized at the obstacles' shoulder; although the resulting pDEP force repels our target cells, the high shear stress and short residence time minimize the role the shoulder region plays in capture. Likewise, cells experiencing nDEP are repelled from regions where capture is likely (i.e., the obstacles' leading edge) and attracted to regions where capture is unlikely (i.e., the obstacles' shoulder). The remainder of this work focuses on simulating cell transport and capture in DEP–immunocapture devices with electrodes offset and along the length of the device.
In addition to the electrode configuration, several other parameters govern cell performance in these systems. Cell transport and cell–obstacle collision dynamics (i.e., the collision frequency) are functions of the array geometry (row spacing, Γ; column spacing, Λ; obstacle diameter, 2r; row offset, Δ), cell diameter (2a), and the mean fluid velocity. For a given field, fCM controls the sign of the DEP response. Once a cell is in contact with the antibody-functionalized obstacle surface, the probability that said contact results in cell capture is a function of the cell-antibody system, the distance and duration of contact, and the shear stress experienced by the cell (τ).28
We have previously reported particle advection and cell capture simulations that predict transport, collision behavior, and capture probability in these obstacle arrays due to fluid advection and immunocapture;11,28,29 these simulations have been adapted to study a range of target cells.30,31 In this study, we expand those existing numerical simulations to also include the effect of DEP forcing, identifying geometries and applied AC electric fields that are optimized for DEP–immunocapture. We build on our previous characterization studies14 to inform a Monte Carlo cell capture simulation, and use that simulation to identify an optimized geometry to enhance the capture of pancreatic cancer cells with pDEP, while rejecting most contaminating leukocytes by with nDEP.
II. COMPUTATIONAL METHODS
We have adapted our previously reported simulations28,29 to calculate cell transport within a microfluidic obstacle array caused by fluid advection and DEP forcing, predicting the cell trajectories in a range of geometries and applied electric fields. These trajectories are then used in a Monte Carlo simulation, informed by experimentally measured capture parameters, to calculate the probability of capturing different cells within each geometry. These simulations occur in four discrete steps for each geometry, cell diameter, and cell–antibody system:
A. Fluid velocity field calculations
First, COMSOL Multiphysics (COMSOL, Inc.) calculated the fluid velocity field within each obstacle array geometry by solving the steady, incompressible, two-dimensional Navier–Stokes equations. The flow within a small domain of 20 × 20 obstacles (determined based on the results of a convergence study) was simulated for a uniform inlet velocity of Uinlet = 100 μm/s in the direction along the −x boundary and a zero-pressure outlet along the boundary. In this system, the Reynolds number is small
| (3) |
where ρ is the fluid density and η is the viscosity, and the resulting flow is laminar and independent of Uinlet so long as remains much less than unity. The flow around the central obstacle in this small domain was separated into its x- and y-components and saved onto a regular grid; this velocity field represents one “unit structure” with periodic boundary conditions that can be tiled to simulate an obstacle array of arbitrarily large size. This process was repeated for each geometry of interest but is independent of the cell diameter and cell–antibody system.
B. Electric field calculations
Next, COMSOL Multiphysics (COMSOL AB; Stockholm, Sweden) calculated the time-averaged electric field in the absence of any particles, , by solving Laplace's equation. A 20 × 20 domain of obstacles was studied; a voltage V was applied to the boundary, the −y boundary was treated as ground, and the remaining boundaries (including the obstacles themselves) were treated as perfect insulators. V was chosen to generate a 100 V/cm gradient between the boundaries. The resulting field around the central obstacle was taken as a unit structure with periodic boundary conditions and saved onto a regular grid, as described in Sec. II A. Again, this process was repeated for each geometry of interest but is independent of the cell diameter and cell–antibody system.
C. Cell transport simulations
Third, a custom, parallelized particle transport simulation was developed in MATLAB (The Mathworks, Inc.; Natick, MA, USA) to track cells through the obstacle arrays. Fluid and DEP forcing is considered using a linear superposition of the fluid velocity field and a time-averaged DEP velocity field to generate an effective velocity field
| (4) |
Noting that the drag force for a spherical particle of radius a in a fluid of velocity u and viscosity η is given by ,32 we can compute the dielectric mobility, , of that particle as
| (5) |
and calculate as
| (6) |
using that would exist in the absence of the cells,33 calculated for each geometry as described in Sec. II B. This approach neglects particle-particle interactions, as DEP microdevices generally use blood samples diluted in buffers of controlled conductivity,1 in which particle-particle interactions are infrequent. We approximate diffusion as negligible (Pe, the Péclet number, ), particle inertial effects as small compared to the fluid and DEP forces (St, the Stokes number, ), and neglect the wall-induced particle migration effects observed in long microchannels.34–36 (As the length of the constriction between adjacent obstacles is on the order of the obstacle diameter, 2a = 100 μm.) In the absence of DEP forces, each cell acts as a Lagrangian tracer, passively following the fluid streamlines unless the cell contacts an obstacle, at which time a no-penetration condition is enforced using an ad hoc quadratic penalty function designed to mimic the compression of a deformable sphere. The penalty function takes the form of an additional velocity component, , acting normal to the obstacle surface when a cell approaches a distance r < a from the surface
| (7) |
where is the maximum velocity in the unit structure, and S is an arbitrary scaling factor; S = 300 was chosen so as to ensure that a cell remained in contact with the obstacle, traveling along the obstacle surface, rather than repeatedly making and breaking cell–obstacle contact.
An initially uniform distribution of particles (spaced 5 μm apart; chosen based on the results of a convergence study) is tracked through a simulated device 100 unit structures long by use of a fourth-order Runge–Kutta integration scheme with adaptive timestepping. Particles that do not transverse through a unit structure in an arbitrarily large time (3000 s in simulation time) are flagged as “trapped,” as occurs when pDEP moves a cell into the stagnation point on the leading edge of an obstacle and the fluid forces are unable to overcome the pDEP forcing; unlike DEP devices that do not use immunocapture,16,18,25 trapping is not our primary design goal, but it does facilitate immunocapture by holding a cell in a region where a low shear stress and long residence time makes capture likely. We do not consider the effect of trapped cells on the local and u fields; this approximation is valid for rare cell capture applications, where there are many more obstacles than rare cells captured.
This process was repeated for each combination of cell diameter, fCM value, and obstacle geometry. The number of cell–obstacle collisions (and misses) were collectively reported as the mean collision frequency for that combination of parameters. For each timestep in which cell–obstacle contact occurs, the fluid shear stress (τ), time-averaged DEP forcing , and timestep duration (dt) were saved for use in calculating the probability of cell capture.
D. Monte Carlo cell capture simulation
Finally, a shear- and -dependent cell capture simulation was developed in MATLAB, based on the model that we have previously reported;28 this model leverages our previous characterization experiments to inform cell adhesion parameters specific to each cell–antibody system. The model was incorporated into a Monte Carlo simulation and used to calculate the probability of capturing a given cell type with a particular geometry, DEP forcing, and antibody combination.
1. Modeling cell capture
The capture of a moving cell on an antibody-terminated surface is a function of many coupled mechanical and chemical events, including mechanical forcing (friction and cell deformation), cell adhesion kinetics,37,38 and the forming and deformation of individual biomolecules.39,40 Although detailed models exist that consider all of these forces and are able to predict cell adhesion, rolling, and release, they require a detailed understanding (or at least estimates) of many adhesion parameters, which are often unknown for rare cells.
We have previously reported on a reduced-order model as an engineering tool for the optimization of rare cell capture microdevices;28 here, we have adapted that model to include -dependent cell capture parameters. Briefly, we begin with an exponential model developed by Decuzzi and Ferrari41 and used to study the capture of cancer cells in a microfluidic device by Wan et al.42 This model predicts , the probability of capturing a given cell rolling along a surface, as
| (8) |
where mr and ml are the receptor and ligand surface densities, is the receptor–ligand association constant at zero load, Ac is the contact area, λ is the characteristic receptor–ligand bond length, is the thermal energy, and is the dislodging force. As these constants are unknown for most rare cells, we group them into two lumped parameters that are functions of the DEP forcing, and , which can be derived from experimental data fitting14
| (9) |
and
| (10) |
Furthermore, we took as proportional to the local shear stress, τ, and discretized the model to predict for the length of each timestep, dt
| (11) |
This model predicts capture probability as a function of the residence time and shear stress; by varying the values of A and B as functions of , the model also accounts for changes in the contact area and normal forces as a result of .
2. Experimental characterization of cell adhesion properties
In this work, we use several pancreatic cancer cell lines (BxPC-3, Capan-1, and PANC-1) to model pancreatic CTCs, and PBMCs to model contaminating leukocytes. We have previously reported a study characterizing A and B as functions of using these cells and an anti-EpCAM antibody in Huang et al.14
Briefly, a hybrid DEP and immunocapture Hele-Shaw flow cell was engineered to simultaneously expose the cells of interest to varying shear stress as they rolled along the antibody-functionalized device surface while an interdigitated electrode array generated a DEP force on the order of N. The electrodes were driven at 50 kHz and 200 kHz in two independent experiments; these frequencies were selected to show that the capture response was frequency-dependent: at 200 kHz, the cancer cells experience pDEP while the PBMCs experience nDEP; at 50 kHz, all cells experience nDEP (Table I). The resulting capture data inform A and B at several values of . For each cell line, we found that A (which governs the magnitude of Pcapture at a given shear stress) increases with pDEP and decreases with nDEP; B (which characterizes the shear dependence of Pcapture) remained constant regardless of DEP forcing.
TABLE I.
The predicted DEP response (i.e., fCM) shows that pancreatic cells undergo pDEP (fCM > 0) at 200 kHz while PBMCs undergo nDEP (fCM < 0); all of the cells undergo nDEP at 50 kHz. Although the value of A varies with ,14 over the range of seen in obstacle arrays with a 100 V/cm applied gradient, A can be approximated as constant. The values of fCM shown here inform the cell transport simulation; the values of A and B shown here are used to calculate Pcapture. Note that the values of A reported in Huang et al. include a factor of μ (μ = 1 mPa⋅s for water); here, we report values of A without this factor, for consistency with our previous description of this capture model28 and for dimensional consistency with Eq. (11) in this work (values from Fig. 2 and Table I in Huang et al.14).
| DEP response (fCM) | Capture parameters | |||
|---|---|---|---|---|
| f = 50 kHz | f = 200 kHz | A (s−1) | B (Pa−1) | |
| BxPC-3 | −0.4188 | 0.1725 | 108.97 | |
| Capan-1 | −0.4080 | 0.2159 | 76.29 | |
| PANC-1 | −0.3763 | 0.3183 | 130.46 | |
| PBMCs | –0.4870 | −0.3199 | 73.98 | |
In this work, the cell transport simulations described in Sec. II C show that the cells are exposed to DEP forcing on the order of 10–13 N when in contact with the obstacle surface at the 100 V/cm applied gradient across the obstacle array. As this is a much smaller range than the cells experience in the Hele-Shaw characterization chamber (±10–9 N), we treated A as constant across the range of the cells encounter in the obstacle array; cell transport is affected by DEP in the obstacle array, but that the DEP forces are too small to affect capture. The values of A and B used in this work are summarized in Table I.
3. Monte Carlo simulation
For each cell of interest, the discrete cell capture probability (dPcapture; Eq. (11)) was calculated with the values of A and B in Table I at each timestep in which cell–obstacle contact occurred. The discrete probability was compared to a pseudorandom number, dPrandom, and a cell was assumed captured if dPcapture ≥ dPrandom. This process was repeated for 103 replicates for each starting particle (determined based on a convergence study), and the average value was reported as the mean capture probability for that combination of cell–antibody system, obstacle array geometry, and applied electric field. Any particles which are flagged as “trapped” by the cell transport simulation (i.e., they do not advect through a unit structure as described in Sec. II C) are assumed captured due to DEP trapping.
III. RESULTS AND DISCUSSION
The effect of DEP on cells in microfluidic obstacle arrays has two components: changes in transport and collision dynamics due to DEP forcing, and changes in the cell capture probability that result from changes in the distance and duration over which cell–obstacle contact occurs. Here, we explore these effects in an illustrative geometry with Γ = Λ = 200 μm spacing and 2R = 100 μm diameter obstacles.
A. Transport and collision dynamics
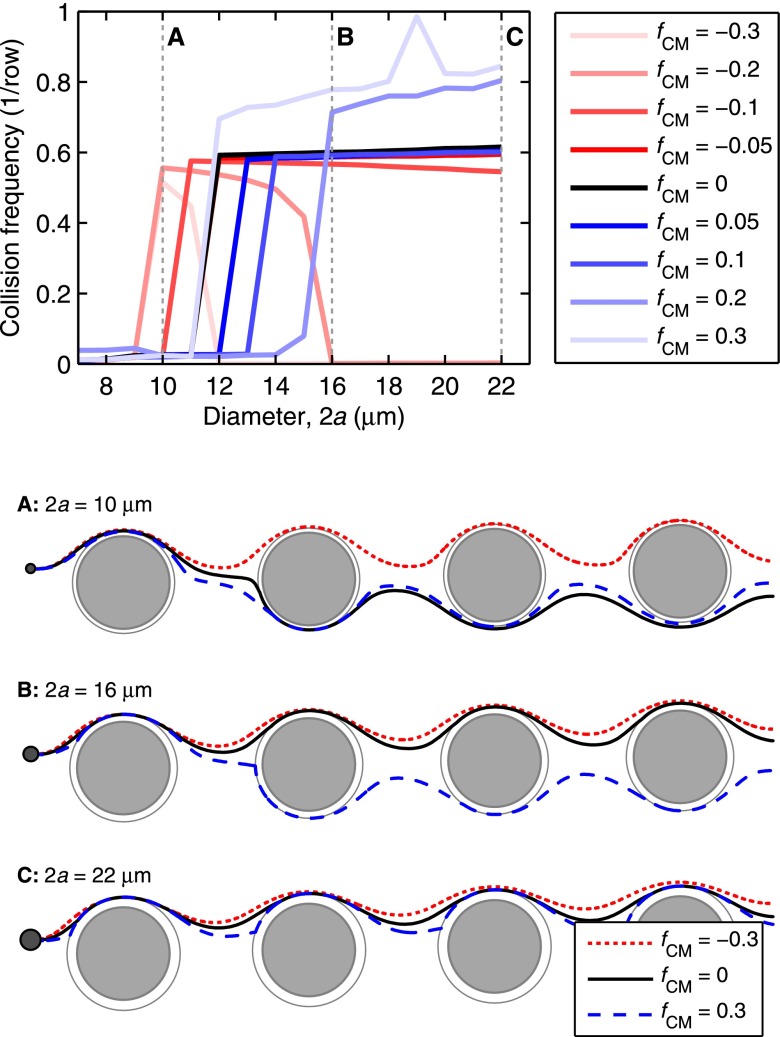
We study DEP's effect on transport and collision dynamics in microfluidic obstacle arrays by comparing the mean collision frequency for different particle diameters with a range of fCM values in a 100 V/cm applied field; this is analogous to experimentally observing the trajectories of a given cell type while varying the frequency of the applied field (and thus fCM). Fig. 2 shows the mean collision frequency as a function of 2a for different values of fCM in a Δ = 4 μm array. Several trends are notable:
FIG. 2.
DEP alters cell trajectories within the microfluidic device, leading to changes in the mean collision frequency for cells within a given device geometry. Advection dominates DEP at the obstacles' shoulder, but the reverse is true at the obstacles' leading and trailing edges, where the fluid flow stagnates; as such, a cell's response in the high electric field magnitude region at the leading and trailing edges has the most effect on its trajectory through the array. For medium and large cells (e.g., diameters B and C in this figure), pDEP attracts the cells to the high field magnitude regions near the leading and trailing edges, increasing the mean collision frequency and the time in contact (which supports capture), whereas nDEP (fCM < 0) repels cells from these regions. Likewise, pDEP forces small diameter cells (e.g., diameter A) toward the region of high field magnitude, increasing collision frequency compared to without DEP, but the overall collision frequency remains low. Although nDEP does indeed repel these small cells from the high field magnitude regions, nDEP displaces particle diameter A enough to cause a brief “grazing” cell-obstacle collision, increasing the collision frequency; these grazing events are brief and occur where the shear stress is highest, so capture of these cells is unlikely. (Shown here for an illustrative Δ = 4 μm array).
First considering the collision dynamics in the absence of DEP (i.e., fCM = 0; black line), we note the sharp transition between infrequent collisions for small particles and frequent collisions for relatively large ones that is characteristic of a GEDI obstacle array geometry.11,29 For a given row and column spacing, this critical particle diameter (2acrit) is a function of the offset, Δ; in Fig. 2, 2acrit = 12 μm. Without DEP, trajectories for particles smaller than 2acrit (e.g., A in Fig. 2) may have the occasional collision with an obstacle, but that collision displaces the particle onto a trajectory which misses subsequent obstacles, reducing the mean collision frequency. In contrast, after a collision event, particles larger than 2acrit (e.g., B and C) are displaced onto a trajectory that collides with the subsequent downstream obstacle, and thus have a high mean collision frequency.
There are several interesting effects when the particles experience pDEP (blue lines). All particles undergoing pDEP are attracted to the leading and trailing edges of the obstacles (i.e., the obstacles' ±x surfaces) due to the high electric field magnitude adjacent to these surfaces; they are repelled from the obstacle surface at the shoulders (i.e., the obstacles' ±y surfaces) due to the low field magnitudes adjacent to these surfaces (right inset, Fig. 5). The fluid velocity is comparatively fast at the shoulder, resulting in much less time for the pDEP force to act on a particle there as compared to a particle near the leading and trailing edges; DEP forcing near the leading and trailing edges having a more significant impact on particle trajectories than DEP forcing at the obstacle shoulders. For particles much larger than 2acrit (e.g., C in Fig. 2), this attraction to the high field magnitude regions leads to an increase in the distance and duration of cell–obstacle contact; the mean collision frequency is increased because the distance required for a particle to have its first collision with an obstacle is decreased. Particles just larger than 2acrit in diameter (e.g., B) are small enough (relative to the array geometry and the pDEP force) that they are deflected around the non-offset side of the obstacle but still have frequent collisions. Small particles (e.g., A) follow a similar trajectory, but the pDEP displacement after a collision is insufficient to cause a collision with the downstream obstacles; their overall collision frequency remains low.
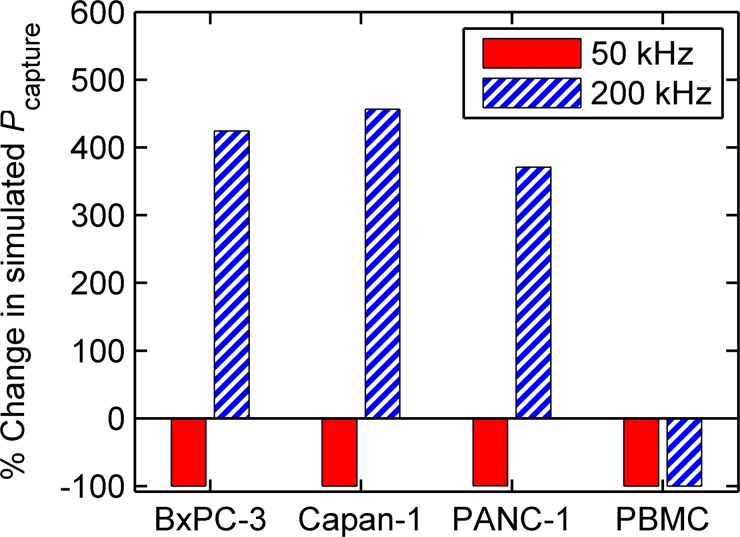
FIG. 5.
DEP significantly effects the capture probability of cells in the obstacle array. Here, the percent change in simulated —i.e., —is shown for pancreatic cancer cells and PBMCs for two independent simulations, one driven at 50 kHz and another at 200 kHz, in an array with Δ = 2 μm. The simulations show that the capture of contaminating PBMCs is reduced by greater than 99% at 200 kHz (from 0.16 to 0.001); simultaneously, the capture of target pancreatic cancer cells is increased by 370%–450% (from 0.03–0.10 to 0.14–0.55, based on cell line). Although the absolute capture probability for pancreatic cancer cells would be greater at a larger offset, the improvement in sample purity (i.e., the large reduction in Pcapture for PBMCs) predicted using DEP at a small offset outweigh a small decrease in capture efficiency, especially for applications such as single-cell genetic analyses.
nDEP (red lines) has a similar, but opposite effect: particles are repelled from the obstacles' leading and trailing edges due to the adjacent region of high electric field magnitude, and are likewise attracted to the shoulders due to the adjacent region of low field magnitude; as is the case for pDEP, the DEP force at the high field magnitude regions is more significant because the fluid velocity is slower there. In general, the collision frequency for a given particle size (e.g., B and C in Fig. 2) is reduced by displacing the particles so that they do not collide with subsequent downstream obstacles. A notable exception occurs for relatively small particles: in the absence of DEP, they which weave around the obstacles and collide infrequently; with DEP, they are displaced just enough to have brief “grazing” collisions with the obstacles (e.g., A in Fig. 2). This leads to an increase in collision frequency as compared to without DEP; the duration of these collisions and the high shear stress in that region reduce the likelihood that they result in capture, reducing the practical significance of this phenomenon.
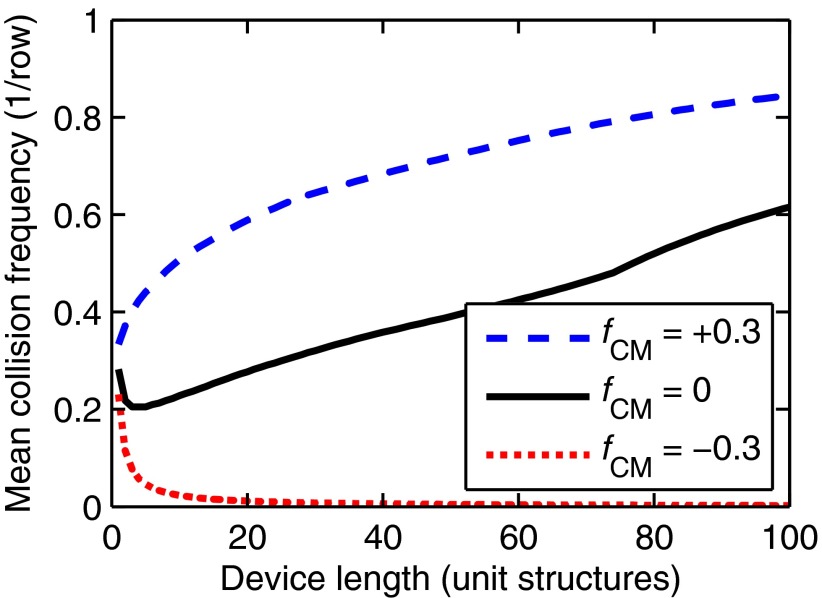
Finally, we note that the collision dynamics in an obstacle array geometry are sensitive to small changes in a particle's position; this effectively amplifies modest displacements due to , as visible in the trajectories shown in Fig. 2, where a small change in position due to DEP significantly alters the trajectories in subsequent unit structures. This amplification is important because large DEP forces require a large applied voltage and are difficult to implement experimentally, especially in blood; for example, the 100 V/cm gradient used here is an order of magnitude lower than the gradient used in filamentary DEP devices.25 Fig. 3 quantifies this effect for an illustrative 22 μm diameter particle in a Γ = Λ = 200 μm array with Δ = 4 μm. Without DEP, we observe that the mean collision frequency increases with increasing device length; each particle that enters an array must travel a finite distance before its first collision, and entrance effects are less prominent in longer devices. With pDEP (fCM > 0), DEP forcing attracts particles toward the obstacles' leading edge (where the field magnitude is high), reducing the entrance effect and increasing the mean collision frequency compared to a device of the same length without DEP; although these particles also experience a repulsive force near the obstacles' shoulder, the locally high fluid velocity minimizes the displacement due to DEP. Likewise, nDEP (fCM < 0) repels particles away from the obstacles' leading edge and onto pathlines which do not result in further downstream collisions, quickly reducing the mean collision frequency to near zero.
FIG. 3.
Modest displacements due to are amplified in the obstacle array geometry. This amplification increases with increasing device length, increasing the mean collision frequency (i.e., the collision frequency for all particles of a given diameter averaged over the length of the device) for particles with fCM > 0 and decreasing the collision frequency for particles with fCM < 0 (shown here for 2a = 22 μm and Δ = 4 μm).
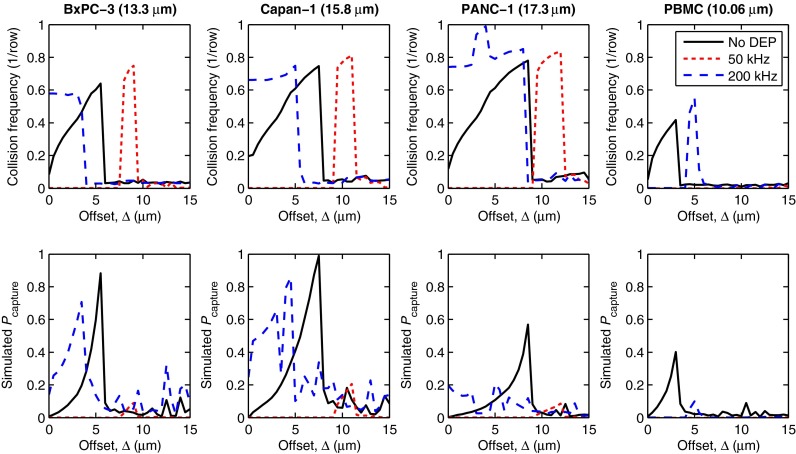
B. Cell capture probability
When considering rare cell capture, Eq. (11) shows that the shear stress, the duration and distance of contact, and the cell-antibody system determine the probability that a given cell–obstacle collision results in a cell being captured onto the obstacle surface. Here, we explore the effect of DEP on cell capture using pancreatic cancer cells (BxPC-3, Capan-1, PANC-1) as our target rare cell and PBMCs as our model contaminating cell; in this example, our aim is to maximize sample purity by selecting a geometry and applied electric field that captures pancreatic cells while capturing as few PBMCs as possible. Fig. 4 shows the collision frequency and capture probability for our cells of interest as a function of row offset (Δ) for three DEP conditions: in the absence of DEP, with a 100 V/cm applied field at 200 kHz, and with a 100 V/cm applied field at 50 kHz. At 200 kHz, the pancreatic cancer cells experience pDEP (fCM > 0) while the PBMCs experience nDEP; at 50 kHz, all of the cells experience nDEP (fCM < 0; Table I). We include the 50 kHz case for completeness, rather than to present a practical design solution, and note that an applied frequency at which target and contaminating cells have the same DEP response is only of practical use in applications where the capture of contaminating cells (i.e., the purity) is unimportant.
FIG. 4.
Simulated collision frequency (top row) and capture probability (Pcapture, bottom row) are shown vs. offset (Δ) for four cell types: BxPC-3, Capan-1, and PANC-1 pancreatic cancer cells; and PBMCs. At 50 kHz, all of the cells experience nDEP. At 200 kHz, the pancreatic cells experience pDEP and are attracted to the obstacles, increasing Pcapture; simultaneously, PBMCs experience nDEP at 200 kHz and are repelled from the obstacles, decreasing Pcapture. Note that Pcapture for PANC-1 is much lower than the other pancreatic cancer cells due its smaller A value (see Table I) and the displacement of some PANC-1 cells onto high collision frequency, high shear stress trajectories at 200 kHz (see supplementary Fig. S143 ).
Briefly considering the effect of DEP and Δ on the predicted collision frequency, we note that at small offsets and 200 kHz, the pancreatic cells exhibit an increase in collision frequency (due to pDEP) while the PBMCs exhibit a decrease (due to nDEP); at small offsets and 50 kHz, collision frequencies are decreased for all cells due to nDEP. At larger offsets and 50 kHz, there is a localized increase in the collision frequency for the pancreatic cells (e.g., for Δ = 7–9 μm for BxPC-3s); this phenomenon is due to brief grazing collisions and cell trajectories similar to those of diameter A and fCM = –0.3 in Fig. 2. The same phenomenon is responsible for the increase in PBMC collision frequency at Δ = 5 μm and 200 kHz; these trends are consistent with the results of Sec. III A and the particle trajectories shown in Fig. 2.
For a given cell type, Pcapture is maximized when the shear stress is low and the cell spends a significant duration (and thus distance) in contact with the obstacle; this is most likely when the cell first contacts the obstacle near the stagnation point on the −x obstacle face.28 At 200 kHz, those trajectories occur for the pancreatic cells at small offsets, maximizing Pcapture for our target cells and thus our capture efficiency. That configuration also leads to infrequent PBMC–obstacle collisions, minimizing Pcapture and maximizing our sample purity. Pcapture for PANC-1 cells is significantly less than the other pancreatic cells, owing to its lower A value (which partially results from PANC-1 cells having fewer antibodies bound per cell than the other pancreatic cells14), and because some PANC-1 cells follow a trajectory with frequent, but high shear stress, collisions at 200 kHz (see supplementary Fig. S143).
At 50 kHz, all of the cells undergo nDEP, which reduces the collision frequency at almost all offsets; the only exception being brief grazing collisions at moderate offsets, as discussed in Sec. III A. These collisions are comparatively brief, and occur in regions of high shear stress; as such, we note that Pcapture is very low for all cells at all offsets at 50 kHz.
These changes in cell trajectories and capture probabilities agree with the trends reported in the DEP literature for a variety of applications. At 50 kHz for all of the cells, and at 200 kHz for PBMCs, the repulsion from the high field magnitude regions near the leading and trailing edge of the obstacles results in the cells traveling in “filaments” through the array, as observed with a different electrode configuration by Cummings and Singh.25 The attraction of the pancreatic cancer cells to the leading edge of the obstacle at 200 kHz causes DEP trapping for cells that approach very near to the stagnation point, similar to that reported by Becker et al.16 and Henslee et al.;18 for geometries where many simulated cells are trapped, there is a corresponding spike in the predicted collision frequency and capture probability (e.g., for PANC-1 cells at Δ = 3 μm in Fig. 4). Finally, the increase in collision frequency observed for cells undergoing pDEP corresponds to those cells being displaced in the direction of offset, at an angle to the bulk fluid flow; these trajectories are consistent with those observed by Beech et al.26 for DEP-driven transport in deterministic lateral displacement arrays. By coupling DEP with immunocapture, we are able to use these phenomena to facilitate the high efficiency, high purity capture of rare cells, immobilizing them on the obstacle surface where they can be subsequently studied.6,9
In our example application where we seek to capture pancreatic cancer cells at high purity, we select an offset and applied electric field that captures as few PBMCs as possible while still capturing some of the pancreatic cells—this is desirable for single-cell analysis for genetic applications, for example.3–9 Fig. 5 shows the normalized change in Pcapture for our example cells with DEP (for two separate cases: one at at 50 kHz, the other at 200 kHz) compared to without DEP in a device with a small offset, Δ = 2 μm; this offset is smaller than would be necessary to optimize the capture of pancreatic cancer cells in an absolute sense, but is optimized for the rejection of contaminating PBMCs using DEP. At 200 kHz (i.e., the on-design case), our simulations predict that PBMC capture is reduced by greater than 99% due to nDEP, while pancreatic cell capture is significantly enhanced (370%–450%) by pDEP. This increase partially mitigates the lower absolute capture probability expected for the pancreatic cancer cells at the small offsets needed to reject PBMCs with nDEP; this tradeoff in efficiency is justified for applications that require high purity, such as single-cell genetic analyses. These results show that it is possible to capture rare cells at high sample purity in a hybrid DEP–immunocapture device, while still maintaining adequate capture efficiency.
IV. CONCLUSIONS
We have presented numerical simulations which predict that DEP can be combined with an antibody-functionalized microfluidic obstacle array to enhance the capture of rare cells, while simultaneously reducing the capture of contaminating leukocytes, in small-offset arrays. An AC electric field applied to electrodes offset from the obstacle array and parallel to the fluid flow generates a spatially varying electric field whose magnitude is maximized at the obstacles' leading and trailing edges, and minimized at the obstacles' shoulder. We show that this field results in a time-averaged DEP force that attracts cells undergoing pDEP to the obstacles' leading edge, where the shear stress is low and the residence time long, resulting in a high probability of capturing those cells; although these cells are also repelled from the obstacles' shoulder, the locally high shear stress and short residence time minimizes the role that DEP force plays on transport and capture. Likewise, we show that cells undergoing nDEP are repelled from regions of high capture probability and attracted to regions where capture is unlikely. A relatively small offset (as compared to the offset needed to maximize the capture efficiency of pancreatic cancer cells without DEP) array of Δ = 2 μm and an electric field applied at 200 kHz results in contaminating PBMCs experiencing nDEP, decreasing their capture probability by greater than 99%, greatly increasing sample purity. Simultaneously, the capture of target pancreatic cancer (BxPC-3, Capan-1, and PANC-1) cells is increased by 370%–450%, partially mitigating the reduced capture efficiency expected in a device with such a small offset. These simulations lay the groundwork for the experimental study of hybrid DEP–immunocapture obstacle array microdevices.
ACKNOWLEDGMENTS
This work was supported by the Cornell Center on the Microenvironment and Metastasis through Award No. U54CA143876 from the National Cancer Institute Physical Sciences Oncology Center (NCI PS-OC). C.H. was supported by a National Science Foundation (NSF) Graduate Research Fellowship.
References
- 1.Pratt E. D., Huang C., Hawkins B. G., Gleghorn J. P., and Kirby B. J., Chem. Eng. Sci. 66, 1508 (2011). 10.1016/j.ces.2010.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Allard W. J., Matera J., Miller M. C., Repollet M., Connelly M. C., Rao C., Tibbe A. G. J., Uhr J. W., and Terstappen L. W. M. M., Clin. Cancer Res. 10, 6897 (2004). 10.1158/1078-0432.CCR-04-0378 [DOI] [PubMed] [Google Scholar]
- 3.Ramsköld D., Luo S., Wang Y.-C., Li R., Deng Q., Faridani O. R., Daniels G. A., Khrebtukova I., Loring J. F., Laurent L. C., Schroth G. P., and Sandberg R., Nat. Biotechnol. 30, 777 (2012). 10.1038/nbt.2282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yu M., Ting D. T., Stott S. L., Wittner B. S., Ozsolak F., Paul S., Ciciliano J. C., Smas M. E., Winokur D., Gilman A. J., Ulman M. J., Xega K., Contino G., Alagesan B., Brannigan B. W., Milos P. M., Ryan D. P., Sequist L. V., Bardeesy N., Ramaswamy S., Toner M., Maheswaran S., and Haber D. A., Nature 487, 510 (2012). 10.1038/nature11217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cann G. M., Gulzar Z. G., Cooper S., Li R., Luo S., Tat M., Stuart S., Schroth G., Srinivas S., Ronaghi M., Brooks J. D., and Talasaz A. H., PLoS One 7, e49144 (2012). 10.1371/journal.pone.0049144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kirby B. J., Jodari M., Loftus M. S., Gakhar G., Pratt E. D., Chanel-Vos C., Gleghorn J. P., Santana S. M., Liu H., Smith J. P., Navarro V. N., Tagawa S. T., Bander N. H., Nanus D. M., and Giannakakou P., PLoS One 7, e35976 (2012). 10.1371/journal.pone.0035976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Russnes H. G., Vollan H. K. M., Lingjaerde O. C., Krasnitz A., Lundin P., Naume B., Sørlie T., Borgen E., Rye I. H., Langerød A., Chin S.-F., Teschendorff A. E., Stephens P. J., Månér S., Schlichting E., Baumbusch L. O., Kåresen R., Stratton M. P., Wigler M., Caldas C., Zetterberg A., Hicks J., and Børresen-Dale A.-L., Sci. Trans. Med. 2, 38ra47 (2010). 10.1126/scitranslmed.3000611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Navin N., Kendall J., Troge J., Andrews P., Rodgers L., McIndoo J., Cook K., Stepansky A., Levy D., Esposito D., Muthuswamy L., Krasnitz A., McCombie W. R., Hicks J., and Wigler M., Nature 472, 90 (2011). 10.1038/nature09807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pratt E. D., Stepansky A., Hicks J., and Kirby B. J., Anal. Chem. 86, 11013 (2014). 10.1021/ac503453v [DOI] [PubMed] [Google Scholar]
- 10.Nagrath S., Sequist L. V., Maheswaran S., Bell D. W., Irimia D., Ulkus L., Smith M., Kwak E. L., Digurmarthy S., Muzikansky A., Ryan P., Balis U., Tompkins R. G., Haber D. A., and Toner M., Nature 450, 1235 (2007). 10.1038/nature06385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gleghorn J. P., Pratt E. D., Denning D., Liu H., Bander N. H., Tagawa S. T., Nanus D. M., Giannakakou P. A., and Kirby B. J., Lab Chip 10, 27 (2010). 10.1039/b917959c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stott S. L., Hsu C.-H., Tsukrov D. I., Yu M., Miyamoto D. T., Waltman B. A., Rothenberg S. M., Shah A. M., Smas M. E., Korir G. K., Floyd F. P., Gilman A. J., Lord J. B., Winokur D., Springer S., Irimia D., Nagrath S., Sequist L. V., Lee R. J., Isselbacher K. J., Maheswaran S., Haber D. A., and Toner M., Proc. Natl. Acad. Sci. U.S.A. 107, 18392 (2010). 10.1073/pnas.1012539107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang S., Liu K., Liu J., Yu Z. T.-F., Xu X., Zhao L., Lee T., Lee E. K., Reiss J., Lee Y.-K., Chung L. W. K., Huang J., Rettig M., Seligson D., Duraiswamy K. N., Shen C. K.-F., and Tseng H.-R., Angew. Chem. Int. Ed. 50, 3084 (2011). 10.1002/anie.201005853 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huang C., Smith J. P., Saha T. N., Rhim A. D., and Kirby B. J., Biomicrofluidics 8, 044107 (2014). 10.1063/1.4890466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hawkins B. G., Gleghorn J. P., and Kirby B. J., in Methods in Bioengineering: Biomicrofabrication and Biomicrofluidics, edited by Zahn J. D. ( Artech House, Boston, MA, 2009), Chap. 6, pp. 133–181. [Google Scholar]
- 16.Becker F. F., Wang X. B., Huang Y., Pethig R., Vykoukal J., and Gascoyne P. R., Proc. Natl. Acad. Sci. U.S.A. 92, 860 (1995). 10.1073/pnas.92.3.860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gascoyne P. R. C., Noshari J., Anderson T. J., and Becker F. F., Electrophoresis 30, 1388 (2009). 10.1002/elps.200800373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Henslee E. A., Sano M. B., Rojas A. D., Schmelz E. M., and Davalos R. V., Electrophoresis 32, 2523 (2011). 10.1002/elps.201100081 [DOI] [PubMed] [Google Scholar]
- 19.Gupta V., Jafferji I., Garza M., Melnikova V. O., Hasegawa D. K., Pethig R., and Davis D. W., Biomicrofluidics 6, 024133 (2012). 10.1063/1.4731647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Salmanzadeh A., Sano M. B., Gallo-Villanueva R. C., Roberts P. C., Schmelz E. M., and Davalos R. V., Biomicrofluidics 7, 011809 (2013). 10.1063/1.4788921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shim S., Stemke-Hale K., Noshari J., Becker F. F., and Gascoyne P. R. C., Biomicrofluidics 7, 011808 (2013). 10.1063/1.4774307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huang C., Santana S. M., Liu H., Bander N. H., Hawkins B. G., and Kirby B. J., Electrophoresis 34, 254 (2013). 10.1002/elps.201200464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang C., Liu H., Bander N., and Kirby B., Biomed. Microdevices 15, 941 (2013). 10.1007/s10544-013-9784-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gascoyne P. R. C., Shim S., Noshari J., Becker F. F., and Stemke-Hale K., Electrophoresis 34, 1042 (2013). 10.1002/elps.201200496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cummings E. B. and Singh A. K., Anal. Chem. 75, 4724 (2003). 10.1021/ac0340612 [DOI] [PubMed] [Google Scholar]
- 26.Beech J. P., Jönsson P., and Tegenfeldt J. O., Lab Chip 9, 2698 (2009). 10.1039/b823275j [DOI] [PubMed] [Google Scholar]
- 27.Rhim A. D., Thege F. I., Santana S. M., Lannin T. B., Saha T. N., Tsai S., Maggs L. R., Kochman M. L., Ginsberg G. G., Lieb J. G., Chandrasekhara V., Drebin J. A., Ahmad N., Yang Y., Kirby B. J., and Stanger B. Z., Gastroenterology 146, 647 (2014). 10.1053/j.gastro.2013.12.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Smith J. P., Lannin T. B., Syed Y. A., Santana S. M., and Kirby B. J., Biomed. Microdevices 16, 143 (2014). 10.1007/s10544-013-9814-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gleghorn J. P., Smith J. P., and Kirby B. J., Phys. Rev. E 88, 032136 (2013). 10.1103/PhysRevE.88.032136 [DOI] [PubMed] [Google Scholar]
- 30.Santana S. M., Antonyak M. A., Cerione R. A., and Kirby B. J., Biomed. Microdevices 16, 869 (2014). 10.1007/s10544-014-9891-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Thege F. I., Lannin T. B., Saha T. N., Tsai S., Kochman M. L., Hollingsworth M. A., Rhim A. D., and Kirby B. J., Lab Chip 14, 1775 (2014). 10.1039/c4lc00041b [DOI] [PubMed] [Google Scholar]
- 32.Batchelor G. K., An Introduction to Fluid Dynamics ( Cambridge, 1967). [Google Scholar]
- 33.Kirby B. J., Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices ( Cambridge, 2010). [Google Scholar]
- 34.Yariv E., Phys. Fluid 18, 031702 (2006). 10.1063/1.2185690 [DOI] [Google Scholar]
- 35.Liang L., Ai Y., Zhu J., Qian S., and Xuan X., J. Colloid Interface Sci. 347, 142 (2010). 10.1016/j.jcis.2010.03.039 [DOI] [PubMed] [Google Scholar]
- 36.Kazoe Y. and Yoda M., Langmuir 27, 11481 (2011). 10.1021/la202056b [DOI] [PubMed] [Google Scholar]
- 37.Bell G. I., Dembo M., and Bongrand P., Biophys. J. 45, 1051 (1984). 10.1016/S0006-3495(84)84252-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dembo M., Torney D. C., Saxman K., and Hammer D., Philos. Trans. R. Soc. London, Ser. B 234, 55 (1988). 10.1098/rspb.1988.0038 [DOI] [PubMed] [Google Scholar]
- 39.Dustin M. L., Ferguson L. M., Chan P. Y., Springer T. A., and Golan D. E., J. Cell Biol. 132, 465 (1996). 10.1083/jcb.132.3.465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhu C., Bao G., and Wang N., Ann. Rev. Biomed. Eng. 2, 189 (2000). 10.1146/annurev.bioeng.2.1.189 [DOI] [PubMed] [Google Scholar]
- 41.Decuzzi P. and Ferrari M., Biomaterials 27, 5307 (2006). 10.1016/j.biomaterials.2006.05.024 [DOI] [PubMed] [Google Scholar]
- 42.Wan Y., Tan J., Asghar W., Kim Y.-T., Liu Y., and Iqbal S. M., J. Phys. Chem. B 115, 13891 (2011). 10.1021/jp205511m [DOI] [PubMed] [Google Scholar]
- 43.See supplementary material at http://dx.doi.org/10.1063/1.4908049E-BIOMGB-9-022501 for an example of such a trajectory.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4908049E-BIOMGB-9-022501 for an example of such a trajectory.