Abstract
Four experiments examined 8- and 9-month-old infants’ expectations about collision events. The infants saw test events in which a small cylinder rolled down a ramp and hit one of several different boxes. These boxes varied in width and height and always remained stationary when hit. The results revealed two separate developments. The first involved infants’ knowledge of the variables relevant to collision events. At 8 months, the infants expected all of the boxes to move when hit, regardless of their sizes; at 9 months, the infants began to take into account the size of the boxes to predict whether they should move when hit. The second development concerned infants’ ability to generate explanations for outcomes that violated their collision knowledge. At both ages, upon observing that a box with a salient vertical dimension did not move when hit, the infants apparently concluded that the box must be one of those objects we term pillars—vertical objects that are attached at one or both ends to adjacent surfaces. At 8 months, the infants considered any vertical box as a potential pillar; at 9 months, the infants considered only boxes that were both vertical and narrow as potential pillars. The development of infants’ knowledge about collision events is thus one that is complex and protracted and weaves together many separate developments.
Keywords: Infant cognition, Physical reasoning, Causal expectations, Statistical expectations, Collision events
1. Introduction
As adults, we possess a great deal of knowledge about the physical world, which we use for many different purposes: for example, to predict and interpret the outcomes of physical events; to guide our actions on objects; to interpret others’ actions; and even to deceive or entertain others. Over the past 20 years, investigators have begun to explore how infants use their developing physical knowledge to predict and interpret the outcomes of the physical events they observe (for a recent review, see Baillargeon, 2002). This research has brought to light two main findings. First, infants form distinct event categories, such as occlusion, containment, support, and collision events (e.g., Aguiar & Baillargeon, 2003; Baillargeon & Wang, 2002; Casasola, Cohen, & Chiarello, 2003; Hespos & Baillargeon, 2001; Luo, 2001; McDonough, Choi, & Mandler, 2003; Needham & Ormsbee, in press; Onishi, 2000; Wang, Baillargeon, & Paterson, in press; Wilcox & Chapa, 2002). Second, for each event category, infants identify a series of variables that enables them to predict outcomes within the category more and more accurately over time (e.g., Aguiar & Baillargeon, 1999; Baillargeon, 1991; Baillargeon, Needham, & DeVos, 1992; Dan, Omori, & Tomiyasu, 2000; Hespos & Baillargeon, 2001; Huettel & Needham, 2000; Kotovsky & Baillargeon, 1998; Luo, 2001; Sitskoorn & Smitsman, 1995; Wang et al., in press). The present research built on these earlier investigations: it focused on collision events, and examined what variables infants consider at 8 and 9 months of age to predict whether a stationary object should be displaced when hit by a moving object.
In the next sections, we review previous findings on infants’ reasoning about collision events, discuss how this knowledge might be conceptualized, and then introduce the present research.
1.1. Infants’ knowledge about collision events
In an extensive series of experiments, Kotovsky and Baillargeon (Baillargeon, 1995; Kotovsky & Baillargeon, 1994, 1998, 2000) examined infants’ responses to a simple collision event in which a cylinder rolled down a ramp and hit a wheeled toy bug at the bottom of the ramp. These experiments were conducted using the violation-of-expectation method (e.g., Baillargeon, 1998), and revealed the following developmental sequence. At 2.5 months of age, infants use a simple impact/no-impact variable to predict the outcomes of collision events: they expect an object to be displaced when hit, and to remain stationary when not hit. Infants aged 2.5 months and older were surprised,1 as evidenced by increased attention, (1) if the bug remained stationary when hit by the cylinder, and (2) if the bug moved when the cylinder did not hit it, because a barrier or other obstacle prevented contact between the cylinder and bug (Baillargeon, 1995; Kotovsky & Baillargeon, 1994, 2000).
By 5.5–6.5 months of age (females precede males by a few weeks in this development, most likely because of their superior depth perception; e.g., Held, Thorn, Gwiazda, & Bauer, 1996), infants have acquired a further collision variable: they now attend to the size of the moving object, and expect a stationary object to be displaced farther when hit by a larger as opposed to a smaller object. Infants aged 5.5 and 6.5 months were habituated to a calibration event in which a medium-size cylinder rolled down the ramp and hit the bug, causing it to roll to the middle of the track. Next, the infants saw test events in which a larger (large-cylinder event) or a smaller (small-cylinder event) cylinder caused the bug to roll to the end of the track. The 6.5-month-old infants, and the 5.5-month-old female infants, looked reliably longer at the small- than at the large-cylinder event. These and control results suggested that the infants considered the size of the moving object when predicting the bug’s trajectory: they realized that the bug could roll farther when hit by a cylinder larger but not smaller than the medium-size cylinder. The 5.5-month-old male infants tended to look equally at the small- and large-cylinder test events. Further experiments revealed that these younger male infants remembered how far the bug rolled when hit by the medium-size cylinder, and expected the bug to continue rolling this same distance when hit by the same or a same-size cylinder; however, they apparently had no basis for predicting how far the bug should roll when hit by a different-size (either larger or smaller) cylinder (Kotovsky & Baillargeon, 1994, 1998).
The research just described suggests that, by 6.5 months of age, infants expect an object (1) to be displaced when hit but not otherwise, and (2) to be displaced farther when hit by a larger as opposed to a smaller object. But how should these expectations be characterized? Do infants, in the course of observing collision events, come to detect statistical regularities involving different events and their outcomes? Or do infants understand something of the causal properties of collision events? In other words, are the collision variables identified by infants best conceptualized as statistical or as causal regularities? We consider this issue in the next section.
1.2. A primitive notion of force
In a recent account of infants’ acquisition of their physical knowledge, we suggested that the identification of a new variable in an event category typically includes three main steps (e.g., Baillargeon, 2002; Wang et al., in press; see DeJong, 1988, 1993, 1997, for a related computational account of explanation-based learning). The first step involves noticing contrastive outcomes for the variable: we believe that what usually triggers the identification of a new variable in an event category is exposure to contrastive outcomes not predicted by infants’ current knowledge of the category. These unpredicted contrastive outcomes may involve the violation of current variables, but not necessarily: infants may simply detect hitherto unnoticed variation in events from the category. For example, in the case of the collision variable “size of the moving object” (Kotovsky & Baillargeon, 1994, 1998), infants might notice that stationary objects hit by moving objects sometimes travel a shorter and sometimes a longer distance.
The second step in the identification process involves the search for relevant conditions: upon noticing the unpredicted contrastive outcomes, infants begin to search for the conditions that map onto these outcomes. To return to our example, infants might notice that stationary objects typically travel farther when hit by larger as opposed to smaller moving objects.
Finally, the last step in the identification process involves building an explanation for the condition-outcome observations that have been gathered. According to our account, only condition-outcome observations for which infants can build causal explanations are identified as new variables. These explanations are no doubt shallow (e.g., Keil, 1995; Wilson & Keil, 2000), and they may even be incorrect (e.g., Baillargeon, 2002); nevertheless, they serve to integrate new variables with infants’ prior causal knowledge. This prior knowledge is assumed to include infants’ previously acquired knowledge as well as their core knowledge—notions that, from birth, guide infants’ interpretations of physical events (e.g., Leslie, 1995; Spelke, Phillips, & Woodward, 1995).
To return to our example once more, what causal explanation could infants generate for their observations that stationary objects typically travel farther when hit by larger as opposed to smaller objects? One possibility comes from the work of Leslie and his colleagues (e.g., Leslie, 1995; Leslie & Keeble, 1987). Leslie suggested that, from birth, infants interpret physical events in accord with a primitive notion of force: when watching a collision between a moving and a stationary object, infants include in their physical representation of the event a mechanical force—a simple unidirectional push—that is exerted by the first object onto the second and brings about its displacement. This notion of force could help infants readily make sense of their observations concerning larger and smaller moving objects: specifically, infants could reason that, relative to smaller objects, larger objects would be likely to exert more force, and hence to cause greater displacements.
Is there evidence that infants do represent collision events causally? Experiments focusing on collision events between self-moving objects support such a possibility (e.g., Leslie & Keeble, 1987; Oakes, 1994; Oakes & Cohen, 1995). In one experiment, for example, Leslie and Keeble (1987) habituated 6-month-old infants to a filmed event. The infants in the immediate condition saw a red brick approach and contact a green brick, which immediately moved off; the infants in the delayed condition saw a similar event except that the two bricks’ motions were separated by a 0.5-s delay. Following habituation, the infants in each condition watched their same event in reverse. Although the infants in two conditions tended to look equally during the habituation trials, the infants in the immediate condition looked reliably longer than those in the delayed condition during the test trials. These results suggested two conclusions. During the habituation trials, the infants in the immediate condition assumed that the red brick caused the green brick’s displacement; in contrast, the infants in the delayed condition assumed that the green brick caused its own displacement (i.e., it moved off on its own). During the test trials, the infants in the immediate condition realized that the red and green bricks’ causal roles were now reversed; no such role reversal occurred in the delayed condition, as each brick continued to cause its own displacement. Thus, although the infants in both conditions saw test events with reversed spatiotemporal properties (the two bricks now moved in the opposite spatial direction and in the opposite temporal order), only those in the immediate causal condition were exposed to a reversal in causal role. The fact that the infants detected this reversal suggests that, by 6 months of age, infants construe a simple collision event between a moving and a stationary object causally: they assume that the moving object causes the stationary object’s displacement, presumably through the application of a mechanical force.
We began this section with the question of whether the variables infants identify as they learn about collision events are best described as statistical or as causal regularities. The research reviewed in this section suggests that these variables (like other variables) are in fact causal rules.
This is not to say, of course, that infants may not also use statistical regularities to interpret the events they observe (there already is evidence in the field of language acquisition that infants are highly skilled at detecting statistical regularities for strings of sounds; e.g., Chambers, Onishi, & Fisher, 2003; Gómez & Gerken, 1999; Saffran, Newport, & Aslin, 1996). Consider, for example, infants who notice through repeated observations that objects with property A sometimes also have property X, which in turn affects the outcomes of various events involving these objects. Because infants do not understand why A and X sometimes co-occur (it may in fact be that only objects with properties A, B, and C also have property X), this statistical regularity has limited predictive power. Upon encountering a novel object with property A, infants cannot predict whether it will also have property X; this can only be established post hoc, through additional observation. Nevertheless, infants may still be able to use these limited statistical regularities to help interpret the physical events they observe. As will soon become clear, and consistent with these speculations, the present research suggested that both causal and statistical regularities contribute to 8- and 9-month-old infants’ responses to collision events. We return to this issue when discussing the results of Experiment 1.
1.3. The present research
The research reviewed in the preceding sections suggests that, by 6.5 months of age, infants expect a stationary object to be displaced farther when hit by a larger as opposed to a smaller object, presumably because they recognize that a larger object is likely to exert a greater force and hence to cause a greater displacement (e.g., Kotovsky & Baillargeon, 1994, 1998; Leslie, 1995; Leslie & Keeble, 1987). The present research built on these findings to explore a different facet of infants’ knowledge about collision events.
In the experiments conducted by Kotovsky and Baillargeon (1994, 1998), the toy bug usually moved when hit by the cylinder. But in many collision events in everyday life, stationary objects are not displaced when hit: consider, for example, a pencil that rolls along a desktop and collides with a stapler, or a grape that rolls along a tabletop and collides with a bowl. At what age do infants begin to realize that stationary objects do not always move when hit? The present research began to address this question.
One important variable adults consider in predicting whether a stationary object is likely to be displaced when hit is its size: all other things being equal, we believe that a moving object is more likely to displace a smaller as opposed to a larger stationary object. The present research asked at what age infants begin to take into account the size of a stationary object to predict whether it should move when hit. Experiments 1 and 2 focused on 8-month-old infants, and Experiments 3 and 4 on 9-month-old infants.
2. Experiment 1
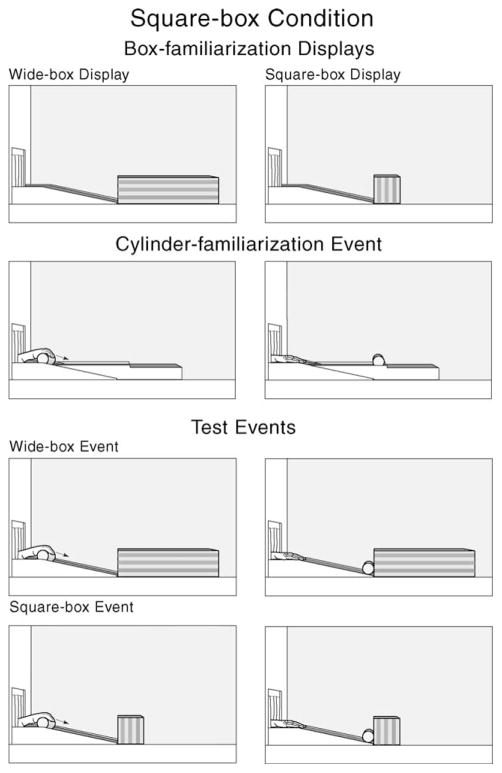
Experiment 1 asked whether 8-month-old infants would expect a small but not a large stationary object to be displaced when hit by a moving object. The infants saw test events in which a cylinder rolled down a ramp and hit a box at the bottom of the ramp. A small and a large box were used on alternate trials; the box always remained stationary when hit. The small and large boxes were of the same height (13 cm) and depth (15.5 cm); they differed only in width. In the square-box condition (see Fig. 1), the small box was 13 cm wide and therefore presented a square front surface (square-box event); the large box was 52 cm wide (wide-box event). In the narrow-box condition (see Fig. 2), the small box was 3.25 cm wide and thus was very narrow (narrow-box event): the large box was again 52 cm wide (wide-box event). The infants in the square-box condition saw the square- and wide-box events on alternate trials, and the infants in the narrow-box condition saw the narrow- and wide-box events on alternate trials.
Fig. 1.
Schematic drawing of the box-familiarization displays, cylinder-familiarization event, and test events shown in the square-box condition of Experiment 1.
Fig. 2.
Schematic drawing of the box-familiarization displays, cylinder-familiarization event, and test events shown in the narrow-box condition of Experiment 1.
At the start of the experiment, the infants in each condition received two box-familiarization trials in which they saw the two boxes used in the test trials; the boxes were shown on alternate trials, resting at the bottom of the ramp. These box-familiarization trials served to acquaint the infants with each box, and to determine whether they possessed an intrinsic preference for either box. Next, the infants received four cylinder-familiarization trials in which they saw the cylinder roll down a ramp; no box was present in these trials, which served to introduce the infants to the rolling cylinder. Following the box- and cylinder-familiarization trials, the infants received four test trials in which they saw, as mentioned earlier, the wide- and either the square- or narrow-box event on alternate trials. At the start of each trial, an experimenter’s gloved hand held the cylinder at the top of the ramp and tapped it lightly to attract the infants’ attention. Next, the hand released the cylinder, which rolled down the ramp and hit the box. All of the boxes remained stationary when hit.
Our reasoning was as follows. If the infants (1) attended to the size of the box used in each test event, and (2) expected the wide box to remain stationary, and the square and the narrow box to move, when hit by the cylinder, then they should be surprised in the square-and narrow-box events when these last expectations were violated. Thus, the infants in the square-box condition should look reliably longer at the square- than at the wide-box event, and those in the narrow-box condition should look reliably longer at the narrow- than at the wide-box event. Similar looking patterns were thus predicted for the two conditions.
2.1. Method
2.1.1. Participants
Participants were 32 healthy term infants, 15 males and 17 females, ranging in age from 7 months, 12 days to 8 months, 16 days (M = 8 months, 6 days). An additional 11 infants were tested but eliminated, 6 because they were fussy (2), inattentive (2), drowsy (1), or overly active (1), and 5 because the observers could not follow the infant’s gaze. Half of the infants were randomly assigned to the square-box condition (M = 8 months, 8 days), and half to the narrow-box condition (M = 8 months, 4 days).
2.1.2. Apparatus
The apparatus consisted of an unpainted wooden box 124 cm high, 152 cm wide, and 61 cm deep that was mounted 76 cm above the floor. The infant faced an opening 48 cm high and 150 cm wide in the front of the apparatus. Between trials, a wooden frame 64 cm high, 152 cm wide, and covered with white muslin, was lowered in front of this opening. The back wall of the apparatus was covered with blue cloth; at the bottom of the wall was a large opening, concealed by a curtain made of the same blue cloth, which was used between trials to insert and remove stimuli.
A wooden ramp 55 cm wide and 13.6 cm deep stood 28 cm from and parallel to the front of the apparatus, against the left wall. The ramp consisted of a horizontal plateau 7.6 cm high and 16 cm long, and an incline 40 cm long that sloped downward at an 11° angle; the top surface of the plateau and incline was covered with black contact paper. At the top of the ramp was a window 21 cm high and 15.5 cm wide that was filled with a white muslin fringe. An experimenter introduced her right hand (in a long green glove) into the apparatus through this window to roll the cylinder down the ramp. The cylinder was 5.9 cm in diameter and 13.3 cm wide; it was made of plastic piping material, closed at both ends, and painted light blue. On either side of the ramp were vertical wood panels 0.5 cm thick that protruded 0.75 cm above the surface of the ramp and prevented the cylinder from rolling off the ramp. The ramp rested on a strip of particle board 0.7 cm thick, 55 cm wide, and 15.5 cm deep. A similar strip 97 cm wide and covered with black felt extended from the bottom of the ramp to the right wall of the apparatus; the boxes were placed on this strip at the bottom of the ramp.
The three boxes used in the box-familiarization and test trials were all 13 cm tall, 15.5 cm deep, made of wood, and covered with red contact paper decorated with green stripes (the narrow and square boxes had vertical stripes and the wide box horizontal stripes). The narrow box was 3.25 cm wide, the square box 13 cm, and the wide box 52 cm wide; each box was thus 25% as wide as the next larger box. To ensure that the boxes did not move when hit by the cylinder in the test trials, two metal posts were screwed into the apparatus floor at the bottom of the ramp before the test trials; these posts were 10.5 cm high, 1.25 cm in diameter, covered with black felt, and located 10.5 cm apart. The narrow box fit tightly over the posts; the square and wide boxes had built-in compartments for the posts, and they were also filled with heavy weights, to prevent any motion.
In the cylinder-familiarization trials, a horizontal wooden platform 6.5 cm high, 68 cm long, and 13.5 cm deep was used (because no box was present at the bottom of the ramp in the cylinder-familiarization trials, the platform served to restrict the motion of the cylinder past the ramp, so that it could easily be retrieved by the experimenter and returned to the top of the ramp). The left half of the platform lay over the right 34 cm of the ramp (the underside of the platform was cut at a steep angle to accommodate the ramp and keep the surface of the platform horizontal); the right half of the platform extended past the ramp. When released at the top of the ramp, the cylinder rolled down the ramp (for about 5 cm) and then onto the platform. The surface of the platform was covered with black felt. Along the sides of the platform were wooden guides 1 cm tall, 0.5 cm thick, and covered with black felt, that prevented the cylinder from rolling off the platform. The guides were 41 cm long; they began at the left edge of the platform and extended for 38.5 cm, at which point they angled inward to form small triangular stops, also covered with black felt. These stops served to gradually slow the cylinder and limit the maximum distance it could travel.
The infants were tested in a well-lit room. Four 40-W clip-on lights attached to the front wall of the apparatus provided additional light. Two wooden frames, each 183 cm tall, 71 cm wide, and covered with yellow cloth, were anchored to the sides of the apparatus; these frames served to isolate the infants from the experimental room.
2.1.3. Events
The numbers in parentheses indicate the time taken to perform each action described. A metronome beat softly once per second to help the experimenter adhere to each event’s script.
2.1.3.1. Box-familiarization displays
The infants in each condition saw the two boxes shown in the test trials on alternate trials (the wide and square boxes in the square-box condition, and the wide and narrow boxes in the narrow-box condition). Each box rested at the bottom of the ramp; the experimenter’s gloved hand and cylinder were not present during these trials.
2.1.3.2. Cylinder-familiarization event
The infants in the square- and narrow-box conditions saw the same cylinder-familiarization event. At the start of each trial, the experimenter’s gloved hand held the cylinder centered on the plateau at the top of the ramp. The hand tapped the cylinder lightly at a rate of about three taps per second until the computer signaled that the infant had looked at the cylinder for 2 cumulative seconds. When this pretrial ended, the trial proper began. The hand slid the cylinder to the top of the incline (1 s) and released it (1 s); the hand then rested on the plateau. After it was released, the cylinder rolled down the ramp and onto the platform (1 s). After a 1-s pause, the hand grasped the cylinder (1 s) and, sliding it along the surface of the platform and ramp, returned it to the top of the incline (2 s). A new event cycle then began: the hand paused for 1 s and then released the cylinder once again. Each cycle (beginning after the pretrial in which the cylinder was tapped) lasted about 7 s. Cycles were repeated until the computer signaled that the trial had ended (see the following).
2.1.3.3. Test events
Prior to the test events, the platform was removed and the posts were screwed into the apparatus floor at the bottom of the ramp. On alternate trials, the wide and the square (square-box condition) or narrow (narrow-box condition) boxes were placed over the posts. At the start of each trial, the experimenter’s gloved hand tapped the cylinder on the plateau at the top of the ramp until the computer signaled that the infant had looked at the cylinder for 2 cumulative seconds. When this pretrial ended, the trial proper began. The hand slid the cylinder to the top of the incline (1 s), released the cylinder (1 s), and then rested on the plateau. After it was released, the cylinder rolled down the ramp and hit the box (1 s), which remained stationary. After a 1-s pause, the hand grasped the cylinder (1 s) and, sliding it along the surface of the ramp, returned it to the top of the incline (2 s). A new event cycle then began: the hand paused for 1 s and then released the cylinder once again. Each cycle thus lasted about 7 s, as in the cylinder-familiarization event. Because the hand had less distance to travel to grasp the cylinder (against the box) or to return it to the top of the incline, it moved slightly more slowly than in the cylinder-familiarization event.
2.1.4. Adult ratings
In implementing the design of Experiment 1, we chose a large box we thought most adults would expect to remain stationary when hit by the cylinder, and two small boxes we thought most adults would expect to move when hit by the cylinder. How accurate were our choices? To address this question, we tested 30 undergraduate students, 12 males and 18 females (M = 21.7 years); half were assigned to the square-box condition, and half to the narrow-box condition. Another four undergraduate students were tested but eliminated because they misunderstood the instructions.
The adults in the square-box condition first received two display trials in which they saw the square (square-box display) or the wide (wide-box display) box resting at the bottom of the ramp; the experimenter’s gloved hand held the cylinder at the top of the incline. Each display trial lasted 10 s. During the trial, the adults were asked to rate how likely the box was to move when hit by the cylinder on a scale of 1–6, where 1 was “very unlikely” and 6 was “very likely.” Next, the adults received two test trials which again began with the hand holding the cylinder at the top of the incline, and the square (square-box event) or the wide (wide-box event) box resting at the bottom of the ramp. Each trial lasted 10 s. The hand paused for 1 s, released the cylinder (1 s), and then rested on the plateau at the top of the ramp for the remainder of the trial. Once released, the cylinder rolled down the ramp and hit the box (1 s), which remained stationary. After seeing the event, the adults were asked to rate how surprised they were by the outcome of the event on a scale of 1–6, where 1 was “not surprised” and 6 was “very surprised.”
The adults in the narrow-box condition received similar display and test trials, except that the square box was replaced by the narrow box. Of the 30 adults in the experiment, 14 saw the wide box first in the display and test trials, and 16 saw the square or narrow box first.
The ratings obtained in the display trials were analyzed by means of a 2 × 2 analysis of variance (ANOVA) with condition (square- or narrow-box) as a between-subjects factor and display (wide- or square-/narrow-box) as a within-subject factor. The only significant effect was that of display, F(1, 28) = 75.67, p < .0001. Planned comparisons indicated that the adults in the square-box condition believed that the square box (M = 4.1, SD = 1.4) was more likely than the wide box (M = 2.2, SD = 1.4) to move when hit, F(1, 28) = 22.42, p < .0001; and that the adults in the narrow-box condition similarly believed that the narrow box (M = 5.3, SD = 1.1) was more likely than the wide box (M = 2.3, SD = 1.1) to move when hit, F(1, 28) = 57.69, p < .0001.
The ratings obtained in the test trials were analyzed in the same manner as above with event (wide- or square-/narrow-box) as the within-subject factor. Again, the only significant effect was that of event, F(1, 28) = 74.88, p < .0001. Planned comparisons indicated that the adults in the square-box condition were more surprised when the square box (M = 4.2, SD = 1.6) than when the wide box (M = 1.9, SD = 1.7) box failed to move when hit, F(1, 28) = 25.26, p < .0001; and that the adults in the narrow-box condition were similarly more surprised when the narrow box (M = 4.8, SD = 1.2) than when the wide box (M = 1.5, SD = 1.1) failed to move when hit, F(1, 28) = 52.42, p < .0001.
Together, these data suggested that the adults readily used information about the size of the boxes to judge whether they should move when hit by the cylinder. Specifically, the adults expected the square and the narrow box, but not the wide box, to move when hit, and they were surprised in the square- and narrow-box events when these expectations were violated. Experiment 1 examined whether 8-month-old infants would share the same expectations as adults about the wide, square, and narrow boxes.
2.1.5. Procedure
During the experiment, each infant sat on parent’s lap in front of the bottom of the ramp. The infant’s head was approximately 43 cm from the front edge of the apparatus. Prior to the experiment, the infant was shown for a few seconds the experimenter’s green glove and the cylinder. Parents were instructed to remain silent and neutral during the experiment and to close their eyes during the test trials.
The infant’s looking behavior was monitored by two observers who watched the infant through peepholes in the cloth-covered frames on either side of the apparatus. The observers could not determine, and were not told, to which condition the infant was assigned and in which order the box-familiarization and test trials were administered. Each observer depressed a button connected to a computer when the infant looked at the display or event shown in the apparatus. The looking times recorded by the primary observer were used to decide when a trial had ended (see the following).
The infants first received two box-familiarization trials in which they saw the two box-familiarization displays appropriate for their condition on alternate trials. These trials served to acquaint the infants with the boxes used in the test trials; they also made it possible to assess whether the infants had an intrinsic preference for one box over the other. Each trial ended when the infant either (1) looked away from the display for 1 consecutive second after having looked at it for at least 4 cumulative seconds or (2) looked for 30 cumulative seconds.
Next, the infants received four cylinder-familiarization trials. These trials were used to acquaint the infants with the rolling cylinder. Each trial ended when the infant either (1) looked away from the event for 1 consecutive second after having looked at it for at least 4 cumulative seconds (beginning at the end of the pretrial, when the hand slid the cylinder to the top of the incline) or (2) looked for 60 cumulative seconds.
Following the box- and cylinder-familiarization trials, the infants received four test trials in which they saw the two test events appropriate for their condition on alternate trials. Half of the infants in each condition saw the wide box first in the box-familiarization and test trials, and half saw the square or narrow box first. Each test trial ended when the infant either (1) looked away from the event for 1 consecutive second after having looked at it for at least 5 cumulative seconds (beginning at the end of the pretrial, when the hand moved the cylinder to the top of the incline) or (2) looked for 60 cumulative seconds. The 5-s minimum value was chosen to ensure that the infants had ample opportunity to see that the box did not move when hit by the cylinder.
To assess interobserver agreement during the box-familiarization, cylinder-familiarization, and test trials, each trial was divided into 100-ms intervals, and the computer determined in each interval whether the two observers were in agreement. Percent agreement was calculated for each trial by dividing the number of intervals in which the observers agreed by the total number of intervals in the trial. Agreement was measured for all 32 infants in Experiment 1 and averaged 95% per trial per infant.
Preliminary analyses of the test data in this and in the following experiments revealed no significant interaction involving condition, event, and either sex or order; the data were therefore collapsed across sex and order in subsequent analyses.
2.2. Results
2.2.1. Box-familiarization trials
The infants’ looking times during the two box-familiarization trials were compared by means of a 2 × 2 ANOVA with condition (square- or narrow-box) as a between-subjects factor and display (wide- or square-/narrow-box) as a within-subject factor. The main effect of display was not significant, F(1, 30) = 1.30, p > .10, nor was the condition × display interaction, F(1, 30) = 0.01, indicating that the infants in the two conditions tended to look equally at the displays they were shown (square-box condition: wide-box, M = 8.7, SD = 5.7, square-box, M = 7.3, SD = 3.5; narrow-box condition: wide-box, M = 9.8, SD = 6.2, narrow-box, M = 8.1, SD = 3.5).
2.2.2. Cylinder-familiarization trials
The infants’ looking times during the four cylinder-familiarization trials were compared by means of a 2 × 4 ANOVA with condition (square- or narrow-box) as a between-subjects factor and trial (first, second, third, or fourth) as a within-subject factor. The analysis revealed a significant main effect of trial, F(3, 90) = 10.36, p < .0001, indicating that the infants looked reliably less across trials. The main effect of condition was not significant, F(1, 30) = 0.86, nor was the condition × trial interaction, F(3, 90) = 0.68, indicating that the infants in the square-box (M = 40.5, SD = 19.6) and narrow-box (M = 36.7, SD = 20.0) conditions did not differ reliably in their responses to the cylinder-familiarization event.
2.2.3. Test trials
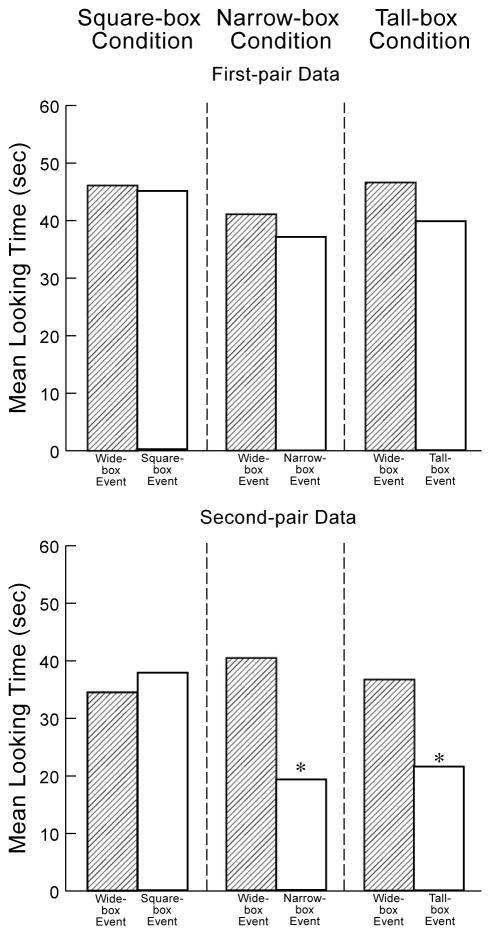
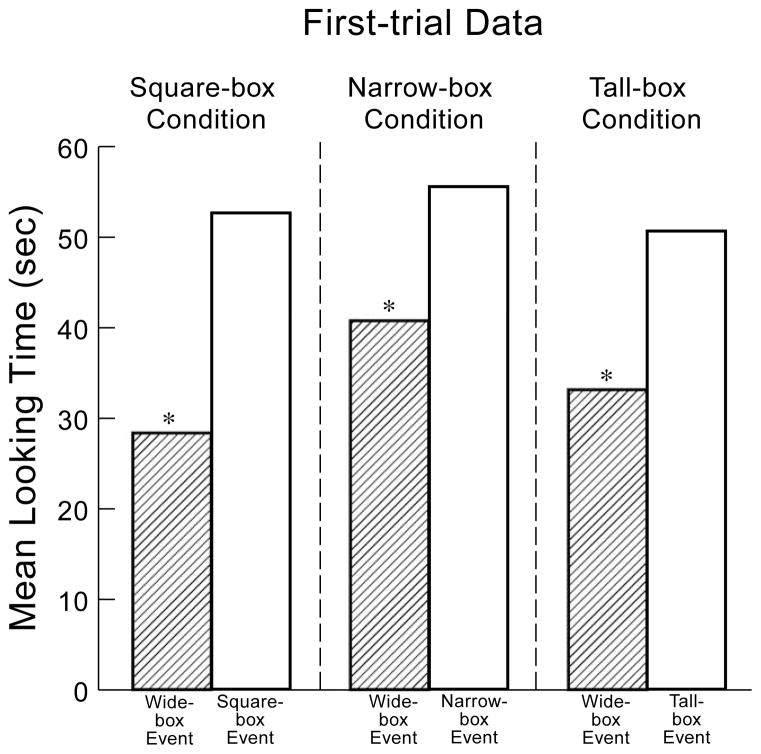
The infants’ looking times during the four test trials (see Fig. 3) were analyzed by means of a 2 × 2 × 2 ANOVA with condition (square- or narrow-box) as a between-subjects factor and with pair (first or second) and event (wide- or square-/narrow-box) as within-subject factors. The analysis yielded significant main effects of pair, F(1, 90) = 14.44, p < .0005, and event, F(1, 90) = 5.51, p < .025, as well as significant interactions between condition and event, F(1, 90) = 7.68, p < .01, and condition, pair, and event, F(1, 90) = 4.84, p < .05.
Fig. 3.
Mean looking times of the 8-month-old infants in Experiments 1 and 2 at the test events during the first and second pairs of trials.
To understand the nature of this three-way interaction, two interaction comparisons were carried out. The first examined the data from the first pair of test trials and was not significant, F(1, 90) = 0.16, suggesting that on the first test pair the infants in the two conditions tended to look equally at the test events they were shown. These negative results were confirmed by additional comparisons focusing exclusively on the square-box condition (wide-box, M = 46.1, SD =16.8, square-box, M = 44.9, SD = 17.2, F(1, 90) = 0.06) and on the narrow-box condition (wide-box, M = 41.1, SD = 19.8, narrow-box, M = 37.1, SD = 16.1, F(1, 90) = 0.65).
The second interaction comparison focused on the second pair of test trials and was significant, F(1, 90) = 12.36, p < .001, indicating that the infants in the two conditions differed in their responses to the wide- and square- or narrow-box events. Additional comparisons revealed that, whereas the infants in the square-box condition again looked about equally at the wide-box (M = 34.5, SD = 20.8) and square-box (M = 37.8, SD = 18.7) events, F(1, 90) = 0.44, those in the narrow-box condition now looked reliably longer at the wide-box (M = 40.4, SD = 17.5) than at the narrow-box (M = 19.2, SD = 13.8) event, F(1, 90) = 18.57, p < .0001.
A final set of comparisons across the two pairs of test trials revealed that (1) there was no reliable difference in the looking times of the infants in the two conditions at the wide-box event on the first (M = 43.6, SD = 18.3) and second (M = 37.5, SD = 19.1) test pairs, F(1, 90) = 3.12, p > .05; (2) there was no reliable difference in the looking times of the infants in the square-box condition at the square-box event on the first (M = 44.9, SD = 17.2) and second (M = 37.8, SD = 18.7) test pairs, F(1, 90) = 2.11, p > .10; and finally (3) there was a reliable difference in the looking times of the infants in the narrow-box condition at the narrow-box event on the two test pairs: the infants looked reliably less on the second (M = 19.2, SD = 13.8) than on the first (M = 37.1, SD = 16.1) test pair, F(1, 90) = 13.31, p < .0005.
2.3. Discussion
The results of Experiment 1 were unexpected. On the first test pair, the infants in the two conditions responded with equal and prolonged attention to the wide- and square- or narrow-box events. On the second test pair, the infants in the square-box condition continued to respond with prolonged attention to the wide- and square-box events. In contrast, the infants in the narrow-box condition continued to respond with prolonged attention to the wide- but not the narrow-box event: they now looked reliably longer at the wide- than at the narrow-box event. How should these results be interpreted?
We speculated that two different factors contributed to the results of Experiment 1. The first factor had to do with the infants’ limited knowledge of collision events. The results suggested that, at 8 months of age, infants do not yet take into account the size of a stationary object to predict whether it should move when hit. At this stage, infants still have available only a simple impact/no-impact variable and hence still expect all stationary objects to be displaced when hit. Thus, on the first test pair, the infants in Experiment 1 expected the wide, square, and narrow boxes to all move when hit, and they responded with prolonged attention to the wide-, square-, and narrow-box events because in all of these events—contrary to their expectations—the box remained stationary when hit.
The second factor that contributed to the infants’ responses had to do with their ability to generate explanations for apparent violations of their collision knowledge. The results suggested that, by 8 months of age, infants have detected a statistical regularity about objects: they have learned that some objects with a salient vertical dimension (i.e., objects that are significantly taller than they are wide) are attached at one or both ends to adjacent surfaces, so that they remain stationary when a force is exerted upon them; for ease of description, we will refer to these attached vertical objects as pillars. Thus, upon observing that the narrow box did not move when hit by the cylinder, the infants in the narrow-box condition of Experiment 1 concluded that the narrow box must be one of those immovable pillars. Because the infants could make sense of the narrow-box event, they ceased responding to it with prolonged attention, and thus looked reliably less at it in the second than in the first test pair. In contrast, the infants continued to respond with prolonged attention to the wide- and square-box events in the first and second test pairs, because they were not able to generate an explanation for these events. At 8 months of age, infants apparently view objects with a salient vertical dimension (like the narrow box), but not objects lacking such a dimension (like the square and wide boxes), as potential immovable pillars.
How might infants come by their knowledge about pillars? Infants might notice, for example, that the slats of cribs, the legs of tables, or the posts of banisters and other railings typically do not move when acted upon (e.g., when pulled, pushed, or kicked by the infants themselves or by their caretakers or siblings). Through these and other observations, infants would come to recognize that, although some vertical objects (e.g., cups, bottles, and tall toys) move when hit, other vertical objects (e.g., crib slats, table legs, and railing posts) do not, because they are attached to adjacent surfaces.
Two bodies of evidence supported our interpretation of the results of Experiment 1. First, there is now considerable evidence that infants aged 3.5 months and older are sometimes able to generate explanations to make sense of events that would otherwise violate their physical knowledge (e.g., Aguiar & Baillargeon, 2002; Baillargeon, 1994; Hespos & Baillargeon, 2003; Spelke, Kestenbaum, Simons, & Wein, 1995; Xu & Carey, 1996). In some cases, these explanations involve positing the presence of additional objects. For example, when an object disappears behind one screen and reappears from behind another screen without appearing in the gap between the two screens, infants aged 3.5 months and older conclude that two identical objects must be involved in the event, one traveling to the left and one to the right of the screens (e.g., Aguiar & Baillargeon, 2002; Baillargeon, 1994; Spelke, Kestenbaum, et al., 1995; Xu & Carey, 1996). Similarly, when two objects are placed behind a screen which is then lowered to reveal three objects, 10-month-old infants conclude that a third object must already have been present behind the screen (Baillargeon, Miller, & Constantino, cited in Baillargeon, 1994). In other cases, infants’ explanations involve positing connections between objects or between objects and surfaces. For example, when a gloved hand’s index finger pushes a box off a platform and the box remains stable in midair at the end of the finger, 3.5-month-old infants conclude that the box must be attached to the finger (Needham & Baillargeon, cited in Baillargeon, 1994). Furthermore, when shown two small toys on a vertical surface, infants aged 5.5 months and older tend to reach for the one of the two toys that also rests on a horizontal surface, as though they realize that the other toy could not remain in place without being attached to the vertical surface and hence is unlikely to be retrievable (Hespos & Baillargeon, 2003). Finally, when shown two small toys, one with its bottom surface resting fully on a platform, and one with only a small portion of its bottom surface resting on a platform, 6.5-month-old infants tend to reach for the first of the two toys, as though they realize that the second toy could not remain in place without being attached to the platform and hence is unlikely to be retrievable (Hespos & Baillargeon, 2003). Infants’ explanations for apparent violations of their physical knowledge are not necessarily correct, but they do serve to reconcile what they see with what they know.
The second body of evidence consistent with our interpretation of the results of Experiment 1 involves findings from experiments on 7.5-month-old infants’ responses to collision events between a moving object and a tall, narrow barrier (Kotovsky & Baillargeon, 2000). The infants were assigned to a contact or a no-contact condition. The infants in the no-contact condition first saw static familiarization displays in which a tall, narrow barrier stood across the bottom of a ramp; a cylinder rested against the left side of the barrier and a wheeled toy bug rested against its right side. The infants in the contact condition saw similar displays except that a large portion of the barrier’s lower half was removed so that the cylinder rested directly against the bug under this half-barrier. Next, a short screen was placed in front of the bottom of the ramp; the portion of the barrier or half-barrier visible above the screen was identical in the two conditions. The infants in both conditions received six test trials in which they saw the same test event: the cylinder rolled to the bottom of the ramp, partly disappearing behind the left edge of the screen, and the barrier or half-barrier and bug remained stationary. The infants in the contact condition looked reliably longer than those in the no-contact condition. This and control results suggested that (1) the infants in the contact condition expected the bug to move when hit by the cylinder and were surprised that it did not, and (2) the infants in the no-contact condition did not expect the barrier to move when hit by the cylinder. Had the infants expected both the bug in the contact condition and the barrier in the no-contact condition to move when hit, they would have tended to look equally in the two conditions. The fact that they did not suggests that the infants in the no-contact condition perceived the barrier to be one of those attached vertical objects—an immovable pillar. Because the infants could make sense of the fact that the barrier but not the bug remained stationary when hit, the infants in the no-contact condition looked reliably less overall than did those in the contact condition.
We have argued that two distinct expectations contributed to the responses of the infants in Experiment 1. First, the infants used a simple, impact/no-impact collision variable—a stationary object is displaced when a moving object exerts a force upon it—to predict the outcomes of the wide-, square-, and narrow-box events. In each case, the infants expected the box to move when hit by the cylinder. The 8-month-old infants in Experiment 1 thus differed from the adults we tested in that they expected all of the boxes—not just the narrow and the square box—to move when hit. Unlike the adults, the infants were not able to take into account the size of each box to predict whether it should move, and they expected even the wide box (52 cm in width) to move when hit.
Second, upon seeing that the narrow box did not move when hit, the infants appealed to a statistical regularity to make sense of this event: some objects with a salient vertical dimension are attached to their adjacent surfaces, and hence remain stationary when forces are exerted upon them. The infants could not use this regularity to predict that the narrow box would remain stationary when hit. The fact that the narrow box was an immovable pillar (e.g., such as a table leg, crib slat, or banister post), rather than a movable vertical object (e.g., such as a cup, bottle, or tall toy), could only be established empirically, post hoc, upon observing that it did not move when hit. In our experiment with adults, participants were not asked how our collision events were produced. Upon seeing that the square and narrow boxes did not move when hit, however, the adults were no doubt able to quickly generate explanations for these unexpected events. Indeed, some adults spontaneously commented that the square and narrow boxes must be somehow anchored to the apparatus floor, whereas others suggested that the boxes must be heavier than they had initially expected (since the boxes were identical except for their widths, the adults tended to assume that their weights were proportional to their sizes; some adults clearly revised this assumption when the outcomes of the events suggested otherwise). Unlike the adults, the infants were apparently able to generate an explanation only for the narrow-box event, by appealing to their prior observations about attached vertical objects.
In sum, the results of Experiment 1 suggested that the infants brought to bear both a causal and a statistical expectation when reasoning about the collision events they were shown: the causal expectation was used to predict the outcomes of the events (“stationary objects move when a force is exerted upon them”), and the statistical expectation was invoked after the fact to make sense of one of the outcomes that violated their predictions (“some vertical objects are attached to their adjacent surfaces”).
3. Experiment 2
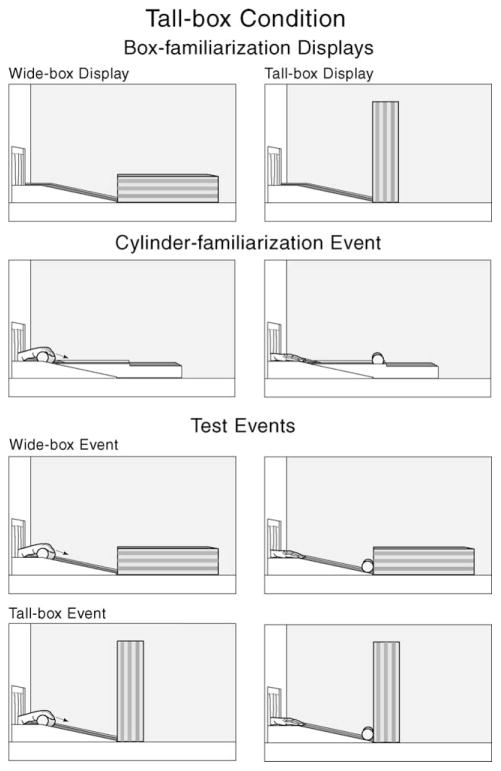
Experiment 2 was designed to extend and confirm the results of Experiment 1. Participants were again 8-month-old-infants, and they were tested using the same procedure as in Experiment 1 with one exception: instead of a square or a narrow box, the infants saw a tall box identical to the wide box in a vertical orientation (see Fig. 4). The infants saw the wide and tall boxes on alternate box-familiarization and test trials.
Fig. 4.
Schematic drawing of the box-familiarization displays, cylinder-familiarization event, and test events shown in the tall-box condition of Experiment 2.
Our interpretation of the results of Experiment 1 led to the following predictions. First, if infants at 8 months of age expect all boxes to move when hit, irrespective of their sizes, then the infants in Experiment 2 should expect both the wide and the tall box to move when hit; the infants should thus respond with prolonged attention to the wide- and tall-box events on the first pair of test trials. Second, if infants can bring to bear a statistical regularity involving vertical objects to make sense of violations of their collision knowledge (“some vertical objects are attached to their adjacent surfaces”), then the infants in Experiment 2 should continue to respond with prolonged attention to the wide- but not the tall-box event on the second pair of test trials; the infants should thus look reliably longer at the wide- than at the tall-box event on the second test pair.
The results of Experiment 2 were thus expected to mirror those of the narrow-box condition in Experiment 1. Although the narrow and tall boxes were markedly different in height and width, they both had a salient vertical dimension and as such were expected to elicit similar responses from the infants.
3.1. Method
3.1.1. Participants
Participants were 16 healthy term infants, 8 males and 8 females, ranging in age from 7 months, 18 days to 8 months, 16 days (M = 8 months, 2 days). An additional eight infants were tested but eliminated, four because they were inattentive, two because the observers could not follow the infant’s gaze, and two because they looked for the maximum amount of time allowed (60 s) on all four test trials.
3.1.2. Apparatus, events, and procedure
The apparatus, events, and procedure used in Experiment 2 were identical to those in the narrow-box condition of Experiment 1, except that the narrow box used in the box-familiarization and test trials was replaced with a tall box identical to the wide box in a vertical orientation; this tall box was thus 52 cm tall, 13 cm wide, and 15.5 cm deep. Interobserver agreement was measured for all 16 infants and averaged 92% per trial per infant.
3.1.3. Adult ratings
Would adults perceive the tall box as likely or as unlikely to move when hit? To find out, 15 undergraduate students, 8 males and 7 females (M = 18.3 years) were tested using the same procedure as in the narrow-box condition of the adult experiment reported in Experiment 1, with one exception: the narrow box was replaced with the tall box. The adults thus saw the wide and the tall box on alternate display and test trials.
The ratings obtained in the display trials were analyzed by means of a one-way ANOVA with display (wide- or tall-box) as a within-subject factor. The main effect of display was significant, F(1, 28) = 14.33, p < .001, indicating that the adults believed that the tall box (M = 3.5, SD = 1.6) was more likely than the wide box (M = 1.7, SD = 1.0) to move when hit. A parallel analysis of the ratings obtained in the test trials again yielded a significant main effect of event, F(1, 28) = 6.45, p < .025, indicating that the adults were more surprised when the tall box (M = 2.9, SD = 1.5) than when the wide box (M = 1.7, SD = 1.2) failed to move when hit.
Because the tall and wide boxes were identical in size, the fact that the adults responded to them differently suggested that they took into account not only the size but also the stability of each box—how much force would be required to topple it. The tall box was less stable than the wide box, and so the adults expected it to move when hit and were surprised when it did not. Consistent with this analysis, several adults spontaneously commented that the box was less stable and should be easier to move in its vertical than in its horizontal orientation.
We predicted that, like the adults, the 8-month-old infants in Experiment 2 would expect the tall box to move when hit (before they arrived at the conclusion that it must be one of those attached vertical objects or pillars). Unlike the adults, however, the infants would also expect the wide box to move when hit.
3.2. Results
Because the results of Experiment 2 were expected to mirror those of the narrow-box condition in Experiment 1, the results obtained with these two groups of infants were directly compared in the analyses of the familiarization and test trials.
3.2.1. Box-familiarization trials
The infants’ looking times during the two box-familiarization trials were compared to those of the infants in the narrow-box condition of Experiment 1 by means of a 2×2 ANOVA with condition (narrow- or tall-box) as a between-subjects factor and display (wide- or narrow-/tall-box) as a within-subject factor. The main effect of display was not significant, F(1, 30) = 0.29, nor was the condition × display interaction, F(1, 30) = 0.48, indicating that the infants in the two conditions tended to look equally at the displays they were shown (narrow-box condition: wide-box, M = 9.8, SD = 6.2, narrow-box, M = 8.1, SD = 3.5; tall-box condition: wide-box, M = 6.8, SD = 2.8, tall-box, M = 7.0, SD = 6.5).
3.2.2. Cylinder-familiarization trials
The infants’ looking times during the four cylinder-familiarization trials were compared to those of the infants in the narrow-box condition of Experiment 1 by means of a 2 × 4 ANOVA with condition (narrow- or tall-box) as a between-subjects factor and trial (first, second, third, or fourth) as a within-subject factor. The analysis revealed a significant main effect of trial, F(3, 90) = 19.78, p < .0001, indicating that the infants looked reliably less across trials. The main effect of condition was not significant, F(1, 30) = 0.00, nor was the condition × trial interaction, F(3, 90) = 0.09, suggesting that the infants in the narrow-box (M = 36.7, SD = 20.0) and tall-box (M = 36.7, SD = 21.0) conditions did not differ reliably in their responses to the cylinder-familiarization event.
3.2.3. Test trials
The infants’ looking times during the four test trials (see Fig. 3) were compared to those of the infants in the narrow-box condition of Experiment 1 by means of a 2 ×2 ×2 ANOVA with condition (narrow- or tall-box) as a between-subjects factor and with pair (first or second) and event (wide- or narrow-/tall-box) as within-subject factors. The analysis yielded significant main effects of pair, F(1, 90) = 21.32, p < .0001, and event, F(1, 90) = 21.76, p < .0001, as well as a significant interaction between pair and event, F(1, 90) = 6.37, p < .025. The interaction among condition, pair, and event was not significant, F(1, 90) = 0.80, suggesting that the infants in the two conditions tended to respond similarly during the two pairs of test trials. Planned comparisons indicated that during the first test pair, the infants tended to look equally at the wide-box (M = 43.8, SD = 16.3) and narrow-/tall-box (M = 38.4, SD = 18.5) events, F(1, 90) = 2.29, p > .10; during the second test pair, however, the infants looked reliably longer at the wide-box (M = 38.6, SD = 18.0) than at the narrow-/tall-box (M = 20.5, SD = 14.8) event, F(1, 90) = 25.83, p < .0001. Further comparisons revealed that this looking pattern held for each condition examined separately (narrow-box condition: first test pair, wide-box, M = 41.1, SD = 19.8, narrow-box, M = 37.1, SD = 16.1, F(1, 90) = 0.62; second test pair, wide-box, M = 40.4, SD = 17.5, narrow-box, M = 19.2, SD = 13.8, F(1, 90) = 17.74, p < .0001. Tall-box condition: first test pair, wide-box, M = 46.6, SD = 12.0, tall-box, M = 39.8, SD = 21.1, F(1, 90) = 1.82, p > .10; second test pair, wide-box, M = 36.7, SD = 18.8, tall-box, M = 21.8, SD = 16.2, F(1, 90) = 8.86, p < .005).
A final set of comparisons across the two pairs of test trials revealed that (1) there was no reliable difference in the looking times of the infants in the two conditions at the wide-box event on the first (M = 43.8, SD = 16.3) and second (M = 38.6, SD = 18.0) test pairs, F(1, 90) = 2.19, p > .10; and (2) there was a reliable difference in the looking times of the infants in the two conditions at the narrow-/tall-box event on the two test pairs: the infants looked reliably less on the second (M = 20.5, SD = 14.8) than on the first (M = 38.4, SD = 18.5) test pair, F(1, 90) = 25.49, p < .0001.
3.3. Discussion
The infants in Experiment 2 responded in the same manner as those in the narrow-box condition of Experiment 1. On the first test pair, the infants responded with equal and prolonged attention to the wide- and tall-box events, suggesting that they expected both boxes to move when hit and were surprised when they did not. On the second test pair, the infants continued to respond with prolonged attention to the wide- but not the tall-box event. This last result suggested that the infants concluded, upon seeing that the tall box did not move when hit, that it must be one of those immovable pillars. Because the infants could generate an explanation for the tall-box event, they were no longer surprised by it, and ceased responding to it with prolonged attention; they thus looked reliably less at the tall-box event on the second than on the first test pair.
The results of Experiment 2 thus provided further support for the conclusions of Experiment 1. At 8 months of age, two different expectations appear to contribute to infants’ responses to collision events: a causal expectation that objects—regardless of their sizes—should move when forces are applied to them; and a statistical expectation that some objects with a salient vertical dimension are attached to their adjacent surfaces and hence remain stationary when forces are applied to them. Infants use the causal expectation to predict whether an object should move when hit, and the statistical expectation to make sense, post hoc, of some outcomes that violate their predictions. Consistent with this analysis, the infants in Experiments 1 and 2 expected the wide, tall, square, and narrow boxes to all move when hit by the cylinder; and they readily inferred, upon seeing that the tall and narrow boxes did not move when hit, that they must belong to that special class of immovable vertical objects or pillars.
Experiment 3 began to examine how infants’ expectations about collision events develop with age. In this experiment, 9-month-old infants were tested in the square-, narrow-, and tall-box conditions used in Experiments 1 and 2.
4. Experiment 3
4.1. Method
4.1.1. Participants
Participants were 48 healthy term infants, 23 males and 25 females, ranging in age from 8 months, 20 days to 9 months, 26 days (M = 9 months, 5 days). An additional five infants were tested but eliminated, three because they were fussy (2) or inattentive (1), and two because they looked for the maximum amount of time allowed (60 s) on all four test trials. Sixteen infants were randomly assigned to the square-box (M = 9 months, 5 days), narrow-box (M = 9 months, 3 days), and tall-box (M = 9 months, 7 days) conditions.
4.1.2. Apparatus, events, and procedure
The apparatus, events, and procedure used in Experiment 3 were identical to those in Experiments 1 and 2. Interobserver agreement was measured for all 48 infants and averaged 93% per trial per infant. Half of the infants in the narrow- and tall-box conditions saw the wide box first in the box-familiarization and test trials, and half saw the narrow or tall box first. In the square-box condition, seven infants saw the wide box first, and nine infants saw the square box first.
4.2. Results
4.2.1. Box-familiarization trials
The infants’ looking times during the two box-familiarization trials were analyzed by means of a 3 × 2 ANOVA with condition (square-, narrow-, or tall-box) as a between-subjects factor and display (wide- or square-/narrow-/tall-box) as a within-subject factor. The main effect of display was not significant, F(1, 45) = 1.26, p > .10, nor was the condition × display interaction, F(2, 45) = 0.34, suggesting that the infants in the three conditions tended to look equally at the displays they were shown (square-box condition: wide-box, M = 8.1, SD = 3.2, square-box, M = 9.3, SD = 6.1; narrow-box condition: wide-box, M = 10.1, SD = 6.5, narrow-box, M = 10.1, SD = 5.2; tall-box condition: wide-box, M = 8.8, SD = 6.2, tall-box, M = 10.5, SD = 7.0).
4.2.2. Cylinder-familiarization trials
The infants’ looking times during the four cylinder-familiarization trials were compared by means of a 3 × 4 ANOVA with condition (square-, narrow-, or tall-box) as a between-subjects factor and trial (first, second, third, or fourth) as a within-subject factor. The analysis revealed a significant main effect of trial, F(3, 135) = 23.32, p < .0001, indicating that the infants looked reliably less across trials. The main effect of condition was not significant, F(2, 45) = 0.86, nor was the condition × trial interaction, F(6, 135) = 0.94, suggesting that the infants in the square-box (M = 32.4, SD = 19.0), narrow-box (M = 31.4, SD = 20.2), and tall-box (M = 36.1, SD = 20.7) conditions did not differ reliably in their responses to the cylinder-familiarization event.
4.2.3. Test trials
The infants’ looking times during the four test trials (see Fig. 5) were analyzed by means of a 3 ×2 ×2 ANOVA with condition (square-, narrow-, or tall-box) as a between-subjects factor and with pair (first or second) and event (wide- or square-/narrow-/tall-box) as within-subject factors. The analysis revealed a significant main effect of pair, F(1, 135) = 18.00, p < .0001, indicating that the infants looked reliably less as the experiment progressed, and a significant main effect of event, F(1, 135) = 14.11, p < .0005. Planned comparisons indicated that (1) the infants in the square-box condition looked reliably longer at the square-box (M = 45.0, SD = 17.6) than at the wide-box (M = 31.4, SD = 16.1) event, F(1, 135) = 12.29, p < .001; (2) the infants in the narrow-box condition tended to look equally at the narrow-box (M = 31.2, SD = 20.8) and wide-box (M = 30.2, SD = 17.9) events, F(1, 135) = 0.07; and (3) the infants in the tall-box condition looked reliably longer at the tall-box (M = 43.4, SD = 16.2) than at the wide-box (M = 32.8, SD = 20.5) event, F(1, 135) = 7.46, p < .01.
Fig. 5.
Mean looking times of the 9-month-old infants in Experiment 3 at the test events.
The ANOVA also yielded a significant condition × pair interaction, F(2, 135) = 5.04, p < .01. Because this interaction did not involve event, it does not bear on the present hypotheses and will not be discussed further.
4.2.4. Additional analyses
The results of Experiment 3 differed markedly from those of Experiments 1 and 2, suggesting that developments already take place between 8 and 9 months of age in infants’ responses to collision events. At least three changes were evident.
First, unlike the 8-month-old infants in Experiments 1 and 2, the 9-month-old infants in Experiment 3 did not expect the wide box to move when hit by the cylinder. The infants looked reliably less at the event involving the wide box (M = 31.5, SD = 18.1) than at the event involving the square, narrow, or tall box (M = 39.9, SD = 19.1) both overall, as indicated by the significant main effect of event in the ANOVA, as well as on each test pair examined alone (first test pair: wide-box, M = 36.6, SD = 16.5, square-/narrow-/tall-box, M = 44.3, SD = 18.1, F(1, 135) = 5.86, p < .025; second test pair: wide-box, M = 26.3, SD = 18.3, square-/narrow-/tall-box, M = 35.5, SD = 19.3, F(1, 135) = 8.35, p < .005). These results suggested that, at 9 months of age, infants have begun to consider size information when predicting whether a stationary object is likely to be displaced when hit. Like the adults tested in Experiments 1 and 2, the 9-month-old infants in Experiment 3 expected the wide box to remain stationary when hit by the cylinder.
Second, the infants in Experiment 3 expected not only the square box but also the tall box to move when hit, and on both test pairs. There was no reliable difference overall in the infants’ responses to the square (M = 45.0, SD = 17.6) and tall (M = 43.4, SD = 16.2) boxes, F(1, 135) = 0.17. Furthermore, no differences were found in the infants’ responses to these boxes when each test pair was examined alone (first test pair: square-box, M = 46.4, SD = 17.2, tall-box, M = 48.9, SD = 14.6, F(1, 135) = 0.19; second test pair: square-box, M = 43.6, SD = 18.4, tall-box, M = 38.0, SD = 16.4, F(1, 135) = 1.03, p > .10). Why did the 8-month-old infants in Experiment 2, but not the 9-month-old infants in Experiment 3, conclude that the tall box must be one of those attached vertical objects that remain stationary when acted upon? One possibility was that, between 8 and 9 months of age, infants begin to refine their expectations about vertical objects: whereas 8-month-old infants would view any vertical object (such as the narrow or the tall box) as a potential pillar, 9-month-old infants would view only slender or narrow vertical objects (such as the narrow box) as potential pillars.
Finally, the third difference between the results of Experiments 1 and 3 involved the narrow box. In Experiment 1, the interaction between pair and event in the narrow-box condition was significant, F(1, 90) = 6.13, p < .025; the 8-month-old infants tended to look equally at the wide- and narrow-box events on the first test pair, but looked reliably less at the narrow-than at the wide-box event on the second test pair. In Experiment 3, the corresponding interaction was not significant, F(1, 135) = 3.25, p > .05; the 9-month-old infants tended to look equally at the wide- and narrow-box events on both the first (F(1, 135) = 1.18, p > .10), and second (F(1, 135) = 2.15, p > .10) test pairs (first test pair: wide-box M = 43.5, SD = 13.7, narrow-box M = 37.5, SD = 21.1; second test pair: wide-box M = 16.9, SD = 9.8, narrow-box M = 25.0, SD = 19.1). Our interpretation of these results was that, like the 8-month-old infants in Experiment 1, the 9-month-old infants in Experiment 2 (1) expected the narrow box to move when hit by the cylinder, and (2) inferred, upon seeing that the narrow box remained stationary, that it must be one of those immovable vertical objects or pillars. The only difference between the 8- and 9-month-old infants, on this interpretation, was that the older infants were faster at generating an explanation for the narrow-box event than were the younger infants. By the end of the first test pair, the infants’ responses to the wide- and narrow-box events were already similar: the infants expected the wide box to remain stationary because of its size, and they expected the narrow box to remain stationary because their observations during the experiment suggested that it constituted an immovable pillar.
The preceding speculations led to the following prediction: if we were to examine the looking times of the infants in the narrow-box condition on the first test trial only, we might observe a different response pattern than that found when the data from the first test pair, or from both test pairs, were analyzed. In particular, evidence that the infants who saw the narrow-box event on their first test trial looked reliably longer than those who saw the wide-box event, would support the notion that the infants initially expected the narrow box to move and were surprised when it did not, but that this surprise rapidly dissipated as the infants generated the explanation that the narrow box must be an immovable pillar.
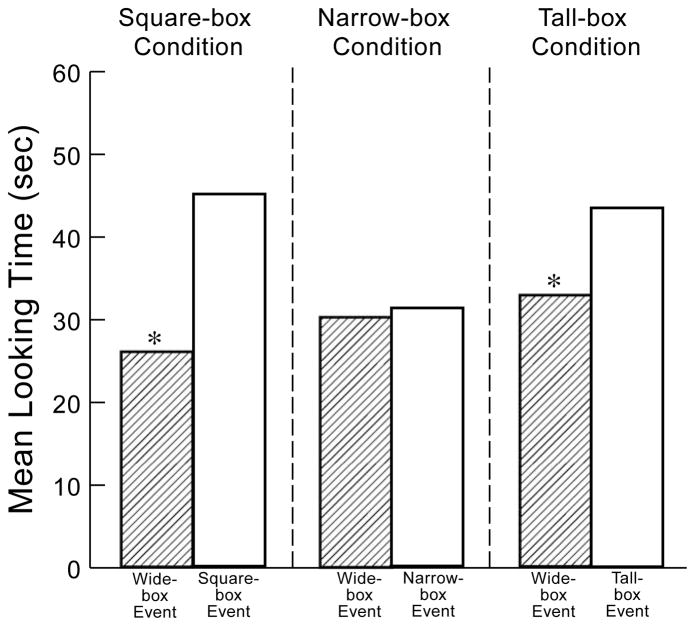
To test this prediction, the looking times of the infants in the square-, narrow-, and tall-box conditions of Experiment 3 on their first test trials (see Fig. 6) were compared by means of a 3×2 ANOVA with condition (square-, narrow-, or tall-box) and event (wide- or square-/narrow-/tall-box event) as between-subjects factors. The only significant effect was that of event, F(1, 42) = 24.00, p < .0001, suggesting that the infants who saw the square-/narrow-/tall-box (M = 52.9, SD = 12.6) event on their first test trial looked reliably longer than those who saw the wide-box (M = 34.3, SD = 14.0) event. Additional comparisons confirmed that this pattern was reliable in each condition (square-box condition: square-box, M = 52.6, SD = 14.0, wide-box, M = 28.3, SD = 12.4, F(1, 42) = 13.16, p < .001; narrow-box condition: narrow-box, M = 55.5, SD = 11.1, wide-box, M = 40.7, SD = 13.1, F(1, 42) = 4.94, p < .05; tall-box condition: tall-box, M = 50.6, SD = 13.8, wide-box, M = 33.1, SD = 15.0), F(1, 42) = 6.91, p < .025).
Fig. 6.
Mean looking times of the 9-month-old infants in Experiment 3 at the test events on the first test trial.
4.3. Discussion
Comparison of the results obtained with the 8-month-old infants in Experiments 1 and 2 and with the 9-month-old infants in Experiment 3 pointed to several significant similarities and differences. With respect to the similarities, the infants at both ages expected the square and narrow boxes to move when hit by the cylinder and were surprised when they did not. Furthermore, upon noticing that the narrow box did not in fact move when hit, the infants at both ages generated an explanation for this outcome: they appealed to the statistical regularity that some vertical objects are attached to their adjacent surfaces. Thus, at both ages, infants brought to bear causal and statistical expectations in their responses to the collision events they were shown.
However, the 9-month-old infants were more sophisticated than the 8-month-old infants in at least three aspects of their reasoning. First, the infants no longer expected the wide box to move when hit. This result suggested that, by 9 months of age, infants have identified a new collision variable. What could be this new variable be? The fact that the infants expected the wide but not the tall box to remain stationary when hit, even though the two boxes were identical in size, suggested two possibilities. One was that, at 9 months of age, infants focus on one particular size dimension, width, and expect very wide objects (such as the wide box), but not narrower objects (such as the narrow, square, and tall boxes), to remain stationary when hit. Another possibility was that, at 9 months of age, infants consider both size and stability information when predicting whether an object is likely to move when hit. On this interpretation, the infants in Experiment 3, like the adults tested in Experiment 2, realized that the tall box was less stable than the wide box and hence was more likely to wobble or fall when hit by the cylinder. Additional research is needed to determine which of these two possibilities is correct. For the present, we overlook these ambiguities and simply conclude that, by 9 months of age, infants have begun to attend to size information when predicting whether an object should move or remain stationary when hit.
Second, the 9-month-old infants in Experiment 3 were faster than the 8-month-old infants in Experiment 1 at coming to the conclusion that the narrow box must be one of those attached vertical objects that remain stationary when forces are applied to them. The 8-month-old infants in Experiment 1 responded with prolonged attention to the narrow-box event on the first but not the second test pair; by contrast, the 9-month-old infants in Experiment 3 responded to the narrow-box event with prolonged attention on their first test trial only. It does not seem very surprising that older infants should be faster than younger infants at generating explanations for events; one would expect much the same difference between younger and older children, or between children and adults (e.g., Bullock, Gelman, & Baillargeon, 1982; Chandler & Lalonde, 1994; Gelman & Baillargeon, 1983).
Finally, although both the 9-month-old infants in Experiment 3 and the 8-month-old infants in Experiment 2 initially expected the tall box to move when hit, only the 8-month-old infants concluded that the tall box must be one of those immovable pillars (recall that the 8-month-old infants in Experiment 2 responded to the tall-box event with prolonged attention on the first but not the second test pair; in contrast, the 9-month-old infants in Experiment 3 did so on both test pairs). Why did the 9-month-old infants in Experiment 3 view the narrow box, but not the tall box, as a potential pillar? As mentioned earlier, one possible explanation was that, between 8 and 9 months of age, infants’ statistical expectations about vertical objects become more refined. Thus, whereas at 8 months infants would accept any vertical object as a potential pillar, at 9 months infants would accept only slender or narrow vertical objects as pillars—that is, only objects resembling fairly closely the legs of tables, the slats of cribs, the posts of banisters, and so on. At this stage, wider vertical objects such as the tall box would no longer be considered possible pillars.
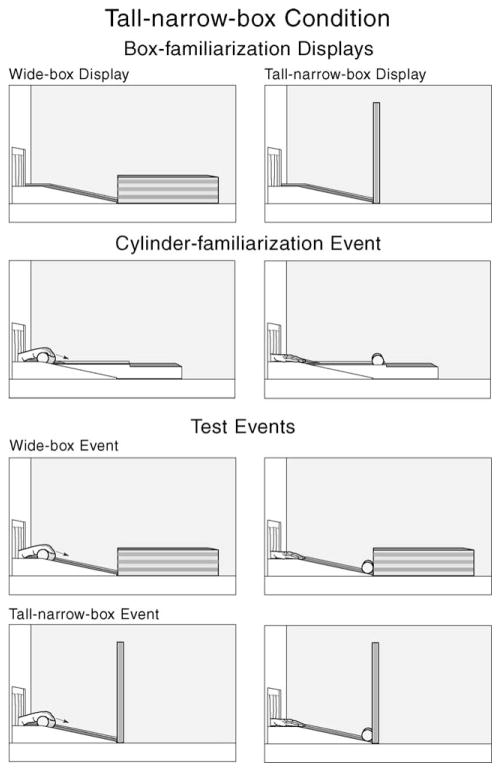
This last speculation led to the following prediction: 9-month-old infants tested with a tall narrow box should respond to this box in the same manner as the 9-month-old infants in Experiment 3 responded to the narrow box. Experiment 4 was designed to test this prediction (see Fig. 7). On alternate test trials, the infants saw the wide-box event and a tall-narrow-box event. This tall narrow box was as wide (3.25 cm) and as deep (15.5 cm) as the narrow box, but much taller (52 cm); it was in fact as tall as the tall box.
Fig. 7.
Schematic drawing of the box-familiarization displays, cylinder-familiarization event, and test events shown in the tall-narrow-box condition of Experiment 4.
We predicted that, like the infants in the narrow-box condition of Experiment 3, the infants in Experiment 4 would look about equally at the tall-narrow- and wide-box events overall, but would look reliably longer at the tall-narrow- than at the wide-box event on their first test trial, before they arrived at an explanation for why the tall narrow box did not move when hit.
5. Experiment 4
5.1. Method
5.1.1. Participants
Participants were 16 healthy term infants, 7 males and 9 females, ranging in age from 8 months, 23 days to 9 months, 26 days (M = 9 months, 12 days).
5.1.2. Apparatus, events, and procedure
The apparatus, events, and procedure used in Experiment 4 were identical to those in the narrow-box condition of Experiment 3, except that the narrow box used in the box-familiarization and test trials was replaced with a box that was similar to the narrow box in width (3.25 cm) and depth (15.5 cm) but was much taller: it was 52 cm instead of 13 cm tall. To make sure that this tall narrow box did not move when hit, it was mounted on the posts in the apparatus floor and also had heavy weights attached to its back wall (out of sight). Interobserver agreement was measured for all 16 infants and averaged 93% per trial per infant.
5.1.3. Adult ratings
Would adults perceive the tall narrow box as likely or as unlikely to move when hit? To find out, 15 undergraduate students, 7 males and 8 females (M = 18.8 years) were tested using the same procedure as in the narrow-box condition of the adult experiment reported in Experiment 1, except that the narrow box was replaced with the tall narrow box. The adults thus saw the wide and the tall narrow box on alternate display and test trials.
The ratings obtained in the display trials were analyzed by means of a one-way ANOVA with display (wide- or tall-narrow-box) as a within-subject factor. The main effect of display was significant, F(1, 28) = 32.09, p < .0001, indicating that the adults believed that the tall narrow box (M = 4.4, SD = 1.4) was more likely than the wide box (M = 1.7, SD = 1.2) to move when hit. A parallel analysis of the ratings obtained in the test trials again yielded a significant main effect of event, F(1, 28) = 61.93, p < .0001, indicating that the adults were more surprised when the tall-narrow-box (M = 3.8, SD = 1.3) than when the wide box (M = 1.1, SD = 0.3) failed to move when hit.
The adults thus expected the tall narrow box to move when hit and were surprised when it did not. In their responses, the adults apparently took into account both the size and the stability of the tall narrow box. Many adults spontaneously commented that the tall narrow box was smaller than the wide box, and less stable, so that it should be easier to move. Upon observing that the tall narrow box did not in fact move when hit, several adults suggested that it must be fastened to the apparatus floor, or more generally that something must be preventing the cylinder from knocking it down.
We predicted that, like the adults, the 9-month-old infants in Experiment 4 would expect the tall narrow box but not the wide box to move when hit, and hence would look reliably longer at the tall-narrow-box than at the wide-box event on the first test trial. Thereafter, the infants would conclude that the tall narrow box must be one of those slender vertical objects that are attached to their adjacent surfaces, and their surprise at the tall-narrow-box test would dissipate, resulting in equal looking times overall at the tall-narrow- and wide-box events.
5.2. Results
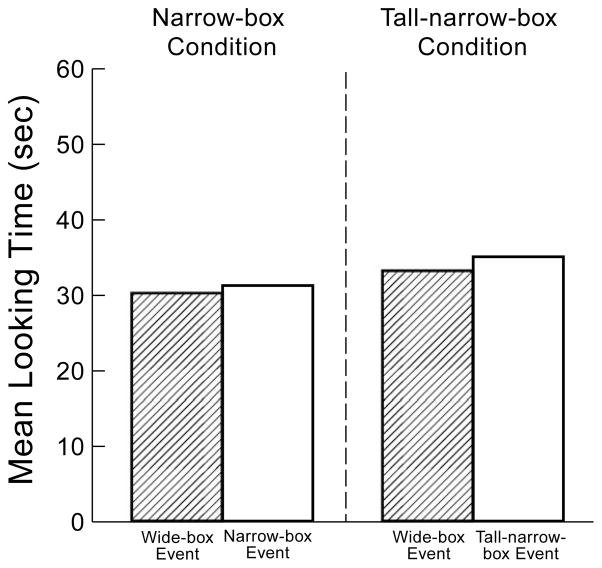
Because the results of Experiment 4 were expected to mirror those of the narrow-box condition in Experiment 3, the results obtained with these two groups of infants were directly compared in the analyses of the familiarization and test trials.
5.2.1. Box-familiarization trials
The infants’ looking times during the two box-familiarization trials were compared to those of the infants in the narrow-box condition of Experiment 3 by means of a 2 × 2 ANOVA with condition (narrow- or tall-narrow-box) as a between-subjects factor and display (wide-or narrow-/tall-narrow-box) as a within-subject factor. The main effect of display was not significant, F(1, 30) = 0.45, nor was the condition × display interaction, F(1, 30) = 0.46, suggesting that the infants in the two conditions did not differ reliably in their pattern of response to the wide- and narrow- or tall-narrow-box displays (narrow-box condition: wide-box, M = 10.1, SD = 6.5, narrow-box, M = 10.1, SD = 5.2; tall-narrow-box condition: wide-box, M = 6.3, SD = 3.1, tall-narrow-box, M = 7.5, SD = 4.0).
The ANOVA also yielded a significant main effect of condition, F(1, 30) = 4.66, p < .05, suggesting that the infants in the narrow-box condition (M = 10.1, SD = 5.8) looked reliably longer overall during the familiarization trials than did those in the tall-narrow-box condition (M = 6.9, SD = 3.6). This effect most likely reflected simple sampling variation; because it did not interact with display, it does not bear on the present hypotheses and will not be discussed further.
5.2.2. Cylinder-familiarization trials
The infants’ looking times during the four cylinder-familiarization trials were compared by means of a 2 × 4 ANOVA with condition (narrow- or tall-narrow-box) as a between-subjects factor and trial (first, second, third, or fourth) as a within-subject factor. The analysis yielded a significant main effect of trial, F(3, 90) = 21.39, p < .0001, indicating that the infants looked reliably less across trials. The main effect of condition was not significant, F(1, 30) = 0.00, nor was the condition × trial interaction, F(3, 90) = 0.71, suggesting that the infants in the narrow-box (M = 31.4, SD = 20.2) and tall-narrow-box (M = 31.3, SD = 17.5) conditions did not differ reliably in their responses to the cylinder-familiarization event.
5.2.3. Test trials
The infants’ looking times during the four test trials (see Fig. 8) were compared to those of the infants in the narrow-box condition of Experiment 3 by means of a 2 × 2 × 2 ANOVA with condition (narrow- or tall-narrow-box) as a between-subjects factor and with pair (first or second) and event (wide- or narrow-/tall-narrow-box) as within-subject factors. The only significant effect was that of pair, F(1, 90) = 29.40, p < .0001, indicating that the infants looked reliably less as the experiment progressed. The main effect of event was not significant, F(1, 90) = 0.28, nor was the condition×event interaction, F(1, 90) = 0.02, or the condition× pair×event interaction, F(1, 90) = 2.41, p > .10. The infants in the two conditions thus tended to look equally at the wide- and narrow- or tall-narrow-box events (narrow-box condition: wide-box, M = 30.2, SD = 17.9, narrow-box, M = 31.2, SD = 20.8, F(1, 90) = 0.07; tall-narrow-box condition: wide-box, M = 33.2, SD = 19.3, tall-narrow-box, M = 35.0, SD = 18.3, F(1, 90) = 0.23).
Fig. 8.
Mean looking times of the 9-month-old infants in the narrow-box condition of Experiment 3 and the tall-narrow-box condition of Experiment 4 at the test events.
5.2.4. Additional analyses
Our interpretation of the results of Experiment 3 was that the infants expected all but the wide box to move when hit. Upon seeing that the narrow box did not in fact move, however, the infants concluded that it must be one of those immovable pillars. Because the infants came to this conclusion very quickly, they showed surprise at the narrow-box event only briefly, during the first test trial. In a final analysis, we compared the looking times on the first test trial of the infants in Experiments 3 and 4 (see Fig. 9). The four conditions in these experiments were formed into two groups: those involving a box that was both vertical and narrow (VAN; narrow-and tall-narrow-box conditions), and those that was not (non-vertical-and-narrow (NVAN); square- and tall-box conditions). The infants’ looking times were compared by means of a 2×2 ANOVA with condition (VAN or NVAN) and event (wide- or other-box) as between-subjects factors. The only significant effect was that of event, F(1, 60) = 17.85, p < .0001, indicating that the infants looked reliably longer at the other-box (M = 51.3, SD = 13.7) than at the wide-box (M = 35.5, SD = 16.5) event. Planned comparisons confirmed that the infants in the each condition showed the same pattern (VAN condition: other-box, M = 50.9, SD = 14.4, wide-box, M = 39.9, SD = 18.1, F(1, 60) = 4.25, p < .05; NVAN condition: other-box, M = 51.7, SD = 13.5, wide-box, M = 30.9, SD = 13.6, F(1, 60) = 15.30, p < .0005).
Fig. 9.
Mean looking times of the 9-month-old infants in the vertical-and-narrow (VAN) and non-vertical-and-narrow (NVAN) conditions at the test events on the first test trial.
5.3. Discussion
The infants in Experiment 4 responded in the same manner as the infants in the narrow-box condition of Experiment 3: they looked reliably longer at the tall-narrow-box than at the wide-box event on the first test trial, but tended to look equally at the two events overall, across the first and second pairs. These responses differed from those of the infants in the tall-box condition of Experiment 3, who looked reliably longer at the tall- than at the wide-box event not only on the first test trial but also overall, on the first and second test pairs.
These results provided support for the conclusions of Experiment 3. By 9 months of age, infants’ causal and statistical expectations have both undergone developments. First, infants now consider size information when predicting whether a stationary object is likely to move when hit. The infants in Experiments 3 and 4, like the adults we tested, but unlike the 8-month-old infants in Experiments 1 and 2, did not expect the wide box to move when hit, from the first test trial. Second, infants have refined their statistical expectations about vertical objects: they now recognize that some objects that are both vertical and narrow—such as the legs of tables, the slats of cribs, or the posts of banisters—are attached to their adjacent surfaces, and are unlikely to move when acted upon. The infants in Experiments 3 and 4 initially expected the narrow and tall narrow boxes to move when hit; upon observing that the boxes did not move, however, the infants came to the conclusion that these boxes must be immovable pillars, and their surprise at these events rapidly dissipated. The infants in Experiment 3 also expected the tall box to move when hit, but their surprise at this event did not dissipate: the infants looked reliably longer at the tall- than at the wide-box event throughout the test trials. The 9-month-old infants in the present research thus perceived the narrow and tall narrow boxes, but not the tall box, as potential pillars.
6. General discussion
The present research suggests that two main developments take place between 8 and 9 months of age in infants’ responses to collision events. The first development involves infants’ knowledge of the variables relevant to collision outcomes; the second development involves infants’ knowledge of what objects in the environment are likely to be attached to adjacent surfaces and hence to remain stationary when acted upon. We discuss each of these developments in turn.
6.1. Identifying a new collision variable
Prior research has brought to light the following developmental sequence in infants’ knowledge about collision events in which a moving object approaches and hits a stationary object (for reviews, see Baillargeon, 1995, 1998). By 2.5 months of age, infants have identified a simple impact/no-impact variable: they expect the stationary object to be displaced when hit and to remain stationary when not hit (e.g., Baillargeon, 1995; Kotovsky & Baillargeon, 1994, 2000). By 5.5–6.5 months of age, infants have identified a further collision variable: they now attend to the size of the moving object, and expect the stationary object to be displaced farther when hit by a larger as opposed to a smaller moving object (e.g., Kotovsky & Baillargeon, 1994, 1998). The present research built on these findings and asked at what age infants begin to take into account the size of the stationary object to predict whether it should be displaced when hit. Infants aged 8 and 9 months saw a cylinder rolling down a ramp and hitting a narrow, square, wide, or tall box; all of the boxes remained stationary when hit.
The results suggested that at 8 months of age infants do not yet take into account the size of a stationary object to predict whether it should move when hit. The 8-month-old infants in Experiments 1 and 2 expected all of the boxes to move when hit by the cylinder. At this stage, infants apparently still use only an impact/no-impact variable or rule and expect all objects to be displaced when hit, irrespective of their sizes. Thus, even though the cylinder was 5.9 cm in diameter and the wide box 13 cm tall and 52 cm wide, the infants expected the cylinder to displace the box and were surprised when it did not. This last finding adds to a growing body of experimental evidence that infants with limited physical knowledge may regard possible and even commonplace events (such as a very wide box remaining stationary when hit by a small cylinder) as unexpected or surprising, when these events happen to contradict their faulty knowledge (e.g., Luo & Baillargeon, 2003; Wang, 2003b). Like some of young children’s speech errors (e.g., “he goed,” “she eated”; e.g., Marcus et al., 1992), infants’ errors when responding to possible events provide strong support for the acquisition of abstract generalizations or rules (for further discussion, see Luo & Baillargeon, 2003).
By 9 months of age, infants have begun to consider the size of a stationary object when predicting whether it should move when hit. Unlike the 8-month-old infants in Experiments 1 and 2, the 9-month-old infants in Experiments 3 and 4 expected the wide box to remain stationary when hit by the cylinder, even in their initial test trial. As was mentioned earlier, the present findings are not sufficient to specify exactly what size information 9-month-old infants attend to. On the one hand, infants might focus on the width of stationary objects, and expect very wide objects (such as the wide box), but not narrower objects (such as the narrow, tall narrow, square, and tall boxes), to remain stationary when hit. On the other hand, infants might attend to both the overall size and the stability of stationary objects, and expect large, stable objects (such as the wide box), but not smaller objects (such as the narrow, square, or tall narrow box), or less stable objects (such as the tall box), to remain stationary when hit. One way to decide between these two possibilities might be to test infants with collision events involving very wide but short objects (e.g., the tall narrow box in a horizontal orientation). Evidence that 9-month-old infants expect these very wide but short (hence small but stable) objects to move when hit would support the second of the two possibilities listed above.
Whichever possibility turns out to be correct, one might ask what experiences lead 9-month-old infants to begin to attend to the size of stationary objects to predict whether they are likely to be displaced when hit. In Section 1, we described a recent account of the process by which infants might identify a new variable in an event category (e.g., Baillargeon, 2002; Wang et al., in press). According to this account, infants notice contrastive outcomes for the variable, search for the conditions that map onto these outcomes, and then build a causal explanation for these new condition-outcome data, using their prior knowledge. In light of this account, how might infants go about identifying the size of the stationary object as a collision variable?
By 9 months of age, infants typically are able to crawl, which allows them to explore new facets of their environment (e.g., Bertenthal & Campos, 1990). Few caretakers would ever give a young infant a large and heavy object to play with; hence, until they begin to crawl and can explore the world on their own, infants generally have few opportunities to act on such objects. With crawling, however, such opportunities soon arise. Many parents will remember their crawling infants dragging pots and pans from cupboards or books from shelves. As a result of such experiences, infants could come to notice that larger objects (e.g., large pots or books, buckets filled with toys, or briefcases) are generally more difficult to displace than are smaller objects (e.g., smaller pots or books, cups, spoons, shoes, or rattles). To make sense of these condition-outcome data, infants might once again build an explanation involving their notion of force (e.g., Leslie, 1995; Leslie & Keeble, 1987). That is, just as 5.5- to 6.5-month-old infants may recognize that larger moving objects can exert more force than smaller moving objects on stationary objects, thus causing greater displacements (e.g., Kotovsky & Baillargeon, 1998), 9-month-old infants may recognize that larger stationary objects can withstand more force than smaller stationary objects from moving objects, resulting in smaller or even no displacements. At this stage, infants would thus appreciate that larger objects can both exert and resist greater forces than can smaller objects (Leslie, 1995).
The preceding analysis not only makes clear why infants might not attend to the size of the stationary object in a collision event until about 9 months—infants have few opportunities before then to act on larger as opposed to smaller objects—but it also helps explain why infants would attend to the size of the moving object in collision events as early as 5.5–6.5 months of age (e.g., Kotovsky & Baillargeon, 1998). To learn that more force typically results in greater displacements and less force in smaller displacements, infants would not need to act on objects of contrastive sizes; they would only have to notice that the same objects, or similar objects, are displaced farther when hit with more force and less far when hit with less force. Infants could gather such condition-outcome data through their own repeated actions on objects, for example when lying on their backs and batting or kicking objects with more or less vigor. Piaget (1952) reported several observations consistent with this analysis. For example, after noticing the doll hung over her feet, Lucienne, aged 0; 5 (1) (or 5 months, 1 day), “gropes until she has felt contact between her naked foot and the doll; she then increases her movements. Same reaction at 0; 5 (7) and the days following” (p. 159). Similarly, upon noticing the wooden Pierrot hung before her, Lucienne, aged 0; 6 (2), “strikes the toy more and more vigorously, without trying to grasp it, and bursts out laughing at the Pierrot’s antics” (p. 167). Finally, Laurent, aged 0; 3 (14) notices the watch chain Piaget has attached to the rattle hanging from his bassinet hood: “he tries to grasp the chain (without looking at it), brushes it with the back of his hand, grasps it but continues to look at the rattle without moving his arms. Then he shakes the chain gently while studying the effect. Afterward he shakes it more and more vigorously. A smile and expression of delight” (p. 163).
In all of the preceding discussions, we focused on the relation between the sizes of objects and the forces they can either exert or resist. But are infants really reasoning in terms of the sizes of objects, or in terms of their weights? At what age do infants expect larger objects to be heavier? And at what age do infants expect heavier objects to exert and resist greater forces than lighter objects, irrespective of their actual sizes?
To begin to address these questions, we have undertaken a new series of experiments focusing on infants’ reasoning about collision events involving moving or stationary objects of different weights (e.g., Wang, 2001; Wang & Baillargeon, 2003). For example, in one experiment, 10-month-old infants were first given two boxes to hold, one at a time. The boxes were identical in size but differed in color: one was yellow and one red. For half of the infants (same-weight condition), the two boxes were equally light; for the other infants (different-weight condition), the yellow box was again light but the red box was much heavier (it was simply laid on the infants’ laps, as they typically could not hold it up). All of the infants first saw a familiarization event in which a medium-size cylinder rolled down a ramp and hit the yellow box, causing it to move a short distance. Next, the infants saw a test event in which the same cylinder rolled down the ramp and hit the red box, which remained stationary.
The infants in the same-weight condition looked reliably longer during the test event than did those in the different-weight condition. This result suggested two conclusions. First, the infants in the same-weight condition (1) remembered that the yellow box weighed about the same as the red one and (2) reasoned that, if the cylinder could displace the yellow box, then it should also be able to displace the red box. Second, the infants in the different-weight condition (1) remembered that the yellow box was lighter than the red box and (2) appreciated that the cylinder might be able to displace the light yellow box but not the heavy red box.
Parallel results were obtained in another experiment in which the weight of the cylinder, rather than that of the box, was manipulated. The infants were given two cylinders to hold, one at a time. The cylinders were identical in size but differed in color: one was yellow and one blue. For half of the infants, the two cylinders were equally light (same-weight condition); for the other infants, the blue cylinder was again light but the yellow cylinder was much heavier (different-weight condition). All of the infants first saw a familiarization event in which the yellow cylinder rolled down a ramp and hit a box, causing it to move a short distance. Next, the infants saw a test event in which the blue cylinder rolled down the ramp and hit the same box, which now remained stationary.
The infants in the same-weight condition looked reliably longer during the test event than did those in the different-weight condition. This result suggested two conclusions. First, the infants in the same-weight condition (1) remembered that the yellow cylinder weighed about the same as the blue one and (2) reasoned that, if the yellow cylinder could displace the box, then the blue cylinder should also be able to do so. Second, the infants in the different-weight condition (1) remembered that the yellow cylinder was heavier than the blue cylinder and (2) appreciated that the heavy yellow cylinder, but not the lighter blue cylinder, might be able to displace the box.
Consistent results were obtained in a final series of experiments in which the infants had to infer the weight of each box or cylinder from its size—they no longer felt the boxes or cylinders, but simply inspected them visually (e.g., in one experiment, the yellow cylinder was the same size as, or much larger than, the blue cylinder). The results were analogous to those of the preceding experiments: the infants in the same-size condition looked reliably longer than did those in the different-size condition.
Together, these findings suggest that 10-month-old infants attend to and remember the weights of objects, and recognize that collision events may have different outcomes depending on the weights of the moving and stationary objects involved. In particular, infants seem to expect heavier objects to both exert and resist greater forces than lighter objects. Finally, infants seem to expect larger objects to be heavier than smaller objects—though they realize that objects of the same size may have different weights and that in such cases it is the objects’ weights rather than sizes that should be considered in predicting and interpreting collision outcomes.
In future experiments, we hope to extend this research to younger infants, to find out at what age infants begin to attend to, remember, and use information about objects’ weights (as opposed to sizes) in reasoning about collision and other physical events.
6.2. Learning about potential pillars
The results of Experiments 1 and 2 suggested that by 8 months of age infants have learned that some objects with a salient vertical dimension (i.e., objects that are noticeably taller than they are wide) are attached at one or both ends to adjacent surfaces and hence do not move when acted upon. Infants cannot use this statistical expectation to predict whether a novel vertical object (such as the narrow or the tall box) is likely to move when hit. However, after observing that the object does not move when hit, infants can appeal to their knowledge of these attached vertical objects or pillars to make sense of what they have seen—to explain why the novel object did not move when a force was exerted upon it.
The results of Experiments 3 and 4 suggested that, by 9 months of age, infants have already begun to refine their expectations about what vertical objects are likely to be attached. They now view only objects that are vertical and narrow (such as the narrow and tall narrow boxes) as potential pillars.
How might infants come by their expectations about vertical objects? As was mentioned before, we suspect that infants derive these expectations from observing the effects of their own or others’ actions on immovable objects such as table legs, crib slats, railing posts, and so on. On this view, infants would first notice the salient verticality of these immovable objects, and then, with additional observation, would come to detect another feature of these objects, their narrowness.
Throughout our discussions so far, we have suggested that infants’ expectations about pillars are statistical rather than causal in nature. Are we correct in doing so? As adults, our notion of what vertical objects might be attached to adjacent surfaces is closely tied to our knowledge of support. We realize that a very narrow object, such as a piece of cardboard, would be unlikely to remain upright for any length of time without being attached to its adjacent surfaces. We would not need to see that the cardboard does not move when hit to conclude that it is attached: our knowledge of support alone would lead us to this conclusion (because an object is stable only when a line drawn through its center of gravity downwards falls within its base of support, any small movement of a thin object can shift its center of gravity outside its base of support). Furthermore, as adults, we may decide that a vertical object is likely to be attached to an adjacent surface because it provides support for that surface. The legs of tables, slats of cribs, and posts of railings all serve as supports for the horizontal surfaces above them. All of the boxes used in the present research were adequately supported (i.e., could remain in place without being attached to the apparatus floor); and none of the boxes provided support for other surfaces. Hence, none of the boxes were viewed as pillars by the adults we tested, who expected all but the wide box to move when hit. Upon seeing that the narrow, square, tall, and tall narrow boxes did not in fact move when hit, the adults could no doubt generate explanations for these surprising outcomes. As noted earlier, several adults did spontaneously comment that the boxes must be anchored to the floor, heavier that they seemed, and so on. For the adults, the idea that the boxes might be attached to the apparatus floor was thus not limited to the vertical boxes, and not related to their notion of pillar.
The infants’ notion of a pillar, by contrast, seemed more diffuse and unlikely to be related to their knowledge of support. By 8 or 9 months of age, infants have already identified several of the variables relevant for predicting under what conditions an object placed on another object is likely to remain in place or fall (for reviews, see Baillargeon, 1995, 1998, 2002). Most of these variables are concerned with the quality and quantity of contact between the two objects: whether the first object is placed on or against the second object, how much of the first object’s bottom surface rests on the second object, and so on. To our knowledge, no one has yet investigated infants’ ability to predict whether a very narrow vertical object, such as a piece of cardboard, can remain upright when placed on a horizontal surface. We hope to begin exploring this question in future experiments. The present results suggest to us that at 8 or 9 months of age infants have not yet learned to take into account such information in reasoning about objects’ support. In this respect, the fact that the 8-month-old infants in Experiment 2 viewed the tall box, which was 13 cm wide, as a pillar seems particularly telling. This finding suggests that at this age infants have gathered only statistical evidence that some vertical objects may be attached, evidence which they readily invoke to make sense of collision events in which vertical objects remain stationary when hit.
The present findings suggest many interesting questions for future research. For example, at what age do infants realize that a very narrow object is unlikely to remain upright without being attached? Do infants at some point take into account the role of vertical objects as supports for other objects to determine whether they are pillars? While infants’ notion of pillar remains primarily statistical rather than causal, what characteristic features do they consider to be relevant? For example, could a pillar be a compressible rather than a rigid vertical object? Could a pillar be a vertical object with an obvious alternative function (e.g., a box with an open top and objects such as pencils or spoons protruding from it)? Tracking the development of infants’ statistical knowledge about pillars, the development of infants’ causal knowledge about support, and how both of these contribute to their responses to collision and other events, should yield rich and detailed insights into the development of infants’ physical reasoning.
6.3. Causal and statistical expectations
In this article, we have argued that the variables infants use to reason about collision events (e.g., “size of the moving or stationary object”) are best characterized as causal expectations, acquired through a process of explanation-based learning (e.g., Baillargeon, 2002; DeJong, 1988, 1993, 1997; Wang et al., in press); and that infants’ knowledge about vertical objects is best characterized (at least initially) in terms of statistical expectations, acquired through a process of correlation-based or statistical learning. Are we right in distinguishing in this fashion between infants’ causal and statistical expectations? Is it possible that all of the expectations revealed by the present research are in fact statistical expectations?
One way to get at this question, we believe, would be to attempt to teach infants collision variables they have not yet acquired. We have already conducted a number of successful teaching experiments focusing on variables in support and covering events (e.g., Baillargeon, Fisher, & DeJong, 2000; Wang, 2003a). In each case, infants abstracted a new variable when exposed in the laboratory to observations (1) that involved appropriate contrastive outcomes; (2) that allowed infants to identify the conditions that mapped onto these outcomes; and (3) that allowed infants to build an explanation, using their prior knowledge, for these new condition-outcome data.
In the same vein, it should be possible to teach infants the collision variable “size of the stationary object” prior to 9 months of age, by exposing them in the laboratory to appropriate teaching observations. Interestingly, our explanation-based learning approach predicts that infants should readily learn the rule that larger (or heavier) objects are less likely than smaller (or lighter) objects to move when hit—but should have great difficulty learning the reverse rule that smaller (or lighter) objects are less likely than larger (or heavier) objects to move when hit. The first rule would be consistent with infants’ prior intuitions about forces, but the second would not. In the present approach, only condition-outcome data consistent with infants’ causal knowledge can become variables.
Additional evidence that infants’ collision variables are causal rather than statistical expectations could come from teaching experiments in which the sizes and weights of objects are manipulated. For example, two groups of infants could be shown that larger boxes are displaced less far than smaller boxes when hit. In this experiment, the infants would not only see but also feel the boxes. For one group of infants, weight would be proportional to size: the larger boxes would weigh more than the smaller ones. For the other infants, this would not be true: weight and size would be inversely related or unrelated. Evidence that the infants in the first but not the second group show evidence of learning would again support the notion that variables are causal rather than statistical expectations, and that infants’ causal knowledge places sharp limits on the variables they can acquire.
6.4. Concluding remarks
The present research revealed two important developments between 8 and 9 months of age in infants’ reasoning about collision events. A first development involves the variables infants have identified as relevant to these events: 9- but not 8-month-old infants take into account the size of a stationary object to predict whether it is likely to be displaced when hit by a moving object. The second development involves infants’ knowledge of what objects are likely to be attached to adjacent surfaces and hence to remain stationary when hit: whereas 8-month-old infants view any vertical object as a potential pillar, 9-month-old infants view only objects that are vertical and narrow (and hence that more closely approximate objects such as the legs of tables, slats of cribs, or posts of railings) as potential pillars. The development of infants’ knowledge about collision events is thus a complex and protracted process that weaves together many separate developments.
Acknowledgments
This research was supported by a Chiang Ching-kuo Foundation fellowship to the first author and an NICHD grant (HD-21104) to the third author. We thank Jerry DeJong, Cindy Fisher, and Wai Yip Kwok for helpful suggestions; the staff of the Infant Cognition Laboratory at the University of Illinois for their help with the data collection; and the parents and infants who generously participated in the research.
Footnotes
In the present research, the term “surprise” is used simply as a short-hand descriptor, to denote a state of heightened interest or attention induced by an expectation violation.
References
- Aguiar A, Baillargeon R. 2.5-monthold infants’ reasoning about when objects should and should not be occluded. Cognitive Psychology. 1999;39:116–157. doi: 10.1006/cogp.1999.0717. [DOI] [PubMed] [Google Scholar]
- Aguiar A, Baillargeon R. Developments in young infants’ reasoning about occluded objects. Cognitive Psychology. 2002;45:267–336. doi: 10.1016/s0010-0285(02)00005-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguiar A, Baillargeon R. Perseverative responding in a violation-of-expectation task in 6.5-month-old infants. Cognition. 2003;88:277–316. doi: 10.1016/s0010-0277(03)00044-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baillargeon R. Reasoning about the height and location of a hidden object in 4.5- and 6.5-month-old infants. Cognition. 1991;38:13–42. doi: 10.1016/0010-0277(91)90021-u. [DOI] [PubMed] [Google Scholar]
- Baillargeon R. Physical reasoning in young infants: Seeking explanations for unexpected events. British Journal of Developmental Psychology. 1994;12:9–33. [Google Scholar]
- Baillargeon R. A model of physical reasoning in infancy. In: Rovee-Collier C, Lipsitt LP, editors. Advances in infant research. Vol. 9. Norwood, NJ: Ablex; 1995. pp. 305–371. [Google Scholar]
- Baillargeon R. Infants’ understanding of the physical world. In: Sabourin M, Craik F, Robert M, editors. Advances in psychological science. Vol. 2. London, UK: Psychology Press; 1998. pp. 503–529. [Google Scholar]
- Baillargeon R. The acquisition of physical knowledge in infancy: A summary in eight lessons. In: Goswami U, editor. Handbook of childhood cognitive development. Oxford: Blackwell; 2002. pp. 47–83. [Google Scholar]
- Baillargeon R, Fisher C, DeJong GF. Teaching infants about support: What data must they see?. Paper presented at the biennial International Conference on Infant Studies; Brighton, UK. 2000. Jul, [Google Scholar]
- Baillargeon R, Needham A, DeVos J. The development of young infants’ intuitions about support. Early Development and Parenting. 1992;1:69–78. [Google Scholar]
- Baillargeon R, Wang S. Event categorization in infancy. Trends in Cognitive Sciences. 2002;6:85–93. doi: 10.1016/s1364-6613(00)01836-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertenthal BI, Campos JJ. A systems approach to the organizing effects of self-produced locomotion during infancy. In: Rovee-Collier C, Lipsitt LP, editors. Advances in infant research. Vol. 6. Norwood, NJ: Ablex; 1990. pp. 1–60. [Google Scholar]
- Bullock M, Gelman R, Baillargeon R. The development of causal reasoning. In: Friedman WJ, editor. The developmental psychology of time. New York: Academic Press; 1982. pp. 209–254. [Google Scholar]
- Casasola M, Cohen L, Chiarello E. Six-month-old infants’ categorization of containment spatial relations. Child Development. 2003;74:679–693. doi: 10.1111/1467-8624.00562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers KE, Onishi KH, Fisher C. Infants learn phonotactic regularities from brief auditory experience. Cognition. 2003;87:B69–B77. doi: 10.1016/s0010-0277(02)00233-0. [DOI] [PubMed] [Google Scholar]
- Chandler MJ, Lalonde CE. Surprising, magical, and miraculous turns of events: Children’s reactions to violations of their early theories of mind and matter. British Journal of Developmental Psychology. 1994;12:83–96. [Google Scholar]
- Dan N, Omori T, Tomiyasu Y. Development of infants’ intuitions about support relations: sensitivity to stability. Developmental Science. 2000;3:171–180. [Google Scholar]
- DeJong GF. An introduction to explanation-based learning. In: Shrobe H, editor. Exploring artificial intelligence. San Mateo, CA: Morgan Kaufman; 1988. pp. 45–81. [Google Scholar]
- DeJong GF. Investigating explanation-based learning. Boston, MA: Kluwer Academic Press; 1993. [Google Scholar]
- DeJong GF. Explanation-based learning. In: Tucker A, editor. Encyclopedia of computer science. Boca Raton, FL: CRC Press; 1997. pp. 499–520. [Google Scholar]
- Gelman R, Baillargeon R. A review of Piagetian Concepts. In: Mussen PH, Flavell JH, Markman EM, editors. Handbook of child psychology. 4. Vol. 3. New York: Wiley; 1983. pp. 167–230. [Google Scholar]
- Gómez RL, Gerken L. Artificial grammar learning by 1-year-olds leads to specific and abstract knowledge. Cognition. 1999;70:109–135. doi: 10.1016/s0010-0277(99)00003-7. [DOI] [PubMed] [Google Scholar]
- Held R, Thorn F, Gwiazda J, Bauer J. Development of binocularity and its sex differentiation. In: Vital-Durand F, Atkinson J, editors. Infant vision. The European brain and behaviour society series. Vol. 2. Cambridge, MA: MIT Press; 1996. pp. 265–274. [Google Scholar]
- Hespos SJ, Baillargeon R. Infants’ knowledge about occlusion and containment events: A surprising discrepancy. Psychological Science. 2001;12:140–147. doi: 10.1111/1467-9280.00324. [DOI] [PubMed] [Google Scholar]
- Hespos SJ, Baillargeon R. Developments in infants’ knowledge about support events: Converging evidence from action tasks. 2003. Manuscript in preparation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huettel SA, Needham A. Effects of balance relations between objects on infants’ object segregation. Developmental Science. 2000;3:415–427. [Google Scholar]
- Keil FC. The growth of causal understandings of natural kinds. In: Sperber D, Premack D, Premack AJ, editors. Causal cognition: A multidisciplinary debate. Oxford, UK: Clarendon Press; 1995. pp. 234–262. [Google Scholar]
- Kotovsky L, Baillargeon R. Calibration-based reasoning about collision events in 11-month-old infants. Cognition. 1994;51:107–129. doi: 10.1016/0010-0277(94)90012-4. [DOI] [PubMed] [Google Scholar]
- Kotovsky L, Baillargeon R. The development of calibration-based reasoning about collision events in young infants. Cognition. 1998;67:311–351. doi: 10.1016/s0010-0277(98)00036-5. [DOI] [PubMed] [Google Scholar]
- Kotovsky L, Baillargeon R. Reasoning about collision events involving inert objects in 7.5-month-old infants. Developmental Science. 2000;3:344–359. [Google Scholar]
- Leslie AM, Keeble S. Do six-month-old infants perceive causality? Cognition. 1987;25:265–288. doi: 10.1016/s0010-0277(87)80006-9. [DOI] [PubMed] [Google Scholar]
- Leslie AM. A theory of agency. In: Sperber D, Premack D, Premack AJ, editors. Causal cognition: A multidisciplinary debate. Oxford, UK: Clarendon Press; 1995. pp. 121–149. [Google Scholar]
- Luo Y. Infants’ knowledge about transparency in occlusion and containment events. Paper presented at the biennial meeting of the Society for Research in Child Development; Minneapolis, MN. 2001. Apr, [Google Scholar]
- Luo Y, Baillargeon R. When the ordinary seems unexpected: Evidence for rule-based physical reasoning in young infants. 2003. Manuscript under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus GF, Pinker S, Ullman M, Hollander M, Rosen TJ, Xu F. Overregularization in language acquisition. Monographs of the Society for Research in Child Development. 1992;57(4) (Serial No. 228) [PubMed] [Google Scholar]
- McDonough L, Choi S, Mandler JM. Understanding spatial relations: Flexible infants, lexical adults. Cognitive Psychology. 2003;46:229–259. doi: 10.1016/s0010-0285(02)00514-5. [DOI] [PubMed] [Google Scholar]
- Needham A, Ormsbee SM. The development of object segregation during the first year of life. In: Kimchi R, Behrmann M, Olson C, editors. Perceptual organization in vision: Behavioral and neural perspectives. Mahwah, NJ: Erlbaum; (in press) [Google Scholar]
- Oakes LM. The development of infants’ use of continuity cues in their perception of causality. Developmental Psychology. 1994;30:869–879. [Google Scholar]
- Oakes LM, Cohen LB. Infant causal perception. In: Rovee-Collier C, Lipsitt LP, editors. Advances in infant research. Vol. 9. Norwood, NJ: Ablex; 1995. pp. 1–54. [Google Scholar]
- Onishi KH. Infants can reason about the support of 2 but not 3 stacked boxes. Paper presented at the biennial International Conference on Infant Studies; Brighton, UK. 2000. Jul, [Google Scholar]
- Piaget J. The origins of intelligence in children. New York: International Universities Press; 1952. [Google Scholar]
- Saffran JR, Newport EL, Aslin RN. Word segmentation: The role of distributional cues. Journal of Memory and Learning. 1996;35:606–621. [Google Scholar]
- Sitskoorn SM, Smitsman AW. Infants’ perception of dynamic relations between objects: Passing through or support? Developmental Psychology. 1995;31:437–447. [Google Scholar]
- Spelke ES, Kestenbaum R, Simons DJ, Wein D. Spatiotemporal continuity, smoothness of motion, and object identity in infancy. British Journal of Developmental Psychology. 1995;13:1–30. [Google Scholar]
- Spelke ES, Phillips A, Woodward AL. Infants’ knowledge of object motion and human action. In: Sperber D, Premack D, Premack AJ, editors. Causal cognition: A multidisciplinary debate. Oxford, UK: Clarendon Press; 1995. pp. 44–78. [Google Scholar]
- Wang S. Ten-month-old infants’ reasoning about the weight of objects in collision events. Paper presented at the biennial meeting of the Society for Research in Child Development; Minneapolis, MN. 2001. Apr, [Google Scholar]
- Wang S. Under what conditions do infants learn about physical events?. Paper presented at the biennial meeting of the Society for Research in Child Development; Tampa, FL, USA. 2003a. Apr, [Google Scholar]
- Wang S. When expected seems unexpected: 7.5-month-old infants’ reasoning about support events. Paper presented at the biennial meeting of the Society for Research in Child Development; Tampa, FL, USA. 2003b. Apr, [Google Scholar]
- Wang S, Baillargeon R. Infants’ reasoning about weight information in collision events. 2003. Manuscript in preparation. [Google Scholar]
- Wang S, Baillargeon R, Paterson S. Detecting continuity and solidity violations: A new account and new evidence from covering events. Cognition. doi: 10.1016/j.cognition.2002.11.001. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox T, Chapa C. Infants’ reasoning about opaque and transparent occluders in an individuation task. Cognition. 2002;85:B1–B10. doi: 10.1016/s0010-0277(02)00055-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson RA, Keil FC. The shadows and shallows of explanation. In: Keil FC, Wilson RA, editors. Explanation and cognition. Cambridge, MA: MIT Press; 2000. pp. 87–114. [Google Scholar]
- Xu F, Carey S. Infants’ metaphysics: The case of numerical identity. Cognitive Psychology. 1996;30:111–153. doi: 10.1006/cogp.1996.0005. [DOI] [PubMed] [Google Scholar]