Abstract
Bayesian model selection or averaging objectively ranks a number of plausible, competing conceptual models based on Bayes' theorem. It implicitly performs an optimal trade-off between performance in fitting available data and minimum model complexity. The procedure requires determining Bayesian model evidence (BME), which is the likelihood of the observed data integrated over each model's parameter space. The computation of this integral is highly challenging because it is as high-dimensional as the number of model parameters. Three classes of techniques to compute BME are available, each with its own challenges and limitations: (1) Exact and fast analytical solutions are limited by strong assumptions. (2) Numerical evaluation quickly becomes unfeasible for expensive models. (3) Approximations known as information criteria (ICs) such as the AIC, BIC, or KIC (Akaike, Bayesian, or Kashyap information criterion, respectively) yield contradicting results with regard to model ranking. Our study features a theory-based intercomparison of these techniques. We further assess their accuracy in a simplistic synthetic example where for some scenarios an exact analytical solution exists. In more challenging scenarios, we use a brute-force Monte Carlo integration method as reference. We continue this analysis with a real-world application of hydrological model selection. This is a first-time benchmarking of the various methods for BME evaluation against true solutions. Results show that BME values from ICs are often heavily biased and that the choice of approximation method substantially influences the accuracy of model ranking. For reliable model selection, bias-free numerical methods should be preferred over ICs whenever computationally feasible.
Keywords: Bayesian model selection, Bayesian model evidence, information criteria
Introduction
The idea of model validation is to objectively scrutinize a model's ability to reproduce an observed data set and then to falsify the hypothesis that this model is a good representation for the system under study [Popper, 1959]. If this hypothesis cannot be rejected, the model may be considered for predictive purposes. Modelers have been encouraged for centuries to create multiple such working hypotheses instead of limiting themselves to the subjective choice of a single conceptual representation, therewith avoiding the “dangers of parental affection for a favorite theory” [Chamberlin, 1890]. These dangers include a significant underestimation of predictive uncertainty due to the neglected conceptual uncertainty (uncertainty in the choice of a most adequate representation of a system). Recognizing conceptual uncertainty as a main contribution to overall predictive uncertainty [e.g., Burnham and Anderson, 2003; Gupta et al., 2012; Clark et al., 2011; Refsgaard et al., 2006] makes model selection an “integral part of inference” [Buckland et al., 1997]. The quantification of conceptual uncertainty is of importance in a variety of scientific disciplines, e.g., in climate change modeling [Murphy et al., 2004; Najafi et al., 2011], weather forecasting [Raftery et al., 2005], hydrogeology [Rojas et al., 2008; Poeter and Anderson, 2005; Ye et al., 2010a], geostatistics [Neuman, 2003; Ye et al., 2004], vadose zone hydrology [Wöhling and Vrugt, 2008], and surface hydrology [Ajami et al., 2007; Vrugt and Robinson, 2007; Renard et al., 2010], to name only a few selected examples from the field of water resources.
Different strategies have been proposed to develop alternative conceptual models, assess their strengths and weaknesses, and to test their predictive ability. Bayesian model averaging (BMA) [Hoeting et al., 1999] is a formal statistical approach which allows comparing alternative conceptual models, testing their adequacy, combining their predictions into a more robust output estimate, and quantifying the contribution of conceptual uncertainty to the overall prediction uncertainty. The BMA approach is based on Bayes' theorem, which combines a prior belief about the adequacy of each model with its performance in reproducing a common data set. It yields model weights that represent posterior probabilities for each model to be the best one from the set of proposed alternative models. Based on the weights, it allows for a ranking and quantitative comparison of the competing models. Hence, BMA can be understood as a Bayesian hypothesis testing framework, merging the idea of classical hypothesis testing with the ability to test several alternative models against each other in a probabilistic way. The principle of parsimony or “Occam's razor” [e.g., Angluin and Smith, 1983] is implicitly followed by Bayes' theorem, such that the posterior model weights reflect a compromise between model complexity and goodness of fit (also known as the bias-variance trade-off [Geman et al., 1992]). BMA has been adopted in many different fields of research, e.g., sociology [Raftery, 1995], ecology [Link and Barker, 2006], hydrogeology [Li and Tsai, 2009], or contaminant hydrology [Troldborg et al., 2010], indicating the general need for such a systematic model selection procedure.
The drawback of BMA is, however, that it involves the evaluation of a quantity called Bayesian model evidence (BME). This integral over a model's parameter space typically cannot be computed analytically, while numerical solutions come at the price of high computational costs. Various authors have suggested and applied different approximations to the analytical BMA equations to render the procedure feasible. Neuman [2003] proposes a Maximum Likelihood Bayesian Model Averaging approach (MLBMA), which reduces computational effort by evaluating Kashyap's information criterion (KIC) for the most likely parameter set instead of integrating over the whole parameter space. This is especially compelling for high-dimensional applications (i.e., models with many parameters). If prior knowledge about the parameters is not available or vague, a further simplification leads to the Bayesian information criterion or Schwarz' information criterion (BIC) [Schwarz, 1978; Raftery, 1995]. The Akaike information criterion (AIC) [Akaike, 1973] originates from information theory and is frequently applied in the context of BMA in social research [Burnham and Anderson, 2003] for its ease of implementation. Previous studies have revealed that these information criteria (IC) differ in the resulting posterior model weights or even in the ranking of the models [Poeter and Anderson, 2005; Ye et al., ,,; Tsai and Li, 2010, 2008; Singh et al., 2010; Morales-Casique et al., 2010; Foglia et al., 2013]. This implies that they do not reflect the true Bayesian trade-off between performance and complexity, but might produce an arbitrary trade-off which is not supported by Bayesian theory and cannot provide a reliable basis for Bayesian model selection. Burnham and Anderson [2004] conclude that “… many reported studies are not appropriate as a basis for inference about which criterion should be used for model selection with real data.” The work of Lu et al. [2011] has been a first step into clarifying the so far contradictory results by comparing the KIC and the BIC against a Markov chain Monte Carlo (MCMC) reference solution for a synthetic geostatistical application.
Our study aims to advance this endeavor by rigorously assessing and comparing a more comprehensive set of nine different methods to evaluate BME. In specific, we will highlight their theoretical derivation, computational effort, and approximation accuracy. As representatives of mathematical approximations, we consider the AIC, AICc (bias-corrected AIC), and BIC in our comparison. We further include the KIC evaluated at the maximum likelihood parameter estimate (KIC@MLE) as introduced in MLBMA, and an alternative formulation that is evaluated at the maximum a posteriori parameter estimate instead (KIC@MAP). We also consider three types of Monte Carlo integration techniques (simple Monte Carlo integration, MC; MC integration with importance sampling, MC IS; MC integration with posterior sampling, MC PS) and a very recent approach called nested sampling (NS) as representatives of numerical methods. By pointing out and comparing the important features and assumptions of these mostly well-known techniques, we are able to argue which methods are truly suitable for BME evaluation, and which ones are suspected to yield inaccurate results. We then present a simplistic synthetic, linear test case where an exact analytical expression for BME exists. With this first-time benchmarking of the different BME evaluation methods against the true solution, we close a significant gap in the model selection literature.
The controlled setup in the simplistic example allows us to systematically investigate the factors which influence the value of BME and the approximation thereof by the nine featured evaluation methods. The two main factors investigated are (1) the size of the data set which determines the “seriousness” of the goodness of fit rating, and (2) the shape of the parameter prior which characterizes the robustness of a model. In a second step, we assess the performance of the different methods when confronted with low-dimensional nonlinear models. In this more challenging scenario of the synthetic example, no analytical solution to compute BME exists. We therefore generate a reference solution by brute-force MC integration, after having proven its suitability as reference solution in the linear case. In a third step, we present a real-world application of hydrological model selection. We chose this application such that the model selection task is still relatively simple and unambiguous. Even in this case the deficiencies of some of the evaluation methods become apparent. Our systematic investigation of methods to determine BME takes an important next step toward robust model selection in agreement with Bayes' theorem, heaving it up on solid ground.
We summarize the statistical framework of BMA in section 2 and discuss assets and drawbacks of the available techniques to determine BME in section 3. In section 4, we present the first-time benchmarking of the featured methods on the simplistic test case. Section 5 compares the approximation performance in a real-world hydrological model selection problem. We summarize our findings and formulate recommendations on which methods to use for reliable model selection in even more complex situations in section 6.
Bayesian Model Averaging Framework
We formulate the BMA equations according to Hoeting et al. [1999]. All probabilities and statistics are implicitly conditional on the set of considered models. While the suite of models is a subjective choice that lies in the responsibility of the modeler, it is the starting point for a systematic procedure to account for model uncertainty based on objective likelihood measures.
Let us consider Nm plausible, competing models Mk. The posterior predictive distribution of a quantity of interest given the vector of observed data
given the vector of observed data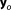 can be expressed as:
can be expressed as:
| (1) |
with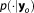 representing a conditional probability distribution and
representing a conditional probability distribution and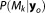 being discrete posterior model weights. The weights can be interpreted as the Bayesian probability of the individual models to be the best representation of the system from the set of considered models.
being discrete posterior model weights. The weights can be interpreted as the Bayesian probability of the individual models to be the best representation of the system from the set of considered models.
The model weights are given by Bayes' theorem:
| (2) |
with the prior probability (or rather subjective model credibility)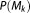 that model Mk could be the best one (the most plausible, adequate, and consistent one) in the set of models before any observed data have been considered. A “reasonable, neutral choice” [Hoeting et al., 1999] could be equally likely priors
that model Mk could be the best one (the most plausible, adequate, and consistent one) in the set of models before any observed data have been considered. A “reasonable, neutral choice” [Hoeting et al., 1999] could be equally likely priors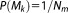 if there is little prior knowledge about the assets of the different models under consideration. The denominator in equation (2) is the normalizing constant of the posterior distribution of the models. It is easily obtained by determination of the individual weights. It could even be neglected, since all model weights are normalized by the same constant, so that the ranking of the individual models against each other is fully defined by the proportionality:
if there is little prior knowledge about the assets of the different models under consideration. The denominator in equation (2) is the normalizing constant of the posterior distribution of the models. It is easily obtained by determination of the individual weights. It could even be neglected, since all model weights are normalized by the same constant, so that the ranking of the individual models against each other is fully defined by the proportionality:
| (3) |
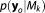 represents the BME term as introduced in section 1 and is also referred to as marginal likelihood or prior predictive because it quantifies the likelihood of the observed data based on the prior distribution of the parameters:
represents the BME term as introduced in section 1 and is also referred to as marginal likelihood or prior predictive because it quantifies the likelihood of the observed data based on the prior distribution of the parameters:
| (4) |
where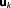 denotes the vector of parameters of model Mk with dimension equal to the number
denotes the vector of parameters of model Mk with dimension equal to the number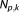 of parameters,
of parameters,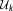 is the corresponding parameter space, and
is the corresponding parameter space, and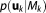 denotes their prior distribution.
denotes their prior distribution.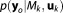 is the likelihood or probability of the parameter set
is the likelihood or probability of the parameter set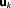 of model Mk to have generated the observed data set. The BME term can either be evaluated via integration over the full parameter space
of model Mk to have generated the observed data set. The BME term can either be evaluated via integration over the full parameter space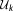 (equation (4), referred to as Bayesian integral by Kass and Raftery [1995]), or via the posterior probability distribution of the parameters
(equation (4), referred to as Bayesian integral by Kass and Raftery [1995]), or via the posterior probability distribution of the parameters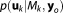 by rewriting Bayes' theorem with respect to the parameter distribution (instead of the model distribution, equation (2)):
by rewriting Bayes' theorem with respect to the parameter distribution (instead of the model distribution, equation (2)):
| (5) |
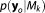 acts as a model-specific normalizing constant for the posterior of the parameters
acts as a model-specific normalizing constant for the posterior of the parameters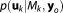 . As a matter of fact, evaluating
. As a matter of fact, evaluating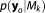 for any given model is a major nuisance in Bayesian updating, and MCMC methods have been developed with the goal to entirely avoid its evaluation. However, in order to evaluate BME, this normalizing constant has to be determined, which is the challenge addressed in the current study. Rearranging equation (5) yields the alternative formulation for equation (4):
for any given model is a major nuisance in Bayesian updating, and MCMC methods have been developed with the goal to entirely avoid its evaluation. However, in order to evaluate BME, this normalizing constant has to be determined, which is the challenge addressed in the current study. Rearranging equation (5) yields the alternative formulation for equation (4):
| (6) |
MacKay [1992] refers to the twofold evaluation of Bayes' theorem (equations (2) and (4) or (6)) as the “two levels of inference” in Bayesian model averaging: the first level is concerned with finding the posterior distribution of the models, the second level with finding the posterior distribution of each model's parameters (or rather its normalizing constant).
The integration over the full parameter space in equation (4) can be an exhaustive calculation, especially for high-dimensional parameter spaces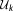 . The alternative of computing the posterior distribution of the parameters (defining the “calibrated” parameter space, equation (5)) is similarly demanding in high-dimensional applications. Analytical solutions are available only under strongly limiting assumptions. In general, mathematical approximations or numerical methods have to be drawn upon instead. We discuss and compare the nine different methods to compute BME in the following section and assess their accuracy in section 4.
. The alternative of computing the posterior distribution of the parameters (defining the “calibrated” parameter space, equation (5)) is similarly demanding in high-dimensional applications. Analytical solutions are available only under strongly limiting assumptions. In general, mathematical approximations or numerical methods have to be drawn upon instead. We discuss and compare the nine different methods to compute BME in the following section and assess their accuracy in section 4.
Available Techniques to Determine BME
We will adopt the notation of Kass and Raftery [1995] for equation (4):
| (7) |
and denote any approximation to the true BME value Ik as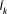 . After explaining two formulations of the analytical solution in detail in section 3.1, we examine mathematical approximations in the form of ICs in section 3.2. Finally, we discuss assets and drawbacks of selected numerical evaluation methods in section 3.3 and summarize our preliminary findings from this theoretical comparison in section 3.4. All BME evaluation methods featured in this study are listed with their underlying assumptions in Table4. All approximation methods (i.e., the nine nonanalytical approaches) follow equation (7) to evaluate BME. We do not use equation (6) here, since typically for medium to highly parameterized applications, the multivariate probability density of posterior parameter realizations cannot be estimated. Knowing the posterior parameter distribution up to its normalizing constant (as in MCMC methods, see section 3.3.3) does not suffice here since the normalizing constant is actually the targeted quantity itself.
. After explaining two formulations of the analytical solution in detail in section 3.1, we examine mathematical approximations in the form of ICs in section 3.2. Finally, we discuss assets and drawbacks of selected numerical evaluation methods in section 3.3 and summarize our preliminary findings from this theoretical comparison in section 3.4. All BME evaluation methods featured in this study are listed with their underlying assumptions in Table4. All approximation methods (i.e., the nine nonanalytical approaches) follow equation (7) to evaluate BME. We do not use equation (6) here, since typically for medium to highly parameterized applications, the multivariate probability density of posterior parameter realizations cannot be estimated. Knowing the posterior parameter distribution up to its normalizing constant (as in MCMC methods, see section 3.3.3) does not suffice here since the normalizing constant is actually the targeted quantity itself.
Table 4.
Overview of Methods to Evaluate Bayesian Model Evidence
| Evaluation method | Abbreviation | Eq. | Underlying Assumptions | Comp. Effort | Performance in Linear Test Case | Performance in Non-linear Test Cases | Recommended Use |
|---|---|---|---|---|---|---|---|
| Analytical solution | |||||||
| Theoretical distribution of BME | - | 9 | Gaussian parameter prior and likelihood, linear model | Negligible | Exact | Not available | Whenever available |
| Normalizing constant of parameter posterior | - | 6 | conjugate prior, linear model | Negligible | Exact | Not available | Whenever available |
| Mathematical approximations | |||||||
| Kashyap's information criterion, evaluated at MLE | KIC@MLE | 14 | Gaussian parameter posterior, negligible influence of prior | Medium | Relatively accurate (assumptions mildly violated) | Inaccurate | KIC@MAP to be preferred |
| Kashyap's information criterion, evaluated at MAP | KIC@MAP | 15 | Gaussian parameter posterior | Medium | Exact (assumptions fulfilled) | Inaccurate | If assumptions fulfilled/ numerical techniques too expensive |
| Bayesian information criterion | BIC | 16 | Gaussian parameter posterior, negligible influence of prior | Low | Potentially very inaccurate (depending on actual data set), ignores prior | Not recommended for BMA | |
| Akaike information criterion | AIC | 18 | (not derived as approximation to BME) | Low | Potentially very inaccurate (depending on actual data set), ignores prior | Not recommended for BMA | |
| corrected Akaike information criterion | AlCc | 19 | (not derived as approximation to BME) | Low | Potentially very inaccurate (depending on actual data set), ignores prior | Not recommended for BMA | |
| Numerical evaluation techniques | |||||||
| Simple Monte Carlo integration | MC | 23 | None | Extreme | Slow convergence, but bias-free | Whenever computationally feasible | |
| MC integration with importance sampling | MC IS | 24 | None | High | Faster convergence, but (potentially) biased | As a more efficient alternative to MC | |
| MC integration with posterior sampling | MC PS | 25 | None | High | Even faster convergence, but even more biased (due to harmonic mean approach) | Not recommended for BMA | |
| Nested sampling | NS | 26 | None | High | Slow convergence for BME (due to uncertainty in prior mass shrinkage), but bias-free | Promising alternative to MC, more research needed | |
Analytical Solution
The Bayesian integral or BME Ik for model Mk can be evaluated analytically for exponential family distributions with conjugate priors [see e.g., DeGroot, 1970]. Thus, analytical solutions for BME are available, if the observed data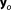 are measurements of the model parameters
are measurements of the model parameters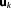 or a linear function thereof and a conjugate prior (i.e., the prior parameter distribution is in the same family as the posterior parameter distribution) exists. This is generally not the case in realistic applications. However, we will briefly outline the analytical solution to BME under these restrictive and simple conditions, before we discuss other evaluation methods that are not limited by these strong assumptions in sections 3.2 and 3.3.
or a linear function thereof and a conjugate prior (i.e., the prior parameter distribution is in the same family as the posterior parameter distribution) exists. This is generally not the case in realistic applications. However, we will briefly outline the analytical solution to BME under these restrictive and simple conditions, before we discuss other evaluation methods that are not limited by these strong assumptions in sections 3.2 and 3.3.
We will focus here on the special case of a linear model Mk with a linear model operator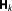 relating multi-Gaussian parameters
relating multi-Gaussian parameters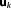 to multivariate Gaussian distributed variables
to multivariate Gaussian distributed variables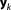 :
:
| (8) |
The prior parameter distribution is defined as a normal distribution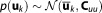 with the prior mean
with the prior mean and the covariance matrix
and the covariance matrix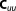 . For simplicity of notation, the index k is dropped from the notation for the parameter covariance matrix.
. For simplicity of notation, the index k is dropped from the notation for the parameter covariance matrix.
The residuals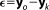 signify any type of error associated with the data set and the models, e.g., measurement errors and model errors. Here we assume the models to be perfect (free of model errors) and only measurement errors to be relevant, and adopt a Gaussian model
signify any type of error associated with the data set and the models, e.g., measurement errors and model errors. Here we assume the models to be perfect (free of model errors) and only measurement errors to be relevant, and adopt a Gaussian model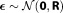 with a diagonal matrix R representing the covariance matrix for uncorrelated measurement errors. This results in a Gaussian likelihood function
with a diagonal matrix R representing the covariance matrix for uncorrelated measurement errors. This results in a Gaussian likelihood function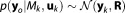 . Using the theory of linear uncertainty propagation [e.g., Schweppe, 1973] and the stated assumptions, BME can be directly evaluated for any given data set
. Using the theory of linear uncertainty propagation [e.g., Schweppe, 1973] and the stated assumptions, BME can be directly evaluated for any given data set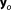 from the Gaussian distribution:
from the Gaussian distribution:
| (9) |
with .
.
As an alternative way to determine BME analytically, the posterior distribution of the parameters can be derived since the Gaussian distribution family is self-conjugate [Box and Tiao, 1973]. In general, the likelihood of the observed data given the prior parameter space of model Mk can be written as a function of the parameters
of the observed data given the prior parameter space of model Mk can be written as a function of the parameters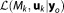 [Fisher, 1922]. Note that the likelihood function is not necessarily a proper probability density function with respect to
[Fisher, 1922]. Note that the likelihood function is not necessarily a proper probability density function with respect to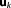 , because it does not necessarily integrate to one. With the assumptions of Gaussian measurement noise and a linear model, the likelihood can be expressed as a Gaussian function of the parameters
, because it does not necessarily integrate to one. With the assumptions of Gaussian measurement noise and a linear model, the likelihood can be expressed as a Gaussian function of the parameters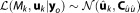 with
with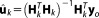 and
and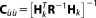 . The mean of the distribution,
. The mean of the distribution,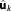 , is the maximum likelihood estimate (MLE) and (in this case) also the estimate obtained by ordinary least squares regression. It represents the parameter vector that yields the best possible fit to the observed data to be achieved by model Mk.
, is the maximum likelihood estimate (MLE) and (in this case) also the estimate obtained by ordinary least squares regression. It represents the parameter vector that yields the best possible fit to the observed data to be achieved by model Mk.
The combination of a Gaussian prior distribution and a Gaussian likelihood function yields an analytical expression for the posterior distribution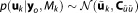 , which is again Gaussian with
, which is again Gaussian with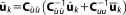 and
and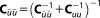 . Under the current set of assumptions, the mean of the posterior distribution,
. Under the current set of assumptions, the mean of the posterior distribution,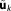 , is the maximum a posteriori estimate (MAP). The MAP represents those parameter values that are the most likely ones for model Mk, taking into account both prior belief about the distribution of the parameters and the performance in fitting the observed data. For a derivation of these statistics, see e.g., Box and Tiao [1973].
, is the maximum a posteriori estimate (MAP). The MAP represents those parameter values that are the most likely ones for model Mk, taking into account both prior belief about the distribution of the parameters and the performance in fitting the observed data. For a derivation of these statistics, see e.g., Box and Tiao [1973].
With the posterior parameter distribution, the quotient in equation (6) (Bayes' theorem rewritten to solve for the normalizing constant, equivalent to the integral in equation (7)) can be determined for any given value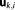 within the limits of
within the limits of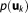 .
.
Mathematical Approximation
If no analytical solution exists to the application at hand, equation (7) can be approximated mathematically, e.g., by a Taylor series expansion followed by a Laplace approximation. We briefly outline this approach in section 3.2.1 and then discuss the derivation of the KIC (section 3.2.2) which is based on this approximation. In this context, it becomes more evident how Occam's razor works in BMA (section 3.2.3). The BIC (section 3.2.4) represents a truncated version of the KIC. Another mathematical approximation, which is based on information theory, results in the AIC(c) (section 3.2.5). We contrast the expected impact of the different IC formulations on model selection in section 3.2.6.
Laplace Approximation
The idea of the Laplace method [De Bruijn, 1961] is to approximate the integral by defining a simpler mathematical function for a subinterval of the original parameter space, assuming that the contribution of this neighborhood almost makes up the whole integral. Here a Gaussian posterior distribution is assumed as simplification to the unknown distribution. This is a suitable approximation if the posterior distribution is highly peaked around its mode (or maximum) . This assumption holds, if a large data set with a high information content is available for calibration. Expanding the logarithm of the integrand in equation (7) by a Taylor series about the posterior mode
. This assumption holds, if a large data set with a high information content is available for calibration. Expanding the logarithm of the integrand in equation (7) by a Taylor series about the posterior mode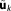 (i.e., the MAP), neglecting third-order and higher-order terms, taking the exponent again and finally performing the integration with the help of the Laplace approximation yields:
(i.e., the MAP), neglecting third-order and higher-order terms, taking the exponent again and finally performing the integration with the help of the Laplace approximation yields:
| (10) |
with the likelihood function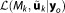 , the prior density
, the prior density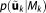 , and the number of parameters
, and the number of parameters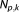 . The
. The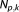 x
x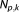 matrix
matrix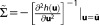 is the negative inverse Hessian matrix of second derivatives and represents an asymptotic estimator of the posterior covariance
is the negative inverse Hessian matrix of second derivatives and represents an asymptotic estimator of the posterior covariance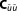 . It is equal to
. It is equal to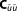 for the case of an actually Gaussian posterior (see section 3.1). For details on the Laplace approximation in the field of Bayesian statistics and an analysis of its asymptotic errors, please refer to Tierney and Kadane [1986].
for the case of an actually Gaussian posterior (see section 3.1). For details on the Laplace approximation in the field of Bayesian statistics and an analysis of its asymptotic errors, please refer to Tierney and Kadane [1986].
If the parameter prior is little informative, the expansion could also be carried out about the MLE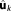 instead of the MAP
instead of the MAP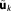 . This approximation will be less accurate in general, with the deterioration depending on the distance between the MAP and MLE estimators. However, the MLE may be easier to find than the MAP with standard optimization routines. The corresponding approximation takes the following form:
. This approximation will be less accurate in general, with the deterioration depending on the distance between the MAP and MLE estimators. However, the MLE may be easier to find than the MAP with standard optimization routines. The corresponding approximation takes the following form:
| (11) |
The inverse of the covariance matrix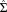 is the observed Fisher information matrix evaluated at the MLE,
is the observed Fisher information matrix evaluated at the MLE,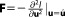 , with l being the log-likelihood function [Kass and Raftery, 1995].
, with l being the log-likelihood function [Kass and Raftery, 1995].
If the normalized (per observation) Fisher information is used,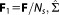 equals
equals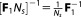 [Ye et al., 2008]:
[Ye et al., 2008]:
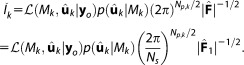 |
(12) |
For clarity in notation, model indices are omitted here for the covariance matrices and for the Fisher information matrix.
The presented mathematical approximations to the Bayesian Integral (equation (7)) are typically known in the shape of ICs, i.e., as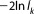 . We subsequently discuss the three most commonly used ICs in the BMA framework. They all generally aim at identifying the optimal bias-variance trade-off in model selection, but differ in their theoretical derivation and therefore in their accuracy with respect to the theoretically optimal trade-off according to Bayes' theorem.
. We subsequently discuss the three most commonly used ICs in the BMA framework. They all generally aim at identifying the optimal bias-variance trade-off in model selection, but differ in their theoretical derivation and therefore in their accuracy with respect to the theoretically optimal trade-off according to Bayes' theorem.
Kashyap Information Criterion
The Kashyap information criterion (KIC) directly results from the approximation defined in equation (12) by applying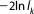 [Kashyap, 1982]:
[Kashyap, 1982]:
| (13) |
The KIC is applied within the framework of MLBMA [Neuman, 2002]. By means of this approximation, MLBMA is a computationally feasible alternative to full Bayesian model averaging if knowledge about the prior of parameters is vague. For applications of MLBMA, see Neuman [2003], Ye et al. [2004], Neuman et al. [2012], and references therein.
If an estimate of the postcalibration covariance matrix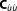 is obtainable, equation (11) can be drawn upon instead:
is obtainable, equation (11) can be drawn upon instead:
| (14) |
Ye et al. [2004] point toward the close relationship of the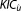 with the original Laplace approximation, but prefer the evaluation at the MLE, because it is in line with traditional MLE-based hydrological model selection and parameter estimation routines. Neuman et al. [2012] appreciate that MLBMA “admits but does not require prior information about the parameters” and include prior information in their likelihood optimization routine, which makes it de facto a MAP estimation routine. We strongly advertise the latter variant, because the Laplace approximation originally involves an expansion about the MAP instead of the MLE, and we understand prior information on the parameters as a vital part of Bayesian inference. Therefore, we propose to explicitly evaluate the KIC at the MAP:
with the original Laplace approximation, but prefer the evaluation at the MLE, because it is in line with traditional MLE-based hydrological model selection and parameter estimation routines. Neuman et al. [2012] appreciate that MLBMA “admits but does not require prior information about the parameters” and include prior information in their likelihood optimization routine, which makes it de facto a MAP estimation routine. We strongly advertise the latter variant, because the Laplace approximation originally involves an expansion about the MAP instead of the MLE, and we understand prior information on the parameters as a vital part of Bayesian inference. Therefore, we propose to explicitly evaluate the KIC at the MAP:
 |
(15) |
We will refer to this formulation as KIC@MAP as opposed to the KIC@MLE (equation (14)) to avoid any confusion within the MLBMA framework, which seems to admit both of the KIC variants discussed here. The evaluation at the MAP is consistent with the Laplace approach to approximate the Bayesian integral and, in case of an actually Gaussian parameter posterior, will yield accurate results; this does not hold if the approximation is evaluated at the MLE. If the assumption of a Gaussian posterior is violated, it needs to be assessed how the different evaluation points affect the already inaccurate approximation. We will investigate the differences in performance between the KIC@MLE and our proposed KIC@MAP in section 4.
Interpretation Via Occam's Razor
In equation (15), we have distinguished different terms of the Laplace approximation in the formulation of the KIC@MAP. They can be interpreted within the context of BMA, and if the assumption of a Gaussian posterior parameter distribution is satisfied, this represents an interpretation of the ingredients of BME (or more specifically, minus twice the logarithm of BME). It incorporates a measure of goodness of fit (the negative log-likelihood term, NLL) and three penalty terms that account for model dimensionality (dimension of the model's parameter space). These three terms are referred to as Occam factor [MacKay, 1992].
The Occam factor reflects the principle of parsimony or Occam's razor: If any number of competing models shows the same quality of fit, the least complex one should be used to explain the observed effects. Any additional parameter is considered to be fitted to noise in the observed data and might lead to low parameter sensitivities and poor predictive performance (due to little robustness of the estimated parameters). Synthesizing the discussions by Neuman [,], Ye et al. [2004], and Lu et al. [2011], and explicitly transferring them to the expansion about the MAP, we make an attempt to explain the role of the three terms that are contained in the Occam factor.
The parameter prior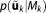 (term 1) implicitly penalizes a growing complexity in that it gives a lower probability density to models with larger parameter spaces (larger
(term 1) implicitly penalizes a growing complexity in that it gives a lower probability density to models with larger parameter spaces (larger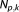 ), since high-dimensional densities have to dilute their total probability mass of unity within a larger space. Thus, a more complex model with its smaller prior parameter probabilities will obtain a higher value of the criterion or a decreased value of BME, which will compromise its chances to rule out its competitors according to Occam's razor.
), since high-dimensional densities have to dilute their total probability mass of unity within a larger space. Thus, a more complex model with its smaller prior parameter probabilities will obtain a higher value of the criterion or a decreased value of BME, which will compromise its chances to rule out its competitors according to Occam's razor.
The opposite is true for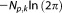 (term 2): here, an increase in dimensionality yields a decrease of the KIC or an increase in model evidence. This term is actually part of the normalizing factor of a Gaussian prior distribution and thus partially compensates the effect of (1).
(term 2): here, an increase in dimensionality yields a decrease of the KIC or an increase in model evidence. This term is actually part of the normalizing factor of a Gaussian prior distribution and thus partially compensates the effect of (1).
Finally, (term 3) accounts for the curvature of the posterior distribution. A strong negative curvature, i.e., a very narrow posterior distribution, represents a high information content in the data with respect to the calibration of the parameters. A narrow posterior leads to a low value for the determinant and thus to a decrease in model evidence or an increase of the KIC. This might seem counter-intuitive at first, but has to be interpreted from the viewpoint that if the data provide a high information content, the resulting likelihood function shall be narrow, and thus, its peak value shall also be high. The determinant is thus a partially compensating counterpart to the NLL term. If two competing models achieve the same likelihood, but differ in their sensitivity to the data, the one with a smaller sensitivity will be chosen because of its robustness [Ye et al., 2010b].
(term 3) accounts for the curvature of the posterior distribution. A strong negative curvature, i.e., a very narrow posterior distribution, represents a high information content in the data with respect to the calibration of the parameters. A narrow posterior leads to a low value for the determinant and thus to a decrease in model evidence or an increase of the KIC. This might seem counter-intuitive at first, but has to be interpreted from the viewpoint that if the data provide a high information content, the resulting likelihood function shall be narrow, and thus, its peak value shall also be high. The determinant is thus a partially compensating counterpart to the NLL term. If two competing models achieve the same likelihood, but differ in their sensitivity to the data, the one with a smaller sensitivity will be chosen because of its robustness [Ye et al., 2010b].
Bayesian Information Criterion
The Bayesian information criterion (BIC) or Schwarz information criterion [Schwarz, 1978] is a simplification to equation (13) in that it only retains terms that vary with Ns:
| (16) |
Evaluating this criterion for the MAP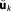 would not be consistent, because the influence of the prior is completely ignored in equation (16). Since only parts of the Occam factor are retained compared to equation (15), the BIC penalizes a model's dimensionality to a different extent. Those differences are not supported by any specific theory. However, the KIC@MLE reduces asymptotically to BIC with growing data set size Ns. The reason is that the prior probability of
would not be consistent, because the influence of the prior is completely ignored in equation (16). Since only parts of the Occam factor are retained compared to equation (15), the BIC penalizes a model's dimensionality to a different extent. Those differences are not supported by any specific theory. However, the KIC@MLE reduces asymptotically to BIC with growing data set size Ns. The reason is that the prior probability of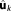 as well as the normalized Fisher information do not grow with data set size, but the likelihood
as well as the normalized Fisher information do not grow with data set size, but the likelihood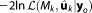 and
and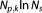 do, rendering contributions that only grow with
do, rendering contributions that only grow with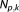 negligible [Neuman, 2003]. The error in approximation by the BIC is therefore expected to reduce to the error made by the KIC for large data set sizes. In section 3.2.6, we will compare the different IC approximations with regard to their penalty terms, and in section 4 we will investigate the convergence behavior of the KIC and BIC in more detail on a synthetic test case.
negligible [Neuman, 2003]. The error in approximation by the BIC is therefore expected to reduce to the error made by the KIC for large data set sizes. In section 3.2.6, we will compare the different IC approximations with regard to their penalty terms, and in section 4 we will investigate the convergence behavior of the KIC and BIC in more detail on a synthetic test case.
Applying the KIC or BIC for model selection (as opposed to averaging) is consistent as the assigned weight for the true model (if it is a member of the considered set of models) converges to unity for an infinite data set size. The truncated form (BIC) still seems to perform reasonably well for model identification or explanatory purposes [Koehler and Murphree, 1988]. It is also much less expensive to evaluate than the KIC for models with high-dimensional parameter spaces, since the evaluation of the covariance matrix is not required.
Akaike Information Criterion
The Akaike information criterion (AIC) or, as originally entitled, “an information criterion,” originates from information theory (as opposed to the Bayesian origin of the KIC and BIC), but has frequently been applied in the framework of BMA [e.g., Poeter and Anderson, 2005]. It is derived from the Kullback-Leibler (KL) divergence that measures the loss of information when using an alternative model Mk with a predictive density function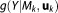 instead of the “true” model with predictive density function
instead of the “true” model with predictive density function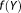 , with Y being a random variable from the true density f of the same size Ns as the observed data set
, with Y being a random variable from the true density f of the same size Ns as the observed data set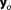 :
:
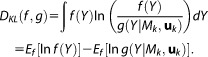 |
(17) |
The first term in the second line of equation (17) is an unknown constant that drops out when comparing differences in the expected KL-information for the competing models in the set [e.g., Kuha, 2004]. Akaike [,] argued that the second term, called relative expected KL-information, can be estimated using the MLE. For reasons not provided here, this estimator is biased by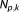 , the number of parameters in the model Mk. Correcting this bias and multiplying by −2 yields the AIC [Burnham and Anderson, 2004]. The AIC formulation contains the NLL term as an expression for the goodness of fit and a penalty term for the number of parameters:
, the number of parameters in the model Mk. Correcting this bias and multiplying by −2 yields the AIC [Burnham and Anderson, 2004]. The AIC formulation contains the NLL term as an expression for the goodness of fit and a penalty term for the number of parameters:
| (18) |
Compared to the BIC in equation (16), the penalty term for the number of parameters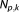 is less severe. For data set sizes
is less severe. For data set sizes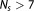 , BIC favors models with less parameters than AIC, since its penalty term
, BIC favors models with less parameters than AIC, since its penalty term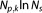 becomes larger than the AIC's
becomes larger than the AIC's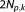 .
.
For a finite data set size Ns, a second-order bias correction has been suggested [Sugiura, 1978; Hurvich and Tsai, 1989]:
| (19) |
Among others, Burnham and Anderson [2004] suggest using the corrected formulation for data set sizes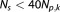 . For increasing data set sizes, the AICc converges to the AIC.
. For increasing data set sizes, the AICc converges to the AIC.
The posterior Akaike model weight is derived from:
| (20) |
with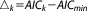 or
or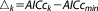 , respectively. Based on its theoretical derivation, the absolute value of AICk or AICck has no explanatory power [Burnham and Anderson, 2004], only the difference
, respectively. Based on its theoretical derivation, the absolute value of AICk or AICck has no explanatory power [Burnham and Anderson, 2004], only the difference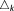 with respect to the lowest AICk or AICck can be interpreted. The BIC or KIC, in contrast, are a direct approximation to BME (equation (7)) and therefore yield meaningful values, also in interpretation as absolute values.
with respect to the lowest AICk or AICck can be interpreted. The BIC or KIC, in contrast, are a direct approximation to BME (equation (7)) and therefore yield meaningful values, also in interpretation as absolute values.
The AIC seems to perform well for predictive purposes, with a tendency to over-fit observed data [see e.g., Koehler and Murphree, 1988; Claeskens and Hjort, 2008]. This tendency is supposedly less severe for the bias-corrected AICc. Both versions of the AIC do not converge to the true model for an infinite data set size. The reason is that, with an increasing amount of data, the model chosen by AIC(c) will increase in complexity, potentially beyond the complexity of the true model (if it exists) [Burnham and Anderson, 2004].
The KIC is expected to provide the most consistent results among the ICs investigated here because it is based on the approximation closest to the true equations. Applications and comparisons of KIC, BIC, and AIC can be found in Ye et al. [2008], Tsai and Li [2010], Singh et al. [2010], Riva et al. [2011], Morales-Casique et al. [2010], and Lu et al. [2011]. In the following, we will summarize the main theoretical differences in the BME approximation by these ICs.
Theoretical Comparison of IC Approximations to BME
Based on equation (10), the Laplace approximated BME can be divided into the likelihood and the Occam factor OF (see section 3.2.3):
| (21) |
The ICs analyzed here all share the same approximation for the goodness of fit term based on the MLE. The only exception is the KIC@MAP, which is evaluated at the MAP instead of at the MLE. However, they all differ in their approximation to the OF. The OF represents the penalty for the dimensionality of a model or what we call the sharpness of Occam's razor. For the different ICs, it is given by:
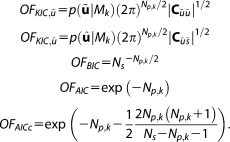 |
(22) |
The OF as approximated by KIC does not explicitly account for data set size, yet Ns typically influences the curvature of the posterior probability (or the likelihood function) and thus implicitly affects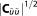 (or
(or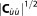 ). In contrast, AICc and BIC explicitly take data set size Ns in account, but do not evaluate the sensitivity of the calibrated parameter set via the curvature. The effects of these differences on the accuracy of the BME approximation will be demonstrated exemplarily on two test case applications in sections 4 and 5.
). In contrast, AICc and BIC explicitly take data set size Ns in account, but do not evaluate the sensitivity of the calibrated parameter set via the curvature. The effects of these differences on the accuracy of the BME approximation will be demonstrated exemplarily on two test case applications in sections 4 and 5.
Numerical Evaluation
Numerical evaluation offers a second alternative to determine BME, if no analytical solution is available or if one mistrusts the approximate character of the ICs. A comprehensive review of numerical methods to evaluate the Bayesian integral (equation (7)) is given by Evans and Swartz [1995]. In the following, we will shortly review selected state-of-the-art methods and discuss their strengths and limitations. Note that conventional efficient integration schemes (e.g., adaptive Gaussian quadrature) are limited to low-dimensional applications [Kass and Raftery, 1995]. In this study, we focus on numerical methods that can also be applied to highly complex models (models with large parameter spaces) in order to provide a useful discussion for a broad range of research fields and applications.
Monte Carlo Integration
Simple Monte Carlo integration [Hammersley, 1960] evaluates the integrand at randomly chosen points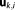 in parameter space. These parameter sets
in parameter space. These parameter sets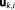 are randomly drawn from their prior distribution
are randomly drawn from their prior distribution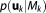 . The integral (or expected value over parameter space, cf. equation (4)) is then determined as the mean value of the evaluated likelihoods (sometimes referred to as arithmetic mean approach):
. The integral (or expected value over parameter space, cf. equation (4)) is then determined as the mean value of the evaluated likelihoods (sometimes referred to as arithmetic mean approach):
| (23) |
with the number of Monte Carlo (MC) realizations N. For large ensemble sizes N and a friendly overlap of the parameter prior and the likelihood function, this method will provide very accurate results. For high-dimensional parameter spaces, however, a sufficient (converging) ensemble might come at a high or even prohibitive computational cost. If the likelihood function is sharp compared to the prior distribution, only very few integration points will contribute a high likelihood value to the integral (making a very skewed variable), and the numerical uncertainty in the approximated integral might be large.
a very skewed variable), and the numerical uncertainty in the approximated integral might be large.
Monte Carlo Integration With Importance Sampling
To reduce computational effort and improve convergence, importance sampling [Hammersley et al., 1965] aims at a more efficient sampling strategy. Instead of drawing random realizations from the prior parameter distribution, integration points are drawn from any arbitrary distribution that is more similar to the posterior distribution. Thus, the mass of the integral will be detected more likely by the sampling points. When drawing from a different distribution q than the prior distribution p, the integrand in equation (7) must be expanded by q / q. This modifies equation (23) to:
| 24 |
with weights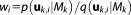 . The improvement achieved by importance sampling compared to simple MC integration will greatly depend on the choice of the importance function q.
. The improvement achieved by importance sampling compared to simple MC integration will greatly depend on the choice of the importance function q.
Monte Carlo Integration With Posterior Sampling
Developing this idea further, it could be most advantageous to draw parameter realizations from the posterior distribution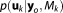 in order to capture the full mass of the integral. Sampling from the posterior distribution is possible, e.g., with the MCMC method [Hastings, 1970].
in order to capture the full mass of the integral. Sampling from the posterior distribution is possible, e.g., with the MCMC method [Hastings, 1970].
For posterior sampling, the approximation to the integral reduces to the harmonic mean of likelihoods [Newton and Raftery, 1994], also referred to as the harmonic mean approach:
| (25) |
Equation (25) can be subject to numerical instabilities, due to small likelihoods that may corrupt the evaluation of the harmonic mean.
According to Jensen's inequality [Jensen, 1906], sampling exclusively from the posterior parameter distribution yields a biased estimator that overestimates BME. Thus, the harmonic mean approach should be seen as a trade-off between accuracy and computational effort. In order to avoid the instabilities of the harmonic mean approach by solving equation (6) instead, it would be necessary to estimate the posterior parameter probability density from the generated ensemble through kernel density estimators [e.g., Härdle, 1991], which is only possible for low-dimensional parameter spaces. We therefore do not investigate this alternative option further within this study.
Integration in Likelihood Space With Nested Sampling
The main challenge in evaluating BME lies in sufficiently sampling high-dimensional parameter spaces. A promising approach which avoids this challenge and instead samples the one-dimensional likelihood space is called nested sampling [Skilling, 2006]. The integral to obtain BME is written as:
| (26) |
where Z represents prior mass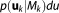 . It is solved by discretizing into m likelihood threshold values with the sequence
. It is solved by discretizing into m likelihood threshold values with the sequence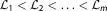 and summing up over the corresponding prior mass pieces
and summing up over the corresponding prior mass pieces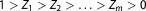 according to a numerical integration rule. How to find subsequent likelihood thresholds is described in Skilling [2006].
according to a numerical integration rule. How to find subsequent likelihood thresholds is described in Skilling [2006].
One of the remaining challenges for this very recent approach lies in finding conforming samples above the current likelihood threshold. We follow Elsheikh et al. [2013] in utilizing a short random walk Markov chain starting from a random sample that overcame the previous threshold. However, instead of using the ratio of likelihoods as acceptance distribution, we take the ratio of prior probabilities instead, to ensure that new samples still conform with their prior. Another challenge lies in ending the procedure with a suitable termination criterion (e.g., stop if the increase in BME per iteration has flattened out or if the likelihood threshold cannot be overcome within a maximum number of MCMC steps).
If the prior mass enclosing a specific likelihood threshold was known, the value of BME could be determined as accurately as the integration scheme allows. However, the fact that the real prior mass pieces Zj are unknown introduces a significant amount of uncertainty into the procedure, which reduces its precision. To quantify the resulting numerical uncertainty, an MC simulation over randomly chosen prior mass shrinkage factor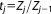 should be performed [Skilling, 2006].
should be performed [Skilling, 2006].
Conclusions From Theoretical Comparison
From our comparison of the underlying assumptions for the nine BME evaluation methods considered here, we conclude that out of the ICs, the KIC@MAP is the most consistent one with BMA theory. It represents the true solution if the assumptions of the Laplace approximation hold (i.e., if the posterior parameter distribution is Gaussian). The other ICs considered here represent simplifications of this approach or, in the case of the AIC(c), are derived from a different theoretical perspective and are therefore expected to show an inferior approximation quality. Among the numerical methods considered here, simple MC integration is the most generally applicable approach because it is bias-free and spares any assumptions on the shape of the parameter distribution, but is also the computationally most expensive one. The other numerical methods vary in their efficiency, but are expected to yield similarly accurate results, except for MC integration with posterior sampling, which yields a biased estimate. We will test these expectations on a synthetic setup in the following section. The underlying assumptions of the nine BME evaluation methods analyzed in this study are summarized in Table4.
Benchmarking on a Synthetic Test Case
The nine methods to solve the Bayesian integral (equation (7)) differ in their accuracy and computational effort, as described in the previous section. To illustrate the differences in accuracy under completely controlled conditions, we apply the methods presented in section 3 to an oversimplified synthetic example. In a first step, we consider a setup with a linear model where an analytical solution exists. We create an ideal premise for the KIC@MAP and its variants (KIC@MLE and BIC) by using a Gaussian parameter posterior, which fulfills their core assumption. We designed this test case as a best-case scenario regarding the performance of these ICs: there is no less challenging case in which the information criteria could possibly perform better. In a second step, we also consider nonlinear models of different complexity that violate this core assumption. Since in this case no analytical solution exists, we use brute-force MC integration as reference for benchmarking. We designed this test case as an intermediate step toward real-world applications that typically entail nonlinear models and a higher number of parameters.
Setup and Implementation
In the first step, a linear model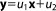 relates bivariate Gaussian distributed parameters
relates bivariate Gaussian distributed parameters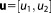 (slope and intersect of a linear function) to multi-Gaussian distributed predictions y at measurement locations x. This linear model is tested against a synthetic data set. The synthetic truth underlying the data set is generated from the same model, but with slightly different parameter values than the prior mean. To obtain a synthetic data set, a random measurement error is added according to a Gaussian distribution
(slope and intersect of a linear function) to multi-Gaussian distributed predictions y at measurement locations x. This linear model is tested against a synthetic data set. The synthetic truth underlying the data set is generated from the same model, but with slightly different parameter values than the prior mean. To obtain a synthetic data set, a random measurement error is added according to a Gaussian distribution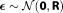 .
.
For this artificial setup, BME can be determined analytically according to equations (9) (determining BME via linear uncertainty propagation) or 6 (solving Bayes' theorem for BME). This exact value is used as reference for the approximate methods presented in section 3. In this simple case, the MAP, , and the MLE,
, and the MLE, , are known analytically. Also, the corresponding covariances
, are known analytically. Also, the corresponding covariances and
and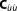 are known. We allow the mathematical approximations to take advantage of this knowledge by evaluating them at these exact values. Normally, these quantities have to be approximated by optimization algorithms first. This initial step represents the computational effort needed to determine BME with mathematical approximations in the form of ICs, since the evaluation of their algebraic equations itself is very cheap. Here we are not concerned with the potential challenge to find these parameter estimates, but merely wish to remind the reader of this fact.
are known. We allow the mathematical approximations to take advantage of this knowledge by evaluating them at these exact values. Normally, these quantities have to be approximated by optimization algorithms first. This initial step represents the computational effort needed to determine BME with mathematical approximations in the form of ICs, since the evaluation of their algebraic equations itself is very cheap. Here we are not concerned with the potential challenge to find these parameter estimates, but merely wish to remind the reader of this fact.
The numerical evaluation schemes do not take advantage of the linearity of the test case. Their computational effort is determined by the number of required parameter realizations, and hence by the number of required model evaluations. To assess the expected improvement in accuracy by investing in computational effort, we repeat the determination of BME for increasing ensemble sizes (MC integration, importance sampling, sampling from the posterior) or increasing sizes of the active set (nested sampling). To determine the lowest reasonable ensemble size, we investigate the convergence of the BME approximation for each method. Simple MC integration is performed based on ensembles of 2000–1,000,000 parameter realizations drawn from the Gaussian prior. MC integration with importance sampling is performed based on the same ensemble sizes. The sampling distribution for importance sampling is chosen to be Gaussian with a mean value equal to the MAP and a variance equal to the prior variance. Realizations of the posterior parameter distribution for MC integration with posterior sampling are generated by the differential evolution adaptive metropolis adaptive MCMC scheme DREAM [Vrugt et al., 2008]. With DREAM, BME is approximated based on ensembles of 5000–1,000,000 parameter realizations. Convergence of the MCMC runs was monitored by the Gelman-Rubin criterion [Gelman and Rubin, 1992] and we chose to take the final 25% of the converged Markov chains as posterior ensemble. Nested sampling is performed with initial ensemble sizes of 10–10,000. A nested sampling run is complete if one of the two following termination criteria is reached. The first termination criterion stops the calculation if the current likelihood threshold could not be overcome within 100 MCMC steps with a scaling vector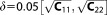 . The second termination criterion stops the calculation if the current BME estimate would not increase by more than 0.5% even if the current maximum likelihood value would be multiplied with the total remaining prior mass. This results in total ensemble sizes (summed over all iterations) of roughly 1000–1,000,000.
. The second termination criterion stops the calculation if the current BME estimate would not increase by more than 0.5% even if the current maximum likelihood value would be multiplied with the total remaining prior mass. This results in total ensemble sizes (summed over all iterations) of roughly 1000–1,000,000.
As a base case, we generate a synthetic data set of size Ns = 15. Figure 1 shows the setup for the synthetic test case. The parameters used in the synthetic example are summarized in Table1.
Figure 1.
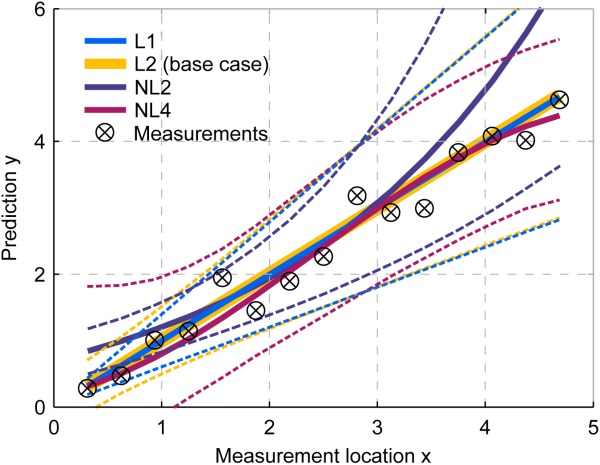
Synthetic test case setup. Measurements marked in black, prior estimate of linear (L1, L2) and nonlinear (NL2, NL4) models in solid lines, 95% Bayesian prediction confidence intervals in dashed lines of the respective color.
Table 1.
Definition of Parameters Used in Different Scenarios of the Synthetic Test Casea
| Parameter | Symbol | Value |
|---|---|---|
| Base Case (L2) | ||
| Prior mean |  |
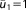 ; ; 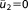
|
| Prior covariance | 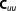 |
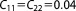 ; ; 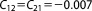
|
| Data set size | Ns | Ns = 15 |
| Meas. error covariance | R |
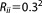 ; Rij = 0 ; Rij = 0 |
| Varied Data Set Size | ||
| Data set size | Ns | 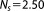 |
| Varied Prior Width | ||
| Prior covariance | 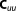 |
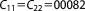 ; ; 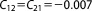
|
| Varied Prior/Likelihood Overlap | ||
| Prior mean |  |
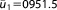 ; ; 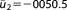
|
| Varied Model Structure | ||
| Prior mean (L1) |  |
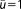 |
| Prior variance (L1) | s2 | 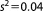 |
| Prior mean (NL2) |  |
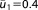 ; ; 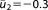
|
| Prior covariance (NL2) | 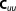 |
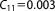 ; ; 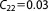 ; ; 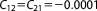
|
| Prior mean (NL4) |  |
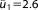 ; ; 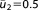 ; ; 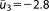 ; ; 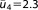
|
| Prior covariance (NL4) | 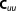 |
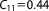 ; ; 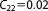 ; ; 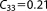 ; ; 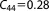 ; ; 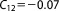 ; ; 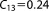 ; ; 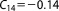 ; ; 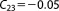 ; ; 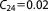 ; ; 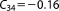
|
For variations of the base case, only differences to the base case parameters are listed.
In our synthetic test case, the computational effort required for one model run is very low. This allows us to repeat the entire analysis for the base case and to average over 500 runs for each ensemble size in order to quantify the inherent numerical uncertainty in the results obtained from the numerical approximation methods. In the case of nested sampling, we additionally average over 200 random realizations of the prior mass shrinkage factor per run.
With the setup described above, we compare the performance of the different approximation methods in quantifying BME. Additionally, we study by scenario variations the impact of varied data set size and varied prior information (different mean values and variances of parameters) on the outcome of BME and on the performance of the different methods. The behavior of the mathematical approximations for small or large data set sizes has been touched upon in the literature [e.g., Burnham and Anderson, 2004; Lu et al., 2011]. We will underpin these discussions by systematically increasing the data set size from Ns = 2 to Ns = 50. Again, the same model is used to generate the synthetic truth as in the base case, and the measurements are taken at equidistant locations on the same interval of x. To show the general behavior of the approximation methods and to eliminate artifacts caused by a specific outcome of measurement error, we generate 200,000 perturbed data sets for each data set size and average over the results of these realizations.
To our knowledge, the impact of prior information on the performance of BME approximation methods has not yet been studied in such a systematic approach. With the help of our synthetic test case, we can assess and then discuss this impact in a rigorous manner. Figure 2a visualizes the prior parameter densities, the likelihood function, and the posterior densities for a range of prior widths, Figure 2b for different prior/likelihood overlaps. The second column represents the base case as described above. Variations in prior width are normalized as fractions of the base case variances (covariance is not varied), variations in overlap of prior and likelihood are measured as distance between the prior mean and the MLE. The varied parameter values are also listed in Table1.
Figure 2.
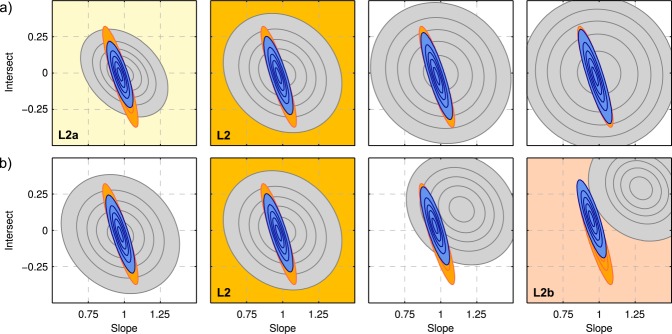
Prior densities (gray), likelihood (orange), and posterior densities (blue) for the different scenarios of the synthetic test case. Contour lines represent 10–90% Bayesian confidence intervals: (a) variations of prior width (fractions of base case variance shown here: 0.5,…,5), (b) variations of prior/likelihood overlap (distance between prior mean and MLE shown here: 0,…,0.3).
Besides the factors explained above, the model structure and dimensionality of the models' parameter spaces is expected to influence the performance of the different approximation methods. In the first step, we consider varying complexity with regard to the allowed parameter ranges as defined by the prior. In the second step, we also consider models with varied structure. Differences in model structure can manifest themselves in either differences in the dimensionality of the model (i.e., the number of parameters), or in the type of model (linear versus nonlinear), or in both. We consider all of these options here by including a linear model with one parameter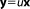 (smaller number of parameters, but same model type; L1), a weakly nonlinear model with two parameters
(smaller number of parameters, but same model type; L1), a weakly nonlinear model with two parameters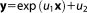 (same number of parameters, but different model type; NL2), and a nonlinear model with four parameters
(same number of parameters, but different model type; NL2), and a nonlinear model with four parameters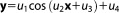 (higher number of parameters and different model type; NL4) into the analysis. All prior distributions are chosen to be Gaussian with their mean and covariance values given in Table1. For nonlinear models, no analytical solution exists. In order to still be able to assess the differences in approximation quality, we generate a reference solution with brute-force MC integration using a very large ensemble of 10 million realizations per model. We choose this exceptionally large number of realizations to obtain a very reliable estimate of BME as a reference. In a numerical convergence analysis (bootstrapping) [Efron, 1979], we determined the variance upon resampling of the ensemble members, which confirmed that the BME estimate is varying less than 0.001%. This variation is insignificant in relation to the lowest error produced by the compared BME evaluation methods, which is two orders of magnitude larger. The average BME approximation quality (and its scattering) achieved by the other numerical methods is based on 500 repeated runs with ensemble sizes of 50,000, which might be considered a reasonable compromise between accuracy and computational effort based on the findings from the first step of our synthetic test case. From the posterior parameter sample generated by DREAM, we determine the MAP and the covariance matrix needed for the evaluation of the KIC@MAP. We obtain the respective ML statistics for the KIC@MLE from a DREAM run with uninformative prior distributions to cancel out the influence of the prior. We also evaluate the AIC(c) and the BIC at this parameter set.
(higher number of parameters and different model type; NL4) into the analysis. All prior distributions are chosen to be Gaussian with their mean and covariance values given in Table1. For nonlinear models, no analytical solution exists. In order to still be able to assess the differences in approximation quality, we generate a reference solution with brute-force MC integration using a very large ensemble of 10 million realizations per model. We choose this exceptionally large number of realizations to obtain a very reliable estimate of BME as a reference. In a numerical convergence analysis (bootstrapping) [Efron, 1979], we determined the variance upon resampling of the ensemble members, which confirmed that the BME estimate is varying less than 0.001%. This variation is insignificant in relation to the lowest error produced by the compared BME evaluation methods, which is two orders of magnitude larger. The average BME approximation quality (and its scattering) achieved by the other numerical methods is based on 500 repeated runs with ensemble sizes of 50,000, which might be considered a reasonable compromise between accuracy and computational effort based on the findings from the first step of our synthetic test case. From the posterior parameter sample generated by DREAM, we determine the MAP and the covariance matrix needed for the evaluation of the KIC@MAP. We obtain the respective ML statistics for the KIC@MLE from a DREAM run with uninformative prior distributions to cancel out the influence of the prior. We also evaluate the AIC(c) and the BIC at this parameter set.
For all cases (base case, varied data set size, varied prior information, varied model structure), the error in BME approximation is quantified as a relative error
| (27) |
with the subscript i representing any of the discussed methods. In the case of numerical techniques, the average Erel value and its Bayesian confidence interval out of all repetitions is provided.
Finally, we determine the impact of BME approximation errors on model weights based on the same setup and implementation details as described for the investigation of the influence of model structure (section 4.5).
Results for the Base Case
Figure 3 shows the relative error of BME approximations with respect to the analytical solution for the base case (see definition of parameters in section 4.1) as a function of ensemble size (number of model calls). Obviously, the accuracy of approximation improves for numerical methods when investing more computational effort, i.e., when increasing the numerical ensemble size. The improvement includes both a reduction in bias (error) and a reduction in variance (numerical uncertainty, shown as 95% Bayesian confidence intervals of the approximation error in Figure 3).
Figure 3.
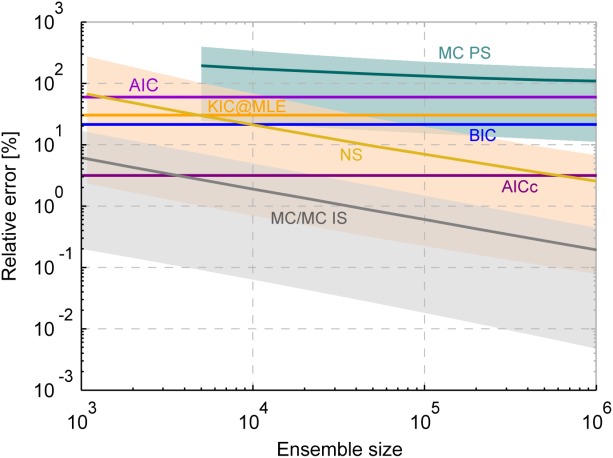
Relative error of BME approximation with respect to the analytical solution for the synthetic base case as a function of ensemble size. IC solutions are plotted as horizontal lines, as they do not use realizations for BME evaluation. Results of the numerical evaluation schemes are presented with 95% Bayesian confidence intervals.
Simple MC integration (MC) and MC integration with importance sampling (MC IS) perform equally well for this setup. MC results improve linearly in quality in this log-log-plot, which complies with its well-known convergence rate of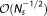 (Central Limit Theorem) [Feller, 1968]. MC integration with sampling from the posterior (MC PS), however, leads to a severe overestimation of BME as anticipated (see section 3.3.3) and does not improve linearly with ensemble size in log-log-space, but shows a slower convergence. It also produces a much larger numerical uncertainty (keep in mind the logarithmic scale of the error axis). Note that the bias in BME approximation stems from the harmonic mean formulation and not from the sampling technique, because the posterior realizations generated with DREAM were checked to be consistent with the (in this case) known analytical posterior parameter distribution.
(Central Limit Theorem) [Feller, 1968]. MC integration with sampling from the posterior (MC PS), however, leads to a severe overestimation of BME as anticipated (see section 3.3.3) and does not improve linearly with ensemble size in log-log-space, but shows a slower convergence. It also produces a much larger numerical uncertainty (keep in mind the logarithmic scale of the error axis). Note that the bias in BME approximation stems from the harmonic mean formulation and not from the sampling technique, because the posterior realizations generated with DREAM were checked to be consistent with the (in this case) known analytical posterior parameter distribution.
Nested sampling (NS) shows a similar approximation quality to MC integration, but is shifted on the x axis, i.e., it is less efficient with regard to numerical ensemble sizes in this specific test case. The convergence behavior shown here might not be a general property of nested sampling, because we found that modifications in the termination criteria significantly influence its approximation quality and uncertainty bounds. For this synthetic linear test case, we conclude that nested sampling is not as efficient as simple MC integration. It is also less reliable due to its somewhat arbitrary formulation with respect to the search for a replacement realization and the choice of termination criteria. In principle, it offers an alternative to simple MC integration and might become more advantageous in high-dimensional parameter spaces. We will continue this discussion for the real-word hydrological test case (section 5) and draw some final conclusions in section 6.
Since the ICs do not use random realizations to approximate BME, they are plotted as horizontal lines. With its assumptions fully satisfied, the KIC@MAP is equal to the analytical solution in this case. Therefore, it does not produce any error to be plotted in Figure 3. Evaluating the KIC at the MLE (KIC@MLE), however, leads to a significant deviation from the exact solution. For this specific setup, the AICc (after the KIC@MAP) performs best out of the mathematical approximations with a tolerable error of 3%. However, we will demonstrate later that this is not a general result. Note that we assess the AIC(c)'s performance in approximating the absolute BME value here for illustrative reasons, although strictly speaking, it is only derived for comparing models with each other, i.e., only the resulting model weights should be assessed (see section 4.6). The other ICs yield approximation errors of 20–60%. Figure 3 shows that, except for MC integration with posterior sampling, the numerical methods outperform all of the ICs evaluated at the MLE, if only enough realizations are used.
Results for Varied Data Set Size
The approximation results as a function of data set size are shown in Figure 4. Since we have demonstrated that the numerical methods (except for posterior sampling) can approximate the true solution with arbitrary accuracy if only the invested computational power is large enough, we do not show their results here, as they would coincide with the solution of the KIC@MAP. Figure 4a shows the approximated BME values, while the relative error in percent with respect to the analytical solution is shown in Figure 4b.
Figure 4.
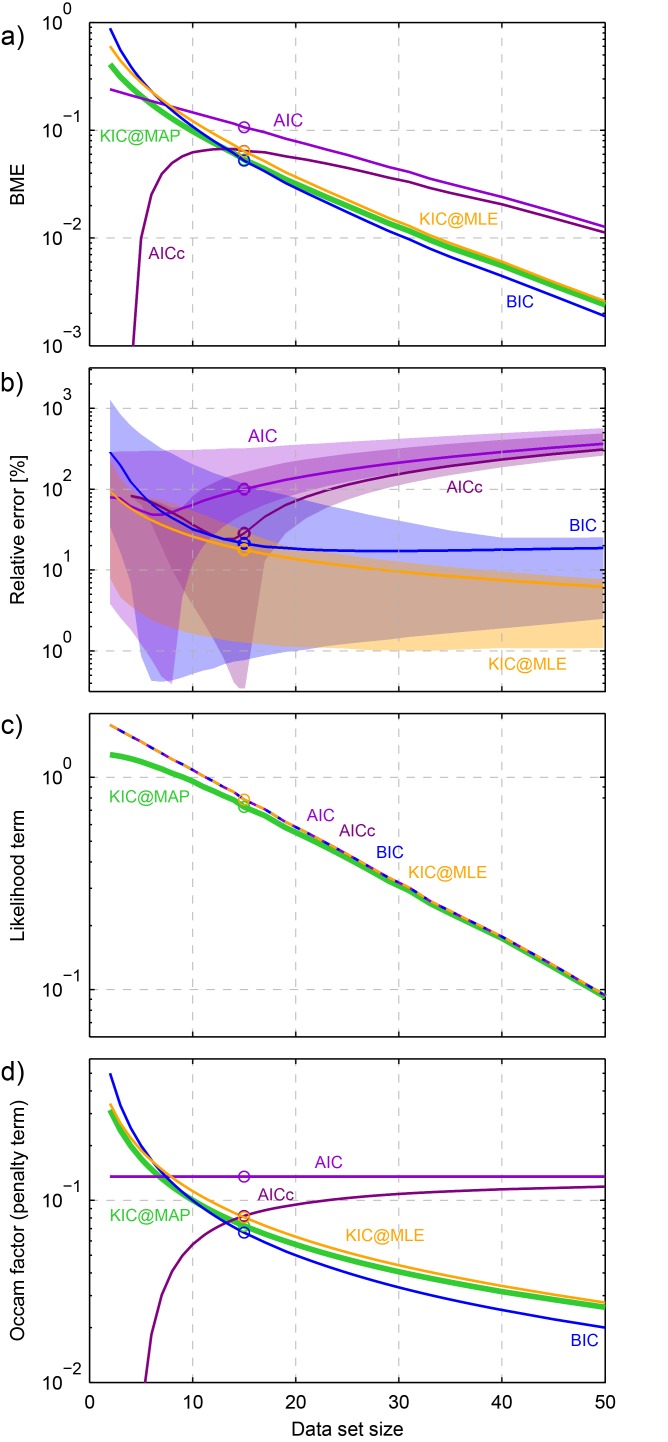
Synthetic test case results as a function of data set size: (a) approximation of BME, (b) relative error with respect to the analytical solution with 95% Bayesian confidence intervals, (c) likelihood term approximation, (d) Occam factor approximation. The result obtained from KIC@MAP represents the analytical solution in this case.
The true BME curve (represented by the KIC@MAP here) is approximated quite well by both the KIC@MLE and by the BIC. However, while the KIC@MLE converges to the KIC@MAP with increasing data set size, the BIC does not. Its relative error with respect to the analytical solution becomes stable at more than 20%. This result is not in agreement with the findings of Lu et al. [2011], who confirmed the general belief that the BIC approaches the KIC with increasing data set size. In our case, the contribution of the terms dismissed by the BIC (see section 3.2) is still significant and hence produces a relevant deviation between the two BME approximations.
The AIC shows a linear dependence on data set size in this semilog plot. As expected, the AICc converges to the AIC with increasing data set size. Still, both variants of the AIC produce a relative error of more than 30%, which even increases with increasing data set size to more than 300% in this specific test case. Again, be reminded that the AIC(c) is only derived for comparing models with each other by the means of model weights, not as an approximation to the absolute BME value.
We investigate the reasons for the different behavior of the ICs over data set size by separating the likelihood term from the Occam factor penalty term (see section 3.2.6). Figure 4c shows how the true likelihood term (here: KIC@MAP) is approximated by the other ICs. Obviously, approximating this term produces negligible errors if the data set size is reasonably large, i.e., if the MAP and the MLE almost coincide. The problems in BME approximation clearly stem from the challenge of approximating the Occam factor (Figure 4d). The true Occam factor (or complexity penalty term) decreases with data set size. The KIC@MLE converges to this true behavior. The BIC is able to closely approximate the true curve, but does not yet converge to it in the range analyzed here. The penalty term of the AIC is a constant, which intersects the BIC's penalty term curve at Ns = 7 (see explanation in section 3.2.5). The penalty term of the AICc variant is converging to the constant AIC from below, i.e., it is increasing in contrast to the true, decreasing behavior. We conclude that the ICs differ substantially in the way they approximate the penalty term and therefore yield very different BME approximations with huge relative errors observed for the AIC and AICc.
Note that the results for Ns = 15 measurements, marked with circles in Figure 4, are similar, but not equal to the results we showed in Figure 3. This is due to the fact that to investigate the influence of data set size, we have marginalized over the random measurement error, while as a base case, we presented results for just one specific outcome of measurement error. We chose this scenario on purpose to illustrate that all those approximation methods which do not explicitly account for the sensitivity of the parameters to the specific data set, suffer from unpredictable behavior. The range of potential relative errors (95% Bayesian confidence intervals) over all 200,000 random realizations of measurement errors are shown as shaded areas in Figure 4b. It becomes clear that, up to a data set size of about Ns = 20 in our test case, none of the specific ICs would be a reliable choice: the AIC, AICc, and BIC could potentially yield very low (<1%) or very high (>100%) relative errors. Choosing the KIC@MLE is a more reliable choice, since it shows narrower bounds of potential relative errors, but still results in intolerable errors up to a data set size of about 30 in this case. We will elaborate on the question of how to make a safe choice of BME evaluation method in section 6.
Results for Varied Prior Information
Next, we investigate the behavior of the ICs for varied prior information. Figure 5 compares the influence of the prior width (left column) with the influence of varied distance between the MLE and the prior mean, i.e., of a shifted prior (right column). Again, we present the BME approximation (Figures 5a and 5e) and its relative error (Figures 5b and 5f), and the KIC@MAP represents the true solution. The AIC, AICc, and BIC approximations are constant over both variations, because they are not able to detect any information about the prior beyond the sheer number of parameters. In theory, however, increasing the prior width and moving the prior away from the area of high likelihood, both lead to a decrease in BME, which can be seen in the BME curve obtained by the KIC@MAP. While BME stabilizes at some point when increasing the prior width to a fully uninformative prior, it falls steeply if the prior is shifted farther away. This is important to keep in mind, because also the systematic relative errors in approximation (Figures 5b and 5f) are much larger for the shifted prior.
Figure 5.
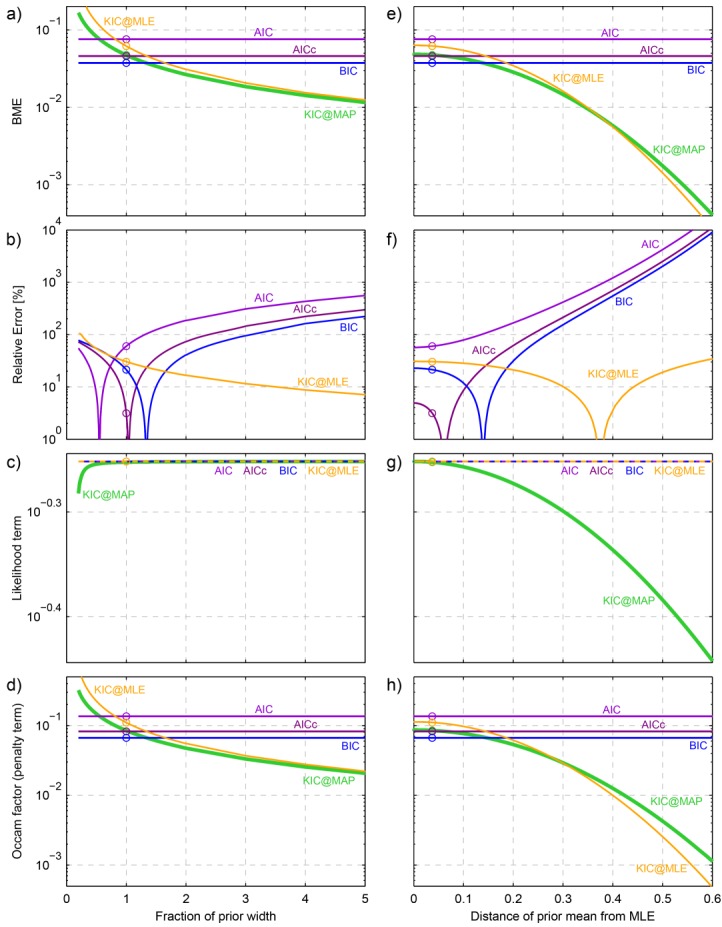
(left) Results obtained for the synthetic test case as a function of prior width and (right) as a function of distance between prior mean and MLE. (a and e) Approximation of BME, (b and f) relative error with respect to the analytical solution, (c and g) likelihood term approximation, (d and h) Occam factor approximation. The result obtained from KIC@MAP represents the analytical solution in this case.
Only the KIC@MLE is able to track the variations in prior information and yields acceptable errors in both BME approximation and the approximation of the individual terms (likelihood term, Figures 5c and 5g, and penalty term, Figures 5d and 5h). Nevertheless, this error is in the range of 10%. In the case of increased prior width, the KIC@MLE converges to the true solution because the MAP moves toward the MLE, and, at the same time, the posterior covariance is approximated more closely by the covariance around the MLE. In contrast, there is no such convergence behavior with decreasing distance between the MLE and the prior mean, because in that case only the MAP moves toward the MLE, but the covariances do not coincide if the prior is still somewhat informative. Therefore, the solution of the KIC@MLE deviates from the true BME value even if the MAP is equal to the MLE, still producing a relative error of 30%.
For increasing distance between the MLE and the prior mean, the approximation of the likelihood term (Figure 5g) by MLE-based criteria deteriorates significantly. Since neither the likelihood term nor the penalty term are adequately approximated by the AIC, AICc, or BIC, substantial errors in BME approximation arise. There are poles in the relative error curves, where they cut the analytical solution. These locations are, however, dependent on the actual model at hand and on the outcome of the measurement error, and can therefore not be predicted a priori. Again, preferring any IC among AIC, AICc, and BIC as an approximation to BME is not a reliable choice as already pointed out when analyzing their performance over data set size. We will discuss implications of this finding in section 6.
Results for Varied Model Structure
In this section, we illustrate the influence of model structure on the BME approximation quality achieved by the nine different evaluation methods. In the previous sections, we have investigated the behavior of the ICs for varied data set size and varied prior information under optimal conditions, i.e., their underlying assumption of a Gaussian posterior distribution was fulfilled. For the nonlinear models considered here, this is no longer the case. This setup therefore represents a more realistic setting where no analytical solution exists. In order to still be able to assess the differences in approximation quality, we generate a reference solution with brute-force MC integration. We choose this method as reference for its absence of assumptions (section 3.3.1), i.e., its unrestricted applicability to any arbitrary (linear or nonlinear) setup, and for its precision and accuracy in BME approximation as demonstrated in the first step of our synthetic test case (section 4.2).
The relative approximation errors made by the different BME evaluation methods for the four different models are listed in Table2. The performance of the numerical methods is comparable to the results shown in the previous sections, since their approximation quality is not directly related to model structure (but might be influenced by the shape of the area of high likelihood). Results for the AIC, AICc, and BIC vary arbitrarily with regard to model type and model dimensionality. We have shown that their approximation quality hugely depends on the actual data set (cf. section 4.3). This effect seems to be similarly strong here, mixing with errors due to the linear approximation of the complexity penalty term and due to violations of the underlying assumptions by the nonlinear models. The KIC variants show a much clearer tendency to fail with increasing nonlinearity of the model. The KIC@MAP is equal to the true solution in the case of the linear models L1 and L2, but not in the nonlinear case of the models NL2 and NL4. Since its approximation is perfect under linear (and multi-Gaussian) conditions, the deterioration in approximation quality for the nonlinear models clearly shows its deficiencies if these assumptions are not fulfilled. The KIC@MLE additionally suffers from differences in the location of the MAP and the MLE, which seems to cause similar trouble in the linear case (L2) and in the weakly nonlinear case (NL2). Note that the KIC@MLE suffers more strongly than the other ICs considered in this study, since not only its likelihood term, but also its Occam factor (penalty) term depends on this chosen point of expansion (see section 4.4).
Table 2.
Relative Error of BME Approximation Methods for Different Model Structures as Compared to the Reference Solution (Analytical Solution Equal to the KIC@MAP in Case of Linear Models, Brute-Force MC Integration in Case of Nonlinear Models, Highlighted in Italic Font)a
| Method |
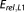 (%) (%) |
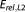 (%) (%) |
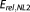 (%) (%) |
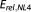 (%) (%) |
|---|---|---|---|---|
| KIC@MLE | 0.9 | 30.4 | 24.9 | 99.8 |
| KIC@MAP | 0.0 | 0.0 | 13.2 | 59.4 |
| BIC | 94.0 | 21.3 | 37.5 | 70.3 |
| AIC | 176.4 | 59.7 | 179.2 | 22.5 |
| AICc | 137.0 | 3.2 | 69.4 | 83.4 |
| MC | 0.0 | 0.0 | 0.0 | 0.0 |
| MC IS | 0.8 [0.0; 2.2] | 0.1 [0.0; 0.4] | 1.1 [0.0; 2.9] | 1.5 [0.1; 4.1] |
| MC PS | 132.0 [25.7; 196.6] | 131.8 [23.5; 221.7] | 324.8 [40.8; 490.3] | 232.8 [18.1; 481.8] |
| NS | 2.4 [0.1; 6.4] | 2.8 [0.4; 27.2] | 4.0 [0.2; 10.7] | 11.2 [3.3; 18.9] |
95% Bayesian confidence intervals of numerical results given in parentheses.
Impact of Approximation Errors on Model Selection
The overestimation or underestimation of BME itself might not be a major concern, if it yielded consistent results in model weighting, i.e., if the estimated BME values were correlated with the exact values, so that ratios of BME between alternative models were consistent. Furthermore, the AIC(c) is derived to assess differences between competing models, and one would expect to see a better approximation to the true model weights than to the absolute BME values. To investigate this, we determine the model ranking for the four models described in section 4.1. We further introduce two additional versions of the base case model L2 by using two different prior distributions: Model L2a (see Figure 2) acts on an informative prior which has a significant overlap with the area of high likelihood. Model L2b uses a slightly less informative prior, which is significantly shifted away from the area of high likelihood. Model L2a is therefore clearly the favorite among those two model versions, because it makes better predictions while being even more parsimonious. We deliberately include those two versions as competing models to illustrate the inability of the AIC(c) and the BIC to detect differences in the parameter prior. We assign equal prior weights to all six models to let BME be the decisive factor in model averaging (see equation (2)).
Figure 6 shows the resulting posterior model weights as obtained from the different approximation methods, with the model weights of L2b, NL2, and NL4 additionally displayed on a logarithmic axis for better visual inspection. The ranking obtained from simple MC integration with an ensemble of 10 million realizations per model is used as reference solution. The solution obtained for the KIC@MAP coincides with the true weighting according to Bayes' theorem in case of the linear models L1, L2a, L2, and L2b, since the underlying assumption for the Laplace approximation is fulfilled. The results of simple MC integration (MC) and MC integration with importance sampling (MC IS) are shown in one bar in Figure 6 because, as demonstrated for the base case, they yield nearly identical results. MC integration with sampling from the posterior (MC PS) yields a biased result for model ranking, while nested sampling (NS) yields, on average, a very accurate result of model weighting, which indicates that the potential bias in overestimation or underestimation of BME induced by the somewhat arbitrary choice of termination criteria is consistent (correlated with the true value across the competing models).
Figure 6.
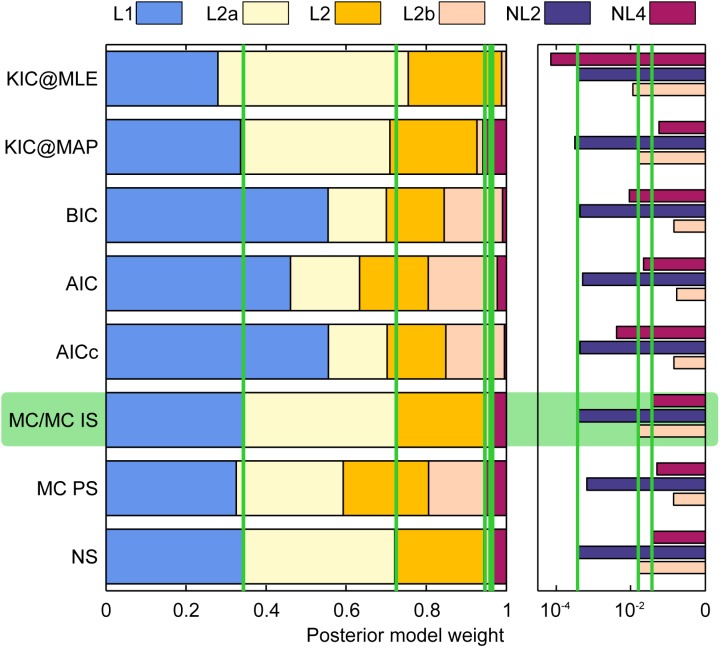
Posterior model weights as obtained from the different BME evaluation methods for linear (L1, L2) and nonlinear (NL2, NL4) models. L2, L2a, and L2b represent the same linear model with differently shaped priors. Green vertical lines indicate reference solution (obtained from brute-force MC integration).
The AIC, AICc, and BIC assign a too large weight to the simplest model in the set (L1). This is due to the fact that these criteria merely count the number of parameters used by a model, instead of considering correlations among the parameters (defined by the parameter prior) which reduce the actual degrees of freedom. Furthermore, these criteria are not able to distinguish between the three models L2a, L2, and L2b, which only differ in their prior parameter assumptions, but not in their respective MLE. The corresponding BME approximations by AIC, AICc, and BIC therefore yield the most indecisive weighting for these three models (equal weights), whereas the true BMA weights convey the clear message that, out of these three models, L2a should be preferred over L2, and L2b should be discarded.
Within this model set, the nonlinear models obtain very small weights (see Figure 6) in the reference solution because the model structure of NL2 does not match the data well and NL4 is already too complex to compete with the simpler linear models. Since the BME approximation errors of the KIC variants increase drastically with the nonlinearity of the models, these errors are expected to impact model ranking significantly if nonlinear models are playing a relevant role in the model selection competition. Here the nonlinear models play an almost irrelevant role and thus model ranking is not too badly compromised when using the KIC@MLE or the KIC@MAP, with the latter still outperforming the former.
Conclusions From Synthetic Test Case
The benchmarking has shown that all ICs (except for the KIC@MAP) potentially yield unacceptably large errors in BME approximation. Their performance depends on the actual data set (including the outcome of measurement error) that is used for calibration. We have learned that the AIC and AICc behave differently from the BIC and KIC for increasing data set size, i.e., the error made by the AIC(c) increases, while the error of the BIC and KIC decreases. Under varied prior information, however, the BIC follows the error behavior of the AIC(c) in that it cannot distinguish models which only differ in their prior definition of the parameter space. This is a crucial finding, since the prior contains all the information about the flexibility of a model and is the basis for an adequate punishment of model complexity. Also, differences in model dimensionality cannot be adequately captured by those ICs. Among the ICs considered here, the KIC@MLE is closest to the true solution, which is identical to the KIC@MAP in the linear case. The performance of the KIC under nonlinear conditions deteriorates toward unacceptable approximation errors in both its versions, while the KIC@MAP still outperforms the KIC@MLE. Except for MC integration with posterior sampling, we have shown that the numerical methods considered here are capable of approximating the true BME value with satisfying accuracy, if the required computational power is affordable. Out of the numerical methods, simple MC integration and MC integration with importance sampling show the highest accuracy and lowest uncertainty for a given computational effort, which is in agreement with the theoretical basis of the respective methods (see section 3.4). Our findings regarding the approximation quality of the absolute BME value also apply to the approximation quality of the resulting model weights in this synthetic case, with one exception: nested sampling proves to yield a similarly accurate model ranking despite its slightly higher BME approximation errors as compared to MC integration.
Real-World Application to Hydrological Model Selection
In this section, we describe the application of the BME approximation methods presented in section 3 to real-world hydrological model selection. Due to the nonlinearity in the hydrological models considered here, no analytical solution exists. As already argued in section 4.5, we generate a reference solution by investing a large amount of computational effort into a brute-force MC integration. Hydrological model selection based on discharge measurements as presented here can be seen as a relatively simple model selection task, since generally a large number of measurements is available, which emphasizes differences in model behavior. In other disciplines, model selection might become more difficult, as the number of measurements and their information content are typically limited. Therefore, this real-world application can still be considered as a rather good-natured case of model selection. BME evaluation methods which fail in this application are expected to perform similarly insufficiently or even worse in other applications.
Setup and Implementation
We use the distributed mesoscale hydrologic model (mHM, Version 4.0) [Samaniego et al., 2010] to illustrate the performance of the different BME approximation methods in hydrological model selection. mHM is based on numerical approximations of dominant hydrological processes that have been tested in various existing hydrological models (e.g., in HBV [Bergström et al., 1997] and VIC [Liang et al., 1996]). It features a novel multiscale parameter regionalization technique to treat subgrid variability of input variables and model parameters [Samaniego et al., 2010; Kumar et al., 2010]. A detailed description of mHM can be found in Samaniego et al. [2010], Kumar et al. [2010], and Wöhling et al. [2013] and is therefore not repeated here. The model is applied to the Fils river catchment (area 361 of the Upper Neckar basin, Southwest Germany, using daily discharge measurements for the time period between 1980 and 1988. Please refer to sub-catchment 17 in Wöhling et al. [2013] for details on the model setup and a multicriteria model calibration. The original model considers two soil layers and employs 53 global parameters, 33 of which have been found sensitive to discharge predictions in a sensitivity analysis conducted prior to this study (results not shown here). This model is subsequently referred to as mHM2L. For the purpose of this study, a slightly simpler model with a single soil layer was built (mHM1L), where 29 of the 53 global parameters have been found sensitive to discharge predictions. Conventional model calibration for these two models yields Nash-Sutcliffe efficiencies (NSE) [Nash and Sutcliffe, 1970] of 0.9309 and 0.9073 for mHM2L and mHM1L, respectively. These values indicate that both models are able to adequately reproduce the observed discharge time series.
of the Upper Neckar basin, Southwest Germany, using daily discharge measurements for the time period between 1980 and 1988. Please refer to sub-catchment 17 in Wöhling et al. [2013] for details on the model setup and a multicriteria model calibration. The original model considers two soil layers and employs 53 global parameters, 33 of which have been found sensitive to discharge predictions in a sensitivity analysis conducted prior to this study (results not shown here). This model is subsequently referred to as mHM2L. For the purpose of this study, a slightly simpler model with a single soil layer was built (mHM1L), where 29 of the 53 global parameters have been found sensitive to discharge predictions. Conventional model calibration for these two models yields Nash-Sutcliffe efficiencies (NSE) [Nash and Sutcliffe, 1970] of 0.9309 and 0.9073 for mHM2L and mHM1L, respectively. These values indicate that both models are able to adequately reproduce the observed discharge time series.
A uniform prior is assumed for the sensitive parameters with parameter ranges set to mHM-recommended values [see Kumar et al., 2010]. The insensitive parameters are fixed at midrange.
From a preprocessing analysis, the residuals between predictions and observations were found to be heteroscedastic, which is often encountered in hydrological modeling [Sorooshian and Dracup, 1980]. To mitigate heteroscedasticity, we applied a Box-Cox transformation [Box and Cox, 1964] to both discharge predictions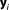 and discharge observations
and discharge observations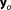 :
:
| (28) |
A value of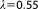 proved to be best suitable to reduce heteroscedasticity and to achieve a satisfying compromise in the fit to both high-flow and low-flow periods. The remaining variance in residuals is attributed to both measurement noise and conceptual errors. If only tested against measurement noise, both models (just like any other conceptual model) would be rejected from the statistical viewpoint [Reichert and Mieleitner, 2009] despite the high NSE values reported above, because not all observations can be reproduced within measurement error bounds. The residuals appeared to be correlated to a varying extent on different time scales (most likely due to superposition of seasonal trends and event-based model deficiencies), such that we could not identify a parsimonious correlation model that would reasonably explain the observed patterns. Since the identification of more elaborate but robust error models [see e.g., Del Giudice et al., 2013; Evin et al., 2014] is beyond the scope of our study, we restricted ourselves to a simple uncorrelated error that increases with discharge in the untransformed space, similar to a relative error. We chose a relatively large and constant standard deviation of 4.4
proved to be best suitable to reduce heteroscedasticity and to achieve a satisfying compromise in the fit to both high-flow and low-flow periods. The remaining variance in residuals is attributed to both measurement noise and conceptual errors. If only tested against measurement noise, both models (just like any other conceptual model) would be rejected from the statistical viewpoint [Reichert and Mieleitner, 2009] despite the high NSE values reported above, because not all observations can be reproduced within measurement error bounds. The residuals appeared to be correlated to a varying extent on different time scales (most likely due to superposition of seasonal trends and event-based model deficiencies), such that we could not identify a parsimonious correlation model that would reasonably explain the observed patterns. Since the identification of more elaborate but robust error models [see e.g., Del Giudice et al., 2013; Evin et al., 2014] is beyond the scope of our study, we restricted ourselves to a simple uncorrelated error that increases with discharge in the untransformed space, similar to a relative error. We chose a relatively large and constant standard deviation of 4.4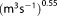 for this lumped error in transformed space as a mild penalty for deviations from the observations. The sheer length of the observed time series nevertheless led to an effective reduction of parameter and prediction uncertainty, i.e., to a successful and reliable calibration. Posterior uncertainty in discharge predictions was reduced to around 5% of prior uncertainty for both models. Our chosen error parameterization is represented as an error matrix
for this lumped error in transformed space as a mild penalty for deviations from the observations. The sheer length of the observed time series nevertheless led to an effective reduction of parameter and prediction uncertainty, i.e., to a successful and reliable calibration. Posterior uncertainty in discharge predictions was reduced to around 5% of prior uncertainty for both models. Our chosen error parameterization is represented as an error matrix with entries on the main diagonal. The Gaussian likelihood function to be evaluated in equation (7) then takes the form:
with entries on the main diagonal. The Gaussian likelihood function to be evaluated in equation (7) then takes the form:
| (29) |
with the last term being the derivative of the transformed observations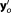 with respect to the untransformed observations
with respect to the untransformed observations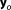 . Prior and posterior predictions of discharge as obtained from both models are shown for the first year of the observation time series in Figure 7.
. Prior and posterior predictions of discharge as obtained from both models are shown for the first year of the observation time series in Figure 7.
Figure 7.
Model predictions of discharge for first year of calibration time series. (a) mHM1L, (b) mHM2L. Prior 95% Bayesian confidence intervals are shaded in gray, posterior 95% Bayesian confidence intervals in respective color.
The reference BME value for each model was determined by MC integration (equation (23)) over ensembles of 1.1 million realizations per model. Effective sample sizes [Liu, 2008] (the number of prior realizations that significantly contribute to the posterior distribution) of 95 for the double-layer model (mHM2L) and of 27 for the single-layer model (mHM1L) were considered to be sufficiently large to produce a reliable statistic of BME. We again performed a numerical convergence analysis (see section 4.1), which confirmed that the BME estimate is varying less than 1%.
Based on this reference solution, we assess the approximation quality of the different methods presented in section 3. From a posterior parameter ensemble of size 25,000 generated by DREAM, we determine the MAP (and the covariance matrix needed for the evaluation of the KIC). In this case, the MAP is equal to the MLE due to the uniform prior parameter distributions, and because the MLE does not fall outside of the bounds of the prior. We evaluate the AIC, BIC, and KIC at this parameter set. Note that, when using the full calibration time series with Ns = 3227 measurements, we do not consider the AICc, because it yields the same results as the AIC. This is expected since the ratio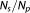 is much larger than 40 and, therefore, there is no need to correct for a small data set size (see section 3.2.5). Importance sampling is performed with Gaussian sampling distributions that are centered about the MLE (obtained from DREAM) with the same standard deviations as specified for the prior parameter distributions. 100,000 realizations are generated from each model. Nested sampling is performed with an initial ensemble size of 500. The same termination criteria as described in the synthetic test case (section 4) are used. This leads to a total ensemble size (number of model calls) of around 110,000.
is much larger than 40 and, therefore, there is no need to correct for a small data set size (see section 3.2.5). Importance sampling is performed with Gaussian sampling distributions that are centered about the MLE (obtained from DREAM) with the same standard deviations as specified for the prior parameter distributions. 100,000 realizations are generated from each model. Nested sampling is performed with an initial ensemble size of 500. The same termination criteria as described in the synthetic test case (section 4) are used. This leads to a total ensemble size (number of model calls) of around 110,000.
All BME approximation methods are assessed with regard to the error in reproducing the absolute BME value as well as with regard to model ranking. Since all mathematical approximation methods drastically underestimate BME in this test case and relative errors would all end up being 100%, we specify the approximation error instead by determining the ratio between approximate and reference BME value and taking the natural logarithm:
| (30) |
A good approximation will hence be characterized by a ratio of close to 1 and an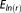 value of close to 0. A negative value indicates that the approximation underestimates the reference value, and a positive value indicates overestimation. The impact on model ranking is evaluated by comparing the resulting model weights (equation (2)).
value of close to 0. A negative value indicates that the approximation underestimates the reference value, and a positive value indicates overestimation. The impact on model ranking is evaluated by comparing the resulting model weights (equation (2)).
Results for Full Observation Time Series
When using the full observation time series of 3227 daily discharge measurements for calibration, BME takes a very small value since the likelihood of a parameter set is the product of the relatively small likelihoods for each data point. We therefore report the natural logarithm of the BME value instead. The reference ln(BME) values as obtained from MC integration are −10,003 for the single-layer model (mHM1L) and −9991 for the double-layer model (mHM2L). While the numerical methods and the KIC arrive relatively close to this reference solution, the AIC and BIC drastically underestimate the reference values (see Table3). Again, the AIC might be excused because it is not derived for approximating the absolute BME value, but for approximating the differences in models via model weights. The numerical methods tend to overestimate BME (especially posterior sampling and importance sampling), while the KIC underestimates instead. Nested sampling yields the most accurate results of all numerical methods (besides the MC reference solution that has a roughly 10-fold computational effort). MC integration with importance sampling leads to an overestimation of BME here. This indicates that the choice of importance density is already close enough to the posterior parameter density to inherit (some of) the biasedness of MC integration with posterior sampling (see section 3.3.3). Results of all approximation methods are summarized in Table3.
Table 3.
Performance of BME Approximation Methods in Hydrological Test Case as Compared to the Brute-Force MC Reference Solution (Highlighted in Italic Font)
| Method | Full Time Series |
Reduced Time Series |
||
|---|---|---|---|---|
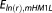 |
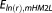 |
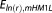 |
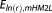 |
|
| KIC | −5.2 | −7.2 | −6.8 | −8.4 |
| BIC | −103.1 | −120.6 | −79.7 | −92.1 |
| AIC | −15.0 | −20.3 | −23.1 | −27.8 |
| AICc | −25.7 | −31.2 | ||
| MC | 0.0 | 0.0 | 0.0 | 0.0 |
| MC IS | 1.4 | 3.3 | 1.0 | 1.5 |
| MC PS | 3.1 | 4.8 | 0.8 | 1.0 |
| NS | 1.1 | 0.5 | 0.3 | −0.1 |
Based on BME values, the double-layer model mHM2L is the clear winner in this model comparison. Although both models exhibit a good predictive performance which is confirmed by NSE values greater than 0.90, mHM2L outperforms mHM1L because the concept of two soil layers is able to mimic the water retention capacity and the water movement in the unsaturated zone better than a single soil layer. This leads to a slightly but notably better fit of the simulated discharge hydrograph to the data. With regard to model complexity, both models use the same number of parameters, but differ in the number of sensitive (nonfixed) parameters. Even though the number of sensitive parameters is slightly smaller for mHM1L than mHM2L (29 versus 33), the size of the parameter space as defined by the prior density is larger in the case of mHM1L due to the actual permitted range of parameter values; i.e., some sensitive parameters of mHM1L, which are fixed in mHM2L, have a larger range of values. As a consequence, there is no trade-off between goodness of fit and model complexity, and model mHM2L obtains a full posterior model weight of 100% (mHM1L obtains a weight of 0.0004% in the reference solution).
All numerical methods as well as the KIC and AIC agree with the reference model weights. The BIC, however, yields the exact opposite: It assigns a weight of 99.4% to the competing model, mHM1L. The BIC's parameterization of the Occam factor is in this case the decisive (and guilty) factor, because the difference in the countable number of parameters is large enough to compensate the slightly better goodness of fit, which is in reality not the case. Posterior model weights are visualized in Figure 8a. Although the quality of approximation achieved by the different methods varies drastically, the model ranking and model selection result is (except for BIC) extremely clear and correct. This is due to the fact that the difference in goodness of fit is significantly large, in favor of mHM2L. This is mirrored in the difference of maximum likelihoods between both models, and is therefore detected by the ICs.
Figure 8.
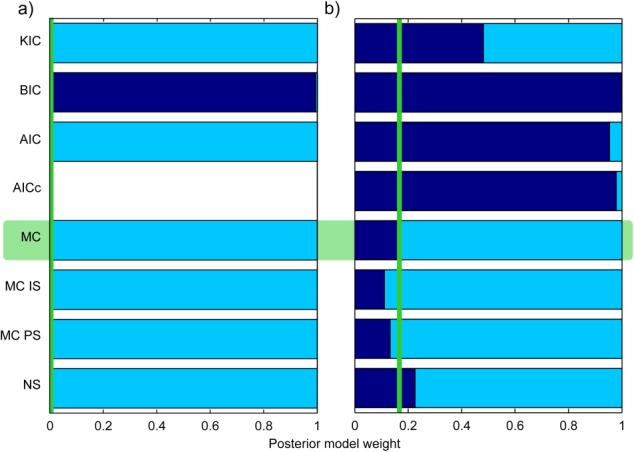
Posterior model weights for (a) full observation time series and b) reduced observation time series as obtained from the different BME evaluation methods for models mHM1L (dark blue) and mHM2L (light blue). Green vertical line indicates reference solution generated by MC integration.
Previous studies on hydrological model selection have yielded similar results in that one model obtained an IC weight of close to 100% [e.g., Meyer et al., 2007]. Lu et al. [2013] have interpreted this clear weighting as too “aggressive,” because it did not seem justified given the available data and prior knowledge. They therefore propose to use a different formulation for the likelihood function which considers not only uncorrelated (measurement) errors, but also correlated model structural errors. This led to a less clear weighting for all of the ICs that are also considered here. Tsai and Li [2010] proposed a different procedure, but following the same line of thought: They suggest to modify the calculation of the model weights by scaling the IC results in order to obtain a less obvious model ranking. Ye et al. [2010a] used the generalized likelihood uncertainty estimation method (GLUE) [Beven and Binley, 1992]), which penalizes deviations from the observed values in a nonformal, user-specified manner. They calculated posterior model weights merely based on GLUE-likelihoods of the calibrated models (which does not incorporate any Bayesian penalty for complexity) and compared them with model weights obtained from ICs, also finding that ICs seem to discriminate too harshly. Rojas et al. [2008], on the other hand, compared different (formal and informal) likelihood formulations within the theoretical BMA framework, but did not find significant differences in the resulting model weights.
We would like to add to this discussion by pointing out that the choice of likelihood function clearly influences the outcome of BME and, potentially, the resulting model weights as a consequence. If uncorrelated errors are assumed, the likelihood for all individual data points are multiplied. If, for a long data series, one model at all times predicted only slightly worse than its opponent, multiplying all the slightly lower likelihoods would lead to a drastically lower total likelihood and hence to a significantly lower BME value. BMA theory therefore supports the finding that, if only enough data points are available for calibration (and such a type of likelihood function is used), one model will be the clear winner—no matter if the competing model is performing very well, too, as it is the case in our application.
This might seem counter-intuitive, as one would argue that there is not necessarily more information about model choice in a more frequently measured time series. But it needs to be kept in mind that the clear model ranking is only based on the calibration period, i.e., the models might behave very differently under changing boundary conditions. Hence, the choice of the calibration period, the sampling frequency and the definition of the likelihood function lie in the responsibility of the modeler and should be subject to further research. In summary, overly decisive weights are not an artifact of BME evaluation via ICs. They are a characteristic of BMA theory (and hence also of BME evaluation via numerical methods). Future investigations on the adequate choice of likelihood functions should therefore consider a suitable numerical method as a reference for the true characteristics of the BMA framework.
We hypothesize that, if the difference in model performance was not as dominant, model ranking would not be as obvious and not as accurately reproduced by approximation methods. To test this hypothesis, we shorten the observation time series in the spirit of a thought experiment and only consider the first year for calibration. By virtue of reducing the number of data points, the difference in goodness of fit will not be as pronounced because the multiplication of likelihoods for each data point of the time series will have a much less drastic effect. We do not advocate to use such a short time series for proper hydrological model calibration, but proceed with it in section 5.3 to illustrate the impact of the number of observations. Note that we do not change the analysis framework here (neither the definition of the likelihood function nor the formulation of how to calculate model weights from ICs) as suggested by the authors listed above, but actually change the amount of information that goes into the BMA analysis. Using the reduced time series for model selection can also be seen as representative for more difficult model selection tasks in other disciplines that have to cope with a limited number of measurements.
Results for Reduced Observation Time Series
When using the reduced observation time series of 365 daily discharge measurements for calibration, BME takes values of −1134 for the single-layer model (mHM1L) and −1132 for the double-layer model (mHM2L) in the reference solution. As intended, the difference in goodness of fit and therefore in BME values is now much less pronounced. Again, the numerical methods and the KIC achieve relatively good results. The AIC, AICc (considered here since ), and BIC again drastically underestimate the reference values. Nested sampling consistently yields the most accurate BME value. Approximation results are summarized in Table3.
), and BIC again drastically underestimate the reference values. Nested sampling consistently yields the most accurate BME value. Approximation results are summarized in Table3.
This setup now leads to a less decisive weighting of 16.5% (mHM1L) versus 83.5% (mHM2L) in the reference solution. Apparently, the difference in performance over the reduced time series is now small enough such that model mHM1L should not be discarded, despite its slightly larger parameter space. Nevertheless, mHM2L still obtains a significantly larger posterior probability of being the better model due to its more suitable representation of water retention capacity and water movement in the unsaturated zone. This time, however, not only the BIC yields model weights erroneously in clear favor of mHM1L, but also the AIC and AICc (even though they are derived for approximating BMA weights). Despite its BME approximation quality being inferior to nested sampling, posterior sampling surprisingly yields weights closest to the reference solution. Nested sampling and importance sampling weights still convey a similar message, but already deviate significantly from the reference weighting. Here the KIC yields indecisive weights of 51.9% versus 48.1% and therefore does not qualify as a reliable approximation method. Resulting model weights are visualized in Figure 8b.
Conclusions From Real-World Test Case
From this real-world test case, we have found that, still, the KIC performs best out of the ICs considered here, but it produces a much larger approximation error than any of the numerical methods. All of the methods used in this study, except for the BIC, are able to reproduce the reference model weighting when using a large calibration data set. The BIC yields exactly the opposite model ranking and therefore contradicts the true Bayesian model ranking, even in such a good-natured model selection problem where a large data set is available. The fact that the BIC did not perform particularly badly (e.g., definitely not worse than the AIC) in the synthetic setup (section 4) is alarming, because this means that there is not necessarily a correlation between the ICs' performance under linear conditions with their performance under nonlinear (but still good-natured) conditions. When using a significantly shorter time series, the quality of BME approximation deteriorates for the AIC and improves in case of the BIC, while the approximation quality of the KIC slightly decreases. This was expected from our investigation of the influence of the data set size in the synthetic test case (see section 4.3). Independently of the actual BME approximation quality, all ICs yield inaccurate posterior model weights. We therefore have to face the fact that the ICs considered here produce a rather arbitrary model ranking result in nonlinear real-world applications, and their accuracy cannot be predicted in a general manner. Only the numerical methods are able to reproduce the true model ranking reliably and sufficiently well.
Summary and Conclusions
In this study, we have compared nine methods to approximate Bayesian model evidence (BME), which is required to perform Bayesian model averaging (BMA) or Bayesian model selection. Since analytical solutions only exist under strongly limiting assumptions, we have investigated the usefulness of four numerical methods (simple MC integration, MC integration with importance sampling, MC integration with posterior sampling, and nested sampling) which do not rely on any assumptions, but suffer from high computational effort and potential inefficiency in high parameter dimensions. We have further considered four different mathematical approximations which are known as information criteria (AIC, AICc, BIC, and KIC evaluated at the MLE) and are frequently used in the context of BMA, but in previous studies yielded contradicting results with regard to model ranking. To be most consistent with approximation theory, we have proposed to evaluate the KIC at the MAP, instead, and also included this variant in our intercomparison. The nine BME evaluation methods analyzed in this study are summarized in Table4.
Summary of Results
We have systematically compared these nine approximation techniques with regard to their theoretical derivations, common features, and differences in underlying assumptions. From this extensive analysis, we conclude that out of the ICs, the KIC evaluated at the MAP (KIC@MAP) is the most consistent one with BMA theory, but also the most expensive one to evaluate. It yields the true solution if the posterior parameter distribution is Gaussian (e.g., if the data set is large). The other ICs considered here are simplified versions of the KIC@MAP (KIC@MLE and BIC) or derived in a non-BMA context (AIC and AICc). Since the ICs' assumptions to calculate BME are too strong for nonlinear models or lack the correct theoretical foundation altogether, the contradicting reports on their performance at various accounts in the literature were to be expected. The numerical methods considered here are not limited by any assumptions. Simple MC integration is bias-free, but computationally very expensive. The other numerical methods are potentially more efficient, but prone to show a bias in their BME estimate. The most important assumptions and limitations of the nine BME evaluation methods analyzed in this study are summarized in Table4.
The main contribution of this study is a first-time benchmarking of the different methods on a simplistic synthetic example where an exact analytical solution exists. The benchmarking has shown that all ICs (except for the KIC@MAP) potentially yield unacceptably large errors in BME approximation, with their performance depending on the actual calibration data set. Therefore, it cannot be recommended to use either of these criteria for a reliable, accurate approximation of BME. Especially, the AIC(c) and BIC cannot distinguish models which only differ in their prior definition of the parameter space. This is a major concern, since the specification of prior information is a fundamental part of Bayesian inference and Bayesian model ranking. It is misleading to think that the AIC(c) or BIC would perform acceptably if prior information is vague or not available; we have demonstrated that actually the opposite is the case. Also, these criteria are incapable of capturing the true dimensionality of a model. It remains an open question for future investigation, whether model dimensionality could be more adequately “encoded” in these ICs to improve their so far unacceptable performance in BME approximation. While the KIC@MAP represents a perfect choice if its assumptions are fulfilled, its performance deteriorates significantly with increasing nonlinearity in the considered models as illustrated in the second part of our synthetic example. The accuracy of BME approximation by the numerical methods considered here is only limited by computational effort (except for MC integration with posterior sampling, which is expected to overestimate BME due to its theoretical formulation). Simple MC integration and MC integration with importance sampling showed the highest accuracy and lowest uncertainty for a given computational effort, which agrees with the expectations based on the theoretical background of the respective methods.
We have continued our analysis with a real-world application to hydrological model selection. We have compared two conceptually slightly different versions of the distributed mesoscale hydrologic model (mHM) [Samaniego et al., 2010], which are applied to the Fils river catchment of the Upper Neckar basin in Southwest Germany. Here the nonlinearity in model equations represents a typical case where the assumptions of the analytical solution or the Laplace approximation are not fulfilled. Based on the findings from our theoretical comparison and the benchmarking, we have therefore used simple MC integration as reference solution. In this realistic setup, the KIC again performs best out of the ICs considered in this study, but it produces a much larger approximation error than any of the numerical methods. Using a long time series of daily discharge measurements between 1980 and 1988 for calibration, model choice turns out to be very clear, such that the conceptually superior model obtains a posterior model weight of 100%. In this case, all of the methods considered in this study, except for the BIC, reproduce this clear model weighting, despite their difficulties in approximating the actual value of BME. Note that the BIC yields exactly the opposite model ranking and therefore contradicts the true Bayesian model ranking, even in this good-natured model selection problem where a large data set is available. The BIC's much worse performance in the real-world application could not be foreseen from its performance in the synthetic setup. This fact is revealing, because it reminds us again that the approximation quality of the ICs is rather arbitrary and application-dependent, which has already become evident in the synthetic test case.
We have pointed out that BMA theory supports the finding from our studies and previous work that, if only enough data points are available for calibration, one model will be the clear winner, even if the competing model is also performing very well as in our application. This might seem counter-intuitive, but is not an artifact of approximating BME via ICs as previously suspected by other authors. To test our hypothesis that also the other ICs discussed here would not be able to yield a consistent ranking if the calibration time series were shorter (as would often be the case for model selection in disciplines other than hydrology), we have repeated the analysis using only the first year of measurements for calibration. We do not advocate to use such a short data set for a robust calibration of mHM, but provide this analysis to make the reader aware of the important role of the data set length. Independently of the actual BME approximation quality, all ICs yield inaccurate posterior model weights in this case, while the numerical methods are able to reproduce the true model ranking sufficiently well.
Implications for Robust Model Selection
Both test case applications have revealed that using ICs to approximate BME potentially can, but not necessarily will, produce acceptable results for both the absolute BME value and the resulting model ranking. The Bayesian trade-off between model performance and model complexity is not represented adequately by the ICs, with the potential exception of the KIC@MAP. However, it cannot be decided in advance if a data set is large enough for the KIC@MAP to perform well for a given application and model set. This is why we advocate to perform a comparison of the KIC@MAP with at least one of the numerical methods presented here, in order to assess the degree of agreement between the methods. If the discrepancy is large, one should continue with numerical methods if computationally feasible. If computation time is limited, nested sampling could be an efficient alternative to full MC integration as indicated by our test case results. If numerical evaluation is not an option at all because large model run times prohibit such an approach, we still do not recommend to compare several ICs amongst each other as frequently suggested in the literature, since this procedure cannot provide any conclusive insight. Instead, we suggest to solely use the KIC, evaluated at the MAP. Note that this still involves nonnegligible computational effort, since the MAP and the posterior covariance need to be determined; this could however be done by more efficient numerical optimization schemes. Nonetheless, finding a reliable alternative to numerical BME evaluation is still an open research question.
Conclusions
In conclusion, the findings from our theoretical intercomparison, the benchmarking results from our synthetic study as well as the insights from the application to a real-world hydrological model selection problem demonstrate that
for real-world applications, BME typically needs to be evaluated numerically or approximated by ICs because no analytical solution exists;
out of the ICs, the KIC evaluated at the MAP is the most consistent one, but might still be heavily biased when applied to nonlinear models;
the choice of evaluation method for BME substantially influences the deviation from the true BME value, the outcome of posterior model weights and model ranking as such;
for reliable model selection, there is still no reliable alternative to bias-free numerical methods.
Acknowledgments
The authors would like to thank the German Research Foundation (DFG) for financial support of the project within the International Research Training Group “Integrated Hydrosystem Modelling” (IRTG 1829) at the University of Tübingen and the Cluster of Excellence in Simulation Technology (EXC 310/1) at the University of Stuttgart. This work was also supported by a grant from the Ministry of Science, Research and Arts of Baden-Württemberg (AZ Zu 33–721.3-2) and the Helmholtz Centre for Environmental Research, Leipzig (UFZ). The authors also thank R. Kumar for setting up the mHM for the Neckar basin. The authors further acknowledge the collaboration of the German Weather Service DWD for providing the observational data set employed in this study, which can be obtained via the WebWerdis data portal (http://www.dwd.de/webwerdis). The discharge data were obtained from LUBW Landesanstalt für Umwelt, Messungen und Naturschutz Baden-Württemberg (http://www.lubw.baden-wuerttemberg.de/servlet/is/35855/). The data are “open to non-commercial research or training institutes, federal or state authorities and national meteorological services, which all fulfill the requirements of receiving the data free of charge.”
Key Points:
The choice of BME evaluation method influences the outcome of model ranking
Out of the ICs, the KIC@MAP is the most consistent one
For reliable model selection, there is still no alternative to numerical methods
References
- Ajami NK, Duan QY. Sorooshian S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007;43:W01403. and, doi: 10.1029/2005WR004745. [Google Scholar]
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Csaki F, editor; Petrov and BN, editor. Second International Symposium on Information Theory. N. Y: Springer; 1973. pp. 367–281. [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Trans. Automatic Control. 1974;19(6):716–723. doi: 10.1109/TAC.1974.1100705. [Google Scholar]
- Angluin D. Smith CH. Inductive inference: Theory and methods. ACM Comput. Surv. 1983;15(3):237–269. [Google Scholar]
- Bergström S, Carlsson B, Grahn G. Johansson B. A more consistent approach to catchment response in the HBV model. Vannet i Norden. 1997;4:1–7. [Google Scholar]
- Beven K. Binley A. The future of distributed models––Model calibration and uncertainty prediction. Hydrol. Processes. 1992;6(3):279–298. and, doi: 10.1002/hyp.3360060305. [Google Scholar]
- Box G. Tiao G. Bayesian Inference in Statistical Analysis. Reading, Mass: Addison-Wesley; 1973. [Google Scholar]
- Box GEP. Cox DR. An analysis of transformations. J. R. Stat. Soc., Ser. B. 1964;26(2):211–252. [Google Scholar]
- Buckland ST, Burnham KP. Augustin NH. Model selection: An integral part of inference. Biometrics. 1997;53(2):603–618. and, doi: 10.2307/2533961. [Google Scholar]
- Burnham KP. Anderson DR. Model Selection and Multimodel Inference: A Practical Information Theoretic Approach. 2nd. XXVI. N. Y: Springer; 2003. p. 488. and, vol. ed., [corr. print.] ed., pp. [Google Scholar]
- Burnham KP. Anderson DR. Multimodel inference––Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004;33(2):261–304. and, doi: 10.1177/0049124104268644. [Google Scholar]
- Chamberlin TC. The method of multiple working hypotheses. Science. 1890;15(366):92–96. doi: 10.1126/science.ns-15.366.92. [DOI] [PubMed] [Google Scholar]
- Claeskens G. Hjort NL. Model Selection and Model Averaging, Cambridge Ser. Stat. Probab. Math. Vol. 330. Cambridge, U. K: Cambridge Univ. Press; 2008. and, vol. [Google Scholar]
- Clark MP, Kavetski D. Fenicia F. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 2011;47:W09301. and, doi: 10.1029/2010WR009827. [Google Scholar]
- De Bruijn N. Asymptotic Methods in Analysis, Bibliotheca Mathematica. Vol. 4. Amsterdam, Netherlands: Dover; 1961. vol. [Google Scholar]
- DeGroot MH. Optimal Statistical Decisions. N. Y: McGraw-Hill; 1970. [Google Scholar]
- Del Giudice D, Honti M, Scheidegger A, Albert C, Reichert P. Rieckermann J. Improving uncertainty estimation in urban hydrological modeling by statistically describing bias. Hydrol. Earth Syst. Sci. 2013;17(10):4209–4225. and, doi: 10.5194/hess-17-4209-2013. [Google Scholar]
- Efron B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979;7(1):1–26. [Google Scholar]
- Elsheikh AH, Wheeler MF. Hoteit I. Nested sampling algorithm for subsurface flow model selection, uncertainty quantification, and nonlinear calibration. Water Resour. Res. 2013;49:8383–8399. and, doi: 10.1002/2012WR013406. [Google Scholar]
- Evans M. Swartz T. Methods for approximating integrals in statistics with special emphasis on Bayesian integration problems. Stat. Sci. 1995;10(3):254–272. [Google Scholar]
- Evin G, Thyer M, Kavetski D, McInerney D. Kuczera G. Comparison of joint versus postprocessor approaches for hydrological uncertainty estimation accounting for error autocorrelation and heteroscedasticity. Water Resour. Res. 2014;50:2350–2375. and, doi: 10.1002/2013WR014185. [Google Scholar]
- Feller W. An Introduction to Probability Theory and its Applications. 3rd. Vol. 1. N. Y: John Wiley; 1968. vol. ed. [Google Scholar]
- Fisher RA. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. London A. 1922;222:309. [Google Scholar]
- Foglia L, Mehl SW, Hill MC. Burlando P. Evaluating model structure adequacy: The case of the Maggia Valley groundwater system, southern Switzerland. Water Resour. Res. 2013;49:260–282. and, doi: 10.1029/2011WR011779. [Google Scholar]
- Gelman A. Rubin DB. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992;7(4):457–472. [Google Scholar]
- Geman S, Bienenstock E. Doursat R. Neural networks and the bias/variance dilemma. Neural Comput. 1992;4(1):1–58. and, doi: 10.1162/neco.1992.4.1.1. [Google Scholar]
- Gupta HV, Clark MP, Vrugt JA, Abramowitz G. Ye M. Towards a comprehensive assessment of model structural adequacy. Water Resour. Res. 2012;48:W08301. and, doi: 10.1029/2011WR011044. [Google Scholar]
- Hammersley JM. Monte Carlo methods for solving multivariable problems. Ann. N. Y. Acad. Sci. 1960;86(3):844–874. doi: 10.1111/j.1749-6632.1960.tb42846.x. [Google Scholar]
- Hammersley JM, Handscomb DC. Weiss G. Monte Carlo methods. Phys. Today. 1965;18:55. [Google Scholar]
- Härdle W. Smoothing Techniques: With Implementation in S, Springer Ser. Stat. N. Y: Springer; 1991. [Google Scholar]
- Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57(1):97–109. doi: 10.2307/2334940. [Google Scholar]
- Hoeting JA, Madigan D, Raftery AE. Volinsky CT. Bayesian model averaging: A tutorial. Stat. Sci. 1999;14(4):382–401. [Google Scholar]
- Hurvich CM. Tsai CL. Regression and time-series model selection in small samples. Biometrika. 1989;76(2):297–307. and, doi: 10.2307/2336663. [Google Scholar]
- Jensen JLWV. Sur les fonctions convexes et les ingalits entre les valeurs moyennes. Acta Math. 1906;30(1):175–193. doi: 10.1007/bf02418571. [Google Scholar]
- Kashyap RL. Optimal choice of AR and MA parts in autoregressive moving average models. IEEE Trans. Pattern Anal. Mach. Intell. 1982;PAMI-4(2):99–104. doi: 10.1109/tpami.1982.4767213. [DOI] [PubMed] [Google Scholar]
- Kass RE. Raftery AE. Bayes factors. J. Am. Stat. Assoc. 1995;90(430):773–795. and, doi: 10.2307/2291091. [Google Scholar]
- Koehler AB. Murphree ES. A comparison of the Akaike and Schwarz criteria for selecting model order. J. R. Stat. Soc. Ser. C. 1988;37(2):187–195. and, doi: 10.2307/2347338. [Google Scholar]
- Kuha J. AIC and BIC: Comparisons of assumptions and performance. Sociol. Methods Res. 2004;33(2):188–229. doi: 10.1177/0049124103262065. [Google Scholar]
- Kumar R, Samaniego L. Attinger S. The effects of spatial discretization and model parameterization on the prediction of extreme runoff characteristics. J. Hydrol. 2010;392(1-2):54–69. and, doi: 10.1016/j.jhydrol.2010.07.047. [Google Scholar]
- Li X. Tsai FT-C. Bayesian model averaging for groundwater head prediction and uncertainty analysis using multimodel and multimethod. Water Resour. Res. 2009;45:W09403. and, doi: 10.1029/2008WR007488. [Google Scholar]
- Liang X, Wood EF. Lettenmaier DP. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Global Planet. Change. 1996;13(1-4):195–206. and, doi: 10.1016/0921-8181(95)00046-1. [Google Scholar]
- Link WA. Barker RJ. Model weights and the foundations of multimodel inference. Ecology. 2006;87(10):2626–2635. doi: 10.1890/0012-9658(2006)87[2626:mwatfo]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Liu JS. Monte Carlo Strategies in Scientific Computing. N. Y: Springer; 2008. [Google Scholar]
- Lu D, Ye M. Neuman SP. Dependence of Bayesian model selection criteria and Fisher information matrix on sample size. Math. Geosci. 2011;43(8):971–993. and, doi: 10.1007/s11004-011-9359-0. [Google Scholar]
- Lu D, Ye M, Meyer PD, Curtis GP, Shi XQ, Niu XF. Yabusaki SB. Effects of error covariance structure on estimation of model averaging weights and predictive performance. Water Resour. Res. 2013;49:6029–6047. and, doi: 10.1002/wrcr.20441. [Google Scholar]
- MacKay DJC. Bayesian interpolation. Neural Comput. 1992;4:415–447. doi: 10.1162/neco.1992.4.3.415. [Google Scholar]
- Meyer PD, Ye M, Rockhold ML, Neuman SP. Cantrell KJ. Tech. Rep. PNNL-16396. Richland, Wash: Pac. Northwest Natl. Lab; 2007. Combined estimation of hydrogeologic conceptual model, parameter, and scenario uncertainty with application to uranium transport at the Hanford Site 300 Area. [Google Scholar]
- Morales-Casique E, Neuman SP. Vesselinov VV. Maximum likelihood Bayesian averaging of airflow models in unsaturated fractured tuff using Occam and variance windows. Stochastic Environ. Res. Risk Assess. 2010;24(6):863–880. and, doi: 10.1007/s00477-010-0383-2. [Google Scholar]
- Murphy JM, Sexton DMH, Barnett DN, Jones GS, Webb MJ. Stainforth DA. Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature. 2004;430(7001):768–772. doi: 10.1038/nature02771. and, doi: 10.1038/nature02771. [DOI] [PubMed] [Google Scholar]
- Najafi MR, Moradkhani H. Jung IW. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Processes. 2011;25(18):2814–2826. and, doi: 10.1002/hyp.8043. [Google Scholar]
- Nash JE. Sutcliffe JV. River flow forecasting through conceptual models part I––A discussion of principles. J. Hydrol. 1970;10:282–290. [Google Scholar]
- Neuman SP. Proceedings of ModelCARE2002. Vol. 277. Prague, Czech Republic: IAHS Publ; 2002. Accounting for conceptual model uncertainty via maximum likelihood Bayesian model averaging; pp. 303–313. , vol. [Google Scholar]
- Neuman SP. Maximum likelihood Bayesian averaging of uncertain model predictions. Stochastic Environ. Res. Risk Assess. 2003;17(5):291–305. doi: 10.1007/s00477-003-0151-7. [Google Scholar]
- Neuman SP, Xue L, Ye M. Lu D. Bayesian analysis of data-worth considering model and parameter uncertainties. Adv. Water Resour. 2012;36:75–85. and, doi: 10.1016/j.advwatres.2011.02.007. [Google Scholar]
- Newton MA. Raftery AE. Approximate Bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. B. 1994;56(1):3–48. [Google Scholar]
- Poeter E. Anderson D. Multimodel ranking and inference in ground water modeling. Ground Water. 2005;43(4):597–605. doi: 10.1111/j.1745-6584.2005.0061.x. and, doi: 10.1111/j.1745-6584.2005.0061.x. [DOI] [PubMed] [Google Scholar]
- Popper KR. The Logic of Scientific Discovery. N. Y: Basic Books; 1959. [Google Scholar]
- Raftery AE. Bayesian model selection in social research. Sociol. Methodol. 1995;25:111–163. doi: 10.2307/271063. [Google Scholar]
- Raftery AE, Gneiting T, Balabdaoui F. Polakowski M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005;133(5):1155–1174. and, doi: 10.1175/mwr2906.1. [Google Scholar]
- Refsgaard JC, van der Sluijs JP, Brown J. van der Keur P. A framework for dealing with uncertainty due to model structure error. Adv. Water Resour. 2006;29(11):1586–1597. and, doi: 10.1016/j.advwatres.2005.11.013. [Google Scholar]
- Reichert P. Mieleitner J. Analyzing input and structural uncertainty of nonlinear dynamic models with stochastic, time-dependent parameters. Water Resour. Res. 2009;45:W10402. and, doi: 10.1029/2009WR007814. [Google Scholar]
- Renard B, Kavetski D, Kuczera G, Thyer M. Franks SW. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010;46:W05521. and, doi: 10.1029/2009WR008328. [Google Scholar]
- Riva M, Panzeri M, Guadagnini A. Neuman SP. Role of model selection criteria in geostatistical inverse estimation of statistical data- and model-parameters. Water Resour. Res. 2011;47:W07502. and, doi: 10.1029/2011WR010480. [Google Scholar]
- Rojas R, Feyen L. Dassargues A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008;44:W12418. and, doi: 10.1029/2008WR006908. [Google Scholar]
- Samaniego L, Kumar R. Attinger S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010;46:W05523. and, doi: 10.1029/2008WR007327. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann. Stat. 1978;6(2):461–464. doi: 10.1214/aos/1176344136. [Google Scholar]
- Schweppe FC. Uncertain Dynamic Systems. Englewood Cliffs, N. J: Prentice Hall; 1973. [Google Scholar]
- Singh A, Mishra S. Ruskauff G. Model averaging techniques for quantifying conceptual model uncertainty. Ground Water. 2010;48(5):701–715. doi: 10.1111/j.1745-6584.2009.00642.x. and, doi: 10.1111/j.1745-6584.2009.00642.x. [DOI] [PubMed] [Google Scholar]
- Skilling J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006;1(4):833–859. [Google Scholar]
- Sorooshian S. Dracup JA. Stochastic parameter-estimation procedures for hydrologic rainfall-runoff models––Correlated and heteroscedastic error cases. Water Resour. Res. 1980;16(2):430–442. and, doi: 10.1029/WR016i002p00430. [Google Scholar]
- Sugiura N. Further analysts of the data by Akaike' s information criterion and the finite corrections. Commun. Stat. 1978;7(1):13–26. doi: 10.1080/03610927808827599. [Google Scholar]
- Tierney L. Kadane JB. Accurate approximations for posterior moments and marginal densities. J. Am. Stat. Assoc. 1986;81(393):82–86. and, doi: 10.2307/2287970. [Google Scholar]
- Troldborg M, Nowak W, Tuxen N, Bjerg PL, Helmig R. Binning PJ. Uncertainty evaluation of mass discharge estimates from a contaminated site using a fully Bayesian framework. Water Resour. Res. 2010;46:W12552. and, doi: 10.1029/2010WR009227. [Google Scholar]
- Tsai FT-C. Li X. Reply to comment by Ming Ye et al. on “Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window,”. Water Resour. Res. 2010;46:W02802. and, doi: 10.1029/2009WR008591. [Google Scholar]
- Tsai FT-C. Li XB. Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window. Water Resour. Res. 2008;44:W09434. and, doi: 10.1029/2007WR006576. [Google Scholar]
- Vrugt JA. Robinson BA. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007;43:W01411. and, doi: 10.1029/2005WR004838. [Google Scholar]
- Vrugt JA, ter Braak CJF, Clark MP, Hyman JM. Robinson BA. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008;44:W00B09. and, doi: 10.1029/2007WR006720. [Google Scholar]
- Wöhling T. Vrugt JA. Combining multiobjective optimization and Bayesian model averaging to calibrate forecast ensembles of soil hydraulic models. Water Resour. Res. 2008;44:W12432. and, doi: 10.1029/2008WR007154. [Google Scholar]
- Wöhling T, Samaniego L. Kumar R. Evaluating multiple performance criteria to calibrate the distributed hydrological model of the upper Neckar catchment. Environ. Earth Sci. 2013;69(2):453–468. and, doi: 10.1007/s12665-013-2306-2. [Google Scholar]
- Ye M, Neuman SP. Meyer PD. Maximum likelihood Bayesian averaging of spatial variability models in unsaturated fractured tuff. Water Resour. Res. 2004;40:W05113. and, doi: 10.1029/2003WR002557. [Google Scholar]
- Ye M, Meyer PD. Neuman SP. On model selection criteria in multimodel analysis. Water Resour. Res. 2008;44:W03428. and, doi: 10.1029/2008WR006803. [Google Scholar]
- Ye M, Pohlmann KF, Chapman JB, Pohll GM. Reeves DM. A model-averaging method for assessing groundwater conceptual model uncertainty. Ground Water. 2010a;48(5):716–28. doi: 10.1111/j.1745-6584.2009.00633.x. and, doi: 10.1111/j.1745-6584.2009.00633.x. [DOI] [PubMed] [Google Scholar]
- Ye M, Lu D, Neuman SP. Meyer PD. Comment on “Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window” by Frank T.-C. Tsai and Xiaobao Li. Water Resour. Res. 2010b;46:W02801. and, doi: 10.1029/2009WR008501. [Google Scholar]