High Accuracy of Karplus Equations for Relating Three-Bond J Couplings to Protein Backbone Torsion Angles

Abstract

³J_C′C′ and ³J_HNHα couplings are related to the intervening backbone torsion angle ϕ by standard Karplus equations. Although these couplings are known to be affected by parameters other than ϕ, including H-bonding, valence angles and residue type, experimental results and quantum calculations indicate that the impact of these latter parameters is typically very small. The solution NMR structure of protein GB3, newly refined by using extensive sets of residual dipolar couplings (RDCs), yields 50–60% better Karplus equation agreement between ϕ angles and experimental ³J_C′C′ and ³J_HNHα values than does the high resolution X-ray structure. In intrinsically disordered proteins, ³J_C′C′ and ³J_HNHα couplings can be measured at even higher accuracy, and the impact of factors other than the intervening torsion angle on ³J will be smaller than in folded proteins, making these couplings exceptionally valuable reporters on the ensemble of ϕ angles sampled by each residue.

1. Introduction

Empirically parameterized Karplus relations^[1] between a wide range of different types of three-bond J couplings and their corresponding intervening dihedral angles continue to be of exceptional value in structural analysis of organic compounds, including peptides and proteins.^[2] Shortly after the initial introduction of the Karplus relation, multiple reports highlighted the dependence of ³J_HH couplings on electronegativity of substituents and ring size for cyclic compounds, thereby limiting the precision at which these couplings can be interpreted.^[3–6] In a subsequent response, Karplus pointed out that indeed ³J couplings not only depend on the intervening torsion angle, but that theory also shows the coupling to be impacted by electronegativity of substituents, H-C-C valence angles, and bond lengths, and that “the person who attempts to estimate dihedral angles to an accuracy of one or two degrees does so at his own peril”.^[7] Although the effect of substituent electronegativity has been accounted for by empirical adjustments to the Karplus equation,^[8] the chemistry community largely has taken Karplus’ advice to heart and does not interpret these couplings to the level of precision at which they often can be measured.

Backbone ³J_HNHα couplings have been widely used for conformational analysis in peptides and proteins. With the exception of Gly residues, the electronegativity of the substituents is very similar for all residue types, suggesting that quantitative analysis of these parameters in terms of the intervening torsion angle ϕ may be quite robust. However, the observation of a relatively large value (0.85 Hz) for the root-mean-square difference (rmsd) between observed ³J_HNHα values and those predicted by a 1.4-Å X-ray structure of the small protein BPTI again pointed to the presence of alternate factors impacting these ³J_HNHα values.^[9] Indeed, deviations from ideal covalent geometry in the protein backbone are well documented,^[10] and variations in H-bonding are expected to impact the H^N σ orbitals and thereby the ³J_HNHα value. Moreover, as pointed out by Brueschweiler and Case,^{[11, 12]} non-uniformity in the amplitude of backbone dynamics along the protein backbone will differentially skew these experimental parameters towards a value of ca 5 Hz, again impacting the relation between ³J_HNHα and the time-averaged intervening dihedral angle. On the other hand, refinement of the 1.1-Å X-ray structure of the protein GB3 yielded a considerable drop from 0.76 to 0.43 Hz between measured ³J_HNHα values and those predicted by an optimized Karplus equation.^[13] For the extensively studied protein ubiquitin, concerted analysis of ³J_HNHα, ³J_HNCβ, ³J_HNC′, ³J_C′Hα, ³J_C′Cβ, and ³J_C′C′, which all report on the backbone torsion angle ϕ, also indicated that uncertainty in the coordinates obtained from a 1.8-Å X-ray structure of this protein dominated the 0.73 Hz rmsd between observed and predicted ³J_HNHα values.^[14]

Here, we report results which confirm that random uncertainty in the X-ray coordinates is the prime contributor to the rmsd between observed ³J_C′C′ values and those predicted by the Karplus equation. For ³J_HNHα, we find that both uncertainties in the coordinates of the C and N backbone atoms as well as deviations from idealized in-peptide-plane positions of H^N and from idealized tetrahedral geometry at C^α significantly impact the residual in the fit. Our results imply that experimental ³J_HNHα and ³J_C′C′ values can be interpreted in angular terms at a precision that approaches that of their measurements. This finding is of particular importance when defining or validating backbone angle distributions in intrinsically disordered proteins, where both ³J_HNHα and ³J_C′C′ are readily measured at an accuracy better than 0.1 Hz.

2. Results and Discussion

The 1.1-Å X-ray structure of GB3,^[15] previously refined by solution NMR RDCs,^[16] was further refined by newly measured ¹D_CαCβ RDCs under three different alignment orientations, as well as previously reported ¹H-¹H RDCs,^[17] and ¹D_CαC′ values measured for a number of GB3 mutants that orient differentially in a Pf1 liquid crystal suspension.^[18] In order to obtain optimal cross-validation results, we found it necessary to reduce by 5-fold the very tight force constants normally used for keeping the peptide bond planar. For details, see the Methods section. The root-mean-square deviation from Ω=180° in the final structures then was 5.0°, close to the values seen in the highest resolution protein X-ray structures.^{[10, 19, 20]} The change in backbone coordinates between the newly calculated structure and the previous RDC-refined structure is quite small (0.37 Å), but nevertheless improves the fit of the ³J_HNHα and in particular the ³J_C′C′ couplings significantly (vide infra).

It is well known that protein structures are subject to relatively large amplitude internal dynamics,^[21–23] which impacts ³J couplings and therefore their fits to Karplus curves.^[11]. For deriving the most accurate average torsion angles it is advantageous to calculate the structure as a single model that best fits all input restraints simultaneously, rather than as the average over an NMR ensemble calculation.^[24] We therefore have chosen the latter approach for evaluating the relation between ³J couplings and backbone torsion angles, while excluding the three residues (L12, D40, and G41) that were shown to have the highest amplitude internal dynamics as judged by ¹⁵N relaxation^[25] and RDC measurements.^[26]

Fit of ³J_HNHα values to Karplus equation

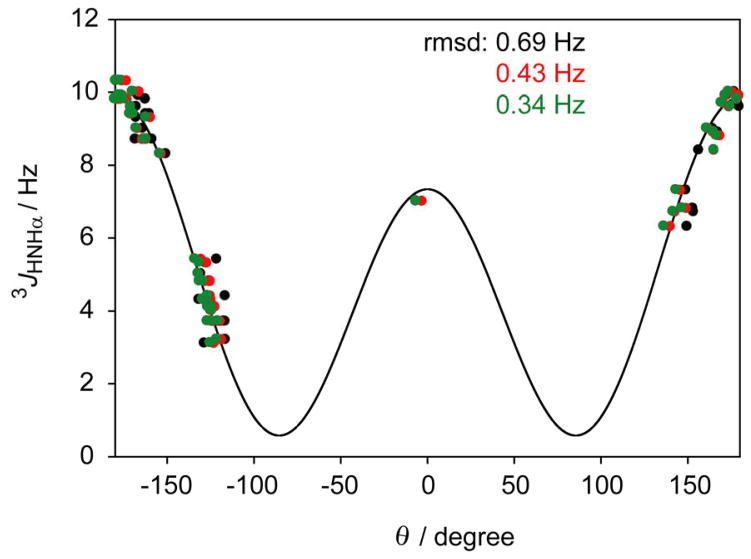
High precision ³J_HNHα values, measured previously^[13] using a multiple-quantum method,^[27] that to a good approximation suppresses effects of cross-relaxation,^[28] were used in this study. A fit of these couplings to the X-ray structure (PDB entry 1IGD)^[15] to which hydrogens were added with the program REDUCE,^[29] yields an rmsd of 0.76 Hz. This rmsd is minimally impacted by the refinement method used, as can be seen from the values obtained for the PDB_REDO structure ^[30] of GB3, obtained using an optimized automated refinement protocol. This result is not surprising, considering that the backbone coordinate rmsd between 1IGD and its PDB_REDO structure is only 0.046 Å (see Table S1 of the Supporting Information). A much better fit (0.43 Hz rmsd)^[17] is observed for the previously RDC-refined model (PDB entry 2OED),^[16] which drops to 0.34 Hz for the newly refined model, which includes many additional RDCs plus decreased peptide bond planarity restraints. The coordinates of a GB3 structure obtained from joint X-ray/NMR refinement, using the 1IGD structure factors and the 2OED NMR (RDC) restraints ^[31], yields rmsd values that are intermediate between 2OED and 1IGD. The relatively high rmsd value for this structure appears to result from the weak weights used for the NMR restraints, also reflected in a very low coordinate rmsd of 0.04 Å relative to 1IGD (see Table S1 of the Supporting Information).

As can be seen in Table 1, a significant fraction of the improvement in fit quality of the newly refined NMR structure over the original X-ray structure stems from the fact that the positions of the hydrogens in X-ray structures are unknown, and are added to the structure by model building using programs such as REDUCE^[29] or MOLMOL.^[32] If the H^N-N-C^α-H^α dihedral angle is derived from the newly refined structure using the common assumption θ = ϕ − 60° the fit quality drops to a level that is not much better than the original X-ray structure (Table 1). As was found previously,^{[14, 24]} and also can be seen from the fifth column in Table 1, most of this increase in rmsd is related to the out-of-peptide-plane angle Δϕ, but small deviations of the C^α-H^α vector from its idealized orientation also contribute a non-negligible amount. Indeed, when H^α is positioned in the plane that bisects the N-C^α-C^β and N-C^α-C′ planes, i.e. θ_HNHα = (θ_HNCβ + θ_HNC′+ 360°)/2, the fit to the Karplus equation is slightly worse (0.37 vs 0.34 Hz).

Table 1.

Rmsd between measured ³J couplings and values predicted by the Karplus equations.^a

	3JHNHα				3JC′C′
	angle used for Karplus equation
Model	θHNHα	(θHNCβ + θHNC′ + 360°)/2	(ϕ − 60°) c	(ϕ − 60° + Δϕ)d	ϕ
1IGD	0.76	0.71	0.74	0.72	0.29
REDOe	0.76	0.74	0.76	0.69	0.28
Xray/NMRf	0.62	0.71	0.68	0.63	0.26
2OED	0.43	0.48	0.58	0.51	0.19
New	0.34 b	0.37 b	0.69	0.43	0.12

^aIn units of Hz, excl. residues L12, D40, and G41. Predicted values are derived from the previously parameterized Karplus equation,^{[13] 3}J_HNHα = 7.97 × cos²θ − 1.26 × cosθ + 0.63 Hz, and the newly parameterized ³J_C′C′ = 1.61 × cos²ϕ − 0.93 × cosϕ + 0.55 Hz.

^bThe rmsd between θ_HNHα and (θ_HNCβ + θ_HNC′ + 360°)/2 in the newly refined model is 1.2°.

^cUsing θ = ϕ − 60°, where ϕ is the C′_i−1-N_i -C^α_i -C′_i dihedral angle.

^dUsing θ = ϕ − 60° + Δϕ, where Δϕ is the out-of-plane angle observed in the newly refined NMR structure.

^eX-ray structure calculated from the 1IGD structure factors using PDB_REDO.^[30]

^fStructure calculated using joint 1IGD X-ray structure factors and 2OED NMR restraints. Coordinates taken from the supporting information of Rinaldelli et al.^[31]

Only in exceptional cases, such as the present study of GB3, are there sufficient experimental restraints to define deviations from idealized geometry for positioning hydrogens in a protein structure from NMR data. In practice, therefore when using ³J_HNHα couplings in structure determination, the 0.69 Hz value in Table 1 represents the limit of precision at which ³J_HNHα can be interpreted in structural terms, even while inherently it is considerably more accurate at describing the H^N-N-C^α-H^α dihedral angle.

Fit of ³J_C′C′ values to Karplus equation

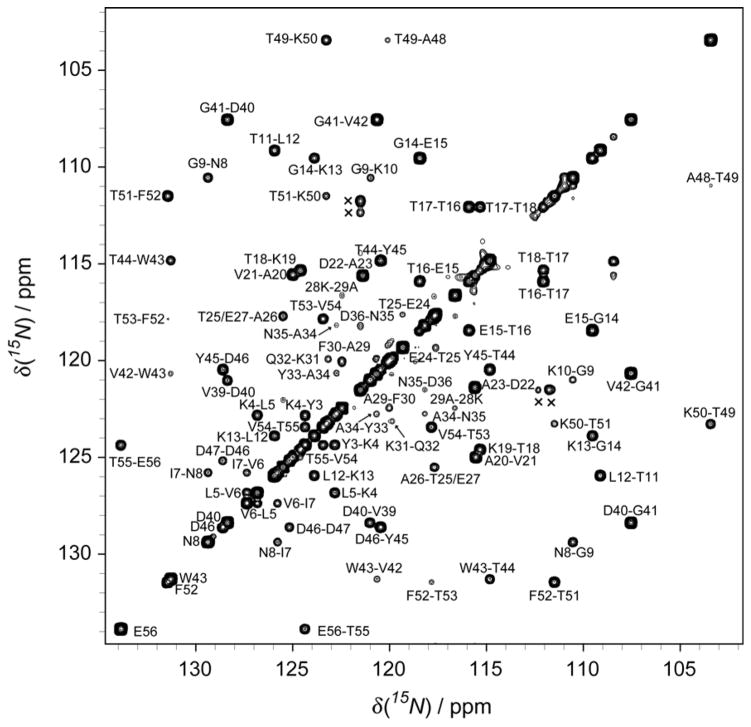
Measurement of ³J_C′C′ in isotopically uniformly enriched proteins has been demonstrated previously,^[33] and was shown to be useful for sequential assignment in intrinsically disordered proteins.^[34] Quantitative measurement of ³J_C′C′ was also shown feasible for rather slowly tumbling proteins (τ_c ≈ 12 ns), even prior to the introduction of highly sensitive cryogenic probeheads.^[35] Here, we used a slightly modified 3D NMR experiment that does not require the 2-spin approximation used in prior work, and which yields cross peak/diagonal peak intensity ratios between sequential amide groups that are proportional to tan²(πJ_C′C′T) (See Figure S1 of the Supporting Information). A projection of the 3D spectrum on the ¹⁵N-¹⁵N plane (Figure 2) illustrates the excellent spectral resolution and sensitivity that can be obtained, enabling the measurement of a nearly complete set of ³J_C′C′ couplings (Table S2 of the Supporting Information). Spectra were recorded at 15 and 25 °C, and the pairwise rmsd between these two sets of measurements was 0.06 Hz, indicating a random error of only 0.03 Hz in their averaged values.

Figure 2.

Projection of the 500 MHz 3D HN(COCO)NH spectrum of GB3 on the ¹⁵N-¹⁵N (F₁, F₂) plane, recorded at 298 K. The projection extended from 10.5 to 7.0 ppm in the H^N (F₃) dimension. Cross peak to diagonal peak ratios correspond to tan²(πJ_C′C′T), with the ¹³C′-¹³C′ de-/re-phasing interval T set to 100 ms. Cross peaks are labeled, and peaks marked × show the correlations between N35 ¹⁵N^δ (with and without ²H isotope shift) and D36 ¹⁵N.

A fit of the ³J_C′C′ values to the newly refined structure of GB3, calculated without using ³J_C′C′ or ³J_HNHα restraints, yields the following optimized Karplus equation:

$${{}^{3}J}_{{\mathrm{C}}^{\prime }{\mathrm{C}}^{\prime }}=1.61\times {\text{cos}}^2\varphi -0.93\times \text{cos}\varphi +0.55\text{Hz}$$ (1)

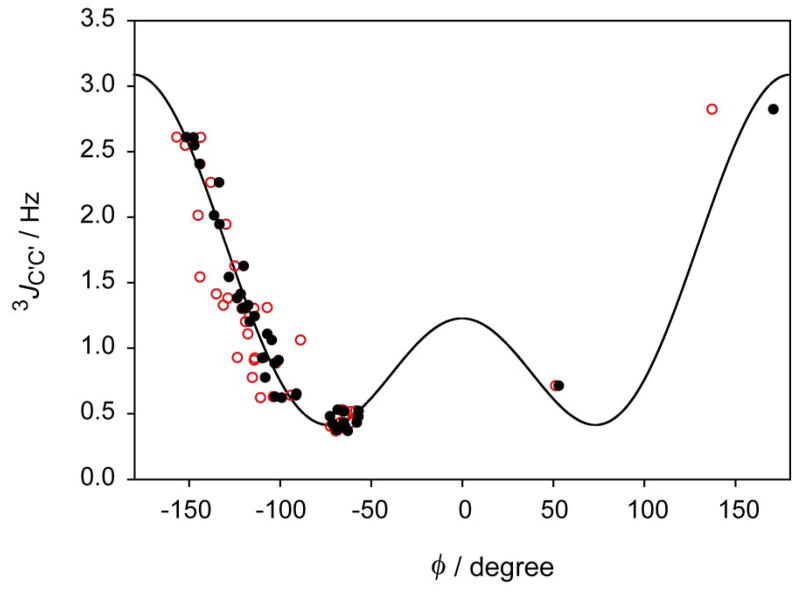
with an rmsd of 0.12 Hz between measured and predicted couplings (Fig. 3). For comparison, this rmsd increases from 0.12 to 0.29 Hz when using ϕ angles taken from the high resolution X-ray structure (PDB entry 1IGD). A small, 4% drop in this rmsd value is obtained when using the PDB-REDO refinement^[30] of the 1IGD structure factors. A slightly larger drop (~10%) is obtained for the joint X-ray/NMR refinement,^[31] but a considerably larger decrease (~35%) is observed for the original 2OED NMR structure (Table 1). As mentioned above, the finding that the improvement in the ³J fit of the joint X-ray/NMR refined structure over the original X-ray structure is modest presumably results from the weak weight assigned to the RDC restraints, also reflected in a minimal backbone coordinate rmsd relative to the 1IGD X-ray structure (see Table S1 of the Supporting Information). However, our finding that the joint X-ray/NMR refinement consistently yields ³J_C′C′ and ³J_HNHα rmsd values that are considerably higher than obtained for the 2OED NMR structure also points to true differences between the structures in the crystalline state and in free solution. Indeed, intermolecular H-bonding results in a continuous plane of β-sheet in the crystalline state,^[15] and in all likelihood contributes to this modest difference in backbone structure.

Figure 3.

Plot of experimental ³J_C′C′ values against the backbone torsion angle ϕ. The solid line corresponds to the Karplus equation (eq 1). Red data points correspond to ϕ angles extracted from the X-ray structure (PDB entry 1IGD)^[15]; black data points correspond to the RDC-refined GB3 structure. Dynamically disordered residues (L12, D40, and G41, previously identified on the basis of ¹⁵N relaxation order parameters S² <0.7, axially symmetric diffusion model,^[25] are excluded from the plot. The rmsd between observed and best-fitted ³J_C′C′ values is 0.12 Hz.

The experimental ³J_C′C′ values in GB3 span a range of 2.46 Hz, which is 20-fold larger than the rmsd in their fit to the Karplus equation. This is nearly the same ratio as observed for ³J_HNHα (range of 7.2 Hz, versus 0.34 Hz rmsd). However, as discussed above, from a practical perspective the interpretation of ³J_HNHα couplings is limited to an uncertainty of 0.69 Hz, due to the fact that the deviations from idealized geometry for hydrogen positions normally cannot be determined. Therefore, ³J_C′C′ couplings intrinsically have much higher restraining power when determining a protein structure from NMR data, in particular for small proteins where these couplings can be measured at very high accuracy.

Factors other than ϕ impacting ³J_C′C′

Although the fit of the ³J_C′C′ couplings to the Karplus equation is very good, the residual we observe is nearly four times larger than the 0.03 Hz experimental measurement uncertainty. Although errors in the coordinates of the NMR-refined structure will contribute to the 0.12 Hz rmsd, the scatter does not correlate with the steepness of the curve, and therefore does not appear to be dominated by uncertainty in ϕ. Variations in the amplitude of ϕ-angle fluctuations among different residues would also scale the couplings differentially and thereby contribute to the scatter.^[11] However, for the protein ubiquitin a very long (1-ms) molecular dynamics trajectory has been reported,^[23] which shows that the amplitude of ϕ-angle fluctuations in the well ordered regions of the protein is quite homogeneous (rmsd of 13±3°), and insufficiently large to lead to significant differential scaling of the ³J_C′C′ couplings.^[11] The same conclusion must apply for GB3, which also is a very well structured protein.

We therefore carried out quantum calculations to evaluate what other geometric factors can be expected to significantly impact ³J_C′C′. A tripeptide Gly-Ala-Gly was first built using the program Molden,^[36] both in helical (ϕ = −50, ψ = −50) and extended (ϕ = −120, ψ = 120) backbone conformations. The tripeptide then was modified in silico to generate a smaller dipeptide analogue (Ac-Ala-NH-CH₃). Four water molecules were placed near the carbonyl and amide groups, in a linear hydrogen bond geometry (Fig. 4a). The water molecule that is hydrogen bonded to the C-terminal amide cap was rotated towards the N-methyl group within the peptide plane by 20° (i.e. making the C′–N–O_water angle 140° instead of 120°) such that this water molecule does not significantly vary its interaction with nearby water molecules when changing backbone torsion angles.

Figure 4.

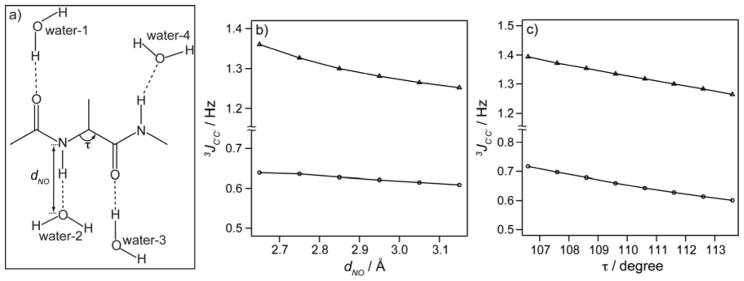
Effect of H-bonding on ³J_C′C′ as obtained from DFT calculations. (a) The dipeptide analog Ac-Ala-NH-CH₃ H-bonded to four water molecules, used in the DFT calculations. (b) ³J_C′C as a function of d_NO, the distance between the O of water-2 and the Ala N atom, for α-helical (circles) and β-sheet (triangles) backbone geometry. (c) ³J_C′C′ as a function of the τ angle, for α-helical (circles) and β-sheet (triangles).

The O–O or N–O distance were independently stepwise increased from 2.65 to 3.15 Å, except for the water H-bonded to the C-terminal N-methyl group, which was kept fixed at d_NO = 2.85 Å. Full results are included in Tables S3–S5 of the Supporting Information. As can be seen from Table S4, the impact of removing H-bonds on ³J_C′C′ is to a first approximation additive, and therefore these H-bonds may be considered separately. The largest impact is observed when altering the distance to water-2 (Fig. 4), which accepts an H-bond from Ala-NH. For the extended backbone geometry, the computed ³J_C′C′ decreases from 1.36 to 1.25 Hz when d_NO is increased from 2.65 to 3.15 Å, but ³J_C′C′ variation for the helical ϕ = −50° value is considerably smaller (Fig. 4b).

Variations in the N C^α C′ bond angle, τ, also are known to occur in protein structures^[37] and according to the DFT calculations can have a significant impact on ³J_C′C′, decreasing by ~0.15 Hz when τ is increased from 106.6 to 113.6°, both in extended and helical geometries (Fig. 4c). The DFT calculations also point to a non-negligible effect of amino acid type, both for ³J_C′C′ and for ³J_HNHα (Table S5 in the Supporting Information) and a substantial effect of the χ₁ torsion angle on both ³J_C′C′ and ³J_HNHα is seen for Ser.

The above calculations confirm that variations in H-bonding and valence angles as well as residue type and their sidechain χ₁ torsion angle are likely responsible for most of the residual scatter seen in Figures 1 and 3. Substantial outliers in these fits would be expected if, for example, an amide group were completely lacking an H-bond, or if a large deviation from ideality for τ would occur. The absence of such large outliers therefore indicates that both H-bonding and backbone valence angles are restricted to narrow ranges in GB3.

Figure 1.

Plot of ³J_HNHα values measured for GB3 against the H-N-C^α-H^α dihedral angle, θ (Note: θ ≈ ϕ − 60°). Dihedral angles derived from the coordinates of the RDC-refined NMR structure with amide protons in their RDC-optimized positions (red data points; θ = ϕ − 60° + Δϕ), with H^N atoms moved to their idealized in-peptide plane positions (black data points; θ = ϕ − 60°), or with both H^N and H^α atoms in their RDC-optimized positions (green data points; θ being the H-N-C^α-H^α dihedral angle).

Resolving degeneracies in the Karplus curve

Ignoring the small out-of-plane angles, Δϕ, and the deviations from ideal tetrahedral geometry at C^α, both ³J_C′C′ and ³J_HNHα report on the same backbone torsion angle, ϕ. However, the corresponding Karplus curves are shifted by 60° relative to one another (Fig. 5a). A plot of Karplus-predicted ³J_C′C′ vs ³J_HNHα values highlights that the ³J_HNHα degeneracy with respect to ϕ, around the extrema of the Karplus curve (ϕ ≈ −120° + N×90°), is lifted by ³J_C′C′, and vice versa, degeneracies in the ³J_C′C′ values around ϕ ≈ 0°, 180°, and ±73° are resolved by ³J_HNHα (Fig. 5b). The combination of these two sets of ³J couplings therefore presents a very precise measure for the ϕ angle in proteins, allowing this torsion angle to be determined at an accuracy that can exceed those of the best X-ray structures. The highly complementary nature of ³J_C′C′ and ³J_HNHα, together with the high precision at which these values can be measured in flexible regions of proteins, also will make their joined use invaluable in defining the distribution of torsion angles sampled in intrinsically disordered proteins (IDPs) or large flexible loop regions.

Figure 5.

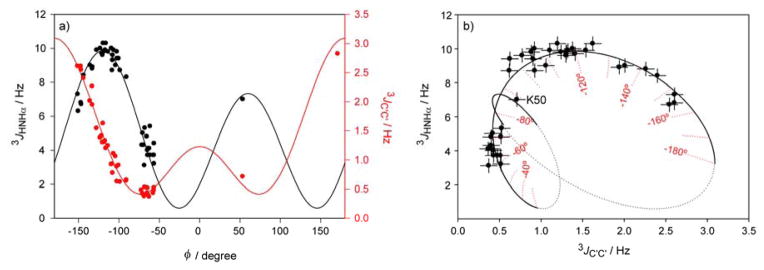
Resolving ambiguities in the Karplus relation for determining the backbone torsion angle ϕ in proteins. (a) Karplus relations between ³J_C′C′ (red) or ³J_HNHα(black) values and the backbone torsion angle, ϕ, assuming the out-of-plane angle Δϕ = 0°. (b) Plot of ³J_C′C′ vs ³J_HNHα values in GB3, again assuming Δϕ = 0°. Only residues that are well-ordered (S² ≥ 0.7) on the basis of prior ¹⁵N relaxation studies^[25] are shown. The solid line corresponds to the relation between the predicted values in the most favored region of the Ramachandran plot (−180°<ϕ< −30°; 30°<ϕ<90°), with the dotted section corresponding to sparsely populated or forbidden ϕ angles. For calculating this curve, Δϕ = 0°. Error bars correspond to ±0.4 Hz for ³J_HNHα and to ±0.1 Hz for ³J_C′C′. Residue K50 adopts a positive ϕ angle (ϕ = 53°).

Methods

NMR Measurements

GB3 ³J_C′C′ values were derived from two 3D HN(COCO)NH spectra, measured with the pulse sequence of Supporting Information Figure 1, using a 2.5 mM sample of uniformly ¹³C/¹⁵N-enriched GB3 in 20 mM sodium phosphate, 50 mM NaCl, 0.05% w/v sodium azide, pH 6.6, 5% D₂O. The two spectra were recorded on a Bruker Avance-III 500 MHz NMR spectrometer equipped with a cryogenic z-gradient probehead, with sample temperatures set to 288 K and 298 K. The ¹³C and ¹⁵N carriers were set at 177 and 118 ppm, respectively. The time domain matrix consisted of 200* × 200* × 1024* complex data points, or acquisition times of 60.0 ms (t₁, ¹⁵N), 60.0 ms (t₂, ¹⁵N) and 146.3 ms (t₃, ¹H), and approximately 88 hours of total measurement time, using 4 scans per free induction decay (FID), and a 1.5-s interscan delay. The time domain data were apodized with a 60°-shifted sine-bell window function in all dimensions, and zero-filled prior to Fourier transformation to yield high digital resolution. The spectra were processed and analyzed using the software package nmrPipe.^[38]

Structure calculations

An extensive set of previously reported backbone ¹D_NH, ¹D_CαC′, ¹D_NC′ and ¹D_CαHα RDCs measured under 5 alignment conditions for wild type GB3, and 6 sets of ¹D_NH values measured for a series of charge-perturbed mutants of GB3 aligned in liquid crystalline Pf1, was supplemented by 3 sets of ¹D_CαHα and ¹D_CαCβ RDCs for wild type GB3, aligned in Pf1,^[39] polyethylene glycol,^[40] and bicelles,^[41] respectively.

The structure of GB3 was refined using the Xplor-NIH program^[42] starting from the coordinates of the RCSB PDB deposition 2OED.^[16] In addition to the N-H, C^α-H^α, C′-C^α, and C′-N RDC restraints collected in five different alignment media, previously used to derive the 2OED model, the refinement protocol included previously reported N-H, C^αH^α, and C′-C^α RDCs measured in Pf1 for GB3 mutants K19A/D47K, K19E/D40N, K19E/K4A-N-His₆, K19E/K4A-C-His₆, K19A/T11K, and K19E/K4A.^[18] The input RDCs also included N-H, C^α-H^α, and H^N-H^α RDCs measured for wild type GB3 in Pf1,^[17] as well as newly collected N-H, C^α-H^α and C^α-C^β RDCs from samples of wild-type GB3 in Pf1, bicelles and PEG, and N-H, C^α-H^α RDCs from K4A/K19E/V42E-CHis₆, K19A/V42E/D47K, and K4A/K19E/V42E mutants in Pf1. Fitting of variable-distance H^N-H^α RDCs was done using the xdip term in XPLOR^[42] with a scaling constant of 11.13 with respect to the N-H RDCs, corresponding to the libration-corrected N-H bond length of 1.041Å. Unlike the 2OED deposition, no non-crystallographic symmetry restraint terms with respect to the 1IGD crystal structure were used in the refinement. Backbone/backbone hydrogen bonding geometries were enforced via a previously described database potential of mean force,^[43] modified to include refinement against experimental through-H-bond ^3hJ_NC′ couplings.^[44]

The empirical force field used in the refinement was slightly modified to better cope with a large number of input backbone RDC restraints. N-H and C^α-H^α bond lengths were set to 1.02 and 1.09 Å, and improper torsion angles governing positioning of the H^N and H^α atoms were softened from their default setting of 500 kcal mol⁻¹ rad⁻² to 50 kcal mol⁻¹ rad⁻². The empirical force field parameters used to describe the alignment tensor pseudo molecules were strengthened by introducing three additional bond and three additional angle restraint terms. In order to evaluate the effect of softening the empirical potential used to restrain the peptide bond angle Ω to 180°, the force constants for the corresponding improper terms were decreased by factors of 3, 5, and 10 with respect to their defaults settings of 500 kcal mol⁻¹ rad⁻², with 5-fold reduction yielding the best agreement between calculated structures and ³J_HαHN and ³J_C′C′ couplings in terms of rmsd observed in a Karplus equation fit. Note that these couplings were not used as input restraints, and that no ϕ torsion angle restraints were used for structure refinement.

Due to differences between the alignment conditions of the individual samples from which the fitted RDC data were extracted, a total of 24 alignment tensors were used to fit the entire set of RDCs. The RDC data were found to fully cover the 5-dimensional space of alignment tensors as judged by SECONDA analysis.^{[45, 46]} Therefore, RDC force constants were optimized by cross-validation, frequently resulting in values lower than those based solely on alignment tensor magnitudes and rhombicities. To account for the differences in static coupling magnitudes of various RDC types, force constant multipliers of 26, 75, 0.24, and 5.0 were used for C-C, C-N, C-H, and H-H RDCs. During structure refinement, both eigenvalues and orientations of the alignment tensors were adjusted every 0.1 ps by SVD-fitting. The structure refinement used Cartesian dynamics and consisted of 200 steps of conjugate gradient minimization, followed by a 2-ps high temperature stage at 2000 K, followed with a 100 ps simulated annealing schedule from 200 K to 0 K, and finishing with 200 steps of conjugate gradient minimization. During the entire procedure, non-bonded interactions were modeled by quartic repulsive-only energy terms, using a force constant of 4.0 kcal mol⁻¹ A⁻². All van der Waals radii are scaled by a factor of 0.81. The actual refinement script and all input tables as well as the coordinates of the refined model can be downloaded from http://spin.niddk.nih.gov/bax/structures/GB3_RDC_refinement_2014.zip

Highlights.

• A convenient, sensitive, and accurate method for ³J_C′C′ measurement is presented

• Karplus equation fits for ³J_C′C′ and ³J_HNHα in proteins are limited by the accuracy of these structures

• Best ³J_HNHα Karplus equation fit is obtained when using the experimentally derived H-N-C^α-H^α dihedral angle, rather than ϕ

• ³J_C′C′ values in proteins are reliable ϕ reporters, minimally impacted by residue type and variations in H-bonding.