Origin of Light-Induced Spin-Correlated Radical Pairs in Cryptochrome

Abstract

Blue-light excitation of cryptochromes and homologs uniformly triggers electron transfer (ET) from the protein surface to the flavin-adenine dinucleotide (FAD) cofactor. A cascade of three conserved tryptophan residues has been considered to be critically involved in this photoreaction. If the FAD is initially in its fully oxidized (diamagnetic) redox state, light-induced ET via the tryptophan triad generates a series of short-lived spin-correlated radical pairs comprising an FAD radical and a tryptophan radical. Coupled doublet-pair species of this type have been proposed as the basis, e.g., of a biological magnetic compass in migratory birds, and were found critical for some cryptochrome functions in vivo. In this contribution, a cryptochrome-like protein (CRYD) derived from Xenopus laevis has been examined as a representative system. The terminal radical-pair state FAD^•⋯W324^• of X. laevis CRYD has been characterized in detail by time-resolved electron-paramagnetic resonance (TREPR) at X-band microwave frequency (9.68 GHz) and magnetic fields around 345 mT, and at Q-band (34.08 GHz) at around 1215 mT. Different precursor states – singlet versus triplet – of radical-pair formation have been considered in spectral simulations of the experimental electron-spin polarized TREPR signals. Conclusively, we present evidence for a singlet-state precursor of FAD^•⋯W324^• radical-pair generation because at both magnetic fields, where radical pairs were studied by TREPR, net-zero electron-spin polarization has been detected. Neither a spin-polarized triplet precursor nor a triplet at thermal equilibrium can explain such an electron-spin polarization. It turns out that a two-microwave-frequency TREPR approach is essential to draw conclusions on the nature of the precursor electronic states in light-induced spin-correlated radical pair formations.

Introduction

Proteins of the cryptochrome/photolyase family share their three-dimensional fold, amino-acid sequence homology, and the redox-active cofactor flavin adenine dinucleotide (FAD), but exhibit rather diverse physiological activities.¹ Members of this family have been identified in various organisms ranging from bacteria to higher organisms including humans. The family proteins are functionally divided into two groups: photolyases repair UV-damaged DNA containing either cyclobutane pyrimidine dimers or (6–4) photoproducts,^2–4 presumably by photo-induced cyclic electron transfer (ET) from the fully reduced FAD to the damage site in single-stranded or double-stranded DNA,⁵ and – once the DNA lesion is repaired – back to the FAD. Despite their high structural conservation with photolyases, cryptochromes exhibit more diverse physiological functions, including regulation of germination, elongation, and photoperiodism in plants.^6–8 Some cryptochromes are also involved in the entrainment of the circadian clock.^1,9 Recent in vivo studies indicate light-induced ET activity from the protein surface toward the FAD cofactor under the participation of redox-active amino acid residues in plant and animal cryptochromes,^10–12 though the relevance for this cofactor photoreduction in the DNA repair by photolyases is controversial.^13,14 Regardless, light-induced ET to fully oxidized FAD in both cryptochromes and photolyases generates spin-correlated radical-pair states.^15,16 In cryptochromes, these are proposed as the basis of a biological magnetic compass in some organisms including migratory birds.^17–20

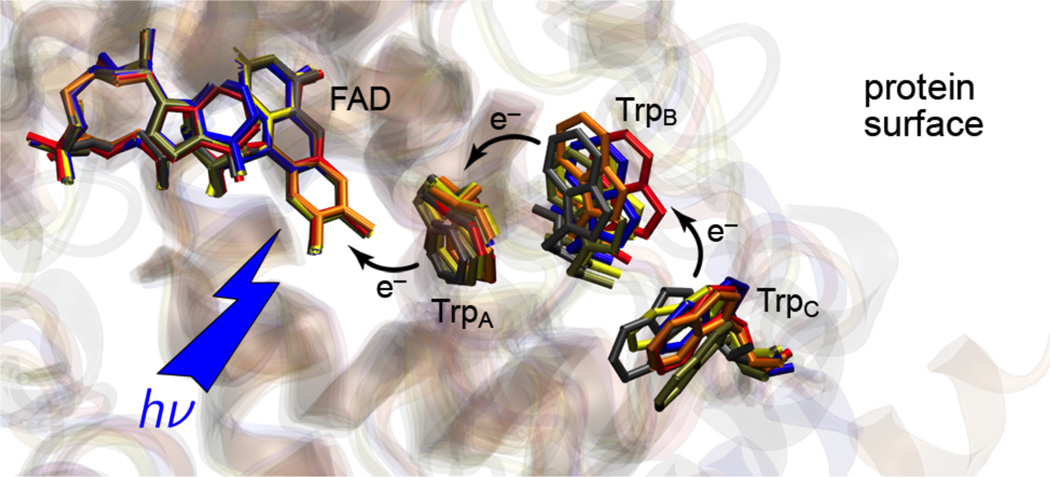
Previous point-mutational studies revealed a conserved triad of tryptophan residues in the cryptochrome/photolyase family that facilitates light-induced ET from exogenous reductants at the protein surface to the FAD cofactor in the protein core (Figure 1).^2,21–24

Figure 1.

Structural alignment of the conserved tryptophan cascade of members of the photolyase/cryptochrome protein family. Shown are the structures of Escherichia coli CPD photolyase (blue) (PDB entry: 1DNP), Thermus thermophilus CPD photolyase (red) (PDB entry: 1IQR), Drosophila melanogaster (6–4) photolyase (grey) (PDB entry: 3CVU), Arabidopsis thaliana cryptochrome-1 (orange) (PDB entry: 1U3D), Synechocystis sp. PCC 6803 Cry-DASH (yellow) (PDB entry: 1NP7), and A. thaliana cry3 (Cry-DASH, brown) (PDB entry: 2J4D). For X. laevis CRYD, the conserved tryptophans are Trp_A ≡ W400, Trp_B ≡ W377, and Trp_C ≡ W324.

In crystal structures of cryptochrome/photolyase-family proteins, the edge-to-edge separations between the individual indole rings of the three tryptophans range from 3.8 to 4.7 Å.^21,25–31 Hence, the aromatic moieties are sufficiently close for efficient directional ET via individual electron-hopping steps, as in a molecular wire, across a total distance of about 20 Å on a picosecond time scale.³² In comparison, direct ET over this long distance would be orders of magnitude slower.^33,34 The highly conserved positions and orientations of the three tryptophans are well defined in all structure-known members of the cryptochrome/photolyase family. The three-dimensional conservation suggests that ET along this pathway is relevant to all of the family members. Indeed, FAD photoreduction has been consistently observed among photolyases and cryptochromes from different organisms regardless of the proteins functions.^{15,23,35–38}

Very recently, we have demonstrated that the conserved tryptophan triad comprising residues W400, W377, and W324 (from inside the protein to outside; Figure 1) in the DASH-type cryptochrome (CRYD) derived from Xenopus laevis is active in FAD photoreduction.³⁹ Upon pulsed laser excitation, a short-lived spin-polarized radical-pair species has been detected by time-resolved X-band (≈9.7 GHz) electron-paramagnetic resonance (TREPR) on a nanosecond to microsecond time scale in the wild-type protein, but was not detected in a mutant W324F, in which the terminal tryptophan has been replaced by phenylalanine. Spectral simulations corroborated the assignment of the TREPR signal to the radical-pair state FAD^•⋯W324^•: The TREPR line shape could be faithfully reproduced using the geometry of the FAD^• and W324^• radicals taken from a model structure of X. laevis CRYD and assuming characteristic g-principal values and principal axes orientations and EPR line widths for the FAD⁴⁰ and tryptophan radicals.⁴¹ Two simultaneous assumptions were, however, critical: (1) radical-pair generation starts out from a pure electronic singlet precursor state, and (2) given the initial singlet-state radical-pair precursor, a small but positive value for the exchange interaction J was required to reproduce the experimental electron-spin polarization pattern.³⁹ The first assumption is in accord with findings from transient optical absorption spectroscopy on the equivalent radical-pair state, FAD^•⋯W306^•, of Escherichia coli DNA cyclobutane pyrimidine dimer (CPD) photolyase,¹⁸ however, conclusive evidence in the case of radical-pair formation in cryptochromes is still missing. Knowledge on the strength of the exchange interaction J is crucial, e.g., for an evaluation of the suitability of flavin-based cryptochrome radical pair magnetoreception in a biological compass.^19,20,42 Only if J is not too large with respect to the dipolar interaction between the two radicals of the radical pair and the strength of the earth’s magnetic field, a radical pair of the type encountered in cryptochromes fulfills the requirements to operate as an efficient magnetic compass sensor based on radical-pair spin chemistry. In this context, the precursor state of radical-pair formation is also of high importance; only if the multiplicity of the excited molecular wavefunction of the direct precursor state of radical-pair generation can be determined, then the electron-spin polarization pattern of the radical pair allows for an unambiguous determination of the sign of J.

In this contribution, we examine the radical-pair state FAD^•⋯W324^• of X. laevis CRYD both experimentally by applying Q-band (34.08 GHz) TREPR, and theoretically by inspection of radical-pair formation from different precursor multiplet states. We demonstrate that a two-frequency TREPR approach in combination with spectral simulations allows for an unambiguous assignment of the precursor spin multiplicity (singlet or triplet), and hence, the sign of the exchange interaction parameter J of the radical pair. Furthermore, a more accurate estimation of J is yielded for the FAD^•⋯W324^• state due to the higher spectral resolution of TREPR at around 34 GHz as compared to the more conventional experiment at around 9.7 GHz.

Experimental Methods

Sample Preparation

X. laevis CRYD was expressed and purified in the dark as described previously.⁴³ For TREPR studies, protein samples stored in a buffer (0.3 M NaCl, 0.1 M Tris·HCl, pH 8.0, 30–50% (v/v) glycerol) were supplemented with 5 mM potassium ferricyanide, K₃[Fe(CN)₆], and incubated overnight to ensure homogeneity of the FAD oxidation state. After removal of excess K₃[Fe(CN)₆] by ultrafiltration, samples were supplemented with 5 mM K₃[Fe(CN)₆] and 35% (v/v) glycerol and used directly for TREPR. Protein concentration and homogeneity of the FAD-cofactor redox state were controlled with a Shimadzu UV-1601PC spectrophotometer using published absorbance coefficients.⁴⁴

Time-Resolved EPR Studies

All Q-band TREPR experiments were performed at 272 K using a commercial EPR spectrometer (Bruker ESP380E) in conjunction with a Bruker microwave bridge (ER050 QGT). The protein sample was placed in a synthetic-quartz (suprasil) sample tube (0.56 mm inner diameter) and irradiated in a cylindrical resonator (Bruker ER5106 QT-W1), which was immersed in a helium gas-flow cryostat (Oxford CF-935). The temperature was regulated to ±0.1 K by a temperature controller (Oxford ITC-503). The time resolution of the experimental setup was in the 10-ns range. A microwave frequency counter (Hewlett Packard HP 5352B) was used to monitor the microwave frequency. The magnetic field at the position of the sample was calibrated against a Li:LiF standard sample with known g-value (2.002293±0.000002).⁴⁵

Optical excitation at a wavelength of 460 nm was carried out with an OPO system (Opta BBO-355-vis/IR) pumped by an Nd:YAG laser (Spectra Physics, Quanta Ray GCR 190-10) with a pulse width of approximately 6 ns, and a pulse energy of 4 mJ. The repetition rate of the laser was set to 1 Hz. A transient recorder (LeCroy 9354A) with a digitizing rate of 2 ns/11 bit was used to acquire the time-dependent EPR signal. To eliminate the background signals from the laser, TREPR signals were accumulated at off-resonance magnetic-field positions (background) and subtracted from those recorded on resonance.

Theoretical Formalism

Photo-induced charge separation produces a pair of interacting radicals (denoted radical A and radical B), whose time evolution is directly recorded by TREPR. The time-dependent EPR spectrum was calculated from the density matrix ${\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },t)$ of the radical pair by solving the quantum Liouville-von Neumann equation

$$\mathrm{i}\hslash \frac{\mathrm{d}{\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },t)}{\mathrm{d}t}=[{Ĥ}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega }),{\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },t)]$$ Eq. (1)

which has the solution

$${\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },t)=\text{exp }(-\frac{\mathrm{i}}{\hslash }{Ĥ}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega })t)·{\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },0)·\text{exp }(+\frac{\mathrm{i}}{\hslash }{Ĥ}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega })t)$$ Eq. (2)

where ${Ĥ}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega })$ is the time-independent radical-pair Hamiltonian in the rotating frame of the microwave frequency ω, and ${\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },0)$ is the density matrix at time zero defined at the instance of the laser pulse that is assumed a delta function since the laser pulse width is short compared to the observation time of the radical pair. The radical-pair Hamiltonian and the density matrix are functions of the orientation Ω of the two radicals with respect to each other and with respect to the direction of the external magnetic field B₀ = (0, 0, B₀) of strength B₀. The (time-independent) radical-pair Hamiltonian in the rotating frame is obtained from the (time-dependent) Hamiltonian in a fixed frame by the transformation

$${Ĥ}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega })=\text{exp }(+\mathrm{i}\omega {Ŝ}_{z}t)·{Ĥ}_{\text{rp}}(\mathrm{\Omega },t)·\text{exp }(-\mathrm{i}\omega {Ŝ}_{z}t)$$ Eq. (3)

The Hamiltonian of the radical pair is given by

$${Ĥ}_{\text{rp}}(\mathrm{\Omega },t)={Ĥ}_{\mathrm{A}}(\mathrm{\Omega })+{Ĥ}_{\mathrm{B}}(\mathrm{\Omega })+{Ĥ}_{\text{SS}}(\mathrm{\Omega })+{Ĥ}_{B_1}(t)$$ Eq. (4)

with

$$\begin{array}{cc}{Ĥ}_{\mathrm{A}}(\mathrm{\Omega })\hfill & ={\mathit{\beta }}_{\mathrm{e}}{\mathit{B}}_0·{\mathbf{g}}_{\mathrm{A}}(\mathrm{\Omega })·{\mathit{Ŝ}}_{\mathrm{A}}+{\displaystyle \sum _j}{\mathit{Î}}_{\mathrm{A},j}·{\mathbf{A}}_{\mathrm{A},j}(\mathrm{\Omega })·{\mathit{Ŝ}}_{\mathrm{A}}\hfill \\ {Ĥ}_{\mathrm{B}}(\mathrm{\Omega })\hfill & ={\mathit{\beta }}_{\mathrm{e}}{\mathit{B}}_0·{\mathbf{g}}_{\mathrm{B}}(\mathrm{\Omega })·{\mathit{Ŝ}}_{\mathrm{B}}+{\displaystyle \sum _k}{\mathit{Î}}_{\mathrm{B},k}·{\mathbf{A}}_{\mathrm{B},k}(\mathrm{\Omega })·{\mathit{Ŝ}}_{\mathrm{B}}\hfill \\ {Ĥ}_{\text{SS}}(\mathrm{\Omega })\hfill & =-J(\frac{1}{2}+2{\mathit{Ŝ}}_{\mathrm{A}}·{\mathit{Ŝ}}_{\mathrm{B}})+\mathit{Ŝ}·{\mathbf{D}}_{\text{rp}}(\mathrm{\Omega })·\mathit{Ŝ}\hfill \end{array}$$ Eq. (5)

and

$$\mathit{Ŝ}={\mathit{Ŝ}}_{\mathrm{A}}+{\mathit{Ŝ}}_{\mathrm{B}}$$ Eq. (6)

The constant β_e is the Bohr magneton. For radicals A and B, respectively, Ŝ_A = (Ŝ_A,x,Ŝ_{A, y},Ŝ_A,z) and Ŝ_B = (Ŝ_B,x,Ŝ_{B, y},Ŝ_B,z) are the electron-spin vector operators, Î_A and Î_B are the nuclear-spin vector operators, g_A (Ω) and g_B (Ω) are the g-tensors, and A_A,j (Ω) and A_B,k (Ω) the hyperfine interaction tensors. J is the isotropic exchange interaction parameter, and D_rp (Ω) is the electron–electron magnetic dipolar interaction tensor between the two unpaired electrons of the radical pair.

In the absence of any microwave magnetic field in Eq. (4) and neglecting all hyperfine interactions, the three contributions Ĥ_A (Ω), Ĥ_B (Ω), and Ĥ_SS (Ω) lead to the well-known four-level energy diagram of spin-correlated coupled radical pairs,^46–49 where |T₊〉 and |T₋〉 are eigenstates, as well as two linear combinations of |S〉 and |T₀〉 with coefficients that depend on the exchange and dipolar interactions as well as the differences in precession frequencies of the two spins of radicals A and B. For one specific orientation of the two radicals of the radical pair with respect to each other and relative to the direction of the external magnetic field B₀, the resulting state-energy diagram leads to four possible EPR transitions between the four eigenstates. In the case of a pure singlet-state precursor, an EPR spectrum comprising two equally intense anti-phase line pairs is expected. The center position of this EPR spectrum corresponds to the average g-value of the two radicals, and if their difference in g-value is large compared to the splitting of the line pairs (i.e., for weak radical–radical coupling) one pair of lines is centered around the g-value of the A^• radical, the other around the g-value of the B^• radical. In a rigid radical pair, the splitting of the line pair is modified by an orientation-dependent dipolar contribution to a value |2J − 2D_rp,zz| where

$$D_{\text{rp},\mathit{\text{zz}}}=D_{\text{rp}}({\text{cos}}^2\xi -\frac{1}{3})$$ Eq. (7)

In Eq. (7) D_rp is the zero-field parameter of the radical pair, and ξ is the angle between the dipolar axis of the system and the magnetic-field direction. When the radicals are relatively far removed from each other, as in the cases of interest here, D_rp can be estimated from a classical point-dipole approximation,

$$D_{\text{rp}}/\mu \mathrm{T}=-\frac{2.782\times {10}^3}{{(r/\text{nm})}^3}$$ Eq. (8)

where r (in nm) is the center-to-center distance between A^• and B^•.

The term

$${Ĥ}_{B_1}(t)=\mathit{ḡ}{\mathit{\beta }}_{\mathrm{e}}{\mathit{B}}_1(t)·\mathit{Ŝ}$$ Eq. (9)

accounts for the microwave magnetic field B₁ = B₁(cos(ω t), sin(ω t), 0) of strength B₁, that induces EPR transitions within the four-state model of spin-correlated radical pairs. In Eq. (9), g̅ = (g̅_A + g̅_B) / 2, where g̅_A and g̅_B are the (average) isotropic g-values of A^• and B^•, respectively.

The time-dependent intensity of the EPR spectrum, Int(B₀, t), is calculated at each value of the external magnetic field B₀ using

$$\text{Int}(B_0,t)={\displaystyle \underset{\mathrm{\Omega }}{\int }}\text{Tr }[{\mathrm{\rho ̂}}_{\text{rp}}^{\mathrm{r}}(\mathrm{\Omega },t)·{Ŝ}_y]\mathrm{d}\mathrm{\Omega }$$ Eq. (10)

where Ŝ_y extracts the y-component of the total electron spin in the rotating frame produced by Ĥ_B1.

In the singlet–triplet representation, the initial density matrix ρ̂_rp (Ω, 0) for a single radical-pair member of the ensemble becomes

$${\mathrm{\rho ̂}}_{\text{rp}}(\mathrm{\Omega },0)=\left(\begin{array}{cccc}\hfill |{\mathrm{T}}_{+}\rangle \hfill & \hfill |\mathrm{S}\rangle \hfill & \hfill |{\mathrm{T}}_0\rangle \hfill & \hfill |{\mathrm{T}}_{-}\rangle \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_{\mathrm{S}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$ Eq. (11)

for a radical pair created by a singlet state precursor, where ρ_S = 1, and

$${\mathrm{\rho ̂}}_{\text{rp}}(\mathrm{\Omega },0)=\left(\begin{array}{cccc}\hfill |{\mathrm{T}}_{+}\rangle \hfill & \hfill |\mathrm{S}\rangle \hfill & \hfill |{\mathrm{T}}_0\rangle \hfill & \hfill |{\mathrm{T}}_{-}\rangle \hfill \\ \hfill {\rho }_{+}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_{-}\hfill \end{array}\right)$$ Eq. (12)

for a triplet state precursor. In both cases, the trace of the initial density matrix is 1. This approach is the same as that used for the TREPR study of radical pairs in the primary events of photosynthesis, except for the added complication, that the cryptochrome photochemistry may involve either a singlet-state or a triplet-state precursor (see below), while in the photosystems and some models for photosynthetic charge separation radical-pair formation occurs only from the singlet state.^50–52 In contrast, the initial density matrix for a radical pair generated from a triplet-state precursor is more complicated.

In general, intersystem crossing from an excited singlet-state molecule to an excited triplet state always takes place in accord with “spin selection rules” that operate in the molecule.⁵³ As a result, the three zero-field sublevels, labeled |T_X〉, |T_Y〉, and |T_Z〉 (X, Y, and Z are the principal axes of the D_T tensor, see below), of the triplet state are unequally populated, far from thermal equilibrium. In the absence of an external magnetic field, the intersystem crossing process results in the initial, non-equilibrium populations ρ_X, ρ_Y, and ρ_Z, whose sum adds up to 1. Typically, the formation of the radical pair from the triplet-state precursor is faster than spin-lattice relaxation in the precursor to thermal equilibrium. In this case, the non-equilibrium populations of the triplet state are passed on to the appropriate radical-pair levels. Since the EPR spectra are recorded in the presence of a (typically rather strong) external magnetic field, the high-field density-matrix elements of the triplet state precursor are required, namely ρ₊, ρ₀, and ρ₋, and not the density-matrix elements, ρ_X, ρ_Y, and ρ_Z, at zero magnetic field.

The anisotropic spin Hamiltonian of the triplet-state precursor in the absence of an external magnetic field (in the principal axis system (X, Y, Z) of the triplet-state dipolar coupling tensor D_T),

$${Ĥ}_{\mathrm{T}}(\mathrm{\Omega },B_0=0)=\mathit{Ŝ}·{\mathbf{D}}_{\mathrm{T}}(\mathrm{\Omega })·\mathit{Ŝ}$$ Eq. (13)

is used to calculate the high-field density matrix, where the appropriate eigenfunctions are accurately represented as the wavefunctions |T₊〉, |T₀〉, and |T₋〉. The zero-field energies are defined with the two zero-field splitting parameters D and E, such that D_X = D/3 − E, D_Y = D/3 + E, and D_Z = −2D/3. The high-field energy levels are calculated by diagonalizing the high-field Hamiltonian

$${Ĥ}_{\mathrm{T}}(\mathrm{\Omega },B_0)=\mathit{g}{\mathit{\beta }}_{\mathrm{e}}{\mathit{B}}_0·\mathit{Ŝ}+\mathit{Ŝ}·{\mathbf{D}}_{\mathrm{T}}(\mathrm{\Omega })·\mathit{Ŝ}$$ Eq. (14)

This yields the transformation matrix R̂ that diagonalizes Ĥ_T(Ω,B₀) in Eq. (14). Ŝ = Ŝ₁ + Ŝ₂ is the total electron-spin operator for the two spins of the triplet state. This matrix transformation is then applied to the density matrix of the zero-field triplet-state precursor to determine the high-field triplet density matrix, where the resulting off-diagonal density-matrix elements are neglected:

$${\mathrm{\rho ̂}}_{\mathrm{T}}(\mathrm{\Omega },t=0)=\mathit{R̂}·\left(\begin{array}{ccc}\hfill |{\mathrm{T}}_X\rangle \hfill & \hfill |{\mathrm{T}}_Y\rangle \hfill & \hfill |{\mathrm{T}}_Z\rangle \hfill \\ \hfill {\rho }_X\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_Y\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_Z\hfill \end{array}\right)·{\mathit{R̂}}^{-1}\equiv \left(\begin{array}{ccc}\hfill |{\mathrm{T}}_{+}\rangle \hfill & \hfill |{\mathrm{T}}_0\rangle \hfill & \hfill |{\mathrm{T}}_{-}\rangle \hfill \\ \hfill {\rho }_{+}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_{-}\hfill \end{array}\right)$$ Eq. (15)

Conservation of spin-angular momentum during the formation of the radical pair requires that the density-matrix elements of the triplet-state precursor at non-zero magnetic field B₀, ρ₊, ρ₀, and ρ₋, are also the initial density matrix elements of the radical-pair density matrix for the |T₊〉, |T₀〉, and |T₋〉 wavefunctions of the singlet-triplet representation (see Eq. (12)).

A further situation has been examined in this study: formation of a radical pair from a triplet-state precursor whose initial electron-spin polarization has decayed by spin-lattice relaxation to the thermally equilibrated high-field triplet sublevel populations. In this case, the density-matrix elements ρ₊, ρ₀, and ρ₋, of the triplet precursor, and consequently of the radical pair, have been calculated using the Boltzmann expressions for the three levels i ∈ {|T₊〉, |T₀〉, |T₋〉}

$${\rho }_{\mathrm{T},i}(\mathrm{\Omega },t=0)=\frac{1}{q}·\text{exp }(-\frac{E_i}{k_{\mathrm{B}}T})$$ Eq. (16)

where E_i is the energy of state i, k_B is the Boltzmann constant, T is the temperature, and q is the partition function

$$q={\displaystyle \sum _i}\text{exp }(-\frac{E_i}{k_{\mathrm{B}}T})$$ Eq. (17)

Computation of EPR Spectra

A FORTRAN program has been developed, in which the initial density matrix ρ̂_rp (0) is calculated as described above, depending on the precursor multiplicity (singlet precursor (Eq. (11)) versus triplet precursor (Eq. (12))). To calculate ρ̂_rp (t) from Eq. (2) for the ensemble of radical pairs, Ĥ_rp (Ω) as a function of t, Ω, B₀, B₁, D_T, D_rp, g_A, g_B, A_A,j and A_B,k, is diagonalized using the Householder/QL-method implemented with subroutines provided in the literature.⁵⁴ The parameters Ω, B₀, B₁, D_rp, g_A, g_B, A_A,j and A_B,k, are reasonably well defined for cryptochromes in advance of the simulations (see below). The zero-field populations ρ_X, ρ_Y, and ρ_Z of the triplet-state precursor and the zero-field splitting parameters D and E were taken from the literature for a flavin in frozen aqueous solution.⁵⁵ TREPR spectra as a function of time were then calculated according to Eq. (10) for the powder average over the Euler angles represented by Ω. Calculations of the radical pairs formed from the singlet state are comparatively straightforward and have been described in the literature.⁴⁹

Results and Discussion

Radical-Pair Detection by TREPR

TREPR spectroscopy, with a time resolution of up to 10 ns, allows real-time observation, e.g., of short-lived radical-pair and triplet states generated by pulsed laser excitation. In contrast to conventional continuous-wave EPR spectroscopy, which usually involves magnetic-field modulation to improve the signal-to-noise ratio, TREPR is recorded in a high-bandwidth direct-detection mode, so as not to constrain the time resolution of the experiment. Consequently, positive and negative signal amplitudes in TREPR correspond to enhanced absorptive (A) and emissive (E) electron-spin polarizations of the EPR transitions, respectively.

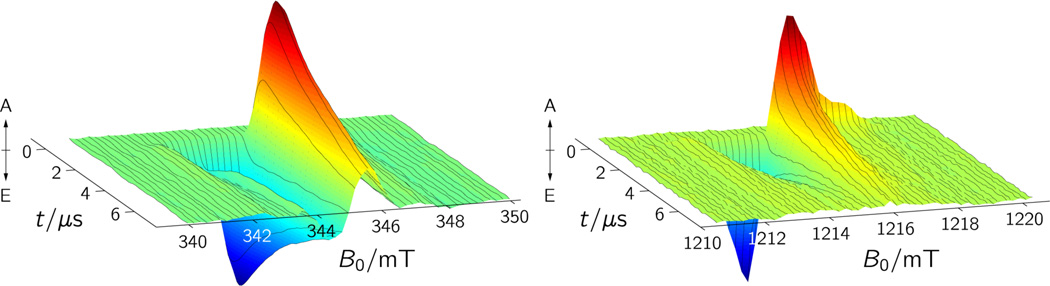
Upon blue-light photoexcitation, wild-type X. laevis CRYD forms a spin-polarized paramagnetic species at ambient temperature, which we assigned to a radical pair based on the spectral shape and narrow width of the signal.³⁹ A spin-polarized flavin triplet state detected under comparable conditions would span more than 150 mT on the magnetic-field axis as a result of the strong dipolar and exchange spin-spin interactions between the two unpaired electrons that are both localized on the 7,8-dimethyl isoalloxazine ring of the FAD cofactor.^55,56 Figure 2 shows a comparison of the two-dimensional TREPR data sets recorded under similar experimental conditions (temperature, solvent, optical sample excitation) at Q-band (34.08 GHz) and at X-band (9.68 GHz) as a function of the magnetic field B₀ and the time t following the laser pulse. Both spectra have a similar overall shape, though the Q-band spectrum is slightly more asymmetric and decays somewhat faster (about 1.6 µs at Q-band as compared to about 6 µs at X-band) than the X-band spectrum. The latter observation clearly indicates that the decay of the TREPR signal does not reflect the lifetime of the radical-pair species but is governed by electron-spin relaxation of the initial electron-spin polarization to thermal (Boltzmann) equilibrium which may depend on the microwave frequency used in the EPR experiment. Closer inspection of the Q-band data even reveals some relaxation anisotropy that is not observed at X-band: the high-magnetic-field range of the TREPR signal decays considerably faster than the spectral components at the center and at the low-magnetic-field range of the spectrum (Figure 2). This observation can be rationalized by the better spectral separation of the contributions of the two radicals typically obtained at higher microwave frequencies due to the direct scaling of the Zeeman interaction with the strength of the external magnetic field (see also below).

Figure 2.

Complete TREPR data sets of X. laevis CRYD showing the signals of the spin-correlated radical pair FAD^•⋯W324^• generated by pulsed laser excitation (460 nm). A, enhanced absorption; E, emission. (a) X-band TREPR. Each time profile is the average of 120 acquisitions recorded at a microwave frequency of 9.68 GHz, and a microwave power of 2 mW at a detection bandwidth of 100 MHz. (b) Q-band TREPR. Each time profile is the average of 50 acquisitions recorded at a microwave frequency of 34.08 GHz, and a microwave power of 3.7 mW at a detection bandwidth of 100 MHz.

The radical-pair signatures are not observed in a single-point mutant of X. laevis CRYD, in which the protein-surface exposed tryptophan W324 of the conserved tryptophan triad (FAD–W400–W377–W324 protein surface; Figure 1) is replaced with a phenylalanine (W324F).³⁹ The three aromatic indole rings of the tryptophan cascade constitute an efficient ET path to the flavin through which electrons can be step-wise transported upon photoexcitation of the flavin. The triad has initially been identified in CPD photolyase of E. coli (FAD–W382–W359–W306 from protein core to surface)²¹ and has since been found in all structure-known members of the cryptochrome/photolyase family except for class-II photolyases with poor amino-acid sequence homology.³⁶ In the E. coli photolyase enzyme, when the FAD cofactor is initially in its neutral radical form, FADH^•, ET from W382 to FADH^• forms FADH⁻ and a tryptophan radical cation, W382^•+, and this is followed by ET from W359 to W382^•+ (thus forming W382 and W359^•+), and finally W306 reduces W359^•+ (forming W359 and W306^•+). These three ET steps are completed within 30 ps.³² In a subsequent step, within 300 ns W306^•+ releases a proton to the solvent, and forms a neutral tryptophan radical, W306^•.⁵⁷ An alternative pathway has been proposed by Saxena and coworkers in which, instead of ET occurring through W382 and W359, an electron tunnels through the α-15 helix from residue D358 to residue W359.⁵⁸

In X. laevis CRYD, when FAD has been prepared fully oxidized, stepwise light-induced ET likely generates a sequence of short-lived radical pairs:

$$\text{FAD }\mathrm{W}400\mathrm{W}377\mathrm{W}324\stackrel{h\nu }{\to }{\text{FAD}}^{*}\mathrm{W}400\mathrm{W}377\mathrm{W}324\to {\text{FAD}}^{•-}{\mathrm{W}400}^{•+}\mathrm{W}377\mathrm{W}324\to {\text{FAD}}^{•-}\mathrm{W}400{\mathrm{W}377}^{•+}\mathrm{W}324\to {\text{FAD}}^{•-}\mathrm{W}400\mathrm{W}377{\mathrm{W}324}^{•+}\to \dots \to {\text{FAD}}^{•}\mathrm{W}400\mathrm{W}377{\mathrm{W}324}^{•}$$

The disappearance of the radical-pair TREPR signature in the W324F mutant led us to the assignment of the wild-type signal to the radical-pair state FAD^•⋯W324^•.³⁹ As the time resolution of our Q-band TREPR instrumentation is about 10 ns, the intermediate radical-pair states escape detection because of their short lifetime.

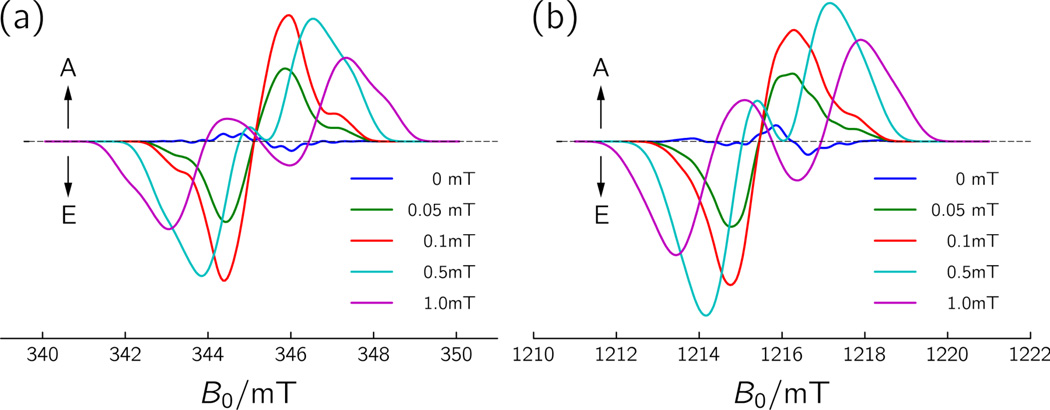
The signal assignment to FAD^•⋯W324^• has been corroborated by spectral simulations carried out under the assumptions that this radical-pair state is generated from a pure singlet-state precursor and that the intermediate radical pairs are too short-lived, as in photolyases,³² for significant singlet-to-triplet interconversion to take place.³⁹ Characteristic g-tensor principal values and principal axes orientations of a flavin radical⁴⁰ and a tryptophan radical,⁴¹ as well as the geometry of the radicals with respect to each other, have been accounted for in the calculations. The strength of the dipolar interaction (D_rp = −0.36 mT) between the unpaired electron spins has been derived from the point-dipole approximation, Eq. (8), using a distance of r = 2.0 nm between FAD^• and W324^•. Assuming characteristic EPR line shapes consistent with the two radicals’ known hyperfine structures, the exchange interaction parameter J was the only variable parameter in the computations. Figure 3 shows spectral simulations of the radical-pair spectra at X-band and Q-band for a range of (positive) J-values, values that are in accord with evaluations of the exchange interaction obtained for other radical-pair states, e.g., from photosynthetic charge separation.⁵⁹ The weak ‘bumps’ in the spectra with small J-values are due to the rather large hyperfine couplings arising from the β-protons at the indole side chain attached to C(3) of W324^•. With increasing J, spectral broadening progressively obliterates the resulting hyperfine structure. The radical pair’s hyperfine signature is less strongly pronounced at Q-band as compared to the X-band, because g-anisotropies become dominant at higher magnetic fields. Clearly a small but non-zero value of J needs to be considered, as otherwise the characteristic E/A pattern of the experimental data set would not be reproduced. It should be noted, that a negative J-value yields virtually the same TREPR pattern, however, with inverted electron-spin polarization. Consequently, the sign of J must remain undetermined as long as the precursor state of radical-pair formation (singlet versus triplet) is not confirmed (see below).

Figure 3.

Simulations of TREPR spectra at (a) X-band (9.68 GHz), and (b) Q-band (34.08 GHz) microwave frequencies using the magnetic interaction parameters of the radical-pair state FAD^•⋯W324^• of X. laevis CRYD. A, enhanced absorption; E, emission. Only the exchange interaction parameter J was varied in a range from 0 to +1 mT. Other (fixed) simulation parameters: g-tensor of the flavin radical g_FAD = (2.00431, 2.00360, 2.00217); g-tensor of tryptophan radical g_W324 = (2.00370, 2.00285, 2.00246); orientation of the g_W324-tensor principal axes with respect to the g_FAD-tensor principal axes: Ω_W324 = (127°, 77°, 247°); dipolar coupling between FAD^• and W324^•, D_rp = −0.36 mT; orientation of the dipolar coupling tensor D_rp with respect to the g_FAD-tensor principal axes: Ω_Drp = (0°, 110°, 110°); 2nd moment of the FAD^• hyperfine line broadening, 〈H²〉_HFS(FAD^•) = 0.252 mT²; 2nd moment of the of the W324^• radical, 〈H²〉_HFS(W324^•) = 0.841 mT². 2nd moment of (Gaussian) inhomogeneous broadening, 〈H²〉_inh = 0.371 mT².

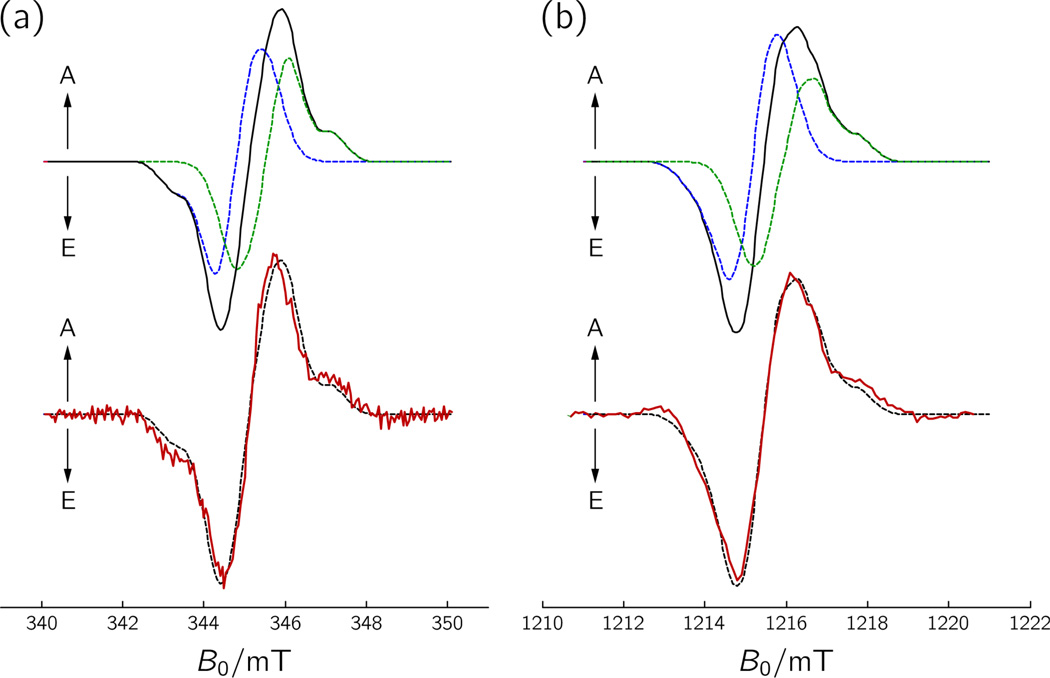
The Q-band radical-pair TREPR signal was recorded 130 ns after pulsed laser excitation (Figure 4). As Q-band has typically better spectral resolution than X-band, the value of J = +0.073 mT extracted from an automated least-squares fitting of the Q-band TREPR spectrum is more reliable than the approximately three times larger value extracted from the X-band data set. In general, the agreement between experimental and calculated TREPR spectra is remarkably good. These experimental observations validate the concern of Izmaylov et al., whose quantum-chemical calculations predict negligible exchange and dipolar interactions for the most distant FAD^•⋯W^• radical pair in cryptochrome, that the specific protein environment of redox partners strongly affects coupling and that calculations in its absence may not be accurate.⁶⁰ Clearly, with J and D_rp simultaneously being zero, electron-spin polarized TREPR signals would have not been detected.

Figure 4.

Simulations of TREPR spectra of FAD^•⋯W324^• of X. laevis CRYD recorded at (a) X-band (9.68 GHz), and (b) Q-band (34.08 GHz) microwave frequencies based on the spin-correlated coupled radical-pair model with a pure singlet-state precursor. The parameters specified in Figure 3 were used in combination with J = +0.073 mT. Lower panel: experimental spectra (red curves) recorded at 1 µs (X-band) and 130 ns (Q-band) after pulsed laser excitation. Spectral simulations are superimposed as black dashed lines. Upper panel: Spectral simulations of the radical pair FAD^•⋯W324^• together with the contributions of the individual radicals to the overall spectrum (black curves), FAD^• (dashed blue curves); W324^• (dashed green curves).

Figure 4 also depicts the individual contributions of the FAD^• and W324^• radicals to the overall radical-pair spectrum. Due to its slightly larger isotropic g-value,⁶¹ the FAD^• signal is shifted to lower magnetic fields as compared to that of W324^•. Consequently, in the Q-band TREPR spectrum of FAD^•⋯W324^• the high-magnetic-field contribution is almost exclusively dominated by the W324^• radical (Figure 4(b)). The even smaller decay time observed in this region (approx. 230 ns) as compared to the value found in the central part of the spectrum (1.6 µs) – where both radicals contribute to the overall TREPR amplitude – indicates that some dynamic process influences electron-spin relaxation in the protein-surface exposed W324 radical. This could be interaction with surrounding solvent molecules or small-angle librational motions of the indole ring of W324^•, which is situated in a short loop region. Such relaxation anisotropy is not observed in our X-band TREPR data due to its inferior spectral resolution and the more limited time resolution (≈900 ns) of the instrumentation.

Singlet and Triplet Radical-Pair Precursor States

Light-induced generation of radical-pair species has been reported from molecular singlet states as well as from triplet states.⁵³ Singlet-precursor radical pairs have been detected, for example, in the primary events of plant and bacterial photosynthesis,⁶² whereas in a number of artificially designed molecular systems for light-induced ET, radical pairs emerge from a molecular triplet state.^63–65 Both multiplets could in principle be relevant to light-induced radical-pair generation in flavoproteins. In the recently discovered blue-light photoreceptor proteins carrying the BLUF (blue light using FAD) domain, for example, hydrogen-bond switching in photoactivation proceeds by means of a radical-pair mechanism involving an excited flavin singlet state.⁶⁶ In contrast, radical-pair formation from an excited flavin triplet state has been suggested, based on spectroscopic and theoretical evidence, to precede flavin–cysteinyl adduct formation in the primary photoreaction of LOV (light-oxygen-voltage) domains in the blue-light receptor phototropin.^56,67 Given this diversity in flavin photochemistry, we have examined the generation of spin-correlated radical pairs in X. laevis CRYD representing cryptochromes starting out from (a) a pure electronic singlet state and from (b) a pure triplet-state precursor. For the latter case, further differentiation is required.

Case (b.1). Due to triplet-sublevel selective spin-orbit intersystem crossing from an excited molecular singlet state to a molecular triplet state, the zero-magnetic-field levels of the triplet, denoted |T_X〉, |T_Y〉, and |T_Z〉, are initially in general unequally populated, far from thermal equilibrium, in a highly electron-spin polarized configuration. This also holds true for molecular triplet states of flavins generated by photoexcitation.^55,56 The electron-spin polarization of the zero-field levels of the triplet is then projected onto the triplet high-magnetic-field levels, |T₊〉, |T₀〉, and |T₋〉, and upon charge separation transferred to the |T₊〉-, |T₀〉-, and |T₋〉-levels of the radical pair, assuming the rate of radical-pair formation is large as compared to the rate of electron-spin relaxation in the triplet state. We expect this to be the case at low temperatures where spin-polarized flavin triplet states show rather long electron-spin lattice relaxation times on the order of several microseconds to milliseconds.

Case (b.2). If however electron-spin relaxation in the molecular triplet is fast as compared to the time constant of radical-pair formation, then the initially highly electron-spin polarized populations of the triplet zero-field and high-field levels will relax to thermal equilibrium before ET can take place. In this case the triplet sublevels of the radical pair will be populated from the thermally equilibrated triplet functions, |T₊〉, |T₀〉, and |T₋〉. We expect this case to occur mostly at elevated temperatures when relaxation of the triplet populations to thermal equilibrium is quite fast.

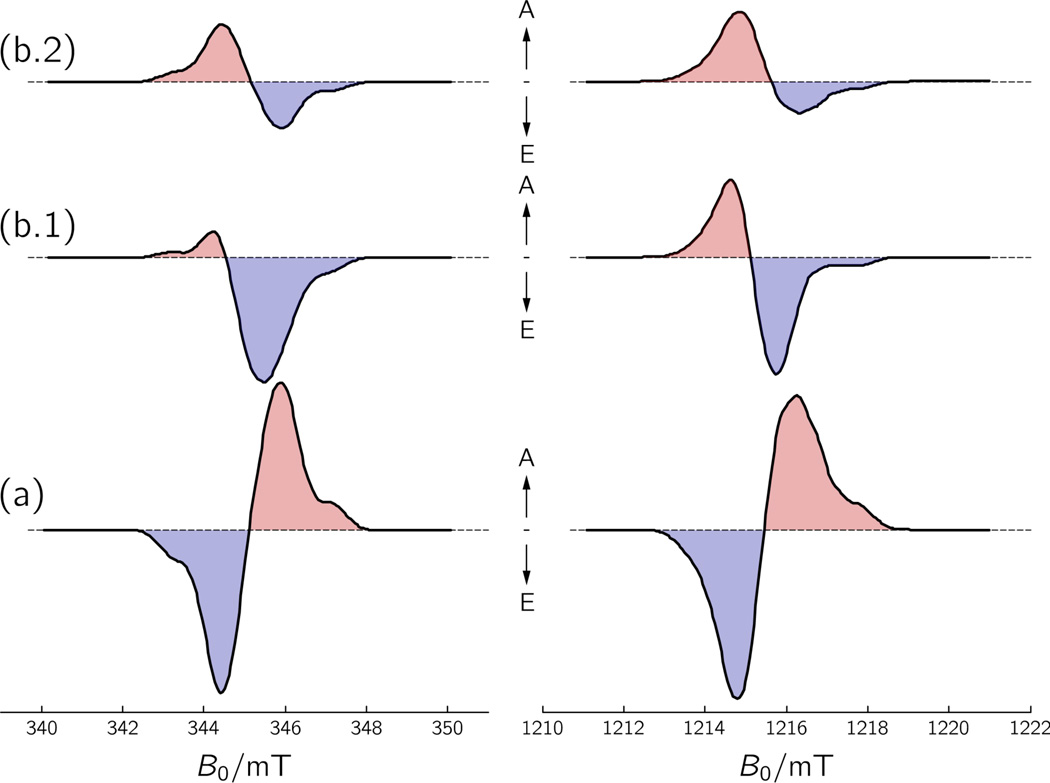
Based on the formalism outlined above, we have performed spectral simulations of radical-pair TREPR spectra for the following three cases: (a) singlet state precursor, (b.1) spin-polarized triplet state precursor, and (b.2) “relaxed” triplet state precursor at thermal equilibrium (T = 274 K). For both triplet computations (b.1 and b.2), characteristic triplet-state parameters of a flavin have been used. The zero-field splitting parameters, D = 68.57 mT, and E = −18.75 mT, and zero-field spin-state populations, ρ_X = 0.67, ρ_Y = 0.33, and ρ_Z = 0, were taken from simulations of TREPR spectra of a flavin mononucleotide (FMN) triplet state recorded in frozen aqueous solution at 80 K.⁵⁵ The results of the triplet-precursor calculations have been compiled in Figure 5 together with results from singlet-state precursor simulations.

Figure 5.

Simulations of TREPR spectra of FAD^•⋯W324^• of X. laevis CRYD recorded at X-band (9.68 GHz, left curves), and Q-band (34.08 GHz, right curves) microwave frequencies, based on a (a) pure singlet-precursor state, (b.1) pure spin-polarized triplet-precursor state, and (b.2) pure (“relaxed”) triplet-precursor state at thermal equilibrium. The simulation parameters for the singlet-precursor radical-pair spectra (a) are given in Figure 3. For the triplet-precursor radical-pair spectra (b.1 and b.2), the following triplet parameters have been used: D = 68.57 mT, and E = −18.75 mT; zero-field spin-state populations, ρ_X = 0.67, ρ_Y = 0.33, and ρ_Z = 0 (case b.1). For the triplet precursor at thermal equilibrium (T = 274 K) (case b.2), the high-field triplet sublevel populations have been calculated using Eqs. (16) and (17). The principal axes of the D_T-tensor of the flavin triplet precursor were assumed collinear with the principal axes of the g_FAD-tensor.

When the radical-pair precursor is a pure singlet state, the initial electron-spin polarized TREPR spectrum has a rather symmetric shape, as in case (a) of Figure 5. One half of the spectrum is in emission, and the other half is in enhanced absorption. Integration of the signal intensity over the magnetic-field range results in zero net electron-spin polarization. The cancelation happens because the singlet state, |S〉, has an equal number of spins with M_S = −1/2 (“spin down”) and with M_S = +1/2 (“spin up”), while the |T₊〉, |T₀〉, and |T₋〉 states of the radical pair are not populated. This situation applies at all values of the magnetic field and is depicted for the radical-pair state of cryptochrome at X-band and Q-band.

When the radical-pair precursor is a spin-polarized triplet state (case b.1), the initial TREPR spectrum typically exhibits either net absorption or net emission. This is understood in terms of the three triplet wavefunctions, |T₊〉, |T₀〉, and |T₋〉. All three states can be populated. Similar to the |S〉 state, the |T₀〉 state has an equal number of “spin up” and “spin down” electrons. The |T₋〉 and |T₊〉 states, on the other hand, may contain different populations because of second-order effects created by the size of the zero-field splitting parameters D and E relative to the strength of the external magnetic field B₀.^68–70 If |T₊〉 is in excess, then net emission occurs, because |T₊〉 contains two “spin up” electrons. Accordingly, if |T₋〉 is in excess, net enhanced absorption occurs because |T₋〉 contains two electrons with “spin down”. However, the stronger the magnetic field B₀ is relative to the size of the dipolar interaction (parameterized by D and E) in the triplet state, the smaller the population difference between the high-field levels |T₊〉 and |T₋〉 despite the non-Boltzmann population of the zero-field levels.⁷⁰ In this so-called “high-magnetic-field limit”, where the energies of |T₊〉 and |T₋〉 states increase and decrease, respectively, in a linear fashion with the external magnetic field B₀, one expects increasingly symmetric TREPR spectra. In other words, the higher the magnetic field, the more efficiently the enhanced absorptive and emissive spectral contributions will cancel out, and the more the integral of the signal intensity over the magnetic field will approach zero. Given the zero-field splitting parameters and zero-field populations of a flavin triplet precursor, a net emissive TREPR spectrum is expected from the cryptochrome radical pair at X-band microwave frequencies, whereas at Q-band the spectrum becomes more symmetric and the net polarization quite small (case (b.1) of Figure 5). In both cases, a TREPR spectrum with a reversed spin-polarization pattern (A/E) as compared to that of a singlet-state precursor (E/A) radical pair with J > 0 is expected.

Finally, for the case when spin-lattice relaxation to thermal equilibrium occurs prior to radical-pair formation (case b.2), the triplet levels are populated according to the Boltzmann factors. At rather low magnetic field (e.g., ≈345 mT in X-band TREPR) and hence rather small energetic differences between the three triplet sublevels, one can assume roughly equal populations in |T₊〉, |T₀〉, and |T₋〉: ρ₊ ≈ ρ₀ ≈ ρ₋ ≈ 1/3. For a radical pair generated by this precursor state, a fairly symmetric TREPR spectrum is predicted, similar to that of a singlet-precursor radical pair except that the electron-spin polarization pattern inverts to A/E, cf. spectra (b.2) and (a) in Figure 5, left side. However, the higher the magnetic field (and hence the larger the energy differences between the three triplet sublevels), the more will the triplet sublevel populations deviate from the value of 1/3 observed at low magnetic field. According to their relative energies, the sublevel populations will then be unequally populated, with ρ₊ < ρ₀ < ρ₋. Consequently, the larger the population differences between the sublevels of the triplet at thermal equilibrium, the more absorptive contributions will dominate the TREPR spectrum of the radical pair. This effect is clearly seen in the comparison of the radical-pair spectra calculated for X-band and Q-band TREPR.

Origin of the Spin-Correlated Radical Pair in Cryptochrome

Closer analysis of the overall electron-spin polarizations in X. laevis CRYD, obtained by integrations of the experimental radical-pair signal intensities over the magnetic field ranges, yields zero polarizations at both X-band and Q-band TREPR. This is due to equal amounts of emissive and enhanced absorptive polarization cancelling each other. Such invariance of the net polarization is observed neither for a spin-polarized triplet-state precursor nor for a triplet precursor at thermal equilibrium (Figure 5). For the former, net-zero electron-spin polarization of the radical pair is only observed in the limiting case of very high magnetic fields relative to the zero-field splitting parameters, D and E, of the precursor triplet state. Due to the large zero-field (dipolar and/or spin orbit) interactions in spin-polarized flavin radicals,⁵⁵ this case would definitely not be fulfilled at the moderate magnetic fields (≈345 mT) of X-band TREPR. Our simulations predict even at the approximately four-fold stronger magnetic fields (≈1216 mT) of Q-band TREPR, significant net emission occurs. On the other hand, for a thermally equilibrated triplet precursor, net-zero electron-spin polarization is only observed at low magnetic fields, where the triplet sublevels are more or less equally populated. Increasing the magnetic field would lead to enhanced absorption dominating. This effect, predicted to be observable at Q-band TREPR, clearly does not show up in the experiment. We therefore conclude that the light-induced radical pair FAD^•⋯W324^• of X. laevis CRYD, detected by TREPR at ambient temperature (274 K), is generated from an FAD excited singlet precursor state. Consequently, this must also hold true for the intermediate radical pairs FAD^•−⋯W400^•+ and FAD^•−⋯W377^•+ that escape TREPR detection and which are too short-lived for significant singlet-to-triplet interconversion to take place.

For the analogous photoreduction of fully oxidized FAD in E. coli CPD photolyase, ET starting out from the FAD triplet state, thus generating a triplet radical pair, has been proposed by Gindt and coworkers.¹⁵ However, neither spectral simulations of the TREPR signal of FAD^•⋯W306^• (recorded with a millisecond time resolution) have been presented, nor has the TREPR detection of the radical-pair species been conducted at different magnetic field ranges. Clearly, further studies need to be carried out in order to substantiate if photolyases – despite their high structural conservation – react differently upon photoexcitation as compared to cryptochromes.

For a proposed magnetoreceptor function of cryptochrome,¹⁷ spin-correlated radical-pair formation by light-induced charge separation via the tryptophan triad from an excited singlet-state precursor of FAD has important implications. The two unpaired electron spins of the radical pair need to be quickly separated over a rather large distance so as to minimize spin-allowed – and energetically favored – backward electron transfer that would regenerate the diamagnetic ground state and thus diminish the yield of required long-lived radical-pair species. Hence, the triad of tryptophan residues not only establishes the required separation of the two radicals such that their mutual magnetic interactions are small with respect to the magnetic field of the Earth, but also prevents radical recombination from intermediate radical pairs by favoring fast forward electron transfer. Consequently, the intermediate radical pairs become too short-lived for significant singlet-to-triplet interconversion to take place, and the terminal radical pair FAD^•−⋯W324^•+ is generated in a pure spin state. This course of events fulfills one prerequisite for an efficient functioning of a magnetoreceptor based on photoinduced radical-pair chemistry. Nevertheless, the general concept of magnetoreception in animals remains under heavy debate.^19,71

In summary, this study shows that high-time resolution TREPR performed at two microwave frequency bands is well suited for probing the detailed features of light-induced charge separation in cryptochromes that are essential to understanding how flavin-based radical-pair spin chemistry may be exploited in an avian magnetic compass.