Effects of gap junction inhibition on contraction waves in the murine small intestine in relation to coupled oscillator theory

Abstract

Waves of contraction in the small intestine correlate with slow waves generated by the myenteric network of interstitial cells of Cajal. Coupled oscillator theory has been used to explain steplike gradients in the frequency (frequency plateaux) of contraction waves along the length of the small intestine. Inhibition of gap junction coupling between oscillators should lead to predictable effects on these plateaux and the wave dislocation (wave drop) phenomena associated with their boundaries. It is these predictions that we wished to test. We used a novel multicamera diameter-mapping system to measure contraction along 25- to 30-cm lengths of murine small intestine. There were typically two to three plateaux per length of intestine. Dislocations could be limited to the wavefronts immediately about the terminated wave, giving the appearance of a three-pronged fork, i.e., a fork dislocation; additionally, localized decreases in velocity developed across a number of wavefronts, ending with the terminated wave, which could appear as a fork, i.e., slip dislocations. The gap junction inhibitor carbenoxolone increased the number of plateaux and dislocations and decreased contraction wave velocity. In some cases, the usual frequency gradient was reversed, with a plateau at a higher frequency than its proximal neighbor; thus fork dislocations were inverted, and the direction of propagation was reversed. Heptanol had no effect on the frequency or velocity of contractions but did reduce their amplitude. To understand intestinal motor patterns, the pacemaker network of the interstitial cells of Cajal is best evaluated as a system of coupled oscillators.

in the small intestine, waves of contraction travel distally from the gastroduodenal junction to the terminal ileum at a regular frequency of 8–12 min⁻¹ in humans (17) and 30–40 min⁻¹ in mice (39). This rhythm originates with the interstitial cells of Cajal (ICCs) of the myenteric plexus (MP), which form a continuous network along the whole length of the small intestine (39, 72, 75). ICCs generate electrical “slow” waves, which in turn drive contraction of the muscle. Electrical slow waves, and thus contraction waves, can be explained by two mechanisms: phase waves and trigger waves (10, 61). In the case of trigger waves, there is a single oscillator (pacemaker ICC), and waves spread from this point by cycles of excitation and refraction. In the case of phase waves, every ICC oscillates by itself, but the phase and frequency of this oscillation can be influenced by neighbors, as described by the phase-response curve and entrainment, respectively. The result of this interaction (coupling) between oscillators is that waves can appear to propagate, although this only represents a coordinated phase difference between oscillators.

Coupled oscillator theory (phase waves) has been used to explain a number of phenomena related to contraction waves in the small intestine. As early as the mid-19th century, it was noticed that the frequency of contractions is higher in the duodenum than the ileum (3, 4). Diamant and Bortoff (19, 20) showed that the gradient was usually steplike, with plateaux in frequency separated by sharp boundaries. Diamant and Bortoff, together with Nelsen and Becker (54), suggested that frequency plateaux could be explained by frequency entrainment. There would be a population of coupled oscillators along the length of the gut (which has been shown to be the network of ICCs) with a gradient in their natural frequency, i.e., the frequency at which each oscillates in isolation. Plateaux result from frequency entrainment, whereby one oscillator pulls up to its own natural frequency (or higher) a series of distal oscillators of lower natural frequency. Plateau boundaries occur where the difference in frequencies is too great for pulling. At these boundaries, waves must be lost (dropped); if neighboring plateaux have contraction intervals of 1.4 and 1.3 s, then every 14th wave must be dropped. The end of the dropped wave is known alternately as a dislocation (56), terminology borrowed from crystallography, or phase singularity (76), because phase at the end point is indeterminate. Mathematical models of chains of coupled oscillators have shown dislocations to have a forked shape (37, 53, 55). Also, such models predict a waxing-waning in the amplitude of the contraction wave at the plateau boundary (7, 53, 55). Both fork dislocations and waxing-waning occur at frequency plateau boundaries in the small intestine (9, 20, 44). They also occur in physical wave phenomena where there is a gradient in frequency, notably, vortex sheets shed from tapered rods (7, 30, 55, 74) and plasma waves (50, 53).

As the coupling between oscillators decreases in strength, the velocity of phase waves is predicted to decrease as the phase lag between oscillators increases (21). Also, plateaux should become shorter and more numerous, as the reduction in coupling reduces the ability for entrainment (73). In electron microscopy studies, the ICC-MP network appears to have infrequent gap junctions (63), and connexin 43 immunohistochemistry does not reveal a significant presence (16). Nevertheless, dye-coupling experiments have left little doubt that every ICC-MP is a pacemaker cell coupled by gap junctions to its neighbors (57). Gap junction inhibitors have been shown to disturb calcium wave propagation between ICCs (57), but there are no data on their effect on frequency plateaux and other phase wave-related phenomena in the small intestine. We wished to address this lack of data by investigating the effects of gap junction blockers on contraction wave propagation in the isolated, ex vivo whole murine small intestine.

METHODS

Intestine preparation.

All procedures were approved and carried out in accordance with regulations of the Animal Ethics Board of McMaster University. Small intestines of 14-wk-old CD1 mice were prepared in chilled and oxygenated Krebs solution containing (mM) 120 NaCl, 3 KCl, 15.5 NaHCO₃, 1.2 NaH₂PO₄, 0.1 citric acid, 0.1 aspartic acid, and 1.2 MgCl₂. The entire mesentery was cut away, and a “cannula head” was inserted into the lumen at the gastroduodenal junction. The cannula head consisted of a 12-mm-long metal tube (fashioned from a 16-gauge needle) terminated by a plastic collar (Fig. 1C, right). The intestine was slipped over the collar and tied just behind it to prevent the intestine from slipping off the cannula head. The intestine was cut to a 25- to 30-cm length distal from the gastroduodenal junction. Typically, this would remove 5–10 cm of terminal ileum. The cannula head was connected to a reservoir of saline (135 mM NaCl-5 mM KCl), and the intestinal contents were flushed out. It was essential to keep the level of the reservoir at ∼10 cm above the intestine. Exertion of larger pressures prevented strong circular contractions from developing during the experiment. After the contents were flushed out, the ileal end of the intestine was also connected to a cannula head.

Fig. 1.

Multicamera rig and organ bath. A and B: a row of 10 cameras (A) mounted 65 cm above the organ bath (B). kk, kit-kat; ht, heating tube (oxygenation tube runs in parallel); bc, bubble cover (lower cover not shown for clarity); co, circulation outflow; ci, circulation inflow. C and D: length of intestine tied to cannula heads (ch) at gastroduodenal junction and 30 cm distal to gastroduodenal junction (C) and held in a lane of the kit-kat by insertion of cannula heads into cannula receivers (cr), which fit tightly into the lane (D).

Organ bath and multicamera rig.

The organ bath consisted of a plastic wallpaper tray (54 × 12 cm; Fig. 1B). A manifold made of metal gutter covering was attached by Velcro to the bottom of the tray. This manifold held a U-bend of 9-mm-bore Tygon tubing connected to a water circulator for heating the bath. Parallel to this, a length of PE-190 tubing, perforated and closed at one end, was installed for oxygenation. The bath was filled with 1.5 liters of Krebs solution containing (mM) 120 NaCl, 5.9 KCl, 15.5 NaHCO₃, 1.2 NaH₂PO₄, 0.1 citric acid, 0.1 aspartic acid, 2.5 CaCl₂, 1.2 MgCl₂, and 6 glucose. A “kit-kat,” a 58 × 5 cm plastic bar with five lengthwise square grooves or lanes, 5 mm wide and deep, was placed inside the U-bend (Fig. 1, B and D). Each lane of the kit-kat held a single intestine. The intestine was held in place by insertion of its cannula heads (one on either end) into a cannula receiver, which was squeezed to fit into the lane (Fig. 1, C and D). The cannula receiver had either a tube to a saline reservoir (gastroduodenal end) or an open-ended tube above the level of the bath (ileal end).

Two brackets, one at either end of the bath, held two lengths of clear plastic that partitioned the solution surface at either side of the kit-kat (bubble covers in Fig. 1B). This prevented passage of surface bubbles (from the U-bend oxygenation tube) over the field of the kit-kat. It was found that proper circulation of the bath solution was essential for the long-term viability of intestines. Two aquarium air pumps (AW-20 Aqua Lifter, Tom Aquarium Products, Shawnee, KS) were used; their outflow was attached to the bracket at one end, and their inflow was attached to the manifold, midway along the bath (Fig. 1B). LED light wands at each end of the bath were used for shallow-angle lighting. Illumination from above gave reflections and illumination from the sides cast shadows in the lanes of the kit-kat, interfering with spatiotemporal mapping.

Miniature CCD board cameras (1/3′ SONY Super HAD CCD, 700 TVL, and SONY Effio-E DSP), with 50-mm focal length lens (F2.0, AOV 9°), were purchased from Security Camera 2000 (Hong Kong). A row of 10 cameras were mounted 65 cm above the organ bath by means of a horizontal L-bar supported by two clamp stands (Fig. 1A). At the height at which the cameras were mounted, the field of each camera was 38 × 52 mm (480 × 960 pixels, 0.079 × 0.054 mm/pixel), so that, arranged in a row with slightly overlapping fields, the total field was 36 × 5.2 cm. Note that the higher resolution orthogonal to the row did not result from barrel distortion in the lens but, rather, from the format of the camera's analog (TV) signal. The high resolution across the width of the intestine (54 μm/pixel) is not excessive with small-diameter intestines from small animals; the amplitude of murine contractions was ≤0.6 mm (see results). Camera signals were recorded by a 16-channel digital video recorder at 30 frames/s (model K4116HMF, Vonnic, Markham, ON, Canada).

All experiments were carried out at 36°C and in the presence of 0.5 mM lidocaine and 9 μM indomethacin. Intestinal intraluminal pressure was ∼2.5 cmH₂O (1.87 mmHg, 250 Pa), as gauged by the height of the cannula reservoir solution surface above the height of the organ bath solution surface. As the organ bath was a closed system (unperfused), drugs had to be added directly as stock solutions or weakly diluted from these. When 18β-glycyrrhetic acid in an ethanol stock was added to the bath, it immediately came out of solution. Carbenoxolone and 1-heptanol were prepared as 1-ml stock solutions at 1,500 times the maximum concentration required (40 μM and 2 mM, respectively). Carbenoxolone was dissolved in 1 ml of ethanol, and 425 μl of 1-heptanol were added to 375 μl of ethanol. The 1-ml stock solution was then added to the bath (1.5-liter volume) incrementally (1/8, 1/8, 1/4, and 1/2) to reach the maximum concentration.

Mapping and analysis.

Calculation of diameter maps (Dmaps) and all other analysis were carried out with custom plugins written for ImageJ (National Institutes of Health, Bethesda, MD). Dmaps were calculated by a thresholding algorithm. This was automated, so that, with two mouse clicks, the movie output from one experiment (≥15 h of total recording from 10 cameras) could be converted to Dmaps overnight by the computer. Dmaps from neighboring cameras were stitched together after registration of their border overlap by difference minimization.

Dmaps are shown as images, with time running horizontally and distance along the intestine running vertically from proximal (top) to distal (bottom). The intensity of the Dmap is the width (“diameter”) of the intestine from black (contracted) to white (relaxed). Positive velocities are proximal-distal, and negative velocities are distal-proximal.

The direction of features in an image, i.e., “local image orientation,” is an important subject in image analysis and computer vision. For instance, in a Dmap such as Fig. 2A, we need the computer to measure the direction of contraction waves and, thereby, their velocity. Orientation is typically measured by calculating the derivatives of the image along the x and y axes. The orientation at any point in the image is equal to the arctangent of the ratio of x to y derivatives at that point. The derivatives can be calculated by convolution of the image with one-dimensional derivative kernels such as the Prewitt, Sobel, and Savitsky-Golay (66). The image is convolved with the kernel and its transpose (90°-oriented version) to calculate the x and y derivatives, respectively. Because of their small size, one-dimensional kernels are vulnerable to image noise without a presmoothing of the image or other noise removal technique. A recent solution has been the use of “steerable filters” (29). These are two-dimensional derivative kernels and, therefore, are naturally less sensitive to noise: they sample more of the pixels around a point. A common steerable filter consists of the derivative of a two-dimensional Gaussian (29). If the kernel/filter is represented as a matrix (square array of numbers), G, then the elements of the kernel (g_ij) are

$$g_{ij}=-{\left(2\pi {\sigma }^4\right)}^{-1}x\exp \left[-\left(x^2+y^2\right)/2{\sigma }^2\right]$$ (1)

$$x=i-0.5n$$ (2)

$$y=j-0.5n$$ (3)

where n is the width of the kernel in pixels. G has the appearance of a dumbbell, with one negative and one positive lobe (Fig. 2A, inset).

Fig. 2.

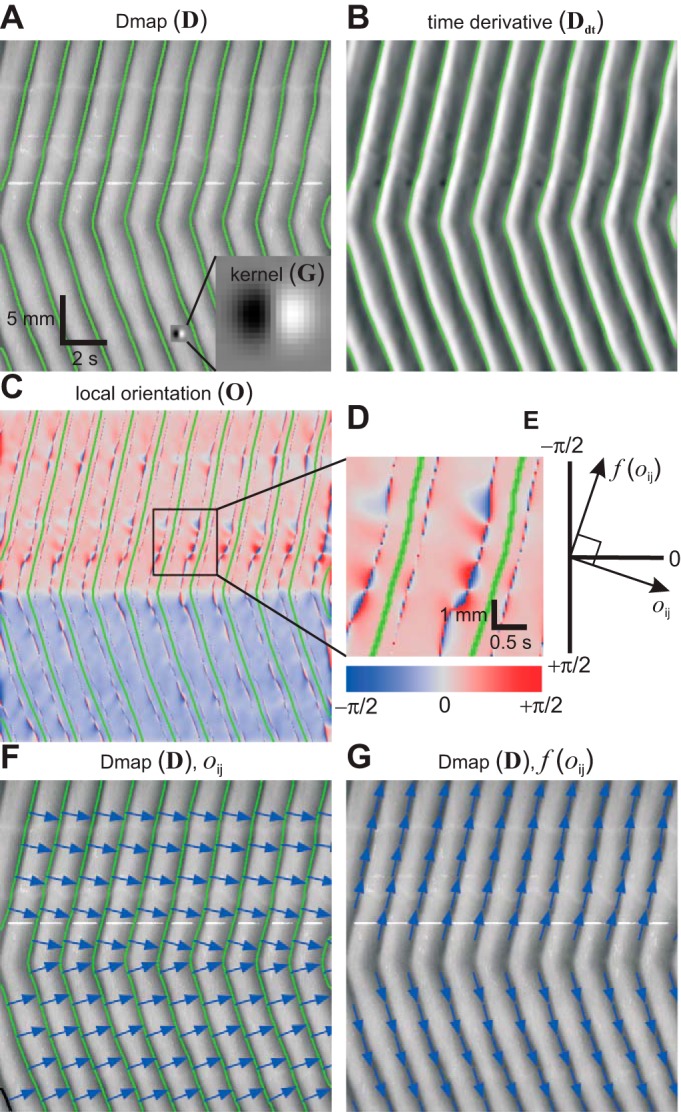
Detection of contractions and calculation of contraction velocity from diameter maps (Dmaps). Bold uppercase letters in parentheses indicate matrix notation of images (see methods). A and B: a Dmap convolved with a steerable filter kernel (magnified in inset) to give its time derivative. Contractions (green lines) occur when time derivative changes from negative to positive. C and D: convolution of the time derivative, the kernel, giving the local orientation. Note divergence of orientation between contraction lines. E: direction of the contraction [f(o_ij)] orthogonal to the local orientation. F: Dmap with local orientation vectors. G: Dmap with contraction direction vectors.

We wished to measure orientation specifically along lines of contraction, i.e., the minima or valleys in the Dmap (Fig. 2A). Minima in a function are defined by the point at which its derivative goes from negative (downward stroke) to positive (upward stroke). The Dmap was convolved with G to give its time derivative. In matrix notation

$${\mathbf{\text{D}}}_{\text{d}t}=\mathbf{\text{D}}\ast \mathbf{\text{G}}$$ (4)

where D is the Dmap, D_dt is its time derivative, and * is the convolution operator. Contraction lines were defined as the point at which D_dt went from negative to positive (green lines in Fig. 2, A and B).

The simplest way to calculate orientation in the Dmaps would have been to convolve the Dmap with G and its transpose (G^T in mathematical notation) to calculate the x and y derivatives. However, along the lines of contraction, the x and y derivatives tend toward zero (by their definition as minima), and so the orientation, as a ratio of these values, diverges (tends to be very large or very small). To put it another way, if you are standing in the valley bottom, you cannot measure the slope of the surrounding hills. However, in D_dt, the contraction lines lie right on the middle of the slope from negative to positive (Fig. 2B). Therefore, orientation was calculated by convolving D_dt, rather than D, with G. Where O is the orientation (Fig. 2C)

$$\mathbf{\text{O}}={\tan }^{-1}\frac{{\mathbf{\text{D}}}_{\text{d}t}\ast {\mathbf{\text{G}}}^{\text{T}}}{{\mathbf{\text{D}}}_{\text{d}t}\ast \mathbf{\text{G}}}$$ (5)

G was 21 pixels on both sides (0.7 s by 1.13 mm) and σ² (the Gaussian variance) was 12.25 pixels (0.4 s or 0.97 mm). As shown in Fig. 2D, the contraction lines (green lines) lie between divergences in orientation (intense blue and red bulges).

The orientation as defined above is orthogonal (at right angles) to the actual direction of the contraction waves (blue arrows in Fig. 2, F and G, respectively). Therefore, the direction of the contraction waves was found by the function

$$f\left(o_{ij}\right)=\{\begin{array}{cc}{o}_{ij}+\pi /2,& o_{ij}<0\\ o_{ij}-\pi /2,& o_{ij}>0\end{array}$$ (6)

where o_ij is an element of O (Fig. 2E). This was then used to calculate velocity (V)

$$v_{if}=\frac{y_{\text{r}}}{x_{\text{r}}}\tan \left[f\left(o_{ij}\right)\right]$$ (7)

where y_r is the spatial resolution (0.079 mm/pixel) and x_r is the temporal resolution (0.033 s/pixel). The set of velocities occurring at contraction lines was found, and their distribution was calculated.

From Eqs. 4–7, it can be shown that

$$\mathbf{\text{V}}=-\frac{y_{\text{r}}}{x_{\text{r}}}\frac{{\mathbf{\text{D}}}_{\text{d}t}\ast \mathbf{\text{G}}}{{\mathbf{\text{D}}}_{\text{d}t}\ast {\mathbf{\text{G}}}^{\text{T}}}$$ (8)

RESULTS

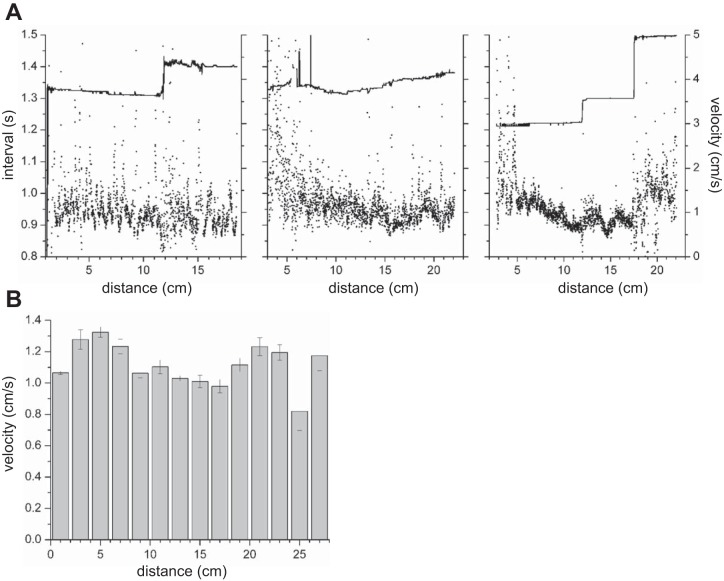
Propulsive circular muscle contractions propagated from the gastroduodenal junction to the ileum with occasional dropping of waves at dislocations (Fig. 3). The proximal 4–5 cm usually had a marked degree of tone, resulting in a dark band along the top of the Dmaps. There were typically two to three frequency plateaux (Fig. 4A), although in some intestines there were none (Fig. 4A, middle). The average change in frequency at plateau boundaries was 0.18 ± 0.03 min⁻¹ (change in interval of 102 ± 18 ms, n = 7). There was no simple pattern to contraction velocities (Fig. 4). There were often local gradients in velocity (Fig. 4A), but there was no overall proximal-distal trend in velocity (Fig. 4B).

Fig. 3.

Dmap of a 20-cm length of small intestine from duodenum (top) to distal intestine (bottom). Arrows, dislocations.

Fig. 4.

Contraction interval (A) and velocity (B) along the length of the small intestine. Interval was calculated as average of the first 5 peaks in the temporal autocorrelation from 3 intestines. Velocity was calculated by local orientation along contractions in 6 intestines over 2-cm distance bins (see methods). Distance is from gastroduodenal junction.

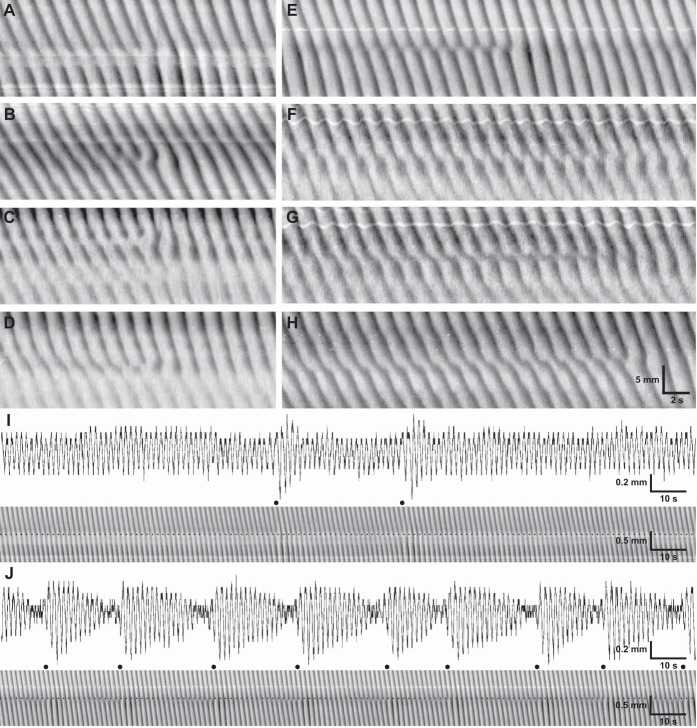
Plateau boundaries were correlated with phase dislocations. Dislocations were variable in appearance (Fig. 5). In some dislocations, distortion was limited to the wavefronts immediately about the terminated wave, giving the appearance of a three-pronged fork, i.e., a fork dislocation (Fig. 5, A–C). In others, a localized decrease in velocity developed across a number of wavefronts, ending with the terminated wave, which could appear as a fork, i.e., slip dislocations (Fig. 5, D–H). In fork dislocations, the phase singularity was clearly visible as the center of the fork. However, in slip dislocations, it was often not clear where the singularity should be defined, because as the dislocation proceeded, wavefronts often coalesced (Fig. 5, E–G). Commonly, this took the form of interdigitation between wavefronts, giving a saw-tooth pattern (Fig. 5, E and F). Generally, dislocations were of a fixed position. However, on rare occasions, slip dislocations could be seen to change position or glide (Fig. 5H). Fork dislocations did not always repeat, whereas slip dislocations were cyclical (Fig. 5J). In temporal profiles of width at the slip dislocation/plateau boundary, a waxing-waning of contraction amplitude was observed at the same frequency as the dislocation (Fig. 5J). Waxing-waning of amplitude was also observed at fork dislocations (Fig. 5I).

Fig. 5.

Phase dislocations at frequency plateau boundaries. A: fork. B: asymmetric fork. C: 2 space-adjacent forks. D: slip. E and F: saw-tooth slips. G: hard slip. H: gliding slip. I and J: waxing-waning associated with fork (I) and slip (J) dislocations. Contraction amplitude profile (top) is shown along dotted line in Dmaps (bottom). ●, Wave drop times.

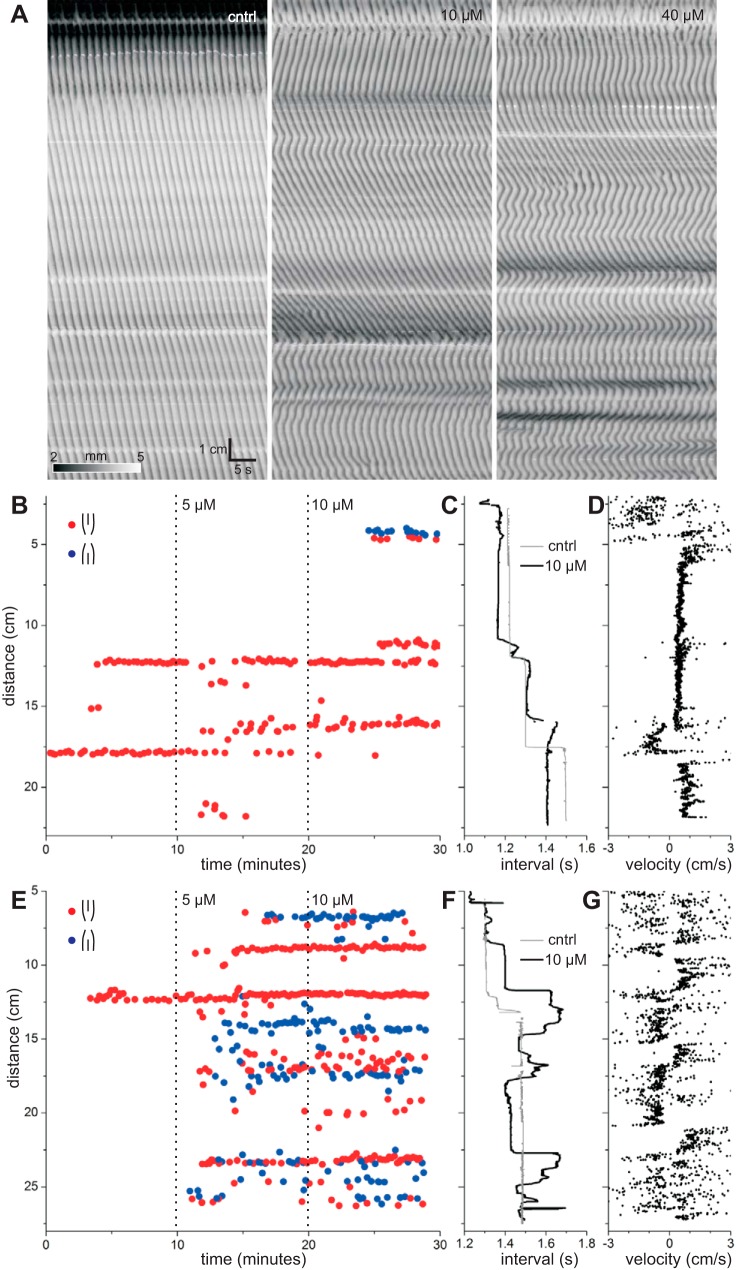
Glycyrrhetic acid (enoxolone) is one of the most commonly used gap junction inhibitors. It is, however, poorly water-soluble and therefore unsuitable for use in our organ bath (see methods). Therefore we used carbenoxolone, a close analog of glycyrrhetic acid, which in contrast to glycyrrhetic acid is highly water-soluble. The concentration of carbenoxolone was doubled every 10 min over the range 5–40 μM. Carbenoxolone broke contractions up into regions of oppositely directed wavefronts (Fig. 6A). Positions of dislocations, corresponding to plateau boundaries, observed under control conditions were usually preserved with the addition of carbenoxolone (Fig. 6, B and E), but sometimes were not (lower boundary in Fig. 6B). Carbenoxolone induced a large number of dislocations at new positions (Fig. 6, B and E). These induced dislocations could be aligned, forming new frequency plateaux, or scattered (Fig. 6, B and E).

Fig. 6.

Effects of carbenoxolone. A: Dmaps from 1 intestine. Left to right: control and 10 and 40 μM carbenoxolone. B: locations and times of wave drops at fork dislocations and ends of slip dislocations in 1 intestine. Distance is from the gastroduodenal junction. At wave drops, the wave is lost distally (red) or proximally (blue). Dotted lines indicate addition of carbenoxolone (control and 5 and 10 μM). C: contraction interval along the length of the intestine. Control (gray) and 10 μM carbenoxolone (black). Interval was calculated as average of the first 5 peaks in the temporal autocorrelation. D: contraction velocity along the length of the intestine with 10 μM carbenoxolone. E–G: same as B–D for another intestine.

Prior to addition of carbenoxolone, frequency always decreased (waves were dropped) distally; thus, fork dislocations (pure or ending a slip) always had the same polarity (Fig. 6, B and E). In the presence of carbenoxolone, frequency sometimes increased distally (Fig. 6F); therefore, waves were dropped proximally, corresponding to forks of the opposite polarity to control (Fig. 6E). Stable lines of dislocations, corresponding to plateau boundaries, usually consisted of forks of a single polarity but, sometimes, of mixed polarity (Fig. 6E). More often, forks of opposite polarity intermingled in close proximity. Between lines of dislocations of opposing polarity, corresponding to hills or valleys in frequency, wavefront direction changed (Fig. 6G). This follows from their geometry. Forks of opposite polarity must run in the opposite direction, given that waves are dropped and not created. Therefore, the wavefront must change direction an odd number of times between forks of opposite polarity.

Carbenoxolone changed the velocity of contractions (Fig. 6, A, D, and G). To quantify this, local orientation velocities were calculated along contraction wavefronts (see methods). Distally directed waves have positive velocity, and proximally directed waves have negative velocity. The distribution of velocities was changed by carbenoxolone, which shifted the peak of positive velocities downward and increased the proportion of negative velocities (Fig. 7A). The largest change was from control to 5 μM carbenoxolone, which shifted the peak of positive contraction velocities from 0.91 ± 0.03 to 0.56 ± 0.02 cm/s (P = 1.04 × 10⁻⁴; Fig. 7B). At >5 μM, this peak shifted little more (Fig. 7B), although the proportion of negative velocities continued to increase (Fig. 7A).

Fig. 7.

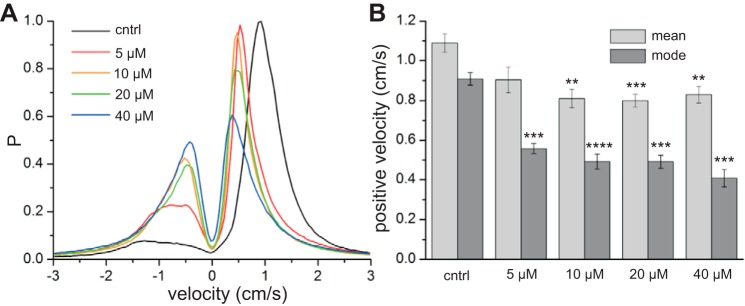
Effect of carbenoxolone on contraction velocity. A: probability density of contraction velocities (see methods). Positive velocities correspond to distal-directed waves and negative velocities to proximal-directed waves. Values were calculated from 6 intestines, over 2 min per intestine, with bins of 0.05 cm/s. B: mean and mode negative velocities. **P < 10⁻², ***P < 10⁻³, ****P < 10⁻⁴ vs. control (by paired t-test).

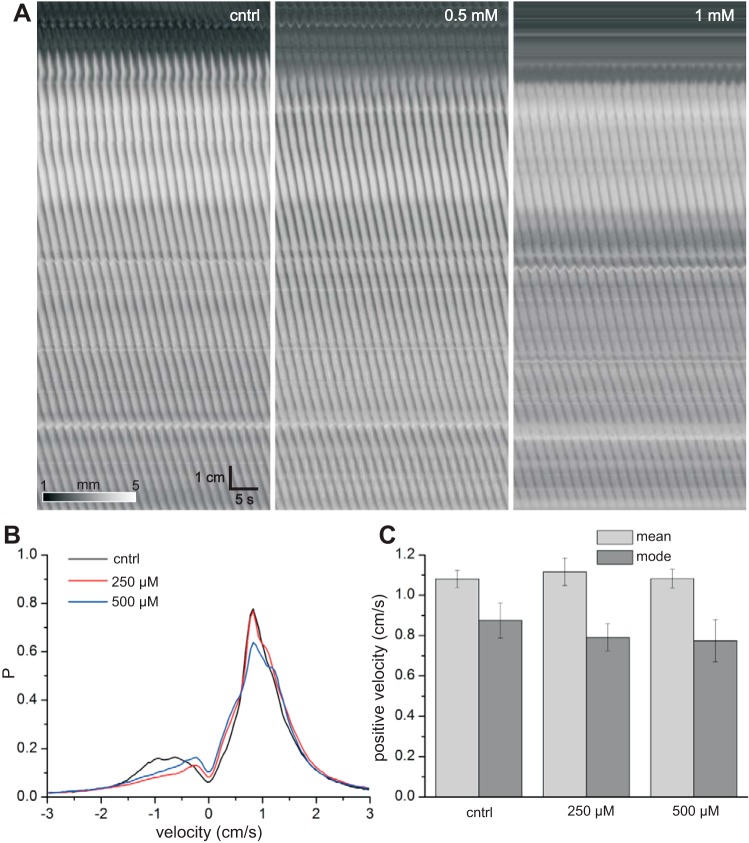
Before glycyrrhetic acid and carbenoxolone were reported as gap junction inhibitors (18), long-chain alcohols and fatty acids were used and are still commonly used. The concentration of 1-heptanol was doubled every 10 min over the range 250 μM–2 mM. Heptanol initially formed droplets on the surface of the organ bath solution. However, after a few seconds, the droplets dissolved, and then the bath shimmered for a few seconds. This was likely due to oscillations in surface tension and convection cells driven by the heptanol, known as the Marangoni effect (8, 31). Heptanol had no effect on contraction velocity or pattern (Fig. 8), but as the concentration reached ≥0.5 mM, contractions were weakened in amplitude (Fig. 8A). At 2 mM, contractions disappeared in all intestines tested (n = 6).

Fig. 8.

Effects of 1-heptanol. A: Dmaps from 1 intestine. Left–right: control and 0.5 and 1 mM heptanol. B: probability density of contraction velocities (see methods). Positive velocities correspond to distal-directed waves and negative velocities to proximal-directed waves. Values were calculated from 6 intestines, over 2 min per intestine, with bins of 0.05 cm/s. C: mean and mode negative velocities.

DISCUSSION

We have shown that frequency plateau boundaries in the small intestine are associated with a wide variety of fork and slip dislocations and that gap junction inhibition increases the number of boundaries (dislocations) and decreases wave velocity. The occurrence of these phenomena indicates that the pacemaker system underlying the contraction patterns is a system of coupled oscillators. We have also shown that regulation of gap junction conductance alone can be a powerful tool to reduce long propulsive contractions and, hence, appears to promote mixing and absorption. Understanding the mechanisms of motor pattern generation in the intestine requires further knowledge about the behavior of coupled oscillators.

Although the frequency gradient of the small intestine has been quantified since the pioneering studies of Walter Alvarez a century ago (3, 4, 6, 14, 15, 17, 23, 34, 60), it was not until 1969 that frequency plateaux were described by Diamant and Bortoff (20; although see Fig. 4 in Ref. 4). This may have been due to a lack of spatial resolution or the averaging of data from different intestines. However, our data and data of others (45, 70) show that plateaux simply do not exist in some preparations; i.e., the frequency gradient is either nonexistent or smooth (Fig. 4A, middle). In the case of no gradient, there may be only a slight natural frequency gradient, so that the whole preparation is entrained to the same frequency (there is only 1 plateau). In the case of a smooth gradient, coupled oscillator chain models show that, given a particular natural frequency gradient, which would normally give frequency plateaux, the addition of a noise term to the phase coupling will, instead, produce a smooth frequency gradient (73). This noise could represent stochastic changes in gap junction conductance or membrane potential.

According to coupled oscillator theory, the direction of the phase wave (sign of its velocity) is dependent on the frequency gradient; its speed (amplitude of its velocity), however, is dependent on coupling strength. Therefore, there is no particular reason for a relationship between frequency and velocity, which is a dispersion relationship. Neither we nor anyone else, as far as we are aware, has observed a velocity gradient in the small intestine of mice. However, a velocity gradient has been observed along the small intestine in dogs and cats (1, 44, 45, 52, 68). In these cases velocity may be more dependent on slow-wave amplitude (see Fig. 5 of Ref. 45), slow-wave upstroke rate, and coupling strength, rather than frequency. We did see local changes in velocity. Some of these changes were associated with slip dislocations (Fig. 5). Others, however, did not occur at plateau boundaries. Subcentimeter fluctuations in measured velocity may have resulted from the measured contraction line passing close to divergences in image orientation (Fig. 2D; see methods). This would also explain the long tails in the velocity distributions (Fig. 7). Supercentimeter fluctuations (Fig. 4) appear to be real phenomena and may be just stochastic, rather than having any particular significance in regards to coupled oscillator theory.

Fork dislocations have been seen in Dmaps of the rabbit distal colon (22) and rat small intestine (9), although neither study associated these with frequency plateau boundaries. A 240-electrode array study of the whole cat intestine (>100 cm) was the first to associate fork dislocations with plateau boundaries (44). By combining a very high spatial resolution with coverage of a long length of intestine, our novel multicamera technique has allowed us to observe details of fork dislocations and has also revealed slip dislocations, which have not been noted previously in the small intestine. In both fork and slip dislocations, the first wave after the dropped wave usually had a (rotated) “V” indentation at the plateau boundary (Fig. 5). This gave the appearance of oral and aboral propagation from a pacemaker at the apex of the V. In a sense, this is correct: the distal plateau is entrained by the ICCs at the boundary, and so these ICCs can be thought of as a “pacemaker.” It is not correct in the sense of an ectopic or “peripheral” pacemaker that arises only transiently at the V and then disappears again, as was proposed when this was seen in electrode array studies of the porcine and canine small intestine (5, 44, 45). Why would the pacemaker emerge for only one wave cycle? Why would the V wave from the pacemaker not propagate further in the proximal (oral) direction? In slip dislocations, the V is preceded by a progressive (regular) slowing of velocity about the dislocation boundary, and slip dislocations are repeated at regular intervals. None of this is explained by a peripheral or ectopic pacemaker but is a natural outcome of phase walk-through: the oscillators at either side of the boundary are not entrained and, therefore, come in and out of phase according to their frequency difference (25). Forks with V indents arise naturally from coupled oscillator models (37, 53, 55).

The superposition (addition) of two waves of different frequency results in a wave with a frequency halfway between the two and an amplitude that waxes-wanes at a frequency equal to their difference. This waxing-waning is known in acoustics as a “beat,” combination tone, difference tone, or Tartini tone (36, 51, 55). Waxing-waning of slow-wave amplitude was observed by Bortoff in the cat small intestine (11, 12) and was found to be associated with frequency plateau boundaries (20). This was explained as a superposition of different frequency slow waves on either side of the boundary. However, it is possible that waxing-waning might arise independently of superposition, as it is seen at frequency plateau boundaries in a chain of van der Pol oscillators without superposition of signals (53). Another possibility is that waxing-waning results from amplitude modulation of a single slow-wave signal by the phase of a signal at the waxing-waning frequency (38). However, there is no evidence for such a low-frequency signal outside the plateaux boundary.

In the presence of carbenoxolone, frequency sometimes increased, rather than decreased, distally, with fork dislocations reversed in polarity. The simplest explanation for this is that carbenoxolone changed the natural frequency in places. Gap junction inhibition has been shown to increase calcium wave frequency in the bladder (33). This could occur through gap junction inhibition effecting calcium homeostasis in ICCs and, thus, changing the frequency of the calcium clock (41). However, such effects were often transient, as forks of opposite polarity often intermingled in close proximity.

The lack of effect of heptanol on smooth muscle conduction properties has been noted in previous studies (32, 77). Long-chain alcohols and fatty acids do not specifically interact with or block the pore of the connexin channel but, instead, change the physical properties of the plasma membrane, primarily membrane fluidity, leading to a mechanoconformational response by the channel (42, 69, 71). The nonspecificity of this mechanism means that many ion channels are inhibited by long-chain alcohols and fatty acids at similar concentrations (42, 71), explaining the effect of heptanol on contraction amplitude. It also explains why heptanol does not always inhibit gap junctions (32, 77), as its effect is dependent on any number of physical factors, e.g., composition of the plasma membrane, mechanical stress on the membrane, and cytoskeletal anchoring of connexins. As Srinivas (69) has suggested, “actions of n-alkanols may depend on the cholesterol content of the membranes and on the localization of gap junctions in such membranes.” In Xenopus oocytes, connexin 50, but not connexin 46, was sensitive to octanol (26).

Through the 1970s and 1980s, a large number of publications described models of slow-wave propagation with chains of coupled relaxation (van der Pol) oscillators (1, 21, 48, 54, 62, 64, 65). A major criticism of these models was their simplicity (usually just 2 ordinary differential equations) and therefore abstraction from biophysics, meaning they were not of much working use to gastrointestinal physiologists (59). This is certainly a fair criticism. In response to this criticism, by 1977, Derek Linkens introduced a model of coupled Hodgkin-Huxley oscillators (49, 58). The Hodgkin-Huxley and the related Fitzhugh-Nagumo oscillator remain popular models of gastrointestinal wave propagation (2, 47), because they produce many of the gross phenomena associated with contraction propagation, while they are practical in simulation of systems with large numbers of elements. Nevertheless, more detailed biophysical models (various ionic currents and calcium dynamics) of systems of coupled oscillators are also possible (13, 24, 27, 40, 41). The criticism of individual models does nothing to prejudice coupled oscillator theory, as this is a general concept that can be used to understand or frame the data. This concept indicates only that all the individual elements (cells) oscillate independently of each other and any external stimulus and that they can influence each other's phase (they are coupled). A model that satisfies these criteria can be as biophysical or abstract as one likes and, if it allows for an external stimulus, can be analyzed in terms of phase-response curves (40). The lack of prejudice against coupled oscillator theory, as against relaxation oscillator models, is reflected by the continued use of such terms as entrainment, pulling phase advance, and intrinsic frequency (13, 27, 35, 43) that necessarily imply coupled oscillator theory (they have no meaning in any other context), even if the theory is not explicitly mentioned.

Distinct from models, conceptually, one can talk about slow-wave (contraction) propagation in terms of excitation and refraction (trigger waves) or the phase-response curve and entrainment (coupled oscillator theory and phase waves). However, the phase-response curve and excitation/refraction really describe the same thing, i.e., the response of a cell to a stimulus as a function of the time of the last excitation. So their biophysics will be much the same: interactions between membrane voltage, ion channels, and intracellular calcium (24, 40, 41, 46). Therefore, in terms of the biophysical reality that we try to approach with more detailed models, the distinction in terminology may dissolve. As Winfree suggested, “the differences between these two approaches [trigger and phase waves] are in part semantic differences and that a quantitative, rather than a verbal, biophysical model may behave much the same way under either description” (76). This is borne out by the fact that the slowing of velocity with gap junction inhibition, as shown here, is predicted by models of both coupled oscillators (21) and trigger waves (67). Nevertheless, there is a clear distinction between phase and trigger waves: all cells oscillate independently, and only one cell (the pacemaker) oscillates. In this context, coupled oscillator theory is a better conceptual framework with which to understand contraction waves in the small intestine.

GRANTS

This study was supported by Canadian Institutes of Health Research Grant MOP12874 and Natural Sciences and Engineering Research Council Grant 386877 to J. D. Huizinga.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.P.P. developed the concept and designed the research; S.P.P. performed the experiments; S.P.P. analyzed the data; S.P.P. and J.D.H. interpreted the results of the experiments; S.P.P. drafted the manuscript; S.P.P. and J.D.H. edited and revised the manuscript; S.P.P. and J.D.H. approved the final version of the manuscript.