Quantitative separation of arterial and venous cerebral blood volume increases during voluntary locomotion

Abstract

Voluntary locomotion is accompanied by large increases in cortical activity and localized increases in cerebral blood volume (CBV). We sought to quantitatively determine the spatial and temporal dynamics of voluntary locomotion-evoked cerebral hemodynamic changes. We measured single vessel dilations using two-photon microscopy and cortex-wide changes in CBV-related signal using intrinsic optical signal (IOS) imaging in head-fixed mice freely locomoting on a spherical treadmill. During bouts of locomotion, arteries dilated rapidly, while veins distended slightly and recovered slowly. The dynamics of diameter changes of both vessel types could be captured using a simple linear convolution model. Using these single vessel measurements, we developed a novel analysis approach to separate out spatially and temporally distinct arterial and venous components of the location-specific hemodynamic response functions (HRF) for IOS. The HRF of each pixel of was well fit by a sum of a fast arterial and a slow venous component. The HRFs of pixels in the limb representations of somatosensory cortex had a large arterial contribution, while in the frontal cortex the arterial contribution to the HRF was negligible. The venous contribution was much less localized, and was substantial in the frontal cortex. The spatial pattern and amplitude of these HRFs in response to locomotion in the cortex was robust across imaging sessions. Separating the more localized, arterial component from the diffuse venous signals will be useful for dealing with the dynamic signals generated by naturalistic stimuli.

Introduction

Changes in cerebral blood volume, flow, and oxygenation are widely used to infer neural activity (Logothetis, 2008). Because increases in neural activity, which can last for only a few milliseconds, are usually much briefer than the hemodynamic response, which evolves over seconds, it is necessary to use a quantitative model to relate the two. The hemodynamic signal is usually assumed to be a convolution of neural activity or sensory stimulus with the hemodynamic response function (HRF, also known as a kernel) (Boynton et al., 1996; Friston et al., 1994; Glover, 1999; Vazquez and Noll, 1998; Hirano et al., 2011; Logothetis et al., 2001; Martindale et al., 2003). Typically, the HRF is fit with a gamma distribution function (Boynton et al., 1996; Hirano et al., 2011), but there is evidence that the CBV HRF may be the sum of multiple components (Silva et al., 2007). Because HRFs differ across cortical location (Handwerker et al., 2004), and layer (Hirano et al., 2011), potentially due to neural and vascular differences (Tsai et al., 2009), it is useful to mechanistically understand their vascular origin.

The CBV HRF will be determined by the dynamics of volume changes in various vascular compartments. Arterial dilation, which is mediated by smooth muscle relaxation and is thought to be under the control of neural activity, follows stimulation within a second (Hillman et al., 2007; Kim et al., 2007; Drew et al., 2011; Tian et al., 2010). The distention of veins takes place over tens of seconds in response to prolonged stimuli (Drew et al., 2011; Kim and Kim, 2010), and is thought to reflect the passive mechanical properties of the vessel wall (Clark, 1933; Edvinsson et al., 1983). Theoretical models incorporating the fast arterial and slow venous components reproduce the observed cerebral hemodynamic response well (Barrett et al., 2012; Kim et al., 2013). However, there is spatial variation in HRFs across the brain (Aquino et al., 2014; Bieβmann et al., 2012; Handwerker et al., 2004), which may underlie the diverse temporal profiles of hemodynamic responses across the entire cortex (Gonzalez-Castillo et al., 2012; Vickery et al., 2011).

The arterial and venous CBV changes induced by long sensory stimulation have different spatial extents (Kim and Kim, 2010), with the arterial component being more spatially restricted. This suggests that spatial variation (Handwerker et al., 2004) in HRFs might be due to differences in arterial and venous contributions to the HRF. Since the spatial pattern of the arterial response is thought to be more closely related to the spatial pattern of neural activity (Moon et al., 2013), brief, temporally isolated stimuli will give a hemodynamic response that more precisely reflects the underlying neural activity. However, using impulse-like stimuli is not always possible, particularly when using ‘naturalistic’ stimuli, which have multiple time-scales (Kay et al., 2008; Ben-Yakov et al., 2012; Honey et al., 2012; Naselaris et al., 2011). A method of separating the more localized arterial response from the less specific venous response to temporally extended stimuli would be very helpful for these stimulation paradigms.

Here, we investigated the vascular mechanisms underlying the hemodynamic response function in the superficial layers of the cortex in response to exercise. Previous work on the existence, localization and even direction of cerebral blood flow and volume changes during exercise are contentious (reviewed in (Ide and Secher, 2000)), with some studies showing no changes (Globus et al., 1983), some showing global, non-specific increases (Herholz et al., 1987), and other showing localized increases (Jørgensen et al., 1992; Linkis et al., 1995). One explanation for the discrepancies among these studies, which use different methodologies and durations of exercise, is that different techniques have different sensitivity to arterial versus venous changes. We have previously shown, using intrinsic optical signal (IOS) imaging in head-fixed, voluntarily locomoting mice, that in the first few seconds of locomotion, the frontal cortex shows little to no change in blood volume, while there are substantial increases in blood volume in the limb representations of sensory cortex (Huo et al., 2014). Because arteries and veins have very different temporal (Kim and Kim, 2010; Drew et al., 2011; Gao and Drew, 2014) and spatial (Moon et al., 2013) dynamics, we wanted to determine if the discrepancies in the spatial extent of the hemodynamic response to exercise could be due to different spatial extents of arterial and venous changes.

Using two-photon laser scanning microscopy (2PLSM) (Drew et al., 2011; Shih et al., 2012), we measured individual vessel dilation dynamics during voluntary locomotion in awake, head-fixed mice (Dombeck et al., 2007; Nimmerjahn et al., 2009; Huo et al., 2014). Based on these single vessel measurements, we developed a HRF model to quantify the spatiotemporal characteristics of optically measured pixel-wise CBV changes in the superficial layers. We demonstrate that using the temporal dynamics of the blood volume signal, distinct spatial maps of the localized arterial and diffuse venous responses could be extracted. The arterial and venous responses to locomotion were linear, and repeatable across trials. Using our linear convolution model to separate the more spatially localized arterial changes from the less localized venous responses should prove useful for experiments using dynamic stimuli (Hasson et al., 2010).

A subset of the IOS data presented here has been previously presented (Huo et al., 2014), and is reanalyzed below.

Methods

Animals

All care and experimental manipulation of animals were done in accordance with the Institutional Animal Care and Use Committee of Pennsylvania State University, University Park. A total of 18 male C57BL/6J mice (Jackson Laboratory) were used. Mice were maintained on a 12-hour light/dark cycle in isolated cages.

Surgery

Mice were 2–10 months old (25–40 g) at the time of surgery. All surgical procedures were performed under isoflurane anesthesia. For 2PLSM imaging, polished and reinforced thinned-skull (PoRTS) windows were implanted (Drew et al., 2010; Shih et al., 2012; Gao and Drew, 2014) in the right parietal cortex (N=10). Under anesthesia, a custom-machined titanium head-bolt was attached to the skull and 3 self-tapping, 3/32″ #000 (J.I. Morris) screws were implanted into the skull and connected to the head-bolt with dental cement. Using a hand drill (Foredome), the skull over the right parietal cortex was carefully thinned to ~30μm with a #7 bit (Fine Science Tools). It was then polished with 3f and 4f lapidary polish (Convington Engineering, Redlands, CA, USA), and a #0 coverslip was attached to the skull with cyanoacrylate glue (Vibra-Tite, 32002). A meniscus-holding well was made with dental cement around the window. For IOS imaging, larger reinforced thinned-skull windows (Huo et al., 2014) that spanned frontal and parietal cortices were made either bilaterally (N=6) or unilaterally (N=2). For animals used for IOS imaging, the skull over frontal and parietal cortices in each hemisphere was thinned to remove skull vessels using a Foredom drill with the frontal-parietal suture sealed with cyanoacrylate glue and dental cement. Then the frontal-parietal suture was exposed and carefully thinned until the suture was flush with the frontal and parietal bones. Successful suture thinning was identified by absence of dural or pial vasculature remodeling after surgery. A #1 coverslip cut to the window size in each hemisphere was mounted using cyanoacrylate glue (Vibra-Tite, 32002). A custom machined titanium head-bolt was glued to the skull, centered on the midline suture, posterior to lambda. One self-tapping, 3/32″ #000 (J.I. Morris) screw was implanted into the skull over the olfactory bulb and connected to the head-bolt via midline suture using cyanoacrylate glue and black dental acrylic resin (Lang Dental Mfg. Co., REF 1530) to minimize skull movement, and to absorb reflected light. Keeping the skull intact is important for accurate measures of hemodynamic signals, as craniotomies are known to cause inflammation (Cole et al., 2011; Xu et al., 2007), changes in brain tissue mechanical properties (Hatashita and Hoff, 1987), and angiogenesis (Arieli et al., 2002; Drew et al., 2010; Sohler et al., 1941), all of which are likely to disrupt the normal hemodynamic response.

Experiments

The treadmill (60 mm diameter) had one degree of freedom, and was covered with nonabrasive antislip tape. An optical rotary encoder (US Digital, E7PD-720-118) (Nimmerjahn et al., 2009) was attached to the treadmill axel to quantify the mouse’s velocity. Mice were habituated to being head-fixed on the spherical treadmill over 3–5 days. All experiments were performed within 8 months of surgery in sound attenuating boxes.

Before each 2PLSM imaging session, the mouse was briefly anesthetized with isoflurane and infraorbitally injected with 50 μL 5% (weight/volume) fluorescein conjugated dextran (70 kDa; Sigma-Aldrich). The two-photon microscope consists of a Sutter Movable Objective Microscope and a MaiTai HP laser, controlled by MPScan software (Nguyen et al., 2006). Images were acquired at 6–9 Hz for ~20 minutes/trial using water dipping objectives (Olympus, 10 × 0.3 N.A. 20 × 0.5 N.A., or 20 × 1.0 N.A.). For imaging of pial vessels, power exiting the objective was typically 15–20 mW at 800 nm. We selected a rectangular field of view containing both arteries and veins (Fig. 2A). A total of 151 arteries and 104 veins in 10 mice were imaged.

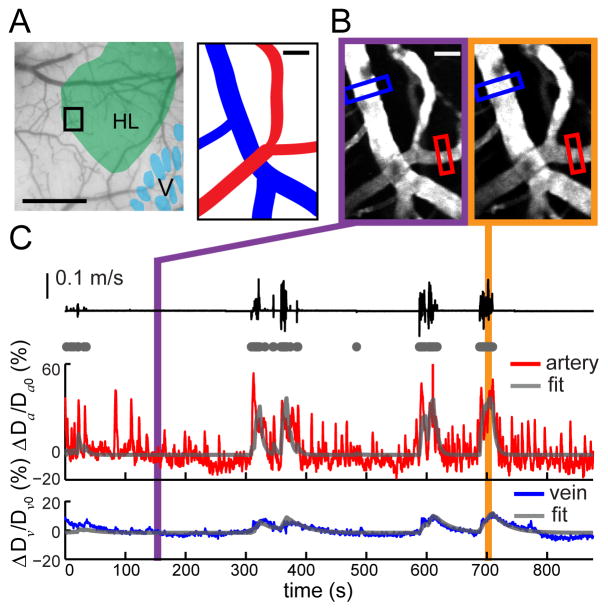
Figure 2. Locomotion-driven pial vessel dilations can be fitted with a linear model.

(A) Left: Histologically identified hindlimb (green) overlaid on an image of a PoRTS window. Scale bar = 0.5 mm. 2PLSM FOV is enclosed in the black rectangle. Right: schematic depicts of an artery (red) and a vein (blue) from FOV. Scale bar = 20 μm. (B) Examples of 1-second average image of FOV under 2PLSM when the animal was at rest (left) and during locomotion (right). Diameter changes of the artery and the vein were recorded from the vessel segments within red and blue rectangular ROIs, respectively. Scale bar = 20 μm. (C) During voluntary locomotion (black trace), fractional change of diameters of the artery (ΔD_a/D_a0, red) and the vein (ΔD_v/D_v0, blue) shown in (B). Using binarized locomotion events (gray dots) as inputs, each diameter was fitted with a linear model (gray trace). The correlation coefficient between the fits and the actual vessel response was 0.83 for the artery and 0.57 for the vein.

IOS and laser Doppler flowmetry (LDF) data were collected using custom-written software in LabView 8.6 (National Instruments). For IOS imaging, four 530 nm LEDs (Thorlabs, M530L2-C1) (Bouchard et al., 2009) passed through a ±10 nm filter (Thorlabs, FB530-10) were used to uniformly illuminate the cortical surface. A CCD camera (Dalsa, Pantera 1M60) was used to acquire 12-bit images (Drew and Feldman, 2009). Each 256 × 256 pixel image had a resolution of 27–37 μm/pixel. A second camera (Microsoft, LifeCam Cinema) was used to observe the mouse’s behavior. After the animal was habituated, we collected IOS data at a frame rate of 3 Hz (~33 minutes/trial). In order to measure the power spectrum of the intrinsic signal (Fig. 1), some trials were collected at 30 Hz, but these were not used for fitting of the arterial and venous parameters due to the short duration of the trial (~3 minutes/trial).

Figure 1. Cortical CBV responses show region-specific dynamics during locomotion.

(A) Experiment setup for IOS imaging. The head-fixed mouse was free to run on a spherical treadmill with one degree of freedom. The cortex of the mouse was illuminated with 530nm light. (B) IOS image of cortex revealed in the thinned-skull window (left). Body representations in the primary somatosenso-ry cortex (SI) and surrounding areas within the window (right) were identified with cytochrome oxidase staining. FC: frontal cortex; FL: forelimb; HL: hindlimb; V: vibrissae. Scale bar = 1 mm. (C) The ball velocity during 60-second trial of voluntary locomotion was recorded with rotary encoder (top), and then converted to binary locomotion events (middle). The average fractional changes of reflectance, ΔR/R₀ (bottom), from the FL/HL representation (enclosed by green polygons in (B)) and FC (enclosed in blue contours in (B)), are plotted within this period, demonstrating the localized response. (D) Power spectrum density (PSD) plots of locomotion events (gray) and averaged ΔR/R₀ in FL/HL area (green) and FC (blue). Arrow denotes heart-rate related oscillations. (E) Fraction of continuous locomotion events at different durations. The height of each bar represents the mean across animals. Error bars show the minimum (lower limit) and the maximum (upper limit) across all animals. N = 8 mice.

For cerebral blood flow (CBF) measurements, an LDF optical probe (Oxford Optronix, OxyFlo) was placed at 30-degree angle to the window plane on the left hemisphere. When the LDF signal and IOS were recorded simultaneously, a 530 ± 5 nm filter was attached to the CCD camera to block light from the LDF probe.

At the conclusion of the experiments, mice were euthanized and the brain was processed for cytochrome oxidase staining (Drew and Feldman, 2007). The limb representations and barrels were aligned with the imaging windows using a combination of vascular images and fiduciary marks (Drew and Feldman, 2009). A polygon enclosing forelimb/hindlimb (FL/HL) representation was selected based on cytochrome oxidase staining (Fig. 1B).

Data Processing

All data analyses and statistical tests were performed in Matlab (MathWorks). To calculate baselines, about ten-second long periods were chosen in at the end of ~30 second period where there was no locomotion. This was long enough for the arterial and venous signal from any short running bouts preceding this period to become negligible.

For 2PLSM data, we removed artifacts from horizontal plane motion using frame-by-frame registration of the vessel images (Drew et al., 2011; Guizar-Sicairos et al., 2008). To quantify the diameter of a vessel, a rectangular box was manually drawn around a short segment (2–5 μm) of vessel (Fig. 2B). The pixel intensities were averaged along the long axis of the vessel, and the diameter, D, was calculated from the full width at half-maximum (Drew et al., 2011). Vessel diameter percentage changes, ΔD/D₀, were calculated by normalizing to the average diameter during a ~10-second period: ΔD/D₀ = (D−D₀)/D₀. Time series of ΔD/D₀ were first filtered with a three-point median filter, and then low-pass filtered (Butterworth) at 3 Hz.

For IOS images, regions of interest (ROIs) enclosing the thinned-skull windows were selected. Data taken on different days were registered off-line. A ~10 second period within a long period of rest was used to calculated the baseline IOS image, R₀, for each day. The calculated fractional change of IOS from baseline, ΔR/R₀, was given by: ΔR/R₀ = (R−R₀)/R₀. The ΔR/R₀ data were mean-subtracted, and low-pass filtered at 1 Hz (Butterworth). We chose this cutoff frequency because it was adequate to capture the dynamics of the arterial response (see Supplementary Fig. S1).

For LDF data, we defined the baseline flux, Q₀, by taking the average value of CBF during a ~10-second period when the animal was stationary. For all trials taken on the same day, we normalized all LDF data against this value to obtain fractional change of CBF, ΔQ/Q₀=(Q−Q₀)/Q₀. The ΔQ/Q₀ data were mean-subtracted and low-pass filtered at 5 Hz (Butterworth).

Linear model

We constructed a linear convolution model to fit the observed changes in hemodynamic signals based on the assumption that the hemodynamic response to locomotion is a linear, time-invariant (LTI) system (Boynton et al., 1996; Cardoso et al., 2012; Glover, 1999; Vazquez and Noll, 1998). The input is the binarized locomotion signal. The output, or response, is any one of our hemodynamic measurements, including changes in diameter, ΔD/D₀ from 2PLSM, changes in reflectance, ΔR/R₀ from IOS, and changes in flux, ΔQ/Q₀ from the LDF signal. The transfer function to individual locomotion event, or the impulse response function, is the hemodynamic response function (HRF). This model can be described as,

$$\frac{\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{m\times 1}}{x_0}={\stackrel{\rightharpoonup }{s}}_{m\times 1}\ast {\stackrel{\rightharpoonup }{h}}_{x,n\times 1}$$ (1)

where x is either the vessel diameter (D), the IOS signal (R), or the cerebral blood flow, Q, and consists of m data points. S⃑ is a vector of the same length as x⃑ that contains binary locomotion events, and h⃑_x is the measurement-specific HRF with n data points, where n≪m.

To identify locomotion events, velocity was low-pass filtered at 10 Hz. Acceleration was calculated as the absolute value of the first derivative of the filtered velocity. The acceleration of the ball should be proportional to the force the paws experience, and thus closely related to the neural activity driven by the tactile sensory input. Acceleration was binarized according to the equation:

$$\delta (T)=H(a_T-a_c)=\{\begin{array}{ll}1,\hfill & if{a}_T\ge a_c;\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}$$ (2)

where the threshold acceleration a_c was chosen at 1×10⁻⁶ m/s²; a_T is the instantaneous acceleration at time T, with a sampling rate of 30 kHz, and H(•) is the binary Heavyside function. We then converted the binarized acceleration signal, δ(T), to binary locomotion events, s(t), at the same temporal resolution as the corresponding hemodynamic measurement. We set s(t) to 1, representing a locomotion event, if at least 10% of δ(T) was 1 within the time spanned between each two consecutive IOS images. Otherwise s(t) = 0. (Huo et al., 2014)

For model fitting, all free parameters in the linear convolution models were estimated by minimizing the mean-squared error (MSE) between the experimental data and estimates of the linear convolution model using the MATLAB function fminsearch. In this algorithm, we performed unconstrained nonlinear optimization by iteratively search for the next best parameter until the improvement of MSE was below a tolerance threshold (1×10⁻⁸) with a marginal change of parameter (<1×10⁻⁸). The initial value of each parameter was fixed at 0.1 for all fittings, which was distant from the final fitted value.

We also solved directly for the kernel (HRF) numerically (Keesman, 2011). Writing the linear convolution model in matrix form, we had

$$X_{(m+n)\times 1}=T{(\stackrel{\rightharpoonup }{s})}_{(m+n)\times (n+1)}\times H_{(n+1)\times 1}$$ (3)

where $X_{(m+n)\times 1}=\left(\begin{array}{c}\mathrm{\Delta }{\stackrel{\rightharpoonup }{x}}_{m\times 1}/x_0\\ {\stackrel{\rightharpoonup }{0}}_{n\times 1}\end{array}\right)$. T(S⃑) is a matrix containing the Toeplitz transformation of locomotion events S⃑:

$$T(\stackrel{\rightharpoonup }{s})=\left(\begin{array}{ccccc}1& s_1& 0& \cdots & 0\\ 1& s_2& s_1& \cdots & 0\\ & & & \ddots & \\ ⋮& s_n& s_{n-1}& \cdots & s_1\\ 1& 0& s_n& \cdots & s_2\\ & & & \ddots & \\ 1& 0& 0& \cdots & s_n\end{array}\right).$$ (4)

The matrix T is real as it contains only binary data. T is full rank column-wise as long as S⃑ is not empty, that is, there is at least one acceleration event above threshold. The vector H containing the impulse response h⃑_x, H={0, h⃑_x}^T, where h₀ is a constant shift, can be solved as:

$$H={(T^{T}T)}^{-1}{T}^{T}X$$ (5)

To avoid boundary effects, we shifted the input S⃑ forward by truncating the first 10 seconds of data (see Supplementary Fig. S3A, S3C).

In order to estimate the maximal change of hemodynamic signal, Δx_max/x₀, we convolved the fitted or numerically solved HRF with a saturating stimulus, mimicking a long bout of locomotion, such that the simulated hemodynamic signal plateaued (see Supplementary Fig. S3B, S3D) at the value of Δx_max/x₀.

Other than early exploratory studies, we did not attempt to fit the CBV HRF with a gamma distribution function (Boynton et al, 1996), as numerical calculations of the CBV locomotion-evoked HRF clearly showed a different profile from gamma distribution (see Supplementary Fig. S3). Numerically calculated HRFs were similar across animals.

All reported summary data were in the form of mean ± standard deviation. All statistical tests using “ANOVA” were one-way ANOVA unless otherwise specified. Animal numbers were not predetermined, and all tests of statistical power were done post hoc.

Results

Spatiotemporal features of locomotion-driven changes in the intrinsic optical signal

We acquired the CBV-related intrinsic optical signal (IOS) in the dorsal frontal and parietal cortices of awake mice that were head-fixed on top of a spherical treadmill. Decreases in fractional reflectance from the baseline, ΔR/R₀, corresponded to increases in CBV (Malonek and Grinvald, 1996; Sirotin and Das, 2009). The hemodynamic response to locomotion had a characteristic multiphasic temporal profile (Fig. 1C). Following locomotion initiation, we observed a strong decrease in ΔR/R₀ in the parietal cortex, especially the forelimb/hindlimb (FL/HL) representations in the primary sensory cortex (SI). At the conclusion of each locomotion event, ΔR/R₀ initially recovered towards baseline rapidly, then with a slower time course, indicative of two distinct processes. For prolonged bouts of locomotion lasting tens of seconds or more, the decrease in ΔR/R₀ in the parietal cortex could be >10%. However, there was little to no locomotion-driven changes in ΔR/R₀ in the frontal cortex (Huo et al., 2014).

In order to accurately estimate the HRF, the input bandwidth must span the output bandwidth (Marmarelis and Marmarelis, 1978). This criterion was satisfied between the binarized locomotion power spectrum (the input) and the power spectrum of the average ΔR/R₀ throughout the entire windows (the output) (Fig. 1D). In addition to the large, low frequency fluctuations in the reflectance signal driven by locomotion, there were small heart rate-induced fluctuations restricted to the frequency range of 8 – 12 Hz (Fig. 1D). Most locomotion events were brief (<1 s) (Fig. 1E). However, most of these short events are correlated in time (Fig. 1C), consistent with the large power at low frequencies in the power spectrum of binarized locomotion (Fig. 1D).

Dynamics of pial arterial and venous dilations

The fast and slow components of CBV increase in SI FL/HL areas measured with IOS (Fig. 1B) could be due to multiple time-scale behavior at the individual vessel level, or to heterogeneous response dynamics across vessel types (Blinder et al., 2013; Shih et al., 2012). To determine how individual vessel dynamics drive CBV changes during locomotion, we employed 2PLSM to visualize individual pial vessels (Drew et al., 2011; Shih et al., 2013) in the SI FL/HL representations of mice head-fixed on the treadmill (Fig. 2A). We focused on pial vessels because voluntary locomotion drives very small dilations of penetrating vessels (Gao, Greene, and Drew, unpublished results), which therefore are not likely to contribute substantially to changes in the intrinsic signal. During periods of quiescence, we observed spontaneous, low-frequency fluctuations in the diameters of pial arteries (Fig. 2C, < 20% peak-to-peak), consistent with measurements in stationary mice (Drew et al., 2011) and with measurements in the IOS (Huo et al., 2014), while pial veins exhibited very small changes in diameter (Fig. 2C).

The pial arteries dilated strongly and rapidly in response to both brief and prolonged voluntary locomotion events (45.1% ± 26.7% peak dilation). At the cessation of locomotion, the arteries constricted back to their baseline diameter within a few seconds (Fig. 2C). In contrast, dilations of pial veins were only apparent after longer bouts of locomotion due to their smaller amplitudes (15.4% ± 15.5% peak dilation). The diameters of veins took tens of seconds to return to baseline (Fig. 2C). Locomotion-driven arterial and venous dilations were very similar in magnitude and time course to those evoked by vibrissae stimulation in stationary mice, and exhibited the same spontaneous dilations in the absence of overt sensory stimulation (Drew et al., 2011) (see Supplementary Fig. S1). However these dilations are substantially larger than those of vessels in anesthetized animals (Drew et al., 2010; Tian et al., 2011), consistent with the observation that anesthesia profoundly disrupts the activity of neurons (Chapin and Lin, 1984) and astrocytes (Thrane et al., 2012), making anesthesia more akin to a coma than reflecting normal brain function (Brown et al., 2010). The similarities of the vascular responses to passively presented sensory stimuli and to somatosensory stimulation that was actively generated suggested that the hemodynamic response was not affected by the behavioral state (locomoting vs. stationary) in the awake condition.

HRFs of pial vessel in response to voluntary locomotion

To quantify the relationship between individual vessel dilation and locomotion stimulus, we used a linear convolution model:

$$\frac{\mathrm{\Delta }\stackrel{\rightharpoonup }{D}}{D_0}=\stackrel{\rightharpoonup }{s}\ast {\stackrel{\rightharpoonup }{h}}_D+c+\stackrel{\rightharpoonup }{e}$$ (6)

where D⃑ is the time series of vessel diameter, D₀ is the baseline diameter at rest, S⃑ is a vector of the binary locomotion events, c is a constant offset term, and e⃑ is the vector of errors (assumed to be Gaussian) that is minimized in the fitting. We used binarized locomotion (thresholded absolute acceleration) because in initial experiments we found that the correlation between the hemodynamic signal and the binarized locomotion was stronger than between the hemodynamic signal and raw velocity (not shown). To characterize the dilation of an individual vessel in response to locomotion, we approximated the HRF, h⃑_D, as a decaying exponential function, where each vessel’s behavior was described by its dilation amplitude (A_D) and time constant (τ_D) of recovery, such that at each time point t,

$$h_D(t;A_D,{\tau }_D)=A_D{e}^{-t/{\tau }_D}$$ (7)

The dynamics of individual arteries and veins were well estimated with this model by fitting the parameters A_D, τ_D, and c to individual trials (Fig. 3) (Pearson’s correlation coefficient, cc = 0.62 ± 0.16 for arteries; cc = 0.52 ± 0.16 for veins).

Figure 3. Quantification of time courses and amplitudes of responses of pial arteries and veins to locomotion using a linear model reveals distinct dynamics.

(A) Fitted time constants (τ_D) of vessel recovery from dilation were significantly smaller for arteries (red) than for veins (blue) (ANOVA: p<0.001). Red and blue arrowheads indicate the mean of for arteries (5.5 ± 5.1 s) and veins (25.1 ± 17.9 s), respectively. (B) Values of integrated areas of the estimated impulse response showed larger arterial (5.57 ± 3.93 s⁻¹, red) than venous (2.61 ± 2.01 s⁻¹, blue) diameter changes (ANOVA: p<0.001). (C) Correlation coefficients (cc) between the data and model fitting for arteries (0.62 ± 0.16) and veins (0.52 ± 0.16) were similar across vessel diameters. Data from a total of 151 arteries and 104 veins were included in each plot.

The fits for the time constants, τ_D, of arteries (5.5 ± 5.1 s) were significantly faster than those of veins (25.1 ± 17.9 s; ANOVA: p<0.001) (Fig. 3A). The amplitudes, A_D, of arterial HRF (10.8% ± 7.0%) were ~10-fold larger than that of the veins (0.9% ± 0.7%; ANOVA: p<0.001). The maximal dilation, A_D,max, obtained by convolving with a simulated stimulus with long enough duration that it saturates the vessel dilatory response, was significantly larger in arteries (33.9% ± 26.7%) than in veins (16.8% ± 12.0%; ANOVA: p<0.001). Similarly, in response to a single locomotion event, the total dilation integrated over time, A_Dτ_D, was significantly larger in arteries (5.57 ± 3.93 s) than in veins (2.61 ± 2.01 s; ANOVA: p<0.001) (Fig. 3B). Time constants, integrated areas and goodness-of-fit, measured by cc, were all consistent across animals (see Supplementary Fig. S2). Smaller arteries had larger dilation amplitudes (log linear regression, slope = −0.02 μm⁻¹, p<0.001), whereas veins showed no size dependence of responses (p>0.05), consistent with previous observations (Drew et al., 2011; Lee et al., 2001).

HRF of CBV-based intrinsic signal changes

Dilations of arteries and veins will increase local blood volume, decreasing reflectance in IOS. The correlation between locomotion and ΔR/R₀ change in the parietal cortex was always significant (Pearson’s correlation coefficient, t-test: p<0.001), but not in the frontal cortex (t-test: p>0.05), implying the linearity in the strongly responding parietal cortex. For each pixel, we fit the ΔR/R₀ measurements in response to locomotion with a linear convolution model, similar to the one used for single vessels:

$$\frac{\mathrm{\Delta }{\stackrel{\rightharpoonup }{R}}_i}{R_{i0}}=\stackrel{\rightharpoonup }{s}\ast {\stackrel{\rightharpoonup }{h}}_{Ri}+c_i+{\stackrel{\rightharpoonup }{e}}_i.$$ (8)

Here ΔR⃑_i/R_i0 is the fractional change of reflectance from baseline of pixel i, c_i is a constant offset associated with pixel i, and e⃑_i is a time-varying error term that is minimized for each pixel during the fitting. We constrained the HRF of the ith pixel, h⃑_Ri, to be weighted sum of a fast arterial and slow venous component:

$$h_{Ri}(t;a_i,v_i)=a_i{e}^{-t/{\tau }_a}+v_i{e}^{-t/{\tau }_v},$$ (9)

where fast decay time constant τ_a was fixed at 4 s, and slow decay τ_v at 40 s, based on our 2PLSM measurements. The pixel-specific weights, a_i and v_i, reflect the individual contributions of arteries and veins to blood volume increases within the area of the ith pixel. We assumed that any responses of capillaries were subsumed into one or both of these terms (Kim & Kim 2011; Hall et al. 2014). The values of a_i and v_i were fitted to the entire trial of each pixel (Fig. 4A). Due to its strong hemodynamic response to locomotion, the parietal cortex yielded a significantly higher average correlation between the fitted and actual responses (cc = 0.70 ± 0.07) than in the frontal cortex (cc = 0.40 ± 0.06; ANOVA: p < 0.001) (Fig. 4B, 5C). This model does not capture the ongoing, spontaneous fluctuation in the hemodynamic signal (Fox and Raichle, 2007; Mayhew et al., 1996; White et al., 2011), effectively setting an upper bound on the quality of our fit. HRFs directly calculated from binarized locomotion and changes in reflectance yielded a similar shape as our bi-exponential HRF construction (see Supplementary Fig. S3A), implying that our parametric simplification captured the essential features of the responses. We found that the exact values of time constants used for the arterial and venous component did not affect fit significantly, so long as they were well separated in value and both resided within the range of time constants for arterial and venous dilation, respectively, to capture the dynamics of the response. More complicated models, potentially including non-linearities, could improve upon the quality of the fits. Varying the time constants by 50% did not change the spatial pattern or the correlation of the fits (see Supplementary Fig. S4). The advantage of using the simplified parameterized HRF is that both a_i and v_i, which have clear physical interpretations, could be visualized and analyzed independently from each other.

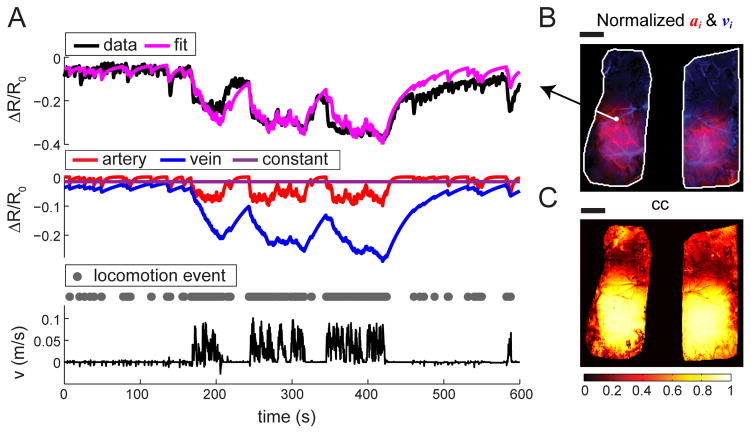
Figure 4. Linear convolution model captures the temporal dynamics of CBV response to locomotion.

(A) Top: Example of pixel-wise model fitting. For a sample pixel signified in (B), we fitted the time series of ΔR/R₀ (top black) with a linear convolution model (magenta; cc = 0.83). Middle: The model consisted of two dynamic components, a fast arterial (red) and a slow venous (blue) component, and a constant offset (purple). Bottom: Binary locomotion events (gray dots) were derived from recorded locomotion velocity (black). (B) Amplitude of the fast component, a_i (red), and amplitude of the slow component, v_i (blue), for all pixels within the ROI (white outline). (C) Correlation coefficients (cc) between the ΔR/R₀ data and the fitted data of all pixels within the ROI. The correlation was highest in the regions with largest decrease in reflectance. Scale bars: 1 mm.

Differing spatial pattern of the arterial and venous responses

We then looked at the spatial patterns of the arterial and venous fitting parameters, a_i and v_i. The fit amplitude of a pixel will not only depend on the fractional change in CBV, but on the relative amount of blood volume in the pixel. The pixels containing large surface vessels will have a larger fractional blood volume than parenchymal pixels, and thus will be more prominent. We found that the patterns of arterial and venous weights consistently separated out the large vessels in the arterial and venous networks (Fig. 5A), with the pixels containing large arteries having large values of a_i, and pixels containing large veins having large values of v_i. The parenchyma exhibited a mixture of the arteries and veins due to the contribution of pial vessels that were smaller than a single pixel, signals from penetrating arterioles and ascending venules, and potentially capillaries (Hall et al., 2014; Stefanovic et al., 2008). Visualizing the spatial pattern of the component fit amplitudes revealed distinct arterial and venous ‘maps’, and that the arterial response to locomotion was more localized than the venous response (Fig. 5A). We quantified this localization by measuring the area of activation of the venous and arterial maps. We defined the area as the area greater than half of the 99%tile peak response. The size of the activation area was 4.2 mm² ± 1.9 mm² in the arterial map, significantly smaller than the 6.1 mm² ± 1.9 mm² in the venous map (ANOVA: p<0.05; N=8) (Fig. 5B). The average window size was 12.9 mm² ± 1.7 mm². The power (1−β) of the ANOVA testing differences in spatial spread between arteries and veins was 0.95.

Figure 5. Spatially distinct arterial and venous contributions to cortical CBV changes during locomotion.

(A) Fitted fast component, a_i (left), and slow component, v_i (right), of all pixels within ROI (white outline) for two different trials. The fast components reliably recovered the arterial network; while the slow components recovered the venous network. Side plots show the medial-lateral average of a_i (red) and v_i (blue) in the left hemisphere. Scale bar = 1 mm. (B) The mean area of arterial (red) or venous (blue) map of pixels with fit amplitudes greater than 50% of the peak response. The peak is defined as the 99%tile of the arterial or venous component amplitude response over the entire window. Activated areas of individual mice are shown in black dots. *: p<0.05. (C) Average fractional contributions to the dynamic component of CBV response for arteries (red), or veins (blue), over the entire window (white bars), or only the SI FL/HL area (filled bars). N=8 mice.

We quantified the relative changes in arterial and venous volumes in response to saturating stimulation from our fits. The fractional contribution of the arterial component was given by:

$$\sum _{i=1}^N\frac{a_{i,max}}{a_{i,max}+v_{i,max}}$$ (10)

where N is the number of pixels in the area of interest (either the FL/HL representation or the entire window area) and i represents the pixel. Based on the construction of HRF (9), the maximum arterial (venous) contribution for each pixel a_i,max (v_i,max) is given by:

$$a_{i,max}=\frac{a_i}{1-e^{-1/f_s{\tau }_a}}$$ (11)

where f_s is the frame rate at which the IOS is measured. The arterial and venous components of CBV response to locomotion had nearly equal magnitude (Fig. 5C) in the FL/HL representation (arterial 45.8% ± 13.6%; venous 54.2% ± 13.6%; ANOVA: p>0.05, N=8). When we examined the relative contributions across the entire window area, the arterial contribution dropped to 32.0% ± 14.2% (venous 68.0% ± 14.2%; ANOVA: p<0.01, N=8) (Fig. 5C). This result was due to the regional ‘negative’ arterial contribution to CBV, as the fitted values of a_i in the frontal cortex were negative (Fig. 5A). These results show that even during prolonged bouts of locomotion, which probably drive venous distention to their physiological limits, the arterial volume contribution to blood volume changes is large and cannot be assumed to be negligible, contrary to the assumptions underlying the balloon model of the BOLD signal (Buxton et al., 1998).

Repeatability and robustness of fit parameters

Since studies using fMRI have typically found hemodynamic responses to be unreliable across trials widely spaced in time (Bennett and Miller, 2010), it is important for us to determine if the changes we observed to relatively natural stimuli are robust across trials. We tested if the parameters fitted on one trial (within-trial fitting) could predict the hemodynamic response to locomotion on a different trial (cross-trial prediction). Voluntary locomotion trials on the same mouse were separated in time by 1 to 94 days (mean of 16 ± 12 days). The measured ΔR/R₀ on one trial and predicted response using the parameters from a different trial were very similar (Fig. 6; also see Supplementary Fig. S5). The temporal dynamics of a single pixel (Fig. 6A) and the spatial specificity of the entire window (Fig. 6B) were both well predicted using the parameters fitted on a different trial. For all trials within an animal, we averaged all correlation coefficients between each cross-trial prediction and the measured data within the FL/HL representations. The fitting quality of cross-trial prediction was 89.3% ± 7.7% of the fitting quality of within-trial estimates (Fig. 6C). The fitted model could also be used to decode locomotion patterns (see Supplementary Fig. S6). These results show that the CBV response to locomotion is spatially and temporally robust and repeatable.

Figure 6. Fitted HRFs are stable across trials.

(A) Example of cross-validation of fit parameters. Averaged IOS across all pixels within the SI FL/HL area (blue polygon in (B)), all model parameters were fitted to one trial (‘fit’, upper panel, cc=0.83) and applied to another trial (‘prediction’, lower panel, cc=0.86). (B) Goodness-of-fit, measured by correlation coefficients between measured data and model fit, of within-trial fitting, cc_fit (upper panel), and of cross-trial prediction, cc_prediction (lower panel), in the entire window. Blue polygons enclose SI FL/HL area in each hemisphere. Scale bars = 1 mm. (C) Comparing the average cc within the SI FL/HL area, with error bars, of within-trial (magenta) and cross-trial (purple) estimates for each animal. N=8 mice.

HRF of cerebral blood flow response to locomotion

Since vessel dilation lowers vascular resistance and thus increases blood flow, we next quantified the relationship between locomotion and changes of CBF. We measured local CBF using LDF in the frontal and parietal cortices (Fig. 7A, also see Supplementary Fig. S7). Again we fit the CBF with a linear convolution model,

Figure 7. Locomotion-induced changes in CBF have linear dynamics.

(A) Example of fitting the linear model (magenta) to 60-second trial of fractional change of CBF from baseline, ΔQ⃑/Q₀ (green), in the FL/HL representation. Locomotion events are shown as gray dots. (B) Comparison of average cc between within-trial model fitting (magenta circle) and cross-trial prediction (purple square), with error bars, for all 3 animals. (C) Fitted time constants, τ_Q, of all trials (black dots) averaged for each animal (bars).

$$\frac{\mathrm{\Delta }\stackrel{\rightharpoonup }{Q}}{Q_0}=\stackrel{\rightharpoonup }{s}\ast {\stackrel{\rightharpoonup }{h}}_Q+c+\stackrel{\rightharpoonup }{e},$$ (12)

where ΔQ⃑/Q₀ represents the fractional change of CBF from baseline, and h⃑_Q is the CBF HRF to locomotion. The HRF is approximated with an exponential kernel,

$$h_Q(t;A_Q,{\tau }_Q)=A_Q{e}^{-t/{\tau }_Q}$$ (13)

where the amplitude A_Q and time constant τ_Q, along with the constant term c, are free parameters. In the parietal cortex, the correlation coefficient between data and the fitted response was consistently high (cc = 0.74 ± 0.07, N=3), showing that this linear model is a good estimation of the CBF response to locomotion. In the frontal cortex, the goodness-of-fit was poor due to the small CBF response (see Supplementary Fig. S7). Again we tested the robustness of CBF response to locomotion in the parietal cortex of each animal. We found that the goodness-of-fit of cross-trial predictions were not significantly different from the within-trial fitting (Fig. 7B). The time constant of the HRF relating CBF to locomotion was slightly shorter than the time constant of arterial dilation (Fig. 7C) (τ_Q = 2.62 ± 1.33 s). These results indicate that the pial arterial dilation in response to locomotion drives a corresponding linear increase in CBF.

Discussion

Hemodynamic signals, such as changes in cerebral blood flow and volume, are several steps removed from the neural activity that drives them (Attwell et al., 2010; Buxton, 2012), and are shaped by the architecture of the vascular network (Gardner, 2010). For this reason it is critical both to have a quantitative description of the hemodynamic response function in order to better interpret observed hemodynamic signals, and to understand the mechanistic basis of the microscopic changes in the vasculature that generate the HRF. Here, we demonstrated that macroscopic blood volume-related hemodynamic response to voluntary locomotion, measured using IOS imaging, could be separated into arterial and venous components with distinct spatial patterns, and that these spatial patterns of HRFs were robust across time.

An important limitation of this study is that though our optical approach gives us a much higher spatial resolution laterally than magnetic-resonance based imaging techniques, our IOS measurements are from hemodynamic changes in the superficial layers, due to light scattering by brain tissue and absorbance by hemoglobin (Tian et al., 2011). This is an important caveat, as several studies have shown small, but significant, laminar differences in stimulus-evoked CBV increases (indicative of dilation), in anesthetized animals (Hirano et al., 2011; Kim & Kim, 2010; Polaowsky & Kim 2014). As the vessels in the deeper layers may respond differently than the pial vessels, it remains to be seen if the dynamics of vessels in deeper layers can be captured using a two-component linear model like the one presented here. Recent advances in non-linear microscopy imaging techniques (Kobat et al., 2009; Horton et al., 2013) should enable measurements of single-vessel dynamics throughout the depth of the cortex in the future.

Interestingly, the HRFs obtained here are similar to the CBV HRF measured in response to electrical stimulation in anesthetized rats (Silva et al., 2007; Hirano et al., 2011), and the dynamics in the visual cortex of anesthetized cats (Kim and Kim, 2010). The distinct fast and slow components of the HRFs are similar to those seen in individual arteries and veins of mice that are stationary, but awake (Drew et al., 2011). This suggests that the combined arterial/venous response to stimulation is a fundamental, invariant feature of the cerebral vascular system across many physiological states. Additionally, for stimuli lasting less than a few seconds, the arterial component of the change in CBV is larger than the venous component, which is important in understanding the physiological basis of the BOLD signal (Buxton, 2012; Kim et al., 2013). Our results cannot be directly compared to BOLD signal HRFs in humans because the BOLD signal reflects primarily venous oxygenation changes, not arterial dilation (Kim and Ogawa, 2012), and thus has different temporal dynamics. We did not explicitly model any capillary dilation, as it is not clear whether the capillary dilation takes place on the time scale of seconds (Hall et al., 2014) or tens of seconds (Stefanovic et al., 2008), slightly and passively in response to upstream arteriole dilation (Kornfield and Newman, 2014), or not at all (Fernandez-Klett et al., 2010; Drew et al., 2011). Due to the light scattering properties of the brain (Tian et al., 2011) and laminar differences in vasculature (Tsai et al., 2009), the IOS from the parenchyma will contain a mix of capillary and large surface vessel signals. Our results show that the dynamics of parenchymal signals can be explained with a sum of arterial and venous signals, which implies that during voluntary locomotion, there is little dilation from capillaries and/or that the capillaries dilate with a mix of fast and slow dynamics that can be subsumed into the arterial and/or venous components.

A second insight obtained from our decomposition of the hemodynamic response into venous and arterial components is that the spatial pattern of the contributions of the components varied across the cortex. By fitting the HRFs in a location-dependent manner, we were able to determine that the spatial extent of the arterial component of the CBV was significantly smaller than the spatial extent of the venous component. This indicates that the ‘point spread function’ of the venous volume change is broader than that of the arterial component. This knowledge, coupled with reconstructions of the vasculature (Blinder et al., 2013; Weber et al., 2008), should help constrain models of blood flow dynamics in the cortex (Boas et al., 2008). By separating the changes in arterial and venous components of the CBV, we are able to show that voluntary exercise immediately induces localized arterial blood volume increase, followed by slow, diffuse venous blood volume increases. These results solve a long-standing issue as to how localized increases in cerebral blood flow and volume are during exercise, showing that diffuse spatial blood volume increases can follow prolonged bouts of locomotion. Additionally, because of the larger venous contribution at locations distant from the center of hemodynamic activation, these more remote areas will have a slower HRF, consistent with a model of a poroelastic brain interacting with a vascular network (Aquino et al., 2014).

The mean correlation coefficients between our fits and the data, which use a behavioral input, are comparable to those of the fMRI BOLD response in anesthetized monkeys, using neural activity as the input to the linear system (Logothetis, 2002). The tight relationship we observed between behavior and the hemodynamic signal is surprising for several reasons. First, awake mice, even at rest, have ongoing neural activity in the brain, which partially contributes to the spontaneous hemodynamic fluctuations we observed and could not account for with our model. Secondly, the locomotion stimulus is of variable duration, which means any temporal non-linearity will reduce the correlation between the data and the predicted response. Lastly, because the level of spontaneous neural activity is substantially higher in the awake animal, one might suspect the proportional change in activity evoked by stimulation, the modulation amplitude of the neural activity, to be lower than in the anesthetized animal (Fiser et al., 2004; Goard and Dan, 2009; Goense and Logothetis, 2008), which would be expected to lower the dynamic range of the locomotion-evoked cerebral hemodynamic signal. Despite all these potential effects that would compromise the correlation between behavior and the resulting hemodynamic signal, we still observed a highly linear cerebral hemodynamic response, suggesting that although the local ‘average’ neural activity measured using electrophysiology may be a poor indicator of changes in cerebral blood flow and volume (Devor et al., 2008; Sirotin and Das, 2009, Huo et al., 2014), these hemodynamic changes are still precisely controlled.

The dilations we observed in the cortical surface arterioles, both in response to locomotion and spontaneously (Figs. 2 & S1), were approximately three to five times larger than those seen in anesthetized mice (Drew et al., 2011; Nizar et al., 2013). Our results build on a substantial body of work showing that anesthesia profoundly disrupts neurovascular coupling, neural metabolism and the hemodynamic responses. The seminal work of Martin and colleagues (Martin et al., 2002, 2006a, &2006b) showed that there is an increase in the strength of neurovascular coupling, and the response to hypercapnia in awake relative to anesthetized rats. The dynamics of these responses are much faster in awake rats than in anesthetized rats. Recent work has found similar slowing and reductions of the hemodynamic responses by anesthesia in the vibrissae and visual cortices of mice (Drew et al., 2011; Pisauro et al., 2013). In addition to changes in the hemodynamic response, anesthesia severely disrupts brain metabolism. The anesthetic alpha-chloralose, widely used in neurovascular coupling studies, decreases glucose metabolism in the cortex by more than 50% relative to the awake state (Dudley et al., 1982), the same magnitude of metabolic decrease of found in vegetative coma patients relative to “locked-in” patients and healthy controls (Levy et al., 1987). The BOLD response is significantly larger in magnitude in awake monkeys than under anesthesia (Goense and Logothetis, 2008). Thus, the awake and anesthetized brains are in profoundly different states, making it problematic to use the results of anesthetized animal studies to interpret the result of human neuroimaging studies.

Although we did not make measurements of blood gases (Drew et al., 2011), the arterial dilation we observed here was unlikely to be caused by changes in CO₂ concentration in the blood for two reasons. Arterial dilations caused by hypercapnia take several minutes under un-physiologically high CO₂ levels to reach the magnitude we observed (Ngai and Winn, 1996), though exposure to high CO₂ in the awake animal can cause faster hemodynamic responses associated with neural desynchronization (Martin et al, 2006a), and the observed increases in blood flow, blood volume and arterial diameter all peaked within seconds of the onset of locomotion, with very similar amplitudes and dynamics as seen during responses to sensory stimulation of the vibrissae (Drew et al., 2011). Secondly, moderate exercise in rats, comparable to our voluntary locomotion paradigm, causes hypocapnia (Fregosi & Dempsey, 1984), which would tend to cause vasoconstriction, not the vasodilation we see here.

Empirical models of the HRF grounded in measurement of individual pial vessel dynamics allow the separation of cerebral hemodynamic signals into distinct vascular components. Particularly, the ability to separate well localized arterial changes from more diffuse venous signals should improve the resolution and accuracy in functional connectivity studies (Fox and Raichle, 2007), reconstructions of stimuli from cerebral hemodynamic signals (Naselaris et al., 2011), and in understanding the microvascular mechanisms of vascular malfunction associated with neurodegenerative diseases (Iadecola, 2013) and aging (D’esposito et al., 2003).

Supplementary Material

1. Figure S1. Arterial and venous dynamics are similar in response to locomotion and passive sensory stimulation.

Diameter traces taken from Fig. 2C, showing fractional changes of arterial diameter ΔD_a/D_a0 (upper) and fractional changes of venous diameter ΔD_v/D_v0 (lower) in response to one locomotion event (~0.33 s), intermediate duration (4 s) of locomotion, and long duration (22 s) of locomotion. The amplitudes and dynamics of both the arterial and venous responses to locomotion are very similar to those in awake mice in response to stimulation of the vibrissae (compare with Fig. 2 and Fig. S3 in Drew et al., 2011).

2. Figure S2. Arterial and venous dynamics fitted with the linear convolution model have similar parameters across animals.

(A) Mean fitted time constant, τ_D, of the single vessel HRFs for both arteries (red) and veins (blue) were consistent across animals. (B) Integrated vessel dilation amplitudes, A_Dτ_D, were consistent across animals. (C) Fitting quality, measured by correlation coefficient (cc), was similar across animals. Error bars show standard deviations.

3. Figure S3. Numerically calculated CBV and CBF HRFs.

(A) Time-invariant, numerically calculated CBV HRF (green), overlaid with the bi-exponential fitted HRF (magenta). The stimulus was the binary locomotion events, and the response was the average ΔR/R₀ in the parietal cortex with duration of 2,000 s and sampling frequency of 3 Hz. Inset: Magnified numerical solution of HRF overlaid with fitted HRF for a duration of 40 s. The stimulus was shifted 10 s backward (only 5 s shown here) in time to avoid boundary effects. Vertical dashed line denotes the onset of locomotion. The horizontal dashed line represents the baseline (0) response. (B) Simulation of maximum ΔR/R₀ changes by convolving the numerically calculated HRF in (A) with a stimulus of 267 s in duration (gray dots). Simulation showed that ΔR/R₀ decreased by 13.5% to a saturating stimulus. Note the fast decrease in ΔR/R₀, followed by a slower decrease, indicating the presence of two different time-scales in the HRF. (C) Fitted responses to 100 s of ΔR/R₀ taken from the 2,000 s trial used in the calculation of (A). Black line shows the average ΔR/R₀ in the parietal cortex. Magenta line shows the bi-exponential model fitting. Green line shows the fitting using numerically calculated HRF. Locomotion events are shown in gray dots. For the entire 2,000 s trial, the fitted correlation coefficient (cc) between the data and the bi-exponential model and numerically calculated HRF were 0.81, and 0.89, respectively. (D–F) Same layout and same trial as in A–C, except the ΔR/R₀ response of a single pixel (same as in Fig. 4B) was fitted with a numerically calculated HRF (green) and a bi-exponential HRF (magenta). The correlation coefficient between the data and the bi-exponential and numerically calculated HRFs for this single pixel were 0.91 and 0.92, respectively. (G–I) Same layout as in A–C, except the CBF change, ΔQ/Q₀, in the parietal cortex over a 2,000 s trial was fitted with a numerically calculated HRF (green) and a single-exponential HRF (magenta). A 100 s sample from this trial is shown in I. The correlation coefficient between the data and the exponential and numerically calculated HRFs were 0.77 and 0.80, respectively.

4. Figure S4. Changing arterial and venous time constants does not appreciably affect the spatial distribution of arterial and venous fits, and the goodness-of-fit.

For a sample trial of 2,000 seconds, the fitted amplitudes of the fast arterial component, a_i (red), and the slow venous component, v_i (blue), were normalized and overlaid (top row). The correlation coefficient (cc) of each pixel composed a cc map (bottom row), the color intensity of each pixel reflecting the value of cc according to the color scale bar. The fit was performed with: (A) τ_a = 4 s, τ_v = 40 s. (B) τ_a = 2 s, τ_v = 20 s. (C) τ_a = 6 s, τ_v = 60 s. Note the similarities of the spatial patterns and correlations of the fits. This is the same mouse as shown in Fig. 4 but a different trial. Scale bars: 1 mm.

5. Figure S5. Cross-trial validation of fitted model measured across multiple days.

Correlation coefficient (cc) matrix between measured data, taken from the histologically defined SI FL/HL area, in trial i and predicted data from the linear convolution model with parameters fit to trial j. The cross validation between 17 trials of 2,000 seconds at 3 Hz taken on 7 different days (over a span of 17 days). Gray lines segment out trials taken on different days. There is no difference between cc for cross-trial fitting within the same day (within each gray-lined grid) or on different days.

6. Figure S6. Decoding locomotion from the CBV signal.

The CBV for each pixel signal was deconvolved using the inverse of its fitted two-component kernel, low-pass filtered at 0.1 Hz to remove false positives caused by spontaneous fluctuations, and then binarized with a threshold of 0. (A) A 200-second sample of locomotion events (black) and the estimated binary locomotion events (purple) from the pixel highlighted in (B). (B) The map of correlation coefficient between locomotion events and the estimated locomotion at every pixel. The average correlation coefficient across the entire ROI was 0.20 ± 0.13, within the FL/HL area it was 0.30 ± 0.09. Scale bar: 1 mm.

7. Figure S7. Negligible increase in CBF in frontal cortex.

(A) Left: Sketch showing the position of the LDF probe in the frontal cortex. Right: Measured fractional change of CBF, ΔQ/Q₀, in the frontal cortex (blue), and model fit (magenta). Locomotion events are shown in gray dots. The correlation coefficient (cc) between the two is 0.21. Black dashed line represents the baseline Q₀. (B) Left: Sketch showing the position of the LDF probe in the parietal cortex. Right: The cc between ΔQ/Q₀ in the parietal cortex (green) and the model fit (magenta) is 0.91. Scale bars = 1 mm.

Abbreviations

CBV

cerebral blood volume

CBF

cerebral blood flow

HRF

hemodynamic response function

IOS

intrinsic optical signal

2PLSM

two-photon laser scanning microscopy

LDF

laser Doppler flowmetry

LTI

linear, time-invariant

MSE

mean-squared error

cc

correlation coefficient

ROI

region of interest

FOV

field of view

FL

forelimb

HL

hindlimb