Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Feb 17;5:8525. doi: 10.1038/srep08525

A General Design Rule to Manipulate Photocarrier Transport Path in Solar Cells and Its Realization by the Plasmonic-Electrical Effect

Wei E I Sha 1,*, Hugh L Zhu 1,*, Luzhou Chen 1, Weng Cho Chew 2,a, Wallace C H Choy 1,b
PMCID: PMC4330524  PMID: 25686578

Abstract

It is well known that transport paths of photocarriers (electrons and holes) before collected by electrodes strongly affect bulk recombination and thus electrical properties of solar cells, including open-circuit voltage and fill factor. For boosting device performance, a general design rule, tailored to arbitrary electron to hole mobility ratio, is proposed to decide the transport paths of photocarriers. Due to a unique ability to localize and concentrate light, plasmonics is explored to manipulate photocarrier transport through spatially redistributing light absorption at the active layer of devices. Without changing the active materials, we conceive a plasmonic-electrical concept, which tunes electrical properties of solar cells via the plasmon-modified optical field distribution, to realize the design rule. Incorporating spectrally and spatially configurable metallic nanostructures, thin-film solar cells are theoretically modelled and experimentally fabricated to validate the design rule and verify the plasmonic-tunable electrical properties. The general design rule, together with the plasmonic-electrical effect, contributes to the evolution of emerging photovoltaics.

Due to a unique ability to localize, guide, and concentrate light at the nanoscale, plasmonics1 finds a special functionality to improve optical properties of thin-film photovoltaic devices2,3,4,5,6. By introducing metallic nanostructures, light absorption at the active layer of devices will be enhanced, which undoubtedly boosts short-circuit current (Jsc) and thus power conversion efficiency (PCE)6,7,8,9,10,11,12,13,14. Currently, a wideband and angle-insensitive light absorption has been achieved by periodic, quasi-periodic and random metallic nanostructures to approach or break the Yablonovitch15,16,17, Lambertian18,19, and Shockley-Queisser limits20,21. However, according to semiconductor physics, bulk recombination of photocarriers (electrons and holes), which is different from light absorption only governed by Maxwell's equations, has a strong influence on electrical properties of solar cells including open-circuit voltage (Voc) and fill factor (FF) and even predominantly determines the PCE. Going beyond the well-known optical enhancement, in this work, plasmonics is explored to control bulk recombination by modifying photocarrier transport path based on a general design rule. Plasmonics, which localizes intense light very close to metallic nanostructures, can spatially redistribute light absorption at the active layer of photovoltaic devices. As a result, the spatial distribution for excitons (or electron-hole pairs) generation can be plasmonically tunable to optimize photocarrier transport path (or bulk recombination) and thus electrical properties of solar cells. The design rule and its realization by the plasmonic-electrical effect can serve as a guideline for designing photovoltaic devices.

Results

Proposed general design rule to reduce bulk recombination

According to semiconductor physics, electrical properties of photovoltaic devices (such as FF and Voc) strongly depend on bulk recombination of photocarriers. Transport path for a photocarrier is the path from the initial site generated to the electrode collected. A short transport path will reduce the recombination and enhance electrical performances of devices. However, the short transport path cannot be achieved for electrons and holes simultaneously because both photocarriers have the same initial sites; and the total length of the electron and hole transport paths is approximately equal to the thickness of active layer, i.e.

graphic file with name srep08525-m1.jpg

where L is the thickness of the active layer. Le and Lh are the lengths respectively for the electron and hole transport paths.

Besides the transport path, mobility of photocarriers also affect bulk recombination strongly. Driven by the same internal electrostatic field, photocarriers with low mobility will move slowly. Thus low-mobility photocarriers require a long transport time before collected by electrodes. An effective way for reducing recombination loss is to let low-mobility photocarriers travel a short path. In other words, we should force the transport time of electrons and holes almost to be the same. Mathematically, we have

graphic file with name srep08525-m2.jpg

where μe and μh represent mobility of electrons and holes, respectively. The above also suggests electron to hole transport length ratio should be balanced with electron to hole mobility ratio, i.e. Le/Lh = μe/μh. The governing equation (1–2) is a general design rule to decide photocarrier transport path tailored to arbitrary photocarrier mobility.

Manipulation of photocarrier transport path by plasmonic-electrical effect

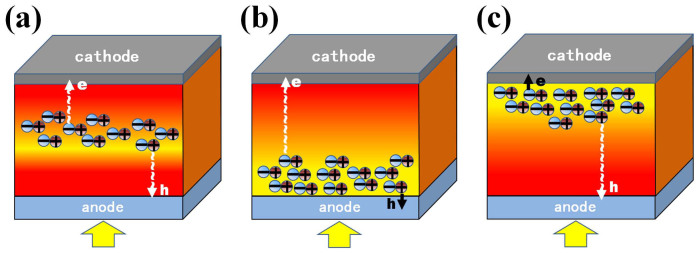
Using Eqs. (1) and (2), one could design transport paths or equivalently optimize initial generation sites of excitons. If mobility between electrons and holes are well balanced, the initial sites should be around the middle of active layer. If hole mobility is smaller than electron mobility, excitons should be initially generated near the anode, which guarantees a short transport path of holes. Figure 1 shows a conceptual diagram to manipulate photocarrier generation by embedding configurable metallic nanoparticles (NPs) into the active layer22,23,24. Spatial locations of NPs and spectral locations of plasmonic resonances should be carefully controlled to shorten transport paths of low-mobility photocarriers and maximize light absorption of active materials. A strong and concentrated optical field around NPs will generate dense and inhomogeneous excitons. These non-uniformly distributed excitons not only increase Jsc but also boost Voc and FF through manipulating transport paths of photocarriers to equalize the transport time of electrons and holes. Additionally, light absorption redistribution can be achieved by metallic grating electrodes as well6,19,25,26, where the coupling between plasmonic modes and waveguide modes will be manipulated.

Figure 1. The conceptual diagram of plasmonic-electrical effect.

Figure 1

Open in a new tab

Light absorption is spatially redistributed at the active layer for manipulating transport paths of photocarriers (minus and plus notations denote electrons and holes, respectively). A desired light absorption distribution is realized by spatially tuning the position of metallic NPs with strongly localized plasmonic effects. Light absorption of active materials is optimized by spectrally tuning the shape-dependent plasmonic resonance. The arrows e and h are the transport paths of electrons and holes. Generated electron-hole pairs (excitons) are concentrated (a) at the middle of the active layer, (b) near the anode, and (c) near the cathode, respectively.

An Approximate Theoretical Model with a Mechanistic Insight

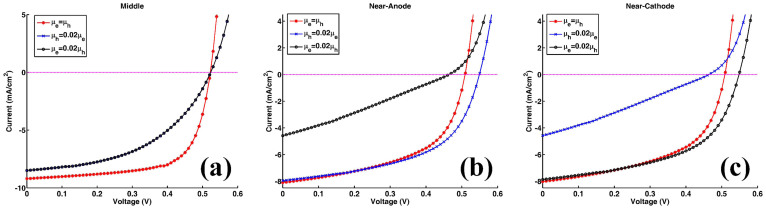
To understand the concept that electrical properties of solar cells will be boosted by spatially redistributing light absorption at the active layer, we theoretically study electrical responses of thin-film organic solar cells (OSCs) by using the multiphysics model27,28,29,30,31,32,33,34,35 developed in literatures (also see Theoretical Method Section). Particularly, OSCs with polymer and small-molecule materials always have unbalanced photocarrier mobility, which depend on material morphology, temperature, and experimental procedures (thermal annealing, etc)26,36. Mobility-dependent current density-voltage (J-V) responses are investigated with different light absorption (exciton generation) distributions, which can be realized by versatile plasmonic solar cell configurations (see Figure 1). The J-V curves and corresponding characteristic parameters are presented in Figure 2 and Table 1, respectively. The active layer thickness is L = 90 nm. μe = μh = 3 × 10−3 cm2/(V·s) are set for the case of balanced mobility. Regarding unbalanced cases, hole (electron) mobility is reduced to 1/50 of electron (hole) mobility. The injection barriers are set to be zero for both electrodes. To model the localized plasmonic effect and understand the plasmonic-electrical effect, spatial distributions of exciton generation inside the active layer are approximately set as follows

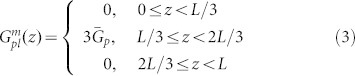graphic file with name srep08525-m3.jpg
graphic file with name srep08525-m4.jpg
graphic file with name srep08525-m5.jpg

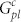where Inline graphic, Inline graphic, and Inline graphic are the exciton generation rates with respect to the three plasmonic solar cells (middle, near-anode, and near-cathode cases) as depicted in Figures 1(a), (b), and (c), respectively. The cathode and anode are located at z = 0 and z = L, respectively. Here all the devices have the same averaged exciton generation rate 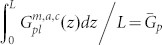Inline graphic. Physically, light absorption at the active layer is spatially redistributed by the localized plasmonic effect.

Figure 2. Photocarrier mobility dependence of J-V characteristics for plasmonic solar cells corresponding to Figures 1(a–c).

Figure 2

Open in a new tab

An approximate theoretical model is adopted for simulating the non-uniform spatial distribution of excitons. Generated electron-hole pairs (excitons) are concentrated (a) at the middle of the active layer, (b) near the anode, and (c) near the cathode, respectively.

Table 1. Electrical parameters for plasmonic solar cells with different photocarrier mobility of active materials and spatial distributions of exciton generation. The Jsc, Voc, FF, and PCE are the short notations of short-circuit current, open-circuit voltage, fill factor, and power conversion efficiency. N-Anode and N-Cathode are the short notations of near-anode and near-cathode.

NPs position Mobility Jsc (mA/cm2) FF Voc (V) PCE (%)
  μe = μh 9.198 0.669 0.522 3.21
Middle μh = 0.02μe 8.494 0.480 0.523 2.13
Fig. 1(a) μe = 0.02μh 8.490 0.480 0.523 2.13
  μe = μh 8.099 0.535 0.509 2.21
N-Anode μh = 0.02μe 7.953 0.535 0.549 2.33
Fig. 1(b) μe = 0.02μh 4.581 0.278 0.464 0.59
  μe = μh 8.022 0.533 0.509 2.18
N-Cathode μh = 0.02μe 4.578 0.278 0.464 0.59
Fig. 1(c) μe = 0.02μh 7.868 0.533 0.548 2.30
Open in a new tab

From the theoretical results (Tables 1–2 and Figure 2), we find that:

  1. The spatial distribution of exciton generation has a pronounced influence on electrical responses of OSCs. The mismatch between exciton distribution (controlled by the spatial location of metallic NPs) and photocarrier mobility will lead to poor photovoltaic devices, such as the near-anode case with low-mobility electrons and the near-cathode case with low-mobility holes.

  2. The best electrical performance (e.g. PCE) can be achieved when electron and hole mobility are well balanced and meanwhile light absorption is concentrated at the middle region of active layer (as listed in the first line of Table 1). For instance, a (standard) planar solar cell cannot achieve best efficiency even if mobility between electron and hole are well balanced. It is because, typically, light intensity is exponentially decayed from the transparent electrode rather than achieving its peak value at the middle region of active layer. On the other hand, although the intensity peak could be around the center of active layer via some smart optical designs, the solar cell does not gain the best efficiency due to unbalanced electron and hole mobility.

  3. Shortening the transport path of low-mobility photocarriers improves electrical properties of OSCs (Voc and FF), such as the near-anode case with low-mobility holes and the near-cathode case with low-mobility electrons. Taking the planar solar cell as an example again, the cell will be particularly helpful for hole collections if its transparent electrode, where light first penetrates, is the anode. This is also the reason why a normal structure of planar OSCs [as shown in Figure 1(b)] has a better performance than an inverted structure when holes have low mobility33,37.

Table 2. Averaged bulk recombination rates under short-circuit Jsc, maximum power Pmax, and open-circuit Voc conditions for plasmonic solar cells with different photocarrier mobility of active materials and spatial distributions of exciton generation. N-Anode and N-Cathode are the short notations of near-anode and near-cathode.

NPs position Mobility Recombination Jsc (1027 m−3s−1) Recombination Pmax (1027 m−3s−1) Recombination Voc (1027 m−3s−1)
  μe = μh 0.014 0.849 13.507
Middle μh = 0.02μe 0.317 2.792 10.916
Fig. 1(a) μe = 0.02μh 0.317 2.789 10.884
  μe = μh 2.762 6.574 15.796
N-Anode μh = 0.02μe 1.678 4.332 12.639
Fig. 1(b) μe = 0.02μh 9.306 11.984 14.759
  μe = μh 2.972 6.574 15.700
N-Cathode μh = 0.02μe 8.434 11.036 13.74
Fig. 1(c) μe = 0.02μh 1.574 4.109 12.118
Open in a new tab

Comparatively studying Table 2 and Table 1, bulk recombination dominates device performance. Under Voc condition (where the total current is equal to zero), recombination rate is very large and is almost equal to generation rate. Therefore, the recombination rates at “different” Voc do not have any significance to device performances. Differently, under Jsc condition or particularly at the maximum power point, larger recombination leads to lower Jsc and FF, which strongly affect PCE of devices. The plasmonic-electrical effect, which shortens the transport path of low-mobility photocarriers, indeed reduces bulk recombination and boosts the device efficiency. It should be noted that we adopted a simplified mathematical model for exciton generation rates which are zeros at some regions of active layer. From the intuitive model, one can understand the importance of light absorption redistribution (without any light absorption enhancements) to the solar cell performance.

A Rigorous Theoretical Model and Validation

The approximate exciton generation model presented in Eqs. (3–5) offers a mechanistic insight for plasmonically induced light redistribution at the active layer. But a rigorous model for calculating exciton generation of a practical solar cell is needed to accurately describe photocarrier transport and validate the proposed design rule. A small-molecule bulk heterojunction solar cell with an active material of copper phthalocyanine (CuPc): Buckminsterfullerene (C60) is theoretically investigated. In contrast to other solar cells, a standard optimized small-molecule solar cell has an ultrathin active layer due to large absorption coefficients of small molecules and a short exciton diffusion length38,39. Hence, by incorporating metallic NPs into active layer, the small-molecule device favors a very strong near-field plasmonic effect. In this work, silver NPs with a size of 10 nm and a spacing distance of 10 nm are embedded into the active layer. Using such small-sized NPs, which have large metal absorption loss, is an unusual design. These small NPs do not significantly enhance the total absorption of active materials; albeit extraordinarily redistribute light absorption at the active layer40. Exciton generation is calculated by the finite-difference frequency-domain method41. Regarding optical simulation details, please see Supplementary Note 1. It should be noted that metal absorption by silver NPs, which does not contribute to exciton generation, has been subtracted from the total absorption of active layer in the calculation23.

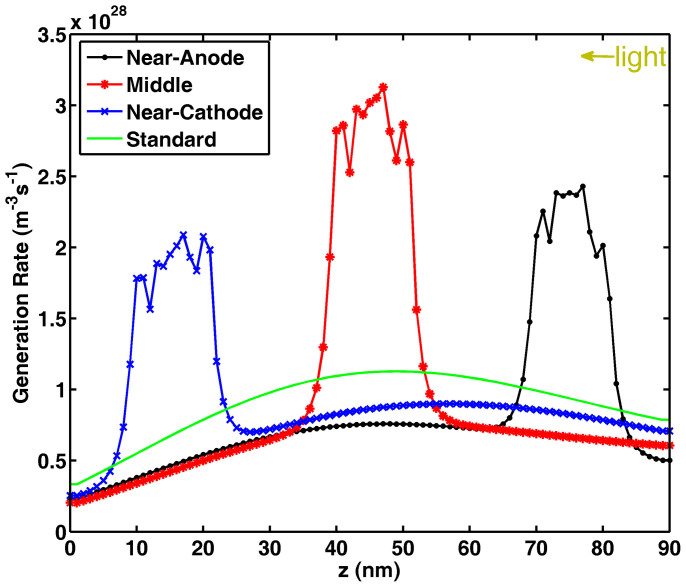
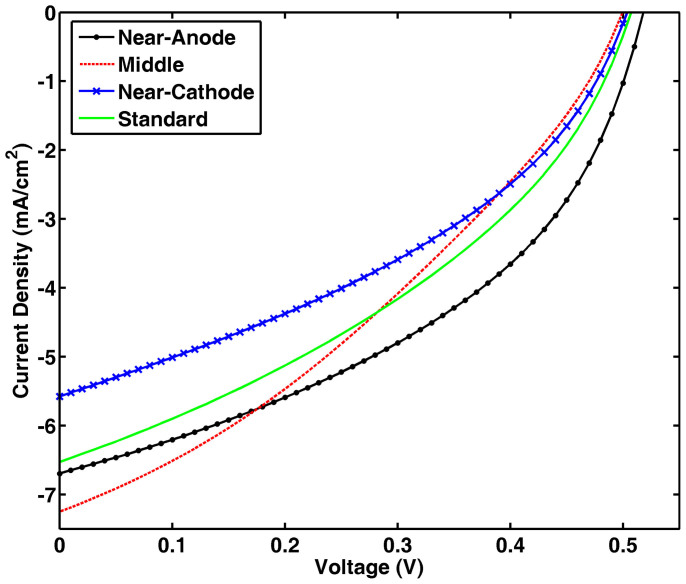
Figure 3 shows the laterally-averaged exciton generation along the vertical direction of active layer. Compared to the standard cell without NPs, plasmonically induced light absorption redistribution and thus non-uniform exciton generation can be clearly observed (also see Figure S2). Hence, the approximate exciton model given by Eq. (4) is quite reasonable. Figure 4 illustrates the J-V response with respect to the exciton generation of Figure 3. The electron and hole mobility are respectively set to be 10−2 cm2/(V·s) and 10−5 cm2/(V·s), which are typical values in small molecule devices39. Due to short transport paths of holes, the near-anode case achieves the best FF, Voc and PCE among all the cells including the standard one, which agrees with the approximate theoretical results as listed in the Table 1 highlighted by bold. However, in view of light blocking effect by metal NPs, the near-anode case induces the worst light absorption according to the exciton generation result (Figure 3). So these unusually-small NPs efficiently redistribute (not significantly enhance) light absorption at the active layer; and boost PCE by the plasmonic-electrical effect.

Figure 3. Laterally-averaged exciton generation 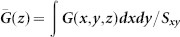Inline graphic at the active layer of a small-molecule bulk-heterojunction solar cell.

Figure 3

Open in a new tab

Silver NPs with a size of 10 nm and a spacing distance of 10 nm are embedded into different locations of the active layer corresponding to Figures 1(a–c). The result of a standard cell without NPs is also given for comparisons. The volume-averaged exciton generation 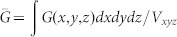Inline graphic (1027 m−3 s−1) are 8.34, 9.26, 9.27, 8.93 respectively for the near-anode, middle, near-cathode, and standard cases.

Figure 4. Theoretical J-V characteristics for plasmonic small-molecule solar cells corresponding to Figures 1(a–c).

Figure 4

Open in a new tab

A rigorous exciton generation result as depicted in Figure 3 is adopted in the simulation. The electron and hole mobility are respectively set to be 10−2 cm2/(V·s) and 10−5 cm2/(V·s). The PCE are 1.50%, 1.23%, 1.09%, and 1.26% respectively for the near-anode, middle, near-cathode, and standard cases.

From Table 1 and Figure 4, Jsc results show an interesting feature that the middle case obtains the largest Jsc, although with a low FF. Firstly, under Jsc condition, the drift current is dominantly larger than the diffusion current; and photocarriers are fast swept out of devices. Consequently, bulk recombination is weak, which can be seen in Table 2. From the theoretical results at Table 1, the middle and near-anode cases have comparable Jsc in contrast to the near-cathode one. The increased Jsc for the middle case in comparison with the near-anode case is due to a nonlinear behavior for bimolecular recombination of photocarriers. However, bulk recombination becomes larger and larger as the built-in electrostatic field is reduced. At the maximum power point or under Voc condition, the diffusion current competes with or even dominates over the drift current. Under this situation, shortening the transport path of low-mobility photocarriers will significantly reduce the bulk recombination and boost electrical properties of devices especially for FF and Voc. Secondly, exciton generation of a practical plasmonic solar cell is the exciton generation of a standard device without metallic NPs multiplied by the spatial-dependent (plasmonic) enhancement factor, which should be obtained with a rigorous simulation. Regarding practical plasmonic devices, the near-anode case [Figure 1(b)] has the shortest transport path of low-mobility holes but blocks a portion of light due to metal absorption. From the results in Figure 3, the volume-averaged exciton generation of the near-anode case gets the lowest value; and is even lower than that of the standard cell without NPs. This is the reason why the near-anode case induces a lower Jsc compared to the middle case. On the other hand, the near-cathode case [Figure 1(c)] has the longest hole transport path to the anode, which causes a large recombination loss and thus the lowest Jsc. From above discussions, Jsc of practical solar cells depends not only on the transport path of photocarriers but also on the magnitude of volume-averaged exciton generation rate.

Although the middle case achieves the largest Jsc, the near-anode case still gains the highest PCE confirmed by the rigorous theoretical results. Therefore, Voc and FF, which strongly depend on bulk recombination and are tunable with photocarrier transport paths, play more important roles than Jsc in determining the overall performance of plasmonic devices.

Experimental Design and Validation

Very recently, it has been reported that device performance of OSCs is affected by the position of a silver film within the active layer42. To understand the underlying physics and experimentally demonstrate the general design rule, we fabricated the small-molecule bulk-heterojunction solar cell with the active material of CuPc:C60. Different-sized Ag NPs are embedded into different positions of the active layer by using thermal evaporation at different stages of film formation of the active layer. Experimental details are discussed at the Experimental Section. It is worthy of noting that the plasmonic solar cells are fabricated within a high-vacuum chamber, and thus metal NPs are not passivated. The device structures corresponding to Figures 1(a–c) are given as follows:

ITO/MoO3 (10 nm)/CuPc:C60 (40 nm)/Ag NPs/CuPc:C60 (40 nm)/BCP (10 nm)/Ag

ITO/MoO3 (10 nm)/CuPc:C60 (20 nm)/Ag NPs/CuPc:C60 (60 nm)/BCP (10 nm)/Ag

ITO/MoO3 (10 nm)/CuPc:C60 (60 nm)/Ag NPs/CuPc:C60 (20 nm)/BCP (10 nm)/Ag

Figure 5 shows the cross sectional scanning electron microscopy (SEM) images of the small molecule solar cells. Ag NPs are well located at a specific region of the CuPc:C60 active layer.

Figure 5. Cross sectional SEM images of small molecule solar cell devices.

Figure 5

Open in a new tab

Ag NPs are embedded (a) at the middle of CuPc:C60 active layer, (b) near the anode, and (c) near the cathode, which respectively correspond to Figures 1(a), (b), and (c).

To study the plasmonic-electrical effect, on one hand, the size of Ag NPs is tuned to be an optimized value for favoring a strong near-field plasmonic effect. Using the structure of ITO/CuPc:C60 (40 nm)/Ag NPs (various sizes)/CuPc:C60 (40 nm), the optical absorptance of CuPc:C60 films incorporating different-sized Ag NPs (see Figure S3) suggests a strong and tunable plasmonic enhancement (see Figure 6). On the other hand, photocarrier mobility in the bulk-heterojunction active material (CuPc:C60) is very unbalanced, which can be confirmed by the experimental results of Figure S4. Here, the hole mobility is four orders of magnitude smaller than the electron one.

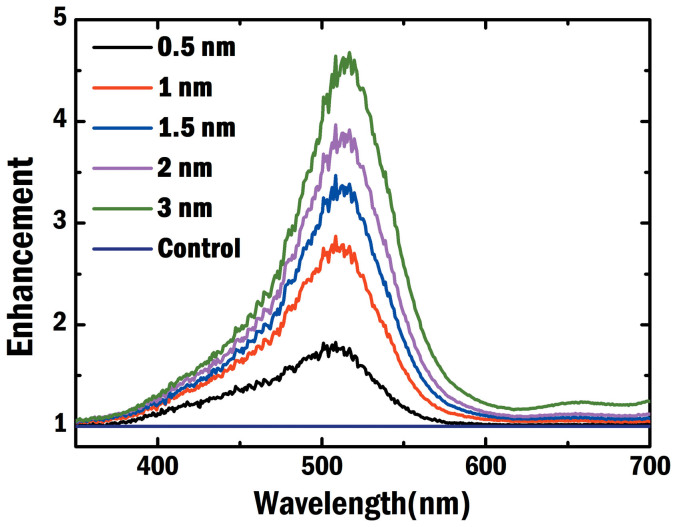
Figure 6. Experimental optical absorption enhancement of CuPc:C60 films after embedding Ag NPs.

Figure 6

Open in a new tab

The absorption enhancement of CuPc:C60 films embedded with different-sized Ag NPs were measured based on the structure of ITO/CuPc:C60 (40 nm)/Ag NPs (various sizes)/CuPc:C60 (40 nm). The enhancement is defined as the absorption of plasmonic cells (with Ag NPs) over that of standard cells without Ag NPs. It should be noted that the thickness of initially evaporated metal film as depicted in the legend is not equal to the size of corresponding metal NPs as shown in Figure S3.

From the experimental results as illustrated in Figures 7 and 8 for different device structures (Figure 5), we find that:

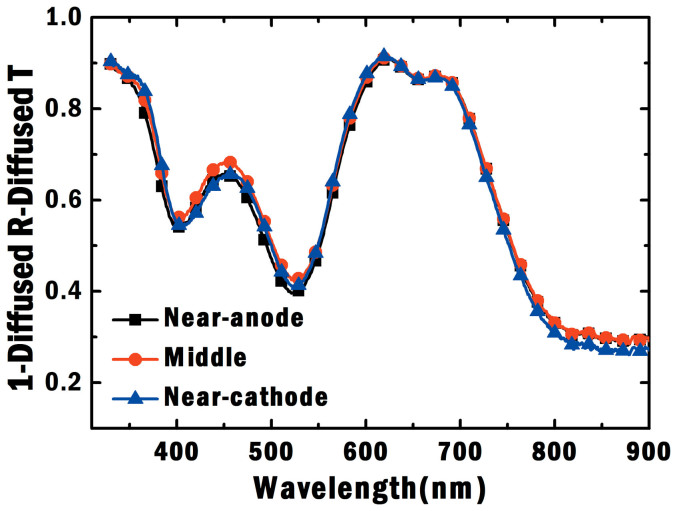
  1. The optical absorption of plasmonic small molecule solar cells, which is almost independent on the NP positions at the active layer, shows no significant differences (see Figure 7). This agrees with our argument and theoretical results (presented in Figure 3), i.e. light absorption is spatially redistributed by the localized plasmonic effects.

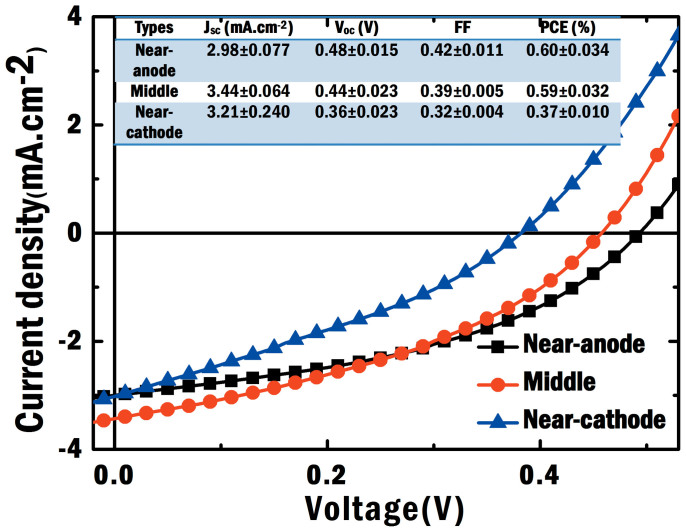
  2. Voc and FF are noticeably improved when Ag NPs are embedded close to the anode (the near-anode case). From experimental results in Figure 8, FF of the near-anode case is 0.42 compared to 0.39 and 0.32 respectively for the middle and near-cathode cases. Moreover, Voc of the near-anode case is 0.48 V in contrast to 0.44 V and 0.36 V for the middle and near-cathode cases, respectively. These experimental results agree with the theoretical predictions as listed in the Table 1 (highlighted by bold) and Figure 4. According to Eq. (2) and relevant physical explanations, shortening the transport path of low-mobility holes will reduce bulk recombination resulting in the improved electrical properties.

  3. Jsc shows peculiar features after comparing experimental results (Figure 8) to theoretical ones (Figure 4). For the theoretical results, Jsc of the near-cathode case is much smaller than that of the near-anode case. For the experimental results, Jsc of the near-cathode case is larger than that of the near-anode case. One of reasons is that bimolecular recombination rate in experimental devices is lower than that in theoretical models based on Langevin theory43. Another reason is the exciton quenching at the surface of unpassivated metallic NPs44. Thus it is not fair or meaningful to make a direct comparison between the plasmonic devices and standard one. In spite of the peculiar feature of Jsc, the near-anode case still achieves the best efficiency among all the plasmonic devices. Again, Voc and FF, highly tunable by the plasmonic-electrical effect, determine the overall plasmonic device performance.

Figure 7. Experimental optical absorption of plasmonic small-molecule solar cells.

Figure 7

Open in a new tab

The optical absorption is obtained by using 1-diffused reflectance (R)-diffused transmittance (T). Ag NPs are embedded at the active layer with different spatial locations corresponding to Figures 1(a–c). The device structure of the middle case is: ITO/MoO3 (10 nm)/CuPc:C60 (40 nm)/Ag NPs/CuPc:C60 (40 nm)/BCP (10 nm)/Ag; The device structure of the near-anode case is: ITO/MoO3 (10 nm)/CuPc:C60 (20 nm)/Ag NPs/CuPc:C60 (60 nm)/BCP (10 nm)/Ag; The device structure of the near-cathode case is: ITO/MoO3 (10 nm)/CuPc:C60 (60 nm)/Ag NPs/CuPc:C60 (20 nm)/BCP (10 nm)/Ag.

Figure 8. Experimental J-V characteristics of plasmonic small-molecule solar cells.

Figure 8

Open in a new tab

Ag NPs are embedded at the active layer with different spatial locations corresponding to Figures 1(a–c). The hole mobility is four orders of magnitude smaller than the electron mobility. The statistical parameters of three different plasmonic solar cells are summarized in the inset.

Extension of the Design Rule to Other Thin-Film Solar Cells

Manipulating photocarrier transport path is not only important to OSCs with low and unbalanced mobility but also important to other thin-film solar cells with high and balance mobility. The amorphous silicon solar cell with a device structure of anode-p+ silicon (10 nm)-intrinsic silicon (460 nm)-n+ silicon (30 nm)-cathode is studied. Most photocarriers are generated at the intrinsic layer with high and balanced photocarriers mobility, i.e. μe = 4.6 × 10−2 cm2/(V·s) and μh = 9.2 × 10−3 cm2/(V·s). According to our theoretical results (see Supplementary Note 2), the near-anode case, which redistributes light absorption (exciton generation) tailored to electron-to-hole mobility ratio, achieves the best PCE with the maximum Voc and FF. Due to a significantly reduced built-in potential at the maximum power point, photocarriers cannot be fast sweep out and thus bulk recombination dominates the device efficiency of solar cells. Additionally, depending on effective mass and average scattering time, mobility of photocarriers, cause different bulk recombination features in different active materials. Consequently, controlling photocarrier transport path by the proposed general design rule is important to thin-film photovoltaics.

In conclusion, we propose a general design rule to manipulate photocarrier transport in photovoltaic devices. Through spatially redistributing light absorption at active layer, the design rule is successfully demonstrated in a configurable plasmonic device with the help of the plasmonic-electrical effect. The dense exciton generation around plasmonic nanostructures provides a flexible and integrated way to both increase Jsc and simultaneously boost Voc and FF. Balancing the transport time for photocarriers with different electron to hole mobility ratio reduces bulk recombination and thus improves the electrical performance of photovoltaic devices. The work is highly important for high-performance photovoltaics.

Methods

Device fabrication

The Ag NPs embedded solar cells were fabricated on clean conductive ITO coated glass substrates (sheet resistance of ~20 Ω/sq, purchased from TINWELL Tech. LTD.), which were previously cleaned in ultrasonic bath in detergent, deionized water, acetone, and ethanol, subsequently. After dried by nitrogen gas, substrates were transferred into a vacuum chamber for thermal deposition. MoO3 (10 nm, purchased from Aladdin China) was evaporated at the speed of 0.04 nm/sec. A blend CuPc:C60 layer (CuPc and C60 were purchased from Kintec and Nichem Taiwan, respectively) was deposited at the evaporation rate of 0.05 nm/sec in the organic chamber. Ag NPs were thermally evaporated at different stages of film formation of the active layer. Finally, electron-blocking layer BCP (10 nm, purchased from Kintec) and Ag cathode (Ag pellets were purchased from Kurt J. Lesker) were evaporated in sequence onto the organic active layer to complete the plasmonic solar cells. The evaporation rate and the final thickness of MoO3, organic active layer, and Ag NPs were controlled by in situ quartz monitors. All of the materials we utilized in this work were commercially available and used without further purification.

Characterization

The absorption spectra of Ag NPs embedded organic active films and plasmonic small-molecule solar cells were determined by the diffused reflection (R) and transmission (T) spectra utilizing a CCD spectrometer (Ocean Optics QE65000) and an integrating sphere. Current-voltage (J-V) curves of plasmonic small-molecule solar cells were measured using a Keithley 2635 SourceMeter and ABET AM1.5G solar simulator. The morphology of Ag NPs thermally deposited on the surface of organic active layers was characterized by LEO 1530 scanning electron microscope (SEM). Cross sectional SEM images of Ag NPs embedded small molecule solar cells were measured by Hitachi S4800 FEG SEM.

Theoretical model

The electrical properties of OSCs can be modeled by solving organic semiconductor equations involving Poisson, drift-diffusion and continuity equations45,46

graphic file with name srep08525-m6.jpg
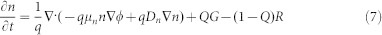graphic file with name srep08525-m7.jpg
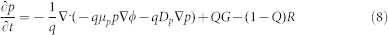graphic file with name srep08525-m8.jpg

where q is the electron charge, ϕ is the potential, and n and p are electron and hole densities, respectively. Moreover, μn and μp are the mobility of electrons and holes respectively. Furthermore, Dn and Dp are the diffusion coefficients of electrons and holes respectively, which are accessible by the Einstein relations and mobility. Jn = −qμnn∇ϕ + qDn∇n and Jp = −qμpp∇ϕ + qDp∇p are respectively electron and hole current densities, and G is the exciton generation rate. Here, the recombination rate R is taken as the Langevin bimolecular form47; and the field-dependent exciton dissociation probability Q is evaluated by the Onsager-Braun theory48,49.

The potential boundary condition at the electrodes is given by

graphic file with name srep08525-m9.jpg

where V is the applied bias voltage and Wm is the work function of the electrode. The electrodes are assumed to be ohmic contacts without injection barriers for understanding the influence of photocarrier transport paths on the electrical properties of solar cells, i.e.

graphic file with name srep08525-m10.jpg

where Nc and Nv are the effective density of states for bulk heterojunction active materials.

Author Contributions

W.E.I.S. and H.L.Z. contributed equally to the work. W.E.I.S. and L.C. conducted theoretical modeling. H.L.Z. fabricated and measured small-molecule solar cells. W.C.H.C. and W.C.C. planned and supervised the project.

Supplementary Material

Supplementary Information

Supplementary Information

srep08525-s1.pdf (1.7MB, pdf)

Acknowledgments

The authors acknowledge the support of the General Research Fund (grants: HKU711813 and HKU711612E), the National Natural Science Foundation of China (NSFC)/Research Grants Council (RGC) grant (N_HKU709/12) and Ministry of Education (MOE)/Research Grants Council (RGC) (M-HKU703/12) from RGC of Hong Kong Special Administrative Region, China. This project is also supported by Collaborated Research Fund (CUHK1/CRF/12G) of RGC and the UGC of Hong Kong (No. AoE/P-04/08), by The National Natural Science Foundation of China (No. 61201122), by Collaborative Research Fund (C7045-14E), by CAS-Croucher Funding (CAS14601), and in part by a Hong Kong UGC Special Equipment Grant (SEG HKU09).

References

  1. Maier S. A. Plasmonics: Fundamentals and Applications. Springer (2007). [Google Scholar]
  2. Catchpole K. R. & Polman A. Design principles for particle plasmon enhanced solar cells. Appl Phys Lett 93, 191113 (2008). [Google Scholar]
  3. Ferry V. E., Sweatlock L. A., Pacifici D. & Atwater H. A. Plasmonic Nanostructure Design for Efficient Light Coupling into Solar Cells. Nano Letters 8, 4391–4397 (2008). [DOI] [PubMed] [Google Scholar]
  4. Pala R. A. et al. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Advanced Materials 21, 3504–3509 (2009). [Google Scholar]
  5. Atwater H. A. & Polman A. Plasmonics for improved photovoltaic devices. Nature Materials 9, 205–213 (2010). [DOI] [PubMed] [Google Scholar]
  6. Li X. H. et al. Dual Plasmonic Nanostructures for High Performance Inverted Organic Solar Cells. Advanced Materials 24, 3046–3052 (2012). [DOI] [PubMed] [Google Scholar]
  7. Lu L. Y., Luo Z. Q., Xu T. & Yu L. P. Cooperative Plasmonic Effect of Ag and Au Nanoparticles on Enhancing Performance of Polymer Solar Cells. Nano Letters 13, 59–64 (2013). [DOI] [PubMed] [Google Scholar]
  8. Wang W. et al. Broadband Light Absorption Enhancement in Thin-Film Silicon Solar Cells. Nano Letters 10, 2012–2018 (2010). [DOI] [PubMed] [Google Scholar]
  9. Wu J. L. et al. Surface Plasmonic Effects of Metallic Nanoparticles on the Performance of Polymer Bulk Heterojunction Solar Cells. Acs Nano 5, 959–967 (2011). [DOI] [PubMed] [Google Scholar]
  10. Yang J. et al. Plasmonic Polymer Tandem Solar Cell. Acs Nano 5, 6210–6217 (2011). [DOI] [PubMed] [Google Scholar]
  11. Bai W. L. et al. Design of plasmonic back structures for efficiency enhancement of thin-film amorphous Si solar cells. Optics Letters 34, 3725–3727 (2009). [DOI] [PubMed] [Google Scholar]
  12. Gan Q. Q., Bartoli F. J. & Kafafi Z. H. Plasmonic-Enhanced Organic Photovoltaics: Breaking the 10% Efficiency Barrier. Advanced Materials 25, 2385–2396 (2013). [DOI] [PubMed] [Google Scholar]
  13. Wang Y. et al. Metamaterial-Plasmonic Absorber Structure for High Efficiency Amorphous Silicon Solar Cells. Nano Letters 12, 440–445 (2012). [DOI] [PubMed] [Google Scholar]
  14. Yang X. et al. High-Efficiency Polymer Solar Cells Achieved by Doping Plasmonic Metallic Nanoparticles into Dual Charge Selecting Interfacial Layers to Enhance Light Trapping. Advanced Energy Materials 3, 666–673 (2013). [Google Scholar]
  15. Callahan D. M., Munday J. N. & Atwater H. A. Solar Cell Light Trapping beyond the Ray Optic Limit. Nano Letters 12, 214–218 (2012). [DOI] [PubMed] [Google Scholar]
  16. Niv A. et al. Near-Field Electromagnetic Theory for Thin Solar Cells. Physical Review Letters 109, 138701 (2012). [DOI] [PubMed] [Google Scholar]
  17. Yu Z. F., Raman A. & Fan S. H. Fundamental limit of nanophotonic light trapping in solar cells. Proceedings of the National Academy of Sciences of the United States of America 107, 17491–17496 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Haug F. J. et al. Super-Lambertian photocurrent-generation in solar cells with periodically textured interfaces. Appl Phys Lett 103, 131108 (2013). [Google Scholar]
  19. Sha W. E. I., Choy W. C. H. & Chew W. C. Angular response of thin-film organic solar cells with periodic metal back nanostrips. Optics Letters 36, 478–480 (2011). [DOI] [PubMed] [Google Scholar]
  20. Sandhu S., Yu Z. F. & Fan S. H. Detailed Balance Analysis and Enhancement of Open-Circuit Voltage in Single-Nanowire Solar Cells. Nano Letters 14, 1011–1015 (2014). [DOI] [PubMed] [Google Scholar]
  21. Yu Z. F., Sandhu S. & Fan S. H. Efficiency above the Shockley-Queisser Limit by Using Nanophotonic Effects To Create Multiple Effective Bandgaps With a Single Semiconductor. Nano Letters 14, 66–70 (2014). [DOI] [PubMed] [Google Scholar]
  22. Lee J. Y. & Peumans P. The origin of enhanced optical absorption in solar cells with metal nanoparticles embedded in the active layer. Opt Express 18, 10078–10087 (2010). [DOI] [PubMed] [Google Scholar]
  23. Sha W. E. I., Choy W. C. H., Liu Y. G. & Chew W. C. Near-field multiple scattering effects of plasmonic nanospheres embedded into thin-film organic solar cells. Appl Phys Lett 99, 113304 (2011). [Google Scholar]
  24. Wang C. C. D. et al. Optical and electrical effects of gold nanoparticles in the active layer of polymer solar cells. Journal of Materials Chemistry 22, 1206–1211 (2012). [Google Scholar]
  25. Min C. J. et al. Enhancement of optical absorption in thin-film organic solar cells through the excitation of plasmonic modes in metallic gratings. Appl Phys Lett 96, 133302 (2010). [Google Scholar]
  26. Sha W. E. I., Li X. H. & Choy W. C. H. Breaking the Space Charge Limit in Organic Solar Cells by a Novel Plasmonic-Electrical Concept. Sci. Rep. 4, 6236 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Koster L. J. A., Smits E. C. P., Mihailetchi V. D. & Blom P. W. M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Physical Review B 72, 085205 (2005). [Google Scholar]
  28. Li X. F. et al. Bridging electromagnetic and carrier transport calculations for three-dimensional modelling of plasmonic solar cells. Opt Express 19, A888–A896 (2011). [DOI] [PubMed] [Google Scholar]
  29. Deceglie M. G., Ferry V. E., Alivisatos A. P. & Atwater H. A. Design of Nanostructured Solar Cells Using Coupled Optical and Electrical Modeling. Nano Letters 12, 2894–2900 (2012). [DOI] [PubMed] [Google Scholar]
  30. Sha W. E. I., Choy W. C. H. & Chew W. C. The roles of metallic rectangular-grating and planar anodes in the photocarrier generation and transport of organic solar cells. Appl Phys Lett 101, 223302 (2012). [Google Scholar]
  31. Sha W. E. I., Choy W. C. H., Wu Y. M. & Chew W. C. Optical and electrical study of organic solar cells with a 2D grating anode. Opt Express 20, 2572–2580 (2012). [DOI] [PubMed] [Google Scholar]
  32. Vervisch W. et al. Optical-electrical simulation of organic solar cells: Influence of light trapping by photonic crystal and ZnO spacer on electrical characteristics. J Appl Phys 111, 094506 (2012). [Google Scholar]
  33. Liu Y. C. et al. Balance between light trapping and charge carrier collection: Electro-photonic optimization of organic photovoltaics with ridge-patterned back electrodes. J Appl Phys 113, 244503 (2013). [Google Scholar]
  34. Li X. F. et al. Multi-dimensional modeling of solar cells with electromagnetic and carrier transport calculations. Progress in Photovoltaics 21, 109–120 (2013). [Google Scholar]
  35. Jiang W. J., Salvador M. & Dunham S. T. Combined three-dimensional electromagnetic and device modeling of surface plasmon-enhanced organic solar cells incorporating low aspect ratio silver nanoprisms. Appl Phys Lett 103, 183303 (2013). [Google Scholar]
  36. Brabec C. J. et al. Polymer-Fullerene Bulk-Heterojunction Solar Cells. Advanced Materials 22, 3839–3856 (2010). [DOI] [PubMed] [Google Scholar]
  37. Kotlarki J. D. & Blom P. W. M. Impact of unbalanced charge transport on the efficiency of normal and inverted solar cells. Appl Phys Lett 100, 013306 (2012). [Google Scholar]
  38. Peumans P., Yakimov A. & Forrest S. R. Small molecular weight organic thin-film photodetectors and solar cells. J Appl Phys 93, 3693–3723 (2003). [Google Scholar]
  39. Rand B. P., Xue J. G., Uchida S. & Forrest S. R. Mixed donor-acceptor molecular heterojunctions for photovoltaic applications. I. Material properties. J Appl Phys 98, 124902 (2005). [Google Scholar]
  40. Rand B. P., Peumans P. & Forrest S. R. Long-range absorption enhancement in organic tandem thin-film solar cells containing silver nanoclusters. J Appl Phys 96, 7519–7526 (2004). [Google Scholar]
  41. Sha W. E. I., Choy W. C. H. & Chew W. C. A comprehensive study for the plasmonic thin-film solar cell with periodic structure. Opt Express 18, 5993–6007 (2010). [DOI] [PubMed] [Google Scholar]
  42. Karatay D. U. et al. Performance limits of plasmon-enhanced organic photovoltaics. Appl Phys Lett 105, 033304 (2014). [Google Scholar]
  43. Nam Y. M., Huh J. & Jo W. H. A computational study on optimal design for organic tandem solar cells. Sol Energ Mat Sol C 95, 1095–1101 (2011). [Google Scholar]
  44. Kirkeminde A. et al. Surface-passivated plasmonic nano-pyramids for bulk heterojunction solar cell photocurrent enhancement. Nanoscale 4, 4421–4425 (2012). [DOI] [PubMed] [Google Scholar]
  45. Selberherr S. Analysis and Simulation of Semiconductor Devices. Springer (1984). [Google Scholar]
  46. Koster L. J. A., Smits E. C. P., Mihailetchi V. D. & Blom P. W. M. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Physical Review B 72 (2005). [Google Scholar]
  47. Langevin P. Recombinaison et mobilites des ions dans les gaz. Ann Chim Phys 28, 433–530 (1903). [Google Scholar]
  48. Onsager L. Initial recombination of ions. Phys Rev 54, 554–557 (1938). [Google Scholar]
  49. Braun C. L. Electric-field assisted dissociation of charge-transfer states as a mechanism of photocarrier production. Journal of Chemical Physics 80, 4157–4161 (1984). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep08525-s1.pdf (1.7MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES