Ocean fronts drive marine fishery production and biogeochemical cycling

Significance

Fronts in the ocean act as oases in a fluid desert that are not fully accounted for in climate or fisheries model projections. Fronts act to increase production by channeling nutrients through multiple trophic levels, including commercially important fishes and marine mammals, and enhance carbon export to the deep ocean. Fronts consequently have immense effects on the ocean, from base of the food chain up through the dinner table and mediation of global climate change. Here we show how fronts can be incorporated into current models, using a technique from fluid dynamics to improve both climate and fisheries models.

Abstract

Long-term changes in nutrient supply and primary production reportedly foreshadow substantial declines in global marine fishery production. These declines combined with current overfishing, habitat degradation, and pollution paint a grim picture for the future of marine fisheries and ecosystems. However, current models forecasting such declines do not account for the effects of ocean fronts as biogeochemical hotspots. Here we apply a fundamental technique from fluid dynamics to an ecosystem model to show how fronts increase total ecosystem biomass, explain fishery production, cause regime shifts, and contribute significantly to global biogeochemical budgets by channeling nutrients through alternate trophic pathways. We then illustrate how ocean fronts affect fishery abundance and yield, using long-term records of anchovy–sardine regimes and salmon abundances in the California Current. These results elucidate the fundamental importance of biophysical coupling as a driver of bottom–up vs. top–down regulation and high productivity in marine ecosystems.

Globally, marine primary production is considered to set the limits of fishery production (1), drive ecosystem functioning (2), and contribute substantially to biogeochemical cycles (3). Recent evidence of increased ocean temperatures (4, 5) and declines in global nutrient supply and primary production (6), combined with overfishing and other increasing human demands on the ocean (7–9), therefore raises significant concerns about fishery sustainability, ecosystem health, and maintaining global biogeochemical cycles (10). However, the degree of patchiness, instead of total biomass, may be the primary regulator of marine production and food web structure (11–16). Fronts in the ocean are boundaries between distinct water masses with sharp gradients in temperature or salinity (density) that can increase patchiness through flow convergence and, for density fronts, increase vertical mixing and nutrient supply (11, 17). Due to flow convergence at fronts, the spatiotemporal overlap of prey and predators can be immense, leading to a cascade of impacts across multiple scales from local prey size structure to global biogeochemical fluxes (11–13). However, the effects of fronts as fishery productivity and biogeochemical cycling hotspots have not been included in models that assess fisheries production and ecosystem health (18) or addressed at scales (tens to hundreds of kilometers) relevant to climate change (19).

Here we use an ecosystem model to explore why fronts appear to have a strong influence on marine fishery production and biogeochemical cycling. Existing ecosystem models currently account only for the mean concentration of predator and prey with relatively large grid cells (20). In a simple case of a single autotrophic prey (A) and a single heterotrophic predator (B) the governing equations are

$$\begin{array}{l}\frac{dA}{dt}={\mu }_{a}NA-gAB-m_{a}A\\ \frac{dB}{dt}=g{\mu }_{b}AB-m_{b}B.\end{array}$$ [1]

These equations describe the change in biomass of predator and prey relative to nutrient supply (N), intrinsic growth (μ), grazing (g), and mortality (m) rates with a reactive term, $g{\mu }_{z}AB$, coupling the two equations, and the mortality terms, $m_{a}A$ and $m_{b}B$, represent the contribution of the interaction to biogeochemical cycling.

In the ocean, concentrations of prey and predator are typically very low, and consequently, the production term in an ecosystem model will be even lower because it depends on the concentration of both (Fig. 1A). However, near fronts and other regions of sharp ocean gradients, the covariance of prey and predators is driven by (i) fluid dynamic processes that concentrate or disperse organisms (convergence/divergence, confluence/diffluence, mixing) and (ii) species-specific behaviors (11). Predator–prey covariance at fronts can be orders of magnitude higher than mean oceanic values (Fig. 1B and Table 1) and is not represented in current ecosystem or fisheries models. We used Reynolds decomposition, a technique used in fluid dynamics to describe turbulent flows, to represent the elevated covariance of prey and predators at fronts. Reynolds decomposition separates the variables of interest into mean and perturbation terms, which creates a closure problem (more unknowns than available equations) where new terms arise due to the covariance of variables. Modelers often use bulk properties to then estimate the magnitude of the covariance terms. However, the averaging in the ecosystem model is applied spatially instead of temporally, as commonly applied in fluid dynamics. In the simple ecosystem model above, the biomasses of prey and predator become $A=\langle A\rangle +A^{\prime }$ and $B=\langle B\rangle +B^{\prime }$, where $\langle \rangle$ indicates the spatial average (Fig. 1B). The decomposition results in an additional term, $\langle A^{\prime }{B}^{\prime }\rangle$, that represents the influence of the spatial covariance of prey and predator on the trophic dynamics of the ecosystem and imposes a similar closure problem to the dynamic equations.

Fig. 1.

Effects of spatial covariance between predators and prey. (A) Evenly dispersed condition currently assumed in models. (B) Highly aggregated condition representative of most ocean environments. (C) Magnitude of the effect of spatial covariance on species production.

Table 1.

${\zeta }_{AB}$ estimated from observations in available literature for multiple trophic interaction

Prey, A	Predator, B	$\langle A\rangle \langle B\rangle$	$\langle A^{\prime }{B}^{\prime }\rangle$	${\zeta }_{AB}$	Ref.
Phytoplankton	Copepods	1,680	21,000	13.5	(14)
Copepods	Micronekton	96	1,340	14.9	(14)
Micronekton	Dolphins	20	480	26.0	(14)
Micronekton	Tunas	0.094	3.24	35.5	(39)
Copepods	Whales	0.066	3.35	56.8	(40)
Salmon	Humans	0.088	7.62	87.5	(41)*

^*Humans are not included explicitly in the present model, but the estimate of ${\zeta }_{AB}$ illustrates the magnitude of the fishing effect on fish populations.

To resolve the ecosystem closure problem, we developed a parameterization for the new covariance term in an ecosystem model (Fig. 1C) that reasonably represents existing field observational data across trophic levels, using a range of front properties (convergence rate, density difference) and species-specific swimming speeds. We define a front as a sharp gradient in ocean temperature or salinity. Whereas density fronts can drive upwelling and be a direct source of nutrients, fronts with no density signature can also lead to aggregation and may be supplied nutrients indirectly through advection of remote sources. Here, we do not directly address the source of nutrients for frontal productivity, but only the aggregative effect of fronts, but a similar technique could be used to address increased nutrient flux at fronts. We used a frontal scaling factor for prey $\left({\zeta }_A=A^{\prime }/\langle A\rangle \right)$ and predator $\left({\zeta }_B=B^{\prime }/\langle B\rangle \right)$ and their covariance $\left({\zeta }_{AB}=1+\langle A^{\prime }{B}^{\prime }\rangle /\langle A\rangle \langle B\rangle \right)$ calculated as the ratio of the covariance term $\left(\langle A^{\prime }{B}^{\prime }\rangle \right)$ to the product of the mean biomass of prey and predator $\left(\langle A\rangle \langle B\rangle \right)$. The frontal scaling factor between two species describes the relative influence of fronts on production (grams per square meter per year) due to enhanced trophic interactions (Fig. 1C). As the strength and stability of a front increase, the production of a species increases due to increased prey availability. Similarly, as the ability of consumers to exploit the front increases, the production of that species increases. For secondary consumers (zooplankton), fronts produce up to a 5-fold increase in production. For larger, commercially important species, such as anchovies, sardines, and salmon, fronts can account for a 20- to 40-fold increase in production and even higher for top predators such as sharks and marine mammals (Fig. 1C), similar to observed values (Table 1).

To show how increased production associated with fronts may explain why (i) the ocean has historically supported immense biomass of higher trophic levels (21), (ii) many large predators migrate to highly active frontal regions such as the California Current (22), and (iii) aggregation plays such an important role in trophic regulation of pelagic ecosystems (2, 13), we incorporated this covariance parameterization into a hybridized size-spectral/higher trophic-level ecosystem model (20, 23). The model contains 40 spectrally distributed size classes each of phytoplankton and microzooplankton and 16 classes of higher trophic levels. We used published values for prey preferences, ingestion rates, and swimming speeds that have been shown to be realistic and stable in the Ecopath model (20). We ran the model for 100 y and discarded the first 25 y as model spin-up for analysis, using a 10-km × 10-km × 20-m deep surface layer ecosystem. Examples of low front (weak convergence, low persistence) and high front (strong convergence, high persistence) runs are given in Figs. S1 and S2. We then computed the mean and 95% confidence intervals of the annual production for several species (Fig. 2 A–C). At low levels of frontal activity, the model performs comparably to other ecosystem models for the California Current [mean production of salmon 0.31 tons (t)⋅km⁻² compared with 0.286 t⋅km⁻²; black dashed line in Fig. 2C] (20). When the covariance term is near zero or negative, the system is highly sensitive to nutrient supply and primary production as has been shown in previous studies (1, 2). However, at moderate and high levels of frontal activity, higher trophic-level production is up to 25-fold higher than in the low front case and relatively insensitive to nutrient supply levels. Ultimately fronts, by changing the susceptibility of prey to consumers, lead to changes in plankton community structure that translate into increased trophic complexity, higher diversity, and higher overall biomass (Fig. 2 and Table 2).

Fig. 2.

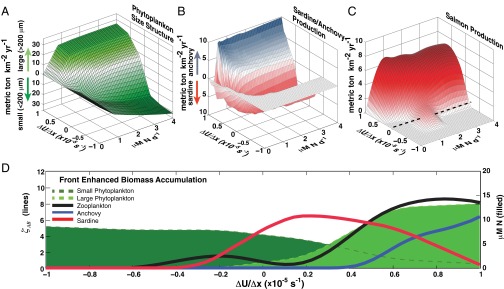
Front parameterized ecosystem model results. (A–C) Productivity vs. frontal strength $\left(\mathrm{\Delta }U/\mathrm{\Delta }x\right)$ and nutrient supply (μM N⋅d⁻¹) for (A) phytoplankton community structure, (B) ardine/anchovy regimes, and (C) salmon production. Dashed black line in C represents production in an ecosystem model of California Current (20). (D) Relationship of phytoplankton size structure, zooplankton abundance, and anchovy–sardine regimes to front parameter.

Table 2.

Stepwise linear model results for anchovy–sardine regimes and salmon abundance

Predictor index	Anchovy–sardine estimate	Predictor index	Salmon estimate
PREV	0.915	FPI	0.530
FSI	−0.436	PDO×FPI	−0.187
PREV×FSI	−0.542	PDO×OUT	−0.187

PREV, previous year anchovy–sardine ratio; FSI, frontal strength index; FPI, frontal probability index; PDO, Pacific Decadal Oscillation; OUT, Sacramento River outflow.

The change in zooplankton size spectra due to front dynamics offers an alternate mechanism for regime shifts from anchovy- to sardine-dominated systems beyond those related to physical, biochemical, and climate drivers (24–27). Weak fronts lead to higher levels of smaller phytoplankton and zooplankton (e.g., dinoflagellates and microzooplankton, Fig. 2 A and D), because top–down forcing of zooplankton on phytoplankton is weaker relative to bottom–up regulation and therefore to a sardine-dominated system (Fig. 2 B and D). Strong fronts lead to a size structure shift from smaller phytoplankton and microzooplankton to larger zooplankton and phytoplankton (e.g., diatoms), because zooplankton can exploit phytoplantkon patches, and eventually to an anchovy-dominated system (Fig. 2 B and D). Although other mechanisms of anchovy–sardine dynamics have been proposed related to coastal vs. wind-stress curl upwelling (24) and oxygen content of waters (27), results here suggest that prey preferences and variation in the feedback loop between bottom–up and top–down forcing due to fronts lead to similar patterns. It is likely that a combination of these mechanisms works in concert to drive observed fluctuations between anchovies and sardines.

To further illustrate the importance of fronts on ocean production, we show that anchovy–sardine regimes and salmon production are closely correlated with front strength and density, using 30+ y of satellite-derived front probability and strength estimates for the central California Current (Fig. 3). Front probability is defined as the probability of a front at a pixel and computed using a probabilistic method from satellite-derived sea surface temperature (28). The front probability index (FPI) is then the first empirical orthogonal function (EOF) of the front probability and represents the frequency of frontal occurrence on the continental shelf (Fig. 3A). The frontal strength index (FSI) is estimated as the distance from the mean to the mode in the sea surface temperature (SST) gradient and represents a skewed lognormal distribution toward high values. We used these two indexes, along with major climate indexes [Pacific Decadal Oscillation (PDO), El Nino Southern Oscillation (ENSO), North Pacific Gyre Oscillation (NPGO), freshwater outflow, and previous year abundance], to develop an integrated index (29) for each that was incorporated into a general linear model for both anchovy–sardine ratios and salmon abundance in the form of the Sacramento index (SI) (30). The best model was selected using the Akaike information criterion corrected for low sample size (AICc). The anchovy–sardine ratio best-fit model (lowest AICc) incorporated an interaction between FSI and previous year abundance (Fig. 3B and Table 2). The addition of the front strength term accurately predicts the two regime shifts in the past 30 y. For salmon, the best-fit model included interaction terms between the PDO and the FPI and Sacramento River outflow (OUT) with the strongest loading on the FPI (Fig. 3D and Table 2). FPI is the strongest predictor of the 2007–2010 salmon collapse for central California.

Fig. 3.

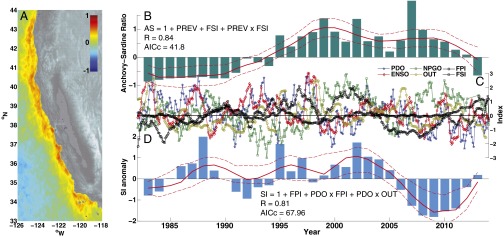
Effects of fronts on ecosystem dynamics. (A) Spatial distribution of the first EOF of front probability, the front probability index (FPI). (B) Anchovy–sardine ratio [AS, normalized (sardine biomass − anchovy biomass)/(combined biomass); − indicates anchovy dominated, + indicates sardine dominated] with best-fit model and predictors. (C) Climate and environmental indexes used in Generalized Linear Models for anchovy–sardine regimes and salmon abundance. (D) Salmon abundance (Sacramento index, SI) with best-fit model and predictors. Dashed red lines in B and C show 95% confidence intervals. Symbols in equations refer to the Pacific Decadal Oscillation (PDO), El Nino Southern Oscillation (ENSO), North Pacific Gyre Oscillation (NPGO), Sacramento River outflow (OUT), front probability index (FPI), front strength index (FSI), and previous year anchovy–sardine ratio (PREV).

Overall, fronts cover ∼4–10% of the area of the California Current during the spring–summer productive upwelling season as estimated from the remote sensing analysis for 1983–2011, yet have disproportionately large contributions to fisheries production (Table 3; 5% front level). Based on the model, fronts can account for more than 59% of salmon production and also a significant increase in the mean trophic level across the entire ecosystem (Table 3; 5% front level). A 1% increase in front probability leads to as much as a 21% increase in fishery production (change in salmon production from 0% to 1% fronts). Increased front activity (more, persistent fronts) consequently may counteract declines in primary production with respect to total ecosystem production (1, 6, 31) (Fig. 3C). These results also suggest that conservation of large marine predators and fishery management that incorporates persistent frontal features may allow for a comparatively rapid return to historical abundances of fishes and other top predators (18).

Table 3.

Fishery production and biogeochemical cycling at fronts

Species/dimension	Mean	At front	1%	5%	10%
Salmon, 103 kg⋅km−⋅y−1	0.23	6.16 (0.15)	0.29 (21)	0.53 (59)	0.77 (71)
Pelagic sharks, 103 kg⋅km−2⋅y−1	0.05	7.78 (0.38)	0.08 (95)	0.39 (99)	0.78 (99)
Baleen whales, 103 kg⋅km−2⋅y−1	0.08	9.34 (0.25)	0.09 (97)	0.47 (99)	0.94 (99)
Shannon diversity index, $H^{\prime }$	0.85	2.79	0.86	1.08	1.22
Simpson reciprocal index of diversity, $1/D$	3.36	9.98	3.67	4.92	6.24
Mean trophic level	1.67	3.33	1.68	2.77	3.18
N, 103 kg⋅km−2⋅y−1	0.11	1.65 (0.08)	0.13 (14)	0.19 (44)	0.26 (63)
C, 103 kg⋅km−2⋅y−1	11.66	148.10 (8.77)	13.02 (11)	18.47 (40)	25.29 (59)
P, 103 kg⋅km−2⋅y−1	1.88	28.29 (1.33)	2.14 (13)	3.20 (41)	4.52 (62)

Percentage columns refer to the amount (1%, 5%, 10%) of the ocean area classified as a front. Values in parentheses are 95% confidence intervals or the percentage of total production that occurs at fronts.

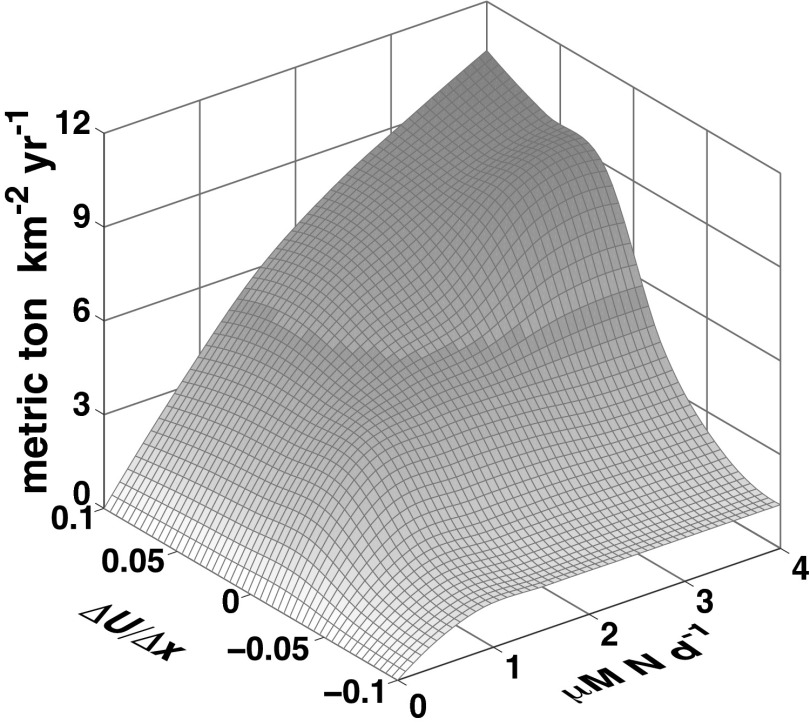
Recent evidence of enhanced vertical mixing along fronts has led to the suggestion that these oceanographic features play an important role in global biogeochemical cycles and consequently must be considered in global climate change models (19, 32, 33). Results from our front-parameterized ecosystem model suggest that in addition to vertical mixing, biogeochemical cycling and carbon export at fronts are also mediated and enhanced by biological processes (Fig. 4). Specifically, the enhanced transfer of nutrients, carbon, and energy to higher trophic levels at fronts increases biogeochemical fluxes to the deep ocean. The resulting carbon and nutrient fluxes at frontal zones are an order of magnitude higher than in surrounding regions (Fig. 4) through processes not currently accounted for in global-scale climate and ecosystem models (19). In the California Current, fronts that cover 5% of the ocean contribute more than 40% of the total biogeochemical fluxes (Table 2). Fronts may thus mediate global climate change impacts on our oceans, including ocean acidification, by vastly increasing carbon export to the ocean floor (Fig. 4) (32).

Fig. 4.

Rates of carbon export vs. frontal strength $\left(\mathrm{\Delta }U/\mathrm{\Delta }x\right)$ and nutrient supply (μM N⋅d⁻¹).

The effects of climate change on fisheries production and biogeochemical cycling will likely be determined by the counteractive effects of stratification (front development and persistence) and winds (front destruction) (33). Increasing sea surface temperatures and stratification related to climate change would likely increase frontal strength and persistence (33) and consequently increase fishery production, as suggested by the model. Conversely, increasing winds may limit front development and persistence and therefore decrease fishery production despite the effects of increased upwelling and nutrient flux (34). Evaluating how these climate change-related scenarios will interact to affect fisheries and ecosystem functioning is critical to our ability to predict and manage future change.

Because fronts are critical, dynamic features of the marine environment, influencing a range of processes from recruitment and fishery production to biogeochemical cycling (1, 18, 19), incorporation of frontal parameterizations into climate and ecosystem models is critical. Current Intergovernmental Panel on Climate Change class models do capture large-scale fronts and important features of primary production, but not the effects of smaller-scale fronts on higher trophic-level interactions and biogeochemical cycling. Reynolds decomposition provides an elegant, computationally inexpensive, easily parameterized mechanism to include fronts in both climate and ecosystem models that will likely improve both climate change and fishery forecasts (Fig. 1D). This formulation is also easily exported to other models that may better represent phytoplankton dynamics using self-selection criteria (35). Explicit data on the spatial covariance of prey and predators due to fronts will be needed to improve the parameterizations used in this study, and novel technological developments in video and acoustic imaging and dynamical systems analysis provide an excellent opportunity to acquire these data across a wide range of oceanographic conditions and trophic levels (14, 36, 37).

Materials and Methods

The Model.

This study used a hybridized size-spectral higher trophic-level ecosystem model with nitrogen as the common currency. The hybridization occurs between a size-spectral model (23) and a mass balance model adapted from Ecopath (20). The model solves equations for the conservation of nitrogen across i size classes of phytoplankton, P; j size classes of microzooplankton, Z; and k higher trophic level classes, H:

$$\begin{array}{l}\frac{dN}{dt}=S-{\displaystyle \sum _i{\mu }_i^P\frac{N}{k_s+N}{P}_i+\left(1-\epsilon -f_{eg}\right)}{\displaystyle \sum _j{\displaystyle \sum _i\frac{{\mathit{\Phi }}_{ij}{P}_i}{K_s+{\displaystyle {\sum }_i{\mathit{\Phi }}_{ij}{P}_i}}{Z}_j}}\\ +\hspace{0.17em}{r}_p{\displaystyle \sum _i{m}_p{P}_i}+r_z{\displaystyle \sum _j{m}_z{Z}_j}+r_h{\displaystyle \sum _k{m}_z{H}_k}\end{array}$$

$$\frac{d{P}_i}{dt}={\mu }_i^P\frac{N}{k_s+N}{P}_i-{\displaystyle \sum _j\frac{{\mathit{\Phi }}_{ij}{P}_i}{K_s+{\displaystyle {\sum }_j{\mathit{\Phi }}_{ij}{P}_i}}{Z}_j}-m_p{P}_i$$

$$\frac{d{Z}_j}{dt}={\mu }_j^Z{\displaystyle \sum _i\frac{{\mathit{\Phi }}_{ij}{P}_i}{K_s+{\displaystyle {\sum }_i{\mathit{\Phi }}_{ij}{P}_i}}{Z}_j}-{\displaystyle \sum _k\frac{{\mathit{\Phi }}_{jk}{Z}_j}{K_s+{\displaystyle {\sum }_j{\mathit{\Phi }}_{jk}{Z}_j}}{H}_k}-m_z{Z}_j$$

$$\begin{array}{l}\frac{d{H}_{k_1}}{dt}={\mu }_{k_1}^H{\displaystyle \sum _j\frac{{\mathit{\Phi }}_{j{k}_1}{Z}_j}{K_H+{\displaystyle {\sum }_j{\mathit{\Phi }}_{j{k}_1}{Z}_j}}{H}_{k_1}}+{\mu }_{k_1}^H{\displaystyle \sum _{k_2}\frac{{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}{K_H+{\displaystyle {\sum }_{k_2}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}}{H}_{k_1}}\\ -{\displaystyle \sum _{k_1}\frac{{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_1}}{K_H+{\displaystyle {\sum }_{k_1}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_1}}}{H}_{k_2}}-m_{k1}^H{\displaystyle \sum _{k1}{H}_{k1}}.\end{array}$$ [2]

Table S1 provides a list and definitions of all terms. The model equations are then solved at each time step, using a fourth-order Runge–Kutta numerical solver. In the current study, 14 size classes of higher trophic levels are used and given with prey preferences in Table S2. Predation by microzooplankton and higher trophic levels is either done using an allometric size distribution or specified directly. Grazing on phytoplankton and microzooplantkon is estimated using an allometric distribution formulation and a prey size variability parameter (23).

To account for the effects of predator–prey covariance, Reynolds decomposition is performed on the set of Eq. 2, yielding an additional growth term for each class interaction. This term is ultimately folded into the existing growth term. An example of this formulation for the higher trophic level Eq. 2 is

$$\begin{array}{c}\frac{d{H}_{k_1}}{dt}={\mu }_{k_1}^H{\displaystyle \sum _j\frac{{\mathit{\Phi }}_{j{k}_1}}{K_H+{\displaystyle {\sum }_j{\mathit{\Phi }}_{j{k}_1}{Z}_j}}\left(Z_j{H}_{k_1}+\langle {Z^{\prime }}_j{H^{\prime }}_{k_1}\rangle \right)}\\ +\hspace{0.17em}{\mu }_{k_1}^H{\displaystyle \sum _{k}2\frac{{\mathit{\Phi }}_{k_1{k}_2}}{K_H+{\displaystyle {\sum }_{k_2}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}}\left(H_{k_2}{H}_{k_1}+\langle {H^{\prime }}_{k_2}{H^{\prime }}_{k_1}\rangle \right)}\\ -\hspace{0.17em}{\displaystyle \sum _{k_1}\frac{{\mathit{\Phi }}_{k_1{k}_2}}{K_H+{\displaystyle {\sum }_{k_1}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}}\left(H_{k_2}{H}_{k_1}+\langle {H^{\prime }}_{k_2}{H^{\prime }}_{k_1}\rangle \right)}-m_{k1}^H{\displaystyle \sum _{k1}{H}_{k1}}\end{array}$$ [3]

$$\begin{array}{c}\frac{d{H}_{k_1}}{dt}={\mu }_{k_1}^H{\displaystyle \sum _j\frac{{\zeta }_{j{k}_1}{\mathit{\Phi }}_{j{k}_1}}{K_H+{\displaystyle {\sum }_j{\mathit{\Phi }}_{j{k}_1}{P}_i}}\left(Z_j{H}_{k_1}\right)}\\ +\hspace{0.17em}{\mu }_{k_1}^H{\displaystyle \sum _{k_2}\frac{{\zeta }_{k_1{k}_2}{\mathit{\Phi }}_{k_1{k}_2}}{K_H+{\displaystyle {\sum }_{k_2}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}}\left(H_{k_2}{H}_{k_1}\right)}\\ -\hspace{0.17em}{\displaystyle \sum _{k_1}\frac{{\zeta }_{k_1{k}_2}{\mathit{\Phi }}_{k_1{k}_2}}{K_H+{\displaystyle {\sum }_{k_1}{\mathit{\Phi }}_{k_1{k}_2}{H}_{k_2}}}\left(H_{k_2}{H}_{k_1}\right)}-m_{k1}^H{\displaystyle \sum _{k1}{H}_{k1}},\end{array}$$ [4]

where

$${\zeta }_{AB}=1+\frac{\langle A^{\prime }{B}^{\prime }\rangle }{\langle A\rangle \langle B\rangle }$$ [5]

is the covariance factor of prey, A, and predator, B. The covariance factor, ${\zeta }_{AB}$, can then be estimated from frontal convergence rate (or change in velocity across a grid cell) and organism swimming speeds as

$${\zeta }_{AB}={\zeta }_A{\zeta }_B=\left(\frac{L_x}{L_x-\left(1/L_x\right){\int }_T{\int }_{Lx}\left(du+w_A\right)dxdt}\right)\left(\frac{L_x}{L_x-\left(1/L_x\right){\int }_T{\int }_{Lx}\left(du+w_B\right)dxdt}\right).$$ [6]

Eq. 6 represents the aggregation (dispersion) of prey and predators due to convergent/confluent (divergent/diffluent, $du$) flow and swimming/sensory capabilities ($w_A$, $w_B$). The first part of [6] represents the aggregative effect of flow and behavior on prey (A). The term is the ratio of the cross-frontal distance $\left(L_x\right)$ to the reduced frontal region due to compression of gradients and behavioral aggregation, $L_x-\left(1/L_x\right){\displaystyle {\int }_T{\displaystyle {\int }_{L_x}\left(du+w_A\right)dxdt}}$. The second part of [6] represents a similar quantity for the predator. In this formulation, we assume that prey or predators will swim toward a region of interest and that the value of w is positive and represents an animal’s ability to search the frontal region. Swimming speeds ($w_A$, $w_B$) are incorporated to factor in the ability of prey or predator to find a region of interest. Swimming speeds for model runs were obtained from available literature or assumed to be one body length per second. This term represents the aggregation (dispersion) of prey and predators due to convergent (divergent) flow and swimming/sensory capabilities within a grid cell (10 km²). Aggregation (dispersion) acts to increase (decrease) the covariance of predator and prey as in Fig. 2A. To estimate ${\zeta }_{AB}$ in the field, we used available observations to compute the mean and perturbation abundance for each trophic interaction based on information such as water depth, area from map or that estimated from the acoustic device used, and the organism distributions/densities. For studies that reported the number of individuals for higher trophic levels, we assumed a mean mass per individual of 100 g for micronekton, 10–20 kg for large pelagic predatory fishes (salmon, tunas), 40 kg for dolphins, and 36,000 kg (40 t) for whales. Acoustic estimates were used to compute mean and perturbation estimates, assuming a linear correlation between biomass and backscatter or echo intensity. We then computed the mean and perturbation concentration in the study region to estimate ${\zeta }_{AB}$.

Biogeochemical fluxes were estimated from the sum of the mortality terms of each class and some fraction of the grazing that did not go into growth. The fraction was estimated as an allometric function based on (i) lower ecotrophic efficiency at higher trophic levels and (ii) increased vertical transport of larger fecal matter from larger species. Percentages of export ranged from 1% for phytoplankton to 10% for highest trophic levels following an inverse of the recycling rates. These percentages potentially underestimate total biogeochemical cycling, but provide a reasonable first-order estimate. Rates of carbon and phosphorus cycling were estimated from the Redfield ratio across all trophic levels in a similar fashion to that for annual production rates for model species.

Sensitivity analyses were conducted over a range of convergence (divergence, −0.1 s⁻¹ to 0.1 s⁻¹) and nutrient supply rates (0–4 μM N⋅d⁻¹). Nutrient supply covers the full range of field observations with 4 μM N⋅d⁻¹ being at the high end of intense upwelling. Typical upwelling systems experience nutrient fluxes of 1–2 μM N⋅d⁻¹ during active upwelling (Fig. S1) (20, 23). The range of convergence rates covers values typically observed in the field from strong convergent fronts to divergent regions of intense upwelling. All model runs were for a period of 100 y. Most of the runs (578 of 625) achieved statistical equilibrium, defined as the point where the mean and variance did not change within the 95% confidence interval of the estimates for all constituents within a 5-y moving window, within 10 y. However, some took as many as 30 y for transient dynamics to diminish. Therefore, the first 25 y of each model run were discarded as initial spin-up. Statistical equilibrium of production terms typically was reached within 5 y. Numerical stability tests were completed and resolved before experimental model runs. We did not perform rigorous sensitivity analyses on other model parameters because (i) this has been done extensively in other studies and these parameters were shown to be stable (20) and (ii) these parameters were not varied within the model for the results presented here. Model runs for a range of biological parameters yielded similar results for the effects of fronts and nutrient supply albeit with different trophic pathways as would be expected. However, the results for trophic complexity, biodiversity, and production at higher trophic levels were found to be robust to these parameter changes. All code was implemented in MatLab and is available online on the author’s website.

Model Results.

Time series of model results for a low front and high front run are shown in Figs. S1 and S2, respectively. We define the low front run as low persistence and weak or no convergence/confluence (0 m⋅s⁻¹) and the high front run as persistent fronts with moderate to strong convergence/confluence rates (0.05 m⋅s⁻¹). Phytoplankton and microzooplankton biomasses are reported in micromolar N. Higher trophic-level biomass was converted from nitrogen, using estimates of %N in tissue around 7%. Annual production rates were estimated directly from model runs for Fig. 2 by integrating the equilibrium production over the final 75 y of the model run and dividing by the number of years in the run (20). We computed the Shannon diversity index ($H^{\prime }={\displaystyle {\sum }_1^N{p}_i\text{log}\hspace{0.17em}{p}_i}$) and the Simpson reciprocal index of diversity ($1/D={\displaystyle {\sum }_1^N{p}_i^2}$), where $p_i$ is the proportion of biomass (in grams C) in each group and N is the number of groups. We also calculated the weighted mean trophic level for no front and high front conditions. For mean trophic level, we assigned trophic level based on the maximum number of links required to go from a species group to nutrients and then computed the weighted mean trophic level as

$$T=\frac{1}{N}{\displaystyle \sum _1^N{p}_i{T}_L}.$$ [7]

Observations.

Time series of front probability and chlorophyll concentration were computed from satellite remote-sensing data obtained from coastwatch.pfeg.noaa.gov. Front probability was computed from monthly composite sea surface temperature images (Pathfinder Day and Night, 4 km resolution, 1983–2003, and MODIS 0.0125° resolution since 2003) over the region from 31° N to 46° N and extending 200 km from the coast, using an adaptive median filter and a frontal probabilistic technique where spatial gradients in SST are fitted to a lognormal distribution based on the monthly mean SST gradient, and the tail of the distribution above 0.1 °C⋅km⁻¹ is integrated to obtain a monthly front probability (28). The front probability index is then the first EOF of the front probability times series, accounts for 12% of the total variance, and represents total frontal activity over the continental shelf (Fig. 1A). The FSI is calculated as the distance between the mode of the lognormal distribution of the SST gradient and the mean SST gradient for each month. Monthly composite chlorophyll data from the MODIS Aqua and SeaWifs satellite data product (science quality, 0.04167° resolution, 2002–2011 and 1997–2006, respectively) were acquired for the same region. Overlapping years were closely correlated and an average of the two data points was used during this period to blend the products and increase temporal coverage. All environmental data were smoothed using a weighted 12-mo moving average filter and then interpolated to 1-y data to match the fisheries data that are recorded annually.

Salmon production was estimated using the Sacramento index (30, 38), which is the total sum of catch and escapement for central California chinook salmon. We chose this metric because it is used as an indicator of salmon abundance by the Pacific Fishery Management Council and the California Department of Fish and Wildlife to set fishery quotas for the California salmon fishery. Anchovy and sardine landings data were obtained from the California Department of Fish and Game. The anchovy–sardine index was computed as the normalized difference between sardine and anchovy abundance divided by total biomass for each year.

To develop the first-order autoregressize (AR-1) predictors for each index (29), we integrated

$$\frac{d\beta \left(t\right)}{dt}=\mathrm{\Pi }\left(t\right)-\frac{\beta \left(t\right)}{{\tau }_{\beta }}$$ [8]

for each index, $\mathrm{\Pi }$, where $\mathrm{\Pi }$ is the PDO, ENSO, NPGO, FPI, or FSI. ${\tau }_{\beta }$ was set to 4 y for anchovies and sardines and to 2 y for salmon to represent the ocean residency period. We then incorporated each predictor into a stepwise general linear model. The Akaike information criterion corrected for small sample sizes was used to select the best-fit model,

$$\text{AICc}=2k-2ln\left(L\right)+\frac{2k\left(k+1\right)}{\left(n+k+1\right)},$$ [9]

where k is the number of parameters, L is the maximum likelihood, and n is the number of samples. All analyses and correlations were performed in Matlab.