ALADYN – a spatially explicit, allelic model for simulating adaptive dynamics

Abstract

ALADYN is a freely available cross-platform C++ modeling framework for stochastic simulation of joint allelic and demographic dynamics of spatially-structured populations. Juvenile survival is linked to the degree of match between an individual’s phenotype and the local phenotypic optimum. There is considerable flexibility provided for the demography of the considered species and the genetic architecture of the traits under selection. ALADYN facilitates the investigation of adaptive processes to spatially and/or temporally changing conditions and the resulting niche and range dynamics. To our knowledge ALADYN is so far the only model that allows a continuous resolution of individuals’ locations in a spatially explicit landscape together with the associated patterns of selection.

It has long been recognized that the dynamics of populations and alleles are tightly coupled: shifts in allele frequencies affecting fitness-relevant traits entail responses in demographic rates and population growth (Lewontin 1974). Changes in population size, in turn, often feed back on genetic processes. In recent years, there has been an acceleration of interest in the coupling of ecological and evolutionary dynamics and a body of theory on these eco-evolutionary dynamics is fast developing. This advance in eco-evolutionary theory has begun to reveal some key features of adaptive processes and their importance across a range of topics including evolutionary rescue, invasive spread and niche and range dynamics in general (e.g. Kuparinen and Schurr 2007, Bridle et al. 2010, North et al. 2010, Holt and Barfield 2011, Bocedi et al. 2013, Henry et al. 2013, Schiffers et al. 2013, Bocedi et al. 2014, Bourne et al. 2014).

Here, we present the modeling framework ALADYN (ALlelic Adaptive DYNamics). Aladyn is a forwards-intime simulator. Unlike backwards-in-time approaches it explicitly simulates the life-cycle of individuals and allows the monitoring of changes of the genetic structure of populations over time. In contrast to most existing population genetics software (these include for example cdpop (Landguth and Cushman, 2010), kernelpop (Strand and Niehaus, 2007), Nemo (Guillaume and Rougemont 2006), QuantiNemo (Neuenschwander et al. 2008), Pedagog (Coombs 2010), Splatche (Currat et al. 2004) and others), ALADYN allows one to describe the location and dispersal of individuals in continuous space as well as associated patters of selection (see Table 1 for a comparison of several softwares, for a more comprehensive overview see Hoban et al. 2012). The continuous resolution of individuals’ dispersal makes the framework especially well suited for studies on population range dynamics. It is possible to simulate two different traits, one coding for the level of adaptation to a spatially variable environmental condition (e.g. edaphic characteristics), the other one coding for a temporally (and spatially) variable condition (e.g. climate). Moreover, the source-code is freely available under the GNU general public license implemented as a C++ console model. The code supports parameterization of the compiled model from the command line, which enables an easy handling on computer clusters with batch files. Several extensions of the model are planned for the coming years. At the same time, we also hope that the release of the software will stimulate further development by the scientific community.

Table 1.

Comparison of selected population genetic software: a) The simulation approach taken, either forwards-in-time or backwards-in-time; b) units of the simulation (individuals or populations) for which x/y-coordinates are modeled and whether the resolution is continuous or on a lattice; c) whether selection of abiotic and/or biotic environment for specific phenotypes is allowed; d) the approach taken to model dispersal. See Hoban et al. (2012) for a more comprehensive overview.

	a) backward/forward	b) x/y - coordinates	c) Selection allowed	d) dispersal
Aladyn	forward	For individuals, continuous resolution	yes	Stage dependent dispersal kernel
cdpop	forward	For individuals/populations, on the lattice	yes	Stepping stone with isolation by distance, sex-specific migration rate and influenced by environmental factors
Kernelpop	forward	For individuals, on the lattice	no	Dispersal kernel
Nemo	forward	For populations on the lattice	yes	Stepping stone with isolation by distance, sex-specific migration rate
Pedagog	forward	-	yes	Age and density dependent, sex-specific migration rate
QuantiNemo	forward	For populations on the lattice	yes	Density dependent, stepping stone, sex-specific migration rate
Splatche	Forward and backward	For populations on the lattice	no	Stepping stone model, migration influenced by environmental factors

Basic functions

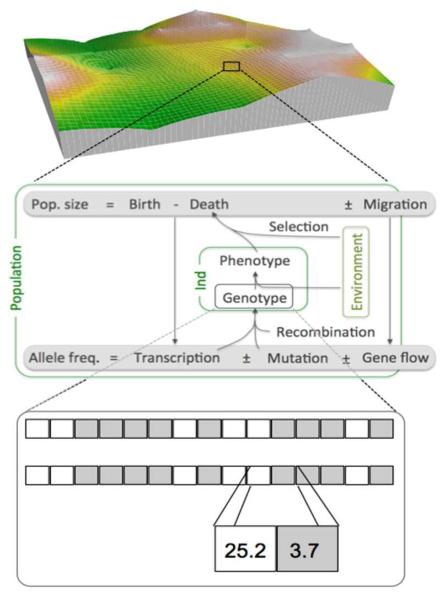
ALADYN models the spatio-temporal dynamics of populations and the underlying genetic processes of an annual, hermaphroditic species (Fig. 1). Individuals are diploid, carrying two copies of a chromosome with a number of loci L, coding for an individual’s level of adaptation to habitat conditions. Alleles are described by continuous values and are additive within and between loci, i.e. neither epistatic nor pleiotropic effects are currently considered. An individual’s phenotype is directly determined by its genotype, that is, heritability is assumed to be 1 and there are no environmental effects.

Figure 1.

Structure of the model. Top: Population dynamics take place on a spatially explicit landscape, here for example with a fractal structure of habitat conditions. Middle: Dynamics are followed on the level of both demographic and genetic processes. Recombination and mutation take place during reproduction, the interaction of resulting phenotypes and the environment affect mortality rates and dispersal and migration affect gene flow. Bottom: Individuals carry two copies of a number of loci, which might code for two different traits (indicated by white and grey squares). Allelic values are continuous and are additive within and between loci.

Population dynamics take place within a continuous region of X by Y grid cells. Edges are joined to form either a cylinder (for gradient landscapes) or a torus (for fractal or patchy landscapes). Single cells are characterized by one or two variables reflecting habitat conditions. The distribution of these values can follow gradients with adjustable slope, patchy range borders or fractal landscapes. Each grid cell can support several individuals, the maximum number given by the local carrying capacity K, which is assumed constant across the region. Apart from being situated in a certain cell, individuals are also assigned continuous x/y-coordinates.

Within each generation, the following processes are simulated in sequential order: (1) reproduction with mutation, recombination, gamete dispersal and subsequent death of the parental generation, (2) dispersal of the offspring, (3) selection in the form of density-independent, hard selection, acting on the survival probabilities of the juveniles for one of the environmental variables and hard or soft selection for the other one and (4) density-dependent mortality.

1. Reproduction

All individuals can potentially bear offspring. The number of ovules produced by each individual is drawn from a Poisson distribution with average R. The mating can be fully outcrossing or include selfing, which might be density dependent. Whether, and by which mating partner, single ovules are fertilized is modeled stochastically with the probabilities of fertilization derived from between-individual distances and the shape of the gamete dispersal kernel (see below). Gametes are composed by duplicating parental alleles, one of each homologous pair being chosen randomly, assuming no linkage between loci. Alleles mutate with a probability of μ. The mutational effect, i.e. the amount by which the allelic value is changed, is drawn from a zero-mean normal distribution with variance α².

2. Dispersal

There are two phases of dispersal in each generation cycle: gamete dispersal and offspring dispersal. Both are characterized by lognormal, isotropic dispersal kernels (see e.g. Greene et al. 2004) with an average distance of d_g for gamete dispersal and d_o for offspring dispersal. Offspring dispersal is simulated explicitly: dispersal distance and direction are determined stochastically with probabilities following the shape of the dispersal kernel. The offspring is positioned at the resulting x/y-coordinates, respecting boundary conditions. Individuals falling off the cylinder are excluded from subsequent simulation dynamics. To gain sufficient computational efficiency, gamete dispersal is simulated in a simplified way according to the following algorithm: For each ovule, first, the grid cell from which the mating partner is drawn is determined, by stochastically choosing x/y-coordinates in the neighborhood of the focal individual, following the gamete dispersal kernel. The mating partner is then randomly drawn from all individuals inhabiting the respective grid cell. In case an empty grid cell is chosen in the first place, the procedure is repeated up to 99 times. If all trials are unsuccessful, the ovule remains unfertilized. To test for undesirable effects of this simplification, we also developed an implementation of gamete dispersal that is more precise in the sense of linking fertilization probability to the exact distance between individuals. Comparison between the two approaches showed that there are no obvious differences at the level of evolutionary or demographic dynamics.

3. Selection

Selection acts on population demography by modulating juvenile survival probability. Individual survival probability W is a function of the difference between the individual’s phenotype z and the optimal phenotype under the local environmental conditions θ(x,y), which may vary with spatial position x,y. This function follows a normal distribution with maximum 1 and variance ω²:

$$W\left(\mathrm{z}\right)=\exp \left[-\frac{{(z-\theta )}^2}{2{\omega }^2}\right]$$

ω² can be interpreted as the selection strength of the environment on the individuals or alternatively as the niche breadth of the species. In case fitness is determined by two traits, overall survival probability W is calculated as the product of survival probability related to climate W_C and survival probability related to the local environment W_E.

4. Density-dependent mortality

We assume the local population regulation occurs following selection, acting on the survivors in a grid cell. We assume a simple ceiling form of density dependence: whenever the number of individuals N within a grid cell exceeds its carrying capacity K, all N resident individuals are subject to density-dependent mortality with probability of mortality equaling 1- K/N.

Sample usage

4. An example for the usage of the model can be found in Schiffers et al. (2013). Here, the effect of local adaptation to a spatially variable environmental condition on the potential for evolutionary rescue during climate change was tested. Habitat conditions were assumed to follow a fractal pattern and climate changed gradually during a period of 100 generations following an earlier stable phase. Depending on the amount of habitat heterogeneity and offspring and gamete dispersal distances, adaptation to local conditions could significantly hamper evolutionary rescue or lead to only partial rescue of the population.

This example can be easily recreated with the material provided in the downloadable files. The only requirements are a C++ compiler and the program ‘make’. A manual (‘Readme.pdf’) explains the installation of these programs, the possible values of each argument in the model and the use of the command line to start the simulation runs. A makefile (‘Make’) controls the compilation of the code. After compilation, the call ‘./aladyn – h’ prints a list of all parameters that can be controlled via the command line. Moreover, a batch file is included (‘batch.sh’) that enables to directly start model runs from the command line without manual parameterization or compilation. It returns results of exemplary scenarios of the above-described study.

Output

Several output files are generated and saved by default in the directory ‘results’. Using batch files, it is easily possible to automatically create a single output directory for each specific parameter combination. The chosen parameter values for the respective scenario are reported in the file ‘parameters.csv’. The file‘landscape.csv’ contains the values for the local habitat conditions in each grid cell allowing a visual control of the landscape structure. The file ‘dynamics.csv’ logs, for each generation and replicate, the actual climate, the average fitness of all individuals with respect to climate, the variance in that fitness, the average fitness of all individuals with respect to environment with its variance, the average overall fitness with variance and the population size.

Finally, the files ‘cpheno.csv’ and ‘epheno.csv’ record the climatic and environmental phenotypes of all individuals for each generation. With some basic coding knowledge output files can be easily adapted to the specific needs of a study.