The Role of Preload and Leakage Correction in Gadolinium-Based Cerebral Blood Volume Estimation Determined by Comparison with MION as a Criterion Standard

Abstract

BACKGROUND AND PURPOSE:

Contrast extravasation in DSC-MRI potentiates inaccurate and imprecise estimates of glioma rCBV. We tested assertions that preload and postprocessing algorithms minimize this error by comparing Gd-rCBV using permutations of these 2 techniques with criterion standard rCBV using MION, an intravascular agent.

MATERIALS AND METHODS:

We imaged 7 Fisher rats with 9L gliosarcomas, by using 3T gradient-echo DSC-MRI with MION (2.0 mg Fe/kg) and staged injection of Gd-diethylene triamine pentaacetic acid: a 0.1-mmol/kg bolus provided no preload (P−) data and served as preload (P+) for a subsequent 0.2-mmol/kg bolus. We computed MION-rCBV (steady-state ΔR2*, tumor versus normal brain) and Gd-rCBV ΔR2* [t] integration) without (C−) and with (C+) postprocessing correction, thereby testing 4 correction permutations: P−C−, P−C+, P+C−, and P+C+. We tested whether each permutation reduced bias and variance of the Gd/MION rCBV differences by using generalized estimating equations and Fmax statistics (P < .05 significant).

RESULTS:

Gd-rCBV progressively better approximated MION-rCBV with increasing leakage correction. There was no statistically significant bias for the mean percentage deviation of Gd-rCBV from MION-rCBV for any correction permutation, but there was significantly reduced variance by using P+C− (22-fold), P−C+ (32-fold), and P+C+ (267-fold) compared with P−C−. P+C+ provided significant additional variance reduction compared with P+C− (12-fold) and P−C+ (8-fold). Linear regression of Gd-rCBV versus MION-rCBV revealed P+C+ to have the closest slope and intercept compared with the ideal, substantially better than P+C−.

CONCLUSIONS:

Preload and postprocessing correction significantly reduced the variance of Gd-rCBV estimates, and bias reduction approached significance. Postprocessing correction provide significant benefit beyond preload alone.

When confined to the intravascular space, paramagnetic contrast agents (eg, Gd-diethylene triamine pentaacetic acid) produce T2*-weighted signal intensity loss in the extravascular space, and DSC-MRI rCBV maps are computed by integrating the transverse relaxivity changes (ΔR2*) that occur dynamically over a first-pass injection.^1,2 There has been extensive clinical application of rCBV mapping during the past decade to the imaging of gliomas, including grading^3,4,5,6–7 and prognosis^8–10 at initial diagnosis; targeting biopsy^11,12 and providing intraoperative guidance;¹³ predicting low-grade to high-grade transformation;^14,15 and monitoring response to treatment,^16,17 including the distinction of tumor recurrence and posttreatment-related enhancement due to radiation necrosis¹⁸ and pseudoprogression.^19,20

In enhancing high-grade gliomas with substantial blood-brain barrier breakdown, typical Gd-based contrast agents extravasate, reducing T2* DSC-MRI signal intensity loss by signal intensity increase in regions where T1 effects are significant.^21,22 In such instances, rCBV will be underestimated and may even be “negative” in highly permeable lesions with rapid contrast extravasation where T1 effects overwhelm the intravascular T2* effects, severely blunting or even eliminating any perceived first-pass susceptibility bolus effect. Conversely, T2* effects due to susceptibility differences between extravasated contrast in the extracellular space and tumor cells can increase ΔR2*.²³ Due to this complex interplay of T1- and T2-weighted effects, contrast agent leakage can lead to either underestimation or overestimation of rCBV in enhancing tumors unless specifically corrected for.^23–25 Because clinical decisions for the applications mentioned above increasingly rely on rCBV quantitation for analysis of temporal trends and absolute thresholds, it is paramount that the DSC technique be optimized to prevent or correct these inaccuracies and ensure that rCBV measurements are accurate and precise.

Whereas early studies neglected leakage-effect contamination,²⁶ more recent studies have acknowledged this pitfall, with most correction schemes focusing on the T1 effects. Generally speaking, T1 leakage-correction schemes can be broadly classified into 3 groups (Table 1): image acquisition (low flip angle, long TE gradient-echo;^11,16 double-echo T2*-weighted^27,28), contrast agent selection (loading dose of contrast agent before DSC-MRI to minimize subsequent changes in T1;^3,21 intravascular agents such as ferumoxytol²⁰), and postprocessing techniques (parametric modeling such as γ-variate fit;^1,4 baseline subtraction;²⁹ limited integration;³⁰ and mathematic leakage-correction models^{21–23,25,31,32}).

Table 1:

Techniques for reducing T1 leakage effects

Category	Technique	Examples
Image acquisition	Low flip angle, long TE, double-echo T2*-weighted	Knopp et al,11 Cha et al38 Vonken et al,27 Uematsu et al28
Contrast agent	Use of loading dosesa	Donahue et al,3 Schmainda et al,21 Simonsen et al35
	Intravascular agents (eg, ferumoxytol)	Gahramanov et al20
Postprocessing	Linear fit + leakage modela	Weisskoff et al,31 Schmainda et al21 Boxerman et al22
	γ-Variate fit	Law et al4
	Limited integration	Wong et al30
	Baseline subtraction	Wetzel et al29

^aDesignates the 2 techniques investigated in this article.

A robust mathematic leakage-correction model was proposed by Weisskoff et al,^21,22,31 which uses linear fitting to determine the voxelwise deviation from nonleaky reference tissue and, by removing the leakage term, generates corrected rCBV values and first-order estimates of vascular permeability. This postprocessing technique is appealing because it does not require nonstandard imaging sequences or contrast agent injection schemes; however, though it theoretically improves rCBV estimation, there is only anecdotal evidence for its effectiveness. For instance, rCBV maps generated with a prebolus loading dose of contrast plus the correction scheme of Weisskoff et al significantly correlate with glioma tumor grade, whereas uncorrected maps do not.^22,24 To our knowledge, there has been no formal validation of the preload and postprocessing correction techniques against a criterion standard. The purpose of this study was to determine the degree to which Gd-based rCBV estimates, by using this increasingly common combination of leakage-correction techniques, match criterion standard rCBV measured with a purely intravascular contrast agent (MION; Massachusetts General Hospital Center for Molecular Imaging Research, Charlestown, Massachusetts). We hypothesized that correction schemes using both techniques would perform better than schemes using only 1 or none, as measured by smaller variance of Gd/MION rCBV ratios and reduced bias.

Materials and Methods

Intracranial Xenograft Transplantation in Rats

Seven male Fisher rats (Charles River Laboratories, Wilmington, Massachusetts) were anesthetized and immobilized, and 10⁵ 9L gliosarcoma cells were injected through a 0.9-mm calvarial burr-hole (1 mm anterior and 2 mm lateral to the bregma) into the right frontal lobe 3 mm deep to the dura.³³ Care of rats followed the National Institutes of Health Guide for the Care and Use of Laboratory Animals (1996). The Institutional Animal Care and Use Committee at the Medical College of Wisconsin approved all protocols.

MR Imaging

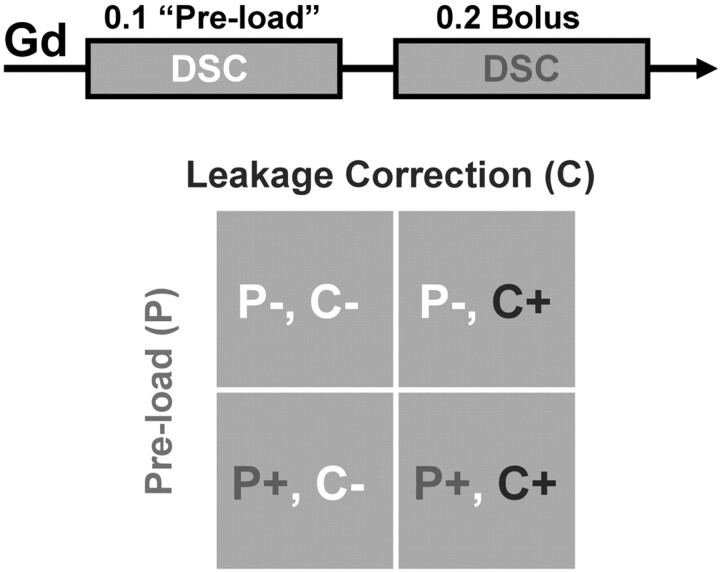
Fourteen days following tumor cell inoculation, MRI was performed (3T Signa Excite; GE Healthcare, Milwaukee, Wisconsin; quadrature birdcage coil; FOV = 4 cm, 4 sections, 2-mm section thickness). DSC-MRI (gradient-echo EPI, TR = 1 second, TE = 34.5 ms, matrix = 64 × 64, 60 seconds before and 60 seconds after injection) was performed with both MION (2.0 mg Fe/kg bolus) and gadodiamide (Omniscan; GE Healthcare) in each rat, with randomly assigned order. For gadodiamide-based DSC-MRI, we used a staged injection technique (Fig 1). Dynamic imaging during an initial single-dose bolus (0.1 mmol/kg) provided no preload (P−) rCBV data and served as preload (P+) for subsequent DSC-MRI using a double-dose (0.2 mmol/kg) bolus. Single-dose (P−) and double-dose (P+) injections were separated by 10 minutes. Finally, T1-weighted spin-echo images (TE/TR = 12/450 ms, 256 × 256 matrix, NEX = 16) were acquired to delineate enhancing tumor.

Fig 1.

Summary of Gd-based DSC methodology: staged injection technique. Gradient-echo DSC-MRI (0.1-mmol/kg gadodiamide bolus) provides no preload (P−) rCBV data and serves as a preload (P+) for subsequent DSC-MRI (0.2 mmol/kg bolus). Gd-rCBV without (C−) and with (C+) application of postprocessing leakage correction are computed for both P− and P+ data, thereby testing P−C−, P−C+, P+C−, and P+C+ permutations of the 2 leakage-correction techniques.

rCBV Computation

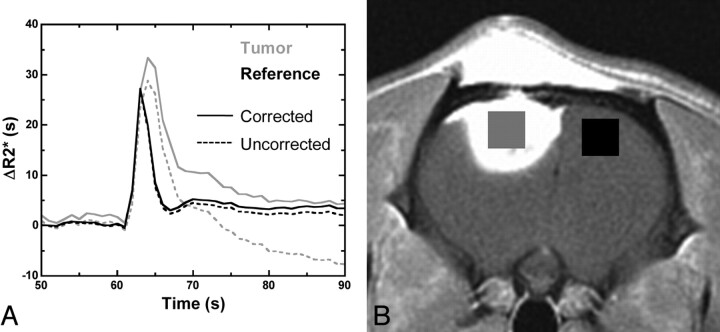
Using custom AFNI-based³⁴ postprocessing software (Bloomington, Illinois), we converted signal intensity time curves to relaxivity time curves (ΔR2*[t]) for each voxel by using a standard technique. For initial (P−) and secondary (P+) injection data, we estimated Gd-rCBV without (C−) and with (C+) application of a leakage-correction algorithm based on the linear fit of uncorrected ΔR2*(t) to constant functions derived from nonenhancing brain parenchyma,^21,22 thereby testing all 4 permutations of the 2 leakage-correction techniques (P−C−, P−C+, P+C−, and P+C+; see Fig 2A for examples of P+C− and P+C+ curves in tumor and reference brain). We generated rCBV maps for each permutation by using numeric trapezoidal integration of ΔR2* (t) over all time points on a voxelwise basis. ROIs of enhancing tumor and normal-appearing reference brain were determined from the postcontrast T1-weighted spin-echo images and coregistered to the rCBV maps for each rat (Fig 2B). Mean rCBV values from the tumor ROI and the reference ROI were extracted, and their ratio was computed, providing a normalized rCBV value for each leakage-correction permutation in all rats.

Fig 2.

Gd-rCBV for initial (P−) and second (P+) injection data was computed by using voxelwise trapezoidal integration of ΔR2* (t) without (C−) and with (C+) postprocessing leakage correction. A, Examples of P+C− and P+C+ curves in tumor and reference brain. B, The ratio of mean rCBV from tumor (gray) and contralateral brain (black) ROIs was computed for all injections, providing normalized rCBV values.

We used MION, an intravascular agent with high T2 relaxivity, as a criterion standard for tumor rCBV, because this agent does not extravasate. Tumor MION-rCBV was estimated by computing the ratio of the steady-state ΔR2* relaxivity value in tumor to that in reference brain by using the same ROIs.³⁵

Data Analysis and Statistical Methods

For each rat, Gd-rCBV estimates from each leakage-correction permutation were normalized to the criterion standard MION-rCBV as a percentage difference (Gd-rCBV − MION-rCBV / MION-rCBV). Using a generalized estimating equation for normally distributed data, we modeled the percentage differences as a function of preload (P+ versus P−), leakage correction (C+ versus C−), and their interaction and tested whether each correction permutation reduced bias and variance of Gd/MION-rCBV ratios by using F_max statistics (http://www.biology.ed.ac.uk/research/groups/jdeacon/statistics/table8.htm) (Holm-adjusted P < .05 was considered significant when comparing correction schemes with each other; unadjusted P values used when comparing correction schemes with ideal or null values). The variances for each correction permutation and covariances between them were modeled by using sandwich estimators and assuming independent variances. The relationships between Gd-rCBV and MION-rCBV for each correction permutation were determined by using another generalized estimating equation that compared slopes and intercepts with the ideal (zero intercept and unity slope) and, in the case of slopes, also with a null of zero, indicating no relationship.

Results

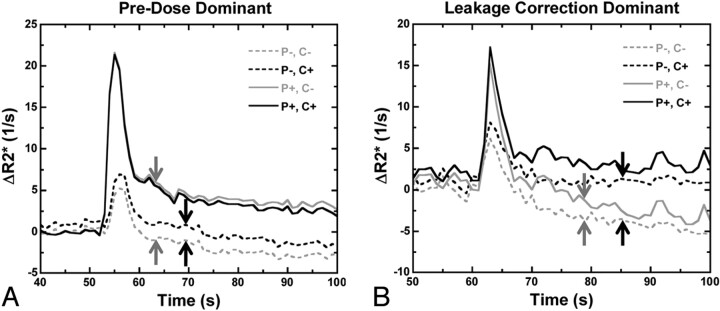
Figure 3 compares the relative effects of preload and the postprocessing algorithm on individual relaxivity time curves. In some tumors, the postprocessing algorithm without preload had minimal corrective effect, whereas inclusion of preload had substantial restorative effects (preload dominant, Fig 3A). In other tumors, the opposite was true, with more substantial corrective effect from the postprocessing algorithm (postprocessing dominant; Fig 3B). These illustrations suggest a complementary role of the 2 leakage-correction schemes. Combining preload and postprocessing algorithms (solid black lines) yields the most robust relaxivity time curves, with the greatest peak ΔR2* and the absence of negative relaxivity values.

Fig 3.

Comparison of preload-dominant and postprocessing-dominant corrective effects on relaxivity time curves for 2 different tumors. A, Preload alone (solid gray line) eliminates most of the T1 leakage contamination (dashed gray line with blunted peak relaxivity and negative ΔR2* values; shift between gray arrows), whereas postprocessing correction does not (dashed black line; shift between black arrows). B, Postprocessing algorithm has more substantial corrective effect than preload in the tail portion of the curves (dashed black versus dashed gray lines; shift between black versus gray arrows), but the converse is true during the first pass (solid versus dashed lines), demonstrating synergy between the 2 correction schemes. Combining preload and postprocessing (solid black lines) yields the greatest peak ΔR2* without negative relaxivity values.

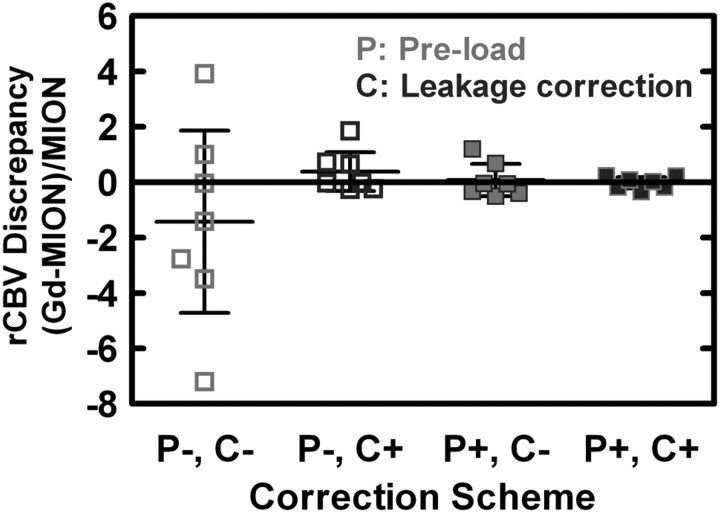
Figure 4 compares the rCBV discrepancies ([Gd − MION] /MION) for each of the 4 correction-scheme permutations (mean, 95% CI). Without preload or leakage-correction algorithms, Gd-rCBV estimates are very discordant, and 3 of the 7 Gd-rCBV values were negative before correction. Although there was no statistically significant bias within or between correction schemes, the mean discrepancy was closest to the ideal of zero for P+C+, followed by P+C−, P−C+, and P−C− (Table 2). There were substantial differences in the variance of discrepancies for the different correction schemes; compared with the variance for P−C−, the variance of discrepancies was statistically significantly lower for P+C− (22-fold, adjusted P = .003), P−C+ (32-fold, adjusted P = .01), and P+C+ (267-fold, adjusted P < .0001). Although there was no significant difference between the variances for P+C− and P−C+ (1.5-fold, adjusted P = .67), the use of both correction techniques (P+C+) further significantly reduced the variance compared with that for each individually (12-fold versus P+C−, adjusted P = .01; 8-fold versus P−C+, adjusted P = .02).

Fig 4.

Comparison of rCBV discrepancies ([Gd − MION] / MION) for each correction scheme permutation (mean and 95% CI). Although there is no statistically significant intrascheme or interscheme bias, mean discrepancy is closest to zero for P+C+ (−1.8%), followed by P+C− (+7.6%), P−C+ (+38.3%), and P−C− (−142.8%). The variance of rCBV discrepancies differed substantially between correction schemes, with P+C− (22-fold), P−C+ (32-fold), and P+C+ (267-fold) all statistically significantly lower compared with P−C−. The use of both correction techniques (P+C+) further significantly reduced the variance compared with that for each individually (12-fold versus P+C−, 8-fold versus P−C+).

Table 2:

Summary of discrepancy between Gd-rCBV and MION-rCBV for each correction scheme permutation

Scheme	rCBV Discrepancy		Intercept		Slope
	Mean (%)	95% CI (%)	Mean	95% CI	Mean	95% CI
P−C−	−142.8	−471.5, +186.0	+1.4	+1.1, +1.6	−0.01	−0.04, +0.02
P−C+	+38.3	−32.0, +108.6	+1.3	+0.8, +1.8	+0.16	+0.02, +0.31
P+C−	+7.6	−50.1, +65.9	+1.0	+0.5, +1.5	+0.02	−0.29, +0.33
P+C+	−1.8	−22.0, +18.3	+0.6	−0.2, +1.4	+0.58	+0.17, +1.00

Note:—rCBV discrepancy indicates (Gd-rCBV − MION-rCBV) / MION-rCBV (ideal equals zero); intercept and slope, the linear fit of MION-rCBV versus Gd-rCBV (ideal equals zero intercept with unity slope).

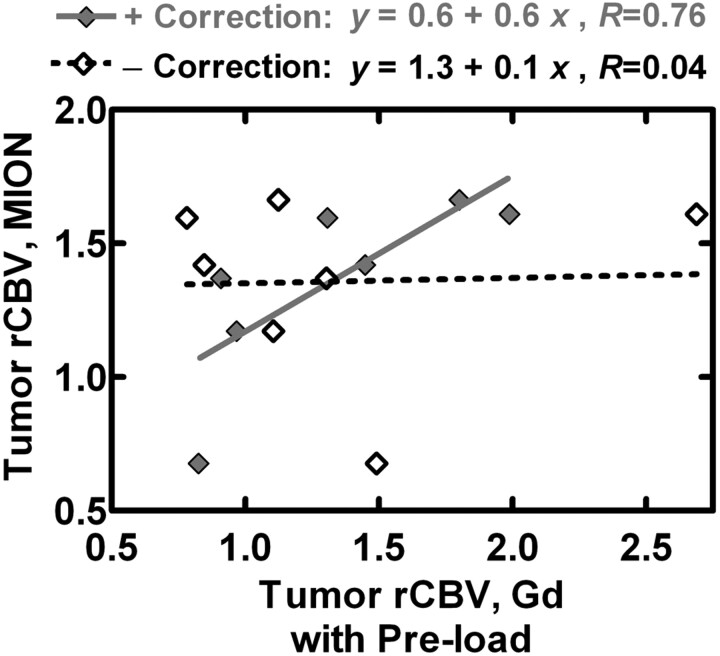
Because the interscheme differences in variance were so striking, we examined the specific relationship between Gd-rCBVs and MION-rCBVs for each correction permutation (Table 2). The intercepts for P−C−, P+C−, and P−C+ each differed significantly from the ideal of zero, whereas the intercept for P+C+ did not. Although the slopes for P−C−, P+C−, P−C+, and P+C+ differed significantly from the ideal of 1, P−C+ (P = .03) and P+C+ (P = .009) produced statistically significant evidence of a greater-than-chance relationship between Gd-rCBV and MION-rCBV, whereas P−C− and P+C− did not. In Fig 5 , Gd-rCBV with preload and with (P+C+) and without (P+C−) postprocessing correction is plotted against MION-rCBV. The linear fit for rCBV data with postprocessing correction is much closer to identity than the linear fit without, arguing that the use of both correction schemes outperforms the use of only 1.

Fig 5.

Gd-rCBV with preload and with (P+C+) and without (P+C−) leakage correction is plotted against MION-rCBV. The linear fit for P+C+ data is much closer to the ideal line of identity than the linear fit for P+C−, arguing that the use of both correction schemes outperforms the use of only preload.

Discussion

Our results offer strong evidence that the combination of preload and postprocessing correction schemes significantly reduces the variance of Gd-rCBV measures relative to criterion standard MION-rCBV compared with either technique alone and no correction. The results also suggest that both techniques may reduce the tendency toward bias observed without correction. The practical implication is that the combined correction scheme improves the accuracy and precision of Gd-rCBV measurements, which is important for clinical applications such as the evaluation of posttreatment gliomas that rely on rCBV quantitation for analysis of temporal trends and absolute thresholds.

Extravasated contrast shortens the extravascular-extracellular compartment T1, counteracting the transient first-pass susceptibility contrast-induced signal intensity drop used to estimate tumor hemodynamics. Preload administration minimizes T1 leakage contamination by saturating the baseline extravascular-extracellular compartment T1-weighted signal intensity, thereby diminishing T1-induced signal intensity increases during subsequent DSC-MRI. It may also reduce the gradient of contrast efflux. The importance of the preload cannot be overemphasized³ and may be the difference between an indiscernible and robust signal intensity drop in very leaky tumors. In some cases without preload, no signal intensity drop is detectable in the signal intensity time curve; in such cases, it may be impossible to “resurrect” legitimate DSC-MRI data by using the postprocessing algorithm. Although the postprocessing algorithm may provide sufficient leakage correction in cases with robust signal intensity drop in the absence of preload, our results suggest a synergistic effect between these 2 techniques, and we advocate their use in tandem.

Preload dose and other factors such as “incubation” time between preload and secondary bolus may impact the adequacy of preload leakage correction.³⁶ Hu et al³⁶ found that a 0.1-mmol/kg preload dose and a 6-minute incubation time helped optimize discrimination of posttreatment-related enhancement and tumor progression compared with uncorrected rCBV measurement, and our use of a 0.1-mmol/kg preload and 10-minute incubation time would certainly be in line with that recommendation. We kept the preload dose and incubation time constant to reduce preload-related variance in Gd-rCBV.

The postprocessing algorithm used herein generates both corrected rCBV maps and first-order estimates of vascular permeability.²² In addition to signal intensity contamination by competing T1 effects, contrast extravasation may also diminish ΔR2* by decreasing the magnetic susceptibility gradient between the intra- and extravascular spaces (Δχ). However, susceptibility differences created between extravascular contrast and tumor cells may increase ΔR2*, providing cell attenuation sensitivity on DSC-MRI, which may help distinguish common enhancing malignant lesions.³⁷ For example, the postbolus plateau of the relaxivity time curves in Fig 3 does not completely return to baseline, even after leakage correction, representing extravasation-related residual T2* effects. The complex interplay between T1- and T2*-weighted effects on DSC-MRI signal intensity is an active area of investigation.^23–25

Other postprocessing correction techniques exist. γ-variate fitting eliminates tail deviation of ΔR2*(t) due to extravasation^4,11 but would not correct first-pass amplitude reduction (Fig 3B), is nonlinear, is often unstable, and has SNR deficiencies.^2,38 Early bolus extravasation may be substantial in high-grade tumors with high vascular permeability, and ignoring first-pass amplitude reduction could yield large rCBV inaccuracies. Considering only peak ΔR2* or only integrating from bolus onset to peak ΔR2* (“limited integration method”³⁰) does not account for first-pass ΔR2* suppression or late bolus ΔR2* effects. The “baseline subtraction method”²⁹ assumes that the ΔR2* (t) tail matches the initial baseline, with homogeneous linear contamination throughout the first pass. The postprocessing model used herein approximately corrects the entire relaxivity time curve by using a stable linear fit, permitting numeric integration during the entire first pass, with associated advantages in accuracy and rCBV SNR.²

There are alternatives to preload with postprocessing correction for minimizing rCBV error. Double-echo T2*-weighted DSC-MRI uses signal intensities at 2 different TEs and an exponential model to compute ΔR2*(t) without T1 contamination.^27,28 This may still have T2* contamination but, if corrected for, significantly correlates with tumor grade, performing on a par, in this sense, with the preload/postprocessing correction scheme; these 2 methods appear to provide the most robust rCBV estimation in the setting of contrast agent extravasation.²⁴ We think that addressing T1 leakage correction remains important because preload/postprocessing correction schemes are becoming commonplace and well cited. Furthermore, residual T2* contamination effects can still confound rCBV estimates, and to the extent that the postprocessing correction herein also addresses T2* contamination (included in the K2 term), the preload/postprocessing correction technique provides some degree of comprehensive leakage correction.

Similar to previously investigated iron oxide contrast agents,^39,40 high-molecular-weight intravascular iron-containing agents with large susceptibility effects (eg, ferumoxytol) would eliminate the need for any leakage correction entirely.^41,42 However, they may introduce practical issues with regard to T1-weighted postcontrast imaging, given that extravasation accounts for most enhancement associated with conventional Gd-based agents. For example, in an intrapatient comparison of gadoteridol and ferumoxytol in intracranial tumors, ferumoxytol rCBV values were significantly larger (P = .0016) than gadoteridol rCBV values⁴³; this finding implies a reduction of T1 leakage contamination.

We found that several Gd-rCBV estimates were negative for the P−C− group, likely due to a predominance of negative ΔR2* secondary to avid contrast enhancement; numeric integration through the tail in such instances can accumulate large negative ΔR2*. This begs the question of how the temporal limits of ΔR2* integration are selected. We collected images for 60 seconds during and after bolus injection, typically yielding 40–50 images following the first pass. It could be argued that an abbreviated integration strategy as previously discussed could minimize sensitivity to T1 leakage effects and reduce the variance of rCBV estimates. However, our methodology mimics that in previous publications documenting significant correlation of rCBV with tumor grade.^22,24 Furthermore, the postprocessing correction technique extends the useful observation time in the dynamic phase of the contrast bolus, potentially increasing the contrast-to-noise ratio of the computed rCBV maps.² The trend toward negative bias for the P−C− case illustrates the fact that T1 contamination, by affecting the first pass and/or tail of the relaxivity time curve, tends to artificially lower rCBV estimates.

The second of our staged bolus injections (P+ cases) was a double-dose injection, compared with a single-dose injection for P− cases, and this would certainly affect the relative SNR of P+ versus P− rCBV measures and consequently the relative group variances. This injection strategy mimics commonly published techniques, though because of nephrogenic systemic fibrosis risk and higher molar T1 relaxivity of newer contrast agents (eg, gadobenate dimeglumine, MultiHance; Bracco Imaging, Milan, Italy; gadobutrol, Gadovist; Bayer Schering Pharma, Berlin-Wedding, Germany), we reduce the preload at our institution to one-fourth dose followed by a single-dose dynamic bolus. This experiment could be repeated to confirm the suspected relevance of our conclusions at this different dosing strategy. In any event, we demonstrated significant variance reduction for P+C+ compared with P+C−, and P−C+ compared with P−C−, both at the same dosing protocols, suggesting the added benefit of postprocessing correction in both preload scenarios.

Because neovascularity in high-grade gliomas is characterized by disorganized large-scale microvessels,⁴⁴ we used gradient-echo EPI because it has ΔR2* sensitivity to microvessels of all sizes, contrary to spin-echo with peak ΔR2* sensitivity to capillary-sized microvessels.⁴⁵ Furthermore, gradient echo–based rCBV is known to be a statistically significant predictor of tumor grade,²² and gradient-echo EPI is probably the most commonly used DSC technique. Nonetheless, we expect that the results of this study should pertain to spin-echo–based rCBV measures as well.

Limitations to our study include a relatively small sample size and the single-versus-double-dose contrast boluses used for P− and P+ cases, respectively. Although multiple investigators have used the postprocessing algorithm tested herein, the limitations of this reference-correction method have been identified, including sensitivity to MTT, whereby elevated tumor MTT may cause rCBV underestimation due to incorrect estimation of K2.²⁵ This may affect comparative rCBV estimates between tumor and reference tissue or between high- and low-grade gliomas typically having relatively lower and higher MTT, respectively. Bjornerud et al²⁵ proposed a novel postprocessing correction algorithm that is insensitive to MTT variations, and the use of more sophisticated postprocessing correction schemes may further improve the residual variance in the P+C+ scheme and the regression of Gd-rCBV estimates versus MION-rCBV criterion standard.

Conclusions

The rat gliosarcoma model with MION provides a viable model for testing T1 leakage-correction schemes against criterion standard rCBV measures. Conventional single-dose rCBV estimates without leakage correction correlate very poorly with true rCBV and should not be trusted in high-grade tumors. Both preload and the postprocessing correction algorithms independently reduce the variance of Gd-rCBV estimates, but there is an additional benefit when used in tandem. It is an ongoing work in our laboratories to better understand and reduce T2* and latent susceptibility components of rCBV error; the MION rat model may be helpful for achieving this goal.

ABBREVIATIONS:

C−

without leakage correction algorithm applied

C+

with leakage correction algorithm applied

CI

confidence interval

DSC

dynamic susceptibility contrast

Gd

gadolinium

K2

linear coefficient in the fitting algorithm used to correct for contrast agent extravasation in CBV estimates as defined in References 21 and 22

MION

monocrystalline iron oxide nanoparticle intravascular contrast agent

P−

without administration of preload contrast agent dose

P+

with administration of preload contrast agent dose

rCBV

relative cerebral blood volume