Covariance Matrix Estimation for the Cryo-EM Heterogeneity Problem

Abstract

In cryo-electron microscopy (cryo-EM), a microscope generates a top view of a sample of randomly oriented copies of a molecule. The problem of single particle reconstruction (SPR) from cryo-EM is to use the resulting set of noisy two-dimensional projection images taken at unknown directions to reconstruct the three-dimensional (3D) structure of the molecule. In some situations, the molecule under examination exhibits structural variability, which poses a fundamental challenge in SPR. The heterogeneity problem is the task of mapping the space of conformational states of a molecule. It has been previously suggested that the leading eigenvectors of the covariance matrix of the 3D molecules can be used to solve the heterogeneity problem. Estimating the covariance matrix is challenging, since only projections of the molecules are observed, but not the molecules themselves. In this paper, we formulate a general problem of covariance estimation from noisy projections of samples. This problem has intimate connections with matrix completion problems and high-dimensional principal component analysis. We propose an estimator and prove its consistency. When there are finitely many heterogeneity classes, the spectrum of the estimated covariance matrix reveals the number of classes. The estimator can be found as the solution to a certain linear system. In the cryo-EM case, the linear operator to be inverted, which we term the projection covariance transform, is an important object in covariance estimation for tomographic problems involving structural variation. Inverting it involves applying a filter akin to the ramp filter in tomography. We design a basis in which this linear operator is sparse and thus can be tractably inverted despite its large size. We demonstrate via numerical experiments on synthetic datasets the robustness of our algorithm to high levels of noise.

1. Introduction

1.1. Covariance matrix estimation from projected data

Covariance matrix estimation is a fundamental task in statistics. Statisticians have long grappled with the problem of estimating this statistic when the samples are only partially observed. In this paper, we consider this problem in the general setting where “partial observations” are arbitrary linear projections of the samples onto a lower-dimensional space.

Problem 1.1

Let X be a random vector on C^p, with E[X] = μ₀ and Var(X) = Σ₀ (Var[X] denotes the covariance matrix of X). Suppose also that P is a random q × p matrix with complex entries, and E is a random vector in C^q with E[E] = 0 and Var[E] = σ²I_q. Finally, let I denote the random vector in C^q given by

$$I=PX+E.$$ (1.1)

Assume now that X, P , and E are independent. Estimate μ₀ and Σ₀ given observations I₁,… , I_n and P₁,… , P_n of I and P , respectively.

Here, and throughout this paper, we write random quantities in boldface to distinguish them from deterministic quantities. We use regular font (e.g., X) for vectors and matrices, calligraphic font (e.g., X ) for functions, and script font for function spaces (e.g., B). We denote true parameter values with a subscript of zero (e.g., μ₀), estimated parameter values with a subscript of n (e.g., μ_n), and generic variables with no subscript (e.g., μ).

Problem 1.1 is quite general, and has many practical applications as special cases. The main application this paper addresses is the heterogeneity problem in single particle reconstruction (SPR) from cryo-electron microscopy (cryo-EM). SPR from cryo-EM is an inverse problem where the goal is to reconstruct a three-dimensional (3D) molecular structure from a set of its two-dimensional (2D) projections from random directions [12]. The heterogeneity problem deals with the situation in which the molecule to be reconstructed can exist in several structural classes. In the language of Problem 1.1, X represents a discretization of the molecule (random due to heterogeneity), P_s the 3D-to-2D projection matrices, and I_s the noisy projection images. The goal of this paper is to estimate the covariance matrix associated with the variability of the molecule. If there is a small, finite number (C) of classes, then Σ₀ has low rank (C − 1). This ties the heterogeneity problem to principal component analysis (PCA) [40]. If Σ₀ has eigenvectors V₁,… , V_p (called principal components) corresponding to eigenvalues λ₁ ≥ ··· ≥ λ_p, then PCA states that V_i accounts for a variance of λ_i in the data. In modern applications, the dimensionality p is often large, while X typically has much fewer intrinsic degrees of freedom [11]. The heterogeneity problem is an example of such a scenario; for this problem, we demonstrate later that the top principal components can be used in conjunction with the images to reconstruct each of the C classes.

Another class of applications closely related to Problem 1.1 is missing data problems in statistics. In these problems, X₁,… , X_n are samples of a random vector X. The statistics of this random vector must be estimated in a situation where certain entries of the samples X_s are missing [31]. This amounts to choosing P_s to be coordinate-selection operators, operators which output a certain subset of the entries of a vector. An important problem in this category is PCA with missing data, which is the task of finding the top principal components when some data are missing. Closely related to this is the noisy low rank matrix completion problem [9]. In this problem, only a subset of the entries of a low rank matrix A are known (possibly with some error), and the task is to fill in the missing entries. If we let X_s be the columns of A, then the observed variables in each column are P_sX_s + E_s, where P_s acts on X_s by selecting a subset of its coordinates, and E_s is noise. Note that the matrix completion problem involves filling in the missing entries of X_s, while Problem 1.1 requires us only to find the covariance matrix of these columns. However, the two problems are closely related. For example, if the columns are distributed normally, then the missing entries can be found as their expectations conditioned on the known variables [51]. Alternatively, we can find the missing entries by choosing the linear combinations of the principal components that best fit the known matrix entries. A well-known application of matrix completion is in the field of recommender systems (also known as collaborative filtering). In this application, users rate the products they have consumed, and the task is to determine what new products they would rate highly. We obtain this problem by interpreting A_i,j as the jth user’s rating of product i. In recommender systems, it is assumed that only a few underlying factors determine users’ preferences. Hence, the data matrix A should have low rank. A high profile example of recommender systems is the Netflix prize problem [6].

In both of these classes of problems, Σ₀ is large but should have low rank. Despite this, note that Problem 1.1 does not have a low rank assumption. Nevertheless, as our numerical results demonstrate, the spectrum of our (unregularized) covariance matrix estimator reveals low rank structure when it is present in the data. Additionally, the framework we develop in this paper naturally allows for regularization.

Having introduced Problem 1.1 and its applications, let us delve more deeply into one particular application: SPR from cryo-EM.

1.2. Cryo-electron microscopy

Electron microscopy is an important tool for structural biologists, as it allows them to determine complex 3D macromolecular structures. A general technique in electron microscopy is called SPR. In the basic setup of SPR, the data collected are 2D projection images of ideally assumed identical, but randomly oriented, copies of a macromolecule. In particular, one specimen preparation technique used in SPR is called cryo-EM, in which the sample of molecules is rapidly frozen in a thin ice layer [12, 63]. The electron microscope provides a top view of the molecules in the form of a large image called a micrograph. The projections of the individual particles can be picked out from the micrograph, resulting in a set of projection images. Mathematically, we can describe the imaging process as follows. Let X : R³ → R represent the Coulomb potential induced by the unknown molecule. We scale the problem to be dimension-free in such a way that most of the “mass” of X lies within the unit ball B ⊂ R³ (since we later model X to be bandlimited, we cannot quite assume it is supported in B). To each copy of this molecule corresponds a rotation R ∈ SO(3), which describes its orientation in the ice layer. The idealized forward projection operator P = P(R) : L¹(R³) → L¹(R²) applied by the microscope is the X-ray transform

$$\left(PX\right)(x,y)={\int }_{\mathbb{R}}X\left(R^{T}r\right)dz,$$ (1.2)

where r = (x, y, z)^T . Hence, P first rotates X by R, and then integrates along vertical lines to obtain the projection image. The microscope yields the image PX , discretized onto an N × N Cartesian grid, where each pixel is also corrupted by additive noise. Let there be q ≈ ^π N ² pixels contained in the inscribed disc of an N × N grid (the remaining pixels contain little or no signal because X is concentrated in B). If S : L¹(R²) → R^q is a discretization operator, then the microscope produces images I given by

$$I=SPX+E$$ (1.3)

with E ~ N (0, σ²I_q ), where for the purposes of this paper we assume additive white Gaussian noise. The microscope has an additional blurring effect on the images, a phenomenon we will discuss shortly, but will leave out of our model. Given a set of images I₁,… , I_n, the cryo-EM problem is to estimate the orientations R₁,… , R_n of the underlying volumes and reconstruct X . Note that throughout this paper, we will use “cryo-EM” and “cryo-EM problem” as shorthand for the SPR problem from cryo-EM images; we also use “volume” as a synonym for “3D structure.”

The cryo-EM problem is challenging for several reasons. Unlike most other imaging modalities of computerized tomography, the rotations R_s are unknown, so we must estimate them before reconstructing X . This challenge is one of the major hurdles to reconstruction in cryo-EM. Since the images are not perfectly centered, they also contain in-plane translations, which must be estimated as well. The main challenge in rotation estimation is that the projection images are corrupted by extreme levels of noise. This problem arises because only low electron doses can scan the molecule without destroying it. To an extent, this problem is mitigated by the fact that cryo-EM datasets often have tens or even hundreds of thousands of images, which makes the reconstruction process more robust. Another issue with transmission electron microscopy in general is that technically, the detector only registers the magnitude of the electron wave exiting the specimen. Zernike realized in the 1940s that the phase information could also be recovered if the images were taken out of focus [60]. While enabling measurement of the full output of the microscope, this out-of-focus imaging technique produces images representing the convolution of the true image with a point spread function (PSF). The Fourier transform of the PSF is called the contrast transfer function (CTF). Thus the true images are multiplied by the CTF in the Fourier domain to produce the output images. Hence, the P_s operators in practice also include the blurring effect of a CTF. This results in a loss of information at the zero crossings of the (Fourier-domain) CTF and at high frequencies [12]. In order to compensate for the former effect, images are taken with several different defocus values, whose corresponding CTFs have different zero crossings.

The field of cryo-EM has recently seen a drastic improvement in detector technology. New direct electron detector cameras have been developed, which, according to a recent article in Science, have “unprecedented speed and sensitivity” [24]. This technology has enabled SPR from cryo-EM to succeed on smaller molecules (up to size ~150 kDa) and achieve higher resolutions (up to 3Å) than before. Such high resolution allows tracing of the polypetide chain and identification of residues in protein molecules [28, 3, 15, 34, 68]. Recently, single particle methods have provided high resolution structures of the TRPV1 ion channel [30] and of the large subunit of the yeast mitochondrial ribosome [1]. While X-ray crystallography is still the imaging method of choice for small molecules, cryo-EM now holds the promise of reconstructing larger, biomedically relevant molecules not amenable to crystallization.

The most common method for solving the basic cryo-EM problem is guessing an initial structure and then performing an iterative refinement procedure, where iterations alternate between (1) estimating the rotations of the experimental images by matching them with projections of the current 3D model and (2) tomographic inversion producing a new 3D model based on the experimental images and their estimated rotations [12, 61, 44]. There are no convergence guarantees for this iterative scheme, and the initial guess can incur bias in the reconstruction. An alternative is to estimate the rotations and reconstruct an accurate initial structure directly from the data. Such an ab initio structure is a much better initialization for the iterative refinement procedure. This strategy helps avoid bias and reduce the number of refinement iterations necessary to converge [70]. In the ab initio framework, rotations can be estimated by one of several techniques (see, e.g., [55, 64] and references therein).

1.3. Heterogeneity problem

As presented above, a key assumption in the cryo-EM problem is that the sample consists of (rotated versions of) identical molecules. However, in many datasets this assumption does not hold. Some molecules of interest exist in more than one conformational state. For example, a subunit of the molecule might be present or absent, have a few different arrangements, or be able to move continuously from one position to another. These structural variations are of great interest to biologists, as they provide insight into the functioning of the molecule. Unfortunately, standard cryo-EM methods do not account for heterogeneous samples. New techniques must be developed to map the space of molecules in the sample, rather than just reconstruct a single volume. This task is called the heterogeneity problem. A common case of heterogeneity is when the molecule has a finite number of dominant conformational classes. In this discrete case, the goal is to provide biologists with 3D reconstructions of all these structural states. While cases of continuous heterogeneity are possible, in this paper we mainly focus on the discrete heterogeneity scenario.

While we do not investigate the 3D rotation estimation problem in the heterogeneous case, we conjecture that this problem can be solved without developing sophisticated new tools. Consider, for example, the case when the heterogeneity is small, i.e., the volumes X₁,… , X_n can be rotationally aligned so they are all close to their mean (in some norm). For example, this property holds when the heterogeneity is localized (e.g., as in Figure 1). In this case, one might expect that by first assuming homogeneity, existing rotation estimation methods would yield accurate results. Even if the heterogeneity is large, an iterative scheme can be devised to alternately estimate the rotations and conformations until convergence (though this convergence is local, at best). Thus, in this publication, we assume that the 3D rotations R_s (and in-plane translations) have already been estimated.

Figure 1.

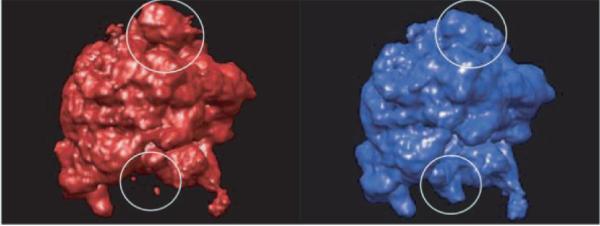
Classical (left) and hybrid (right) states of 70S E. Coli ribosome (image source: [29]).

With the discrete heterogeneity and known rotations assumptions, we can formulate the heterogeneity problem as follows.

Problem 1.2 (heterogeneity problem)

Suppose a heterogeneous molecule can take on one of C different states: X ¹,… , X ^C ∈ B, where B is a finite-dimensional space of bandlimited functions (see section 3.2). Let Ω = {1, 2,… ,C} be a sample space, and p₁,… , p_C probabilities (summing to one) so that the molecule assumes state c with probability p_c. Represent the molecule as a random field X : Ω × R³ → R, with

$$\mathbb{P}[X=X^c]=p_c,c=1,\dots ,C.$$ (1.4)

Let R be a random rotation with some distribution over SO(3), and define the corresponding random projection P = P(R) (see (1.2)). Finally, E ~ N (0, σ²I_q ). Assume that X , R, E are independent. A random image of a particle is obtained via

$$I=SPX+E,$$ (1.5)

where S : L¹(R²) → R^q is a discretization operator. Given observations I¹,… , I_n and R₁,… , R_n of I and R, respectively, estimate the number of classes C, the structures X ^c, and the probabilities p_c.

Note that SP|_B is a (random) linear operator between finite-dimensional spaces, and so it has a matrix version P : R^p → R^q , where p = dim B. If we let X be the random vector on R^p obtained by expanding X in the basis for B, then we recover the equation I = PX + E from Problem 1.1. Thus, the main factors distinguishing Problem 1.2 from Problem 1.1 are that the former assumes a specific form for P and posits a discrete distribution on X. As we discuss in section 4, Problem 1.2 can be solved by first estimating the covariance matrix as in Problem 1.1, finding coordinates for each image with respect to the top eigenvectors of this matrix, and then applying a standard clustering procedure to these coordinates.

One of the main dificulties of the heterogeneity problem is that, compared to usual SPR, we must deal with an even lower effective signal-to-noise ratio (SNR). Indeed, the signal we seek to reconstruct is the variation of the molecules around their mean, as opposed to the mean volume itself. We propose a precise definition of SNR in the context of the heterogeneity problem in section 7.1. Another dificulty is the indirect nature of our problem. Although the heterogeneity problem is an instance of a clustering problem, it differs from usual such problems in that we do not have access to the objects we are trying to cluster—only projections of these objects onto a lower-dimensional space are available. This makes it challenging to apply any standard clustering technique directly.

The heterogeneity problem is considered one of the most important problems in cryo-EM. In his 2013 Solvay public lecture on cryo-EM, Dr. Joachim Frank emphasized the importance of “the ability to obtain an entire inventory of coexisting states of a macromolecule from a single sample” [13]. Speaking of approaches to the heterogeneity problem in a review article, Frank discussed “the potential these new technologies will have in exploring functionally relevant states of molecular machines” [14]. It is stressed there that much room for improvement remains; current methods cannot automatically identify the number of conformational states and have trouble distinguishing between similar conformations.

1.4. Previous work

Much work related to Problems 1.1 and 1.2 has already been done. There is a rich statistical literature on the covariance estimation problem in the presence of missing data, a special case of Problem 1.1. In addition, work on the low rank matrix sensing problem (a generalization of matrix completion) is also closely related to Problem 1.1. Regarding Problem 1.2, several approaches to the heterogeneity problem have been proposed in the cryo-EM literature.

1.4.1. Work related to Problem 1.1

Many approaches to covariance matrix estimation from missing data have been proposed in the statistics literature [31]. The simplest approach to dealing with missing data is to ignore the samples with any unobserved variables. Another simple approach is called available case analysis, in which the statistics are constructed using all the available values. For example, the (i, j) entry of the covariance matrix is constructed using all samples for which the ith and jth coordinates are simultaneously observed. These techniques work best under certain assumptions on the pattern of missing entries, and more sophisticated techniques are preferred [31]. One of the most established such approaches is maximum likelihood estimation (MLE). This involves positing a probability distribution on X (e.g., multivariate normal) and then maximizing the likelihood of the observed partial data with respect to the parameters of the model. Such an approach to fitting models from partial observations was known as early as the 1930s, when Wilks used it for the case of a bivariate normal distribution [66]. Wilks proposed to maximize the likelihood using a gradient-based optimization approach. In 1977, Dempster, Laird, and Rubin introduced the expectation-maximization (EM) algorithm [10] to solve maximum likelihood problems. The EM algorithm is one of the most popular methods for solving missing data problems in statistics. Also, there is a class of approaches to missing data problems called imputation, in which the missing values are filled either by averaging the available values or through more sophisticated regression-based techniques. Finally, see [32, 33] for other approaches to related problems.

Closely related to covariance estimation from missing data is the problem of PCA with missing data. In this problem, the task is to find the leading principal components, and not necessarily the entire covariance matrix. Not surprisingly, EM-type algorithms are popular for this problem as well. These algorithms often search directly for the low rank factors. See [18] for a survey of approaches to PCA with missing data. Closely related to PCA with missing data is the low rank matrix completion problem. Many of the statistical methods discussed above are also applicable to matrix completion. In particular, EM algorithms to solve this problem are popular, e.g., [51, 27].

Another more general problem setup related to Problem 1.1 is the low rank matrix sensing problem, which generalizes the low rank matrix completion problem. Let A ∈ R^p×n be an unknown rank-k matrix, and let M : R^p×n → R^d be a linear map, called the sensing matrix. We would like to find A, but we only have access to the (possibly noisy) data M(A). Hence, the low rank matrix sensing problem can be formulated as follows [19]:

$$\mathrm{minimize}\Vert M\left(A\right)-b\Vert s.t.rank\left(A\right)\le k.$$ (1.6)

Note that when Σ₀ is low rank, Problem 1.1 is a special case of the low rank matrix sensing problem. Indeed, consider putting the unknown vectors X₁,… , X_n together as the columns of a matrix A. The rank of this matrix is the number of degrees of freedom in X (in the cryo-EM problem, this relates to the number of heterogeneity classes of the molecule). The linear projections P₁,… , P_n can be combined into one sensing matrix M acting on A. In this way, our problem falls into the realm of matrix sensing.

One of the first algorithms for matrix sensing was inspired by the compressed sensing theory [46]. This approach uses a matrix version of l₁ regularization called nuclear norm regularization. The nuclear norm is the sum of the singular values of a matrix, and is a convex proxy for its rank. Another approach to this problem is alternating minimization, which decomposes A into a product of the form UV ^T and iteratively alternates between optimizing with respect to U and V . The first proof of convergence for this approach was given in [19]. Both the nuclear norm and alternating minimization approaches to the low rank matrix sensing problem require a restricted isometry property on M for theoretical guarantees.

While the aforementioned algorithms are widely used, we believe they have limitations as well. EM algorithms require postulating a distribution over the data and are susceptible to getting trapped in local optima. Regarding the former point, Problem 1.1 avoids any assumptions on the distribution of X, so our estimator should have the same property. Matrix sensing algorithms (especially alternating minimization) often assume that the rank is known in advance. However, there is no satisfactory statistical theory for choosing the rank. By contrast, the estimator we propose for Problem 1.1 allows automatic rank estimation.

1.4.2. Work related to Problem 1.2

Several approaches to the heterogeneity problem have been proposed. Here we give a brief overview of some of these approaches.

One approach is based on the notion of common lines. By the Fourier projection slice theorem (see Theorem 3.1), the Fourier transforms of any two projection images of an object will coincide on a line through the origin, called a common line. The idea of Shatsky et al. [52] was to use common lines as a measure of how likely it is that two projection images correspond to the same conformational class. Specifically, given two projection images and their corresponding rotations, we can take their Fourier transforms and correlate them on their common line. From there, a weighted graph of the images is constructed, with edges weighted based on this common line measure. Then spectral clustering is applied to this graph to classify the images. An earlier common lines approach to the heterogeneity problem is described in [16].

Another approach is based on MLE. It involves positing a probability distribution over the space of underlying volumes, and then maximizing the likelihood of the images with respect to the parameters of the distribution. For example, Wang et al. [65] model the heterogeneous molecules as a mixture of Gaussians and employ the EM algorithm to find the parameters. A challenge with MLE approaches is that the resulting objective functions are nonconvex and have a complicated structure. For more discussion of the theory and practice of maximum likelihood methods, see [53] and [50], respectively. Also see [49] for a description of a software package which uses maximum likelihood to solve the heterogeneity problem.

A third approach to the heterogeneity problem is to use the covariance matrix of the set of original molecules. Penczek, Kimmel, and Spahn outline a bootstrapping approach in [43] (see also [41, 42, 67, 29]). In this approach, one repeatedly takes random subsets of the projection images and reconstructs 3D volumes from these samples. Then, one can perform PCA on this set of reconstructed volumes, which yields a few dominant “eigenvolumes.” Penczek, Kimmel, and Spahn propose to then produce mean-subtracted images by subtracting projections of the mean volume from the images. The next step is to project each of the dominant eigenvolumes in the directions of the images, and then obtain a set of coordinates for each image based on its similarity with each of the eigenvolume projections. Finally, using these coordinates, this resampling approach proceeds by applying a standard clustering algorithm such as K-means to classify the images into classes.

While existing methods for the heterogeneity problem have their success stories, each suffers from its own shortcomings: the common line approach does not exploit all the available information in the images, the maximum likelihood approach requires explicit a priori distributions and is susceptible to local optima, and the bootstrapping approach based on covariance matrix estimation is a heuristic sampling method that lacks in theoretical guarantees.

Note that the above overview of the literature on the heterogeneity problem is not comprehensive. For example, very recently, an approach to the heterogeneity problem based on normal mode analysis was proposed [20].

1.5. Our contribution

In this paper, we propose and analyze a covariance matrix estimator Σ_n to solve the general statistical problem (Problem 1.1), and then apply this estimator to the heterogeneity problem (Problem 1.2).

Our covariance matrix estimator has several desirable properties. First, we prove that the estimator is consistent as n → ∞ for fixed p, q. Second, our estimator does not require a prior distribution on the data, unlike MLE methods. Third, when the data have low intrinsic dimension, our method does not require knowing the rank of Σ₀ in advance. The rank can be estimated from the spectrum of the estimated covariance matrix. This sets our method apart from alternating minimization algorithms that search for the low rank matrix factors themselves. Fourth, our estimator is given in closed form and its computation requires only a single linear inversion.

To implement our covariance matrix estimator in the cryo-EM case, we must invert a high-dimensional matrix L_n (see definition (2.8)). The size of this matrix is so large that typically it cannot even be stored on a computer; thus, inverting L_n is the greatest practical challenge we face. We consider two possibilities of addressing this challenge. In the primary approach we consider, we replace L_n by its limiting operator L, which does not depend on the rotations R_s and is a good approximation of L_n as long as these rotations are distributed uniformly enough. We then carefully construct new bases for images and volumes to make L a sparse, block diagonal matrix. While L has dimensions on the order of $N_{\mathrm{res}}^6\times N_{\mathrm{res}}^6$, this matrix has only $O\left(N_{\mathrm{res}}^9\right)$ total nonzero entries in the bases we construct, where N_res is the grid size corresponding to the target resolution. These innovations lead to a practical algorithm to estimate the covariance matrix in the heterogeneity problem. The second approach we consider is an iterative inversion of L_n, which has a low storage requirement and avoids the requirement of uniformly distributed rotations. We compare the complexities of these two methods, and find that each has its strengths and weaknesses.

The limiting operator L is a fundamental object in tomographic problems involving variability, and we call it the projection covariance transform. The projection covariance transform relates the covariance matrix of the imaged object to data that can be acquired from the projection images. Standard weighted back-projection tomographic reconstruction algorithms involve application of the ramp filter to the data [38], and we find that the inversion of L entails applying a similar filter, which we call the triangular area filter. The triangular area filter has many of the same properties as the ramp filter, but reflects the slightly more intricate geometry of the covariance estimation problem. The projection covariance transform is an interesting mathematical object in its own right, and we begin studying it in this paper.

Finally, we numerically validate the proposed algorithm (the first algorithm discussed above). We demonstrate this method’s robustness to noise on synthetic datasets by obtaining a meaningful reconstruction of the covariance matrix and molecular volumes even at low SNR levels. Excluding precomputations (which can be done once and for all), reconstructions for 10000 projection images of size 65 × 65 pixels takes fewer than five minutes on a standard laptop computer.

The paper is organized as follows. In section 2, we construct an estimator for Problem 1.1, state theoretical results about this estimator, and connect our problem to high-dimensional PCA. In section 3, we specialize the covariance estimator to the heterogeneity problem and investigate its geometry. In section 4, we discuss how to reconstruct the conformations once we have estimated the mean and covariance matrix. In section 5, we discuss computational aspects of the problem and construct a basis in which L is block diagonal and sparse. In section 6, we explore the complexity of the proposed approach. In section 7, we present numerical results for the heterogeneity problem. We conclude with a discussion of future research directions in section 8. Appendices A, B, and C contain calculations and proofs.

2. An estimator for Problem 1.1

2.1. Constructing an estimator

We define estimators μ_n and Σ_n through a general optimization framework based on the model (1.1). As a first step, let us calculate the first- and second-order statistics of I, conditioned on the observed matrix P_s for each s. Using the assumptions in Problem 1.1, we find that

$$\mathbb{E}[I\mid P=P_s]=\mathbb{E}[PX+E\mid P=P_s]=\mathbb{E}[P\mid P=P_s]\mathbb{E}\left[X\right]=P_s{\mu }_0$$ (2.1)

and

$$\mathrm{Var}[I\mid P=P_s]=\mathrm{Var}[PX\mid P=P_s]+\mathrm{Var}\left[E\right]=P_s{\Sigma }_0{P}_s^H+{\sigma }^2{I}_q.$$ (2.2)

Note that $P_s^H$ denotes the conjugate transpose of P_s.

Based on (2.1) and (2.2), we devise least-squares optimization problems for μ_n and Σ_n:

$${\mu }_n=\underset{\mu }{\mathrm{argmin}}\frac{1}{n}\sum _{s=1}^n\Vert I_s-P_s\mu {\Vert }^2,$$ (2.3)

$${\Sigma }_n=\underset{\Sigma }{\mathrm{argmin}}\frac{1}{n}\sum _{s=1}^1\Vert (I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H-(P_s\Sigma P_s^H+{\sigma }^2{\mathrm{I}}_p){\Vert }_F^2.$$ (2.4)

Here we use the Frobenius norm, which is defined by $\Vert A{\Vert }_F^2={\Sigma }_{i,j}\mid A_{i,j}{\mid }^2$

Note that these optimization problems do not encode any prior knowledge about μ₀ or Σ₀. Since Σ₀ is a covariance matrix, it must be positive semidefinite (PSD). As discussed above, in many applications Σ₀ is also low rank. The estimator Σ_n need not satisfy either of these properties. Thus, regularization of (2.4) is an option worth exploring. Nevertheless, here we only consider the unregularized estimator Σ_n. Note that in most practical problems, we only are interested in the leading eigenvectors of Σ_n, and if these are estimated accurately, then it does not matter if Σ_n is not PSD or low rank. Our numerical experiments show that in practice, the top eigenvectors of Σ_n are indeed good estimates of the true principal components for high enough SNR.

Note that we first solve (2.3) for μ_n, and then use this result in (2.4). This makes these optimization problems quadratic in the elements of μ and Σ, and hence they can be solved by setting the derivatives with respect to μ and Σ to zero. This leads to the following equations for μ_n and Σ_n (see Appendix A for the derivative calculations):

$$\frac{1}{n}\left(\sum _{s=1}^n{P}_s^H{P}_s\right){\mu }_n=\frac{1}{n}\sum _{s=1}^n{P}_s^H{I}_s=:b_n,$$ (2.5)

$$\frac{1}{n}\sum _{s=1}^n{P}_s^H{P}_s{\Sigma }_n{P}_s^H{P}_s=\frac{1}{n}\sum _{s=1}^n{P}_s^H(I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H{P}_s-{\sigma }^2\frac{1}{n}\sum _{s=1}^n{P}_s^H{P}_s=:B_n.$$ (2.6)

When p = q and P = I_p, μ_n and Σ_n reduce to the sample mean and sample covariance matrix. When P is a coordinate-selection operator (recall the discussion following the statement of Problem 1.1), (2.5) estimates the mean by averaging all the available observations for each coordinate, and (2.6) estimates each entry of the covariance matrix by averaging over all samples for which both coordinates are observed. These are exactly the available-case estimators discussed in [31, section 3.4].

Observe that (2.5) requires inversion of the matrix

$$A_n=\frac{1}{n}\sum _{s=1}^n{P}_s^H{P}_s,$$ (2.7)

and (2.6) requires inversion of the linear operator L_n : C^p×p → C^p×p defined by

$$L_n\left(\Sigma \right)=\frac{1}{n}\sum _{s=1}^n{P}_s^H{P}_s\Sigma P_s^H{P}_s.$$ (2.8)

Since the P_s are drawn independently from P , the law of large numbers implies that (2.9) A_n → A and L_n → L almost surely,

$$A_n\to A\mathrm{and}{L}_n\to L\mathrm{almost}\mathrm{surely},$$ (2.9)

where the convergence is in the operator norm, and

$$A=\mathbb{E}\left[P^{H}P\right]\mathrm{and}L\left(\Sigma \right)=\mathbb{E}\left[P^{H}P\Sigma P^{H}P\right].$$ (2.10)

The invertibilities of A and L depend on the distribution of P . Intuitively, if P has a nonzero probability of “selecting” any coordinate of its argument, then A will be invertible. If P has a nonzero probability of “selecting” any pair of coordinates of its argument, then L will be invertible. In this paper, we assume that A and L are invertible. In particular, we will find that in the cryo-EM case, A and L are invertible if, for example, the rotations are sampled uniformly from SO(3). Under this assumption, we will prove that A_n and L_n are invertible with high probability for sufficiently large n. In the case when A_n or L_n are not invertible, we cannot define estimators from the above equations, so we simply set them to zero. Since the RHS quantities b_n and B_n are noisy, it is also not desirable to invert A_n or L_n when these matrices are nearly singular. Hence, we propose the following estimators:

$${\mu }_n=\{\begin{array}{cc}{A}_n^{-1}{b}_n\hfill & \mathrm{if}\Vert A_n^{-1}\Vert \le 2\Vert A^{-1}\Vert ,\hfill \\ 0\hfill & \mathrm{otherwise};\hfill \end{array}\phantom{\}}{\Sigma }_n=\{\begin{array}{cc}{L}_n^{-1}\left(B_n\right)\hfill & \mathrm{if}\Vert L_n^{-1}\Vert \le 2\Vert L^{-1}\Vert ,\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\phantom{\}}$$ (2.11)

The factors of 2 are somewhat arbitrary; any α> 1 would do.

Let us make a few observations about A_n and L_n. By inspection, A_n is symmetric and PSD. We claim that L_n satisfies the same properties, with respect to the Hilbert space C^p×p equipped with the inner product (A, B) = tr(B^H A). Using the property tr(AB) = tr(BA), we find that for any Σ₁, Σ₂,

$$\begin{array}{cc}\hfill \langle L_n\left({\Sigma }_1\right),{\Sigma }_2\rangle & =\mathrm{tr}\left({\Sigma }_2^H{L}_n\left({\Sigma }_1\right)\right)=\mathrm{tr}\left[\frac{1}{n}\sum _s{\Sigma }_2^H{P}_s^H{P}_s{\Sigma }_1{P}_s^H{P}_s\right]\hfill \\ \hfill & =\mathrm{tr}\left[\frac{1}{n}\sum _s{P}_s^H{P}_s{\Sigma }_2^H{P}_2^H{P}_s{\Sigma }_1\right]=\langle {\Sigma }_1,L\left({\Sigma }_2\right)\rangle .\hfill \end{array}$$ (2.12)

Thus, L_n is self-adjoint. Next, we claim that L_n is PSD. Indeed,

$$\begin{array}{cc}\hfill \langle L_n\left(\Sigma \right),\Sigma \rangle & =\mathrm{tr}\left({\Sigma }^H{L}_n\left(\Sigma \right)\right)=\mathrm{tr}\left[\frac{1}{n}\sum _s{\Sigma }^H{P}_s^H{P}_s\Sigma P_s^H{P}_s\right]\hfill \\ \hfill & =\frac{1}{n}\sum _s\mathrm{tr}\left[{\left(P_s\Sigma P_s^H\right)}^H\left(P_s\Sigma P_s^H\right)\right]=\sum _s\frac{1}{n}\Vert P_s\Sigma P_s^H{\Vert }_F^2\ge 0.\hfill \end{array}$$ (2.13)

2.2. Consistency of µ_n and Σ_n

In this section, we state that under mild conditions on P , X, E, the estimators μ_n and Σ_n are consistent. Note that here, and throughout this paper, ∥·∥ will denote the Euclidean norm for vectors and the operator norm for matrices. Also, define

$$\mid \Vert Y\mid {\Vert }_j=\mathbb{E}{[\Vert Y-\mathbb{E}\left[Y\right]{\Vert }^j]}^{1∕j},$$ (2.14)

where Y is a random vector.

Proposition 2.1

Suppose A (defined in (2.10)) is invertible, that lP l is bounded almost surely, and that |||X|||₂, |||E|||₂ < ∞. Then, for fixed p, q we have

$$\mathbb{E}\Vert {\mu }_n-{\mu }_0\Vert =O\left(\frac{1}{\sqrt{n}}\right).$$ (2.15)

Hence, under these assumptions, μ_n is consistent.

Proposition 2.2

Suppose A and L (defined in (2.10)) are invertible, that lP l is bounded almost surely, and that there is a polynomial Q for which

$$\mid \Vert X\mid {\Vert }_j,\mid \Vert E\mid {\Vert }_j\le Q\left(j\right),j\in \mathbb{N}.$$ (2.16)

Then, for fixed p, q, we have

$$\mathbb{E}\Vert {\Sigma }_n-{\Sigma }_0\Vert =O\left(\frac{Q\left(\log n\right)}{\sqrt{n}}\right).$$ (2.17)

Hence, under these assumptions, Σ_n is consistent.

Remark 2.3

The moment growth condition (2.16) on X and E is not very restrictive. For example, bounded, subgaussian, and subexponential random vectors all satisfy (2.16) with deg Q ≤ 1 (see [62, sections 5.2 and 5.3]).

See Appendix B for the proofs of Propositions (2.1) and (2.2). We mentioned that μ_n and Σ_n are generalizations of available-case estimators. Such estimators are known to be consistent when the data are missing completely at random (MCAR). This means that the pattern of missingness is independent of the (observed and unobserved) data. Accordingly, in Problem 1.1, we assume that P and X are independent, a generalization of the MCAR condition. The above propositions state that the consistency of μ_n and Σ_n also generalizes to Problem 1.1.

2.3. Connection to high-dimensional PCA

While the previous section focused on the “fixed p, large n” regime, in practice both p and n are large. Now, we consider the latter regime, which is common in modern high-dimensional statistics. In this regime, we consider the properties of the estimator Σ_n when Σ₀ is low rank, and the task is to find its leading eigenvectors. What is the relationship between the spectra of Σ_n and Σ₀? Can the rank of Σ₀ be deduced from that of Σ_n? To what extent do the leading eigenvectors of Σ_n approximate those of Σ₀? In the setting of (1.1) when P = I_p, the theory of high-dimensional PCA provides insight into such properties of the sample covariance matrix (and thus of Σ_n). In particular, an existing result gives the correlation between the top eigenvectors of Σ_n and Σ₀ for given settings of SNR and p/n. It follows from this result that if the SNR is sufficiently high compared to √p/n, then the top eigenvector of Σ_n is a useful approximation of the top eigenvector of Σ₀. If generalized to the case of nontrivial P , this result would be a useful guide for using the estimator Σ_n to solve practical problems, such as Problem 1.2. In this section, we first discuss the existing high-dimensional PCA literature, and then raise some open questions about how these results generalize to the case of nontrivial P .

Given independently and identically distributed (i.i.d.) samples I₁,… , I_n ∈ R^p from a centered distribution I with covariance matrix ${\tilde{\Sigma }}_0$ (called the population covariance matrix), the sample covariance matrix ${\tilde{\Sigma }}_n$ is defined by

$${\tilde{\Sigma }}_n=\frac{1}{n}\sum _{s=1}^n{I}_s{I}_s^H.$$ (2.18)

We use the new tilde notation because in the context of Problem 1.1, ${\tilde{\Sigma }}_0$ is the signal-plus-noise covariance matrix, as opposed to the covariance of the signal itself. High-dimensional PCA is the study of the spectrum of ${\tilde{\Sigma }}_n$ for various distributions of I in the regime where n, p →∞ with p/n → γ.

The first case to consider is X = 0, i.e., I = E, where E ~ N (0, σ²I_p). In a landmark paper, Marc̆cenko and Pastur [35] proved that the spectrum of ${\tilde{\Sigma }}_n$ converges to the Marc̆cenko– Pastur (MP) distribution, which is parameterized by γ and σ²:

$$MP\left(x\right)=\frac{1}{2\pi {\sigma }^2}\frac{\sqrt{({\gamma }_{+}-x)(x-{\gamma }_{-})}}{\gamma x}{1}_{[{\gamma }_{-},{\gamma }_{+}]},{\gamma }_{\pm }={\sigma }^2{(1\pm \sqrt{\gamma })}^2.$$ (2.19)

The above formula assumes γ ≤ 1; a similar formula governs the case γ > 1. Note that there are much more general statements about classes of I for which this convergence holds; see, e.g., [54]. See Figure 2(a) for MP distributions with a few different parameter settings.

Figure 2.

Illustrations of high-dimensional PCA

Johnstone [21] took this analysis a step further and considered the limiting distribution of the largest eigenvalue of ${\tilde{\Sigma }}_n$. He showed that the distribution of this eigenvalue converges to the Tracy–Widom distribution centered on the right edge of the MP spectrum. In the same paper, Johnstone considered the spiked covariance model, in which

$$I=X+E,$$ (2.20)

where E is as before and ${\Sigma }_0=\mathrm{Var}\left[X\right]=\mathrm{diag}({\tau }_1^2,\dots ,{\tau }_r^2,0)$, so that the population covariance matrix is ${\tilde{\Sigma }}_0=\mathrm{diag}({\tau }_1^2+{\sigma }^2,\dots ,{\tau }_r^2+{\sigma }^2,{\sigma }^2,\dots ,{\sigma }^2)$. Here, X is the signal and E is the noise. In this view, the goal is to accurately recover the top r eigenvectors, as these will determine the subspace on which X is supported. The question then is the following: for what values of τ₁,… , τ_r will the top r eigenvectors of the sample covariance matrix be good approximations to the top eigenvectors of the population covariance? Since we might not know the value of r a priori, it is important to first determine for what values of τ₁,… , τ_r we can detect the presence of “spiked” population eigenvalues. In [5], the spectrum of the sample covariance matrix in the spiked model was investigated. It was found that the bulk of the distribution still obeys the MP law, whereas for each k such that

$$\frac{{\tau }_k^2}{{\sigma }^2}\ge \sqrt{\gamma },$$ (2.21)

the sample covariance matrix will have an eigenvalue tending to $({\tau }_k^2+{\sigma }^2)(1+\frac{{\sigma }^2}{{\tau }_k^2}\gamma )$. The signal eigenvalues below this threshold tend to the right edge of the noise distribution. Thus, (2.21) defines a criterion for detection of signal. In Figure 2(b), we illustrate these results with a numerical example. We choose p = 800, n = 4000, and a spectrum corresponding to r = 3, with τ₁, τ₂ above, but τ₃ below, the threshold corresponding to γ = p/n = 0.2. Figure 2(b) is a normalized histogram of the eigenvalues of the sample covariance matrix. The predicted MP distribution for the bulk is superimposed. We see that indeed we have two eigenvalues separated from this bulk. Moreover, the eigenvalue of ${\tilde{\Sigma }}_n$ corresponding to τ₃ does not pop out of the noise distribution.

It is also important to compare the top eigenvectors of the sample and population covariance matrices. Considering the simpler case of a spiked model with r = 1, [4, 37] showed a “phase transition” effect: as long as τ₁ is above the threshold in (2.21), the correlation of the top eigenvector (V_PCA) with the true principal component (V ) tends to a limit between 0 and 1:

$$\mid \langle V_{PCA},V\rangle {\mid }^2\to \frac{\frac{1}{\gamma }\frac{{\tau }_1^4}{{\sigma }^4}-1}{\frac{1}{\gamma }\frac{{\tau }_1^4}{{\sigma }^4}+\frac{{\tau }_1^2}{{\sigma }^2}}.$$ (2.22)

Otherwise, the limiting correlation is zero. Thus, high-dimensional PCA is inconsistent. However, if ${\tau }_1^2∕{\sigma }^2$ is sufficiently high compared to $\sqrt{\gamma }$, then the top eigenvector of the sample covariance matrix is still a useful approximation.

While all the statements made so far have concerned the limiting case n, p → ∞, similar (but slightly more complicated) statements hold for finite n, p as well (see, e.g., [37]). Thus, (2.21) has a practical interpretation. Again considering the case r = 1, note that the quantity ${\tau }_1^2∕{\sigma }^2$ is the SNR. When faced with a problem of the form (2.20) with a given p and SNR, one can determine how many samples one needs in order to detect the signal. If V represents a spatial object as in the cryo-EM case, then p can reflect the resolution to which we reconstruct V . Hence, if we have a dataset with a certain number of images n and a certain estimated SNR, then (2.21) determines the resolution to which V can be reconstructed from the data.

This information is important to practitioners (e.g., in cryo-EM), but as of now, the above theoretical results only apply to the case when P is trivial. Of course, moving to the case of more general P brings additional theoretical challenges. For example, with nontrivial P , the empirical covariance matrix of X is harder to disentangle from that of I, because the operator L_n becomes nontrivial (see (2.6) and (2.8)). How can our knowledge about the spiked model be generalized to the setting of Problem 1.1? We raise some open questions along these lines.

1. In what high-dimensional parameter regimes (in terms of n, p, q) is there hope to detect and recover any signal from Σ_n? With the addition of the parameter q, the traditional regime p ≈ n might no longer be appropriate. For example, in the random coordinate-selection case with the (extreme) parameter setting q = 2, it is expected that n = p² log p samples are needed just for L_n to be invertible (by the coupon collector problem).

2. In the case when there is no signal (X = 0), we have I = E. In this case, what is the limiting eigenvalue distribution of Σ_n (in an appropriate parameter regime)? Is it still the MP law? How does the eigenvalue distribution depend on the distribution of P ? This is perhaps the first step towards studying the signal-plus-noise model.

3. In the no-signal case, what is the limiting distribution of the largest eigenvalue of Σ_n? Is it still Tracy–Widom? How does this depend on n, p, q, and P ? Knowing this distribution can provide p-values for signal detection, as is the case for the usual spiked model (see [21, p. 303]).

4. In the full model (1.1), if X takes values in a low-dimensional subspace of R^p, is the limiting eigenvalue distribution of Σ_n a bulk distribution with a few separated eigenvalues? If so, what is the generalization of the SNR condition (2.21) that would guarantee separation of the top eigenvalues? What would these top eigenvalues be, in terms of the population eigenvalues? Would there still be a phase-transition phenomenon in which the top eigenvectors of Σ_n are correlated with the principal components as long as the corresponding eigenvalues are above a threshold?

Answering these questions theoretically would require tools from random matrix theory such as the ones used by [21, 5, 37]. We do not attempt to address these issues in this paper, but remark that such results would be very useful theoretical guides for practical applications of our estimator Σ_n. Our numerical results show that the spectrum of the cryo-EM estimator Σ_n has qualitative behavior similar to that of the sample covariance matrix.

At this point, we have concluded the part of our paper focused on the general properties of the estimator Σ_n. Next, we move on to the cryo-EM heterogeneity problem.

3. Covariance estimation in cryo-EM heterogeneity problem

Now that we have examined the general covariance matrix estimation problem, let us specialize to the cryo-EM case. In this case, the matrices P have a specific form: they are finite-dimensional versions of P (defined in (1.2)). We begin by describing the Fourier-domain counterpart of P, which will be crucial in analyzing the cryo-EM covariance estimation problem. Our Fourier transform convention is

$$\widehat{f}\left(\xi \right)={\int }_{{\mathbb{R}}^d}f\left(x\right)e^{-ix\cdot \xi }dx,f\left(x\right)=\frac{1}{{\left(2\pi \right)}^d}{\int }_{{\mathbb{R}}^d}\widehat{f}\left(\xi \right)e^{ix\cdot }d\xi .$$ (3.1)

The following classical theorem in tomography (see, e.g., [38] for a proof) shows that the operator P takes on a simpler form in the Fourier domain.

Theorem 3.1 (Fourier projection slice theorem)

Suppose Y ∈ L²(R³)∩L¹(R³) and J : R² → R. Then

$$PY=\widehat{J}\iff \widehat{P}\widehat{Y}=\widehat{J},$$ (3.2)

where P : C(R³) → C(R²) is defined by

$$\left(\widehat{P}\widehat{Y}\right)\left(\begin{array}{c}\hfill \widehat{x}\hfill \\ \hfill \widehat{y}\hfill \end{array}\right)=\widehat{Y}\left(R^T{(\widehat{x},\widehat{y},0)}^T\right)=\widehat{y}(\widehat{x}{R}^1+\widehat{y}{R}^2).$$ (3.3)

Here, Rⁱ is the ith row of R.

Hence, p̂ rotates a function by R and then restricts it to the horizontal plane ẑ = 0. If we let ξ = (x̂, ŷ, ẑ), then another way of viewing p̂ is that it restricts a function to the plane ξ · R³ = 0.

3.1. Infinite-dimensional heterogeneity problem

To build intuition for the Fourier-domain geometry of the heterogeneity problem, consider the following idealized scenario, taking place in Fourier space. Suppose detector technology improves to the point that images can be measured continuously and noiselessly and that we have access to the full joint distribution of R and Î. We would like to estimate the mean m̂ ₀ : R³ → C and covariance function Ĉ₀: R³ × R³ → C of the random field X , defined by

$${\widehat{m}}_0\left(\xi \right)=\mathbb{E}\left[\widehat{X}\left(\xi \right)\right],{\widehat{C}}_0({\xi }_1,{\xi }_2)=\mathbb{E}\left[(\widehat{X}\left({\xi }_1\right)-{\widehat{m}}_0\left({\xi }_1\right))\overline{(\widehat{X}\left({\xi }_2\right)-{\widehat{m}}_0\left({\xi }_2\right))}\right].$$ (3.4)

Heuristically, we can proceed as follows. By the Fourier projection slice theorem, every image I provides an observation of X (ξ) for ξ ∈ R³ belonging to a central plane perpendicular to the viewing direction corresponding to P. By abuse of notation, let ξ ∈ p̂ if p̂ carries the value of P(ξ), and let P(ξ) denote this value. Informally, we expect that we can recover m̂ ₀ and Ĉ₀

$${\widehat{m}}_0\left(\xi \right)=\mathbb{E}[\widehat{I}\left(\xi \right)\mid \xi \in \widehat{I}],{\widehat{C}}_0({\xi }_1,{\xi }_2)=\mathbb{E}[(\widehat{I}\left({\xi }_1\right)-{\widehat{m}}_0\left({\xi }_1\right))\overline{(\widehat{I}\left({\xi }_2\right)-{\widehat{m}}_0\left({\xi }_2\right))}\mid {\xi }_1,{\xi }_2\in \widehat{I}].$$ (3.5)

Now, let us formalize this problem setup and intuitive formulas for m̂ ₀ and Ĉ₀ .

Problem 3.2

Let $\widehat{X}:\Omega \times R^3\to C$ be a random field, where (Ω, F , ν) is a probability space. Here X (ω, ·) is a Fourier volume for each ω ∈ Ω. Let R : Ω → SO(3) be a random rotation, independent of P , having the uniform distribution over SO(3). Let P= P(R) be the (random) projection operator associated with R via (3.3). define the random field ^I : Ω × R² → C by

$$\widehat{I}=\widehat{P}\widehat{X}.$$ (3.6)

Given the joint distribution of ^I and R, find the mean mC ₀ and covariance function X̂ of P , defined in (3.4). Let X̂ be regular enough that

$${\widehat{m}}_0\in C_0^{\infty }\left({\mathbb{R}}^3\right),{\widehat{C}}_0\in C_0^{\infty }({\mathbb{R}}^3\times {\mathbb{R}}^3).$$ (3.7)

In this problem statement, we do not assume that X̂ has a discrete distribution. The calculations that follow hold for any Î satisfying (3.7).

We claim that m̂ ₀ and Ĉ can be found by solving

$$\widehat{A}\left({\widehat{m}}_0\right):=\mathbb{E}\left[{\widehat{P}}^{\ast }\widehat{P}\right]{\widehat{m}}_0=\mathbb{E}\left[{\widehat{P}}^{\ast }\widehat{I}\right]$$ (3.8)

and

$$\widehat{L}\left({\widehat{C}}_0\right):=\mathbb{E}\left[{\widehat{P}}^{\ast }\widehat{P}{\widehat{C}}_0{\widehat{P}}^{\ast }\widehat{P}\right]=\mathbb{E}\left[{\widehat{P}}^{\ast }(\widehat{I}-{\widehat{P}}_{{\widehat{m}}_0}){(\widehat{I}-{\widehat{P}}_{{\widehat{m}}_0})}^{\ast }\widehat{P}\right],$$ (3.9)

equations whose interpretations we shall discuss in this section. Note that (3.8) and (3.9) can be seen as the limiting cases of (2.5) and (2.6) for σ² = 0, p → ∞, and n → ∞.

In the equations above, we define ${\widehat{P}}^{\ast }:C_0^{\infty }\left(R^2\right)\to C_0^{\infty }{\left(R^3\right)}^{\prime }\mathrm{by}\langle {\widehat{P}}^{\ast }\widehat{J},\widehat{Y}\rangle :=\langle \widehat{J},\widehat{P}\widehat{Y}\rangle L^2\left(R^2\right)\mathrm{where}\widehat{J}\in C_0^{\infty }\left(R^2\right),\widehat{Y}\in C_0^{\infty }\left(R^3\right),\mathrm{and}{C}_0^{\infty }{\left(R^3\right)}^{\prime }$ is the space of continuous linear functionals $C_0^{\infty }\left(R^3\right)$. Thus, both sides of (3.8) are elements of $C_0^{\infty }{\left(R^3\right)}^{\prime }$. To verify this equation, we apply both sides to a test function Ŷ:

$$\begin{array}{cc}\hfill \langle \mathbb{E}\left[{\widehat{P}}^{\ast }\widehat{I}\right],\widehat{Y}\rangle & =\mathbb{E}\left[\langle \widehat{I},\widehat{P}\widehat{Y}\rangle L^2\left({\mathbb{R}}^2\right)\right]=\mathbb{E}\left[\mathbb{E}\left[\langle \widehat{I},\widehat{P}\widehat{Y}\rangle L^2\left({\mathbb{R}}^2\right)\mid \widehat{P}\right]\right]\hfill \\ \hfill & =\mathbb{E}\left[\langle {\widehat{P}}_{{\widehat{m}}_0},\widehat{P}\widehat{Y}\rangle L^2\left({\mathbb{R}}^2\right)\right]=\langle \mathbb{E}\left[{\widehat{P}}^{\ast }{\widehat{P}}_{{\widehat{m}}_0}\right],\widehat{Y}\rangle .\hfill \end{array}$$ (3.10)

Note that

$$\begin{array}{cc}\hfill \langle {\widehat{P}}^{\ast }{\widehat{P}}_{\widehat{m}},\widehat{Y}\rangle & =\langle {\widehat{P}}_{\widehat{m}},\widehat{P}\widehat{Y}\rangle L^2\left({\mathbb{R}}^2\right)={\int }_{{\mathbb{R}}^2}\widehat{m}(\widehat{x}{R}^1+\widehat{y}{R}^2)\overline{\widehat{Y}(\widehat{x}{R}^1+\widehat{y}{R}^2)}d\widehat{x}d\widehat{y}\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^3}\widehat{m}\left(\xi \right)\overline{\widehat{Y}\left(\xi \right)}\delta (\xi \cdot R^3)d\xi ,\hfill \end{array}$$ (3.11)

from which it follows that in the sense of distributions,

$$\left({\widehat{P}}^{\ast }\widehat{P}\widehat{m}\right)\left(\xi \right)=\widehat{m}\left(\xi \right)\delta (\xi \cdot R^3)$$ (3.12)

Intuitively, this means that P * P inputs the volume m̂ and outputs a “truncated” volume that coincides with m̂ on a plane perpendicular to the viewing angle and is zero elsewhere. This reflects the fact that the image Î = PX only gives us information about X̂ on a single central plane. When we aggregate this information over all possible R, we obtain the operator Â:

$$\begin{array}{cc}\hfill \widehat{A}\widehat{m}\left(\xi \right)& =\mathbb{E}\left[\widehat{m}\left(\xi \right)\delta (\xi \cdot R^3)\right]=\widehat{m}\left(\xi \right)\frac{1}{4\pi }{\int }_{S^2}\delta (\xi \cdot \theta )d\theta \hfill \\ \hfill & =\frac{\widehat{m}\left(\xi \right)}{\mid \xi \mid }\frac{1}{4\pi }{\int }_{S^2}\delta \left(\frac{\xi }{\mid \xi \mid }\cdot \theta \right)d\theta =\frac{\widehat{m}\left(\xi \right)}{2\mid \xi \mid }.\hfill \end{array}$$ (3.13)

We used the fact that R³ is uniformly distributed over S² if R is uniformly distributed over SO(3). Here, dθ is the surface measure on S² (hence the normalization by 4π). The last step holds because the integral over S² is equal to the circumference of a great circle on S², so it is 2π.

By comparing (3.8) and (2.7), it is clear that P is the analogue of A^Pn for infinite n and p. Also, (3.8) echoes the heuristic formula (3.5). The backprojection operator Ĉ simply “inserts” a 2D image into 3D space by situating it in the plane perpendicular to the viewing direction of the image, and so the RHS of (3.8) at a point ξ is the accumulation of values Ĉ(ξ). Moreover, the operator P is diagonal, and for each ξ, P reflects the measure of the set ξ ∈ Ĉ; i.e., the density of central planes passing through ξ under the uniform distribution of rotations. Thus, (3.8) encodes the intuition from the first equation in (3.5). Inverting P involves multiplying by the radial factor 2|ξ|. In tomography, this factor is called the ramp filter [38]. Traditional tomographic algorithms proceed by applying the ramp filter to the projection data and then backprojecting. Note that solving $\frac{1}{2\mid \xi \mid }{\widehat{m}}_0\left(\xi \right)=E[\widehat{P}\ast \widehat{I}]$ implies performing these operations in the reverse order; however, backprojection and application of the ramp filter commute.

Now we move on to (3.9). Both sides of this equation are continuous linear functionals on $C_0^{\infty }\left(R^3\right)\times C_0^{\infty }\left(R^3\right)$. Indeed, for ${\widehat{Y}}_1,{\widehat{Y}}_2\in C_0^{\infty }\left(R^3\right)$, the LHS of (3.9) operates on $({\widehat{Y}}_1,{\widehat{Y}}_2)$ through the definition

$$\left({\widehat{P}}^{\ast }\widehat{P}\widehat{C}{\widehat{P}}^{\ast }\widehat{P}\right)({\widehat{Y}}_1,{\widehat{Y}}_2)=\langle \widehat{C},({\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_1,{\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_2)\rangle ,$$ (3.14)

where we view $\widehat{C}\in C_0^{\infty }(R^3\times R^3)$ as operating on pairs (η₁, η₂) of elements in $C_0^{\infty }{\left(R^3\right)}^{\prime }$ via

$$\langle \widehat{C},({\eta }_1,{\eta }_2)\rangle :={\int }_{{\mathbb{R}}^3\times {\mathbb{R}}^3}\overline{{\eta }_1\left({\xi }_1\right)}{\eta }_2\left({\xi }_2\right)\widehat{C}({\xi }_1,{\xi }_2)d{\xi }_{1}d{\xi }_2.$$ (3.15)

Using these definitions, we verify (3.9):

$$\begin{array}{cc}\hfill & \mathbb{E}\left[{\widehat{P}}^{\ast }(\widehat{I}-{\widehat{P}}_{{\widehat{m}}_0}){(\widehat{I}-{\widehat{P}}_{{\widehat{m}}_0})}^{\ast }\widehat{P}\right]({\widehat{Y}}_1,{\widehat{Y}}_2)\hfill \\ \hfill & :=\mathbb{E}\left[\langle {\widehat{P}}^{\ast }(\widehat{I}-\widehat{P}{\widehat{m}}_0),{\widehat{Y}}_1\rangle \overline{\langle {\widehat{P}}^{\ast }(\widehat{I}-\widehat{P}{\widehat{m}}_0),{\widehat{Y}}_2\rangle }\right]\hfill \\ \hfill & =\mathbb{E}\left[\overline{\langle {\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_1,\widehat{X}-{\widehat{m}}_0\rangle }\langle {\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_2,\widehat{X}-{\widehat{m}}_0\rangle \right]\hfill \\ \hfill & =\mathbb{E}\left[{\int }_{{\mathbb{R}}^3\times {\mathbb{R}}^3}\overline{{\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_1\left({\xi }_1\right)}(\widehat{X}\left({\xi }_1\right)-{\widehat{m}}_0\left({\xi }_1\right)){\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_2\left({\xi }_2\right)\overline{(\widehat{X}\left({\xi }_2\right)-{\widehat{m}}_0\left({\xi }_2\right))}d{\xi }_{1}d{\xi }_2\right]\hfill \\ \hfill & =\mathbb{E}\left[{\int }_{{\mathbb{R}}^3\times {\mathbb{R}}^3}\overline{{\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_1\left({\xi }_1\right)}{\widehat{C}}_0({\xi }_1,{\xi }_2){\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_2\left({\xi }_2\right)d{\xi }_{1}d{\xi }_2\right]\hfill \\ \hfill & =\mathbb{E}\left[\langle {\widehat{C}}_0({\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_1,{\widehat{P}}^{\ast }\widehat{P}{\widehat{Y}}_2)\rangle \right]=\mathbb{E}\left[{\widehat{P}}^{\ast }\widehat{P}{\widehat{C}}_0{\widehat{P}}^{\ast }\widehat{P}({\widehat{Y}}_1,{\widehat{Y}}_2))\right].\hfill \end{array}$$ (3.16)

Substituting (3.12) into the last two lines of the preceding calculation, we find

$$\left({\widehat{P}}^{\ast }\widehat{P}\widehat{C}{P}^{\ast }\widehat{P}\right)({\xi }_1,{\xi }_2)=\widehat{C}({\xi }_1,{\xi }_2)\delta ({\xi }_1\cdot R^3)\delta ({\xi }_2\cdot R^3)$$ (3.17)

This reflects the fact that an image Î gives us information about P (ξ ,ξ ) for ξ ,ξ ∈ Ĉ.

Taking the expectation over R, we find that

$$\begin{array}{cc}\hfill \left(\widehat{L}\widehat{C}\right)({\xi }_2,{\xi }_2)& =\mathbb{E}\left[\widehat{C}({\xi }_1,{\xi }_2)\delta ({\xi }_1\cdot R^3)\delta ({\xi }_2\cdot R^3)\right]\hfill \\ \hfill & =\widehat{C}({\xi }_1,{\xi }_2)\frac{1}{4\pi }{\int }_{S^2}\delta ({\xi }_1\cdot \theta )\theta ({\xi }_2\cdot \theta )=:\widehat{C}({\xi }_1,{\xi }_2)K({\xi }_1,{\xi }_2).\hfill \end{array}$$ (3.18)

Like Â, the operator P is diagonal. P is a fundamental operator in tomographic inverse problems involving variability; we term it the projection covariance transform. In the same way that (3.8) reflected the first equation of (3.5), we see that (3.9) resembles the second equation of (3.5). In particular, the kernel value K(ξ₁, ξ₂) reflects the density of central planes passing through ξ₁, ξ₂.

To understand this kernel, let us compute it explicitly. We have

$$K({\xi }_1,{\xi }_2)=\frac{1}{4\pi }{\int }_{S^2}\delta ({\xi }_1\cdot \theta )\delta ({\xi }_2\cdot \theta )d\theta .$$ (3.19)

For fixed ξ₁, note that δ(ξ₁ · θ) is supported on the great circle of S² perpendicular to ξ₁. Similarly, δ(ξ₂ · θ) corresponds to a great circle perpendicular to ξ₂. Choose ξ₁, ξ₂ ∈ R³ so that |ξ₁ × ξ₂| /= 0. Then, note that these two great circles intersect in two antipodal points θ = ±(ξ₁ × ξ₂)/|ξ₁ × ξ₂|, and the RHS of (3.19) corresponds to the total measure of δ(ξ₁ · θ)δ(ξ₂ · θ) at those two points.

To calculate this measure explicitly, let us define the approximation to the identity ${\delta }_{∊}\left(t\right)=\frac{1}{2∊}{X}_{[-∊,∊]}\left(t\right)$. Fix E₁, E₂ > 0. Note that δ₁ (ξ₁ · θ) is supported on a strip of width 2E₁/|ξ₁| centered at the great circle perpendicular to ξ₁. δ₂ (ξ₂ · θ) is supported on a strip of width 2E₂/|ξ₂| intersecting the first strip transversely. For small E₁, E₂, the intersection of the two strips consists of two approximately parallelogram-shaped regions, S₁ and S₂ (see Figure 3).

Figure 3.

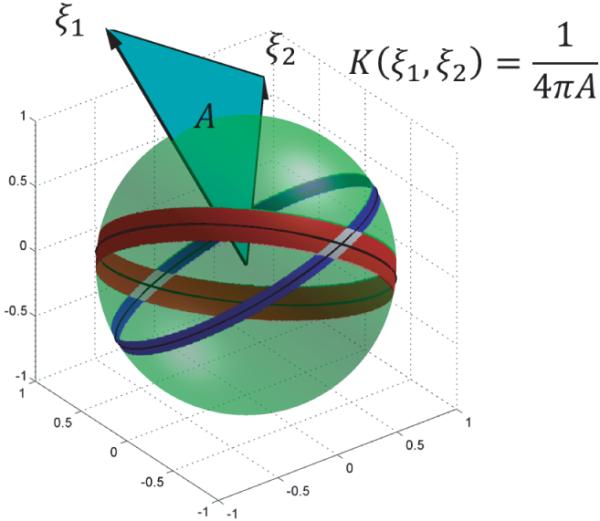
The triangular area filter. ξ1 induces a strip on S2 of width proportional to 1/|ξ1 ^{| (blue); ξ}2 ^{induces a strip of width proportional to 1/|ξ}2 | (red). The strips intersect in two parallelogram-shaped regions (white), each with area proportional to 1/|ξ1 ^{× ξ}2^{|. Hence, K(ξ}1 ^{, ξ}2) is inversely proportional to the area of the triangle spanned by ξ1^{, ξ}2 (cyan).

The sine of the angle between the diagonals of each of these regions is |ξ₁ × ξ₂|/|ξ₁||ξ₂|, and a simple calculation shows that the area of one of these regions is 2E₁2E₂/|ξ₁ × ξ₂|. It follows that

$$\begin{array}{cc}\hfill K({\xi }_1,{\xi }_2)& =\frac{1}{4\pi }{\int }_{S^2}\delta ({\xi }_1\cdot \theta )\delta ({\xi }_2\cdot \theta )d\theta =\underset{{∊}_1,{∊}_2\to 0}{\lim }\frac{1}{4\pi }{\int }_{S^2}\delta ({\xi }_1\cdot \theta )\delta ({\xi }_2\cdot \theta )d\theta \hfill \\ \hfill & =\underset{{∊}_1,{∊}_2\to 0}{\lim }\frac{1}{4\pi }{\int }_{S_1\cup S_2}\frac{1}{2{∊}_1}\frac{1}{2{∊}_2}d\theta =\underset{{∊}_1,{∊}_2\to 0}{\lim }\frac{1}{4\pi }2\frac{4{∊}_1{∊}_2}{{\xi }_1\times {\xi }_2\mid }\frac{1}{2{∊}_1}\frac{1}{2{∊}_2}\hfill \\ \hfill & =\frac{1}{4\pi }\frac{2}{{\xi }_1\times {\xi }_2\mid }.\hfill \end{array}$$ (3.20)

This analytic form of K sheds light on the geometry of Ĉ. Recall that K(ξ₁, ξ₂) is a measure of the density of central planes passing through ξ₁ and ξ₂. Note that this density is nonzero everywhere, which reflects the fact that there is a central plane passing through each pair of points in R³. The denominator in K is proportional to the magnitudes |ξ₁| and |ξ₂|, which indicates that there is a greater density of planes passing through pairs of points nearer the origin. Finally, note that K varies inversely with the sine of the angle between ξ₁ and ξ₂; indeed, a greater density of central planes pass through a pair of points nearly collinear with the origin. In fact, there is a singularity in K when ξ₁, ξ₂ are linearly dependent, reflecting the fact that infinitely many central planes pass through collinear points. As a way to sum up the geometry encoded in K, note that except for the factor of 1/4π, 1/K is the area of the triangle spanned by the vectors ξ₁ and ξ₂. For this reason, we call 1/K the triangular area filter.

Note that the triangular area filter is analogous to the ramp filter: it grows linearly with the frequencies |ξ₁| and |ξ₂| to compensate for the loss of high frequency information incurred by the geometry of the problem. So, this filter is a generalization of the ramp filter appearing in the estimation of the mean to the covariance estimation problem. The latter has a somewhat more intricate geometry, which is reflected in K.

The properties of K translate into the robustness of inverting P (supposing we added noise to our model). In particular, the robustness of recovering P (ξ ,ξ ) grows with K(ξ ,ξ ). For example, recovering higher frequencies in Ĉ is more dificult. However, the fact that K is everywhere positive means that P is at least invertible. This statement is important in proving theoretical results about our estimators, as we saw in section 2.2. Note that an analogous problem of estimating the covariance matrix of 2D objects from their one-dimensional line projections would not satisfy this condition, because for most pairs of points in R², there is not a line passing through both points as well as the origin.

3.2. The discrete covariance estimation problem

The calculation in the preceding section shows that if we could sample images continuously and if we had access to projection images from all viewing angles, then P would become a diagonal operator. In this section, we explore the modifications necessary for the realistic case where we must work with finite-dimensional representations of volumes and images.

Our idea is to follow what we did in the fully continuous case treated above and estimate the covariance matrix in the Fourier domain. One possibility is to choose a Cartesian basis in the Fourier domain. With this basis, a tempting way to define P^Ps would be to restrict the Fourier 3D grid to the pixels of a 2D central slice by nearest-neighbor interpolation. This would make P^Ps a coordinate-selection operator, making L^Pn diagonal. However, this computational simplicity comes at a great cost in accuracy; numerical experiments show that the errors induced by such a coarse interpolation scheme are unacceptably large. Such an interpolation error should not come as a surprise, considering similar interpolation errors in computerized tomography [38]. Hence, we must choose other bases for the Fourier volumes and images.

The finite sampling rate of the images limits the 3D frequencies we can hope to reconstruct. Indeed, since the images are sampled on an N × N grid confining a disc of radius 1, the corresponding Nyquist bandlimit is ω_Nyq = Nπ/2. Hence, the images carry no information past this 2D bandlimit. By the Fourier slice theorem, this means that we also have no information about X past the 3D bandlimit ω_Nyq. In practice, the exponentially decaying envelope of the CTF function renders even fewer frequencies possible to reconstruct. Moreover, we saw in section 3.1 and will see in section 6.2 that reconstruction of Σ₀ becomes more ill-conditioned as the frequency increases. Hence, it often makes sense to take a cuto? ω_max < ω_Nyq. We can choose ω_max to correspond to an effective grid size of N_res pixels, where N_res ≤ N . In this case, we would choose ω_max = N_resπ/2. Thus, it is natural to search for X in a space of functions bandlimited in B_ωmax (the ball of radius ω_max) and with most of their energy contained in the unit ball. The optimal space B with respect to these constraints is spanned by a finite set of 3D Slepian functions [56]. For a given bandlimit ω_max, we have

$$p=\dim \left(B\right)=\frac{2}{9\pi }{\omega }_{\max }^3.$$ (3.21)

This dimension is called the Shannon number, and is the trace of the kernel in [56, eq. 6].

For the purposes of this section, let us work abstractly with the finite-dimensional spaces VP ⊂ C₀(B_ωmax ) and IP ⊂ C₀(D_ωmax ), which represent Fourier volumes and Fourier images, respectively (D_ωmax ⊂ R is the disc of radius ω_max). For example, VP could be spanned by the Fourier transforms of the 3D Slepian functions. Let

$$\widehat{V}=\mathrm{span}\left\{{\widehat{h}}_j\right\},\widehat{I}=\mathrm{span}\left\{{\widehat{g}}_i\right\}$$ (3.22)

with dim(VĈ) = pP and dim(IĈ) = qP. Assume that for all R, Ĉ(VĈ) ⊂ IP (i.e., we do not need to worry about interpolation). Denote by PP the matrix expression of Ĉ . Thus, PP ∈ C^qP×pP. Let X^P1,… , X^Pn be the representations of P ,… , Ĉ in the basis for VĈ.

Since we are given the images I_s in the pixel basis R^q , let us consider how to map these images into IĈ. Let Q₁ : R^q → IP be the mapping which fits (in the least-squares sense) an element of IP to the pixel values defined by a vector in R^q. It is easiest to express Q₁ in terms of the reverse mapping Q₂ : IP → R^q . The ith column of Q₂ consists of the evaluations of g_i at the real-domain grid points inside the unit disc. It is easy to see that the least-squares method of defining $Q_1=Q_2^{+}={\left(Q_2^H{Q}_2\right)}^{-1}{Q}_s^H$

Now, note that

$$I=SPX+E\Rightarrow Q_{1}I=Q_{1}SPX+Q_{1}E\approx \widehat{P}\widehat{X}+Q_{1}E.$$ (3.23)

The last approximate equality is due to the Fourier slice theorem. The inaccuracy comes from the discretization operator S. Note that $\mathrm{Var}\left[Q_{1}E\right]={\sigma }^2{Q}_1{Q}_1^H={\sigma }^2{\left(Q_2^H{Q}_2\right)}^{-1}$. We would like the latter matrix to be a multiple of the identity matrix so that the noise in the images remains white. Let us calculate the entries of $Q_2^H{Q}_2$ in terms of the basis functions g_i. Given the fact that we are working with volumes h_i which have most of their energy concentrated in the unit ball, it follows that g_i have most of their energy concentrated in the unit disc. If x₁,… , x_q are the real-domain image grid points, it follows that

$$\begin{array}{cc}\hfill {\left(Q_2^H{Q}_2\right)}_{ij}& =\sum _{r=1}^q\overline{g_1\left(x_r\right)}{g}_j\left(x_r\right)\approx \frac{q}{\pi }{\int }_{\mid x\mid \le 1}\overline{g_i\left(x\right)}{g}_j\left(x\right)dx\hfill \\ \hfill & \approx \frac{q}{\pi }\overline{\langle g_i,g_j\rangle L^2\left(R^2\right)}=\frac{q}{\pi }\frac{1}{{\left(2\pi \right)}^2}\overline{\langle {\widehat{g}}_i,{\widehat{g}}_j\rangle \rangle L^2\left(R^2\right)}.\hfill \end{array}$$ (3.24)

It follows that in order for $Q_2^H{Q}_2$ to be (approximately) a multiple of the identity matrix, we should require {gP_i} to be an orthonormal set in L²(R²). If we let c_q = 4π³/q, then we find that

$$Q_1{Q}_1^H\approx c_q{I}_{\widehat{q}}.$$ (3.25)

It follows that, if we make the approximations in (3.23) and (3.25), we can formulate the heterogeneity problem entirely in the Fourier domain as follows:

$$\widehat{I}=\widehat{P}\widehat{X}=\widehat{E},$$ (3.26)

where Var[EĈ] = σ²c_q I_qP. Thus, we have an instance of Problem (1.1) with σ² replaced by σ²c_q , q replaced by qP, and p replaced by pP. We seek μP₀ = E[XP] and Σ^{P 0} = Var[XP]. Equations (2.5) and (2.6) become

$${\widehat{A}}_n{\widehat{\mu }}_n:=\left(\frac{1}{n}\sum _{s=1}^n{\widehat{P}}_s^H{\widehat{P}}_s\right){\widehat{\mu }}_n=\frac{1}{n}\sum _{s=1}^n{\widehat{P}}_s^H{\widehat{I}}_s$$ (3.27)

and

$$\begin{array}{cc}\hfill {\widehat{L}}_n{\widehat{\Sigma }}_n:& =\frac{1}{n}\sum _{s=1}^n{\widehat{P}}_s^H{\widehat{P}}_s{\widehat{\Sigma }}_n{\widehat{P}}_s^H{\widehat{P}}_s\hfill \\ \hfill & =\frac{1}{n}\sum _{s=1}^n{\widehat{P}}_s^H({\widehat{I}}_s-{\widehat{P}}_s{\widehat{\mu }}_n){({\widehat{I}}_s-{\widehat{P}}_s{\widehat{\mu }}_n)}^H{\widehat{P}}_s-{\sigma }^2{c}_q{\widehat{A}}_n=:{\widehat{B}}_n.\hfill \end{array}$$ (3.28)

3.3. Exploring AP and LĈ

In this section, we seek to find expressions for AP and LĈ like those in (3.13) and (3.18). The reason for finding these limiting operators is twofold. First of all, recall that the theoretical results in section 2.2 depend on the invertibility of these limiting operators. Hence, knowing AP and LP in the cryo-EM case will allow us to verify the assumptions of Propositions 2.1 and 2.2. Second, the law of large numbers guarantees that for large n, we have A^Pn ≈ AP and L^Pn ≈ LĈ. We shall see in section 5 that approximating A^Pn and L^Pn by their limiting counterparts makes possible the tractable implementation of our algorithm.

In section 3.1, we worked with functions m̂ : R³ → C and P : R³ × R³ → C. Now, we are in a finite-dimensional setup, and we have formulated (3.27) and (3.28) in terms of vectors and matrices. Nevertheless, in the finite-dimensional case we can still work with functions as we did in section 3.1 via the identifications

$$\widehat{\mu }\in C^{\widehat{p}}\leftrightarrow \widehat{m}=\sum _{i=1}^{\widehat{p}}{\widehat{\mu }}_i{\widehat{h}}_i\in \widehat{V},\widehat{\Sigma }\in C^{\widehat{p}\times \widehat{p}}\leftrightarrow \widehat{C}=\sum _{i,j=1}^{\widehat{p}}{\widehat{\Sigma }}_{i,j}{\widehat{h}}_i\otimes {\widehat{h}}_j\in \widehat{V}\otimes \widehat{V},$$ (3.29)

where we define

$$({\widehat{h}}_i\otimes {\widehat{h}}_j)({\xi }_1,{\xi }_2)={\widehat{h}}_i\left({\xi }_1\right)\overline{{\widehat{h}}_j\left({\xi }_2\right)},$$ (3.30)

and VP ⊗ VP = span{h^Pi ⊗ h^Pj }. Thus, we identify C^pP and C^pP×pP with spaces of bandlimited functions. For these identifications to be isometries, we must endow VP with an inner product for which the h^Pi are orthonormal. We consider a family of inner products, weighted by radial functions w(|ξ|):

$$\langle {\widehat{h}}_i,{\widehat{h}}_j\rangle L_w^2\left(R^3\right)={\int }_{R^3}{\widehat{h}}_i\left(\xi \right)\overline{{\widehat{h}}_j\left(\xi \right)}w(\mid \xi \mid )d\xi ={\delta }_{ij}.$$ (3.31)

The inner product on VP ⊗ VP is inherited from that of VĈ.

Note that A^Pn and L^Pn both involve the projection-backprojection operator P^PH P^Ps. Let us see how to express P^PH P^Ps as an operator on VĈ. The ith column of P^Ps is the representation of in the orthonormal basis for I . Hence, using the isomorphism C^qP ↔ I and reasoning along the lines of (3.11), we find that

$${\left({\widehat{P}}_s^H{\widehat{P}}_s\right)}_{i,j}=\overline{\langle {\widehat{P}}_s{\widehat{h}}_i,{\widehat{P}}_s{\widehat{h}}_j\rangle L^2\left(R^2\right)}={\int }_{R^3}\overline{{\widehat{h}}_i\left(\xi \right){\widehat{h}}_j}\left(\xi \right)\delta (\xi \cdot R_s^3)d\xi .$$ (3.32)

Note that here and throughout this section, we perform manipulations (like those in section 3.1) that involve treating elements of VP as test functions for distributions. We will ultimately construct VP so that its elements are continuous, but not in C^∞(R³), as assumed in section 3.1. Nevertheless, since we are only dealing with distributions of order zero, continuity of the elements of VP is sufficient.

From (3.32), it follows that if μP ∈ C^pP ↔ m̂

$$\begin{array}{cc}\hfill \left({\widehat{P}}_s^H{\widehat{P}}_s\right)\widehat{\mu }\leftrightarrow \sum _{i=1}^{\widehat{p}}{\widehat{h}}_i\sum _{j=1}^{\widehat{p}}{\left({\widehat{P}}_s^H{\widehat{P}}_s\right)}_{ij{\mu }_{\widehat{j}}}& =\sum _{i=1}^{\widehat{p}}{\widehat{h}}_i\sum _{j=1}^{\widehat{p}}{\int }_{R^3}\overline{{\widehat{h}}_i\left(\xi \right)}{\widehat{\mu }}_j{\widehat{h}}_j\left(\xi \right)\delta (\xi \cdot R_s^3)d\xi \hfill \\ \hfill & =\sum _{i=1}^{\widehat{p}}{\widehat{h}}_i{\int }_{R^3}\left(\widehat{m}\left(\xi \right)\delta (\xi \cdot R_s^3)\right)\overline{{\widehat{h}}_i\left(\xi \right)}d\xi \hfill \\ \hfill & =:{\pi }_{\widehat{V}}\left(\widehat{m}\left(\xi \right)\delta (\xi \cdot R_s^3)\right),\hfill \end{array}$$ (3.33)

where ${\pi }_{\widehat{\gamma }}:C_0^{\infty }{\left(R^3\right)}^{\prime }\to \widehat{V}$

$${\pi }_{\widehat{V}}\left(\eta \right)=\sum _i{\widehat{h}}_i\langle \eta ,{\widehat{h}}_i\rangle ,\eta \in C_0^{\infty }{\left(R^3\right)}^{\prime }$$ (3.34)

is a projection onto the finite-dimensional subspace VĈ.

In analogy with (3.8), we have

$${\widehat{A}}_{\widehat{\mu }}\leftrightarrow E\left[{\pi }_{\widehat{V}}\left(\widehat{m}\left(\xi \right)\delta (\xi \cdot R^3)\right)\right]={\pi }_{\widehat{V}}\left(\frac{\widehat{m}\left(\xi \right)}{2\mid \xi \mid }\right).$$ (3.35)

Note AP resembles the operator P obtained in (3.8), with the addition of the “low-pass filter” π_VP. As a particular choice of weight, one might consider w(|ξ|) = 1/|ξ| in order to cancel the ramp filter. For this weight, note that

$$\widehat{A}\widehat{\mu }\leftrightarrow {\pi }_{\widehat{V}}\left(\frac{\widehat{m}\left(\xi \right)}{2\mid \xi \mid }\right)={\pi }_{\widehat{V}}^w\left(\frac{1}{2}\widehat{m}\left(\xi \right)\right)=\frac{1}{2}\widehat{m}\left(\xi \right),w(\mid \xi \mid )=1∕\mid \xi \mid ,$$ (3.36)

where ${\pi }_{\widehat{V}}^w$ is the orthogonal projection onto VP with respect to the weight w. Thus, for this weight we find that $\widehat{A}=\frac{1}{2}{I}_{\widehat{p}}$

A calculation analagous to (3.33) shows that for ΣP ∈ C^pP×pP ↔ Ĉ

$${\widehat{P}}_s^H{\widehat{P}}_s\widehat{\Sigma }{\widehat{P}}_s^H{\widehat{P}}_s\leftrightarrow {\pi }_{\widehat{V}\otimes \widehat{V}}\left(\widehat{C}({\xi }_1,{\xi }_2)\delta ({\xi }_1\cdot R_s^3)\delta ({\xi }_2\cdot R_s^3)\right).$$ (3.37)

Then, taking the expectation over R³, we find that

$$\widehat{L}\widehat{\Sigma }\leftrightarrow {\pi }_{\widehat{V}\otimes \widehat{V}}\left(\widehat{C}({\xi }_1,{\xi }_2)K({\xi }_1,{\xi }_2)\right).$$ (3.38)

This shows that between LĈ is linked to P via the low-pass-filter π _P analogously to (3.34).

3.4. Properties of AP and LĈ

In this section, we will prove several results about AP and LĈ, defined in (3.35) and (3.38). We start by proving a useful lemma.

Lemma 3.3

For $\eta \in C_0^{\infty }{\left(R^3\right)}^{\prime }$ and Ŷ Ĉ, we have

$${\langle }_{\pi \widehat{V}}\eta ,\widehat{Y}\rangle L_w^2\left(R^3\right)=\langle \eta ,\widehat{Y}\rangle .$$ (3.39)

Likewise, if $\eta \in C_0^{\infty }{(R^3\times R^3)}^{\prime }\mathrm{and}\widehat{C}\in \widehat{V}\otimes \widehat{V}$, we have

$$\langle {\pi }_{\widehat{V}\otimes \widehat{V}}\eta ,\widehat{C}\rangle L_w^2(R^3\times R^3)=\langle \eta ,\widehat{C}\rangle .$$ (3.40)

Proof

Indeed, we have

$$\begin{array}{cc}\hfill \langle {\pi }_{\widehat{V}}\eta ,\widehat{Y}\rangle L_w^2\left(R^3\right)& =\sum _{i=1}^{\widehat{p}}\langle \eta ,{\widehat{h}}_i\rangle \langle {\widehat{h}}_i,\widehat{Y}\rangle L_w^2\left(R^3\right)\hfill \\ \hfill & =\langle \eta ,\sum _{i=1}^{\widehat{p}}\langle \widehat{Y},{\widehat{h}}_i\rangle L_w^2\left(R^3\right){\widehat{h}}_i\langle =\langle \eta ,\widehat{Y}\rangle .\hfill \end{array}$$ (3.41)

The proof of the second claim is similar.

Note that AP and LP are self-adjoint and PSD because each A^Pn and L^Pn satisfies this property. In the next proposition, we bound the minimum eigenvalues of these two operators from below.

Proposition 3.4

Let M_w(ω_max) = max^|ξ|≤ωmax |ξ|w(|ξ|). Then,

$${\lambda }_{\min }\left(\widehat{A}\right)\ge \frac{1}{2M_w\left({\omega }_{\max }\right)},{\lambda }_{\min }\left(\widehat{L}\right)\ge \frac{1}{2M_w^2\left({\omega }_{\max }\right)}.$$ (3.42)

Proof

Let μP ∈ C^pP ↔ m̂ find

$$\begin{array}{cc}\hfill \langle \widehat{A}\widehat{\mu },\widehat{\mu }\rangle C^{\widehat{p}}& =\langle {\pi }_{\widehat{V}}\left(\widehat{m}\frac{1}{2\mid \xi \mid }\right),\widehat{m}\rangle L_w^2\left(R^3\right)=\langle \widehat{m}\frac{1}{2\mid \xi \mid },\widehat{m}\rangle \hfill \\ \hfill & ={\int }_{B_{\omega max}}\mid \widehat{m}\left(\xi \right){\mid }^2\frac{1}{2\mid \xi \mid w(\mid \xi \mid )}w(\mid \xi \mid )d\xi \ge \frac{1}{2M_{w\left({\omega }_{max}\right)}}\Vert \widehat{m}{{\Vert }^2}_{L_w^2\left(R^3\right)}^2=\frac{1}{2M_{w\left({\omega }_{max}\right)}}\Vert \widehat{\mu }{\Vert }^2.\hfill \end{array}$$ (3.43)

The bound on the minimum eigenvalue of LP follows from a similar argument, using (3.38) and the following bound:

$$\underset{{\xi }_1,{\xi }_2\in B_{w\max }}{\min }\frac{K({\xi }_1,{\xi }_2)}{w(\mid \xi {\mid }_1)w\left({\xi }_2\right)}=\underset{{\xi }_1{\xi }_2\in B_{w\max }}{\min }\frac{1}{2\pi \mid {\xi }_1\times {\xi }_2\mid w(\mid {\xi }_1\mid )w(\mid {\xi }_2\mid )}\ge \frac{1}{2\pi M_w^2\left({\omega }_{\max }\right)}.$$ (3.44)

By inspecting M_w (ω_max), we see that choosing w = 1/|ξ| leads to better conditioning of both AP and LĈ, as compared to w = 1. This is because the former weight compensates for the loss of information at higher frequencies. We see from (3.36) that for w = 1/|ξ|, AP is perfectly conditioned. This weight also cancels the linear growth of the triangular area filter with radial frequency. However, it does not cancel K altogether, since the dependency on sin γ in the denominators in (3.44) remains, where γ is the angle between ξ₁ and ξ₂.

The maximum eigenvalue of LP cannot be bounded as easily, since the quotient in (3.44) is not bounded from above. A bound on λ_max(LĈ) might be obtained by using the fact that a bandlimited P can only be concentrated to a limited extent around the singular set {ξ₁, ξ₂ : |ξ₁ × ξ₂| = 0}.

Finally, we prove another property of AP and LĈ: they commute with rotations. Let us define the group action of SO(3) on functions R³ → C as follows: for R ∈ SO(3) and P : R³ → C, let R. Ĉ(ξ) = Ĉ(R^T ξ). Likewise, define the group action of SO(3) on functions P : R³ × R³ → C via R. Ĉ(ξ₁, ξ₂) = Ĉ(R^T ξ₁, R^T ξ₂).

Proposition 3.5

Suppose that the subspace VP is closed under rotations. Then, for any Y ∈ V , C ∈ V ⊗ V , and R ∈ SO(3), we have

$$R.\left(\widehat{A}\widehat{Y}\right)=\widehat{A}(R.\widehat{Y}),R.\left(\widehat{L}\widehat{C}\right)=\widehat{L}(R.\widehat{C}),$$ (3.45)

where APX and LPX are understood via the identifications (3.29).

Proof

We begin by proving the first half of (3.45). First of all, extend the group action of SO(3) to the space $C_0^{\infty }{\left(R^3\right)}^{\prime }$, via

$$\langle R.\eta \widehat{Y},\widehat{Y}\rangle :=\langle \eta ,R^{-1}.\widehat{Y}\rangle ,\widehat{Y}\in C_0^{\infty }\left(R^3\right).$$ (3.46)

We claim that for any $\eta \in C_0^{\infty }{\left(R^3\right)}^{\prime }$, we have R.(π _Pη) = π _P(R.η). Since VP is closed under rotations, both sides of this equation are elements of VĈ. We can verify their equality by taking an inner product with an arbitrary element Ĉ VĈ. Using Lemma 3.3 and the fact that VP is closed under rotations, we obtain

$$\begin{array}{cc}\hfill \langle R.\left({\pi }_{\widehat{V}}\eta \right),\widehat{Y}\rangle L_w^2\left(R^3\right)& =\langle {\pi }_{\widehat{V}}\eta ,R^{-1}.\widehat{Y}\rangle L_w^2\left(R^3\right)=\langle \eta ,R^{-1}.\widehat{Y}\rangle \hfill \\ \hfill & =\langle R.\eta ,\widehat{Y}\rangle =\langle {\pi }_{\widehat{V}}(R.\eta ),\widehat{Y}\rangle L_w^2\left(R^3\right).\hfill \end{array}$$ (3.47)

Next, we claim that for any Ĉ VĈ, we have R.( ^{P P}) = Ĉ(R. Ĉ). To check whether these two elements of $\eta \in C_0^{\infty }{\left(R^3\right)}^{\prime }$ are the same, we apply them to a test function $\widehat{Z}\in C_0^{\infty }\left(R^3\right)$:

$$\begin{array}{cc}\hfill \langle R.\left(\widehat{A}\widehat{Y}\right),\widehat{Z}\rangle & =\langle \widehat{A}\widehat{Y},R^{-1}.\widehat{Z}\rangle ={\int }_{R^3}\frac{\widehat{Y}\left(\xi \right)}{2\mid \xi \mid }\widehat{Z}\left(R\xi \right)d\xi \hfill \\ \hfill & ={\int }_{R^3}\frac{\widehat{Y}\left(R^H\xi \right)}{2\mid \xi \mid }\widehat{Z}\left(\xi \right)d\xi =\langle \widehat{A}(R.\widehat{Y}),\widehat{Z}\rangle .\hfill \end{array}$$ (3.48)

Putting together what we have, we find that

$$R.\left(\widehat{A}\widehat{Y}\right)=R.\left({\pi }_{\widehat{V}}\left(\widehat{A}\widehat{Y}\right)\right)={\pi }_{\widehat{V}}=(R.\left(\widehat{A}\widehat{Y}\right))\left(\widehat{A}(R.\widehat{Y})\right)=\widehat{A}(R.\widehat{Y}),$$ (3.49)

which proves the first half of (3.45). The second half is proved analogously.

This property of AP and LP is to be expected, given the rotationally symmetric nature of these operators. This suggests that LP can be studied further using the representation theory of SO(3).

Finally, let us check that the assumptions of Propositions 2.1 and 2.2 hold in the cryo-EM case. It follows from Proposition 3.4 that as long as M_w (ω_max) < ∞, the limiting operators AP and LP are invertible. Of course, it is always possible to choose such a weight w. In particular the weights already considered, w = 1, 1/|ξ| satisfy this property. Moreover, by rotational symmetry, lPĈ(R)l is independent of R, and so of course this quantity is uniformly bounded. Thus, we have checked all the necessary assumptions to arrive at the following conclusion.

Proposition 3.6

If we neglect the errors incurred in moving to the Fourier domain and assume that the rotations are drawn uniformly from SO(3), then the estimators μP_n and Σ^{P n} obtained from (3.27) and (3.28) are consistent.

4. Using ${\widehat{\mu }}_n,{\widehat{\Sigma }}_n$ to determine the conformations

To solve Problem 1.2, we must do more than just estimate μP₀ and Σ^{P 0}. We must also estimate C, X^{P c}, and p_c, where X^{P c} is the coefficient vector of ^Pc in the basis for VĈ. Once we solve (3.27) and (3.28) for μP_n and Σ^{P n}, we perform the following steps.

From the discussion on high-dimensional PCA in section 2.3, we expect to determine the number of structural states by inspecting the spectrum of Σ^{P n}. We expect the spectrum of Σ^{P n} to consist of a bulk distribution along with C − 1 separate eigenvalues (assuming the SNR is sufficiently high), a fact confirmed by our numerical results. Hence, given Σ^{P n}, we can estimate C.

Next, we discuss how to reconstruct X^{P 1},… , X^{P C} and p₁,… , p_C . Our approach is similar to Penczek, Kimmel, and Spahn’s [43]. By the principle of PCA, the leading eigenvectors of ${\widehat{\Sigma }}_n$ span the space of mean subtracted volumes ${\widehat{X}}^1-{\widehat{\mu }}_0,\dots ,{\widehat{X}}^C-{\widehat{\mu }}_0.\mathrm{If}{\widehat{V}}_n^1,\dots ,{\widehat{V}}_n^{C-1}$ are the leading eigenvectors of ${\widehat{\Sigma }}_n$, we can write

$${\widehat{X}}_s\approx {\widehat{\mu }}_n+\sum _{c^{\prime }=1}^{C-1}{\alpha }_{s,c^{\prime }}{\widehat{V}}_n^{c^{\prime }}.$$ (4.1)

Note that there is only approximate equality because we have replaced the mean μP₀ by the estimated mean μP_n, and the eigenvectors of Σ^{P 0} by those of Σ^{P n}. We would like to recover the coefficients α_s = (α_s,1,… , α_s,C−1), but the X^Ps are unknown. Nevertheless, if we project the above equation by P^Ps, then we get

$$\sum _{c^{\prime }=1}^{C-1}{\alpha }_{s,c^{\prime }}{\widehat{P}}_s{\widehat{V}}_n^{c^{\prime }}\approx {\widehat{P}}_s{\widehat{X}}_s-{\widehat{P}}_s{\widehat{\mu }}_n=({\widehat{I}}_s-{\widehat{P}}_s{\widehat{\mu }}_n)-{\widehat{∊}}_s.$$ (4.2)

For each s, we can now solve this equation for the coefficient vector α_s in the least-squares sense. This gives us n vectors in C^C−1. These should be clustered around C points ${\alpha }^c=({\alpha }_1^c,\dots ,{\sigma }_{C-1}^c)$ for c = 1,… ,C, corresponding to the C underlying volumes. At this point, Penczek, Kimmel, and Spahn propose to perform K-means clustering on α_s in order to deduce which image corresponds to which class. However, if the images are too noisy, then it would be impossible to separate the classes via clustering. Note that in order to reconstruct the original volumes, all we need are the means of the C clusters of coordinates. If the mean volume and top eigenvectors are approximately correct, then the main source of noise in the coordinates is the Gaussian noise in the images. It follows that the distribution of the coordinates in C^C−1 is a mixture of Gaussians. Hence, we can find the means α^c of each cluster using either an EM algorithm (of which the K-means algorithm used by Penczek is a limiting case [8]) or the method of moments, e.g., [23]. In the current implementation, we use an EM algorithm. Once we have the C mean vectors, we can reconstruct the original volumes using (4.1). Putting these steps together, we arrive at a high-level algorithm to solve the heterogeneity problem (see Algorithm 1).

5. Implementing Algorithm 1

In this section, we confront the practical challenges of implementing Algorithm 1. We consider different approaches to addressing these challenges and choose one approach to explore further.

5.1. Computational challenges and approaches

The main computational challenge in Algorithm 1 is solving for Σ^{P n} in

$${\widehat{L}}_n\left({\widehat{\Sigma }}_n\right)={\widehat{B}}_n,$$ (5.1)

given the immense size of this problem. Two possibilities for inverting L^Pn immediately come to mind. The first is to treat (5.1) as a large system of linear equations, viewing Σ^{P n} as a vector in C^pP2 and LĈ as a matrix in C^pP2×pP2 . In this scheme, the matrix LĈcould be computed once and stored. However, this approach has an unreasonably large storage requirement. Since $\widehat{p}=O\left(N_{\mathrm{res}}^3\right)$, it follows that L^Pn has size $N_{\mathrm{res}}^6\times N_{\mathrm{res}}^6$. Even for a small N_res value such as 17, each dimension of L^Pn is 1.8 × 10⁶. Storing such a large L^Pn requires over 23 terabytes. Moreover, inverting this matrix naively is completely intractable.

The second possibility is to abandon the idea of forming L^Pn as a matrix, and instead to use an iterative algorithm, such as the conjugate gradient (CG) algorithm, based on repeatedly applying L^Pn to an input matrix. From (3.28), we see that applying L^Pn to a matrix is dominated by n multiplications of a qP × pP matrix by a pP × pP matrix, which costs $n\widehat{q}{\widehat{p}}^2=O\left(n{N}_{\mathrm{res}}^o\right)$. If κ_n is the condition number of L^Pn , then CG will converge in O(^√κ_n ) iterations (see, e.g., [58]). Hence, while the storage requirement of this alternative algorithm is only $O{\widehat{p}}^2=O\left(n{N}_{\mathrm{res}}^o\right)$, the computational complexity is O(nN ^{8 √}κ_n). Thus, the price to pay for reducing the storage requirement is that n matrix multiplications must be performed at each iteration. While this computational complexity might render the algorithm impractical for a regular computer, one can take advantage of the fact that the n matrix multiplications can be performed in parallel.

We propose a third numerical scheme, one which requires substantially less storage than the first scheme above and does not require O(n) operations at each iteration. We assume that the R_s are drawn from the uniform distribution over SO(3), and so for large n, the operator L^Pn does not differ much from its limiting counterpart LP (defined in (3.38)). Hence, if we replace L^Pn by LP in (5.1), we would not be making too large an error. Of course, LP is a matrix of the same size as L^Pn, so it is also impossible to store on a computer. However, we leverage the analytic form of LĈ in order to invert it more efficiently. At this point, we have not yet chosen the spaces VP and IĈ, and by constructing these carefully we give LP a special structure. This approach also entails a tradeo?: in practice the approximation L^Pn ≈ LĈ is accurate to the extent that R³,… , R³ are uniformly distributed on S². Hence, we must extract a subset of the given rotations whose viewing angles are approximately uniformly distributed on the sphere. Thus, the sacrifice we make in this approach is a reduction in the sample size. Moreover, since the subselected viewing directions are no longer statistically independent, the theoretical consistency result stated in Proposition 3.6 does not necessarily extend to this numerical scheme.

Nevertheless, the latter approach is promising because the complexity of inverting LP is independent of the number of images, and this computation might be tractable for reasonable values of N_res if LP has enough structure. It remains to construct VP and IP to induce a special structure in LĈ, which we turn to next.

5.2. Choosing VP to make LP sparse and block diagonal

In this section, we write down an expression for an individual element of LĈ, and discover that for judiciously chosen basis functions Ĉh_i, the matrix LP becomes sparse and block diagonal.

First, let us fix a functional form for the basis elements h^Pi: let

$${\widehat{h}}_i(r,\alpha )=f_i\left(r\right)a_i\left(\alpha \right),r\in R^{+},\alpha \in S^2,$$ (5.2)

where f_i : R⁺ → R are radial functions and a_i : S² → C are spherical harmonics. Note, for example, that the 3D Slepian functions have this form [56, eq. 110]. If the h^Pi are orthogonal with respect to the weight w, then

$$\langle f_i,f_j\rangle L_{r^{2}w\left(r\right)}^2\langle a_i,a_j\rangle L^2\left(S^2\right)={\delta }_{ij},$$ (5.3)

where we use $L_w^2$ as a shorthand for $L_w^2\left(R^{+}\right)$. The 3D Slepian functions satisfy the above condition with w = 1, because they are orthogonal in L²(R³).

Next, we write down the formula for an element L^{Pi1 ,i2,j1,j2} (here, j₁, j₂ are the indices of the input matrix, and i₁, i₂ are the indices of the output matrix). From (3.38) and Lemma 3.3,

we find

$$\begin{array}{cc}\hfill {\widehat{L}}_{i_1,i_2,j_1,j_2}& =\langle {\pi }_{\widehat{V}\otimes \widehat{V}}\left(({\widehat{h}}_{j_1}\otimes {\widehat{h}}_{j_2})K\right),{\widehat{h}}_{i_1}\otimes {\widehat{h}}_{i_2}\rangle L_{\omega }^2(R^3\times R^3)\hfill \\ \hfill & ={\int }_{R^3\times R^3}(h_{j_1}\otimes {\widehat{h}}_{j_2})({\xi }_1,{\xi }_2)K({\xi }_1,{\xi }_2)\overline{({\widehat{h}}_{i_1}\otimes {\widehat{h}}_{i_2})({\xi }_1,{\xi }_2)}d{\xi }_{1}d{\xi }_2\hfill \\ \hfill & ={\int }_{S^2\times S^2}{\int }_{R^{+}\times R^{+}}({\widehat{h}}_{j_1}\otimes {\widehat{h}}_{j_2})({\xi }_1,{\xi }_2)\overline{({\widehat{h}}_{i_1}\otimes {\widehat{h}}_{i_2})({\xi }_1,{\xi }_2)}\frac{1}{2\pi r_1{r}_2\mid \alpha \times \beta \mid }{r}_1^2{r}_2^{2}d{r}_{1}d{r}_{2}d\alpha d\beta \hfill \\ \hfill & =\langle f_{j_1},f_{i_1}\rangle L_{\tau }^2\langle f_{j_2},f_{i_2}\rangle L_r^2{\int }_{S^2\times S^2}(a_{j_1}\otimes a_{j_2})(\alpha ,\beta )\overline{(a_{i_1}\otimes a_{i_2})(\alpha ,\beta )}\frac{1}{2\pi \mid \alpha \times \beta \mid }d\alpha d\beta .\hfill \end{array}$$ (5.4)

Thus, to make many of the radial inner products in LP correct weight is vanish, we see from (5.3) that the

$$w\left(r\right)=\frac{1}{r}.$$ (5.5)

Recall that this is the weight needed to cancel the ramp filter in AP (see (3.36)). We obtain a cancellation in LP as well because the kernel of this operator also grows linearly with radial frequency. From this point on, w will represent the weight above, and we will work in the corresponding weighted L² space.

What are sets of functions of the form (5.2) that are orthonormal in L² (R³)? If we chose 3D Slepian functions, we would get the functional form

$${\widehat{h}}_{k,l,m}(r,\alpha )=f_{k,l}\left(r\right)Y_l^m\left(\alpha \right).$$ (5.6)

However, these functions are orthonormal with weight w = 1 instead of w = 1/r. Consider modifying this construction by replacing the f_k,R(r) by the radial functions arising in the 2D Slepian functions. These satisfy the property

$$\langle f_{k_1,l_1},f_{k_2,l_2}\rangle L_r^2=0\mathrm{if}{l}_1=l_2,k_1\ne k_2.$$ (5.7)

With this property (5.6) becomes orthonormal in L² (R³). This gives LP a certain degree of sparsity. However, note that the construction (5.6) has different families of L²-orthogonal radial functions corresponding to each angular function. Thus, we only have orthogonality of the radial functions f_k^1,R1 and f_k^2,R2 when l₁ = .e₂. Thus, many of the terms f_j , f_i)^L2 in (5.4) are still nonzero.

A drastic improvement on (5.6) would be to devise an orthogonal basis in L² that used one set of r-weighted orthogonal functions f_k for all the angular functions, rather than a separate set for each angular function. Namely, suppose we chose

$${\widehat{h}}_{k,l,m}(\tau ,\alpha )(r,\alpha )=f_k\left(r\right)Y_l^m\left(\alpha \right),(k,l,m)\in J,$$ (5.8)

where J is some indexing set. Note that f_k and J need to be carefully constructed so that span{h_k,R,m}≈ B (see section 5.3 for this construction). We have

$$f_k\left(r\right)Y_{l,m}\left(\alpha \right)={\widehat{h}}_{k,l,m}(r,\alpha )={\widehat{h}}_{k,l,m}(-r,-\alpha )=f_k(-r)Y_{l,m}(-\alpha )={(-1)}^l{f}_k(-r)Y_{l,m}\left(\alpha \right).$$ (5.9)

Here, we assume that each f_k is either even or odd at the origin, and we extend f_k(r) to r ∈ R according to this parity. The above calculation implies that f_k should have the same parity as .e. Let us suppose that f_k has the same parity as k. Then, it follows that (k, .e, m) ∈ J only if k = .e mod 2. Thus, h_k,R,m will be orthonormal in L² if

$$\{f_k:k=0\mathrm{mod}2\}\mathrm{and}\{f_k:k=1\mathrm{mod}2\}\mathrm{are}\mathrm{orthonormal}\text{in}{L}_r^2.$$ (5.10)

If we let k_i be the radial index corresponding to i, then we claim that the above construction implies

$${\widehat{L}}_{i_1,i_2,j_1,j_2}={\delta }_{k_{i_1}{k}_{j_1}}{\delta }_{k_{i_2}{k}_{j_2}}{\int }_{S^2\times S^2}(a_{j_1}\otimes a_{j_2})(\alpha ,\beta )\overline{(a_{i_1}\otimes a_{i_2})(\alpha ,\beta )}\frac{1}{2\pi \mid \alpha \times \beta \mid }d\alpha d\beta .$$ (5.11)

This statement does not follow immediately from (5.10), because we still need to check the case when k_i1 /= k_j1 mod 2. Note that in this case, the dependence on α in the integral over S² × S² is odd, and so indeed L^{Pi ,i ,j ,j} = 0 in that case as well. If VĈ is the space spanned by f_k(r)Y ^m(α) for all .e, m, then the above implies that LP operates separately on each V^Pk ⊗ V^Pk2 . In the language of matrices, this means that if we divide Σ^{P n} into blocks Σ^{P k1,k2} based on radial indices, LP operates on these blocks separately. We denote each of the corresponding “blocks” of LP by L^Pk1,k2 . Let us reindex the angular functions so that a^k denotes the ith angular basis function paired with f_k. From (5.11), we have

$${\widehat{L}}_{i_1,i_2,j_1,j_2}^{k_1,k_2}={\int }_{S^2\times S^2}(a_{j_1}^{k_1}\otimes a_{j_2}^{k_2})(\alpha ,\beta )\overline{a_{i_1}^{k_1}\otimes a_{i_2}^{k_2}(\alpha ,\beta )}\frac{1}{2\pi \mid \alpha \times \beta \mid }d\alpha d\beta .$$ (5.12)

This block diagonal structure of LP makes it much easier to invert. Nevertheless, each block L^Pk1,k2 is a square matrix with dimension $O\left(k_1^2{k}_2^2\right)$. Hence, inverting the larger blocks of LĈ can be dificult. Remarkably, it turns out that each block of LP is sparse. In Appendix C, we simplify the above integral over S² × S². Then, (5.12) becomes

$${\widehat{L}}_{i_1,i_2,j_1,j_2}^{k_1,k_2}=\sum _{l,m}c\left(l\right)C_{l,m}\left(\overline{a_{i_1}^{k_1}}{a}_{j_1}^{k_1}\right)\overline{C_{l,m}\left(\overline{a_{i_2}^{k_2}}{a}_{j_2}^{k_2}\right)},$$ (5.13)

where the constants c(.e) are defined in (C.8) and C_R,m(ψĈ) is the .e, m coefficient in the spherical harmonic expansion of ψP : S² → C. It turns out that the above expression is zero for most sets of indices. To see why, recall that the functions a^k are spherical harmonics. It is known that the product Y ^mY ^m* can be expressed as a linear combination of harmonics Y ^M , where M = m + m¹ and |.e − .e¹|≤ L ≤ .e + .e¹. Thus, C^m (a_ia_j ) are sparse vectors, which shows that each block L^Pk1,k2 is sparse. For example, L^P15,15 has each dimension approximately 2 × 10⁴. However, only about 10⁷ elements of this block are nonzero, which is only about 3% of its total number of entries. This is about the same number of elements as a 3000 × 3000 full matrix.

Thus, we have found a way to tractably solve the covariance matrix estimation problem: reconstruct Σ^{P n} (approximately) by solving the sparse linear systems

$${\widehat{L}}^{k_1,k_2}{\widehat{\Sigma }}_n^{k_1,k_2}={\widehat{B}}_n^{k_1,k_2},$$ (5.14)

where we recall that B^Pn is the RHS of (3.28). Also, using the fact that ${\widehat{A}}_n\approx \widehat{A}=\frac{1}{2}{I}_{\widehat{q}}$, we can estimate μP_n from

$${\widehat{\mu }}_n=\frac{2}{n}\sum _{s=1}^n{\widehat{P}}_s^H{\widehat{I}}_s.$$ (5.15)

In the next two sections, we discuss how to choose the radial components f_k(r) and define IP and VP more precisely.

5.3. Constructing f_k(r) and the space VP

We have discussed so far that

$$\widehat{V}=\mathrm{span}\left(\{f_k\left(r\right)Y_l^m(\theta ,\phi ):(k,l,m)\in J\}\right)$$ (5.16)

with (k, .e, m) ∈ J only if k = .e mod 2. Moreover, we have required the orthonormality condition (5.10). However, recall that we initially assumed that the real-domain functions X_s belonged to the space of 3D Slepian functions B. Thus, we must choose VP to approximate the image of B under the Fourier transform. Hence, the basis functions f_k(r)Y ^m(θ, ϕ) should be supported in the ball of radius ω_max and have their inverse Fourier transforms concentrated in the unit ball. Moreover, we must have dim(VĈ) ≈ dim(B). Finally, the basis functions h^Pi should be analytic at the origin (they are the truncated Fourier transforms of compactly supported molecules). We begin by examining this condition.

Expanding h^Pi in a Taylor series near the origin up to a certain degree, we can approximate it locally as a finite sum of homogeneous polynomials. By [57, Theorem 2.1], a homogeneous polynomial of degree d can be expressed as

$$H_d\left(\xi \right)=r^d(c_d{Y}_d\left(\alpha \right)+c_{d-2}{Y}_{d-2}\left(\alpha \right)+\cdots ),$$ (5.17)

where each Y_R represents a linear combination of spherical harmonics of degree .e. Hence, if (k, .e, m) ∈ J , then we require that f_k(r) = α_Rr^R + α_R+2r^R+2 + ··· , where some coefficients can be zero. We satisfy this requirement by constructing f₀, f₁,… so that

$$f_k\left(r\right)={\alpha }_{k,k}{r}^k+{\alpha }_{k,k+2}{r}^{k+2}+\cdot$$ (5.18)

for small r with α_k,k /= 0, and combine f_k with Y ^m if k = .e mod 2 and .e ≤ k. This leads to the following set of 3D basis functions:

$$\left\{{\widehat{h}}_i\right\}=\{,f_0{Y}_0^0,f_1{Y}_1^{-1},f_1{Y}_1^0,f_1{Y}_1^1,f_2{Y}_0^0,f_2{Y}_2^{-2},\dots ,f_2{Y}_2^2,\dots \}.$$ (5.19)

Written another way, we define

$$\widehat{V}=\mathrm{span}\left(\{f_k\left(r\right)Y_l^m(\theta ,\phi ):0\le k\le K,l=k\left(\mathrm{mod}2\right),0\le l\le k,\mid m\mid \le l\}\right).$$ (5.20)

Following the reasoning preceding (5.17), it can be seen that near the origin, this basis spans the set of polynomial functions up to degree K.

Now, consider the real- and Fourier-domain content of h^Pi. The bandlimitedness requirement on X_s is satisfied if and only if the functions f_k are supported in the interval [0, ω_max]. To deal with the real domain requirement, we need the inverse Fourier transform of f_k(r)Y ^m(θ, ϕ). With the Fourier convention (3.1), it follows from [2] that

$$\begin{array}{cc}\hfill F^{-1}\left(f_k\left(r\right)Y_l^m(\theta ,\phi )\right)(r_x,{\theta }_x,{\phi }_x)& =\frac{1}{2{\pi }^2}{i}^l\left({\int }_0^{\infty }{f}_k\left(r\right)j_l\left(r{r}_x\right)r^{2}dr\right)Y_l^m({\theta }_x,{\phi }_x)\hfill \\ \hfill & =\frac{1}{2{\pi }^2}{i}^l\left(S_l{f}_k\right)\left(r_x\right)Y_l^m({\theta }_x,{\phi }_x).\hfill \end{array}$$ (5.21)

Here, j_R is the spherical Bessel function of order .e, and S_R is the spherical Hankel transform. Also note that (r, θ, ϕ) are Fourier-domain spherical coordinates, while (r_x, θ_x, ϕ_x) are their real-domain counterparts. Thus, satisfying the real-domain concentration requirement amounts to maximizing the percentage of the energy of S_Rf_k that is contained in [0, 1] for 0 ≤ k ≤ K, 0 ≤ .e ≤ k, .e = k mod 2.

Finally, we have arrived at the criteria we would like f_k(r) to satisfy:

1. supp f_k ⊂ [0, ω_max];

2. {f_k : k even} and {f_k : k odd} orthonormal in L²(R⁺, r);

3. f_k(r) = α_k,kr^k + α_k,k+2r^k+2 + ··· near r = 0;

4. under the above conditions, maximize the percentage of the energy of S_Rf_k in [0, 1], for 0 ≤ k ≤ K, 0 ≤ .e ≤ k, .e = k mod 2.

While it might be possible to find an optimal set of such functions {f_k } by solving an optimization problem, we can directly construct a set of functions that satisfactorily satisfies the above criteria.

Note that since .e ranges in [0, k], it follows that for larger k, we need to have higher-order spherical Hankel transforms S_Rf_k remain concentrated in [0, 1]. Since higher-order spherical Hankel transforms tend to be less concentrated for oscillatory functions, it makes sense to choose f_k to be less and less oscillatory as k increases. Note that the functions f_k cannot all have only few oscillations because the even and odd functions must form orthonormal sets. Using this intuition, we construct f_k as follows. Since the even and odd f_k can be constructed independently, we will illustrate the idea by constructing the even f_k. For simplicity, let us assume that K is odd, with K = 2K₀ + 1. define the cuto? χ = χ([0, ω_max]). First, consider the sequence

$$J_0(z_{0,k_0+1}r∕{\omega }_{\max })\chi ,J_2(z_2,K_{0}r∕{\omega }_{\max })\chi ,\cdots ,J_{2K_0}(z_{2K_0,1}r∕{\omega }_{\max })\chi$$ (5.22)

where z_k,m is the mth positive zero of J_k (the kth-order Bessel function). Note that the functions in this list satisfy criteria 1 (by construction) and 3 (due to the asymptotics of the Bessel function at the origin). Also note that we have chosen the scaling of the arguments of the Bessel functions so that the number of zero crossings decreases as the list goes on. Thus, the functions become less and less oscillatory, which is the pattern that might lead to satisfying criterion 4. However, since these functions might not be orthogonal with respect to the weight r, we need to orthonormalize them with respect to this weight (via Gram–Schmidt). We need to be careful to orthonormalize them in such a way as to preserve the properties that they already satisfy. This can be achieved by running the (r-weighted) Gram–Schmidt algorithm from higher k towards lower k. This preserves the supports of the functions, their asymptotics at the origin, and the oscillation pattern. Moreover, the orthogonality property now holds as well. See Figure 4 for the first several even radial basis functions. Constructing the odd radial functions requires following an analogous procedure. Also, changing the parity of K requires the obvious modifications.

Figure 4.

The even basis functions up to f14 (r). Note that they become less oscillatory as k increases, and that f^k (r) ~ r^k at the origin. The odd basis functions have a similar structure and so are not pictured.

It remains to choose K. We do this based on how well criterion 4 is satisfied. For example, we can calculate how much energy of S_Rf_k is contained in the unit interval for all 0 ≤ k ≤ K, 0 ≤ .e ≤ k, .e = k mod 2. Numerical experiments show that K = N_res − 2 is a reasonable value. For each value of N_res that we tested, this choice led to S_Rf_k having at least 80% of its energy concentrated in the unit interval for each relevant (.e, k), and at least 95% on average over all such pairs (.e, k). Thus our experiments show that for our choice of f_k, choosing roughly K ≈ N_res leads to acceptable satisfaction of criterion 4. A short calculation yields

$$\widehat{p}=\dim \left(\widehat{V}\right)=\sum _{k=0}^K\frac{(k+1)(k+2)}{2}=\frac{(K+1)(K+2)(K+3)}{6}\approx \frac{N_{\mathrm{res}}^3}{6}=\frac{4{\omega }_{\max }^3}{3{\pi }^3}.$$ (5.23)

$${\widehat{P}}_s\left(f_k\left(r\right)Y_l^m(\theta ,\phi )\right)=f_k\left(r\right){\widehat{P}}_s\left(Y_l^m(\theta ,\phi )\right).$$ (5.24)

Hence, we have pP/p = 6/π² ≈ 0.6. Hence, the dimension of the space VP we have constructed is within a constant factor of the dimension of B. This factor is the price we pay for the computational simplicity VP provides.

Note that a different construction of f_k might have even better results. Choosing better radial functions can be the topic of further research. In any case, the specific choice of f_k does not affect the structure of our algorithm at all because LP is independent of these functions, as can be seen from (5.12). Thus, the selection of the radial basis functions can be viewed as an independent module in our algorithm. The radial functions we choose here work well in numerical experiments; see section 7.

5.4. Constructing IP

Finally, the remaining piece in our construction is the finite dimensional space of Fourier images, IĈ. To motivate our construction, consider applying P_s to a basis element of V . The first observation to make is that the radial components f_k(r) factor through Ĉ completely:

Recall from (3.21) that

$${\widehat{P}}_s\left(Y_l^m(\theta ,\phi )\right)=\underset{m^{\prime }=l\mathrm{mod}2}{\sum _{\mid m^{\prime }\mid \le l}}{c}_{l,m,m^{\prime }}\left(R_s\right)\frac{1}{\sqrt{2\pi }}{e}^{i{m}^{\prime }\phi },$$ (5.25)

Note that the Ĉon the LHS should be intepreted as C(R³) → C(R²), whereas the one on the RHS is the restricted map C(S²) → C(S¹), which we also call P . The correct interpretation should be clear in each case. Viewed in this new way, Ĉ : C(S²) → C(S¹) rotates a function on the sphere by R_s ∈ SO(3), and then restricts the result to the equator.

By the rotational properties of spherical harmonics, a short calculation shows that

$$f_k\left(r\right)Y_l^m(\theta ,\phi )\in \widehat{V}\Rightarrow \frac{1}{\sqrt{2\pi }}{f}_k\left(r\right)e^{im\phi }\in \widehat{J},m=-l,-l+2,\dots ,l-2,l.$$ (5.26)

where the constants c_R,m,m* depend on the Wigner D matrices D^R [36]. Hence, P (VĈ) ⊂ IP if

$$\left({\widehat{g}}_i\right)=\{\frac{1}{\sqrt{2\pi }}{f}_0\left(r\right),\frac{1}{\sqrt{2\pi }}{f}_1\left(r\right)e^{-i\phi },\frac{1}{\sqrt{2\pi }}{f}_1\left(r\right)e^{i\phi },\frac{1}{\sqrt{2\pi }{f}_2}\left(r\right)e^{-2i\phi },\frac{1}{\sqrt{2\pi }}{f}_2\left(r\right),\frac{1}{\sqrt{2\pi }}{f}_2\left(r\right)e^{2i\phi },\cdots \}.$$ (5.27)

Thus, we construct IP by pairing f_k with $\frac{1}{\sqrt{2\pi }}{e}^{im\phi }$ if k = m mod 2 and m ≤ k. This leads to the 2D basis functions

$$\widehat{J}=\mathrm{span}\left(\{\frac{1}{\sqrt{2\pi }}{f}_k\left(r\right)e^{im\phi }:0\le k\le K,m=k\left(\mathrm{mod}2\right),\mid m\mid \le k\}\right).$$ (5.28)

Written another way, we construct

$$\widehat{q}=\dim \left(\widehat{J}\right)=\sum _{k=0}^K(k+1)=\frac{(K+1)(K+2)}{2}\approx \frac{N_{\mathrm{res}}^2}{2}=\frac{2{\omega }_{\max }^2}{{\pi }^2}.$$ (5.29)

If I^Pk is the subspace of IP spanned by the basis functions with radial component f_k, (5.24) shows that P (VP ) ⊂ IĈ for each k. Thus, PĈ has a block diagonal structure, as depicted in Figure 5.

Figure 5.

Block diagonal structure of PPs. The shaded rectangles represent the nonzero entries. For an explanation of the specific pairing of angular and radial functions, see (5.27) and (5.19) and the preceding discussion. A short calculation shows that the kth block of PĈs has size $(k+1)\times \frac{(k+1)(k+2)}{2}$.

Let us now compare the dimension of IP to that of the corresponding space of 2D Slepian functions, as we did the previous section. We have

$$\mathrm{nnz}\left({\widehat{L}}^{k_1,k_2}\right)\le \frac{1}{k_1+k_2+1}{\left(\frac{(k_1+1)(k_1+2)(k_2+1)(k_2+2)}{4}\right)}^2,$$ (6.1)

The Shannon number in 2D corresponding to the bandlimit ω_max is ω² 4. Thus, we are short of this dimension by a constant factor of 8/π² ≈ 0.8. Another comparison to make is that the number of grid points in the disc inscribed in the N_res × N_res grid is ^π N ² = ω²/π. Thus, dim(IĈ) is short of this number by a factor of ² . Note that this is the same factor that was obtained in a similar situation in [69], so IP is comparable in terms of approximation to the Fourier–Bessel space constructed there.

Thus, by this point we have fully specified our algorithm for the heterogeneity problem. After finding Σ^{P n} numerically via (5.14), we can proceed as in steps 6–9 of Algorithm 1 to solve Problem 1.2.

6. Algorithm complexity

In this section, we explore the consequences of the constructions of VP and IP for the complexity of the proposed algorithm. We also compare this complexity with that of the straightforward CG approach discussed in section 5.1.

To calculate the computational complexity of inverting the sparse matrix L^Pk1,k2 via the CG algorithm, we must bound the number of nonzero elements of this matrix and its condition number.

6.1. Sparsity of LP and storage complexity

Preliminary numerical experiments confirm the following conjecture.

Conjecture 6.1

$$\mathrm{maximum}\mathrm{eigenvalue}\mathrm{of}{\widehat{L}}^{k,k}=0.2358+0.1357k.$$ (6.2)

where nnz(A) is the number of nonzero elements in a matrix A, and the term involving the square is the total number of elements in L^Pk1,k2 .

Hence, the percentage of nonzero elements in each block of LĈ decays linearly with the frequencies associated with that block. This conjecture remains to be verified theoretically.

We pause here to note the storage complexity of the proposed algorithm, which is dominated by the cost of storing LĈ. In fact, since we process all the blocks separately, only storing one L^Pk1,k2 at a time will suffice. Hence, the storage complexity is the memory required to store the largest block of LĈ, which is nnz(L^PK,K ) = O(K⁷) = O(N ⁷ required storage for a full matrix of the size of LĈ, which is $\mathrm{nnz}\left({\widehat{L}}^{K,K}\right)=O\left(K^7\right)=O\left(N_{\mathrm{res}}^7\right)$. Compare this to the required storage for a full matrix of the size of L, which is $O\left(N_{\mathrm{res}}^{12}\right)$.

6.2. Condition number of LĈ

Here we find the condition number of each L^{Pk1 ,k2} . We already proved in Proposition 3.4 that λ_min(LĈ) ≥ 1/2π. For any k₁, k₂, this implies that λ_min(L^{Pk1 ,k2} ) ≥ 1/2π. This is confirmed by a numerical experiment: in Figure 6(a) are plotted the minimum eigenvalues of L^Pk,k for 0 ≤ k ≤ 15. Note that the eigenvalues actually approach the value 1/2π (marked with a horizontal line) as k increases. We remarked in section 3.4 that an upper bound on the maximum eigenvalue is harder to find. Nevertheless, numerical experiments have led us to the following conjecture.

Figure 6.

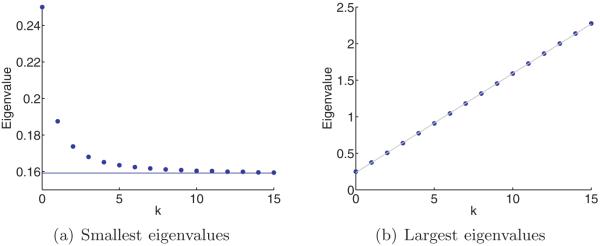
The smallest and largest eigenvalues of (the continuous version of ) LPk,k, for 0 ≤ k ≤ 15. The smallest eigenvalues approach their theoretical lower bound of 1/2π as k increases. The largest eigenvalues show a clear linear dependence on k.

Conjecture 6.2

The maximal eigenvalue of L^Pk1,k2 grows linearly with min(k₁, k₂).

Moreover, a plot of the maximal eigenvalue of L^Pk,k shows a clear linear dependence on k. See Figure 6(b). The line of best fit is approximately

$$k\left({\widehat{L}}^{k_1,k_2}\right)\le 1.4818+0.8524\min (k_1,k_2).$$ (6.3)

Taken together, Proposition 3.4 and Conjecture 6.2 imply the following conjecture about the condition number of L^Pk1,k2 , which we denote by κ(L^{Pk1 ,k2} ).

Conjecture 6.3

$$k\left(\widehat{L}\right)\le 1.4818+.852K.$$ (6.4)

In particular, this implies that

$$\begin{array}{cc}\hfill & \mathrm{complexity}\mathrm{of}\mathrm{inverting}\widehat{L}\hfill \\ \hfill & \lesssim \sum _{k_1,k_2=0}^K\sqrt{k\left({\widehat{L}}^{k_1,k_2}\right)}\mathrm{nnz}\left({\widehat{L}}^{k_1,k_2}\right)\hfill \\ \hfill & \lesssim \sum _{k_1,k_2=0}^K\sqrt{\min (k_1,k_2=0)}\frac{1}{k_1+k_2+1}{\left(\frac{(k_1+1)(k_1+2)(k_2+1)(k_2+2)}{4}\right)}^2\hfill \\ \hfill & \lesssim \sum _{k_1,k_2=0}^K{\left(k_1{k}_2\right)}^{1∕4}\frac{1}{\sqrt{k_1{k}_2}}{k}_1^4{k}_2^4\hfill \\ \hfill & \lesssim \sum _{k_1=0}^K{k}_1^{3.75}\sum _{k_2=0}^K{k}_2^{3.75}\lesssim K^{4.75}{K}^{4.75}=K^{9.5}.\hfill \end{array}$$ (6.5)

6.3. Algorithm complexity

Using the above results, we estimate the computational complexity of Algorithm 1. We proceed step by step through the algorithm and estimate the complexity at each stage. Before we do so, note that due to the block diagonal structure of P^Ps (depicted in Figure 5), it can be easily shown that an application of P^Ps or P^PH costs O(K⁴).

Sending the images from the pixel domain into IP requires n applications of the matrix Q₁ ∈ C^qP×q , which costs O(nqqP) = O(nN ²N ²). Note that this complexity can be improved using an algorithm of the type [39], but in this paper we do not delve into the details of this alternative.

Finding μP_n from (5.15) requires n applications of the matrix ${\widehat{P}}_s^H$, and so has complexity $O\left(n{K}^4\right)=O\left(n{N}_{\mathrm{res}}^4\right)$.

Next, we must compute the matrix B^Pn. Note that the second term in B^Pn can be replaced by a multiple of the identity matrix by (3.36), so only the first term of B^Pn must be computed.

Note that B^Pn is a sum of n matrices, and each matrix can be found as the outer product of P_s (I^Ps − P^PsμP_n) ∈ C^pP with itself. Calculating this vector has complexity O(K⁴), from which it follows that calculating B^Pn costs O(nK⁴) = O(nN ⁴ ).

Next, we must invert LĈ. As mentioned in section 5.1, the inversion of a matrix A via CG takes √κ(A) iterations. If A is sparse, than applying it to a vector has complexity nnz(A). Hence, the total complexity for inverting a sparse matrix is √κ(A)nnz(A). Conjectures 6.1 and 6.3 imply that

$$O(n{N}^2{N}_{\mathrm{res}}^2+N_{\mathrm{res}}^{9.5}).$$ (6.6)

Since LP has size of the order K⁶ × K⁶, note that the complexity of inverting a full matrix of this size would be K¹⁸. Thus, our efforts to make LP sparse have saved us a K^8.5 complexity factor. Moreover, the fact that LP is block diagonal makes its inversion parallelizable.

Assuming that C = O(1), solving each of the n least-squares problems (4.2) is dominated by a constant number of applications of P^Ps to a vector. Thus, finding α_s for s = 1,… ,n costs $O\left(N_{\mathrm{res}}^{12}\right)$

Next, we must fit a mixture of Gaussians to α_s to find α^c. An EM approach to this problem requires O(n) operations per iteration. Assuming that the number of iterations is constant, finding α^c has complexity O(n).

Finally, reconstructing X^{P c} via (4.1) has complexity O(N ³ ).

Hence, neglecting lower-order terms, we find that the total complexity of our algorithm is

$$O{(}_n{N}_{\mathrm{res}}^{7.5}).$$ (6.7)

6.4. Comparison to straightforward CG approach

We mentioned in section 5.1 that a CG approach is possible in which at each iteration, we apply L^Pn to ΣĈ using the definition (3.28). This approach has the advantage of not requiring uniformly spaced viewing directions. While the condition number of L^Pn depends on the rotations R₁,… , R_n, let us assume here that κ(L^Pn) ≈ κ(LĈ). We estimated the computational complexity of this approach in section 5.1, but at that point we assumed that each P^Ps was a full matrix. If we use the bases VP and IĈ, we reap the benefit of the block diagonal structure of P^Ps. Hence, for each s, evaluating P^PH P^PsΣP P^PH P^Ps is dominated by the multiplication P^PsΣP , which has complexity N ⁷. Hence, applying L^Pn to ΣĈ has complexity nN ⁷. By (6.4), we assume that κ(L^Pn) = O(N_res). Hence, the full complexity of inverting LP using the conjugate gradient approach is (6.7) O(nN ^7.5).

$$\mathrm{SNR}=\frac{P\left(\mathrm{signal}\right)}{P\left(\mathrm{noise}\right)},$$ (7.1)

Compare this to a complexity of O(N ^9.5) for inverting LĈ. Given that n is usually on the order of 10⁵ or 10⁶, for moderate values of N_res we have N ^9.5 ≤ nN ^7.5. Nevertheless, both algorithms have possibilities for parallelization, which might change their relative complexities. As for memory requirements, note that the straightforward CG algorithm only requires O(N ⁶ ) storage, whereas we saw in section 6.1 that the proposed algorithm requires O(N ⁷ ) storage.

In summary, these two algorithms each have their strengths and weaknesses, and it would be interesting to write parallel implementations for both and compare their performances. In the present paper, we have implemented and tested only the algorithm based on inverting LĈ.

7. Numerical results

Here, we provide numerical results illustrating Algorithm 1, with the bases IP and VP chosen so as to make LĈ sparse, as discussed in section 5. The results presented below are intended for proof-of-concept purposes, and they demonstrate the qualitative behavior of the algorithm. They are not, however, biologically significant results. We have considered an idealized setup in which there is no CTF effect, and have assumed that the rotations R_s (and translations) have been estimated perfectly. In this way, we do not perform a “full-cycle” experiment, starting from only the noisy images. Therefore, we cannot gauge the overall effect of noise on our algorithm because we do not account for its contribution to the misspecification of rotations; we investigate the effect of noise on the algorithm only after the rotation estimation step. Moreover, we use simulated data instead of experimental data. The application of our algorithm to experimental datasets is left for a separate publication.

7.1. An appropriate definition of SNR

Generally, the definition of SNR is

$$P\left(\mathrm{noise}\right)=\frac{N_{\mathrm{res}}^2}{N^2}{\sigma }^2.$$ (7.2)

where P denotes power. In our setup, we will find appropriate definitions for both P (signal) and P (noise). Let us consider first the noise power. The standard definition is P (noise) = σ². However, note that in our case, the noise has a power of σ² in each pixel of an N × N grid, but we reconstruct the volumes to a bandlimit ω_max, corresponding to N_res. Hence, if we downsampled the N × N images to size N_res × N_res, then we would still obey the Nyquist criterion (assuming the volumes actually are bandlimited by ω_max). This would have the effect of reducing the noise power by a factor of N ² /N ². Hence, in the context of our problem, we define

$$P\left(\mathrm{signal}\right)=\frac{1}{n}\sum _{s=1}^n\frac{1}{q}\Vert P_s{X}_s{\Vert }^2.$$ (7.3)

Now, consider P (signal). In standard SPR, a working definition of signal power is

$$P\left({\mathrm{signal}}_{\mathrm{het}}\right)=\frac{1}{n}\sum _{s=1}^n\frac{1}{q}\Vert P_s(X_s-{\mu }_0){\Vert }^2.$$ (7.4)

However, in the case of the heterogeneity problem, the object we are trying to reconstruct is not the volume itself, but rather the deviation from the average volume, due to heterogeneity. Thus, the relevant signal to us is not the images themselves, but the parts of the images that correspond to projections of the deviations of X_s from μ₀. Hence, a natural definition of signal power in our case is

$${\mathrm{SNR}}_{\mathrm{het}}=\frac{P\left({\mathrm{signal}}_{\mathrm{het}}\right)}{P\left(\mathrm{noise}\right)}=\frac{\frac{1}{qn}{\Sigma }_{s=1}^n\Vert P_s(X_s-{\mu }_0){\Vert }^2}{{\sigma }^2{N}_{\mathrm{res}}^2∕N^2}.$$ (7.5)

Using the above definitions, let us define SNR_het in our problem by

$$\mathrm{SNR}=\frac{P\left(\mathrm{signal}\right)}{P\left(\mathrm{noise}\right)}=\frac{\frac{1}{n}{\Sigma }_{s=1}^n\frac{1}{q}\Vert P_s{X}_s{\Vert }^2}{{\sigma }^2{N}_{\mathrm{res}}^2∕N^2}.$$ (7.6)

Even with the correction factor $N_{\mathrm{res}}^2∕N^2$ values are lower than the SNR values usually encountered in structural biology. Hence, we also define

$$X^c\left(r\right)=\sum _{i=1}^{M_c}{a}_{i,c}\exp (-\frac{\Vert r-r_{i,c}{\Vert }^2}{2{\sigma }_{i,c}^2}),{\tau }_{i,c}\in R^3,a_{i,c},{\sigma }_{i,c}\in R_{+},c=1,\dots ,C.$$ (7.7)

We will present our numerical results primarily using SNR_het, but we will also provide the corresponding SNR values in parentheses.

To get a sense of the difference between this definition of SNR and the conventional one, compare the signal strength in a projection image to that in a mean-subtracted projection image in Figure 7.

Figure 7.

This figure depicts the effect of mean subtraction on projection images in the context of a two-class heterogeneity. The bottom row projections are obtained from the top row by mean subtraction. Columns (a) and (b) are clean projection images of the two classes from a fixed viewing angle. Columns (c) and (d) are both noisy versions of column (a). The image in the top row of column (c) has an SNR of 0.96, but the SNR of the corresponding mean-subtracted image is only 0.05. In column (d), the top image has an SNR of 0.19, but the mean-subtracted image has SNR 0.01. Note: the SNR values here are not normalized by N ² /N ² in order to illustrate the signal present in a projection image.

7.2. Experimental procedure

We performed three numerical experiments: one with two heterogeneity classes, one with three heterogeneity classes, and one with continuous variation along the perimeter of a triangle defined by three volumes. The first two demonstrate our algorithm in the setup of Problem 1.2, and the third shows that we can estimate the covariance matrix and discover a low-dimensional structure in more general setups than the discrete heterogeneity case.

As a first step in each of the experiments, we created a number of phantoms analytically. We chose the phantoms to be linear combinations of Gaussian densities:

$$\begin{array}{cc}\hfill D_{z^{\ast }}\left(z^{H}a\right)& =a,\hfill \\ \hfill D_{z^{\ast }}\left(z^{H}Az\right)& =Az,\hfill \\ \hfill D_Z\left(tr\left(AZ\right)\right)& =A,\hfill \\ \hfill D_Z\left(tr\left(ZA{Z}^{H}A\right)\right)& =A{Z}^{H}A.\hfill \end{array}$$ (A.1)

For the discrete heterogeneity cases, we chose probabilities p₁,… , p_C and generated X₁,… , X_n by sampling from X ¹,… , X ^C accordingly. For the continuous heterogeneity case, we generated each X_s by choosing a point uniformly at random from the perimeter of the triangle defined by X ¹, X ², X ³.

For all of our experiments, we chose n = 10000, N = 65, N_res = 17, K = 15, and selected the set of rotations R_s to be approximately uniformly distributed on SO(3). For each R_s, we calculated the clean continuous projection image P_sX_s analytically, and then sampled the result on an N × N grid. Then, for each SNR level, we used (7.5) to find the noise power σ² to add to the images.

After simulating the data, we ran Algorithm 1 on the images I_s and rotations R_s on an Intel i7-3615QM CPU with 8 cores, and 8 GB of RAM. The runtime for the entire algorithm with the above parameter values (excluding precomputations) is 257 seconds. For the continuous heterogeneity case, we stopped the algorithm after computing the coordinates α_s (we did not attempt to reconstruct individual volumes in this case). To quantify the resolution of our reconstructions, we use the Fourier shell correlation (FSC), defined as the correlation of the reconstruction with the ground truth on each spherical shell in Fourier space [48]. For the discrete cases, we calculated FSC curves for the mean, the top eigenvectors, and the mean-subtracted reconstructed volumes. We also plotted the correlations of the mean, top eigenvectors, and mean-subtracted volumes with the corresponding ground truths for a range of SNR values. Finally, we plotted the coordinates α_s. For the continuous heterogeneity case, we tested the algorithm on only a few different SNR values. By plotting α_s in this case, we recover the triangle used in constructing X_s.

7.3. Experiment: Two classes

In this experiment, we constructed two phantoms X ¹ and X ² of the form (7.7), with M₁ = 1, M₂ = 2. Cross sections of X ¹ and X ² are depicted in the top row panels (c) and (d) in Figure 8. We chose the two heterogeneity classes to be equiprobable: p₁ = p₂ = 1/2. Note that the theoretical covariance matrix in the two-class heterogeneity problem has rank 1, with dominant eigenvector proportional to the difference between the two volumes.

Figure 8.

Cross-sections of reconstructions of the mean, top eigenvector, and two volumes for three different SNR values. The top row is clean, the second row corresponds to SNR_het = 0.013 (0.25), the third row to SNR_het = 0.003 (0.056), and the last row to SNR_het = 0.0013 (0.025). (a) SNR_het = 0.013(0.25) (b) SNR_het = 0.003(0.056) (c) SNR_het = 0.0013(0.025)

Figure 8 shows the reconstructions of the mean, top eigenvector, and two volumes for SNR_het = 0.013, 0.003, 0.0013 (0.25, 0.056, 0.025). In Figure 9, we display eigenvalue histograms of the reconstructed covariance matrix for the above SNR values. Figure 10 shows the FSC curves for these reconstructions. Figure 11 shows the correlations of the computed means, top eigenvectors, and (mean-subtracted) volumes with their true values for a broader range of SNR values. In Figure 12, we plot a histogram of the coordinates α_s from step 7 of Algorithm 1.

Figure 9.

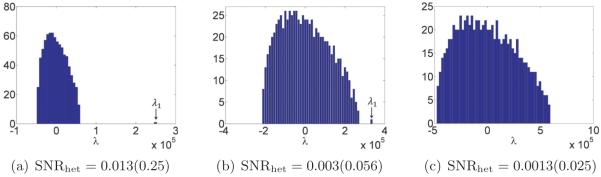
Eigenvalue histograms of ΣP n xin the two-volume case for three SNR values. Note that as the SNR decreases, the distribution of eigenvalues associated with noise comes increasingly closer to the top eigenvalue that corresponds to the structural variability, and eventually the latter is no longer distinguishable.

Figure 10.

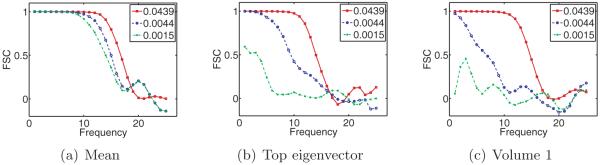
FSC curves for the mean volume, top eigenvector, and one mean-subtracted volume at the same three SNRs as in Figure 8. Note that the mean volume is reconstructed successfully for all three SNR levels. On the other hand, the top eigenvector and volume are recovered at the highest two SNR levels but not at the lowest SNR.

Figure 11.

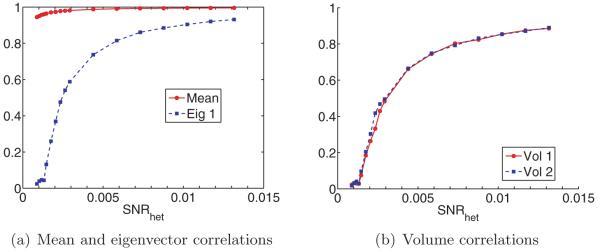
Correlations of computed quantities with their true values for different SNRs (averaged over 10 experiments) for the two-volume case. Note that in the two-volume case, the mean-subtracted volume correlations are essentially the same as the eigenvector correlation (the only small discrepancy is that we subtract the true mean rather than the computed mean to obtain the former).

Figure 12.

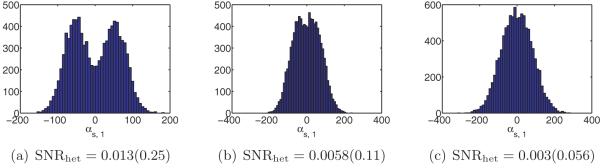
Histograms of αs for two-class case. Note that (a) has a bimodal distribution corresponding to two heterogeneity classes, but these two distributions merge as SNR decreases. (0.002) and 0.003 (0.006). Note that this behavior is tied to the spectral gap (separation of top eigenvalues from the bulk) of Σ^{P n}. Indeed, the disappearance of the spectral gap going from panel (b) to panel (c) of Figure 9 coincides with the estimated top eigenvector becoming uncorrelated with the truth, as reflected in Figures 10(b) and 11(a). This phase transition behavior is very similar to that observed in the usual high-dimensional PCA setup, described in section 2.3.

Our algorithm was able to meaningfully reconstruct the two volumes for SNR_het as low as about 0.003 (0.06). Note that the means were always reconstructed with at least a 94% correlation to their true values. On the other hand, the eigenvector reconstruction shows a phase-transition behavior, with the transition occurring between SNR_het values of 0.001

Regarding the coefficients α_s depicted in Figure 12, note that in the noiseless case, there should be a distribution composed of two spikes. By adding noise to the images, the two spikes start blurring together. For SNR values up to a certain point, the distribution is still visibly bimodal. However, after a threshold the two spikes coalesce into one. The proportions p_c are reliably estimated until this threshold.

7.4. Experiment: Three classes

In this experiment, we constructed three phantoms X ¹, X2_{, X} 3 of the form (7.7), with M₁ = 2, M₂ = 2, M₃ = 1. The cross sections of X ¹, X 2_{, X} 3 are depicted in Figure 13 (top row, panels (d)–(f)). We chose the three classes to be equiprobable: p₁ = p₂ = p₃ = 1/3. Note that the theoretical covariance matrix in the three-class heterogeneity problem has rank 2.

Figure 13.

Cross sections of clean and reconstructed objects for the three-class experiment. The top row is clean, the second row corresponds to SNR_het = 0.044 (0.3), the third row to SNR_het = 0.0044 (0.03), and the last row to SNR_het = 0.0015 (0.01).

Figures 13, 14, 15, 16, 17 are the three-class analogues of Figures 8, 9, 10, 11, 12 in the two-class case.

Figure 14.

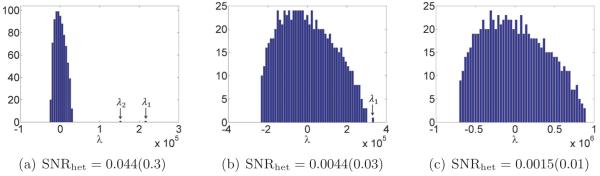
Eigenvalue histograms of reconstructed covariance matrix in the three-class case for three SNR values. Note that the noise distribution initially engulfs the second eigenvalue, and eventually the top eigenvalue as well.

Figure 15.

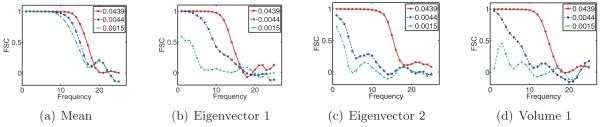
FSC curves for the mean volume, top eigenvector, and one mean-subtracted volume at the same three SNRs as in Figure 13. Note that the mean volume is reconstructed successfully for all three SNR levels, and that the second eigenvector is recovered less accurately than the first.

Figure 16.

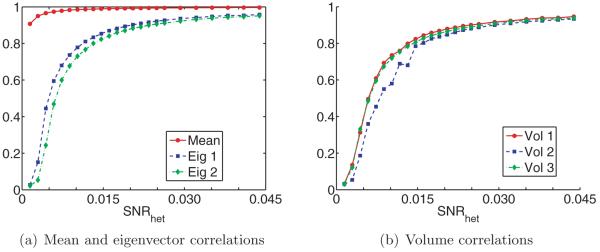
Correlations of computed means, eigenvectors, and mean-subtracted volumes with their true values for different SNRs (averaged over 30 experiments). Note that the mean volume is consistently recovered well, whereas recovery of the eigenvectors and volumes exhibits a phase-transition behavior.

Figure 17.

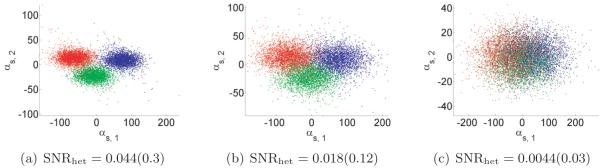
The coordinates αs for the three-class case, colored according to true class. The middle scatter plot is near the transition at which the three clusters coalesce.

Qualitatively, we observe behavior similar to that in the two-class case. The mean is reconstructed with at least 90% accuracy for all SNR values considered, while both top eigen-vectors experience a phase-transition phenomenon (Figure 16(a)). As with the two-class case, we see that the disappearance of the eigengap coincides with the phase-transition behavior in the reconstruction of the top eigenvectors. However, in the three-class case we have two eigenvectors, and we see that the accuracy of the second eigenvector decays more quickly than that of the first eigenvector. This reflects the fact that the top eigenvalue of the true covariance Σ^{P 0} is 2.1 × 10⁵, while the second eigenvalue is 1.5 × 10⁵. These two eigenvalues differ because X ¹³ has greater norm than X ² −X , which means that the two directions of variation have different associated variances. Hence, recovering the second eigenvector is less robust to noise. In particular, there are SNR values for which the top eigenvector can be recovered, but the second eigenvector cannot. SNR_het = 0.0044 (0.03) is such an example. We see in Figure 14 that for this SNR value, only the top eigenvector pops out of the bulk distribution. In this case, we would incorrectly estimate the rank of the true covariance as 1, and conclude that C = 2.

The coefficients α_s follow a similar trend to those in the two-class case. For high SNRs, there is a clearly defined clustering of the coordinates around three points, as in Figure 17(a). As the noise is increased, the three clusters become increasingly less defined. In Figure 17(b), we see that in this threshold case, the three clusters begin merging into one. As in the two-class case, this is the same threshold up to which the p_c are accurately estimated. By the time SNR = 0.0044 (0.03), there is no visible cluster separation, just as we observed in the two-class case. Although the SNR threshold for finding p_c from the α_s coefficients comes earlier than the one for the eigengap, the quality of volume reconstruction roughly tracks the quality of the eigenvector reconstruction. This suggests that the estimation of cluster means is more robust than that of the probabilities p_c.

7.5. Experiment: Continuous variation

In this experiment, we sampled X_s uniformly from the perimeter of the triangle determined by volumes X ¹, X ², X ³ (from the three-class discrete heterogeneity experiment). This setup is more suitable to model the case when the molecule can vary continuously between each pair X ⁱ and X ^j . Despite the fact this experiment does not fall under Problem 1.2, Figure 18 shows that we still recover the rank two structure. Indeed, it is clear that all the clean volumes still belong to a subspace of dimension 2. Moreover, we can see the triangular pattern of heterogeneity in the scatter plots of α_s (Figure 19). However, note that once the images get moderately noisy, the triangular structure starts getting drowned out. Thus, in practice, without any prior assumptions, just looking at the scatter plots of α_s will not necessarily reveal the heterogeneity structure in the dataset. To detect continuous variation, a new algorithmic step must be designed to follow covariance matrix estimation. Nevertheless, this experiment shows that by solving the general Problem 1.1, we can estimate covariance matrices beyond those considered in the discrete case of the heterogeneity problem.

Figure 18.

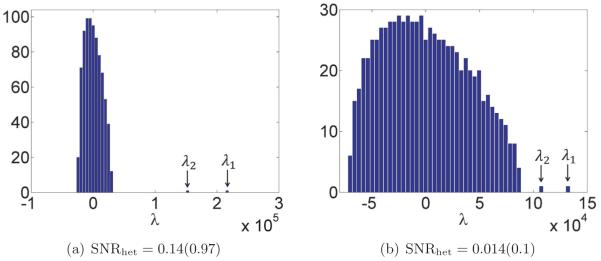
Eigenvalue histograms of covariance matrix reconstructed in continuous variation case.

Figure 19.

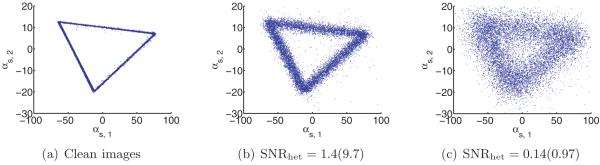
Scatter plots (with some outliers removed) of αs for high SNR values.

8. Discussion

In this paper, we proposed a covariance matrix estimator from noisy linearly projected data and proved its consistency. The covariance matrix approach to the cryo-EM heterogeneity problem is essentially a special case of the general statistical problem under consideration, but has its own practical challenges. We overcame these challenges and proposed a methodology to tractably estimate the covariance matrix and reconstruct the molecular volumes. We proved the consistency of our estimator in the cryo-EM case and also began the mathematical investigation of the projection covariance transform. We discovered that inverting the projection covariance transform involves applying the triangular area filter, a generalization of the ramp filter arising in tomography. Finally, we validated our methodology on simulated data, producing accurate reconstructions at low SNR levels. Our implementation of this algorithm is now part of the ASPIRE package at spr.math.princeton.edu. In what follows, we discuss several directions for future research.

As discussed in section 2.3, our statistical framework and estimators have opened many new questions in high-dimensional statistics. While a suite of results are already available for the traditional high-dimensional PCA problem, generalizing these results to the projected data case would require new random matrix analysis. Our numerical experiments in the cryo-EM case have shown many qualitative similarities between the estimated covariance matrix in the cryo-EM case and the sample covariance matrix in the spiked model. There is again a bulk distribution with eigenvalues separated from it. Moreover, there is a phase-transition phenomenon in the cryo-EM case, in which the top eigenvectors of the estimated covariance lose correlation with those of the population covariance once the corresponding eigenvalues are absorbed by the bulk distribution. Answering the questions posed in section 2.3 would be very useful in quantifying the theoretical limitations of our approach.

As an additional line of further inquiry, note that the optimization problem (2.4) for the covariance matrix is amenable to regularization. If n ≥ f (p, q) is the high-dimensional statistical regime in which the unregularized estimator still carries a signal, then of course we need regularization when n ≤ f (p, q). Here, f is a function depending on the distribution of the operators P_s. Moreover, regularization increases robustness to noise, so in applications like cryo-EM, this could prove useful. Tikhonov regularization does not increase the complexity of our algorithm, but has the potential to make L^Pn invertible. Under what conditions can we still achieve accurate recovery in a regularized setting? Other regularization schemes can take advantage of a priori knowledge of Σ₀, such as using nuclear norm regularization in the case when Σ₀ is known to be low rank. See [25] for an application of nuclear norm minimization in the context of dealing with heterogeneity in cryo-electron tomography. Another special structure Σ₀ might have is that it is sparse in a certain basis. For example, the localized variability assumption in the case of the heterogeneity problem is such an example; in this case, the covariance matrix is sparse in the real Cartesian basis or a wavelet basis. This sparsity can be encouraged using a matrix 1-norm regularization term. Other methods, such as sparse PCA [22] or covariance thresholding [7] might be applicable in certain cases when we have sparsity in a given basis.

We developed our algorithm in an idealized environment, assuming that the rotations R_s (and in-plane translations) are known exactly and correspond to approximately uniformly distributed viewing directions, and that the molecules belong to B. Moreover, we did not account for the CTF effect of the electron microscope. In practice, of course rotations and translations are estimated with some error. Also, certain molecules might exhibit a preference for a certain orientation, invalidating the uniform rotations assumption. Note that as long as L^Pn is invertible, our framework produces a valid estimator, but without the uniform rotations assumption, the computationally tractable approach to inverting this matrix proposed in section 5 no longer holds. Moreover, molecules might have higher frequencies than those we reconstruct, which could potentially lead to artifacts. Thus, an important direction of future research is to investigate the stability of our algorithm to perturbations from the idealized assumptions we have made. An alternative research direction is to devise numerical schemes to invert L^Pn without replacing it by LĈ, which could allow incorporation of CTF and obviate the need to assume uniform rotations. We proposed one such scheme in section 5.1.

As we discussed in the introduction, our statistical problem (1.1) is actually a special case of the matrix sensing problem. In future work, it would be interesting to test matrix sensing algorithms on our problem. In the cryo-EM case, it would be useful to compare our approach with matrix sensing algorithms. It would also be interesting to explore the applications of our methodology to other tomographic problems involving variability. For example, the field of four-dimensional (4D) electron tomography focuses on reconstructing a 3D structure that is a function of time [26]. This 4D reconstruction is essentially a movie of the molecule in action.

The methods developed in this paper can in principle be used to estimate the covariance matrix of a molecule varying with time. This is another kind of “heterogeneity” that is amenable to the same analysis we used to investigate structural variability in cryo-EM.

Appendix A. Matrix derivative calculations

The goal of this appendix is to differentiate the objective functions of (2.3) and (2.4) to verify formulas (2.5) and (2.6). In order to differentiate with respect to vectors and matrices, we appeal to a few results from [17]. The results are as follows:

$$\Vert I_s-P_s\mu {\Vert }^2=(I_s^H-{\mu }^H{P}_s^H)(I_s-P_s\mu )={\mu }^H{P}_s^H{P}_s\mu -{\mu }^H{P}_s^H{I}_s-I_s^H{P}_s\mu +\mathrm{const}$$ (A.2)

Here, the lowercase letters represent vectors and the uppercase letters represent matrices. Also note that z^* denotes the complex conjugate of z. The general term of (2.3) is

$$D_{{\mu }^{\ast }}\Vert I_s-P_s\mu {\Vert }^2=P_s^H{P}_s\mu -P_s^H{I}_s.$$ (A.3)

We can differentiate this with respect to μ^* by using the first two formulas of (A.1). We get

$$\begin{array}{cc}\hfill & \Vert (I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H-(P_s\Sigma P_s^H+{\sigma }^{2}I){\Vert }_F^2\hfill \\ \hfill & =\Vert A_s-P_s\Sigma P_s^H{\Vert }_F^2\hfill \\ \hfill & =\mathrm{tr}(A_s^H-P_s{\Sigma }^H{P}_s^H)(A_s-P_s\Sigma P_s^H)\hfill \\ \hfill & =\mathrm{tr}\left(P_s{\Sigma }^H{P}_s^H{P}_s\Sigma P_s^H\right)-\mathrm{tr}\left(P_s{\Sigma }^H{P}_s^H{A}_s\right)-\mathrm{tr}\left(A_s^H{P}_s\Sigma P_s^H\right)+\mathrm{const},\hfill \\ \hfill & =\mathrm{tr}\left(\Sigma P_s^H{P}_s{\Sigma }^H{P}_s^H{P}_s\right)-\mathrm{tr}\left(P_s^H{A}_s{P}_s{\Sigma }^H\right)-\mathrm{tr}\left(P_s^H{A}_s^H{P}_s\Sigma \right)+\mathrm{const},\hfill \end{array}$$

Summing in s gives us (2.5).

If we let A_s = (I_s − P_sμ_n)(I_s − P_sμ_n)^H − σ²I, then the general term of (2.4) is

$$P_s^H{P}_s{\Sigma }^H{P}_s^H{P}_s-P_s^H{A}_s^H{P}_s.$$

Using the last two formulas of (A.1), we find that the derivative of this expression with respect to Σ is

$$E\left[Y_s\right]=0and\Vert Y_s\Vert \le Ralmostsurely.$$ (B.1)

Taking a Hermitian and summing in s gives us (2.6).

Appendix B. Consistency of µ_n and Σ_n

In this appendix, we will prove the consistency results about μ_n and Σ_n stated in section 2.2. Recall μ_n and Σ_n are defined nontrivially if ^IA^−1I ≤ 2 ^IA^−1I and ^IL^−1I ≤ 2 ^IL^−1I. As a necessary step towards our consistency results, we must first prove that the probability of these events tends to 1 as n → ∞. Such a statement follow from a matrix concentration argument based on Bernstein’s inequality [59, Theorem 1.4], which we reproduce here for the reader’s convenience as a lemma.

Lemma B.1 (matrix Bernstein’s inequality)

Consider a finite sequence Y_s of independent, random, self-adjoint matrices with dimension p. Assume that each random matrix satisfies

$$P\left\{\Vert \sum _s{Y}_s\Vert \ge t\right\}\le p\cdot exp\left(\frac{-t^2∕2}{{\sigma }^2+Rt∕3}\right),\mathrm{where}{\sigma }^2:=\Vert \sum _{s}E\left(Y_k^2\right)\Vert .$$ (B.2)

Then, for all t ≥ 0,

$$P\left\{\Vert \frac{1}{n}\sum _{s=1}^n{Z}_s-E\left[Z\right]\Vert \ge t\right\}\le d\exp \left(\frac{-3n{t}^2}{6B^2+4Bt}\right).$$ (B.3)

Next, we prove another lemma, which is essentially the Bernstein inequality in a more convenient form.

Lemma B.2

Let Z be a symmetric d × d random matrix, with lZl≤ B almost surely. If Z₁,… , Z_n are i.i.d. samples from Z, then

$$E\Vert \frac{1}{n}\sum _{s=1}^n{Z}_s-E\left[Z\right]\Vert \le CB\max (\sqrt{\frac{\log d}{n}},\frac{2\log d}{n}),$$ (B.4)

Moreover,

$$\Vert Y_s^{}\Vert \le \frac{1}{n}(\Vert Z_s\Vert +E[\Vert Z\Vert ])\le \frac{2B}{n}=:R\mathrm{almost}\mathrm{surely}.$$ (B.5)

where C is an absolute constant.

Proof

The proof is an application of the matrix Bernstein inequality. Let $Y_s=\frac{1}{n}(Z_s-EZ)$. Then, note that E[Y_s] = 0 and

$$E\left[Y_s^2\right]=\frac{1}{n^2}E[Z_s^2-Z_{s}E\left[Z\right]-E\left[Z\right]Z_s+E{\left[Z\right]}^2]=\frac{1}{n^2}(E\left[Z_s^2\right]-E{\left[Z\right]}^2)\le \frac{1}{n^2}E\left[Z_s^2\right].$$ (B.6)

Next, we have

$${\sigma }^2:=\Vert \sum _{s=1}^{n}E\left[Y_s^2\right]\Vert \le \sum _{s=1}^n\Vert E\left[Y_s^2\right]\Vert \le \sum _{s=1}^n\frac{1}{n^2}\Vert E\left[Z_s^2\right]\Vert \le \sum _{s=1}^n\frac{1}{n^2}E[\Vert Z_s{\Vert }^2]\le \frac{B^2}{n}.$$ (B.7)

It follows that

$$P\left\{\Vert \frac{1}{n}\sum _{s=1}^n{Z}_s-E\left[Z\right]\Vert \ge t\right\}=P\left\{\Vert \sum _{s=1}^n{Y}_s\Vert t\right\}\le d\exp \left(\frac{-t^2∕2}{{\sigma }^2+Rt∕3}\right)\le d\exp \left(\frac{-3n{t}^2}{6B^2+4Bt}\right).$$ (B.8)

Now, by the matrix Bernstein inequality, we find that

$$P\{\Vert A_n-A\Vert \le t\}\le p\exp \left(\frac{-3n{t}^2}{6B_P^4+4B_P^{2}t}\right).$$ (B.9)

$$E\Vert A_n-A\Vert \le C{B}_P^2\max (\sqrt{\frac{\log p}{n}},\frac{2\log p}{n})=C{B}_P^2\sqrt{\frac{\log p}{n}},$$ (B.10)

This proves (B.3). The bound (B.4) follows from [59, Remark 6.5].

P^HP_s, where P₁,… , P_n are i.i.d. samples from P . Then,

Corollary B.3

Let P be a random q × p matrix such that lP l ≤ B_P almost surely. Let A = E[P^HP ] and let

$$P\{\Vert L_n-L\ge t\}\le p^2\exp \left(\frac{-3n{t}^2}{6q^4{B}_P^8+4q^2{B}_P^{4}t}\right).$$ (B.11)

Moreover,

$$E\Vert L_n-L\Vert \le C{q}^2{B}_P^4\max \left(\sqrt{\frac{2\log p}{n}},\frac{4\log p}{n}\right)=C_q^2{B}_P^4\sqrt{\frac{2\log p}{n}},$$ (B.12)

where the last equality holds if n ≥ 4 log p.

Proof

These bounds follow by letting Z = P^HP in Lemma B.2 and noting that lZl≤ B² almost surely.

Corollary B.4

Let P be a random q × p matrix such that lP l ≤ B_P almost surely. Let $L\Sigma =E\left[P^{H}P\Sigma P^{H}P\right]andlet{L}_n\Sigma =\frac{1}{n}{\Sigma }_{s=1}^n{P}_s^H{P}_s\Sigma P_s^H{P}_s$, where P₁,… , P_n are i.i.d. samples from P . Then,

$$\begin{array}{cc}\hfill \Vert Z\Vert & =\underset{\Vert \mathrm{vec}\left(\Sigma \right)\Vert =1}{\max }\Vert Z_{\mathrm{vec}}\left(\Sigma \right)\Vert =\underset{\Vert \Sigma {\Vert }_F=1}{\max }\Vert Z\Sigma {\Vert }_F\hfill \\ \hfill & =\underset{\Vert \Sigma {\Vert }_F=1}{\max }\Vert P^{H}P\Sigma P^{H}P{\Vert }_F\le \Vert P{\Vert }_F^4\le q^2\Vert P{\Vert }^4\le q^2{B}_P^4.\hfill \end{array}$$ (B.13)

$$P\left[{\epsilon }_n^A\right]\ge 1-{\alpha }_n^A,P[{\epsilon }_n^L\ge 1-{\alpha }_n^L],$$ (B.14)

Moreover,

where the last equality holds if n ≥ 8 log p.

Proof

We wish to apply Lemma B.2 again, this time for ZΣ = P^HP ΣP^HP . In this case we must be careful because Z is an operator on the space of p × p matrices. We can view it as a p² × p² matrix if we represent its argument (a p × p matrix Σ) as a vector of length p² (denoted by vec(Σ)). Then, almost surely,

$${\alpha }_n^A=p\exp \left(\frac{-3n{\lambda }_{\min }{\left(A\right)}^2∕4}{6B_P^4+2B_P^2\lambda \min \left(A\right)}\right)and{\alpha }_n^L=p^2\exp \left(\frac{-3n{\lambda }_{\min }{\left(L\right)}^2∕4}{6q^4{B}_P^8+2q^2{B}_P^4\lambda \min \left(L\right)}\right).$$ (B.15)

In the penultimate inequality above we used the fact that lAl_F ≤ √rank(A) lAl for an arbitrary matrix A. Now, (B.11) follows from (B.3) by setting B = q²B⁴ and d = p².

Proposition B.5

Let E ^A be the event that ^IA^−1I ≤ 2 ^IA^−1I, and let E ^L be the event that

$$P[\Vert A_n^{-1}\Vert >2\Vert A^{-1}\Vert ]=P[{\lambda }_{\min }\left(A_n\right)<\frac{1}{2}{\lambda }_{\min }\left(A\right)]\le P[\Vert A_n-A\Vert >\frac{1}{2}{\lambda }_{\min }\left(A\right)].$$ (B.16)

where

$$P[\Vert A_n-A\Vert >\frac{1}{2}{\lambda }_{\min }\left(A\right)]\le p\exp \left(\frac{-3n{\lambda }_{\min }{\left(A\right)}^2∕4}{6B_P^4+2B_P^2\lambda \min \left(A\right)}\right)={\alpha }_n^A.$$ (B.17)

Proof

Note that λ_min(A_n) ≥ λ_min(A) − lA_n − Al. It follows that

$$P[\Vert L_n-L\Vert >\frac{1}{2}{\lambda }_{\min }\left(L\right)]\le p^2\exp \left(\frac{-3n{\lambda }_{\min }{\left(L\right)}^2∕4}{6q^4{B}_P^8+2q^2{B}_P^4\lambda \min \left(L\right)}\right)={\alpha }_n^A.$$ (B.18)

By Corollary B.3, it follows that

$$B_I^2:=E[\Vert I-P{\mu }_0{\Vert }^2].$$ (B.19)

Analogously, Corollary B.4 implies that

$$B_I^2\le B_P^{2}E[\Vert X-{\mu }_0{\Vert }^2]+E{[\Vert E\Vert ]}^2.$$ (B.20)

Now, we prove the consistency results, which we restate for convenience. In the following propositions, define

$$\mid \Vert V\Vert {\mid }_m=E{[\Vert V-E\left[V\right]{\Vert }^m]}^{\frac{1}{m}},$$ (B.21)

Note that

$$E\Vert {\mu }_n-{\mu }_0\Vert =O\left(\frac{1}{\sqrt{n}}\right).$$ (B.22)

Also, recall the following notation introduced in section 2.2:

$$\begin{array}{cc}\hfill E[\Vert {\mu }_n-{\mu }_0\Vert ]& =P\left[{∊}_n^A\right]E[\Vert {\mu }_n-{\mu }_0\Vert \mid {∊}_n^A]+(1-P\left[{∊}_n^A\right])E[\Vert {\mu }_n-{\mu }_0\Vert \mid \overline{{∊}_n^A}]\hfill \\ \hfill & \le P\left[{∊}_n^A\right]E[\Vert A_n^{-1}{b}_n-{\mu }_0\Vert \mid {∊}_n^A]+{\alpha }_n^A\Vert {\mu }_0\Vert \hfill \\ \hfill & \le P\left[{∊}_n^A\right]E[\Vert A_n^{-1}(b_n-A_n{\mu }_n)\Vert \mid {∊}_n^A]+{\alpha }_n^A\Vert {\mu }_0\Vert \hfill \\ \hfill & \le P\left[{∊}_n^A\right]a\Vert A^{-1}\Vert E[\Vert b_n-A_n{\mu }_0\Vert \mid {∊}_n^A]+{\alpha }_n^A\Vert {\mu }_0\Vert \hfill \\ \hfill & \le 2\Vert A^{-1}\Vert E[\Vert b_n-A_n{\mu }_0\Vert ]+{\alpha }_n^A\Vert {\mu }_0\Vert .\hfill \end{array}$$ (B.23)

where V is a random vector. For example, (B.20) can be written as $B_I^2\le B_P^2\mid \Vert X\mid {\Vert }_2^2+\mid \Vert E\mid {\Vert }_2^2$.

Proposition B.6

Suppose A (defined in (2.10)) is invertible, that lP l≤ B_P almost surely, and that |||X|||₂, |||E|||₂ < ∞. Then, for fixed p, q we have

$$E[\Vert b_n-A_n{\mu }_0{\Vert }^2]\le E[\Vert b_n-A_n{\mu }_0{\Vert }^2]=\frac{1}{n}E[\Vert P^H(I-P_{{\mu }_0}){\Vert }^2]\le \frac{1}{n}{B}_P^2{B}_I^2.$$ (B.24)

Hence, under these assumptions, μ_n is consistent.

Proof

Since P[lµ_n − μ₀l ≥ t] ≤ t⁻¹E[lµ_n − μ₀l] by Markov’s inequality, it is sufficient to prove that E[lµ_n − μ₀l] → 0 as n → ∞. Note that by the definition of µ_n and Proposition B.5,

$$E[\Vert {\mu }_n-{\mu }_0\Vert ]\le \frac{2\Vert A^{-1}\Vert B_P{B}_I}{\sqrt{n}}+{\alpha }_n^A\Vert {\mu }_0\Vert .$$ (B.25)

$$P\left[{∊}_n^A\right]E[\Vert {\mu }_n-{\mu }_0{\Vert }^2\mid {∊}_n^A]\le \frac{4\Vert A^{-1}{\Vert }^2}{n}{B}_P^2{B}_I^2.$$ (B.26)

where these summands are i.i.d., we find

Since

$$E\Vert \frac{1}{n}\sum _{s=1}^n{V}_s{V}_s^H-{\Sigma }_V\Vert \le C\Vert {\Sigma }_V\Vert \Vert {\Sigma }_V^{-1∕2}\Vert \frac{\sqrt{\log p}}{\sqrt{n}}{(E\Vert V{\Vert }^{\log n})}^{1∕\log n},$$ (B.27)

Putting together what we have, we arrive at

$$\mid \Vert X\mid {\Vert }_j,\mid \Vert E\Vert {\mid }_j\le Q\left(j\right),j\in N.$$ (B.28)

Inspecting this bound reveals that E[lµ_n − μ₀l] → 0 as n → ∞, as needed.

Remark B.7

Note that with a simple modification to the above argument, we obtain

$$E\Vert {\Sigma }_n-{\Sigma }_0\Vert =O\left(\frac{Q\left(\log n\right)}{\sqrt{n}}\right).$$ (B.29)

This bound will be useful later.

Before proving the consistency of Σ_n, we state a lemma.

Lemma B.8

Let V be a random vector on C^p with E[VV^H ] = Σ_V , and let V₁,… , V_n be i.i.d. samples from V . Then, for some absolute constant C,

$$\begin{array}{cc}\hfill E[\Vert {\Sigma }_n-{\Sigma }_0\Vert ]& =P[{∊}_n^A\cap {∊}_n^L]E[\Vert {\Sigma }_n-{\Sigma }_0\Vert \mid {∊}_n^A\cap {∊}_n^L]+(1-P[{∊}_n^A\cap {∊}_n^L])E[\Vert {\Sigma }_n-{\Sigma }_0\Vert \mid \overline{{∊}_n^A\cap {∊}_n^L}]\hfill \\ \hfill & \le P[{∊}_n^A\cap {∊}_n^L]E[\Vert L_n^{-1}{B}_n-{\Sigma }_0\Vert \mid {∊}_n^A\cap {∊}_n^L]+({\alpha }_n^A+{\alpha }_n^L)\Vert {\Sigma }_0\Vert \hfill \\ \hfill & \le P[{∊}_n^A\cap {∊}_n^L]E[\Vert L_n^{-1}{B}_n-L_n{\Sigma }_0\Vert \mid {∊}_n^A\cap {∊}_n^L]+({\alpha }_n^A+{\alpha }_n^L)\Vert {\Sigma }_0\Vert \hfill \\ \hfill & \le 2\Vert L^{-1}\Vert P[{∊}_n^A\cap {∊}_n^L]E[\Vert (B_n-L_n{\Sigma }_0)\Vert \mid {∊}_n^A\cap {∊}_n^L]+({\alpha }_n^A+{\alpha }_n^L)\Vert {\Sigma }_0\Vert \hfill \\ \hfill & \le 2\Vert L^{-1}\Vert P\left[{∊}_n^A\right]E[\Vert B_n-L_n{\Sigma }_0\Vert \mid {∊}_n^A]+({\alpha }_n^A+{\alpha }_n^L)\Vert {\Sigma }_0\Vert .\hfill \end{array}$$ (B.30)

provided the RHS does not exceed lΣ_V l.

Proof

This result is a simple modification of [47, Theorem 1].

Proposition B.9

Suppose A and L (defined in 2.10) are invertible, that lP l≤ B_P almost surely, and that there is a polynomial Q for which

$$\begin{array}{cc}\hfill B_n-L_n{\Sigma }_0& =(\frac{1}{n}\sum _{s=1}^n{P}_s^H(I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H{P}_s-\frac{1}{n}\sum _{s=1}^n{P}_s^H(I_s-P_s{\mu }_0){(I_s-P_s{\mu }_0)}^H{P}_s)\hfill \\ \hfill & +(\frac{1}{n}\sum _{s=1}^n{P}_s^H(I_s-P_s{\mu }_0){(I_s-P_s{\mu }_0)}^H{P}_s-({\sigma }^{2}A+L{\Sigma }_0))+{\sigma }^2(A-A_n)+(L-L_n){\Sigma }_0\hfill \\ \hfill & =:D_1+D_2+D_3+D_4.\hfill \end{array}$$ (B.31)

Then, for fixed p, q, we have

$$E[\Vert D_1\Vert \mid {∊}_n^A]\le B_P^2\frac{1}{n}\sum _{s=1}^{n}E[\Vert (I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H-(I_s-P_s{\mu }_0){(I_s-P_s{\mu }_0)}^H\Vert \mid {∊}_n^A].$$ (B.32)

Hence, under these assumptions, Σ_n is consistent.

Proof

In parallel to the proof of Proposition B.6, we will prove that E[lΣ_n − Σ₀l] → 0 as n → ∞. We compute

$$\begin{array}{cc}\hfill & (I_s-P_s{\mu }_n){(I_s-P_s{\mu }_n)}^H-(I_s-P_s{\mu }_0){(I_s-P_s{\mu }_0)}^H\hfill \\ \hfill & =\{(I_s-P_s{\mu }_0)+P_s({\mu }_0-{\mu }_n)\}{\{(I_s-P_s{\mu }_0)+P_s({\mu }_0-{\mu }_n)\}}^H-(I_s-P_s{\mu }_0){(I_s-P_s{\mu }_0)}^H\hfill \\ \hfill & =(I_s-P_s{\mu }_0){({\mu }_0-{\mu }_n)}^H{P}_s^H+P_s({\mu }_0-{\mu }_n){(I_s-P_s{\mu }_0)}^H+P_s({\mu }_0-{\mu }_n){({\mu }_0-{\mu }_n)}^H{P}_s^H.\hfill \end{array}$$ (B.33)

Now, we will bound E $E[\Vert B_n-L_n{\Sigma }_n\Vert \mid {∊}_n^A]$. To do this, we write

$$\begin{array}{cc}\hfill & E{[\Vert (I_s-P_s{\mu }_0){({\mu }_0-{\mu }_n)}^H{P}_s^H\Vert \mid {∊}_n^A]}^2\hfill \\ \hfill & \le B_P^{2}E{[\Vert I_s-P_s{\mu }_0\Vert \Vert {\mu }_0-{\mu }_n\Vert \mid {∊}_n^A]}^2\hfill \\ \hfill & \le B_P^{2}E[\Vert I_s-P_s{\mu }_0{\Vert }^2\mid {∊}_n^A]E[\Vert {\mu }_0-{\mu }_n{\Vert }^2\mid {{∊}_n^A}^2]\hfill \\ \hfill & \le \frac{4\Vert A^{-1}{\Vert }^2}{nP{\left[{∊}_n^A\right]}^2}{B}_P^4{B}_I^4.\hfill \end{array}$$ (B.34)

Let us consider each of these four difference terms in order. Note that

$$E[\Vert P_s({\mu }_0-{\mu }_n){({\mu }_0-{\mu }_n)}^H{P}_s^H\Vert \mid {∊}_n^A]\le B_P^{2}E[\Vert {\mu }_0-{\mu }_n{\Vert }^2\mid {∊}_n^A]\le \frac{4\Vert A^{-1}{\Vert }^2}{nP\left[{∊}_n^A\right]}{B}_P^4{B}_I^2.$$ (B.35)

Moreover,

$$\begin{array}{cc}\hfill P\left[{∊}_n^A\right]E[\Vert D_1\Vert \mid {∊}_n^A]& \le P\left[{∊}_n^A\right]B_P^2(2\frac{2\Vert A^{-1}\Vert }{\sqrt{n}P\left[{∊}_n^A\right]}{B}_P^2{B}_I^2+4\frac{\Vert A^{-1}{\Vert }^2}{nP\left[{∊}_n^A\right]}{B}_P^4{B}_I^2)\hfill \\ \hfill & =\frac{4B_P^4{B}_I^2\Vert A^{-1}\Vert }{n}(\sqrt{n}+\Vert A^{-1}\Vert B_P^2).\hfill \end{array}$$ (B.36)

Using the Cauchy–Schwarz inequality and (B.26), we find

$${\Sigma }_V=E\left[V{V}^H\right]=E\left[P^{H}P(X-{\mu }_0){(X-{\mu }_0)}^H{P}^{H}P\right]+E\left[P^{H}E{E}^{H}P\right]=L{\Sigma }_0+{\sigma }^{2}A.$$ (B.37)

Here, we used (B.26). This bound also holds for the second term in the last line of (B.33). As for the third term,

$$P\left[{∊}_n^A\right]E[\Vert D_2\Vert \mid {∊}_n^A]\le E\Vert \frac{1}{n}\sum _{s=1}^n{V}_s{V}_s^H-{\Sigma }_V\Vert \le C\Vert {\Sigma }_V\Vert \Vert {\Sigma }_V^{-1∕2}\Vert \frac{\sqrt{\log p}}{\sqrt{n}}{(E\Vert V{\Vert }^{\log n})}^{\frac{1}{\log n}}.$$ (B.38)

Putting these bounds together, we arrive at

$$\Vert L{\Sigma }_0\Vert \le \Vert L{\Sigma }_0{\Vert }_F\le q^4{B}_P^4\Vert {\Sigma }_0{\Vert }_F\le q^4{B}_P^4\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\Vert {\Sigma }_0\Vert q^4{B}_P^4\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\mid \Vert X\mid {\Vert }_2^2.$$ (B.39)

$$\begin{array}{cc}\hfill {(E\Vert V{\Vert }^{\log n})}^{\frac{1}{\log n}}& \le B_p\left(B_p(E{[\Vert X-{\mu }_0{\Vert }^{\log n}]}^{\frac{1}{\log n}}+E{[\Vert E{\Vert }^{\log n}]}^{\frac{1}{\log n}})\right)\hfill \\ \hfill & =B_p\left(B_p(\mid \Vert X\mid {\Vert }_{\log n}+\mid \Vert E\mid {\Vert }_{\log n})\right).\hfill \end{array}$$ (B.40)

Next, we move on to analyzing D₂. If V = P^H (I − P μ₀), note that

$$\begin{array}{cc}\hfill P\left[{∊}_n^A\right]E[\Vert D_2\Vert \mid {∊}_n^A]& \le C{B}_P^3(q^4{B}_P^2\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\mid \Vert X\mid {\Vert }_2^2+{\sigma }^2)\hfill \\ \hfill & \times \Vert {(L{\Sigma }_0+{\sigma }^{2}A)}^{-1∕2}\Vert \frac{\sqrt{\log p}}{\sqrt{n}}\left(B_p(\mid \Vert X\mid {\Vert }_{\log n}+\mid \Vert E\Vert {\mid }_{\log n})\right).\hfill \end{array}$$ (B.41)

By Lemma (B.8), we find (B.38)

Since Σ₀ = E[(X − μ₀)(X − μ₀)^H ], it follows that lΣ₀l ≤ E[lX − μ₀l ] = |||X|||₂. Further, the calculation (B.13) implies that

$$P\left[{∊}_n^A\right]E[\Vert D_3\Vert \mid {∊}_n^A]\le E[\Vert D_3\Vert ]={\sigma }^{2}E[\Vert A-A_n\Vert ]\le {\sigma }^2{C}^{\prime }{B}_P^2\sqrt{\frac{\log n}{p}}.$$ (B.42)

Also, it is clear that $\Vert A\Vert \le B_P^2$. Furthermore, Minkowski inequality implies that

$$\begin{array}{cc}\hfill P\left[{∊}_n^A\right]E[\Vert D_4\Vert \mid {∊}_n^A]& \le E[\Vert D_4\Vert ]\le E[\Vert L-L_n\Vert ]\Vert {\Sigma }_0{\Vert }_F\hfill \\ \hfill & \le {\sigma }^2{C}^{\prime }{q}^2{B}_P^4\sqrt{\frac{2\log p}{n}}\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\mid \Vert X\Vert {\mid }_2^2.\hfill \end{array}$$ (B.43)

Hence, (B.38) becomes

$$\begin{array}{cc}\hfill E[\Vert {\Sigma }_n-{\Sigma }_0\Vert ]& \le 2\Vert L^{-1}\Vert \frac{4B_P^4(B_P^2\mid \Vert X\mid {\Vert }_2^2+\mid \Vert E\mid {\Vert }_2^2)\Vert A^{-1}\Vert }{n}(\sqrt{n}+\Vert A^{-1}\Vert B_P^2)\hfill \\ \hfill & +C{B}_P^3(q^4{B}_P^2\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\mid \Vert X\mid {\Vert }_2^2+{\sigma }^2)\Vert {(L{\Sigma }_0+{\sigma }^{2}A)}^{-1∕2}\Vert \hfill \\ \hfill & \times \frac{\sqrt{\log p}}{\sqrt{n}}\left(B_P(\mid \Vert X\mid {\Vert }_{\log n}+\mid \Vert E\mid {\Vert }_{\log n})\right)\hfill \\ \hfill & +{\sigma }^2{C}^{\prime }{B}_P^2\sqrt{\frac{\log p}{n}}+{\sigma }^2{C}^{\prime }{q}^2{B}_P^4\sqrt{\frac{2\log p}{n}}\sqrt{\mathrm{rank}\left({\Sigma }_0\right)}\mid \Vert X\mid {\Vert }_2^2\hfill \\ \hfill & +({\alpha }_n^A+{\alpha }_n^L)\mid \Vert X\mid {\Vert }_2^2.\hfill \end{array}$$ (B.44)

Next, a bound for D₃ follows immediately from (B.10):

$${\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1,k_2}={\int }_{S^2\times S^2}(a_{j_1}^{k_1}\otimes a_{j_2}^{k_2})(\alpha ,\beta )\overline{(a_{j_1}^{k_1}\otimes a_{j_2}^{k_2})(\alpha ,\beta )}K(\alpha ,\beta )d\alpha d\beta .$$ (C.1)

Similarly, (B.12) gives

$${\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1,k_2}={\int }_{S^2\times S^2}{A}_{i_1{j}_1}^{k_1}\left(\alpha \right)\overline{A_{i_2{j}_2}^{k_2}\left(\beta \right)}K(\alpha ,\beta )d\alpha d\beta .$$ (C.2)

Combining the four bounds (B.36), (B.39), (B.42), (B.43) with (B.30) and (B.31), we arrive at

$$A_{i_1{j}_1}^{k_1}\left(\alpha \right)=\sum _{l=0}^{2k_1}\sum _{\mid m\mid \le l}{C}_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)Y_l^m\left(\alpha \right),A_{i_2{j}_2}^{k_2}\left(\beta \right)=\sum _{l=0}^{2k_2}\sum _{\mid m^{\prime }\mid \le l^{\prime }}{C}_{l,m}\left(A_{i_2{j}_2}^{k_2}\right)Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right).$$ (C.3)

Fixing all the variables except n, we see that the largest term is the one in the second line, and it decays as Q(log n)/^√n due to the moment growth condition (B.28).

Appendix C. Simplifying (5.12)

Here, we simplify the expression for an element of L^Pk1,k2:

$${\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1,k_2}=\sum _{l,m}\sum _{l^{\prime ,}{m}^{\prime }}{C}_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}{\int }_{S^2}{\int }_{S^2}{Y}_l^m\left(\alpha \right)K(\alpha ,\beta )\overline{Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right)}d\alpha d\beta .$$ (C.4)

Let $A_{i,j}^k=\overline{a_i^k}{a}_j^k$. Then, (C.1) becomes

$${\int }_{S^2}{Y}_l^m\left(\alpha \right)K(\alpha ,\beta )d\alpha =c\left(l\right)Y_l^m\left(\beta \right),$$ (C.5)

Recall from section 5.3 that $a_i^k$ is a spherical harmonic of order up to k. It follows that $A_{i_1{j}_1}^{k_1}$ has a spherical harmonic expansion up to order 2k₁ (using the formula for the product of two spherical harmonics, which involves the Clebsch–Gordan coefficients). The same holds for $A_{i_2{j}_{12}}^{k_2}$, where the order goes up to 2k₂. Let us write $C_l^m\left(A_{ij}^k\right)$ for the l, m coefficient of the spherical harmonic expansion of $A_{ij}^k$. Thus, we have

$$c\left(l\right)=\frac{2\pi }{P_l\left(1\right)}{\int }_{-1}^{1}K\left(t\right)P_l\left(t\right)dt.$$ (C.6)

It follows that

$$c\left(l\right)=2{\int }_0^1\frac{1}{\sqrt{1-t^2}}{P}_l\left(t\right)dt.$$ (C.7)

Since K(α, β) depends only on α · β, by an abuse of notation we can write K(α, β) = K(α · β). Thus, the Funk–Hecke theorem applies [38], so we may write

$$c\left(l\right)=2{\int }_0^1\frac{1}{\sqrt{1-t^2}}{P}_l\left(t\right)dt=\pi {\left(\frac{l!}{2^l{(\frac{l}{2}!)}^2}\right)}^2.$$ (C.8)

where

$$\begin{array}{cc}\hfill {\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1{k}_2}& =\sum _{l,m}\sum _{l^{\prime },m^{\prime }}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}{\int }_{S^2}{Y}_l^m\left(\beta \right)\overline{Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right)}d\beta \hfill \\ \hfill & =\sum _{l,m}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}.\hfill \end{array}$$ (C.9)

Note that the P_R are the Legendre polynomials. Since K is an even function of t and P_R has the same parity as .e, it follows that c(.e) = 0 for odd .e. For even .e, we have

$$\begin{array}{cc}\hfill {\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1{k}_2}& =\sum _{l,m}\sum _{l^{\prime },m^{\prime }}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}{\int }_{S^2}{Y}_l^m\left(\beta \right)\overline{Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right)}d\beta \hfill \\ \hfill & =\sum _{l,m}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}.\hfill \end{array}$$ (C.9)

It follows from formula 3 on p. 423 of [45] that

$$\begin{array}{cc}\hfill {\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1{k}_2}& =\sum _{l,m}\sum _{l^{\prime },m^{\prime }}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}{\int }_{S^2}{Y}_l^m\left(\beta \right)\overline{Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right)}d\beta \hfill \\ \hfill & =\sum _{l,m}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}.\hfill \end{array}$$ (C.9)

Using Stirling’s formula, we can find that c(.e) ~ .e⁻¹ for large .e.

Finally, plugging the result of Funk–Hecke into (C.4), we obtain

$$\begin{array}{cc}\hfill {\widehat{L}}_{i_1{i}_2,j_1{j}_2}^{k_1{k}_2}& =\sum _{l,m}\sum _{l^{\prime },m^{\prime }}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}{\int }_{S^2}{Y}_l^m\left(\beta \right)\overline{Y_{l^{\prime }}^{m^{\prime }}\left(\beta \right)}d\beta \hfill \\ \hfill & =\sum _{l,m}c\left(l\right)C_{l,m}\left(A_{i_1{j}_1}^{k_1}\right)\overline{C_{l^{\prime },m^{\prime }}\left(A_{i_2{j}_2}^{k_2}\right)}.\hfill \end{array}$$ (C.9)

Thus, we have verified (5.13).