Quantitative Assessment of Single-Image Super-Resolution in Myocardial Scar Imaging

Abstract

Single-image super resolution is a process of obtaining a high-resolution image from a set of low-resolution observations by signal processing. While super resolution has been demonstrated to improve image quality in scaled down images in the image domain, its effects on the Fourier-based image acquisition technique, such as MRI, remains unknown. We performed high-resolution ex vivo late gadolinium enhancement (LGE) magnetic resonance imaging (0.4×0.4×0.4 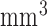) in postinfarction swine hearts 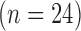. The swine hearts were divided into the training set 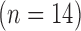and the test set 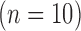, and in all hearts, low-resolution images were simulated from the high-resolution images. In the training set, super-resolution dictionaries with pairs of small matching patches of the high- and low-resolution images were created. In the test set, super resolution recovered high-resolution images from low-resolution images using the dictionaries. The same algorithm was also applied to patient LGE 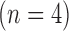to assess its effects. Compared with interpolated images, super resolution significantly improved basic image quality indices 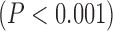. Super resolution using Fourier-based zero padding achieved the best image quality. However, the magnitude of improvement was small in images with zero padding. Super resolution substantially improved the spatial resolution of the patient LGE images by sharpening the edges of the heart and the scar. In conclusion, single-image super resolution significantly improves image errors. However, the magnitude of improvement was relatively small in images with Fourier-based zero padding. These findings provide evidence to support its potential use in myocardial scar imaging.

I. Introduction

Late gadolinium enhancement (LGE) MRI can visualize the regions of fibrosis or scar in the heart, mainly from previous myocardial infarction (MI) [1]. Recent evidence suggests that the complex geometry of the scar determines the propensity to ventricular arrhythmia [2], and predicts death [3]. Our previous work using high-resolution ex vivo MRI demonstrated a critical link between the complex scar geometry and electrical circuits of ventricular arrhythmia [4]. However, the spatial resolution of clinical cardiac MRI is not sufficiently high to allow reconstruction of the complex scar geometry. Improved resolution of clinical cardiac MRI would allow qualitative assessment of the scar and more appropriate utilization of clinical image data to predict lethal arrhythmia, guide therapy and prevent death.

To improve the spatial resolution of an imaging system, one straightforward approach is to directly acquire a high-resolution image. This solution, however, may not be feasible due to higher noise levels associated with high-resolution image acquisition, longer acquisition time and higher hardware cost such as in high and ultra-high field system. Another approach is to accept the image degradations, and use signal processing to post-process the captured images, to trade off computational cost with the hardware cost. These techniques are referred to as super-resolution reconstruction. Specifically, super resolution is the process of obtaining a high-resolution image from a set of low-resolution observations, thereby increasing the high-frequency components and removing the degradations caused by the process of inherently blurred image acquisition. There are a number of methods to perform super resolution while preserving edges and small details [5].

In this work, we applied an algorithm for single-image super resolution [6] to myocardial scar imaging to quantitatively assess its effects. The algorithm uses sparse representation and operates by training a pair of low- and high-resolution dictionaries, using either training images or exploiting a lower-resolution version of the same image to be handled. While this algorithm of super resolution has been demonstrated to improve image quality in scaled down images in the image domain [6], its effects on the Fourier-based image acquisition technique such as MRI remains unknown. To investigate the effects of single-image super resolution on Fourier-based and image-based methods of scale-up, three separate data analyses were conducted using the same sets of images.

II. Methods

A. Animal Study Protocol

The animal protocol was approved by the Animal Care and Use Committee of the Johns Hopkins University School of Medicine. In domestic swine (25 to 35 kg, ), the mid–left anterior descending coronary artery was occluded for 150 minutes using a balloon angioplasty catheter (2.7 Fr) via a carotid artery to create MI under general anesthesia [4]. Ten to twelve weeks after MI, high-resolution ex vivo MRI [4] was conducted to visualize myocardial scar geometry. Fifteen minutes after intravenous administration of heparin 5,000 IU and Gd-DTPA (Magnevist, gadolinium diethylene triamine pentaacetic acid, Berlex) at 0.20 mmol/kg, the animals were euthanized, and the hearts were removed and filled with vinyl polysiloxane. Each heart was scanned in a 1.5-Tesla scanner (Avanto, Siemens Medical Solutions) with a 3D gradient recalled echo (GRE) sequence to visualize the myocardial scar (bandwidth, ; flip angle, 20°; echo time/repetition time, 4.02/9.7 ms; field of view, 100×100 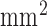; image matrix, 256×256; spatial resolution, 0.4×0.4×0.4 ).

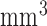B. Data Analysis

The high-resolution image data sets (0.4×0.4 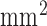in-plane) from swine ex vivo imaging were divided into the training set 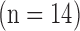and the test set 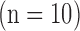. In both sets, the image data from each heart consisted of 100 short-axis (SAX) images and 50 long-axis (LAX) images to only include the ventricles. MATLAB R2013a (Mathworks, Inc., Natick, MA) was used for data analysis. The single-image super-resolution algorithm (available at http://www.cs.technion.ac.il/~elad/software/) was modified to fit the objectives of the study and the specific computational environment (3.4 GHz Intel Core i7×4, 32 GB RAM and 3TB hard drive).

C. Training Set

The details of the original algorithm are described in Zeyde et al. [6]. Briefly, in the training sets (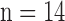 hearts, total 1,400 SAX images and 700 LAX images), the high-resolution image 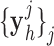(a 256×256 matrix) was blurred and scaled-down by a factor of 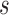(Fig. 1).

where 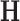represents an operator to create the low-resolution image 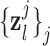(a 64×64 matrix) from the high-resolution image 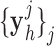(a 256×256 matrix), and 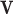an additive white Gaussian noise. In this study 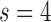was chosen because the in-plane resolution of clinical myocardial scar imaging 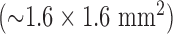is approximately 4 times lower than that of the high-resolution image data sets (0.4×0.4 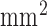). The low-resolution image 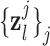(a 64×64 matrix) was then scaled-up by a factor of 4 to the original size (a 256×256 matrix) by an interpolation operator .

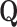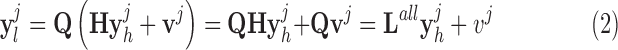The methods of scale-up and scale-down are described in Section III (“. Three comparative analyses”). Both the high-resolution 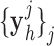and interpolated images 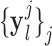were pre-processed with high-pass filters, and were divided into small overlapping patches 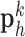and 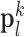, and the pairs of matching patches were extracted to form the training dictionary 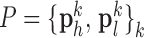. Each of these patch-pairs underwent a pre-processing stage that removes the low-frequency components from 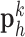and extracts features from 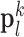. Dimensionality reduction using principal component analysis (PCA) was also applied on the features of 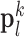, making the dictionary training step much faster. A low-resolution dictionary 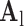was trained for the low-resolution patches using the K-SVD algorithm [7], such that they could be represented sparsely. A corresponding high-resolution dictionary 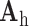was constructed for the high-resolution patches, such that it matched the low-resolution dictionary .

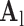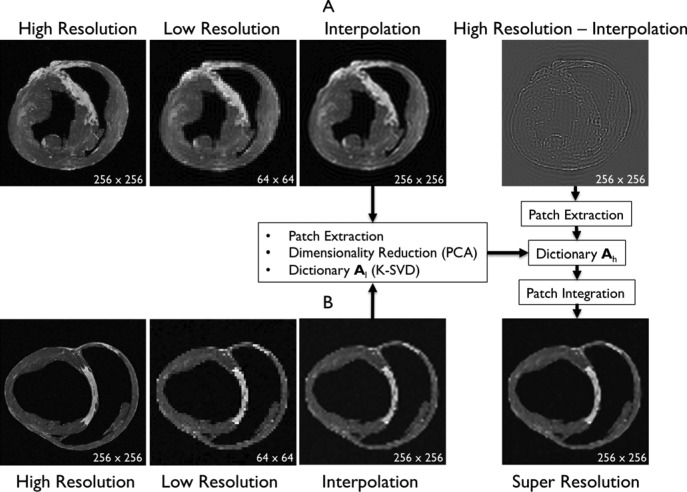
Fig. 1. Algorithm of single-image super-resolution using sparse representation. The details of the algorithm are described in Zeyde et al. [6]. A. Training set (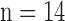 hearts, total 2,100 images). In the original high-resolution late gadolinium enhancement (LGE) image (a 256×256 matrix), the region of high signal intensity (SI) 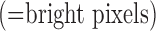indicates myocardial infarction (MI). The high-resolution image was scaled down by a factor of 4 to generate a low-resolution image (a 64×64 matrix). The low-resolution image was then scaled up by a factor of 4 to the original size (a 256×256 matrix) by interpolation. The methods of scale-up and scale-down are shown in Fig. 2. Both the high-resolution and interpolated images were divided into small overlapping patches, and the pairs of matching patches were extracted to form the training dictionary. Each of these patch-pairs underwent a pre-processing stage that removes the low-frequency components from high-resolution patches and extracts features from low-resolution patches. Dimensionality reduction using principal component analysis (PCA) was also applied on the features of the low-resolution patches, making the dictionary training step much faster. A low-resolution dictionary 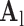was trained for the low-resolution patches using the K-SVD algorithm [7], such that they could be represented sparsely. A corresponding high-resolution dictionary 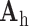was constructed for the high-resolution patches, such that it matched the low-resolution dictionary 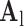. B. Test set ( 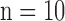hearts, total 1,500 images). As in the training set, low-resolution images (a 64×64 matrix) were also constructed from the high-resolution images (a 256×256 matrix) by scale-down by a factor of 4, and the low-resolution images (a 64×64 matrix) were scaled up to the destination size (a 256×256 matrix) by interpolation. Pre-processed low-resolution patches were extracted from each location, and then sparse-coded using the trained low-resolution dictionary 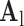. The representations found in the low-resolution dictionary 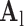were then used to recover the high-resolution patches by multiplying them with the high-resolution dictionary 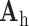. The recovered high-resolution patches were merged by averaging in the overlap area to create the resulting image (a 256×256 matrix) A. Training set B. Test set.

D. Test Set

In the test image sets (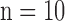 hearts, total 1,000 SAX images and 500 LAX images), as in the training set, low-resolution images (a 64×64 matrix) were also constructed from the high-resolution images (a 256×256 matrix) by scale-down by a factor of 4, and the low-resolution images (a 64×64 matrix) were scaled up to the destination size (a 256×256 matrix) by interpolation. Pre-processed low-resolution patches 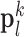were extracted from each location, and then sparse-coded using the trained low-resolution dictionary 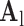. The representations 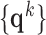found in the low-resolution dictionary 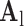were then used to recover the high-resolution patches 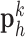by multiplying them with the high-resolution dictionary 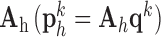. The recovered high-resolution patches 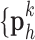were merged by averaging in the overlap area to create the resulting image (a 256×256 matrix).

E. Three Comparative Analyses

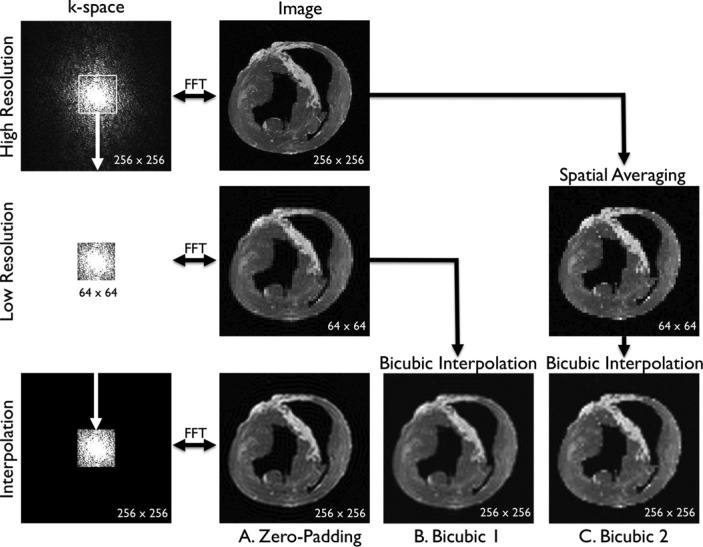
In this study, to compare the effects of super resolution on different methods of scale-up, three separate data analyses were conducted using the same sets of LGE images (Fig. 2). Separate sets of dictionaries were created for each analysis. A. Zero-padding. Because MRI is a Fourier-based image acquisition technique and the image data are acquired in k-space, the most logical method to simulate a low-resolution image from a high-resolution image is to remove coefficients in k-space. A fast Fourier transform (FFT) was applied to the high-resolution image to compute the high-resolution k-space (a 256×256 matrix). The low-resolution k-space was simulated by extracting the central, low-frequency components (a 64×64 matrix) of the high-resolution k-space. The magnitude of the low-resolution k-space was corrected by a factor of 16 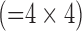and smoothed by a Fermi window to simulate a low-resolution acquisition. The low-resolution image (a 64×64 matrix) was obtained as an FFT of the low-resolution k-space. The interpolated image (a 256×256 matrix) was obtained by padding zeros around the low-resolution k-space to restore the original size (a 256×256 matrix), and by applying inverse FFT to the zero-padded k-space. This is mathematically equivalent to convolution with a sinc function. The process of zero-padding in k-space is the typical interpolation routine used in MRI systems. B. Bicubic 1. This analysis was conducted to compare the effects of super resolution between zero-padding and bicubic interpolation, a commonly used interpolation method outside the MRI field. The low-resolution image (a 64×64 matrix) was simulated as in the zero-padding group. The interpolated image (a 256×256 matrix) was created by applying bicubic interpolation to the low-resolution image. C. Bicubic 2. This analysis was conducted to serve as a positive control of the super resolution technique. Spatial averaging as a method of scale-down and bicubic interpolation as a method of scale-up are commonly used to evaluate the effects of super-resolution techniques [6]. The low-resolution image (a 64×64 matrix) was created by spatially averaging the high-resolution image (a 256×256 matrix). The interpolated image (a 256×256 matrix) was created by applying bicubic interpolation to the low-resolution image.

Fig. 2. Three comparative analyses. A. Zero-padding. A fast Fourier transform (FFT) was applied to the high-resolution image to compute the high-resolution k-space (a 256×256 matrix). The low-resolution k-space was created by extracting the central, low-frequency components (a 64×64 matrix) of the high-resolution k-space. The magnitude of the low-resolution k-space was corrected by a factor of 16 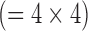and smoothed by a Fermi window to simulate a low-resolution acquisition. The low-resolution image (a 64×64 matrix) was obtained as an FFT of the low-resolution k-space. The interpolated image (a 256×256 matrix) was obtained by padding zeros around the low-resolution k-space to restore the original size (a 256×256 matrix), and by applying inverse FFT to the zero-padded k-space. This is mathematically equivalent to convolution with a sinc function. B. Bicubic 1. The low-resolution image (a 64×64 matrix) was created as in the zero-padding group. The interpolated image (a 256×256 matrix) was created by applying bicubic interpolation to the low-resolution image. C. Bicubic 2. The low-resolution image (a 64×64 matrix) was created by spatially averaging the high-resolution image (a 256×256 matrix). The interpolated image (a 256×256 matrix) was created by applying bicubic interpolation to the low-resolution image.

F. Error Analysis

To measure the differences between the original high-resolution image and the interpolated image or the super resolution image, we used 4 separate indices: mean absolute error (MAE), root mean square error (RMSE), peak signal-to-noise ratio (PSNR) and universal image quality index (UIQI) [8], [9].

MAE between a reference image 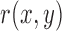and a test image 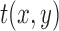of the size 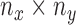is defined as

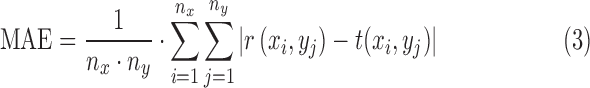RMSE is defined as

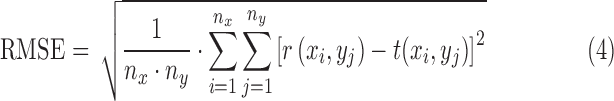PSNR (in dB) is defined as

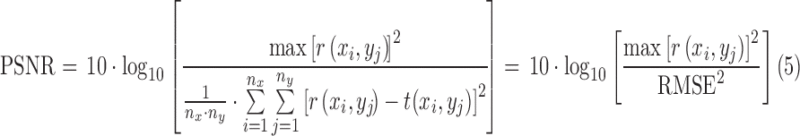UIQI is defined as

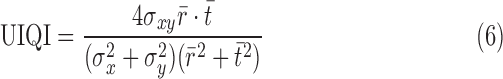where

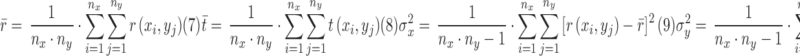G. Patient Protocol

We applied the super resolution algorithm to clinical MRI of the patients with ischemic heart disease . The study was approved by the Institutional Review Board of the Johns Hopkins Medical Institutions. The patients underwent cardiac MRI with LGE on a 1.5-Tesla scanner (Avanto, Siemens Medical Solutions) with the standard 6-element cardiac phased-array receiver coil and the spine coil. Ten to twelve contiguous short-axis slices were prescribed to cover the entire left ventricle. LGE images were acquired 15 to 30 minutes after an intravenous injection of Gd-DTPA at 0.20 mmol/kg with a standard non-phase-sensitive inversion recovery sequence. Representative imaging parameters were as follows: repetition time 1 heartbeat , echo time 3.32 ms, in-plane spatial resolution 1.25–1.9 mm, 10-mm slice thickness, 0–2-mm gap, inversion time 175 to 280 ms (adjusted to null the signal of normal myocardium), flip angle 25° and a GRE readout. Each image acquisition was ECG gated, and the image was acquired during a single, typically end-expiration, breath hold.

H. Super Resolution in Patient Images

The original, standard clinical MRI (low-resolution) images were scaled up to the destination size by a factor of 4 using the zero padding and the bicubic 1 methods described above. Bicubic 2 was not used because there was no original high-resolution patient image available from which to create a spatially averaged image. Using the respective dictionaries created using the swine training sets, high-resolution images were reconstructed as described above.

I. Statistical Analysis

Values are 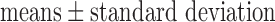(SD). A Student's t-test was used to compare super-resolution and interpolated images for each error index. A Student's t-test was also used to compare zero-padding and two other interpolation methods (bicubic 1 and bicubic 2). A 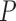value 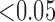is considered statistically significant. Statistical analysis was performed using MATLAB (Statistical Toolbox, MathWorks, Inc, Natick, MA).

III. Result

A. Computation Time

Training of each set of dictionary took approximately 1.5 hours. The process of super resolution took less than 2 seconds per image.

B. Qualitative Pixelwise Error Analysis

In Fig. 3, each column shows pixelwise absolute error in signal intensity (SI) between the high-resolution image and the interpolated image or the super resolution image. The bottom row represents the absolute difference in SI between the interpolated image and the super resolution image. The columns indicate the results from three comparative analyses, including zero padding, bicubic 1, and bicubic 2. In zero padding (left column), the absolute error of the interpolated image was relatively low (top row). The region of high error was concentrated at the edges of the heart and was evenly spread out throughout the heart. The absolute error of the super-resolution image was equally low (middle row) and there was only small difference between the interpolated and the super-resolution images (bottom row). In contrast, in bicubic 1 (middle column), the absolute error of the interpolated image was substantially higher at the edges, particularly in the scar region (septum), reflecting the blurring effect of image-based interpolation (top row). The absolute error of the super-resolution image was visually lower overall (middle row), particularly in the scar region (septum), making the difference between the interpolated and super-resolution images relatively high (bottom row). In addition, the absolute error of the super resolution image (middle row) was somewhat higher compared to that of the super-resolution image in zero padding. In bicubic 2 (right column), the absolute error of the interpolated image (top row) appears slightly higher than that of zero padding. The regions of high errors were spotty and not contiguous. This is likely the effect of image-based spatial averaging to create a low-resolution image from the high-resolution image. The absolute error of the super-resolution image (middle row) was visually similar to that of the interpolated image and there was small difference between the interpolated and the super-resolution images (bottom row), except in the scar region.

Fig. 3. Pixelwise absolute error vs. high-resolution image. Each column shows pixelwise absolute error in SI between the high-resolution image and the interpolated image (“Interpolation”) or the super resolution image (“Super Resolution”). The bottom row represents the absolute difference in SI between the interpolated image and the super resolution image. The columns indicate the results from three comparative analyses, including A. Zero-padding, B. Bicubic 1, and C. Bicubic 2.

C. Quantitative Error Analysis

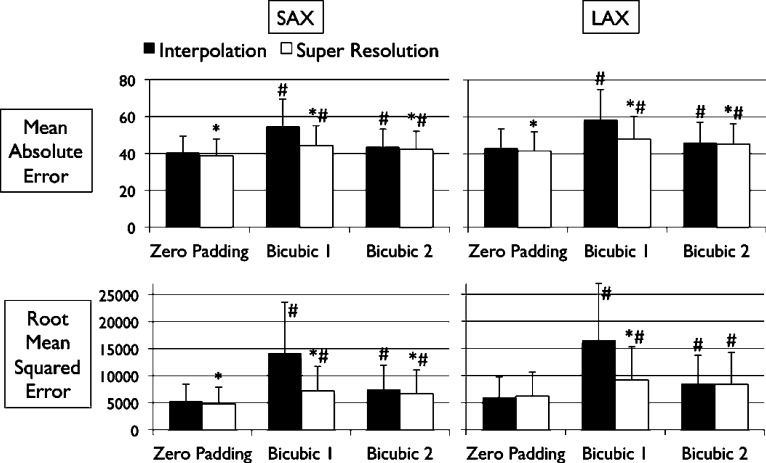
Figs. 4 and 5 show the results of quantitative error analysis using the indices described above. The sample size was 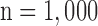for SAX images, and 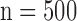for LAX images. Super resolution significantly improved MAE compared with the interpolated image in both SAX and LAX images, regardless of the interpolation method (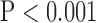, top row, Fig. 4). Importantly, zero padding achieved the lowest MAE in both the interpolated and super-resolution images (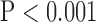, top row, Fig. 4). Similarly, super resolution significantly improved RMSE in SAX images regardless of the interpolation method (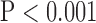, bottom row, Fig. 4). However, super resolution did not significantly improve RMSE in LAX images in zero padding and bicubic 2. 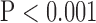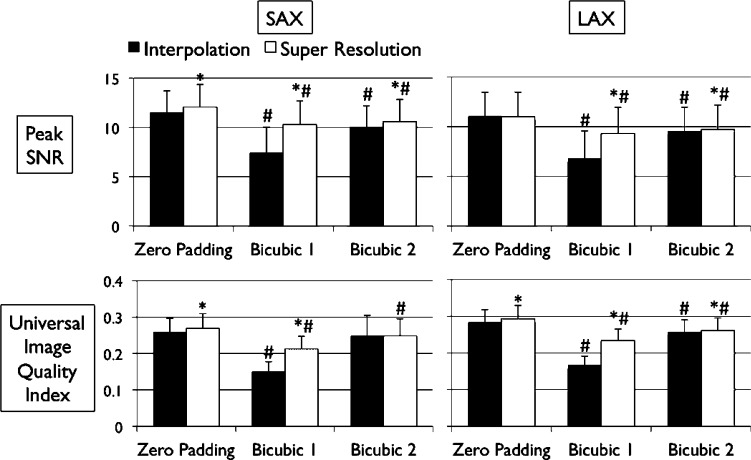Zero padding achieved the lowest RMSE in both the interpolated and super-resolution images (, bottom row, Fig. 4). Super resolution significantly improved peak SNR in SAX images regardless of the interpolation method (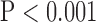, top row, Fig. 5). However, super resolution did not significantly improve peak SNR in LAX images in zero padding. Zero padding achieved the highest peak SNR in both the interpolated and super-resolution images (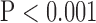, top row, Fig. 5). Finally, super resolution significantly improved UIQI in LAX images regardless of the interpolation method (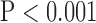, bottom row, Fig. 5). However, super resolution did not significantly improve UIQI in SAX images in bicubic 2. Zero padding achieved the highest UIQI in both the interpolated and super-resolution images (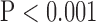, bottom row, Fig. 5).

Fig. 4. Error measurements vs. high-resolution image. Values are 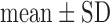. Black and white bars represent interpolated and super resolution images, respectively. The sample size was for short-axis (SAX) images, and 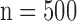for long-axis (LAX) images. 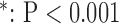vs. Interpolation; 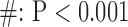vs. zero Padding.

Fig. 5. Error measurements vs. high-resolution image (continued). Values are 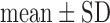. Black and white bars represent interpolated and super resolution images, respectively. The sample size is 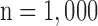for short-axis (SAX) images, and 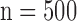for long-axis (LAX) images. 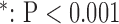vs. Interpolation; 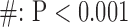vs. zero Padding.

Among the indices that super resolution significantly improved, the magnitude of improvement was the greatest in bicubic 1 (20%-50%), and equally smaller in zero padding (3%-10%) and bicubic 2 (1%-10%) (Table I).

TABLE I. Magnitude of Improvement by Super Resolution. Percent Improvement is Based on the Mean Values of Each Index. SAX, Short-Axis; LAX, Long-Axis; MAE, Mean Absolute Error; RMSA, Root Mean Squared Error; PSNR, Peak Signal-to-Noise Ratio; UIQI, Universal Image Quality Index. 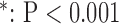vs. Interpolation.

	Zero Padding		Bicubic 1		Bicubic 2
	SAX	LAX	SAX	LAX	SAX	LAX
MAE	4.1%*	3.2%*	19.0%*	18.4%*	3.2%*	2.1%*
RMSE	10.3%*	−3.1%	49.5%*	44.4%*	10.9%*	1.7%
PSNR	4.7%*	−0.4%	38.3%*	36.9%*	5.7%*	1.7%*
UIQI	3.8%*	3.5%*	41.6%*	40.2%*	0.0%	1.4%*

D. Patient Images

The same super resolution algorithm was applied to patient MRI to assess improvement in image quality. Representative images are shown in Fig. 6 (SAX) and Fig. 7 (LAX). Zero padding and bicubic 1 were used for scale-up by a factor of 4. In both zero padding and bicubic 1, interpolation improved the spatial resolution by a factor of 4 but smoothed edges. Super resolution created subtle but qualitatively distinct improvement in image quality. Super resolution images showed sharper geometric features (e.g., edges between the heart and the scar, border between the myocardium and the blood pool). In addition, the effect of super resolution was quantitatively analyzed by calculating the absolute difference in SI between the interpolated image and the super resolution image. As indicated by consistently larger absolute difference in SI, the magnitude of improvement in image quality by super resolution was quantitatively higher with bicubic 1 compared with zero padding. However, the image quality of super resolution was visually better in zero padding compared with bicubic 1. These results are consistent with Figs. 3 –5.

Fig. 6. Super resolution applied to patient images: short-axis images. Original, low-resolution images of patients A and B with clinical standard spatial resolution were interpolated (zero padding or Bicubic 1) to scale up by a factor of 4. Super resolution was applied to the interpolated image. The bottom row represents the absolute difference in SI between the interpolated image and the super resolution image, as in Fig. 3. Note sharper geometric features in super resolution images (e.g., edges, endocardial border with blood pool).

Fig. 7. Super resolution applied to patient images: long-axis images. See the legend of Fig. 6.

IV. Discussion

The aim of the present study was to investigate the effects of single-image super resolution on Fourier-based and image-based methods of scale-up.

Our results demonstrated that the current algorithm of single-image super resolution significantly improved the errors of the images both qualitatively and quantitatively. Importantly, super resolution consistently provided additional error improvement regardless of interpolation methods, which indicates that the current algorithm was successful in recovering edges and details that tend to be blurred by interpolation. This finding supports the validity of the current approach of super resolution, and provides evidence to support its potential use in myocardial scar imaging. The importance of this study relates to the overall conservative nature of medical image processing, where less is generally considered better than more image processing. In this case, however, qualitatively and quantitatively, the super resolution approach appears better than the standard approach, and may have a direct clinical application. For example, super resolution may be suitable for automated post-processing as it provides edge sharpening and denoising demonstrated in patient images (Figs. 6 and 7).

Our results also indicate that super resolution using Fourier-based zero padding achieved the best image quality. However, the magnitude of improvement by super resolution compared with interpolation was small in images with zero padding. The magnitude of improvement was the greatest in bicubic 1 (20%-50%), and equally smaller in zero padding (3%-10%) and bicubic 2 (1%-10%) (Table I). This was largely due to the fact that zero padding and bicubic 2 were a significantly better interpolation method than bicubic 1 (Figs. 4 and 5). This finding suggests that the current algorithm of super resolution may be less effective in a Fourier-based scale-up method than an image-based bicubic interpolation. In addition, this finding indicates that the current algorithm requires further technical improvements to enhance its output quality.

Super resolution can be a useful tool to improve the clinical management of the patients with scar-related arrhythmia. Previous studies have shown that myocardial scar imaging with LGE can predict fatal arrhythmia and death [2], [3], [10]. In addition, we have demonstrated that LGE can identify the potential target of ablation therapy to treat fatal arrhythmia [11], [12]. Improvement in image quality by super resolution is expected to improve the diagnostic accuracy of these important clinical indices to provide better care to the patients.

There are several limitations of the current study. First, we did not evaluate the effect of super resolution on images of different slice thickness. Slice thickness of the original image is a realistic and critical factor in visualizing accurate scar structures in clinical MRI. Even with a high in-plane resolution, increasing slice thickness substantially blurs the scar geometry due to the partial volume effect [1], [13]. The error improvement with super resolution would be greater with thicker slices due to the more substantial partial volume effect, because the smoother the original image is, the easier it is for the algorithm to recover the original image with smaller errors. Second, we did not explore resolution improvement greater than a factor of 4. In reality, however, given a typical in-plane spatial resolution of 1.2–1.9 mm in clinical LGE, resolution improvement by a factor of 4 provides an in-plane spatial resolution of 0.3–0.5 mm, which would resolve finer details at the edges of the scar, as shown in Figs. 6 and 7. Third, because of the lack of ex vivo, high-resolution images of human heart, we applied super resolution to patient images using the dictionaries created by high-resolution images of the swine heart. Although the heart anatomy is similar between human and swine, it is possible that some of the detailed features may be misrepresented. A viable solution to this potential issue is to create dictionaries from ex vivo, high-resolution myocardial scar imaging from patients post mortem who are known to have had heart disease. Finally, the current super-resolution algorithm is limited to two-dimensional (2-D) images. However, the vast majority of medical imaging, including MRI that was used in this work, provides three-dimensional (3-D) volumetric data to represent 3-D structures of the human anatomy. To provide more accurate and quantitative data, a similar algorithm should be developed to apply super-resolution to 3-D volumetric images.

V. Conclusion

Single-image super resolution significantly improves the errors of the images both qualitatively and quantitatively. However, the magnitude of improvement by super resolution compared with interpolation was relatively small in images with Fourier-based scale-up method. These findings provide evidence to support its potential use in myocardial scar imaging, but suggest that the current algorithm of super resolution may be less effective in a Fourier-based scale-up method than an image-based bicubic interpolation.

Biographies

Hiroshi Ashikaga received the M.D. degree from the University of Tokyo, Japan, in 1996. He completed clinical training in internal medicine with the Beth Israel Medical Center, New York, NY, USA, in 2001. He completed research training in biomedical engineering at the University of California, San Diego and Cardiovascular MRI at the National Institutes of Health, Bethesda, MD, USA, in 2006. He received the Ph.D. degree from the University of Tokyo in 2007. His Ph.D. research was in application of cardiac electromechanics to assess the substrate for sudden cardiac death. He completed clinical training in cardiology and cardiac electrophysiology with Johns Hopkins Hospital, Baltimore, MD, USA, in 2012.

He joined John Hopkins in 2012 as an Assistant Professor of medicine and biomedical engineering. He is an Attending Cardiac Electrophysiologist with Johns Hopkins Hospital. His research interests include cardiac electromechanical mapping, cardiovascular MRI/CT, mathematical modeling, cardiac biomechanics, and image-guided diagnosis and intervention.

His awards include a finalist for the Young Investigator Award at the Heart Rhythm Society in 2006, the Elite Reviewer for the Journal of the American College of Cardiology in 2006, the winner of the Howard S. Silverman Award at the Johns Hopkins University in 2010, the winner of the Young Investigator Award at the Asia-Pacific Heart Rhythm Society in 2011, and a finalist for the Melvin Judkins Young Investigator Award at the American Heart Association in 2011. He is a member of the American Heart Association, the American College of Cardiology, and the Heart Rhythm Society.

Heidi L. Estner received the M.D. degree from Ludwig-Maximilians-University, Munich, Germany, in 2002. She completed clinical training in internal medicine and cardiology including cardiac electrophysiology with Deutsches Herzzentrum München, Germany, in 2010. Since 2011, she has been the Head of the Department for Clinical Electrophysiology, Ludwig-Maximilians-University.

She joined John Hopkins in 2008 and 2009 as a Research Fellow. Her research interests include cardiac mapping, cardiovascular MRI, and clinical studies including image-guided diagnosis and intervention.

The award enabling the research at Johns Hopkins was a European Award called Marie-Curie PEOPLE 2007-4-1-IOF. She is a member of the American Heart Association and the German and European Heart Association.

Daniel A. Herzka (M'09) was born in Lima, Peru. He received the B.S. degree in electrical engineering from Cornell University, Ithaca, NY, USA, in 1997, the M.S.E. degree in biomedical engineering from Johns Hopkins University, Baltimore, MD, USA, in 1999, and the Ph.D. degree in biomedical engineering from the Johns Hopkins University School of Medicine in 2004.

After his graduate work, he became a Senior Member of Research Staff with Philips Research North America, where he worked in magnetic resonance imaging technique development while embedded in a clinical environment. In 2008, he joined the Johns Hopkins University School of Medicine, Baltimore, MD, USA, as an Assistant Professor of biomedical engineering. His current research focuses on MRI acquisition and reconstruction technique development. His interest is centered on dynamic imaging with MRI, and encompasses fast and high-resolution cardiac imaging, musculoskeletal system imaging, and fetal imaging.

Dr. Herzka is a member of the International Society for Magnetic Resonance in Medicine, the Society for Cardiovascular Magnetic Resonance, and the American Heart Association.

Elliot R. Mcveigh received the Undergraduate degree in physics from the University of Toronto in 1984, and the Ph.D. degree from the Department of Medical Biophysics, University of Toronto, in 1988. He joined the faculty of radiology with the Johns Hopkins University School of Medicine, working with E. Zerhouni to develop a research program in cardiac MRI.

In 1991, he founded the Medical Imaging Laboratory, Department of Biomedical Engineering as part of a Whitaker Development Award. Many novel MR imaging techniques were developed during this period: myocardial tagging for evaluating local muscle contraction, myocardial perfusion estimates with dynamic imaging of contrast injections, and late enhancement imaging to clearly image myocardial infarction. These techniques form the foundation of the modern cardiac MRI exam. His laboratory also demonstrated the ability of MRI to evaluate the benefit of cardiac resynchronization therapy (CRT) in the failing heart; these studies were seminal in understanding how CRT should be used.

In 1999, he joined the Laboratory of cardiac energetics with the NIH, Bethesda, to develop a research program in cardiovascular interventional MRI. Working with clinical colleagues, his laboratory demonstrated numerous novel applications for the first time, three of which were: the first MRI guided injections of therapeutic agents directly into the myocardium, the first simultaneous electrical and mechanical measurements of cardiac function with MR, the first MR guided aortic valve replacement in the beating heart.

In 2007, he was appointed as a Massey Professor and Director of the Department of Biomedical Engineering, Johns Hopkins.

Henry R. Halperin received the B.S. degree in physics with highest distinction from Purdue University in 1971, the M.A. degree in physics from the University of California, Berkeley in 1972, and the M.D. degree from Louisiana State University, New Orleans, LA, USA, in 1977. He was a fellow of cardiology with The Johns Hopkins Hospital, Baltimore, MD, USA, from 1981 to 1984. He is a member of Phi Beta Kappa; an Established Investigator, Fellow, and Distinguished Scientist of the American Heart Association; a fellow of the Heart Rhythm Society; and a McClure Fellow of the Johns Hopkins University Applied Physics Laboratory.

Dr. Halperin is currently the David J. Carver Professor of medicine, and Professor of radiology and biomedical engineering with Johns Hopkins Medical Institutions, and is a Clinical Electrophysiologist with Johns Hopkins Hospital. He is the Co-Director of the Johns Hopkins Cardiovascular Imaging Center of Excellence, and the Director of Advanced Cardiovascular Life Support with Johns Hopkins Hospital. He serves on the editorial board of the journal Resuscitation, and is the past Chair of a number of the American Heart Association Emergency Cardiac Care Sub-Committees. His current research interests include cardiopulmonary resuscitation, electrophysiology, magnetic resonance imaging, magnetic resonance imaging—implanted device interactions, and advanced image-guided interventions. Ten of his students have received young investigator awards from the American Heart Association and Heart Rhythm Society, and he has ongoing support from the National Institutes of Heath for his research programs. He has published over 160 peer-reviewed publications and over 50 patents issued.

Funding Statement

This work was supported by the National Institutes of Health under Grants Z01-HL004609, R01-HL64795, and R01-HL094610.