MODEL OF CALCIUM-INDUCED CALCIUM RELEASE MECHANISM IN CARDIAC CELLS

Abstract

A model with which to elucidate the mechanism of Ca²⁺ release from, and Ca²⁺ loading in the sarcoplasmic reticulum (SR) by Ca²⁺ current (I_Ca) in cardiac cells is proposed. The SR is assumed to be comprised of three functional subcompartments: (1) the main calcium store (MCS), which contains most of the calcium (both free and bound); (2) the releasable terminal (RT), which contains the calcium readily available for release; and (3) the longitudinal network of the SR (LSR), which sequesters and the transfers the sarcoplasmic calcium to the RT. A rapid increase of the Ca²⁺ concentration at the outer surface of the SR (Ca_e) due to the fast component of I_Ca activates and inactivates this surface, inducing the release of Ca²⁺ from the RT to the sarcoplasmic space. The RT in turn is further activated and inactivated by a increase in the concentration of sarcoplasmic Ca²⁺. The Ca²⁺ in the sarcoplasmic space is then sequestered by the LSR, leading to the reactivation of the RT. Further increase of Ca_e due to the slow component of I_Ca enhances the entry of Ca²⁺ into the MCS to be bound by the binding substance. The free Ca²⁺ released from the Ca–binding substance complex is transferred to the RT for subsequent release. The activation, inactivation and reactivation are Ca²⁺-mediated and time-dependent. The proposed model yields simulation of the many events qualitatively similar to those observed experimentally in skinned cardiac cells.

Introduction

A transient increase of intracellular calcium is an important step coupling membrane excitation to muscular contraction. In mammalian cardiac muscle, calcium entry through the sarcolemma during the plateau of the action potential have been considered necessary for contraction. More than a decade ago, Bassingthwaighte and Reuter (1972) postulated that the trans-sarcolemmal Ca²⁺ influx was insufficient for activating the myofilaments and that additional Ca²⁺ released from the internal stores was required.

Experiments on skinned cells (Fabiato and Fabiato, 1978; Fabiato, 1982) demonstrated that no stimulated trans-sarcolemmal influx of Ca²⁺ of any magnitude could activate the myofilaments directly. In isolated rat ventricular cells, the computed [total Ca²⁺] was 7 µM and 10 µM during the initial 10 and 20 ms respectively of the fast Ca²⁺ current (Fabiato, 1983). This Ca²⁺ influx and the resting [Ca²⁺] (7 µM) resulted in pCa values of 6.8 and 6.71 respectively. This meager rise in [free Ca²⁺] is insufficient to induce any direct activation of the myofilaments.

The role of the trans-sarcolemmal Ca²⁺ seems to be to induce the release of Ca²⁺ from the intracellular Ca store—the sarcoplasmic reticulum (SR). The Ca²⁺-induced release of Ca²⁺ had been demonstrated in skinned cardiac cells (Fabiato and Fabiato, 1975, 1977, 1978). Recent advances in single-channel conduction and gating experiments on canine (Rousseau et al., 1986) and human cardiac SR (Holmberg and Williams, 1989) strongly support the concept of Ca²⁺-induced Ca²⁺ release. These single-channel experiments did not elucidate the release mechanism or processes. However, Fabiato’s experiements have suggested that the release mechanism is not an all-or-none process but is determined by three factors:

1. the level of preload of the SR with Ca²⁺;

2. the rate of change of trigger [free Ca²⁺];

3. the level of [free Ca²⁺] used as trigger.

Fabiato (1985b) demonstrated that in skinned Purkinje cells, the mechanism of Ca²⁺-induced release of Ca²⁺ from the SR appeared to be via a channel with time- and Ca²⁺-dependent activation and inactivation. Based on this concept, a preliminary model (Wong et al., 1987) for Ca²⁺-dependent Ca²⁺ release from the SR was proposed. Although the model fits well all experimental data tested, it does not include the mechanism involved in Ca²⁺ release from the SR by the fast component and Ca²⁺ loading in SR by the slow component of the trans-sarcolemmal Ca²⁺ influx (Fabiato, 1985c). Thus, the present model is an improved version in that it not only produces results quantitatively similar to the experimental observations, but also includes some processes not considered in the previous model.

This model formulation contains some features which have not been demonstrated experimentally, but which appear to be needed to provide behavior similar to the observed behavior of cardiac single cells and fiber bundle preparations. Thus, the model should be regarded as descriptive overall, and explicative in only certain well-defined features. The main innovative feature is the desription of Ca²⁺-dependent Ca²⁺ release, which is expressed in a fashion analogous to Hodgkin–Huxley kinetics, but the channel “conductance” is time- and [Ca²⁺]-dependent rather than time- and voltage-dependent.

Overall Description of the Proposed Model

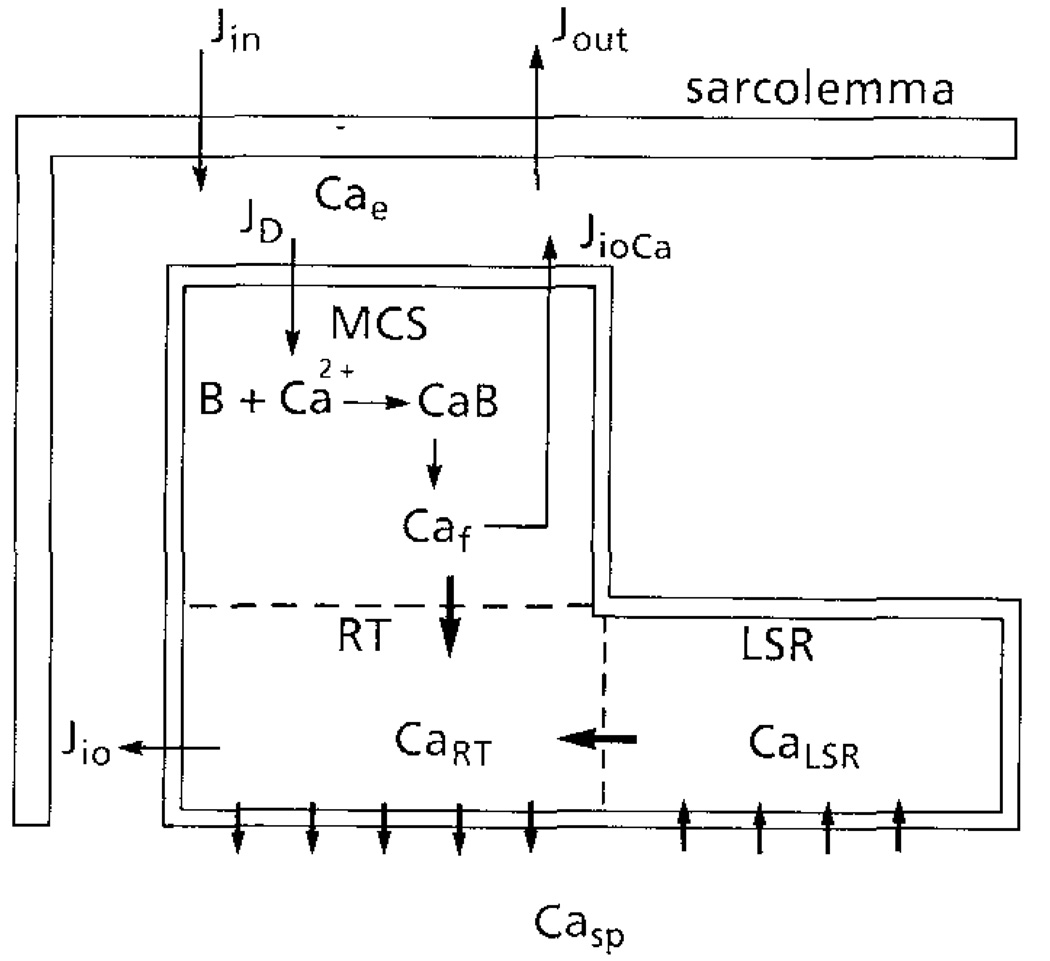
The schematic diagram shown in Fig. 1 represents a cardiac cell with intact sarcolemma. The SR comprises three subcompartments: (1) the main calcium store (MCS), which contains most of the calcium store in the SR and in which the calcium is predominantly bound; (2) the “releasable” terminal (RT), in which the calcium is mostly free and which releases a fraction of its calcium content to the myofibrils to activate the contractile machinery; and (3) the longitudinal network (LSR), which sequesters the calcium from the sarcoplasmic space and transfers it to the RT.

Figure 1.

Schematic diagram of the model. The sarcoplasmic reticulum (SR) comprises of: (1) Main Calcium Store (MCS) into which Ca²⁺ entering by diffusion is bound by the binding substance B; (2) a Releasable Terminal (RT) which releases Ca²⁺ to the sarcoplasmic space; (3) the longitudinal SR which sequesters Ca²⁺ from the sarcoplasmic space. Free Ca from MCS (Ca_f) and LSR (Ca_LSR) are transferred to RT with time constants τ_fr and τ_LSRJ_in and J_out are the trans-sarcolemmal influx and efflux respectively. J_ioCa and J_io are Ca–Ca exchange between Ca_e and Ca_RT. Ca_e is the [Ca²⁺] between sarcolemma and SR; Ca_sp is the sarcoplasmic Ca²⁺.

To simulate experiments on skinned cardiac cells, the membrane in Fig. 1 is removed. At resting state, the calcium concentration at the outer surface of the SR (Ca_e) is low and this surface is completely inactivated. No calcium is released from the RT. When Ca_e increases rapidly, the outer surface of the SR is activated and inactivation of this surface is also initiated at a slower rate. Both the activation and inactivation are calcium (Ca_e)- and time-dependent, as described by Hodgkin–Huxley kinetics.

The activation of the SR outer surface triggers the release of calcium from the RT, resulting in an increase of calcium concentration in the sarcoplasmic space (Ca_sp). As the activation and inactivation of the RT is also Ca_sp- and time-dependent, more calcium release can be induced until inactivation becomes dominant. While Ca²⁺ is being released from the RT, [free Ca²⁺] (Ca_f) in the MCS is increased due to the diffusion of Ca²⁺ from outside the SR and the dissociation of the Ca–binding substance complex. The free Ca²⁺ from the MCS and the LSR is transferred to the RT for subsequent release. The Ca²⁺ in the sarcoplasmic space is sequestered by an active process (J_pump). The decrease of Ca_sp results in the activation and reactivation of the RT.

Assumption and Formulation

(1) Calcium concentration at the outer surface of the SR (Ca_e). The calcium concentration at the outer surface of the SR is determined by:

1. the rate and the amount of increase or decrease of Ca²⁺ from the external source (J_in);

2. the diffusion (J_D) of Ca²⁺ across the outer SR membrane into the MCS; and

3. the calcium efflux (J_ioCa) from the MCS.

The rate of change of Ca_e is

$${\text{dCa}}_{\mathrm{e}}/\mathrm{d}t=J_{\text{in}}+J_{\text{ioCa}}-J_{\mathrm{D}}.$$

In experiments on skinned cells, the calcium source and sink can be considered very large. Therefore:

$${\text{dCa}}_{\mathrm{e}}/\mathrm{d}t=J_{\text{in}},$$ (1)

where J_in represents the rate of injection or aspiration of trigger Ca²⁺.

(2) Free calcium concentration in the MCS (Ca_f). Calcium-binding substance exists in the SR (Solaro and Briggs, 1974). It is assumed that the free Ca²⁺ that enters the MCS binds to the free binding substance B (calsequestrin) by a simple first-order absorption, one Ca²⁺ molecule per site. The free calcium concentration in the MCS can be described in relation to the concentration of free binding substance B and bound Ca²⁺ (CaB) within the MCS:

$$\begin{array}{cc}\hfill {\text{dCa}}_{\mathrm{f}}/\mathrm{d}t& =-K_1·\mathrm{B}·{\text{Ca}}_{\mathrm{f}}+K_2·\text{CaB}+J_{\text{net}},\hfill \\ \hfill \text{dB}/\mathrm{d}t& =K_1·\mathrm{B}·{\text{Ca}}_{\mathrm{f}}-K_2·\text{CaB},\hfill \\ \hfill J_{\text{net}}& =J_{\mathrm{D}}-J_{\text{ioCa}}-K_{\text{fr}}·{\text{Ca}}_{\mathrm{f}}/{\tau }_{\text{fr}},\hfill \end{array}$$ (2)

where J_D = D(α) (Ca_e – Ca_f), D(α) is the diffusion coefficient, τ_fr is the time constant associated with the transfer of Ca_f to the RT, the K_fr is a constant of proportionality.

Binding is assumed at all times to be essentially at an equilibrium (Bassingthwaighte and Reuter, 1972), i.e.:

$${\text{Ca}}_{\mathrm{f}}·\mathrm{B}/\text{CaB}=K/K_2=K_{\mathrm{a}},$$ (3)

where K_a is a dissociated constant. Taking the derivative of equation (3) and substituting in equation (2) gives:

$$\begin{array}{cc}\hfill {\text{dCa}}_{\mathrm{f}}/\mathrm{d}t& =J_{\text{net}}\frac{{(K_{\mathrm{a}}+{\text{Ca}}_{\mathrm{f}})}^2}{{(K_{\mathrm{a}}+{\text{Ca}}_{\mathrm{f}})}^2+{\mathrm{B}}_{\mathrm{t}}{K}_{\mathrm{a}}},\hfill \\ \hfill {\mathrm{B}}_{\mathrm{t}}& =\mathrm{B}+\text{CaB}.\hfill \end{array}$$ (4)

(3) Calcium concentration in the releasable terminal (Ca_RT). The RT is assumed to differ only functionally from the MCS. The calcium content in the RT is free and is replenished by the free calcium transferred from the MCS and the LSR. The rate of release is determined by:

1. the calcium gradient between the RT and the sarcoplasmic space;

2. the degree of activation and inactivation of the outer SR membrane, described by the kinetic parameters p(t) and q(t); and

3. the degree of activation and inactivation of the RT, which is described by the parameter r(t), itself a function of Ca_sp.

The rate of change of Ca_RT is given by:

$$\begin{array}{cc}{\text{dCa}}_{\text{RT}}/\mathrm{d}t=\hfill & K_{\text{fr}}{\text{Ca}}_{\mathrm{f}}/{\tau }_{\text{fr}}+K_{\text{LSR}}{\text{Ca}}_{\text{LSR}}/{\tau }_{\text{LSR}}\hfill \\ \hfill & -g_{\text{Ca}}·p(t)·q(t)·r(t)({\text{Ca}}_{\text{RT}}-{\text{Ca}}_{\text{sp}})\hfill \\ \hfill & -J_{\text{io}},\hfill \end{array}$$ (5)

where K_fr and K_LSR are constants, τ_fr and τ_LSR are time constants associated with the process of calcium transfer, g_Ca is the maximal rate of release, and J_io is the calcium efflux from the RT to the outside of the cell.

(4) Calcium concentration in the sarcoplasmic space (Ca_sp). The calcium concentration in the sarcoplasm is determined by the amount of calcium released from the SR, the uptake of calcium and the passive diffusion of calcium between the sarcoplasm and the outside of the cell. The rate of change of Ca_sp is:

$$\begin{array}{c}\hfill {\text{dCa}}_{\text{sp}}/\mathrm{d}t=g_{\text{Ca}}·p(t)·q(t)·r(t)({\text{Ca}}_{\text{RT}}-{\text{Ca}}_{\text{sp}})\hfill \\ \hfill -J_{\text{pump}}+D_{\mathrm{e}}({\text{Ca}}_{\mathrm{e}}-{\text{Ca}}_{\text{sp}}),\hfill \end{array}$$ (6)

where J_pump is the uptake rate of the LSR and D_e is the diffusion coefficient.

(5) Calcium concentration in the longitudinal sarcoplasmic reticulum (Ca_LSR). The calcium content in the LSR depends on the Ca²⁺ uptake rate and the transfer of its content to the RT. This model assumes transmembrane transport to be the uptake mechanism. Kitazawa (1976) demonstrated that the Ca²⁺ uptake of fragmented chicken cardiac SR increased sigmoidally with free Ca²⁺ concentrations. At a certain free Ca²⁺ concentration, the Ca uptake increased exponentially with time and the initial uptake rate varies with the free Ca²⁺ concentration. The Ca uptake data suggests a process empirically described as:

$$J_{\text{pump}}=\frac{x(t)V_{\text{max}}{\text{Ca}}_{\text{sp}}^2}{(K_{\mathrm{m}}+{\text{Ca}}_{\text{sp}}^2)}+\frac{f(t){V\prime }_{\text{max}}{\text{Ca}}_{\text{sp}}}{{K\prime }_{\mathrm{m}}+{\text{Ca}}_{\text{sp}}}$$

and

$${\text{dCa}}_{\text{LSR}}/\mathrm{d}t=J_{\text{pump}}-K_{\text{LSR}}{\text{Ca}}_{\text{LSR}}/{\tau }_{\text{LSR}},$$ (7)

where V_max, V′_max are maximum pump rates and K_m, K′_max are the concentrations at which the half-maximal pump rate occurs; K_LSR is a constant; τ_LSR, a time constant, is related to the apparent diffusion coefficient.

Both x(t) and f(t) are kinetic parameters describing the “conductance” of the channels of the RT surface. As x(t) is slow-varying and its value is significant only at relatively high Ca_sp, Ca²⁺ uptake by the LSR starts near the end of Ca²⁺ release. The second term in J_pump accounts for the removal of Ca²⁺ during the relaxation phase.

(6) Activation, inactivation and reactivation. The activation and inactivation of the outer SR surface are characterized by two parameters—p and q. These parameters are governed by the first-order kinetic equation:

$$\begin{array}{cc}\hfill \mathrm{d}y/\mathrm{d}t& =[{\alpha }_y(1-y)-{\beta }_{y}y],y=p,q;\hfill \\ \hfill y_{\infty }& ={\alpha }_y/({\alpha }_y+{\beta }_y),\hfill \\ \hfill {\tau }_y& =1/({\alpha }_y+{\beta }_y).\hfill \end{array}$$

The rate constants α_y, β_y are functions of Ca_e. Thus, the steady-state parameters p_∞, q_∞ and the time constants τ_p, τ_q are functions of Ca_e. To explain the experimental observations that the release and accumulation of Ca²⁺ are influenced by the rate (α) of change of Ca_e, it is necessary to assume that τ_p is inversely proportional to, and τ_q proportional to, the rate of change of Ca_e. Thus:

$$\begin{array}{c}\hfill D(\alpha )=D{\alpha }_0/\alpha ,\hfill \\ \hfill {\tau }_p(\alpha ,{\text{Ca}}_{\mathrm{e}})={\alpha }_0{\tau }_p({\text{Ca}}_{\mathrm{e}})/\alpha ,\hfill \\ \hfill {\tau }_q(\alpha ,{\text{Ca}}_{\mathrm{e}})=\alpha {\tau }_p({\text{Ca}}_{\mathrm{e}})/{\alpha }_0;\hfill \end{array}$$ (8)

$${\text{Ca}}_{\mathrm{e}}={\text{Ca}}_{\mathrm{o}}[1-\text{exp}(-\alpha t)],$$ (9)

where Ca_o is the maximal calcium concentration injected or aspired and α₀ is a certain rate constant chosen as standard. Equation (8) indicates that τ_p, τ_q are linearly and inversely proportional to the rate of change of Ca_e respectively. When dCa_e/dt is high, the outer SR surface is rapidly activated, but slowly inactivated. At low rate, the opposite occurs.

The activation, inactivation and reactivation of the RT is described by the parameter r(t). However, r(t) is comprised of four parameters: d, f, X̅, and x, such that:

$$\begin{array}{c}\hfill r(t)=d(t)f(t)-\lambda \overline{X}(t)x(t),\hfill \\ \hfill y(t)+{\tau }_y\mathrm{d}y/\mathrm{d}t=y_{\infty }y=d,f,\hfill \\ \hfill \mathrm{d}\overline{X}/\mathrm{d}t={\alpha }_{\overline{X}}{\mathrm{\Delta }\text{pCa}}_{\mathrm{e}}[(1-X)-{\beta }_{\overline{X}}\overline{X}],\hfill \\ \hfill {\mathrm{\Delta }\text{pCa}}_{\mathrm{e}}=7.2-{\text{pCa}}_{\mathrm{e}},\hfill \\ \hfill \mathrm{d}x/\mathrm{d}t=\eta ({\text{pCa}}_{\mathrm{e}})[{\alpha }_x(1-x)-{\beta }_{x}x],\hfill \\ \hfill \eta ({\text{pCa}}_{\mathrm{e}})=\text{exp}[0.6({\text{pCa}}_{\mathrm{e}}-6.4)].\hfill \end{array}$$

The steady-state parameters d_∞, f_∞, x_∞ and the time constants τ_d, τ_f and τ_x are functions of Ca_sp; X̅ and τ_X̅ are functions of the trigger calcium concentration (Ca_e). The parameter r(t) should be considered as a variable that varies with Ca_sp and Ca_e, rather than as a Hodgkin–Huxley-type kinetic parameter. The formulations of the kinetic equations for X̅ and x are similar to those used by Standen and Stanfield (1982).

(7) Calcium efflux. Calcium efflux is assumed to take place at two locations within the SR: the MCS and the RT. At the MCS, free Ca²⁺ is extruded across the SR membrane by a Ca²⁺–Ca²⁺ exchange process (Wong and Bassingthwaighte, 1981):

$$J_{\text{ioCa}}=\varphi ({\text{Na}}_{\mathrm{o}})[{\text{Ca}}_{\mathrm{f}}/(K_1+{\text{Ca}}_{\mathrm{f}})][{\text{Ca}}_{\mathrm{e}}/(K_2+{\text{Ca}}_{\mathrm{e}})],$$

where ϕ(Na_o) is a function of [Na⁺]_o in the oppositional space or outside the SR, and K₁, K₂ are constants.

In the present model, the RT is preplenished by free Ca²⁺ from the LSR and the MCS. When high [Ca²⁺] outside the cell is maintained, there will be a continuous production of free Ca²⁺ in the MCS and a continuous transfer of Ca²⁺ to the RT. If there were no Ca²⁺ extrusion from the RT to the outside of the cell, the RT would be loaded infinitely with Ca²⁺—an impossible situation.

To prevent an unreasonable overloading of RT, a Ca²⁺ extrusion mechanism is assumed. This mechanism is described as:

$$J_{\text{io}}=K_{\text{RT}}[{\text{Ca}}_{\mathrm{e}}/(K_3+{\text{Ca}}_{\mathrm{e}})]F({\text{Ca}}_{\text{RT}}).$$

The function F(Ca_RT) should be such that J_io is insignificant when Ca_RT is equal or below its resting value (14 µM) but increases otherwise. An exponential function of the form:

$$F({\text{Ca}}_{\text{RT}})=1.0/\{1+\text{exp}[2(18-{\text{Ca}}_{\text{RT}})]\}$$

seems to give the most satisfactory results.

(8) Time constant associated with the calcium transfer. The two time constants τ_fr and τ_LSR associated with the transfer of Ca_f and Ca_LSR to the RT are assumed to be inversely proportional to the apparent diffusion coefficient for Ca. Based on the study of Safford and Bassingthwaighte (1977), the apparent diffusion coefficient for Ca_f is related to the degree of binding of Ca²⁺ by the binding substance. Thus:

$${\tau }_{\text{fr}}\propto [{(K_{\mathrm{a}}+{\text{Ca}}_{\mathrm{f}})}^2+{\mathrm{B}}_{\mathrm{t}}{K}_{\mathrm{a}}]/{(K_{\mathrm{a}}+{\text{Ca}}_{\mathrm{f}})}^2.$$

The rate of transfer of Ca²⁺ from LSR to RT is again assumed to be related to [Ca²⁺] in the LSR. This is based on the assumption that some degree of binding occurs in the LSR and that the apparent diffusion coefficient for Ca_LSR varies nonlinearly with Ca_LSR. Therefore:

$${\tau }_{\text{LSR}}\propto [K_{\mathrm{a}}^{\prime }+{{\text{Ca}}_{\text{LSR}})}^2+B_{\mathrm{t}}^{\prime }{K}_{\mathrm{a}}^{\prime }+{{\text{Ca}}_{\mathrm{f}})}^2.$$

Numerical Parameters

All model responses in this study were simulated with the same set of kinetic parameters, time constants and the following numerical constants:

$$\begin{array}{c}\hfill {\text{Resting}\text{pCa}}_{\mathrm{e}},{\text{pCa}}_{\mathrm{f}},{\text{pCa}}_{\text{sp}},{\text{pCa}}_{\text{LSR}}=7.4,\hfill \\ \hfill {\text{Resting}\text{Ca}}_{\text{RT}}=14\mu \mathrm{M},D=0.005/\text{ms},D_{\mathrm{e}}=0.0001/\text{ms},\hfill \\ \hfill K_{\text{fr}}=0.005/\text{ms},K_{\text{LSR}}=0.005/\text{ms},K_{\text{RT}}=1.0\mu \text{M/ms},\hfill \\ \hfill K_{\mathrm{a}}=0.14\mu \mathrm{M},K_{\mathrm{a}}^{\prime }=4.0\mu \mathrm{M},{\mathrm{B}}_{\mathrm{t}}=B_{\mathrm{t}}^{\prime }=50\mu \mathrm{M},\hfill \\ \hfill K_1=K_2=K_3=10\mu \mathrm{M},\surd K_{\mathrm{m}}=10\mu \mathrm{M},K_m^{\prime }=100\mu \mathrm{M},\hfill \\ \hfill {\varphi }_{\text{Ca}}=0.15/\text{ms},V_{\text{max}}=0.5\mu \text{M/ms},\hfill \\ \hfill \varphi {(\text{Na}}_{\mathrm{o}})0.5\mu \text{M/ms},\lambda =\mathrm{5.0.}\hfill \end{array}$$

The above numerical values were chosen to produce an optimal performance of the model. The only variable in all simulations was the trigger [Ca²⁺] at the outer surface of the SR, described by equation (9).

Kinetic Parameters and Time Constants

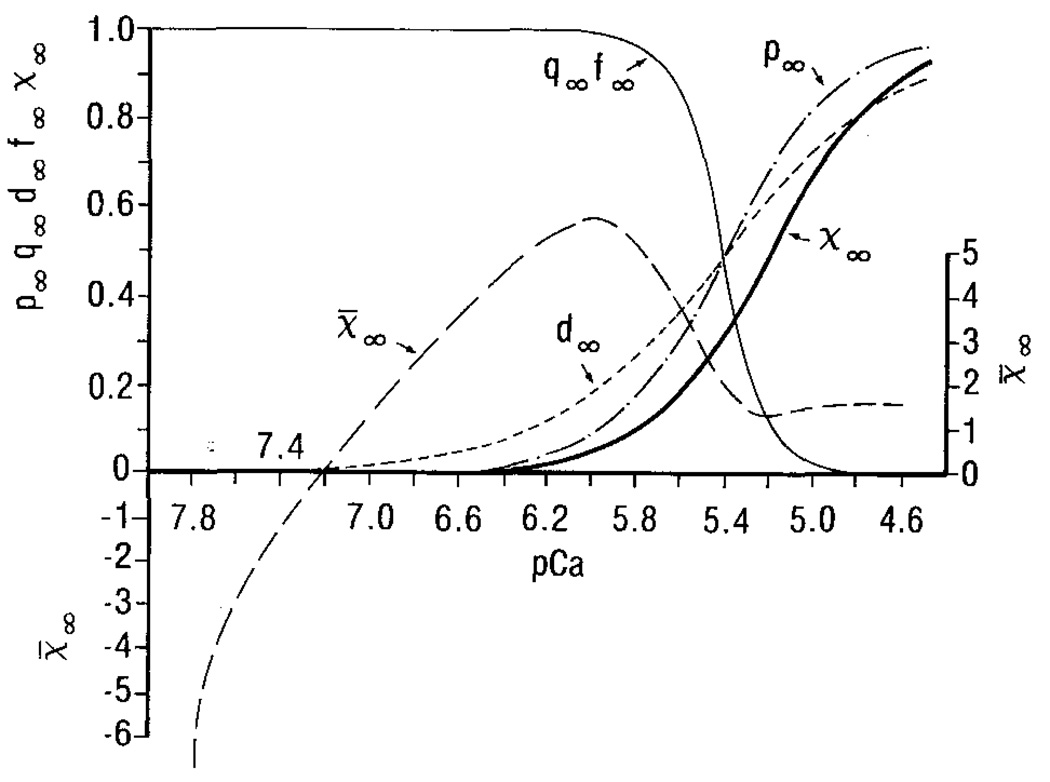
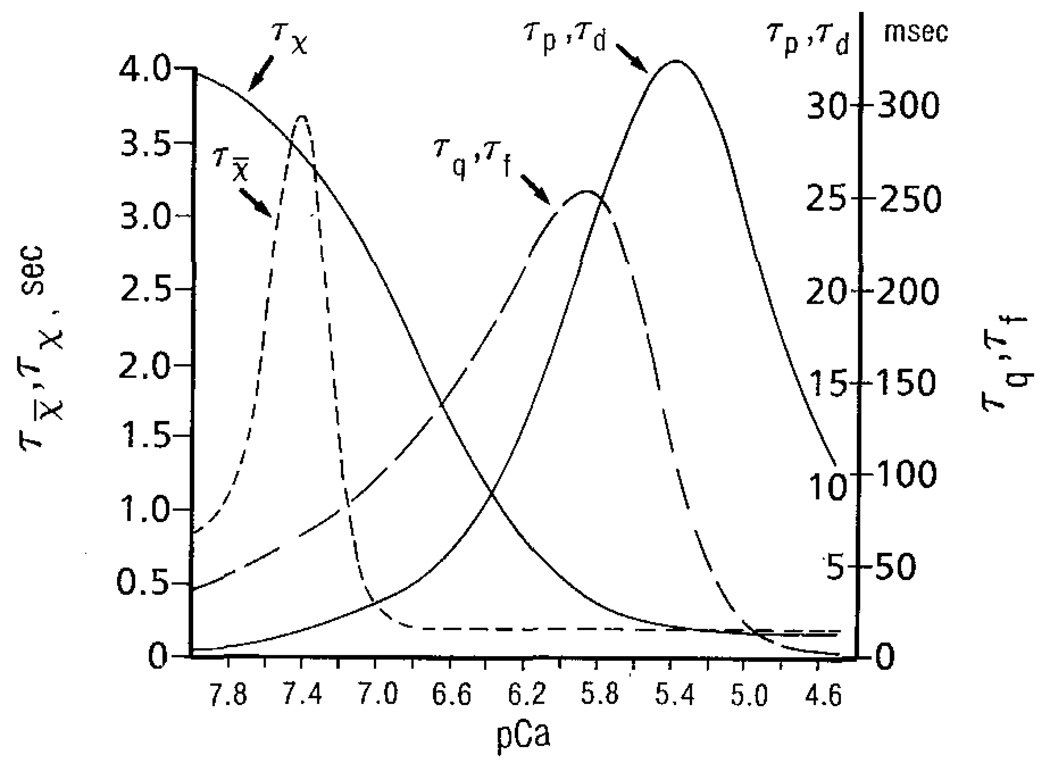
Figure 2 depicts the steady-state parameters as functions of trigger pCa or sarcoplasmic pCa. The time constants, as functions of pCa, are shown in Fig. 3. These functions are chosen after trial and error so that the model produces results qualitatively similar to those observed experimentally.

Figure 2.

The steady-state values for the activation (q_∞) and inactivation (p_∞, λx̅) parameters as functions of pCa at the outer SR surface. The activation (d_∞) and inactivation (f_∞x_∞) parameters for the RT are functions of the pCa of the sarcoplasmic space.

Figure 3.

Time constants τ_p, τ_q, and τ_X̅ are functions of the pCa of the outer SR surface; τ_f, τ_d, and τ_x are functions of the pCa of the sarcoplasmic space.

Cyclic Release

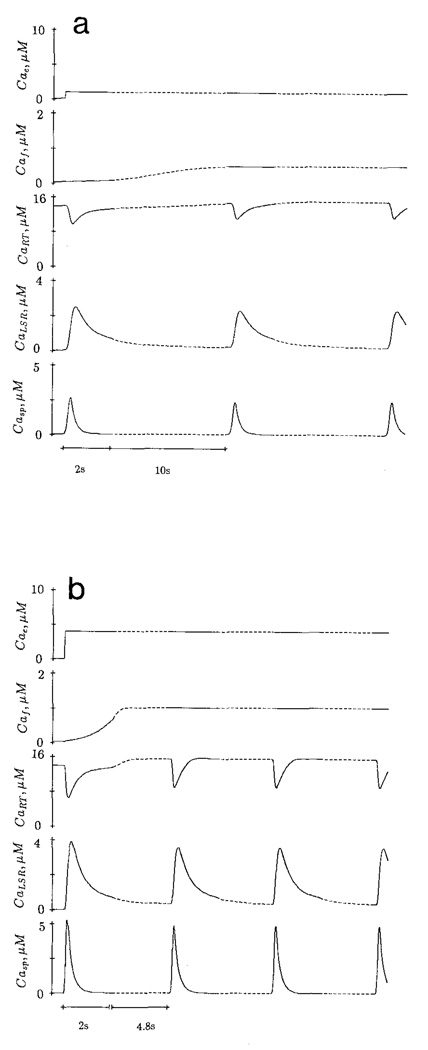
Cyclic release of Ca from the SR of skinned cardiac cells of rat (Fabiato and Fabiato, 1975) and Purkinje cells (Fabiato, 1985b) occurs when the trigger Ca²⁺ above a critical level is maintained outside the cell. The amplitude and frequency of the cyclic release depends on the trigger Ca concentration. The cycle release of Ca was simulated with the present model. With a trigger [Ca] of 1 µM (pCa = 6.0), the peak sarcoplasmic Ca (Ca_sp) is 2.62 µM with a cycle period of 11.6 s (Fig. 4a). At trigger pCa = 5.4, the peak Ca_sp is 5.27 µM and the cycle period is 6.8 s (Fig. 4b). At supraoptimal trigger Ca (pCa = 5.2), both peak Ca_sp (4.38 µM) and cycle period (5.25 s) are reduced (Fig. 4c). The simulation is in agreement with the experimental observations on skinned ventricular cell of rat (Fig. 8 of Fabiato and Fabiato, 1975).

Figure 4.

Simulated cyclic release of Ca at constant trigger Ca²⁺ (Ca_e). The cycle period is 11.6 s at pCa_e 6.0 (a), 6.8 s at pCa_e 5.4 (b) and 5.25 s at pCa_e 5.2 (c). The change of time scale (– – – –) should be noted.

Effect of Concentration and the Rate of Increase of Trigger Ca (Ca_e) on Ca Release

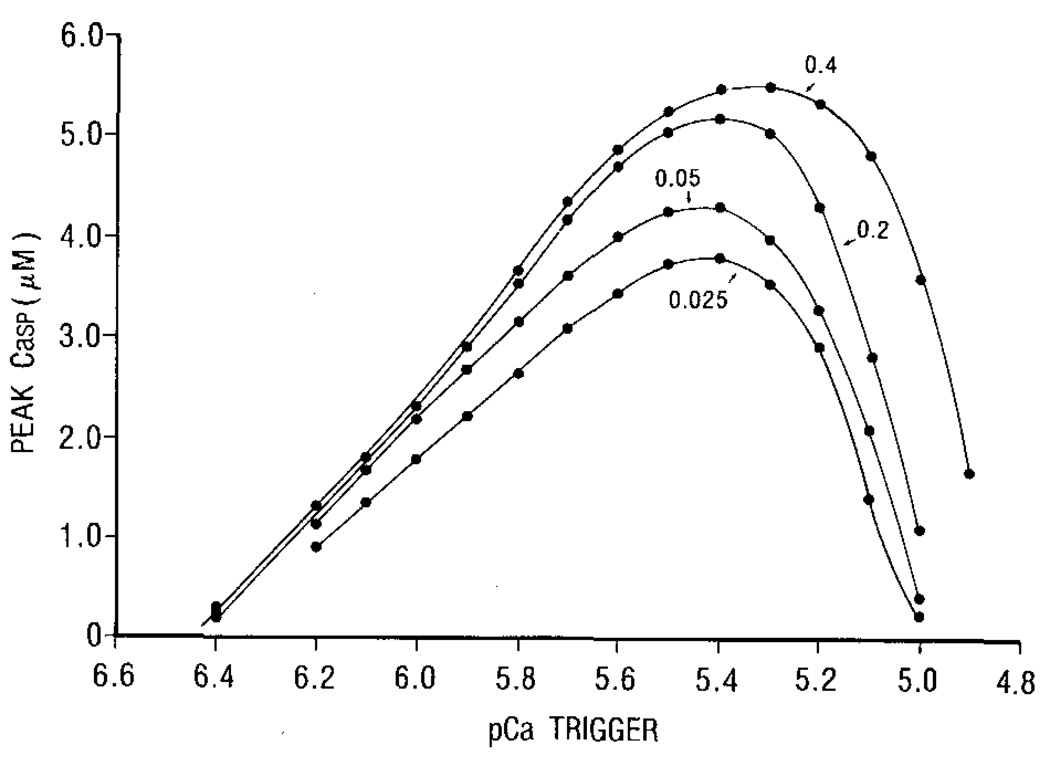
The bell-shaped relationship between the trigger pCa and peak sarcoplasmic Ca transient (Fig. 5) is mainly due to the activation p and the inactivation q of the outer SR surface. This is equivalent to the relation of peak Ca current and voltage. The effect of the rate of increasing trigger Ca on Ca release is indicated by the value of α [see equation (9)]. A higher value of α means a faster rate of increase.

Figure 5.

The relation between the trigger pCa, the rate of rise of trigger PCa and the peak Ca_sp in the sarcoplasmic space. The numbers indicate the value of rate constant (α) in Ca_e = Ca_o[1 – exp(–αt)]. The larger the number, the faster the increase of Ca_e.

The higher the rate of increase of trigger Ca, the greater the peak sarcoplasmic Ca, similar to the peak tension and trigger pCa relation shown by Fabiato (1985b). These are the consequences of the assumption that the time constants of activation (τ_p) and inactivation (τ_q) are functions of α (equation (8)]. When trigger Ca is increased slowly (α is small), the outer SR surface is slowly activated, but rapidly inactivated, resulting in a reduction of the value of p · q.

Rate of Inactivation and of Removal of Inactivation

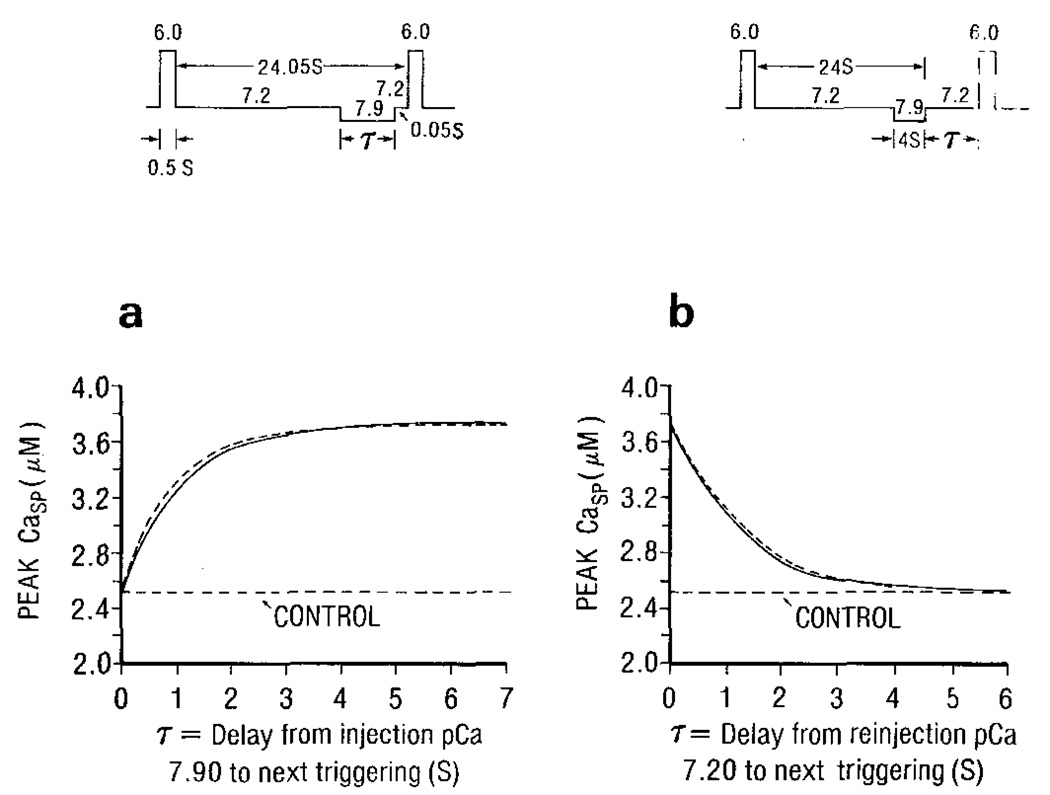
Fabiato’s experiments (1985b, Fig. 18) to demonstrate the rate of inactivation and of removal of inactivation were mimicked. The model response, shown in Fig. 6, is qualitatively similar to the experimental observations. The curve in Fig. 6a can be expressed as:

$$\text{Ca}={\text{Ca}}_{\mathrm{c}}+({\text{Ca}}_{\mathrm{m}}-{\text{Ca}}_{\mathrm{c}})[1-\text{exp}(-\tau /T)],$$ (10)

where Ca_c is the control peak Ca_sp; Ca_m is the maximal peak Ca_sp; τ is the delay from injection pCa 7.9 to the next triggering; T is the time constant of the exponential curve.

Figure 6.

The simulated protocols (upper panels) and the model’s results (lower panel) demonstrate the rate of removal of inactivation (a) and the rate of inactivation (b). The duration of trigger Ca at pCa 6.0 is 0.5 s. The dotted curve in (a) is described by equation (10) with T = τ_X̅ (7.9) = 0.903 s, and in (b) by equation (11) with T = τ_X̅ (7.9) = 1.43 s.

According to the present model scheme, it can be speculated that Ca_m reflects the magnitude of X̅_∞ and T, the time constant, τ_X̅ at pCa_e = 7.9. The speculation is based on the release expression: p · q · r (Ca_RT – Ca_sp), r = d · f – X̅ · x. At pCa_e = 7.2, p · q ≈ 0, d · f ≈ 0, X̅ · x ≠ 0 but slowly decreases toward zero in 24 s or longer. Therefore, r is negative and the releasable terminal is inactivated. When pCa_e of 7.9 is introduced at a delay (τ) from the next trigger, X̅(τ) at the end of τ is:

$$\overline{X}(\tau )={\overline{X}}_{\infty }(7.9)-[{\overline{X}}_0(7.2)]\text{exp}[-\tau /{\tau }_{\overline{X}}(7.9)],$$

where X̅₀(7.2) is the value of X̅ just before pCa_e = 7.9 is introduced.

In the present model, X̅₀(7.2)≈0, and x, being very slow-varying, does not vary much within τ. Thus:

$$r\propto {\overline{X}}_{\infty }(7.9)[1-\text{exp}(-\tau /{\tau }_{\overline{X}}(7.9)].$$

As X̅_∞ is negative, r has a positive value. The degree of activation of the releasable terminal increases exponentially with a time constant = τ_X̅(7.9). To show that the time constant (T) in Fig. 6a is equal to τ_X̅(7.9), Ca in equation (10) was computed (dotted curve) with Ca_c = 2.51 µM, (Ca_m – Ca_c) = 1.20 µM and T = τ_X̅(7.9) = 0.903 s, a value used in the present model.

The curve in Fig. 6b can be described as:

$$\text{Ca}={\text{Ca}}_{\mathrm{c}}+({\text{Ca}}_{\mathrm{m}}-{\text{Ca}}_{\mathrm{c}})\text{exp}(-\tau /T),$$ (11)

where τ is the delay from reinjection of pCa 7.2 to the next triggering, and T is the time constant; Ca_m is the peak Ca_sp at τ = 0.

When pCa 7.2 is reinjected after τ seconds, the value of X̅ at the end of τ is:

$$\overline{X}(\tau )={\overline{X}}_{\infty }(7.2)-[{\overline{X}}_{\infty }(7.2)-{\overline{X}}_0(4,7.9)\text{exp}[-\tau /{\tau }_{\overline{X}}(7.2)],$$

where X̅₀(4, 7.9) is the value of X̅ at the end of 4 s at pCa = 7.9.

As X̅(7.2) = 0, X̅(τ) = X̅₀(4, 7.9) exp[−τ/τ_X̅(7.2)] indicates that before the next triggering, the degree of activation of the releasable terminal decays exponentially with a time constant of τ_X̅(7.2) The dotted curve in Fig. 6b is described by equation (11) with Ca_c = 2.51 µM, (Ca_m – Ca_c) = 1.20 µM and T = τ_X̅(7.2) = 1.43 s, which is the value chosen in this model.

Simulation of Ca²⁺ Current

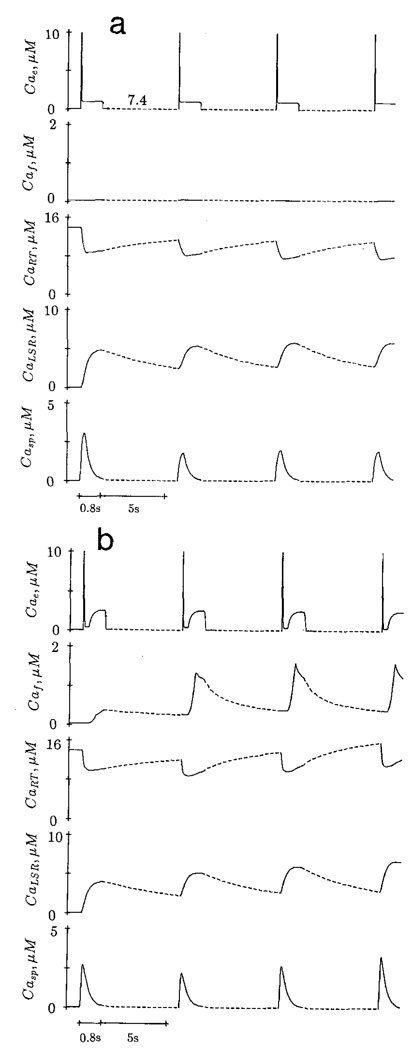
To simulate the fast component of Ca²⁺ current, Fabiato (1985c) injected trigger Ca²⁺ at pCa 5.0 in 10 ms and mixed with a volume of solution at pCa 7.0 injected at a slow rate. The slow component was made by mixing pCa 5.0 and pCa 7.0 solution at a slower rate. In the present study, the fast component was simulated by increasing the [free Ca²⁺] from pCa 7.4 to pCa 5.0 in 10 ms (i.e. α = 0.6 in equation (9)], which decayed to either pCa 6.4 or pCa 6.0 in 40 ms (α = 2.0), and lasted for 200 ms. The [free Ca²⁺] was slowly increased to a final pCa of 5.6 at two rates: α = 0.01 for 300 ms and α = 0.025 for the next 300 ms. This [free Ca²⁺] was rapidly reduced to resting pCa level (e.g. 7.4). The total duration of fast and slow components was 810 ms.

Potentiation of Subsequent Ca²⁺ Transient by the Slow Component

Figure 7 shows the effect of adding a slow component to the trigger Ca²⁺ on the subsequent sarcoplasmic Ca²⁺ transient (Ca_sp). The first trigger Ca²⁺ (i.e. third pulse), comprising of fast and slow components, does not potentiate the sarcoplasmic Ca²⁺, but increases the [free Ca²⁺] sequestered by LSR are then transferred to the releasable terminal and become available for subsequent release.

Figure 7.

Demonstration of the potentiation of subsequent Ca transient by the slow component of trigger Ca. The first two trigger Ca pulses (uppermost panel) consist of fast component only. The third pulse, comprising of fast and slow component, does not modify the corresponding sarcoplasmic Ca transient immediately. The fourth and fifth trigger Ca pulses potentiate the subsequent transient. Note the change of time scale (– – –).

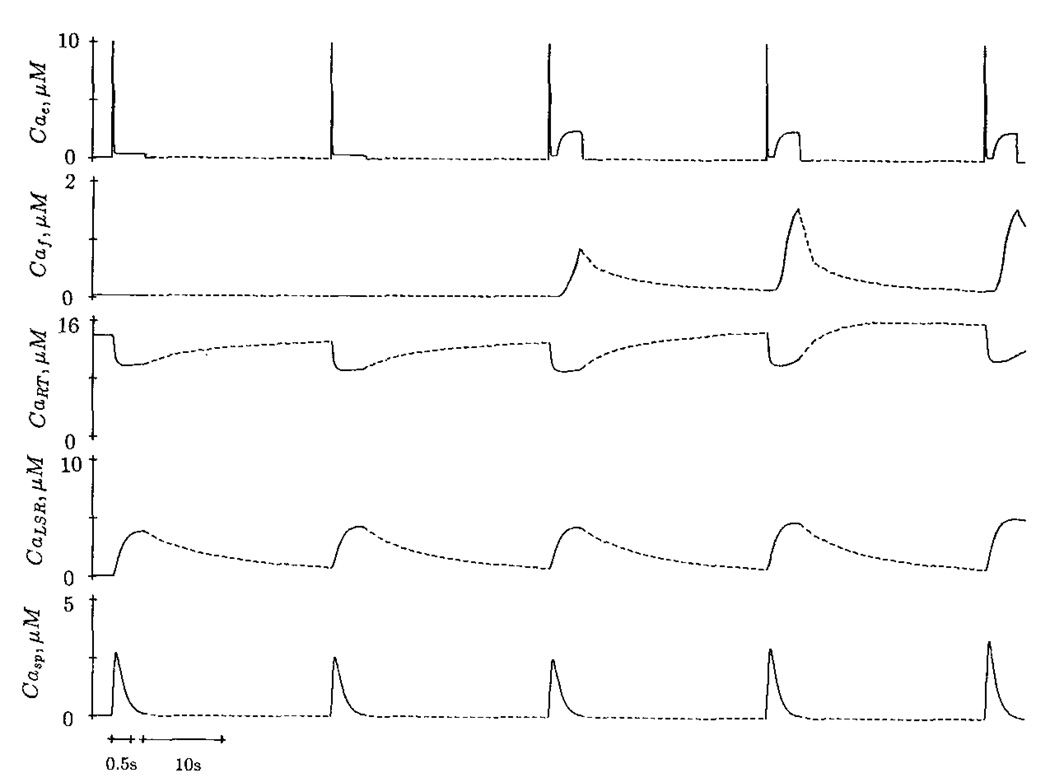
Positive and Negative Staircase

An increase of frequency of stimulation by trigger Ca²⁺ with fast component only results in a negative staircase. In Fig. 8a, the first sarcoplasmic Ca²⁺ (Ca_sp) transient is triggered by a fast component after a long rest period. Subsequent stimulation at one per 6 s produces decreasing Ca²⁺ transient. In the absence of slow component, the [free Ca²⁺] production in MCS (Ca_f) is minimal. The higher frequency of stimulation reduces the time for the releasable terminal to be replenished by the [Ca²⁺] from MCS and LSR, resulting in a progressive reduction of calcium content in this compartment. In contrast, trigger Ca²⁺ with fast and slow components elicits a positive staircase (Fig. 8b) at the same frequency of stimulation (one per 6 s). The calcium content of the releasable terminal progressively increases due to the increase of [Ca²⁺] in the MCS.

Figure 8.

Negative staircase (a) is elicited by trigger Ca²⁺ with fast component only, and stimulated at a frequency of one per 6 s. Positive staircase (b) is caused by trigger Ca²⁺ with fast and slow components, stimulated at the same frequency. Change of time scale is indicated by the dotted line.

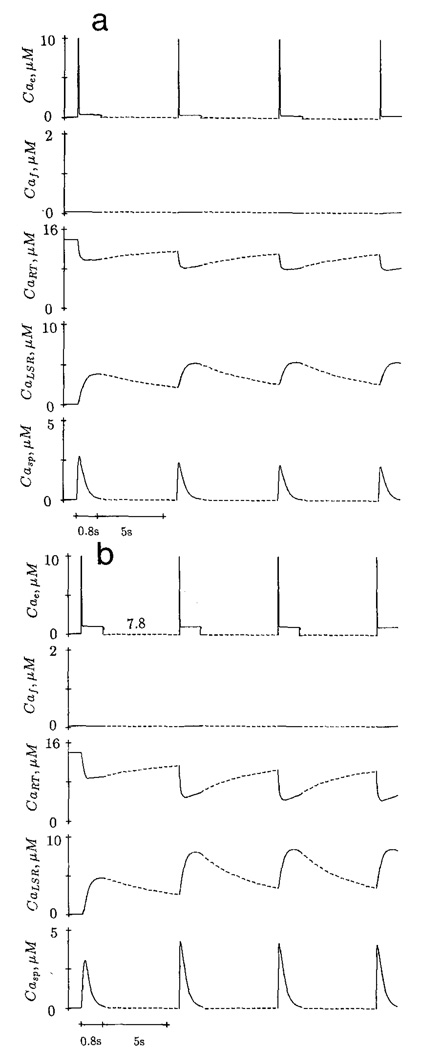
Effect of Resting [free Ca²⁺] on the Subsequent Calcium Release

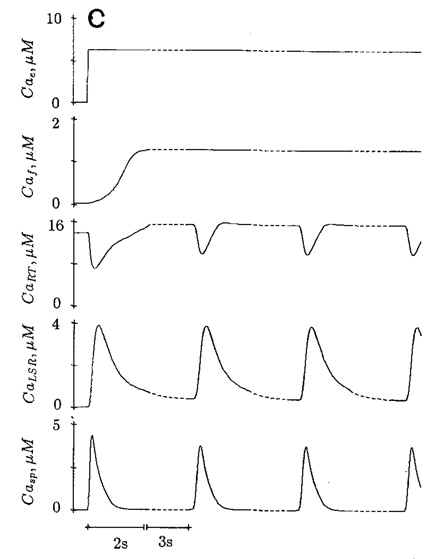
The initial conditions in Fig. 9a,b are identical. The trigger Ca²⁺ consists of a fast component only; a 10 ms pCa 5.0 decays rapidly to pCa 6.0 in 40 ms and lasts for 800 ms. The first sarcoplasmic Ca²⁺ transient is elicited by the trigger Ca²⁺ after a long rest period; it has a peak value of 3.1 µM. When the resting [Ca²⁺] during the interval between stimuli is lowered to pCa_e = 7.8 and stimulation frequency is increased (one per 6 s), the subsequent sarcoplasmic Ca²⁺ transient is potentiated (Fig. 9a). However, at a resting [free Ca²⁺] of pCa_e = 7.4, higher stimulation frequency produces a reduced Ca²⁺ transient in the next beat.

Figure 9.

Effect of resting pCa_e during the interval between two stimuli on subsequent Ca²⁺ transient. The initial resting pCa_e is 7.4. After the first Ca²⁺ transient, the resting pCa_e is changed to 7.8. Dotted lines indicate smaller time scale.

Fabiato (1985c) reasoned that when the resting [free Ca²⁺] was higher, the negative staircase elicited was caused by a progressive reduction in the degree of refilling of the SR during the interval between tension transients resulting from the increase of frequency. According to the model response, the potentiated Ca²⁺ transient at higher resting [free Ca²⁺] is not due to the loading of the releasable terminal. In fact, the calcium content in this compartment is reduced. The potentiation is caused by the elevated degree of reactivation of the releasable terminal (r = d · f – λX̅ · x).

At resting pCa_e = 7.8, X̅_∞ is more negative, resulting in a larger positive value of r during the interval between stimuli. At pCa_e = 7.4, X̅_∞ is less negative. The releasable terminal at the end of the of the resting period (6 s) has a smaller value of r and thus less Ca²⁺ is released in the subsequent beat.

Discussion

The present model has demonstrated that trans-sarcolemmal Ca²⁺ influx, such as Ca²⁺ current, can trigger Ca²⁺ release from and load the sarcoplasmic reticulum in cardiac cells. The demonstration is made possible by assuming that the activation, inactivation and the reactivation of the SR membrane is Ca²⁺-mediated and time-dependent.

In many aspects, the proposed model is phenomenological as some of the assumptions do not seem to have a molecular basis. For example, it is difficult to explain how the rate of change of trigger Ca²⁺ affects τ_p, τ_q, the diffusion of Ca²⁺ into the MCS, or how trigger [Ca²⁺] can influence τ_x, which is primarily a function of sarcoplasmic [Ca²⁺]. Another objectionable feature is J_io, the calcium efflux from the RT to the outside of the cell. J_io can be eliminated by (1) making the free Ca²⁺ transferred from LSR to MCS instead of to RT. By modifying the numerical values of parameters of constants in Fig. 2, the free Ca²⁺ in RT can be limited to about 18 µM (Adler et al., 1985). (2) Considering the MCS as the compartment which can store, release and sequester Ca²⁺, then LSR is not necessary.

In the above two cases, it is necessary to modify or adjust the parameters and constants so that the amount of free Ca²⁺ produced in MCS is equal to the amount of Ca²⁺ sequestered, otherwise the free [Ca²⁺] in RT cannot be maintained. In other words, it is necessary to assume a high free Ca² in the MCS during resting state, as in the other E–C coupling models (Cannell and Allen, 1984; Adler et al., 1985). If the free Ca²⁺ in the MCS were high, calcium would be extruded continuously across the SR membrane to the outside diffusion. High resting free Ca²⁺ within the MCS could be maintained only if the SR membrane was nondiffusible at the resting condition, or some “calcium pump” similar to the Na–K pump was was assumed. However, these assumptions do not seem reasonable.

The releasable terminal, being part of the SR, does contain relatively high free Ca²⁺; this calcium is not extruded by diffusion. The separation of the SR into a “main calcium store” and the Releasable Terminal is for the convenience of mathematical formulation. One should perceive the MCS and RT together as one single compartment (i.e. SR), in which the resting free Ca²⁺ is high and calcium is extruded by a Ca–Ca exchange mechanism.

Cannell et al. (1987) reported the effect of depolarization duration on the time course of calcium transient (indicated by the fluorescent Ca²⁺ indicator fura-2) in single rat cardiac cells. They suggested that Ca release might be mediated by Calcium-Induced Calcium Release (CICR) and modulated directly by changes in voltage. An alternative scheme of Ca²⁺ release from the SR based on CICR and a voltage-dependent mechanism (Hilgemann and Noble, 1987) should be considered. However, in a review article, Fabiato (1985d) cited studies which demonstrated no change of SR potential during Ca²⁺ release induced by Ca²⁺ or caffeine, or no Ca²⁺ release induced by change of potential in single skinned cardiac cells. The effect of depolarization duration on calcium transient is equivalent to the effect of decreasing trigger [Ca²⁺] at different phases of Ca²⁺ transient (Fabiato, 1985b) and can be explained by the present model. The release parameter r(t) = (f · d – λX̅ · x) is dependent on the sarcoplasmic calcium (Ca_sp) or intracellular Ca²⁺ and trigger Ca²⁺ (Ca_e) concentration. In a cardiac cell with sarcolemma, repolarization at different phases of the Ca²⁺ transient alters Ca²⁺ influx into the appositional space, changing Ca_e and X̅(t). Subsequently, r(t) is altered, affecting the amount of Ca²⁺ released and intracellular Ca²⁺ concentration.

Studies by Winegrad (1979, 1982) showed no evidence for different sites for Ca²⁺ release and accumulation in cardiac muscle. Experiments on skinned cardiac cells (Fabiato, 1981, 1983) suggest that the longitudinal SR is capable of both accumulating and releasing Ca²⁺. A recent study by Fabiato (1985c) suggests a mechanism through which Ca²⁺ release and accumulation could take place with only a functional compartment caused by the time and Ca²⁺ dependence of activation and inactivation of Ca²⁺ release from the SR and of the Ca²⁺ accumulation into the SR.

The present model appears to be in conflict with the above concept as the release and accumulation of Ca²⁺ occurs at different sites or compartments (RT and LSR). However, the kinetic parameters f(t) and x(t) are involved in Ca²⁺ release and uptake. Furthermore, the LSR transfers free Ca²⁺ directly to RT for subsequent release. Arbitrarily, both RT and LSR could be lumped together as one functional unit capable of releasing and accumulating Ca²⁺.

The model is consistent with the concept that the trans-sarcolemmal Ca²⁺ influx loads the SR with Ca²⁺ when it is slow and occurs during the refractory period of the process of Ca²⁺-induced release of Ca²⁺ (Fabiato, 1985c). The refractory period in the model is determined by the release expression (d · f – λX̅ · x). After the fast component of the Ca²⁺ influx triggers the release of Ca²⁺, x(t) increases and f(t) decreases, making (d · f – λX̅ · x) negative and model refractory. Within the refractory period, the slow component of the influx increases the [Ca²⁺] outside the SR. Subsequently, [Ca²⁺] enters the MCS, increasing its free Ca²⁺ content.

In many aspects, the kinetics of the proposed Ca release mechanism are similar to those of cardiac action potential (Beeler and Reuter, 1977). The parameters p, q, d and f can be considered equivalent to the activation and inactivation of inward currents, and X · x to the outward current. The rate of Ca released from releasable terminal, given as:

$$g_{\text{Ca}}·p·q·(d·f-\lambda \overline{X}·x)({\text{Ca}}_{\text{RT}}-{\text{Ca}}_{\text{sp}}),$$

differs little conceptually from the kinetics of ionic current, I = g(E – E_r), in which g is the conductance and (E – R_r) the driving force. The first term of the Ca release equation is equivalent to conductance, the second term to the driving force.

The expression for J_pump, despite its empirical nature, has its physiological function. As X(t) is slow-varying and its value is small when Ca²⁺ is being released, Ca uptake is not significant, thus allowing the increase of sarcoplasmic Ca²⁺ at a faster rate to activate the myofilaments. Near the end of release, when x(t) has become relatively large and the sarcoplasmic Ca²⁺ is high, the Ca uptake is accelerated. This is in agreement with the experimental observation (Fabiato, 1985b) that Ca uptake starts at the end of the release.

The delay of Ca uptake is physiologically significant. If release and uptake occurred simultaneously, more Ca²⁺ had to be released than necessary in order to be sufficient to activate the myofilaments; energy expenditure would be greater to keep the uptake process operating all the time.

An alternative and realistic scheme for J_pump is:

$$J_{\text{pump}}=K_{\text{ATP}}[\text{ATP}]{[{\text{Ca}}_{\text{sp}}]}^2-K_{\text{ADP}}{[\mathrm{P}]}_{\mathrm{i}}[\text{ADP}]{{\text{Ca}}_{\text{LSR}}]}^2.$$

In this equation, ATP promotes Ca uptake while ADP and P_i inhibits it. If ATP is depleted early there is an accumulation of P_i and ADP, for example during moderate or severe hypoxia (Nayler et al., 1979), and the Ca accumulation by the LSR and the transport of Ca to the releasable terminal will be depressed. However, the variation of local concentrations of ATP, P_i and ADP with time on a beat-to-beat basis is not clear.

Despite the fact that the “steady state” kinetic parameters and the time constants are “guessed” or speculated, the model is able to simulate many events qualitatively similar to those observed experimentally (Fabiato, 1985c). Perhaps the model can be refined if the kinetic parameters are determined more realistically. The amplitudes and rate of rise of aequorin light data vs trigger pCa of the Fabiato’s experiments (1985a,b) on skinned cells can provide clues for estimating p, q, d, f and their associated time constants. X̅, x and τ_x can be estimated from the periodicity and amplitude of the cyclic release.

The present model can be applied directly to cardiac cells with intact sarcolemma by replacing the space at the outer surface of the SR with the oppositional space (APS). Thus equation (1) becomes:

$${\text{dCa}}_{\mathrm{e}}/\mathrm{d}t=J_{\text{in}+}{J}_{\text{ioCa}}-(J_{\text{out}}+J_{\mathrm{D}}).$$

J_in is the transmembrane calcium influx during a depolarization such as the calcium current. J_out is the transmembrane calcium efflux from APS to the extracellular space. The efflux is probably due to Ca–Na exchange and/or calcium pump. Both J_D and J_ioCa have the same meaning as defined in equation (1).

A small number of experiment observations on skinned cells cannot be simulated by the present model. This is because many mechanistic and molecular details of Ca²⁺ release and accumulation are still lacking in this study. Nevertheless, the model appears to confirm the hypothesis that the activation, inactivation and reactivation of Ca²⁺ release and accumulation processes are calcium-mediated and time-dependent, analogous in principle to Hodgkin–Huxley channel regulation by voltage.

Conclusion

A model has been proposed to describe the mechanism of calcium-induced calcium release from cardiac sarcoplasmic reticulum (SR). Based on the assumption that the activation, inactivation and reactivation of the SR calcium channels are Ca²⁺-mediated and time-dependent, the model satisfactorily explains (a) how an increase of [free Ca²⁺] outside the SR membrane induces a release of Ca²⁺ from the lumen of the SR, (b) why this phenomenon is graded rather than all-or-none, and (c) why trans-sarcolemmal Ca²⁺ influx such as Ca²⁺ current can trigger Ca²⁺ release from and also load the SR.