An empirical comparison of meta-analysis and mega-analysis of individual participant data for identifying gene-environment interactions

Abstract

For analysis of the main effects of SNPs, meta-analysis of summary results from individual studies has been shown to provide comparable results as “mega-analysis” that jointly analyzes the pooled participant data from the available studies. This fact revolutionized the genetic analysis of complex traits through large GWAS consortia. Investigations of gene-environment (G×E) interactions are on the rise since they can potentially explain a part of the missing heritability and identify individuals at high risk for disease. However, for analysis of gene-environment interactions, it is not known whether these methods yield comparable results. In this empirical study, we report that the results from both methods were largely consistent for all four tests; the standard 1 degree of freedom (df) test of main effect only, the 1 df test of the main effect (in the presence of interaction effect), the 1 df test of the interaction effect, and the joint 2 df test of main and interaction effects. They provided similar effect size and standard error estimates, leading to comparable p-values. The genomic inflation factors and the number of SNPs with various thresholds were also comparable between the two approaches. Mega-analysis is not always feasible especially in very large and diverse consortia since pooling of raw data may be limited by the terms of the informed consent. Our study illustrates that meta-analysis can be an effective approach also for identifying interactions. To our knowledge, this is the first report investigating meta- versus mega-analyses for interactions.

Introduction

Over the past several years, genome wide association studies (GWAS) have identified hundreds of common genetic variants associated with many common complex disease traits (http://www.genome.gov), thereby accelerating the progress in the genetic dissection of complex human disease traits. The confidence and funding invested in GWAS approaches have led to unprecedented levels of collaboration, spawning a number of highly productive consortia such as the CHARGE (Cohorts for Heart and Aging Research in Genetic Epidemiology) [Psaty, et al. 2009], GIANT (Genetic Investigation of Anthropometric Traits) [Willer, et al. 2009], and ICBP (International Consortium of Blood Pressure) [International Consortium for Blood Pressure Genome-Wide Association, et al. 2011]. It is standard practice in these consortia to perform meta-analysis that combines the summary results from multiple studies for the same phenotype of interest [de Bakker, et al. 2008]. As recently reviewed [Evangelou and Ioannidis 2013], meta-analysis provides an efficient and practical strategy for overcoming the limitations of power that can compromise any individual study.

However, these hundreds of successfully identified genetic variants typically have very subtle effects, thus explaining only a fraction of the heritability of most complex traits [Manolio, et al. 2009]. It is increasingly recognized that the near-exclusive focus on main effects has become a barrier to the identification of additional genes underlying these disease traits. Increasingly greater emphasis is being placed in recent years on gene-environment (G×E) interaction analyses, also relying on meta-analysis in large consortia. The identification of G×E interactions is important for many reasons [Le Marchand and Wilkens 2008; Thomas 2010a]. G×E interactions or more complex pathways involving multiple genes and environments can potentially explain at least part of the missing heritability [Eichler, et al. 2010; Manolio, et al. 2009; McCarthy and Hirschhorn 2008; Visscher, et al. 2012]. They can further elucidate the biological networks underlying complex disease risk and enable “profiling” of individuals at highest risk for disease. Although identifying G×E interactions is important, it requires larger sample sizes than those needed to identify genetic main effects alone [Thomas 2010b]. Therefore, it is important to have very large sample sizes. Meta-analysis which has been useful for identifying genetic main effects will be even more useful for identifying G×E interactions.

To increase sample sizes, collaborative groups are increasingly collating the raw individual participant data from studies that are able to participate and jointly analyze the pooled individual-level data (such analysis is referred to here as mega-analysis). This approach, also known as meta-analysis of individual patient data (IPD) in statistical literature [Stewart and Clarke 1995], is regarded as the gold standard in randomized clinical trials (e.g, see [Chalmers 1993]). For example, a general framework for this IPD meta-analysis for clinical trials has been described by Higgins et al [Higgins, et al. 2001]. However, meta-analysis that combines results from the participating studies has several advantages as compared to mega-analysis. First, obtaining individual level data is challenging and limited by the terms of the informed consent within each study. Second, integration of very large genotype and phenotypic data sets from different studies is time-consuming and poses additional challenges with data management, storage, and harmonization issues. Third, meta-analysis allows for analyses of individual studies to account for local population substructure, relationships among subjects, study-specific covariates, and other ascertainment-related issues which may be optimally dealt with within each study. Reviews on advantages and disadvantages of each approach can be also found elsewhere [Steinberg, et al. 1997; Stewart and Tierney 2002].

Although mega-analysis is arguably more powerful than meta-analysis of separate results, in so far as analysis of main effects is concerned, it has been shown that meta-analysis also yields highly comparable results. Olkin and Sampson [Olkin and Sampson 1998] showed that, for comparing treatments with respect to a continuous outcome in clinical trials, meta-analysis is equivalent to mega-analysis if the treatment effects and error variances are constant across trials. The equivalence has been extended even if the error variances are different across trials [Mathew and Nordström 1999]. Lin and Zeng theoretically proved asymptotic equivalence between meta- and mega-analyses when the effect sizes are the same for all studies [Lin and Zeng 2010b]. This was further illustrated empirically by combining results from two phases of data [Lin and Zeng 2010a].

However, for analysis of G×E interaction effects, it is unknown whether meta- and mega-analyses yield comparable results. In this paper, we addressed this issue using empirical data. Using data from the four studies, we analyzed each study separately and meta-analyzed the results using METAL [Willer, et al. 2010]. We also combined the raw phenotypic and GWAS data from all 4 studies and analyzed the pooled data (i.e., mega-analysis). In addition to the standard 1 degree of freedom (df) test of interaction effect, we used the joint 2 df test of main and interaction effects by Kraft et al [Kraft, et al. 2007] and the joint meta-analysis by Manning et al [Manning, et al. 2011].

Study Samples

We used data for European American participants from four studies presented in Table I: the Framingham Heart Study (FHS), GENOA, HERITAGE and HyperGEN. All four studies obtained informed consent from participants and approval from the appropriate institutional review boards. All four studies have participated in several GWAS consortia publications (based on main effects), and therefore much is already known about them. Our analysis was restricted to a total of 131,880 imputed SNPs on chromosomes 16 and 18, for which preliminary analysis of G×E interactions in the FHS data yielded significant results. Imputation for these SNPs was performed using MACH [Li, et al. 2010] using the reference panels of the HapMap Phase II data with European ancestry subjects.

Table I. Summary statistics for the four studies.

	FHS	GENOA	HERITAGE	HyperGEN
# Subjects	6,686	1,420	469	1,216
% Male	46.6%	44.9%	48.6%	49.7%
Age (mean ± SD)	49.1 ± 13.6	54.7 ± 10.7	36.9 ± 14.2	49.5 ± 13.8
BMI (mean ± SD)	27.4 ± 5.4	30.4 ± 6.2	26.0 ± 5.0	29.3 ± 5.9
% on Anti-HT Meds	19.0%	55.7%	0.0%	46.0%
SBP (mean ± SD)	120.4 ± 16.4	133.5 ± 19.6	116.5 ± 11.2	123.2 ± 19.2
Pack Years (mean ± SD)	9.9 ± 17.6	13.6 ± 21.6	5.0 ± 10.9	7.2 ± 16.3

Values shown represent mean value ± the standard deviation or percentage. FHS = Framingham Heart Study; GENOA = Genetic Epidemiology Network of Arteriopathy; HERITAGE = health, risk factors, exercise training and genetics; HyperGEN = Hypertension Genetic Epidemiology Network

The Framingham Heart Study (FHS) is a longitudinal family-based study for identifying the factors that contribute to cardiovascular disease, sponsored by the National Heart, Lung, and Blood Institute (NHLBI). FHS began in 1948 with the recruitment of an original cohort of 5,209 men and women who were 28 to 62 years of age at entry [Dawber, et al. 1951]. Clinic examinations took place approximately every 2 years. In 1971, a second generation of study participants, 5,124 children and spouses of children of the original cohort were enrolled [Feinleib, et al. 1975]. Clinic examinations took place approximately every 4 years. Enrollment of the third generation cohort of 4,095 children of offspring cohort participants began in 2002 [Splansky, et al. 2007]. In this analysis we used the FHS SNP Health Association Resource (SHARe) data, as obtained through the database of Genotypes and Phenotypes (dbGaP). Our analysis was restricted to cross-sectional data on 6,686 European American subjects involving all 3 generations with GWAS data.

The Genetic Epidemiology Network of Arteriopathy (GENOA) is a family-based study of hypertension and diabetes (e.g., see [Daniels, et al. 2004]). GENOA recruited sibships with at least two hypertensive siblings and any additional available siblings, regardless of hypertension status. In total, it has collected data on over 5,000 European-American, African-American, and Hispanic-American subjects, from Minnesota, Mississippi, and Texas, respectively. GENOA subjects were brought in for a complete physical examination and questionnaire. We used the 1,420 European American subjects with GWAS data in this analysis.

The Health, risk factors, exercise training and genetics (HERITAGE) Family Study was designed to evaluate the role of genetic and non-genetic factors in cardiovascular, metabolic, and hormonal responses to aerobic exercise training [Bouchard, et al. 1995]. Extensive data, including body composition, cardiovascular risk factors, and lifestyle habits, were gathered on approximately 800 subjects in over 200 families, both before and after 20 weeks of supervised training. We used 469 European American subjects with GWAS data in this analysis.

The Hypertension Genetic Epidemiology Network (HyperGEN) is a multicenter family-based study for investigating the genetic causes of hypertension and related conditions [Williams, et al. 2000]. HyperGEN recruited African American and European American participants at five field centers. It recruited sibships with at least two hypertensive siblings, non-medicated offspring of these hypertensive siblings, and an age-matched random sample. Subjects were brought into the clinic for an exam, and data were collected from questionnaires, a physical exam, and blood and urine samples. In total, HyperGEN collected data from 2,471 European American subjects and 2,300 African-American subjects. We used the 1,216 European American subjects with GWAS data in this analysis.

Statistical Analyses

To compare meta-analysis and mega-analysis, we considered four analysis options. First, as most GWAS use a main-effect-only analysis, we also performed a main-effect-only analysis. The expected response trait (Y) has the regression model

$$E[Y]={\delta }_0+{\delta }_{e}E+{\delta }_{g}G,$$ (1)

where δ_e is the environmental main effect and δ_g is the genetic main effect. We used the Wald test statistic that follows a chi-squared distribution with 1 degrees of freedom (df) under the hypothesis H₀: δ_g=0 (i.e., testing for the genetic main effect). Second, we followed the standard approach to identify G×E interactions. The regression model is generalized to

$$E[Y]=\alpha +{\beta }_{e}E+{\beta }_{g}G+{\beta }_{ge}GE,$$ (2)

where β_e and β_g respectively are the environmental and genetic main effects and β_ge is their multiplicative interaction effect. We used the Wald test statistic that also follows a chi-squared distribution with 1 df under the H₀: β_ge=0 (i.e., testing for the G×E interaction effect in the presence of the genetic main effect). Third, we also tested the genetic main effect in the presence of G×E interaction effect by using Wald test statistic that follows a chi-squared distribution with 1 df under the H₀: β_g=0. Finally, we performed the test proposed by Kraft et al [Kraft, et al. 2007] that jointly tests the genetic main and G×E interaction effects using the same regression model as in the second analysis. We used a Wald test statistic that follows a chi-squared distribution with 2 df under the H₀: β_g=β_ge=0. This Wald test statistic is based on estimates of β_g and β_ge and their corresponding 2×2 covariance matrix. The regression models for mega-analysis of pooled individual data were analogous except that they included study-specific intercepts (i.e., α₁ – α₄).

To combine the results from the four studies, we performed fixed effects meta-analysis. We used the inverse-variance weighting method in METAL [Willer, et al. 2010] by computing inverse-variance-weighted coefficients. It is straightforward to combine the 1 df results from three analysis options: main-effect-only analysis, interaction effect, and main effect in the presence of interaction effect. Manning et al [Manning, et al. 2011] developed the joint meta-analysis and modified METAL [Willer, et al. 2010] to combine the joint 2 df tests across multiple studies. The joint meta-analysis provides inference on the genetic main effect and interaction effect pooled across all studies. To combine the joint 2 df results (estimates of β_g, β_ge and their corresponding 2×2 covariance matrix) from these 4 studies, we used a modified version of METAL that implements this joint 2 df meta-analysis by Manning et al [Manning, et al. 2011].

Fixed effects meta-analysis that we used is the most popular approach in GWAS consortia and is shown to be the most powerful for prioritizing and discovering SNPs [Pfeiffer, et al. 2009]. In particular, fixed effects models have an advantage over random effects models in terms of increased power for discovery [Pereira, et al. 2009]. However, because fixed effects meta-analysis assumes that true effect-size is constant across the studies, we examined whether there was evidence of heterogeneity among studies using p-value based on Cochran's Q-test [Cochran 1954] for each SNP for all four analysis options. We also examined the I² index that quantifies the proportion of total variation due to heterogeneity (i.e., between-study variance) [Higgins and Thompson 2002].

Increased Type I error due to inflation of test statistics in G×E interactions can be a concern as recently shown [Voorman, et al. 2011]. We plotted quantile-quantile (QQ) plots and computed the genomic inflation factor λ_GC, the degree of inflation of the median test statistic, for all four analysis options. We also computed the genomic controlled p-values by dividing test statistics by λ_GC, as they are widely used to correct for minor substructure problems [Ganesh, et al. 2009]. In addition, we performed genomic controlled meta-analysis (also using METAL), where genomic control correction was applied before combining study-specific results.

To compare meta-analysis and mega-analysis in the context of G×E interactions, we analyzed systolic blood pressure (SBP) and used pack-years of smoking as an interacting covariate. In addition, we included age, sex, body mass index (BMI) and use of anti-hypertensive medications as common covariates. Because all four studies are family studies in which relatedness must be taken into account, we used ProbABEL [Aulchenko, et al. 2010] and GenABEL/MixABEL [Aulchenko, et al. 2007] for each cohort study and mega-analysis of pooled individual participant data.

Results

Table I presents select characteristics of the four studies. Roughly half of the subjects are female within each study. The subjects in the HERITAGE tended to be younger, relatively leaner and low pack years with no anti-hypertensive medications (e.g., hypertension was an exclusion criterion). In contrast, the subjects in GENOA were older and had high pack years and higher SBP with over 55% on anti-hypertensive medications. The HyperGEN study has characteristics similar to GENOA. The FHS has intermediate values for SBP, medication use and pack years. We found that meta-analysis of interaction results had more SNPs with evidence of heterogeneity across studies.

Table II presents the number of SNPs and I² index across multiple ranges of heterogeneity p-values based on Cochran's Q-test for heterogeneity. For main effect only analysis, heterogeneity p-values roughly followed a uniform distribution; about 5% of SNPs had heterogeneity p-values below 0.05. In contrast, meta-analysis for the interaction effect encountered the greatest heterogeneity among studies (13% of the SNPs had heterogeneity p-values < 0.05). The 2df test of joint main and interaction effects provided 10% heterogeneous results. Values of I² index also provided evidence of higher heterogeneity in the interaction analysis (I² values of 25, 50, 75 are considered low, moderate, high heterogeneity, respectively). I² index ranged from 0 to 77.5 with a mean value of 4.3 for the main effect only analysis, whereas it ranged from 0 to 81.9 with a mean value of 9.9 for the interaction analysis.

Table II.

The number of SNPs (out of 131,880 SNPs) and I² index across multiple ranges of heterogeneity p-values (HetP) based on Cochran's Q-test for heterogeneity.

Range of HetP	1DF Main Only		1DF Main		1DF Interaction		2DF Joint Main and Int.
	SNPs Count (%)	I2 index Mean (Min, Max)	SNPs Count (%)	I2 index Mean (Min, Max)	SNPs Count (%)	I2 index Mean (Min, Max)	SNPs Count (%)
HetP ≥ 0.1	119,421 (90.6%)	0.8 (0, 20)	119,776 (90.8%)	0.8 (0, 20)	103,726 (78.7%)	1.3 (0, 20)	109,302 (82.9%)
0.05 ≤ HetP < 0.1	6,047 (4.6%)	27.6 (20, 36)	6,084 (4.6%)	27.6 (20, 36)	11,264 (8.5%)	28.0 (20, 36)	9,566 (7.3%)
HetP < 0.05	6,412 (4.9%)	48.2 (36, 77.5)	6,020 (4.6%)	48.0 (36, 76.5)	16,890 (12.8%)	50.8 (36, 81.9)	13,012 (9.9%)
All		4.3 (0,77.5)		4.2 (0,76.5)		9.9 (0,81.9)

I² index for the 2df joint main and interaction test is unavailable.

We found that the results between meta- and mega-analyses were largely consistent. In particular, as shown in Figure I, the two analysis approaches provided similar effect sizes and standard error (SE) estimates. Effect sizes between the two approaches had a correlation of 0.95, 0.94, and 0.96 for main effect only 7[δ_g in equation (1)], main effect [β_g in equation (2)], and interaction effect [β_ge in equation (2)] estimates, respectively. When the results were restricted to SNPs with heterogeneous effect sizes across studies (i.e., p-values of Cochran's Q-test < 0.05), there was larger variation in the meta- and mega-analysis results, leading to smaller correlations (as expected). Finally, SE estimates for all three effect sizes were almost identical (with correlations of 0.999).

Figure I.

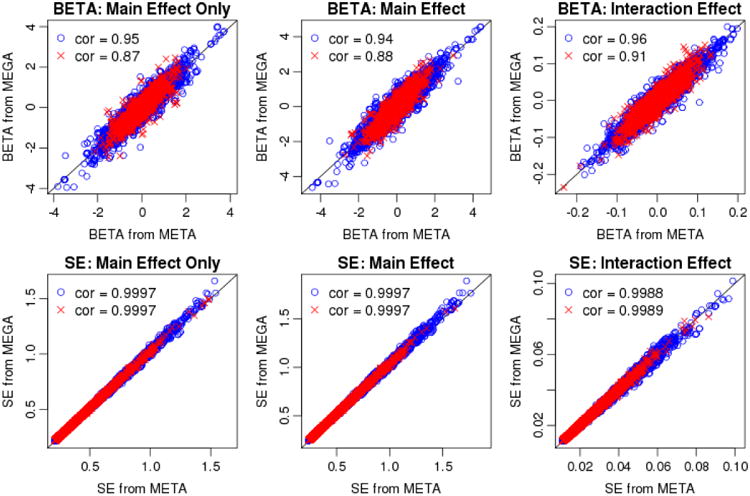
Scatterplots showing effect sizes (1^st row) and standard errors (2^nd row) from mega-analysis versus meta-analysis. The main effect only BETA (1^st column) corresponds to δ_g in equation (1). The main effect BETA (2^nd column) and interaction effect BETA (3^rd column) correspond to β_g and β_ge in equation (2), respectively. Red crosses are SNPs with heterogeneous effect sizes across studies (i.e., p-value of Cochran's Q-test < 0.05), and blue circles are SNPs with p-value of Cochran's Q-test ≥ 0.05. The correlations between the two methods across all SNPs were identical to the correlations across blue circles (up to two decimal places). The black diagonal line indicates where the values on the two axes are equal.

Figure II presents −log(p) values between meta- and mega-analyses for all four analysis options: main-effect-only analysis, main effect in the presence of the interaction effect, interaction effect in the presence of the main effect, and 2 df joint tests of main and interaction effects. Supplemental Table I presents summary statistics of −log(p) differences between mega- and meta-analyses. Surprisingly, the joint 2 df test provided the highest overall correlation (0.91); the correlations between the two methods across all SNPs were identical to the correlations across homogeneous SNPs only (up to two decimal places). Overall, although mega-analysis provided slightly better results as expected, both methods yielded very similar results for the most promising SNPs (with the smallest p values). For these promising SNPs, heterogeneity p-values were greater than 0.05, indicating their effects are homogenous across studies. High concordance of the smallest p values between mega- and meta-analysis methods is particularly noteworthy since they are the most important discoveries for further follow up.

Figure II.

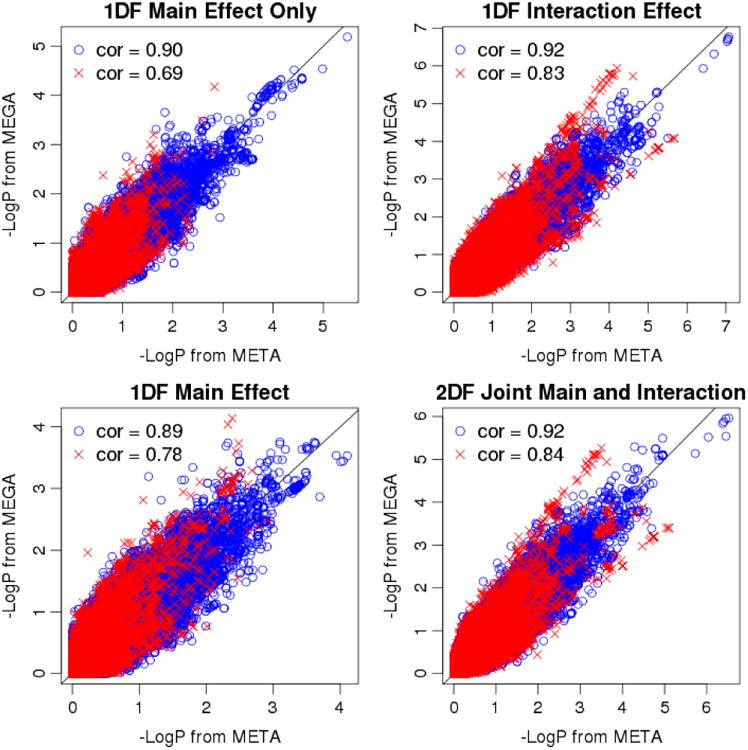
Scatterplots showing -log(p) values from mega-analysis versus meta-analysis for the 4 analysis options: 1 df test of the main effect only (without interaction effect) (top left), 1 df test of main effect in the presence of interaction effect (bottom left), 1 df test of interaction effect in the presence of the main effect (top right), and 2 df joint test of the main and interaction effects (bottom right). Red crosses are SNPs with heterogeneity effect sizes across studies (i.e., p-value of Cochran's Q-test < 0.05), and blue circles are SNPs with p-value of Cochran's Q-test ≥ 0.05. The correlations between the two methods across all SNPs were identical to the correlations across blue circles (up to two decimal places). The black diagonal line indicates where −log (p) values from meta- and mega-analyses are equal.

When the effect sizes are constant across studies, the meta-analysis method using inverse-variance weighting is shown to be optimal [Zhou, et al. 2011]. In particular, weights proportional to the square root of study sample sizes can be suboptimal when the trait variance differs across studies. In addition to the weighting method, we also performed another commonly-used approach that converts the direction of effect and p-value observed in each study into a signed Z-score; these Z-scores are then combined across studies in a weighted sum, with weights proportional to the square-root of the sample size for each study. Although trait variance of SBP differs somewhat, as shown in Table I, the results between the inverse-variance weighting method and the sample size weighted signed Z score method were remarkably similar, providing a correlation of 0.98.

Table III presents genomic inflation factor λ_GC for all 4 analysis options. QQ plots for meta- and mega-analyses are shown in Figure III (study-specific QQ plots are shown in Supplemental Figure I). We found that both meta- and mega-analyses behaved similarly. Main effect analysis had no inflation of Type I error. However, 1 df test of interaction effect had high inflation of type I error (λ_GC = 1.45 for both meta- and mega-analyses). The genomic controlled meta-analysis (GC-Meta), where genomic control correction was applied before combining study-specific results, removed most of the inflation (λ_GC = 1.02). The 2 df joint test of main and interaction effects had lower levels of inflation of type I error (λ_GC = 1.15 and 1.20 for meta- and mega-analysis, respectively), which was also removed by GC-Meta (λ_GC = 0.99). As shown in Table IV, the proportion of SNPs with p-value < 0.05 stayed at 5% with genomic control correction. We note that, as the primary purpose of this investigation is to evaluate the comparability of meta- versus mega-analysis, inflation of type I error rate in G×E analyses is in itself not as relevant as whether such inflation, when it exists, is also comparable between the two approaches.

Table III.

Genomic control λ_GC values for study-specific analysis, mega-anlysis, and meta-analysis.

	1DF Main Only	1DF Main	1DF Interaction	2DF Joint Main and Int.
Study-specific analysis:
FHS	0.905	0.927	1.466	1.161
GENOA	0.998	1.108	1.228	1.117
HERITAGE	1.047	0.954	1.518	1.238
HyperGEN	1.015	0.933	1.549	1.234
Mega-analysis:	1.036	0.988	1.451	1.204
Meta-analysis:
No genomic control correction	0.976	0.927	1.447	1.154
Genomic control correction	0.971	0.914	1.015	0.994

QQ-plots for study-specific analysis are shown in Supplemental Figure I. QQ-plots for meta- and mega-analyses are shown in Figure III.

Figure III.

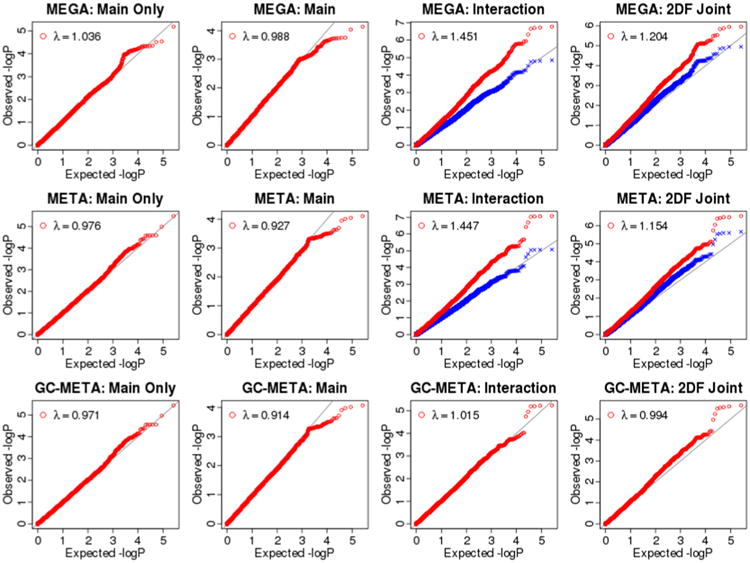
Quantile-quantile (QQ) plots for the 4 analysis options: main effect only analysis (1st column), main effect in the presence of interaction (2nd column), interaction in the presence of main effect (3rd column), and 2 df joint test of main and interaction effects (4th column). The red circle points are p-values and the blue cross points are genomic controlled p-values. The genomic control value for the blue cross points is 1. Study-specific QQ plots are shown in Supplemental Figure I.

Table IV.

The number of SNPs with p-values below thresholds (0.05 and 1×10^-4) out of 131,880 SNPs. Gonomic control (GC) correction preserved type I error.

	Analysis	1DF Main Only	1DF Main	1DF Interaction	2DF Joint Main and Int.
P < 0.05	Mega-analysis	6,617 (6%)	5,935 (5%)	13,584 (11%)	11,691 (9%)
	Meta-analysis	6,617 (6%)	5,935 (5%)	13,584 (11%)	11,691 (9%)
	Mega-GC analysis	6,896 (5%)	7,167 (5%)	6,469 (5%)	7,529 (6%)
	Meta-GC analysis	6,970 (5%)	7,024 (5%)	6,604 (5%)	7,945 (6%)
	GC-Meta analysis	6,527 (5%)	5,710 (4%)	6,752 (5%)	7,790 (6%)
P < 1×10-4	Mega-analysis	37	2	215	108
	Meta-analysis	20	3	188	118
	Mega-GC analysis	20	2	8	35
	Meta-GC analysis	32	4	9	36
	GC-Meta analysis	20	2	8	35

For Mega-GC and Meta-GC, GC correction was applied after mega-analysis and meta-analysis, respectively. For GC-Meta, GC correction was applied for each study-specific analysis before meta-analysis.

For mega-analysis, we also used the robust option in the ProABEL suite (results shown in Supplemental Figure II) following a recent recommendation [Voorman, et al. 2011]. This robust option is based on the “sandwich” estimate for variance, which is known to provide robust and asymptotically consistent estimator under miss-specified models [Huber 1967; Liang and Zeger 1986; White 1980]. Because the robust option in ProbABEL is currently applicable to population-based data, this ignores familial correlation. As shown in Supplemental Figure II, the p-values from this robust option were similar to the genomic controlled p-values from the mega-analysis (Mega-GC).

We compared the performance of the four analyses in terms of the evidence for association, using the genomic controlled mega-analysis (Mega-GC) results. Figure IV presents the scatterplots of the results [- log (p) values] across these 4 analysis options. As shown in Table V, the number of SNPs with p-value < 1×10^-4 was 24, 2, 18, and 35 from main effect only, main effect (in the presence of interaction), interaction effect (in the presence of main effect), and the 2 df joint test, respectively. They are plotted as red, green, blue, and cyan points in Figure IV. The 18 blue SNPs (with p-value < 1×10^-4 from the interaction effect) also had p-value < 1×10^-4 from the 2 df joint test; 17 additional SNPs with p-value < 1×10^-5 from the 2 df joint test are plotted as cyan points. Table V presents the effect sizes and standard errors (SE) for a subset of these SNPs, one SNP selected from each linkage disequilibrium (LD) block, as our results were based on 131,880 imputed SNPs. We found that the genetic main and interaction effects were in the opposite direction for every SNP in group 2. For these SNPs, the main effect only analysis (without interaction) provided a much smaller main effect estimate, leading to no evidence of association. This phenomenon is well known as Simpson's paradox in the statistics literature [Simpson 1951; Wagner 1982]. We found that the main and interaction effects were in the same direction for every SNPs in groups 1 and 3. Although this evaluation was based on results from the mega-analysis, as they are considered a gold standard, results based on meta-analysis were almost identical (which is not surprising given the high concordance between mega- and meta-analysis).

Figure IV.

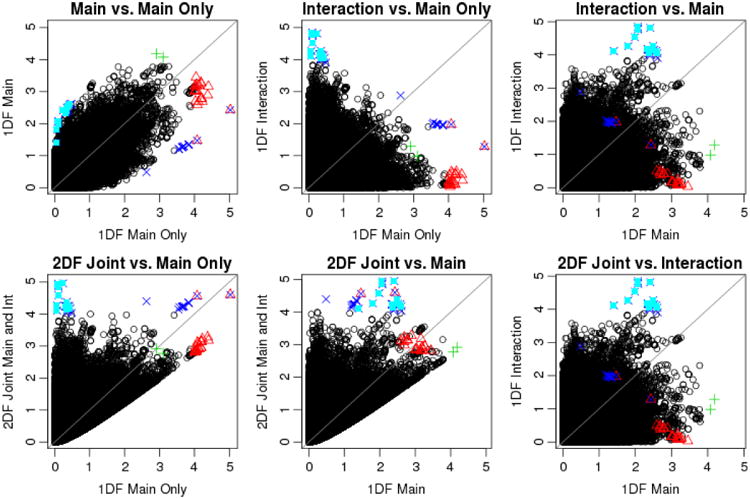
Scatterplots of -log(p) values across the 4 analysis options using genomic controlled mega-analysis. Red points are 24 SNPs with p-value < 1×10^-4 from the main effect only test. Green points are 2 SNPs with p-value < 1×10^-4 from the main effect test. Blue points are 18 SNPs with p-value < 1×10^-4 from the 1 df test of interaction effect (in the presence of main effect). Cyan points are additional 17 SNPs with p-value < 1×10^-4 from the 2 df test of joint main and interaction effects.

Table V.

Independent SNPs with p-values < 1×10^-4, one SNP selected from each linkage disequilibrium (LD) block from the genomic controlled mega-analysis.

SNP	Main Only		Main		Interaction		Genomic controlled P-values
	Beta	SE	Beta	SE	Beta	SE	Main Only	Main	Int	2df
Group 1 (selected from 22 red SNPs in Figure IV)
rs8050871	1.10	0.24	0.80	0.28	0.03	0.01	9.4×10-6	0.004	0.05	2.5×10-5
rs4788828	-1.23	0.30	-1.18	0.34	-0.01	0.02	6.5×10-5	0.0005	0.79	0.001
rs948638	1.30	0.31	1.13	0.35	0.02	0.02	4.2×10-5	0.001	0.38	0.0005
rs6499538	1.21	0.30	1.18	0.34	0.00	0.02	8.7×10-5	0.0005	0.84	0.001
rs2247603	1.26	0.32	1.18	0.36	0.01	0.02	8.8×10-5	0.0009	0.69	0.001
rs9930015	1.24	0.31	1.16	0.35	0.01	0.02	9.7×10-5	0.0009	0.68	0.001
Group 2 (selected from 18 blue SNPs in Figure IV)
rs733123	0.18	0.32	1.03	0.36	-0.09	0.02	0.57	0.004	1.5×10-5	1.1×10-5
rs9954614	0.08	0.32	0.94	0.36	-0.09	0.02	0.80	0.008	1.4×10-5	1.1×10-5
rs6420435	-0.21	0.27	-0.92	0.31	0.07	0.01	0.45	0.003	5.3×10-5	4.1×10-5
rs1558949	0.06	0.31	0.85	0.36	-0.08	0.02	0.84	0.015	5.4×10-5	5.4×10-5
rs11859599	-0.24	0.27	-0.90	0.30	0.07	0.01	0.38	0.003	7.5×10-5	5.6×10-5
rs2405214	0.05	0.23	-0.54	0.26	0.06	0.01	0.85	0.039	7.6×10-5	7.8×10-5
Group 3 (selected from 2 green SNPs and 17 cyan SNPs in Figure IV)
rs963267	0.91	0.23	0.55	0.26	0.04	0.01	8.4×10-5	0.03	0.01	2.7×10-5
rs949184	-1.24	0.33	-0.72	0.37	-0.05	0.02	0.0002	0.05	0.01	5.7×10-5
rs9960318	-1.39	0.42	-1.89	0.48	0.05	0.02	0.001	6.5×10-5	0.05	0.001

Discussion

Meta-analysis has become the most effective approach in GWAS for utilizing large sample sizes available from multiple studies and a standard practice in most consortia, since each study can analyze its own data optimally by customizing data adjustments as needed [Evangelou and Ioannidis 2013]. Increasingly greater emphasis is being placed on G×E interaction analyses, also relying on meta-analysis in large consortia [Aschard, et al. 2012]. Mega-analysis is not readily feasible owing to several challenges including limitations of the informed consent for sharing raw data, data management, and data harmonization for combining multiple huge data sets. All these challenges render meta-analysis as the convenient and expedient method of choice especially because meta-analysis yields results comparable to mega-analysis.

In this paper, we empirically evaluated whether meta-analysis also provides results comparable to mega-analysis for identifying G×E interactions. We found that results from meta- and mega-analyses were largely consistent even for identifying G×E interaction effects. In particular, they provided similar effect size and standard error estimates, leading to similar p-values. The number of SNPs significant at various thresholds was also comparable between the two approaches. We observed increased type I error due to inflation of test statistics for identifying interactions. To address this issue, we adjusted for genomic control before and after meta-analysis in addition to correction after mega-analysis. Although inflation of type I error rate has been observed for the analysis of G×E interactions, the levels of inflation were fairly comparable between meta- and mega-analyses. Our study illustrates that meta-analysis can be an effective approach for investigating interaction effects also.

To our knowledge, this is the first report investigating meta- versus mega-analyses for interactions. The validity of our findings is somewhat limited as it is based on an empirical investigation using a relatively small number of studies (four) that are readily available to us. Therefore, they may not be generalized to all situations. A more comprehensive simulation study covering the various scenarios regarding the number of studies, variation of study sizes and types of genetic variation, among others, would strengthen our findings.