Methodology for Evaluating a Partially Controlled Longitudinal Treatment Using Principal Stratification, With Application to a Needle Exchange Program

Abstract

We consider studies for evaluating the short-term effect of a treatment of interest on a time-to-event outcome. The studies we consider are only partially controlled in the following sense: (1) Subjects’ exposure to the treatment of interest can vary over time, but this exposure is not directly controlled by the study; (2) subjects’ follow-up time is not directly controlled by the study; and (3) the study directly controls another factor that can affect subjects’ exposure to the treatment of interest as well as subjects’ follow-up time. When factors 1 and 2 are both present in the study, evaluating the treatment of interest using standard methods, including instrumental variables, does not generally estimate treatment effects. We develop the methodology for estimating the effect of treatment 1 in this setting of partially controlled studies under explicit assumptions using the framework for principal stratification for causal inference. We illustrate our methods by a study to evaluate the efficacy of the Baltimore Needle Exchange Program to reduce the risk of human immunodeficiency virus (HIV) transmission, using data on distance of the program’s sites from the subjects.

1. INTRODUCTION

We consider studies for evaluating the short-term effect of a treatment of interest on a time-to-event outcome. For practical or ethical reasons, assume that the study design has the following features: (1) Subjects’ exposure to the treatment of interest can be longitudinal, that is, can vary over time, but this exposure is not directly controlled by the study; (2) subjects’ follow-up time is not directly controlled by the study; and (3) the study directly controls another factor that can affect subjects’ exposure to the treatment of interest as well as subjects’ follow-up time.

A motivating example is the needle exchange program (NEP) in Baltimore (ALIVE and NEP studies; Vlahov et al. 1997; Strathdee et al. 1999). In particular, a cohort of injection drug users has been enrolled and is being followed, with regular 6-month visits in which the subjects are offered clinic services, including blood tests for human immunodeficiency virus (HIV; Vlahov et al. 1991). Independently of the clinic, the NEP also operates sites in Baltimore where drug users can visit and exchange a used needle for a clean one (and receive other services such as counseling), with the hope of reducing HIV transmission. Studies for other NEP’s have generally been positive, but some have shown mixed results (Bruneau, Lamothe and Franco 1997; Hagan et al. 2000). However, such studies control neither who exchanges at the NEP nor how long subjects continue the clinic visits, so comparisons of available HIV seroconversion measures between observed exchangers and nonexchangers do not generally estimate the effect of exchange. Importantly, though, the NEP staff does control placement of the NEP sites and, hence, distance of the sites from the subjects. Moreover, there have been earlier indications (e.g., Rockwell, Des Jarlais, Friedman, Rerlis, and Paone 1999) that proximity of drug users to the sites increases needle exchange. Therefore, we wish to formulate explicitly the distance as a controlled factor to provide an alternative evaluation of the NEP’s effect on HIV transmission.

When there is a single partially controlled factor, the structure of studies with features 1 and 3 in general share some aspects with the more standard method of instrumental variables (IV’s) in some earlier studies for other evaluations. For example, Card (1986) used families’ proximity to colleges to evaluate the impact that attending college can have on later income, and McClellan, McNeil, and Newhouse (1994) used elders’ proximity to hospitals to assess whether intensive treatment after myocardial infarction reduces mortality. More recently, there has also been increasing interest in using IV’s to estimate the effects of treatment received in trials where some subjects do not comply with their assigned treatment (e.g., Sommer and Zeger 1991; Robins and Greenland 1994; Baker and Lindeman 1994, 2001; Imbens and Rubin 1994, 1997; Angrist and Imbens 1995; Angrist, Imbens, and Rubin 1996; Baker, Lindeman, and Kramer 2001).

Evaluation of the effect of a treatment on an outcome is more demanding in studies where that treatment as well as other factors, such as observation of the outcome, are only partially controlled. Existing frameworks for time-dependent factors such as those discussed in Robins, Greenland, and Hu (1999); Hernan, Brumback, and Robins (2000), and Murphy et al. (2001) are appropriate for their assumptions and goals. Our framework is fundamentally different from such existing frameworks in terms of the partial control for the factors we consider and in terms of the goals we have (for a comparison of frameworks, see Frangakis and Rubin 2002). In particular, in studies where such partially controlled factors as (1) and (2) given previously can interact, standard methods, including standard IV’s, are not adequate to evaluate the treatment of interest (Frangakis and Rubin 1999). Moreover, in such studies, more flexible methods under more plausible assumptions have been limited to singletime treatments and all-or-none levels of the controlled factor (Frangakis and Rubin 1997, 1999; Baker 1998, 2000).

We propose a framework that evaluates transient (short-term) effects in studies with features 1–3 and that better addresses the limitations of existing methods under certain assumptions. The next section formulates the general framework, the assumptions, the data, and the causal effects that are the estimation goal. Under the general assumptions Section 3 shows identifiability of the causal effects without parametric assumptions in large samples, and Section 4 discusses a class of parametric models and estimation that is appropriate for smaller samples. In Section 5 we demonstrate our methods in the NEP study introduced previously. In Section 6 we discuss the limitations of our method and extensions.

2. FORMULATING THE GENERAL STUDY

2.1 Principal Strata of Exposure and Principal Effects on Outcome

Consider a study that begins follow-up of a cohort of subjects, at discrete time periods t = 1, …, t_max, to investigate a discrete time-to-event outcome. At a certain period t for subject i, define X_i,t to be the indicator such that {i : X_i,t = 1} denotes the subgroup of subjects who are still in the study but have not had the outcome by the end of period t – 1. At the beginning of the next period t, we distinguish between the controlled and uncontrolled factors. At that period, assume each subject i in the risk set {i : X_i,t = 1} can be potentially assigned different levels of a controlled factor D (e.g., distance of clinic from subject), and consider outcomes that can be potentially observed as the controlled factor would take different levels (Neyman 1923; Rubin 1974, 1977, 1978). In particular, if subject i at time t is assigned level d of the controlled factor, then let E_i,t(d) be the potential exposure (e.g., to the needle exchange program) that subject i will have during that period, let Y_i,t(d) be the indicator for whether the event (e.g., HIV positive) will occur during period t or not, and let C_i,t(d) be the indicator for whether t will be the first period the subject will not provide the outcome Y_i,t(d) (in which case we say the person will be censored at t). Also, here we focus on studies with sufficiently many time periods so that the potential values for exposure E at each time t can have one of two levels (0, 1), but where the levels can vary across time. Moreover, we allow the controlled factor D to have one of possibly multiple levels d = 1, …, d_max at each time t. Finally, we let H_i,t denote the observed history variables of the subject up to the beginning of period t, including the past indicators for observed outcomes, censoring, and exposure, past levels of the controlled factor, as well as covariates.

We are interested in defining and estimating the transient effect of the controlled factor D on outcome Y that is attributable to exposure E. We define this effect here as the effect of the factor D on outcome Y for subjects and at times for which the controlled factor D also affects the exposure E; a technical definition is given in Section 2.2. However, the explicitly controlled factor in the study is D, not exposure E, which is possibly also affected by the factor D. Therefore, and adopting Rubin’s (1978) convention that potential outcomes in the study are written as functions only of factors that are explicitly controlled by the researcher, the potential outcome Y, as a function of the controlled factors, is formally a function only of factor D, not of exposure E. For this reason, before we define the causal effects of interest, we define the vector S_i,t of all possible exposures, S_i,t = (E_i,t(1), …, E_i,t(d_max)) that subject i at time t can have at different levels of D. The vector S_i,t is called a principal stratum of exposure, and comparisons of potential outcomes at different levels of the controlled factor D within principal strata S_i,t are called principal effects (Frangakis and Rubin 2002).

Principal strata S_i,t and principal effects have two general properties. First, because the stratum S_i,t is equivalent to the function that describes how exposure is affected by the controlled factor D for subject i at time t, the stratum S_i,t itself is not affected by the controlled factor D for that subject at that time. Second, principal effects are well-defined causal effects of the factor D on outcome Y (Frangakis and Rubin 2002). Principal strata and effects are important because, as we show in Sections 2.2 and 3, they can define the causal effect of the controlled factor D on outcome Y that is attributable to exposure E. We also show that this causal effect is estimable under certain assumptions that can be different from and often more plausible than those of more standard approaches.

By limiting focus on the preceding outcomes for each subject i as functions of the factor D separately at each time t, as opposed to jointly across all times, we treat the observed actual levels of that factor, of exposure, outcome, and censoring up to period t, as components of the history variables H_i,t specific to subject i at time t. We do this because we wish to study the transient effect of D on outcome Y that is attributable to exposure E.

An important example for evaluating transient effects is the NEP study introduced in Section 1, and for which a preliminary formulation using principal stratification is given in Frangakis, Rubin, and Zhou (2002). In this project, the factor that the NEP’s staff controlled was the NEP sites’ locations and, therefore, the distance D_i,t of the closest NEP site at time t from subject i’s residence. (Note: Subjects’ residence was recorded at enrollment but because, subsequently, different NEP sites were placed at different semesters, the distances D_i,t can change over time.) If the closest NEP site is placed at distance d from subject i at semester t, then let E_i,t(d) be the indicator for whether the person will visit and exchange at the NEP during that semester, and which we label for brevity as “exchange”; let Y_i,t(d) be the indicator for whether the subject will become HIV positive during semester t; and let C_i,t(d) 0 if the subject will stay in the study and have the HIV test so = that Y_i,t(d) will be observed. The principal stratum S_i,t = (E_i,t(1), …, E_i,t(d_max)), then, is the vector of all potential exchange behaviors of subject i at time t as a function of the distance of the NEP from the subject at that time. In the NEP distance can affect exchange (E_i,t(d)), outcome (Y_i,t(d)), and censoring (C_i,t(d)). Moreover, the time from HIV infection, for example, because of exposure to an HIV-contaminated needle, until being positive on the HIV antibody test is, for all practical purposes, less than 6 months, which is the unit of time between different measurements of data. For this reason we are interested in the transient effect that distance can have on HIV status and that is attributable to exchange within a semester.

More generally, one can set up the framework to study longterm cumulative effects, although, with partially controlled factors, that would require increasing the notation and structure in the assumptions of the next section. For simplicity, we focus here on transient effects.

2.2 Data, Assumptions, and Goal

Let D_i,t be the actual level of the factor D of subject i during period t, and let E_i,t = E_i,t(D_i,t), Y_i,t = Y_i,t(D_i,t), and C_i,t = C_i,t(D_i,t) be the actual exposure, outcome, and indicator for whether that outcome is censored, respectively, in the study. For the actual outcomes for time to event and censoring in the study, the values Y_i,t = 1 and C_i,t = 1 are absorbing states for the risk set in the sense that if either occurs during period t, then the subject will not be in the risk set {i′ : X_i′,t′ = 1} for t′ > t. Assume, then, that for each subject i we observe the indicator X_i,t for whether the subject is in the risk set, that is, has not had the outcome and has not been censored by the beginning of period t, and, if the subject is in that risk set, then the observed data during period t also include the following: the levels of the factors D_i,t and E_i,t; the censoring indicator C_i,t for the outcome Y_i,t; the outcome Y_i,t if the subject is not censored during period t; and history variables H_i,t, which can include the levels of the factors D_i,t′ and E_i,t′, as well as covariates, for times t′ < t. (Note: The assumption that D_i,t and E_i,t are observed even at the time of possible censoring of the person’s Y_i,t can be relaxed; it is made here because it is true in the NEP example, owing to the different sources supplying information in that study; see Vlahov et al. 1997.)

We consider the subjects i as a random sample from a large population to which we wish to generalize, and assume that the following conditions hold.

1. Sequential Ignorability of Assignment to the Controlled Factor

$$(S_{i,t},\{Y_{i,t}\left(d\right),C_{i,t}\left(d\right),d=1,\dots ,d_{\max }\left\}\right)⫫D_{i,t}\mid H_{i,t},X_{i,t}=1\text{for times}t\ge 1,$$

where Dawid’s (1979) symbol ⫫ denotes independence. The assumption expresses that, among subjects still in the risk set by time t, the study assigns levels D_i,t of the controlled factor at random with probabilities that can depend on the observed history variables H_i,t. Sequential ignorability for a controlled factor has been considered earlier, for example, by Rubin (1978), Robins (1986), Robins et al. (1999), Scharfstein, Rotnitzky, and Robins (1999), and Murphy et al. (2001) but in settings with fundamentally different structure from ours in the degree of control for exposure and censoring behavior.

In the NEP example, where the controlled factor was the distance D_i,t of the closest NEP site from each drug user, within areas of past high risk for HIV transmission, the NEP sites were placed in a nonsystematic way. This makes sequential ignorability more plausible when we include in H_i,t main variables, such as sexual and drug use behavior, that can be confounders with D_i,t in the sense that they cluster in some of Baltimore’s areas. More generally, sequential ignorability is an explicit way to express conditional comparability of subjects at different levels of the controlled factor D.

2. Multilevel Monotonicity of Exposure

We assume that increasing levels of the factor D provide decreasing encouragement for exposure, or, formally, that E_i,t(d^′) ≤ E_i,t(d) if d^′ > d. Multilevel monotonicity is a generalization of the monotonicity assumption of Imbens and Rubin (1994) for a binary controlled factor. For a single partially controlled factor, in particular, with no outcome censoring, the previous assumption was considered by Angrist and Imbens (1995) for estimation of linear models in instrumental variables and by Baker et al. (2001).

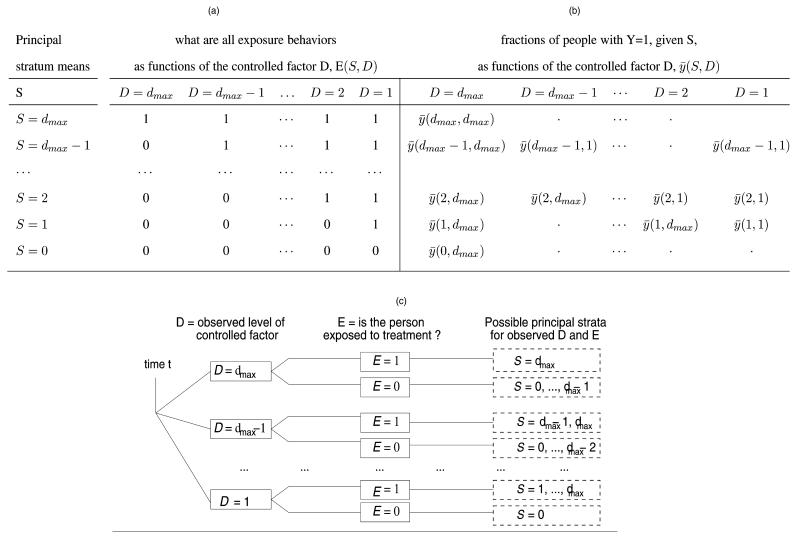
Under multilevel monotonicity in our framework, subject i’s principal stratum S_i,t is one of d_max + 1 levels, say, 0, 1, …, d_max, and is equivalent to the subject-specific threshold (maximum) level that the controlled factor can be, above which subject i at time t would not become exposed to treatment E. This ordered structure is represented in Figure 1(a).

Figure 1. Principal Stratification at a Particular Time (time index is omitted). Relations in (a) follow by multilevel monotonicity, and in (b) by compound exclusion restriction.

In the NEP example monotonicity formally reflects that if a subject at time t is one who would not visit the NEP to exchange needles if the NEP were at a distance d, then the subject would also not visit the NEP to exchange if the NEP were at a longer distance, which is a generally plausible condition (e.g., Rockwell et al. 1999). Moreover, under monotonicity, a statement about the principal stratum S_i,t = (E_i,t(1), …, E_i,t(d_max)) of subject i, that is, about all d_max exposure behaviors of the subject as a function of distance, is equivalent to a statement about the closest distance we can place the NEP beyond which that subject will not exchange needles at it during period t. For this reason we will henceforth be using the notation S_i,t = d, d = 0, …, d_max, for that closest distance to indicate the principal stratum of that subject at that time.

Note that, even under monotonicity, a subject’s principal stratum S_i,t generally is not fully observed and is different from the observed strata defined by (D_i,t, E_i,t). For example, as Figure 1, (a) and (c), shows, subjects who exchange when being at the closest distance from the NEP (D_i,t = 1, E_i,t = 1) are a mixture of all subjects with principal stratum S_i,t ≥ 1.

3. Compound Exclusion Restriction

A subject with E_i,t(d) = E_i,t(d′) at time t is, by definition, someone whose exposure behavior E would be the same if the controlled factor D were set at level d or d′. For this reason we assume that assigning such a subject to either level d or d′ of D would not change the subject’s outcome, Y, or the behavior, C, of censoring of the outcome. That is,

$$\text{if}{E}_{i,t}\left(d\right)=E_{i,t}\left(d^{\prime }\right)\text{then}{Y}_{i,t}\left(d\right)=Y_{i,t}\left(d^{\prime }\right)\text{and}{C}_{i,t}\left(d\right)=C_{i,t}\left(d^{\prime }\right).$$

For a particular time Figure 1(b) displays the pattern that compound exclusion implies for the average, say, $\stackrel{‒}{y}(S,D)$, of the potential outcomes when principal stratum S is at level D of the controlled factor (the time index is omitted); average censoring rates follow an analogous pattern.

Special cases of the preceding compound exclusion restriction have been explored for no censoring, for example, by Imbens and Rubin (1994) and Baker et al. (2001), and with censoring but binary controlled factor, for example, by Frangakis and Rubin (1997, 1999), Baker (1998), and Barnard, Frangakis, Hill, and Rubin (2002).

More generally, the principal strata and compound exclusion restriction help define causal effects of interest. In particular, at time t, for subjects in the two principal strata, S_i,t = 0 and S_i,t = d_max, whose exposure is the same for all levels of the controlled factor D [Fig. 1(a)], there is no causal effect of D on Y [Fig. 1(b)]. For subjects in any one of the remaining principal strata, S_i,t = d, 1 ≤ d ≤ d_max − 1, consider the comparison between two proportions: the proportion of subjects who get the event if assigned D = 1 versus the proportion of subjects who get the event if assigned D = d_max, that is,

$$\begin{array}{cc}\hfill & \mathrm{pr}\left(Y_{i,t}\right(1)=1\mid H_{i,t},X_{i,t}=1,S_{i,t}=d)\hfill \\ \hfill & \text{versus}\hfill \\ \hfill & \mathrm{pr}\left(Y_{i,t}\right(d_{\max })=1\mid H_{i,t},X_{i,t}=1,S_{i,t}=d).\hfill \end{array}$$ (2.1)

Such comparisons of potential outcomes within principal strata, called principal effects, date back at least to Imbens and Rubin (1994) for randomized studies with noncompliance, and were formulated by Frangakis and Rubin (2002) to principal strata for general partially controlled variables. Before the general definition of such estimands, standard definitions of treatment effects in settings with both a controlled and a partially controlled factor were comparisons between populations of different groups of subjects (“net-treatment effects,” e.g., Cochran 1957; Rosenbaum 1983), and so were not generally causal effects (see, for example, Rosenbaum 1983; Frangakis and Rubin 2002). The importance of principal effects in (2.1) is that both proportions in (2.1) are conditional on the same group of subjects, so that their comparison is a well-defined causal effect (Frangakis and Rubin 2002). Moreover, every subject in the top expression of (2.1) gets exposure to treatment E, whereas no subject in the bottom expression of (2.1) gets exposure to treatment E [Fig. 1, (a) and (b), for S_i,t = 1, …, d_max − 1]. Therefore, a principal effect of the form (2.1) better quantifies an effect of the controlled factor D on outcome Y that is attributable to exposure E. For this reason we set (2.1) to be our main goal for estimation.

In the NEP compound exclusion means that two different distances of the NEP location from a specific subject might result in different HIV status Y or censoring of that status (e.g., by discontinuation of follow-up), but only if those two distances would result in different needle exchange (and visiting) behavior at the NEP, an assumption that is expected to be approximately true. In this case a principal effect of the form (2.1) quantifies an effect that distance from the NEP can have on HIV transmission and that is attributable to exchange of needles at the NEP. This effect is of main interest in the application.

4. Latent Ignorability of the Censoring Mechanism

Because the principal stratum S_i,t is a characteristic of the subject, effectively representing the willingness to become exposed to treatment, S_i,t can be associated with both the potential outcome and the censoring of the outcome. In the NEP example that would mean that subjects willing to exchange at different distances can have different risk for HIV and/or different willingness to stay in the study. More generally, then, if we knew the principal stratum S_i,t for all subjects, we should first stratify subjects by it, before connecting outcomes of censored subjects (i.e., without measured outcomes) to uncensored subjects (i.e., with measured outcomes). An assumption that formalizes this is

$$Y_{i,t}\left(d\right)⫫C_{i,t}\left(d\right)\mid D_{i,t},H_{i,t},X_{i,t}=1,\text{and}{S}_{i,t}$$

for times t ≥ 1 and each level d of the controlled factor. (Note: By definition, observed exposure E_i,t is a function of D_i,t and S_i,t, so the right side of the previous expression also includes E_i,t.) The preceding assumption extends the latent ignorability for single time points introduced by Frangakis and Rubin (1999) for randomized trials with noncompliance.

Because neither exposure nor censoring is controlled, of course, any set of assumptions, including the previous four, is not guaranteed to be absolutely correct. Therefore, the set of assumptions is best judged not by whether it is certain to be absolutely correct, but in comparison to other existing approaches, on the inferences and the sensitivity analyses it can produce for estimating the effects (2.1). Specifically, a framework that allows the more general condition, “A” = “the mechanism of censoring C can depend on the latent principal stratum S,” is richer and so can produce (a) inferences for (2.1) that are better than inferences that do not allow “A” and (b) sensitivity analyses around inferences that allow “A” and, thus, are more informative than sensitivity analyses around inferences that do not allow “A” (for a related discussion, see Frangakis and Rubin 1999, sec. 4.2). To our knowledge, the framework using latent ignorability is the first in this longitudinal setting that both allows “A” and also allows identifiability of the causal effects (2.1), as discussed in the next section. In Section 4 we discuss parametric models for our set of assumptions, although study of sensitivity to models around those assumptions and alternative assumptions that would allow “A” is also of interest.

3. IDENTIFIABILITY OF PRINCIPAL CAUSAL EFFECTS

We show that, under the assumptions of the previous section, the probabilities in (2.1), and, hence, comparisons among them, are identifiable with no parametric assumptions. Without loss of generality, for this section, suppose we are already within an observed stratum of the subjects at risk at the beginning of a specific period t and already within an observed stratum defined by history H_i,t. The first three of the following six expressions define the notation for the proportions of principal strata, of no censoring, and of positive outcome within principal strata and when the subjects get assigned D = d. The last three expressions define the notation for the directly estimable proportions of observed exposure within strata D = d, of no censoring within strata D = d and exposure E = e, and of positive outcome within strata (D = d, E = e) and among uncensored subjects (C = 0),

$$\begin{array}{cc}\hfill \stackrel{‒}{s}\left(d\right)& ≔\mathrm{pr}(S_i=d),\hfill \\ \hfill \stackrel{‒}{c}(d^{\prime },d)& ≔\mathrm{pr}\left(C_i\right(d)=0\mid S_i=d^{\prime }),\hfill \\ \hfill \stackrel{‒}{y}(d^{\prime },d)& ≔\mathrm{pr}\left(Y_i\right(d)=1\mid S_i=d^{\prime }),\hfill \\ \hfill {\stackrel{‒}{e}}^{\mathrm{obs}}\left(d\right)& ≔\mathrm{pr}(E_i=1\mid D_i=d),\hfill \\ \hfill {\stackrel{‒}{c}}^{\mathrm{obs}}(e,d)& ≔\mathrm{pr}(C_i=0\mid D_i=d,E_i=e),\hfill \\ \hfill {\stackrel{‒}{y}}^{\mathrm{obs}}(e,d)& ≔\mathrm{pr}(Y_i=1\mid D_i=d,E_i=e,C_i=0),\hfill \end{array}$$

where the indexing for time t is omitted. Assuming the probabilities in the first two lines are in (0, 1), we derive the probabilities in the left column as a function of those in the right column.

Proportions of Principal Strata

Note that the observed stratum (D = d_max, E = 1) contains only the principal stratum S = d_max. By multilevel monotonicity an observed stratum (D = d, E = 1) of exposed subjects at level D = d is the mixture [Fig. 1, (a) and (c)] of the principal strata, S = d, …, d_max,

$${\stackrel{‒}{e}}^{\mathrm{obs}}\left(d_{\max }\right)=\stackrel{‒}{s}\left(d_{\max }\right),{\stackrel{‒}{e}}^{\mathrm{obs}}\left(d\right)=\stackrel{‒}{s}\left(d_{\max }\right)+\dots +\stackrel{‒}{s}\left(d\right),$$

and so

$$\stackrel{‒}{s}\left(d\right)={\stackrel{‒}{e}}^{\mathrm{obs}}\left(d\right)-{\stackrel{‒}{e}}^{\mathrm{obs}}(d+1).$$

Proportions of Uncensored Subjects Within Principal Strata

Because the observed stratum (D = d_max, E = 1) contains only subjects with S = d_max, we have that ${\stackrel{‒}{c}}^{\mathrm{obs}}(1,d_{\max })=\stackrel{‒}{c}(d_{\max },d_{\max })$, which equals $\stackrel{‒}{c}(d_{\max },1)$ by compound exclusion. The noncensoring proportions in the remaining observed strata (D = d, E = 1), for 1 ≤ d ≤ d_max − 1, are mixtures across principal strata. Let ${\stackrel{‒}{s}}_{(+)}\left(d\right)=\stackrel{‒}{s}\left(d\right)+\dots +\stackrel{‒}{s}\left(d_{\max }\right)$. Then

$$\begin{array}{cc}\hfill {\stackrel{‒}{c}}^{\mathrm{obs}}(1,d)& =\frac{\stackrel{‒}{s}\left(d_{\max }\right)\stackrel{‒}{c}(d_{\max },d)+\dots +\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,d)}{{\stackrel{‒}{s}}_{(+)}\left(d\right)}\hfill \\ \hfill & =\frac{\stackrel{‒}{s}\left(d_{\max }\right)\stackrel{‒}{c}(d_{\max },1)+\dots +\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,1)}{{\stackrel{‒}{s}}_{(+)}\left(d\right)},\hfill \end{array}$$

where the last equality follows by compound exclusion. Considering the last equality for d + 1 and using induction in the numerators, we get

$$\stackrel{‒}{c}(d,1)=\frac{{\stackrel{‒}{s}}_{(+)}\left(d\right){\stackrel{‒}{c}}^{\mathrm{obs}}(1,d)-{\stackrel{‒}{s}}_{(+)}(d+1){\stackrel{‒}{c}}^{\mathrm{obs}}(1,d+1)}{\stackrel{‒}{s}\left(d\right)}.$$

Working similarly with induction for strata (D = d, E = 0), we obtain that $\stackrel{‒}{c}(0,d_{\max })={\stackrel{‒}{c}}^{\mathrm{obs}}(0,1)$, and, for the remaining principal strata S = d, for 1 ≤ d ≤ d_max − 1, that

$$\stackrel{‒}{c}(d,d_{\max })=\frac{\{1-{\stackrel{‒}{s}}_{(+)}(d+1\left)\right\}{\stackrel{‒}{c}}^{\mathrm{obs}}(0,d+1)-\{1-{\stackrel{‒}{s}}_{(+)}(d\left)\right\}{\stackrel{‒}{c}}^{\mathrm{obs}}(0,d)}{\stackrel{‒}{s}\left(d\right)}.$$

Proportions of Potential Outcomes Within Principal Strata

As with censoring rates, because the observed stratum (D = d_max, E = 1) contains only the principal stratum S = d_max, we have ${\stackrel{‒}{y}}^{\mathrm{obs}}(1,d_{\max })=\stackrel{‒}{y}(d_{\max },d_{\max })=\stackrel{‒}{y}(d_{\max },1)$, where the first equality follows by latent ignorability, and the second by compound exclusion. For the remaining observed strata (D = d, E = 1), 1 ≤ d ≤ d_max − 1, the proportion for the outcome that is observable, ${\stackrel{‒}{y}}^{\mathrm{obs}}(1,d)$, is a mixture over principal strata S:

$${\stackrel{‒}{y}}^{\mathrm{obs}}(1,d)=E\left\{E\right(Y=1\mid D=d,E=1,S)\mid D=d,E=1,C=0\},$$

where, in the inner expectation, C = 0 is canceled by latent ignorability. After some algebra the previous expression can be written as

$${\stackrel{‒}{y}}^{\mathrm{obs}}(1,d)=\frac{\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,1)\stackrel{‒}{y}(d,1)+\dots +\stackrel{‒}{s}\left(d_{\max }\right)\stackrel{‒}{c}(d_{\max },1)\stackrel{‒}{y}(d_{\max },1)}{\stackrel{‒}{c}+\left(d\right)},$$

where ${\stackrel{‒}{c}}_{+}\left(d\right)=\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,1)+\dots +\stackrel{‒}{s}\left(d_{\max }\right)\stackrel{‒}{c}(d_{\max },1)$. By considering the preceding expression also for d + 1 and using induction, we obtain the outcome proportion within principal strata as a function of quantities that we have already shown are estimable:

$$\stackrel{‒}{y}(d,1)=\frac{{\stackrel{‒}{c}}_{+}\left(d\right){\stackrel{‒}{y}}^{\mathrm{obs}}(1,d)-{\stackrel{‒}{c}}_{+}(d+1){\stackrel{‒}{y}}^{\mathrm{obs}}(1,d+1)}{\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,1)}.$$ (3.1)

With an analogous argument, with induction for the outcome probability on the strata (D = d, E = 0), we obtain that $\stackrel{‒}{y}(0,d_{\max })={\stackrel{‒}{y}}^{\mathrm{obs}}(0,1)$, and, for the remaining principal strata S = d, for 1 ≤ d ≤ d_max − 1, that

$$\stackrel{‒}{y}(d,d_{\max })=\frac{{\stackrel{‒}{c}}_{(-)}(d+1){\stackrel{‒}{y}}^{\mathrm{obs}}(0,d+1)-{\stackrel{‒}{c}}_{(-)}\left(d\right){\stackrel{‒}{y}}^{\mathrm{obs}(0,d)}}{\stackrel{‒}{s}\left(d\right)\stackrel{‒}{c}(d,d_{\max })},$$ (3.2)

where ${\stackrel{‒}{c}}_{(-)}\left(d\right)=\stackrel{‒}{s}\left(0\right)\stackrel{‒}{c}(0,d_{\max })+\dots +\stackrel{‒}{s}(d-1)\stackrel{‒}{c}(d-1,d_{\max })$. Expressions (3.1) and (3.2) establish identifiability, using observed data, of the outcome probabilities within principal strata and, therefore, identifiability of the principal causal effects (2.1).

There are two more general notes regarding the principal effects. First, note that their expressions (3.1) and (3.2) involve the censoring mechanism $\stackrel{‒}{c}(d^{\prime },d)$ (estimable as shown earlier), which, therefore, is not ignorable in the sense of Rubin (1976). Second, we can write (3.1) and (3.2) as

$$\begin{array}{cc}\hfill \stackrel{‒}{y}(d,1)& =\frac{\frac{\delta }{\delta \left(d\right)}{\stackrel{‒}{c}}_{(+)}\left(d\right){\stackrel{‒}{y}}^{\mathrm{obs}}(1,d)}{\frac{\delta }{\delta \left(d\right)}{\stackrel{‒}{c}}_{(+)}\left(d\right)},\hfill \\ \hfill \stackrel{‒}{y}(d,d_{\max })& =\frac{\frac{\delta }{\delta \left(d\right)}{\stackrel{‒}{c}}_{(-)}\left(d\right){\stackrel{‒}{y}}^{\mathrm{obs}}(0,d)}{\frac{\delta }{\delta \left(d\right)}{\stackrel{‒}{c}}_{(-)}\left(d\right)},\hfill \end{array}$$ (3.3)

where δ/δ(d) denotes the finite-difference derivative with respect to d. The last two expressions, although ratios of differences, are not those used in standard IV models with additive error terms (e.g., Wald 1940; Bowden and Turkington 1984). Therefore, the causal effects (2.1) are identifiable as before, but not using IV’s.

4. ESTIMATION USING PARAMETRIC MODELS

Expressions (3.3) are useful for establishing identifiability of the causal effects without parametric assumptions in large samples at any time period and given past history, but are not directly useful for practical estimation of the effects with many time periods and with continuous covariates. In such cases parametric models can smooth the relation between the variables across the many strata.

A useful class of parametric models is obtained when we place models on the distributions in the left column of the expression at the beginning of Section 3, which are of direct interest. Allowing now, explicitly, dependence on time and past covariates, we can model the distribution of the ordinal principal strata by the proportional odds model, where

$$\mathrm{logit}\mathrm{pr}(S_{i,t}\ge d\mid H_{i,t}=h,X_{i,t}=1,{\beta }^{\left(S\right)})={\beta }_{\left(d\right)}^{\left(S\right)}+{\text{link}}^{\left(S\right)}(h,t){\beta }_{\left(h\right)}^{\left(S\right)},$$ (4.1)

where link^(S)(h, t) is a link function, ${\beta }_{\left(d\right)}^{\left(S\right)}\ge {\beta }_{\left(d^{\prime }\right)}^{\left(S\right)}$ for 1 ≤ d < d′ ≤ d_max, logit(·) = log(·/(1 − ·)), and where the probability for S_i,t = 0 is determined by the previous ones.

We can model the target probability of the event Y = 1 in (2.1) and the analogous probability of censoring C = 1 of that event as functions of the factor D and given principal strata, respectively, by the logistic models:

$$\mathrm{logit}\mathrm{pr}\left(Y_{i,t}\right(d)=1\mid H_{i,t}=h,X_{i,t}=1,S_{i,t}=d^{\prime },{\beta }^{\left(Y\right)})={\text{link}}^{\left(Y\right)}(d,d^{\prime },h,t){\beta }^{\left(Y\right)},$$ (4.2)

$$\mathrm{logit}\mathrm{pr}\left(C_{i,t}\right(d)=1\mid H_{i,t}=h,X_{i,t}=1,S_{i,t}=d^{\prime },{\beta }^{\left(C\right)})={\text{link}}^{\left(C\right)}(d,d^{\prime },h,t){\beta }^{\left(C\right)},$$ (4.3)

where we require that link^(Y)(d, d′, h, t) and link^(C)(d, d′, h, t) be functions that satisfy the implications of the compound exclusion restriction in the population. An example is the function link^(Y) (d, d′, h, t) = link^(C)(d, d′, h, t) = [1, h, t, d′, E_(S,D)(d′, d)], where E_(S,D)(d′, d) is the matrix of Figure 1(a), with (d′, d) entry equal to the exposure that principal stratum d′ has when assigned level d of the factor D. Moreover, the parameters β^(S), β^(Y), and β^(Y) can be tied together by additional plausible conditions, if warranted, to increase precision of estimation.

Using models (4.1)–(4.3), and noting that the actual exposure data E_i,t are functions of the person’s principal stratum S_i,t and the factor level D_i,t, we can obtain the likelihood of observing the data of person i at period t as if these data also included the current principal stratum S_i,t = d′, and conditionally on the risk set X_i,t = 1, history H_i,t = h, and level D_i,t = d, as

$$l(d^{\prime },d,y,c,h,t;\beta )≔\mathrm{pr}(S_{i,t}=d^{\prime }\mid H_{i,t}=h,X_{i,t}=1,{\beta }^{\left(S\right)})\times {\left\{\mathrm{pr}\right(Y_{i,t}\left(d\right)=y\mid H_{i,t}=h,X_{i,t}=1,S_{i,t}=d^{\prime },{\beta }^{\left(Y\right)}\left)\right\}}^{(1-c)}\times \mathrm{pr}\left(C_{i,t}\right(d)=c\mid H_{i,t}=h,X_{i,t}=1,S_{i,t}=d^{\prime },{\beta }^{\left(C\right)}),$$

where the last product follows by latent ignorability and where β := (β^(S), β^(Y), β^(C)). Now let $\mathcal{S}(D_{i,t},E_{i,t})$ be the set of possible principal strata that subject i can belong to at time t, as a function of the observed factor level D_i,t and observed exposure E_i,t; that is, $\mathcal{S}(D_{i,t},E_{i,t})=\{d:d\ge D_{i,t}\}$ if E_i,t = 1, and $\mathcal{S}(D_{i,t},E_{i,t})=\{d:d<D_{i,t}\}$ if E_i,t = 0 [Fig. 1(c)]. Then, using the previous likelihood function, we can obtain a partial likelihood function L(β) as the product of the likelihood of observed data over all subjects in the risk set at period t, and over all periods t, as

$$L\left(\beta \right)=\prod _t\prod _{i:X_{i,t}=1}\sum _{s\in \mathcal{S}(D_{i,t},E_{i,t})}l(s,D_{i,t},Y_{i,t},R_{i,t},X_{i,t},t;\beta ).$$

The function L(β) is a partial likelihood, not in the usual sense of Cox’s (Cox and Oakes 1984) partial likelihood, but in the sense that L(β) omits the distributions of the variables in H_i,t that are not past observed outcome, censoring, or exposure indicators. Nevertheless, as with partial likelihood in other settings (e.g., Cox and Oakes 1984; Robins et al. 1999), the estimator that maximizes L(β) enjoys properties analogous to those of the usual maximum likelihood estimators (MLE’s), in the sense that, in large samples, its distribution is approximately normal, centered around the true parameter vector, and with variance estimated consistently by the inverse of the negative second derivative of log L(β), evaluated at the MLE. Then a comparison between the probabilities in (2.1) can be estimated by expressing them in terms of the models (4.2) and estimating them by the MLE.

We have developed a program for maximizing L(β) for general levels of principal strata S and periods t, using an EM algorithm (Dempster, Laird, and Rubin 1977) that treats the partially observed principal strata as incomplete data. The Hessian matrix is obtained numerically at the MLE. The program was checked using limited preliminary simulations and is available from the authors.

5. EXAMPLE ON NEEDLE EXCHANGE

We return to the NEP study, introduced in Section 1, and the goal is to evaluate the NEP’s impact on HIV seroconversion. In Section 5.2 we present an evaluation based on a standard method, and in Section 5.3, an evaluation based on the new method. First, we discuss some additional background.

5.1 Background

The cohort in this evaluation consists of the 1,170 subjects who were HIV negative in 1994 and for whom residence information was available at that time. Since then, the average follow-up was 9 semesters, during which time 54 subjects tested HIV positive (5 per 1,000 person-semesters), and the overall rate of subjects’ needle exchange visits was 14 per 100 personsemesters. In addition, before starting to place NEP sites in 1994, the NEP staff requested a set of 25 baseline covariates for each subject in the study, measuring various aspects of sexual and drug use behaviors. Directly fitting all these covariates in a model (4.1)–(4.3) is not possible, because many covariate values were missing across subjects, and also because of the proportionally small number of HIV cases.

To address the missing values for the covariates only, but to limit further complexity, we used multiple imputation (Rubin 1987, 1996). Specifically, we fitted a standard Bayesian general location model on the contingency table of the discrete covariates and on the continuous covariates conditionally on that contingency table, assuming missing covariate values are missing at random and fitting all the second-order interactions, using software by Schafer (1998). We ran five independent dataaugmentation chains, and, after they mixed, as judged by the potential scale reduction criterion (Gelman and Rubin 1992), the covariate missing values were imputed from their joint posterior predictive distribution conditionally on the observed covariate values, giving five complete-data covariate matrices. Each such matrix was then matched to the data matrix for the longitudinal distance D, exchange E, HIV status Y, and censoring C of Y, creating five sets of data, each of whose structure is as described in the first paragraph of Section 2.2. Each of the five datasets was analyzed as described in Sections 4 and 5, and the analyses were combined at the end by the general multiple imputation rules (Rubin 1987).

To handle the small number of HIV cases up to the calendar time of this analysis, we had to limit distance levels to two, d_max for more than 3 miles (far) and d = 1 for 3 miles or less (close) of the NEP from each subject. To address the multitude of covariates, after the imputations described previously, we transformed them into their principal components. The first component, as expected, gave positive weights to those levels of the covariates that were positive on risky sexual and drug use behaviors. For this reason, we used the first principal component of subject i, denoted by B_i, as a summary index of an observed baseline risk behavior for HIV transmission in our models. The uncertainty in the final results was almost entirely from within imputations, which suggests that results are robust to the preceding preparatory computations.

5.2 Evaluation With Observed Stratification

Table 1 gives direct estimates of the percentage of at-risk of subjects who exchange at the NEP, that is, who visit an NEP at least once in the semester, stratified by whether the NEP is far or close to them, and stratified by whether their baseline risk score B is above or below its median, m_B. These descriptive measures show that subjects with high observed baseline risk exchange considerably more than the others. Moreover, subjects closer to the NEP also exchange more frequently than subjects farther from the NEP, a result that confirms an earlier finding by Rockwell et al. (1999).

Table 1. Percentage (%) of Subjects Exchanging at the NEP as a Function of Distance From the NEP, at Each Semester, and Stratified by Above (high) and Below (low) the Median Baseline Risk Score.

	Semester (t)
Distance (D)	1	2	3	4	5	6	7	8	9	10	11	12	Average
	(a) For subjects with low baseline risk score:
Far	4	5	6	6	6	5	6	4	6	5	7	2	5
Close	8	7	7	8	7	12	12	11	13	13	12	9	10
	(b) For subjects with high baseline risk score:
Far	16	18	21	19	18	16	14	14	12	14	7	5	14
Close	24	24	24	19	18	19	19	20	21	21	20	16	20

To quantify these relations while also modeling past exchange, for subjects concurrently at the risk set, we fit the model

$$\mathrm{logit}\mathrm{pr}(E_{i,t}=1\mid D_{i,t},H_{i,t},X_{i,t}=1)={\alpha }_t^{\left(E\right)}+{[D_{i,t}\cdot 1(B_i<m_B),D_{i,t}\cdot 1(B_i\ge m_B),B_i,E_{i,t-1},D_{i,t-1}]}^{\prime }{\alpha }^{\left(E\right)}$$

by conditional logistic regression using its partial likelihood. In this and later models, the baseline risk score and first past lags of exchange and distance are included in the model as history variables to make the strata more comparable in past behaviors. With this model we obtain that, for subjects with low baseline risk, there is a 2.2 odds ratio for exchanging at close compared to far distance from the NEP (95% CI: 1.64, 2.96), and for subjects with high baseline risk, these odds are 1.70 (95% CI: 1.29, 2.41). Moreover, within a given distance D_i,t, there is a 9% increase (95% CI: 5%, 13%) in the odds of exchanging needles associated with an increase of 1 standard deviation in the baseline risk B. In addition, the odds of exchanging were 26-fold higher (95% CI: 22, 29) for subjects who exchanged during the previous period compared to those who did not, given distance and baseline risk score.

For a standard approach to HIV seroconversion, we fitted the discrete survival model

$$\mathrm{logit}\mathrm{pr}(Y_{i,t}=1\mid E_{i,t},D_{i,t},H_{i,t},X_{i,t}=1)={\alpha }_t^{\left(Y\right)}+{\alpha }_{\left(e\right)}^{\left(Y\right)}{E}_{i,t}+{\alpha }_{\left(d\right)}^{\left(Y\right)}{D}_{i,t}+{\alpha }_{\left(b\right)}^{\left(Y\right)}{B}_i+{\alpha }_{(e-)}^{\left(Y\right)}{E}_{i,t-1}+{\alpha }_{(d-)}^{\left(Y\right)}{D}_{i,t-1}.$$

The two main results of interest from this approach are shown in Table 2. In particular, as would be expected, a higher baseline risk score B predicts more HIV seroconversion [Table 2(a)]. Moreover, conditionally on the other variables in that model, observed exchangers have 32% lower odds of HIV seroconversion than observed nonexchangers, although this result is not statistically significant (OR = .68; 95% CI: .26, 1.77).

Table 2. Results From the Standard Stratification Model of Section 5.2 on Exchanging Needles at the NEP and HIV Seroconversion.

Estimand	Estimate	95% CI
(a) Odds ratio of HIV seroconversion for   1 standard deviation increase in base-   line risk score B: $\exp \left({\alpha }_{\left(b\right)}^{\left(Y\right)}\right)$	1.17	(1.05, 1.30)
(b) Odds ratio of HIV seroconversion for   comparing exchangers versus nonex-   changers, given fixed baseline risk   score B: $\exp \left({\alpha }_{\left(e\right)}^{\left(Y\right)}\right)$	.68	(.26, 1.77)

The relatively wide uncertainty about the preceding difference is likely a result of the low overall seroconversion in the cohort. Moreover, for $\exp \left({\alpha }_{\left(e\right)}^{\left(Y\right)}\right)$ in this approach to have interpretation of causal effect as the odds ratio of HIV seroconversion attributable to exchange, three assumptions must hold: (1) Exchange can only affect HIV seroconversion in the same period; (2) given D_i,t, H_i,t, and X_i,t = 1, observed exchangers and nonexchangers are comparable in=their potential outcomes of HIV seroconversion; and (3) given D_i,t, H_i,t, and X_i,t = 1, subjects at a time t who provide the outcome Y are comparable with subjects who do not provide the outcome. The first assumption is physiologically appropriate, and we assume it also in the framework of principal stratification. However, the second and third assumptions are not necessarily plausible because, given D_i,t, H_i,t, and X_i,t = 1, exchangers and nonex-changers are different mixtures of principal strata [Fig. 1(c)]. For these reasons we also evaluated the NEP using principal stratification.

5.3 Evaluation With Principal Stratification

We now set our goal to estimate the causal effect of distance on HIV seroconversion that is the odds ratio comparison (2.1), that is, that is attributable to exchanging versus not exchanging needles, using principal stratification. To do so, we fitted the model described in Section 4. To have the structure of history variables comparable to that of the standard model, we fitted the same history vector, that is, the baseline riskscore, the past exchange status, and the past distance from the NEP, H_i,t = (B_i, E_i,t−1, D_i,t−1). To have the models for outcome and censoring satisfy the compound exclusion restriction, we fitted the link function introduced in Section 4. In particular, we parameterize links (4.1)–(4.3) as

$${\text{link}}^{\left(S\right)}(H_{i,t},t){\beta }_{\left(h\right)}^{\left(S\right)}≔{\beta }_{\left(b\right)}^{\left(S\right)}{B}_i+{\beta }_{(e-)}^{\left(S\right)}{E}_{i,t-1}+{\beta }_{(d-)}^{\left(S\right)}{D}_{i,t-1}+{\beta }_{\left(t\right)}^{\left(S\right)}t,$$ (5.1)

$${\text{link}}^{\left(Y\right)}(D_{i,t},S_{i,t},H_{i,t},t){\beta }^{\left(Y\right)}≔{\beta }_{\left(0\right)}^{\left(Y\right)}+{\beta }_{\left(b\right)}^{\left(Y\right)}{B}_i+{\beta }_{(e-)}^{\left(Y\right)}{E}_{i,t-1}+{\beta }_{(d-)}^{\left(Y\right)}{D}_{i,t-1}+{\beta }_{\left(t\right)}^{\left(Y\right)}t+{\beta }_{\left(s\right)}^{\left(Y\right)}{S}_{i,t}+{\beta }_{(s,d)}^{\left(Y\right)}{E}_{(S,D)}(S_{i,t},D_{i,t}),$$ (5.2)

$${\text{link}}^{\left(C\right)}(D_{i,t},S_{i,t},H_{i,t},t){\beta }^{\left(C\right)}≔{\beta }_{\left(0\right)}^{\left(C\right)}+{\beta }_{\left(b\right)}^{\left(C\right)}{B}_i+{\beta }_{(e-)}^{\left(C\right)}{\mathrm{E}}_{i,t-1}+{\beta }_{(d-)}^{\left(C\right)}{D}_{i,t-1}+{\beta }_{\left(t\right)}^{\left(C\right)}t+{\beta }_{\left(s\right)}^{\left(C\right)}{S}_{i,t}+{\beta }_{(s,d)}^{\left(C\right)}{\mathrm{E}}_{(S,D)}(S_{i,t},D_{i,t}).$$ (5.3)

With the parameterization (4.2) and (5.2), the causal effect that is the odds ratio between the top and bottom probabilities in (2.1) for principal strata S_i,t = d, 1 ≤ d ≤ d_max − 1, is equal to $\exp \left[{\beta }_{(s,d)}^{\left(Y\right)}\right\{{\mathrm{E}}_{(S,D)}(d,1)-{\mathrm{E}}_{(S,D)}(d,d_{\max })\left\}\right]$, which, by multilevel monotonicity [Fig. 1(a)], equals $\exp \left\{{\beta }_{(s,d)}^{\left(Y\right)}\right(1-0\left)\right\}=\exp \left({\beta }_{(s,d)}^{\left(Y\right)}\right)$. Estimation, then, of this odds ratio causal effect can follow fromjoint estimation of the principal stratificationmodel (5.1)–(5.3).

Fitting this model without further assumptions gives an estimated causal effect of 89% reduction in the odds of HIV attributable to exchange, or OR = .11, with a wide CI of (.002, 7.99). This means that, although, as shown in Section 3, the causal effect is theoretically estimable without further assumptions, and here is estimated substantially larger than in the standard method, some plausible additional structure is required to increase precision.

Because the principal stratification model accounts for any unmeasured risk for HIV between exchangers and nonexchangers, the 89% estimated reduction with this method compared to the 32% reduction with the standard method [Table 2(b)] suggests the hypothesis H_mis|obs = “even after adjusting for the observed baseline risk factors, exchangers were at higher, thus unmeasured, risk for HIV than nonexchangers, independently of the act of exchange and of their distance from the NEP.” Moreover, Table 2(a) [and comparison between Table 1, (a) and (b)] supports the hypothesis H_obs = “exchangers were at higher risk for HIV in the observed baseline factors compared to nonexchangers.” By recalling that the principal stratum is the subjectspecific unmeasured threshold distance for not exchanging, we can formalize the hypothesis that H_obs and H_mis|obs are either both true or both false using our model, by

$${\beta }_{\left(b\right)}^{\left(S\right)}\cdot {\beta }_{\left(s\right)}^{\left(Y\right)}\ge 0.$$

This condition still allows the standard assumption, that all confounders are measured, as a special case, but also allows for the possibility of some types of unmeasured confounding. Substantively in the NEP, (5.4) allows that in the variables H_i,t we may not have measured the baseline sexual and drug risk behaviors in sufficient detail (e.g., due to underreporting), and, as a result, observed exchangers and nonexchangers may not be comparable in their risk for HIV seroconversion given H_i,t and independently of exchange. Put another way, (5.4) means that we allow unmeasured confounding, but that it would be implausible if the unmeasured association in hypothesis H_mis|obs, after measuring 25 relevant baseline covariates, carries the opposite message from that of the measured association in H_obs about exchangers being at higher (or lower) risk than nonexchangers. Mathematically, (5.4) is not forced to be true or false in our general assumptions in Section 2 and so, by Section 3, (5.4) is testable in our framework. In the earlier fit of the model without constraint (5.4), we obtained estimates for ${\beta }_{\left(b\right)}^{\left(S\right)}$ and ${\beta }_{\left(s\right)}^{\left(Y\right)}$ equal to .14 and 1.07, respectively, and so the estimate for ${\beta }_{\left(b\right)}^{\left(S\right)}\cdot {\beta }_{\left(s\right)}^{\left(Y\right)}$ equals .15 > 0. Therefore, our data can provide no evidence against (5.4) and, so we take our model to be (5.1)–(5.4).

To obtain inference for this model, the MLE’s of L(β) remain unchanged because they satisfy (5.4). To incorporate the implications of (5.4) on the uncertainty about the causal effect $\exp \left({\beta }_{(s,d)}^{\left(Y\right)}\right)$, we take the ellipsoidal three-dimensional joint 95% confidence region R′ for ${\beta }_{(s,d)}^{\left(Y\right)}$ and the two estimands, ${\beta }_{\left(b\right)}^{\left(S\right)}$ and ${\beta }_{\left(s\right)}^{\left(Y\right)}$, involved in (5.4), and find the subset R of R′ that satisfies (5.4). The resulting region R, then, is a 95% joint confidence region for the three estimands.

These results are given in Table 3. The estimated effect of the NEP that is attributable to exchanging versus not exchanging needles is a reduction by 89% in HIV seroconversion, as in the fit of this model without (5.4). The point estimate, thus, means that the data point to a larger benefit of the NEP, compared to the standard method. The uncertainty about the effect (OR = .11, 95% joint CR: .00, 2.23) is larger than that of the standard = approach [Table 2(b)]. This wider uncertainty fairly reflects that the new method accounts for possible confounding remaining in the standard approach because exchangers and nonexchangers are different mixtures of the partially unmeasured principal strata.

Table 3. Results From the Principal Stratification Model of Section 5.3 on Exchanging Needles at the NEP and on HIV Seroconversion.

Estimand	Estimate	95% CR b
(a) Odds ratio of higher versus lower   principal stratumaS for 1 standard   deviation increase in baseline risk   score B: $\exp \left({\beta }_{\left(b\right)}^{\left(S\right)}\right)$	1.15	(1.11, 1.20)
(b) Odds of HIV seroconversion under   fixed exchange for higher versus   lower principal stratumaS, given fixed   baseline risk score B: $\exp \left({\beta }_{\left(s\right)}^{\left(Y\right)}\right)$	2.92	(.99, 96.36)
(c) Odds ratio of HIV seroconversion   for close versus far distance from   the NEP and attributable to needle   exchangec: $\exp \left({\beta }_{(s,d)}^{\left(Y\right)}\right)$	.11	(.0003, 2.23)

^aA subject’s principal stratum is the closest distance to place the NEP beyond which that subject would not exchange at it.

^bJoint confidence region.

^cConditionally on baseline risk score B and principal stratum S.

6. DISCUSSION

We proposed a method based on principal stratification for evaluating studies where (1) subjects take a longitudinal treatment, whose transient effect on a time-to-event outcome is of interest, but where this treatment is not directly controlled; (2) the subject’s follow-up time is not directly controlled; and (3) the study directly controls another longitudinal factor that can affect both exposure to the treatment of interest as well as follow-up time. The new method based on principal strata has three advantages over existing methods. First, the method based on principal strata can better address studies with coexistence of partially controlled factors such as exposure and censoring of outcomes. Second, the method of instrumental variables is, in principle, based on estimation of coefficients in additive equations with error terms, and so can only estimate causal effects that happen to be expressible in terms of such equations. In contrast, the method based on principal strata estimates causal effects whose definition and interpretation does not require parametric models. Rather, the role of parametric models is in assisting estimation. Finally, the method based on principal strata can make the assumptions explicit. Making assumptions such as those of Section 2.2 explicit can allow researchers to evaluate their plausibility.

The notation we used for a subject’s potential outcomes, exposure, and censoring behaviors as functions of that subject’s level of the controlled factor D also embodies the implicit assumption that those values are not a function of other subjects’ levels of the controlled factor, namely, the no-interference assumption (Cox 1958, p. 19; Rubin 1978). Such an assumption is typically made, and relaxing it leads to many more potential outcomes and principal strata, so that inferences without it would require additional assumptions. For example, as pointed out by a reviewer, interference in the NEP between a couple of cohabiting drug users can exist if they are both recruited in the study and their network for sharing needles is limited to only the two of them. Then the exchanging behavior at the NEP for one member of the couple is expected to be very influential on the potential outcome of the other member, even when the latter member does not exchange at the NEP. On the other hand, interference is not expected to be a serious concern if any impact of the study on its subjects does not result in a big change on the larger network of drug users with which the study drug users interact. Inference using this assumption in this study is relevant because (a) the study subjects are only a subset of the larger network of drug users with whom they interact; (b) within the study, and at any time, only a small fraction of subjects exchange at the NEP; and (c) small deviations from the assumption would mean that the effect of distance attributable to exchange as estimated in Section 5 is a conservative estimate of the target impact that can be realized if the larger part of the community of drug users is to visit and exchange at the NEP. Nevertheless, our framework can, in principle, allow interference by allowing the subject-specific potential values of outcomes, exchange, and censoring at a given time to be also a function of the subjects’ collective behaviors at previous times. Such models require additional assumptions to identify causal effects and are of interest in further work.

The described method also assumes observations across subjects are independent, which, if not true unconditionally, becomes more realistic when conditioning on important covariates. However, direct fitting of a large number of covariates to address possible spatial clustering can be avoided by modeling instead a correlation structure unconditionally on the covariates. In data of simpler structure than that described here, work related to this issue is discussed in Frangakis, Rubin, and Zhou (1998, 2002) and Korhonen, Loeys, Goetghebeur, and Palmgren (2000), and generalizations to the longitudinal data structure of Section 2 can be useful.

Principal stratification can also be used in conjunction with other methods, for example, propensity scores (Rosenbaum and Rubin 1983). With settings such as those considered here, for example, for the NEP, estimating propensity scores is conceivable for the distribution of the controlled factor, or of the partially controlled observed exposured or of censoring. It is important to note, however, that the full advantage of using propensity scores comes mostly in simpler settings where assignment of a binary factor is assumed ignorable, given observed variables. Therefore, such full advantage of using propensity scores is not likely achievable in our setting where the controlled factor is generally multilevel and where exposure and censoring are allowed to be nonignorable. Nevertheless, further study of the role of propensity scores, for example, for dimension reduction without introducing bias, in settings such as ours is also of interest.

With better methods of analysis, there is also a need for better retrospective and prospective designs. An example of the former in the NEP could be: Choose the known cases of HIV and, from the controls of the study (at each time point), select only the most informative ones, by means of appropriate measures of covariates, of controlled distance, and of partially controlled exposure. The motivation for such approaches is that, although we would be using reduced data, we would have more accurate estimates than if we were using the full data if model extrapolation in the latter case can introduce large bias relative to gains in efficiency. In this case one can use the conditional likelihood that is induced by the matching scheme on the unconditional likelihood of models such as those of Section 4. An important issue, however, in such a problem is to select informative matching schemes, given the different role of the controlled and partially controlled factors in the study. For prospective designs, methods are needed to develop guidelines for the controlled factor, for example, in the NEP, about how many sites, and at what locations, should be used to achieve balance between, on the one hand, current practical and ethical concerns and, on the other hand, precision of estimation of effects of a program that can be beneficial in the future for the larger community. Work on prospective designs that anticipate noncompliance discussed by Jo (1999) and Frangakis and Baker (2001) provides some preliminary directions that are relevant to the role of prospective designs in such more general settings.

Regarding evaluation of the Baltimore NEP, the method that uses principal stratification points to a substantially larger benefit of the NEP in reducing HIV transmission than the standard method, although the results for both methods are associated with considerable uncertainty. More important than the results of each method alone is that the different methods give consistent results and in relative magnitudes that are explainable if the NEP does lower HIV transmission and also attracts subjects who are at higher risk. Such consistency between the two different perspectives provides more confidence on the effectiveness of the NEP, although continued follow-up can provide more conclusive information.