Mechanosensitive Gating of Kv Channels

Abstract

K-selective voltage-gated channels (Kv) are multi-conformation bilayer-embedded proteins whose mechanosensitive (MS) P_open(V) implies that at least one conformational transition requires the restructuring of the channel-bilayer interface. Unlike Morris and colleagues, who attributed MS-Kv responses to a cooperative V-dependent closed-closed expansion↔compaction transition near the open state, Mackinnon and colleagues invoke expansion during a V-independent closed↔open transition. With increasing membrane tension, they suggest, the closed↔open equilibrium constant, L, can increase >100-fold, thereby taking steady-state P_open from 0→1; “exquisite sensitivity to small…mechanical perturbations”, they state, makes a Kv “as much a mechanosensitive…as…a voltage-dependent channel”. Devised to explain successive g _K (V) curves in excised patches where tension spontaneously increased until lysis, their L-based model falters in part because of an overlooked IK feature; with recovery from slow inactivation factored in, their g(V) datasets are fully explained by the earlier model (a MS V-dependent closed-closed transition, invariant L≥4). An L-based MS-Kv predicts neither known Kv time courses nor the distinctive MS responses of Kv-ILT. It predicts Kv densities (hence gating charge per V-sensor) several-fold different from established values. If opening depended on elevated tension (L-based model), standard g _K (V) operation would be compromised by animal cells’ membrane flaccidity. A MS V-dependent transition is, by contrast, unproblematic on all counts. Since these issues bear directly on recent findings that mechanically-modulated Kv channels subtly tune pain-related excitability in peripheral mechanoreceptor neurons we undertook excitability modeling (evoked action potentials). Kvs with MS V-dependent closed-closed transitions produce nuanced mechanically-modulated excitability whereas an L-based MS-Kv yields extreme, possibly excessive (physiologically-speaking) inhibition.

Introduction

Overview

Kv channels which are voltage-gated channels (VGC). Their four voltage-sensing domains are biological hydrophobic cations bearing well-hydrated charge in close proximity to the embedding bilayer’s hydrophobic interior [1,2]. Via fine positional control the sensors’ motions let them regulate pore openness according to membrane voltage [3]. Perhaps not surprisingly, bilayer deformations modulate Kv activities [4,5]. Native bilayers are far-from equilibrium structures of asymmetric lipid leaflets and complex lateral arrangements. Lateral pressure profiles for simple bilayers vary strikingly depending on lipid constituents, a reminder that bilayer structure impacts the energetics of membrane proteins [6,7]. Imposed bilayer deformations that alter that structure (thickness, lipid-packing order, local curvatures and so on) can, therefore, potentially modify protein’s conformational stabilities. A bilayer’s profile can change irreversibly (chemical constituent changes, bleb-type denaturing of lipid organization [8]) or reversibly (reversibly imposed stretch, hyperbaric pressure, temperature changes, surface active molecules [7,9,10]). Membrane proteins, be they, say, rhodopsin [11] or VGCs are mechanosensitive (MS) if their conformational equilibria are modulated by such bilayer mechanical changes [4,7,12,13,14,15]; electrophysiologically speaking, an ion channel whose open probability (P _open) is sensitive to bilayer structure [5,16] is a MS channel.

Though MS channels are generally studied using pipette aspiration to increase bilayer tension in plasma membrane patches, tension control is not straightforward [17,18] as re-emphasized by Schmidt et al [19]. Membrane/glass adhesion forces associated with gigaohm seal formation [20] combined with residual pipette pressures [21] result in “resting” patch tensions of uncertain magnitude. Moreover, insofar as seal formation disrupts cytoskeleton/bilayer adhesions and other cellular processes that maintain native bilayer structures in situ, it inflicts bleb-type damage (denatured bilayer structure [8,22]). But even if the bilayer denatures and acquires a non-zero resting tension, channels in patches can remain functional. If their activity or responses to stimuli become irreversibly altered [23,24,25,26], this represents a patch artifact [23] or epiphenomenon.

For MS channels, patch epiphenomena involving irreversibly altered gating have been acknowledged (or dodged) with terms like “hysteresis”, “patch history” and even “exercising the patch” [27,28]. Except where putatively mechanical effects are explicitly demonstrated as reversible, it should not be assumed that the epiphenomenon represents a MS gating phenomenon [29], a caveat relevant to a patch clamp epiphenomenon reported by Schmidt et al [19], i.e., “conversion”. Conversion describes irreversible changes in macroscopic Kv channel current recorded from outside-out oocyte patches [19], the reconfigured components of which are depicted in Fig. 1A (right).

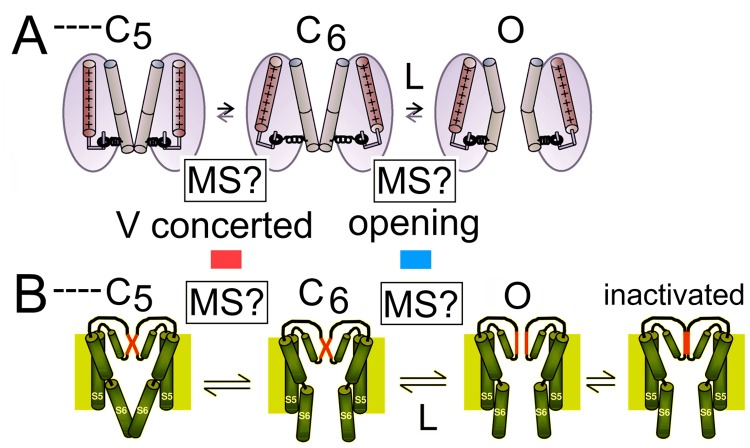
Fig 1. Kv channels and their mechanosensitivity.

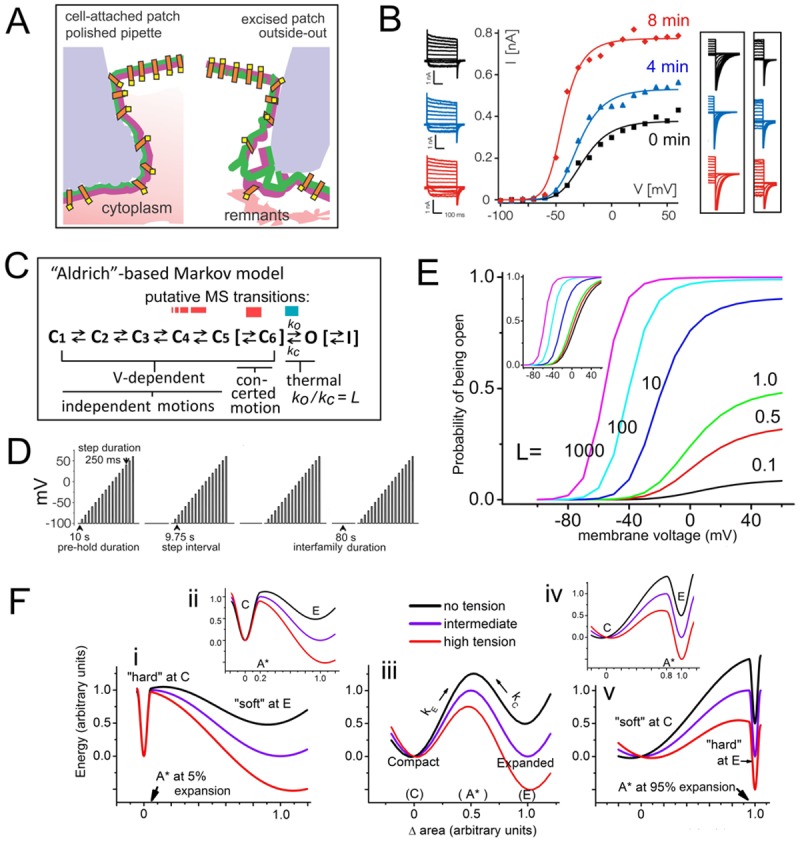
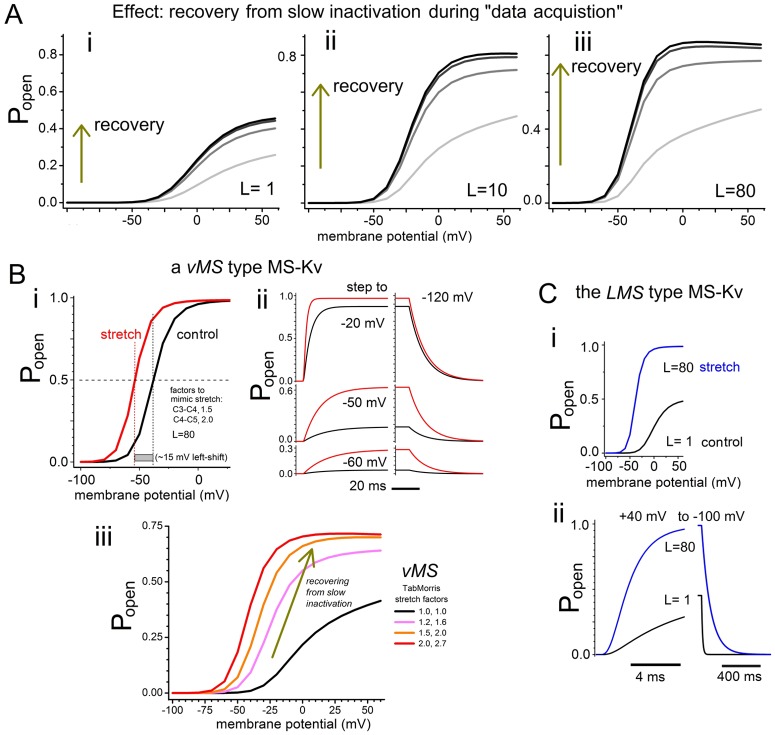
A. Cartoon of some differences at the gigaohm seal zones for (left) cell-attached versus (right) excised outside-out oocyte patches. Left, the uneven surface (pale blue) depicts pipette tip glass sputtered with molten soda glass during fire polishing [18]. Right, outside-out patches (whose structure would resemble that of pinched off blebs or multi-lipid artificial bilayers or [30,31]) reseal within the pipette’s unmodified borosilicate interior surface, then creep inward, developing progressively higher tension [19]. Membrane-glass interactions are extensive and stable at soft-glass sputtered tips (Left) and spontaneous tension build-up is less evident [17]; patches withstand multiple prolonged bouts of applied suction [32,33,34,35]. B. Exemplar data from Schmidt et al [19] (modified from their Fig. 1) showing “conversion” for Kv-Shaker, plus (boxed) tail currents for other Kvs. C. A kinetic scheme for Kv channels, extending Scheme 1 with optional addition (square brackets) of C₆ (“pre-open”) and I (slow inactivated) states. Putative MS transitions color-coded red for V-dependent (variants explained in the text), blue for thermal. D. V(t) clamp protocol for acquiring g(V) data (from “tail-I_K”): as per [19], except that to confirm trends we simulated acquisition of 4 g(V)s (not 3). E. Effect of varying L on P _open (V) (values from Ref. [36]); inset, same curves normalized to P _open-max (similar to Fig. 2 of ref [37]). F, i-v. Reaction co-ordinate (drawn by eye) depicting MS transition energetics. Some area, A*, between area, C, of the smaller compacted and area, E, of the larger expanded protein conformation will be the area of the unstable “activated” or transition state [38] (for V-dependent transitions, A*-C compares to the equivalent charge moved through the electric field to put a two-state V-sensor in its transition state; see [37]). A MS channel transition could be between two distinct closed states [38,39], or, as per Schmidt et al [19] a closed and an open state. Activation barriers at the extrema, A* = C and A* = E, would imply extreme rigidities at those locations. Protein energetics depicted here at zero, intermediate and high membrane tensions (i, iii, v) are for A* marginally >C (5% of its expansion), or A* midway between C and E (50% of its expansion), or A* marginally <E (95% of its expansion), with two cases (ii, iv) of moderate barrier asymmetry (20% and 80% area expansion) as insets. In vMS and LMS models here (as in a previous MS-Kv channel model [39]) symmetry is implied (A*midway between C and E) as it is the simplest assumption in the absence of structural data for transition states (see also [38,40,41,42]).

Conversion is attributed to spontaneous progressive increases in bilayer tension leading to patch rupture; purportedly conversion reflect an overlooked aspect of MS gating in Kv channels[19]. The epiphenomenon is a progressive and irreversible increase in apparent gK _max, accompanied by slope-steepening and by hyperpolarizing shifts (“left-shifts”) of gK(V) (Fig. 1B). Sometimes, irreversibly-increasing patch tension was augmented by pipette suction. Their native bilayer arrangements [14] degraded, the outside-out patches (Fig. 1A) underwent tension-inducing [28] patch-creep [19] (see, however, Ref. [17]). We concur that patches were under increasing tension and that this would explain part of the “conversion” epiphenomenon (specifically, left-shifted activation [39]), but the apparently novel MS aspect of “conversion” (i.e., the growth in apparent g _max), we argue, can be explained by recovery from slow inactivation.

In their studies of MS Kv gating, Morris and colleagues [39,43,44,45] used the more robust cell-attached patch configuration (Fig. 1A) and focused principally on demonstrably reversible I _K time courses before, during and after applied stretch (pipettes suction) over a wide range of voltages. Though the outside-out patches of Schmidt et al [19] did not allow for relief of tension, they regard conversion as an inherently reversible MS phenomenon, modeling it as such based on g(V) data. Here, we use computations to consider their findings and model in comparison to those of Morris and colleagues (for several Kv Shaker constructs).

Mechanisms of MS-Kv gating have physiological implications since mammalian nociceptor neurons use Kv1 mechanosensitivity to mechanically modulate pain signals [46] and atrial rhythmicity is putatively under mechanical regulation via MS Kv7 gating [47]. With the neuronal case in mind, we checked the impact of subjecting to “stretch” a model excitable membrane comprised in part with a MS g _K (V). We used either 1) the Schmidt et al [19] model (Kvs had a MS V-insensitive closed↔open transition) or 2) a model like that of Tabarean and Morris [39] (Kvs had a MS V-dependent concerted closed↔closed transition). The Schmidt et al MS-Kv powerfully inhibited excitability while the other model mechanically modulated excitability in a smoothly graded fashion.

Our analysis does not favor the proposition [19] that Kv mechanosensitivity can be attributed to a MS voltage-insensitive opening transition. But while a MS voltage-dependent closed-closed transition [39] is a better explanation for MS-Kv gating in Shaker type channels, it cannot be proffered as a global explanation for MS-Kv gating phenomena, let alone for MS gating in all VGCs. Other explanations are needed for the voltage-independent MS acceleration of slow inactivation [44] and for MS gating in members of the Kv3 subtype [29,45]. The putatively MS gating of a Kv7 channel [47] seems worth re-examining in light of the two classes of models addressed here. A key point emerging from the present analysis is that even though membranes cannot be “tension clamped”, hypothesis testing about putatively MS gating transitions is possible where reversible MS responses have been obtained for time courses (kinetics) and equilibria over a range of known voltages and imperfectly known tensions.

Models for MS-Kvs

Two mechanisms have been proposed for the mechanosensitivity of Shaker type Kv channels, both assuming a transition in which the channel expands↔compacts in the plane of the bilayer, with the expanded conformation energetically favored by increased tension. In modeling these MS transitions here (as previously [39]), a simple assumption was used for the channel’s condition when in its transition (or “active”) state, A*, namely that it displaces an area halfway between the areas of the compacted (C) and expanded (E) states, as depicted in Fig 1 Fiii. As discussed previously [36], qualitatively different behaviors result if, instead of being roughly balanced, deformation into A* is heavily biased towards either the compacted or expanded state (Fig 1F i,v). Via MS rates, barrier characteristics would be apparent in I _K time courses, as will be pointed out as appropriate.

An earlier model (Fig. 1C, red), vMS, posits expansion associated voltage-dependent closed-closed transition(s) near the open state [39]. The new model (Fig. 1C, blue), LMS, posits expansion during the voltage-independent closed-open transition [19]. For a MS VGC, the issue of whether or not a MS transition involves the conductive state is pivotal, and with a strictly MS opening (the basic LMS model) P _open would only reach its operational maximum at elevated membrane tension.

Unlike the LMS model, the vMS models explored here are not confounded by the oft confirmed [48,49,50,51,52,53] fixed P _{open-max =} ~0.8 feature of Shaker Kv channels, thought to reflect flickery transitions off the voltage-activation path [49,51]. Thus, following Smith-Maxwell et al [36], the 2002 “TabMor” version of vMS [39] was able to ignore L (by making it large, i.e., 80) and the flickery open state being irrelevant in that context was not included. For the L-based MS-Kv model, however, large MS variations in L are precisely what underlie the (putative) MS increase in apparent P _open-max and by their reckoning (given the fits in [19]), in situ rest tension L values should be ~0.5 or less. As a compromise resolution where direct comparisons were made between vMS and LMS (see also Section Excitability and a MS-Kv: vMS versus LMS ), we used L = 4. This would correspond to a “pre-stressed” rest-tension L value for LMS and it corresponds to P _open-max = 0.8. At L = 80 [36] the LMS rest-tension apparent P _open-max would approach unity, obliterating the central feature of LMS whereas the smaller fixed value of L in vMS does no violence to its central MS features (MS gV left-shift, no MS change in g _max).

Markov type models [37] were used to predict gK(V,t) without and with simulated tension as prescribed by LMS or vMS models. Results are principally but not exclusively given as conductance time courses plus equilibrium g(V) and Q(V) curves. Use of vMS and LMS in connection with excitability modeling will be described further in the appropriate context.

Results

The g(V) data sets behind LMS

Schmidt et al [19] generated their LMS Kv model to account for sequentially acquired g(V) families (see Fig. 1B) obtained immediately upon forming outside-out oocyte patches (Fig. 1A, right). With patch tension increasing spontaneously for several minutes prior to rupture, their g(V) curves (4 min intervals; see V(t) protocol, Fig. 1D) grew in magnitude ~2–3 fold, with hyperpolarizing shifts and steepening slopes. In some cases, pipette suction applied between successive g(V)s augmented the “creep”-induced tension increases. Their LMS model assumes four V-dependent closed-closed transitions followed by a voltage-independent (“thermal”) opening, C ₅ →O, shown in Fig. 2 as Scheme 1.

Fig 2. Scheme 1.

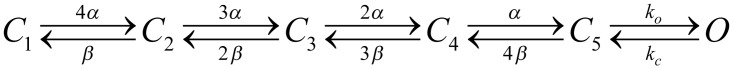
The kinetic constants α and β can be expressed (using values at V = 0 mV) as:

$$\alpha ={\alpha }_0{e}^{z_{\alpha }FV/RT}=e^{z_{\alpha }F(V-V_{0.5})/RT};\beta \text{=}{\beta }_0{e}^{-z_{\beta }FV/RT}=e^{z_{\beta }F(V-V_{0.5})/RT},$$ [1]

where V _0.5 is the midpoint membrane voltage for activation of individual voltage sensors and z _α and z _β are effective charges for voltage sensor activation and deactivation respectively (F, R and T have their usual meanings). The constants used in Scheme 1are listed in Table 1. In LMS, the “pore opening” last transition, C ₅ ↔O, is “thermal” (insensitive to voltage) but is sensitive to bilayer stretch. Assuming their g(V) plots represented equilibria for sequentially higher (albeit unknown) membrane tensions, Schmidt et al (2012) [19] performed global fits to the equilibrium formulation for Scheme 1:

Table 1. Kv model for Schemes 1 and 2(^*).

(as presented in Fig. 4 of Ref. [36] and Figure 11 of Ref. [39]).

α0	1120s-1	zα	0.25e
β0	373s-1	zβ	1.0e
ko	8000s-1	kc	100s-1
*inac	0.05s-1	*recov	0.005s-1

* refers to parameters associated with Scheme 2.

$$P_{open}=\frac{{\left[\frac{K}{1+K}\right]}^4\cdot L}{1+{\left[\frac{K}{1+K}\right]}^4\cdot L}.$$ [2]

The kinetic constants are embedded in ratios, K and L. K characterizes the V-dependent activation/deactivation transitions ($K=\frac{\alpha }{\beta }=e^{zF(V-V_{0.5})/RT}$where z = z _α +z _β) and L the voltage-independent pore opening/closing transition (L = k _o /k _c). In “L-based” Kv mechanosensitivity, the channel would displace more bilayer in its O than in its C ₅ state, so k _o and k _c show inverse MS responses. To globally fit a patch’s g(V)s to Eq. 2, they held z and V _0.5 constant, and they varied the putatively MS equilibrium constant, L. Note from Eq. 2 that the maximal value of P _open (= L/(1+L)) increases with L. Given the g(V) characteristics of their (LMS) model, Schmidt et al (2012) [19] conclude that “the Kv channel is as much a mechanosensitive channel as it is a voltage-dependent channel.”

When a voltage-independent entry-to/exit-from the K⁺-conducting state was first considered [48], Zagotta et al [37] showed (their Fig. 2) how such a transition impacts the V-dependence of gK, plotting normalized P _open (V) for L from 0.1 up to 1000 (see inset, Fig. 1E). A changeable g _max (i.e., a ∆ apparent g _max) would be physiologically critical, so we replotted this here without normalization (Fig. 1E). The resemblance to Schmidt et al (2012)’s Kv datasets [19] (fitted L-values ranged from ~0.5 to >150) is self-evident (e.g., their Fig. 1L, 0.56⇾165; their Kv-Shaker data, reproduced in our Fig. 1B, 1.8⇾62). Although as explained above variability in P _open-max is at odds with other measurements from excised oocyte patches (noise and unitary currents, e.g.[54]) we note that for LMS, P _open-max = 0.8 corresponds to L≈4.

Recovery from slow inactivation

Unlike previous studies of Kv mechanosensitivity from cell-attached patches (Fig. 1A) Schmidt et al [19] mostly used outside-out patches, with V _m = 0 mV during excision/resealing in high [K⁺] saline. A sealed patch was immediately clamped from 0 mV to V _m = -100 mV and data acquisition (series of g(V)s) started. With V _m = 0 mV until seal reformation, Kv channels would be slow inactivated [55]. Data acquisition occurred, therefore, in out-of-equilibrium systems. To mimic these “start” conditions, we ran the Schmidt et al [19] protocol (Fig. 1D) for Scheme 2 (see Fig. 3), which includes the slow inactivated state, I:

Fig 3. Scheme 2.

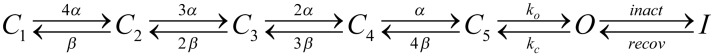
Constants for Scheme 2 are listed in Table 1. Fig. 4A plots outcomes for L = 1, 10, 80, covering much of the L range inferred by the Schmidt et al [19] fits. The four g(V)-runs we simulated show the system approaching equilibrium (recovery-from-inactivation). Schmidt et al, assuming tension-dependent L and with no mention of slow inactivation, use the term “post-conversion” for the last of their 3 g(V)s to signify gating under near-lytic (albeit unmeasured) patch tension.

Fig 4. Mimicking excised patch datasets by adding slow inactivation and progressive vMS-type g(V) left-shifts to Scheme 1.

A, B, and C are explained in the text and by figure labels. For A and Biii, the systems are initiated (i.e., t = 0, Fig. 1D protocol) from the slow inactivated state. Note (Bi versus C) that the vMS and LMS models make qualitatively different predictions for the effect of “membrane stretch” on tail time courses (i.e., closing kinetics).

In Fig. 4A, three fixed L values (1, 10, 80) are simulated; in each case, g(V) curves grow in amplitude with time, with upwardly inclined “plateaus” on the first g(V) plots and progressively steeper slope regions. Thus, recovery (more available channels) of this initially far-from-equilibrium system resembles the Schmidt et al [19] datasets, suggesting that recovery from slow inactivation (and not increasing values of L) underlies the ∆ apparent g _max in their data sets. Granted, a (tension-induced) L increase predicts the experimentally observed progressive g(V) left-shifts (note V-axis positions of g(V)-sets for L = 1,10,80), but so too does vMS. We therefore next look at a vMS version of Scheme 2 operating during recovery from inactivation.

Kv mechanosensitivity in a voltage-dependent transition

Stretch-modulation of Kv-Shaker and its short-S3-S4-linker mutant (“5aa”) in cell-attached oocyte patches was previously described with a vMS version (“TabMor”) of Scheme 2 [39]. Mechanosensitivity was attributed to a closed-closed V-dependent conformation change near the open state. Tabarean and Morris [39] approximated a MS concerted pre-opening by reciprocally “stretch modulating” the forward and backward rates of the penultimate and ultimate V-dependent transitions of Scheme 2 (as in the example of Fig. 4Bi MS modulation was depicted as stronger in the second transition). For a given (unspecified) tension, rates at C ₃ ↔ C ₄ and at C ₄ ↔ C ₅ change by “stretch factors” ms _3↔4 and ms _4↔5 respectively. Since Tabarean and Morris [39] simulated selected g(V,t) without plotting P _open (V) for control and “stretch” conditions, we rectify that here (Fig. 4Bi), calculating g(V) (10 mV intervals) for the parameters as labeled. Unlike LMS, g _max is unaffected as g(V) left-shifts with “stretch” (in those simulations, L = 80 following [36] but for any fixed L g _max is invariant). Fig. 4Bii shows that vMS-simulated stretch weakly modulates the rate of conductance onset but, importantly, not the offset rate (i.e., the tails).

For Fig. 4Biii, the Schmidt et al [19] V(t) protocol (Fig. 1D) was used with Scheme 2 and the vMS parameters of Fig. 4Bi except that L = 4. Henceforth for vMS, L = 4 = k _o/k _c (= 400/100). Importantly, all channels were initially in state I. Then, to mimic membrane tension progressively increasing above its rest (control) level, stretch factors (ms _3↔4 and ms _4↔5) were increased for successive g(V)s. The “TabMor stretch” version of vMS used here are as labeled; in terms of Scheme 2 kinetic parameters, this produces a small increase in the ratio 2α/3β and a slightly larger one for α/4β. Notice how closely the resulting g(V) set mimics the exemplar datasets of Schmidt et al [19] (e.g. Fig. 1B, here).

Thus, using 1) a fixed L magnitude consistent with established values of P _open-max (e.g., [48,49]), and 2) realistic magnitudes for a vMS-type left-shift (i.e., consistent with I(V,t) data before/during/after stretch [39]), and 3) known rates of Kv Shaker slow inactivation [55], the outcome is a g(V) set (Fig. 4Biii) with all the features of the Schmidt et al [19] g(V) datasets.

LMS predictions for tail currents under stretch

The LMS model postulates a ∆-area at C ₅ ↔O. Recall that the models used here assume an activated (transition) state, A*, symmetrically located between the compacted and expanded states, which for LMS would be C ₅ and O. The unlikely situation of A* being at or almost at the expanded state (Fig. 1Fv) will be addressed below, but ignoring that for the moment, LMS predicts that “tail current” (measured at hyperpolarized voltages to track closing, O→C ₅) should slow dramatically at elevated membrane tensions, as illustrated for L = 1 = 100/100 going to L = 80 = 894.4/11.20 in a Scheme 1 simulation (Fig. 4C). Schmidt et al [19] do not address this prediction, but Kv Shaker tail currents, which have been monitored before/during/after stretch in cell-attached patches [45], show no consistent change with increased tension. Schmidt et al’s exemplar datasets include tail currents; inspection reveals no consistent changes as tension grows. These experimental findings agree with the vMS models here (e.g., Fig. 4Bi); they predict tail currents at hyperpolarized potentials almost unaffected by stretch, as in Fig. 4Bii (see also Fig. 5D).

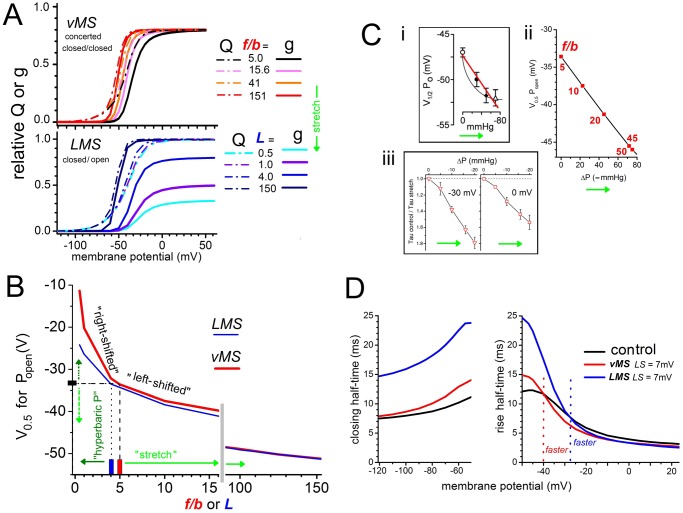
Fig 5. Comparing vMS and LMS using Scheme 3 (concerted pre-opening).

A. g(V)s and coinciding Q(V)s (normalized to g(V)s of vMS, where P _open-max = 0.8 because L = 4) at the listed equilibrium constant values. For the vMS case, rest tension (no applied stress) is (f/b) ₀ = 5 and for LMS, the rest tension L value would be near 1 as discussed in the text. B. g(V) midpoint (V _0.5) as a function of the MS equilibrium constants for each model. Ci. g(V) left-shift data redrawn from Hao et al (2013)[46]. The red line overlay is our “by-eye” fit. ii, Scheme 3 vMS- Kv g(V) left-shift calculated as a function of ∆P; P _open (vMS-Kv) was modeled for a hemispherical-section patch whose increasing radius of curvature for 0 to 80 mmHg suction caused membrane-area to increase by 1.4% (the patch model was a perfect hemisphere for a 4% area-increase which is a bilayer’s typical lytic limit; other parameter values were K_A = 250 mN/m for bilayer stiffness, conformation change ∆area = 3 nm^2; patch radius = 0.5 μm). LMS left-shift behavior (not shown) is similarly quasi-linear. iii. Replotted data from Fig. 5 of Ref. [56] for MS changes in Nav1.5 fast inactivation kinetics (tight kinetic coupling makes this inactivation process a good proxy for V-dependent Nav1.5 activation; and as for Kv1, the g(V) for Nav1.5 left-shifts reversibly with patch stretch). D. Half times for Kv conductance tails and onset, for a control condition ((f/b) ₀ = 5, L = 4) of Scheme 3 and after parameter changes yielding 7 mV g(V) left-shifts according to vMS and LMS models. Note, with LMS, the pronounced slowing of tail decay. Note, also, that for onset, in the vMS case conductance rise would be accelerated by stretch at-40 mV and beyond, but in the LMS case it would rise more slowly with stretch till about-27 mV.

Stretch, we note, accelerates tail current for another VGC, HCN2 (Lin et al [57]; see their Fig. 6). Though HCN channels resemble Kv channels, they close in response to depolarization and while details are sketchy, HCN tail currents should reflect V-dependent sensor motions [58]. Stretch-accelerated closing of HCN2 is inexplicable by a LMS ∆-area model whose underlying mechanism involves compaction to the closed state and expansion to the open state.

Fig 6. Scheme 3.

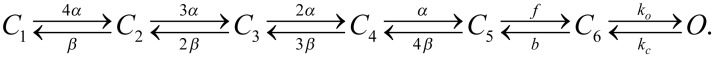
We now return to the conjecture raised earlier that Kv tail current insensitivity to stretch is explicable via LMS if A* = E (or say, at ~95% in its area expansion) (see Fig. 1Fv) which would make current onset (regardless of voltage) accelerate strongly with stretch and leave tail currents unaffected. For the Schmidt et al exemplars (their Fig. 1), inferred L values increased ~60-fold (L = ~1.5 for controls going to L = ~90 for g(V)) upon “conversion”. In the notation of Fig. 1F (L = K _E /K _C), K _C would be invariant with tension so current rise would be ~60-fold faster than control at the higher tension. The traces reveal no such changes and none are mentioned. By contrast, small (reversible) MS changes are seen for Shaker-type Kv rise times [39,43,44,45] along the lines summarized in Fig. 5D (red), a vMS depiction of what (experimentally) would represent application of near-lytic stretch (explained further in the next section; as in all modeling here, the rates for that vMS’s MS transition—the equivalent of Fig. 1F’s generic K _E and K _C—operate over an area-symmetric energy barrier). Thus, while an a priori rejection of LMS based on the insensitivity of tail currents to stretch is too facile, MS rise time changes for Shaker channels are entirely inconsistent with such an explanation, whereas both rising current and tail current time courses patterns are fully consistent with the proposed vMS model.

For both vMS and LMS models Q(V) limits MS left-shifts of g(V)

Previously [39] (the “TabMor” vMS) we approximated a MS concerted V-dependent pre-opening but with that transition now better understood, we can use Scheme 3 (see Fig. 6), which includes an explicit concerted V-dependent C ₅ ↔C ₆ before the open state:

Table 2 lists the constants for this 7-state scheme. The C ₅ ↔C ₆ concerted voltage sensor motion (involving ~13% of total gating charge) is thought to exert a laterally-acting (centripetal) force to destabilize the cytoplasmic “bundle crossing gate” (see [35,59]). By making C ₅ ↔C ₆ versus C ₆ ↔O the sole MS transition, Fig. 5 compares the predictions of Scheme 3-based vMS versus LMS models.

Table 2. Scheme 3 (7-state) Kv model for WT and ILT.

	WT	ILT		WT	ILT
α0	2000s-1	1540s-1	zα	0.5e	0.5e
β0	100s-1	0.16s-1	zβ	1.5e	2.5e
f0	1000s-1	0.072s-1	zf	0.2e	1.0e
b0	200s-1	0.162s-1	zb	0.8e	0.8e
ko	400s-1	400s-1	kc	100s-1	100s-1

For WT, model based on Ref. [15] equilibrium model for g(V) and Q(V)curves with kinetic constants and effective charges inspired from Ref. [50]; for ILT, charges and rate constants started from Ref. [35], but shifted to give g(V) and Q(V) midpoints consistent with those in the literature V _0.5 ^Q(V) ≈ -80 mV and a V _0.5 ^g(V) ≈ 100 mV (see Refs. [35] (Fig. 5), [15,60]).

$C_6\rightleftarrows O$, the thermal transition, is the same for ILT and the WT, L = k _o /k _c = 400/100, yielding P _open-max = 0.8.

Fig. 5A depicts relative g(V)s with the corresponding Q(V)s for vMS and LMS models for a range of “stretch intensities”. Increasing tension is mimicked by increasing f/b for vMS or by increasing L (= k _o /k _c) for LMS. For a tension-dependent L, the low end of the Schmidt et al [19] L values (from their global fits) would approach rest tension values. In vMS, g _max is unchanging as stretch left-shifts the g(V), while in LMS, true rest tension g _max should be less than experimental estimates while at large L values (say 100) apparent g _max and true g _max converge (Fig. 1B). Over the inferred L range from Schmidt et al’s [19] fits (~ 0.5 to >150), apparent g _max increases ~3-fold. Note how, as the simulated “stretch intensity” grows, the left-shift of g(V) is increasingly limited by the Q(V) curve which always lies to the left of g(V). Unlike the “TabMor” version of vMS, neither the LMS nor the vMS models assume any MS effect at the voltage sensors’ independent transitions. Nevertheless, as evident from the co-plotted g and Q curves, mechanosensitivity in either the charge-poor concerted pre-opening transition or the entirely charge-free opening transition would yield appreciable MS shift/steepening of Q(V). Conversely, experimentally-observed MS Q(V) changes of this ilk would not signify MS effects on independent voltage sensor motions.

Fig. 5B summarizes MS g(V) shifts for both models over as a function of their MS equilibrium constants. Rest tension values are indicated by boxes on the axes, with increasing stretch (bright green arrows) or hyperbaric pressure regimes (dark green arrows) associated with the labeled ranges. In both models, g(V)s left-shift under tension and right-shift under hyperbaric pressures but neither gives a tension-induced “saturation” of left-shift.

For vMS, the rest tension value of the equilibrium constant, (f/b) ₀ (f/b at V = 0 mV), is 5 (red marker, x-axis) (Fig. 5B, see labels). Although values >5 signify stretched membrane while <5 would signify compressed membrane (hyperbaric pressures right-shift Kv and Nav activation (Conti and colleagues [56], discussed in Ref. [39]) this x-axis should not be misconstrued as a “membrane tension” axis. The relationship between f/b (or L) and membrane tension is derived below.

For Kv1.1 channels in HEK cells, Hao et al [46] report MS g(V) left-shifts which, they thought, saturated at large patch pipette pressures. Part of their Fig. 5D is redrawn in Fig. 5Ci; our red line overlay shows that the data comfortably fit a straight line. This matters, since for both vMS and LMS models, a near-straight line, but definitely not a saturation, is predicted as a function of pipette pressure (Fig. 5Cii). Direct calibration of the models’ MS equilibrium constants against pipette pressure (the x-axis of the Hao et al [46] plot) or even against membrane tension, is not possible. Instead, we derived the Fig. 5Cii plot using simple arguments that relate the g(V) midpoint, V _0.5, to applied pipette pressure and the MS equilibrium constants. We first note the order in which the relevant quantities can be related:

$$V_{0.5}\leftrightarrow \left(\frac{f}{b}\right)\text{or}L\leftrightarrow \gamma =K_A\epsilon \leftrightarrow \mathrm{\Delta }P$$ [3]

The first two are related through Fig. 5B. Next, (f/b)₀ (or L) are related to membrane tension γ, through a Boltzmann relationship. The ratio f/b (or L = k _o /k _c) gives the ratio of probabilities of occupation of states C ₅ and C ₆ (or C ₆ and O), hence:

$$\frac{{(f/b)}_{\gamma \ne 0}}{{(f/b)}_{\gamma =0}}=\exp \left(\frac{\gamma \mathrm{\Delta }A}{k_{B}T}\right),\text{or}\gamma \text{=}\frac{k_{B}T}{\mathrm{\Delta }A}\ln \left(\frac{{(f/b)}_{\gamma \ne 0}}{{(f/b)}_{\gamma =0}}\right),$$ [4]

where ΔA is the area change of the MS transition. This holds for all V, and if one assumes that stress affects the free energy of the channel only through the term (-γ ΔA), then the V = 0 value of the two (f/b)₀ can be used in the expressions. Next, γ is proportional to the lateral expansion of the membrane, ε, through γ = K _A ε, where K _A is the compressibility modulus for membrane expansion. And finally Laplace’s law relates ε to ΔP, the specific values depending on the initial curvature of the patch. When standard values for membrane patches are used for the various quantities, the predicted effect of applied pressure, ΔP, on V _0.5 is as seen in the essentially linear relationship of Fig. 5Cii. For a different VGC, Nav1.5, Fig. 5Ciii shows a similar outcome in the MS rates of inactivation (Nav1.5 inactivation couples tightly to activation and thence to the MS-modulated g(V) midpoint [61]); as with the MS-Kv data, ΔP has an essentially linear effect.

Why the linearity? Although g(V) left-shift declines strongly as the MS equilibrium constant increases (i.e., (f/b)₀ or L for vMS or LMS models respectively, as per Fig. 3B), g(V) left-shift grows exponentially with γ and consequently these behaviors largely neutralize each other. Thus, neither statistics nor theory support saturation of the MS g(V) shifts observed [46] for the neuronal MS-Kv.

The neuronal MS-Kv is, nevertheless, physiologically compelling, and the MS g(V) left-shift observed by Hao et al [46], i.e., ~7 mV at large pipette pressures, we take to represent a physiological extremum given that near-lytic tension (not “saturation”) is likely what sets the upper limit. This amount of shift accords with MS shift extrema reported for Kv-Shaker and Nav1.5 channels in oocyte patches [39,62].

From time courses (g(V,t)), Fig. 5D plots onset and tail halftimes for control (no stretch) and both vMS and LMS stretch (7 mV left-shifts in each case). For vMS, the rest tension value of the concerted closed-closed transition equilibrium constant, (f/b)₀, was 5. To facilitate comparison, L = 4 was used for rest tension in both models. Had we modeled the 7 mV g(V) shift interval of the LMS case starting from say L = 0.5 or 1.0 (see Fig. 5B y-and-x axes for the relevant upper value for L) results would be quantitatively but not qualitatively different. Fig. 5D, then, compares halftimes for vMS vs LMS versions of Scheme 3 before then after a 7 mV g(V) left-shift ((f/b) ₀ at 5 then 15.6 for vMS; L at 4 then 14.4 for LMS)). The key outcome: for vMS, the tail time course at a hyperpolarized test voltage (say, -120 mV) will be essentially insensitive to stretch while that for LMS will slow markedly with stretch. As explained above (section on tail currents), this vMS kinetic pattern is consistent with experimental observations, thereby casting strong doubt on the LMS model.

Some subtler features could also be useful for experimentalists. In both models, onset half times during depolarizing steps (right side of plot) go through a “crossover” voltage. Its value left-shifts as stretch intensity increases (not shown). Kinetically, vMS produces net stretch acceleration starting at more hyperpolarized V _m than with LMS (see labeled crossover points). Left-shifting g(V)s would ensure stretch-augmented steady-state currents in either models but, especially for steps to near the foot of the g(V), stretch-induced time course changes could be baffling if one was unaware of the crossovers. For excitable cells, vMS would be a simpler mechanical tuner than LMS. LMS would be powerful yet ungainly, with stretch substantially increasing absolute gK (Fig. 5Aii) albeit with slower kinetics over much of the physiological voltage range (compare the crossover points). We return briefly to the relative mechano-electrical “competencies” of the two models in the last section.

ILT mechanosensitivity: consistent with a vMS model, inconsistent with the LMS model

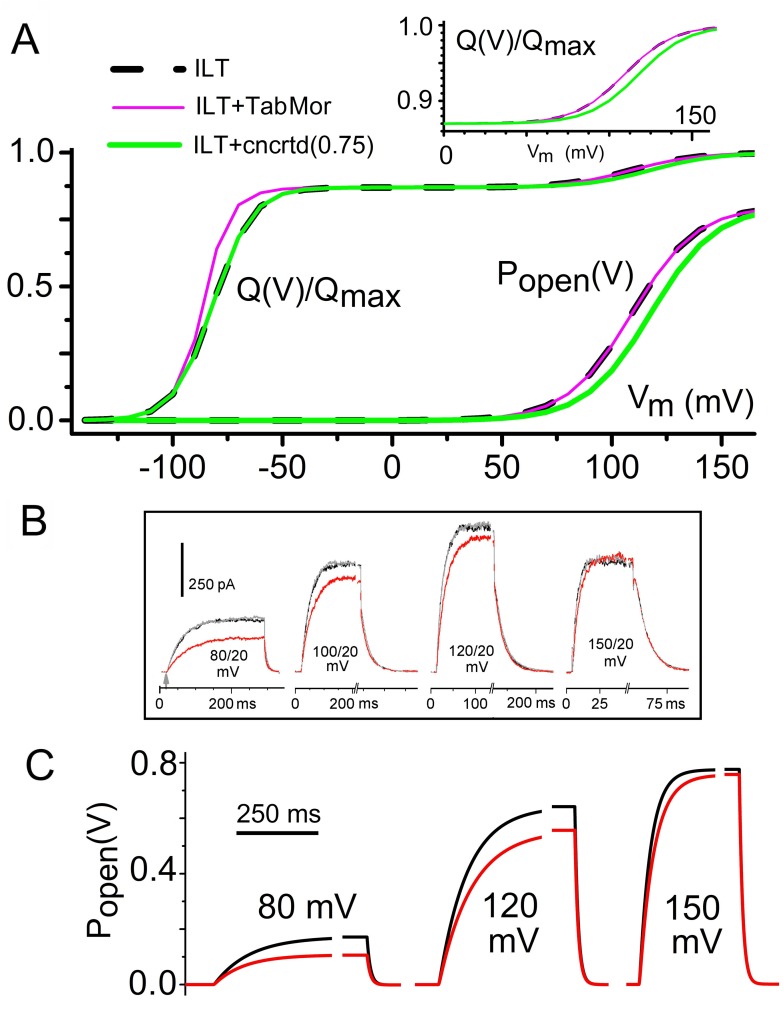
The Kv-Shaker-ILT mutant isolates the independent voltage-driven motions of the four Kv voltage sensor domains from the ensuing concerted voltage-sensitive pre-opening [37,63,60]. In wild type (WT) Kv-Shaker, pre-opening (see Scheme 3) couples tightly to the last of the four independent motions. In ILT, independent charge motion is facilitated while the concerted motion is severely hampered, so the Q(V) component associated with independent charge movements is left-shifted even as g(V) and the small concerted motion Q(V) component right-shift. Dashed black lines in Fig. 7A depict normalized Q(V) and the P _open (V) for ILT; the corresponding curves for WT (not shown) both lie near-50 mV (Q(V) near-50mV, and G(V) about-25 to-40 mV) [15,35,60,63]; parameters are in Table 2. To open ILT requires extreme depolarization, perhaps because [60] altered interactions between the mutated S4 segments and the lipid bilayer, plus abnormally strong protein-protein interactions stabilize the closed bundle crossing (“activation gate”). Since open ILT and open WT channels have identical unitary conductances, opening in ILT, C ₆ ⇾O, is presumably not to some novel conformation. Accordingly, for both ILT and WT, a LMS model predicts a stretch-induced increase in apparent g _max, a left-shifted g(V) and slowed current offset (i.e., tail currents). Patch recordings of ILT channels show that none of these LMS expectations are met: with stretch, the ILT g(V) right-shifts, current onset slows, and tail currents are unaffected [59] (see sample currents in Fig. 7B).

Fig 7. A 7-state vMS model of Shaker ILT: Q(V), g(V), and time courses.

The four independent V-dependent transitions account for 87% [50] of charge movement and the concerted V-dependent closed-closed transition accounts for the remaining 13% [63],[59],[15]. Kinetic constants are Table 2. A. For a Scheme 3 Kv-ILT model, the Q(V)s for rest tension (dashed black line) and with applied tension acting on the concerted transition (green) (Q(V) from 0 to 150 mV is expanded above). To illustrate that any “stretch effects” on V-dependent transitions prior to C ₅ ↔C ₆ would be uncoupled from the ILT-g(V), an ILT simulation (pink line) using the same “TabMor” parameters as previously (Fig. 4B) was included (Note that P _open (V) = g(V)/g _max). Comparison of B (experimental I _K (V,t) data for ILT, where black, red and gray traces are before, during and after patch stretch [45]) and C (time course simulations, with black and red signifying rest and elevated tension, respectively) shows that a g(V) right-shift due to MS rate changes in the concerted transition (i.e., green in A) yields appropriate g(V,t) behavior.

Clearly, ILT is not a Kv-LMS. But can a vMS model predict ILT’s strange MS behavior? As a first point, any vMS model of ILT using Scheme 3 (which terminates in a thermal closed-open transition) predicts its stretch-insensitive tail currents. However, the vMS explanation that worked nicely for WT does not predict ILT’s stretch-slowed current onset nor the attendant stretch-induced g(V) right-shift. We modeled ILT as shown in Fig. 7A then tested vMS variants. Not surprisingly, a Q(V) left-shift (done like TabMor on WT [39]) has no impact on the ILT P _open (V) curve. A vMS version of Scheme 3 that does yield a ILT-like MS-g(V,t) response pattern is as follows: a stretch-induced decrease by a factor 0.75 in the forward rate of the concerted voltage-dependent transition C ₅ ↔C ₆ and a corresponding increase by the same factor in the backward rate (result plotted in Fig. 7C). The corresponding P _open (V) change or g(V) right-shift (green) is shown in Fig. 7A. The ILT I(V,t) data [45] in Fig. 7B illustrate that MS rate changes in this range mimic large but experimentally available membrane tension increases. In both experimental and vMS-simulated traces, onset decelerates under stretch but tails (closing) are insensitive to stretch.

Thus, membrane stretch/deformation further slows an already difficult V-dependent closed-closed transition in ILT, a channel in which the rate-limiting V-dependent transition has been pinpointed as the next-to-last in a multi-step transition [60]. If, in both ILT and WT, a V-dependent component of a step-wise concerted transition involves an in-plane expansion closed-closed expansion (vMS), how might one envisage a subsequent stretch-insensitive (thermal) transition in and out of the open state? Two possibilities suggested by experimental findings are suggested in the discussion.

Excitability and a MS-Kv: vMS versus LMS

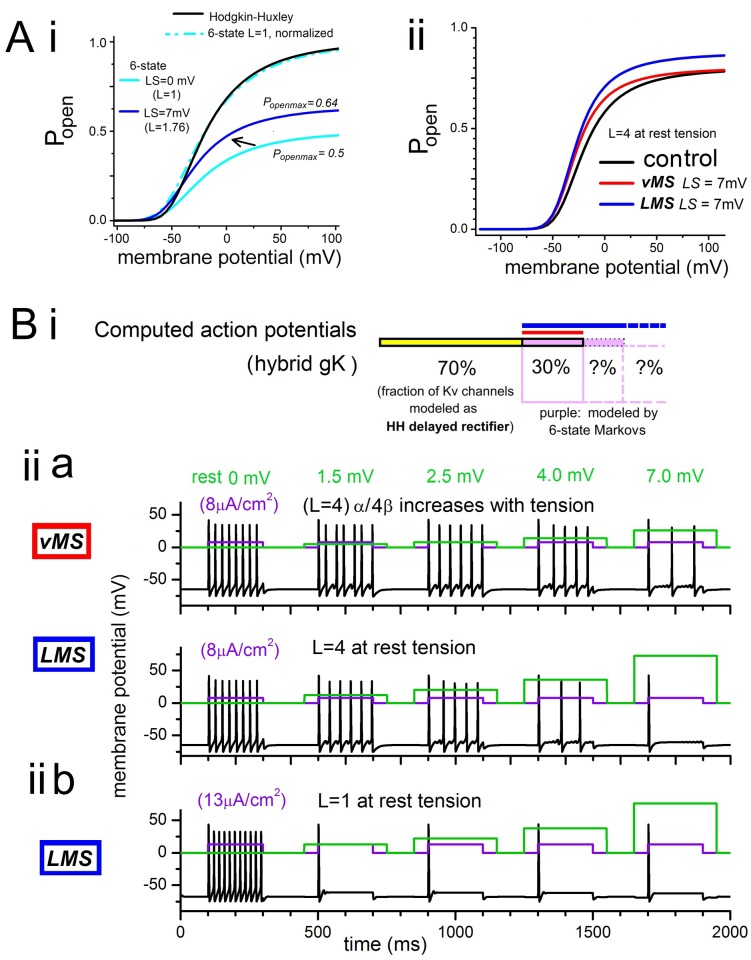
For excitable membranes that experience tension fluctuations, MS-Kvs could be physiological modulators. MS-Kv7 channels, for example, might signal strong atrial myocyte distension [33]. Especially pertinent here neuronal MS-Kv1.1 alluded to already; in pain sensing mechanoreceptor neurons, it can mechanically tune the characteristic mechanosensory firing patterns [46]. The recombinant channels exhibit MS-g(V) left-shifts of up to 7 mV, but since kinetic specifics in the neuronal gK(V,t) have yet to be studied detailed neuronal modeling would thus be premature. Basic comparisons of vMS-Kv versus LMS-Kv performance in a simple excitability setting are, however, warranted. To do so, we substituted a fraction (30%) of a Hodgkin-Huxley (HH) [64] system’s g _K with a Markov g _K that distinguishes the two putative MS-Kv types (see Appendix). Fig. 8Ai,ii plots the various g _K (V)s.

Fig 8. Effects of stretch-modulated MS Kv (3 versions) on electrically stimulated APs.

In these excitability models, 70% of gK _max is a Hodgkin-Huxley (HH) type gK and the remaining 30% is a Scheme 1 (6-state) Markov adjusted to approximate the HH-type gK with respect to V _0.5 and steepness (see Table 3 for the parameter values). Ai. Normalized P _open (V)s for HH and 6-state systems with L = 1.0 (rest), plus non-normalized plots for L = 1.0 and L = 1.76 (i.e., 7 mV of LMS left shift). Aii. For the 6-state Markov using L = 4 as rest value, P _open (V) for that rest value and for a 7 mV left-shift (LMS: L changes from “pre-stressed rest” of 4.0 to 6.9; vMS: the ratio of C ₄ ↔C ₅ kinetic constants α/4β changes by a factor of 1.76). Bi. Diagram of contributions to gK _max (two sub-populations of Kv channels as labeled). Biia. Responses of the vMS and LMS excitability systems to an 8 μA/cm² stimulus, with rest tension (LS = 0) corresponding to L = k _o /k _c = 400/100 = 4.0. MS left-shifts (LS) are modeled by accelerating the forward rate by the same factor by which the backward rate is reduced. The LS values (1.5, 2.5, 4.0, 7.0 mV) are obtained as follows: for vMS, α/4β increases by factors 1.05, 1.079, 1.14, 1.26 respectively and for LMS, with L = 4.5, 4.8, 5.4, 6.9 respectively (green lines represent % increases of α/4β or L). Biib. As in Biia, for LMS but with L = k _o /k _c = 100/100 = 1.0 at LS = 0 and L = 1.13, 1.22, 1.38, 1.76 for the other values of LS = 1.5, 2.5, 4.0, 7.0 mV respectively. I _stimulus for this case, 13 μA/cm².

For this purpose, MS-g(V)s were described using Scheme 1 (“6-state”) (Fig. 8Bi) with stretch modulation affecting only C ₄ ↔C ₅ (α/4β) for vMS, and only C ₅ ↔O (L = k _o /k _c) for LMS. Use of L = 4 at rest tension allowed for direct inter-model comparison (Fig. 8Biia). In another simulation, use of a lower value (L = 1 (Fig. 8Biib)) approximated more closely what Schmidt et al [19] would see as a near-physiological rest tension L value. We reverted to Scheme 1 in these excitability tests for electrophysiological simplicity because Scheme 3 differs too much from HH; each of the two “rest tension (control)” MS-gK(V) used were adjusted to closely match the HH-gK(V). Parameters are listed in Table 3. Mechanical stimuli would deform only part of an excitable cell (e.g., in the Hao et al [46] DRG neuron clamp experiments); for this reason the vMS- or LMS-modulated gK were made to account for only part of total rest-tension gK _max (30% was chosen arbitrarily) (Fig. 8Bi). Fig. 8Ai shows the HH g(V) and an L = 1 version of LMS-gK(V) normalized to each other (black and dashed turquoise lines). As depicted in Fig. 8Bi, for the L-based MS-Kv (i.e., LMS), the excitability model deals with gK _max as an apparent value (see Eq. 2 and the Appendix); under stretch conditions, it exceeds its rest-tension value (as for the 7-state LMS Markov of Fig. 5A, intense enough stretch, apparent gK _max could triple if rest tension L ~0.5, albeit not for a 7 mV g(V) shift). Fig. 8Aii shows g(V)s for “rest tension” (control, L = 4) then after a 7 mV left-shift (“LS”) produced by increased L or increased α/4β.

Table 3. Parameters for two sub-populations of Kv (one MS, one not) used to study the effect of a MS-Kv on HH type excitability.

	HH model(s-1)(V in mV)	Scheme 1 with L = 4(s-1)(V in mV)	Scheme 1 with L = 1(s-1)(V in mV)
αn	$10\frac{(V+55)}{1-\exp \left(-\frac{V+55}{10.0}\right)}$	$\frac{10}{1.55}\frac{(V+55)}{1-\exp \left(-\frac{V+55}{12.0}\right)}$	$\frac{10}{1.55}\frac{(V+18+55)}{1-\exp \left(-\frac{V+18+55}{12.0}\right)}$
βn	$125\exp \left(-\frac{V+65}{80}\right)$	$1.55\times 125\exp \left(-\frac{V+65}{85}\right)$	$1.55\times 125\exp \left(-\frac{V+18+65}{85}\right)$
ko	not applicable	400	100
kc	not applicable	100	100

Fig. 8 Biia (vMS vs LMS) and 8Biib (LMS, L = 1) show action potentials (APs) elicited by fixed intensity depolarizing currents (excitation threshold is higher for 8Biib, hence the larger I _stim). In Fig. 8Biia the excitability model responds to a marginally supra-threshold I _stim (on/off as per purple lines) first without stretch at rest tension (i.e., “LS” = 0 mV) then with stretch described by vMS or by tM S (stretch “on/off “as per green lines) to give 1.5, 2.5, 4 or 7 mV of left-shift (LS). The corresponding α/4β and k _o /k _c = L changes are listed in the legend. For rest tension proportion of MS-gK greater (or less) than the 30% used here, MS impacts on excitability would be more (or less) powerful than shown. Since it would be inconsistent with the Schmidt et al [19] analysis for the LMS model to have L = 4 at rest tension (4 would, by their reckoning, correspond to a high membrane tension) this could be regarded as a “pre-stressed” condition. Direct comparison between models requires this since in vMS, L = 4 at all stresses. With that proviso, Fig. 8Biia shows that for both models, increasing “stretch intensity” causes a graded inhibition of AP firing frequency. With L = 4 at rest tension in both models, outcomes for LMS and vMS are not substantially different though double-faceted MS (left-shift plus ↑apparent g _max) inhibits the electrically stimulated APs slightly more than does vMS.

Next, to compare LMS and vMS when neither has an appreciable pre-stress, we look to the lower rest tension L simulation. For true rest tension, L should, by the arguments of Schmidt et al, be lower than their smallest L values since their patches are assumed to have elevated rest tensions. Nevertheless, we chose L = 1, i.e., near the low end of their fitted range. As Fig. 8Biib shows, this puts an outright brake on excitability at the smallest tested “stretch” intensity. Any nuance disappears; even for the lowest “stretch intensity” tested (equivalent to a 1.5 mV left-shift), the stretch-induced apparent g_max increase of this LMS extinguishes excitability. By contrast, in the vMS scenario (top line of Fig. 8Biia), over the 1.5–7 mV MS-left-shift range, the AP patterns convey information about mechanical stimulus intensity and duration. We again point out however, that “braking” and modulation efficacy would depend dramatically with the proportion of total gK experiencing stretch. Additionally, MS braking requirements increase substantially once a MS-cation channel is present. Once additional native cell MS-Kv kinetic data become available, the approach used here could incorporate those features along with a MS-g _cation and the cell’s full complement of channels.

Discussion

Overview

In 2002 it was proposed that Kv mechanosensitivity [39] is explained by a cooperative voltage-dependent closed-closed transition near the open state and structure function studies showed that the Kv pore is more stable closed than open so “to open the pore the voltage sensors must exert positive work by applying an outward lateral force near the inner helix bundle” [66]. But interestingly, Mackinnon and colleagues recently argued that the final voltage independent transition in/out of the conducting state, not a preceding voltage-dependent transition, accounts for Kv mechanosensitivity [19]. Here, we addressed the known mechano-electrophysiological behaviors of Kv channels in light of these two mechanistic models. Because “tail current” decay would almost certainly be stretch-sensitive in one case but not in the other, the demonstrated stretch-insensitivity of tail currents favors the latter model. We nevertheless suggest that the oft-overlooked final transition may have an adaptive role in the Kv activation pathway. Paradoxically, a strictly thermal (insensitive to membrane voltage and to tension) entry to and exit from the conducting state would preserve a MS-Kv channel’s predominant role as V-sensitive conductance, allowing a Kv to be modulated by but not dominated by the mechanics of the bilayer. Since MS-Kv current in mechanosensory neurons was recently shown to be physiologically important [46] we also tested the two models in an excitability setting.

Identity of the critical MS transition in Kv channels

Prokaryotic MS channels are acknowledged mechanical specialists [16,34] but Kv channels, too, have been called exquisite mechanosensors [19]. While we think this needs to be tempered, modulation of VGCs by membrane stress, reported first for calcium channels [67], occurs among members of all VGC families [4]. MS modulation of VGCs does not require that channels be co-expressed with auxiliary subunits (e.g., [61,68]) and it seems safe to expect that the deformable lipid/protein interface (and not, say, a cytoskeletal linker) will prove to be the “gating spring” [4,12,62] in all cases, but beyond that, no universal mechanism for VGC mechanosensitivity has emerged. In prokaryote MS channels, dramatic differences in cross-sectional areas and transverse thickness in closed versus open conformations underlie mechanosensitivity. In Kv channels, dimensional changes are far more minimal by comparison [69,70,71,72]. In-plane shape changes for comformations along the activation path (e.g. see Fig. 9 in Ref. [73]) would, however, require structural repacking at the adjacent bilayer interface. Given that stretch-induced left-shifts and right-shifts respectively are seen in the g(V) of Kv-WT and Kv-ILT a universal “∆ area” explanation for all MS-VCG already seems ruled out, though the possibility that a MS thermal transition could serve as such a mechanism was mooted [19]. A hypothetical universal mechanism would, further, need to explain how Nav and Kv1 but not Cav and Kv3 channels (all of which exhibit reversible stretch-induced increases in steady state P _open (V)) respond to stretch with accelerated current onset. We focused narrowly here, on two postulated mechanisms of mechanosensitivity in Shaker type Kv channels. The MS opening transition model of Schmidt et al, we termed “LMS”. We fleshed it out as a Markov model with standard rate constants (except for L, which needed MS-dependent rates) to allow the models to operate in the time domain. g(V,t) comparisons were done against “vMS” models in which a voltage-dependent closed-closed transition(s) near the open state underlies Kv mechanosensitivity [39].

Fig 9. Two postulated versions for MS transitions and for the thermal open/closed transition in Kv channels.

Cartoons A and B were originally designed not to address Kv mechanosensitivity, but to illustrate ideas about the concerted pre-opening and opening transitions. We have relabeled them showing, in each, how vMS puts the MS (expand-compact) transition at C ₅ ↔C ₆, and likewise, in both, how LMS would put it at C ₆ ↔O. In A (modified from Ref. [59]), C ₆ ↔O is the opening of a bundle crossing gate while in B (modified from Ref. [79], release of the bundle crossing gate is necessary but not sufficient to allow for an I _K flow, which requires the opening of a selectivity filter gate (slow inactivation changes at the selectivity filter are also cartooned in B).

Does the model really matter?

Tabarean and Morris [39] indicated that a V-dependent closed-closded expansion near the open state in the range 2 to 9 nm² would account for their data. Schmidt et al [19], alluding to atomic structural differences of closed and open pores near the inner bilayer leaflet, suggested a 3 to 4 nm² area expansion during channel opening, emphasizing that to stabilize the open state, their model requires elevated membrane tension as much depolarization. The final arbiter of “openness” in their model (a LMS-Kv in our terms) is tension in the plane of the membrane, not transmembrane voltage. By contrast, for vMS-Kv models, tension modulates the rate of approach to the open state and shifts the V _0.5 for activation without affecting the maximal P _open.

In animal cells, plasma membranes, when not stressed by applied forces or osmotic swelling, are generally near-flaccid (neurons sustain small non-zero membrane tensions [32,74] and so the consequences of a MS opening as envisaged by Schmidt et al would be biologically non-trivial (e.g., see Fig. 8iib). The biophysical consequences would also be striking: Kv channel gating currents measured under rest tension conditions (near-flaccid) would yield true Q _max values but for true gK _max (several-fold beyond the apparent value measured at rest tension; see Fig. 5A) the V-clamped membrane would need to be subjected to untenably high stress. Kv channel density calculated using unitary conductance and rest tension gK _max would systematically be underestimated several-fold. In molecular models of V-sensing, attributions of gating charge per Kv channel would consequently be too high [75]. Inappropriate channel density measurements would also distort cell biological expectations regarding rates of Kv biogenesis and demands on trafficking machinery. Pharmacological quantities whose calculation assumes accurate channel density numbers (e.g. Kv/toxin binding interactions) would be assessed wrongly.

The concerted V-dependent pre-opening transition

In the Kv tetramer, a concerted V-dependent pre-opening motion generates a centripetally acting force to untwist the intracellular bundle crossing, [76],[77],[66] yielding an “activated-closed” state (C ₆ in Scheme 3) [63]. Channel opening occurs at the next transition C ₆ →O. Comparison of the responses of Kv WT and Kv ILT channels to stretch can help discriminate between vMS or LMS mechanisms. In vMS, an area increase is assumed to occur at the C ₅ →C ₆ transition, while in LMS it occurs at C ₆ →O. In WT, stretch yields a g(V) left-shift, in ILT, a right shift [45]. Mechanical stretch, whether acting on the C ₅ →C ₆ or the C ₆ →O transition would decrease the enthalpy of the corresponding transition, and hence would yield a left shifted g(V), the result observed for WT. ILT activation however exhibits g(V) right-shift during stretch [45]. This could be explained if stretch-deformation of the ILT/lipid interface increased the number of ways of being in C ₅ (= increased entropy and stability in C ₅) enough so that the free energy change at C ₅ →C ₆ is dominated not by the enthalpic decrease in C ₅ →C ₆ (as in WT) but by the entropic change. In summary, a net positive free energy change of this sort would result in a g(V) right-shift.

Co-operative bundle crossing movements close to Kv pore opening involve substeps [60,71,78]. A V-dependent in-plane expansion-substep (e.g., Fig. 9A) could readily underlie vMS but for LMS a late V-dependent concerted closed-closed transition would need to store elastic energy [4] without laterally expanding the channel (unlike cartoon Fig. 9A). In LMS expansion opens the permeation path. For LMS, a conundrum is that Kv closing’s demonstrable insensitivity to tension would imply a transition state essentially identical in area to the open state (Fig. 1Fv), thus implying I _K (V) onsets far more strongly accelerated by tension than observed. The identity of the final opening transition is, in any case, unsettled. A standard picture invokes bundle crossing motions (Fig. 9A) but another speculation (Fig. 9B; relabeled cartoon) [79] is that the closed bundle crossing allosterically constrains the selectivity filter (SF) in a non-conducting state while V-dependent opening of the bundle crossing relieves that constraint. Opening of the SF would be a final V-independent transition in the activation path. Voltage and tension working together to destabilize the penultimate closed state in a vMS version of Fig. 9B would be essentially as envisaged by Yifrach and Mackinnon [4].

Operational sensitivity to membrane tension and to V _m in LMS versus vMS models

Terminating a vMS-Kv activation path with a strictly thermal closed/open transition diminishes the impact of bilayer mechanics on ion currents. A LMS-Kv is essentially a V-modulated MS channel whereas a vMS-Kv is a tension-modulated V-gated channel.

In a Hodgkin-Huxley gK, P _open approaches unity at large depolarizations, while, as per Hoshi et al [48], in our vMS Schemes (1,2 or 3), maximal P _open = 0.8. In LMS, extreme membrane tensions allow P _open to approach unity. This could add scope for signalling about bilayer mechanics where extreme tension is relevant (e.g., in walled cells that move vertically in water columns and/or that experience osmotic turgor pressure changes). Although the data argue against LMS-Kv for Shaker type channels, data for Kv3 channels are not consistent with a vMS model; Kv3s show one key feature of a LMS-Kv (reversible MS increase in apparent g _max) but have neither a MS-tau or a MS-g(V) shift [44]. Since smooth muscle maxi-Kv channels are strongly modulated by a dietary lipid [80] that appears to stabilize the open state it would be interesting to know if earlier reports of mechanosensitivity in similar channels [81] reflect MS modulation of a lipid-sensitive thermal C-O transition.

We concur with Schmidt et al that a channel such as they propose (the LMS-Kv model) would be “exquisitely mechanosensitive”, but for reasons noted above, the descriptor is apt only from certain perspectives. From a per-channel perspective, a LMS mechanism “disenfranchises” a portion of expressed channels. For example, in Fig. 8Ai (L = 1 ⇾ L = 1.76) the apparent half-g _max at rest tension is not 0.5 but 0.25, and even with near-lytic stretch, LMS precludes ~35% of channels from contributing current. Nevertheless, from a cellular excitability perspective, LMS-Kv channels would indeed be powerful mechano-effectors (Figs. 8Ai and 5Bii).

Our excitability modeling indicates, in fact, that a LMS-Kv could menace normal excitability (Fig. 8Biib). With LMS, excitability is extinguished by a 1.5 mV g(V) left-shift of only 30% of Kv channels, so if 100% of Kv channels were LMS-type, the most minor mechanical perturbation would likely be intolerable. However, cells have diverse MS channels [22] some of which are excitatory, and our basic excitability model ignored them. What our admittedly rudimentary excitability modeling demonstrates is that “stretch-induced” left-shifts of a MS component of gK will modulate evoked AP trains. Assuming an excitable membrane initially at rest tension (no pre-stress), vMS can produce graded MS modulation while LMS simply extinguishes excitability (as in Fig. 5Biib). Physiologically, all else being equal, a LMS-Kv would be a dramatically powerful MS brake on excitability, whereas a vMS-Kv would be a nuanced MS brake, conveying rather than supressing information about the strength and duration of mechanical deformations of the bilayer.

Conclusion

The recent proposal that Kv channel mechanosensitivity resides with MS thermal (i.e. voltage-independent) closed-open transition has not, in our view, been established. Issues addressed here regarding recovery from slow inactivation, reversibility of MS responses, and tail current kinetics undermine the LMS case, as do the model’s implications for experimental determinations of Kv channel density and thence gating charge per channel. While we do not propose vMS as a universal mechanism for VGC mechanosensitivity (or even for all Kv channels), it remains a satisfying model for the MS responses of Shaker type Kv channels.

Appendix: The two gK(V,t) subpopulations, one being an MS-Kv, for an HH excitability system

This Appendix explains how we subdivide the Kv conductance gK(V,t) in a Hodgkin Huxley (HH) excitability system, as discussed in Section Excitability and a MS-Kv: vMS versus LMS. This allows us to implement different versions of an MS-Kv. The total K⁺ current density (in μA/cm²) in the two-population system is given by:

$$I_K=gK\left(f_{HH}{n}^4+f_M\frac{P_o}{P_{o,\max }(L_0)}\right)(V-E_K),$$ [5]

where the potential terms V are in mV, and f _HH and f _M are respectively the fractions of the total conductance arising from HH-like and Markov like Kv channels at rest tension. The f _HH fraction obeys HH like kinetics and the f _M fraction Scheme 1 like Markov kinetics (with f _HH + f _M = 1). In our calculations f _M was 0.3. P _o is the open probability of the Scheme 1 channels; P _o,max (L₀) is the maximum P _o at L ₀, the “rest tension” value of L = k _o /k _c. The total steady-state Kv conductance is given by:

$$g\left(V\right)=gK\left(f_{HH}n{\left(V\right)}^4+f_M\frac{P_o\left(V\right)}{P_{o,max}\left(L_0\right)}\right)$$ [6]

Its maximum value at L = L ₀, gK is the apparent gK _,max. Only the f _M component is mechanosensitive. Increase in L leads to an increase in the maximal current density g _K (V—E _K) of:

$$\Delta I_{K,\max }=gK{f}_M\frac{L-L_0}{L_0(1+L)}(V-E_K),$$ [7]

or an increase in the maximum conductance from gK, to gK + Δg _max where:

$$\Delta g_{\max }=gK{f}_M\frac{L-L_0}{L_0(1+L)}.$$ [8]

The other physical constants for the Nav and Kv channels and the leak conductance are the same as in Table 1 of Ref. [65] (e.g. gNa = 120.0 mS/cm², gK = 36.0 mS/cm², g _leak = 0.25 mS/cm², etc…, with equation constants adjusted to give time units as s). The kinetic parameters of the models (HH like and Markov) are given in Table 3.

Data Availability

The paper alludes to published data which are referred to in the References.

Funding Statement

This work was supported by Natural Sciences and Engineering Research Council (Canada) (BJ, Discovery grant and EAP, undergraduate student research award) and Ottawa Hospital Research Institute (CEM). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.