Considering the kinetics of mRNA synthesis in the analysis of the genome and epigenome reveals determinants of co-transcriptional splicing

Abstract

When messenger RNA splicing occurs co-transcriptionally, the potential for kinetic control based on transcription dynamics is widely recognized. Indeed, perturbation studies have reported that when transcription kinetics are perturbed genetically or pharmacologically splice patterns may change. However, whether kinetic control is contributing to the control of splicing within the normal range of physiological conditions remains unknown. We examined if the kinetic determinants for co-transcriptional splicing (CTS) might be reflected in the structure and expression patterns of the genome and epigenome. To identify and then quantitatively relate multiple, simultaneous CTS determinants, we constructed a scalable mathematical model of the kinetic interplay of RNA synthesis and CTS and parameterized it with diverse next generation sequencing (NGS) data. We thus found a variety of CTS determinants encoded in vertebrate genomes and epigenomes, and that these combine variously for different groups of genes such as housekeeping versus regulated genes. Together, our findings indicate that the kinetic basis of splicing is functionally and physiologically relevant, and may meaningfully inform the analysis of genomic and epigenomic data to provide insights that are missed when relying on statistical approaches alone.

INTRODUCTION

Messenger RNA (mRNA) synthesis is a highly regulated process in which transcription factors and chromatin modifying factors coordinate with Pol II to produce a nascent strand of RNA. The nascent pre-mRNA is processed by 5′ capping, 3′ polyadenylation and pre-mRNA splicing—the removal of non-coding introns. Complete splicing is necessary for proper mRNA export, stability and protein function. RNA processing steps can in principle be initiated and completed during the transcription process, i.e. co-transcriptionally, but may also occur post-transcriptionally (1–9). It is now well established that a large fraction of splicing occurs co-transcriptionally in metazoan genomes (9,10).

Because of the constraints imposed on co-transcriptional splicing (CTS) by the parallel process of transcriptional elongation, an intron's fate may be dramatically affected by the elongation dynamics of Pol II. Indeed, a slower Pol II can result in increased use of a weak 5′ splice site in reporter gene constructs (11,12) or alternative exon skipping by allowing a negative factor to bind (13). Splice site choice can be altered in human cell lines by removing downstream pausing sites (14) or pharmacologically slowing down Pol II (15), and Pol II pausing may cause an increase in CTS (5,6,16). Also, spliceosome recruitment may be coordinated with transcription (17–21), for example via the carboxy-terminal domain (CTD) of Pol II (22), and Pol II mutants lacking the CTD produce splicing defects (23). Further, CTS may regulate chromatin modifications to reinforce transcription initiation (24) or may facilitate rapid gene induction during the inflammatory response (25,26).

However, splicing may also occur post-transcriptionally (27–29), and studies of how splice patterns of specific genes are achieved have generally identified trans-acting splicing factors, which may function both co- and post-transcriptionally, as key determinants. Indeed, statistical machine learning approaches are the basis for computational tools that predict splice patterns based on splice factor expression and cognate binding site sequences (30).

Thus, whether the kinetic control implicit in co-transcriptional splicing is in general functionally important remains an open question. The answer determines (i) whether a kinetic modeling framework will be required to improve predictions of splice patterns. Indeed, no scalable mechanistic modeling framework amenable to genome-wide experimental testing has yet been established. It also determines (ii) whether the annotation of the genome itself may gain from applying kinetic considerations.

Here, we examined how the kinetics of transcription and splicing may affect the control of CTS within the normal ranges of metazoan physiologies. We constructed a scalable mathematical model of splicing coupled to transcriptional elongation in order to identify genetic and epigenetic features that regulate CTS. Using this model we developed methods to extract kinetic information from next generation sequencing (NGS) data (29,31), thus allowing us to parameterize the kinetic CTS model in a species-specific manner. We reasoned that while splicing of specific introns may be critically determined by trans-acting splicing factors, the common kinetic basis of CTS may be apparent when considering cohorts of introns.

Our analysis revealed a variety of gene features that contribute to CTS efficiency and that these are over-represented in specific cohorts of genes. By expanding the model we were able to simulate co-transcriptional outcomes of multi-intron genes genome-wide as a function of genomic and epigenomic determinants. Our results show that while genes may differ widely in their cis-determinants of CTS, the kinetic integration of transcription and splicing is an intrinsic feature of gene expression control, and that mechanistic mathematical models that account for these kinetic processes may form the basis for genome analysis tools that usefully complement statistical approaches.

MATERIALS AND METHODS

Computational modeling

We simulate the elongation of a single polymerase and the transformation of its associated transcript. The probability that an intron has spliced by the time that transcription has terminated is a function of the time it takes to cleave and polyadenylate the mRNA subsequent to the intron's synthesis, and the kinetic rate of splicing. Splicing can be modeled as a series of j sequential reactions (32). By assuming that the time of each reaction is an independent, exponentially distributed random variable with forward rate constant k_s*j, we can model the probability of splicing at time t as a gamma-distributed random variable with shape j and mean 1/k_s. Thus, the probability that an intron i has spliced by time t is the cumulative distribution:

For a single-step reaction (j = 1), this simplifies to the exponential distribution:

If we assume a constant elongation rate k_E, the total elongation time T_i downstream of intron I is proportional to the distance D_i from intron I to the poly(A) site:

Splicing rate constants are reported in the manuscript as k_E/(k_s*j).

Multi-intron model

Each potential transcript for a gene with N introns and N + 1 exons can be represented as a string , where S_i = 1 if intron i has been spliced out, and 0 if it is retained. Therefore the probability of each transcript S is:

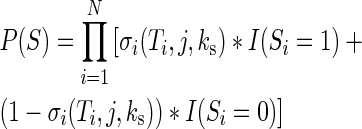where I(x) is the indicator function. To predict the abundance of each transcript at the end of CTS, we calculate P(S) for all possible transcripts: co-transcriptional splicing efficiency was defined as the abundance of the transcript S whose introns have all been removed (all ). Therefore, CTS efficiency can be computed simply as:

This is an O(n) operation and is therefore extremely fast, making this model scalable to genes of any complexity.

RESULTS

A model of co-transcriptional constitutive splicing

We first modeled co-transcriptional splicing of individual introns using a one- or two-step splicing model (cf. (32)). An intron's probability of being spliced co-transcriptionally σ is determined by its splicing rate constant and the duration of the transcriptional phase following the synthesis of the 3′ splice site but prior to mRNA polyadenylation (Supplementary Figure S1A). We next combined models of independent introns to generate a model of co-transcriptional constitutive splicing (CTCS). Our CTCS model enables simulations of multi-intron genes of any complexity and allows us to quantitatively assess the effects of genome structure and kinetic rates on genome-wide splicing outcomes (Figure 1A). Using parameters fit to RNA-seq data to simulate a test gene (see Supplemental Methods, and Supplementary Figure S1B), the CTCS model recapitulated a central point of the kinetic theory of CTS control (6,7,9): namely, that long genes (Figure 1B, left), and specifically genes with long last exons (Figure 1B, right) would favor CTS (because they provide more time for splicing), whereas the length of the penultimate exon (which has no influence on the splicing time of the last intron) would be less important (Figure 1B middle). These conclusions are robust to specific splicing parameter values (data not shown).

Figure 1.

Model of co-transcriptional constitutive splicing (CTCS). (A) Model schematic showing all possible reactions and species for a 3-intron gene. The eight possible isoforms that can exist when transcription is complete are color-coded at right. (B) Model simulations of the 3-intron gene. Each column represents the distribution of the eight species after each simulation. Left: the lengths of all introns and exons were scaled up and down by a constant factor. Middle: length of exon 3 was varied; Right: length of exon 4 was varied. (C) Distribution of exon lengths among last and internal exons in the human genome. (All error bars indicate SEM; P-values are the results of t-tests). (D) Average splicing acceptor scores in last and non-last introns genome-wide. (E) Nucleosome stability scores in the first 147 bp of last versus internal exons. (F) Average genome-wide MNase-seq signal in K562 cells and GM12878 cells over internal exon starts versus last exon starts. t-Test was performed by averaging the signal across the 147 bp and comparing this average in internal versus last exons.

It has previously been suggested that long last exons may have evolved to optimize CTS (Figure 1C, Supplementary Figure S2A; (6)). We expected that if complex genomes evolved under pressure to maintain high CTS efficiency, other genomic signatures besides last exon length, that influence CTS, may be identifiable. Since our model predicted the excision of last introns to be the limiting step in determining the CTS efficiency, we compared acceptor splice site strengths across several genomes based on species-specific sequence motifs. Indeed, we found evidence for conservation of higher average acceptor scores in last introns compared to non-last introns in several vertebrate genomes (Figure 1D, Supplementary Figure S2B: 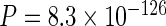). Since the presence of nucleosomes can inhibit transcription elongation (33) and thus provide more time for CTS, we next tested whether nucleosome stability was enriched at 3′ exons. We first evaluated nucleosome stability across several species using a simple algorithm based on biophysical considerations (34), and found that nucleosomes are indeed expected to be more stable at terminal exons than at internal exons (Figure 1E, Supplementary Figure S2C: 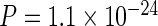). Furthermore, analysis of human cell MNase-seq data (ENCODE Project 35) revealed that nucleosomes are enriched in the proximity of last exons compared to internal exons (Figure 1F). Interestingly, it was previously observed that nucleosomes are present in higher abundance in exons flanking weaker splice sites, both in internal and last exons (36), reinforcing the hypothesis that nucleosome occupancy and splice sites may balance each other to control CTS.

Fitting the model to RNA-seq data

To parameterize our model, we took advantage of existing RNA-seq measurements of purified cellular compartments in K562 cells (31) to estimate the steady-state spliced fraction (Σ) for each intron (17 266 introns in 2768 genes; see ‘Materials and Methods’ section). For this analysis, we restricted our set of genes to those that use their most downstream annotated poly(A) site, as determined by RNA-seq of the cytoplasmic fraction (13 650 introns in 2136 genes). Examining non-poly-adenylated nuclear transcripts, median Σ strongly correlates with distance to the poly(A) site, in K562 cells, as reported previously (9), and in other cell types (Supplementary Figure S3). By fitting our model to the median Σ of introns binned according to distance from poly(A) site, we obtained a ratio of splicing rate to elongation speed (see Supplemental Methods). We also examined RNA-seq data from the chromatin fraction of mouse macrophages (29), but this dataset contains many polyadenylated mRNAs that are post-transcriptionally associated with chromatin (Supplementary Figure S4, (26,29)).

Fitting the CTCS model to the nuclear poly(A)-depleted K562 data resulted in a ratio of elongation rate to splicing rate of 615 bp/splicing event, equating to an intron half-life of 9 s if elongation is 3 kb/min (37). The fit was robust to the binning procedure used (Supplementary Figure S1B and C), and a two-step model did not improve the fit to the model (Supplementary Figure S1C). However, previous studies have derived estimates of co-transcriptional splicing rates in diverse organisms ranging from a 30 second half-life to a 5–10 min ‘splicing completion time’ (4,27,32,38).

A close inspection of the poly(A)-depleted nuclear RNA-seq data revealed that the CTCS model underestimated the steady-state spliced fraction of introns proximal to the poly(A) site (Figure 2A, Supplementary Figure S1B), similar to findings in yeast (6). This disconnect could be due in part to conditions that prolong association of nascent, un-polyadenylated RNA with the chromatin template beyond the time predicted by the poly(A) site (39), such as a transcriptional pause near 3′ ends (6), or transcriptional read-through past the poly(A) site. We therefore modified our CTCS model to include a post-poly(A) site time delay (model CTCS + T), and fit this model to the chromatin-associated RNA-seq data.

Figure 2.

Pol II read-through may contribute to delay time following transcription of the poly(A) site. (A) Deriving kinetic parameters by fitting CTCS model to median spliced fraction Σ of 100 equally populated bins of introns. Green and blue lines are the fits to the CTCS or CTCS + T_FIT models, respectively. T_FIT refers to the average additional time after Pol II transcribes the poly(A) site, as determined by the model fit. (B) UCSC browser tracks showing GRO-seq traces in mouse macrophages for representative gene irf2bp2. Schematic boxes indicate the read-through lengths and transcription units determined computationally (40). (C) Distribution of transcriptional read-through as measured by GRO-seq in human MCF7 cells (top) and mouse macrophages (bottom). (D) Simulations of CTS in all human genes (left) and mouse genes (right). Genes were split into four evenly sized groups based on total gene length [short (<6444 bp), medium short (6444–20 252 bp), medium long (20 257–57 229 bp) and long (>57 229 bp)], and further subdivided by the number of introns. Boxplots of CTS efficiency for short and long groups are shown for simulations in three models: CTCS, CTCS + T_FIT, and CTCS + T_GRO. T_GRO refers to the additional time after Pol II transcribes the poly(A) site if transcription proceeds to the termination sites identified by GRO-seq, in individual genes for which GRO-seq measurements are available. All boxes show the extent of the 50% inter-quartile range and the notches estimate a 95% confidence interval for the median.

Remarkably, allowing for this additional time interval (T_FIT) in our model dramatically improved the fit to the data (Figure 2A, Supplementary Figure S3). The best fit was obtained when the median time delay was equivalent to elongating 4.7 kb past the poly(A) site (see Supplemental Methods), and with a new value of 3.1 kb/splicing event for the elongation to splicing ratio. Assuming an elongation rate of 3 kb/min, these values equate to a median 3′ delay of 94 s and a median intron half-life of 43 s. This second estimate of median splicing half-life is more consistent with, though still on the fast side of those previously reported (4,27,32,38). If elongation rates turned out to be slower, those half-life estimates would proportionally increase.

To investigate whether transcriptional read-through could account for the extra time observed in CTCS + T_FIT, we measured the extent of active transcription associated with each gene using a novel software tool (40) to analyze GRO-seq (41) data. We used our GRO-seq dataset (42) in mouse macrophages (Figure 2B), and an existing dataset of human MCF7 cells (43) to measure how far pol II activity extends. As cleavage and polyadenylation may occur prior to termination of pol II activity, these measurements put an upper limit on the pre-cleavage read-through distance.

Most genes showed pol II activity well beyond the annotated poly(A) site (Figure 2B) indicating median read-through distances in macrophages and MCF7 of 3.2 and 3.8 kb (equivalent to 68 and 76 s), respectively (Figure 2C). These data suggest that transcriptional read-through may contribute but does not fully account for the estimated delay in polyadenylation after traversing the poly(A) site.

To investigate the effect of the 3′ delay T on CTS, we calculated the CTS efficiency of all human and mouse genes using the CTCS and CTCS + T models and a splicing rate of 3.1 kb/splice (Figure 2D). CTS efficiency was defined as the fraction of transcripts in which all introns are removed prior to cleavage and polyadenylation (see Supplemental Methods), though some level of co-transcriptional splicing may be occurring even for transcripts that are scored as incompletely spliced. With no 3′ delay T, <50% of transcripts were predicted to be completely spliced upon polyadenylation. Genes with many introns, especially short genes, showed even lower CTS efficiency. With the 3′ delay equated to either the median fitted delay time (+T_FIT), or to the time equivalent of GRO-seq-measured read-through distances in individual genes (+T_GRO), resulted in an increase in CTS efficiency. However, CTS efficiency remained dependent on gene length and the number of introns, such that even these time delays are not sufficient to ensure that all introns are spliced in short genes, especially those with many introns.

Predicting selective Pol II pausing at 3′ ends

Our model revealed that some genes’ structures predispose their transcripts for inefficient CTS. However, if efficient CTS were selected for during the evolution of complex genomes, we would expect to find compensatory signatures of other CTS determinants. Indeed, we found that nucleosome stability of genes is markedly higher in short genes than long genes in vertebrate genomes (Figure 3A, Supplementary Figure S5A). This trend could explain the finding that Pol II elongation rate is positively correlated with gene length (44). Furthermore, among short genes, those with high numbers of introns had very high average nucleosome stability scores. No similar compensatory signatures were observed for splice site scores (Supplementary Figure S5B), which correlate with intron length and are universally stronger in last introns (Supplementary Figures S2C and S5C). We examined nucleosome occupancy in K562 and GM12878 cells using the MNase-seq data. Within short genes, nucleosome density increased with increasing numbers of introns (Figure 3B).

Figure 3.

Variable Pol II elongation kinetics favor CTS. (A) Boxplots (50% inter-quartile range and 95% confidence interval of the median) of the nucleosome stability score of each gene in indicated gene categories based on gene length and intron numbers. Nucleosome scores were averaged over the region of the gene that encompassed the second through final exon. Stability scores of exons in genes with 1–4 introns are significantly lower (P < 10e−10, indicated by **), or higher (P < 0.005, indicated by ‡) than stability scores of exons in genes with 8+ introns (t-tests). (B) Average MNase-seq signal over all exon starts in K562 (left) and GM12878 cells (right) in short and long genes, split up by intron number. (C) Average PolS2 ChIP-seq signal in the 1 kb upstream of the poly(A) site (left), and gene expression (right) for short and long genes split up by number of introns, in K562 cells. PolS2 ChIP-seq signal in genes with 1–4 introns is significantly lower (P < 0.005 indicated by *) than PolS2 ChIP-seq signal in genes with 8+ introns (t-tests). FPKM stands for fragments per kb per million reads sequenced. (D) Average PolS2 signal downstream of the poly(A) site. Traces are normalized to the average of the 1 kb upstream of the poly(A) site for each category. (E) Simulations of CTS efficiency in short and long human genes using model CTCS + T_FIT. Boxplots of simulations in four separate modeling conditions (see Supplemental Methods) are shown: T_FIT: same as Figure 2D; + Δelong: elongation rate of each gene was modulated as an inverse function of nucleosome stability. + Δsplice: kinetic splicing rate was modulated so that last introns had a rate twice the speed of other introns. + Δboth: both elongation and splicing rates were modulated.

We next tested whether we could find evidence of differential Pol II dynamics in long and short genes by examining Pol II CTD SerineS2 phosphorylation (PolS2) in K562 cells in the vicinity of poly(A) sites that were not within 1 kb of any other genes’ starts or ends. In the 1 kb upstream of the poly(A) site, PolS2 read densities were higher for short genes than long genes (Figure 3C) (though PolS2 read densities also correlate with gene expression levels), and genes with more introns have disproportionately high PolS2 densities. Furthermore, short genes generally had prominent peaks of PolS2 signal after the poly(A) site (Figure 3D), whereas long genes had lower and broader peaks. These data indicate that differential regulation of Pol II elongation could be sufficient to confer high CTS efficiency to all genes, regardless of gene structure.

To test this hypothesis we simulated all human genes (Figure 3E) and mouse genes (Supplementary Figure S5E) with our CTCS + T_FIT model using variable elongation parameters. Using experimentally determined elongation rates of long genes in K562 cells (44), we tested that elongation rates were negatively correlated with nucleosome stability (Supplementary Figure S5D), and we used this correlation to extrapolate elongation rates for each gene based on the nucleosome stability scores shown in Figure 3A (see Supplemental Methods). Allowing for a variable elongation parameter (+ Δelong) resulted in preferentially marked increases in CTS efficiency for short genes with many introns (Figure 3E). Next, we tested the effect of having stronger splice sites in last introns (+ Δsplice). This change increased CTS efficiency in most gene categories, but exacerbated the differences between genes with many or few introns. When we took into account both variable elongation and splicing rates (+ Δboth), there was an increase in CTS efficiency across all categories. These modeling results are consistent with a central role for elongation control in the regulation of CTS efficiency. Moreover, these data illustrate the power of modeling to elucidate the combined contributions of several factors, such as elongation, nucleosome stability, and splice site strength, for regulating co-transcriptional splicing.

Distinct genomic CTS-determinants of housekeeping genes

Since CTS efficiency depends on Pol II dynamics, we hypothesized that differentially regulated gene groups would show distinct signatures of CTS. We compared constitutively-expressed housekeeping (HK) genes with genes whose expression is more variable across cell types (non-HK; 45). Nascent RNA-seq revealed that HK genes have overall higher steady-state intron spliced fraction Σ than non-HK genes, especially for introns close to the poly(A) site (Figure 4A). The CTCS + T_FIT model, when fit to this data, predicts a significantly longer post-poly(A) site delay for HK genes (equivalent to 7.3 kb) compared to non-HK genes (3.8 kb). Interestingly, our mouse GRO-seq data, indicates that the average read-through is significantly longer in HK genes than non-HK genes (4.4 versus 3.6 kb, respectively: Figure 4B: ).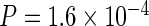

Figure 4.

Housekeeping genes have distinct CTS determinants. (A) Splicing completion in nuclear poly(A)-depleted RNA-seq is higher in housekeeping genes (red) than other genes (black). Inset shows parameter fits to CTCS + T_FIT. The asterisks indicate statistical significance (P < 0.001). (B) Read-through in mouse genes as measured by GRO-seq. Error bars indicate SEM; P-values are the results of t-tests. Acceptor scores (C) and exonic nucleosome stability scores in the first 147 bp (D) in HK versus non-HK genes based on human genome sequence. (E) Normalized PolS2 ChIP-seq signal at the poly(A) site of HK and non-HK genes, for long and short genes.

Next, we analyzed how the combination of other CTS determinants could contribute to the higher CTS efficiency of HK genes. The model fit resulted in a higher elongation/splicing ratio in HK genes: 3.5 kb/splice compared 3.0 kb/splice in non-HK genes (Figure 4A). Interestingly, introns throughout HK genes in fact have stronger splice sites than non-HK gene introns (Figure 4C, Supplementary Figure S6A: ): therefore the elongation/splicing ratio in HK genes is consistent with a faster elongation rate instead of a slower splicing rate. In support of this hypothesis, HK genes have on average lower nucleosome stability than non-HK genes (Figure 4D, Supplementary Figure S6B: ). This faster elongation/splicing ratio implies that HK genes would have lower CTS efficiency were it not for a longer post-poly(A) site delay time. As transcriptional read-through measured by GRO-seq (4.4 kb) does not account for the expected delay (equivalent to 7.3 kb), we hypothesized that transcriptional pause sites may provide additional time. Strikingly, in support of this hypothesis, HK genes have much stronger PolS2 peaks downstream of their poly(A) sites in K562 cells than non-HK genes (Figure 4E).

DISCUSSION

In this study, we constructed a scalable computational model of CTS to identify and interpret the biological significance of genetic, sequence, and epigenetic features in vertebrate genomes. We found that distinct combinations of genetic and epigenetic determinants apply to different cohorts of genes; regulated genes appear to have evolved to rely more on nucleosomal control of pol II elongation to achieve high CTS efficiency than housekeeping genes, which contain more introns (46) but have higher splice site scores and exhibit longer Pol II read-through. As nucleosome density is a component of the regulated chromatin landscape, our observation suggests that splice patterns of non-HK genes are an integral part of their gene expression regulation.

Model simulations further suggested that many transcripts remain incompletely spliced when Pol II reaches the poly(A) site (Figure 2D), but that several mechanisms may contribute to ensuring completed splicing prior to transcript release. Indeed, our analysis estimates an average interval of ∼1.5 min between transcription of the poly(A) site and cleavage of the pre-mRNA (Figure 2A). One mechanism may involve transcriptional read-through by which Pol II terminates well past the poly(A) site (Figure 2C). A second may involve increased PolS2 occupancy indicative of pausing at the 3′ end of shorter genes. And third, several studies have shown that even cleaved and polyadenylated but incompletely spliced mRNAs are retained on the chromatin (26,29,47). The delay in transcript release could result from the complex requirements of termination (48), or perhaps reflects a checkpoint that prevents release of pre-mRNA transcripts (5). Even if the ultimate catalytic steps of splicing occur post-transcriptionally, the recruitment and assembly of splicing complexes likely occur co-transcriptionally (7,8,27,47), and are therefore subject to the kinetic considerations addressed here. Indeed, a detailed quantitative delineation of post-transcriptional events will require refinement of the current model so that the chemical reaction of splicing is delineated starting with the recruitment of splicing factors (cf. (49)). Similarly, the quantitative impact on CTS of other mechanisms such as splicing enhancers or suppressors and associated trans-acting factors (30,50), the chromatin-mediated recruitment of splicing factors, or alternative splicing may be studied by extending the current model formulation.

The present work suggests that mathematical modeling frameworks of splicing must include a kinetic component, and that kinetic considerations encoded in such models lead to new insights about the organization of the genome and epigenome, as well as the patterns of gene expression observed in RNAseq datasets. As such, the present work illustrates that simple kinetic considerations of gene expression processes can be brought to bear on the analysis of genome-wide datasets produced by Next Gen Sequencing approaches, revealing novel insights by mechanistically connecting measurements of gene structure, sequence elements, chromatin modification, and the abundance of mRNA isoforms.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online. Code is available at https://github.com/jdavisturak/CTCSmodel.

FUNDING

National Institutes of Health (NIH) grant funding, specifically the ‘San Diego Center of Excellence for Systems Biology’ [P50 GM085764 to A.H.]; University of California at Los Angeles to Center for ‘Ribonomics of Gene Regulation’ [U01 HG007912 to A.H.]; investigator grants [R01 GM085474 to T.L.J. and R01ES024995 to A.H.]; National Science Foundation Graduate Research Fellowship Program (to J.D.-T., M.N.S.). Funding for open access charge: NIH [P50 GM085764].

Conflict of interest statement. None declared.