Five checkpoints maintaining the fidelity of transcription by RNA polymerases in structural and energetic details

Abstract

Transcriptional fidelity, which prevents the misincorporation of incorrect nucleoside monophosphates in RNA, is essential for life. Results from molecular dynamics (MD) simulations of eukaryotic RNA polymerase (RNAP) II and bacterial RNAP with experimental data suggest that fidelity may involve as many as five checkpoints. Using MD simulations, the effects of different active site NTPs in both open and closed trigger loop (TL) structures of RNAPs are compared. Unfavorable initial binding of mismatched substrates in the active site with an open TL is proposed to be the first fidelity checkpoint. The leaving of an incorrect substrate is much easier than a correct one energetically from the umbrella sampling simulations. Then, the closing motion of the TL, required for catalysis, is hindered by the presence of mismatched NTPs. Mismatched NTPs also lead to conformational changes in the active site, which perturb the coordination of magnesium ions and likely affect the ability to proceed with catalysis. This step appears to be the most important checkpoint for deoxy-NTP discrimination. Finally, structural perturbations in the template DNA and the nascent RNA in the presence of mismatches likely hinder nucleotide addition and provide the structural foundation for backtracking followed by removing erroneously incorporated nucleotides during proofreading.

INTRODUCTION

Maintaining high fidelity during transcription is essential for the accurate transfer of genetic information from DNA to RNA. RNA polymerase (RNAP) misincorporates only one wrong nucleotide per ∼100 000 bases (1). Multi-subunit RNAP structures differ overall between bacteria and eukaryotic organisms, but because the central structural features and functions are similar, overall mechanisms are expected to be conserved. The energetics of base pair formation is assumed to be a key contribution to fidelity. However, because many mismatched bases can be maintained with marginal stability, base pairing alone is not a sufficient explanation of the very low error rate of RNAPs. In principle, fidelity checkpoints could be achieved during any or all of the following steps: initial binding of a nucleoside triphosphate (NTP), isomerization into a catalytically competent conformation coupled with trigger loop (TL) closing, catalysis, pyrophosphate release associated with TL opening and translocation (2,3). While fidelity control during the first three steps would prevent misincorporation, delay or inhibition of the last two steps in the case of misincorporation could lead to backtracking, followed by endonucleolytic cleavage and expulsion of an incorrect nucleotide.

It is generally believed that NTP binding and pairing with the DNA template requires an open TL and involves three steps: (i) in the prevailing model, the NTP would first enter through the secondary channel or the main channel and bind at the template-independent entry (E) site (4,5). (ii) After rotation, the NTP would bind at a template-dependent pre-selection (PS) site (6) before, (iii), transferring into a catalytically competent configuration in the active (A) site. Structural data show incorrect NTPs only in E (4) and PS (6,7) sites suggesting that the transition to the A site is either prevented or unfavorable for incoming incorrect NTPs. A conformational change preceding catalysis has also been suggested as a key fidelity checkpoint based on evidence for RNA-dependent RNA polymerase (RdRp) (8) and, more recently, for RNAP involving the mobile TL (9). The TL is believed to close the active site in the presence of a complementary NTP (cNTP) thereby allowing the subsequent catalysis (10). Mutations of the TL and neighboring residues often result in a loss of ability to discriminate against non-complementary NTPs (ncNTPs) (9,11–16). These results suggest that the TL may contribute to either providing sufficient time for selecting a correct NTP or for favoring the catalysis of the correct NTP. Therefore, the TL may be tuned to strike a critical balance between enabling catalytic activity while maintaining transcriptional fidelity (10). An active role of the TL comes from the observation that the inhibition of TL closing of Saccharomyces cerevisiae (Sc) RNAP II by α-amanitin resulted not just in a slowdown of transcription but also in a substantial decrease of correct NTP addition relative to deoxy-NTP (dNTP) misincorporation (11). On the other hand, a mutation of Sc Rpb1 E1103 in the TL that is believed to favor a closed TL has also been found to promote misincorporation (11,12) while increasing the elongation rate (11,12,17). The latter finding supports the idea of kinetic proofreading by the TL (18). Additional studies on Escherichia coli (Ec) RNAP also suggest that the open TL may play a major role in discrimination against ncNTPs (15). The prevailing hypothesis of DNA polymerases (DNAPs) holds that fidelity might be controlled at the isomerization step, an open–closed conformation transition, following dNTP binding (19,20).

RNAP also has to prevent misincorporation of dNTPs, especially complementary dNTPs (cdNTPs) that cannot be discriminated based on mismatch formation. Previous studies have identified certain RNAP residues that are likely involved in recognizing the 2′-OH group (14,16,21), and there is evidence from misincorporation assays that the TL is essential for dNTP discrimination (11,14). This suggests that, for dNTP discrimination, TL closing preceding catalysis is likely the main fidelity checkpoint.

Despite some insight from previous studies (22), the details of how cNTPs are distinguished from ncNTPs and cdNTPs have remained elusive. Here, modeling and simulation are integrated with available structural and biochemical data to obtain atomic-level insight into the mechanistic details of fidelity control. Extending our previous work on TL dynamics in the presence of an active site cNTP (23–25), we are comparing molecular dynamics (MD) simulations of RNAP with cNTP, ncNTPs and cdNTP. Together, our simulation results suggest a robust fidelity control mechanism that consists of several complementary checkpoints for discriminating against ncNTP and cdNTP misincorporation. We distinguished five distinct checkpoints that likely evolved to allow RNAP to achieve an exceptionally high fidelity when faced with different possible mismatches and dNTPs. The overall multi-step fidelity control mechanism appears to be conserved between eukaryotic RNAP II and bacterial RNAP with only slight differences in the specific molecular details of how each step is realized. Furthermore, it appears likely that at least part of the mechanism described here outlines the general strategy for preventing nucleotide misincorporation not just in RNAP but also DNAP and RdRp because of functional and mechanistic parallels between different polymerases while being subjected to the same evolutionary pressures.

MATERIALS AND METHODS

System setup

Crystallographic structures of the 10-subunit S. cerevisiae (Sc) RNAP II complex (Rpb1-3, Rpb5-6, Rpb 8-12) (9) with open (PDB ID: 2E2J) and closed (PDB ID: 2E2H) TL conformations were used as starting structures for Sc MD simulations (Figure 1A). Construction of missing non-surface-loop residues was described in our previous works (23). In all simulations, Rpb1 H1085 was protonated as suggested by Huang et al. (26). Truncated octahedral boxes of explicit water molecules with box lengths of 169 Å were adopted to decrease the number of the total atoms of the systems. This leads to a reduction to ∼360 000 atoms, compared to a cubic box with ∼460 000 atoms. At least a 9-Å margin was kept from any atom of the RNAP II complex to the edge of the box. Furthermore, by randomly replacing water molecules, 334 Cl⁻ and 405 or 398 Na⁺ were added for the closed and open TL structures, respectively, yielding a 0.15-M NaCl solution and neutralized closed and open TL complexes. Ten systems were built with all combinations of open and closed TL systems and the following active site NTPs: GTP (complementary), ATP (non-complementary), UTP (non-complementary), CTP (non-complementary) and dGTP (complementary deoxynucleotide). All the incorrect NTPs and E-site GTP were taken from crystal structures by superposing all of the Cα and P atoms of the enzyme.

Figure 1.

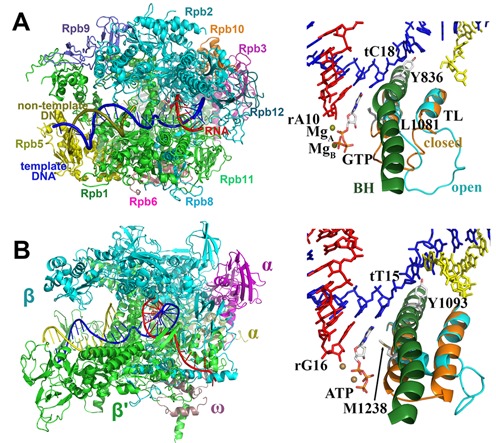
The structures of Sc RNAP II (A) and Tt RNAP (B). The active sites shown on the right panels are rotated by 180° relative to the enzyme orientation on the left.

Crystallographic structures of the 5-subunit (α₂ββ′ω) Thermus thermophilus (Tt) RNAP complex (6) with open (PDB ID: 2PPB) and closed (PDB ID: 2O5J) TL conformations were used as starting structures for Tt MD simulations (Figure 1B). Missing TL residues, β′ 1244–1250 were constructed by MODELLERv9 (Figure 1B and Supplementary Figure S2) (27). In all simulations, β′ H1242 was also protonated. The complexes were fully solvated in cubic boxes of explicit water, ∼300 000 atoms in total. Box lengths were ∼155/128/146 Å (closed) or 152/138/143 Å (open), also with at least 9 Å remained from any atom of the RNAP complex to the edge of the box. Furthermore, 224 or 238 Cl⁻ and 312 or 327 Na⁺ were added for the closed and open TL structures, respectively, also yielding a 0.15-M NaCl solution and neutralized complexes. Because the conformational changes with an open TL are less dependent on the protein sequence and similar conformational changes were observed in the dC:CTP and dC:UTP simulations with closed TLs, four systems with different active site NTPs were built for Tt: ATP (complementary), GTP (non-complementary), CTP (non-complementary) and dATP (complementary deoxynucleotide).

Simulation details

The CHARMM27/36 force field (28,29) was used for Sc RNAP II and Tt RNAP, respectively. The CHARMM version of the TIP3P (30) model was used for explicit water and Na⁺, Mg²⁺ and Zn²⁺ parameters were used as described previously (31,32). Parameters of deprotonated cysteines and the 3′-OH group of the terminal RNA base were modified to favor Zn²⁺ and Mg²⁺ binding, respectively. The modifications were expatiated in our previous paper (23). The parameters for GTP, UTP, CTP, dATP and dGTP were built by combining the existing parameter for ATP and nucleic acids. All of the simulations were carried out with NAMD 2.8 (33) in conjunction with the Multiscale Modeling Tools for Structural Biology (MMTSB) Tool Set (34). The electrostatic interactions were calculated by the particle-mesh Ewald method (35). The non-bonded interactions were truncated at 10 Å with a switching function effective at 8.5 Å. All of the heavy atom-hydrogen bonds were constrained holonomically by the SETTLE algorithm (36) allowing an integration time step of 2 fs. A Langevin-type thermostat and barostat (37,38) were used to maintain an NPT ensemble at 298 K and 1 bar. The complete systems were first minimized over 5000 steps with the protein/DNA/RNA fixed and 5000 steps without any restraints followed by gradual heating from 5 to 298 K over 400 ps with a step of 50 K and a weak harmonic restraint on Cα and P atoms with a force constant of 10 kcal/mol/Ų. Then, the force constant was reduced to zero in steps of 1 kcal/mol/Ų. Subsequent simulations were run without any restraints. About 300 ns of MD simulations were accumulated for each of the Sc RNAP II and Tt RNAP systems (three independent trajectories each over 100 ns with different initial velocities) for a total simulation time of about 4.2 μs for all systems.

Additional umbrella sampling simulations were carried out in NAMD 2.8 (33) to determine the free energy during the A–E transitions of different NTPs. The active site DNA:GTP/ATP/CTP C1′-C1′ distances were selected as the reaction coordinate with umbrella windows covering distance values between 10.0 and 20.5 Å with a window width of 0.5 Å (21 windows). A 50-ns steered MD simulations was first performed to obtain the initial structures for the umbrella sampling simulations. To prevent the Mg_A going along NTPs and leaving the 3′-terminal RNA, and make sure the transition of different NTPs in similar environment, a restraint was applied on the Mg_A-rA10/O3′ distance for the steered MD simulations. In all umbrella sampling simulations, a force constant of 20 kcal/mol/Ų was used, and each simulation at each window was carried out for 20 ns. The last 15 ns samplings were used for calculating the potentials of mean force (PMF) and error bars through the weighted histogram analysis method by Alan Grossfield (http://membrane.urmc.rochester.edu/content/wham) (39,40).

The analysis was carried out primarily with the MMTSB Tool Set (34). All structural figures were generated using VMD (41). Details of the simulation analysis methods are provided in the Methods section in the Supplementary data.

RESULTS

The fidelity of RNAP with respect to mismatch incorporation is expected to be fundamentally related to an inability to form Watson–Crick hydrogen bonding, which leads to unfavorable energetics and structural distortions. Furthermore, especially purine:purine and pyrimidine:pyrimidine base pairs are likely resulting in poor steric fits at the active site (42). The discrimination of cdNTPs versus cNTPs, however, is likely a result of loss of the interactions between the 2′-OH and the enzyme. To study both mechanisms in more detail, we carried out extensive MD simulations of Sc RNAP II and Tt RNAP with different NTPs opposite the template DNA: dC:GTP/ATP/UTP/CTP/dGTP (Sc with open and closed TLs) and dT:ATP/GTP/CTP/dATP (Tt with a closed TL).

The overall RMSD of the complex and the active site are stable, maintained in most cases at ∼4 and 3 Å, respectively (Supplementary Figure S1). For the Tt TL, the sampled structures had RMSD values close to their respective starting structures with all NTPs (Supplementary Figure S2). But there were much larger changes for the Sc TL because of the flexibility due to the non-helical structure (Supplementary Figure S3). Large dynamics in a complex system such as RNAP raise concerns about sufficient convergence. However, when measuring changes in specific local conformational properties induced by incorrect NTPs, it appears that sufficient levels of convergence have been reached within our simulations (Supplementary Figure S4). In the following, a detailed analysis of the simulation results and implications for fidelity control are presented.

Flexibility of the active-site NTPs with an open TL

In all of the trajectories started from the open TL structure, the active site ncNTPs and cdNTP were more flexible than the cGTP according to the sampling of C1′-C1′ distances for the active site DNA:NTP base pair and the NTP glycosidic torsion angle (Figure 2). The complementary dC:GTP pair favored a conformation stabilized by Watson–Crick hydrogen bonds with the i+1 site template DNA (tC18) and base pair stacking with the 3′ terminal RNA (rA10) base (as evidenced by C1′-C1′ and base–base distances that remained near 10.6 and 5 Å). On the other hand, mismatches sampled configurations with different C1′-C1′ and/or base–base distances, indicating a loss of base pairing with the template DNA base and a loss of stacking with the nascent RNA. Generally, C1′-C1′ distances were increased, but in the case of dC:ATP we also observed shortened C1′-C1′ distances that resulted from intercalation of the NTP into the DNA template chain. In some cases, wobble base pairs were formed (dC:ATP), but ncNTPs often formed interactions with the neighborhood residues, such as the fork loop I (Sc Rpb2 E529 and G530), Rpb1 N479, S476, A480, P765 and rA10. These structures correspond to an intermediate ‘half-rotated’ state on the exit pathway. A fraction of the dC:dGTP conformations also deviated from ideal base pair geometries while forming hydrogen bonds between the dGTP base and Sc Rpb1 R446, Rpb2 E529 and rA10.

Figure 2.

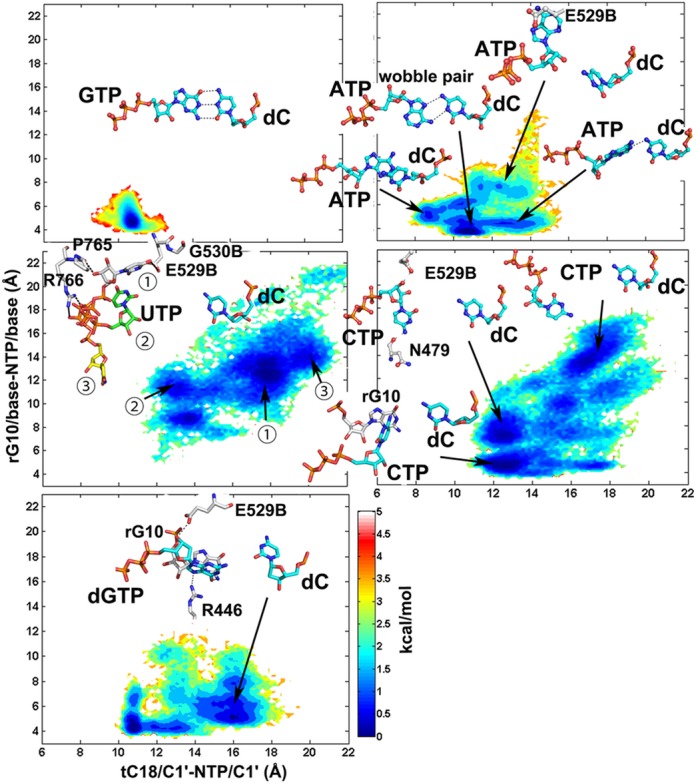
Conformational sampling of NTPs opposing the template DNA dC base in RNAP II with an open TL. Potentials of mean force are plotted as a function of glycosidic torsion angles and NTP/C1′-DNA/C1′ distances. Representative structures are shown in stick representation. The three dC:UTP representative structures () were superimposed on all of the Cα and P atoms. The residues ending with a ‘B’ denote subunit Sc Rpb2/Tt β, all other residues refer to Sc Rpb1/Tt β′.

With an open TL, stable binding of ncNTPs to the A site resulted in significant instability compared to cNTP binding to the A site. In detail, the conformational changes of ATP and dGTP were limited to a rotation of the bases. The base of the CTP turned away from the DNA template toward the E site, but the triphosphate moiety remained trapped by the interactions with the active site ions and basic residues (Figure 2). For UTP, the entire nucleotide was rotated out of the active site. UTP turned to three different directions () in three trajectories. Incorrect NTPs were observed at the E site in several crystal structures suggesting an intermediate state toward exit through the secondary pore. One of those trajectories (UTP3) was following the major A-E pathway (Supplementary Figure S5 and Supplementary Movie S1), and conformation (Figure 2) was thought to be the E site state, locating below the E-site NTPs from the crystal structures, but close to one of them (ncATP from 1R9T). Another rotated-out states for the mismatched UTP () involve stabilizing interactions with Rpb2 E529/G530/Rpb1 P765. Conformation locates at the entrance of the main channel, may indicate possible intermediates on alternate NTP entry or exit pathways through the main channel. Trajectory 2 sampled a broad space (Supplementary Figure S5). Such conformations have not been characterized before, may undergo a different A-E pathway from the major one. On the other hand, it may offer many possibilities of other exit pathways, except the secondary pore.

The spontaneous A-E transitions of mismatched CTP and UTP nucleotides contrast the case of a correctly matched dC:GTP pair where base pairing is maintained stably in unbiased simulations (Figure 2). Therefore, an initial fidelity checkpoint may be a tendency of ncNTPs that reach the A site to rotate back into the E site, from which ncNTPs could exit through the secondary pore and/or the main channel.

The A-E conformational transition PMFs

Incorrect NTPs were observed at the E site in several crystal structures, indicating that the A-E transition may play a role in preventing misincorporation of incorrect NTPs. An exact definition of the E site is somewhat challenging because the base of the NTP is flexible when not interacting with the enzyme (Supplementary Figure S5). However, the C1′-C1′ distances between the E site NTP and the template DNA in the crystal structures all locate around 19 Å. To further confirm this, we performed a 100-ns MD simulation with an E site GTP, which also resulted in most favorable C1′-C1′ distances of ∼19 Å (Supplementary Figure S6) and the base having minimal interactions with the enzyme.

Our simulations suggest that mismatches tend to transfer from the A site to the E site. This was observed spontaneously in one of the dC:UTP simulations (Figure 2 and Supplementary Movie S1). During this transition, the TL was maintained in a stable open conformation. Once in the E site, the base of the NTP is turned toward the secondary pore, but no further motion toward the exit of the pore occurred during the time of the simulation. A PMF calculated from the MD simulations along the C1′-C1′ distance suggests an energy barrier between the A site and E site of less than 1 kcal/mol while favoring the E site by just less than 0.5 kcal/mol (Figure 3A). In order to further quantify these results, we performed umbrella sampling simulations along the tC18/C1′-NTP/C1′ distance for dC:GTP, dC:ATP and dC:CTP with an open TL.

Figure 3.

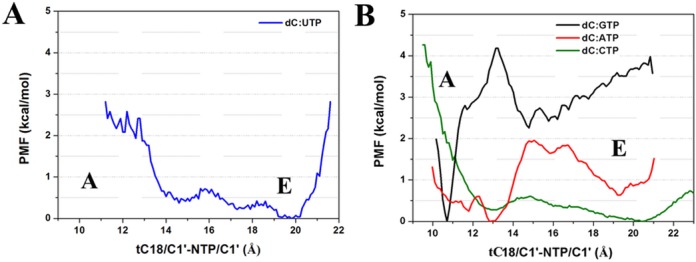
Potential of mean force of the A–E conformational transition along the NTP/C1′-DNA/C1′ distance from MD simulations for dC:UTP (A) umbrella sampling for dC:GTP/ATP/CTP (B) with an open TL.

With the correct NTP, there is a pronounced global minimum at the A site (at 10.6 Å) as expected (Figures 2 and 3B and Supplementary Figure S7). The A site is estimated to be favored by more than 3.0 kcal/mol with a significant kinetic barrier of ∼4.0 kcal/mol inhibiting the A→E transition according to the simulations. On the other hand, the PMF for the ncCTP has a global minimum at the E site (at 20.5 Å), where the E site is stabilized by ∼0.4 kcal/mol and the A→E energy barrier is just ∼0.6 kcal/mol. In addition, the free energy profile of dC:ATP also shows a global minimum at the A site (at ∼13.0 Å), but that state is favored by just 0.7 kcal/mol and again the barrier separating the A from the E site is lower (of 2 kcal/mol) compared to the correct NTP. Taken together, these results clearly demonstrate that a transition to the E site is much more likely for mismatched bases than for a correctly paired base.

Steric hindrance between closed TL and mismatched NTPs

Previous simulations have suggested that TL closing is key for the efficient progression to a catalytically competent state and for subsequent catalysis (23,24). Furthermore, TL closing appears to be spontaneous in the presence of a cNTP in the active site. Meanwhile, it is known experimentally that the TL keeps a balance between maximizing both the elongation rate and fidelity (10). The interactions between the closed TL and the active site NTPs are therefore presumed to be essential for both catalysis and fidelity. Given the additional contacts with the closed TL (Supplementary Figure S8), the conformational sampling of ncNTPs becomes more restricted (Supplementary Figure S9) compared to the open TL case. This indicates that at least some of the states sampled in the presence of the open TL are not compatible with TL closing because of clashes that would occur otherwise.

When the TL is closed, Sc Rpb1 L1081 (Tt β′ M1238) play a key role by positioning the active site NTPs via hydrophobic interactions (26). In the presence of the cNTP, the L1081/M1238-NTP distances were narrowly distributed around 5 Å, but when ncNTPs were present, significantly larger distances as well as closer distances were observed (Figure 4). Larger distances mean that the NTPs are not optimally positioned in the active site while shorter distances suggest unfavorable interactions between the TL and the NTP. Too close interactions between the TL and an ncNTP (such as in the dC:ATP simulations) would presumably favor either nucleotide expulsion or reopening of the TL. Taking the i-2 RNA base (Sc rG9/Tt rC15) as a stable reference point, L1081/M1238 moved closer to RNA, and occupied the active site in some mispairs. Overall, the Tt TL adopted a more tightly closed conformation (Figure 4 and Supplementary Figure S2), especially for dT:CTP, while insufficiently closed TL states were found for dT:dATP, again suggesting a competition between TL closing and interactions with active site mismatches.

Figure 4.

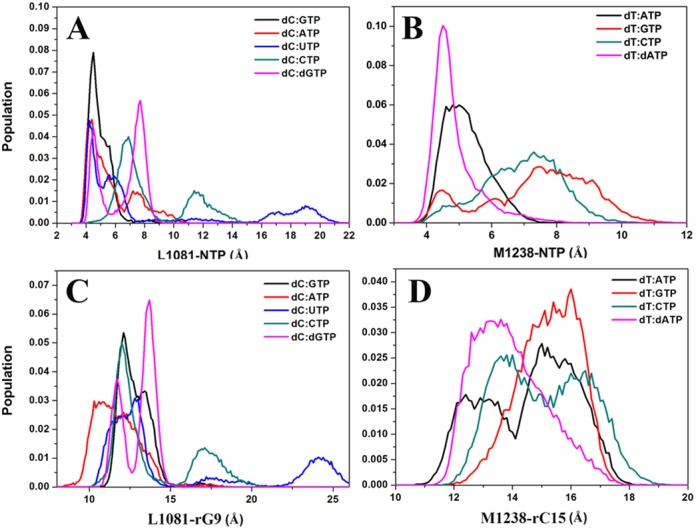
Sampling of centers of mass distances between TL Sc L1081 (A, C)/Tt M1238 (B, D) and NTP(A, B)/i−2 RNA (C, D) base (Sc rG9 /Tt rC15) with a closed TL as a function of an active site NTP.

Taken together, our simulations propose a secondary fidelity checkpoint consisting of either hindered TL closing when ncNTPs are present in the active site or increased interactions between a closed TL and ncNTPs likely favoring NTP expulsion. Delayed or prevented TL closing would delay progression to the catalytic step and increase the chance for an ncNTP to leave the active site instead of being misincorporated, which could be supported by fast kinetic experiments (14).

Mismatch-induced disruption of the active-site geometry

Based on the two-magnesium catalytic mechanism (43), the two ions Mg_A and Mg_B were suggested to play critical roles during catalysis: Mg_A lowers the pKa of the primer 3′-OH group thus facilitating the incorporation of the incoming nucleotide; Mg_B provides structural support, stabilizing the phosphorane transition state, and aids in PPi release (44,45). Both magnesium ions form perfect six-coordinated octahedral geometry with the cNTP in the crystal structure (9). In the Sc structure, the rA10 O3′ atom was not obtained, but modeling suggests that Mg_A locates between the 3′ RNA base rA10 (O3′) and GTP (O2A), coordinating with rA10 (O3′), GTP (O2A), Rpb1 D485 (OD1 and OD2), Rpb1 D483 (OD2) and presumably a water molecule. Mg_B locates between GTP (O2B) and GTP (O2G), coordinating with GTP (O2B and O2G), Rpb1 D481 (OD1 and OD2), Rpb1 D483 (OD1) and Rpb2 D837 (OD1) (Figure 5). Because Mg_A coordinates with both rA10 (O3′) and a Pα oxygen, it may function as a link for keeping the Pα-O3′ distance within a range suitable for catalysis.

Figure 5.

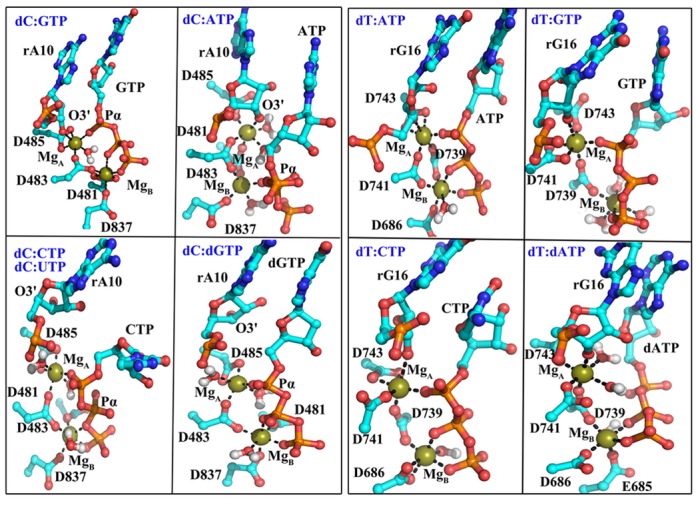
Representative snapshots of active site geometries with different active site NTPs with a closed TL (Sc dC:GTP/ATP/UTP/CTP/dGTP and Tt dT:ATP/GTP/CTP/dATP). The conformation of the dC:UTP is similar to that of dC:CTP, so we did not show it here. Coordination of magnesium ions to surrounding oxygen atoms is indicated with black lines.

In the simulations with the closed TL, the complementary pairs dC:GTP and dT:ATP maintained close Pα-O3′ distances while both magnesium ions remained coordinated in a similar manner as seen in the crystal structures. However, the geometry was distorted for all mispairs. Such a non-ideal geometry may result in a higher energy of the transition state during catalysis. The position of Mg_B was largely maintained, but with an altered coordination (Figure 5 and Supplementary Figure S10, and Table 1 and Supplementary Table S1). On the other hand, Mg_A shifted substantially from the catalysis competent configurations, ending up far from the primer O3′ in some cases (dC:ATP/UTP/dGTP) or the Pα atom in the case of dC:ATP and dT:dATP. The distortion of the active site geometry was also seen in the crystal structure with GMPCPP in the active site (PDB ID: 2NVT) (9). Furthermore, for most mispairs, additional water molecules coordinate the catalytic Mg (Figure 5 and Supplementary Figure S11), which was also observed in simulations of DNAP with ncdNTPs in the active site (46,47).

Table 1. Average active site interatomic distances with the closed TL.

	Distance (Å)
	dC:GTP	dC:ATP	dC:UTP	dC:CTP	dC:dGTP	2E2H
NTP/Pα-rA10/O3′	3.74 ± 0.21	7.33 ± 2.67	3.82 ± 0.37	6.04 ± 1.34	4.78 ± 1.52	NAa
MgA coordination
MgA- rA10/O3′	2.47 ± 0.68	3.03 ± 1.49	2.38 ± 0.70	4.57 ± 0.73	3.15 ± 1.56	NA
MgA-NTP/O?Ab	1.83 ± 0.04	5.71 ± 1.87	1.83 ± 0.04	1.83 ± 0.05	1.83 ± 0.05	2.02
MgA-D483/Oδ2	1.83 ± 0.04	1.84 ± 0.05	1.82 ± 0.04	1.82 ± 0.04	1.82 ± 0.04	2.32
MgA-D485/Oδ1	1.87 ± 0.05	1.87 ± 0.05	1.86 ± 0.06	1.88 ± 0.06	1.89 ± 0.06	2.24
MgA-D485/Oδ2	2.01 ± 0.32	2.36 ± 0.64	2.51 ± 0.63	2.43 ± 0.70	2.44 ± 0.71	3.94
MgB coordination
MgB-NTP/O?Bb	1.90 ± 0.06	1.84 ± 0.06	1.94 ± 0.07	1.95 ± 0.06	1.88 ± 0.06	3.13
MgB-NTP/O?Gb	1.83 ± 0.05	5.37 ± 0.80	2.79 ± 1.17	1.81 ± 0.04	1.83 ± 0.05	1.97
MgB-D483/Oδ1	1.85 ± 0.05	1.85 ± 0.05	1.83 ± 0.05	1.82 ± 0.04	1.86 ± 0.05	2.22
MgB-D481/Oδ1	2.00 ± 0.32	1.84 ± 0.05	1.99 ± 0.50	2.12 ± 0.69	1.86 ± 0.05	2.19
MgB-D481/Oδ2	2.36 ± 0.73	3.55 ± 0.12	3.50 ± 0.70	3.35 ± 0.73	3.78 ± 0.21	4.15
MgB-D837/Oδ1	1.88 ± 0.05	1.86 ± 0.07	1.85 ± 0.05	1.83 ± 0.04	1.86 ± 0.06	2.25
MgA-MgB	4.54 ± 0.16	4.47 ± 0.16	4.65 ± 0.25	4.89 ± 0.19	4.43 ± 0.12	3.43

^aThe 3′-OH is not available in the crystal structure.

^bThis value is the distance between Mg_B and the closest oxygen atom on NTP PA/PB/PG atoms distance.

The case of dNTPs is especially interesting because Watson–Crick base pairing can be maintained, whereas only the lack of the 2′-OH group allows discrimination from NTPs. In the crystal structure of Sc RNAP II, the conserved Rpb1 R446 lies close to the NTP 2′-OH group. In the simulations with the cNTP, R446 formed hydrogen bonds with O2′ either directly or mediated by water (Supplementary Figure S12). At the same time, R446 also coordinated with rA10, which likely contributed to stabilizing the correct active site geometry (Supplementary Figure S8). However, R446 lost the interaction with dGTP and partly formed a salt bridge with D485. This may be weakening the connection between dGTP and nascent RNA and also coordination of Mg_A, and shift its position consequently. Dynamic network analysis furthermore suggested that the selection for a 2′-OH group in the ribose ring does not involve the analogous β′ R704 in Tt RNAP (with the dT:dATP pair), but instead involves β′ N737 and Q1235 (analogous to Sc Rpb1 N479 and Q1078) (Supplementary Figure S8). Mutations of these two bacterial RNAP residues do indeed lead to a decrease in dNTP discrimination (14,16,21). An arginine in the active site of DNAP was also suggested to play a key role in discrimination of dNTP and NTP by comparing the crystal structures of DNAP binding dNTP and NTP (47). The network analysis (Supplementary Figure S8) furthermore revealed an overall stronger interaction network for cNTPs compared to ncNTPs and cdNTPs involving an additional highly conserved residue, Sc Rpb1 P448 (Tt β′ P706). To dissect the exact mechanism further we suggest Sc Rpb1 R446, D485, P448, N479 and Q1078 and Tt β′704, N737, Q1235 and P706 as mutation targets in experimental studies to confirm the similar but slightly different mechanisms for 2′-OH discrimination in Sc RNAP II and Tt RNAP proposed by our simulations.

Corresponding to the movement of the two magnesium ions from the crystal structure (PDB: 2E2H), the starting structure for all the closed TL simulations, the incorrect NTPs underwent conformational rearrangements of the triphosphates relative to the correct NTPs (Supplementary Figure S13). As a result, the Pα atom moved far from the 3′ terminal RNA leading to increased Pα-O3′ distances. In addition, the cGTP pucker conformations mainly located in the C3′-endo, but ncATP and cdGTP puckers mostly showed the C2′-endo conformation (Supplementary Figure S14). This difference of pucker conformations may play a role in preventing catalysis. The pucker conformation was demonstrated to be a key factor in DNAP catalysis (48). This suggests that a third fidelity checkpoint may involve active site distortions away from catalytically competent conformations that arise when incorrect nucleotides are still present in the active site after TL closing.

Backward translocation of the DNA template

In the Brownian Ratchet Model (49), the correct active site NTP is proposed to work as a pawl to keep the enzyme in the post-translocation state. Without a correct NTP, the complex may undergo a thermal fluctuation of forward and backward translocation. Although we did not observe significant backward translocation of the entire DNA/RNA hybrid, partial backward translocation in the neighborhood of the i+1 site template DNA base was observed in mismatch simulations (Figure 6). Rpb1 Y836, analogous β′ Y1093 in Tt RNAP, is proposed to provide important stacking interactions with the transition nucleotide (Sc tC18 and Tt tT14 in our case) (50). Therefore we analyzed translocation by monitoring the distances between the tC18/tT14 bases and the Y836/Y1093 benzene rings. During thermal fluctuations the distance varies between 9 and 12 Å, but in dC:ATP and dT:GTP simulations, tC18 shifted further away from the active site, decreasing the distance to less than 4 Å (Figure 6). The consequence is an empty site across the active site, which was subsequently occupied by the i-1 template DNA base. Furthermore, the fraying of the template DNA base also resulted in a rearrangement of the bridge helix (BH), such as the local reorientation of the side chain of this tyrosine.

Figure 6.

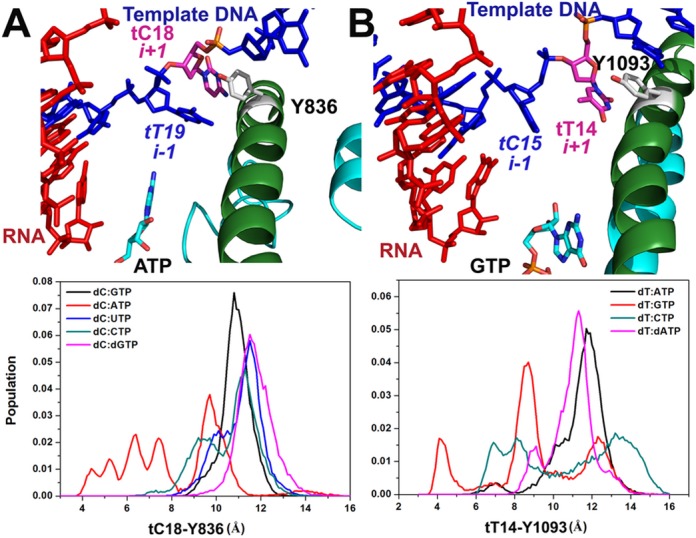
Backward translocation of the template DNA with closed TLs for Sc RNAP II (A) and Tt RNAP (B).

Perturbations in the nascent DNA:RNA hybrid base pair

The nascent (i−1) hybrid RNA–DNA base pair has been demonstrated to play a role in distinguishing cNTPs in both RNAP and DNAP (51–53). In our simulations with closed TLs, the nascent base pair deviated slightly from ideal Watson–Crick pairing for cNTP, while the deviations were much greater for ncNTPs and cdNTPs (Figure 7 and Supplementary Figure S15). Dynamic network analysis furthermore indicated that correlations within the i−1 RNA–DNA base pair (Sc rA10-tT19 and Tt rG16-tC15) are strong, while the correlations became much weaker or disappeared entirely for active site ncNTPs and cdNTPs indicative of a destabilized i−1 base pair (Supplementary Figure S8). For the dC:dGTP pair, the 3′ terminal RNA base shifted far away from dGTP and disrupted the base pair with DNA. For the ncNTP simulations, the 3′ terminal RNA/DNA base frayed (Figure 7 and Supplementary Figure S15).

Figure 7.

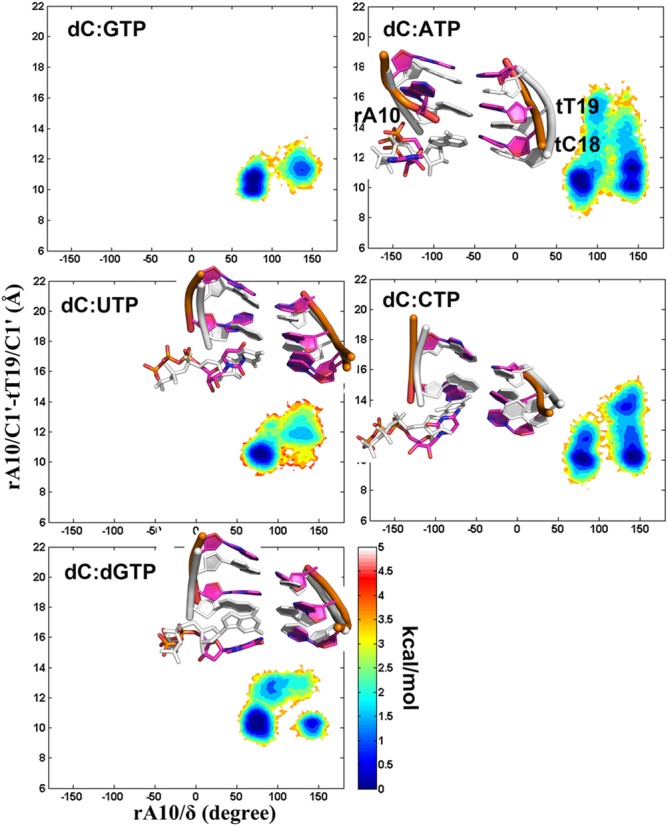
Conformational sampling of the Sc nascent DNA:RNA base pair (tT19:rA10) with a closed TL. PMFs are plotted as a function of the rA10/δ torsion angle and the rA10/C1′-tT19/C1′ distance. Representative structures of the active site base pairs and two nascent base pairs in the initial structure (white) versus the simulated structure (magenta) after superimposing the entire complex on all of the Cα and P atoms are also shown.

Distortions in the DNA:RNA hybrid likely hinder nucleotide addition but also may provide the structural foundation for backward translocation and backtracking. Interestingly, in simulations of DNAP, similar distortions were observed before or after catalysis (46). Thus, backward translocation of the template base and distortions in the nucleic acid as a result of incorrect NTPs may be a fourth and a fifth checkpoint that would stall misincorporation or allow removal of misincorporated nucleotides. In the latter case, external cleavage factors (Gre in bacteria, TFIIS in eukaryotes and TFS in archaea) would be expected to aid (54–57).

DISCUSSION

While copying the genetic information from DNA into RNA, transcription exhibits a high degree of fidelity. Because single-stranded RNA, once synthesized, cannot be repaired if nucleotides have been misincorporated, RNAP is the first and last fidelity checkpoint for correct RNA synthesis. It is therefore not surprising that RNAP may involve several steps for ensuring transcriptional fidelity. Based on the results from the MD simulations presented here, it appears that as many as five separate checkpoints may be at work (Figure 8). The contribution of each checkpoint to the overall fidelity may differ in its effectiveness for detecting different mismatch combinations, but taken altogether the different checkpoints are likely to result in discrimination of all possible misincorporation types. It appears that the different fidelity mechanisms employ a combination of thermodynamics and kinetics, where either binding of ncNTPs to the active site is energetically unfavorable or the transition to a catalytically competent state is delayed.

Figure 8.

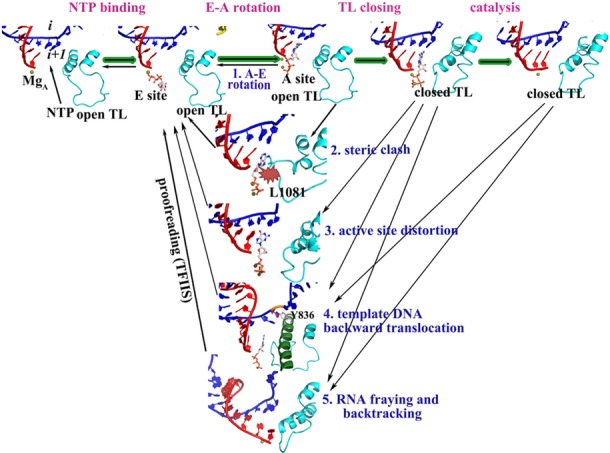
Proposed stepwise mechanism of RNAP fidelity checkpoints.

NTPs approach RNAP with an empty active site by thermally driven diffusion while the TL is open (58). The entrance of NTPs is not confirmed so far, and both the main channel and the secondary channel may take the charge. In the available crystal structures, incorrect NTPs were found in the E site or both the A and E sites (4,9). According to our simulations, ncNTPs and dNTPs are not bound as stably in the A site and may therefore transition to the E site from which they could be expelled through the secondary pore. We observed spontaneous transitions between the A and E sites for an ncNTP suggesting that this transition may occur easily on sub-μs time scales. On the other hand, a cNTP bound in the active site appears to be highly stable with an energy barrier for leaving the A site of more than 4 kcal/mol. Based on our previous work, TL closing is estimated to occur on time scales between 1 μs and 1 ms (24). Hence, there would be enough time to ‘try’ different NTPs until a cNTP is found that would remain stably bound to the A site until the TL closes.

Exit of ncNTPs through the secondary may potentially conflict with simultaneous secondary pore entry. However, based on previous work, NTP entry faces a significant kinetic barrier in the ms range due to unfavorable electrostatics (58) so that the rate of NTP entry through the secondary pore is presumed to be much lower than ncNTP exit via the same pathway. Nevertheless, NTP entry through the main channel remains a possibility and even exit of ncNTPs through the main channel may occur as indicated by our simulation results for mismatched UTP (Figure 2). How exactly NTPs enter and exit remains an intriguing question that will require further studies to gain a complete understanding.

Our simulations show A-E transitions only for pyrimidine:pyrimidine mismatches but dC:ATP and dC:dGTP also display large conformational flexibility in the active site when the TL is open. Therefore, we speculate that other mismatch bases would also be expelled eventually. The energy barrier of dC:ATP A-E transitions is ∼2.0 kcal/mol, much lower than the TL closing. Discrimination against dC:dGTP base pairs is probably most difficult at this step, though, as cdNTPs can form stable Watson–Crick base pairing with the template base. Our results agree with experimental data that found that the discrimination against dC:CTP and dT:CTP mismatches in RNAP without a TL is much higher (about 1:10³), while it is 1:10¹ for dC:ATP, dT:GTP, dC:dGTP and dT:dATP (Table 2) (14). In the case of dC:UTP experimental data indicate a discrimination of only 1:20. This could be explained by our simulation data if the alternate non-E site rotated-out states do not lead to expulsion but require a transition back to the A site and then the E site before the ncNTP can be expelled through the secondary pore.

Table 2. Contributions of individual fidelity steps.

Fidelity contributiona	dC:ATP	dC:UTP	dC:CTP	dC:dGTP	dT:GTP	dT:CTP	dT:dATP
Open TL	Medium	High	High	Medium	-	-	-
Closed TL steric hindrance	High	Medium	Medium	Low	Medium	Medium	Medium
Distortion of active site geometry	High	Low	Medium	Medium	Low	Low	Medium
Template DNA backward translocation	High	Low	Low	Low	High	Low	Low
Damage of nascent RNA–DNA base pair	High	Medium	Medium	Medium	Medium	Medium	Low
Kinetic discrimination (14) (ΔTL)	40	20	5000	3	4	1500	6
Efficiencies (60) (misincorporation/cleavage)	60/24%	54/18%	8/19%		12/24%	54/18%

^aThe contributions are estimated by the degree that the mismatched samplings deviated from the matched samplings.

The next step after NTP binding is TL closing. This leads to tightening of the active site and to the formation of a catalytically competent conformation (23). Sc Rpb1 L1081 plays a role in positioning the active site cNTP via hydrophobic interaction (26). However, in the case of ncNTPs, the flexibility of the base may result in the steric competition with L1081. This could either prevent TL closing or cause an ncNTP to be actively expelled as the TL closes or attempts to close. If L1081 indeed plays a critical part, the length of the side chain is likely a key factor. In bacterial RNAP, the residue equivalent to L1081 is methionine (Tt β′ M1238). Interestingly, the ability to discriminate against ncNTPs in a M1238A mutant is close to that of the ΔTL mutant. On the other hand, M1238V exhibits intermediate rates between those of M1238A and the WT while M1238L is indistinguishable from WT (14). While L1081 on the closed TL likely stabilizes the active site in the presence of a cNTP, it created steric competition in the case of ncNTPs that should slow down and/or prevent the formation of a closed TL state with an ncNTP bound in the active site. TL closing improves the overall transcription fidelity by around an order of magnitude (14). From our simulations, we saw the strongest effect for the dC:ATP mismatch (Table 2) again indicating that the effectiveness of discriminating against mismatches in this manner likely varies as a function of mismatch type.

When NTPs bind initially, they are not in an ideal catalytic conformation. TL closing is presumed to induce a transition to such a state. A key aspect is the location of two Mg²⁺ ions in the RNAP active site. With an open TL, the coordination of the two Mg²⁺ ions is not as stable as in the case of a closed TL. With the cNTP in the active site, the closed TL kept the two Mg²⁺ ions stably with perfect six-coordinated octahedral geometry, resulting in close Pα-O3′ distances in a conformation that appeared to be poised for catalysis. In contrast, the presence of incorrect NTPs led to a significant shift and a distortion of the coordinates of the two Mg²⁺ ions also with increased hydration. The movement of the Mg²⁺ ions was furthermore coupled to a population shift of the active site NTP conformations, an A-PS conformational switch. As a result, the Pα-O3′ distance became larger and a progression toward catalysis appeared unlikely. According to our simulations, this step is a major checkpoint for preventing dNTP incorporation. Interestingly, the pyrimidine:pyrimidine mismatches just led to a slight deviation of the coordination of the two Mg²⁺ ions from the perfect six-coordinated octahedral geometry, and there was even no significant increase in the Pα-O3′ distance in dC:UTP and dT:CTP simulations. This indicates that a closed TL may accommodate small NTPs and this third checkpoint is less effective for such mismatches.

After the NTP selection, the proofreading of external cleavage factors further contributes to the overall fidelity by removing misincorporated nucleotides (54–57). As a possible detailed mechanistic explanation for how proofreading is accomplished, we propose distortions in the nascent DNA:RNA hybrid and i+1 template DNA base when ncNTPs and dNTPs are present in the active site. Structural perturbations of the RNA and template DNA would likely oppose further nucleotide addition (55) or may lead to backtracking (59,60) and subsequent mismatch removal if misincorporation has occurred. The perturbations were apparent for all cases, consistent with similar experimentally observed efficiencies for cleaving a 3′-terminal misincorporation (∼20%) from the nascent RNA (Table 2) (60).

A systematic quantitative analysis of misincorporation in Sc RNAP II (60) showed misincorporation resulting in dC:CTP and dT:GTP mismatches to be least likely (∼8 and 12%), while dC:ATP, dC:UTP and dT:CTP mismatches incorporated with medium probability (∼60, 54 and 54%) (Table 2). Because our simulations suggest especially effective dC:CTP discrimination, the initial fidelity checkpoint with an open TL, the A→E transition, may be most effective for Sc RNAP II. However, misincorporation rates in Thermus aquaticus RNAP (14) differ suggesting that the efficiencies of the fidelity checkpoints on discriminating against different ncNTPs and dNTPs may depend on the sequence of the complex and/or subtle differences between RNAPs from different species.

CONCLUSIONS

In this study, we have compared Sc RNAP II and Tt RNAP with cNTPs, ncNTPs and cdNTP through MD and umbrella sampling simulations. It appears that as many as five different mechanisms may be at work for ensuring a high degree of transcriptional fidelity. The first step would select cNTPs based on more favorable and more stable binding to the active site. Then, TL closing would be hindered if ncNTPs are present in the active site. In the case of successful TL closing, active site distortions appear to be more likely for ncNTPs and dNTPs, disfavoring the following catalysis. Finally, distortions of the i+1 template DNA and i−1 DNA:RNA hybrid appear to constitute final checkpoints by preventing nucleotide addition and/or triggering backtracking and the removal of a misincorporated nucleotide. The results presented here open the door to further studies, both computational and experimental, to confirm the proposed mechanisms and to understand in more detail how the large number of possible mismatches may be recognized differentially at different steps.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [GM092949 to M.F., Z.B.]; National Science Foundation [MCB 1050867 to Z.B.]; XSEDE Facilities [TG-MCB090003, TG-MCB120005]. Funding for open access charge: National Institutes of Health [NIH GM092949]; National Science Foundation.

Conflict of interest statement. None declared.