Testing the Vesicular Morphology to Destruction: Birth and Death of Diblock Copolymer Vesicles Prepared via Polymerization-Induced Self-Assembly

Abstract

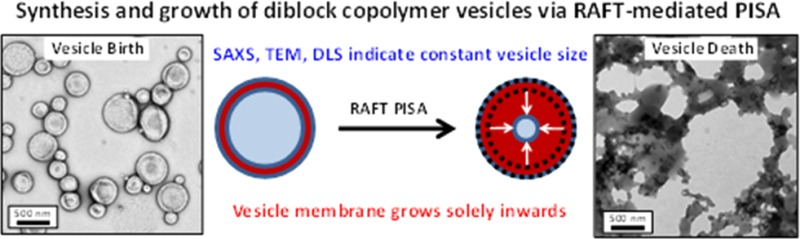
Small angle X-ray scattering (SAXS), electrospray ionization charge detection mass spectrometry (CD-MS), dynamic light scattering (DLS), and transmission electron microscopy (TEM) are used to characterize poly(glycerol monomethacrylate)₅₅-poly(2-hydroxypropyl methacrylate)_x (G₅₅-H_x) vesicles prepared by polymerization-induced self-assembly (PISA) using a reversible addition–fragmentation chain transfer (RAFT) aqueous dispersion polymerization formulation. A G₅₅ chain transfer agent is utilized to prepare a series of G₅₅-H_x diblock copolymers, where the mean degree of polymerization (DP) of the membrane-forming block (x) is varied from 200 to 2000. TEM confirms that vesicles with progressively thicker membranes are produced for x = 200–1000, while SAXS indicates a gradual reduction in mean aggregation number for higher x values, which is consistent with CD-MS studies. Both DLS and SAXS studies indicate minimal change in the overall vesicle diameter between x = 400 and 800. Fitting SAXS patterns to a vesicle model enables calculation of the membrane thickness, degree of hydration of the membrane, and the mean vesicle aggregation number. The membrane thickness increases at higher x values, hence the vesicle lumen must become smaller if the external vesicle dimensions remain constant. Geometric considerations indicate that this growth mechanism lowers the total vesicle interfacial area and hence reduces the free energy of the system. However, it also inevitably leads to gradual ingress of the encapsulated water molecules into the vesicle membrane, as confirmed by SAXS analysis. Ultimately, the highly plasticized membranes become insufficiently hydrophobic to stabilize the vesicle morphology when x exceeds 1000, thus this PISA growth mechanism ultimately leads to vesicle “death”.

Introduction

It is well-known that amphiphilic diblock copolymers self-assemble in water to form either spherical micelles, cylindrical micelles (a.k.a. “worms”), or vesicles, depending on the relative volume fractions of each block.¹⁻³ Vesicles have attracted particular attention because of their potential applications for drug delivery.⁴ Copolymer vesicles comprise a polymeric bilayer membrane encapsulating an aqueous cavity or lumen. The membrane consists of interdigitated hydrophobic chains, with brush-like hydrophilic chains being expressed at both the inner and outer surfaces.^3,5 Unlike their small-molecule liposome counterparts,⁶ diblock copolymer vesicles are usually considered to be non-ergodic (kinetically frozen) nanostructures: with the notable exception of Pluronic-type block copolymers,^7,8 there is normally little or no exchange of individual copolymer chains between vesicles and the (typically aqueous) continuous phase.⁹

Recently, polymerization-induced self-assembly (PISA) has provided a highly versatile route to self-assembled nano-objects at much higher concentrations (up to 25% w/w solids) than can be achieved using conventional post-polymerization processing techniques.¹⁰⁻¹⁴ For example, detailed phase diagrams have been constructed for the reversible addition–fragmentation chain transfer (RAFT) polymerization of 2-hydroxypropyl methacrylate (HPMA) that allow pure phases comprising spherical diblock copolymer micelles, anisotropic worms, or polydisperse vesicles to be consistently produced using either poly(glycerol monomethacrylate) (PGMA)¹² or poly(2-(methacryloyloxy)ethyl phosphorylcholine) (PMPC)¹⁴ or poly(ethylene glycol)-based macro-CTAs.¹⁵ Such formulations provide an excellent opportunity to investigate the properties of these nano-objects, since the synthesis and self-assembly of the diblock copolymer chains can be conducted efficiently and simultaneously at high solids via one-pot protocols.

Herein we utilize PISA as a convenient method for preparing a series of PGMA₅₅-PHPMA_x (denoted as G₅₅-H_x) diblock copolymer vesicles with varying PHPMA degrees of polymerization (DP) at 10% w/w solids (Figure 1). These vesicles are characterized by small-angle X-ray scattering (SAXS), dynamic light scattering (DLS), and transmission electron microscopy (TEM) to investigate the effect of varying the DP of the core-forming block on the copolymer morphology. In addition, electrospray ionization charge detection mass spectrometry (CD-MS)¹⁶ studies have been conducted on the vesicles. This technique has been previously utilized to accurately determine the mass of water droplets,¹⁷ high molecular weight polymers,^18,19 nanoparticles,¹⁸ and viruses.^20,21 In particular, CD-MS has been recently used to determine the absolute mass of spherical diblock copolymer micelles synthesized via RAFT aqueous emulsion polymerization.^22,23 However, as far as we are aware, the present study is the first time that the CD-MS technique has been used to characterize diblock copolymer vesicles. CD-MS measures both the m/z ratio and the charge (i.e., z) for individual species (see Figure 3a). These results can be combined with the copolymer number-average molecular weight (M_n,pol) determined by ¹H NMR spectroscopy to calculate a mean aggregation number (N_agg^CD-MS) for these vesicles. Such data have been traditionally obtained for copolymer micelles using static light scattering²⁴⁻²⁷ but are seldom reported in the literature for copolymer vesicles. Exceptionally, Nardin et al. and Egli et al. reported mean aggregation numbers of 10,000–30,000 for PMOXA-PDMS-PMOXA triblock copolymer vesicles.^28,29

Figure 1.

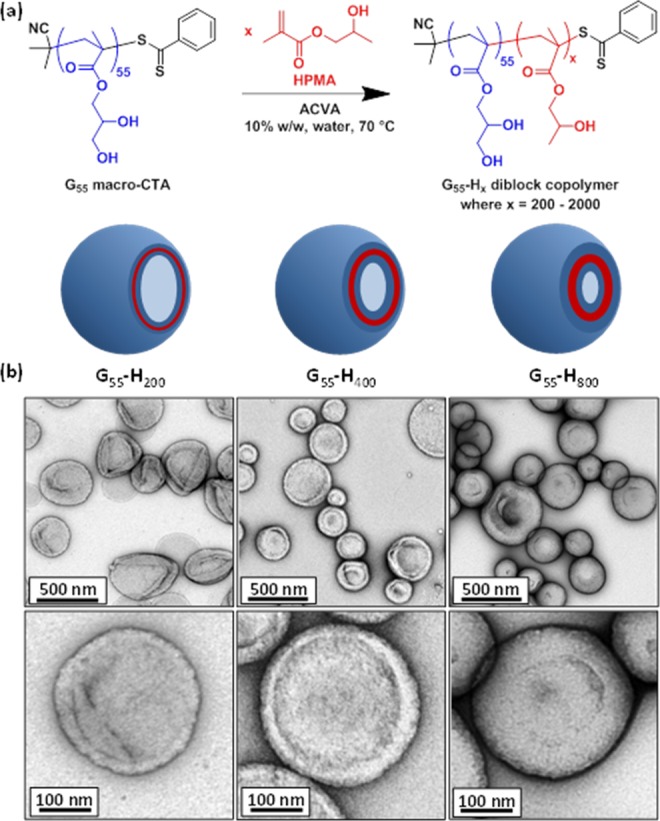
(a) Synthesis of PGMA₅₅-PHPMA_x (or G₅₅-H_x) diblock copolymer vesicles via RAFT aqueous dispersion polymerization and the effect of increasing the target degree of polymerization (x) of the membrane-forming PHPMA block on the mean thickness of the vesicle membrane. (b) Transmission electron micrographs obtained after drying 0.10% w/v dispersions of G₅₅-H₂₀₀, G₅₅-H₄₀₀, and G₅₅-H₈₀₀ vesicles.

Figure 3.

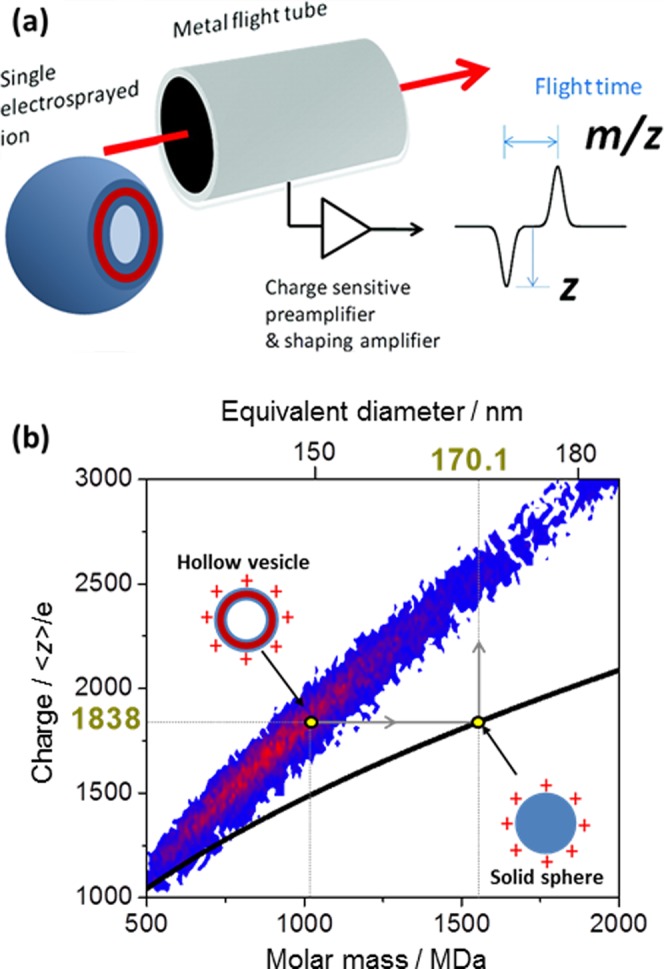
(a) Principle of electrospray ionization CD-MS as applied to vesicle characterization. (b) 3D mass–charge image of ionized G₅₅-H₅₀₀ vesicles obtained via CD-MS; the red color indicates a relatively high number of particles in this region of the plot. The black curve corresponds to the predicted limiting curve for water droplets at 60% of Rayleigh’s limiting charge (see text for details).

Results and Discussion

First, a well-defined PGMA₅₅ macro-CTA was synthesized by RAFT solution polymerization in ethanol (DMF GPC, M_n = 15,600 g mol^–1, M_w/M_n = 1.10; vs poly(methyl methacrylate) calibration standards). This homopolymer precursor was subsequently chain-extended with HPMA via RAFT aqueous dispersion polymerization to produce a series of G₅₅-H_x diblock copolymers, targeting x values ranging from 200 to 2000. High monomer conversions (>98%) were achieved in each diblock copolymer synthesis, as judged by the disappearance of the vinyl proton signals at 5.6 and 6.2 ppm in the ¹H NMR spectra (see Figure S1). A systematic increase in M_n was observed as higher core-forming block DP values were targeted (see Table S1). A high molecular weight shoulder in the GPC traces gradually became more prominent as a result of light branching caused by a small amount of dimethacrylate impurity in the HPMA monomer.¹¹ Incomplete monomer conversions (≤90%) were obtained for the G₅₅-H₁₅₀₀ and G₅₅-H₂₀₀₀ formulations along with partial loss of colloidal stability, as judged by the concomitant macroscopic precipitation.

According to DLS studies (see particle size distributions shown in Figure S2), z-average diameters for G₅₅-H₂₀₀ and G₅₅-H₃₀₀ copolymer vesicles are 239 and 219 nm, respectively, whereas G₅₅-H_400–800 vesicles all lie between 200 and 205 nm. There was only a very modest increase in the z-average diameter of the G₅₅-H₁₀₀₀ vesicles (up to 229 nm), whereas much larger increases were observed for G₅₅-H₁₅₀₀ (455 nm) and G₅₅-H₂₀₀₀ (752 nm). Moreover, these latter two diameters were obtained for aqueous copolymer dispersions after filtration through glass wool to remove macroscopic precipitate. These observations suggest that the vesicular morphology eventually becomes unstable when targeting DPs in excess of 1000 for the membrane-forming block.

TEM studies (see images shown in Figures 1b and S3) confirmed that the series of G₅₅-H_x diblock copolymers adopt an exclusively vesicular morphology when targeting x values up to 1000. It is also apparent that shorter membrane-forming blocks resulted in vesicles with relatively flexible membranes, which are prone to buckling and tend to collapse on drying, whereas the longer hydrophobic blocks produce vesicles with much more resilient membranes that exhibit minimal deformation during TEM inspection under ultrahigh vacuum (Figure 1b). TEM studies confirm loss of the vesicular morphology for both G₅₅-H₁₅₀₀ and G₅₅-H₂₀₀₀, while SEM studies indicate that the G₅₅-H₂₀₀₀ copolymer phase comprises aggregated spheres (see Figure 2).

Figure 2.

Transmission electron micrographs obtained from dried 0.10% w/v aqueous copolymer dispersions of (a) G₅₅-H₁₅₀₀ and (b) G₅₅-H₂₀₀₀. (c) Scanning electron micrograph obtained for the G₅₅-H₂₀₀₀ copolymer, which forms a macroscopic precipitate comprising wholly spherical (i.e., non-vesicular) particles.

Charge Detection Mass Spectrometry (CD-MS)

Electrospray ionization CD-MS was used to determine the absolute molecular weight of the individual vesicles (see experimental schematic shown in Figure 3a).^22,23 The CD-MS raw data can be displayed as a 3D mass–charge distribution, where the charge and mass of individual aggregates is plotted. Typical data obtained for the G₅₅-H₅₀₀ vesicles are shown in Figure 3b, where the color range indicates the number of charged vesicles (with the red data signifying higher counts/more particles than the blue data). The former plot produces an essentially monomodal distribution with maxima ranging from ∼800 to ∼4,000 MDa (see Table 1). The mass distributions can be characterized statistically by the weight-average particle mass (M_w^CD-MS) and the number-average particle mass (M_n), leading to determination of the polydispersity index, M_w^CD-MS/M_n. Polydispersities ranging from 1.08 to 1.21 were calculated for the various G₅₅-H_x vesicles shown in Table 1. Mean masses reported for G₅₅-H₄₀₀ to G₅₅-H₈₀₀ vesicles are relatively constant, ranging between ∼1,000 and ∼1,400 MDa. A reduction in vesicle polydispersity from ∼1.2 to ∼1.1 was observed over this range, which correlates with the lower polydispersities observed by DLS. A long tail to higher mass in the particle mass distribution is observed for PHPMA DPs >1000 (see Figure S4). This tail indicates the presence of significantly larger structures. The G₅₅-H₂₀₀₀ sample exhibits a bimodal distribution, with a number-average particle mass of 97 MDa along with a population of aggregates much larger than those found for any of the other copolymer samples (M_n^CD-MS = 35,700 MDa). This is consistent with TEM studies of G₅₅-H₂₀₀₀, which suggest the presence of ill-defined, non-vesicular aggregates for this sample (see Figure 2).

Table 1. DLS z-Average Diameter (D_z) and Polydispersity Index (PDI) and Various SAXS Structural Parameters Obtained by Analysis of a Series of G₅₅-H_x Copolymer Vesicles^a.

DLS			SAXS									CD-MS
PHPMA DP (x)	Dz, nm	PDI	Dv, nm	Vm, nm3	RmSAXS, nm	σRm, nm	TmSAXS, nm	σTm, nm	Rg, nm	xsol	NaggSAXS/103	MnCD-MS, MDa	MwCD-MS/Mn	NaggCD-MS /103	⟨z⟩ / e	D, nm	TmCD-MS, nm
200	239	0.28	244(5)	40(4)	111(3)	45(2)	12.8(1)	1.3(1)	2.2(1)	0.38(1)	31.0 ± 5.3	–	–	–	–	–	–
			233(7)		105(3)	50(2)	12.6(1)	1.1(1)	2.5(3)	0.51(1)	22.0 ± 3.9
300	219	0.14	236(6)	59(6)	105(3)	45(1)	17.8(1)	2.1(1)	2.1(1)	0.38(1)	25.7 ± 4.7	800	1.19	15.3	1952	177	12.6
			228(6)		101(4)	51(2)	17.8(1)	2.1(1)	2.4(1)	0.52(1)	18.2 ± 3.8
400	201	0.12	208(4)	79(9)	89(2)	39(1)	20.2(1)	2.2(1)	2.2(1)	0.45(1)	14.2 ± 2.5	1307	1.18	13.5	2076	184	20.8
			213(3)		91(1)	45(1)	20.3(1)	2.3(1)	2.4(1)	0.56(1)	11.8 ± 1.9
500	208	0.02	197(2)	99(11)	82(1)	34(1)	24.7(1)	2.3(1)	2.3(1)	0.38(2)	13.0 ± 2.0	1023	1.09	12.6	1838	170	19.2
			197 (2)		81(1)	36(1)	25.1(1)	2.6(1)	2.4(1)	0.52(2)	10.2 ± 1.8
600	204	0.04	205(2)	119(13)	83(1)	38(1)	29.7(1)	2.7(1)	2.3(1)	0.51(2)	10.8 ± 1.8	1366	1.12	14.3	2060	184	22.6
			206(1)		83(1)	40(1)	30.4(1)	3.0(1)	2.3(1)	0.58(2)	9.5 ± 1.8
700	204	0.04	205(2)	139(15)	82(1)	34(1)	34.1(1)	3.0(1)	1.7(1)	0.63(1)	7.9 ± 1.3	1421	1.08	12.9	2181	190	21.4
			205(2)		82(2)	40(1)	34.5(1)	3.0(1)	1.8(1)	0.63(1)	7.9 ± 1.3
800(A)	205	0.02	204(3)	158(17)	79(1)	32(1)	37.7(1)	2.9(1)	2.0(1)	0.62(1)	7.3 ± 1.2	1282	1.11	10.3	2046	183	21.1
			206(3)		80(2)	35(1)	38.9(1)	3.1(1)	1.9(1)	0.61(2)	7.9 ± 1.5
800(B)	201	0.03	197(1)	158(17)	75(1)	30(1)	37.1(1)	4.8(1)	2.3(4)	0.57(1)	7.4 ± 1.1	1220	1.11	9.8	2000	180	20.7
			194(1)		73(4)	32(1)	39.1(1)	5.3(1)	2.3(1)	0.62(1)	6.4 ± 0.8
1000	229	0.02	243(3)	198(21)	95(2)	41 (1)	45.7(1)	3.8(1)	1.7(1)	0.68(1)	8.4 ± 1.6	2003	1.15	17.9	2413	204	27.8
			247(3)		97(2)	52 (1)	46.9(1)	3.9(1)	1.6(1)	0.66(1)	9.7 ± 1.6
1500	455	0.23	–	–	–	–	–	–	–	–	–	4027	1.21	19.1	3070	240	45.6
2000	752	0.14	–	–	–	–	–	–	–	–	–	97/35700b	n/a	0.362/125.2	–	–	–

^aD_v is the mean vesicle diameter, R_m^SAXS is the radius from the center of the vesicle to the center of the membrane and σ_Rm is the associated standard deviation, T_m is the membrane thickness, and σ_Tm is the associated standard deviation, R_g is the radius of gyration of the coronal stabilizer (PGMA) chains, x_sol is the average water content of the hydrophobic PHPMA membrane, and N_agg^SAXS is the mean vesicle aggregation number. Numbers in brackets represent the error in the last significant digit of the SAXS fitting parameters. The volume of a PGMA₅₅ block (V_vc) was calculated to be 11.2 ± 0.12 nm³ and V_m is the volume of the hydrophobic PHPMA_x block. Two sets of SAXS fitting parameters are given for each sample: the first line corresponds to a ‘simple’ model fit, and the second line corresponds to a ‘complex’ model fit that accounts for the vesicle corona scattering length density profile. CD-MS results obtained for the same series of copolymer vesicles are also summarized, including the number-average particle mass of the vesicles (M_n), weight-average particle mass of the vesicles (M_w^CD-MS), polydispersity index (M_w/M_n^CD-MS), mean vesicle aggregation number (N_agg), average number of charges per vesicle (⟨z⟩; as calculated from the charge distribution), equivalent vesicle diameter (D) and vesicle membrane thickness (T_m^CD-MS); see main text for details.

^bA bimodal mass distribution was observed for this particular sample.

CD-MS can also be used to explore the charging capacity of nano-objects.²³ The charging of spherical self-assembled amphiphilic diblock copolymer micelles in water by electrospray ionization has been shown to be ∼60% of Rayleigh’s limiting charge for charged water droplets of the same dimensions.²³ In the present work, we assume that the charging capacity of the diblock copolymer vesicles is the same as that of the previously reported spherical nanoparticles. Figure 3b displays the mass–charge distribution for ionized G₅₅-H₅₀₀ vesicles obtained via CD-MS as a function of molecular weight, together with the predicted limiting curve for water droplets at 60% of Rayleigh’s limiting charge. An equivalent vesicle diameter can be estimated by comparing their average charge to the corresponding charge of a water droplet at 60% of Rayleigh’s limiting charge. For example, ionized G₅₅-H₅₀₀ vesicles possess on average 1838 charges per vesicle (as calculated from the charge distribution). This charge corresponds to a water droplet with a diameter of ∼170 nm, as shown in Figure 3b. We postulate that the vesicle diameter (indicated in Figure 3b as a yellow point associated with the hollow vesicle) is given by this equivalent water droplet diameter. The same analysis was performed for the other vesicle dispersions, which allows calculation of an equivalent vesicle diameter (D). The results are summarized in Table 1.

Small-Angle X-ray Scattering (SAXS)

SAXS characterization of the G₅₅-H_x vesicles was conducted by fitting scattering patterns obtained for various copolymer dispersions to an appropriate model for polydisperse vesicles (see Theory section for a description of the ‘simple’ and ‘complex’ models used to fit the data model). From these data (see Figure 4), it was possible to determine the mean vesicle membrane thickness, (T_m^SAXS), the volume-average diameter (D_v), the radius of gyration of the PGMA stabilizer chains (R_g), the average water content of the vesicle membrane (x_sol), and the mean vesicle aggregation number (N_agg), see Table 1. The vesicle model described by eq A1 fits the SAXS data well over five orders of magnitude in X-ray scattering intensity (Figure 4). The calculated R_g of the PGMA₅₅ coronal block (Table 1) of ∼2.0 nm is comparable to the theoretical value. The latter can be estimated from the total contour length of the PGMA₅₅ block, L_PGMA = 55 × 0.255 nm =14.03 nm (since the projected contour length per GMA monomer repeat unit is defined by two carbon bonds in an all-trans conformation, or 0.255 nm) and the Kuhn length of 1.53 nm [based on the literature value for poly(methyl methacrylate)³⁰] results in an approximate R_g of (14.03 × 1.53/6)^1/2 = 1.89 nm. The SAXS fitting parameters [total particle diameter, D_v = 2(R_out + 2R_g)] are consistent with the DLS data (Table 1). Fitting SAXS data to either the ‘simple’ model or the ‘complex’ model produced similar parameters (see Table 1, PGMA₅₅-PHPMA₃₀₀ and PGMA₅₅-PHPMA₈₀₀). Significant differences between data fits are only noticeable for x_sol when analyzing copolymers with shorter membrane-forming (hydrophobic) blocks (x ≤ 500).

Figure 4.

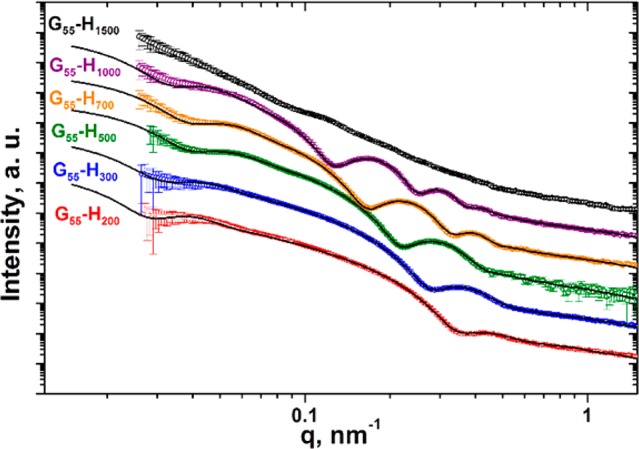
Selected experimental SAXS patterns (circles) obtained for a series of PGMA₅₅-PHPMA_x (abbreviated to G₅₅-H_x for brevity) diblock copolymers, where x = 200, 300, 500, 700, 1000, or 1500, along with the corresponding vesicle model fittings (solid black lines). No appropriate structural model or data fit could be found for G₅₅-H₁₅₀₀, which strongly suggests that this sample has a non-vesicular morphology. For clarity, each SAXS pattern is multiplied by an arbitrary intensity coefficient.

This suggests that the vesicle aggregation number, N_agg^SAXS, calculated for these copolymer compositions is sensitive to the chosen model. Thus this parameter has a relatively large range of uncertainty [e.g., from 25,700 ± 4,700 for the ‘simple’ model to 18,200 ± 3,800 for the ‘complex’ model for PGMA₅₅-PHPMA₃₀₀, see Table 1]. In contrast, N_agg values obtained for copolymers containing a relatively long hydrophobic block, and therefore less scattering signal originating from the corona blocks, appear to be essentially model-independent (e.g., 7,400 ± 1,100 for the ‘simple’ model vs 6,400 ± 800 for the ‘complex’ model in the case of PGMA₅₅-PHPMA₈₀₀, see Table 1).

For the vesicle SAXS model (Figure 5), it is assumed that the number of PGMA corona blocks located at the outer and the inner leaflet of a vesicle is the same. This is a good approximation for large vesicles with relatively thin membranes, but produces a systematic error in the SAXS analysis when considering vesicles with relatively thick membranes. In the latter case, the number of outer leaflet blocks can significantly exceed the number of inner leaflet blocks, and in principle this difference should be included in the model.³¹ However, in practice the relatively short corona block for the vesicle series studied herein produces only a weak contribution to the X-ray scattering for vesicles that comprise relatively thick membranes [see (β_vc/β_m)² ratio for the PGMA₅₅-PHPMA₈₀₀ previously estimated in the text]; thus the difference between the outer and inner leaflet blocks actually makes a negligible contribution to the scattering from vesicles with relatively thick membranes.

Figure 5.

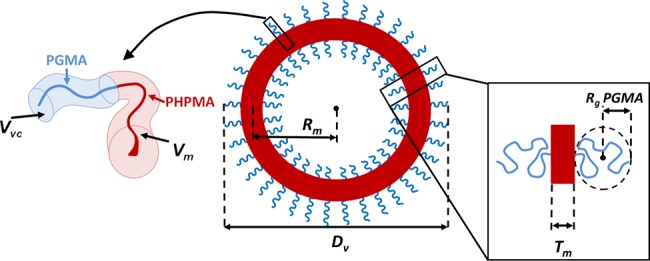
Schematic representation of the various parameters used to fit the SAXS data to a polydisperse vesicle model.

The D_v, R_g, and T_m^SAXS values calculated from the SAXS data fits are virtually independent of the two vesicle models employed (Table 1), suggesting a robust data set. A reduction in D_v from around 244 to 208 nm was observed for G₅₅-H₂₀₀ to G₅₅-H₄₀₀, with this parameter then remaining approximately constant (between 197 and 208 nm) for G₅₅-H₅₀₀ to G₅₅-H₈₀₀. These SAXS observations are consistent with the DLS data discussed earlier (see Table 1). Thus, it seems that some degree of vesicle compaction initially occurs as x is increased from 200 to 400. A physically reasonable explanation for this observation is that PHPMA gradually becomes more hydrophobic as it grows longer, which leads to greater attractive forces between these chains within the vesicle membrane. The essentially constant outer diameters observed for vesicles prepared targeting x = 400 to 800 was not expected. Naively, we anticipated that the thickening of the vesicle membranes that occurs when targeting higher x values would involve a gradual increase in the outer vesicle diameter with a concomitant reduction in the inner vesicle diameter. However, as we shall see, this proved not to be the case.

Mechanism of Vesicle Growth During PISA

In principle, there are four possible particle growth mechanisms once vesicles are initially formed during PISA. These scenarios are depicted in Figure 6. In case A, both the inner and outer diameters increase during vesicle growth. In case B, the inner vesicle diameter remains constant, while the outer diameter increases. Alternatively, the outer diameter increases and the inner diameter is simultaneously reduced, as shown in case C.

Figure 6.

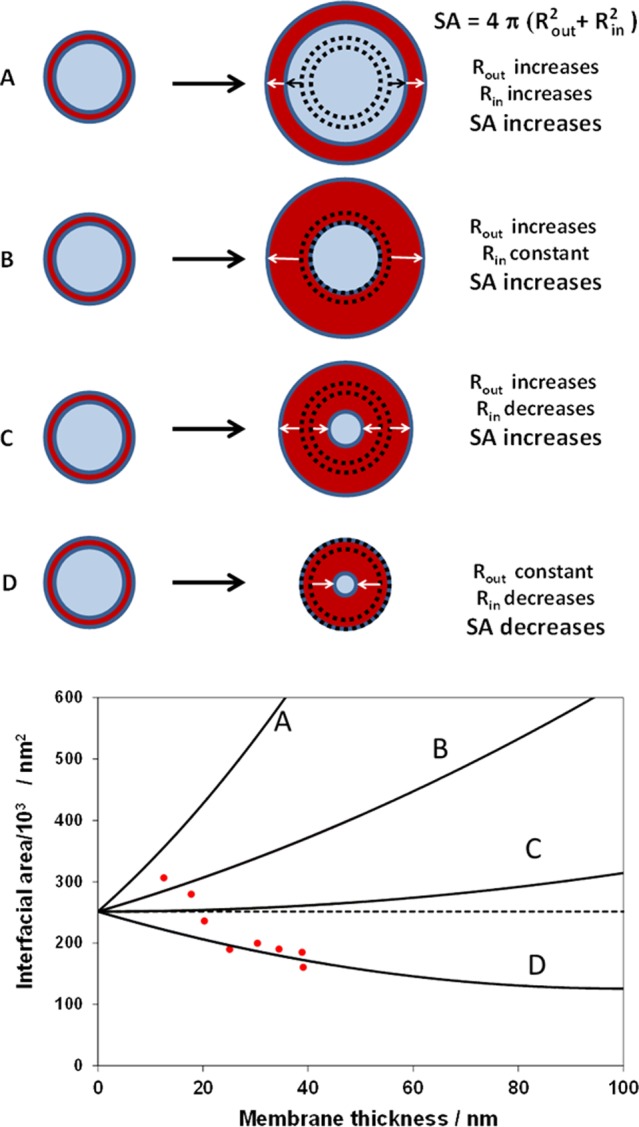
Variation of total vesicular interfacial area (SA) with membrane thickness on increasing the mean degree of polymerization (x) of the core-forming block for the growth of PGMA₅₅-PHPMA_x diblock copolymer vesicles during polymerization-induced self-assembly (PISA). Four possible vesicle growth mechanisms (see A–D) are considered for perfectly monodisperse vesicles with an initial diameter of 200 nm. Only one of these mechanisms (case D) allows the growing vesicles to reduce their interfacial area and hence minimize their free energy. SAXS studies enable the vesicle dimensions (i.e., their inner and outer diameters and hence mean membrane wall thicknesses) to be determined, and these experimental data (see red circles) lie close to the theoretical curve calculated for the vesicle growth mechanism shown in case D.

Finally, in case D, the outer vesicle diameter is fixed, and the inner vesicle diameter is reduced as the membrane thickens, i.e., the vesicles grow solely inward, which progressively reduces the lumen volume. Also shown in Figure 6 are the corresponding four relationships between the total vesicle interfacial area and the membrane thickness (which is directly related to the mean degree of polymerization of the membrane-forming block) for these four scenarios, as calculated from simple geometric considerations.

It is immediately apparent that only case D reduces the total vesicle interfacial area, which in turn provides a mechanism for minimizing the free energy of the system. Moreover, SAXS analysis alone provides sufficient experimental data to discriminate between these four vesicle growth mechanisms, since this technique simultaneously reports the mean outer diameter of the vesicles and the mean membrane thickness (and hence also the mean inner diameter of the vesicles by difference), see Table 1. The experimental SAXS results (see red data points) obtained for the initial vesicles (x = 200–400) do not lie on the theoretical curve calculated for case D. However, the overall vesicle diameter is not yet constant in this regime, since compaction of the initial vesicles occurs as the growing PHPMA chains gradually become more hydrophobic. In contrast, remarkably good agreement is observed for the x = 500–800 regime, for which the external vesicle dimensions remain constant (see Table 1). Thus, we conclude that these vesicle membranes display a strong preference for solely growing inward, resulting in a gradual reduction of the encapsulated lumen volume. This growth mechanism imposes an intrinsic constraint on the stability of the vesicle phase, which has important consequences as higher degrees of polymerization are targeted for the membrane-forming PHPMA block. The inward growth inevitably leads to gradual plasticization of the thickening membrane by the water molecules encapsulated within the lumen. This in turn creates increasingly hydrated membranes that comprise 60% water for G₅₅-H₈₀₀ vesicles, as compared to ∼40% water for the initial G₅₅-H₂₀₀ vesicles (see Table 1). The water content of the vesicle membrane increases up to 70% for G₅₅-H₁₀₀₀, which accompanies the increase in vesicle diameter up to around 240 nm. The steric congestion experienced by the PGMA stabilizer chains expressed at the inner vesicle leaflet increases significantly at higher (inner) curvatures. In principle, this congestion can be relieved by allowing copolymer chains to migrate across the vesicle membrane from the inner leaflet to the outer leaflet. Moreover, this transfer should be facilitated by plasticization of the vesicle membrane by the encapsulated water molecules, since this reduces the hydrophobic attractive forces between the PHPMA chains. Ultimately, the outer leaflet also becomes sterically congested, hence excess copolymer chains are expelled from the vesicle. This phenomenon accounts for the observed significant reduction in aggregation number as the DP of the PHPMA block increases from 200 to 800 (see Table 1). Notwithstanding the weakly hydrophobic nature of the PHPMA block, it is unlikely that the expelled copolymer chains remain molecularly dissolved. Indeed, surface tension measurements conducted on the supernatant solution obtained from centrifugal sedimentation of a G₅₅-H₈₀₀ vesicle dispersion indicated no evidence for surface activity (the supernatant surface tension was ∼70 mN m^–1 at 20 °C, which is close to the surface tension of pure water). Thus the expelled copolymers appear to reform vesicles, rather than exist as molecularly dissolved chains. On targeting a higher core-forming block DP, the vesicle aggregation number is reduced by a factor of around three (see entries 1–8 in Table 1). Since the total number of copolymer chains remains unchanged and the outer vesicle diameter is approximately constant, these observations imply a three-fold increase in the number of vesicles in the aqueous phase.

A cryo-TEM image obtained for a dispersion of G₅₅-H₈₀₀ vesicles suggests that the relatively hydrated PHPMA membranes can undergo fusion on contact (see Figure S5). Eisenberg and co-workers have invoked a fusion–fission model to account for the changes in dimensions of polystyrene-poly(acrylic acid) vesicles observed by TEM during subtle variation of the solvent composition.³² In this earlier work, the gradual addition of water led to the formation of a smaller number of larger vesicles, which produced a reduction in the overall vesicle interfacial area. In the present study, the reduction in interfacial area for the PGMA–PHPMA vesicles is instead achieved via inner growth of the membrane at an approximately constant external vesicle diameter (see case D shown in Figure 6). In unpublished work, we have made similar observations for at least two other diblock copolymer vesicle formulations prepared via aqueous or non-aqueous PISA, hence this behavior is likely to be generic.

Self-assembly was also achieved in aqueous solution by slow rehydration of a thin G₅₅-H₈₀₀ copolymer film originally deposited from methanol, which is a good solvent for both the PGMA and PHPMA blocks. After stirring a 10% w/w aqueous copolymer suspension for 1 week, an aqueous dispersion of vesicles was obtained with a comparable size distribution to that of the original G₅₅-H₈₀₀ vesicles produced via PISA (see Figure S6). This suggests that the vesicular morphology is the equilibrium morphology for this G₅₅-H₈₀₀ diblock copolymer composition. Moreover, this supports our observation that the copolymer chains expelled from vesicles as a result of the growing steric congestion can reform new vesicles of approximately the same size.

A systematic increase in membrane thickness (T_m) was observed when targeting longer membrane-forming blocks, e.g., from 13 nm for G₅₅-H₂₀₀ to 47 nm for G₅₅-H₁₀₀₀ (see Table 1 and Figure 7). Previously, it has been reported that T_m should increase according to the scaling relationship, T_m = kx^a, where x is the degree of polymerization of the membrane-forming block, k is a constant related to the Flory–Huggins interaction parameter at the block junction, and a is a scaling exponent that is determined by the conformation of the membrane-forming chains.^6,33−35 It has been reported that a = 0.50 for completely collapsed coils and a = 1.00 for fully stretched chains (e.g., for the alkyl chains in phospholipid-based liposomes). The data shown in Figure 7 indicate an intermediate scaling exponent of 0.79 for the SAXS data, which suggests that the vesicle membranes comprise partially stretched chains. This seems physically realistic given the relatively high degrees of hydration of the vesicle membranes indicated by SAXS studies (see Table 1).

Figure 7.

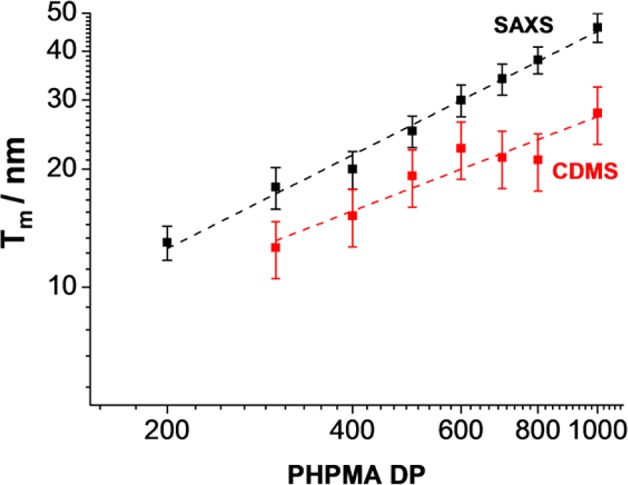
Evolution of vesicle membrane core thickness (T_m) with PHPMA DP (x) for a series of G₅₅-H_x block copolymer vesicles, as measured using SAXS (black squares) and CD-MS (red squares). The error bars in the SAXS data indicate the membrane polydispersity. The error bars in the CD-MS data indicate the variation in membrane thickness assuming 50–70% of Rayleigh’s limiting charge for a charged water droplet of the same dimensions.

Comparison between SAXS and CD-MS Data

In general, the equivalent CD-MS diameters are slightly lower than those reported by DLS and SAXS. Presumably, this reflects the hydrated nature of the vesicles in aqueous solution, as opposed to the highly dehydrated particles interrogated by CD-MS. Since the CD-MS analysis assumes that the vesicles are completely dehydrated in the gas phase, N_agg^CD-MS can be calculated by using the molecular weight of the individual diblock copolymer chains according to the relation:

where M_n^CD-MS is the number-average particle mass of the vesicles (obtained from CD-MS), and M_n,pol is the molar mass (or molecular weight) of the corresponding G₅₅-H_x copolymer, as calculated using ¹H NMR spectroscopy. There is a systematic reduction in N_agg from 15,200 (G₅₅-H₃₀₀) to 9800 (G₅₅-H₈₀₀), followed by an increase up to 17,900 and 19,100 for the G₅₅-H₁₀₀₀ and G₅₅-H₁₅₀₀ vesicles.

The bimodal CD-MS molecular weight distribution observed for G₅₅-H₂₀₀₀ indicates N_agg^CD-MS values of 362 and 125,200, respectively. However, neither of these values are characteristic of well-defined vesicles. This suggests the presence of diblock copolymer aggregates that are significantly smaller than vesicles, as well as the presence of much larger aggregates. This observation is yet not fully understood, but it is certainly consistent with SAXS and TEM studies of this copolymer, which confirm the absence of any vesicular morphology.

Assuming that vesicles can be approximated to hollow spheres with an outer radius (R = D/2) and a membrane thickness, T_m^CD-MS, the relationship between M_n, the copolymer mass density ρ_p, the outer vesicle radius R, and the membrane thickness T_m^CD-MS, is given by the following third-order polynomial equation:

Knowing R, M_n^CD-MS, and ρ_p (which ranges between 1.21 and 1.23 g cm^–3, depending on the precise copolymer composition of the vesicles), T_m can be calculated by solving the above equation numerically. The membrane thicknesses extracted from the CD-MS measurements (given in Table 1 and displayed in Figure 7) show a systematic increase in T_m^CD-MS from 13 to 28 nm as x increases from 300 to 1000.

It is evident that the membrane thicknesses determined by SAXS are larger than those obtained by CD-MS for the same vesicles. When the log–log plot of T_m^CD-MS vs PHPMA DP (or x) is plotted for G₅₅-H_x (x = 300–1000), a scaling exponent, a, of 0.58 is obtained from the linear fit. In contrast, SAXS analysis of the same vesicles yielded a = 0.79, which suggests that the membrane-forming PHPMA chains are more stretched.³⁵ This difference is physically reasonable because the vesicles are substantially dehydrated when ionized in the gas phase for CD-MS analysis.³⁶

Bearing in mind the various assumptions involved, the reasonable correlation between the CD-MS and SAXS data is encouraging. Not only do these techniques report comparable results but also some of the discrepancies can be rationalized by the differing degrees of hydration of the vesicles during these two sets of measurements. Moreover, it is apparent that these vesicles are sufficiently robust to survive on the time scale of the CD-MS experiment. This is most likely the result of a relatively thick membrane and perhaps also multiple entanglements between the hydrophobic core-forming PHPMA blocks. In contrast, liposomes might be expected to undergo dissociation during electrospray measurements.

The SAXS pattern obtained for G₅₅-H₁₅₀₀ is relatively featureless and cannot be satisfactorily fitted using a vesicle form factor. It is possible that this non-vesicular morphology might be a large compound micelle, as previously described by Eisenberg and co-workers.³⁷ Presumably, the relatively short hydrophilic PGMA block is no longer capable of maintaining colloidal stability, leading to partial macroscopic precipitation. In addition, the high degree of plasticization of the vesicle membranes reduces the attractive hydrophobic forces between the PHPMA chains, eventually leading to destruction of the vesicle morphology (or vesicle “death”).

Conclusions

In summary, RAFT aqueous dispersion polymerization enables a series of diblock copolymer vesicles to be conveniently prepared via PISA. Using a suitable PGMA₅₅ macro-CTA enables the mean vesicle membrane thickness to be readily controlled simply by varying the mean degree of polymerization of the membrane-forming hydrophobic PHPMA block. Membrane thicknesses can range from 13 nm up to 47 nm and scale with an exponent of 0.79 according to SAXS analysis. This suggests that the PHPMA chains are somewhat more stretched than membrane-forming blocks in many other diblock copolymer vesicles. This is attributed to the substantial water content (∼40–68 vol %) within the membrane, which is consistent with the weakly hydrophobic nature of the PHPMA chains. When targeting PHPMA DPs of up to 1000, the vesicle membrane becomes progressively thicker, but there is almost no change in the overall vesicle dimensions. Thus the vesicle membrane thickens solely via inward growth, so the volume of the internal cavity (or lumen) necessarily becomes smaller. This growth mechanism leads to a reduction in total interfacial area for the growing vesicles, which in turn minimizes the free energy of the system. However, water molecules within the shrinking lumen gradually permeate the thickening PHPMA membrane. At some critical degree of membrane hydration, the attractive hydrophobic forces between the PHPMA blocks are no longer sufficient to stabilize the vesicular morphology. This triggers the formation of ill-defined colloidally unstable aggregates, as judged by both TEM and SAXS. The absolute mass of these PGMA₅₅-PHPMA_x vesicles can be determined using CD-MS, which is the first time that this technique has been applied to this copolymer morphology. In particular, the CD-MS data indicate little or no increase in vesicle mass when targeting a higher DP (x) for the membrane-forming PHPMA block. Mean vesicle aggregation numbers were calculated from both CD-MS and SAXS data and were in reasonably good agreement. Both techniques indicate a reduction in vesicle aggregation number with increasing x, which suggests that exchange of copolymer chains between vesicles occurs as the membranes become more hydrated.

Theory

The scattering intensity equation used for SAXS analysis is based on a previously reported model,³⁸ but it comprises two polydispersity functions, rather than a single function:

A1

where SZ(R_m^SAXS,σ_Rm) is a Schulz–Zimm distribution describing the vesicle radius polydispersity (R_m is the distance from the center of the vesicle to the middle of the membrane core, as indicated in the vesicle model shown in Figure 5, and σ_Rm is the standard deviation) and G(T_m^SAXS, σ_Tm) is a Gaussian function describing the polydispersity of the membrane thickness (T_m is the thickness and σ_Tm is the standard deviation).

Preliminary analysis indicated that using the Schulz–Zimm distribution in the model, see eq A1, produced a better data fit than when assuming Gaussian distributions for both R_m^SAXS and T_m. This is understandable as the size polydispersity should be linked to the molecular weight distribution of a diblock copolymer, which usually corresponds to a Schulz–Zimm distribution.³⁹ Incorporating the membrane thickness polydispersity into the model significantly improved the quality of the data fits. Indeed, using two polydispersity functions is physically reasonable for the vesicle model. The vesicle radius polydispersity is associated with the surface curvature (which is defined by the packing of the hydrophilic PGMA chains within the vesicle corona), while the membrane thickness polydispersity is directly related to the molecular weight distribution of the hydrophobic PHPMA block.

Programming tools within the Irena SAS Igor Pro macros⁴⁰ were used to implement the scattering model. The vesicle form factor in eq A1 is expressed as³⁸

A2

The X-ray scattering length contrast for the membrane-forming block (PHPMA) and the coronal stabilizer block (PGMA) is given by β_m = V_m (ξ_m – ξ_sol) and β_vc = V_vc (ξ_vc – ξ_sol), respectively, where ξ_m, ξ_v, and ξ_sol are the X-ray scattering length densities of the membrane-forming block (ξ_PHPMA = 11.11 × 10¹⁰ cm^–2), the coronal stabilizer block (ξ_PGMA = 11.94 × 10¹⁰ cm^–2) and the solvent (ξ_H2O = 9.42 × 10¹⁰ cm^–2). V_m and V_vc are the volumes of the membrane-forming block and the coronal stabilizer block, respectively. Using the molecular weights of the PHPMA and PGMA blocks and their respective mass densities (ρ_PHPMA = 1.21 ± 0.01 g cm^–3 and ρ_PGMA = 1.31 ± 0.01 g cm^–3, as determined using helium pycnometry), the individual block volumes can be calculated from V = ((M_n,pol)/(N_Aρ)) (Table 1), where M_n,pol corresponds to the number-average molecular weight of the block determined by ¹H NMR spectroscopy. The amplitude of the membrane self-term is

A3

where R_in = R_m^SAXS – 1/2T_m is the inner radius of the membrane, R_out = R_m^SAXS + 1/2T_m is the outer radius of the membrane, V_in = 4/3πR_in³, V_out = 4/3πR_in³, and Φ(qR) = 3[sin(qR) – qR cos(qR)]/(qR)³ is the form factor amplitude for a sphere.

It should be noted that eqs A2 and A3 differ from the original work in which they were first described.³⁸ The exponent term represents a sigmoidal interface between the blocks, with a width σ_in accounting for a decaying scattering length density at the core surface. This parameter was fixed at 0.3 nm during fitting. The mean vesicle aggregation number, N_agg^SAXS is given by

A4

where x_sol is the solvent (i.e., water) concentration within the vesicle membrane, which represents the volume fraction of water distributed within the layer of the membrane-forming PHPMA blocks. This parameter allows calculation of the mean volume occupied by the PHPMA blocks within a single vesicle, which is given by the expression (1 – x_sol)(V_out – V_in). The ratio of this mean volume to the volume of a single PHPMA block, V_m, enables the average number of copolymer chains in a single vesicle, N_agg^SAXS, to be determined, see eq A4. The self-correlation term for the corona block in eq A2 is given by the Debye function:

A5

where R_g is the radius of gyration of the vesicle corona block. Assuming that there is no penetration of the hydrophilic coronal blocks into the hydrophobic membrane, the amplitude of the corona self-term is expressed as

A6

where the term outside the square brackets is the factor amplitude of the corona block chain such that

A7

It should be noted that the X-ray scattering contribution from the corona block can be comparable to that from the membrane-forming block, especially for copolymers comprising relatively short membrane-forming blocks [i.e., PGMA₅₅-PHPMA₃₀₀ with (β_vc/β_m)² ≈ 0.08 versus PGMA₅₅-PHPMA₈₀₀ with (β_vc/β_m)² ≈ 0.01]. Thus, a more rigorous description of the corona electron density profile has also been examined for the fitting model (see eq A1) in order to estimate the effect of the approximate description of the corona profile on the SAXS fitting parameters, particularly the vesicle aggregation number. In this case, the amplitude of the corona self-term, A_vc(q), is obtained from a normalized Fourier transform of the radial density distribution function of the vesicle corona chains:

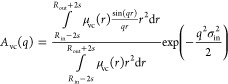A8

The radial profile, μ_vc(r), is expressed as a linear combination of two cubic b splines using two fitting parameters s and a that correspond to the width of the profile and the weight coefficient, respectively.³⁸ The precise analytical expression of the integration applied in the SAXS analysis is not given in the original paper,³⁸ but it can be obtained by using a mathematical software package such as Maple or MatLab. In accordance with previous results,^7,38 a confinement s = 2R_g was introduced into the model. From a preliminary SAXS analysis of the vesicle dispersions, it was found that the parameter a tended to zero for this condition. Thus, a = 0 was assumed for μ_vc(r) in eq A8. The vesicle model, eq A1, using either eq A4 or A8 for A_vc is denoted as the ‘simple model’ or ‘complex model’, respectively.

Supporting Information Available

Copolymer characterization and further TEM and SEM images. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.