Charge Transfer in Dynamical Biosystems, or The Treachery of (Static) Images

Conspectus

The image is not the thing. Just as a pipe rendered in an oil painting cannot be smoked, quantum mechanical coupling pathways rendered on LCDs do not convey electrons. The aim of this Account is to examine some of our recent discoveries regarding biological electron transfer (ET) and transport mechanisms that emerge when one moves beyond treacherous static views to dynamical frameworks.

Studies over the last two decades introduced both atomistic detail and macromolecule dynamics to the description of biological ET. The first model to move beyond the structureless square-barrier tunneling description is the Pathway model, which predicts how protein secondary motifs and folding-induced through-bond and through-space tunneling gaps influence kinetics. Explicit electronic structure theory is applied routinely now to elucidate ET mechanisms, to capture pathway interferences, and to treat redox cofactor electronic structure effects. Importantly, structural sampling of proteins provides an understanding of how dynamics may change the mechanisms of biological ET, as ET rates are exponentially sensitive to structure. Does protein motion average out tunneling pathways? Do conformational fluctuations gate biological ET? Are transient multistate resonances produced by energy gap fluctuations? These questions are becoming accessible as the static view of biological ET recedes and dynamical viewpoints take center stage.

This Account introduces ET reactions at the core of bioenergetics, summarizes our team’s progress toward arriving at an atomistic-level description, examines how thermal fluctuations influence ET, presents metrics that characterize dynamical effects on ET, and discusses applications in very long (micrometer scale) bacterial nanowires. The persistence of structural effects on the ET rates in the face of thermal fluctuations is considered. Finally, the flickering resonance (FR) view of charge transfer is presented to examine how fluctuations control low-barrier transport among multiple groups in van der Waals contact. FR produces exponential distance dependence in the absence of tunneling; the exponential character emerges from the probability of matching multiple vibronically broadened electronic energies within a tolerance defined by the rms coupling among interacting groups. FR thus produces band like coherent transport on the nanometer length scale, enabled by conformational fluctuations. Taken as a whole, the emerging context for ET in dynamical biomolecules provides a robust framework to design and interpret the inner workings of bioenergetics from the molecular to the cellular scale and beyond, with applications in biomedicine, biocatalysis, and energy science.

1. Introduction

1.1. Significance

The electron flux across cell membranes is essentially a constant in biology, amounting to 10⁶ electrons per second in bacteria.^1,2 It is remarkable that life on earth is energized by the stepwise vectorial transport of individual electrons and protons. The electrons do not flow as a current in a wire but are fired one-by-one or two-by-two as they flow (mostly) downhill among redox cofactors, sometimes synchronized with proton transfer, finally generating a diffuse transmembrane electrochemical gradient.³ At a cost of about three protons per ATP molecule, the proton gradient powers the formation of the ubiquitous energy-storing phosphate bond.⁴ Establishing the underpinnings of bioenergetics in general and the mechanism of electron transfer (ET) in photosynthetic and mitochondrial membranes in particular led to no fewer than six Nobel prizes (Szent-Györgyi; Mitchell; Taube; Deisenhofer, Huber, and Michel; Marcus; Boyer, Walker, and Skou). Yet, developing an understanding of the molecular-level schemes that control and couple processes in molecular bioenergetics is very challenging. For example, what are the origins of the efficiency and specificity of biomolecular charge flow? How are high-energy redox species directed without creating destructive moieties in the soft, wet biological milieu? In the case of carrier flow to aromatic residues and nucleobases,^5,6 or across water clefts,⁷ how transferrable is the physics of protein-mediated ET? In the last two decades, increasing attention has turned to ultrafast ET, DNA electron transfer,⁸ proton-coupled ET (PCET),^9,10 bacterial nanowires,² and multielectron catalysis, processes that may require extending the frameworks of adiabatic and nonadiabatic single electron transfer.¹¹ As well, new developments in theory and experiment are beginning to describe the formation and decay of transient coherences among species in van der Waals contact; these emerging themes are of great interest throughout biological ET and photobiology, and atomic-resolution understanding is yet to emerge.¹²⁻¹⁴

1.2. Prehistory

With early ideas of bridge-mediated tunneling (superexchange) in chemical and biological systems sketched by Halpern and Orgel¹⁵ and by Hopfield,¹⁶ early estimates of superexchange interactions in molecules were based on bold empirical models. McConnell’s computation of spin–spin interactions via hydrocarbons invoked virtual carbon d-orbitals,¹⁷ but these superexchange states are too far off resonance to provide the observed donor–acceptor couplings needed to understand biological ET. Hopfield’s estimate of a 2 eV tunneling barrier,¹⁶ posited to be less than the one-half of σ→ σ* optical gap of proteins but not so small as to allow thermal injection of carriers from photoexcited cofactors, captured the correct energy scale for protein-mediated superexchange. This early estimate could not address issues of through-bond and through-space tunneling nor of hole vs electron-mediated superexchange. We began to resolve these fascinating mechanistic issues about a decade later. Our studies of small molecules in the 1980s¹⁸ and of proteins in the 1990s^19,20 indicated that, at the redox potentials relevant to biology, hole-mediated superexchange often dominates. For photoinduced ET, the mechanism is likely mixed electron and hole superexchange.

Because of their central role in biology, chemistry, and physics, ET and PCET reactions are widely reviewed.²¹⁻²⁵ What continues to surprise us is the extremely wide range of length (centimeters to nanometers), energy (10^–1 to 10^–11 eV), and time scales (hours to picoseconds) associated with biological redox function.^{7,9,10,26−28}

1.3. Biological Electron Tunneling

Since bioenergetics employs single-electron motion, evolution directly confronts the dual particle–wave nature of matter. Studies of charge transfer in the bacterial photosynthetic apparatus^16,29,30 established vibronically coupled electron tunneling as the ET mechanism. And so, over the past two decades, we have pursued an atomic-resolution theory for transport in these structurally diverse, soft, wet systems. Moving from structureless square barrier models¹⁶ to tunneling pathway theories captured the heterogeneous through-bond and through-space characteristics of protein-mediated superexchange. Now, ensemble averaged fully quantum treatments of ET, including computation of redox potentials and reorganization energies, are powerful in their predictive and interpretive capacity.³¹⁻⁴¹ Semiempirical descriptions of electronic couplings provide a satisfactory compromise between accuracy and cost in studying large fluctuating systems. Such methods allow enhanced structure sampling that may not be accessible to more costly ab initio methods.⁴²⁻⁴⁴ Indeed, explorations of the critical fluctuations and time scales at play in ET and PCET are of great general interest.^10,45,46

The capacity to probe the biophysics of ET with atomistic resolution places compelling biophysical questions within reach: How is multielectron catalysis coordinated? What structures and mechanisms enable charge transfer on the micrometer to centimeter scales in bacterial nanowires and filaments? When is transport through multiple redox cofactors in van der Waals contact coherent? How do the multiple electronic and nuclear time scales play out across these diverse reactions?

1.4. Scope

This Account discusses the views emerging from our laboratory regarding how fluctuations in atomic positions and the consequent changes in electronic structure influence long-range charge flow in biology. We highlight progress in ET theory that has led to a deeper understanding of mechanism, has produced an emerging capacity to design functional synthetic systems, and is exposing some of the logic of biological function. We set the stage by reviewing the mechanisms of charge propagation in proteins and in nucleic acids. We then explore cases where either the average protein structure controls ET or fluctuations away from the mean dominate (section 2). We next examine the emerging understanding of multistep hopping and multicenter resonant transport in biomolecules in the context of bacterial nanowires (section 3). Finding that thermal fluctuations can bring multiple chemical groups into simultaneous redox-state resonance, we describe the new concept of flickering resonance transport, a mechanism that produces exponential distance decay of ET rates in the absence of tunneling. Flickering resonance is of particular importance when donor–bridge (DB) and bridge–acceptor (BA) energy gaps are on the same scale as the vibronic broadenings of the redox state energies (section 4 and Figure 5a) and electronic couplings among groups are strong, as may arise in π-stacked DNA and multiheme proteins. Finally, we conclude by mentioning new directions for our studies (section 5).

Figure 5.

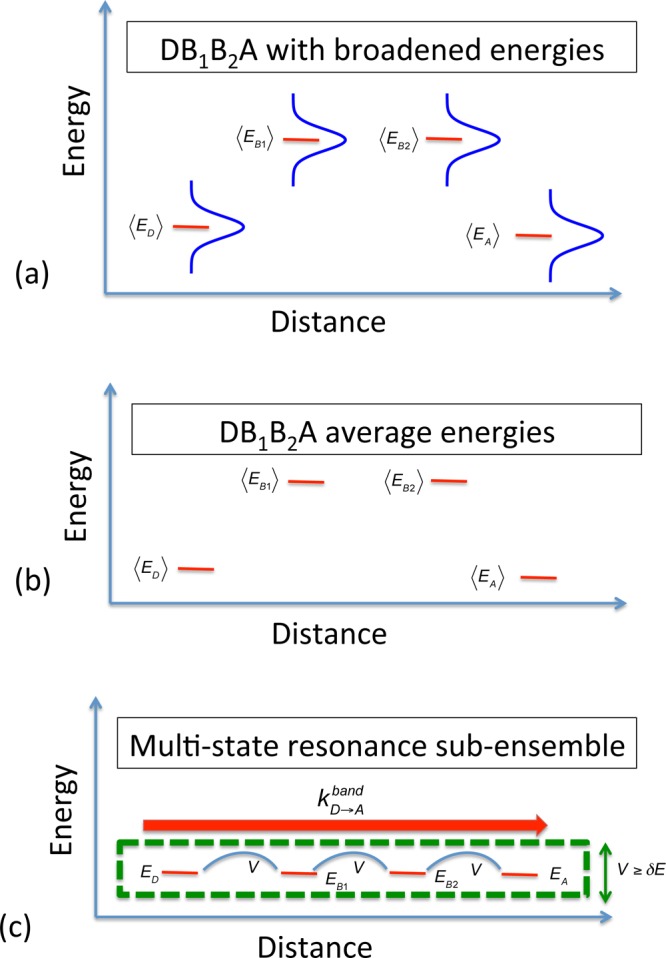
Site energies associated with a model DBBA system. (a) Assuming uncorrelated Gaussian fluctuations of site energies, each ET unit has an energy standard deviation of σ_E(i) = (2λ_ik_BT)^1/2.¹⁴ (b) Most static pictures for transport “freeze” the energy levels at their mean values and apply transport theories on this energy landscape. (c) Flickering resonance transport considers the subensemble of energy matched D, B_n, and A sites that support coherent transport (with rate k_D→A^band). Formation probabilities require that the coupling between groups (V) exceeds any energy mismatch (δE) among the sites energies. The probability of forming FR structures drops exponentially with distance (eq 1), as does the FR mechanism ET rate.¹⁴

2. Tunneling through Fluctuating Biomacromolecules

2.1. Mechanisms

Transport through biomacromolecules can proceed in many ways: by coherent tunneling, multistep and multirange hopping, and flickering resonance. Coherent band-like transport over long distances (with weak coupling to phonons), familiar in periodic solids, is believed to be inaccessible in ET molecules as a result of their aperiodicity and high barriers to electron or hole injection.^23,24 Nonetheless, we recently found that transient band-like transport on the scale of nanometer distances can be accessed for medium- to low-barrier ET systems (section 4).¹⁴ In this regime, multiple transport mechanisms may coexist, including multistep hopping, fast carrier injection followed by partially coherent transport,⁴⁷ and mechanisms determined by initial state preparation.⁴⁸ With hopping, the Boltzmann probability for placing an electron or hole on the bridge exceeds the D-to-A tunneling probability. Since k_BT is 1/40 eV at room temperature and typical tunneling decay exponents in proteins are 1.2 Å^–1, one expects hopping mechanisms to become operative beyond ∼30 Å for a ∼1 eV carrier injection energy.

2.2. Redox Energy Landscape

The redox window for one electron half-cell reactions of biological cofactors ranges from about −900 to about +1200 mV vs NHE.^4,49 When translated to electronic binding energies,⁵⁰ the energies fall in the −5.6 to −3.5 eV range. In a 1D square barrier model, a state bound by 5 eV has a through-space squared wave function decay exponent (β) of ∼2.2 Å^–1. This numerical value is double the measured tunneling decay rates observed experimentally in biomolecules. Thus, biological media (protein, DNA, solvent, ions, etc.) lower the effective barrier height by more than 2-fold. Intensive effort over the last two decades has focused on understanding how the tunneling medium places β into the observed range of 1–2 Å^–1 in proteins and to even lower values in nucleic acids.

2.3. Tunneling Pathways

The Pathway theoretical framework is the simplest model that captures the influence of a protein’s fold on its electron-tunneling kinetics. This model assigns pairwise through-bond and through-space decay factors to all interactions, based on parameters drawn from chemical model systems and back-of-envelope theory.²⁰ The most compelling predictions of the model are that (1) a larger β value is expected for random coils and α-helices compared with β-sheet structures, (2) “hot and cold spots” for electron transfer arise in proteins and these regions can be identified in advance of experimental validation, and (3) since protein structures are inhomogeneous, rates at fixed distances (and with fixed reaction free energies and reorganization energies) can differ by orders of magnitude because of coupling pathway structure.⁵¹⁻⁵⁴

Quantum chemistry is now used widely to explore even more refined questions about tunneling mediation,^31,32,43 as tunneling pathways appear in bundles or tubes in proteins and the multitude of paths interfere with one another. Indeed, theoretical analysis and extensive experimental data support the view that secondary structure and atomic details of pathway structure set the average β value for tunneling decay in proteins, producing structure-specific rates as discussed next.

A crucial and nuanced question is, under what circumstances do tunneling pathways limit ET rates in proteins? That is, does thermal motion erase pathway structure effects? Theory and experiment indicate that the answer is no (vide infra). We have found (in our analysis of heme and blue copper Ru-modified proteins of Winker and Gray⁵⁵) that about 15% of the derivatives studied require detailed pathway (or higher-level) analysis to make a reliable prediction of relative ET rates.²⁶ In this 15% of the derivatives, a through-space gap is found that substantially weakens the coupling compared with that found in the average activationless tunneling-limited rates for the proteins. This circumstance arises in proteins with dominant pathway families that couple into an axial heme ligand. Apparently heme protein folding tends to insulate the axial heme pathways from the protein surface. This causes anomalously slow ET rates (for their distance) in specific ruthenated myoglobin, cytochrome c, and cytochrome b₅₆₂ derivatives.^26,31 The other 85% of the derivatives have rates that can be predicted from knowledge of their bridging secondary structure, without zooming in to examine pathway structure at full atomistic resolution. Of course, comparisons among proteins with different cofactors require detailed quantum chemical analysis since the coupling pre-exponential factors are different for flavins, blue coppers, hemes, FeS clusters, redox active tryptophan residues, etc.

2.4. Water Pathways in ET and PCET

Tunneling can certainly be mediated by water at protein–protein interfaces and in clefts.⁵⁶ Our studies of self-exchange ET indicate that thin water layers at protein–protein interfaces can establish multiple constructively interfering pathways that enhance ET. For azurin dimers, the interplay of water-mediated pathways was interpreted in terms of electrostatically driven structuring of those pathways.³⁷ Indeed, rates accelerated by such effects could be larger than predicted by tunneling estimates based on frozen water models.²²

Recent studies also point to a possible role for structured water in PCET. Long-distance PCET was proposed to occur through the water-exposed interface between monooxygenase copper domains via cleavage and formation of hydrogen bonds along a water chain.⁵⁷ Such a chain could establish a “H atom wire,” providing effective long-range ET that is coupled to many short-range proton transfers. In tyramine β-monooxygenase, mutation of a conserved tyrosine residue in the interdomain solvent cleft produces a decreased protein contribution to the (PC)ET pathways and a corresponding disruption of the structured water regime, with a dramatic decrease in the ET rate.^7,56,58

2.5. Do Pathway Effects Persist in the Face of Thermal Fluctuations?

Pathway structures fluctuate, although pathway-coupling effects discussed above are often analyzed in fixed protein geometries. Consider a protein ET system with structure that partially unfolds and refolds on the time scale of ET (see Figure 1). In this case, one expects the mean-squared coupling to represent the average tunneling characteristics of the medium and the pathway effects to be ensemble averaged. Do protein fluctuations wash out all sequence and folding effects on ET couplings; does a protein’s time-averaged structure control its ET coupling? We have addressed these questions by performing D–A coupling analysis on protein geometries sampled along classical MD trajectories. Our studies found that the scatter of ⟨H_DA²⟩ values for different Ru-proteins with similar DA distances is of the same order as the scatter of ⟨H_DA⟩², the square of the mean coupling, computed for that family of proteins.^26,43 If thermal fluctuations completely erased structure-dependent pathway signatures, the ratio of the (many protein) standard deviation of ⟨H_DA²⟩ values at a given DA distance to the many protein ⟨H_DA²⟩ value for that distance would be zero, not of order unity.⁴³ This conclusion does not mean that coupling fluctuations are unimportant. Indeed, we find that for D–protein–A systems with average D–A distance larger than 6–7 Å, structural fluctuations cause large fluctuations in the D–A coupling, that is, ⟨H_DA²⟩ > ⟨H_DA⟩². Thus, nonequilibrium conformations of the D–bridge–A system provide much larger D–A couplings than the equilibrium conformation and thus enhance the ET rate. In this regime, tunneling pathway or electronic structure analysis should be performed for the large-coupling nonequilibrium conformations. However, even in the large-fluctuation limit, the values of ⟨H_DA²⟩ for different D–protein–A species with the same average D–A distances will be different (i.e., the coupling fluctuations depend on the underlying structure, as do the average couplings). Figure 1 shows schematically how DA couplings (mediated by direct contact, intervening atoms, or water) fluctuate with geometry, modulating H_DA.

Figure 1.

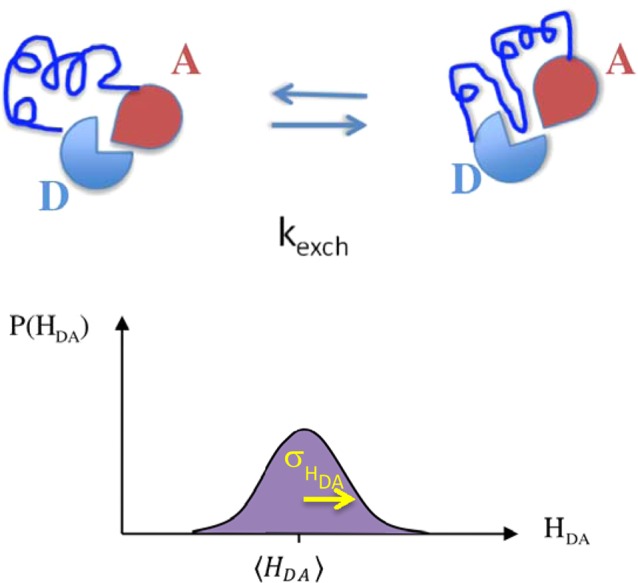
Donor–bridge–acceptor structural fluctuations cause coupling values, H_DA, to vary. When exchange among molecular conformations is much faster than the ET rate, ⟨H_DA²⟩ enters the nonadiabatic rate expression in place of a single coupling value. The probability density for couplings, P(H_DA), is determined by structures accessed.^27,43,70 In the regime of slow exchange among conformations (k_exch ≪ k_ET), nonexponential or gated kinetics may be measured.

3. Energy Gap Fluctuations and ET: Transition to Hopping

While tunneling describes protein-mediated ET on length scales up to a few tens of angstroms, it does not describe ET at much longer distances. Thermal Boltzmann populations of states drop exponentially as a function of energy above the ground state. Thus, bridge energies that are ∼1 eV above the donor and acceptor states will have thermal populations that compete with tunneling probabilities at distances of more than ∼30 Å for β values ∼1.2 Å^–1 (i.e., exp(−ΔE/(k_BT)) ≈ exp(−βR_DA)). Transport across photosynthetic and mitochondrial membranes can be described as multistep hopping among multiple redox cofactors, and long-distance hopping via multiple aromatic residues in key proteins is known as well.⁵⁹ Indeed, installation of strong oxidants in proteins can trigger tryptophan-mediated hopping at shorter distances.¹² Describing the transition between coherent single-step transport and incoherent multistep dynamics theoretically and mapping it experimentally remain a great challenge,⁶⁰ with important parallels in photobiology.^13,23,24

Our recent studies of charge recombination between hemes in the cytochrome c/cytochrome c peroxidase couple explored the tunneling/hopping transition. We performed classical MD simulations of the protein–protein complex based on docked protein structures determined by X-ray crystallography (see Figure 2).⁶¹ Interestingly, the experimental studies on a number of mutant proteins produced rates that were not understood using simple distance scaling or coupling pathway arguments.⁶¹ We found in the simulations that tryptophan residues came in and out of resonance with a redox cofactor, indicating that charge recombination via a hopping mechanism is accessible. Combining this principle with a description of the distance dependent reorganization energy provides a consistent view of the observed ET recombination kinetics. Other theoretical and experimental studies on this redox couple also support a hopping charge-recombination mechanism.⁶²

Figure 2.

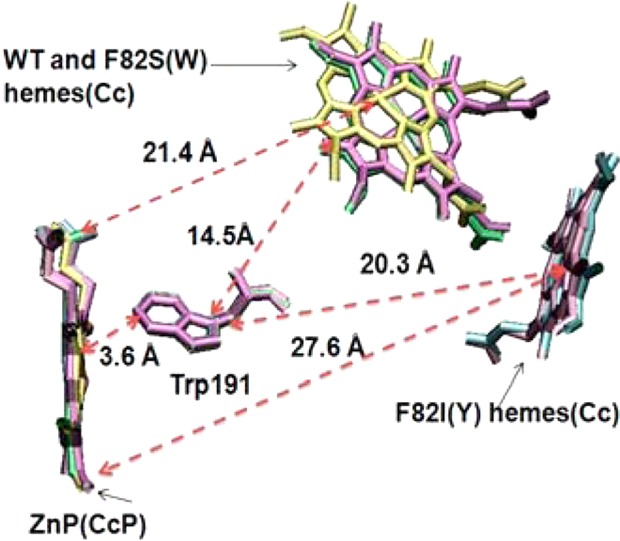
Studies of charge recombination in the cytochrome c/Zn-cytochrome c peroxidase complexes indicate hopping transport via Trp191. The very long heme-to-heme distances (and weak couplings), combined with the redox potentials, favor hopping recombination. Reproduced with permission from ref (61). Copyright 2013 American Chemical Society.

Some bacterial ET chains employ long extracellular appendages that extend for micrometers outside of the cell (see Figure 3). These appendages, known as nanowires, are believed to help deliver electrons to extracellular inorganic substrates (like iron oxide) when the organisms are respiring anaerobically (i.e., “rock breathers”²). Recent studies of dried nanowires indicate that nanoampere currents are conducted on the micrometer scale through these appendages.^63,64 We built multistep hopping models to explore the physical constraints under which such high currents could flow.⁶⁵ We found that the hopping-transport model could reproduce the experimental I–V curves, with plausible values of reaction free energies, reorganization energies, and a packing density for redox cofactors (e.g., hemes) consistent with that of multiheme proteins found in the bacterial cell surface (Figure 4).⁶⁶ If somewhat delocalized intermediates form (say, among two or three neighboring cofactors), the observed currents can be described with less stringent requirements. Because of their potential value as charge conduits for both biofuels-to-electricity and electricity-to-biofuels schemes, bionanowires are of intensive interest (and controversy).^2,67,68

Figure 3.

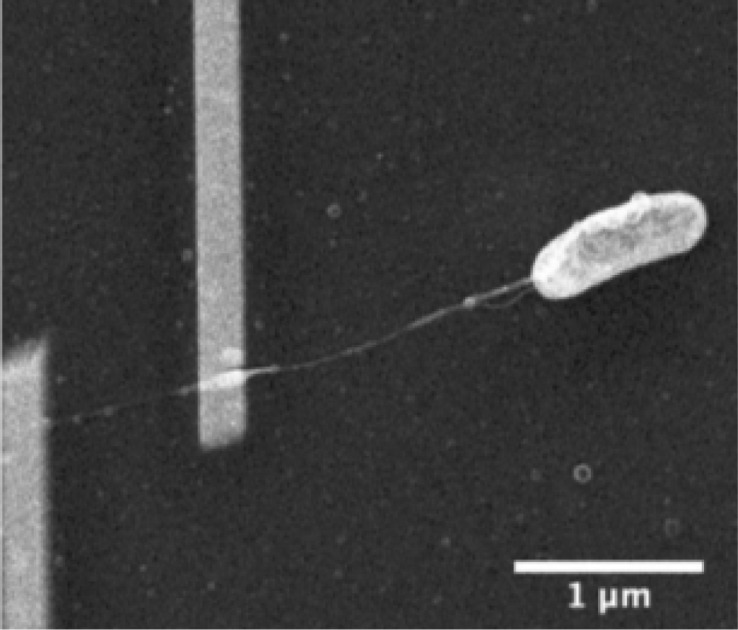
A nanowire from a Shewanella oneidensis MR-1 cell bridges two platinum electrodes. Used with permission from ref (64). Copyright 2012 Royal Society of Chemistry.

Figure 4.

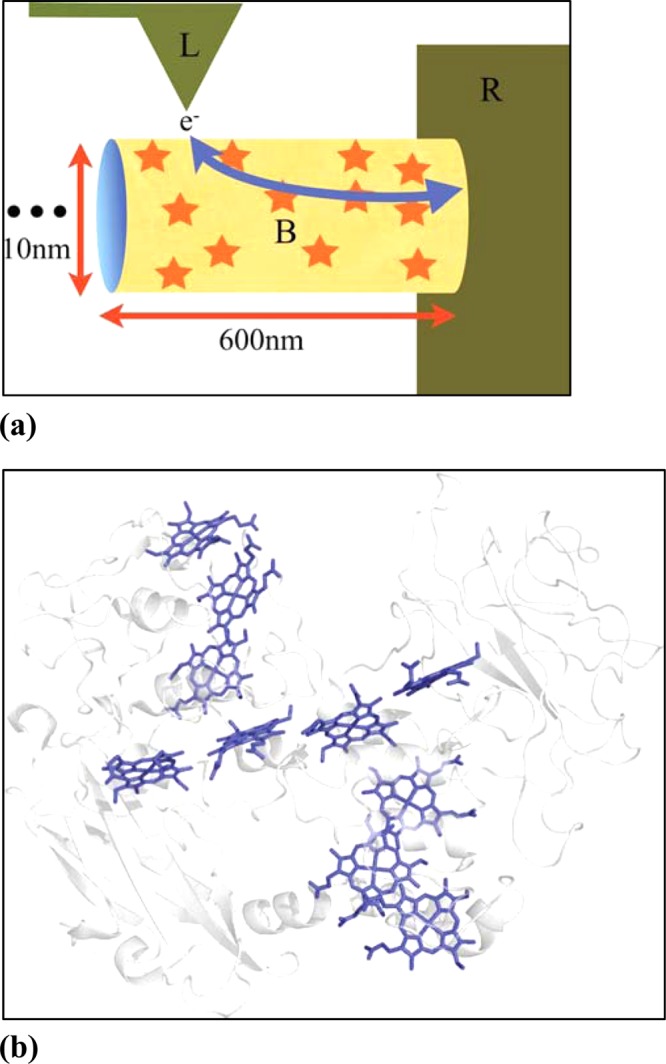
(a) Representation of the hopping network used to model transport in bacterial nanowires.⁶⁶ Star shapes represent hopping sites. (b) Rendering of the decaheme protein structure from the outer-membrane of Shewanella oneidensis.(65) Note the near van der Waals contact among cofactors. Used with permission from ref (66). Copyright 2012 Royal Society of Chemistry.

Fascinating open challenges remain concerning biological ET on the micrometer to centimeter length scale.^2,28 Band-like coherent conduction was proposed as an alternative to hopping for nanowire transport (see Figure 4). In our analysis, this band conduction was found to be unlikely because it requires nonphysical parameter choices.⁶⁶ Moreover, biological systems with vibronic site energy broadenings on the scale of tenths of an electronvolt (typical of condensed phase systems) would be ill-suited to create band-like states. In the next section, however, we explore the possibility of forming short-lived coherences among multiple electronic states. Such transient species may contribute to charge transport but are predicted to produce ET rates that decay exponentially with distance, thus limiting the functional significance of this mechanism to the nanometer regime before incoherent hopping takes over.

4. Flickering Resonance and Long Range ET

The traditional theory of vibronically coupled ET may be cast in terms of Gaussian spectral functions for electron removal from D and insertion on A.^16,21 If D and A broadenings are equal, the standard deviation of each broadened level (i) is σ_E(i) = (2λ_ik_BT)^1/2, where λ_i is the site’s contribution to the reorganization energy.¹⁶ At room temperature, σ_E is expected to be on the scale of tenths of an electronvolt. The nonadiabatic ET rate may be described as the probability for matching the initial and final electronic state energies within a range set by the DA coupling (i.e., the product of the Franck–Condon factor and the DA coupling) multiplied by the two-level system electronic oscillation frequency.^14,16 When energy barriers for carrier injection to the bridge are similarly on the tenths of electronvolt scale, there is a significant probability that the donor, bridge, and acceptor states will match, creating transient multisite resonances. As such, FR transport rates at short distances may plausibly compete with superexchange rates.¹⁴

Since the probability of many uncorrelated events occurring simultaneously is the product of independent probabilities, the matching probability drops exponentially with distance. For N sites with equal average energies,¹⁴ we found P_match(N) ≈ ((2/π)^1/2(σ_E/V_RMS))^N, where σ_E is the standard deviation of the site energies and V_RMS is the root-mean-square coupling among nearest-neighbor sites. Thus,

1a

If the donor and acceptor are off-resonance (on average) with the bridge sites, with an average D(A)-to-B energy gap of E_B,

1b

As in familiar ET theory, there are many possible rate limiting time scales that may control the ET dynamics,^14,23 and the FR ET rate prefactor 1/τ is determined by this time scale: k_ET^FR = P_match(N)/τ. Interestingly, FR rates decay exponentially with distance, even though the transfer mechanism is not tunneling.¹⁴

The distance decay exponent, Φ, for FR is approximately proportional to the logarithm of σ_E/V_RMS. We computed these energy level matching probabilities and found that their distance decays match observed ET rate distance decays in several DNA-ET experiments.¹⁴ It is thus possible that the strong distance dependence in DNA ET rates at short distance arises from a FR mechanism or from a mixed FR/tunneling mechanism, rather than from pure tunneling.

FR is described schematically in Figure 5. Figure 5a shows the probability density distributions of site (electronic) energies for D–B–A species. Although the average site energy picture indicates that the D and A states are not resonant with the bridge (Figure 5b), the site-energy distributions may overlap substantially for medium to low barrier heights. For the subensemble of systems with all sites resonant (Figure 5c), ET from D to A is band-like and fast, limited by the multiresonance (FR) lifetime and the prefactor, 1/τ.¹⁴ For short bridges, this mechanism can provide an efficient ET channel. The FR model is equally valid in the adiabatic and nonadiabatic regimes, reflected in a multisite adiabaticity factor that also appears in the FR rate.¹⁴ It is possible, also, to consider sequential FR transport steps, which might take on some characteristics that arise in multirange hopping theories.⁶⁹

What signatures of FR transport distinguish it from conventional tunneling or hopping? The key features are 2-fold. First, the FR distance decay exponent (Φ) grows with temperature so the distance dependence will become steeper as the temperature grows (since σ_E grows with temperature, V_RMS is expected to be weakly temperature dependent). Second, the energy barrier prefactor (eq 1b) is expected to grow with temperature. Figure 6 thus indicates the expected temperature signatures for FR rates as a function of distance.

Figure 6.

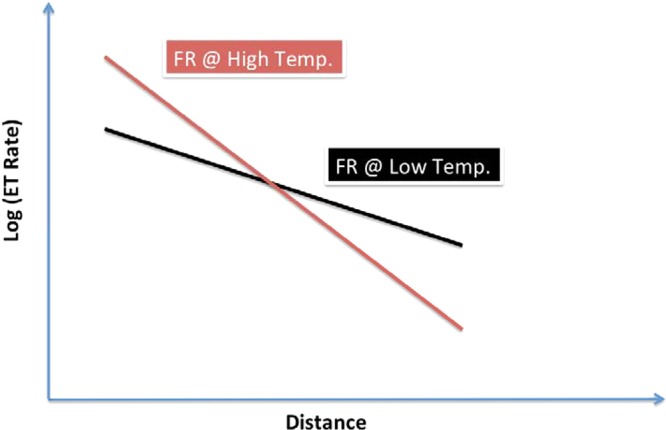
Prediction of distance-dependent transport rates for FR at low and high temperatures. Elevating the temperature grows the injection prefactor (e^{–E_B2/2σ_E2}) but also increases the distance decay exponent Φ (eq 1), assuming that V_RMS is weakly temperature dependent. Traditional nonadiabatic ET rates would produce parallel lines in this plot.

5. Conclusions and Prospects

We have described progress in our group over the last 20 years to establish atomic-resolution theories for biological electron transfer and transport rates. In recent years, biomolecular dynamics has captured center stage as we have examined the features of tunneling in biology that are either averaged out or robust in the face of thermal fluctuations. Importantly, for low-barrier transport among groups in van der Waals contact, we have identified a flickering resonance mechanism for coherent band-like transport that can masquerade as tunneling because of its exponential distance dependence. Applications of this theoretical framework to complex systems for transport in molecular bioenergetics, biocatalysis, DNA nanostructures, bacterial nanowires, and biosensors seem poised for exploitation. Static reduced dimensional views, like Magritte’s rendering in the Conspectus, have tremendous value but do not convey the richness of the three-dimensional, dynamical, functional object.

Experimental studies increasingly indicate the importance of fine quantum effects in biological systems, associated with coherences on the nanometer length scale. Elucidating the physics and biochemistry of these subtle effects requires theoretical frameworks to describe the quantum dynamics with as few ad hoc mechanistic assumptions as possible, while taking the nature of the fluctuations into account. In this spirit, we are developing methods in our lab that solve the time-dependent Schrödinger equation for molecular systems in the presence of thermal fluctuations with characteristic correlation times, correlation lengths, and energy fluctuations. We expect that principles emerging from these simulations will provide insights of value at the confluence of the quantum and the biological worlds, and the emerging framework may lead to useful guidance for the de novo design of functional nanostructures based on biomolecular architectures.

Biographies

David Beratan (B.S., Duke; Ph.D., Caltech; NRC Resident Research Associate, JPL) is the Reynolds Professor of Chemistry at Duke.

Chaoren Liu (B.S. Physics, University of Science and Technology of China; M.S. Physics, Chinese Academy of Sciences) is a Ph.D. candidate at Duke.

Agostino Migliore (Physics Laurea, Palermo; Ph.D. Physics, Modena and Reggio Emilia, postdoctoral researcher at Pennsylvania and Tel Aviv) is an Assistant Research Professor of Chemistry at Duke.

Nicholas F. Polizzi (B.S. Biology, Cornell) is a Ph.D. candidate at Duke.

Spiros Skourtis (B.S., Physics and Mathematics, Miami, Ph.D. Biophysics, UC-Berkeley, postdoc UCSD, Rochester, and Pittsburgh) is Associate Professor of Physics at University of Cyprus. He held visiting faculty positions at Duke, the Israel Institute of Advanced Studies (Hebrew University), and the Freiburg Institute of Advanced Studies (University of Freiburg).

Peng Zhang (B.S., Zhengzhou; M.S., Peking; Ph.D., Emory; postdoc Harvard) is an Assistant Research Professor of Chemistry at Duke.

Yuqi Zhang (B.S., Nankai) is a Ph.D. candidate at Duke.

Author Contributions

All authors contributed to and approve the paper’s submission.

This research was supported by the National Science Foundation (Grants CHE-1012357 and DMR-1413257), Office of Naval Research (Grant N00014-11-1-0729), National Institutes of Health (Grants GM-48043 and GM-71628), and the Cyprus Foundation for the Promotion of Research.

The authors declare no competing financial interest.

Special Issue

Published as part of the Accounts of Chemical Research special issue “Protein Motion in Catalysis”.

Funding Statement

National Institutes of Health, United States