Efficiently mining Adverse Event Reporting System for multiple drug interactions

Abstract

Efficiently mining multiple drug interactions and reactions from Adverse Event Reporting System (AERS) is a challenging problem which has not been sufficiently addressed by existing methods. To tackle this challenge, we propose a FCI-fliter approach which leverages the efforts of UMLS mapping, frequent closed itemset mining, and uninformative association identification and removal. By applying our method on AERS, we identified a large number of multiple drug interactions with reactions. By statistical analysis, we found most of the identified associations have very small p-values which suggest that they are statistically significant. Further analysis on the results shows that many multiple drug interactions and reactions are clinically interesting, and suggests that our method may be further improved with the combination of external knowledge.

Introduction

It is well understood that adverse drug reactions may pose serious health concerns on patients. The situation becomes more complicated when two or more drugs are taken together. Interactions between multiple drugs may yield additional reactions than taking them separately. To monitor the adverse drug reactions, the US Food and Drug Administration built an Adverse Event Reporting System (AERS), a post-marketing drug safety surveillance database which contains adverse reports from various sources.

However, AERS is essentially a large collection of drug reaction reports. A report involving multiple drugs and reactions does not necessarily indicate a causal relationship between them. In fact, records in AERS come from multiple sources coded as “Foreign”, “Study”, “Literature”, “Consumer”, “Health Professional”, etc. It is not clear whether all sources produce similar accurate reports to AERS.

Thus, mining such a large data for causative adverse drug reactions poses a major challenge in drug safety studies.

The existing work on AERS data mining and analysis mainly focuses on using statistic approaches. Some studies identify the reactions caused by one drug, or the drug-drug interactions between two drugs, using statistical approaches such as Bayesian methods [1] [2] and propensity score matching [3]. Some studies focus on the analysis of a few specific adverse reactions [4] or a few drug-drug interaction pairs [5]. In [2], the authors also extend the self-controlled case series (SCCS) to analyze multiple drug interactions. However, these methods did not answer the question of how to efficiently discover multiple drug interactions, i.e., drug-drug interactions that involve two or more drugs. There are many reports in AERS involving more than 2 drugs.

To tackle this challenge, Harpaz et al. [6] used association rules mining technique to find frequent patterns. A frequent pattern (a.k.a., frequent itemset) in AERS is a set of drugs and reactions that appear in at least k reports, where k is an adjustable parameter that is known as minimum support. The lower k is, the more patterns will be found and thus more computational time is needed. However, using frequent pattern mining has two major limitations.

First, it is computationally very costly. If a pattern is frequent, then all its sub patterns are frequent and should be outputted under the same support level k. A pattern with length x will have 2^x sub patterns (including the empty pattern and itself). This implies that it is computationally intractable to find a lengthy pattern because the number of sub patterns is exponential to its length. The counter measurement is to increase k or limit the output pattern size. But by doing this, we will miss a large volume of lengthy patterns and low support patterns. In [6], authors use 50, a quite high support level for mining AERS, and obtained only 2603 itemsets.

Second, the association rules suggested by frequent patterns are not sufficient to support the causative relationships between drug interactions and reactions. For example, if (drug_A, drug_B, reaction_A, reaction_B) is a frequent itemset, we cannot conclude that it is supportive evidence that the interaction of drug_A and drug_B leads to the reaction_A and reaction_B. It may be caused by the facts that (1) drug_A causes reaction_A; drug_B causes reaction_B, drug_A and drug_B are often taken together.

Given the above challenging background, in this work we propose a very efficient mining method based on UMLS mapping, Frequent Closed Itemset Mining and filtering (FCI-filter) for mining multiple drug interactions from AERS. Our method efficiently finds a large number of multiple drug interactions and effectively prunes out uninformative patterns. It is important to point out that in this work we do not target on finding causative relationships between drug interactions and reactions, but on finding informative associations by eliminating associations that are not sufficient to support causative relationships.

Methods

UMLS Mapping

A drug or a reaction may have different names in the AERS, for example: Alpha Lipoic Acid is also known as ALA or Lipoic Acid. In many cases a drug name in AERS not only includes the drug but also its dosage. Therefore, it is not accurate to build a transactional database based on the drug or reaction names in AERS. To tackle this issue, we map each drug or reaction name to a UMLS concept, by LDPMap [7]. The UMLS is a very comprehensive collection of medical terms from various sources, such as HUGO, SNOMED CT, RxNorm, ICD9, MedDRA, etc. The RxNorm contains a large collection of drug names and has been successfully used in [6] for mapping drug names. The MedDRA was used for coding reactions in AERS. In the UMLS, a medical term may have various synonyms and may appear in more than one source, but it has only one unique identifier known as a CUI. In [7], we designed a layered dynamic programming mapping method (LDPMap) to effectively find a best matching UMLS CUI for any input of medical term. We have known that LDPMap is much more accurate in mapping medical terms to the UMLS than the UMLS Metathesaurus Browser [8] and MetaMap [9]. Here, we utilize LDPMap to map each drug and reaction to a UMLS CUI. In order to increase the accuracy, dosage related characters such as “oz”, “ml” and “mg” in drug names were removed before applying LDPMap. After applying LDPMap on the AERS data of 2012q3, we obtained 10297 unique drugs and 6838 unique reactions, and built a transactional database AERS_tdb containing 134508 records.

Frequent Closed Itemset Mining

In data mining, a closed itemset is defined as an itemset which does not have a superset that has the same support as this itemset, and a frequent closed itemset is an itemset that is both closed and frequent. By using the concept of closed itemset, we will be able to eliminate the problem of enumerating exponential numbers of subsets. For example, if drug_A, drug_B, reaction_A, reaction_B is a frequent closed itemset, then we do not need to output any of its subsets (such as drug_A, reaction_A) unless such a subset appears in a record that does not contain all items of drug_A, drug_B, reaction_A, reaction_B. Thus, we can see that by using the concept of frequent closed itemset, it is possible to significantly reduce the computational cost and eliminate the output of redundant information.

In this study, we use MAFIA [10], an efficient frequent closed itemset mining tool, to mine frequent closed itemset in AERS_tdb, with support level set to be 0.00005, which implies that any closed itemset appearing in 6.7254 or more records in AERS_tdb will be outputted. As a result, we obtained 4811379 frequent closed itemsets. Since we are interested in drug reaction relationships, we removed any itemset that contains only drugs or only reactions, and finally we got 1903630 itemsets containing both drugs and reactions. This is several orders of magnitude larger than the 2603 items obtained in [6]. In addition, we observed that the maximum number of drugs contained in one itemset is 20. This suggests that these 20 drugs are often taken together and with common reactions.

Uninformative Association Identification and Removal

As mentioned above, the association rules suggested by frequent closed itemsets are not equivalent to the causative relationships between drug interactions and reactions. An itemset is not sufficient to support a causative relationship if its items and supporting transactions (i.e., transactions containing these items) can be obtained from the interaction of other itemsets and their supporting transactions. In this case, this itemset is considered uninformative. Formally, Let I denote an itemset, and T denote the complete set of transactions containing this itemset. We have the following rule:

Rule 1: I is not sufficient to support causative relationships if there exist a list of itemset-transaction pairs I₁×T₁, I₂×T₂, … I_n×T_n, I = I₁ ∪ I₂… ∪ I_n and T = T₁ ∩ T₂… ∩ T_n such that none of T_1, T₂…,T_n is equal to T.

In other words, if we view an itemset and its supporting transactions as a block, the above interaction can be described as a “block horizontal union” [11]. Thus, an itemset is not sufficient to support causative relationships if its block can be obtained by a block horizontal union on other blocks with different transaction sets. Here is an example:

drug_A, reaction_A, appears in and only in records 1, 3, 5

drug_B, reaction_B, appears in and only in records 1, 2, 5

drug_A, drug_B, reaction_A, reaction_B appears in and only in records 1, 5.

Then drug_A, drug_B, reaction_A, reaction_B is not sufficient to support a causative relationship such that the interaction of drug_A and drug_B causes reaction_A and reaction_B, because this relationship is a logical result of taking both drugs together.

However, if in the above, drug_A, reaction_A appears in and only in records 1, 5, then we cannot judge drug_A, drug_B, reaction_A, reaction_B as “not sufficient to support a causative relationship”.

In the following, we will use the above rule to eliminate frequent closed itemsets that are not sufficient to establish a causative relationship. Interestingly, we find that block interaction is not necessary for frequent closed itemsets and rule 1 can be simplified as:

Rule 2: A frequent closed itemset I is not sufficient to support causative relationships if there exist a list of frequent closed itemsets I₁, I₂, … I_n where I = I₁ ∪ I₂... ∪ I_n.

This is because for frequent closed itemsets, if I = I₁ ∪ I₂... ∪ I_n, we can conclude that for T = T₁ ∩ T₂… ∩ T_n, none of T₁, T₂…, T_n is equal to T. Othewise, if one of the transaction set, say T_k, is equal to T, then it is a contradiction to the assumption that I_k is a closed itemset, because in this case I_k ∪ I would be a superset of I_k with the same support as I_k.

Next we will design an efficient filtering algorithm based on Rule 2. For an itemset I with p drugs, if I = I₁ ∪ I₂… ∪ I_n, we can observe that for any I_k (1≤ k ≤n), it must not contain more than p drugs. Thus, the filtering algorithm does not need to consider all itemsets in order to decide whether an itemset needs to be filtered out. We organize itemsets into groups by the number of drugs they contains. Let IS_k denote the itemset with k drugs, our filtering algorithm can be summarized by the following pseudo code:

By applying FCI-Filter to the 20 frequent closed itemsets mined from AERS_tdb, we filtered out 654484 frequent closed itemsets and kept 1249146 frequent closed itemsets as the candidate associate rules.

Statistical validation

We use the following statistical method to validate the filtered itemsets. Assume the counts for taking drug(s) and have reaction(s) follows a Poisson distribution. For any drug(s) and reaction(s), we will have the following frequency:

Total cases: N

Taking drug(s): a

Have reaction(s): b

If the drug(s) will not affect the rate of having reaction(s), the expected counts of taking drug(s) and having reaction(s) would be $\mu =b\times \frac{a}{N},\text{as}\frac{a}{N}$ is the portion of people taking drug.

The P-value is based on the observed counts of taking drug(s) and having reaction(s) denoted by X and its expectation μ, which is P(X > μ), X~Pois(μ)

Results

By applying UMLS mapping and Frequent Closed Itemset Mining, we obtained a large number of itemsets of drug interactions and reactions (Table 1). After applying algorithm FCI-Filter, we removed a significant amount of itemsets that are insufficient to support causative relationships (Table 1).

Table 1.

Summary of results of Frequent closed mining and frequent closed itemset filtering on AERS_tdb.

Number of drugs	Itemsets before filtering	Itemsets after filtering
1	1246948	48033
2	543037	1320
3	99755	144
4	11238	33
5	1231	14
6	267	12
7	155	9
8	100	3
9	83	3
10	57	2
11	42	1
12	43	1
13	57	0
14	96	0
15	139	1
16	159	0
17	135	1
18	70	2
19	17	0
20	1	0

We subjected the itemsets (i.e., drug interactions and reactions) after filtering in Table 1 to statistical validation, and found that most itemsets have very significant low p-values (Figure 1). In addition, for drug counts greater than 10, p-value histogram (Figure 2) is similar to Figure 1, which further confirms the effectiveness of our drug interaction mining approach.

Figure 1.

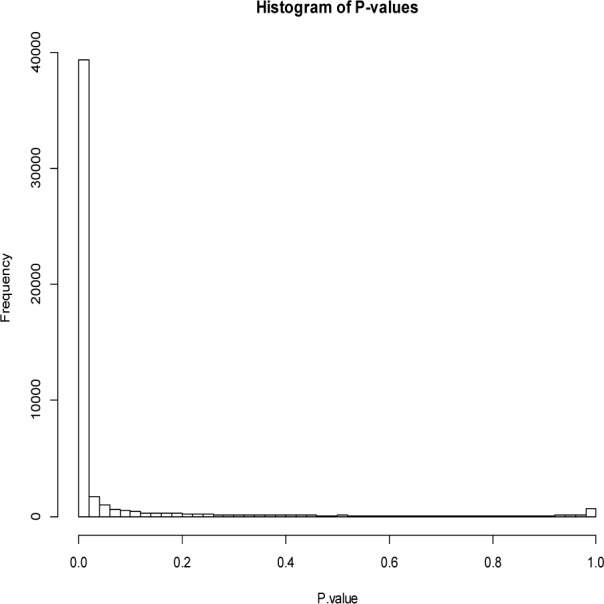
P-value histogram for all itemsets after filtering

Figure 2.

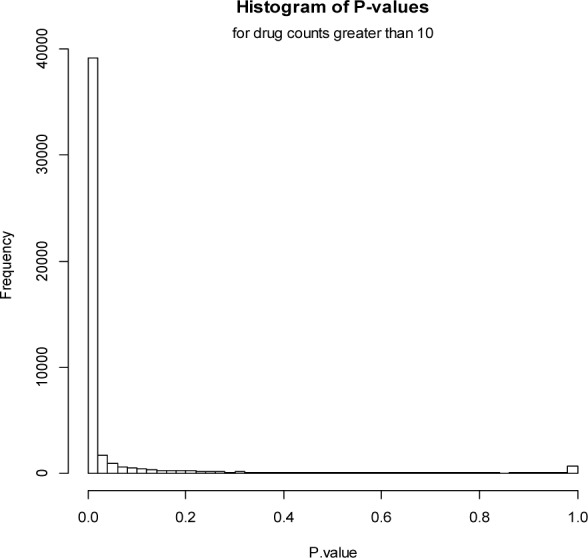
P-value histogram for drug counts greater than 10

Discussions

A clinical evaluation of the data mining results reveals some interesting findings as listed in Table 2.

Table 2.

Interesting drug drug interactions and reactions.

Case	Drugs	Adverse Event
1	ARIPIPRAZOLE|CITALOPRAM HYDROBROMIDE|MIRTAZAPINE	CARDIAC FAILURE CONGESTIVE|CONGESTIVE CARDIOMYOPATHY
2	DULOXETINE HYDROCHLORID E|MIRTAZAPINE|RISPERIDONE	LIVER FUNCTION TEST ABNORMAL
3	ASPIRIN|BISOPROLOL FUMARATE|GLYBURIDE|MIGLITOL|ONON|PLAVIX	HYPOGLYCAEMIA
4	AMARYL|SITAGLIPTIN PHOSPHATE	HYPOGLYCAEMIA
5	BROMOCRIPTINE MESYLATE|CLARITHROMYCIN|KETOCONAZOLE	HYPOTENSION

For instance, Aripiprazole, Citalopram hydrobromide and Mirtazapine, the three antidepressants sometimes used in combination therapies, were found to be in association with adverse cardiovascular events (Case 1 of Table 2). This result is highly interesting, since the potential cardiovascular side effects of antidepressants and antipsychotics have long been under debate [12] [13]. Recently in 2011, the US Food and Drug Administration (FDA) announced that “Citalopram causes dose-dependent QT interval prolongation. Citalopram should no longer be prescribed at doses greater than 40 mg per day.” Further clinical study of Aripiprazole, Citalopram hydrobromide and Mirtazapine is required to explore their association with adverse cardiovascular events.

In addition to the above findings, we also observed interesting interactions involving a good number of drugs. For example, the following interaction contains 7 drugs and many reactions:

Drugs:

AMINOPYRIDINE|DANTRIUM|GILENYA|LEVO CARNIL|PIROXICAM|TROSPIUM CHLORIDE|VESICARE|

Reactions:

ALANINE AMINOTRANSFERASE INCREASED | ASPARTATE   AMINOTRANSFERASE INCREASED  |  BLOOD  CREATININE INCREASED  |BLOOD  GLUCOSE INCREASED|BLOOD   LACTATE DEHYDROGENASE INCREASED|BLOOD UREA INCREASED|BLOOD URIC ACID DECREASED||HAEMOGLOBIN   DECREASED|…(18 other reactions)

The actions of this combination of drugs along with the reported biochemical effects is interesting. Many of these drugs act on ion channels or receptors, and the diverse array of biochemical effects that they result in is overwhelming. They result in increased activities of alanine aminotransferase, aspartate aminotransferase and blood lactate dehydrogenase. They also result in increased concentrations of blood creatinine, glucose and urea, as well as decreased concentrations in hemoglobin and blood uric acid. Many of these outcomes can be partly accredited to abnormal kidney or liver function, but they along with the other associated symptoms make analyzing their overall effects quite complex. However, this type of data analysis can provide valuable pieces of information that can act as a starting point in order to investigate why this combination of drugs has the resulting effects.

Future work

We have demonstrated in the above that FCI-filter is very effective in identifying important multiple drug interactions and reactions. However, the clinical evaluation also suggests some future improvements of our data mining strategy. An integration of clinical knowledge outside of the AERS database can be helpful (Case 3, 4, and 5 of Table 2). For instance, in Case 5 of Table 2, the hypotension side effect of Bromocriptine (single drug) is not statistically revealed from the AERS data set, although it is well known clinically to cause potential hypotension. As such, external knowledge can make the filtering of the Frequent Closed Itemset Mining more effective.