Protein Conformational Landscapes and Catalysis. Influence of Active Site Conformations in the Reaction Catalyzed by L-Lactate Dehydrogenase

Abstract

In the last decade L-Lactate Dehydrogenase (LDH) has become an extremely useful marker in both clinical diagnosis and in monitoring the course of many human diseases. It has been assumed from the 80s that the full catalytic process of LDH starts with the binding of the cofactor and the substrate followed by the enclosure of the active site by a mobile loop of the protein before the reaction to take place. In this paper we show that the chemical step of the LDH catalyzed reaction can proceed within the open loop conformation, and the different reactivity of the different protein conformations would be in agreement with the broad range of rate constants measured in single molecule spectrometry studies. Starting from a recently solved X-ray diffraction structure that presented an open loop conformation in two of the four chains of the tetramer, QM/MM free energy surfaces have been obtained at different levels of theory. Depending on the level of theory used to describe the electronic structure, the free energy barrier for the transformation of pyruvate into lactate with the open conformation of the protein varies between 12.9 and 16.3 kcal/mol, after quantizing the vibrations and adding the contributions of recrossing and tunneling effects. These values are very close to the experimentally deduced one (14.2 kcal·mol⁻¹) and ~2 kcal·mol⁻¹ smaller than the ones obtained with the closed loop conformer. Calculation of primary KIEs and IR spectra in both protein conformations are also consistent with our hypothesis and in agreement with experimental data. Our calculations suggest that the closure of the active site is mainly required for the inverse process; the oxidation of lactate to pyruvate. According to this hypothesis H4 type LDH enzyme molecules, where it has been propose that lactate is transformed into pyruvate, should have a better ability to close the mobile loop than the M4 type LDH molecules.

INTRODUCTION

Enzymes are flexible biological proteins that accelerate biological reactions to take place in time scales compatible with life.¹ The understanding of the origin of the rate enhancement achieved by enzymes can be used in the rational design of new biocatalysts capable of working in aqueous solutions at aqueous mild conditions of temperature and pressure, showing high efficiency, selectivity and fewer unwanted side products.² Meanwhile, the fact that many enzymes catalyse chemical processes consisting of a cascade of reactions in a unique active site, or the promiscuous activity shown by some enzymes, have attracted the attention of academia and industry to design catalysts for one-pot procedures, with the corresponding decrease of energy consuming steps such as separation and purification of intermediates, and the obvious consequent economical savings.

The seminal Pauling's postulate that explained the origin of enzymes catalytic activity has been now rationalized in terms of the electrostatic stabilization that the protein provides for the transient structures that appear during the transformation of reactants into products and, in particular, for the transition state (TS).³ Nevertheless, the protein has to adopt different conformations from the substrates binding step to the products release, passing through the chemical step. Obviously, protein flexibility is necessary to understand how a cavity created during millions of years to interact and stabilize the TS of a chemical reaction, is also capable to accommodate, for instance, reactant state structures. Thus, enzymes must be stable to retain their three-dimensional structure but flexible enough to change among the different conformations relevant at each step of the catalytic cycle.^4,5 Moreover, the presence of different conformations in any of the states along the full catalytic process is essential to explain experimental results such as the temperature dependence of kinetic isotope effects (KIEs)⁶,⁷ or the significant different rate constants observed in single-molecule spectroscopy.⁸ In this regard, Yeung and co-workers monitored differences in the chemical reactivity of individual Lactate Dehydrogenase (LDH) molecules, finding that the activity of individual enzyme molecules could vary by a factor of three or four.⁹ This pioneering single molecule-experiment on LDH have been recently supported by temperature jump infrared spectroscopy studies performed by Dyer and co-workers,¹⁰ revealing the presence of multiple reactive conformations of pyruvate bound to the enzyme, each of them forming a heterogeneous branched reaction pathway with a different rate of pyruvate to lactate conversion. Correlated with this work, Callender and co-workers have used isotope-edited difference Fourier transform infrared spectroscopy measurements on the NADH·pyruvate Michaelis complex for the wild type LDH and a mutant (Asp168Asn) with an impaired catalytic efficiency, suggesting that their results provide direct evidence of a restricted ensemble of more reactive conformational substates in the enzyme system than in the non-catalyzed reaction in solution.¹¹ Experiments of single-molecule enzymatic dynamics have been carried out on other systems such as flavin adenine dinucleotide (FAD),¹² or horseradish peroxidase (HRP).^13,14 The presence of a wide distribution of rates in individual enzyme molecules have also been predicted by computer simulations on different enzymatic systems,^15,16,17 including LDH.^18,19 The results of these studies have been interpreted as evidence for subtly distinct conformations of enzyme molecules, rendering different reactivity. Single-molecule enzymology, based on both experiments and computer simulations, provides the proper tools for understanding the dynamic disorder of enzymes,²⁰ a requisite to define the mechanism of action of natural biocatalysts and the implementation of this knowledge into the development of new biocatalysts.² The use of isotopically substituted enzymes has been also revealed as a useful tool to quantify the role of protein motions in the recent years, although the interpretations of experimental and theoretical studies carried out in this field have not arrived to a consensus.²¹

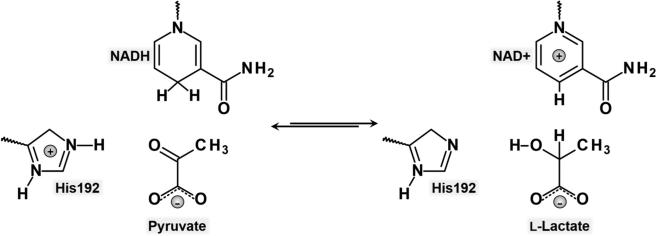
LDH, which is the system object of study in this paper, catalyses the interconversion of pyruvate and L-lactate using the NADH/NAD pair as redox cofactor. The chemical step of LDH (scheme 1) in the pyruvate to L-lactate direction involves a hydride transfer from the dihydronicotinamide ring of NADH to the carbonyl C atom of pyruvate and a proton transfer to the carbonyl O atom from a protonated histidine residue (His192 in rabbit muscle LDH).

Scheme 1.

Reversible transformation of pyruvate to L-lactate catalysed by LDH.

Site directed mutagenesis experiments have been extensively applied to LDH to explore the role of various aminoacids. These included acylation of His195 (in Bacillus stearothermophilus LDH) that inhibited the enzyme, an observation that was interpreted in terms of a model in which the substrates could bind only when His195 was protonated;²² replacement of Asp168 with either Asn or Ala that provoked the chemical step becoming rate limiting, but surprisingly, pKa of His195 did not change and activity of the enzyme was not dramatically reduced;²³ the Arg171Lys mutation, that affected the catalytic properties of the enzyme by weakening the substrate binding;²⁴ Arg109Gln that supported the role of the arginine in polarizing the pyruvate carbonyl group;²⁵ Asn140Asp that was used to explain the charge balance in the active site;²⁶ or Ala245Lys that made the rearrangement much faster and hydride transfer becoming the first slow step.²⁷

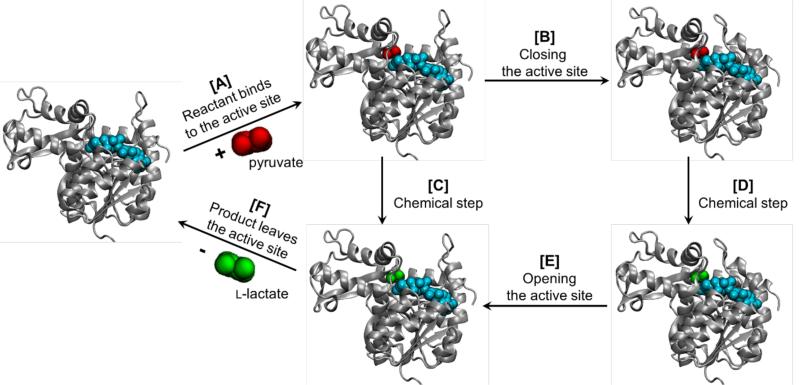
According to the experimental data, the whole catalytic process has been proposed to go through several stages (see [A]-[B]-[D]-[E]-[F] transformation steps in Figure 1): substrate binding; unimolecular rearrangement involving the closure of a surface loop (99–110) down over the active site; pyruvate reduction; reverse protein conformational change; and products release.²⁷ The loop closure would enforce isolation of the active site from the bulk solvent and it has been proposed that a conserved arginine residue of the loop would interact with the carbonyl group of the pyruvate and stabilize the TS. According to this proposal, this loop closuring would be necessary for the reaction to proceed at a noticeable rate.^28,29 In the wild-type Bacillus stearothermophilus LDH, this conformational rearrangement was demonstrated to be in fact the rate-limiting step.²⁹

Figure 1.

Representation of full LDH catalytic process as proposed by Holbrook and co-workers:²⁷ involving [A] binding of pyruvate, [B] closure of the active site, [D] the chemical step, opening the active site, and [F] product release. An alternative path would involve [A] binding of pyruvate, [C] chemical step, and [F] product release.

LDH has been the subject of a large number of theoretical studies, starting from the early empirical valence-bond study of Warshel and co-workers that was focused on the role of solvent reorganization.³⁰ Further theoretical studies based on hybrid quantum mechanics/molecular mechanics (QM/MM) potentials were focused on the exploration of the potential energy surface (PES) of the chemical step to define the controversial timing of the proton and hydride transfers.^31,32 The use of a fully flexible QM/MM molecular model rendered results suggesting that both mechanisms, concerted and step-wise, could take place in the active site of LDH,³³ a conclusion later supported from calculations based on transition path sampling.³⁴ As pointed out by Gao and Truhlar, although the classification of transition state (TS) structures into the two mechanisms was not as sensitive to initial conditions of the optimization, the energetics of the two mechanisms were similar enough that it would be hard to tell which is preferred by nature.³⁵ The fact that myriads of reactants state (Michaelis complex) conformations of the protein-substrate can exist in the protein environment in solution was demonstrated by exploration of PES starting from different protein conformations generated from a molecular dynamics (MD) simulation¹⁸ and from calculations based on free energy perturbation (FEP) methods starting from slightly different TS structures.¹⁹ Transition path sampling technique has been applied to LDH to study the impact of dynamics in the reaction catalyzed by LDH.³⁶ Despite the effect of the mass change on the rate constant was not quantified with this technique, an increase in the time of barrier crossing in the heavy enzyme was interpreted as the existence of the controversial concept of promotion vibrations.³⁶

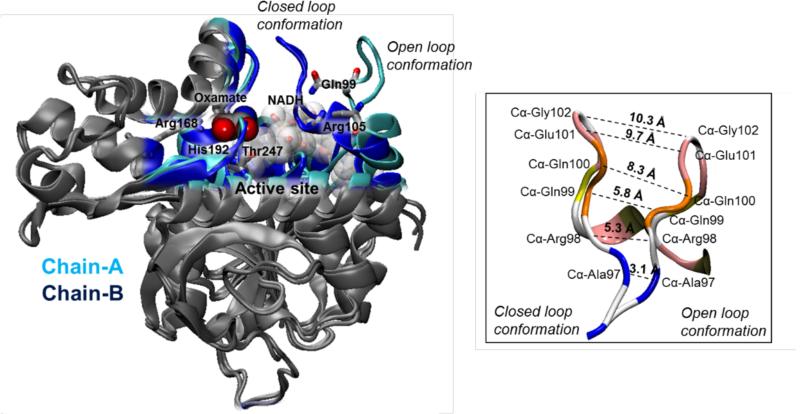
Evidences of dramatic geometrical fluctuations on LDH can be deduced from crystal structures of rabbit muscle LDH recently determined by X-ray crystallography (PDB code 3H3F).³⁷ This structure, that contained two tetramers, each of them with a unique constitution of two active sites with the open loop conformation (residues 97 to 107 in this LDH enzyme) and two with the loop closed over the actives site with a bounded inhibitor (oxamate), provides an excellent starting point to perform further studies on the dynamic diversity of enzymes and the structure-activity relationship in LDH catalysis (see Figure 2). From the geometrical point of view, LDH is a tetramer. There are five different isoforms for this enzyme: H4, H3M, H2M2, HM3, and M4, where H and M refers to heart or skeletal muscle type, respectively.³⁸ QM/MM calculations have shown differences in geometries of active sites of M4 and H4 isoforms of human LDH ligated with oxamate, pyruvate or L-lactate.³⁹ Measurements of binding isotope effects (BIEs) of the methyl hydrogen atoms of pyruvate and L-lactate were proposed as a tool to distinguish these isoforms,^39,40,41 which can be used for medical and biological applications. In fact, the specificity of LDH isoforms makes it an extremely useful marker in both clinical diagnosis and in monitoring the course of many diseases, ranging from myocardial infarction,⁴² breast cancer,⁴³ colon cancer,⁴⁴ lung cancer,⁴⁵ brain metastases,⁴⁶ etc...

Figure 2.

Superposition of rabbit LDH chain monomers from X-ray crystallography PDB code 3H3F.³⁷ Chain A with open loop conformation and chain B with closed loop conformation.

This work is focused in getting a deeper analysis into the correlation between the protein movements and the chemical reaction coordinate by studying the conversion between pyruvate to lactate in two limit cases: the protein with the open and closed mobile loop conformation. The description of reaction mechanism of LDH will be done by means of hybrid QM/MM methods, where the QM region will be described at different levels of theory including semiempirical, DFT and ab initio methods. The results will be used to test the reliability of semiempirical methods, and to question whether previous assumptions of the consecutive steps in the full LDH catalyzed process have to be revisited. Our initial hypothesis is to check if the large distribution of rate constants experimentally observed in single molecule experiments can be the consequences of variations in protein conformations but also on the possible presence of parallel reaction paths with dramatic protein conformation differences (process through the steps [A]-[C]-[F] in Figure 1). Reconciliation of experimental methods and computational simulations is a promising strategy to understand the mechanisms that enzyme employ to catalyze chemical reactions. Keeping in mind the interest of this system in medical applications, the knowledge deduced from our study can have a great interest for pharmaceutical industries.

THEORETICAL METHODS

System setup

The starting geometry for the simulations was the structure of LDH from rabbit muscles that contains two tetramers (Protein Data Bank code 3H3F).³⁷ Since the biologically active form of the enzyme is a tetramer only one tetramer was taken into consideration. Moreover, the use of the full tetramer was shown to be crucial to get reliable results in previous computational studies on LDH.⁴⁷ The structure of tetramer involves four active sites localized each in a different chain and all with bound NADH cofactor and oxamate inhibitor. Each oxamate molecule was replaced by pyruvate, the natural substrate of LDH. To assign accurate protonation states to all titratable residues at pH = 7, the pKa values for these amino acids has been calculated using the empirical propKa program of Jensen et al.^48,49 According to the results, most residues were found at their standard protonation state, except for the His-192 from chains A, B, C and D that were protonated at δ and ε positions. Subsequently, the charge of the system was neutralized adding eight Cl⁻ ions and the model of enzyme was soak in a box of water (110× 110×110 ų). Any water with an oxygen atom lying within 2.8 Å from a heavy atom of the protein was deleted. The remaining water molecules were then relaxed using optimization algorithms.

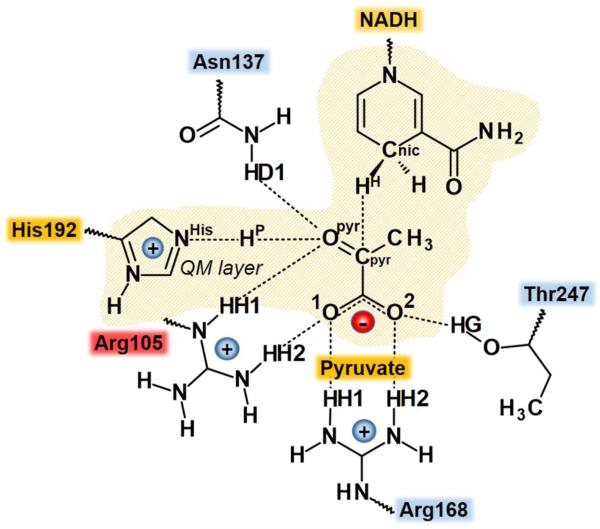
In order to carry out theoretical studies for such large molecular systems (the total number of atoms is equal to 131,472) hybrid QM/MM potentials were used, where a small part of the system, the pyruvate molecule, the nicotinamide ring of NADH and the side chain of His-192, is described by quantum mechanics while the protein and solvent water molecules are represented by classical force fields. Two link atoms⁵⁰ were inserted where the QM/MM boundary intersected covalent bonds: these were placed along the C-N bond between the nicotinamide and ribose rings of NADH and the Cα-Cβ bond of His-192. The QM region (shown as the orange-shaded region in Scheme 2) contained a total of 39 QM atoms, including the link atoms.

Scheme 2.

Active site of LDH. Nicotinamide ring of NADH and pyruvate and imidazole ring of His192 (in orange) are treated quantum mechanically in all calculations. Arg105 belongs to the mobile loop.

During the QM/MM energy optimizations the atoms of the QM region were treated by the semiempirial Hamiltonians AM1,⁵¹ PM3,⁵² PDDG/PM3,⁵³ and RM1;⁵⁴ by three hybrid density functional theory (DFT) methods B3LYP,⁵⁵ M06-2X,⁵⁶ and mPW1PW91,⁵⁷ and by the ab initio Møller-Plesset second-order perturbation theory (MP2).⁵⁸ The standard 6-31G+(d,p) basis set was used in the DFT and MP2 calculations The rest of the system, protein and water molecules, are described using the OPLS-AA⁵⁹ and TIP3P⁶⁰ force fields, respectively, as implemented in the fDYNAMO library.⁶¹ Due to the large amount of degrees of freedom, any residue or water molecule 25 Å apart from any of the atoms of the pyruvate molecule located in active site selected to study the reaction were kept frozen in the remaining calculations. Cut-offs for the non-bonding interactions are applied using a force switching scheme, within a range radius from 14.5 to 16 Å. After thermalization, QM/MM MD simulations of the system in the NVT ensemble (with the QM region treated at AM1 level) were ran during 500 ps at a temperature of 300 K using the Langevin-Verlet algorithm using a time step of 1 fs. According to the time-dependent evolution of the RMSD of those atoms belonging to the protein backbone, the system can be considered equilibrated.

Potential Energy Surfaces

Potential energy surfaces (PESs) are obtained by grid scanning of two antisymmetric combinations of distances defining: a) the proton transfer, from His192 to carbonyl oxygen of pyruvate, ξ1 = d(N^His-H^P) – d(H^P-O^pyr); and b) the hydride transfer, from C4 of nicotinamide ring of NADH to C2 atom of pyruvate, ξ2 = d(C^nic-H^H) – d(H^H-C^pyr). The procedure was performed in two active sites, using two initial protein configurations of different monomers of the 3H3F tetramer presenting an open or closed mobile loop conformation, respectively. A micro-macro iteration optimization algorithm^18,62 was used to localize, optimize and characterize the TS structures using a Hessian matrix containing all the coordinates of the QM subsystem, while the gradient norm of the remaining movable atoms was maintained less than 0.01 kcal·mol⁻¹·Å⁻¹. Intrinsic reaction coordinates (IRCs) were traced down from located TSs to the valleys of the reactants and products in mass-weighted Cartesian coordinates.

Free energy surfaces

In order to obtain the free energy surfaces, FES, we have traced two-dimensional Potentials of Mean Force (2D PMFs) using as initial structures those generated in the PESs exploration for the open and closed loop conformations. The procedure for the PMFs calculation requires a series of molecular dynamics simulations in which the distinguished reaction coordinates are constrained around these particular values with the umbrella sampling procedure.⁶³ The values of the variables sampled during the simulations are then pieced together to construct a distribution function using the weighted histogram analysis method (WHAM).⁶⁴

Because of the large number of structures that must be evaluated during free energy calculations, QM/MM MD calculations are restricted to the use of the four selected semiempirical Hamiltonians. In order to improve the quality of our MD simulations, following the work of Truhlar et al.,^65,66,67 a spline under tension⁶⁸ is used to interpolate this correction term at any value of the reaction coordinates ξ₁ and ξ₂ selected to generate the free energy surfaces. In this way we obtain a continuous function in a new energy function to obtain corrected PMFs:^69,70,71

$$E=E_{AM1∕MM}+S\left[\Delta E_{LL}^{HL}({\xi }_1,{\xi }_2)\right]$$ (1)

where S denotes a two-dimensional cubic spline function, and its argument is a correction term evaluated from the single-point energy difference between a high-level (HL) and a low-level (LL) calculation of the QM subsystem. In particular, S is adjusted to a grid of 71×71 points obtained as HL single energy calculation corrections. The semiempirical Hamiltonians were used as LL method, while B3LYP M06-2X, mPW1PW91 and MP2 methods were selected for the HL energy calculations. These calculations were carried out using the Gaussian09 program.⁷²

Quantum mechanical tunneling, dynamic recrossing effects and rate constants

Deviations from classical Transition State Theory (TST) as a result of quantum-tunneling and dynamical recrossings effects have been estimated by means of the inclusion of a prefactor in the expression of the rate constant:^73,74,75

$$k_r\left(TST\right)=\Gamma \cdot \frac{k_{B}T}{h}{e}^{[-\frac{\Delta G_{act}^{QC}}{RT}]}$$ (2)

where k_B is the Boltzmann constant, T the temperature, h the Planck constant, R the constant of ideal gases, $\Delta G_{act}^{QC}$ is the quasiclassical activation free energy that includes the classical mechanical activation free energy deduced from the PMF $\left(\Delta G_{act}^{CM}\right)$ plus the quantized vibrations of the QM region $\left(\Delta W_{wb,QM}\right)$, and Γ the generalized transmission coefficient, obtained as the product of recrossing (γ) and tunneling (κ) contributions:

$$\Gamma =\gamma \cdot \kappa$$ (3)

Recrossing transmission coefficients γ were computed using the “positive flux” formulation⁷⁶ that assumes that the trajectories are initiated at the barrier top with forward momentum along the reaction coordinate. Then for a given reaction time t, with t = 0 being the starting time for the downhill trajectory, the time-dependent transmission coefficient can be calculated as:

$$\gamma \left(t\right)=\frac{\langle j_{+}\theta \left[\xi (+t)\right]-j_{+}\theta \left[\xi (-t)\right]\rangle }{\langle j_{+}\rangle }$$ (4)

where ξ is the reaction coordinate, j₊ represents the initially positive flux at given by ξ (t = 0), and θ (ξ) is a step function equal to one in the product side of the reaction coordinate and zero on the reactant side. The average is calculated over all the downhill trajectories. 200 TS structures selected from the maximum along the Minimum Free Energy Path traced along the 2D-PMFs were used as the starting points for the free downhill trajectories. Initial velocities were assigned from a Maxwell-Boltzmann distribution corresponding to 300 K. The equations of motion were integrated to positive times, where the obtained velocities were multiplied by one, and to negative times, the velocities were multiplied by minus one. The simulations were extended from −1 to +1 ps, using a time step of 0.5 fs and the microcanonical thermodynamical collective (NVE), by means of the velocity-Verlet integrator algorithm. The trajectories obtained can be classified as reactive, when they connect reactants to products (RP), or nonreactive, when they connect reactants to reactants (RR) or products to products (PP). These later trajectories account for barrier recrossings. From 200 computed free downhill trajectories, the time dependent transmission coefficient is calculated by means of equation (4). The time-dependent evolution of the recrossing transmission coefficient, γ(t), obtained for both conformations of the enzyme decays very fast during the first 30–50 fs until they reach a constant value (see Figure S1 of Supporting Information), which is the number pluged into equation (3). This procedure is equivalent to the use of previous “positive flux” formulations, which calculates the recrossing from the eventual outcome of trajectories without having to define a function of time.⁷⁷

The tunneling transmission coefficients, κ, were calculated with the small-curvature tunneling (SCT) approximation, which includes reaction-path curvature appropriate for enzymatic hydrogen transfers.^78,79,80

Finally, the phenomenological free energy of activation, $\Delta G_{act}^{eff}$, can be obtained by the following equation:

$$\Delta G_{act}^{eff}=\Delta G_{act}^{QC}-RT\ln \Gamma$$ (5)

Due to the computer limitations to run the large amount of QM/MM MD simulations, quantum-tunneling and dynamical recrossings were obtained based on AM1/MM simulations from the lowest energy TS at each protein conformation; open loop and closed loop conformations.

Kinetic isotope effects (KIEs)

Kinetic isotope effects (KIE) have been computed for isotopic substitutions of key atoms, from the transition states and the reactant complex localized at all levels of theory described above. From the definition of the free energy of a state, G_i, as a function of the internal energy U_i, the total partition function Q_i, and the zero point vibrational energy, ZPE_i,

$$G_i=U_i-RT\ln Q_i+ZP{E}_i$$ (6)

Then, from equation (6) and using TST, the ratio between the rate constants corresponding to the light atom “L” and the heavier isotope “H” can be computed as:

$$KIE=\frac{{\left(\frac{Q_{TS}}{Q_R}\right)}_L}{{\left(\frac{Q_{TS}}{Q_R}\right)}_H}{e}^{\frac{1}{RT}(\Delta ZP{E}_L-\Delta ZP{E}_H)}$$ (7)

In equation (7), the total partition function, Q, was computed as the product of the translational, rotational, and vibrational partition functions for the isotopologs in reactants and TS in the active site of the open and closed loop conformation monomers. The Born-Oppenheimer, rigid-rotor and harmonic oscillator approximations were considered to independently compute the different contributions. Keeping in mind that both involved states, reactants and TS, are in a condensed media (the active site of a protein), contribution of translation and rotation to KIEs are negligible. Nevertheless, the full 3N × 3N Hessians have been subjected to a projection procedure to eliminate translational and rotational components, which give rise to small non-zero frequencies, as previously described.⁸¹ Thus, it has been assumed that the 3N - 6 vibrational degrees of freedom are separable from the 6 translational and rotational degrees of freedom of the substrate. Hessians have been also used to compute infra red, IR, spectra.

RESULTS AND DISCUSSION

QM/MM PESs corresponding to the transformation between pyruvate and lactate have been computed at different levels of theory in open loop conformation of the protein active site of LDH by scanning the two coordinates described in previous section; ξ1 and ξ2. The schematic representation of the obtained QM/MM PESs is shown in Figure 3.

Figure 3.

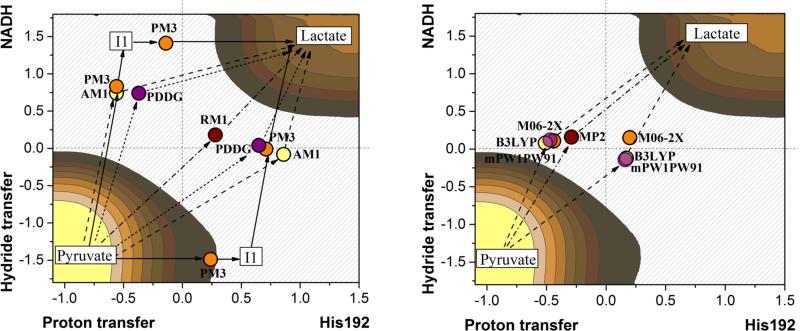
Summary of TS localized in the open active site at different level of QM theory during QM/MM calculations. On left panel the semiempirical (AM1 – yellow, PM3 – orange, PDDG/PM3 – purple, RM1 – brown) methods and on right DFT and ab initio methods (B3LYP – yellow, M06-2X – orange, mPW1PW91 – purple, MP2 – brown). See the text for definition of the two reaction coordinates.

As observed in Figure 3, where the positions of the TSs refined at the different QM/MM levels of calculations are indicated, a different description of the mechanism can be deduced depending on the Hamiltonian employed to define the QM region of the full QM/MM system. Thus, RM1/MM describes the double transfer as an almost perfectly concerted process. PM3/MM provides a picture where two reaction mechanisms can take place as step-wise processes with localization of two possible intermediates, corresponding to the proton and hydride completely transferred to pyruvate from His192 or NADH, respectively. Two competitive concerted but very asynchronous mechanisms are obtained from semiempirical AM1/MM, PDDG/MM and the three functionals used for the DFT/MM calculations: one with the hydride transfer more advanced than the proton transfer in the TS, and the other way around for the alternative path. And finally, just one TS structure was localized with MP2/MM calculations, corresponding to a concerted and quite synchronous process. When repeating the computational protocol but starting from one of the monomers of the rabbit muscle LDH with a closed loop conformation, similar results were obtained but with a smaller deviation on the position of the TSs on the PESs (see Figure S1 of Supporting Information). This is probably due to the constrains imposed by a closed cavity of the active site.

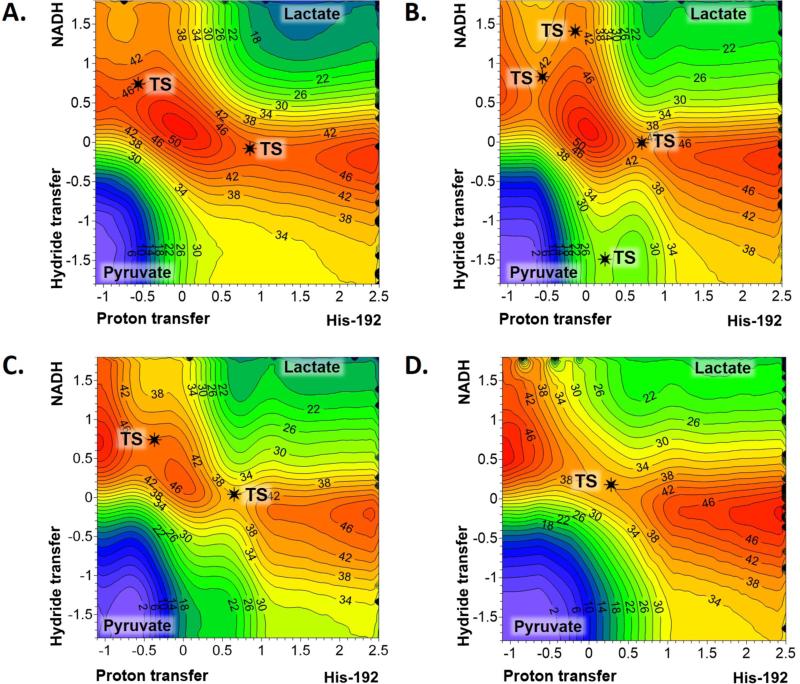
Keeping in mind the discussion on single molecule experiments presented in the Introduction, and that PESs describe just the behaviour of a single molecule, the next stage in our study was to compute the FESs, as described in previous section. At this point, and since MD simulations have to be performed, the four semiempirical methods were selected to get preliminary QM/MM FES that will be afterwards corrected at DFT/MM and MP2/MM level. The resulting free energy surfaces are presented in Figure 4, where the structures of first order saddle points located and refined at the four different levels of theory fit into the TS quadratic region of each FES (see the black stars depicted in Figure 4). As observed in the figure, the reaction mechanism deduced from the FESs are basically coincident with the description obtained from the exploration of the PESs at their corresponding level of theory. Interestingly, the minimum energy reaction paths that can be traced on the FES obtained at PM3/MM level are now quite close to the ones obtained at AM1/MM level (Fig. 4B and 4A). The FESs are much smoother than the PESs. Concurrently, a very swallow minimum that would correspond to an intermediate with the hydride completely transferred from NADH can be guest on the AM1/MM surface (upper left corner of Fig. 4A). Nevertheless, this state does not appear as kinetically relevant. FESs obtained at PDDG/MM and RM1/MM (Fig. 4C and 4D) are definitely very close to the topology of their corresponding PESs: two competitive asynchronous concerted mechanisms and one quite synchronous mechanism at PDDG/MM and RM1/MM levels, respectively. As observed in Fig. 4A and 4C, the TS with the proton transfer more advanced than the hydride transfer is more stable than the TS with the proton still bonded to the His192. In the case of PM3/MM surface, both TSs would render a very similar free energy barrier.

Figure 4.

Free energy surfaces for the pyruvate to lactate transformation catalysed by LDH with open loop conformation, computed as 2D PMFs with different semiempirical methods: A) AM1/MM; B) PM3/MM; C) PDDG/MM; and D) RM1/MM. Values of isoenergetical contour lines are reported in kcal·mol⁻¹, and distances in Å. Black stars indicate the position of the TSs localized on the PESs of Figure 3.

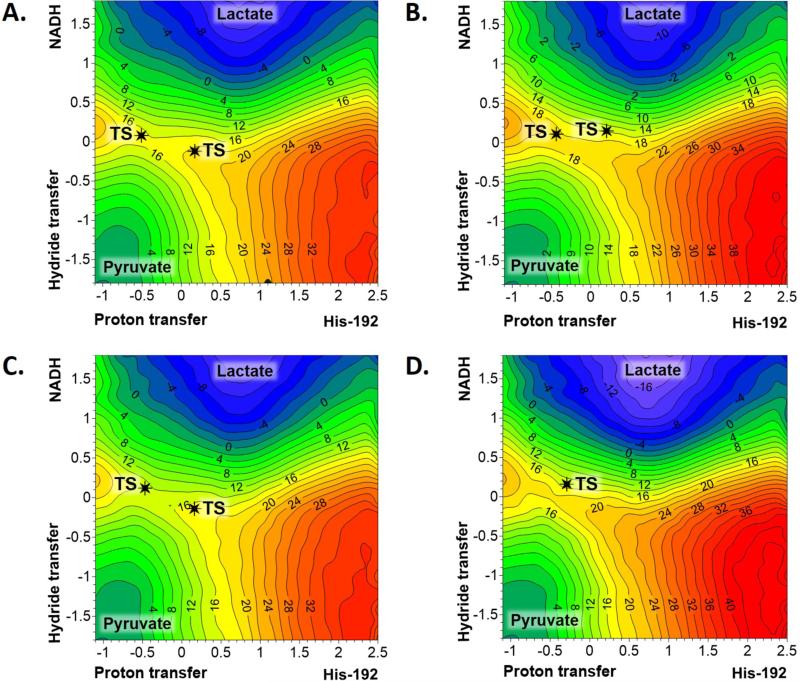
Then, keeping in mind that the results obtained from AM1/MM and RM1/MM methods cover the two possible different scenarios that describe the pyruvate to lactate transformation catalysed by the open conformation of LDH, spline corrections with DFT and MP2 Hamiltonians were carried out on these two FESs. The corrected FESs obtained from the AM1/MM surface, presented in Figure 5, are equivalent to the ones obtained from the RM1/MM FES (see Figure S2 of Supporting Information). Moreover, and probably more significantly, the FESs obtained at B3LYP/MM, M06-2X/MM, mPW1PW91/MM and MP2/MM levels all describe a reaction taking place through a concerted mechanism with a single transition state. Slight differences can be identified regarding the synchronicity of the hydride and proton transfers, and the barrier height. Analysis based on the FESs, as well as the free energy barriers (see Table 1) and the averaged key interatomic distances of the TSs (see Table 2) allow stressing very interesting observations. First of all, the quasiclassical activation free energies range between 15.0 kcal·mol⁻¹ (mPW1PW91/MM) and 19.0 kcal·mol⁻¹ (M06-2X/MM and MP2/MM). The range of the barriers obtained based on corrections of the RM1/MM FES is very similar; from 17.0 kcal·mol⁻¹ (B3LYP/MM and mPW1PW91/MM) to 20.0 kcal·mol⁻¹ (M06-2X/MM and MP2/MM). Keeping in mind the low dependency of the FESs topology on the method, the FESs with the close conformation of our LDH enzyme has been computed only at B3LYP and M06-2X level (reported in Figure S3 of Supporting Information). In any case, structures corresponding to reactants (Michaelis complex) and TS have been located and refined at mPW1PW91/MM and MP2/MM level, that will be used to support further analysis (see below). Interestingly, and probably unexpectedly, the free energy barriers obtained with the closed loop conformations (see Table 1) are very close to the ones obtained for the open loop conformations. The values of the free energy of activation for the pyruvate to lactate transformation in the active site of LDH with the open loop conformations are significantly close to previous free energy barriers obtained for the transformation in the active site of LDH with the closed loop conformations.¹⁹ The free energy barriers, computed by means of QM/MM FEP methods on a monomer of LDH from Bacillus stearothermophilus ranged between 16.7 and 23.5 kcal·mol⁻¹, depending on slightly different protein conformations used as starting point, but all of them with the mobile loop closed over the active site.¹⁹ It is important to point out that the QM/MM energy function employed in this previous study was also based on MP2/6-31G(d,p) corrections to the AM1/MM energy function. The free energy values were deduced from QM/MM FEP technique, which implies sampling of the protein environment but on IRC paths of the atoms of the QM region obtained from short QM/MM MD simulations constraining the chemical coordinates at the TS values.

Figure 5.

AM1/MM free energy surfaces, computed as 2D PMFs, with spline corrections at: A) B3LYP/MM; B) M06-2X/MM; C) mPW1PW91/MM; and D) MP2/MM level of theory for the pyruvate to lactate transformation catalysed by LDH with open loop conformation. Values of isoenergetical contour lines are reported in kcal·mol⁻¹, and distances in Å. Black stars indicate the position of TSs localized on the PESs at the corresponding levels of theory.

Table 1.

Classical mechanical free energy of activation, $\Delta G_{act}^{CM}$, quantized nuclear vibrational corrections, W_vib,QM, recrossing transmission coefficient, γ, tunnelling transmission coefficient, κ, and the effective phenomenological free energy of activation, $\Delta G_{act}^{eff}$, and reaction free energies, ΔG_reac, obtained at different levels of theory for the pyruvate to lactate LDH catalysed reaction with the open loop conformations and including the quantized nuclear vibrational corrections. All values of energies in kcal·mol⁻¹.

	B3LYP/MM	M06-2X/MM mPW1PW91/MM		MP2/MM
Open loop conformation
$\Delta G_{act}^{CM}$	17.0	19.0	15.0	19.0
Wvib,QM	2.0	2.5	1.9	2.8
γ	0.29
κ	4.90
$\Delta G_{act}^{eff}$	14.8	16.3	12.9	15.9
Δ Greac	−15.2	−11.2	−11.2	−15.1
Closed loop conformation
$\Delta G_{act}^{CM}$	19.0	21.0
Wvib,QM	2.3	2.6
γ	0.23
κ	4.03
$\Delta G_{act}^{eff}$	16.5	18.2
Δ Greac	−7.1	−7.1

Table 2.

Key inter-atomic distances (in Å) obtained at different levels of theory for the Michaelis complex (RC), and TS of the pyruvate to lactate LDH catalysed reaction with the open and closed loop conformations. All results for open loop conformation and B3LYP/MM and M06-2X/MM for close loop conformation come from the saddle point of the FESs while results of mPW1PW91/MM and MP2/MM of the closed loop conformation come from single optimizations on their PESs.

	B3LYP		M06-2X		mPW1PW91		MP2
	RC	TS	RC	TS	RC	TS	RC	TS
open loop conformation
Cnic- HH	1.11	1.39	1.10	1.39	1.11	1.40	1.10	1.44
Cpyr - HH	2.45	1.31	2.42	1.28	2.42	1.28	2.60	1.28
Opyr - Hp	1.93	1.58	1.96	1.53	1.91	1.55	1.84	1.42
NHis192 - Hp	1.03	1.07	1.03	1.09	1.03	1.08	1.04	1.13
Cnic...Cpyr	3.28	2.67	3.23	2.64	3.27	2.66	3.42	2.70
Opyr ... NHis192	2.91	2.63	2.91	2.60	2.89	2.61	2.83	2.54
HH1Arg105 ··· Opyr	12.73	12.89	12.68	12.93	12.69	12.91	12.59	12.89
HD1Asn137 ··· Opyr	1.68	1.66	1.68	1.67	1.69	1.67	1.66	1.67
HGThr247 ··· O2pyr	1.83	1.78	1.84	1.80	1.84	1.78	1.82	1.77
HH1Arg168 ··· O1pyr	1.56	1.51	1.58	1.52	1.57	1.51	1.55	1.48
HH2Arg168 ··· O2pyr	1.53	1.52	1.54	1.52	1.53	1.52	1.53	1.51
HWAT ··· Opyr	1.73	1.71	1.82	1.75	1.75	1.72	3.24	3.41
HWAT ··· O1pyr	1.70	1.67	1.70	1.67	1.70	1.67	1.68	1.66
closed loop conformation
Cnic-HH	1.11	1.46	1.11	1.46	1.11	1.49	1.10	1.49
Cpyr - HH	2.68	1.29	2.54	1.26	2.65	1.26	2.52	1.22
Opyr - Hp	1.87	1.58	1.88	1.51	1.86	1.54	1.88	1.53
NHis192 – Hp	1.03	1.05	1.02	1.10	1.03	1.09	1.02	1.09
Cnic ··· Cpyr	3.55	2.73	3.41	2.68	3.52	2.72	3.41	2.67
Opyr ··· NHis192	2.89	2.65	2.89	2.61	2.87	2.63	2.88	2.61
HH1Arg105 ··· Opyr	2.56	2.67	2.61	2.75	2.55	2.68	2.63	2.97
HDlAsn137 ··· Opyr	1.90	1.97	1.94	2.00	1.90	1.97	1.93	1.98
HGThr247 ··· O2pyr	1.74	1.72	1.72	1.74	1.75	1.74	1.72	1.71
HH1Arg168 ··· O1pyr	6.00	5.97	6.03	5.99	6.02	5.98	5.99	5.97
HH2Arg168 ··· O2pyr	1.70	1.69	1.72	1.70	1.70	1.69	1.72	1.71
HWAT ··· Opyr	1.55	1.53	1.55	1.53	1.55	1.54	1.56	1.54
HWAT ··· O1pyr	-	-	-	-	-	-	-	-
HH1Arg105 ··· Opyr	-	-	-	-	-	-	-	-

The obtained activation free energy for the reaction for the open loop conformation is close to the value deduced from the experimental rate constants (14.4 kcal·mol⁻¹). This agreement is improved when quantum vibrations, recrossing and tunnelling corrections are included in our estimations, since they contribute to a reduction in the phenomenological free energy barrier of ca. 3-4 kcal·mol⁻¹ (see Table 1). The obtained values do not depend on the protein conformation, being of the same order of magnitude as previous calculations for the reaction catalysed Bacillus stearothermophilus LDH with the closed loop conformation.¹⁹ Finally, a significant difference between both conformations is detected, nevertheless, on the reaction energies: the reduction of pyruvate to lactate is significantly more exothermic with the open loop conformation than with the closed loop conformation. This result implies a higher barrier with the open loop conformation for the inverse process; the lactate to pyruvate transformation.

It is important to point out that most of the previous hybrid QM/MM theoretical studies on the reaction catalysed by LDH have been based on the use of the AM1 semiempirical Hamiltonian to describe the QM region. Nowadays semiempirical methods are widely used for describing quantum region in QM/MM calculations in order to understand reaction mechanism and dynamic effects occurring in large enzymatic systems within a reasonable computational effort. These QM methods play a very important role especially when the long dynamic simulations are required. Time reduction of dynamic simulation by applying semiempirical methods is so large in comparison to ab initio methods that the fact of being a source of inaccuracy still does not discourage researchers from using them. In fact application of the semiempirical methods in reaction mechanism studies usually provides reasonable mechanistic description with wrong energetic of reaction barriers. Nevertheless, as it was already shown, the energetic correction can be done using results obtained at higher level of theory, using density functional theory (DFT) or MP2 methods by applying, for instance, spline correction methods, or re-parameterizing semiempirical methods by using the so-called specific reaction path (SRP) parameters, a procedure originally proposed by Truhlar and coworkers.⁸² Besides being capable of rendering a correct presentation of reaction mechanisms, semiempirical methods have additional advantage such as the fact that KIEs and BIEs computed at this level of theory are rather satisfactory and usually in agreement with experimental data.^16,18,19,40 In the case of LDH, the semiempirical AM1 method produces two possible reaction mechanisms, one with the hydride transfer more advanced than the proton transfer in the TS, and another where the proton transfer precedes the hydride transfer. However, free energy surfaces corrected at high level shows that the reaction proceeds through a unique concerted reaction mechanisms. In this sense, Schwarz and coworkers,³⁴ using Transition Path Sampling methods combined with a AM1/MM potentials, described different reactive trajectories for the reaction catalyzed by human heart LDH and attributed their result to the role of protein fluctuations that could determine the nature of the reaction. However, as shown in the present study, these different trajectories can correspond to the different mechanisms observed at the AM1 level, just reflecting the inaccuracy of the quantum method selected and not the proposed role of the protein.

Geometrical analysis of the stationary structures obtained at the different levels of calculation show that the structures of first order saddle points located and refined at the four different levels of theory fit into the TS quadratic region of each corrected FES (see the black stars depicted in Figure 5), confirming the goodness of the correction scheme and the fact that the conclusions derived from single structures can be representative of the average structures that define the transition states. As can be deduced from the data reported in Table 2, the TS obtained by any of the four methods is described by the hydride in an advanced stage of the transfer while the proton is still bonded to the nitrogen donor atom of His192. These results are in agreement with previous TS located at AM1/MM level with gas phase corrections at MP2/6-31G(d,p) for the reduction of pyruvate with the closed loop conformation, which were 1.43 and 1.31 Å for donor-hydride and hydride-acceptor distances, respectively, and 1.09 and 1.57 Å for donor-proton and proton-acceptor distances, respectively.³³

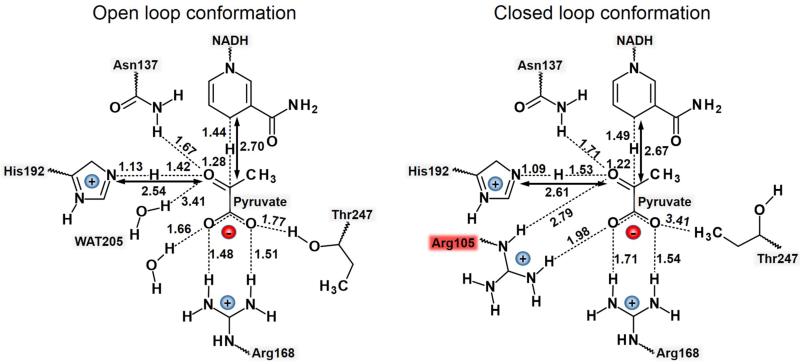
The interactions between the chemical system and the residues of the active site when the protein presents an open loop conformation render very interesting conclusions. First, the polarization of the carbonyl group of pyruvate by an arginine residue that belongs to the mobile loop (Arg105 in our system, or Arg109 in Bacillus stearothermophilus LDH) that was suggested to stabilize the TS, can not take place in the open loop conformation. As expected, the distance between Arg105 and carbonyl oxygen of pyruvate is, in all cases where the loop was open, over 12 Å. Instead, Asn137 could be doing this role according to the distances H_d1(Asn137) – O_pyr reported in Table 2. The values measured for this distance, that ranges between 1.66 and 1.69 Å, would describe a strong hydrogen bond interaction that could be polarizing the carbonyl group of pyruvate. Interestingly, the DFT/MM results show how the open cavity allows an additional water molecule to interact with the carbonyl group of pyruvate contributing, together with Asn137, to this polarization of the bond that would favor the proton transfer from His192. Moreover, it appears that the open loop conformation does not preclude the anchoring and stabilization of the negative charge of pyruvate by residues such as Thr247, Arg168 and a water molecule. Finally, and although quite obvious, the chemical reaction from the Michaelis complex to the TS implies not only the movement of two hydrogen atoms, but also a reduction in the proton and hydride donor-acceptor distances, that oscillate from 0.3 to 0.7 Å. Any theoretical model constraining these distances would involve a significant error.

The results obtained for the monomer of 3H3F³⁷ with a closed loop conformation, listed in Table 2, reveal a reaction mechanism with a TS with a slightly less advanced hydride transfer than in the previous TSs located with the open loop conformation, while the proton is also found still bonded to His192. Interestingly, some of the observations of the TSs structures located in the present work can be compared with those families of TS structures of the closed loop conformation of Bacillus stearothermophilus LDH published before where the carbonyl bond of pyruvate was polarized basically through an interaction with an asparagine residue (Asn140 in Bacillus stearothermophilus LDH and Asn137 in the present study) of the active site¹⁸. As observed in Table 2, this interaction ranges from 1.71 to 1.75 Å, which corresponds to a strong hydrogen bond interaction. The pose of this Asn137 is probably correlated with a shift in the position of Arg105 that mainly interacts not with the carbonyl bond of pyruvate but with one of its carboxylate oxygen atom. A weak hydrogen bond interaction nevertheless is still maintained with O_pyr (distances ranging from 2.67 to 2.97 Å at the TSs). The anchoring of pyruvate with Asp168 is also reproduced in this conformation (see interactions of Arg168 with O1 and O2 of pyruvate in Table 2) but now, and probably due to the strong interaction between one of the oxygen atoms of the carboxylate group of pyruvate and Arg105, Thr247 is not doing this role anymore (see distances with O2 of pyruvate in Table 2). Finally, it is important to point out that no water molecules have been detected in the surroundings of pyruvate carbonyl group when the active site is closed. Schematic representations of the TS structures localized at MP2/MM level of theory in the open and closed conformation of the protein are presented in Figure 6.

Figure 6.

Schematic representation of the active site at the TS localized at MP2/MM level of theory for the pyruvate to lactate transformation in the open and closed conformation of the protein 97-107 loop.

Once the analysis of geometries has been done, in order to get a deeper insight into the origin and differences of the catalytic efficiency of LDH in its open and close loop conformations, the electrostatic properties can be analysed by calculation of the atomic charges of key atoms, the electrostatic potential created by the protein in these atoms, and estimating the electric field created by the protein projected into the direction defined by the donor and acceptor atoms of the transferring hydride (see Table 3 and Table 4). First of all, as observed in Scheme 1, independently in the conformation of the protein, the process can be described as a negative charge transfer from the nicotinamide ring of the NADH cofactor to the pyruvate, and a positive charge transfer from His192 to the pyruvate. This is confirmed by analysis of charges and, in particular, by sum of charges on the three involved species; pyruvate, His192 and nicotinamide ring of NADH (see Table S1 of Supporting Information). It is interesting to point out that pyruvate presents its most negative charge at the TS (-1.634 and -1.510 a.u. in the open and closed loop conformations, respectively), where the charge on the transferring hydride is close to zero (0.154 a.u. in the open loop conformation and 0.039 a.u. in the closed loop conformation). Keeping in mind that the proton is still not transferred at the TS and that the hydride is in between its donor and acceptor atoms, the definition of the transfer of the hydride should the revised since the process should be better described as a electron transfer followed by the transfer of a hydrogen atom. The atoms showing the most dramatic charge variations from reactants to TS are: the C4 donor atom of NADH that becomes less positively charged, the N1 atom of NADH that becomes less negatively charged, and the carbonyl oxygen atom of pyruvate that becomes more negatively charged. Within these data on hand, it can be observed how the open loop conformation creates a more favourable electrostatic potential on C^nic atom in the TS, -39.8 kJ·mol⁻¹·e⁻¹, than the closed conformation, -65.0 kJ·mol⁻¹·e⁻¹ (a more negative potential would stabilize the positive charge of reactants). On the other side, an opposite behaviour is observed on the N1 NADH atom; the developed positive charge in this atom is better stabilized by the closed conformation (-135.8 kJ·mol⁻¹·e⁻¹) than the open conformation (-70.6 kJ·mol⁻¹·e⁻¹). The effect on the O^pyr atom is more complex: the open conformation creates a more favourable potential (more positive) on this atom than the close conformation (218 vs 130 kJ·mol⁻¹·e⁻¹ in the open and close conformations, respectively) to stabilize the negative developed charge, but a larger change in the potential is observed from reactants to the TS in the open conformation (ca. 71 kJ·mol⁻¹·e⁻¹) than in the closed conformation (ca. 14 kJ·mol⁻¹·e⁻¹). This behaviour, that is consistent with the presence of water molecules in the active site of the open loop conformation, would imply a larger reorganization penalty in the open loop conformation but a better preorganization in reactants. In both conformations, a positive potential on the acceptor C^pyr atom of pyruvate would stabilize the transfer of a negative charge from the cofactor.

Table 3.

ChelpG atomic charges computed on key atoms of the reaction (in e) and averaged electrostatic potentials (in kJ·mol⁻¹·e⁻¹) created by the environment in these atoms. Results obtained at M06-2X/MM level for the open and closed loop conformation

atoms	charges		electrostatic potential
	RC	TS	RC	TS
Open loop conformation
Cnic	0.631	0.148	−47.3 ± 20.0	−39.8 ± 18.1
HH	−0.051	0.154	32.5 ± 20.0	66.1 ±19.2
Cpyr	0.665	0.518	103.2 ± 24.3	152.5 ± 22.4
Opyr	−0.798	−1.025	146.9 ± 32.8	217.8 ± 28.8
Hp	0.361	0.349	36.4 ± 22.4	108.1 ± 25.2
NHis	0.029	0.109	−37.2 ± 21.7	10.3 ± 23.4
N1NADH	−0.451	−0.273	−70.2 ± 23.0	−70.6 ± 21.9
Closed loop conformation
Cnic	0.826	0.227	−60.3 ± 18.8	−64.9 ± 15.8
HH	−0.140	0.039	−8.3 ± 18.6	20.4 ± 17.0
Cpyr	0.547	0.588	100.7 ± 24.4	100.8 ± 21.4
Opyr	−0.666	−0.944	116.5 ± 30.1	130.9 ± 31.0
Hp	0.310	0.308	8.9 ± 21.9	42.0 ± 21.8
NHis	−0.034	−0.008	−81.9 ± 20.4	−62.8 ± 18.8
N1NADH	−0.625	−0.241	−104.6 ± 24.9	−135.8 ± 23.1

Table 4.

Averaged electric field created by the environment (in kJ·mol⁻¹·e⁻¹·Å⁻¹) on key atoms and projected in the vector defined by the donor (C^nic) and acceptor (C^pyr) atoms position of the transferring hydride.

	RC	TS	RC	TS
	Open loop conformation		Closed loop conformation
CPyr	−0.240 ± 0.127	−0.751 ± 0.062	−0.527 ± 0.104	−0.833 ± 0.048
HH	−0.726 ± 0.044	−0.859 ± 0.040	−0.812 ± 0.048	−0.881 ± 0.034
Cpyr	−0.644 ± 0.060	−0.835 ± 0.048	−0.703 ± 0.063	−0.791 ± 0.045

Combination of the analysis of charges with the electric field created by the environment on key atoms and projected in the vector defined by the donor and acceptor atoms position of the transferring hydride show how both environments generate a net electrostatic force on the hydride to be transferred to the pyruvate. The magnitude of this force in the closed loop conformation (0.11 kJ·mol⁻¹·Å⁻¹) is more favourable than in the open conformation (0.04 kJ·mol⁻¹·Å⁻¹). The net force on the donor and acceptor carbon atoms would favour the forming of the H^H-C^pyr bond and the breaking of the C^nic-H^H bond that, once again, it is slightly favoured in the closed conformation. In the TS, in both conformations the effect on the hydride would be negligible but significant value of the net electrostatic forces to approach the donor and acceptor carbon atoms (0.3 and 0.2 kJ·mol⁻¹·Å⁻¹ in the open and closed conformations, respectively) appears. This effect would then favour the transfer of the light particle.

Kinetic isotope effects (KIE)

Finally, in an attempt to check whether the proposed mechanism of the reduction of pyruvate to lactate in the open loop conformation of the LDH can be consistent with the experimental data of KIEs, they have been computed from the TS localized on the PESs obtained at the different levels of theory. In particular, semiclassical KIEs have been computed for the substitution of the key atoms involved in the reaction. As deduced from the results listed in Table 5, all DFT/MM methods and the MP2/MM calculations give KIEs in the range from 3.36 to 2.80 for the primary ²H KIE of replacing the transferring hydride with a deuterium (NADH vs NADD). These values may be compared with the experimental values for wild type and mutants of LDH from Bacillus stearothermophilus that were between 2.4 and 2.8.^25,83 Regarding the values deduced from three of the four selected semiempirical/MM methods, the deviations between the primary ²H KIE computed with the two possible TSs that appear on their corresponding PESs (see Figure 3) are consistent with the degree of advance of the transferring hydride. If doing a simple arithmetic mean between the couple of values obtained with each method, we obtained KIEs ranging from 2.44 and 3.38. The single KIE obtained at RM1/MM level, 2.64, fits in this interval. These values are very close to the corresponding primary ²H KIE for the closed loop conformation reported in Table 5, and with previous calculations of LDH that were in the range between 3.3 and 3.9, depending on the specific protein conformation.¹⁸ Consequently, primary ²H KIE for the transferring hydride can not be used to distinguish the loop conformation of the monomer since both set of values are very similar and in agreement with experimental data.

Table 5.

Kinetic isotope effects (KIEs) obtained for the pyruvate to lactate transformation in the LDH active site computed from the TSs located in its open and closed loop conformation at different levels of calculations. Results obtained according to eq. 7 at 298 K.

open loop conformation
	AM1		PM3		PDDG/PM3		RM1	B3LYP	M06-2X	mPW1PW91	MP2
	TS1	TS2	TS1	TS2	TS1	TS2
13CNADH	1.029	1.018	1.030	1.001	1.002	1.003	1.004	1.000	0.999	0.999	1.000
2HNADH	1.299	3.588	1.450	1.019	1.664	3.686	2.641	3.364	3.138	2.799	3.206
13CPYR	1.015	1.035	1.019	1.011	1.022	1.039	1.025	1.022	1.024	1.019	1.020
18OPYR	1.001	1.027	1.023	1.020	1.035	1.014	1.010	1.019	1.023	1.019	1.018
2HHis192	2.105	1.304	1.499	11.770	2.987	0.906	2.846	1.323	1.658	1.416	2.093
15NHis192	1.001	1.017	1.001	1.011	1.005	1.013	1.011	1.000	1.002	1.001	1.003

closed loop conformation.
	AM1		PM3		PDDG/PM3		RM1	B3LYP	M06-2X	mPW1PW91	MP2
	TS1	TS2	TS1	TS2	TS1	TS2
13CNADH	1.028	1.017	1.029	1.016	1.040	1.017	1.019	1.028	1.026	1.036	1.035
2HNADH	1.279	3.503	1.401	5.113	1.678	3.405	1.836	3.347	3.211	2.716	2.398
13CPYR	1.018	1.037	1.021	1.035	1.023	1.039	1.018	1.023	1.023	1.020	1.014
18OPYR	1.030	1.008	1.030	1.010	1.035	1.013	1.015	1.022	1.027	1.024	1.023
2HHis192	1.358	1.656	1.281	1.013	1.708	1.141	4.435	1.406	1.788	1.542	1.613
15NHis192	0.999	1.014	0.999	1.013	1.002	1.010	1.008	1.001	1.001	1.002	1.002

The rest of KIEs computed for the isotopically labelling of other key atoms involved in the reaction do not allow rendering decisive conclusions. Apart from the other primary ²H KIE corresponding to replacing the transferring proton of His192, which is difficult to measure since it is exchangeable with protons of the solvent, the rest of computed values are close to unity.

Infrared spectra (IR)

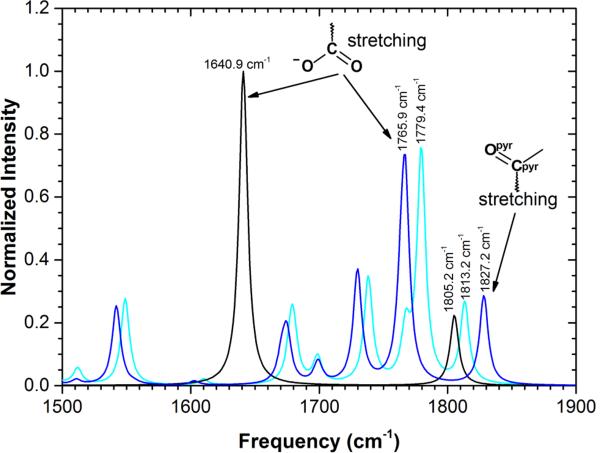
Using the C^pyr=O^pyr stretch frequency of bound pyruvate within the enzyme-substrate Michaelis complex as a monitor of the protein's ensemble nature,⁸⁴ Dyer and co-workers have recently measured the presence of three different frequencies between 1674 and 1686 cm⁻¹. The authors claimed that their results provide direct evidence of a restricted ensemble of reactive conformational substates. The IR spectra computed at M06-2X/MM level for the open and closed conformations of the protein (see Figure 7) show, indeed, a shift in the C^pyr=O^pyr stretching of 14 cm⁻¹, almost coincident with the range measured experimentally, 12 cm⁻¹. This match can be interpreted as the existence of a possible equilibrium between open and loop conformers at the Michaelis complex.

Figure 7.

IR spectra, computed at M062X/MM level, of pyruvate in water (black line) and in the active site of LDH in the closed conformation (dark blue line) and open conformation (light blue line).

CONCLUSIONS

LDHs catalyse the reversible transformation of pyruvate into L-lactate with the concomitant conversion of the nicotinamide adenine dinucleotide cofactor from the NADH form to NAD⁺. It has been assumed from the early works of Holbrook and co-workers that the full catalytic process starts with the binding of the cofactor that is followed by the binding of the substrate and the enclosure of the active site by a mobile loop of the protein. This last step would be the rate-limiting step in the wild-type enzyme. The chemical step of the enzymatic process involves the transfer of a proton from a protonated histidine to the carbonyl oxygen atom of pyruvate and a hydride transfer from the dihydronicotinamide ring of the cofactor to the carbonyl carbon atom of the substrate. Previous experimental studies have revealed the importance of the closure of this mobile loop for the chemical reaction step to take place, including a conserved arginine that has been proposed to stabilize the TS of the reaction by polarizing the carbonyl group of the pyruvate. Previous theoretical studies localized different TS structures on the QM/MM PES, basically differing on the conformation of the active site but, in all cases, within the closed loop conformation. Small movements of the loop were detected in other QM/MM studies based on FEP calculations, also revealing well-characterized reactant valleys, each one acting as an independent enzyme, with its own individual reaction rate constant.

In this paper we show that the forward chemical step of the LDH catalyzed reaction (transformation of pyruvate into lactate) can take place within the open conformation of the loop 97-107. Starting from a X-ray diffraction structure of rabbit muscle LDH tetramer that presented an open loop conformation in two of the four chains, QM/MM free energy surfaces have been obtained at different levels of theory depending on the method employed to describe the atoms treated quantum mechanically. In particular, using semiempirical, DFT and MP2 Hamiltonians, the free energy barriers for the pyruvate reduction to lactate varies between 12.9 and 16.3 kcal·mol⁻¹, after quantizing the vibrations and adding the contributions of recrossing and tunneling effects. These vales are ~2 kcal·mol⁻¹ smaller than in the closed loop conformer. The catalytic rate constant of Bacillus stearothermophilus LDH enzyme at 25°C is 250 s⁻¹, and it is assigned to the active-site loop closure.⁸³ This result, according to the Transition State Theory, implies that the upper limit of the barrier for the chemical step should be 14.2 kcal·mol⁻¹, a value which is very well comparable to our values obtained for the open loop conformation. It is important to stress that the equilibrium between the open and closed loop conformations at the reactant states, steps B and C in Figure 1, has not been explored in the present study. In principle, two different scenarios are possible. If the interconversion rates between open and closed conformations is much faster than the chemical transformation, an equilibrium could be assumed, and the individual rate constants would be governed by the free energy barriers of the pyruvate to lactate transformation. Otherwise, a kinetic control would govern the population of each protein conformation, and one of them could not be kinetically reliable. Nevertheless, we must keep in mind that pyruvate, and more noticeably NADH, has to enter into the active site when the loop adopts an open conformation and, consequently, our results suggest the viability of the process through the path A-C-F in Figure 1.

Our results of primary ²H KIEs for the substitution of the transferring hydride of NADH are in agreement with previous experimental data and calculations from closed loop conformations of LDHs. Analysis of the geometries of the TSs located with the open loop conformation shows that the previously assigned role of Arg105, that in this conformation is located more than 12 Å away from the pyruvate, can be done by an asparagine residue that does not belong to the loop, and by water molecules that now have access to the cavity.

The calculation of atomic charges of key atoms of the reaction together with the electrostatic potential created by the protein in both conformations of the loop reveal that in both situations, a proper environment is created to promote the reaction. This is confirmed by the estimation of the electric field created by the protein and projected in the vector defined by the donor and acceptor carbon atoms of the transferring hydride; the set of electric forces exhorted by the protein in both conformations would push the donor and acceptor atoms to approach and the hydride to be transferred to the substrate.

Fluctuations of catalytic rate constants, as shown by single-molecule spectroscopy studies in this enzyme and others, can be due not only to different conformations of the TS and different reactive valleys within the closed loop conformation but also to the possibility that the reaction can take place also with the open loop conformation. The shift observed in signals of the C^pyr=O^pyr stretch frequency IR spectra, recently measured by Dyer and co-workers⁸⁴ could be considered in agreement with our hypothesis, since our simulations for the open and closed loop conformations reproduce such results.

Despite having similar reactivity, our simulations reveal that the reaction is much more exothermic in the open loop conformation than in the closed form. Considering that LDH catalyzes the reversible transformation between pyruvate and lactate, this notable difference between the free energy of the reaction obtained in our simulations for the open and closed conformations would suggest that the closure of the active site is mainly required for the inverse process, the oxidation of lactate to pyruvate. If however the active site is closed during the forward enzymatic process, then it is not related to the efficiency of the chemical step. The fact that closed conformations are obtained in the X-ray diffraction studies can be associated with interactions established between a glutamine residue (Gln99 in rabbit muscle LDH) and the amine group of inhibitor (oxamate) used during the experiments. The natural substrate, pyruvate, contains a methyl group in this position. From the lactate shuttle hypothesis proposed by Brooks in 1985,⁸⁵ lactate would not be the dead-end metabolite of glycolisis process. It has been latter hypothesized that twitch fibers, where the H4 type of LDH is dominant, take up lactate from fast twitch fibers with a high concentration of M4 type of LDH and convert it to pyruvate.⁸⁶ However, there are opinions that oxidation and production of lactate have to take place in the same cell, and it can depend only on local environment.⁸⁷ Our results suggest that H4 type LDH enzyme molecules should have a better ability to close the mobile loop than the M4 type LDH molecules, which in turn implies a lower barrier for the oxidation of lactate.