Abstract
Stimulus discrimination depends on the selectivity and variability of neural responses, as well as the size and correlation structure of the responsive population. For direction discrimination in visual cortex, only the selectivity of neurons has been well characterized across development. Here we show in ferrets that at eye opening, the cortical response to visual stimulation exhibits several immaturities, including: a high density of active neurons that display prominent wave-like activity, a high degree of variability, and strong noise correlations. Over the next three weeks, the population response becomes increasingly sparse, wave-like activity disappears, and variability and noise correlations are markedly reduced. Similar changes are observed in identified neuronal populations imaged repeatedly over days. Furthermore, experience with a moving stimulus is capable of driving a reduction in noise correlations over a matter of hours. These changes in variability and correlation contribute significantly to a marked improvement in direction discriminability over development.
Introduction
Accurate visual discrimination depends critically on the selective responses of neurons in visual cortex for features of the visual scene such as the orientation of edges and their direction of motion. Other aspects of cortical responses, especially those that influence the spatial and temporal patterns of neuronal activity, also play an important role in visual discrimination. These include response variability1–3, the number of responsive neurons4–6, and the degree of correlation in neuronal response, all of which impact the performance of population coding in the mature visual cortex. 7. 8–10. How these four features of the population response emerge and reach their mature state during the development of the visual cortex remains unclear.
Most is known about the development of stimulus selectivity, and studies in the ferret indicate that the time course of emergence and the role of experience differ according to the type of selectivity. For example, orientation selectivity is present and organized in a columnar fashion around the time of eye opening11, while tuning for direction selectivity emerges shortly after eye opening in a process that requires visual experience12. Much less is known about the development of the temporal properties of the cortical population response, beyond the characterization of single units as “sluggish” and unreliable prior to and around the time of eye opening, becoming more crisp and reliable with continued experience13, 14. Moreover, how these changes in single unit properties are related to the number of responsive neurons and the correlation structure of evoked responses remains unclear. However, two recent reports in rodents suggest that both of these properties may undergo significant postnatal maturation15, 16.
In this study we used 2-photon in vivo calcium imaging to characterize the spatial and temporal response properties of large numbers of single neurons in ferret visual cortex in order to assess how these factors change during postnatal development. We found that cortical responses at eye opening are characterized by a high density of active neurons that display prominent wave-like activity, a high degree of variability, and strong noise correlations. Over the next three weeks, the population response becomes increasingly sparse, wave-like activity disappears, and variability and noise correlations are markedly reduced. The decrease in variability and noise correlations both contribute significantly to improvements in the ability of cortical neuronal activity to discriminate motion direction, and both the decrease in noise correlations and improvement in direction discriminability appear highly sensitive to visual experience. Taken together with previous observations in the ferret12, 17, the period following eye opening is distinguished by rapid changes in a number of neuronal response properties that are critical for motion discrimination.
Results
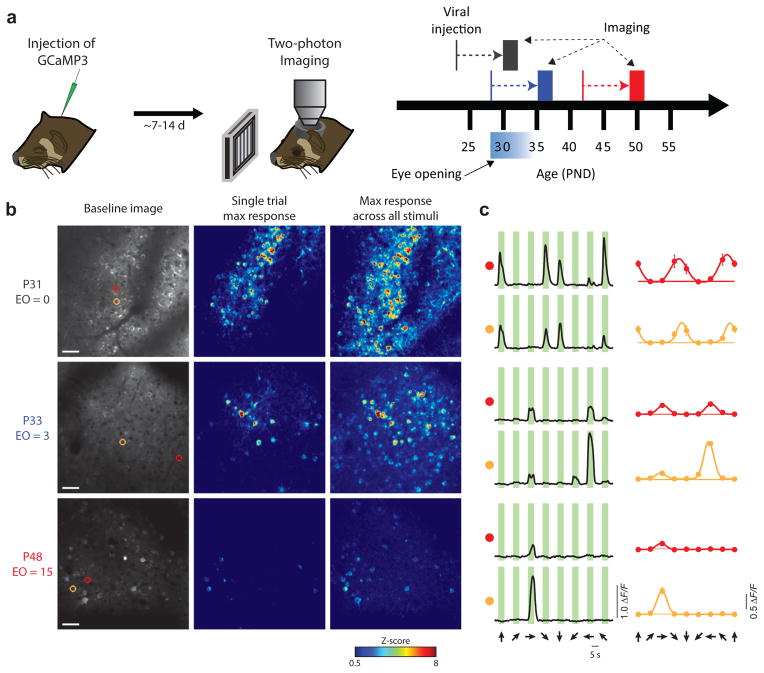
Ferrets were imaged in 3 age groups (naive: P29–32, immature: P33–36, and mature: P48–50, with 0–1, 4–6, and >15 days visual experience, respectively) following intracortical injections of AAV-expressing GCaMP3 (Fig. 1a). In animals imaged at eye opening, we observed dense and vigorous responses with strong orientation selectivity but weak direction selectivity, whereas in older animals, responses were considerably sparser and direction selectivity was greatly increased (Fig. 1b,c). Pooling across animals, we observed similar results to previous work12, with strong selectivity for orientation and weak selectivity for direction in naive animals, both of which increased significantly over the following weeks (Fig. 2a, orientation: Kruskal-Wallis test (KW): Χ2(2)=309.45, p<0.001, pairwise Mann-Whitney U test (MW): naive: Z(1811)=−12.23, p<0.001; immature: Z(1447)= −15.30, p<0.001; mature: Z(992)= −6.99, p<0.001, Fig 2b, direction: KW: Χ2(2)=473.87, p<0.001, pairwise MW: naive: Z(1555)= −16.51, p<0.001; immature: Z(1174)= −18.06, p<0.001; mature: Z(883)= −7.56, p<0.001). Beyond these expected changes, we found that the trial-to-trial response variability decreased significantly in immature and mature animals compared to naive animals (Fig. 2c, KW: Χ2(2)=190.24, p<0.001; MW: naive vs. immature: Z(1555)= −16.51, p<0.001; naive vs. mature: Z(1174)= −18.06, p<0.001). Variability rebounded slightly but significantly from immature to mature animals (MW: Z(883)= −7.56, p=0.001;). Over this same period, the amplitude of the response evoked by the preferred stimulus did not change (Fig. 2d, ΔF/F mean ± SEM: 0.148±0.004, 0.147±0.006, and 0.138±0.007 for naive, immature, and mature respectively; KW: Χ2(2)=2.99, p=0.22).
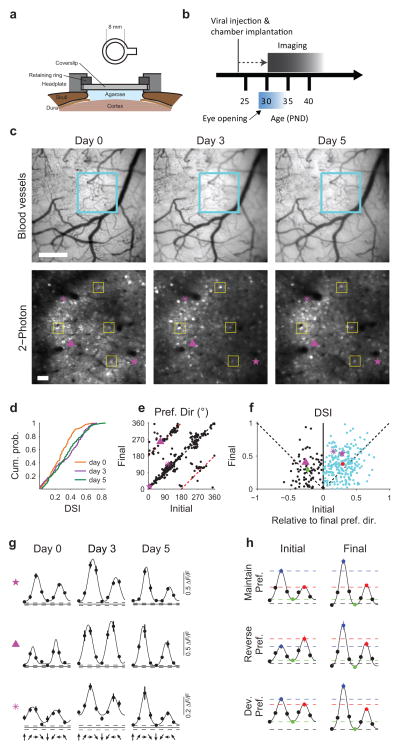
Figure 1. Response properties change dramatically following eye-opening.
(a) Experimental timeline. GCaMP3.3-expressing AAV was delivered intracortically via microinjection and two-photon imaging was performed 7–14 days later. Animals were imaged at either P29–32 (naive), P32–36 (immature), or P48–50 (mature). (b) Representative responses from animals in each age group. Left column: Baseline image. Scale bar = 50 μm. Middle: Single trial response to preferred stimulus, maximum projection across stimulus duration. Right: Maximum response across all stimuli and all trials. (c) Responses for individual neurons highlighted in b. Left column: Response to 8 directional stimuli, averaged across trials. Right column: Tuning curves fit with a 2-peaked Gaussian. Horizontal line indicates the mean response to a blank stimulus.
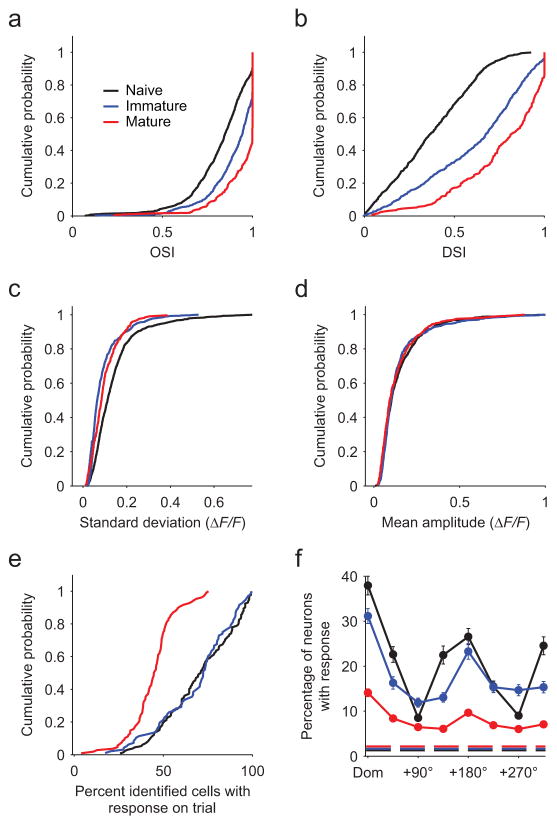
Figure 2. Stimulus selectivity increases and population response density decreases with age and experience.
Black: Naive (P29–32, n = 9 animals). Blue: immature (P33–36, n = 5 animals). Red: mature (P48–50, n = 5 animals). (a) Orientation selectivity (OSI) increases significantly with age (n = 1134, 679, and 315 neurons for naive, immature, and mature, respectively). (b) Direction selectivity (DSI) increases significantly with age (n = 924, 633, and 252, for naive, immature, and mature, respectively). (c) Response variability (shown as standard deviation across trials) to the preferred stimulus decreases with age. (d) Response amplitude to the preferred stimulus does not change across age (mean response across trials). (e) The response density (fraction of active neurons on a given trial out of all identified neuronal ROIs with at least 1 response) declines significantly from the naive and immature groups to the mature group. (f) Response density is stimulus specific. In all age groups, the fraction of neurons active on a given trial is significantly greater for the dominant stimulus (the stimulus producing activity in the largest fraction of neurons, aligned across animals) versus a stimulus with opposite direction of motion (null, +180°) or an orthogonal orientation. Dashed line indicates mean fraction of neurons active during blank stimuli. Error bars are mean ± SEM across animals.
To quantify the population sparseness4, we examined the fraction of identified neurons within a field of view that exhibited a response to at least one stimulus on a given trial, making this measurement resistant to changes in direction selectivity. The fraction of responsive cells did not change from naive to immature animals (Fig. 2e; mean ± SEM across all trials for all stimuli: 70.2±1.7% vs. 68.7±2.1%; KW across groups: Χ2(2)=103.2, p<0.001; MW: naive vs. immature: Z(226)=0.35, p=0.72). However, responses in mature animals were considerably sparser (44.4±1.2%; MW: naive vs. mature: Z(238)=9.38, p<0.001; immature vs. mature: Z(202)=8.13, p<0.001). These results cannot be explained through enhanced direction selectivity, decreased responsivity to preferred stimuli (Fig. 2d), a change in the density of labeled neurons (KW: Χ2(2)=2.69, p=0.26), or toxicity related to GCaMP expression (correlations between expression time and response density are non-significant in all groups; naive: r(7)=0.48, p=0.19; immature: r(3)= −0.65, p=0.24; mature: r(3)= −0.27, p=0.65), but rather may result from developmental changes in receptive field structure13, 18. Notably, the response density in naive animals does not reflect a global non-specific hyper-excitability, but rather was highly specific for both stimulus orientation and direction (Fig. 2f, within group KW across stimuli: naive: Χ2 (7)=227.03, p<0.001; immature: Χ2 (7)=107.99, p<0.001; mature: Χ2 (7)=139.40, p<0.001; dominant vs. orthogonal: naive: Z(526)=14.12, p<0.001; immature: Z(382)=8.36, p<0.001; mature: Z(430)=9.53, p<0.001; dominant vs. opposite: naive: Z(262)=4.09, p<0.001; immature: Z(190)=3.31, p<0.001; mature: Z(214)=4.78, p<0.001;).
Wave-like propagating responses in naive animals
In addition to the high density of the responsive neurons, a prominent feature of the visual response in young animals was a wave-like propagation of activity during the stimulus period (Fig. 3a, Supplemental movie 1). The spatial-temporal pattern of activity was largely consistent both within and across stimuli (Fig. 3b,c), and frequently resembled a linear traveling wave (Fig. 3d). Both the fraction of trials eliciting a linear wave and the wave velocity exhibited age-dependent declines (wave incidence: Fig. 3e, mean ± SEM: naive: 30.7±5.0%, n=3 FOV from 3 animals; immature: 10.2±4.5%, n=6 FOV from 3 animals; mature: 1.6±0.5%, n=4 FOV from 2 animals; KW: Χ2(2)=8.62, p=0.013; wave velocity: Fig. 3f, naive: 256±24 μm/sec, n=115; immature: 91±11 μm/sec, n=60; mature: 44±7 μm/sec. n=6, KW: Χ2(2)=65.07, p<0.001).
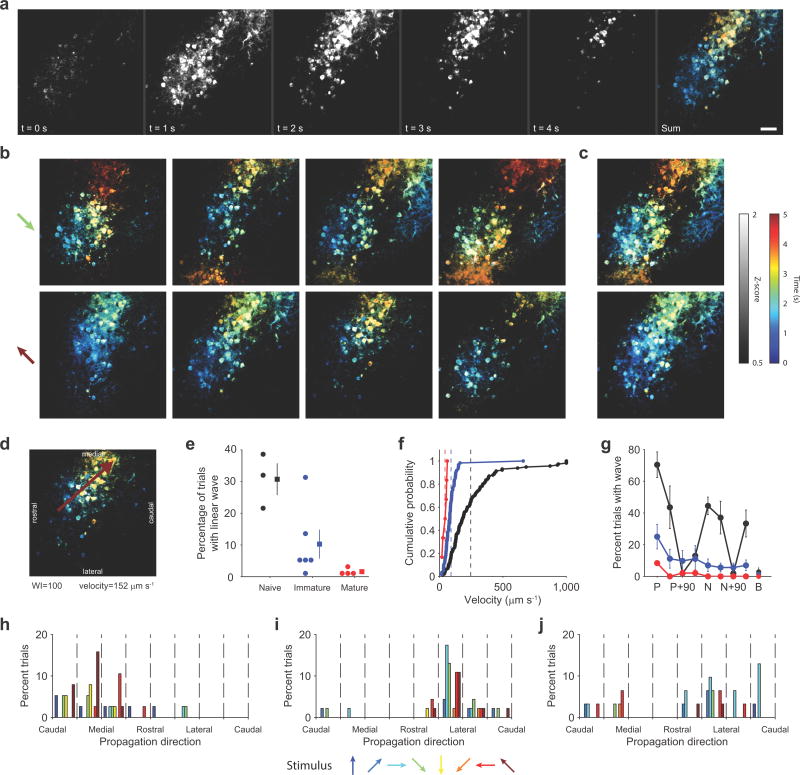
Figure 3. Wave-like responses to visual stimulation in young animals.
(a) Pseudocolored timecourse of response to single stimulus. Propagating activity appears as a gradient from blue to orange. Scale bar = 50 μm; applies to a–d. (b) Single-trial example responses. Top row: responses to grating drifting down and to the left, bottom row: responses to stimulus of same orientation but opposite direction of motion. (c) Average response across all trials with strong wave-like activity. (d) Example response well fit by a linear traveling wave (wave index (WI) = 100) (e) Frequency of linear waves declines significantly with age (n=3 FOV from 3 animals, 6 FOV from 3 animals, and 4 FOV from 2 animals for naive, immature, and mature, respectively). Circles indicate individual FOVs, with squares indicating mean ± SEM. (f) Velocity of linear waves declines significantly with age (mean ± SEM: naive: 256.8 ± 23.7 μm/sec, n=115 waves; immature: 91.3 ± 10.6 μm/sec, n=60 waves; mature: 44.2 ± 7.1 μm/sec n=6 waves). Dashed lines indicate geometric means. (g) Occurrence of linear waves is stimulus specific. Labels: ‘P’-preferred stimulus. ‘N’-null stimulus with opposite direction of motion from preferred, ‘B’-blank stimulus. Error bars are mean ± SEM across animals. (h–j) Wave direction is largely consistent across all stimuli within an animal, but differs across animals. Each histogram shows propagation directions for one animal in the naive group. Bar color indicates the stimulus identity.
The stimulus-evoked wave-like pattern of activity demonstrated here does not propagate continuously over the surface of the cortex but is limited to domains that are tuned to the orientation of the stimulus. Consistent with the significant orientation tuning that is present at eye opening, the likelihood of eliciting a linear wave within the field of view was highly dependent on the orientation of the stimulus (Fig. 3g, Friedman’s test: naive: Χ2(7)=19.05, p=0.008; immature: Χ2(7)=16.00, p=0.025; mature: Χ2(7)=21.00, p=0.004). There was also a bias towards a directional preference in the likelihood of eliciting a linear wave in all age groups (compare preferred to null stimulus in Fig. 3g).
The waves had a strong tendency to travel across the cortex in a consistent direction that was distinct for each animal (Fig. 3h–j; for FOVs with minimum 10 traveling waves (5 of 13, 3 naive and 2 immature; Hodges-Ajne test for non-uniformity: p<0.05 in 4 of 5 cases with ≥30 waves each; fifth case p=0.49 with 13 waves, statistics in Supplementary table 1). The propagation direction varied significantly across animals (circular non-parametric multi-sample test for equal medians (CM)19: P(4)=35.075, p<0.001), and did not vary as a function of the direction of stimulus motion (CM within animal: p>0.14 in all cases, statistics in Supplementary table 2).
Noise correlations decrease with age
The presence of highly variable but highly dense responses in naive animals suggests a large degree of correlated variability at this age. As shared trial-to-trial variability has strong implications for neural coding8, 10, we examined pairwise noise correlations across development. Across all neuronal pairs, noise correlations exhibited a significant decline with age (mean ± SEM across animals after averaging pairs within each FOV: 0.125±0.023, 0.020±0.003, 0.010±0.002 for naive, immature, and mature, respectively; KW: Χ2(2)=19.94, p<0.001; MW: naive vs. immature: U(15)=72, p<0.001; naive vs. mature: U(16)=81, p<0.001; immature vs. mature: U(15)=63, p=0.008).
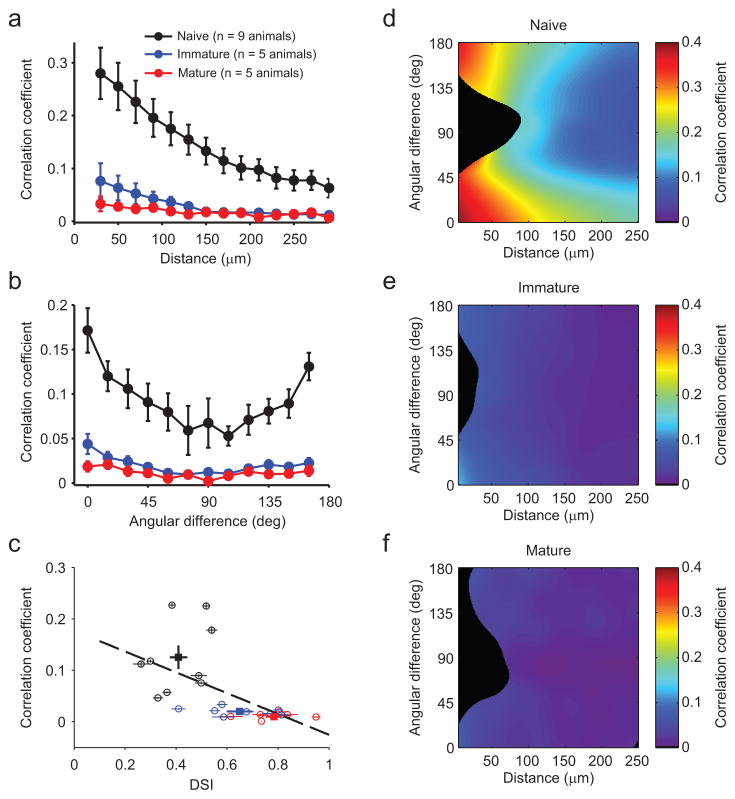
In mature animals, noise correlations tend to be higher between nearby neurons with similar tuning properties20–22 and we examined how this difference emerged during development. Noise correlations declined with increasing spatial distance for all groups (Fig. 4a, Friedman’s test within group: naive: Χ2(13)=106.55, p<0.001, r(98643)= −0.49, p<0.001; immature: Χ2(13)=84.23, p<0.001, r(34222)= −0.19, p<0.001; mature: Χ2(12)=35.79, p<0.001, r(7617)= −0.14, p<0.001), and the decrease in correlations with age was evident at all distances examined (Mack-Skillings test for age while controlling for distance: Χ2(2)=253.76, p<0.001). Noise correlations also decreased with age for all intra-pair tuning differences (Fig. 4b, Mack-Skillings test for age while controlling for angular difference: Χ2(2)=130.44, p<0.001). We further observed a strong relationship across ages between the mean noise correlation and the mean direction selectivity of each neuronal population we imaged (Fig. 4c, r(24)= −0.59, p=0.001), indicating that these changes occur over similar timescales during development. Notably, neuron pairs with similar tuning and small spatial separation exhibited the highest noise correlations in naive animals (Fig. 4d, lower left corner), and also showed the largest decreases with age (Fig. 4e,f).
Figure 4. Noise correlations decline with age and experience.
(a) Pairwise noise correlation as a function of intra-pair spatial distance. There is a significant decrease in noise correlation across age groups, as well as a significant decrease in noise correlation as a function of distance within each group. (b) Pairwise noise correlation as a function of the intra-pair difference in preferred direction. For all age groups, noise correlations are significantly higher for pairs with similar orientation preferences than for those with orthogonal preferences. Likewise, all age groups exhibited significantly higher correlations for pairs with similar as opposed to opposite direction preferences. Data in a and b are represented as the mean ± SEM across animals after taking the mean across all pairs within an animal. (c) Noise correlations decrease and DSI increases with age. Circles: mean ± SEM for each FOV, squares: mean ± SEM across all animals in each age group. There is a significant correlation (R = −0.59; p<0.01) between noise correlation and DSI across all experiments. (d–f) Maps of pairwise noise correlation as a function of intra-pair spatial distance and difference in preferred direction (local average based on Gaussian kernel, σx=15 micron, σy=15 deg). Early, noise correlation is large for small distances, in particular in pairs with similar preferred direction. In the mature cortex, this bias is reduced and noise correlations are small irrespective of distance and tuning difference. Black regions indicate regions with insufficient data (less than 20 pairs per 30 micron by 22.5 deg region).
To determine if the strong wave-like activity present in naive animals contributes to high noise correlations, we selected stimuli capable of eliciting linear waves and calculated noise correlations using only trials with and without waves. Trials with wave-like activity showed significantly higher noise correlations than those without (mean ± SEM across 3 animals: wave present, 0.266±0.019, absent, 0.125±0.021; WSR: Z(2195)=39.54, p<0.001, n=2197 pairs from 3 animals), indicating that wave-like responses are a major, albeit not the only source of correlated variability in the naive cortex.
Chronic 2P imaging of emergence of direction selectivity
To track the developmental changes that occur in individual neurons, we performed longitudinal imaging of a defined neuronal population over several days following eye opening. We successfully imaged 4 ferrets over 2–3 imaging sessions starting around eye opening (Fig. 5a, b). In these experiments, we only considered neurons that could be conclusively identified across all imaging sessions (73.8±7.8 of cells identified in first imaging session, mean ± SEM across 4 animals). In the example shown in Fig. 5c,d, we imaged 126 visually-responsive neurons over 3 imaging sessions from P32 to P37. In this population, we found an increase in direction selectivity from P32 to P35, which did not change further by P37 (Fig. 5d, Friedman’s test: Χ2(2)=14.02, p<0.001; post-hoc WSR: P32 vs P35: Z(124)= −3.84, p<0.001; P32 vs P37: Z(124)= −3.33, p<0.001; P35 vs P37: Z(124)= −0.31, p=0.754). In order to examine the changes underlying this increase in selectivity, we compared orientation and direction preferences for identified neurons across imaging sessions. We found that orientation preference is largely stable over this period, while orientation selectivity increased significantly as would be expected from previous work11 (Supplemental figures 1 & 2a, c, e; WSR: Z(317)=12.66, p<0.001). Interestingly, direction preference exhibited approximately 180° reversals in a subset of neurons (Fig. 5e, example neuron shown in 5g middle row). Amongst neurons with a stable preferred direction, selectivity increased significantly over imaging sessions (Fig. 5f cyan points; WSR: Z(239)=5.61, p<0.001).
Figure 5. Longitudinal 2P imaging reveals emergence of direction selectivity in identified neurons.
(a) Schematic of chronically implanted headplate. (b) Timecourse of imaging experiments. (c–d) Longitudinal imaging across 5 days following eye opening. (c) Top row: cortical blood vessel pattern from day 0 to day 5. Blue box indicates area for functional imaging. Bottom row: Imaging field over days. Yellow boxes outline examples of corresponding neurons. 126 neurons (63% of day 0) remained visible and visually responsive across all imaging sessions. Images were aligned across days with an affine transform. Purple symbols indicate example neurons shown in (g). Scale bar: top: 500 μm, bottom: 50 μm. (d) Direction selectivity increases in a population of neurons imaged from a single animal over 5 days (n = 126 neurons). (e) Direction preference is stable in the majority of neurons, whereas a subset of cells exhibit 180 degree reversals. Red dashed lines indicate 180 degree shift from d0. (f) DSI increases in neurons with stable preferences (blue symbols, mean ± sem indicated with red circle) from the initial to final imaging session. Neurons that reverse preference (black, mean ± SEM in green) do not show an increase in selectivity. (g and h) Example (g) and average (h) tuning curves showing neurons that maintain a preferred direction (top), reverse preferred direction (middle), and develop a clear preferred direction (bottom). Purple symbols in c, & e–g indicate corresponding neurons. For ease of comparison, tuning curves were shifted to align preferred stimuli on day 5.
Increased direction selectivity could occur through either potentiation of responses to the preferred direction, suppression of null responses, or both. In neurons which maintain a stable direction preference (see methods, e.g. Fig. 5g, top), the rise in selectivity was due to a potentiation of the response to the preferred direction (Fig. 5h, top; mean ΔF/F ±SEM, with WSR: initial vs. final: preferred: 0.33±0.02 vs. 0.43±0.02, Z(113)=5.051, p<0.001; null: 0.17±0.01 vs. 0.18±0.01, Z(113)=1.066, p=0.286; orthogonal: 0.04±0.01 vs. −0.01±0.00, Z(113)=–7.725, p<0.001; n=115), consistent with the initial changes reported using pooled acute single-unit recordings23. Interestingly, neurons that exhibited reversals in preference (e.g. Fig. 5g, middle) showed both a potentiation of the final preferred response and a depression of the initial preferred (final null) (Fig. 5h, middle; mean ΔF/F ±SEM, with WSR: initial vs. final: preferred: 0.24±0.03 vs. 0.53±0.06, Z(22)=4.286, p<0.001; null: 0.34±0.04 vs. 0.27±0.03, Z(22)=–2.171, p=0.030; orthogonal: 0.04±0.01 vs. −0.04±0.01, Z(22)=–3.829, p<0.001; n=24), as did cells with an initially uncertain preference which developed over time (Fig. 5g & h, bottom; mean ΔF/F ±SEM, with WSR: initial vs. final: preferred: 0.26±0.02 vs. 0.37±0.02, Z(96)=5.732, p<0.001; null: 0.21±0.02 vs. 0.17±0.01, Z(96)=–2.748, p=0.006; orthogonal: 0.07±0.01 vs. 0.00±0.01, Z(96)=–6.844, p<0.001; n=98).
These changes in single-cell response were accompanied by a significant decline in pairwise noise correlation amongst the longitudinally imaged populations (Fig. 6a, Supplementary Fig. 3, WSR: Z(18946)=–98.10, p<0.001, n=18948 pairs). We next assessed the relationship between the change in selectivity of individual neurons and the structure of the population response during the period following eye opening (Fig. 6b). In 3 of 4 longitudinal imaging experiments, direction selectivity had increased from the initial to the final imaging session (Friedman’s test: p<0.05 for each experiment with 33, 147, and 126 neurons per experiment, respectively, statistics in Supplementary table 3), while pairwise noise correlations amongst this same population decreased (Friedman’s test: p<0.001 for each experiment, with 489, 10618, and 7770 pairs per experiment, respectively, statistics in Supplementary table 3). In the fourth experiment, only 13 neurons were both identifiable and visually responsive across days and neither changes in in direction selectivity nor in noise correlation were significant (Friedman’s test: direction selectivity: p=0.58, n=13 cells, correlation: p=0.49, n=69 pairs). We also observed a strong decrease in trial-to trial variability over this same period (initial vs. final imaging session, WSR: Z(317)=15.48, p<0.001). These results clearly show that individual neurons in defined populations become both more selective for direction of motion, less variable, and less correlated following eye opening.
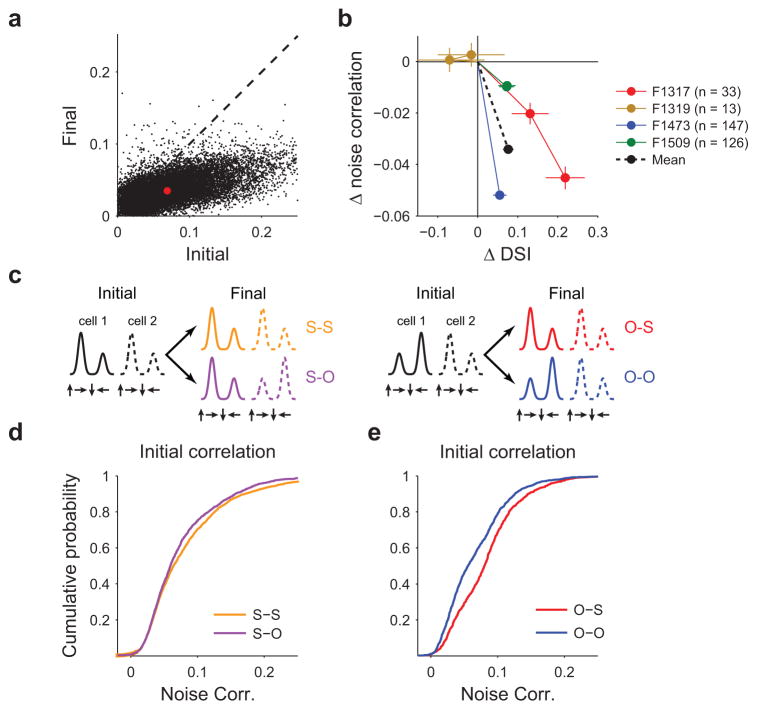
Figure 6. Correlation between decrease in noise correlation and direction selectivity.
(a) Pairwise noise correlations decrease significantly from the initial to the final imaging session. Red dot indicates mean across all pairs and animals. (b) Relationship between change in pairwise noise correlation and direction selectivity (relative to day 0) for 4 animals in which chronic imaging was performed. In 3 of 4 cases, noise correlations exhibited a significant decrease by the final imaging session, whereas direction selectivity significantly increased (n = 33, 147, and 126 neurons per experiment). In one experiment (F1319, shown in orange, n=13 neurons) neither changes in DSI nor correlations were significant. Data are shown as mean ± SEM across all neurons. Averaging across all neurons and pairs on the final imaging session (black line) reveals a significant decrease in noise correlation and a significant rise in direction selectivity. (c) Cartoon depicting possible relationships in pairwise angular preference across imaging sessions. (d) Initial pairwise noise correlations are higher for pairs that will maintain similar preferences (S-S pairs) than those that adopt opposite preferences (S-O pairs). (e) Initial correlations are higher for pairs with opposite preferences if that pair will adopt matching preferred directions on the final imaging session (O-S) than for pairs that maintain opposite preferences (O-O).
Given that noise correlations can reflect the influence of common inputs and recurrent connectivity24, 25, it is possible that high noise correlations amongst pairs of neurons early in development may predict shared tuning properties later on. To examine this, we compared noise correlations during the initial imaging session for neurons with similar preferred directions (within 45°), which maintained that similarity (S–S pairs) versus those which adopted opposite preferences by the final imaging session (S–O pairs) (Fig. 6c, Supplementary Fig. 4). Initial noise correlations were significantly higher for S–S pairs than S–O pairs (Fig. 6d, MW: Z(4857)=3.01, p<0.001, n=3098, 1761 for S–S and S–O, respectively). Likewise, initial noise correlations were higher amongst pairs with opposite preferences that would ultimately adopt similar tuning (O–S pairs) than for pairs which would maintain opposing preferred directions (O–O pairs) (Fig. 6e, MW: Z(2448)=8.74, p<0.001, n=921, 1529 for O–S and O–O, respectively). Taken together, these results indicate that initial pairwise noise correlations may predict future tuning similarity, suggesting the presence of functionally interconnected subpopulations destined to adopt similar tuning.
Decline in variance improves direction discriminability
Traditional measures of direction selectivity are based on the average response of neurons over multiple stimulus trials in order to ‘average out’ the noise that can be present on a single trial. However, reliable behavioral discriminations of motion direction are made based on neuronal responses to a single stimulus presentation. Thus, in addition to selectivity, the variability in single neuron response and correlation in response of the active population may impact the capacity of network activity to discriminate different directions of motion.
As would be expected, the direction discriminability (Supplementary Fig. 5a) of single neurons improved considerably from the naive to immature groups (Fig. 7a, MW: Z(1920)=–18.3, p<0.001). To assess whether this increase resulted primarily from an increase in the selectivity of individual neurons (Fig. 2b), or a decrease in the variance of their response (Fig. 2c), we computing direction discriminability for two hybrid data sets (see Methods). Replacing the variance in naive neurons with that of immature neurons resulted in much higher direction discriminability than using immature tuning together with naive variance (Fig. 7a). This suggests that within a few days after eye opening, the reduction of variance, albeit modest, has a stronger impact on improvements in direction discriminability than the increase in direction selectivity (MW: Z(1998)=–4.10, p<0.001). Between the immature and the mature stage, single neuron discriminability changed little (Fig. 7a) despite an increase in direction selectivity during this period (Fig. 2b), which is consistent with the slight increase in variability observed over the same period (Fig. 2c).
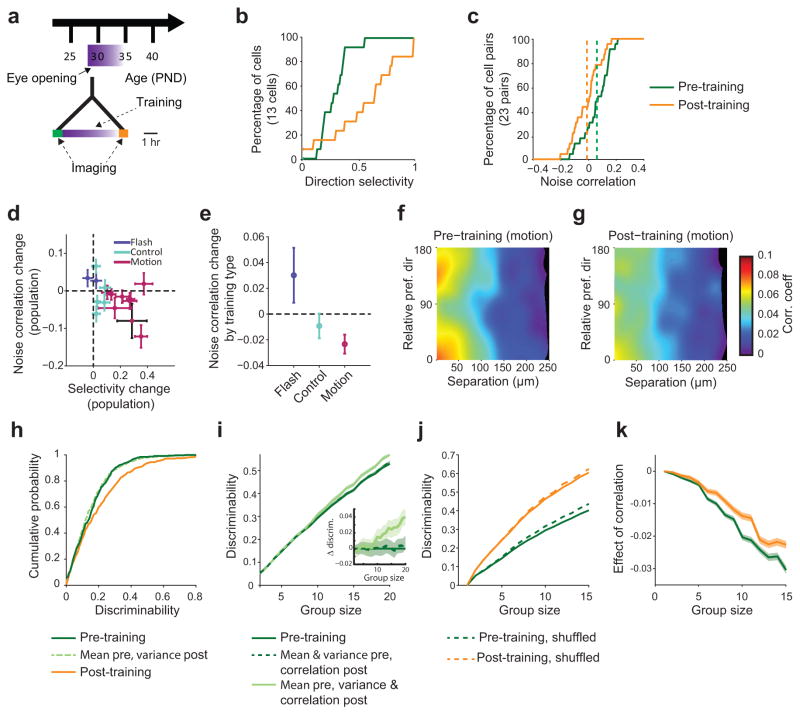
Figure 7. Changes in variance and correlation structure contribute to increased discriminability over development.
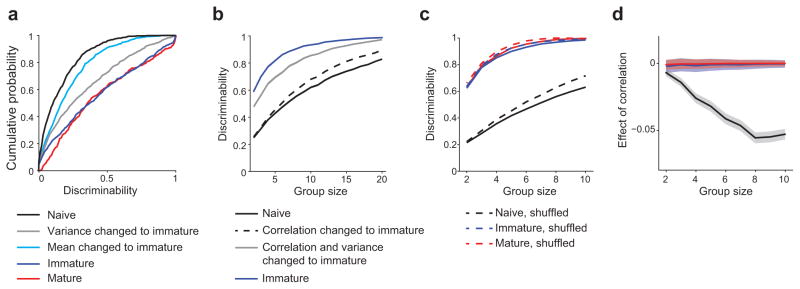
(a) Single-cell direction discriminability increases significantly between the naive and immature ages (black vs. dark blue). Combining immature levels of variance with naive levels of selectivity (gray) results in near immature levels of discriminability, whereas the gain in selectivity alone between the naive and immature ages (light blue) has a much smaller effect on discriminability (gray vs. blue). (b) Effects of variance and structure of noise correlations on discriminability by groups of cells. The overall change in variance and correlation structure increases discriminability substantially between the naive and immature ages. A considerable fraction (increasing with group size) is due to a change in the structure of noise correlations alone (black dashed line). (c) Effect of eliminating correlations by trial shuffling on discriminability by groups of cells. (d) Differences between solid and dashed lines from c. Shaded region shows ±1 SEM.
To determine the degree to which developmental reductions in trial-to-trial variability enhance discriminability in individual neurons, we examined direction discriminability in longitudinally imaged animals. We find a significant increase in discriminability over days (Supplementary Fig. 6a, b; WSR: WSR: Z(201)=–6.56, p<0.001), including within a subset of neurons which exhibited reduced selectivity (termed LS, for low selectivity; Supplementary Fig. 6c). In LS neurons, the response amplitude to both the preferred and null stimuli did not change (Supplementary Fig. 6d WSR: preferred: Z(30)=1.46, p=0.145; null: Z(30)=0.79, p=0.432, n=32), in contrast to neurons with increased selectivity (termed HS neurons), in which the preferred response was enhanced and the null suppressed (Supplementary Fig. 6e; WSR: preferred: Z(110)=5.33, p<0.001; null: Z(110)=–5.20, p<0.001 n=112). Notably, although in both groups variability decreased and this decrease contributed significantly to a rise in discriminability, the decline in variability and corresponding contribution to improved discriminability were both significantly greater in cells lacking an increase in selectivity (Supplementary Fig. 6f–i; WSR: variance: LS: Z(30)=–3.85, p<0.001, HS: Z(110)=–4.26, p<0.001; MW: LS vs. HS: Z(142)=–2.38, p=0.017; effect of variance on discriminability: WSR: LS: Z(30)=4.02, p<0.001, HS: Z(110)=4.23, p<0.001; MW: LS vs. HS: Z(142)=3.09, p=0.002). These results show that developmental reductions in variability are capable of driving increased discriminability in the absence of improved selectivity.
Decrease in noise correlations improves discriminability
While direction discriminability based on the responses of single neurons is enhanced with age, behaviorally relevant direction discriminations are likely to depend on the distribution of activity in populations of cortical neurons where both trial-to-trial variance and noise correlations are contributing factors (Supplementary Fig. 5b). Therefore we sought to assess changes in discriminability in groups of neurons over the course of development and the contribution of a reduction in noise correlation and variance to these changes. As expected, the median discriminability increased with group size (Fig. 7b, c). Consistent with the single cell results, discriminability improved considerably from the naive to the immature stage for group sizes up to N=20 (Fig. 7b). To disentangle the different factors contributing to this improvement, we again constructed hybrid data sets combining aspects of both the naive and immature data sets (see Methods). Combining direction selectivity of the naive set with the variance and correlation structure of the immature cortex, we obtained levels of discriminability close to those reached by the true immature set (Fig. 7b), confirming the single cell result above that early on the increase in direction selectivity is not the prevalent factor in strengthening direction discriminability.
To estimate how much of this enhancement is due to a change in noise correlation, rather than a decrease in (single cell) variance, we generated a second hybrid set, which shared the direction tuning and variance with the naive, but the structure of noise correlations with the immature set. For group sizes of four or larger, discriminability was higher in this set compared to the true naive set (Fig. 7b, MW: p<0.05, full statistics in Supplementary table 4) and nearly as high as when destroying all noise correlations in the naive set by shuffling (Fig. 7c), with the effects of noise correlations increasing with group size (Fig. 7b,d). For the immature and mature sets, differences between the real and trial-shuffled controls were close to zero for all group sizes. These results indicate that on a population level, changes in the structure of correlations contribute considerably to the improvement in direction discrimination early in development.
Motion training decreases noise correlations
Our results showing changes in variance and noise correlation, and their contributions to improvements in discriminability raise two important questions: 1) how rapidly can these changes in selectivity, variance, and correlation, as well as their contributions to discriminability, occur? and 2) are these changes affected by the visual experience of the animal?
Previous results have shown that the emergence of direction selectivity is highly sensitive to the impact of visual experience shortly after eye opening. Stimulation with a moving (but not static) grating for as little as 4–6 hours can induce significant changes in direction selectivity17, 26, indicating that the nature of visual stimulation is critical. We therefore asked, does exposure to a moving stimulus induce a rapid decrease in variability and noise correlations, and if so, do these changes improve discriminability beyond that expected from gains in selectivity alone?
Data originally reported in Li et al. (2008)17 from ferrets that underwent 4–6 hours of motion training (Fig. 8a) was analyzed for changes in pairwise noise correlations as a function of training. In a population of 13 neurons from an example animal shown in Fig. 8b and c, we observed a strong increase in direction selectivity as would be expected following motion training (Fig. 8b, single FOV, n=13 cells, mean difference ± SEM: +0.29±0.11, MW: Z(24)=2.46, p=0.014; for all experiments: n=396 cells, +0.22±0.02, MW: Z(394)=–11.80, p<0.001). Among this same population, we also observed a significant decrease in pairwise noise correlations (Fig. 8c, single FOV: n=14 pairs, mean difference ± SEM: −0.10±0.04, MW: Z(26)=–2.37, p=0.018; for all experiments: n=1247 pairs, −0.022±0.004, MW: Z(1245)=–4.47, p<0.001). In contrast, flash training with non-moving stimuli, which fails to elicit changes in direction selectivity17, not only failed to produce a decrease in noise correlations but actually significantly increased noise correlations (change +0.05±0.01, MW: Z(253)=4.78, p<0.001, n=255 pairs). Importantly, in control experiments where no training stimulus was given, neither direction selectivity nor noise correlations exhibited significant changes (change −0.006±0.005; MW: Z(1026)=–1.19, p=0.234, n=1028 pairs). When analyzed over all experiments, there was a clear relationship between increasing direction selectivity and decreasing noise correlations (Fig. 8d, e; correlation r(13)=–0.57; p=0.025, n=15 experiments (10 motion; 2 flash; 3 control)). These results demonstrate that visual experience with moving stimuli drives rapid changes in both selectivity and in noise correlation, and demonstrate that these changes depend on the nature of visual experience.
Figure 8. Motion training induces decrease in noise correlations and increase in direction selectivity.
(a) Experimental timeline. Shortly after eye opening animals received 4–6 hours of motion training. (b) Example of (black point in d) direction selectivity increase following motion training. (c) Example of decrease in pairwise noise correlations following motion training. (d) Following motion training, noise correlations decrease and direction selectivity increases, while direction selectivity did not change and noise correlations increased following flash training. In control (no training) animals, noise correlations and direction selectivity remained unchanged. (e) Change in noise correlation as a function of training type, pooled across all animals. (f) Before training, noise correlation is highest in pairs for which the difference in preferred direction and cortical distance is small (map generated as in Fig. 4d–f using a Gaussian smoothing kernel, σx=15 micron, σy=15 deg). (g) The correlation in this group is reduced after training, primarily due to the subset of pairs maintaining a small difference in preferred direction, as opposed to those preferring opposite directions after training. (h–k): Discriminability measures in training data set. (h) Discriminability of the trained orientation increases with training. Switching the pre- and post-training variances (light green) does not change discriminability. (i) In larger groups of cells, the change in variance, but not noise correlation, had a detectable effect on discriminability. (j) Effect of eliminating noise correlations by trial shuffling on discriminability in training dataset. (k) Difference between solid and dashed lines from j. Shaded regions show ±1 SEM.
Next, we tested the degree of specificity by which changes in noise correlations are interrelated with changes in direction selectivity. Similar to what we observed during normal development, the largest training induced decrease in noise correlations occurred in pairs with similar tuning properties (similar preferred direction and small cortical distance; Fig. 8f and g; compare Fig. 4d–f). However, only the cell pairs with similar tuning before and after training (the prevalent case) showed a significant decrease in noise correlation, whereas for pairs that changed from same to opposite preferred direction over training, noise correlations remained significantly larger (change in correlation: similar: −0.016±0.007, n=314; opposite: +0.007±0.009, n=121; MW: Z(433)=–2.35, p=0.018). Similar results were obtained when comparing noise correlations from identified populations in longitudinally imaged animals, where correlations for cell pairs with similar preferences on the final day underwent greater reductions than those for pairs with opposite final day preferences (Supplementary Fig. 7; MW: S–S vs. S–O: Z(4857)=–3.55, p<0.001, n=3098, 1761; O–S vs. O–O: Z(2448)=–2.60, p=0.009, n=921, 1529). As positive noise correlations are most detrimental amongst pairs with similar tuning10, 27, our results suggest the changes in noise correlations both over normal development and induced by motion training are not simply a general decrease in the strength of all correlations, but may be specifically structured in such a way as to improve discriminability.
Motion training significantly improved discriminability in single cell responses along the trained orientation (Fig. 8h, mean ± SEM: 0.05±0.19, n=396 cells, MW: Z(394)= −3.28, p<0.001). Unlike in our acute data set, we failed to detect a significant change in variance (Supplementary Fig. 8, Z(394)=–0.64, p=0.52), and the increase in single cell discriminability could be explained by an increase in selectivity (Fig. 8h). However, the impact of altered variability became apparent when examining larger populations (Fig. 8i). Removing noise correlations through shuffling resulted in improved discriminability, both pre- and post-training (Fig. 8j, k, pre-training: p<0.05 for group size >3, post-training: p<0.05 for group size > 7; full statistics in Supplementary table 5). However changes in variance made a larger contribution to improved discriminability than changes in correlation (Fig. 8i, MW: for group size > 2, p<0.05; full statistics in Supplementary table 6). These results demonstrate not only that changes in noise correlations and discriminability can occur rapidly in as little as hours, but also that these changes are dependent on the nature of visual experience.
Discussion
Over a brief period of time following eye opening, the population response in the visual cortex of the ferret undergoes a series of changes that dramatically improve stimulus discriminability. In addition to previously documented increases in direction selectivity12, we find that in the two to three weeks following eye opening, the active population undergoes a striking transformation from a highly dense response with complex spatiotemporal wave-like dynamics to a sparse distribution of active neurons. This transformation is characterized by a decline in variance and pairwise noise correlations over this period, occurring with the same timecourse and in the same neuronal population as the rise in direction selectivity. The high noise correlations present at eye opening limit the direction discriminability of the neuronal population, which improves significantly with the decline in noise correlation. In naive animals, the nature of visual experience appears to play a major role in these processes: experience with moving, but not static, stimuli drives both an enhancement in direction selectivity and a decrease in noise correlations, resulting in improved discrimination.
Dense wave-like responses dominate at eye opening
At eye opening, visual stimulation engages a high percentage of layer 2/3 neurons and the calcium responses in these neurons exhibit complex spatiotemporal dynamics that have the appearance of propagating waves. Spontaneous wave-like activity appears to be a common feature throughout the developing brain including the retina, thalamus, and cortex, and is thought to play a role in establishing orderly maps of retinotopy and ocular dominance through its ability to synchronize the activity of nearby neurons28–30. This supra-threshold activity is distinct from the traveling waves of fast sub-threshold depolarization observed in adult visual cortex in response to focal sensory stimulation31, 32.
The wave-like responses and the sparsification with age that we report here are reminiscent of changes observed in the spontaneous calcium activity in the developing mouse cortex, which is especially prominent prior to eye opening15. However, there are several notable differences between the waves we observe and those described previously in mice15, 33–35. First, wave-like activity in naive ferrets is stimulus specific and local, rather than propagating across the entire cortical surface33, 35. Secondly, the propagation direction varies greatly across animals, suggesting the absence of a stereotypic wave pattern34. Lastly, the developmental profile of cortical waves appears to differ across species, with waves in mice reflecting, at least in part, the transmission of spontaneous retinal wave activity through the early visual system33, 34, whereas spontaneous retinal wave activity is thought to have diminished by eye opening in the ferret36.
Regardless of whether the wave-like patterns of activity evoked in the developing ferret cortex are a reflection of retinal waves or downstream processes, it is clear that these patterns of activity reflect an interaction of this input with cortical circuitry37, 38 as they are constrained by the architecture of orientation selective domains. It is possible that these intracolumnar waves serve as a source of local temporal correlation that promotes map refinement and local response coherence.
Response decorrelation with visual experience
In visually naive ferrets, we find that removing noise correlations via shuffling results in considerable improvements in direction discriminability. Thus in the developing ferret cortex, correlated noise limits the performance of the population. As noise correlations decrease with visual experience, these limits are relaxed and the population nears the performance achievable by a completely decorrelated network. Moreover, by factoring out any increase in direction selectivity taking place over the considered period, we find that the observed early changes in noise correlation and variance alone can lead to strong improvements in direction discriminability. The relative contribution of noise correlations becomes more apparent when considering larger groups of neurons (n<20). We expect their impact to be even more pronounced in larger groups or neurons, but a direct assessment was not possible in our data, due to the limited number of stimulus repetitions and the early saturation in discriminability encountered with moving grating stimuli.
One concern that may arise is whether the use of anesthesia for these experiments undermines the significance of the observations. It is possible that the patterns of cortical activity in the awake animal at these ages differ from those encountered in our preparation; however, our results show that animals maintained under the same anesthetic regime at different ages exhibit profoundly different patterns of activity in response to an identical stimulus, which results in major differences in discriminability. How the developmental changes in cortical responses observed under these conditions manifest in the awake animal, and how these changes contribute to behavioral performance remain important questions for future studies.
Potential circuit mechanisms for response maturation
The decline in noise correlations during the period following eye opening represents a major operational shift for the developing cortex, from a design that is well suited for maximizing the correlations in patterns of spontaneous activity necessary to build circuits, to a design that minimizes correlation in order to improve discrimination of activity patterns evoked by sensory stimulation. A refinement of feedforward inputs along with an increase in the degree of preferential interconnectivity amongst similarly tuned cells39, 40 could account for many of our results, including the increases in selectivity and sparseness, as well as the decrease in wave-like activity. As noise correlations can reflect common inputs24, 25, such refinement could also drive reductions in noise correlations.
An additional role is likely played by the maturation of intracortical inhibition over this period of development41, 42, which likewise can promote response selectivity43 and sparsification44, dampen wave-like activity, and decrease noise correlations45–49. Ultimately, whether the result of a refinement of excitatory connections, a maturation of inhibition, or both, population response properties undergo dramatic changes following eye-opening which have profound effects on stimulus discriminability.
Materials and Methods
All experimental procedures were approved by the Max Planck Florida Institute for Neuroscience or the Duke University Institutional Animal Care and Use Committee, and were performed in accordance with guidelines from the US National Institutes of Health.
Female ferrets were obtained from Marshall Farms and were housed with a jill on a 16 hour light / 8 hour dark cycle. Kits were examined daily to determine the precise date of eye opening.
Viral injections and GCaMP imaging
Microinjections of AAV2/1.hSyn.GCaMP3.WPRE.SV4050(obtained from University of Pennsylvania Vector Core) were made into the visual cortex approximately 7–14 days prior to imaging (range 6–22 days) using pulled glass pipettes and aseptic surgical technique. Anesthesia was induced with ketamine (50 mg/kg) and maintained with isoflurane (1–2%) and nitrous oxide (0 – 50% in oxygen). Atropine (0.2 mg/kg) was given at induction to reduce bronchial secretions. Animals were maintained at approximately 37 °C with a homeothermic heating blanket. Skin and muscle overlying visual cortex were reflected, and a small burr hole was made with a hand held drill (Fordom Electric Co.). Approximately 1 μL of virus was injected over 10 minutes using a Nanoject-II (WPI). Following the injection, muscle and skin were sutured closed, and the animal was recovered and returned to its home cage.
After allowing time for expression of GCaMP3, animals were anesthetized as before, a tracheotomy was performed and an IV catheter was inserted into either the femoral vein or the external jugular vein. Animals were mechanically ventilated and heart rate and end-tidal CO2 were monitored throughout the experiment. A metal headplate was implanted over the injected region and a crainiotomy (~5 mm) was performed. Dura was resected and the brain was stabilized with 2% agarose and a coverslip.
For imaging, isoflurane was reduced to 0.5–1% and animals were paralyzed with vecuronium bromide (2 mg/kg/hr in lactated ringers, delivered IV). This anesthetic regime produced highly stable heart rates of 280–300 bpm for the duration of imaging, with end-tidal CO2 levels stably maintained between 35–40 mmHg. Phenylephrine (5 %) and tropicamide (0.5%) were applied to the eyes to retract the nictitating membrane and dilate the pupil, and the cornea was protected with silicon oil.
Visual stimulation and 2-photon imaging
Visual stimuli were delivered on an LCD screen placed approximately 25–30 cm in front of the eyes. Stimuli were full field sinusoidal gratings at 100% contrast, at 0.06–0.08 cycles per degree, drifting at 4 Hz, presented at one of 8 directions of motion. Stimuli were randomly interleaved, and were presented for 5 seconds followed by a five second gray screen. A 5 second gray screen was used as a “blank” stimulus and was interleaved with grating stimuli. Stimuli were produced using either MATLAB (The Mathworks Inc.) and Psychtoolbox51, 52 or PsychoPy53.
Two-photon imaging was performed with an Ultima IV (Prairie Technologies) driven by a Mai-Tai DeepSee (Spectra Physics) at 910 nm. 512 x 512 pixel images were collected at 0.6 – 1.6 Hz. In a subset of experiments, imaging was performed using a resonant scanner (Prairie Technologies). In these experiments, rectangular images (512 pixel by 256 line images with a 1:2 aspect ratio) were collected at 60 Hz and downsampled to 15 Hz by averaging every 4 successive frames. Prior to analysis, these images were resized to 512 x 512 via bilinear interpolation along the vertical dimension.
Data analysis
Data analysis was performed in ImageJ and MATLAB, utilizing MIJ54. In this study, we utilized fluorescent calcium sensors to report the activity levels of large populations of neurons simultaneously. The relative change in fluorescence of all three calcium sensors used in this study (GCaMP3, GCaMP6s, and OGB) has been shown to be proportional to firing rate and this relationship is roughly linear over the range of firing rates commonly observed in the visual cortex of juvenile ferrets13, 23, 50, 55–58. To extract fluorescence traces from image stacks, ROIs were manually drawn around identified neurons, and raw fluorescence for each frame was computed as the mean of all pixels in the ROI. Fluorescence traces were filtered with a first-order high-pass Butterworth filter with a cut-off time (TC) of 300 seconds. Similar results were obtained using F/F with F0 taken as the last 2 seconds of the ISI immediately preceding stimulus onset. Stimulus evoked responses were taken as the average high-pass filtered fluorescence over the full stimulus interval. Neurons were considered visually responsive and analyzed further if the response to the preferred stimulus (averaged across trials) was both greater than zero and 2 standard deviations above the “blank” response.
To determine the density of the population response, a neuron was considered responsive on a given trial if its response to any stimulus on that trial was greater than 2 standard deviations above the response to a blank stimulus. Only neurons exhibiting at least 1 response during the imaging session (>90% of neurons) were included in this analysis to prevent counting poorly labeled or unhealthy neurons as unresponsive. To examine the stimulus-specificity of response density, we aligned all FOVs by the dominant stimulus - that which evoked a response in the largest fraction of neurons within the imaging field.
To compute tuning curves and determine the preferred direction (θpref), responses were averaged across trials and fit with a 2 peaked Gaussian function, where the peaks were constrained to be 180° apart. Poorly fit (correlation between fit and actual responses with p>0.05) or unresponsive neurons were excluded from further analysis. Orientation and direction selectivity were computed as described17:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Only neurons with significant orientation selectivity (Hotelling’s t2-test with p < 0.05, see ref. 17) were included for analysis of direction selectivity.
Pairwise noise correlations were calculated by first attempting to remove all signal correlations between neurons. This was achieved by filtering the data with a short cut-off time first-order Butterworth filter (TC=5 seconds), then Z-scoring the data individually for each stimulus with respect to the mean of that stimulus. The z-scored responses (containing all data points acquired during the stimulus presentation) were then concatenated across all stimuli and the blank condition. Pairwise noise correlations were then computed using the MATLAB corrcoef function. To prevent contamination of the fluorescence signal from neighboring neurons, we only considered pairs separated by at least 30μm. Due to the slower scanning rate (0.5–0.7 Hz) for the training data, two cells were required to be sampled within 100 ms of each other to be included in the pairwise correlation analysis.
Non-parametric statistics were used unless noted, with Kruskal-Wallis (KW) tests followed by post-hoc Mann-Whitney U tests (MW). Wilcoxon signed-rank tests (WSR) were used for paired comparisons. Data are presented as mean ± SEM.
Analysis of wave-like responses
Only experiments performed with a resonant scanner were used for the analysis of wave-like responses. To compute temporally colored images (Fig. 3a,b), images were Z-scored pixel-wise relative to the mean and standard deviation of images collected during blank simuli. Images were then smoothed with a mean filter (2 x 2 pixels in x and y and 2 frames (.133 sec) in t). Frames were then binned into 0.26 second intervals, averaged, and pseudocolored by time. Finally, pseudocolored images were summed across the full stimulus period. For calculating the average wave image (Fig 3c), only trials with a significant linear wave (see below) were included.
To determine the presence of a linear wave we utilized methods based upon Siegel et al. (2012)34. First we found the peak response time (tpeak) for each responsive neuron on a given trial. For this analysis, a neuron was considered responsive if its fluorescence was > 3 standard deviations above the response to a “blank” stimulus for 6 successive frames. Response onset was defined as the first time during the response that the fluorescence exceeded 1 standard deviation above the blank. Peak response times were then fit with a linear traveling wave, where the response time (tfit) is given by
| (6) |
where v is the velocity of the wave along its propagation direction, and t0 is the time the wave crossed the origin of the image coordinate system (positioned at upper left pixel). p is the projection of the neuron’s x and y coordinates onto a unit vector describing the waves propagation angle:
| (7) |
where x and y define a neuron’s position, and θ is the propagation angle of the wave. The error of the fit was defined as the SSE of tfit relative to tpeak, and v, θ and t0 were adjusted to minimize this error. For each stimulus, we then calculated a goodness-of-fit by shuffling tpeak 100 times, re-fitting each shuffled data set, and determining an error. The fraction of shuffled responses with errors larger than that of the original data set acts as a waviness index, giving an indication of the waviness of the response (for a wave-like event, shuffling the response times should produce fits with higher errors). Only responses with waviness indices > 0.9 were considered as waves and included for determining velocity and propagation direction.
Given the frame rate of our microscope and the size of our FOVs, there is an upper limit to the wave velocity which we are able to observe. We estimate that this detection limit is faster than 1500 μm/sec. At such a velocity, a wave would traverse our FOV (512 pixels at 0.77 μm/pixel) in 4 imaging frames, ensuring that the wavefront position could be captured by at least three images. This threshold is approximately 6x greater than the mean velocity (and 8x greater than the median velocity) that we observed in naive animals (Fig. 3g).
If neurons are distributed in an elongated manner within a FOV, it is possible that our ability to detect waves propagating along the short axis could be reduced. If such an aperture effect is present in our data, then the ability to detect a wave traveling along the short axis should depend on the wave velocity, and fast moving waves should be underrepresented along this axis. To determine if such an effect is present in our data, we computed the velocity of waves travelling within 22.5° of either the long or short axis of a FOV. Considering only naive animals, in which both the frequency and velocity of waves are relatively high, there is no significant difference between velocity distributions for the two propagation directions (mean ± SEM: 310.0±63.2 vs. 281.2±58.9 μm/sec; n=30 and 17, respectively; MW: p=0.816). Furthermore, the asymmetry in wave propagation direction we report is present even if we discard from our analysis all waves that moved faster than the short-axis velocity detection limit (taken conservatively to be 400 μm/sec, see below), showing that this effect cannot be from a bias in detectability.
To demonstrate the robustness of our detection algorithm, we performed a sensitivity analysis using simulated wavefronts. We construct FOVs of 200 neurons with positions drawn from a 2-D gaussian distribution with covariance similar to our actual data. Propagation directions were drawn from a uniform distribution of 0 to 2pi, and velocities drawn from a uniform distribution of 2000–3000 μm/sec. To simulate a wave, response times were calculated for a subset of cells, with the number of cells participating in each wave drawn from a uniform distribution between 5 and 40, with a random selection of cells from within the 200 cell FOV for each wave. Detection is more difficult with low numbers of participating neurons, and this range covers the lower range observed in naive animals (mean ± stdev: 38 ± 28, with quartiles of 16, 31.5, and 53 cells / wave), where we required at least 5 active neurons to define a wave. After calculating the response times of participating cells, uniform noise (scaled to be 50% of the range of response times on a given wave) was added and response times were binned into 1/15 second intervals to match the imaging frame rate. Each simulated wave was then fit, and the same detection threshold used for the actual data was applied.
In simulated data, our algorithm readily detected waves travelling between 2000 and 3000 μm/sec (84.5%, 845/1000, with 5–40 active neurons per wave), suggesting that 1500 μm/sec is a conservative estimate of the upper limit for detection.
We also repeated our simulations using highly elliptical FOVs (mean ellipticity >0.84), with wave velocities drawn from a normal distribution with mean and standard deviation of 1000 μm/sec. In these FOVs, our detection algorithm identified 92.7% (395/426) of waves travelling 1000–2000 μm/sec, containing on average 23 active neurons per wave, including 87.8% (101/115) of waves travelling within 22.5° of the short axis. For waves travelling under 1000 μm/sec, the detection rate along the short axis increased to 98.1%. Within our dataset, FOVs have much lower ellipticity (< 0.61) and the majority of waves have velocity much less than 1000 μm/s (average is approximately 250 μm/s). Thus, for realistic ellipticity and wave velocity, we are able to detect waves travelling in all directions and that the asymmetries in propagation direction which we observe are not due to an inability to detect certain wave trajectories.
To determine the contribution of wave-like responses to noise correlations in the naive group, we calculated correlations using only trials with linear waves and compared these to correlations on trials with the same stimuli, but without waves. Only stimuli which evoked at least 2 waves were included in this analysis.
Longitudinal 2-photon calcium imaging
Kits were implanted with a custom-designed headplate at P24–25. The headplate design accommodates an 8 mm diameter coverslip (World Precision Instruments) held in place by a stainless steel retaining ring (McMaster Carr) that fits securely underneath a lip in the headplate, securing the coverslip in place and providing mild pressure (Fig. 5a). The headplate also features a protruding tab allowing the headplate to be clamped in a custom built animal holder during surgery and imaging. The imaging chamber was designed to allow ready and repeated access to the cortex in order to remove any tissue or neo-membrane (see 59) that can regrow over the imaging field.
During surgery, animals were anesthetized as above, except that animals were intubated and ventilated mechanically. Respiration parameters were adjusted to maintain end-tidal CO2 at 35–40 mmHg. During some portions of the surgery (durotomy and microinjection) animals were mildly hyperventilated to ~30 mmHg to reduce edema. The skull overlying visual cortex was exposed, and a thin layer of cyanoacrylate (Vetbond, 3M) was applied and allowed to dry. The headplate was then positioned in place, and attached to the skull with dental cement (C&B Metabond, Parkell Inc.). Once the cement had dried, a second layer of black cement (OrthoJet, Lang Dental mixed with powdered pigment: Iron Oxide, Dick Blick Art Supply) was applied.
A craniotomy (~5 mm diameter) was performed over visual cortex and dura was carefully removed. In two animals (F1317 and F1319) AAV expressing GCaMP3 was injected as above. In an additional two experiments (F1473 and F1509) conducted after the release of GCaMP6, AAV1.Syn.GCaMP6s.WPRE.SV40 (ref. 58, obtained from University of Pennsylvania Vector Core) was injected in place of GCaMP3. Following the injection, warm agarose (2% in ACSF with Baytril (0.45 mg/mL)) was applied to the cortex and a glass coverslip was quickly inserted into place. The coverslip was secured with a retaining ring coated in silicone polymer (Kwik-Kast, World Precision Instruments) to seal the chamber. Following surgery, animals were recovered from anesthesia and returned to their home cage.
Approximately one week following this surgery, animals were returned to the imaging room, anesthesia was induced with ketamine, atropine was administered, and anesthesia was maintained with isoflurane as above. Animals were intubated and ventilated, and an IV catheter was placed in the cephalic vein. In some imaging sessions, it was not possible to catheterize the cephalic vein, in these cases an IP catheter was inserted. If necessary, the chamber was opened under aseptic conditions, any regrown tissue or neomembrane was removed, agarose and a coverslip were reapplied, and the chamber was resealed. This was usually necessary after about 1–2 weeks following implantation, and could typically be performed without causing apparent damage to the underlying cortex. In approximately half of the imaging sessions, the chamber remained optically clear and no tissue regrowth was apparent. Immediately prior to imaging, animals were paralyzed with vecuronium bromide (0.1 mg/kg/hr in lactated ringers).
2-photon imaging was performed as above and lasted approximately 3 hours, containing approximately 45 minutes of visual stimulation. Imaging sessions were kept as short as possible in order to minimize the potential for inducing training effects, which can be observed in young ferrets following 4–6 hours of continuous exposure to moving stimuli 17. The imaged field of view could be identified approximately based on surface blood vessel patterns, and 2-photon Z-stacks were taken from the cortical surface through the imaging plane to aid alignment. Following imaging, vecuronium was stopped and paralysis was antagonized with neostigmine (0.06 mg/kg), delivered with atropine (0.2 mg/kg). Isoflurane was discontinued, and animals were removed from the ventilator once spontaneous respiration was observed.
Sessions were repeated every 2–3 days until imaging quality degraded or the imaging FOV could not be conclusively identified. The imaging area was found on the basis of cortical blood vessel patterns, which were highly stable over days and on the local 3D pattern of GCaMP expression imaged with 2-photon Z-stacks.
Alignment of images across sessions was performed with an affine transform, and data was analyzed as above. Only neurons that were visible and could be conclusively identified across all imaging sessions were included in this analysis.
To identify neurons with stable and reversing direction preferences, a bootstrapping analysis was performed as in Li, et al. 200817. Neurons with less than a 10% likelihood of reversing preference were considered stable, and neurons with >90% likelihood of reversing were considered reversing neurons. Neurons in which the initial direction preference was highly uncertain17 (uncertainty > 10%) but became certain (uncertainty < 10%) by the final session were classified as having initially lacked a preferred direction but developed on over sessions. To compare average tuning curves across neurons, curves were aligned based on the preferred direction on the final imaging session.
OGB data and analysis
Data from Li et al.17 was analyzed for changes in noise correlations as described above. Briefly, in these experiments animals were imaged shortly following eye opening after bulk-loading the calcium indicator OGB1 (full methods available in ref 17). Direction tuning curves were measured both prior to and following 4–6 hours of motion training. Motion training consisted of repeated presentations of a grating drifting in a single orientation (both directions of motion were interleaved). An additional group of animals received flash training, in which a static grating stimulus was shown. As a control, a third group of animals received no training and viewed a static gray screen during the entire training period. To ensure continuity within the studied population, we have restricted analysis to neurons that could be conclusively identified both before and after motion training and which were visually responsive throughout the experiment. We assessed responsiveness by computing the signal to noise ratio (SNR): the size of response to the preferred direction relative to size of fluctuations during unstimulated periods of each cell. We restrict our analysis to a subpopulation of cells for which the distribution of SNR did not change significantly over the training period. In this way, we insure that a net change in cell responsiveness did not underlie the change in mean correlation in the population.
Discrimination analysis
For a given set of neurons, we defined discriminability to be one minus the normalized overlap between the population-response distributions using a Gaussian approximation, which captured the observed responses well (Supplemental Figure 9). More concretely, consider a set of N neurons with ri,t being the response of N neurons at trial t = 1 …Nt to stimulus i = 1…Ns. We computed r̄i, the sample mean response to stimulus i:
| (8) |
Covariance was assumed to be stimulus-independent and computed over all eight stimuli after subtracting stimulus means:
| (9) |
With the covariance matrix C and mean responses to stimuli i and j, discriminability of stimulus pair {i,j} is
with
| (10) |
where Ioverlap is the integrated product of the stimulus-dependent response distributions:
| (11) |
Here we assumed a multivariate Gaussian distribution of cell responses with covariance C. Equation 11 reduces to
| (12) |
Large overlap is a small discriminability. If the stimulus means r̄i are equal, the discriminability is 0. No overlap is perfect discriminability (1).
To compute the shuffled discriminability, we computed the covariance matrix from trial-shuffled responses. Means r̄i are unchanged. The measure of discriminability used here is related to the sensitivity index, d′ (ref. 60), the argument of the exponential in Eqn (12). For a subset of the data, we computed discriminability using a low-rank approximation of the noise covariance matrix, which was obtained from the singular value decomposition (SVD) of the noise covariance matrix, and obtained results consistent with the full covariance matrix discriminability results.
In longitudinally imaged animals, discriminability was only assessed for neurons in which the stimulus orientation evoking the largest response did not change across sessions.
Variance and covariance exchange across datasets
To disentangle the effects of a shift in mean and a shift in variance over development, we computed direction discriminability for two hybrid cell sets: the first one was composed by using the average activities (direction selectivities) from the naive data set, but taking the variances from the immature set; the second one combined the variances of the naive set with the averages of the immature set. Since cells from the two data sets were not identical (typically from different animals), we assigned cell pairs across sets by matching the rank of their average activity, or variance, respectively.
Specifically, we computed discriminability by drawing mean responses from a population of cells in naive animals and variances from populations of cells in immature animals. Mean responses are rank-matched to variance in the following manner. We drew from the available naive (N = 1159 cells) and immature (N = 763 cells) populations equal-sized subsets of N = 700 cells. For each cell in the naive population, we computed the rank of the mean response to the preferred direction and the rank of the variance. This was repeated for the immature population. We then assigned cell pairs across sets to be rank-matched. For instance, if a cell in the naive population had mean response with rank m, it was matched with the variance of the cell in the immature population that had mean response with rank m. This gives the set of “cells” with naive means and immature variances. For the reverse, naive variances with immature means, we took t nth rank variance from the naive population and matched it with the mean response corresponding to the nth rank variance in the immature population. This method ensures that the statistical relationship between mean activity and its variance is preserved.
The method for exchanging variance and covariance among subsets of cells is a two-step process: first, to match each group of cells from the naive set to a group of cells from the immature set, and second, to determine the cell-by-cell matching between each pair of groups. To construct groups of cells, we rank-matched as described above based on the highest group-average response and the determinant of the covariance matrix. Within each group of N cells, we used rank matching based on the N mean responses to the preferred direction and on the N individual-cell variances. Effectively, this reorders the rows and columns of the covariance matrix. At this stage, we can compute discriminability with naive means and immature variance and covariance. To separate covariance and variance, we computed the correlation matrix rij from the (immature) covariance matrix (Cij) using immature single-cell variances ( )
| (13) |
and transformed this back to a covariance matrix using the individual cell variances from the naive dataset ( ):
| (14) |
The matrix was used to compute discriminability with immature correlation structure and naive mean and variance.
In the training dataset, we have the same populations of cells so rank matching was not required to match pre- and post-training covariance and means. Variance and covariance were separated as described above, by first converting to a correlation matrix and then using pre-training single-cell variance to compute the covariance matrix from the correlation matrix.
A supplementary methods checklist is available.
Supplementary Material
Acknowledgments
This research was supported by grants EY011488 (D.F.), EY022001 (G.B.S.), 5T32HG003284 (A.J.S.), and BFNT 01GQ0840 (M.K.), as well as the Max Planck Florida Institute. We would like to thank Dominique Ouimet and Valerie Hoke for technical and surgical assistance, and Rebekah Corlew for administrative support.
Footnotes
Author contributions
G.B.S, A.S., M.K. and D.F. designed the study, analyzed the results, and wrote the paper. G.B.S. performed the acute and longitudinal GCaMP imaging. Y.M.E. developed the method for longitudinal imaging. S.D.V.H. originally acquired the motion training data and prepared this data for the additional analyses reported here.
References
- 1.Tomko GJ, Crapper DR. Neuronal variability: non-stationary responses to identical visual stimuli. Brain Res. 1974;79:405–418. doi: 10.1016/0006-8993(74)90438-7. [DOI] [PubMed] [Google Scholar]
- 2.Tolhurst DJ, Movshon JA, Dean AF. The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res. 1983;23:775–785. doi: 10.1016/0042-6989(83)90200-6. [DOI] [PubMed] [Google Scholar]
- 3.Tolhurst D. The amount of information transmitted about contrast by neurones in the cat’s visual cortex. Visual neuroscience. 1989:409–413. doi: 10.1017/s0952523800002212. [DOI] [PubMed] [Google Scholar]
- 4.Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12:255–270. [PubMed] [Google Scholar]
- 5.Yen SC, Baker J, Gray CM. Heterogeneity in the responses of adjacent neurons to natural stimuli in cat striate cortex. J Neurophysiol. 2007;97:1326–1341. doi: 10.1152/jn.00747.2006. [DOI] [PubMed] [Google Scholar]
- 6.Weliky M, Fiser J, Hunt RH, Wagner DN, York N. Coding of natural scenes in primary visual cortex. Neuron. 2003;37:703–718. doi: 10.1016/s0896-6273(03)00022-9. [DOI] [PubMed] [Google Scholar]
- 7.Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]
- 8.Shadlen MN, Newsome WT. Noise, neural codes and cortical organization. Curr Opin Neurobiol. 1994;4:569–579. doi: 10.1016/0959-4388(94)90059-0. [DOI] [PubMed] [Google Scholar]
- 9.Abbott LF, Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11:91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- 10.Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7:358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- 11.Chapman B, Stryker MP, Bonhoeffer T. Development of orientation preference maps in ferret primary visual cortex. J Neurosci. 1996;16:6443–6453. doi: 10.1523/JNEUROSCI.16-20-06443.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li Y, Fitzpatrick D, White LE. The development of direction selectivity in ferret visual cortex requires early visual experience. Nat Neurosci. 2006;9:676–681. doi: 10.1038/nn1684. [DOI] [PubMed] [Google Scholar]
- 13.Chapman B, Stryker MP. Development of orientation selectivity in ferret visual cortex and effects of deprivation. J Neurosci. 1993;13:5251–5262. doi: 10.1523/JNEUROSCI.13-12-05251.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Krug K, Akerman CJ, Thompson ID. Responses of neurons in neonatal cortex and thalamus to patterned visual stimulation through the naturally closed lids. J Neurophysiol. 2001;85:1436–1443. doi: 10.1152/jn.2001.85.4.1436. [DOI] [PubMed] [Google Scholar]
- 15.Rochefort NL, et al. Sparsification of neuronal activity in the visual cortex at eye-opening. Proc Natl Acad Sci U S A. 2009;106:15049–15054. doi: 10.1073/pnas.0907660106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ikezoe K, Tamura H, Kimura F, Fujita I. Decorrelation of sensory-evoked neuronal responses in rat barrel cortex during postnatal development. Neurosci Res. 2012;73:312–320. doi: 10.1016/j.neures.2012.05.009. [DOI] [PubMed] [Google Scholar]
- 17.Li Y, Van Hooser SD, Mazurek M, White LE, Fitzpatrick D. Experience with moving visual stimuli drives the early development of cortical direction selectivity. Nature. 2008;456:952–956. doi: 10.1038/nature07417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Derrington AM, Fuchs AF. The development of spatial-frequency selectivity in kitten striate cortex. J Physiol. 1981;316:1–10. doi: 10.1113/jphysiol.1981.sp013767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berens P. CircStat: a MATLAB toolbox for circular statistics. Journal of Statistical Software. 2009:31. [Google Scholar]
- 20.Bair W, Zohary E, Newsome WT. Correlated firing in macaque visual area MT: time scales and relationship to behavior. J Neurosci. 2001;21:1676–1697. doi: 10.1523/JNEUROSCI.21-05-01676.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ecker AS, et al. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327:584–587. doi: 10.1126/science.1179867. [DOI] [PubMed] [Google Scholar]
- 22.Smith MA, Kohn A. Spatial and temporal scales of neuronal correlation in primary visual cortex. J Neurosci. 2008;28:12591–12603. doi: 10.1523/JNEUROSCI.2929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Clemens JM, Ritter NJ, Roy A, Miller JM, Van Hooser SD. The laminar development of direction selectivity in ferret visual cortex. J Neurosci. 2012;32:18177–18185. doi: 10.1523/JNEUROSCI.3399-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kriener B, Tetzlaff T, Aertsen A, Diesmann M, Rotter S. Correlations and population dynamics in cortical networks. Neural Comput. 2008;20:2185–2226. doi: 10.1162/neco.2008.02-07-474. [DOI] [PubMed] [Google Scholar]
- 26.Van Hooser SD, et al. Initial neighborhood biases and the quality of motion stimulation jointly influence the rapid emergence of direction preference in visual cortex. J Neurosci. 2012;32:7258–7266. doi: 10.1523/JNEUROSCI.0230-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jeanne JM, Sharpee TO, Gentner TQ. Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron. 2013;78:352–363. doi: 10.1016/j.neuron.2013.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Blankenship AG, Feller MB. Mechanisms underlying spontaneous patterned activity in developing neural circuits. Nat Rev Neurosci. 2010;11:18–29. doi: 10.1038/nrn2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Huberman AD, Feller MB, Chapman B. Mechanisms underlying development of visual maps and receptive fields. Annu Rev Neurosci. 2008;31:479–509. doi: 10.1146/annurev.neuro.31.060407.125533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ackman JB, Crair MC. Role of emergent neural activity in visual map development. Curr Opin Neurobiol. 2014;24:166–175. doi: 10.1016/j.conb.2013.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wu JY, Xiaoying H, Chuan Z. Propagating waves of activity in the neocortex: what they are, what they do. Neuroscientist. 2008;14:487–502. doi: 10.1177/1073858408317066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sato TK, Nauhaus I, Carandini M. Traveling waves in visual cortex. Neuron. 2012;75:218–229. doi: 10.1016/j.neuron.2012.06.029. [DOI] [PubMed] [Google Scholar]
- 33.Ackman JB, Burbridge TJ, Crair MC. Retinal waves coordinate patterned activity throughout the developing visual system. Nature. 2012;490:219–225. doi: 10.1038/nature11529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Siegel F, Heimel JA, Peters J, Lohmann C. Peripheral and central inputs shape network dynamics in the developing visual cortex in vivo. Curr Biol. 2012;22:253–258. doi: 10.1016/j.cub.2011.12.026. [DOI] [PubMed] [Google Scholar]
- 35.Stroh A, et al. Making waves: initiation and propagation of corticothalamic Ca2+ waves in vivo. Neuron. 2013;77:1136–1150. doi: 10.1016/j.neuron.2013.01.031. [DOI] [PubMed] [Google Scholar]
- 36.Wong RO, Meister M, Shatz CJ. Transient period of correlated bursting activity during development of the mammalian retina. Neuron. 1993;11:923–938. doi: 10.1016/0896-6273(93)90122-8. [DOI] [PubMed] [Google Scholar]
- 37.Hanganu IL, Ben-Ari Y, Khazipov R. Retinal waves trigger spindle bursts in the neonatal rat visual cortex. J Neurosci. 2006;26:6728–6736. doi: 10.1523/JNEUROSCI.0752-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Colonnese MT, et al. A conserved switch in sensory processing prepares developing neocortex for vision. Neuron. 2010;67:480–498. doi: 10.1016/j.neuron.2010.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ko H, et al. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ko H, et al. The emergence of functional microcircuits in visual cortex. Nature. 2013;496:96–100. doi: 10.1038/nature12015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Le Magueresse C, Monyer H. GABAergic interneurons shape the functional maturation of the cortex. Neuron. 2013;77:388–405. doi: 10.1016/j.neuron.2013.01.011. [DOI] [PubMed] [Google Scholar]
- 42.Gao WJ, Newman DE, Wormington AB, Pallas SL. Development of inhibitory circuitry in visual and auditory cortex of postnatal ferrets: immunocytochemical localization of GABAergic neurons. J Comp Neurol. 1999;409:261–273. doi: 10.1002/(sici)1096-9861(19990628)409:2<261::aid-cne7>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 43.Van Hooser SD, Escobar GM, Maffei A, Miller P. Emerging feed-forward inhibition allows the robust formation of direction selectivity in the developing ferret visual cortex. J Neurophysiol. 2014 doi: 10.1152/jn.00891.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.King PD, Zylberberg J, DeWeese MR. Inhibitory interneurons decorrelate excitatory cells to drive sparse code formation in a spiking model of V1. J Neurosci. 2013;33:5475–5485. doi: 10.1523/JNEUROSCI.4188-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bernacchia A, Wang XJ. Decorrelation by recurrent inhibition in heterogeneous neural circuits. Neural Comput. 2013;25:1732–1767. doi: 10.1162/NECO_a_00451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tetzlaff T, Helias M, Einevoll GT, Diesmann M. Decorrelation of neural-network activity by inhibitory feedback. PLoS Comput Biol. 2012;8:e1002596. doi: 10.1371/journal.pcbi.1002596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.van Vreeswijk C, Sompolinsky H. Chaotic balanced state in a model of cortical circuits. Neural Comput. 1998;10:1321–1371. doi: 10.1162/089976698300017214. [DOI] [PubMed] [Google Scholar]
- 48.Renart A, et al. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Renart A, van Rossum MC. Transmission of population-coded information. Neural Comput. 2012;24:391–407. doi: 10.1162/NECO_a_00227. [DOI] [PubMed] [Google Scholar]
- 50.Tian L, et al. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat Methods. 2009;6:875–881. doi: 10.1038/nmeth.1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- 52.Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
- 53.Peirce JW. PsychoPy--Psychophysics software in Python. J Neurosci Methods. 2007;162:8–13. doi: 10.1016/j.jneumeth.2006.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sage D, Dimiter P, Tinevez J-Y, Schindelin J. MIJ: Making Interoperability Between ImageJ and Matlab Possible. ImageJ User & Developer Conference. 2012 [Google Scholar]
- 55.Ohki K, Chung S, Ch’ng YH, Kara P, Reid RC. Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature. 2005;433:597–603. doi: 10.1038/nature03274. [DOI] [PubMed] [Google Scholar]
- 56.Kara P, Boyd JD. A micro-architecture for binocular disparity and ocular dominance in visual cortex. Nature. 2009;458:627–631. doi: 10.1038/nature07721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hendel T, et al. Fluorescence changes of genetic calcium indicators and OGB-1 correlated with neural activity and calcium in vivo and in vitro. J Neurosci. 2008;28:7399–7411. doi: 10.1523/JNEUROSCI.1038-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chen TW, et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chen LM, et al. A chamber and artificial dura method for long-term optical imaging in the monkey. J Neurosci Methods. 2002;113:41–49. doi: 10.1016/s0165-0270(01)00475-7. [DOI] [PubMed] [Google Scholar]
- 60.Averbeck BB, Lee D. Effects of noise correlations on information encoding and decoding. J Neurophysiol. 2006;95:3633–3644. doi: 10.1152/jn.00919.2005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.