Abstract
Malaria parasites exhibit great diversity in the coordination of their asexual life cycle within the host, ranging from asynchronous growth to tightly synchronized cycles of invasion and emergence from red blood cells. Synchronized reproduction should come at a high cost— intensifying competition among offspring—so why would some Plasmodium species engage in such behavior and others not? We use a delayed differential equation model to show that synchronized infections can be favored when: (1) there is limited interference among parasites competing for red blood cells; (2) transmission success is an accelerating function of sexual parasite abundance; (3) the target of saturating immunity is short-lived; and (4) coinfections with asynchronous parasites are rare. As a consequence, synchrony may be beneficial or costly, in line with the diverse patterns of synchronization observed in natural and lab infections. By allowing us to characterize diverse temporal dynamics, the model framework provides a basis for making predictions about disease severity and for projecting evolutionary responses to interventions.
Keywords: synchrony, malaria, interference competition, saturating immunity, transmission, Jensen’s inequality
Introduction
Synchronized reproduction represents a significant challenge to evolutionary theory: what benefits outweigh the costs of escalating competition among offspring? Despite the costs, many organisms do coordinate their reproductive efforts. Extreme examples are mass emergence of periodical cicadas (Williams et al. 1993) and mast-seeding of bamboos (Janzen 1976), but more subtle examples are common throughout the natural world (reviewed in Ims 1990, Kelly and Sork 2002). Yet even among organisms sharing similar life-histories, some synchronize their reproduction while others do not. Theory suggests that synchronized reproduction can be an adaptation to expedite mate-finding and overwhelm natural enemies (Ims 1990, Kelly and Sork 2002). These obstacles are not confined to free-living organisms, however; parasites likewise vary in how closely they coordinate their life cycles, with malaria species provide a striking example (Mideo et al. 2013). We apply an ecological approach to identify plausible mechanisms that could favor synchronized infection cycles in malaria parasites even at the cost of intensifying within-host competition.
Synchronized cycles of blood stage infection are a fascinating aspect of malaria biology, with parasites invading red blood cells, reproducing asexually, and bursting out in unison (e.g., Garnham 1966, Hawking et al. 1968, Hawking 1970). Even considering a single malaria species, some human infections appear synchronous and some do not (Färnert et al. 1997, Bruce et al. 2000 b, Simpson et al. 2002, Dobaño et al. 2007, Touré-Ndouo et al. 2009); these observations highlight variability in a fundamental aspect of within-host ecology, with critical implications for human health. Synchrony should limit host exploitation by intensifying competition for resources. The degree of synchronization should also influence parasites’ susceptibility to anti-malarial drugs, which act against a subset of life stages (e.g., Yayon et al. 1983, Slater and Cerami 1992, ter Kuile et al. 1993, Dhar et al. 1998, Delves et al. 2012). The synchrony inherent to parasite dynamics thus represents a source of variation that could influence the course of evolution within the host, modulating the degree of virulence and drug susceptibility.
All else equal, synchrony should be costly. Malaria parasites face intense competition for red blood cells in vitro (Reilly et al. 2007, Boyle et al. 2010), and parasites have only minutes to invade red blood cells before their viability is lost (Boyle et al. 2010). By bursting out of red blood cells in unison, synchronous parasites should pay a vastly increased cost of competition. Whether synchrony is ultimately beneficial or costly to the parasite will be determined by its effects on the transmission to the mosquito vector. Accordingly, synchrony was first thought to be an adaptation to enhance transmission (Hawking et al. 1968, Hawking 1970). Infecting mosquitoes requires sexual gametocytes that spawn from a small fraction of the asexual, blood-stage parasites (reviewed in Drakeley et al. 2006, Bousema and Drakeley 2011). Coordinated waves of red blood cell invasion generate periodic oscillations in gametocyte numbers that could be advantageous if peak gametocyte numbers occur when mosquitoes are most likely to feed (Hawking et al. 1968, Hawking 1970). However, neither peak infectivity (Bray et al. 1976, Githeko et al. 1993) nor peak gametocyte density (Magesa et al. 2000) have been shown to correspond with peak vector activity time for human cases.
More recent theory has focused on the success of the asexual parasites that ultimately produce transmission stages. Synchrony has been hypothesized to be a consequence of host defenses that intensify with parasite numbers (Kwiatkowski and Nowak 1991, Rouzine and McKenzie 2003). The reasoning is that if a particular parasite stage is immunogenic, and a later stage is vulnerable to immune clearance, then a large cohort of parasites may trigger an intense immune response that would effectively clear away other cohorts of parasites, leaving a synchronized group of parasites behind. While escalation might be characteristic of an adaptive immune response (Antia and Koella 1994), innate host defenses may instead saturate as parasite numbers increase. These early immune responses may be most effective against small numbers of parasites, as suggested by data from rodent infections (Haydon et al. 2003, Metcalf et al. 2011) and malaria parasites in vitro (P. falciparum cultured with platelets, McMorran et al. 2009; and γδ T cells, Costa et al. 2011).
If immunity can saturate, pulses in parasite numbers may overwhelm host defenses, analogous to the way many organisms use synchronized reproduction as a way to satiate predators. If immunity targets a transient part of the parasite life cycle, synchronization would allow parasites in the vulnerable life stage to disappear between brief periods of overwhelming numbers, analogous to the way periodical cicadas emerge synchronously—and briefly—to satiate predators. If immunity targets a long-lived part of the parasite life cycle, then even small variation in timing would result in vulnerable parasites persisting between peaks in abundance. As parasite numbers increase, their survival saturates, and this saturating fitness curve renders oscillations between high and low abundance costly (fig. 1). For synchrony to be advantageous, vulnerable parasites need to oscillate between high and zero abundance, a scenario most likely with a short period of vulnerability. The brevity of the life-stage vulnerable to immunity may help determine whether synchronous parasites perform better in spite of increased competition for host resources.
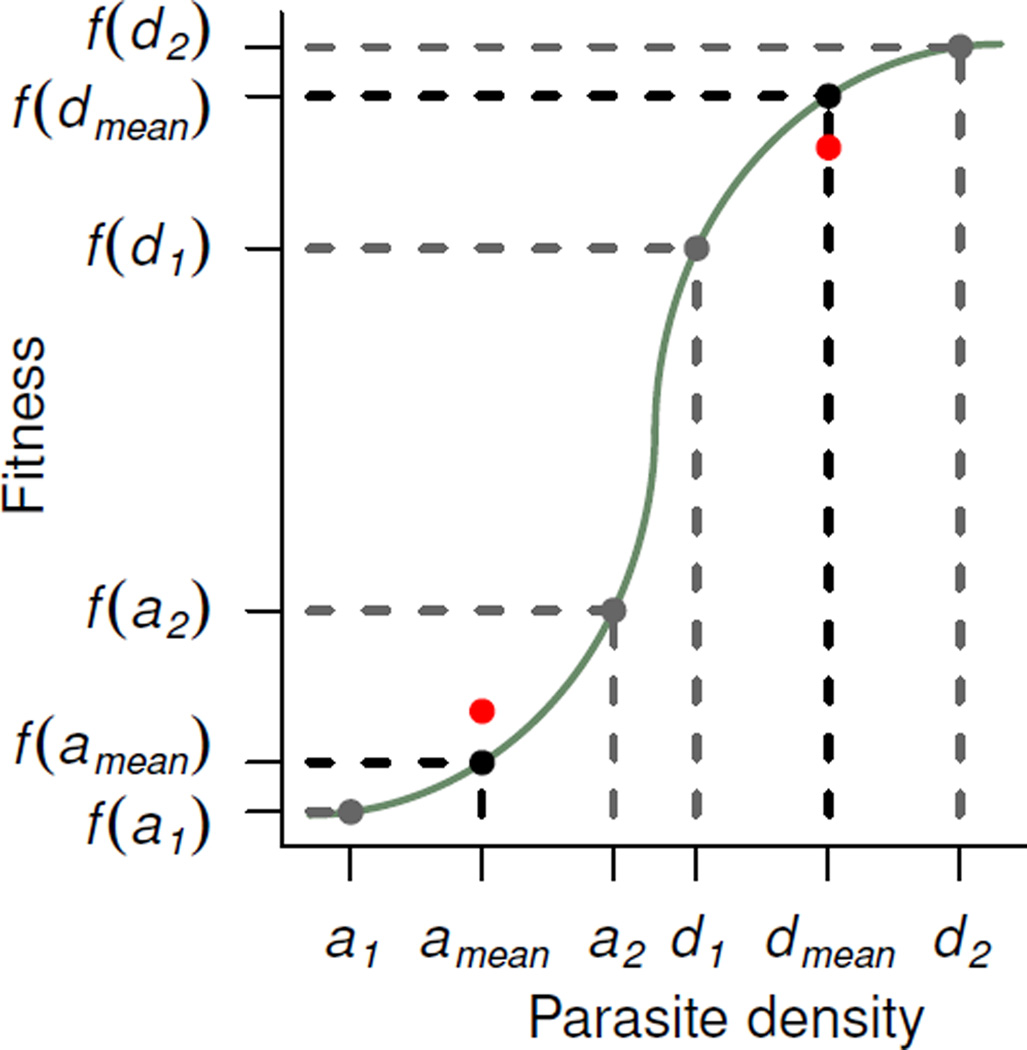
Figure 1.
When fitness is a convex function of density (e.g., the a values in the accelerating part of the curve), oscillations in density can increase mean fitness as a consequence of Jensen’s inequality (reviewed in Ruel and Ayres 1999). A strain that alternates between densities a1 and a2 has higher mean fitness (red point) than a strain that maintains a constant density amean (black point). If fitness is a concave or decelerating function of density (d values), oscillations in numbers decrease mean fitness compared to a strain that maintains a constant density (red versus black point). Cumulative fitness is altered in an identical manner.
Distinct from the success of blood-stage infection, synchrony may improve transmission by allowing the parasites to overcome Allee effects—where fitness declines as a result of dwindling numbers (Courchamp et al. 2008)—that would jeopardize the success of the small numbers of gametocytes present in a mosquito bloodmeal. Sexual organisms may experience sharp increases in fitness as population sizes increase and mates become easier to find (Courchamp et al. 2008). Consequently, malaria transmission is a sigmoidal function of gametocyte density, with the probability of mosquito infection first accelerating as gametocytes increase and then saturating with large numbers of gametocytes (Paul et al. 2007, Huijben et al. 2010, Bell et al. 2012). In the accelerating part of the transmission curve when gametocyte numbers are low, oscillations may improve mean fitness (through Jensen’s inequality, fig. 1). In contrast, fluctuating densities may become a liability in the saturating part of the curve where gametocytes are abundant (fig. 1).
Here we develop a within-host model to estimate the probability of transmission from synchronous versus asynchronous malaria infections while accounting for the possibility of competition for red blood cells and saturating immunity. Treating the intra-erythrocytic part of the life cycle as a fixed delay, the model predicts that synchronous parasites have higher fitness when gametocyte investment is low, both in single and coinfections. Competition for red blood cells may subtly favor synchronous parasites in single infections by damping extreme changes in parasite density, but in coinfections, competition strongly disfavors synchronous strains. Saturating immunity favors synchrony, but only if the target is a brief life stage. These model results lay out a framework for explaining the varied patterns of synchronization observed in natural infections.
Methods
Delayed differential model
We model infection using a system of delayed differential equations, parameterized for the rodent malaria Plasmodium chabaudi. The model framework assumes that a fixed period of time is required for parasite development within red blood cells. Any infected red blood cells that persist through the delay will burst to release the parasite stages capable of invading new red blood cells (merozoites) or will develop into mature transmission stages (gametocytes). This time delay before bursting is essential for capturing synchronous infection dynamics (Hoshen et al. 2000). The delayed system also solves many of the problems associated with continuous time malaria models (reviewed in Crooks 2008), namely the implicit assumption that merozoite release and gametocyte production can occur at any time, even if a red blood cell was only just infected. With a conventional compartmental model, infected cells would burst at a fixed rate (i.e., exponentially-distributed developmental periods). In our model, we assume that the developmental period is fixed (i.e., Dirac-Delta distributed), with all surviving infected cells bursting exactly one day postinfection. We address the implications of assuming a fixed delay in the discussion.
Single infections
The model tracks five life stages critical to the dynamics of malaria infection: uninfected red blood cells (R), infected red blood cells, either committed to the asexual life cycle and bound to produce more merozoites (I) or committed to the sexual life cycle and destined to produce transmissible gametocytes (IG), merozoites (M), and gametocytes (G). The dynamics of uninfected red blood cells are governed by the influx of new red blood cells via erythropoiesis and the outflux of red blood cells due to intrinsic mortality (μ) or infection (p(t)):
| (1) |
where Kstart = λR*/(λ − μR*) so that in the absence of infection red blood cells remain at a homeostatic equilibrium (R*). The rate of erythropoiesis following malaria infection in mice has been approximated as a linear function of red blood cell numbers, with erythropoiesis responding to the loss of red blood cells after a time lag of one or three days, depending on the immune status of the mice (Metcalf et al. 2011). A time lag in the erythropoietic response might select for parasites with a corresponding life cycle length, but it need not alter the fitness of synchronous versus asynchronous parasites. We therefore keep erythropoiesis as a linear function of red blood cell numbers and omit the time lag for simplicity. Red blood cells are infected by merozoites at a rate of p(t). Invasion success declines in an approximately hyperbolic fashion as the ratio of merozoites to red blood cells increases, according to in vitro assays of P. falciparum (Reilly et al. 2007, Boyle et al. 2010), although the biological mechanisms underlying this pattern have not yet been worked out. We introduce the q parameter to specify the degree of merozoite interference:
| (2) |
When q = 0, p(t) reduces to the maximum invasion rate, pmax, and for q > 0, the invasion rate declines hyperbolically as the ratio of merozoites to red blood cells increases. We hence refer to this form of intereference as ”hyperbolic”. We also examine dynamics with an alternate invasion rate, z(t), analogous to functional forms used to describe parasitoid inteference (Hassell 2000):
| (3) |
Unless otherwise specified, we assumed hyperbolic merozoite inteference (Eqn. 2). Whenever red blood cells become infected, a small fraction c are assumed to be committed to the sexual cycle, while the rest continue to propagate blood-stage infection through the production of merozoites:
| (4) |
Infected red blood cells are lost to intrinsic mortality (assumed to be equal to mortality rate of uninfected red blood cells, μ) and to immune clearance, with a proportion S surviving the length of the erythrocytic cycle (α) to burst and release merozoites. Immune clearance is assumed to be a saturating function of infected red blood cell density (type II functional response in ecological terminology, Metcalf et al. 2011), with a per capita clearance of . The proportion, S, of infected red blood cells that survive background mortality and immune clearance to produce merozoites is found by integrating the mortality rates over the developmental period, α.
| (5) |
Each infected red blood cell that survives for α days bursts to release β merozoites:
| (6) |
Merozoites can infect red blood cells at the time-varying rate, p(t), but are subject to intense background mortality (μZ).
We also consider the case where merozoites are the sole target of saturating immunity, to determine how abbreviating the vulnerable life stage can affect the benefit of synchrony. If saturating immunity targets merozoites instead of infected red blood cells, Eqns. 4–6 become:
| (7) |
| (8) |
| (9) |
No complicated survival functions are needed for merozoites (Eq. 9), because their waiting times are assumed to be exponentially distributed (i.e., having fixed hazard rates). To generalize the results from this modified model, we also consider the case where immunity targets a brief portion of the intra-erythrocytic cycle (details of age-structured model in appendix A.1). The rate of immune removal competes with the rate of background mortality, so immunity was set to be stronger when acting against a brief portion of the life cycle. To simplify our model, we omit adaptive immunity, which is not likely to alter dynamics until later in the infection (Metcalf et al. 2011).
For infected red blood cells committed to making gametocytes, the dynamics are similar to Eq. 4 save that there is a longer delay, αG, before an infected red blood cell can develop into a gametocyte (Gautret et al. 1996).
| (10) |
We simulate a range of c values suggested by studies of P. chabaudi infections (0.1% to 5%, Pollitt et al. 2011). We assume that the innate immune response ignores parasites developing into gametocytes (IG) because immune measures most effective against sexual blood stages have so far been reported as antibody-dependent rather than innate (reviewed in Bousema and Drakeley 2011, Riley and Stewart 2013). Given the low proportion of parasites developing into gametocytes, innate immune measures that act against sexual and asexual blood stages are unlikely to qualitatively alter the benefits of synchrony. At peak infection immune measures are already saturated, and this peak generates the bulk of gametocytes.
The proportion surviving to become gametocytes, SG, is
| (11) |
Unlike the asexual cycle, where one infected cell becomes several merozoites (according to the burst size, β), each infected cell committed to the sexual cycle develops into a single gametocyte.
| (12) |
Gametocytes are assumed to have an average lifespan of 1/μG. Gametocytes are maximally infectious for six hours (Gautret et al. 1996), so the infective lifespan of a P. chabaudi gametocyte is shorter than the length of the asexual life cycle (24 hours, Landau and Boulard 1978). We also extend gametocyte lifespan, a scenario more relevant to P. falciparum infections, where it is longer than the length of the asexual life cycle (reviewed in Bousema and Drakeley 2011).
The probability of transmission to the mosquito is assumed to be a sigmoidal function of gametocyte density, as has been shown for both P. falciparum (Huijben et al. 2010) and P. chabaudi (Bell et al. 2012). We sum transmission probability over the first 20 days of infection, which encompasses the first and largest peak in parasite numbers, as our fitness measure. We use a sigmoidal curve parameterized for drug-sensitive P. chabaudi infections (Bell et al. 2012) to calculate the cumulative the probability of transmission for synchronous versus asynchronous strains.
| (13) |
Due to the extreme stiffness of this delayed system, the interpolating algorithm occasionally returned abundances slightly below zero (most negative result on the order of −10−19). Since negative values cannot be evaluated by Eqn. 13, we set gametocyte abundance to zero whenever it became negative. We also calculate the cumulative probability of transmission using two other sigmoidal curves representing the extreme curves reported in the literature (fig. A1, equations and parameter values from Huijben et al. 2010, Bell et al. 2012). Parameter values are shown in Table 1, and all simulations were run in R version 2.15.2 (The R Project for Statistical Computing, http://www.r-project.org/), using the PBSddesolve package.
Table 1.
Parameter values, units, and sources
| Parameter | Value | Source |
|---|---|---|
| R* (red blood cell count at homeostasis) | 8.5 × 106 cells/μL | Savill et al. 2009 |
| λ (maximum new red blood cells) | 3.7 × 105 RBCs/μL/day | Savill et al. 2009 |
| μ (red blood cell mortality rate) | 0.025/day | Miller et al. 2010 |
| p (max. per merozoite invasion rate) | 4 × 10−6/day | Mideo et al. 2008* |
| α (blood-stage delay) | 1 day | Landau and Boulard 1978 |
| αG (gametocyte delay) | 2 days | Gautret et al. 1996 |
| β (burst size) | 10 merozoites | Mideo et al. 2008* |
| μZ (merozoite mortality rate) | 48/day | used in Hetzel and Anderson 1996, Mideo et al. 2008 |
| μG (gametocyte mortality rate) | 4/day | Gautret et al. 1996† |
within realistic range
length of most infectious stage
Initial conditions
Infection is initialized with infected red blood cells to mimic the parasites being released from the liver over a short or long time period, initiating a synchronous or asynchronous infection respectively. Simulated synchronous versus asynchronous infections differ only in the age structure of the initial inoculum, specified by a beta distribution. The initially infected red blood cells (I0) are all committed to producing merozoites. For t ≤ α, Eqns 4, 5, & 6 are
| (14) |
| (15) |
| (16) |
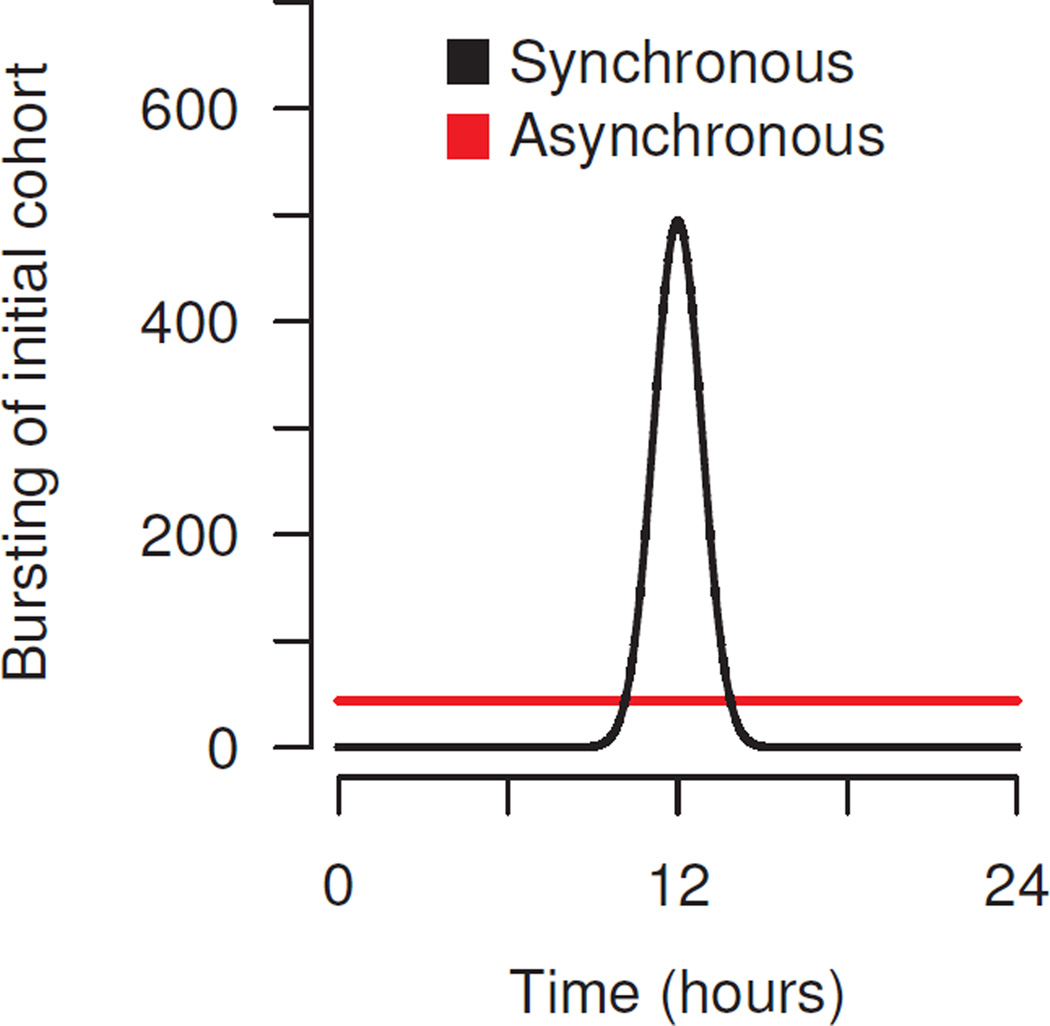
The beta distribution takes two shape parameters, both of which are set equal to sP. With sP = 1, the starting population bursts uniformly over the first delay, while sP = 100 yields a narrow bell curve centered around 0.5 (fig. 2). The underlying assumption is that the degree of synchronization is determined by the genetics (or epigenetics) of the parasite strain at the start of infection.
Figure 2.
Synchronous versus asynchronous infections are initialized using a beta distribution with large or small shape parameter, sP, to specify the bursting of the initial inoculum (synchronous in black, sP = 100; and asynchronous in red sP = 1).
Coinfection model
Synchronous infections of humans seem to be more highly related than asynchronous infections, which tend to show more diversity (Touré-Ndouo et al. 2009). The advantages of synchrony may then depend on the presence of a competing strain. We therefore expand the single strain model into a coinfection model (details in appendix A.2). In short, two strains are assumed to be released from the liver on the same day, with the two strains differing only in the degree of synchronization. The invasion rate per merozoite declines based on the ratio of total merozoites to uninfected red blood cells, with both strains equally sensitive to competition for resources. The immune response is assumed to be non-specific, dependent on the total density of vulnerable parasites as has been suggested by data from human infections (Bruce et al. 2000a). Since we are modeling early infection, we again neglect adaptive immunity.
Results
Low gametocyte investment favors synchrony
In the absence of immunity or interference competition among merozoites, simulated infections peak near day 10 (fig. 3), with subsequent damped oscillations towards an equilibrium. Infections peak due to resource limitation: parasite numbers begin to drop when there are more merozoites than uninfected red blood cells to infect. In this simulation, immunity and merozoites interference are set to zero, resulting in greater numbers of infected than uninfected red blood cells at peak infection. In addition to the multi-day oscillations, synchronous strains showed pronounced daily oscillations in abundance due to the 24 hour cycle length of the parasite P. chabaudi (Landau and Boulard 1978).
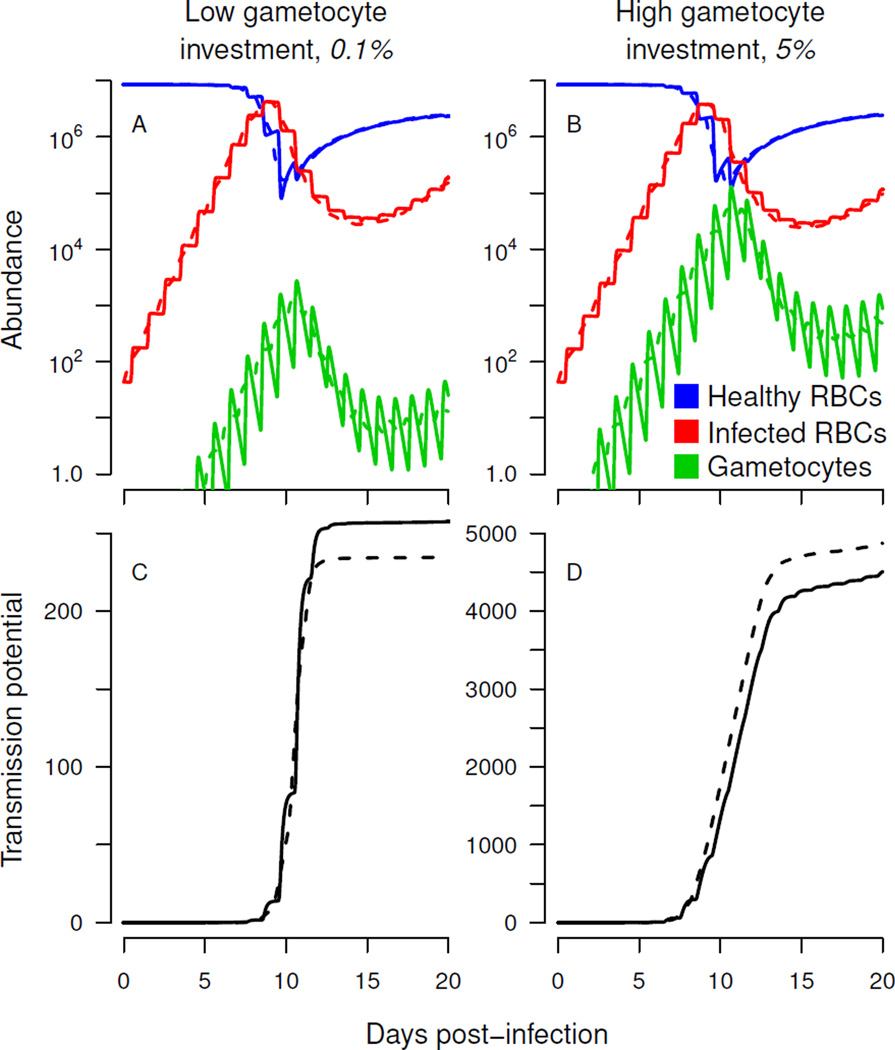
Figure 3.
Synchronous infections transmit better at low gametocyte investment—without any qualitative change in dynamics—due to the sigmoidal shape of the relationship between gametocyte numbers and probability of transmission. Single-strain infections were simulated in the absence of merozoite interference (q = 0) and immune clearance (a = 0), with solid curves indicating synchronous infections and dashed lines referring to asynchronous dynamics. Abundance of uninfected and infected red blood cells (RBCs) in the asexual cycle are shown with gametocyte (transmission stage) numbers (A & B, logarithmic scale), with total transmission potential—the cumulative transmission probability—shown below (C & D). Simulations in panels A & C assume low gametocyte investment (c = 0.001), while panels B & D show dynamics with relatively high gametocyte investment (c = 0.05).
With low gametocyte investment, synchronous strains have higher fitness (i.e., greater cumulative transmission potential). As a smaller proportion of infected cells are committed to the sexual part of the life cycle, gametocyte abundance decreases, but dynamics are qualitatively similar (fig. 3A & B). The critical difference is that the probability of transmission is an accelerating function of gametocyte density at low gametocyte investment, so that oscillations in gametocyte density increase fitness (fig. 3C). At high gametocyte investment, transmission probability saturates (at day 10 in fig. 3D) and oscillations reduce the transmission potential. From fig. 1, it can be seen that when numbers fluctuate in the accelerating part of the curve, mean and cumulative fitness are increased compared to when numbers hold steady. Fluctuations in the saturating part of the curve reduce fitness—the parasite strain would have done better to maintain steady numbers.
Interference among merozoites can benefit synchronous parasites
Interference competition increases uninfected red blood cell density and reduces gametocyte abundance by limiting merozoite invasion success (fig. 4). In the absence of interference competition, gametocyte numbers are predicted to rise to a high peak due to efficient depletion of uninfected red blood cells (fig. 4A, B, blue curves). Once red blood cells become limiting, there is a precipitous drop in gametocyte numbers. When merozoites interfere with each other, red blood cells cannot be depleted to the same degree (fig. 4A), resulting in a lower peak gametocyte density and subsequent shallower trough especially for synchronous infections (fig. 4B, orange curves). For certain parameter values, synchronous infections can catch up and sometimes even exceed the transmission potential of asynchronous infections (fig. 4C).
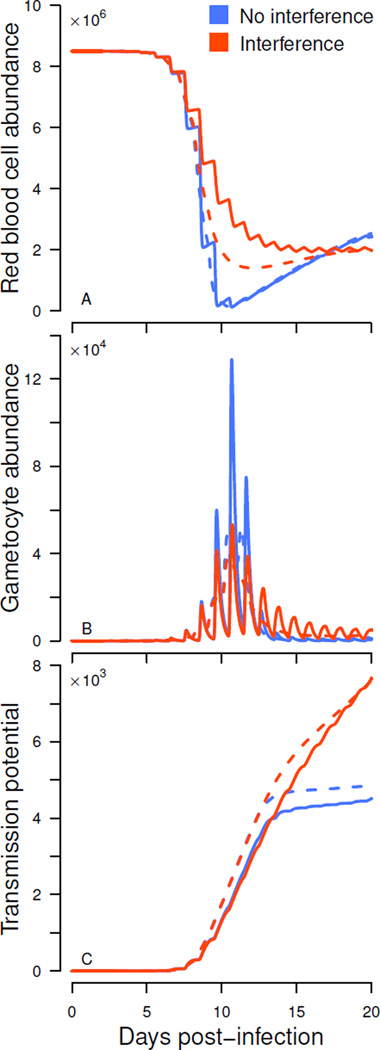
Figure 4.
Merozoite interference reduces anemia (A) and gametocyte abundance (B), but increases transmission potential (cumulative probability of transmission, C). Synchronized and asynchronous dynamics (solid and dashed lines, respectively) when merozoite interference is present (orange curve, q = 10) or absent (blue curve, q = 0). Gametocyte investment is set relatively high (c = 0.05) and immunity is absent (a = 0). The blue curves are identical to the red blood cell and gametocyte abundance shown in Fig. 3B, save that here they are plotted on a conventional rather than logarithmic scale.
Though asynchronous infections have superior gametocyte production in the face of interference, greater gametocyte production does not always result in greater transmission because of the sigmoidal relationship between gametocyte density and probability of infecting a mosquito. Despite large differences in peak gametocyte density, the corresponding probabilities of transmission saturate to similar values (fig. 4C). In the absence of interference competition, the synchronous strain exhibits lower cumulative transmission potential than the asynchronous infection (high transmission investment, fig. 4C). Merozoite interference gives the synchronous strain a larger pool of un- infected red blood cells post-peak, allowing gains in gametocyte production and increasing transmission potential above that of the asynchronous infection (fig. 4C).
Synchronous strains can transmit better from single infections
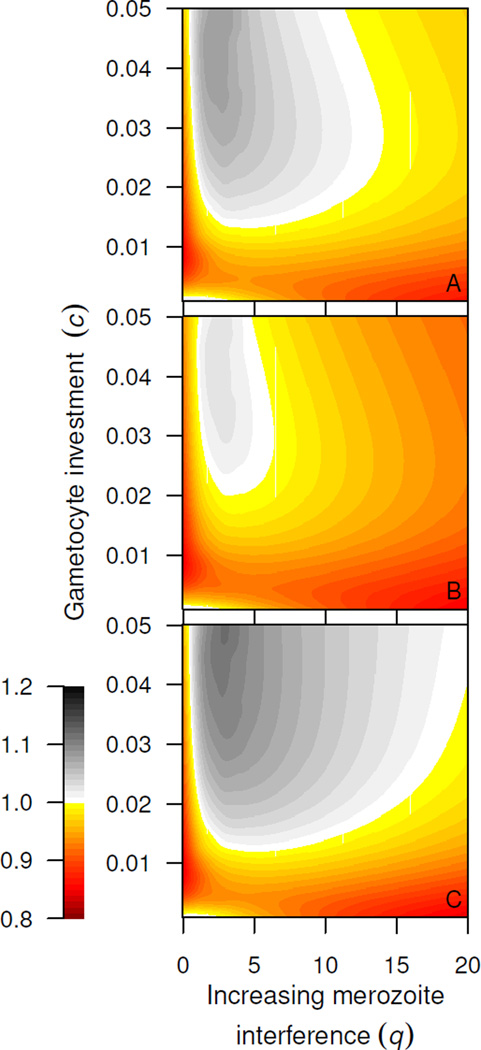
We simulate single infections as a function of interference among merozoites and gametocyte investment for three different immunity scenarios: (1) no immune response; (2) saturating immunity targeting infected red blood cells in the asexual cycle; (3) saturating immunity targeting merozoites. In simulations without immunity, synchrony is only advantageous with minimal merozoite interference and low gametocyte investment, and at intermediate levels of merozoite interference with greater investment in gametocytes (fig. 5A). When immunity removes infected red blood cells, it reduces the region of the parameter space where synchronous strains have a relative fitness advantage (fig. 5B versus A). When immunity targets merozoites, synchronous strains transmit better over a wide range of parameter values because of efficient saturation of the immune response (fig. 5C). The parameter space favorable to synchronous strains is similarly increased when immunity targets only a brief part of the intra-erythrocytic cycle (fig. A2). In both cases, synchrony is advantageous because the vulnerable life-stage is either present in overwhelming numbers or absent altogether.
Figure 5.
Synchronous parasites frequently transmit better from single infections. Smoothed relative fitness (ratio of cumulative probability transmission for synchronous:asynchronous strain) with increasing competition among merozoites (x axis) and investment in producing transmission stages (y axis). Synchronous infections transmit better in the white/gray areas. Immunity is set to zero (A, a = 0), to target infected red blood cells (B, a = 150, b = 100) or to remove merozoites (C, a = 7200, b = 100). Immunity targeting short-lived merozoites increases the parameter space favorable to synchronous infections.
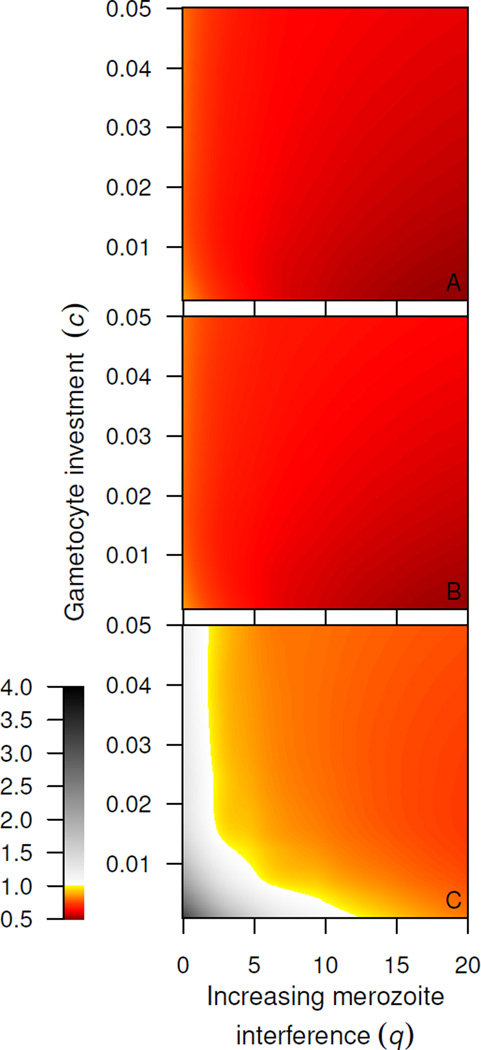
Synchronous strains perform poorly in coinfections
When immunity is absent or when immunity acts on infected red blood cells, asynchronous strains out-transmit synchronous strains in the same host for all parameter values simulated (fig. 6A & B). The success of asynchronous strains suggests that interference competition among merozoites is much more devastating to synchronous strains in coinfections. Synchronous strains do not deplete red blood cells as efficiently in single infections (fig. 4), and in coinfections, synchronous parasites face more severe resource limitation as asynchronous strains efficiently remove uninfected red blood cells. For these substantial costs, synchronous strains are only predicted to out-transmit their asynchronous counterparts when immunity targets the short-lived merozoite stage (fig. 6C).
Figure 6.
Coinfections. Smoothed relative fitness of synchronous:asynchronous strain, with increasing levels of merozoite competition and gametocyte investment. As in fig. 5, values greater than 1 (white areas) indicate superior transmission of the synchronous strain. Immunity is absent (A, a = 0), immunity acts on the total number of red blood cells infected by asexual parasites of both strains (B, a = 150, b = 100) or on merozoites of both strains (C, a = 7200, b = 100). Again, synchronous strains perform better when immunity targets short-lived parasite stage.
Sensitivity to model assumptions
Choice of transmission function
We find that the benefits of synchrony vary with the transmission function used to calculate relative fitness, but two generalities emerge: (1) synchronous strains have higher relative fitness over a greater portion of the parameter space when immunity targets a short-lived life stage (figs. 5C, A3C, A4C); (2) the relative fitness of synchronous strains can be broadly understood in terms of Jensen’s inequality (fig. 1). The three different transmission curves vary in the exact location of their inflection points—that is, the point where the curve switches from accelerating to saturating (fig. A1). The inflection point for the P. falciparum curve occurs at a lower gametocyte abundance than the drug-sensitive P. chabaudi curve; thus there is a smaller range of gametocyte numbers where transmission is an accelerating function, and the region of the parameter space where synchronous strains transmit better is accordingly reduced (compare fig. A4A to fig. 5A). The drug-resistant P. chabaudi transmission curve is always saturating; thus the transmission of synchronous infections suffers and is relatively insensitive to changes in gametocyte investment (compare fig. A3A to fig. 5A).
Functional form of merozoite interference
We also examine infection dynamics for parasitoid-like merozoite interference (Eqn. 3). We observe damped oscillations in parasite abundance— qualitatively similar to early infections of rodents, e.g.,Metcalf et al. (2011)—for only a small range of m values (approx. 0 ≤ m ≤ 0.35). Larger m values cause infection to saturate at an equilibrium with minimal oscillations. For m = 0.05, peak infection is substantially delayed (fig. A5A, B) and transmission potential is reduced for synchronous and asynchronous strains (fig. A5C). In contrast, hyperbolic interference (Eqn. 2) yields damped oscillations for a much wider range of q values with only minimal shifts in the timing of peak infection (fig. 4). This form of competition increases transmission potential even while depressing gametocyte abundance (figs. 4B and C). Using parasitoid-like merozoite interference therefore dramatically alters the relative fitness landscape (fig. A5), but there are still portions of the parameter space where synchronous strains have greater relative fitness because of merozoite inteference (fig. A6). As with hyperbolic interference (fig. 4), parasitoid-like interference can preferentially increase the transmission potential of synchronous infections. Gametocyte production is reduced by interference (fig. A6B), so the improved transmission potential results from alterations to the timing of gametocyte production.
Impact of gametocyte lifespan
Synchrony was initially viewed as an adaptation to ensure that short-lived gametocytes would be present in the blood when mosquitoes were feeding (Hawking et al. 1968). However P. falciparum gametocytes are infectious for about a week in culture (Lensen et al. 1999) and circulate for days in hosts (reviewed in Bousema and Drakeley 2011). Thus the parasites’ asexual cycle need not be precisely timed to ensure that infectious gametocytes are present when mosquitoes are feeding (e.g., Bray et al. 1976). Although we do not assume any particular vector feeding behavior, lengthening the infectious period of gametocytes could still change the advantages of synchrony by damping the otherwise sharp oscillations in gametocyte density. We therefore simulate infections relaxing the assumption that gametocytes have a short infectious lifespan. When gametocytes’ infectious lifespan is extended from a mean of six hours to approximately 20 hours, the net effect is to substantially increase the parameter space where synchrony is advantageous (fig. A7). Individual simulations at high gametocyte investment (5%) and no merozoite interference show that lengthening gametocyte longevity has two effects: damping the extreme daily oscillations of synchronous strains and increasing gametocyte abundance (fig. A8A). Longer gametocyte lifespan can improve the mean transmission probability of synchronous strains by damping otherwise costly oscillations in gametocyte density late in infection (as in fig. A8B, 20 hour lifespan). When gametocyte lifespan is increased to 36 hours (longer than the length of the asexual cycle), mean transmission probability is similar between synchronous and asynchronous infections (fig. A8B).
Discussion
Synchronized reproduction increases the cost of competition for resources among offspring while simultaneously easing the burden of natural enemies and mate-finding. The optimal degree of synchronization strikes a balance between these constraints; thus synchrony may shift from beneficial to costly with changes in ecology. We apply these principles to malaria parasites to predict the fitness consequences of synchronization across different within-host environments. Modeling the malaria life cycle using our delayed differential equation framework, we find that synchronized infection cycles may help malaria parasites (1) transmit efficiently by ensuring successful mate-finding in the mosquito midgut; (2) overwhelm host defenses; and (3) avoid over-exploiting host resources. Notably, these properties are sometimes but not always advantageous. The first two situations are analogous to the evolution of synchronized reproduction in plants, which is most likely for wind-pollinated species—that is, species at low risk of overwhelming their means of dispersing sexual stages—and for species contending with predators capable of being satiated (Kelly and Sork 2002). The current modeling framework builds on previous theory for malaria dynamics (e.g., Kwiatkowski and Nowak 1991, Hoshen et al. 2000) to provide a more comprehensive explanation of diverse temporal behavior.
Model assumptions
Malaria life history is enormously complicated, and we make simplifying assumptions—most notably a fixed life cycle length—to illustrate the key fitness consequences of synchrony. The fixed delay framework allows us to compare transmission from synchronous versus asynchronous infections by varying only the initial age-structure of the parasites. Synchrony breaks down if the simulation is run long enough due to the variability in life cycle length added by modest differences in how long merozoites take to invade red blood cells, but this minimal variability allows strongly synchronized dynamics to be maintained over the 20 days simulated so that we can compare the costs and benefits of synchrony early in infection. Whether a fixed life cycle length is a good approximation of within-host dynamics remains an open question. There is some evidence for within-strain variation in the life cycle length in vitro in that some strains maintain synchrony much more readily than others (Reilly et al. 2007), but that variability could be lost as host circadian rhythms constrict the timing of parasite development. Detailed data on the loss of synchrony in in vivo infections may justify the use of distributed delay models (e.g., Lloyd 2001) that can account for within-strain variability in life cycle length and explore how selection may act on that variability.
Synchrony as an adaptation to improve transmission
Past theory suggested that synchrony should carry a transmission advantage by ensuring that gametocytes will be mature when mosquito vectors are most active (Hawking et al. 1968, Hawking 1970). Synchrony has since been discounted as an adaptation to improve transmission by this mechanism, because daily peaks in gametocyte density and infectivity do not align with peak mosquito activity times (Bray et al. 1976, Githeko et al. 1993, Magesa et al. 2000). It has also been argued that since P. falciparum gametocytes maintain their infectiousness for weeks (Smalley and Sinden 1977), there is no need to produce gametocytes on a circadian schedule (Bray et al. 1976). With such a long lifespan, mature gametocytes will be present when mosquitoes are biting, regardless of what time of day red blood cells are infected.
Independent of any circadian rhythm in mosquito feeding behavior, Jensen’s inequality suggests that oscillations in gametocyte numbers will improve transmission, even if the period of those oscillations is several days. Our model shows a 24-hour periodicity in transmissibility due to the length of the blood-stage life cycle in P. chabaudi, but the periodicity need not be on that time scale for other malaria species. Since P. falciparum has an asexual life cycle lasting approximately 48 hours (Garnham 1966), any periodicity in transmission should be on that time scale (Gautret 2001). Two-day oscillations could still substantially improve transmission over the long infectious periods sustained by human malaria parasites, where strains can persist for weeks in coinfections (Daubersies et al. 1996) or hundreds of days in single infections (Miller et al. 1994). Any periodicity in transmission success would be most easily detected where infectivity is an accelerating function of gametocyte density, such that small changes in gametocyte numbers translate into large changes in infectivity to mosquitoes.
Human infections often contain extremely small numbers of gametocytes (reviewed in Bousema and Drakeley 2011), suggesting that synchronized dynamics could frequently enhance transmission. Minimal investment in gametocytes may be selected for if large numbers of gametocytes increase mosquito mortality or trigger transmission-blocking immunity (Taylor and Read 1997). Low transmission investment may also be favored when strains find themselves in competition with other strains, as has been predicted by theory (McKenzie and Bossert 1998, Mideo and Day 2008) and shown for rodent malaria infections (Pollitt et al. 2011). Modest gametocyte investment may often be selected for, and synchronous dynamics along with it.
Even at low gametocyte densities, periodic changes in infectivity may begin to disappear if gametocytes persist for a long time. Discrete oscillations in gametocyte numbers would then blur together as the infection progressed, making it difficult to tell synchronous from asynchronous gametocyte dynamics. Nevertheless, synchronized fluctuations could still benefit strains early in infection, and, incidentally, that is when gametocyte populations are small and finding mates in the mosquito midgut presents the greatest challenge. Synchrony may become costly later on, when gametocyte populations have grown large enough to render periodic fluctuations costly (fig. 1), but simulations suggest that long gametocyte persistence may help by smoothing away the oscillations later in infection (fig. A7). Further, any transmission benefits garnered by synchronous strains early on could be amplified by superior survival against saturating immune measures, which should be most severe for the small parasite numbers present early in infection (Metcalf et al. 2011). Whether synchrony can be maintained through chronic infection—and whether the fitness advantages carry over—will depend on the functional form and target of immune clearance.
Merozoite interference and virulence
Synchronized dynamics have the potential to improve transmission, but may also limit the exploitation of host resources and hence the virulence of infection. Theory has suggested that synchronous infections should cause less severe anemia than asynchronous infections as periodic spikes above the host’s detection threshold trigger a more effective immune response (McQueen and McKenzie 2008). Our model also shows that synchronous infections result in less severe anemia, but without making any assumptions about the immune response. The reduced anemia of synchronous infections emerges as a consequence of interference among merozoites as they compete for red blood cells. Consistent with this idea, synchronous infections are frequently encounted in asymptomatic children (Färnert et al. 1997, Bruce et al. 2000b) and less frequently encountered in symptomatic or fatal cases (Touré-Ndouo et al. 2009 and Dobaño et al. 2007, respectively). Among symptomatic individuals, there are some indications that asynchronous infections are associated with more severe symptoms (Touré-Ndouo et al. 2009), a trend that warrants further examination. While a correlation is all that can be assessed from human infections, rodent malaria systems could be used to test whether synchronous growth limits virulence by synchronizing parasites in the initial inoculum as has been done in previous experiments (Deharo et al. 1994, Deharo et al. 1996).
Asynchronous parasites are less susceptible to interference among merozoites, simply by virtue of their dynamics, and can exploit red blood cell populations to a greater degree. More intense host exploitation leads to a sharper drop-off in parasite numbers that synchronous parasites are able to avoid. Synchrony may then represent a prudent or risk-averse way of utilizing host resources. Surprisingly, we find that interference among merozoites can improve transmission potential, but that result depends critically on the functional form of competition, and further in vitro work is needed to elucidate the underlying biology. Our model suggests that any benefits of interference competition for synchronous parasites disappear in the presence of an asynchronous competitor. As the asynchronous strain severely depletes the red blood cell population, the synchronous strain bears the cost of overexploitation without receiving any of the benefits. In more diverse infections, there is a greater chance that a synchronized strain would suffer from competition with a less synchronized strain. Correspondingly, asynchronous infections of humans are likely to be more diverse than synchronous ones (Touré-Ndouo et al. 2009). If synchronization is fixed, the model simulations suggest that synchronous parasites would often be outcompeted when coinfection is frequent. If synchrony is instead a facultative response, selection should tend to favor parasites that de-synchronize in response to competitors. However, both reproductive restraint and relatedness could mitigate the predicted costs of synchrony in coinfections. Selection may act to reduce gametocyte investment when parasites have to compete with other strains (Pollitt et al. 2011), driving dynamics into a parameter space favorable to synchrony. Though multiple strain infections are extremely common, recent data from P. falciparum-infected patients shows much higher relatedness than expected (Nkhoma et al. 2012), meaning that synchronous parasites might often share their hosts with parasites that exhibit similar temporal dynamics.
Synchrony as a means of overwhelming natural enemies
Even in the absence of benefits to transmission and host exploitation, theory suggests that synchrony may arise due to the nature of host defenses (Kwiatkowski and Nowak 1991). Theory so far has focused on synchronous infections faced with host defenses that intensify with density (such as fever), but our model shows that saturating immunity could selectively benefit synchronous parasites in the same way that predator satiation favors synchronized reproduction in free-living organisms (Ims 1990, Williams et al. 1993, Kelly and Sork 2002). It has been speculated that synchronization might allow merozoites to overwhelm immune measures (Hoshen et al. 2000), and we use simulations to expand on that idea. The model suggests that saturating immunity should benefit synchronous strains only when the target of defenses is a transient stage, for example either short-lived merozoites or late-stage schizonts. Thus immunity against brief portions of the parasite life cycle could select for synchronous strains. Recent experiments show that components of the human immune system may behave in a way that should maximize the benefit of synchrony: P. falciparum merozoites are cleared by γδ T cells—while intracellular life-stages are relatively protected—and merozoite clearance declines with increasing numbers of parasites per γδ T cells (Costa et al. 2011). Malaria parasites may therefore have a lengthy, relatively protected life stage followed by a transient, vulnerable stage, analogous to the life cycle of the periodical cicadas. In this way, synchrony may be a strategy to overwhelm natural enemies.
Synchrony and drug treatment
Plasmodium falciparum infections exhibit both synchronous and asynchronous dynamics (e.g., Färnert et al. 1997, Simpson et al. 2002), and these diverse temporal dynamics may correspond to critically different patterns of drug susceptibility. A variety of anti-malarials, including the front-line drug artemisinin, disrupt particular portions of the life cycle, while leaving other stages relatively unscathed (e.g., ter Kuile et al. 1993). With a short half-life (reviewed in Meshnick et al. 1996), artemisinin will be largely metabolized by the time drug-insensitive life stages have matured into drug-sensitive ones, making it fundamentally different from other drugs in its ability to select for particular temporal dynamics in malaria parasites. If artemisinin were administered at the wrong time, a synchronous infection might not be cleared effectively, hence the advocacy for monitoring the synchronization of infections and treating accordingly (chronotherapy, Landau et al. 1991, White et al. 1992, ter Kuile et al. 1993). If the timing of drug administration varies greatly from person to person and clinic to clinic, asynchronous parasites may fare better on average, since there are likely to be life stages able to survive drugs no matter what time of day the anti-malarial is administered. Asynchronous growth could therefore function as a form of non-classical resistance. Predicting the evolutionary consequences of intervention requires putting the synchronization and timing of the malaria life cycle into the context of host and parasite fitness (outlined in Mideo et al. 2013). Efforts to disrupt disease transmission may incidentally shift the balance to favor or disfavor synchrony, with the potential to select for within-host dynamics inherently more devastating to human health.
Broader implications
Using a set of models, we have studied the costs and benefits of synchrony in the within-host dynamics of malaria. Our conclusions are broadly similar to those used to explain synchrony in free-living organisms (e.g., Kelly and Sork 2002, Rees et al. 2002): synchrony is favored when competition is limited, when mate-finding is difficult at low abundance, and when top-down controls can be saturated. However, we show that the fitness associated with synchrony versus asynchrony is a surprisingly complex function of the dynamics within the vertebrate host as well as nonlinearities in vector transmission. Relatively small changes in interference competition among asexual stages, frequency of coinfections and allocation to sexual versus asexual reproduction can shift a synchronous parasites from having a robust fitness advantage to a severe disadvantage. The interplay between these density-dependent relationships could explain the range of synchronization patterns observed both within and among malaria species. The case study of malaria further suggests that the transmission biology of the system could generate strong selection for or against synchrony, with synchrony unlikely to evolve where parasites are close to saturating their means of transmission. For instance, if lengthy blood meals allow efficient transmission of small numbers of parasites to vectors, then we might expect the probability of transmission to rapidly saturate with increasing parasite abundance, favoring asynchronous dynamics. The question remains whether similar factors can shed light on the enormous variation in developmental synchrony across diverse parasites.
Supplementary Material
Acknowledgements
The authors wish to thank L. Beck-Johnson and W.A. Nelson for their assistance with delay-differential equation techniques, S. Huijben for helpful discussion, and N. Mideo and F. Ellis McKenzie for invaluable comments on earlier drafts of this manuscript. We also thank members of the Research and Policy in Infectious Disease Dynamics Program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, National Institutes of Health, for stimulating discussion. This study was funded by the National Institute of General Medical Sciences, NIH grants R01GM089932 (AFR) and the Bill and Melinda Gates Foundation (ONB). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Fogarty International Center, the National Institute of General Medical Sciences, the National Institutes of Health, or the Gates Foundation.
References
- Antia R, Koella JC. A model of non-specific immunity. Journal of Theoretical Biology. 1994;168:141–150. doi: 10.1006/jtbi.1994.1094. [DOI] [PubMed] [Google Scholar]
- Bell AS, Huijben S, Paaijmans KP, Sim DG, Chan BHK, Nelson WA, Read AF. Enhanced transmission of drug-resistant parasites to mosquitoes following drug treatment in rodent malaria. PLoS ONE. 2012;7:e37172. doi: 10.1371/journal.pone.0037172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bousema T, Drakeley C. Epidemiology and infectivity of Plasmodium falciparum and Plasmodium vivax gametocytes in relation to malaria control and elimination. Clinical Microbiology Reviews. 2011;24:377–410. doi: 10.1128/CMR.00051-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle MJ, Wilson DW, Richards JS, Riglar DT, Tetteh KKA, Conway DJ, Ralph SA, Baum J, Beeson JG. Isolation of viable Plasmodium falciparum merozoites to define erythrocyte invasion events and advance vaccine and drug development. Proceedings of the National Academy of Sciences of the USA. 2010;107:14378. doi: 10.1073/pnas.1009198107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray RS, McCrae AWR, Smalley ME. Lack of a circadian rhythm in the ability of the gametocytes of Plasmodium falciparum to infect Anopheles gambiae. International Journal for Parasitology. 1976;6:399–401. doi: 10.1016/0020-7519(76)90025-4. [DOI] [PubMed] [Google Scholar]
- Bruce MC, Donnelly CA, Alpers MP, Galinski MR, Barnwell JW, Walliker D, Day KP. Cross-species interactions between malaria parasites in humans. Science. 2000a;287:845–848. doi: 10.1126/science.287.5454.845. [DOI] [PubMed] [Google Scholar]
- Bruce MC, Donnelly CA, Packer M, Lagog M, Gibson N, Narara A, Walliker D, Alpers MP, Day KP. Age- and species-specific duration of infection in asymptomatic malaria infections in Papua New Guinea. Parasitology. 2000b;121:247–256. doi: 10.1017/s0031182099006344. [DOI] [PubMed] [Google Scholar]
- Costa G, Loizon S, Guenot M, Mocan I, Halary F, de Saint-Basile G, Pitard V, Déchanet-Merville J, Moreau J-F, Troye-Blomberg M, Mercereau-Puijalon O, Behr C. Control of Plasmodium falciparum erythrocytic cycle: gd T cells target the red blood cell-invasive merozoites. Blood. 2011;118:6952–6962. doi: 10.1182/blood-2011-08-376111. [DOI] [PubMed] [Google Scholar]
- Courchamp F, Berec L, Gascoigne J. Allee Effects in Ecology and Conservation. 1st ed. New York: Oxford University Press, Inc; 2008. Reproductive mechanisms. Chap. 2, pages 20–34. [Google Scholar]
- Crooks L. Problems with continuous-time malaria models in describing gametocytogenesis. Parasitology. 2008;135:881–896. doi: 10.1017/S0031182008004502. [DOI] [PubMed] [Google Scholar]
- Daubersies P, Sallenave-Sales S, Magne S, Trape J-F, Contamin H, Fandeur T, Rogier C, Mercereau-Puijalon O, Druilhe P. Rapid turnover of Plasmodium falciparum populations in asymptomatic individuals living in a high transmission area. American Journal of Tropical Medicine and Hygiene. 1996;54:18–26. doi: 10.4269/ajtmh.1996.54.18. [DOI] [PubMed] [Google Scholar]
- Deharo E, Coquelin F, Chabaud AG, Landau I. The erythrocytic schizogony of two synchronized strains of Plasmodium berghei NK65 and ANKA, in normocytes and reticulocytes. Parasitology Research. 1996;82:178–182. doi: 10.1007/s004360050091. [DOI] [PubMed] [Google Scholar]
- Deharo E, Gautret P, Ginsburg H, Chabaud AG, Landau I. Synchronization of Plasmodium yoelii nigeriensis and P. y. killicki infection in the mouse by means of Percollglucose gradient stage fractionation: determination of the duration of the schizogonic cycle. Parasitology Research. 1994;80:159–164. doi: 10.1007/BF00933785. [DOI] [PubMed] [Google Scholar]
- Delves M, Plouffe D, Scheurer C, Meister S, Wittlin S, Winzeler EA, Sinden RE, Leroy D. The activities of current antimalarial drugs on the life cycle stages of Plasmodium : A comparative study with human and rodent parasites. PLoS Medicine. 2012;9:e1001169. doi: 10.1371/journal.pmed.1001169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhar R, Zhang K, Talwar GP, Garg S, Kumar N. Inhibition of the growth and development of asexual and sexual stages of drug-sensitive and resistant strains of the human malaria parasite Plasmodium falciparum by Neem ( Azadirachta indica ) fractions. Journal of Ethnopharmacology. 1998;61:31–39. doi: 10.1016/s0378-8741(98)00012-9. [DOI] [PubMed] [Google Scholar]
- Dobaño C, Rogerson SJ, Taylor TE, McBride JS, Molyneux ME. Expression of merozoite surface protein markers by Plasmodium falciparum -infected erythrocytes in peripheral blood and tissues of children with fatal malaria. Infection and Immunity. 2007;75:643–652. doi: 10.1128/IAI.01527-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drakeley C, Sutherland C, Bousema JT, Sauerwein RW, Targett GAT. The epidemiology of Plasmodium falciparum gametocytes: weapons of mass dispersion. Trends in Parasitology. 2006;22:424–430. doi: 10.1016/j.pt.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Färnert A, Snounou G, Rooth I, Bjorkman A. Daily dynamics of Plasmodium falciparum subpopulations in asymptomatic children in a holoendemic area. American Journal of Tropical Medicine and Hygiene. 1997;56:538–547. doi: 10.4269/ajtmh.1997.56.538. [DOI] [PubMed] [Google Scholar]
- Garnham PCC. Malaria Parasites And Other Haemosporidia. 1st ed. Oxford: Blackwell Scientific Publications; 1966. [Google Scholar]
- Gautret P. Plasmodium falciparum gametocyte periodicity. Acta Tropica. 2001;78:1–2. doi: 10.1016/s0001-706x(00)00174-1. [DOI] [PubMed] [Google Scholar]
- Gautret P, Miltgen F, Gantier JC, Chabaud AG, Landau I. Enhanced gametocyte formation by Plasmodium chabaudi in immature erythrocytes: pattern of production, sequestration, and infectivity to mosquitoes. Journal of Parasitology. 1996;82:900–906. [PubMed] [Google Scholar]
- Githeko AK, Brandling-Bennett AD, Beier M, Mbogo CM, Atieli FK, Owaga ML, Juma F, Collins FH. Confirmation that Plasmodium falciparum has aperiodic infectivity to Anopheles gambiae. Medical and Veterinary Entomology. 1993;7:373–376. doi: 10.1111/j.1365-2915.1993.tb00708.x. [DOI] [PubMed] [Google Scholar]
- Hassell MP. The Spatial and Temporal Dynamics of Host-Parasitoid Interactions. New York: Oxford University Press; 2000. [Google Scholar]
- Hawking F. The clock of the malaria parasite. Scientific American. 1970;222:123–131. doi: 10.1038/scientificamerican0670-123. [DOI] [PubMed] [Google Scholar]
- Hawking F, Worms MJ, Gammage K. 24- and 48-hour cycles of malaria parasites in the blood; their purpose, production and control. Transactions of the Royal Society of Tropical Medicine and Hygiene. 1968;62:731–760. doi: 10.1016/0035-9203(68)90001-1. [DOI] [PubMed] [Google Scholar]
- Haydon DT, Matthews L, Timms R, Colegrave N. Top-down or bottom-up regulation of intra-host blood-stage malaria: do malaria parasites most resemble the dynamics of prey or predator? Proceedings of the Royal Society B: Biological Sciences. 2003;270:289–298. doi: 10.1098/rspb.2002.2203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hetzel C, Anderson RM. The within-host cellular dynamics of bloodstage malaria: theoretical and experimental studies. Parasitology. 1996;113:25–38. doi: 10.1017/s0031182000066245. [DOI] [PubMed] [Google Scholar]
- Hoshen MB, Heinrich R, Stein WD, Ginsburg H. Mathematical modelling of the within-host dynamics of Plasmodium falciparum. Parasitology. 2000;121:227–235. doi: 10.1017/s0031182099006368. [DOI] [PubMed] [Google Scholar]
- Huijben S, Nelson WA, Wargo AR, Sim DG, Drew DR, Read AF. Chemotherapy, within-host ecology and the fitness of drug-resistant malaria parasites. Evolution. 2010;64:2952–2968. doi: 10.1111/j.1558-5646.2010.01068.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ims RA. The ecology and evolution of reproductive synchrony. Trends in Ecology & Evolution. 1990;5:135–140. doi: 10.1016/0169-5347(90)90218-3. [DOI] [PubMed] [Google Scholar]
- Janzen DH. Why bamboos wait so long to flower. Annual Review of Ecology and Systematics. 1976;7:347–391. [Google Scholar]
- Kelly D, Sork VL. Mast seeding in perennial plants: Why, how, where? Annual Review of Ecology and Systematics. 2002;33:427–447. [Google Scholar]
- Kwiatkowski D, Nowak M. Periodic and chaotic host-parasite interactions in human malaria. Proceedings of the National Academy of Sciences of the USA. 1991;88:5111–5113. doi: 10.1073/pnas.88.12.5111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau I, Boulard C. Life Cycles and Morphology. Chap. 2, pages 53–84. In: Killick-Kendrick R, Peters W, editors. Rodent Malaria. New York: Academic Press Inc.; 1978. [Google Scholar]
- Landau I, Chabaud A, Cambie G, Ginsburg H. Chronotherapy of malaria: an approach to malaria chemotherapy. Parasitology Today. 1991;7:350–352. doi: 10.1016/0169-4758(91)90218-d. [DOI] [PubMed] [Google Scholar]
- Lensen A, Bril A, van de Vegte M, van Gemert GJ, Eling W, Sauerwein R. Plasmodium falciparum : infectivity of cultured, synchronized gametocytes to mosquitoes. Experimental Parasitology. 1999;91:101–103. doi: 10.1006/expr.1998.4354. [DOI] [PubMed] [Google Scholar]
- Lloyd AL. Realistic distributions of infectious periods in epidemic models: changing patterns of persistence and dynamics. Theoretical Population Biology. 2001;60:59–71. doi: 10.1006/tpbi.2001.1525. [DOI] [PubMed] [Google Scholar]
- Magesa SM, Mdira YK, Akida JA, Bygbjerg IC, Jakobsen PH. Observations on the periodicity of Plasmodium falciparum gametocytes in natural human infections. Acta Tropica. 2000;76:239–246. doi: 10.1016/s0001-706x(00)00110-8. [DOI] [PubMed] [Google Scholar]
- McKenzie FE, Bossert WH. The optimal production of gametocytes by Plasmodium falciparum. Journal of Theoretical Biology. 1998;193:419–428. doi: 10.1006/jtbi.1998.0710. [DOI] [PubMed] [Google Scholar]
- McMorran BJ, Marshall VM, de Graaf C, Drysdale KE, Shabbar M, Smyth GK, Corbin JE, Alexander WS, Foote SJ. Platelets kill intraerythrocytic malarial parasites and mediate survival to infection. Science. 2009;323:797–800. doi: 10.1126/science.1166296. [DOI] [PubMed] [Google Scholar]
- McQueen PG, McKenzie FE. Host control of malaria infections: constraints on immune and erythropoeitic response kinetics. PLoS Computational Biology. 2008;4:e1000149. doi: 10.1371/journal.pcbi.1000149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meshnick SR, Taylor TE, Kamchonwongpaisan S. Artemisinin and the antimalarial endoperoxides: from herbal remedy to targeted chemotherapy. Microbiological Reviews. 1996;60:301–315. doi: 10.1128/mr.60.2.301-315.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metcalf CJE, Graham AL, Huijben S, Barclay VC, Long GH, Grenfell BT, Read AF, Bjørnstad ON. Partitioning regulatory mechanisms of within-host malaria dynamics using the effective propagation number. Science. 2011;333:984–988. doi: 10.1126/science.1204588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mideo N, Barclay VC, Chan BHK, Savill NJ, Read AF, Day T. Understanding and predicting strain-specific patterns of pathogenesis in the rodent malaria Plasmodium chabaudi. American Naturalist. 2008;172:214–238. doi: 10.1086/591684. [DOI] [PubMed] [Google Scholar]
- Mideo N, Day T. On the evolution of reproductive restraint in malaria. Proceedings of The Royal Society B: Biological Sciences. 2008;275:1217–1224. doi: 10.1098/rspb.2007.1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mideo N, Reece SE, Smith AL, Metcalf CJE. The Cinderella Syndrome: Why do malaria-infected cells burst at midnight? Trends in Parasitology. 2013;29:10–16. doi: 10.1016/j.pt.2012.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LH, Good MF, Milon G. Malaria pathogenesis. Science. 1994;264:1878–1883. doi: 10.1126/science.8009217. [DOI] [PubMed] [Google Scholar]
- Miller MR, R°aberg L, Read AF, Savill NJ. Quantitative analysis of immune response and erythropoiesis during rodent malarial infection. PLoS Computational Biology. 2010;6:e1000946. doi: 10.1371/journal.pcbi.1000946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nkhoma SC, Nair S, Cheeseman IH, Rohr-Allegrini C, Singlam S, Nosten F, Anderson TJC. Close kinship within multiple-genotype malaria parasite infections. Proceedings of The Royal Society B: Biological Sciences. 2012;279:2589–2598. doi: 10.1098/rspb.2012.0113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul REL, Bonnet S, Boudin C, Tchuinkam T, Robert V. Aggregation in malaria parasites places limits on mosquito infection rates. Infection, Genetics and Evolution. 2007;7:577–586. doi: 10.1016/j.meegid.2007.04.004. [DOI] [PubMed] [Google Scholar]
- Pollitt LC, Mideo N, Drew DR, Schneider P, Colegrave N, Reece SE. Competition and the evolution of reproductive restraint in malaria parasites. American Naturalist. 2011;177:358–367. doi: 10.1086/658175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reece SE, Duncan AB, West SA, Read AF. Sex ratios in the rodent malaria parasite, Plasmodium chabaudi. Parasitology. 2003;127:419–425. doi: 10.1017/s0031182003004013. [DOI] [PubMed] [Google Scholar]
- Rees M, Kelly D, Bjø rnstad ON. Snow tussocks, chaos, and the evolution of mast seeding. American Naturalist. 2002;160:44–59. doi: 10.1086/340603. [DOI] [PubMed] [Google Scholar]
- Reilly HB, Wang H, Steuter JA, Marx AM, Ferdig MT. Quantitative dissection of clone-specific growth rates in cultured malaria parasites. International Journal for Parasitology. 2007;37:1599–1607. doi: 10.1016/j.ijpara.2007.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley EM, Stewart VA. Immune mechanisms in malaria: new insights in vaccine development. Nature medicine. 2013;19:168–178. doi: 10.1038/nm.3083. [DOI] [PubMed] [Google Scholar]
- Rouzine IM, McKenzie FE. Link between immune response and parasite synchronization in malaria. Proceedings of the National Academy of Sciences of the USA. 2003;100:3473–3478. doi: 10.1073/pnas.262796299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruel JJ, Ayres MP. Jensen’s inequality predicts effects of environmental variation. Trends in Ecology & Evolution. 1999;14:361–366. doi: 10.1016/s0169-5347(99)01664-x. [DOI] [PubMed] [Google Scholar]
- Savill NJ, Chadwick W, Reece SE. Quantitative analysis of mechanisms that govern red blood cell age structure and dynamics during anaemia. PLoS Computational Biology. 2009;5:e1000416. doi: 10.1371/journal.pcbi.1000416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson JA, Aarons L, Collins WE, Jeffery GM, White NJ. Population dynamics of untreated Plasmodium falciparum malaria within the adult human host during the expansion phase of the infection. Parasitology. 2002;124:247–263. doi: 10.1017/s0031182001001202. [DOI] [PubMed] [Google Scholar]
- Slater AFG, Cerami A. Inhibition by chloroquine of a novel haem polymerase enzyme activity in malaria trophozoites. Nature. 1992;355:167–169. doi: 10.1038/355167a0. [DOI] [PubMed] [Google Scholar]
- Smalley ME, Sinden RE. Plasmodium falciparum gametocytes: their longevity and infectivity. Parasitology. 1977;74:1–8. doi: 10.1017/s0031182000047478. [DOI] [PubMed] [Google Scholar]
- Taylor LH, Read AF. Why so few transmission stages? Reproductive restraint by malaria parasites. Parasitology Today. 1997;13:135–140. doi: 10.1016/s0169-4758(97)89810-9. [DOI] [PubMed] [Google Scholar]
- ter Kuile F, White NJ, Holloway P, Pasvol G, Krishna S. Plasmodium falciparum: in vitro studies of the pharmacodynamic properties of drugs used for the treatment of severe malaria. Experimental Parasitology. 1993;76:85–95. doi: 10.1006/expr.1993.1010. [DOI] [PubMed] [Google Scholar]
- Touré-Ndouo FS, Zang-Edou ES, Bisvigou U, Mezui-Me-Ndong J. Relationship between in vivo synchronicity of Plasmodium falciparum and allelic diversity. Parasitology International. 2009;58:390–393. doi: 10.1016/j.parint.2009.07.011. [DOI] [PubMed] [Google Scholar]
- White NJ, Chapman D, Watt G. The effects of multiplication and synchronicity on the vascular distribution of parasites in falciparum malaria. Transactions of the Royal Society of Tropical Medicine and Hygiene. 1992;86:590–597. doi: 10.1016/0035-9203(92)90141-x. [DOI] [PubMed] [Google Scholar]
- Williams KS, Smith KG, Stephen FM. Emergence of 13-Yr periodical cicadas (Cicadidae: Magicicada ): phenology, mortality, and predators satiation. Ecology. 1993;74:1143–1152. [Google Scholar]
- Yayon A, Vande Waa JA, Yayon M, Geary TG, Jensen JB. Stage-dependent effects of chloroquine on Plasmodium falciparum in vitro. Journal of Protozoology. 1983;30:642–647. doi: 10.1111/j.1550-7408.1983.tb05336.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.