Extreme value analyses of VOC exposures and risks: A comparison of RIOPA and NHANES datasets

Abstract

Extreme value theory, which characterizes the behavior of tails of distributions, is potentially well-suited to model exposures and risks of pollutants. In this application, it emphasizes the highest exposures, particularly those that may be high enough to present acute or chronic health risks. The present study examines extreme value distributions of exposures and risks to volatile organic compounds (VOCs).

Exposures of 15 different VOCs were measured in the Relationship between Indoor, Outdoor and Personal Air (RIOPA) study, and ten of the same VOCs were measured in the nationally representative National Health and Nutrition Examination Survey (NHANES). Both studies used similar sampling methods and study periods. Using the highest 5 and 10% of measurements, generalized extreme value (GEV), Gumbel and lognormal distributions were fit to each VOC in these two large studies. Health risks were estimated for individual VOCs and three VOC mixtures. Simulated data that matched the three types of distributions were generated and compared to observations to evaluate goodness-of-fit. The tail behavior of exposures, which clearly neither fit normal nor lognormal distributions for most VOCs in RIOPA, was usually best fit by the 3-parameter GEV distribution, and often by the 2-parameter Gumbel distribution. In contrast, lognormal distributions significantly underestimated both the level and likelihood of extrema. Among the RIOPA VOCs, 1,4-dichlorobenzene (1,4-DCB) caused the greatest risks, e.g., for the top 10% extrema, all individuals had risk levels above 10⁻⁴, and 13% of them exceeded 10⁻². NHANES had considerably higher concentrations of all VOCs with two exceptions, methyl tertiary-butyl ether and 1,4-DCB. Differences between these studies can be explained by sampling design, staging, sample demographics, smoking and occupation.

This analysis shows that extreme value distributions can represent peak exposures of VOCs, which clearly are neither normally nor lognormally distributed. These exposures have the greatest health significance, and require accurate modeling.

1. Introduction

Exposure to volatile organic compounds (VOCs) can cause a wide range of adverse health effects, including irritation, asthma exacerbation, allergy and respiratory effects (Lippy and Turner, 1991; Mendell, 2007; Rumchev et al., 2007). Both acute or short-term exposures, which can result from activities such as smoking, cooking and gasoline pumping (US EPA, 2010), and chronic or long-term exposures, which can occur due to emissions from building materials (Brown, 2002), use of cleaners and air fresheners, vehicle emissions and other sources (US EPA, 2011a), are of concern. Most VOC exposures are dominated by indoor and occupational sources (OSHA, 2011; US EPA, 2011a), and exposures and risks can vary greatly among individuals. For indoor exposures, variability is dominated by house-to-house variability, as compared to seasonal, neighborhood or measurement variability (Jia et al., 2012). Similar heterogeneity is suggested by the few population-based studies that have examined personal exposures (Adgate et al., 2004; Rappaport and Kupper, 2004; Sexton et al., 2007). Although exposures of most VOCs for most persons fall below acute and chronic guidelines, a subset of individuals experience much higher exposures that can exceed risk-based guidelines. For example, in the nationally representative 1999–2000 National Health and Nutrition Examination Survey (NHANES), the estimated lifetime cancer risk exceeded 10⁻⁴ for 10% of adults due to benzene exposure, and 16% of adults exceeded the same risk level for chloroform (Jia et al., 2008).

The significance of acute exposures is evaluated using the hazard quotient (HQ), defined as the ratio of the exposure concentration to an acute reference concentration (RfC) for the specific VOC. A HQ value below 1 indicates that adverse effects are not expected, while values over 1 suggest that such effects could, but not necessarily will, occur (US EPA, 2011b). Chronic non-cancer exposures are similarly evaluated, but long term exposure estimates and chronic RfC are used. Lifetime individual excess cancer risks are estimated by multiplying lifetime (e.g., 70 year) exposure concentrations by the unit risk factor (URF) specific to the VOC (US EPA, 2009). The calculated risk is compared to de minimis or acceptable values, which typically range from 10⁻⁶ to 10⁻⁴. Some VOCs are carcinogens and also have acute or chronic RfCs. These comparisons and calculations form the basis of quantitative risk assessments.

1.1. Extreme value theory and applications

While there are several definitions, extreme events can be defined as low probability and high consequence events (Lenox and Haimes, 1996). Extreme value theory (EVT) describes the probability and magnitude of such events. A variety of EVT models have been developed. These include the Gumbel extreme value distribution (Gumbel, 1958), the Fréchet distribution (Fisher and Tippett, 1928), and the Weibull distribution (Weibull, 1951; Ang and Tang, 1975). These three distributions, respectively called type I, II and III extreme value distributions, belong to the broad class of generalized extreme value (GEV) distributions, which use shape, location and scale parameters to fit the tails of a distribution (Jenkinson, 1955).

Classical extreme value analysis characterizes maxima (or minima) from large samples in which each value (of extrema) is considered to be independent. For a river’s flow rate, for example, maxima might be selected as the highest daily discharge rate in a year from decades of daily observations. If the sample size is small, in which case relatively few maxima can be obtained, then extrema can be selected as observations above specified cut-off (threshold) or percentile. This approach helps to balance the sample size needed to assure statistical validity with the goal of identifying “real” extreme values. In practice, the top 5–10% of observations are selected (Hüsler, 2009).

EVT has been applied in engineering and design analyses for highways, bridges, dams and nuclear power plants (McCormick, 1981), in finance (Embrechts et al., 1997), and elsewhere. Most environmental applications have dealt with hydrology, e.g., estimating the probability of floods and droughts (Katz et al., 2002; Engeland et al., 2004). Additional environmental applications include the likelihood of adverse meteorological conditions (Hüsler, 1983; Sneyer, 1983), exceedances of thresholds relevant to dietary intake of pesticides and heavy metals (Tressou et al., 2004; Paulo et al., 2006), concentrations of metals Mn and Pb in blood (Batterman et al., 2011), deposition of pollutants in surface soils (Huang and Batterman, 2003), and risks of leakage due to pipe corrosion (HSE, 2002). Air quality applications of EVT include the exceedance of air quality standards (Surman et al., 1987; Hopke and Paatero, 1994), exposure to ambient air pollutants (Kassomenos et al., 2010), indoor concentrations of radon (Tuia and Kanevski, 2008), and VOC exposures in the NHANES mentioned earlier (Jia et al., 2008).

Extrema can include observations that are considered to be outliers, which can be defined in a statistical sense as observations that are numerically distant from the rest of the data (Grubbs, 1969). In exposure and risk applications, while not representative of the population, such observations may represent those persons most at risk from exposure. However, these observations may also result from instrument error, coding error, contamination, or other errors. A number of techniques have been used to detect and minimize the influence of outliers, including the use of robust statistics, e.g., medians. Distributional assumptions used to help to account for skewed data, e.g., the widely used lognormal distribution (Rousseeuw and Hubert, 2011) can help to address the influence of outliers, at least to an extent.

The objective of the present study is to characterize extreme value distributions of exposures and risks found in two large studies examining personal exposures of VOCs. We first present descriptive statistics and predicted health risks for each VOC, and then select a subset of VOCs and outcomes for further analysis. These data are fit to GEV, Gumbel and lognormal distributions, and the likelihood of exposures above risk-based criteria is evaluated for individual VOCs as well as VOC mixtures. We evaluate the goodness of fit of these distributions to observations. We conclude by discussing the potential advantages and disadvantages of EV distributions in such applications.

2. Materials and methods

2.1. Data sources

The first dataset uses the Relationship between Indoor, Outdoor and Personal Air (RIOPA) study, which was designed to explore how outdoor and indoor sources contribute to personal exposures of air pollutants. It contrasted three cities (Elizabeth, NJ; Houston, TX; Los Angeles, CA) that were expected to have different contributions from mobile and industrial emissions (Weisel et al., 2005a). Approximately 100 non-smoking households and non-smoking adults and children living in households in each city were recruited and studied from summer 1999 to spring 2001. Each of the 239 adult subjects was sampled twice about three months apart. Outdoor, indoor and personal air samples were collected using 48-h sampling periods. VOCs were collected using passive samplers (OVM3500, 3M Company, St. Paul, MN, USA) and analyzed by gas chromatography–mass spectrometry for 18 compounds (benzene, toluene, ethylbenzene, m,p-xylene, o-xylene, methyl tertiary-butyl ether (MTBE), styrene, 1,4-dichlorobenzene (1-4 DCB), methylene chloride (MC), trichloroethylene (TCE), tetra-chloroethylene (PERC), chloroform, carbon tetrachloride (CTC), D-limonene, α-pinene, β-pinene, 1,3-butadiene and chloroprene). Data for 1,3-butadiene and chloroprene were not reported due to low recovery. We excluded the MC measurements due to measurement issues (inconsistent blank contributions) (Weisel et al., 2005a). Method detection limits (MDLs) ranged from 0.2 (ethylbenzene and PERC) to 7.1 (toluene) μg m⁻³, and detection frequencies for the personal measurements exceeded 50% (Weisel et al., 2005a). Further details of RIOPA and its design are provided elsewhere (Weisel et al., 2005b). The present study focuses on personal measurements, which should be the most representative of exposure. We selected adult subjects due to the larger sample size, namely, 544 measurements for 305 participants (299 and 245 measurements in first and second visits, respectively, of which 239 adults had valid samples in both visits). Child exposures were not used due to the smaller sample size and because several households included measurements from several children (only one adult was sampled in a household), which would cause a cluster effect.

A second dataset was compared to RIOPA. The 1999/2000 cohort of the National Health and Nutrition Examination Survey (NHANES) included personal VOC measurements for 851 participants (NCHS, 2011). NHANES used 48–72 h exposure periods and a stratified, multistage cluster design, and analyses must use weights to obtain representative national averages. The RIOPA and NHANES studies shared ten VOCs in common (benzene, toluene, ethylbenzene, m,p-xylene, o-xylene, MTBE, 1,4-DCB, TCE, PERC and chloroform). While the recruitment strategy and study purposes differed, NHANES and RIOPA used similar sampling methods and study periods. However, NHANES did not include repeated measurements. Thus, comparisons between NHANES and RIOPA used data from only the first RIOPA visit. Unfortunately, available functions and codes used to fit extreme value distributions and perform Kolmogorov–Smirnov (K–S) tests do not include sample weights. Thus, the NHANES sample weights were used to specify a repeat frequency for each observation, forming a much larger dataset (n = 14,320 to 14,524, depending on the VOC), which is needed since most methods used to analyze distributions (described below) do not account for sample weights. The many ties in the derived dataset, which could affect distribution fitting and p-values, were broken by adding a randomly generated normal quantity (±30% of the measurement) to each observation. Because the sample sizes of unweighted and weighted datasets were unbalanced, which may be an issue for distribution fitting, we also used a bootstrap analysis to repeatedly (300 times) generate samples of the same size as the original dataset (n = 635–648 depending on the VOC) by randomly drawing from the weighted dataset.

2.2. Risk evaluation

Screening-level estimates of acute and chronic risks were estimated using standard approaches. For cancer risks, the URFs for the ten VOCs were taken from the US EPA Integrated Risk Information System (IRIS; US EPA, 2011c), the Office of Environmental Health Hazard Assessment’s Air Toxics Hot Spots Program Risk Assessment Guidelines (OEHHA, 2005), or EPA’s Cumulative Exposure Project (Caldwell et al., 1998). Each URF and its basis are shown in Supplemental Table S1, along with the RfC and toxic endpoints. URFs are not available for toluene, m,p-xylene, o-xylene, D-limo-nene, α-pinene and β-pinene. The two seasonal measurements for each adult in RIOPA were averaged as an estimate of the long-term exposure concentration. The excess individual lifetime cancer risk for a specific VOC i was calculated as:

$$R_{\mathrm{i}}=C_{\mathrm{i}}{\text{URF}}_{\mathrm{i}}$$ (1)

where R_i = excess individual lifetime cancer risk (probability), C_i = concentration (μg m⁻³), and URF_i = unit risk factor (cancer cases per μg m⁻³).

Following guidance for mixtures (US EPA, 2000), risks were calculated by response addition for those VOCs that cause the same toxic effect on same target organ. In this case, results of eq. (1) were summed for each participant for the several chemicals in the mixture. Three mixtures were considered: VOCs associated with blood cancers (lymphomas and leukemia), which included benzene, MTBE, 1,4-DCB, TCE and PERC; VOCs associated with liver and renal tumors, which included ethylbenzene, MTBE, 1,4-DCB, TCE, PERC, chloroform and CTC; and total VOCs (TVOC) (Borgert et al., 2004; IARC, 2011). TVOC also serves as a general indicator of VOC exposure, and can be used to identify the dominant contributors to VOC risks.

Acute non-cancer risks were evaluated using HQ computed on a visit basis for available valid data. The RfC for acute effects was taken as the minimal risk level (MRL; Supplemental Table S1), as listed by the Agency for Toxic Substances and Disease Registry (ATSDR, 2011).

2.3. Statistical analyses

After replacing measurements below the MDL with one-half of this value, descriptive statistics were computed for each VOC for the long-term exposure estimates (averaged over the two visits) as well as on a visit basis (without averaging). We next identified outliers, which initially were defined as a value twice that of the next highest observation, and also influential observations, identified as observations which clearly altered statistical results. Observations identified as being both outliers and influential were excluded in subsequent analyses; these very few observations are noted. Two datasets of extrema for each VOC were defined using the percentile method and the top 5% and the top 10% of observed concentrations, which formed sample sizes of 12 and 24, respectively, for RIOPA, and 32 and 64 for NHANES. For mixtures, the cumulative risk was computed for each subject by summing the risks of components in the mixture, and extreme values of the cumulative risk were taken as the top 5% and top 10% of this sum over all persons.

GEV distributions were fit to each extrema dataset (5 and 10% cut-offs for both individual VOCs and VOC mixtures). The GEV probability density function is expressed as:

$$f_{\mathrm{\xi },\mathrm{\mu },\mathrm{\sigma }}(x)=\left(\left({(1+(\mathrm{\xi }(x-\mathrm{\mu })/\mathrm{\sigma }))}^{-1-1/\mathrm{\xi }}\right)/\mathrm{\sigma }\right)\times exp\left(-{(1+(\mathrm{\xi }(x-\mathrm{\mu })/\mathrm{\sigma }))}^{-1/\mathrm{\xi }}\right)\text{if}\mathrm{\xi }\ne 0$$ (2)

where ξ = shape parameter, μ = location parameter, σ = scale parameter, and x = data observation. If ξ > 0, the GEV distribution belongs to Fréchet family; if ξ < 0, the GEV distribution belongs to Weibull family (Jenkinson, 1955); and if ξ = 0, the GEV distribution belongs to the Gumbel family, which permits simplification of eq. (2):

$$f_{0,\mathrm{\mu },\mathrm{\sigma }}(x)=\left(\left(e^{-(x-\mathrm{\mu })/\mathrm{\sigma }}\right)/\mathrm{\sigma }\right)exp\left(-e^{-(x-\mathrm{\mu })/\mathrm{\sigma }}\right)$$ (3)

The three parameters of the GEV distribution were determined by maximum-likelihood estimation (MLE).

Goodness-of-fit (GOF) was examined using Anderson–Darling (A–D) tests with the null hypothesis that data subset comes from the GEV distribution. The A–D test, a modification of the K–S test, emphasizes tail behavior (Stephens, 1974), so it is the most appropriate for evaluating extreme value distributions. Empirical A–D test p-values were calculated for the repeated (bootstrap) samples in the NHANES weighted dataset. For Gumbel distributions, a probability plot was used as follows. First, extrema were ranked in descending order. Then, each observation was plotted against −ln[−ln(Pv)], where Pv was computed as:

$$\text{Pv}=(r-0.44)/(n+0.12)$$ (4)

where r = reverse rank of VOC concentrations, and n = sample size. This method allows GOF to be visualized as agreement to a regression line, and quantitative agreement is noted by the regression’s R² statistic (Barnett, 1975).

As noted earlier, lognormal distributions are commonly employed for exposure data. These distributions were fit to the full datasets by MLE, and the evaluation focused on extrema, again defined as the top 5% and top 10% of the full distribution.

For further evaluation, simulated extreme value datasets (n = 10,000) were generated for each VOC that followed the fitted GEV, Gumbel and lognormal distributions. Simulated datasets were generated for the GEV and Gumbel distributions that matched the top 5% and top 10% of observations. Simulated data (n = 10,000) were also generated for the lognormal distributions that matched the full distribution of observations. The simulated data, including the repeated bootstrap samples, were then compared to observations using K–S tests and graphical analyses, and p-values were estimated. Finally, in a risk assessment-oriented application, we compared the fraction of persons with cancer risks exceeding 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, and 10⁻² cut-offs for the three sets of distributions to observed fractions. These analyses were conducted for both individual VOCs and mixtures.

Statistical analyses used SAS version 9.2 (SAS Institute, Cary, North Carolina, USA). Distribution fitting, simulations of GEV, Gumbel and lognormal distribution used GEV, RGEV, GUM.FIT, RGUMBEL, FIT-DISTR and RLNORM in R version 2.13.1 (R Development Core Team, Vienna, Austria) and Excel (Microsoft, Redmond, WA).

3. Results and discussion

3.1. Descriptive analysis

Table 1 lists statistics for the average VOC exposures in RIOPA. The VOCs with the highest median concentrations were toluene (13 μg m⁻³), D-limonene (13 μg m⁻³) and MTBE (8.0 μg m⁻³). With the exception of CTC, distributions were highly skewed, e.g., upper percentile values typically were 10 or more times the median, and sometimes much more, e.g., the peak 1,4-DCB concentration was nearly 1000 times higher. VOC concentrations measured during the first and second visits were moderately correlated (Spearman rank correlation coefficients ranged from 0.15 (toluene) to 0.59 (PERC and α-pinene; Supplemental Table S2); CTC had notably low correlation (r = 0.11, p = 0.098)). This VOC is a long-lived and globally distributed pollutant which has been banned from most uses since 2002, and its concentration and exposure pattern differ from the other VOCs, most of which have strong and localized sources. Exposure measured in the first and second visits did not differ for most VOCs, based on both paired t tests using log-transformed data and Wilcoxon signed rank sum tests (Supplemental Table S2). The exceptions were benzene, ethyl-benzene, o-xylene, 1,4-DCB and chloroform.

Table 1.

Descriptive statistics of VOC exposures (μg m⁻³) for RIOPA and NHANES.

VOCs	Sample size			Mean			SD			50th			90th			95th			98th			Maximum
	N	RA	R1	N	RA	R1	N	RA	R1	N	RA	R1	N	RA	R1	N	RA	R1	N	RA	R1	N	RA	R1
Benzene	644	239	298	5.3	3.6	3.3	7	3.3	4.1	2.8	2.6	2.1	13.5	6.8	6.8	18.7	9.8	11.9	26.4	17.2	15.9	120	22.1	32.0
Toluene	635	239	298	36.4	18.3	18.8	107	20.9	31.1	17.4	13.2	12.5	59.8	31.7	32.1	98.3	45.8	49.9	237	84.8	125	1611	195	313
Ethylbenzene	639	239	299	8.4	2.9	2.7	41.3	4	5.7	2.6	1.8	1.6	14.2	5.2	4.9	25.2	7.6	7.1	69.4	17.3	15.6	837	33.1	64.6
m,p-Xylene	643	239	299	18.8	8.3	7.8	43.2	11.9	17.5	6.5	5	4.2	38.7	14.5	14.0	69.8	24.2	19.7	181	42.6	46.6	729	112	219
o-Xylene	643	239	299	6.5	2.9	2.8	14.5	4.3	6.6	2.4	1.8	1.7	14.1	5.1	4.6	26.4	9.3	6.4	50.1	13.6	21.0	202	44.7	79.6
MTBE	641	238	298	5.2	13.5	13.3	15.6	17.7	24.2	0.6	8.0	6.9	10.7	25.3	26.3	21.3	44.8	43.1	42.3	67.2	85.7	182	143	232
Styrene	NA	239	299	NA	1.6	1.7	NA	3.5	5.2	NA	0.7	0.4	NA	2.9	2.2	NA	6.4	6.1	NA	11.9	14.7	NA	30	59.5
1,4-DCB	641	239	299	27.3	57	61.0	121	202	241	1.7	2.2	2.0	34.8	82.6	84.5	143	329	305	291	865	1110	2236	1743	2153
TCE	641	237	299	3.4	0.7	1.9	22.7	2.1	13.6	0.3	0.2	0.2	1.2	1.1	1.4	7.4	2.3	3.2	23.6	8.0	15.8	327	20.5	200
PERC	639	238	298	5.2	2.2	2.2	31.2	4.4	6.5	0.7	1	0.9	6.6	4.1	3.8	18.5	8	6.4	40.1	16.5	13.6	659	41.1	80.2
Chloroform	648	239	298	2.7	2	2.3	4.5	2.7	4.2	1.1	1.3	1.1	5.9	4.2	4.7	12.1	6.4	7.0	17.2	10.8	14.1	53.9	23.4	46.5
CTC	NA	238	299	NA	0.7	0.9	NA	0.2	3.3	NA	0.6	0.6	NA	0.9	0.9	NA	1	1.1	NA	1.1	1.6	NA	1.9	42.3
D-Limonene	NA	238	298	NA	26.9	28.6	NA	34.4	102	NA	13.4	11.8	NA	69.1	60.7	NA	107	90.3	NA	145	136	NA	209	1690
α-Pinene	NA	239	299	NA	7.1	6.6	NA	13.3	9.7	NA	3.8	2.9	NA	15.3	16.1	NA	20.2	28.4	NA	33.6	39.3	NA	121	79.7
β-Pinene	NA	239	299	NA	5.6	5.0	NA	10.7	9.8	NA	2.3	1.3	NA	13.1	13.6	NA	20.8	21.5	NA	47.7	34.1	NA	83.6	92.3

N, observations in NHANES; R_A, average observations of first and second visits in RIOPA; R₁, observations in first visit in RIOPA; SD, standard deviation; NA, not available.

Previous analyses of the RIOPA VOC data have examined temporal patterns, indoor/outdoor relationships (Weisel, 2002), and effects of nearby emission sources (Kwon et al., 2006). For most VOCs, indoor and personal concentrations greatly exceeded outdoor levels (applying to means, medians, and extrema), and no obvious seasonal pattern was observed. Outdoor concentrations have been associated with meteorological factors (e.g., temperature, wind speed), and the inverse distance to emission sources (e.g., highways and gas stations for benzene, toluene, ethylbenzene, m,p-xylene, o-xylene (BTEX) and MTBE, and dry cleaners for PERC).

3.2. Comparison to NHANES

Comparisons of the ten VOCs measured in both NHANES and RIOPA studies show many differences (Table 1). Based on K–S tests, distributions differed significantly for all VOCs. For the BTEX compounds, NHANES had higher means, medians, upper percentile and maximum concentrations, and differences tended to increase at higher percentiles, e.g., the relative differences for the 50th and 95th percentile concentrations of ethylbenzene were 40% and 72%, respectively. For PERC and chloroform, NHANES also had higher means, top percentiles and maximum concentrations, although medians were slightly lower. TCE in NHANES also had higher means, median, upper percentiles (except for the 90th percentile) and maximums. Only MTBE and 1,4-DCB levels were generally lower in NHANES.

Several factors can explain the differences in VOC concentrations between the RIOPA and NHANES studies. First, NHANES used extensive staging, including two trips by participants, in most cases by private vehicle, to a centrally-located mobile examination center. These centers consisted of multiple trailers in a parking lot, which were used for surveys, blood collection, sampler deployment, and other purposes. In contrast, RIOPA used in-home measurements, and thus common staging and the associated trips were not required. Staging may have affected both the level and variability of NHANES data and caused other differences, e.g., we have noted discrepancies in some of the NHANES blood VOC data in earlier cohorts and the surprisingly low correlation between VOC levels in blood and personal air (Su et al., 2011).

Second, NHANES included smokers. In the VOC subset, 32% of participants were considered as active smokers due to blood cotinine levels above 10 ng mL⁻¹, and an additional 3% were exposed to environmental tobacco smoke as shown by cotinine levels between 2 and 10 ng mL⁻¹ (Supplemental Table S3). The prevalence of smoking increased for those participants with the highest BTEX and TCE exposures, e.g., smokers constituted 34–56% of persons for the top 5% and top 10% of VOC concentrations, respectively. Participants with cotinine levels above 2 ng mL⁻¹ had higher average, median and 95th percentile concentrations of BTEX compounds than participants with lower cotinine levels (Supplemental Table S4). In contrast, RIOPA recruited only non-smoking households. VOC emissions from smoking may explain the higher concentrations of BTEX and other some VOCs in NHANES.

The demographics of the study samples differed (Supplemental Table S3). NHANES participants were generally younger (81% were less than 50 years of age compared to 66% in RIOPA), and included more males (49% of the sample compared to 25% in RIOPA). These differences affect VOC concentrations as males had higher mean, median and 95th percentile concentrations of most VOCs in both RIOPA and NHANES (Supplemental Tables S4 and S5). Exceptions were 1,4-DCB in NHANES, as well as TCE and chloroform in RIOPA.

Although difficult to evaluate, the potential for occupational exposure also appeared to differ between the two studies (Supplemental Table S3). In NHANES, occupations dealing with services, precision production, craft and repair, operators, fabricators, and laborers, totaled 40% of the sample (Su et al., 2011); these occupations were judged to have potential for VOC exposure. Narrower job definitions were possible in RIOPA. Occupations with the potential for VOC exposure, identified if an individual’s work involves chemicals, had a prevalence of only 26% in RIOPA. Employment rates in the two studies also differed. In RIOPA, 53% of participants were unemployed (classified as full-time students, home makers, retired, or unable to work), compared to 23% in NHANES (not working or looking for work). Compared to unemployed persons, working individuals in RIOPA had higher average exposures of TCE and PERC, but lower exposures of benzene (Supplemental Table S5). In NHANES, employed persons had higher exposures of BTEX, TCE and PERC, but lower exposures of 1,4-DCB and chloroform (Supplemental Table S4).

The differences in study protocols, recruitment, demographics, smoking and occupation are quite substantial, and generally they imply that NHANES’ participants had a greater potential for VOC exposures than RIOPA’s. Interestingly, of the two VOCs that did not have higher levels in NHANES, 1,4-DCB is strongly associated with exposures in the home due to its use as a deodorant and repellant (moth balls and cakes) and is not associated with smoking or workplace exposure. The higher exposure of this VOC in RIOPA appears to reflect the sample demographics (e.g., many older woman) and behaviors (e.g., stayed at home). The reason for higher MTBE levels in RIOPA likely reflects geographic factors since this gasoline additive was not used in all states.

NHANES was designed as a nationally representative sample that reflected population heterogeneity. If this applies to VOCs and their extrema, then this study should better represent extreme value distributions than the RIOPA study. These differences, the exclusion of smokers, and the more limited stratified geographic sampling all suggest that RIOPA may not be representative of the US population. Again, the primary purpose of RIOPA was to contrast exposures in three cities. Analysis of the RIOPA data can provide insights regarding the nature of VOC exposure, including outliers, with the recognition that these results pertain to the study sample. RIOPA has several advantages in the present study, including its repeated measures, the lack of (potential) bias due to centralized staging, the exclusion of smokers, and the more refined descriptors available.

3.3. Outliers

The previous analyses omitted observations identified as influential outliers (at least twice as high as the next observation and not fitting extreme value distributions). For the averaged measurements in RIOPA, this included six outliers in five different households for five VOCs (ID = NJ090 with MTBE = 440 μg m⁻³; NJ063 with TCE = 102 μg m⁻³, TX050 with TCE = 97 μg m⁻³, NJ063 with PERC = 1340 μg m⁻³; NJ080 with CTC = 20 μg m⁻³; TX068 with D-limonene = 1462 μg m⁻³). The two TCE observations had similar concentrations, but both were four times higher than the next value. For the first visit measurements in RIOPA (for the comparison to NHANES), six influential outliers were identified (ID = CA079 with benzene = 85 μg m⁻³, toluene = 641 μg m⁻³, chloroform = 1224 μg m⁻³, and D-limonene = 5114 μg m⁻³; NJ063 with PERC = 2618 μg m⁻³; NJ090 with MTBE = 844 μg m⁻³). In NHANES, four observations were deleted (two cases, participant ID = 468 and 578, that had excessively long sampling periods, and two cases, participant ID = 3852 and 4076, with extremely high concentrations of benzene, xylenes or toluene), also described by Jia et al. (2008).

3.4. Predicted health risks

Estimates of individual excess lifetime cancer risks for the median, 90th and 95th percentile concentrations are shown in Table 2 (Additional statistics are shown in Supplemental Table S6). Using median concentrations, chloroform, 1,4-DCB and benzene presented the highest (and very similar) risks, 2.0 to 2.9 × 10⁻⁵, respectively; risks for other VOCs were below 10⁻⁵. For the 95th percentile concentrations, the same three VOCs also presented the highest risks, 1.5 × 10⁻⁴, 3.6 × 10⁻³ and 7.7 × 10⁻⁵, respectively; risks above 10⁻⁵ are also caused by ethylbenzene, MTBE, styrene, PERC and CTC. Among the RIOPA VOCs, 1,4-DCB presented the greatest risks, e.g., for the top 10% extrema, all individuals had risks exceeding 10⁻⁴, 88% exceeded 10⁻³, and 13% exceeded 10⁻², a high level. Additionally,1,4-DCB’s share of the total carcinogenic risk (the sum of risks across individual VOCs) increased greatly at higher percentiles, e.g., 1,4-DCB represented 17% of the total risk using median concentrations, 81% using 90th percentile concentrations, and 98% using 95th percentile concentrations. As discussed later, the dominance of 1,4-DCB is partly a function of the specific VOCs measured.

Table 2.

Predicted excess cancer risks for adult participants in RIOPA (n = 239).

VOCs	Unit risk (μg m−3)−1	Predicted excess cancer cases per million population
		50th	90th	95th
Benzene	7.8 × 10−6	20.4	53.0	76.6
Ethylbenzene	2.5 × 10−6	4.4	13.0	19.0
MTBE	2.6 × 10−7	2.1	6.6	11.6
Styrene	2.0 × 10−6	1.5	5.8	12.9
1,4-DCB	1.1 × 10−5	24.5	908.9	3620.7
TCE	2.0 × 10−6	0.4a	2.2	4.6
PERC	5.9 × 10−6	5.9	24.1	47.1
Chloroform	2.3 × 10−5	28.9	97.1	147.5
CTC	1.5 × 10−5	9.3	12.9	15.0
Immunotoxicant mixture	NA	76.4	965.4	3651.5
Liver and kidney toxicant mixture	NA	111.1	1102.2	3683.6
Total VOCs	NA	141.1	1125.0	3710.1

NA, not available.

Immunotoxicant mixture includes benzene, MTBE, 1,4-DCB, TCE and PERC; Liver and kidney toxicant mixture includes ethylbenzene, MTBE, 1,4-DCB, TCE, PERC, chloroform and CTC.

^aConcentrations were based on MDLs.

Predicted risks for the three VOC mixtures also are shown in Table 2 and Supplemental Table S6. For immunological toxicity, the median and 95th percentile risks were 7.6 × 10⁻⁵ and 3.7 × 10⁻³, respectively, most of which was due to benzene and 1,4-DCB among the five VOCs (benzene, MTBE, 1,4-DCB, TCE and PERC) in this mixture. For liver and renal toxicity, the median and 95th percentile risks were 1.1 × 10⁻⁴ and 3.7 × 10⁻³, respectively, mostly contributed by 1,4-DCB and chloroform among the seven VOCs (ethyl-benzene, MTBE, 1,4-DCB, TCE, PERC, chloroform and CTC) in this mixture.

The RIOPA VOCs show small risks of non-cancer acute health effects. The HQ for benzene exceeded 1, but for only 3 of 299 persons in the first visit, and for 1 of 245 persons in the second visit. The 90th and 95th percentile HQs for benzene were 0.2 and 0.4, respectively (Supplemental Table S7). The critical effects for the benzene RfC are immunological effects. Similarly, the NHANES data showed small risks of non-cancer acute effects, e.g., 8 of 644 participants had benzene concentrations above the acute RfC. For all other VOCs in RIOPA and NHANES, all measurements fell below RfC, suggesting that acute effects are unlikely.

These risks and hazard quotients represent preliminary screening-level predictions and have several limitations. They include only a subset of VOCs among those known or suspected to be toxicants, e.g., RIOPA did not include naphthalene, which is associated with anemia (ATSDR, 2005), or include reliable measurements of 1,3-butadiene, which is associated with blood and lymphatic system cancers (ATSDR, 2009). The two personal exposure measurements averaged together for each RIOPA participant may not be a robust measure of lifetime average exposure. The uncertainty in the RfC and URF is considerable, and the values used are believed to be conservative. Finally, the exposure measurements represent multiday averages; shorter term exposures (1–24 h) can be higher and could possibly exceed RfC or other guidance levels for acute effects.

3.5. Extreme value distributions for the RIOPA data

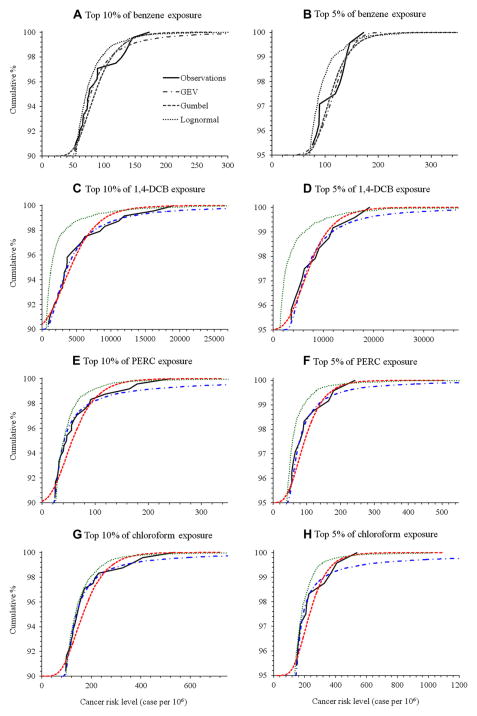
Table 3 shows parameters of GEV distributions fitted to the VOC data, and goodness-of-fit statistics. Fig. 1 shows cumulative distributions of cancer risks for four VOCs for simulated data matching GEV, Gumbel and lognormal distributions, as well as the observed data. Separate plots are shown for the top 5 and 10% extrema. The GEV distributions closely fitted both the top 5 and 10% of observations of all VOCs based on A–D tests (Table 3), and comparisons of simulated and observed distributions matched based on K–S tests, with the exception of the top 10% of β-pinene (Supplemental Table S8). With the exception of the top 5% of benzene concentrations, the shape parameters of the GEV distribution were close to or larger than 0, indicating Gumbel or Fréchet distributions, and the location and scale parameters reflected the high percentile concentrations shown earlier (Table 3). While the GEV distributions closely fitted the extrema, including both individual VOCs and the three VOC mixtures, simulations sometimes produced extremely high values that greatly overpredicted maxima, e.g., concentrations >20,000 μg m⁻³. This occurred for the top 10% of ethylbenzene, styrene, 1,4-DCB, TCE and PERC concentrations, and the top 5% of ethylbenzene, MTBE, styrene, 1,4-DCB, TCE and chloroform concentrations. These problems were limited to the extreme right-hand tails, e.g., values above the 98th or 99th percentile.

Table 3.

GEV parameters and goodness-of-fit (p-value) for average VOC exposures (μg m⁻³) in RIOPA.

VOCs	Top 10% (n = 24)				Top 5% (n = 12)
	Shape	Location	Scale	p-value	Shape	Location	Scale	p-value
Benzene	0.4	9.1	2.4	0.876	30.2	13.6	3.6	0.684
Toluene	1.6	35.8	7.3	0.672	0.6	63.6	19.2	0.829
Ethylbenzene	1.2	6.3	1.7	0.951	0.8	10.6	3.9	0.943
m,p-Xylene	0.8	19.9	6.6	0.963	1.2	28.7	6.9	0.905
o-Xylene	0.9	6.8	2.1	0.900	1.8	10.0	1.3	0.915
MTBE	0.6	36.3	12.5	0.988	0.9	53.0	11.4	0.958
Styrene	1.3	3.9	1.6	0.676	0.9	8.4	2.8	0.895
1,4-DCB	0.5	258.0	188.0	0.991	0.5	516.0	234.9	0.953
TCE	1.1	1.7	0.8	0.987	1.7	2.8	1.0	0.909
PERC	1.0	5.9	2.6	0.882	0.7	11.4	4.2	0.988
Chloroform	0.7	5.5	1.6	0.954	1.1	7.6	1.7	0.943
CTC	0.7	0.9	0.1	0.854	0.7	1.1	0.1	0.991
D-Limonene	0.6	85.8	20.0	0.725	0.4	124.8	19.7	0.890
α-Pinene	1.1	18.0	4.0	0.959	1.7	23.4	6.0	0.797
β-Pinene	0.9	18.2	6.5	0.897	0.1	35.2	13.8	0.905

p-values shown for Anderson–Darling tests.

p-value >0.05 indicating that observations fit to generalized extreme value distributions.

Fig. 1.

Comparison of cancer risks for top 10% and 5% of VOC exposure using observed measurements, generalized extreme value, Gumbel and lognormal simulations for the RIOPA data.

Gumbel distributions fitted several of the VOCs (e.g., top 5 and 10% of benzene, ethylbenzene, MTBE, styrene, 1,4-DCB, PERC and chloroform concentrations), based on K–S tests (Supplemental Table S8). However, the probability plots indicate that the top 10% of the data did not follow Gumbel distributions for several compounds, e.g., the fitted regression line for PERC and chloroform did not match the curvature of the data, and R² values were below 0.9 (Supplemental Table S9 and Fig. S1). For benzene, the two cutoffs gave similar results, e.g., the lines representing fitted Gumbel distributions overlap, suggesting that differences were not consequential. With the exceptions of benzene and D-limonene, the top 5% of observations provided a better fit to Gumbel distributions (e.g., R² > 0.90). Sometimes the lowest values (i.e., the left tail) were lower than observations, and some values even went negative (The plots in Fig. 1 are truncated and do not make this visible.)

Lognormal distributions fitted extrema for several VOCs (e.g., top 10% of benzene and ethylbenzene observations, the top 5 and 10% of MTBE, PERC and chloroform, and the top 5% of CTC, shown in Supplemental Table S8). However, these distributions typically diverged from observations, and the “fat” right-hand tails were greatly unrepresented (Fig. 1). We note that the lognormal distributions were fitted for the full dataset, not just the top 5 and 10% used for the GEV and Gumbel distributions.

The observed and predicted fraction of individuals with risks that exceed 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³ and 10⁻², risk cut-offs that might be considered “bright lines”, are examined in Supplemental Table S10. This analysis is performed for the top 5% and 10% of the data, and the three distributions. GEV and Gumbel predictions were very close to observed frequencies, and differences were usually within a few percent. As an example, for the top 10% of the benzene data, the observed, GEV, Gumbel and lognormal simulations showed risk levels exceeding 10⁻⁴ for 29%, 26%, 31% and 18% of the population, respectively. As a second example, using the top 5% of 1,4-DCB values, the corresponding frequencies were 25%, 27%, 24% and 10%. As noted earlier, GEV simulations sometimes overpredicted the very highest upper percentiles (seen at the 10⁻⁴ risk level for ethylbenzene, MTBE, styrene, TCE, PERC, chloroform and CTC), and such risks were not seen in the data. However, such cases were rare, comprising less than about 1% of the entire dataset. Gumbel distributions also overpredicted extrema (although maxima were lower), and also underpredicted lower risks, in part due to its unbounded nature that can generate small and negative values. For example, all (100%) observed individuals had risks exceeding 10⁻⁶ for MTBE, styrene, 1-4-DCB, TCE, PERC and CTC, but Gumbel predictions ranged from 77% (TCE) to 99% (MTBE). As noted above, lognormal predictions did not match observations, and the differences could be large, e.g., for the top 5% of PERC risks, 33% of the observations exceeded the 10⁻⁴ risk level, but the lognormal predictions showed percentages less than half of this level. Similar results were seen for benzene, styrene, TCE and other VOCs.

Overall, these evaluations show that GEV distributions provided a good fit to pollutant and risk extrema for the VOCs and VOC mixtures measured in RIOPA. Occasionally, GEV distributions overpredicted some concentrations and risks, but this was limited to the very highest values. The 3-parameter GEV distributions provided better fit than the 2-parameter Gumbel distribution. In contrast, lognormal distributions provided poor fits to extrema.

3.6. Extreme value distributions for NHANES data

In most cases, the top 5% and top 10% of the NHANES data did not match GEV distributions fitted to either the larger dataset, which used sample weights to specify repeat frequencies, or to the smaller (equal size) datasets that used bootstrap methods and repeated sampling (Supplemental Tables S11 and S12). Using the latter approach, for example, GEV distributions matched only the top 5% of 1,4-DCB and TCE (marginally significant) based on the A–D tests, but not the K–S test. Possibly the two approaches used to incorporate the sampling weights did not decrease the “staircase” nature of the weighted datasets, which caused these tests to reject the hypothesis that the original and fitted distributions did not differ. Another possible explanation is that the repeated observations violated the assumption that extreme values should be drawn from a set of independent, identically distributed samples (Fisher and Tippett, 1928). We tried a third approach, fitting GEV distributions to the unweighted NHANES data, which did match on basis of A–D and K–S tests (Supplemental Table S13). These results suggest that the fitting or possibly the evaluation approaches used for the GEV distributions are inappropriate for weighted datasets.

Gumbel distributions fitted to the weighted NHANES data had R² above 0.8 for VOCs with a few exceptions (top 10% of toluene, eth-ylbenzene and TCE, and the top 5% of MTBE) (Supplemental Table S9). As seen with the RIOPA data, the top 5% of the exposure data provided a better fit (except for MTBE). Based on R² values, the Gumbel distributions had slightly better fits to the RIOPA data than the NHANES data, although the differences were small.

4. Application

Extreme values of pollutant concentrations must be accurately modeled to establish exposure/risk guidelines and to estimate risks across a population. As an example, a guideline or standard might be set to limit the likelihood of excessively high exposures, possibly using the 98th percentile concentration. The distributions investigated in this paper easily permit such analyses. Considering 1,4-DCB and Fig. 1D, for example, moving horizontally across at the 98th percentile level shows that the GEV model predicts an individual risk of 7.8 × 10⁻³, the Gumbel model 8.1 × 10⁻³, and the lognormal model 3.4 × 10⁻³, compared to the 8.4 × 10⁻³ observed. As a second and related example, an impact analysis often requires an estimate of the number of individuals affected, for example, the number that exceed a specific (“acceptable”) cancer risk. In the case for 1,4-DCB, moving vertically from the (high) risk level of 10⁻² (10,000 cases per million population), the GEV, Gumbel and lognormal predict 1.33%, 1.22% and 0.52% exceeding this threshold, respectively, compared to the 1.67% observed (Fig. 1D). In these and most other cases, the lognormal model considerably underestimates risks and impacts, while both the GEV and Gumbel distributions accurately represent the extreme value exposures and risks. The lognormal distribution also tends to underestimate the very highest risks and exposures, e.g., 98th percentile and above.

Poor fits to lognormal distributions also suggest possible violations of the normality assumption for certain statistical analyses, e.g., linear regression models, and the need for some other transformation. If an appropriate transformation is not available, robust non-parametric methods that resist the effects of extreme values may provide a reasonable alternative, such as quantile regression (Koenker and Bassett, 1978).

5. Limitations

This work has several limitations. GEV and Gumbel distributions describe only one tail of a distribution, and cannot be used for the remainder of the distribution. Cancer risk estimates require long-term exposure estimates, and averaging the two visits in the RIOPA dataset may not be representative of long-term exposure. Additionally, individuals lacking either data from either visit were excluded, which reduced the sample size. Extrema were defined using two cut-offs (90 and 95th percentiles). The use of a higher cut-off, e.g., the 98th percentile, was not feasible due to sample size issues. The results for RIOPA are limited to personal exposure measurements of 15 VOCs made in three large cities in the USA. Because RIOPA included only non-smoking households, and for other reasons noted earlier, its results are not generalizable to other cities. We did not evaluate extreme value distributions for other VOCs (e.g., formaldehyde) or other pollutants (e.g., PM_2.5). There may be additional explanations for the differences between the RIOPA and NHANES results beyond those noted (i.e., different sampling designs, staging, demographics, and presence of smokers).

6. Conclusions

Extreme value analyses focus on the highest exposures and risks, which are the most significant in terms of health risks. These highest values become the determinants or “drivers” of environmental decisions and policies, even though most individuals are exposed to far lower concentrations and risks. This work makes clear that the use of lognormal distributions for pollutant concentration, the usual “default” distributional assumption, will underestimate concentrations and risks from extrema. Despite their importance, few studies have fitted distributions or otherwise characterized such extrema, and better ways to accurately characterize pollutant distributions and predict the numbers of individuals that exceed risk-based exposure guidelines are needed.

Data from the RIOPA study show that extreme value distributions can represent tail behavior of exposure and risk distributions. The highest VOC measurements closely fitted generalized extreme value distributions and, in many cases, Gumbel distributions, a reduced form of the GEV distribution. Generally, these distributions worked well for the 15 VOCs measured in RIOPA, as well as risks posed by three VOC mixtures. Personal exposure measurements of the 10 VOCs in NHANES, a separate and nationally representative study, differed from those in RIOPA, in particular, the NHANES exposures were higher for nearly all VOCs. VOC levels in the three-city RIOPA study are not nationally representative due to differences in the study population (e.g., demographics and exclusion of smokers) and protocols (e.g., differences in staging). While better methods are needed to incorporate the sampling weights in the NHANES data, fitted GEV and Gumbel distributions provided accurate modeling of high exposures and risks in the national study. GEV distributions will be useful in impact and policy analyses to describe concentrations, exposures and risks.

HIGHLIGHTS.

• Personal VOC exposures drawn from two studies, RIOPA and NHANES, were used.

• Generalized extreme value (GEV) and Gumbel distributions were fit to VOC extrema.

• The tail behavior of exposure was usually best fit by GEV and Gumbel distributions.

• Lognormal distributions underestimated both the level and likelihood of extrema.

• NHANES had considerably higher concentrations of most VOCs, including extrema.

Abbreviation list

1,4-DCB

1,4-dichlorobenzene

A–D

Anderson–Darling

BTEX

benzene, toluene, ethylbenzene, m,p-xylene, o-xylene

CTC

carbon tetrachloride

EVT

extreme value theory

GEV

generalized extreme value

GOF

goodness-of-fit

HQ

hazard quotient

IRIS

Integrated Risk Information System

K–S

Kolmogorov–Smirnov

MC

methylene chloride

MDL

method detection limit

MLE

maximum-likelihood estimation

MRL

minimal risk level

MTBE

methyl tertiary-butyl ether

NHANES

National Health and Nutrition Examination Survey

OEHHA

Office of Environmental Health Hazard Assessment

PERC

tetrachloroethylene

RfC

reference concentration

RIOPA

relationship between indoor, outdoor and personal air

TCE

trichloroethylene

TVOC

total VOCs

URF

unit risk factor

VOC

volatile organic compound

Appendix A. Supplementary data

Supplementary data related to this article can be found online at http://dx.doi.org/10.1016/j.atmosenv.2012.06.038.