Are Conditional Cash Transfers Effective in Urban Areas? Evidence from Mexico

Abstract

Conditional cash transfer (CCT) programs have spread worldwide as a new form of social assistance for the poor. Previous evaluations of CCT programs focus mainly on rural settings, and little is known about their effects in urban areas. This paper studies the short-term (one- and two-year) effects of the Mexican Oportunidades CCT program on urban children/youth. The program provides financial incentives for children/youth to attend school and for family members to visit health clinics. To participate, families had to sign up for the program and be deemed eligible. Difference-in-difference propensity score matching estimates indicate that the program is successful in increasing school enrollment, schooling attainment and time devoted to homework for girls and boys and in decreasing working rates of boys.

1 Introduction

Conditional Cash Transfer (CCT) programs have spread quickly internationally as a new form of social assistance for poor populations.¹ The programs aim to lessen current poverty and to promote human development by stimulating investments in health, education and nutrition, particularly over the early stages of the life cycle. CCT programs provide cash incentives for families to engage in certain behaviors, such as sending children to school and/or attending health clinics for regular check-ups, obtaining prenatal care and receiving infant nutritional supplementation. One of the earliest and largest scale CCT programs is the Mexican Oportunidades program (formerly called PROGRESA), in which 30 million people are currently participating. Cash benefits are linked both to regular school attendance of children and to regular clinic visits by beneficiary families. Average household benefits amount to about US35 to 40 dollars monthly.

The Oportunidades program was first initiated in 1997 in rural areas of Mexico. Impact evaluations based on a randomized social experiment carried out in rural villages demonstrated significant program impacts on increasing schooling enrollment and attainment, reducing child labor and improving health outcomes.² In 2001, the program began to expand at a rapid rate into semiurban and urban areas. Impacts in urban areas might be expected to differ from those in rural areas, both because some features of the program changed and because access to schooling and health facilities as well as work opportunities differ. Although there have been a number of evaluations of the schooling impacts of Oportunidades and other CCT programs in rural areas, relatively little is known about their effectiveness in urban areas. Evaluations of CCT programs in other Latin American countries in rural areas have shown overall similar impacts to those in rural Mexico (Parker, Rubalcava, and Teruel, 2008).

Although the structure of benefits is identical in rural and urban areas, the procedure by which families become beneficiaries differs. In the rural program, a census of the targeted localities was conducted and all families that met the program eligibility criteria were informed of their eligibility. For cost reasons, this type of census could not be carried out in urban areas, and an alternative system of temporary sign-up offices was adopted. The location of the sign-up offices was advertised and households that considered themselves potentially eligible had to visit the offices to apply for the program during a two month enrollment period when the office was open. About 40% of households who were eligible did not apply for the program, which contrasts sharply with the very high participation rates in rural areas. About one third of nonparticipating but eligible urban households report not being aware of the program. Another important difference between the initial rural program and the current program is that the schooling subsidies were initially given for attendance in grades 3 through 9, but were extended in 2001 to include grades 10 to 12 (high school). We might therefore expect to see impacts of the program on older children as well as potentially larger impacts on younger children than observed under the original rural program.

This paper evaluates the effectiveness of Oportunidades in influencing schooling and working behaviors of adolescent youth using observational data. Specifically, it examines how participation in the program for two years affects schooling attainment levels, school enrollment rates, time devoted to homework, working rates and monthly wages. Our analysis focuses on girls and boys who were 6–20 years old in 2002, when the Oportunidades program was first introduced in some urban areas. The treated group are households who were eligible for the program and elected to participate during the two month incorporation window. The comparison group consists of eligible households living in localities where the program was not yet available. These localities were preselected to be otherwise similar to the treatment localities in terms of observable average demographics and other characteristics, such as regional location, and availability of schools and health clinics. Nonetheless, in making comparisons between individuals in the treated and comparison groups, it is important to account for program self-selection to avoid the potential for selection bias. We conjecture that participating households differ from nonparticipating households; for example, households who expect a larger gain from participation in terms of subsidies are more likely to seek incorporation. The methodology that we use to take into account nonrandom program selection is difference-in-difference matching (DIDM). Matching methods are widely used in both statistics and economics to evaluate social programs.³ The DIDM estimator compares the change in outcomes for individuals participating in the program to the change in outcomes for matched nonparticipants. The advantage of using a DIDM estimator instead of the more common cross-sectional matching estimator is that the DIDM estimator allows for time-invariant unobservable differences between the participant and nonparticipant groups that may affect participation decisions and outcomes. Such differences might plausibly arise, for example, from variation across regional markets in earnings opportunities. For comparison, we also report impact estimates based on a standard difference-in-difference estimator.

This paper makes use of data on three groups: (a) households who participated in the program, (b) households who did not participate but were eligible for the program and lived in intervention areas, and (c) households living in areas where the program was not available but who otherwise met the program eligibility criteria.⁴ Groups (a) and (b) are used to estimate a model of the program participation decision, and groups (a) and (c) are used for impact evaluation. Importantly, group (b) is not used as a comparison group for the purposes of impact evaluation, because of the potential for spillover effects of the program onto nonparticipating households in intervention areas. For example, if the school subsidy component of the program draws large numbers of children participating in the program into school, then it can lead to increased pupil-teacher ratios that represent a deterioration in school quality for children who are not directly participating.⁵ By drawing the comparison group instead from geographic areas that had not yet received the intervention and assuming that the same program participation model applies to those areas, matching estimators can still be applied. Specifically, we apply the participation model estimated from groups (a) and (b) to predict which of the households in (c) would likely participate were the program made available.

Our analysis samples come from the Urban Evaluation Survey data that were gathered in three rounds. One round is baseline data, gathered in the fall of 2002 prior to beneficiary households beginning to receive program benefits. The 2002 survey gathered information pertaining to the 2001–2002 school year. The other two rounds were gathered post-program initiation in the fall of 2003 and fall of 2004 after participating households had experienced one and two years in the program and pertain to the 2002–2003 and 2003–2004 school years. In all rounds, data were gathered on households living in both intervention and nonintervention areas.

The paper proceeds as follows. Section 2 briefly summarizes the main features of the Oportunidades program. Section 3 describes the parameters of interest and the estimation approach. Section 4 discusses the data and Section 5 describes how we estimate the model for program participation. Section 6 presents estimated program impacts on education and work and Section 7 concludes.

2 Description of the Oportunidades Program

The Oportunidades program is targeted at poor families as measured by a marginality index summarizing characteristics of the household, such as education, type of housing and assets. Households with index scores below a cutoff point are eligible to participate. The program has two main subsidy components: a health and nutrition subsidy and a schooling subsidy. To receive the health and nutrition benefit, household members have to attend clinics for regular check-ups and attend informational health talks. To receive the school subsidy, children or youth in participating households have to attend school in one of the subsidy-eligible grade levels (grades 3–12) for at least 85% of school days. They cannot receive a subsidy more than twice for the same grade.

Because of these conditionalities, one would expect to find positive program impacts on school enrollment and schooling attainment. However, the magnitude of these impacts is not predictable, because households can participate to different degrees in the program. For example, households can choose to participate only in the health and nutrition component, so it is possible that the program has no direct impact on schooling for some households, though there may be indirect effects if better health and nutrition increase schooling enrollment and attendance. Second, households can choose to send only a subset of their children to school for the required time. For example, rather than send two children to school fifty percent of the time, households might send their older child to school 85% of the time (to receive the subsidy) and keep the other child at home. Thus, children within the household may differentially be affected by the program. The goal of this paper is to assess the magnitude of the Oportunidades impacts on a variety of school and work-related outcome measures. Some of these outcomes, such as school enrollment, schooling attainment and grade accumulation, are closely tied to program coresponsibilies on which transfer payments are conditional; other outcomes, such as time spent doing homework, whether parents help with schoolwork, and employment and earnings, are not.⁶

Table 1 shows the subsidy amounts and how they increase with grade level, a design that attempts to offset the higher opportunity costs of working for older children. The slightly higher subsidies for girls reflect one of the emphases of the program, which is to increase the schooling enrollment and schooling attainment for girls, who in Mexico traditionally have lower enrollment in post-primary grade levels.

Table 1.

Monthly amount of educational subsidies (pesos)^*

Level/Grade	Boys			Girls
	2002	2003	2004	2002	2003	2004
Primary
3rd grade	100	105	110	100	105	110
4th grade	115	120	130	115	120	130
5th grade	150	155	165	150	155	165
6th grade	200	210	220	200	210	220
Secondary
1st grade	290	305	320	310	320	340
2nd grade	310	320	340	340	355	375
3rd grade	325	335	360	375	390	415
High School
1st grade	490	510	540	565	585	620
2nd grade	525	545	580	600	625	660
3rd grade	555	580	615	635	660	700

^*Amounts in second semester of the year. 1US = 11pesos.

3 Parameters of Interest and Estimation Approach

The general evaluation strategy used in this paper compares outcomes for program participants (the treatment group) to those of a comparison group that did not participate in the program. Data were gathered on households living in urban areas served by Oportunidades (intervention areas) and on households living in urban areas that had not yet been incorporated (non intervention areas), as described further below in section four. We distinguish among the following three groups of households:

1. Participant Group - Households that applied to the program, were deemed eligible for it and chose to participate.

2. Eligible Non-Participant Group - Households living in program intervention areas that did not apply to the program but were eligible for it.

3. Outside Comparison Group – Households living in localities where Oportunidades was not yet available but who otherwise meet the eligibility criteria for the program. These localities were planned for incorporation after the 2004 data collection, but the households living in these localities did not know about plans for future incorporation.

We refer to group (a) as the treatment group and groups (b) and (c) as the comparison groups. The main parameter of interest in this paper is the average impact of treatment on the treated, for various subgroups of children/youth defined by age, gender and preprogram poverty status. Let Y₁ denote the potential outcome of a child/youth from a household that participates in the program and let Y₀ denote the potential outcome if not exposed to the program. The treatment effect for an individual is:

$$\mathrm{\Delta }=Y_1-Y_0.$$

Because no individual can be both treated and untreated at the same time, the treatment effect is never directly observed. This paper uses matching methods to solve this missing data problem and focuses on recovering mean program impacts.⁷

Let Z denote a set of conditioning variables. Also, let D = 1 if an individual is from a participating household, D = 0 if not. The average impact of treatment on the treated, conditional on some observables Z, is:

$$E(\mathrm{\Delta }|Z,D=1)=E(Y_1-Y_0|Z,D=1)=E(Y_1|Z,D=1)-E(Y_0|Z,D=1)$$

We can use the data on treated households to estimate E(Y₁|Z, D = 1), but the data required to estimate E(Y₀|Z, D = 1) are missing.

Estimators developed in the evaluation literature provide different ways of imputing E(Y₀|Z, D = 1). Traditional matching estimators pair each program participant with an observably similar non-participant and interpret the difference in the outcomes of the matched pairs as the treatment effect (see, e.g., Rosenbaum and Rubin, 1983). Matching estimators are typically justified under the assumption that there exists a set of observable conditioning variables Z for which the nonparticipation outcome Y₀ is independent of treatment status D conditional on Z:

$$Y_0⫫D|Z.$$ (1)

It is also assumed that for all Z there is a positive probability of either participating (D = 1) or not participating (D = 0), i.e.

$$0<\text{Pr}(D=1|Z)<1,$$ (2)

so that a match can be found for all treated (D = 1) persons. Under these assumptions, after conditioning on Z, the Y₀ distribution observed for the matched nonparticipant group can be substituted for the missing Y₀ distribution for participants.⁸ If there are some observations for which Pr(D = 1|Z) = 1 or 0, then it is not possible to find matches for them.

Matching methods can be difficult to implement when the set of conditioning variables Z is large.⁹ To address this difficulty, Rosenbaum and Rubin (1983) provide a useful theorem that shows that when matching on Z is valid, then matching on the propensity score Pr(D = 1|Z) is also valid. Specifically, they show that assumption (1) implies

$$Y_0⫫D|\text{Pr}(D=1|Z).$$

Provided that the propensity score can be estimated at a rate faster than the nonparametric rate (usually parametrically), the dimensionality of the matching problem is reduced by matching on the propensity score. Much of the recent evaluation literature focuses on propensity score-based methods.¹⁰

As described above, cross-sectional matching estimators assume that mean outcomes are conditionally independent of program participation. However, for a variety of reasons, there may be systematic differences between participant and nonparticipant outcomes even after conditioning on observables. Such differences may arise, for example, because of program selectivity on unmeasured characteristics, or because of level differences in outcomes across different geographic locations in which the participants and nonparticipants reside.

A difference-in-differences (DIDM) matching strategy, as proposed and implemented in Heckman, Ichimura and Todd (1997), allows for temporally invariant sources of differences in outcomes between participants and nonparticipants and is therefore less restrictive than cross-sectional matching.¹¹ It is analogous to the standard DID regression estimator but does not impose the linear functional form restriction in estimating the conditional expectation of the outcome variable and reweights the observations according to the weighting functions used by the matching estimator. Letting t′ denote a pre-program time period and t a post-program time period, the DIDM estimator assumes that

$$Y_{0t}-Y_{0t\prime }⫫D|\text{Pr}(D=1|Z),$$

or the weaker condition

$$E(Y_{0t}-Y_{0t\prime }|\mathit{\text{Pr}}(D=1|Z),Z)=E(Y_{0t}-Y_{0t\prime }|D=0,\mathit{\text{Pr}}(D=1|Z))$$

along with assumption (2) (the support condition), which must now hold in both periods t and t′ (a non-trivial assumption given the attrition present in many panel data sets). The local linear DIDM estimator that we apply in this paper is given by

$${\mathrm{\alpha ̂}}_{DD}=\frac{1}{n_1}(\sum _{i\in I_1\cap S_P}(Y_{1ti}-Y_{0t\prime i})-\sum _{j\in I_0\cap S_P}W(i,j)(Y_{0tj}-Y_{0t\prime j})),$$

where I₁ denotes the set of program participants, I₀ the set of non-participants, S_P the region of common support and n₁ the number of persons in the set I₁ ∩ S_P. The match for each participant i ∈ I₁ ∩ S_P is constructed as a weighted average over the difference in outcomes of multiple nonparticipants, where the weights W(i, j) depend on the distance between P_i and P_j. Appendix A gives the expression for the local linear regression weights and describes the method that we use to impose the common support requirement.¹²

Estimating the propensity score P(Z) requires first choosing a set of conditioning variables, Z. It is important to restrict the choice of Z variables to variables that are not influenced by the program, because the matching method assumes that the distribution of the Z variables is invariant to treatment. As described below, our Z variables are baseline characteristics of persons or households that are measured prior to the introduction of the program. We estimate the propensity scores by logistic regression.

Lastly, the propensity score model is estimated from groups (a) and (b) and then applied to groups (a) and (c) to determine the impacts. Thus, our matching procedure assumes that the model for program participation decisions is the same for intervention areas as in nonintervention areas. However, the DIDM estimator allows for households in nonintervention localities to have a potentially different distribution of observed characteristics Z.¹³

4 The Data

We use the Urban Evaluation Survey (Encelurb) baseline carried out in the fall of 2002 and two follow-up rounds carried out in the fall of 2003 and 2004. The baseline was carried out before the program was advertised and before any monetary benefits had been received. The Encelurb data include rich information on schooling (pertaining to the 2001–2002 school year) and labor force participation, as well as information on income, consumption, assets and expectations about future earnings. The database contains information on 2972 households in the eligible participant group (group a), 2556 households who were eligible but did not participate (group b) and 3607 households from nonintervention areas who satisfied the eligibility criteria for the program (group c). Appendix B in Behrman et al. (2011) provides further information on the selection of the subsamples used in our analysis, on the construction variables and on how we identified and dealt with different kinds of data inconsistencies. The sample sizes for groups (a), (b) and (c), comprised of boys and girls age 6–20 in 2002 (age 8–22 in 2004) are 5819, 3078 and 6342, respectively.¹⁴

4.1 Interpretation of the estimator in the presence of attrition

In this study, we focus on children and youth that were observed across all the survey years. The percentage of children who are lost between rounds in groups (a) and (c) (the groups used for the impact analysis) tends to increase with age from 17–20% for 6–7 year-olds and to 35–37% for the oldest age category (19–20 year-olds) for 2002–2004 (see Behrman et al. (2011, Table 3) for details on attrition that are summarized here). The higher attrition rate for the oldest group is not surprising given that older children are more likely to leave home and get married than younger children. Of more relevance for our impact analysis is whether the patterns differ substantially between the treatment and the control groups. Between 2002 and 2004 there are slightly higher attrition rates for most age groups (except for 15–18 year-olds) and on average for the control (22%) than the treatment (19%). But the overall difference (3%) and the differences for each of the age groups (−1% to 4%) are fairly small, and therefore not likely to affect substantially the estimates presented below. Nevertheless, we describe below the extent to which our estimation method accommodates attrition.

Table 3.

a Estimated Impacts on Percentage Enrolled in School Subgroup: Boys, Age 6–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	84	90	4.7 (2.6)	4.6 (2.8)	5.1 (2.3)	4.7 (2.6)	97	97	859	771
8–11	.3	95	98	2.4 (0.9)	2.2 (1.1)	2.3 (0.9)	2.4 (1.1)	97	97	1947	1753
12–14	.3	93	90	1.3 (2.0)	−3.0 (3.1)	1.4 (1.8)	−1.8 (2.6)	97	97	1038	947
15–18	.3	60	53	8.5 (4.1)	2.6 (4.8)	5.6 (3.4)	3.8 (4.1)	96	96	614	523
19–20	.3	22	13	10.2 (9.3)	−4.1 (8.1)	3.7 (5.1)	−4.9 (5.5)	96	97	146	120
6–20	.3	85	86	3.6 (1.0)	1.2 (1.2)	3.1 (0.8)	1.7 (1.0)	97	97	4604	4114

b Estimated Impacts on Percentage Enrolled in School Subgroup: Girls, Age 6–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	84	92	6.0 (2.6)	7.6 (2.5)	6.9 (2.1)	9.1 (2.2)	97	97	927	835
8–11	.3	96	98	1.7 (0.9)	2.4 (1.4)	2.0 (0.8)	1.9 (1.2)	97	97	1989	1796
12–14	.3	88	92	1.0 (2.5)	0.1 (3.3)	4.1 (1.9)	3.6 (2.7)	97	97	972	860
15–18	.3	58	61	3.1 (4.7)	1.2 (6.2)	2.6 (3.8)	4.8 (4.6)	97	97	609	486
19–20	.3	13	22	8.2 (7.7)	−2.1 (10.1)	4.7 (6.2)	−1.4 (6.6)	97	95	129	103
6–20	.3	84	89	2.8 (1.1)	2.7 (1.3)	3.6 (0.8)	4.0 (1.1)	97	97	4626	4080

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

As described in the previous section, our impact analysis aims to recover the average effect of treatment on the treated. In our application, the treated correspond to children observed over the three survey rounds. For the DIDM estimator to be valid in the presence of some attrition, we require an additional assumption on the attrition process. Let A = 1 if the individual attrited between time t′ and t, else A = 0 and, for ease of notation, denote ΔY = Y_0t − Y_0t′. By Bayes rule,

$$\text{Pr}(D=1|A=0,\mathrm{\Delta }Y,Z)=\frac{\text{Pr}(A=0|D=1,\mathrm{\Delta }Y,Z)\text{Pr}(D=1|\mathrm{\Delta }Y,Z)}{\text{Pr}(A=0|\mathrm{\Delta }Y,Z)}=\frac{\text{Pr}(A=0|D=1,\mathrm{\Delta }Y,Z)\text{Pr}(D=1|\mathrm{\Delta }Y,Z)}{\text{Pr}(D=1|\mathrm{\Delta }Y,Z)\text{Pr}(A=0|\mathrm{\Delta }Y,Z,D=1)+\text{Pr}(D=0|\mathrm{\Delta }Y,Z)\text{Pr}(A=0|\mathrm{\Delta }Y,Z,D=0)}$$

Under the DIDM assumption,

$$\text{Pr}(D=1|\mathrm{\Delta }Y,Z)=\text{Pr}(D=1|Z).$$

We invoke an additional assumption that attrition is not selective on the change in potential outcomes in the no-treatment state conditional on Z and D, then

$$\text{Pr}(A=0|\mathrm{\Delta }Y,D,Z)=\text{Pr}(A=0|D,Z)$$

we get

$$\text{Pr}(D=1|\mathrm{\Delta }Y,Z,A=0)=\frac{\text{Pr}(A=0|D=1,Z)\text{Pr}(D=1|Z)}{\text{Pr}(A=0|Z)}=\text{Pr}(D=1|Z,A=0),$$

which would imply that the DIDM estimator is valid for nonattritors. Attrition is allowed to depend on time-invariant unobservables that are eliminated by the differencing, so attrition on unobservables is permitted.¹⁵ However, the estimation approach does rule out certain types of attrition, for example, that individuals with particularly high or low differences in potential earnings or schooling outcomes (that are not explainable by the observed characteristics Z) are the ones who attrit. Also, the application of the DID matching estimator does not require assuming that attrition is symmetric in the treatment and comparison groups. The method would allow, for example, for the case of no attrition in the treated group and substantial attrition in the comparison group, as long as the attrition in the comparison group is not selective on ΔY, conditional on Z.

4.2 Descriptive analysis and comparison of groups at baseline

There are six key outcome variables for boys and for girls. The basic patterns in these variables and comparison of the means for the participant group (a) and the eligible nonintervention group (c) at baseline in the 2001–2002 school year follow (see Behrman et al. 2011, Section 4.2 and Figures 1–6 for details):

1. Mean schooling attainment increases steadily with age until about age 15 after which age the rate of increase declines. Schooling attainment averages about eight grades by age 20. Mean schooling attainment is higher for group (c) than for group (a) for boys until age 14 (after which the averages are about the same) and for girls for all ages;

2. School enrollment rates are near 100% for the primary school age years, after which they steadily decline. Mean enrollment rates for girls are higher for the nonintervention than for the participant group over most of the age range, but for boys mean enrollment rates are higher for the participant group for ages older than 12.

3. The average percentages of children receiving help at home with homework increase at first with age to a peak between 50 and 60 percent in the 7–10 year old range and then declines to less than 20 percent by age 15. For children age 6 the nonintervention group averaged more help, but for other ages the patterns are fairly similar for the two groups.

4. The average number of hours spent doing homework are 5–6 hours per week for ages 7–15 with a slight increasing age pattern for girls but basic stability for boys. The patterns are fairly similar for the participant and the nonintervention groups.

5. The average employment rates in paid activities increase steadily with age from less than 10 percent at age 12 to over 80 percent at age 20 for boys and from less than 10 percent at age 12 to about 25 percent at age 20 for girls. For boys the average rates are very similar for the two groups, but for girls the average rates are higher for the participant than for the nonintervention group.

6. The patterns in the average incomes earned are parallel to the average employment rates. Important points that come out of these baseline data are that (a) there are definite age patterns for both schooling and employment, (b) there are some important gender differences particularly in paid employment, and (c) there are some important preprogram differences that should be taken into account in the analysis (as they are with the DIDM estimates).

5 Propensity Score Estimation

The propensity score DIDM method requires first estimating Pr(D = 1|Z), which we estimate using logistic regression applied to data on households who are eligible to participate and live in areas where the program is available, that is groups (a) and (b) described in Section 2 of this paper. Participating in the program (D=1) means that a household member attended the module to sign up for the program (see Section 1) and that the household was deemed eligible and elected to participate. We use administrative data to determine which households are or are not participating.

An important question in implementing any evaluation estimator is how to choose the set of conditioning variables Z. We include in Z variables that are designed to capture key determinants of program participation decisions, such as measures of the benefits the family expects to receive from the program (based on the number of children in the family of various ages attending school), variables related to costs associated with signing up and participating in the program (such as poverty status of the family, employment status of family members, availability of schools and health clinics), and variables that potentially affect whether the family is aware of the program (such as geographic location, population living in the locality, average poverty score of people living in the locality, schooling of household members). All of the variables are measured prior to program initiation and are therefore unlikely to be influenced by the program. We chose the set of regressors to maximize the percentage of observations that are correctly classified under the model.¹⁶

Appendix B describes the variables used to estimate the program participation model. 73% of the observations are correctly classified under the estimated model as being either a participant or nonparticipant. In general, most of the coefficients are statistically significant at the 10 percent level. The results show that having a dirt floor or walls or ceilings made of provisional materials (cardboard, plastic, tires, etc.) increases the probability of participating in the program. Having piped water inside the house decreases the probability of participating, although this coefficient is small in magnitude. Having a truck or a refrigerator also decreases the probability of participation in the program, which is consistent with these goods being indicators of higher economic status for a household.

Participating in some other in-kind subsidy program has a positive effect on the probability of participation. The other relevant programs operating under the Mexican social support system are the free tortilla program, the milk subsidy program, the free groceries program, and the free school breakfast program.¹⁷

Having more children in the ages range associated with attendance at primary or secondary school increases the probability of program participation, which is to be expected as their presence increases the household’s potential benefits from the school enrollment transfers. Being a female-headed household also increases the participation probability. Being poor, as classified by the Oportunidades poverty score, is associated with higher rates of program participation. Poorer households may be more likely to attend the sign-up offices, either because they live in high density poverty areas where information about the program is better disseminated or because they are more likely to believe that their application to get Oportunidades benefits will be successful.

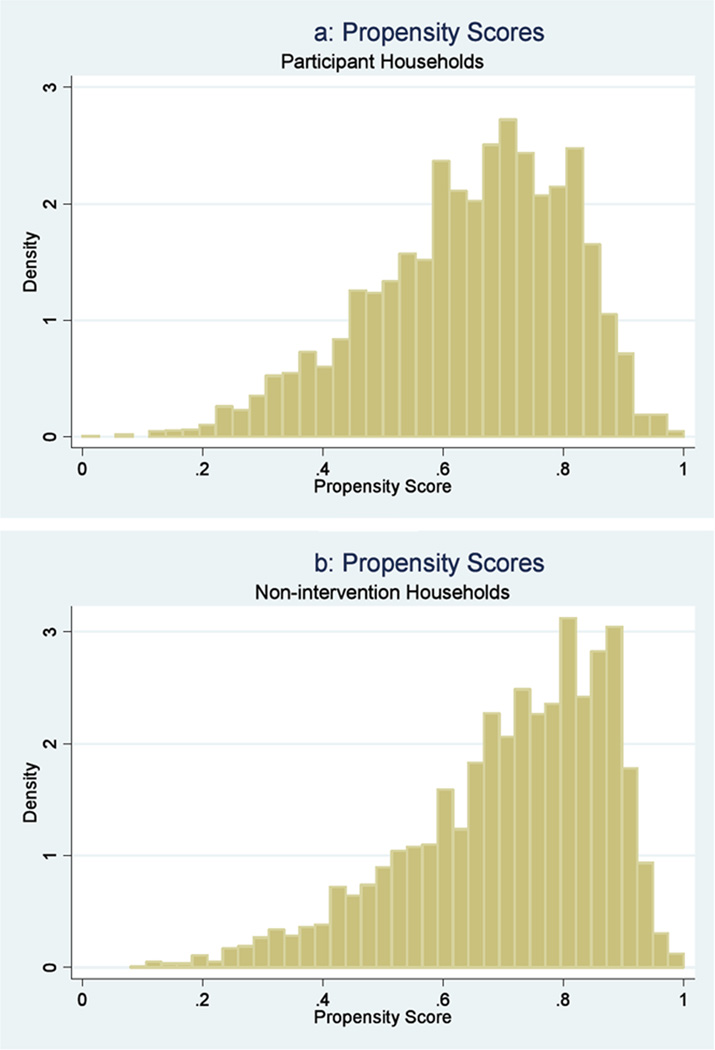
Figures 1a and 1b show the histograms of the propensity scores that are derived for each household from the logit model estimates. The figures compare propensity scores for participant households (group a) to those for nonintervention households (group c). The histograms for both groups are similar. Most importantly, the figures reveal that there is no problem of nonoverlapping support. For each participant household, we can find close matches from the nonintervention group of households (as measured by similarity of the propensity scores).

Figure 1.

Propensity score distribution.

6 Program Impacts

We next evaluate the impacts of participating in the program on schooling and work. Given the relatively high school enrollment levels for young children and lower levels for older children prior to the start of the program, we expect the impacts on school enrollment to be greater for older children. Because the program requires regular attendance, we also expect to see improvements in grade progression as measured by educational attainment. The school attendance requirements would be expected to increase the amount of time spent in school relative to work, so in addition we expect the program to decrease the working rates of children/youth, with a corresponding decrease in earnings. Our expectations for the one-year impact analysis are guided in part by the results of the short-term rural evaluation, which found no effects on primary school enrollment levels but statistically significant effects on increasing enrollment at secondary grades.¹⁸

As described previously, our evaluation strategy compares children/youth from households who participate in the program (group a) to observably similar (matched) children/youth from households living in the areas where the program was not yet available (group c). We impute propensity scores for the households in the nonintervention areas using the estimated logistic model, as described in Section 4.

For these households, the estimated propensity scores represent the probability of the household participating in the program had the program been made available in their locality. Because the propensity score model is estimated at the household level, all children within the same household receive the same score. However, the impact estimation procedure allows children of different gender and age groups from a given household to experience different program impacts.

Lastly, the program subsidies start at grade 3 (primary level), so 6 and 7 year-old children do not receive benefits for enrolling in school. However, we include these children in our impact analysis, because they may benefit from the subsidies received by older siblings and/or the expectation of cash payments at higher grades could provide an incentive to send younger children to school, as was found in rural areas (Behrman, Sengupta and Todd 2005).

6.1 Schooling Attainment

Tables 2a and 2b show the estimated program impacts on total grades of schooling attainment for boys and girls who are age 6 to 20 at the time of the 2002 survey (8–22 at the time of the 2004 survey). The columns labeled ”Avg Trt 2002” and ”Avg Con 2002” give the average schooling attainment at baseline (year 2002) for children in treatment and comparison households, respectively, and show that controls had slightly higher grades of attainment in that year. The program can achieve increases in grades of schooling attainment through earlier matriculation into school, lower rates of grade repetition and lower rates of dropping out. The columns labeled ”1 Year DID Match” and ”2 Year DID Match” give the one-year and two-year program impact estimates obtained through DID matching, where we match on propensity scores after exact matching by age and gender. Also, we do not impose any restriction on the estimation that the two-year impacts exceed the one-year impact. The program might over the short run increase school attendance and educational attainment, but over the longer run might lead to lower attendance at older ages if youth attain their targeted schooling levels at earlier ages. For example, suppose that before the program, a child’s targeted schooling level was ninth grade and it took eleven years to complete ninth grade (because some grades were repeated). The program might encourage the child to attend school more regularly and to increase the targeted schooling level from ninth to tenth grade. If as a result of the program the child completes ten grades in ten years as opposed to nine grades in eleven years, then the child finishes school at an earlier age with more grades completed. In this sense, schooling attainment could increase without necessarily increasing enrollment at older ages.¹⁹

Table 2.

a Estimated Impacts on Years of Schooling Subgroup: Boys, Age 6–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	0.69	0.90	0.04 (0.04)	−.03 (0.06)	0.06 (0.04)	0.02 (0.04)	97	97	843	753
8–11	.3	3.08	3.44	0.11 (0.02)	0.05 (0.03)	0.11 (0.02)	0.06 (0.03)	97	97	1884	1712
12–14	.3	5.78	6.49	0.17 (0.03)	0.25 (0.05)	0.17 (0.03)	0.23 (0.05)	97	97	1003	901
15–18	.3	7.60	7.67	0.13 (0.04)	0.28 (0.09)	0.11 (0.04)	0.22 (0.08)	96	95	595	477
19–20	.3	7.81	8.01	0.04 (0.06)	0.06 (0.17)	0.03 (0.04)	−0.06 (0.10)	96	96	145	106
6–20	.3	4.09	4.25	0.11 (0.02)	0.11 (0.03)	0.12 (0.01)	0.11 (0.02)	97	97	4470	3949

b Estimated Impacts on Years of Schooling Subgroup: Girls, Age 6–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	0.73	0.88	0.10 (0.04)	0.08 (0.04)	0.11 (0.03)	0.09 (0.04)	97	97	900	812
8–11	.3	3.11	3.50	0.12 (0.02)	0.12 (0.03)	0.13 (0.02)	0.13 (0.03)	97	97	1930	1744
12–14	.3	5.87	6.48	0.14 (0.04)	0.17 (0.06)	0.14 (0.03)	0.15 (0.05)	97	97	947	821
15–18	.3	7.54	8.19	0.07 (0.05)	0.19 (0.10)	0.05 (0.04)	0.16 (0.08)	96	97	583	446
19–20	.3	7.00	8.26	0.00 (0.08)	−.06 (0.19)	−.01 (0.05)	0.01 (0.11)	97	96	129	93
6–20	.3	3.98	4.29	0.11 (0.02)	0.13 (0.02)	0.11 (0.01)	0.13 (0.02)	97	97	4489	3916

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

The columns labeled ”1 Year DID” and ”2 Year DID” give impact estimates obtained using an unadjusted DID estimator where as the next two columns contain the DID matching estimates. The one-year impacts correspond to the 2003–2004 school year and two-year impacts to the 2004–2005 school year. As seen in the columns labeled ”% Obs in Support,” the supports for the most part overlap and not many of the treated observations were eliminated from the analysis for support reasons. Each of the tables presents impact estimates obtained using a bandwidth equal to 0.3. The bandwidth controls how many control observations are used in constructing the matched outcomes. As the estimates may depend on bandwidth choice and there are a variety of criteria for choosing bandwidths, it is important to consider a range of choices. We found that the program impact estimates are relatively insensitive to bandwidth choices in the range of 0.2–0.4, so for the sake of brevity we only report results for one bandwidth.²⁰

For boys (Table 2a), there is strong evidence of an effect of the program on schooling attainment at ages 8–18, with the two-year impact (2003–2004) being about 40% larger than the one-year impact. For girls (Table 2b), one year and two-year program impacts are statistically significant over ages 6–14. The two-year impacts for girls are generally of similar magnitude to the one-year impacts and are somewhat lower than for boys, despite the higher subsidy rates for girls. For both girls and boys, the largest impacts are observed in the 12 to 14 age range (approximately 0.20 grades, which represents about a 4% increase in schooling attainment). The estimated impacts are largest for boys age 12 to 14, ranging from 0.23 to 0.30 grades. These ages coincide with the transition from primary to secondary school, when preprogram enrollment rates dropped substantially and when when the subsidy level increases substantially (See Table 1). The DIDM and the simple DID estimates are often similar. The similarity of the estimates, however, does not imply that self-selection into the program is not an issue. As discussed in Heckman, Ichimura and Todd (1997), selection biases can sometimes fortuitously average to close to zero.

Tables 3a and 3b show the estimated impacts on school enrollment for boys and girls. The third and fourth columns (labeled Avg Trt in 20002 and Avg Con in 2002) give the enrollment rates of the children in the baseline 2001–2002 school year. The enrollment rates are usually over 90% for ages up to age 14, after which there is a significant drop. We observe statistically significant impacts of the program on enrollment rates mainly for boys and girls ages 6–14. Both the one-year and two-year impacts are larger for girls age 6–7 than for similar age boys. The impacts for the age 8–11 group are similar across boys and girls and are roughly of the same magnitude (around 2–3 percentage point increases in enrollment, which represents an increase of about 2–3%). The two-year impact is not necessarily larger than the one-year impact, but this is to be expected given that children are aging over the two years and enrollment rates generally decline with age.

Tables 4a and 4b examine the estimated impacts of the program on the percentage of children whose parents help them on their schoolwork, for the subsample of children reported to be in school at the baseline year. The potential impact of the program on parents helping with homework is theoretically difficult to predict. On the one hand, the subsidies may provide an incentive for parents to help their children so that they pass grades levels according to the pace required under the program rules. On the other hand, if the subsidies enable children/youth to work less (outside of school) and spend more time on schoolwork, then they may not require as much help. As children/youth increase school enrollment and decrease their time spent working at home or outside their home, parents may also decide to increase their time spent working and so may have less time available to help children on their schoolwork.

Table 4.

a Estimated Impacts on Percentage Helped with Homework, in school in 2001–2002 Subgroup: Boys, Age 6–18 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	52	61	5.2 (5.7)	−7.3 (8.1)	6.3 (4.5)	−3.3 (4.9)	97	97	754	676
8–11	.3	52	49	−10.0 (3.2)	−12.3 (3.4)	−7.5 (2.9)	−10.4 (3.1)	97	97	1880	1692
12–14	.3	30	33	2.1 (4.2)	2.0 (4.0)	2.0 (3.6)	2.7 (3.7)	97	97	950	870
15–18	.3	17	13	−4.7 (5.6)	−3.1 (5.9)	−4.9 (4.4)	−2.0 (4.5)	94	94	342	304
6–18	.3	43	46	−3.8 (2.3)	−6.8 (2.5)	−2.5 (2.0)	−4.9 (1.9)	97	97	3926	3542

b Estimated Impacts on Percentage Helped with Homework, in school in 2001–2002 Subgroup: Girls, Age 6–18 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	57	58	−4.7 (4.7)	−5.2 (5.3)	−3.6 (4.3)	−5.9 (5.0)	97	97	818	739
8–11	.3	50	52	−5.3 (3.0)	−6.5 (3.3)	−4.1 (2.8)	−6.0 (2.8)	98	97	1931	1743
12–14	.3	26	29	2.3 (4.5)	−6.4 (4.7)	2.3 (3.7)	−5.2 (3.9)	97	97	876	783
15–18	.3	10	14	0.4 (4.5)	−2.9 (5.5)	3.0 (3.6)	−0.2 (4.0)	96	96	362	308
6–18	.3	42	45	−2.9 (2.0)	−5.9 (2.2)	−1.9 (1.8)	−5.3 (1.9)	97	97	3987	3573

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

As seen in Table 4a, for boys there are statistically significant impacts only at ages 8–11, when parents in households participating in the program have a rate of helping with homework that is lower by around 10 percentage points in the first year and 12 percentage points in the second year. Similar negative impacts on homework help are observed for girls, who also show lower two-year impacts on receiving homework help at ages 8–11, though the estimates for girls are for the most part statistically insignificantly different from zero. The general pattern of a decrease in help on homework is consistent with parents in participating households spending more time on work activities to substitute for their children working less (see discussion of employment impacts below).

Tables 5a and 5b examine the impacts of the program on the amount of time that boys and girls dedicate weekly to their studies, for the subsample of children reported to be in school in the 2001–2002 school year. For boys, the average number of hours devoted to homework at the baseline is increasing with age and is in the range of 5–8 hours. The largest one-year and two-year impacts of the program are observed for boys age 12–14 (in 2002), who devote an additional 0.85–1.3 hours to homework, which represents an increase of about 14– 21% over their baseline hours. We also observe statistically significant one-year impacts for boys age 6–7 and for boys age 8–11, who devote an additional 20 to 50 minutes per week on homework. For girls of all ages, however, the estimated two-year impacts are statistically insignificant.

Table 5.

a Estimated Impacts on Hours Spent Doing Homework, in school in 2001–2002 Subgroup: Boys, Age 6–18 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	4.36	4.69	0.87 (0.40)	0.42 (0.56)	0.60 (0.36)	0.03 (0.38)	97	97	754	676
8–11	.3	5.86	5.89	0.51 (0.23)	0.33 (0.29)	0.41 (0.21)	0.22 (0.25)	97	97	1880	1692
12–14	.3	6.26	6.40	1.29 (0.43)	1.08 (0.44)	0.96 (0.40)	0.69 (0.41)	97	97	950	870
15–18	.3	7.86	6.46	1.15 (1.05)	−0.07 (1.07)	0.46 (0.88)	−0.60 (0.82)	96	96	257	228
6–18	.3	5.86	5.80	0.83 (0.18)	0.52 (0.22)	0.59 (0.16)	0.25 (0.19)	97	97	3841	3466

b Estimated Impacts on Percentage Helped with Homework, in school in 2001–2002 Subgroup: Girls, Age 6–18 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
6–7	.3	4.19	4.98	1.38 (0.40)	0.34 (0.41)	1.17 (0.35)	0.45 (0.34)	97	97	818	739
8–11	.3	5.83	5.80	0.39 (0.25)	0.32 (0.25)	0.15 (0.23)	0.04 (0.23)	98	97	1931	1743
12–14	.3	7.27	6.67	0.19 (0.78)	−0.69 (0.64)	0.03 (0.47)	−0.69 (0.50)	97	97	876	783
15–18	.3	8.53	7.56	1.38 (1.57)	0.39 (1.33)	0.12 (1.08)	0.04 (1.00)	97	97	258	217
6–18	.3	6.03	5.93	0.61 (0.27)	0.09 (0.23)	0.33 (0.20)	−0.04 (0.19)	97	97	3883	3482

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

Tables 6a and 6b show the estimated impacts of the program on the percentage of children working for pay. The tables only show estimates for ages 12–20, because very few children work at younger ages, probably in part because of legal restrictions on work for children younger than age 14. As seen in the third and fourth columns, showing the baseline work patterns, the percentage of children working for pay increases sharply with age. From age 12–14 to 15–18, the percentage increases from 10% to 44% for boys and 10% to 27% for girls. Participation in the program is associated with a reduction in the percentage of boys age 12–14 working of about 8 percentage points in the first year and 12–14 percentage points in the second year. For girls, the percentage of youth who work is lower at all ages than for boys, and the program does not seem to affect the percentage of girls who work. The only statistically significant impact for girls is observed at ages 15–18, when the program lowers the percentage working by around 11%, but only in the first year. Thus the gender difference in working and in time spent on homework are consistent with significant shifts away from market work to homework for boys but no significant changes in either for girls.

Table 6.

a Estimated Impacts on Percentage Employed Subgroup: Boys, Age 12–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
12–14	.3	10	6	−7.7 (2.7)	−12.4 (3.6)	−6.9 (2.4)	−13.4 (3.0)	97	97	938	857
15–18	.3	44	42	2.8 (5.9)	−5.1 (8.2)	0.6 (4.4)	−6.8 (5.2)	95	95	548	469
19–20	.3	81	78	−5.9 (9.9)	−15.4 (15.2)	3.1 (6.1)	−6.0 (9.4)	96	96	132	107
6–20	.3	28	24	−4.1 (2.6)	−10.3 (3.6)	−3.6 (2.1)	−10.8 (2.5)	96	96	1618	1433

b Estimated Impacts on Percentage Employed Subgroup: Girls, Age 12–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
12–14	.3	10	5	0.7 (2.6)	−1.0 (2.8)	0.3 (1.9)	−1.1 (2.4)	97	97	886	787
15–18	.3	27	18	−10.5 (6.5)	0.4 (9.2)	−5.8 (4.1)	0.2 (5.0)	97	97	562	452
19–20	.3	32	22	−5.0 (8.0)	8.7 (23.6)	−4.9 (7.5)	−0.3 (9.9)	95	96	116	92
6–20	.3	17	11	−3.8 (2.7)	0.2 (3.8)	−2.3 (1.8)	−0.6 (2.2)	97	97	1564	1331

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

Lastly, Tables 7a and 7b present estimates of the program’s impact on monthly earnings of children and youth 12 to 20 years old, where earnings are set to zero for children who report not working. The average earnings combines information on the proportion working and on the average earnings of those who work. We observe an impact of the program on earnings only for boys age 12–14, for whom earnings decline in the first year after the program started. The other estimates are statistically insignificantly different from zero. This result is not necessarily inconsistent with the statistically significant effects on employment noted above, as it is possible that the decrease in the supply of child labor induced by the program increases the wages of the children who remain in the labor market.

Table 7.

a Estimated Impacts on Monthly Income in Pesos Subgroup: Boys, Age 12–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
12–14	.3	82	53	−66 (35)	−47 (46)	−49 (27)	−45 (39)	97	96	909	800
15–18	.3	454	452	32 (119)	183 (168)	12 (75)	65 (101)	95	96	435	369
19–20	.3	1151	1109	−537 (401)	−289 (489)	−128 (187)	−162 (226)	96	94	83	65
6–20	.3	261	239	−67 (50)	8 (63)	−36(31)	−19 (41)	96	96	1427	1234

b Estimated Impacts on Monthly Income in Pesos Subgroup: Girls, Age 12–20 Local Linear matching†
Age in 2002	BW	Avg Trt in 2002	Avg Con in 2002	1 Year DID Match	2 Year DID Match	1 Year DID	2 Year DID	% Obs in Support~	%Obs in Support~~	1 Year Obs T+C	2 Year Obs T+C
12–14	.3	77	30	3 (28)	3 (33)	−5 (22)	−7 (30)	97	97	871	775
15–18	.3	243	172	−100 (75)	−36 (77)	−53 (53)	−13 (65)	96	97	534	431
19–20	.3	349	274	4 (115)	121 (452)	25 (107)	33 (201)	96	96	106	88
6–20	.3	157	99	−34 (32)	−2 (45)	−20 (25)	−6 (32)	96	97	1511	1294

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

^†Difference-in-Difference estimator, imposing common support (2% trimming)

Standard errors based on bootstrap with 500 replications

^~Percentage of observations in the support region for 1-year estimations

^~~Percentage of observations in the support region for 2-year estimations

7 Conclusions

This paper analyzes the one- and two-year impacts of participation in the Oportunidades program on schooling and work of children/youth who were age 6–20 in 2002 (8–22 in 2004) who live in urban areas and whose families were incorporated into Oportunidades program in 2002. An important difference between the implementation of the program in urban areas in comparison to rural areas is that families in urban areas had to sign up for the program at a centralized location during an enrollment period. Only a subset of the households eligible for the program chose to participate. Another important difference is that the data collection in urban areas is nonexperimental, and the estimators used to evaluate program impacts must therefore take into account nonrandomness in the program participation process.

This paper makes use of data on three groups: (a) a group of eligible households who participate in the program, (b) a group of eligible households who do not participate but who live in intervention areas, and (c) a group of eligible households who live in areas where the program was not available. The difference-in-difference matching estimator compares the change in outcomes for individuals participating in the program with the change in outcomes for similar, matched individuals who are not in the program.

Our analysis finds significant positive impacts for both boys and girls on schooling attainment, school enrollment, proportions working, and amount of time children spend doing homework. In addition, we find a statistically significant negative impact of the program on the percentage of children whose parents help them with their homework and no discernible impact on average earnings.

Overall, the education impacts deriving from one and two years of program operation are sizeable. They are generally encouraging, given that the data come from the initial phase of expansion to urban areas, a time period where one might expect operational problems.²¹ The impacts thus far are consistent with the program, at least in the area of education, being carried over to urban areas in a successful manner. The parameter estimated in this paper was average treatment on the treated. An intent-to-treat estimator, which would include eligibles who did not apply to the program, would indicate smaller size impacts.

One concern in implementing the Oportunidades school subsidies in urban areas is that the level of subsidies in urban areas was identical to rural areas, but the opportunity costs of school for children/youth from urban areas are likely to be greater because of greater earnings potential. It is therefore remarkable that the impact estimates for the urban areas are similar to results found in the rural evaluation in the initial phases of the program. A difference, however, in the urban areas compared with the initial rural implementation is that school subsidies are now offered at grades 10–12, which provides incentives for older children to enroll in school and may also provide extra incentives for younger children to reach those grade levels.

With respect to gender, we found fairly similar impacts for boys and girls on schooling outcomes, which suggests that the slightly higher grants given to girls attending grades 7–12 are not generating large differences in impacts by gender (although one cannot say, based on the current analysis, whether impacts on girls would be different if grant amounts were changed to be the same for girls as boys). Prior to the program, enrollment rates for girls in the participant groups started to fall at earlier ages than those for boys which could justify the higher grants to girls for secondary school grades. However, there are not strong differences in education levels between boys and girls (see Behrman et al (2011) figures 1a and 1b). An evaluation of the short-term impacts in rural areas (Behrman, Sengupta and Todd, 2005) demonstrated that girls tend to progress more quickly than boys through the primary grades (i.e. have lower failure rates), which can explain why their completed average schooling is higher than that of boys despite leaving school on average at earlier ages.²²

Boys report spending more time doing homework as a result of the program, so it is perhaps surprising that they seem to be receiving less help from parents/other relatives with the program than they would without. As described earlier, this may reflect either that they need less help or that other adults are working more in response to the program (perhaps as a response to their children working less) and thus have less time to spend during after school hours with their children. In any case, the impact of the program on the time allocation of different family members seems an important topic for further research.

In addition to program impacts on schooling, we find some evidence that the program affects youth working behavior. Boys age 12–14 in 2002 (14–16 in 2004) experience a significant decrease in working, ranging from 7–13 percentage points. Girls’ work behavior is not significantly affected by the program, in part because a lower proportion of girls than boys work for pay.

We noted that there is little scope for an effect of the program on enrollment rates at primary grades when enrollment rates preprogram were already very high. If increasing average schooling levels is a primary aim of the program, then it is worth considering further whether decreasing or eliminating the subsidies at the lower grades and using the resources to increase the level of payments to higher grade levels would be a more effective program design.²³ Of course, changing the subsidy schedule in this way would have distributional consequences and would shift resources towards families whose children have higher schooling attainment levels. Further study of the urban data would be useful to evaluate the effectiveness of alternative program designs.

Appendix A. Local Linear Regression and Method for Determining Common Support

This appendix gives expressions for the local linear regression weighting function (as introduced in Fan (1992a,b)) and also describes the method we use to impose the common support requirement of matching estimators. Letting P̃_ik = P_k − P_i, the local linear weighting function is given by

$$W(i,j)=\frac{G_{ij}\sum _{k\in I_0}{G}_{ik}{\mathrm{P̃}}_{ki}^2-[G_{ij}{\mathrm{P̃}}_{ji})][\sum _{k\in I_0}{G}_{ik}{\mathrm{P̃}}_{ki}]}{\sum _{j\in I_0}{G}_{ij}\sum _{k\in I_0}{G}_{ij}{\mathrm{P̃}}_{ki}^2-{\left(\sum _{k\in I_0}{G}_{ik}{\mathrm{P̃}}_{ki}\right)}^2}.$$

where G(·) is a kernel function and a_n is a bandwidth parameter.²⁴

To implement the matching estimator given above, the region of common support S_P needs to be determined. By definition, the region of support includes only those values of P that have positive density within both the D = 1 and D = 0 distributions. Following the procedure in Heckman, Ichimura and Todd (1997), we require that the densities exceed zero by a threshold amount determined by a “trimming level” q. That is, after excluding P points for which the estimated density is exactly zero, we exclude an additional q percentage of the remaining P points for which the estimated density is positive but very low. The set of eligible matches are therefore given by

$${Ŝ}_P=\{P\in I_1\cap {Ŝ}_P:\mathrm{f̂}(P|D=1)>c_q\text{and}\mathrm{f̂}(P|D=0)>c_q\},$$

where c_q is the density cut-off trimming level.²⁵

Appendix B: Sample Inclusion Criteria, Construction of Variables and the Propensity Score Specification

In this appendix, we describe the sample inclusion criteria, the construction of key variables and the propensity score model.

Sample Inclusion Criteria

Only individuals between ages 6 and 20 years old in 2002 were included in the outcomes analysis. Individuals with no age information for any of the rounds were deleted as well as individuals with inconsistencies in age between rounds. Individuals with no information in the baseline were excluded as were individuals with contradictory information in the follow-up rounds with respect to grades completed and enrollment. These restrictions left a sample of 12,160 individuals in group (a) or (c) in the baseline. Due to attrition, there is no information on some of those children in the data gathered in 2003 and 2004. The 2003 data have information on 10,541 individuals and the 2004 data on 9,652 observations. Additional observations were dropped in the impact analysis if the information required to obtain propensity scores or outcome variables was missing. In the cases where information was only available in 2003 or 2004 but not in 2002, the missing value was imputed from other years, e.g. if the age for 2003 was available but not for 2002, we imputed the age in 2002.

Construction of Variables

The variable grades of education specifies the completed grades of education, not including kindergarten. In the data, individuals report the highest level of schooling obtained along with the number of years within that level. We determined the total number of years completed according to the years required for each type of degree, as described in table B.1 below. Individuals that made a report that exceeded the upper bound were imputed the maximum number of grades, according to the degree reported.

Table B.1.

Grade equivalencies for schooling levels

Primary school	At most six grades (grades 1–6)
Secondary school	At most 3 grades above primary (grades 7,8,9)
Highschool (upper secondary)	At most 3 grades above secondary (grades 10,11,12)
Normal school	Schooling required to become a teacher. At most 3 grades in addition to high school.
Technical or commercial	Maximum grades for this degree is three in addition to the stated prerequisite (primary, secondary or upper secondary)
College or university degree up to a maximum of 5	12 grades of school plus the number of grades of college reported.
	Masters or doctorate is assumed to a minimum of 17 grades plus up to 3 additional grades.

An individual could have at most 20 grades of educational attainment. Once the total grades of education were computed, we applied some additional rules regarding consistency.²⁶

The school enrollment variable was defined by the question: Did you attend school last year? We did not allow for discrepancies between school enrollment and number of school grades attained. Individuals that reported non-enrollment on the school year 2002 but reported an increase in school grades over that year were dropped. The variables hours spent doing homework and whether the child receives help with homework were constructed conditional on attending school in the 2001–2002 school year. The variables equal zero if the individual reports enrollment in the 2001–2002 school year but non-enrollment in the current school year.

An individual is considered employed in either year if he or she worked the week before being surveyed or reported having a job but not working in the reference week. The income variable is measured on a monthly basis. It includes the monthly income from both the principal job and the secondary job when it exists. Income is set to zero if an individual is unemployed, Also, if individuals report income in weekly or annual terms, we convert the income to a monthly measure. Propensity Score Estimation: The propensity scores were computed using a logit model using as covariates an extensive set of variables that are predictive of program participation. The scores were estimated at the household level. For the logit model, a household was considered to be a participant (treated) if it was located in an intervention area, was eligible and was incorporated by the program. A household was considered non-participant if was located in an intervention area, was eligible but was not incorporated (according to the administrative data). The estimated propensity score model included too many variables to be fully described here. The variables pertain to measures of household wealth, measures of participation in other social programs, demographic variables, measures of employment of household head and spouse, measures of maximum education levels of household members (at baseline), geographic region indicators, measures of what the household ate in the survey week (pork, chicken, beef, fish), household expenditure measures, number of primary schools, secondary schools, and health clinics in the nearby vicinity, measures of population size in the region where the household lives. The coefficient estimates from the propensity score model are reported in Behrman et. al. (2011) and are also available upon request.