A Unified Kernel Regression for Diffusion Wavelets on Manifolds Detects Aging-Related Changes in the Amygdala and Hippocampus

Abstract

We present a new unified kernel regression framework on manifolds. Starting with a symmetric positive definite kernel, we formulate a new bivariate kernel regression framework that is related to heat diffusion, kernel smoothing and recently popular diffusion wavelets. Various properties and performance of the proposed kernel regression framework are demonstrated. The method is subsequently applied in investigating the influence of age and gender on the human amygdala and hippocampus shapes. We detected a significant age effect on the posterior regions of hippocampi while there is no gender effect present.

1 Introduction

The end results of many existing surface-based anatomical studies are statistical parametric maps (SPM) that show statistical significance at each mesh vertex. To obtain stable and robust SPM, various methods have been proposed. Among them, diffusion, kernel, and wavelet-based approaches are probably most popular. Diffusion equations have been widely used in image processing as a form of noise reduction starting with Perona and Malik in 1990’s [1]. Although numerous techniques have been developed for performing diffusion along surfaces, most approaches require numerical schemes which are known to suffer various numerical instabilities [2, 3]. Kernel based models have been also proposed for surface and manifolds data [4, 3, 5]. The kernel approaches basically regress data as the weighted average of neighboring data using mostly a Gaussian kernel and its iterative application can approximates the diffusion process. Recently, wavelets have been popularized for surface and graph data [6, 7]. Although diffusion-, kernel- and wavelet-based methods all look different from each other, it is possible to develop a unified kernel regression framework that relates all of them in a coherent mathematical fashion for the first time.

The focus of this paper is on the unification of diffusion-, kernel- and wavelet-based techniques as a simpler kernel regression problem on manifolds for the first time. The contributions of this paper are as follows. (i) We show how the proposed kernel regression is related to diffusion-like equations. (ii) We establish the equivalence between the kernel regression and recently popular diffusion wavelet transform for the first time. This mathematical equivalence bypasses a need for constructing wavelets on manifolds using a complicated machinery employed in previous studies [6, 7]. Although there have been kernel methods in machine learning [4], they mainly deal with a linear combination of kernels as a solution to penalized regressions, which significantly differ from our framework that does not have any penalty term. The kernel method in the log-Euclidean framework [5] deals with regressing over manifold data. In this study, we are not dealing with manifold data but a scalar data defined on a manifold.

As an application, we illustrate how the kernel regression procedure can be used to localize anatomical signal within the multiple subcortical structures of the human brain. The proposed surface-based morphometric technique is a substantial improvement over the voxel-based morphometry study on hippocampus [8] that projects the statistical results to a surface for interpretation.

2 Kernel Regression and Wavelets on Manifolds

SPD Kernels

Consider a functional measurement f defined on a manifold ℳ ⊂ ℝ^d. We assume the following additive model:

$$f(p)=h(p)+\in (p),p\in \mathcal{M}$$ (1)

where h is the unknown signal and ε is a zero-mean random field, possibly Gaussian. We further assume f ∈ L²(ℳ), the space of square integrable functions on ℳ with the inner product 〈f, g〉 = ∫_ℳ f(p)g(p) dμ(p), where μ is the Lebesgue measure. Consider a self-adjoint operator ℒ satisfying 〈g₁, ℒ_g2〉 = 〉 ℒg₁, g₂〉 for all g₁, g₂ ε L²(ℳ). The operator ℳ induces the orthonormal eigenvalues λ_j and eigenfunctions ψ_j on ℳ: ℒψ_j = λ_jψ_j. Without loss of generality, we can order the eigenvalues 0 = λ₀ ≤ λ₁ ≤ ⋯. The eigenfunctions ψ_j can be numerically computed by solving the generalized eigenvalue problem [9]. Then any symmetric positive definite (SPD) kernel can be written as $K(p,q)={\displaystyle {\sum }_{j=0}^{\infty }{\tau }_j}{\psi }_j(p){\psi }_j(q)$ for some τ_j (Mercer’s theorem). The kernel convolution K*ψ_j(p) = ∫_ℳ K(p, q)ψ_j(q) dμ(q) can be written as K*ψ_j(p) = τ_jψ_j(p). Therefore, τ_j and ψ_j must be the eigenvalues and eigenfunctions of the convolution. For given kernel K, Galerkins method can be used to compute τj.

Kernel Regression

The unknown signal h can be estimated in the subspace ℋ_k ⊂ L²(ℳ) spanned by the orthonormal basis {ψ_j}, i.e. ${\mathscr{H}}_k=\{{\displaystyle {\sum }_{j=0}^k{\beta }_j{\psi }_j(p):{\beta }_j\in ℝ}\}$. Instead of estimating the function h by finding the closest function in ℋ_k, which results in the usual Fourier series, we weight the distance with a positive definite symmetric kernel K:

$$\widehat{h}(p)=\arg \underset{h\in {\mathscr{H}}_k}{\min }{\int }_{ℳ}{\int }_{ℳ}K(p,q){\left|f(q)-h(p)\right|}^{2}d\mu (q)d\mu (p).$$ (2)

Without loss of generality, we will assume the kernel to be a probability distribution so that ∫_ℳ K(p, q) dμ(q) = 1 for all p ε ℳ. If the kernel is a Dirac-delta function, the kernel regression simply collapses to the usual Fourier series expansion. We can show that the solution to optimization (2) is analytically given as

$$\widehat{h}(p)=\arg \underset{h\in {\mathscr{H}}_k}{\min }{\int }_{ℳ}{\int }_{ℳ}K(p,q){\left|f(q)-h(p)\right|}^{2}d\mu (q)d\mu (p)={\displaystyle \sum _{j=0}^k{\tau }_j{f}_j{\psi }_j}.$$ (3)

(3) generalizes the case of spherical harmonics on a sphere [3] to an arbitrary manifold. (3) implies that the kernel regression can be done by simply computing the Fourier coefficients f_j = 〈f, ψ_j〉 without doing messy numerical optimization. As k → ∞, the kernel regression $\widehat{h}={\displaystyle {\sum }_{j=0}^k{\tau }_j{f}_j{\psi }_j}$ converges to convolution K*f establishing the connection to the kernel smoothing framework [4, 3]. Hence, asymptotically kernel regression should inherit many statistical properties of kernel smoothing on manifolds.

Heat Diffusion

For an arbitrary self-adjoint differential operator ℒ, the proposed kernel regression can be shown to be related to the following diffusion-like Cauchy problem

$$\frac{\partial g(p,t)}{\partial t}+ℒg(p,t)=0,g(p,t=0)=f(p),$$ (4)

where the unique solution is given by $g(p,t)={\displaystyle {\sum }_{j=0}^{\infty }{e}^{-{\lambda }_{j}t}}{f}_j{\psi }_j(p)$. If we let τ_j = e^−λjt, the proposed kernel regression $\widehat{h}={\displaystyle {\sum }_{j=0}^k{\tau }_j{f}_j{\psi }_j}$ converges to the solution of diffusion-like equation (4). Further, if we let ℒ be the Laplace-Beltrami (LB) operator, (4) becomes the isotropic diffusion equation as a special case and the kernel becomes the heat kernel $H_t(p,q)={\displaystyle {\sum }_{j=0}^{\infty }{e}^{-{\lambda }_{j}t}}{\psi }_j(p){\psi }_j(q)$. Figure 1 shows diffusion like property of the proposed kernel regression with 1000 LB-eigenfunctions and t = 1.

Fig. 1.

The displacement length, its Fourier series expansion using the Laplace-Beltrami eigenfunctions and the kernel regression with t = 1 for a subject. The strip patterns visible in the amygdale in the original data and Fourier series are image discretization artifacts. They actually correspond to image slices passing through them. In the kernel regression, which is equivalent to diffusion wavelets, such artifacts are reduced.

Wavelet Transform

In order to construct wavelets on an arbitrary graph and mesh, diffusion wavelets have been proposed recently [6, 7]. The diffusion wavelet construction has been fairly complicated. However, it can be shown to be a special case of the proposed kernel regression. Thus its construction is straightforward than previous thought. For some scale function g that satisfies the admissibility conditions, diffusion wavelet W_t,p(p) at position p and scale t is given by $W_{t,q}(p)={\displaystyle {\sum }_{j=0}^{k}g({\lambda }_{j}t){\psi }_j(p){\psi }_j(q)}$. If we let τ_j = g(λ_jt), the diffusion wavelet transform, or wavelet coefficients, can be written as

$$\langle W_{t,p},f\rangle ={\displaystyle {\int }_{ℳ}{W}_{t,q}(p)f(p)d\mu (p)={\displaystyle \sum _{j=0}^k{\tau }_j}{f}_j{\psi }_j(q)},$$

which is the exactly kernel regression we introduced. Hence, diffusion wavelet transform can be simply obtained by doing the kernel regression without a complicated wavelet machinery [7]. Further, if we let $g({\lambda }_{j}t)=e^{-{\lambda }_{j}t}$, we have W_t,p(q) = H_t(p, q), a heat kernel. The bandwidth t of heat kernel controls resolution while the translation is done by shifting one argument in the kernel.

Although the kernel regression is constructed using global basis functions, remarkably the kernel regression at each point p coincides with the wavelet transform at that point. Hence, it inherits all the localization property of wavelets. This is clearly demonstrated in an example given in Figure 2, where a step function of value 1 in the circular band 1/8 < θ < 1/4 (angle from the north pole) and of value 0 outside of the band is constructed. Then the step function is reconstructed using the Fourier series expansion using up to degree 78 spherical harmonics (SPHARM). For the kernel regression, the heat kernel with the small bandwidth t = 0.0001 is used. SPHARM clearly shows severe Gibbs phenomenon (ringing artifacts) compared to the kernel regression.

Fig. 2.

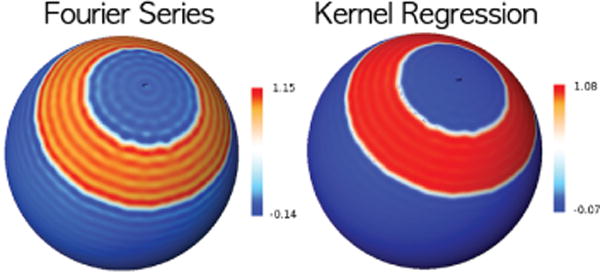
Gibbs phenomenon is visible in the Fourier series expansion of the step function defined on a sphere using SPHARM. The kernel regression (wavelet coefficients) shows less visible artifacts.

3 Statistical Inference on Manifolds

The proposed kernel regression can be naturally integrated into the random field theory based statistical inference [9]. Given a collection of functional measurements in (1), we are interested in determining the significance of h in (1), i.e.

$$H_0:h(p)=0\text{for all}p\in ℳ\text{vs}.H_1:h(p)>0\text{for some}x\in ℳ.$$ (5)

Any point p₀ that gives h(p₀) > 0 is considered as signal. (5) is an infinite dimensional multiple comparisons problem for continuously indexed hypotheses. Given T-field T(p) as a test statistic, we need to compute the multiple comparison corrected type-I error of rejecting the null hypothesis (there is signal) when the null hypothesis is true (there is no signal). For sufficiently high threshold z, which corresponds to the observed maximum T-statistic value, the corrected type-I error is given by $P\left({\sup }_{p\in ℳ}T(p)>z\right)={\displaystyle {\sum }_{j=0}^d{\mu }_j(ℳ){\rho }_j(z)}$, where μ_d(ℳ) is the j-th Minkowski functional of ℳ and ρ_j is the j-th Euler characteristic (EC) density of T-field [9] Hippocampus and amygdala surfaces are compact with no boundary so the Minkowski functionals are simply μ₂(ℳ) = area(ℳ)/2, μ₁(ℳ) = 0 and μ₀(ℳ) = χ(ℳ) = 4 × 2, the Euler characteristic of ℳ. The EC-densities of the T-field with ν degrees of freedom are

$$\begin{array}{l}{\rho }_0(z)=1-P(T_{\nu }\le z),{\rho }_1(z)=\frac{1}{\sqrt{2t^2}}·\frac{1}{2\pi }{(1+\frac{z^2}{\nu })}^{-(\nu -1)/2},\\ {\rho }_2(z)=\frac{1}{2t^2}·\frac{1}{{(2\pi )}^{3/2}}\frac{\Gamma (\frac{\nu +1}{2})}{{(\frac{\nu }{2})}^{1/2}\Gamma (\frac{\nu }{2})}z{\left(1+\frac{z^2}{\nu }\right)}^{-(\nu -1)/2}·\end{array}$$

Note that EC-densities has the term 2t² which relates the scale of wavelets to p-value directly. In the usual SPM framework [9], signals are usually convolved with a kernel with much larger bandwidth t effectively masking the smoothness of noise. Figure 3 shows the type-I error plot over different bandwidth t of the kernel regression. As the bandwidth t decreases, the type-I error decreases. The optimal bandwidth was selected by checking if the decrease of the type-I error is statistically significant. Our approach differs from the usual effective smoothness approach [9]. When t = 0, the kernel regression collapse to the usual Fourier series expansion. Hence, the kernel regression can be viewed as having smaller type-I error compared to the usual Fourier series expansion.

Fig. 3.

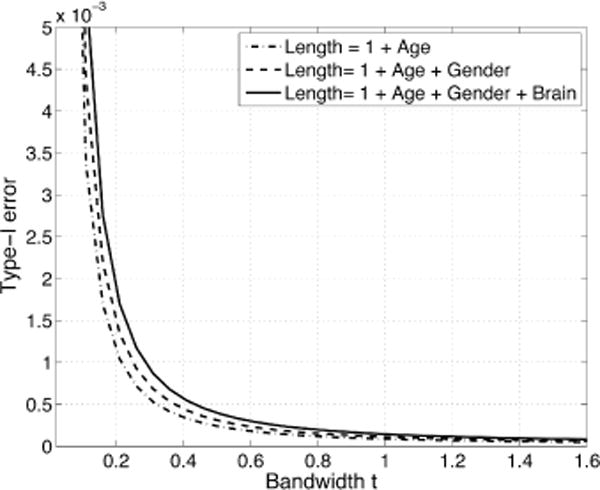
Type-I error plot over bandwidth t for three different models for the study. As t increases, the type-I error decreases.

4 Experiments

Implementation

The LB-operator is chosen as the self-adjoint operators ℒ of choice. We discretized the problem ℒψ_j = λ_jψ_j using the Cotan formulation and solved it as a generalized eigenvalue problem [9]. For the LB-operator, the heat kernel is the corresponding kernel. Bandwidth t = 1 and k = 1000 number of basis are chosen for this study. It is algebraically not possible to have more basis than the number of vertices in a mesh. The average numbers of mesh vertices are 1300 for amygdala. Hence, k = 1000 is used to account for possibly smaller amygdala. The number of eigenfunctions used is more than sufficient to guarantee relative error less than 0.3% against the ground truth. At degree 1000 expansion, the final statistical results are extremely stable and do not change much if we add or delete few terms.

Simulations

Simulations with the known ground truths were used to determine the performance of the proposed method. The type-I error (false positives) can be quantified in the real data. However, since there is no ground truth in the real data, the type-II error (false negatives) cant be quantified without additional assumptions. We performed two simulations with small and large signal-to-noise ratios (SNR). The both simulations were performed on a small T-junction shaped surface (Figure 2). Three black signal regions of different sizes were taken as the ground truth. 60 independent functional measurements on the T-junction were simulated as |N (0, γ²)|, the absolute value of Gaussian distribution with mean 0 and variance γ², at each mesh vertex. Value 1 was added to the black regions in 30 of measurements which served as group 1 while the remaining 30 measurements were taken as group 2. Then the proposed method is compared against the original data without any smoothing and often used iterated kernel smoothing [3]. Two sample t-test with the random field theory based threshold was used to detect the group difference at 0.05 level.

For study I (large SNR), γ² = 0.5² and bandwidth σ = 0.1 were used. All the methods correctly identified the signal regions with almost 100% accuracy as expected. However, due to the increased sensitivity, heat kernel regression incorrectly identified 0.9% non-signal regions as signal (false positives), which is negligible. So it seems for a large SNR setting, all the methods were reasonably able to detect the correct signal regions without significant error.

For study II (small SNR), γ² = 2² and bandwidth σ = 0.5 was used. Smaller SNR requires larger amount of smoothing. In the small SNR setting, iterated kernel smoothing as well as without any smoothing (original) was not able to detect any signal regions after multiple comparison corrected thresholding of 4.9. However, kernel regression was able to identify 94% of the signal regions demonstrating superior performance in extremely low SNR setting. Figure 2 shows the simulation results for study II, where the T-statisic values are all below 4.9 in the two methods, while kernel regression was able to recover most of the signal regions. Due to its sensitivity, heat kernel regression incorrectly identified 0.26% non-signal regions as signal but this is negligible. Although we have shown two extreme cases of high and low SNR, the simulation results are very robust under the change of different parameters.

5 Application

Imaging Data

The study consists of 3T T1-weighted inverse recovery fast gradient echo anatomical 3D images, collected in 124 contiguous 1.2-mm axial slices (TE=1.8 ms; TR=8.9 ms; flip angle = 10°; FOV = 240 mm; 256 × 256 data acquisition matrix) of 69 middle age and elderly adults ranging between 38 to 79 years (mean age = 58.0 ± 11.3 years). There are 23 males and 46 females. The amygdalae and hippocampi were manually segmented by a trained individual rater in the native space. The segmented volumes did not yield any age or gender effects at 0.05 level. This gives a need for developing a sophisticated surface-based method. A nonlinear image registration using the diffeomorphic shape and intensity averaging technique with cross-correlation as similarity metric was performed [10]. The normalized binary masks were then averaged to produce the template. We used the length of surface displacement vector from the template to an individual subject as a response variable. Since the length on the template surface is expected to be noisy due to image acquisition, segmentation and image registration errors, the proposed kernel regression was performed to reduce the type-I error. Figure 1 shows an example of kernel regression on our data.

Results

The smoothed displacement Length is regressed over the total brain volume, age and gender: Length = β₁ + β₂ Brain + β₃ Age + β₄ Gender + ε, where ε is zero mean Gaussian noise. The Age and Gender effects are determined by testing the significance of parameters β₃ and β₄ at α = 0.05 using T-statistic and corrected for the random field based multiple comparisons. We found the region of significant effect of age on the posterior part of hippocampi (left: max. T-stat = 6.25, p-value = 0.00014; right: max. T-stat = 4.78, p-value = 0.024) (Figure 3). Particularly, on the caudal regions of the left and right hippocampi, we found highly localized age effect. Possibly due t small sample size, no age effects are detected on the amygdala surface at α = 0.05. No significant gender effects are detected on amygdale or hippocampi at 0.05 level as well.

6 Conclusion

We have developed a new kernel method that unifies kernel regression, heat diffusion and wavelets in a single mathematical framework. The kernel regression is both global and local in a sense it uses global basis functions to perform regression but locally equivalent to the diffusion wavelet transform. The proposed framework is demonstrated to perform better than existing methods.

Fig. 4.

Simulation study II (small SNR) where three black signal regions of different sizes are taken as the ground truth. All the mesh vertices were assigned value 0. Value 1 was added to the black regions in 30 of measurements, which served as group 2 while the other 30 measurements were taken as group 1. Then noise |N (0, γ²)| is added to each vertex. T-statistics results are shown for the simulation (original) and iterated kernel smoothing [9] and heat kernel regression. Kernel regression performed the best.

Fig. 5.

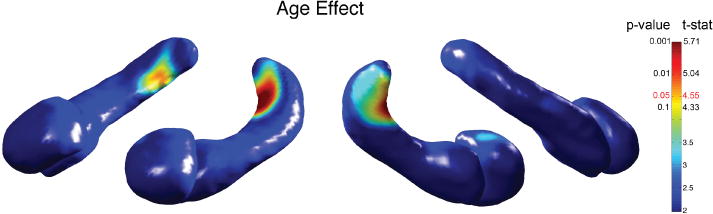
T-statistic and corrected p-value maps on the amygdala/hippocampus template showing age effect. The posterior regions of the both left and right hippocampi show age effects at 0.05 level. There is no gender effect present in any structure.